Left-right differences in proximal femur strength of post-menopausal women: a multicentric Finite Element study

Abstract

Summary

The strength of both femurs was estimated in 198 post-menopausal women through subject-specific finite element models. Important random differences between contralateral femurs were found in a significant number of subjects, pointing to the usefulness of further studies to understand if strength-based classification of patients at risk of fracture can be affected by laterality issues.

Introduction

Significant, although small, differences exist in mineral density and anatomy of contralateral proximal femurs. These differences, and their combined effect, may result in a side difference in femurs’ strength. However this has never been tested on a large sample of a homogenous population.

Methods

The strength of both femurs was estimated in 198 post-menopausal women through CT-derived finite element models, built using a validated procedure, in sideways fall conditions. The impact of the resulting asymmetry on the classification of subjects at risk of fracture was analysed.

Results

The small difference observed between sides (right femur on average 4% stronger than left) was statistically significant but mechanically negligible. In contrast, higher random differences (absolute difference between sides with respect to mean value) were found: on average close to 15% (compared to 9.2% for aBMD alone), with high scatter among the subjects. When using a threshold-based classification, right and left femurs were discordant up to over 20% of cases (K always lower than 0.60), but the left femur was concordant (mean K = 0.84) with the minimum strength between right and left.

Conclusion

Considering both femurs may be important when trying to classify subjects at risk of failure with strength estimates. Future studies including fracture assessment would be necessary to quantify the real impact.

INTRODUCTION

The diagnosis of osteoporosis (OP) is currently done on the basis of areal bone mineral density (aBMD) at the proximal femur [1]. There is common consensus on the possibility of improving the actual ability of aBMD in classifying subjects at risk for osteoporotic fractures [2] with estimation of strength obtained with Finite Element (FE) modelling technique [3]. The rationale behind this is that FE models can account for more determinants of strength (i.e. three dimensional geometry and mineral density distribution) [4] with respect to aBMD that is two-dimensional and provides only an integral measure of the mineral content. An issue that has been always neglected by the FE studies presented so far regards the assumption of symmetry in strength between left and right femur, which has been on the contrary deeply studied for aBMD. All presented studies use a single side, either explicitly indicating which one ([3, 5, 6] left femur), or without any specific indication [7, 8], to classify subjects in clinical studies without sound evidence that this assumption does not influence the results.

A consensus on the clinical opportunity of scanning both sides in routinely DXA exams of the proximal femur has not been reached yet. Some authors maintain that the increase in radiation exposure and complexity of the procedure that a bilateral DXA exam would require is not justified by the number of possible false negatives [9, 10]. Others recommend scanning both sides [11, 12]. However, it is now accepted that a difference in aBMD between right and left proximal femur exists and, although small, is statistically significant [9, 11]. Another major determinant of strength, together with mineral density, is geometry. The geometry of the proximal femur shows as well a certain level of asymmetry. The relevance of this asymmetry is still debated: differences in geometry are small, in the order of 5% [13, 14], but when measurements are performed on a consistent number of subjects, such in [14] that examined 780 cadavers, these differences are significant. It is not clear if and to which extent the asymmetries in mineral density and in geometry can combine and may result in a possible asymmetry in proximal femur strength.

To the authors’ knowledge, the only study that addressed this issue is an experimental work [15] where paired femurs from 54 cadavers (24 men and 30 women) were mechanically tested to failure under sideways fall condition. In this study a small difference was found between the mean left and right femur strengths. The right side seemed to be slightly stronger than the left one, but this difference was not statistically significant. On the contrary, quite high absolute differences between sides were found and the average random difference (i.e. the mean for all subjects of the absolute difference between left and right femoral strength divided by the mean strength of each pair of femurs) was 17%. When adjusted for aBMD the average random difference remained high (16%) but it could not be derived from that study to which extent such difference could be explained by a limited repeatability of the experimental set-up conditions or, on the contrary, by a significant mechanical strength side difference.

The aim of the present work was to estimate the difference in contralateral femurs strength, as assessed through validated CT-based FE models. To this end we analysed 198 post-menopausal women, who represent the group at highest risk of osteoporotic fractures, and we calculated strength in sideways fall loading conditions. In addition the impact of this asymmetry on the classification of subjects at risk of osteoporosis fracture was analysed.

MATERIALS AND METHODS

Bilateral CT scans of intact proximal femurs in 198 subjects were retrieved from three different studies: 106 from The Osteoporotic Virtual Physiological Human (VPHOP, EC grant #223865) multicentric¹ clinical study; 71 from the population based AgeGene/Environment Suceptibility Reykjavik study (AGES- Reykjavik) [16]; 21 from the project “Advanced diagnostics in osteoporosis with predictive models of the risk of fracture in elders” of the Emilia Romagna Region-University Program in Italy (control group of the study [17]). All subjects were post-menopausal women affected by no known pathology at the skeletal apparatus apart from osteopenia/osteoporosis (Table 1). The CT datasets were obtained with different equipments (SIEMENS Sensation 4; Philips MX8000 ITD 10; SIEMENS Volume Zoom; GE MEDICAL SYSTEMS BrightSpeed) but were all densitometrically calibrated (phantom used: European Spine Phantom [18] for IOR and CHA datasets, InTable™ calibration Phantom, Image Analysis, Columbia, KY, USA for AGES-Reykjavik study datasets and Model 3 CT Calibration Phantom, Mindways Software, Inc, Austin, TX, USA for INSERM datasets). For the latter phantom, based on K₂HPO₄, differently from the other two that are based on calcium hydroxyapatite (HA), a correction on the calibration equation was applied following [19]. For 91 subjects a bilateral measurement of aBMD was also obtained: in the 20 subjects of the VPHOP study enrolled at CHA, a DXA scan (Lunar Prodigy Advance, GE Company, Wisconsin, USA, EnCore Software v9.3) was performed, in the 71 subjects belonging to the AGES project aBMD was simulated from CT data with a validated procedure [5, 20].

Table 1.

Descriptive statistics for the 198 enrolled subjects.

	Mean	SD	Min	Max
Age (yrs)	73.3	6.9	61	89
Height (cm)	159.1	6.1	143	184
Weight (kg)	65.1	12.0	41	112
BMI (kg/m2)	26.0	4.5	17.5	38.9

Starting from the CT images, the FE models of both femurs were generated for each patient with a subject-specific FE procedure already described in [21]. This procedure has been validated in-vitro for the prediction of strains [21], and of fracture load [22, 23] obtaining in both studies R² ≥ 0.9 between FE-predicted and experimental variables. The strength of each femur in fall conditions was estimated using a new approach that takes into account the possible variability of loading of the hip joint proposed in [17]. This FE-based estimate of strength classified osteoporotic fractures better than aBMD [17]. The whole procedure is detailed in the cited papers, however a short description of the procedure is provided in the following paragraph for sake of completeness.

FE model generation

All CT datasets were semi-automatically segmented (ITK-Snap 2.0.0, free software, University of Pennsylvania) to extract the three-dimensional bone surfaces. Unstructured 10-noded tetrahedral meshes were generated using an automatic algorithm (Ansys Icem CFD 12.1, Ansys Inc., PA, USA), with an average element size of 2–3 mm that guarantees convergence according to [24].

Material properties were obtained from CT datasets with the BoneMat software [25]. This algorithm uses the densitometric calibration to obtain a QCT density (ρ_QCT), then translates it into ash apparent density (ρ_ash) with a linear correction equation (ρ_ash= 0.877ρ_QCT + 0.079), normalises ρ_ash to wet apparent density (ρ_app) with a constant ratio of 0.6 [26], applies a density-elasticity relationship (E = 6.950ρ_app^1.49 [27], where elastic modulus (E) is expressed in GPa and ρ_app in g/cm³) to obtain elastic modulus estimates from ρ_app, and finally performs a numerical integration to map CT-grid values to FE elements [28].

FE predicted strength in fall conditions

Failure criterion

FE-strength was evaluated in a region of interest (ROI) of the femoral neck (Figure 1), and was defined, for each loading scenario, as the load that induced a principal strain value in the ROI external surface exceeding a threshold value. This value (0.73% tensile limit strain, 1.04% compressive) considered asymmetry in the tensile/compressive bone mechanical behaviour [29].

Figure 1.

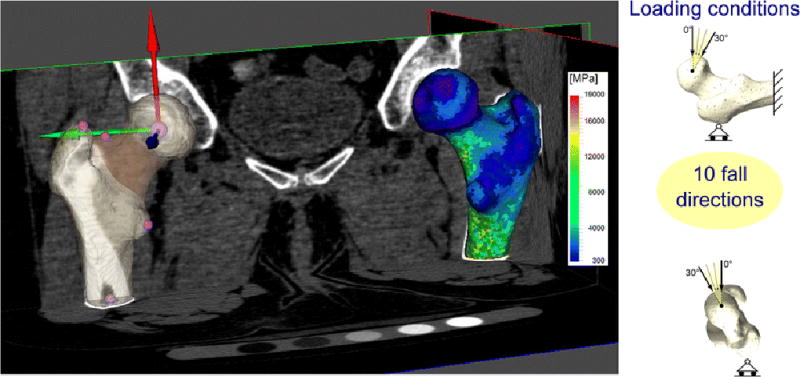
On the left: the solid model of the patient’s left femur, as segmented from the CT dataset, is shown. Relevant skeletal landmarks used to build the proximal femur coordinate systems (whose origin is the femoral head centre) are shown with spherical markers. The femoral neck ROI used for the evaluation of the fracture risk is highlighted. The finite element model of the right femur with the mapped material properties (Young’s module) is also shown superimposed to the CT dataset. On the right: a schematic of the boundary conditions adopted to simulate a fall to the side.

Loads and constraints

Each femur was tested under multiple loading directions representing an accidental condition (i.e. sideways fall (hereinafter: fall)). In detail we simulated 10 fall directions (Figure 1) tilting the applied load from 0 to 30 degrees both in the frontal plane and in the transverse plane [31, 32].

All force directions were identified in the models with respect to a femoral reference system whose definition (Figure 1) was slightly modified with respect to the one presented in [17] to take into account that in the majority of cases only the proximal portion of the femurs were scanned (at least up to 1cm under the lesser trochanter) and consequently the information on the position of the epicondyles was not available.

Each femur was then fully constrained at its distal extremity, and a slider was added to the greater trochanter (Figure 1).

FE-based strength

The minimum strength obtained for each femur among the different simulated loading conditions was taken as the fall FE-based strength.

The underlying rationale is that multiple loading conditions can capture localised weak features. This has already proved to better classify fracture patients versus controls in [17] with respect to a single loading condition.

The estimates of strength in each single loading condition were retained to document changes in strength estimates and contralateral differences between the single loading and multiple loading approaches. All FE analyses were performed with ANSYS v 13 (Ansys Inc, PA, USA).

In order to limit to the least possible the random errors in contralateral bone strength differences, which was the primary object of the study, (i) each couple of femurs was modelled by the same operator, thus avoiding the interoperator bias in the identification of anatomical landmarks; (ii) the segmentation of each couple of bones was performed simultaneously, using the same thresholds and algorithm settings. A repeatability study focused on the purpose of this study, where both femurs from five subjects from the INSERM Lyon cohort were selected and analysed by three different operators, revealed that the repeatability in the assessment of contralateral strength differences in fall conditions was on average 5% (range 0 – 12%).

Assessment of differences in contralateral femurs

Descriptive statistic was used to examine both the aBMD and FE-based strength values of the left and right femurs of the subjects. Correlation between aBMD and FE-strength of the two sides was evaluated and a paired t-test was used to verify the significance of the differences. To elucidate differences between sides, without assuming one side as a reference, the percentage Average Random Difference was computed for aBMD and FE-strength as:

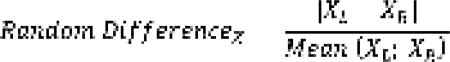Bland Altman Plots for FE-based strength and aBMD were built. Correlation and difference metrics were computed also for strength estimates obtained in each single loading condition.

Analysis of agreement in classification

To elucidate the impact of choosing one single hip for the prediction of patients at risk of fracture, the agreement in classification was calculated, using contingency tables and the Kappa statistic. The agreement in classification was calculated for right vs. left estimated strength, to better characterise contralateral differences, and for both right and left vs. the minimum strength between right and left, to quantify the extent to which using both femurs in the classification is better than using just one side.

In absence of normative data on risk thresholds for FE-derived strength, due to the limited and non standardized sample of population analysed by FE studies so far, the risk threshold for strength was varied, to span the lower range of estimated strength in our sample of the population (2000–3500N).

RESULTS

aBMD

For the 91 subjects with data available on both sides, we found that left and right femoral neck aBMDs were highly correlated (r = 0.91) (Figure 2). Differences were, on average, small and not statistically significant (paired t-test, p=0.33). Although the average left and right aBMD (Table 2) were similar, appreciable differences were common: in 38% of subjects differences between left and right aBMB exceeded 0.047 g/cm² (reference value of least significant change for femoral neck aBMD chosen for comparison with [11]). Differences (aBMD_R–aBMD_L) are plotted against the average value between left and right femur for each subject in the Bland Altman Plot (Figure 2) and showed no visible trend with average aBMD values. The Average Random Difference was 9% (Table 2).

Figure 2.

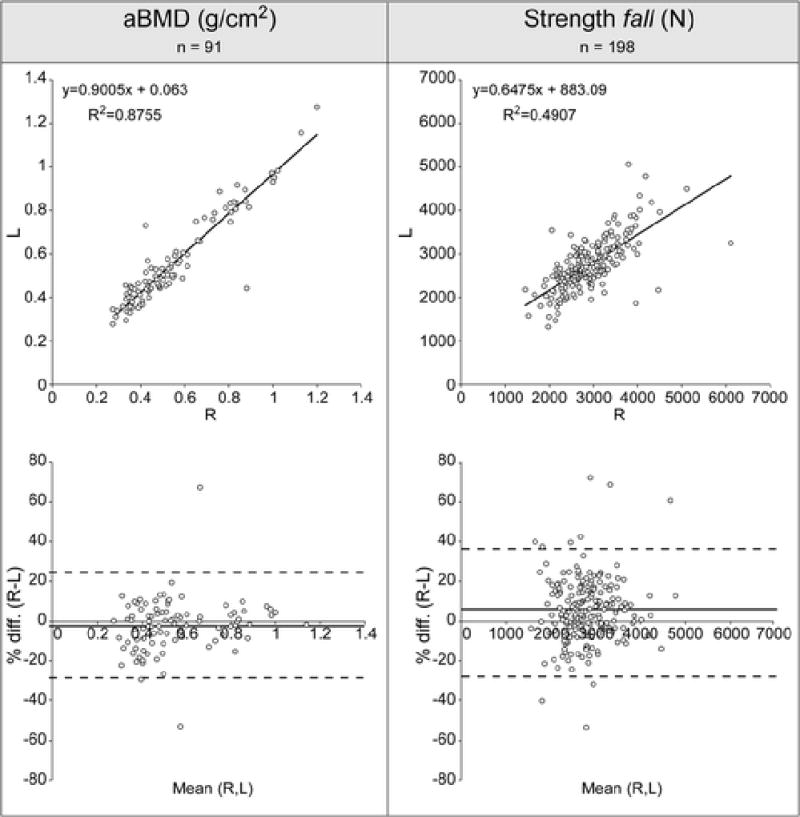
For both aBMD and strength the linear regression between values obtained in the left and right femur is shown at the top, and the Bland-Altman plot at the bottom.

Table 2.

Descriptive statistics of aBMD and relative left-right differences

n = 91	Mean	Min	Max
Neck aBMDL	0.554 (0.213)	0.275	1.201
Neck aBMDR	0.562 (0.205)	0.275	1.271
Differences(R-L)	−0.008 (0.075)	−0.304	0.444
Random Differences	9.2% (10.1%)	0%	67.1%

In two cases, both from the AGES study, a very high difference was found between left and right aBMD (>50%) (Figure 2). For one case (corresponding to the difference of −53%) this high difference in aBMD was not reflected in an analogous difference in strength (difference in fall 15%, in stance 16%) possibly indicating an error could have been done in the evaluation of the aBMD. In the other case a correspondent and very high difference in strength (60%) was found as well.

Strength

Minimum Strength from multiple loading conditions

Although the fall conditions with the highest internal rotation were most often associated with minimum strength, there was a notable spread in the load direction yielding the minimum strength (Table 3). The distribution of the loading conditions determining the minimum strength was similar for right and left femurs.

Table 3.

Occurrences of minimum strength for each analysed combination of force components in fall, for right (italic) / left (underlined) femurs

Minimum strength occurrences (per fall loading direction) in Right / Left femurs	0° Medial	10° Medial	15° Medial	30° Medial
0° Anterior	2 / 0	na	4 / 1	9 / 8
15° Anterior	3 / 2	9 / 4	9 / 17	30 / 27
30° Anterior	10 / 14	na	41 / 46	81 / 79

Concordance between right and left femur in the loading direction determining the minimum strength was perfect (0° difference) in 29% of the subjects, moderate (≤ 15°) in 42% of the subjects, and low (> 15°) in another 29% of the subjects. In fact, although only 58 subjects showed perfect concordance, 84 differed only for 15° in one direction (i.e. one step of load variation in the proposed scheme, see Figure 1).

Strength in the left and right femurs were correlated but to a lower extent than the relative aBMD (r = 0.7) (Figure 2), the standard error of the estimate (SEE) was 427N (15% of the mean value).

Proximal femoral strength was predicted to be, on average, slightly higher on the right side with respect to left side (Table 4). Differences were, on average, small (4%), although statistically significant (paired t-test, p= 0.0002). The coefficient of variation was equal in both sides, close to 22%).

Table 4.

descriptive statistics of femoral strength and relative left-right differences

Minimum strength from multiple loading conditions	Mean (SD)	Min	Max
StrengthL	2748 (599)	1314	5063
StrengthR	2881 (648)	1443	6062
Differences(R-L)	132 (484)	−1508	2813
Random differences	13% (12%)	0.1%	72%

Percentage differences in strength between sides (R-L), with respect to the average value, were highly scattered (95% CI [−28%; 39%]), and did not show any clear trend with the average strength (Bland Altman Plot, Figure 2). Consistent differences were common: 32% of subjects showed a strength difference greater than 15% (RMSE in the in-vitro prediction of failure loads [23]).The average random difference was appreciable (13%, Table 4).

Strength in single loading conditions

An analysis of strength estimates for each single loading condition revealed that the observed differences and scatter between contralateral limbs was not due to the changing load. In fact, for all loading conditions taken singularly, correlation and difference metrics for right and left femur strength were equivalent to, or slightly worse than those observed for minimum strength. In all fall conditions correlations (R²) between right and left femur strength ranged 0.38–0.52., and random differences 15% – 18%. Results from the single fall loading configuration most used in the literature (combination of 15° of internal rotation and 10° of femoral shaft inclination with respect to the ground) are detailed in Table 5.

Table 5.

Descriptive statistics of femoral strength and relative left-right differences in the most commonly used single fall loading conditions.

Strength in single loading condition (the most used for fall: 15° internal rotation, 10° shaft inclination)	Mean (SD)	Min	Max
StrengthL	3648 (1083)	1453	8653
StrengthR	3500 (954)	1799	8991
Differences(R-L)	−147 (770)	−2864	3631
Random differences	15% (12%)	0.01%	51

Agreement in classification

Right and left femurs showed an appreciable disagreement in the classification of cases at risk over the whole range of threshold explored. Kappa statistic was always significant (p < 0.05) but never larger than 0.60 (mean 0.50, range 0.28 – 0.60), which is usually assumed as the lower limit for good accordance, being a unitary Kappa value the perfect agreement. Contingency tables yielded up to 50 discordances (mean 34).

When quantifying the extent to which using strength from both femurs in the classification is better than using just one side, a lower level of discordance was found. Significant differences emerged between right and left strength estimates, being left femur in closer agreement with the minimum value between both limbs. The mean value of the Kappa statistic (p always < 0.001) was 0.84 (range 0.81 – 0.90) for left femur vs. both, and 0.67 (range 0.55 – 0.78) for right femur vs. both. Contingency tables indicated fewer discordances for left femur, throughout the whole range of strength threshold explored (Figure 3).

Figure 3.

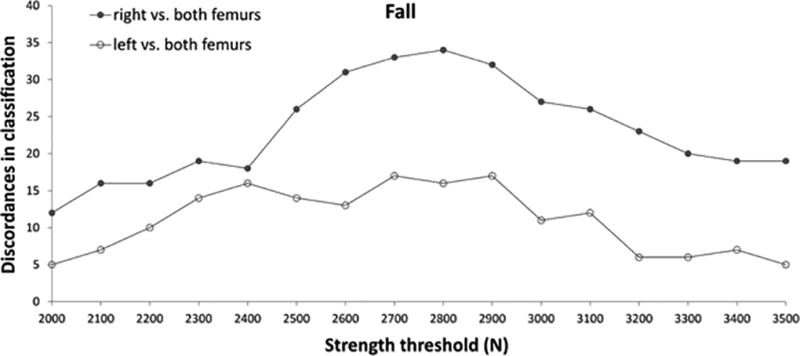
Trends of discordance in classification over a range of strength threshold values.

DISCUSSION

The aim of the present work was to verify if and to which extent differences exist between left and right proximal femurs’ strength, using personalised FE models from CT datasets. In addition an estimate of misclassification rate of subjects at risk of fracture was attempted over a range of plausible threshold values. For a subsample of the studied group, contralateral differences were assessed also for aBMD. The focus was on post-menopausal women that represent the group at highest risk of osteoporotic fractures. The study was performed on 198 subjects, for which a bilateral calibrated CT dataset of the proximal femur was available, and considered, as recently proposed [17], the minimum FE-estimated strength from multiple loading conditions in sideways fall (fall) conditions. Results were compared to strength estimates obtained in single loading conditions to exclude a possible artefact in contralateral differences caused by the minimum strength approach. To the authors’ knowledge the studied cohort is the largest on which side differences in proximal femur strength were evaluated, and meets the most stringent criteria on sample size proposed by [33] to correctly identify contralateral differences in strength parameters.

The results showed that, on average, the difference in the proximal femur strength between left and right sides over the reference population is small (4%), being the right side, in general, slightly stronger than the left one. This difference, although statistically significant, is close to the estimated precision of the numerical modelling workflow adopted, hence may not be mechanically meaningful. The average random difference in strength is instead more notable, being close to 15% and higher than the average random difference in aBMD (9% on the sub-cohort where both values were available). A consistent number of subjects showed differences far higher than the average values (Figure 2). This percentage strength difference did not show any dependence on the magnitude of the average strength.

When trying to address the effects of this contralateral difference in the classification of subjects at risk, incorporating through a variable threshold the existing uncertainty in the definition of FE-derived strength thresholds, we partially confirmed its potential relevance. In fact, discordances in classification when relying only on one bone vs. the contralateral were generally from 10% to over 20% (Kappa statistic never higher than 0.6). However, this discordance picture was damped, when comparing the classification for strength on one side vs. the minimum of both sides (Figure 3), which is likely the most relevant analysis to be done if looking at a clinical perspective. A side-related difference emerged also in this case: classification based on left femur appeared as a good surrogate of classification based on both femurs. It seems that the slight but statistically significant weakness observed for left femurs, which we initially disregarded as mechanically irrelevant, comes again into play here, determining a consistent effect in classification. We may thus speculate on the suitability of analysing the strength of the left femur in clinical analysis, but this statement would need to be put at test in fracture studies.

The obtained results compare overall well with what reported in the literature. The correlation r=0.94 between left and right aBMD is very similar to what found in larger cohorts (number of subjects = 3012, [11]) where r=0.93 was reported for the femoral neck region. With respect to the same work, the percentage of subjects for which the difference exceeded the threshold of 0.047 g/cm² was slightly higher in our cohort (38% against 31% in [11]). Our cohort was however older than the one considered in the cited study, (average age 73 yrs, range 61–89, against 64 yrs, range 50–92 in [11]), hence this result is consistent with their finding that the prevalence of left-right differences was greater in women >65yrs compared with those women aged 50–64yrs. The differences found in FE-derived proximal femur strengths are in good agreement with the only study available [15] in which paired femurs were mechanically tested to failure in fall conditions. Consistently with [15] we found a slightly higher strength (4% in our study, 1% in [15]) in the right with respect to the left femur. The average random difference we found (14% in stance and 13% in fall) is smaller but fully comparable to the value reported in the cited work on the women group (19%). The major difference between our results and what reported in [15] is in the neatly lower correlation between left and right proximal femur strengths found in our cohort (r = 0.70 vs. r = 0.89 in [15]). Interpreting this low correlation is not straightforward. One possibility is that this low correlation may be related to the precision error of the adopted modelling workflow. In this respect, the repeated analysis test we performed showed however an acceptable, although not optimal, repeatability level of 5%. Further experiments with repeated CT measurements could also be beneficial, but dose exposure would suggest using cadaver bones, and it was out of the scope of the present work. While this remains indeed a possibility, several other indicators seem to confirm that our findings and our linear regression model are in good agreement with what reported in [15]. The scatter of the percentage differences reported in [15] is very similar to that observed in our data: in both cases the vast majority of data falls in the [−40%, +40%] range, with an almost uniform distribution within the range, and only very sparse values exceeding this range. Few cases of either very high aBMD differences associated to moderate strength differences or vice-versa are present in both cohorts. The SE of the estimate of the two linear regression models are comparable, being our indeed even lower than the one found in [15] (15% vs. 19.5% of the mean value). The two cohorts are indeed not overlapping being their main difference, apart from size, in the range spanned by the strengths. The cohort considered in [15] is far less homogeneous than ours (including both sexes with broad age-range), consequently the range of strengths is more than 35% broader than ours, which could, evidently, positively influence the correlation coefficient. Finally, a great contribution to the moderate correlation found in our work is given by four subjects (out of 198): without these subjects r rises to 0.80, not so far to that found in [15]. Of those four subjects, one shows a high (60%) right/left strength asymmetry, but also aBMD asymmetry is over 50%; one has a marked (42%) strength asymmetry, but also a notable, though lower, aBMD asymmetry (24%); one has no aBMD values available for one femur, yet shows quite evident geometrical asymmetries (neck-shaft angle, antetorsion) that may alone explain a notable difference in strength, as 3D FE models can capture strength determinants that are not captured by aBMD; finally, only one shows an evident discrepancy between strength (70%) and aBMD (5%) asymmetry. Since cases with similar evident discrepancy between strength and aBMD were present also in [15] there is no evident reason to think these subjects are outliers to be excluded. More studies would be needed to further investigate the actual correlation between left and right proximal femur strengths but the explained accordance with the literature corroborates the hypothesis that the differences found in contralateral bones are unlikely to be the result of analysis artefacts.

More caution is needed in the interpretation of the results on the misclassification of subjects at risk for fracture. This result would indeed need a further validation from a hip fracture study that was not available and out of the scope of the present work. This is actually the main limitation of the present study in a clinical application perspective.. The interest in the topic of our study is however reinforced by the first report of a significant improvement in classification for FE strength estimates over aBMD [3].

Another factor that may be perceived confounding is the strength estimate through a minimum strength criterion (among different loading configurations) instead of a more common single loading configuration. The analysis of the results from each simulated loading condition indeed confirmed to a large extent, and on a larger cohort, the observations made in [17] about the variability of strength estimates with changing loading condition. In few words: (i) loads inducing higher flexural and torsional stresses in the femoral neck generally cause the least strength, while inducing more compression by limiting off-axis loads brings to higher strength values; (ii) the combination of femur anatomy and boundary conditions, characterised by a shorter free length in fall, make stress states, and thus loading conditions inducing the least strength, quite variable among femurs in fall.. When looking at right and left bones of a same subject, however, marked variations in the loading condition inducing the minimum strength were observed only in a few subjects. What is instead very interesting is that the overall data scatter in contralateral strength estimates seem to be slightly reduced rather than enlarged (as it might have been expected) when sorting out the minimum strength from multiple loading conditions instead of using single loading conditions, as commonly done in literature studies. We may try to interpret this finding through an example: if contralateral bones are quite symmetrical (both for geometry and density distribution) then their strength will be similar irrespective of the loading condition imposed; if on the contrary contralateral bones show notable differences in geometry and density distribution, then their strength in a given loading condition will likely be significantly different, while seeking for minimum strength among a range of plausible loads may discover different patterns of structural weakness, thus limiting differences in minimum strength. Deeper studies, trying to single out the often subtle effects of geometry and density combinations to structural weakness, possibly incorporating information on cortical/trabecular compartments [34, 35, 36], are needed to prove this speculation. Nonetheless we believe this observational finding further corroborates the use of a minimum strength approach. Again, a desirable focus of future works would be the robust definition of relevant, admissible and possibly subject-specific loading conditions [37].

Another limitation of the present study is that bilateral aBMD was not available for all study subjects, and for some of them was not directly derived from DXA, but simulated from CT. However, the procedure used to derive aBMD from CT has been previously validated [5, 20] and the data obtained, globally, showed that the subjects considered in the study were aligned in terms of aBMD with far more numerous populations studied [11]. Finally, it was not possible to investigate the correlation between the differences in strength between the two sides with any information on the dominant limb. Self-reported limb dominance information was available only for 69 out of 71 subjects of the IHA cohort. However, 52 subjects were not able to discriminate the dominant leg, answering “Neither” when asked “Which leg is weaker?”. This translated in the impossibility, for us, to make any meaningful analysis on the correlation between leg dominance and strength. More generally, this points to the inadequacy of a simple questionnaire to reliably assess leg dominance. More sophisticated methods, involving likely bilateral muscle strength and balance/coordination measurements would be needed.

In summary the study investigated for the first time, to the authors’ knowledge, in-vivo and on a very focused cohort of post-menopausal women, the difference between left and right proximal femoral strength as derived from FE models. The results showed that, as commonly expected, on average the strength of left and right femurs is similar, but the random difference, (i.e. the absolute difference between left and right femoral strength over their mean) is instead notable (around 15% on average), and can be high in an appreciable number of subjects. The simulation performed to estimate the misclassification level resulting from the adoption of a monolateral instead of bilateral strength estimate, conducted on our cohort over a variable strength threshold, showed that using the left femur, as frequently done in the literature, minimised misclassification. This result cannot however be considered conclusive since a hip fracture study was not available to further test this hypothesis.