Accuracy evaluation of distance inverse square law in determining virtual electron source location in Siemens Primus linac

Abstract

Aim

The aim of this study is to evaluate the accuracy of the inverse square law (ISL) method for determining location of virtual electron source (S_Vir) in Siemens Primus linac.

Background

So far, different experimental methods have presented for determining virtual and effective electron source location such as Full Width at Half Maximum (FWHM), Multiple Coulomb Scattering (MCS), and Multi Pinhole Camera (MPC) and Inverse Square Law (ISL) methods. Among these methods, Inverse Square Law is the most common used method.

Materials and methods

Firstly, Siemens Primus linac was simulated using MCNPX Monte Carlo code. Then, by using dose profiles obtained from the Monte Carlo simulations, the location of S_Vir was calculated for 5, 7, 8, 10, 12 and 14 MeV electron energies and 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm and 25 cm × 25 cm field sizes. Additionally, the location of S_Vir was obtained by the ISL method for the mentioned electron energies and field sizes. Finally, the values obtained by the ISL method were compared to the values resulted from Monte Carlo simulation.

Results

The findings indicate that the calculated S_Vir values depend on beam energy and field size. For a specific energy, with increase of field size, the distance of S_Vir increases for most cases. Furthermore, for a special applicator, with increase of electron energy, the distance of S_Vir increases for most cases. The variation of S_Vir values versus change of field size in a certain energy is more than the variation of S_Vir values versus change of electron energy in a certain field size.

Conclusion

According to the results, it is concluded that the ISL method can be considered as a good method for calculation of S_Vir location in higher electron energies (14 MeV).

1. Background

Unlike photon beams, which have a clear focusing point on the X-rays target of a medical linear accelerator (linac), electron beams are not emitted from a determined physical source in a medical linac. These beams are converted to a wide and extensive form after passing through the vacuum window, bending magnetic field, monitoring chambers, scattering foils and intervening column air. It looks as if the electrons originated from a specific point. This point is called virtual electron source (S_Vir) and it is defined as the confluence point of back projected electron beams along the most possible path of the movement of electrons on the surface of a patient or phantom.¹ In this condition, with determining the location of virtual electron source, output of a machine or other dosimetric quantities can be calculated.²

So far, different experimental methods have been presented to determine virtual and effective electron source location, such as Full Width at Half Maximum (FWHM),³ Multiple Coulomb Scattering (MCS),⁴ Multi Pinhole Camera (MPC),⁵ and Inverse Square Law (ISL)⁶ methods. Of these methods, the ISL method is the most commonly used one.¹

There are several studies which have evaluated different methods of determining the location of virtual and effective electron source. Jamshidi et al.⁷ obtained the location of virtual electron source in different electron energies and field sizes for Varian Clinac-2500 linac using FWHM, MPC and MCS methods. They also obtained the location of effective electron source using ISL and MCS methods. They proved that the location of virtual electron source, which was obtained from different methods, is related to electron energy and field size. In addition, in determination of the location of S_Vir, there was a small difference between different methods at high energies and large field sizes. Ravindran⁸ calculated S_Vir location for a Movatron MD class linac in 5, 7, 9, 10, 12 and 14 MeV energies using ISL and FWHM methods. He showed that for low energies and small field sizes, the positions of virtual electron source obtained from the ISL method are not in agreement with those measured with the FWHM method. Additionally, his results demonstrated that the measured virtual source position depends on machine type and should be obtained for each accelerator independently. In addition, the virtual source position is dependent on the field size as well as the situation where the lead cut-out is kept and on the applicator design. Tynan et al.⁹ compared the distance of virtual electron source and distance of effective electron source at 6, 9, 12, and 16 MeV energies for 10 cm × 10 cm and 20 cm × 20 cm field sizes. Their results showed that with the increase of electron energy and field size, effective source distance calculated for electron fields using the inverse slope method increases. In addition, the increase of source effective distance with increment of the field size was steeper at lower energies than high energies. Finally, they concluded that the obtained effective source distance strongly depends on both electron energy and field size.

To the best of our knowledge, accuracy of the ISL method and the effect of field size and beam energy in determining S_Vir location has not been evaluated yet for a Siemens Primus linac. In this study, the accuracy of the ISL method in determining the location of S_Vir is evaluated for the above-mentioned linac in various electron energies and field sizes using Monte Carlo simulation.

2. Aim

The aim of this study is to evaluate the accuracy of the inverse square law (ISL) method for determining location of virtual electron source (S_Vir) in Siemens Primus linac.

3. Materials and methods

3.1. Determination of virtual electron source location by Monte Carlo simulation

3.1.1. Validation of Monte Carlo simulation of Siemens Primus linac

The radiation source used in this study was a Siemens Primus linac (Siemens AG, Erlangen, Germany). This machine can produce electron beams with 5, 7, 8, 10, 12 and 14 MeV energies and photon beams with 6 and 15 MV energies. The Monte Carlo simulation of the linac's head was performed by MCNPX code (Version 2.6.0).¹⁰ In the current study, the electron energies of 5, 7, 8, 10, 12 and 14 MeV and field sizes of 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm and 25 cm × 25 cm were simulated based on the geometry information acquired from the Siemens manufacturer.

The accelerator's head components, including exit window, primary foil, primary collimator, secondary foil, ionization chamber, mirror, X and Y jaws and electron applicator were simulated. For dose calculation, a water phantom in dimensions of 50 cm × 50 cm × 50 cm was simulated and positioned under the linac's head at a source to surface distance (SSD) of 100 cm. To obtain percentage depth dose (PDD) on the central beam axis, a cylinder was defined with the radius of 2.5 mm and then it was divided into small cells with 1 mm heights that were named scoring cells. The axis of these cells was assumed to be on the central axis of the beam. To calculate dose profiles, some cylindrical scoring cells with a radius and height similar to the PDD calculation scoring cells were utilized; as the axes of these scoring cells were perpendicular to the central axis of the beam. The cylinders were positioned at the depth of maximum dose in the water phantom. To calculate PDD and dose profile, *F8 tally was used. In MCNP code, a tally card is used to specify the quantity which the user wants to gain from the Monte Carlo calculation; for example, current across a surface, flux at a point, heating in a region. This information is requested by the user. *F8 tally was used to calculate the photon dose in the predefined volumes (the scoring cells). In all of these calculations, energy cut-off of photons and electrons was defined equal to 10 keV and 100 keV, respectively. In all of the simulation programs, the MCNP statistical uncertainties were less than 2% in the output files.

3.1.2. In-phantom measurements

The Technical Reports Series (TRS) No. 398 dosimetry protocol¹¹ was followed to perform in-phantom measurements. Dosimetry was executed using a p-type Si diode detector (PTW, Freiburg, Germany) with a sensitive volume of 1 mm² × 30 μm, in a MP3-M water phantom (PTW, Freiburg, Germany). The dimensions of the water phantom were 50 cm × 50 cm × 50 cm. Dosimetric data were obtained for 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm, and 25 cm × 25 cm applicators at 5, 7, 8, 10, 12 and 14 MeV electron energies. The dosimetry results from the in-phantom measurements were analyzed using a Mephysto computer software (PTW, Freiburg, Germany).

To verify the Monte Carlo simulation data, the MC results were compared with the corresponding measured values by the following formula:

$$\text{Dose}\text{difference}(\%)$$

3.1.3. Determination of virtual electron source location

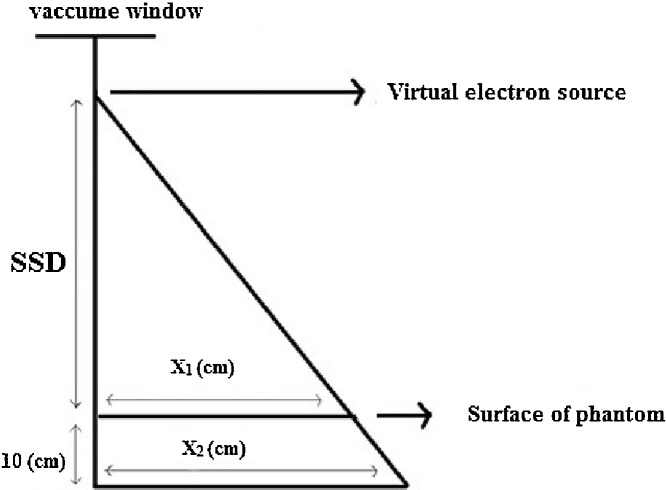
The method used in this study for determination of the location of S_Vir is based on the use of dose profiles³ which were obtained from Monte Carlo simulation. In this method, with back projection of 50% dose profile width in different distances, the location of virtual source was calculated. Firstly, a dose profile was obtained on the phantom surface at SSD of 100 cm and the distance from the central axis of dose profile at 50% dose profile width was calculated. Again, a dose profile at another SSD, for example SSD of 110 cm (the phantom was moved 10 cm toward the downward direction), was taken on the phantom surface and the distance from the central axis of dose profile at 50% dose profile width was calculated. Considering of Thales’ theorem¹² between two triangles that one of them is 10 cm lower than the other, virtual electron source distance was calculated (Fig. 1). To have less uncertainty, this task was repeated for three different SSDs (96, 100, and 110 cm) and by comparing them, the virtual electron source location was computed.

Fig. 1.

Diagram related to the calculation method used for determination of virtual source location using dose profiles.

Due to the time-consuming nature of electron transport in Monte Carlo calculation and with respect to a fast drop-off of electron dose in water compared to air, electron tallies for determination of virtual electron source were considered on the water phantom surface (cylinders from the water surface to 1 mm depth). In all programs run for calculations of dose profiles, energy cut-off for electrons was defined ≤3 MeV. In other words, the maximum energy cut-off was 3 MeV, which is related to 14 MeV electron energy. For the other electron energies, the energy cut-off was decreased by 0.5 MeV steps, i.e. energy cut-offs for 12, 10, 8, 7, and 5 electron beams were 2.5, 2, 1.5, 1, and 0.5 MeV, respectively. Furthermore, it is notable that for each electron energy, the energy cut-off was the same for all the used materials in this code. An energy cut-off means that the electrons are transported until their energies reach the specified energy cut-off. Then, their energies are deposited locally at this position and they are not transported.

Based on the geometry presented in Fig. 1 and the following equation, X is calculated:

$$\frac{X}{X+10}=\frac{X_1}{X_2}$$ (1)

where X₁ and X₂ are 50% dose profile widths in 100 cm and 110 cm SSDs, respectively.

It is clear that after calculation of f or SSD with the mentioned method, the obtained values should be subtracted from the depth which the dose profile was calculated (0.05 cm depth). Finally, the location of S_Vir was determined by Monte Carlo simulation in 5, 7, 8, 10, 12 and 14 MeV electron energies and 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm and 25 cm × 25 cm field sizes.

Given that our aim was only to obtain the location of S_Vir and since the size of the reference applicator is 10 cm × 10 cm, percentage depth dose and dose profile curves were evaluated only for this applicator. The electron energy spectra obtained from validation of Monte Carlo simulation of 10 cm × 10 cm applicator were used for the other applicators.

3.1.4. Calculation of virtual electron source location by the ISL method

Khan et al.¹ proposed a method that is suitable for clinical situations. In this method, dose value is measured in a phantom and the depth of maximum dose (d_m) is obtained in different situations relative to the electron applicator. Firstly, the dose value is measured at a point in contact with the applicator or in standard SSD point (without air gap) and then measured in different distances ranging from 3 cm to 15 cm. To increase the precision of these measurements, each measurement was repeated three times at each point and the average of these values was considered as the final value. If the electrons obey the inverse square law of distance, the following relation can be obtained:

$$\frac{I_0}{I_g}={\left(\frac{g+f+d_m}{f+d_m}\right)}^2$$ (2)

where f is the effective SSD, g is the distance between the standard SSD point (air gap of 0 cm) and the surface of phantom, I₀ is the dose value in air gap of 0 cm, and I_g is the dose value in air gap of g cm. Therefore, can be calculated from the following equation:

$$\sqrt{\frac{I_0}{I_g}}=\frac{g}{f+d_m}+1$$ (3)

With plotting as a function of g distance, a straight line is obtained with a slope of. Therefore:

$$f=\frac{1}{Slope}-d_m$$ (4)

Based on the above-mentioned method, f or SSD can be calculated using the slope of plot as a function of gap (g).

Finally, the location of S_Vir was calculated at 5, 7, 8, 10, 12 and 14 MeV electron energies and 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm and 25 cm × 25 cm field sizes.

4. Results

4.1. Validation of Monte Carlo simulation of Siemens Primus linac

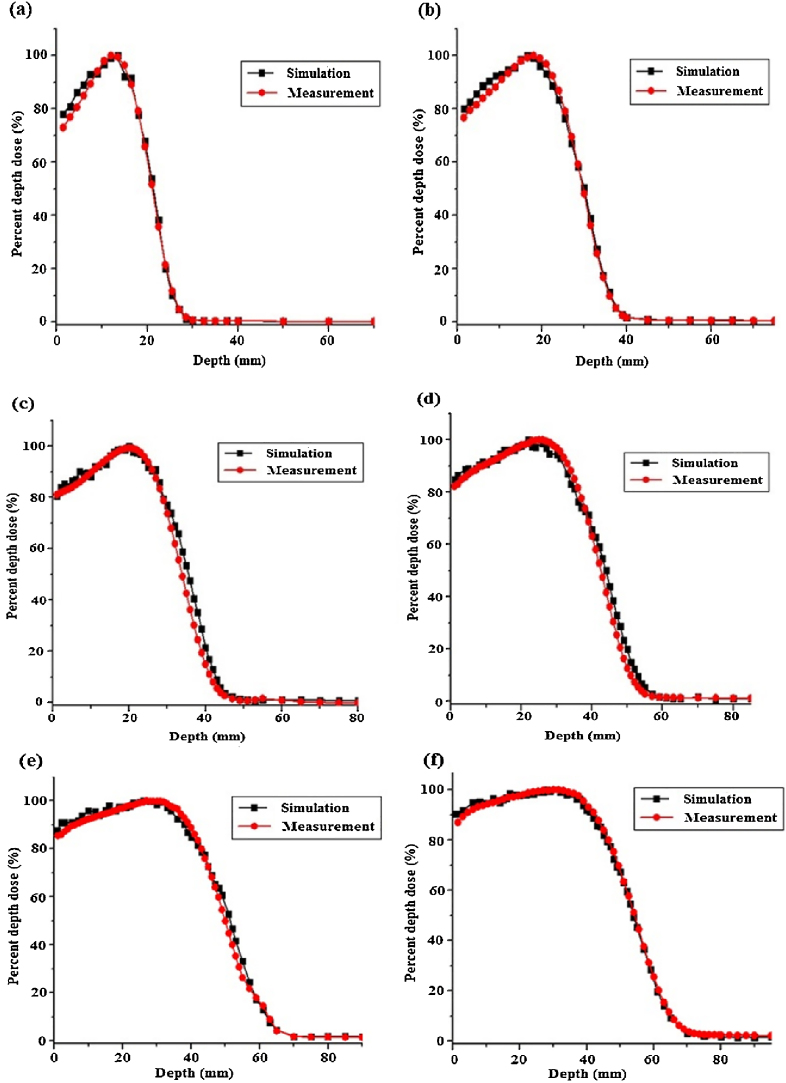
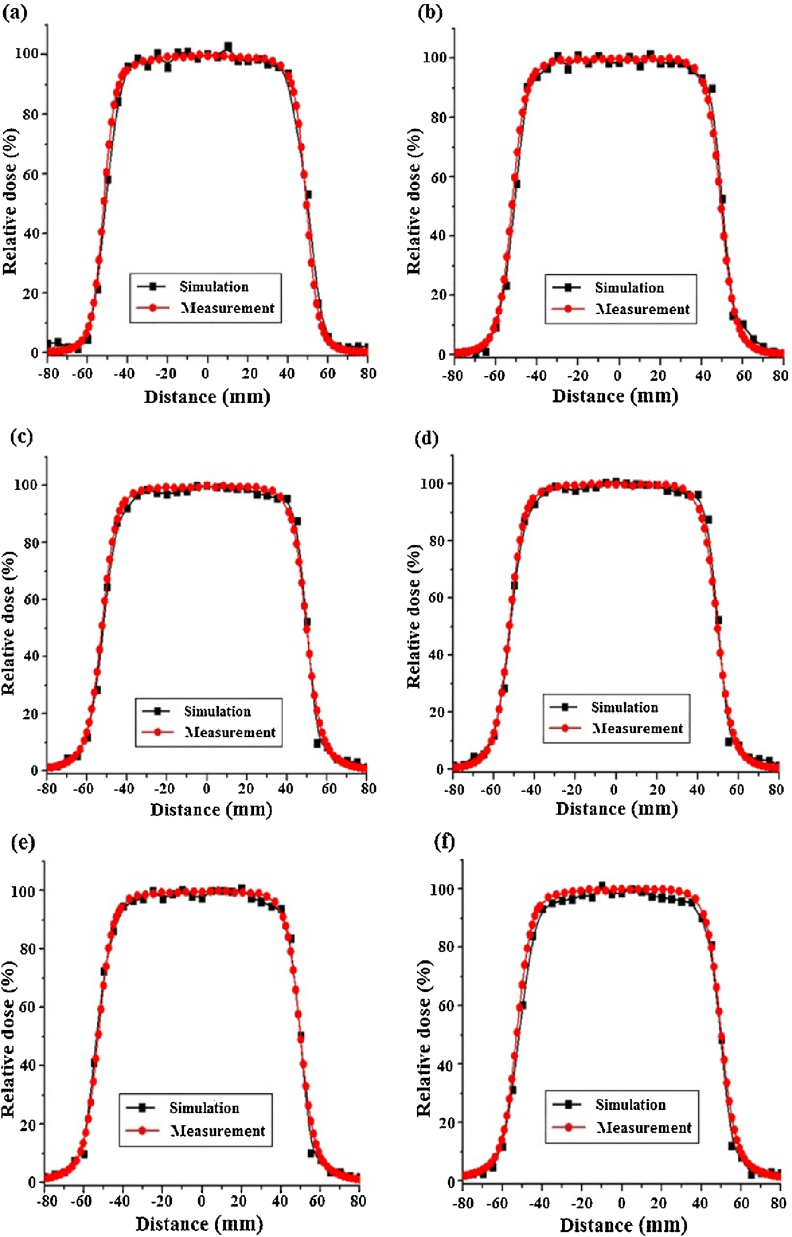
PDD and dose profile values obtained from Monte Carlo simulations and measurements for 10 cm × 10 cm applicator at 5, 7, 8, 10, 12 and 14 MeV electron energies are plotted in Fig. 2 (parts (a)–(f)) and Fig. 3 (parts (a)–(f)), respectively. The data in these figures are related to 10 cm × 10 cm field size and SSD of 100 cm.

Fig. 2.

Percent depth dose (%) values obtained from Monte Carlo simulations and measurements for 10 cm × 10 cm applicator at different electron energies. (a) 5 MeV electron energy, (b) 7 MeV electron energy, (c) 8 MeV electron energy, (d) 10 MeV electron energy, (e) 12 MeV electron energy, and (f) 14 MeV electron energy.

Fig. 3.

Dose profile (%) values obtained from Monte Carlo simulations and measurements for 10 cm × 10 cm applicator at different electron energies. (a) 5 MeV electron energy, (b) 7 MeV electron energy, (c) 8 MeV electron energy, (d) 10 MeV electron energy, (e) 12 MeV electron energy, and (f) 14 MeV electron energy.

4.2. Determination of virtual electron source location

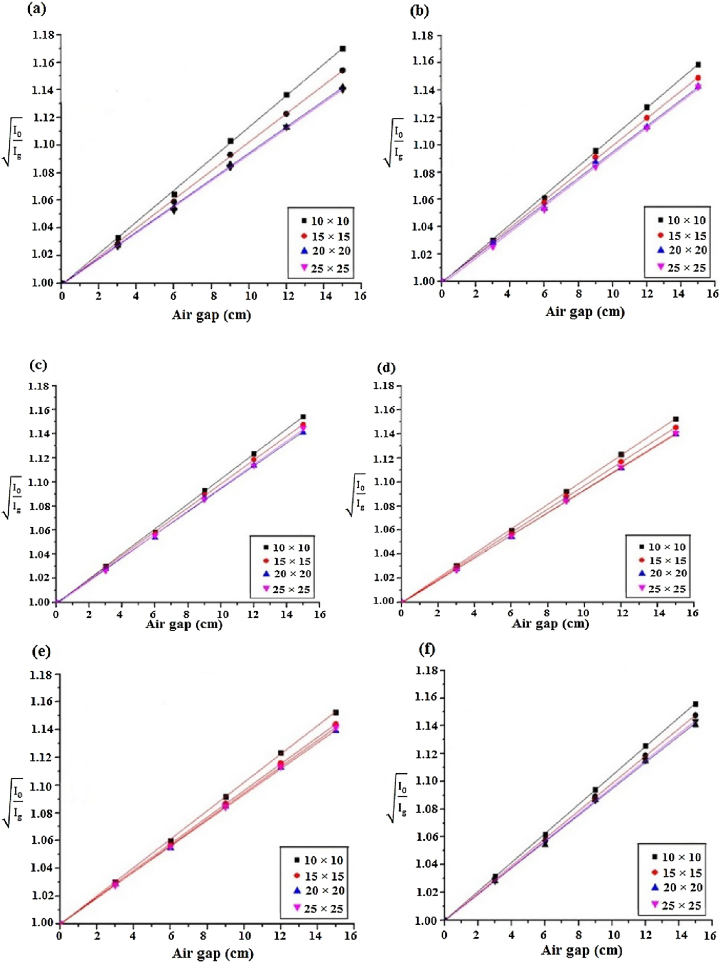
The plots of versus air gap (g) calculated by the ISL method at various electron energies and field sizes are illustrated in Fig. 4 (parts (a)–(f)). The slopes of these lines and d_m for calculation of the location of virtual electron source are listed in Table 1, for various electron energies and field sizes.

Fig. 4.

Plots calculated by the inverse square distance (ISL) method versus air gap for various field sizes. (a) 5 MeV electron energy, (b) 7 MeV electron energy, (c) 8 MeV electron energy, (d) 10 MeV electron energy, (e) 12 MeV electron energy, and (f) 14 MeV electron energy.

Table 1.

The d_m (cm) values and slopes of plots versus air gap (g) for different electron energies and field sizes.

Field size (cm2)	10 × 10		15 × 15		20 × 20		25 × 25
Electron energy (MeV)	dm	Slope	dm	Slope	dm	Slope	dm	Slope
5	1.2	0.01142	1.2	0.01035	1.2	0.00949	1.2	0.00945
7	1.8	0.01068	1.8	0.01003	1.8	0.00953	1.8	0.00956
8	2.1	0.01037	2.0	0.00990	2.1	0.00949	2.1	0.00968
10	2.5	0.01022	2.4	0.00974	2.6	0.00934	2.5	0.00943
12	2.9	0.01022	2.9	0.00960	2.8	0.00930	3.1	0.00946
14	3.0	0.01041	3.0	0.00987	3.0	.0.00949	3.2	0.00960

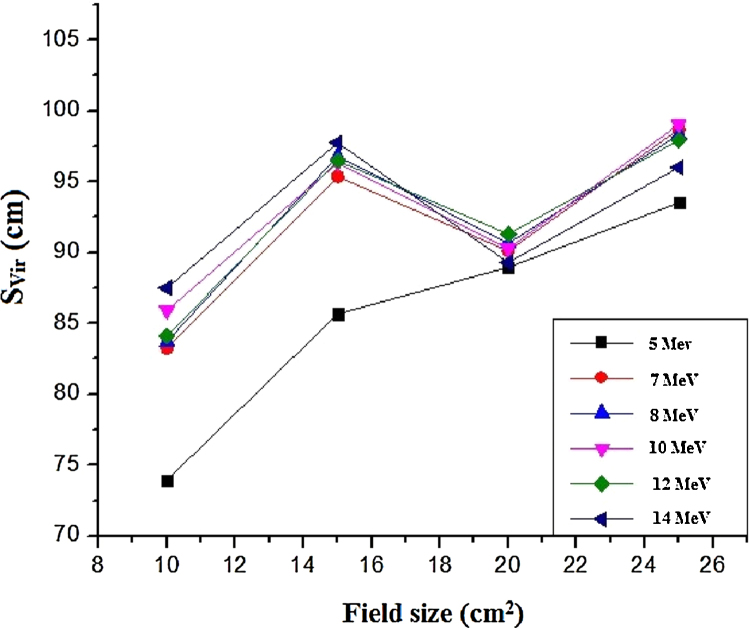
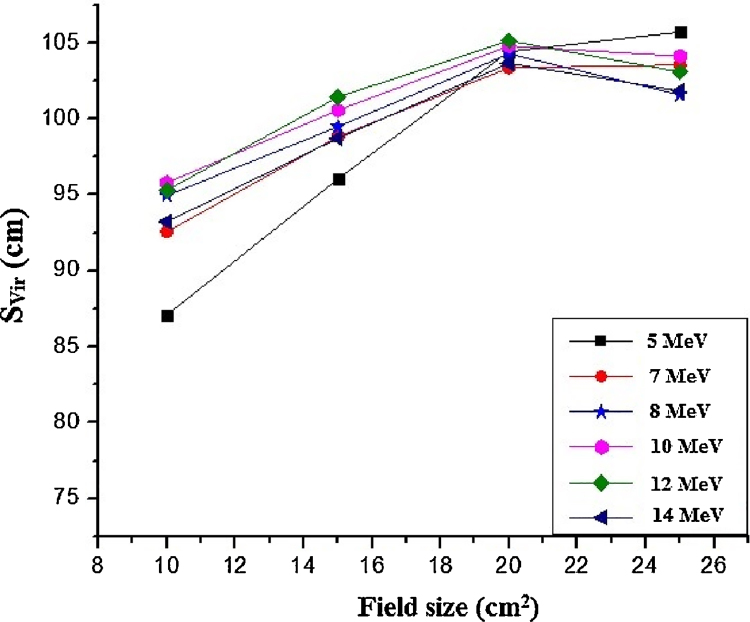
The S_Vir curves obtained by Monte Carlo simulation and ISL methods for various electron energies and field sizes are plotted in Fig. 5, Fig. 6, respectively. Furthermore, the calculated S_Vir values for various electron energies and field sizes are presented in Table 2.

Fig. 5.

S_Vir value (cm) versus field size for various electron energies obtained from Monte Carlo simulation.

Fig. 6.

S_Vir value (cm) versus field size for various electron energies calculated from inverse square distance (ISL) method.

Table 2.

The S_Vir (cm) results from Monte Carlo (MC) simulations and inverse square distance (ISL) methods in different electron energies and field sizes. The percent differences (PDs) between the results from MC and ISL methods are also presented.

Field size (cm2)	10 × 10			15 × 15			20 × 20			25 × 25
Electron energy (MeV)	MC	ISL	PD (%)	MC	ISL	PD (%)	MC	ISL	PD (%)	MC	ISL	PD (%)
5	73.9	87.1	18	85.7	96.0	12	89	104.4	17	93.5	105.7	13
7	83.2	92.6	11	95.4	98.8	4	90.1	103.4	15	98.7	101.6	3
8	83.7	95	14	96.8	99.5	3	90.7	104.3	15	98.3	101.6	3
10	85.9	95.8	12	96.3	100.6	4	90.3	104.8	16	99.0	104.1	5
12	84.1	95.3	13	96.5	101.4	5	91.3	105.1	15	97.9	103.1	5
14	87.5	93.3	7	97.7	98.7	1	89.3	103.7	16	96.0	101.8	6

5. Discussion

In this study, accuracy of ISL method in determining virtual electron source location in Siemens Primus linac was evaluated. Additionally, the effect of electron beam energy and field size on the location of S_Vir was investigated. As it is observed from the findings (Fig. 2, Fig. 3), there is a good agreement between the PDD and dose profile values obtained by the Monte Carlo simulations and the measured values. Therefore, the Monte Carlo simulation of the linac's head is validated. However, there are only a few points with dose differences (between MC simulation and measurement values) greater than 3%, which are interpreted as disagreement at these points. It is notable that dose difference greater than 3%, are seen only in regions where there is a high-dose gradient (e.g. penumbra and build-up regions). Since dose gradient is high in these regions, it seems that the difference between the size of sensitive volume of the measurement dosimeter and the size of the scoring cells in Monte Carlo calculations, and also other factors such as small variation in the set-up of dosimeter can cause dose differences between the calculation and measurement. These findings are consistent with the study by Konefal et al., as their results showed that there are large dose differences between measured and calculated doses in the surface areas.¹³

The findings of the present study show that the calculated S_Vir values depend on the electron beam energy and field size. However, for a certain energy, with the increase of field size, these values mostly increase, but in some cases, this dependence is small and there is no increase in source location distance with the increase of field size. One of the reasons for this trend may be the complexity of the behavior of electrons. Furthermore, for a special applicator size, with increase of electron energy, the location of S_Vir increases, the increment being more evident in small fields and larger than that in large field sizes. According to the results of this study, the variation of S_Vir values with change of field size in a certain energy is higher than the variation of S_Vir values with change of electron energy in a certain field size. These results are consistent with other studies. Various studies showed that the location of virtual electron source depends on the energy of electron beam and the field size.7, 9, 14, 15

It was reported that the location of S_Vir depends on machine type and the experimental method which was used to determine it.⁷ By comparing the results obtained by Monte Carlo simulations and ISL method in the present study, it is shown that ISL method can be applied well in higher electron energies (14 MeV). However, for small field sizes (10 cm × 10 cm), especially at low energies, there is less agreement by using this method, which may be due to the lack of lateral electron equilibrium in small field sizes. It seems that the main factor in the variation of calculated virtual electron source location with field size is the variations in the reached scattered radiation from the applicator walls and phantom to the center of the radiation field. Therefore, these scattered radiations cause the change of dose on the central axis of the beam. In larger field sizes, due to the larger distance between the central beam axis and the treatment field edge, fewer electrons (scattered by the applicator and phantom) can reach the center of the treatment field. They have almost no effect on depth dose distribution in central beam axis, as almost 90% of the dose on the central beam axis at the depth of d_m is caused by primary electrons (not those scattered by the applicator). On the other hand, with the increase of distance from the end of the applicator, the electrons scattered by the applicator walls and the phantom can reach the d_m depth and can prevent further reduction of dose on the central beam. However, in small field sizes, the scattered electrons can be effective on dose distribution on the central beam axis and d_m depth, because the distance between the edge of the treatment field and the central beam axis is smaller than the range of the scattered electrons. On the other hand, the edge of the treatment field is closer to the central beam axis (d_m depth) than in the large field sizes. With the increase of distance from the edge of applicator, these electrons cannot reach the d_m depth and, thereby, cannot compensate the reduction in dose in the lack of primary electrons reaching this region.

Another factor that may reduce the S_Vir values in low energy electrons is related to the scattered electrons in air. In high electron energies, these scattered electrons are almost ineffective, due to a lot of forward scattered electrons and their contributions in dose value in the central beam axis. However, in low electron energies and, especially, in small field sizes, these scattered electrons cause dose values to decrease be more rapidly with the increase of distance from the applicator.

In the current study, the accuracy of the ISL method in determining virtual electron source location was evaluated only for Siemens Primus linac. Therefore, it cannot be concluded whether this method can also be extended for other accelerator models or not. Therefore, the evaluation of the accuracy of application of the ISL method in determining virtual electron source location for other linac models can be suggested as a future study. It is also suggested that location of S_Vir be determined separately for each linac type by different methods and finally, the most accurate method be used in clinical situations where an electron beam is used.

5. Conclusion

By comparing the results obtained from Monte Carlo simulation and ISL methods, it is concluded that the ISL method can be applied as a good method for calculation of S_Vir location in high electron energies (14 MeV). Additionally, the location of S_Vir determined by the ISL method depends on the electron energy and field size. This dependence for low electron energies and small field sizes is higher than that in high electron energies and large field sizes.

Conflict of interest

The authors declare that they have no conflict of interest.

Financial disclosure

The authors would like to acknowledge Alborz Cancer Institute and Radiation Medicine Department of Shahid Beheshti University for contribution in this research. Shahid Beheshti University should be thanked for financial support.