Evidence for the speed-value trade-off: human and monkey decision making is magnitude sensitive

Abstract

Complex natural systems from brains to bee swarms have evolved to make adaptive multifactorial decisions. Recent theoretical and empirical work suggests that many evolved systems may take advantage of common motifs across multiple domains. We are particularly interested in value sensitivity (i.e., sensitivity to the magnitude or intensity of the stimuli or reward under consideration) as a mechanism to resolve deadlocks adaptively. This mechanism favours long-term reward maximization over accuracy in a simple manner, because it avoids costly delays associated with ambivalence between similar options; speed-value trade-offs have been proposed to be evolutionarily advantageous for many kinds of decision. A key prediction of the value-sensitivity hypothesis is that choices between equally-valued options will proceed faster when the options have a high value than when they have a low value. However, value-sensitivity is not part of idealised choice models such as diffusion to bound. Here we examine two different choice behaviours in two different species, perceptual decisions in humans and economic choices in rhesus monkeys, to test this hypothesis. We observe the same value sensitivity in both human perceptual decisions and monkey value-based decisions. These results endorse the idea that neural decision systems make use of the same basic principle of value-sensitivity in order to resolve costly deadlocks and thus improve long-term reward intake.

1 Introduction

Adaptive decision-making is a hallmark of intelligent complex systems at all levels of biological complexity. Such systems can monitor inputs and then calculate effective responses to them with impressive efficiency and flexibility. A major goal is the elucidation of the basic computational principles underlying mechanisms for decision making, from perceptual decision making, to economic decision making to social decisions (Krajbich, Hare, Bartling, Morishima, & Fehr, 2015).

Decision mechanisms are often studied from the perspective of the speed-accuracy trade-off. That is, the decision-maker is assumed to optimize choices based on two competing cost functions, the cost of inaccurate choices and the cost of delays imposed by longer deliberations. This trade-off function has been a central aspect of models of decision-making in psychology, neuroscience, and behavioural ecology (e.g., Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Chittka, Skorupski, & Raine, 2009). However for many decisions, such as food choice, decision-makers should optimize value, not accuracy, and decision-making processes should take this fact into account (Pirrone, Stafford, & Marshall, 2014; Teodorescu, Moran, & Usher, 2015). Both the cost of a decision – in time taken and risk of error – and benefit of a decision – in reward – may frequently depend on the value of options. When referring to ‘overall value’ we mean the magnitude or intensity of the stimuli or reward under consideration; in this case value can have a relation with hedonistic concepts as ‘reward’ or be related to the physical dimension of stimuli. For example, by comparing two lights, we would say that the brighter one has a higher value. At the same time, of two sources of the same food we would say that the bigger has an higher value. It seems reasonable to assume a correlation in many ecological scenarios between stimulus magnitude (or salience) and fitness value; for example, a brighter fruit may be riper and thus more nutritionally beneficial (Schaefer, McGraw, & Catoni, 2008), or a high intensity cue may indicate a more dangerous situation (Teodorescu et al., 2015). Prominent computational models of choice work by integrating difference (Ratcliff & McKoon, 2008) or ratio (Brown & Heathcote, 2008) in evidence between alternatives, thus disregarding information related to the absolute value of the alternatives under consideration (Pirrone et al., 2014; Teodorescu et al., 2015). Such systems may also exhibit decision deadlock between equal alternatives, which can be solved by adding urgency signals, asymmetry of inhibition or collapsing thresholds (Ditterich, 2006; Thura, Beauregard-Racine, Fradet, & Cisek, 2012), however, these additions are motivated by avoiding long reaction times in low evidence trials, without explicit reference to implementing ecologically-relevant option magnitude sensitivity.

Consider, for example, a forager who encounters two food items. Laboratory formalism treats this choice as independent of other events (Bogacz, Hu, Holmes, & Cohen, 2010), but if in the subject’s natural environment food item availabilities and qualities are drawn from typical environmental distributions, then an optimal agent will be more willing to reject both items if they are matched and relatively low in value and instead search for a larger food item. However, if both items are matched and high in value, there is no sense in waiting, nor is there any benefit in deliberation between them. This decision-maker will thus be faster to respond to high-value stimuli than to low-value ones, even if their ratio or difference is identical.

A nonlinear model of decision-making, inspired by observations of house-hunting honeybees (Seeley et al., 2012), has been proposed that implements precisely this value-sensitive deadlock-breaking behaviour (Pais et al., 2013). The dynamics of the model are such that decisions between equal options below a value threshold result in deadlock, but deadlock is spontaneously broken for options above this value threshold; the value threshold is determined by a single biologically-relevant parameter, strength of cross-inhibition between evidence accumulating populations (Pais et al., 2013). An adaptive strategy is to progressively increase this parameter so that equal low-value alternatives that result in decision deadlock will eventually result in deadlock breaking (Pais et al., 2013); under this schedule high-value equal alternatives will result in deadlock breaking before low-value equal alternatives, and hence exhibit shorter reaction times in the former case. As the decision-maker moves from maintaining to breaking decision deadlock, change in the stochastic dynamics around the deadlock point corresponds to a sign change in the Ornstein-Uhlenbeck (O-U) process

$$\dot{x}=Bx+\sigma \eta$$ (1)

from stable (B < 0) to unstable (B > 0) (Pais et al., 2013). In equation 1 x represents state of the decision process, with 0 corresponding to decision deadlock and a decision being reached when x crosses a positive or negative threshold, η is a Wiener process, or Brownian motion, and σ is its standard deviation.

Additionally, when differences between options are large enough the decision-mechanism approximates the classical drift-diffusion model of decision-making (Pais et al., 2013)

$$\dot{x}=A+\sigma \eta ,$$ (2)

where x represents integrated evidence with 0 corresponding to equal evidence, and A is the strength of drift, which is a function of the difference between mean evidence strengths (Ratcliff, 1978). If there is no such difference then A = 0 and the decision variable will only cross a decision threshold through integrating sufficient noise; importantly, if decision thresholds have been set high (indicating a prioritisation of decision accuracy) and do not change, then this will take a correspondingly long time. While Pais et al. present a model of collective behaviour, corresponding non-linear neural models with qualitatively similar properties can be found (Bose, Reina, & Marshall, n.d.).

A first demonstration of value sensitivity in human decision making comes from Teodorescu et al. (2015), and some preliminary results about magnitude sensitivity are also present in Teodorescu and Usher (2013). In Teodorescu et al. (2015) subjects were required to choose the brighter of two grey patches presented on the screen. Compared to a baseline condition, the authors increased the overall value of the alternatives while holding the ratio or the difference between the mean luminances of the two grey patches constant. Their results demonstrate that subjects show a sensitivity to the overall value of the alternatives both in the condition where the difference and the condition where the ratio are maintained constant but the overall value is increased. However, to the best of our knowledge, no study to date has investigated value sensitivity as a mechanism to break decision deadlocks for equal alternatives. We hypothesized that value sensitivity, exhibited by a model of decision-making in honeybee swarms (Pais et al., 2013), will also be observed in neural decision systems. We therefore measured the effects of value on matched-value decisions in two different contexts, perceptual decisions in humans and reward-based decisions in rhesus monkeys. In both cases, decisions of interest (i.e., equal alternatives) were embedded in a larger set of decisions between options of unequal value. In both cases, we observed a significant decrease in reaction time with increasing value for matched-value options. These findings are readily predicted by a value-sensitive model, but are not predicted by many classical models, except under implementations or assumptions that we discuss in our final remarks.

2 Methods

2.1 Human Perceptual Decision Task

For the Human Perceptual Decision Task, all procedures were approved by the University of Sheffield, Department of Psychology Ethics Sub-Committee (DESC), and carried out in accordance with the University and British Psychological Society (BPS) ethics guidelines. Subjects gave their informed consent before participation. The sample size was chosen to be similar to that of Teodorescu et al. (2015); we examined the behaviour of 9 human subjects (1 male, mean age = 18.8 years, SD = 1.64). All subjects had normal or corrected-to-normal vision and participated voluntarily in the experiment in exchange for course credit. Each subject was tested in a single sixty minute session.

Stimuli were programmed in Matlab, using the Psychophysics Toolbox extensions (Brainard, 1997; Kleiner et al., 2007; Pelli, 1997), and were presented on a Mitsubishi Diamond Pro 2070sb 22 CRT monitor. Materials and procedure were similar to those used by Teodorescu et al. (2015), with the only exceptions being the addition of the equal-alternatives conditions, and the elimination of trial by trial feedback.

As done by Teodorescu et al. (2015), we defined as ‘multiplicative’ the condition that held the same ratio between the two alternatives as in a baseline condition while increasing the overall value, and we defined as ‘additive’ the condition in which the difference between the two alternatives was kept constant as in a baseline condition while the overall value of the alternatives was increased.

Stimuli consisted of two homogeneous, round, grey patches on a black background. The width of each patch was 1.2 cm; the distance between the centres of the two grey patches was 6.2 cm. A fixation cross was positioned between the two patches. The baseline array consisted of grey levels normally distributed around means of 0.4 and 0.3 (scale: 0 to 1.0), the multiplicative condition around means of 0.6 and 0.45, the additive condition of 0.6 and 0.5 and the four equal alternatives conditions were distributed respectively around means of 0.3, 0.4, 0.5 and 0.6; all conditions had a standard deviation of 0.1. On each frame, a Gaussian random variable with mean 0 and standard deviation of 0.01 was added to the mean grey level of each patch. If the final computed grey level was below 0.1, it was rounded to 0.1. The screen had a refresh rate of 60 Hz and subjects were positioned at 57 cm with their head on a chin rest. Order presentation of the two grey patches was counter-balanced for each subject. In the remainder we will refer to the four equal-alternatives conditions of increasing value with regards to their intensity (i.e., condition 0.3, condition 0.4, condition 0.5 and condition 0.6). Typical stimuli and value luminance distributions for the two alternatives are represented in Figure 1.

Figure 1.

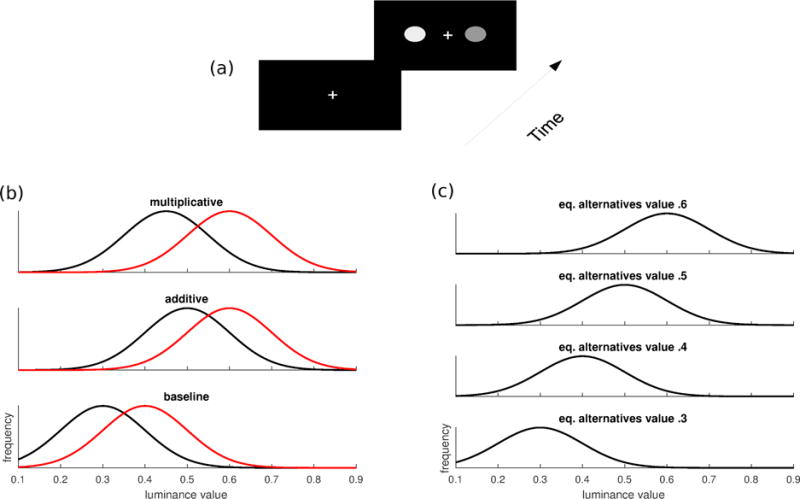
Top (a) Time course of an experimental trial; the stimulus remained on screen until subjects responded and 1 second after that subjects were presented a new trial. Bottom-left (b) Luminance value distributions for the target (red; distribution on the right) and non-target (black; distribution on the left) alternatives. In the baseline condition alternatives had a mean of 0.4 and 0.3 respectively, hence a difference of 0.1 and a ratio of 4/3. In the additive condition, alternatives had a mean of 0.6 and 0.5 respectively, hence maintaining the same difference of 0.1 as in the baseline condition but giving a ratio of 6/5. In the multiplicative condition alternatives had a mean of 0.6 and 0.45 respectively, hence a difference of 0.15 but same ratio of 4/3 as in the baseline condition. Bottom-right (c) Equal alternative conditions of increasing value, respectively 0.3, 0.4, 0.5, 0.6.

2.1.1 Procedure

The two grey patches were presented simultaneously on the screen and subjects were asked to decide which of the two was brighter by pressing ‘left’ or ‘right’ on a keyboard using their left and right index fingers. One second after giving a response they were presented with a new trial. Subjects were not informed about the presence of equal-alternatives conditions or about the presence of a multiplicative and additive condition. Subjects performed 1400 trials of which 320 (22.9 %) were baseline trials and 180 (12.9 %) for each of the remaining conditions. After each block of 60 trials, subjects were asked to take a break and were presented on the screen with their accuracy and reaction times for the block. Accuracy was only computed for non-equal alternatives trials. Subjects were instructed to be as fast and accurate as possible and to maintain their fixation on the cross at the centre of the screen throughout each block. Before the experiment they were presented with 14 training trials (2 trials for each condition) to familiarise them with the task. No feedback was provided after each trial. No additional conditions or measures were collected.

2.2 Results of Human Study

No fast data were excluded from the following analyses, given that fast responses are particularly relevant for this study. However, we excluded slow responses over 3 seconds excluding in this way about 1 % of the data.

Recall that our interest is in the equal alternatives. To assess whether the effect of value on equal alternatives was consistent across subjects (Figure 2) we ran for each of the nine subjects a linear regression on mean RTs with value as predictor. Given the typical skewness of RTs data, for the regression analysis we used Box-Cox transformations of RTs (Entink, Linden, & Fox, 2009). For eight out of nine participants the regression slope was significantly non-zero; for one participant the regression slope had a non-zero trend. Estimates of the slope, and significance levels are reported in Table 1.

Figure 2.

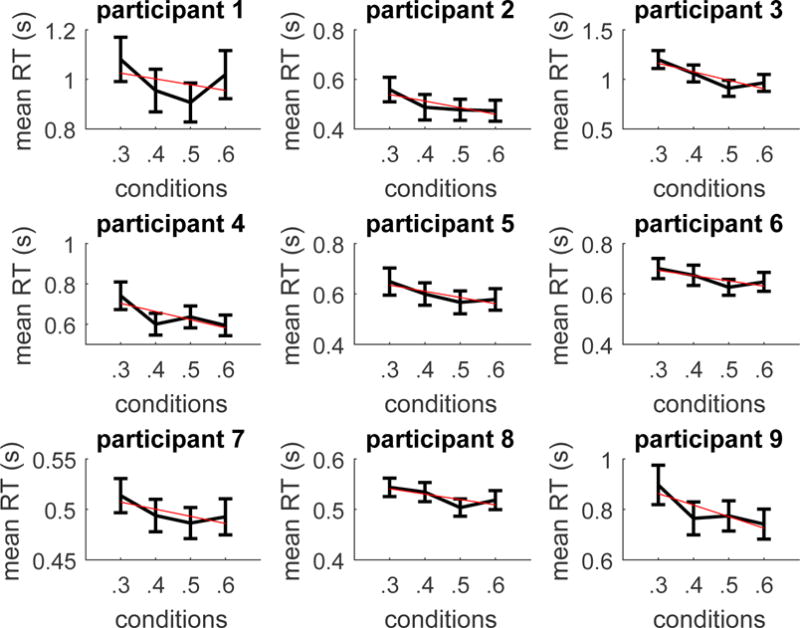
Mean RTs for the equal alternatives conditions of increasing magnitude for each subject (human study). Bars represents 95% confidence intervals. The red (straight) line represents the linear regression line on mean RTs.

Table 1.

Estimate of slope, t statistic, and p value for the linear effect of value on RTs for the equal alternatives conditions (human participants).

	slope est.	t stat.	p. value
participant 1	−.042	−2.215	.027
participant 2	−.033	−2.279	.023
participant 3	−.093	−5.494	.000
participant 4	−.040	−2.410	.016
participant 5	−.025	−1.756	.080
participant 6	−.039	−2.774	.006
participant 7	−.024	−2.115	.035
participant 8	−.027	−2.661	.008
participant 9	−.044	−2.441	.015

Regarding the baseline, the additive and the multiplicative conditions, in an attempt to replicate the results of Teodorescu et al. (2015), we show for each participant mean RTs, and mean accuracy, Figure 3, with bars representing 95% confidence intervals of the mean. In interpreting a graph that shows 95% confidence intervals, when a confidence interval does not overlap with a specific value, it is possible to conclude that there is a statistical difference between the estimates of the values of interest at a false negative rate equal or lower than .05. For example, for the first participant, for mean RTs the graphs show that for the additive condition the subject was significantly slower than for the baseline or the multiplicative condition. For the multiplicative conditions the first participant did not differ from the baseline in mean RT. Regarding accuracy levels, the trend is consistent across subjects with subjects being generally less accurate for the additive condition compared to the baseline or the multiplicative, while the multiplicative condition remains the same as the baseline. Generally the accuracy of subjects is high especially for the baseline and the multiplicative condition with participant 1 and 3 being at ceiling level for all conditions. Regarding RTs however, there is no consistent pattern in how decision time varies across the three unequal conditions.

Figure 3.

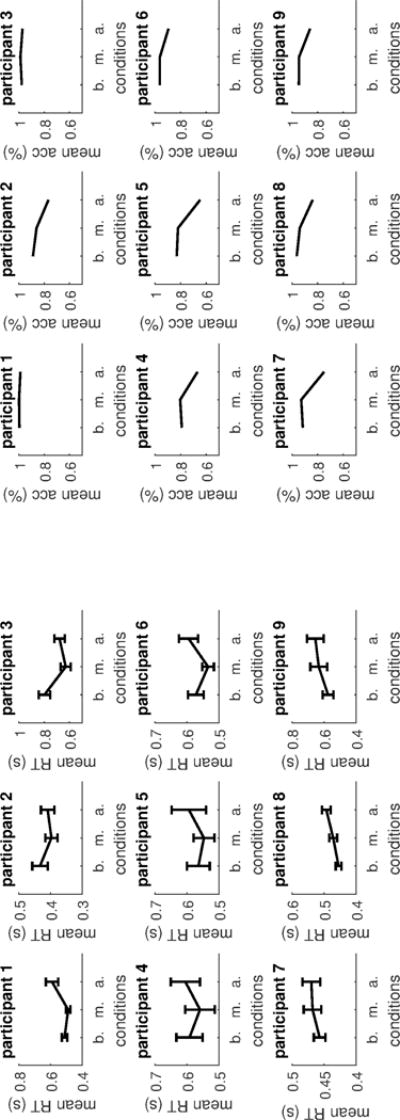
Left: mean RTs for the baseline (b.), multiplicative (m.) and additive (a.) conditions for each subject. Bars represents 95% confidence intervals. Right: mean accuracy levels for the baseline, multiplicative and additive conditions for each subject.

2.3 Experiment on Monkeys

2.3.1 Basic Procedures

The basic procedures used in this study were based on existing protocols we have used for other experiments (Blanchard, Pearson, & Hayden, 2013). All procedures were approved by the University of Rochester Institutional Animal Care and Use Committee and were designed and conducted in compliance with the Public Health Service’s Guide for the Care and Use of Animals. Four male rhesus monkeys (Macaca mulatta) served as subjects. Each animal was outfitted with a small prosthesis using a standard technique (Hayden, Nair, McCoy, & Platt, 2008). Animals received analgesics and antibiotics after all surgeries. Animals were slowly habituated to laboratory conditions and trained to perform oculomotor tasks for liquid reward. Standard reinforcement training was used with only positive rewards; punishment was never used, nor was aversive conditioning.

In each session, the animal was transported from the colony at the University of Rochester to the testing room, about 100 feet away in the same building. The testing room was built specifically for primate studies and houses a computer screen and floor plate for firm mounting of the ergonomically designed primate chair (Crist). Animals made all task-relevant decisions using gaze shifts to selected targets. Horizontal and vertical eye positions were sampled at 1000 Hz by an infrared eye-monitoring camera system (SR Research). Stimuli were controlled by a computer running Matlab (MathWorks) with Psychtoolbox (Brainard, 1997) and Eyelink Toolbox (Cornelissen, Peters, & Palmer, 2002).

A standard solenoid valve controlled the duration of water delivery (Parker). We estimated the precision of fluid volume delivered by the solenoid across the range of open time commands used in this study. All reward volumes were measured and confirmed. Fluid access was controlled outside of experimental sessions.

2.3.2 Monkey Behavioural Task

We used a two-alternative forced choice task to study the effect of overall magnitude of the decision variable on reaction time in macaques. The task is a computerized implementation of a simple economic choice task, of the type we and others have long used. Our task uses the same basic structure as several other tasks in the lab, including those used to study risk (Blanchard, Wilke, & Hayden, 2014), intertemporal choice and foraging (Blanchard & Hayden, 2015), and curiosity (Blanchard, Hayden, & Bromberg-Martin, 2015). The key novel elements of this task were the use of simultaneous option presentation with speeded responses. We used a computerized presentation, with a standard LCD monitor placed 144.8 cm (57 inches) inches in front of the monkey in a darkened room. Screen resolution was 1024×768. All trials were identical aside from the specific values and colours used. On each trial, monkeys first fixated on a small white central spot (50 px diameter, 200 ms duration) to indicate their willingness to initiate the trial. Successful fixation led to the immediate presentation of two choice options; monkeys were allowed to select the choice option (by shifting gaze to it) immediately; no minimum initial fixation was required, nor were monkeys required to look at both options before making a choice. The computer selected two options independently and at random, with a uniform distribution. It then presented them 300 pixels to the left and right of the central spot. Both stimuli were squares (200 pixels wide) in one of 10 colours. The colors we used were red, off-white, orange, indigo, yellow, blue, lime green, pink, purple and cyan. These colours indicated the size of the reward offered by this option, according to the following scheme: red: 50¼L, off-white: 60¼L, orange: 66¼L, indigo: 100¼L, yellow: 110¼L, blue: 132¼L, lime green: 200¼L, pink: 220¼L purple: 240¼L, and cyan: 264¼L. We chose these particular reward values carefully to allow us to have several ratios with different magnitudes. Thus, while subjects saw trials in all possible combinations of the above 10 stimuli, we were particularly interested in subsets of trials that form the focus of our analyses. Subjects had extensive experience with the reward-colour mappings of most colours in this hierarchy of rewards from previous experiments (specifically: red, orange, yellow, blue, lime green, purple and cyan; Blanchard & Hayden, 2015; Strait et al., 2016). To ensure that this familiarity did not introduce any special bias, we extensively familiarized our subjects with the rewards offered by new colours in several training sessions prior to testing. Following presentation, the subject then selected an option by shifting their gaze toward it. Subjects were required to maintain fixation on their choice for 300ms. Failure to maintain fixation led to deselection of the option and returned the monkey to the choice state. Thus, monkeys were allowed to inspect the options without committing to them if they wanted. Once the subject successfully completed fixation, the reward was given and an inter-trial interval of 1 s, 1.5 s, or 2 s began. The particular ITI on a given trial was selected at random from a uniform distribution. Options remained on the screen during reward delivery and throughout the inter-trial interval. Typical stimuli and reward values for the two alternatives are represented in Figure 4. No additional measures or conditions were collected.

Figure 4.

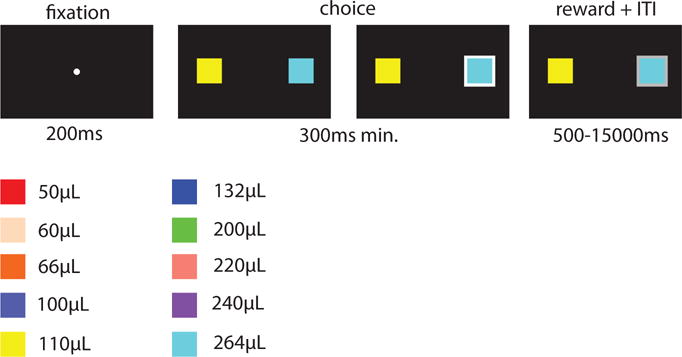
Time course of an experimental trial and reward values for the two alternatives for the monkey experiment. RGB values for stimuli were as follows: – red: [255 0 0] – off-white: [255 218 185] – orange: [255 102 0] – indigo: [78 90 200] – yellow: [255 255 0] – blue: [0 0 255] – lime green: [0 255 0] – pink: [250 128 114] – purple: [160 32 240] – cyan: [0 255 255] – white (fixation dot): [255 255 255].

2.4 Results of Monkey Study

All subjects initially performed over 9000 trials of this task (subject B: 9132 trials, subject H: 11652 trials, subject J: 11150 trials, subject K: 10230 trials). The exact number of trials performed by each subject was constrained by the subject’s willingness to work on any given day, and the need to start them on different tasks. Monkeys performed anywhere between approximately 800 and 1,200 trials per day, depending on their motivation. Session length was entirely determined by the monkeys: sessions were terminated when monkeys stopped performing the task for a considerable period of time. Subjects were highly accurate in their choices (overall accuracy: 85.41%; subject B: 87.64%; subject H: 87.69%; subject J: 88.93%; subject K: 77.01%). These values are all significantly greater than chance (two-sided binomial test, all p < 0.0001). No fast data were excluded from the following analyses but we removed the slowest 0.5 % of trials per subject, which represents unreasonably slow RTs. Given the variability across subjects in mean RT, we could not use a single common value for an upper cutoff as done for the human data.

Our condition of interest is in the condition for which the ratio is 1, Figure 5, meaning that the two alternatives that the subject were presented with were equal in value – hence, subjects were presented with two identical squares. For these conditions, as done for the human experiment, we ran for each of the four subjects a linear regression on RTs with value as predictor. For three subjects the regression slope was significantly non-zero while for one subject it was non significant, although Figure 5 shows a non-zero, negative trend. Estimates of the slope, and significance levels are reported in Table 2; also in this case, results are based on Box-Cox transformation of RTs (Entink et al., 2009).

Figure 5.

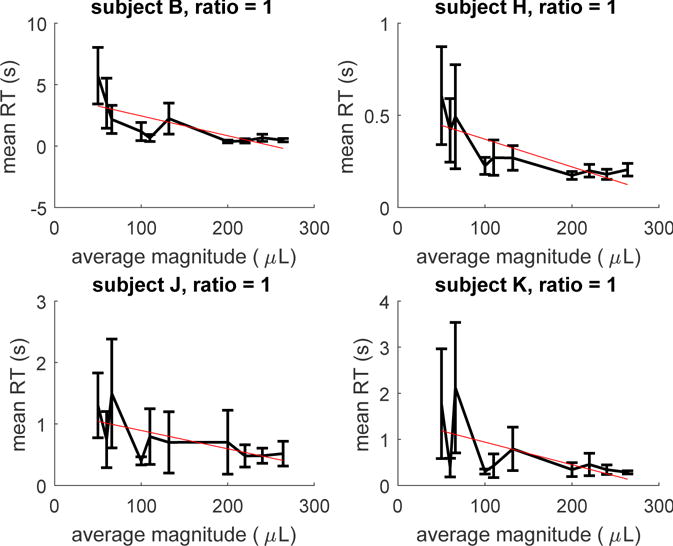
Mean RTs for the equal alternatives conditions of increasing magnitude for each subject (monkey study). Bars represents 95% confidence intervals. The red (straight) line represents the linear regression line on mean RTs.

Table 2.

Estimate of slope, t statistic, and p value for the linear effect of value on RTs for the equal alternatives conditions (monkey participants).

	slope est.	t stat.	p. value
subject B	−.002	−6.477	<.001
subject H	−.001	−9.516	<.001
subject J	−.001	−3.361	.001
subject K	<−.001	−.133	.894

Regarding unequal alternatives, in the Appendix we show for each subject mean RTs with bars representing 95% confidence intervals for all those ratio conditions for which more than three magnitude levels were present, separately for each participant; Figure A1, Figure A2 and Figure A3. We did not analyse these conditions as for these conditions it is not possible to assess whether the decrease in RTs is due to the increase in magnitude, or to scaling factors; however, except for the easiest discrimination (i.e., ratio =4), there is a decreasing trend in RTs when magnitude increases.

3 Discussion

Influenced by a model of value-sensitive decision-making (Pais et al., 2013) and by evolutionary and ecological arguments (Pirrone et al., 2014; Teodorescu et al., 2015) we have investigated the effect of the overall value of the alternatives on decision making, in humans and in monkeys. In line with these arguments, our initial prediction was that an effect of the overall value of the alternatives should be present also for ‘equal’ alternatives: fast decision times when the overall value of the alternatives is high and slow decisions when the overall value is low. Both the perceptual decision-making experiment on humans and the economic decision-making experiment on monkeys provide evidence that the overall value of the alternatives affects response times. These effects are not predicted by classical models of choice which integrate only differences between or ratios of alternatives. Value sensitivity might seem to be counter-intuitive if considered from a speed-accuracy trade-off perspective. From a speed-accuracy point of view, choices involving more valuable options may be more costly to make mistakes on, so we might expect decision making to shift towards a low error regime and, hence, be slower. Instead, we observe the opposite since when the overall value is increased, subjects are faster and could open themselves to making more errors. This result, for the value-based task is in line with a ‘satisficing’ perspective where a ‘good enough’ choice is preferred rather than the ‘best’, and as a consequence accuracy in decisions over small differences is sacrificed in favour of quick responses (Kacelnik, Vasconcelos, Monteiro, & Aw, 2011; Pirrone et al., 2014).

Unfortunately, due to a programming error, in our experiment the display screen was not linearised with respect to brightness. This means that our results hold for physical rather than perceived multiplicative and additive shifts with respect to the baseline. As a consequence, our results on non-equal alternative conditions are not directly comparable to those of Teodorescu et al. (2015). For example, they found a difference in RTs between the baseline and multiplicative conditions which we did not, probably due to our stimuli being shifted by a smaller physical amount. Our results for the multiplicative and additive conditions coincide with what is predicted given the non-linear increase in brightness. However, the equal alternative conditions, which are the focus of our work – and, importantly, are absent from Teodorescu et al. (2015), and thus completely novel – do not suffer from issues related to linearisation. The consistency across subjects for these conditions, as shown in Figure 2, represents a simple but effective test of value-sensitivity in human perceptual decision-making for deadlock breaking.

Relevant to our monkey experiment, regarding the unequal conditions (i.e., the ratio between the two alternatives is not 1), no analyses were performed. These conditions were presented to allow subjects to focus on the task; clearly an experiment consisting only of equal alternatives would be unreasonable as for all trials each choice would be random by necessity. Moreover, these unequal conditions do not allow to test for value sensitivity given that when the ratio between two alternatives is kept constant but the overall value is increased, also the discriminability between the two alternatives increases -assuming constant noise-resulting in decreasing RTs. This means that although for unequal alternatives RTs generally decrease as magnitude increases, it is not possible to dissociate the effect of magnitude from the effect of increased disriminability between the two alternatives. However, also for the monkey data the presence of equal alternatives conditions (e.g., ratio=1) allows us to test and confirm value sensitivity in monkey reward-based decision making.

A strength of presenting both sets of data using different species and domains is that this finding seem to suggest that value guides decision making, regardless of the specific domain. We believe that this supports the idea of a single common mechanism underlying decision making that given evolutionary pressures is value sensitive for perceptual stimuli and for rewards (Pirrone et al., 2014; Teodorescu et al., 2015).

Our point, argued in Pirrone et al. (2014), is that most naturalistic decisions are value-based rather than accuracy-based, in the sense that decision-makers are rewarded by the value of the alternative chosen, regardless of whether it was the best available. Although decision-making is traditionally studied within the speed-accuracy trade-off perspective, this alternative viewpoint suggests that a speed-value trade-off (Pirrone et al., 2014) could be the most relevant decision trade-off to manage in various naturalistic settings (Bateson & Kacelnik, 1998). We believe that the value-sensitivity shown in simple tasks such as those presented in this paper is a signature of this evolutionarily-plausible strategy.

These findings stand in contrast to celebrated models of choice. For example, the Drift Diffusion Model (Ratcliff & McKoon, 2008) assumes that the subject integrates difference in evidence supporting two alternatives until a decision boundary is crossed and a decision is made in favour of that alternative. This reliance on evidence difference rather than evidence value entails predictions of equal RTs for choices between two options of equal difference regardless if they are two high value options or two low value options.

Theoretically, value sensitivity of the kind we have demonstrated here can be explained by a number of models in addition to the one we took as our starting point (Pais et al., 2013). Teodorescu et al. (2015) show that under the neurally plausible assumption that processing noise increases with stimulus value, then a difference-based diffusion model becomes value sensitive and can make similar predictions. Other computational models of choice such as the Leaky Competing Accumulator (Usher & McClelland, 2001, LCA) can also give rise to similar patterns, as directly demonstrated in Teodorescu et al. (2015). The LCA at the early stages of accumulation shows a sensitivity to the overall value of the alternatives and at the later stages approximates a DDM (Bogacz et al., 2006), hence it is a value sensitive model. At the same time, other models such as sequential choice ‘race’ models (as compared to models in which the decision maker explicitly compares options) in which agents choose an option that exceeds a fixed threshold of acceptability (Kacelnik et al., 2011) are in line with the value sensitive reaction time results presented here. Further theoretical effort should be made to determine which empirical data on value-sensitivity can be explained by which models, and attempt to discriminate between them on this basis; an extensive, though surely not complete, model comparison effort of this nature was performed by Teodorescu et al. (2015). As noted in earlier work, the nonlinear dynamics of models that explicitly implement value-sensitive decision-making give rise to a further prediction, of decision hysteresis (Pais et al., 2013), which may motivate further experimental investigation.

Our results were inspired by a model of choice that involves explicit mutual inhibition in economic and perceptual decisions. Neural activity in several reward regions in the brain shows evidence of mutual inhibition during economic decisions. These regions include the ventromedial prefrontal cortex (Strait, Blanchard, & Hayden, 2014), ventral striatum (Strait, Sleezer, & Hayden, 2015), orbitofrontal cortex (Padoa-Schioppa, 2011), dorsal premotor area (Pastor-Bernier, Tremblay, & Cisek, 2012), and parietal cortex (Louie, Grattan, & Glimcher, 2011). Human neuroimaging results also support this (Hunt, Behrens, Hosokawa, Wallis, & Kennerley, 2015; Hunt et al., 2012; Jocham, Hunt, Near, & Behrens, 2012). While a direct link between this literature and the present study remains speculative, the similarity is nonetheless striking. Future work will be required to determine whether these neural processes instantiate the mechanism that our investigation was motivated by.

In conclusion, we hypothesise that far from being an artefact of imperfect implementation, longer RTs with low-value alternatives and shorter RTs with high-value alternatives are diagnostic of an adaptive decision strategy for the uncertain environments faced by decision making systems, at different level of biological complexity, and in various domains.

Appendix

Figure A1.

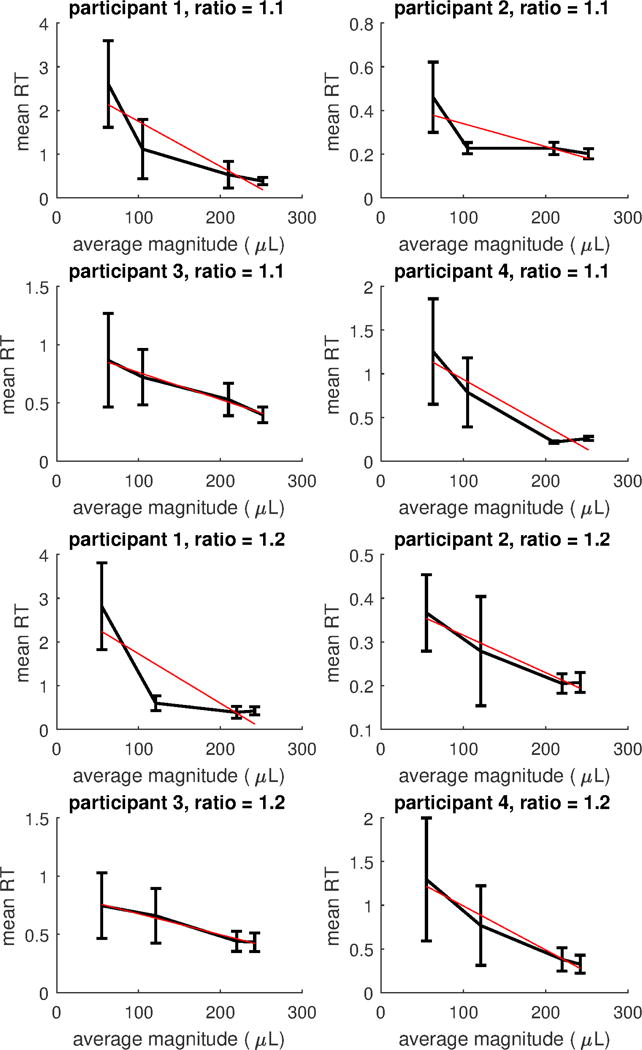
Mean RTs for conditions with constant ratios of increasing magnitude for each subject. Bars represents 95% confidence intervals. The red (straight) line represents the linear regression line on mean RTs. Top: ratio =1.1. Bottom: ratio =1.2.

Figure A2.

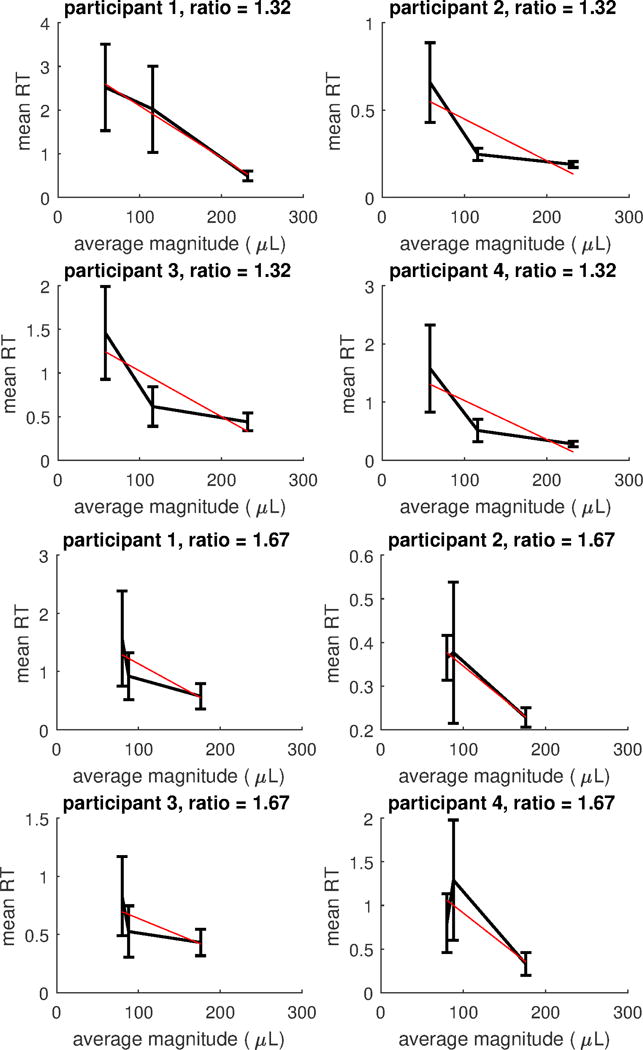
Mean RTs for conditions with constant ratios of increasing magnitude for each subject. Bars represents 95% confidence intervals. The red (straight) line represents the linear regression line on mean RTs. Top: ratio =1.32. Bottom: ratio =1.67.

Figure A3.

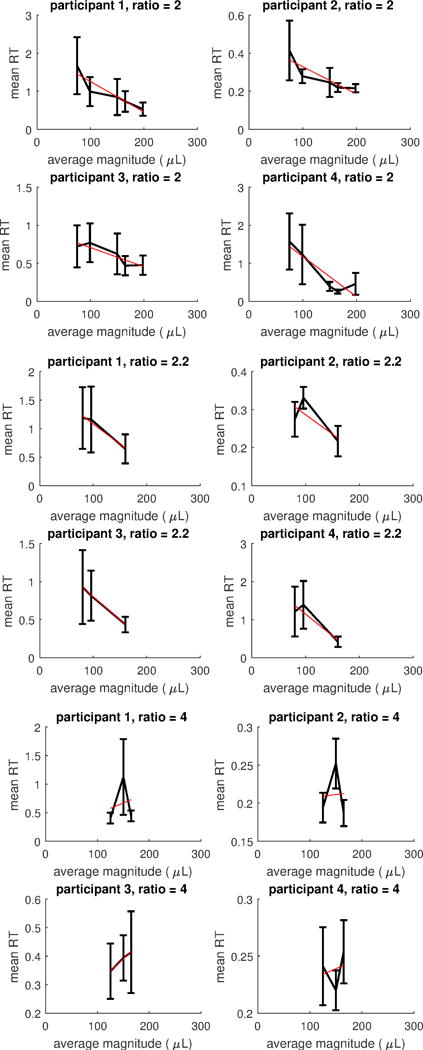
Mean RTs for conditions with constant ratios of increasing magnitude for each subject. Bars represents 95% confidence intervals. The red (straight) line represents the linear regression line on mean RTs. Top: ratio =2. Middle: ratio =2.2. Bottom: ratio =4.