A model-based analysis of tissue targeting efficacy of nanoparticles

Abstract

Tissue targeting is a critical challenge for systemic delivery of drug nanocarriers. To overcome this challenge, major research efforts have been undertaken to design ligand-conjugated nanoparticles. However, limited work has been done to quantitatively assess the effectiveness of such approach. In this work, using a mechanistic spatio-temporal model, I investigate the effectiveness of ligand-directed tissue targeting. By applying an approach from the colloidal filtration theory, I develop a Brownian dynamics model of nanoparticle–cell interaction. The model incorporates a single cell and its surrounding flow field. It considers both specific (receptor-mediated) and non-specific (bare cell surface-mediated) recognition of nanoparticles subject to convective and diffusive motion. Using the model, I investigate how the specific and non-specific interactions compare in determining the overall targeting efficacy. My analysis provides some interesting findings that contradict the general notion that effective targeting is possible based upon the differential receptor expression in cancer and non-cancer cells. I show that such strategy may yield only a marginal gain in the targeting efficacy. Moreover, non-specific interaction may have an important influence on particle recognition by cells even at high receptor expression levels.

1. Introduction

Tissue targeting remains a critical challenge for nanotechnology-based drug delivery. A very small fraction of intravenously injected nanoparticles can reach the target tissues [1,2], while most of them are lost in a variety of mechanisms [3–5]. To overcome this challenge, significant efforts have been made to develop ligand-conjugated nanoparticles [6]. The key idea of ligand conjugation relies on the fact that cancer cells overexpress certain receptor proteins that are found minimally expressed in the normal (non-malignant) cells [7]. Therefore, attachment of receptor-specific ligand may direct the particle to the target tissue while avoiding non-specific recognition by the normal cells [8]. However, there are growing concerns about this approach because of the lack of quantitative evidence [9,10]. Many studies now indicate that active targeting may have little effect on the localization of ligand molecules in target tissues [11–15].

There might be several caveats in the approach of active targeting through ligand conjugation. Nanoparticles in a systemic delivery could be lost even before encountering the target tissue. It is quite misleading to think that ligand attachment can direct a particle to a tissue; rather, a circulating particle first arrives at the target site and is retained through the ligand–receptor binding [9–11]. Another caveat is the formation of protein biocorona on the surface of a circulating nanoparticle [11,16,17]. Biocorona modifies the surface of a particle and may compromise the ligand–receptor specificity [18]. Moreover, particles may get captured by the non-malignant cells in the tumour interstitium [17]. A tumour tissue usually contains only 3–15% malignant cells [17]. The rest of the tissue is composed of a variety of non-malignant healthy cells minimally expressing the target receptors. However, the aggregate amount of receptor proteins expressed by the non-malignant cells could be significant. In addition, these cells can also recognize a particle through non-specific binding. Moreover, the bare regions of a cancer cell surface should be able to mediate non-specific interaction like the non-cancer cells. The effects of such non-specific particle capture on targeting remain poorly understood.

In this modelling work, I investigated the effectiveness of receptor-directed nanoparticle targeting. I focused on the following questions: to what extent may differential receptor expression affect tissue targeting of particles? What roles does the non-specific particle–cell interaction play in determining the overall targeting efficacy? More specifically, I investigated parameter k in equation (1.1) at different levels of cellular expression of receptors and non-specific particle–cell interactions:

1.1

The above equation describes particle transport in a heterogeneous advection–diffusion–reaction system, such as a porous medium or biological tissue. In a biological tissue, C represents particle concentration, D_e represents effective diffusion constant, and k represents the rate constant for particle capture by cells. The value of k is directly related to the targeting efficacy. My goal was to dissect this constant based on the contributions from the specific (receptor-mediated) and non-specific (bare cell surface-mediated) particle–cell interactions. For effective targeting, k should be sensitive to the level of cell-surface receptor expression, which is the key rationale behind targeted drug delivery. On the other hand, for cells devoid of receptors (or particle lacking the targeting ligand), k should account for a weak non-specific recognition. In order for the ligand-directed targeting to be effective, the value of k in a cancer tissue overexpressing the receptors should be large compared with a normal tissue.

To investigate the above questions, I developed a detailed spatio-temporal model of particle–cell interaction. The model is an extension of a theoretical framework called Happel sphere-in-cell model [19]. In colloidal filtration theory, the framework has been extensively used for studying particle deposition in porous media [20–24]. It has also been used to model particle transport in biological tissues [25].

In a Happel model, a porous medium or biological tissue is represented by a unit spherical body (cell) and its surrounding flow field. Particles entrained in the flow field can get captured upon making a contact with the surface of the spherical cell. The surface of the spherical cell is considered to be smooth (homogeneous) that captures a particle in a single contact. I modify the Happel sphere-in-cell framework to explicitly incorporate cell-surface features that represent receptor molecules and non-receptor (bare) regions. In the model, I account for both receptor-mediated (specific) and bare cell-surface-mediated (non-specific) particle–cell interaction. I couple the Happel model with a time-adaptive Brownian dynamics approach to simulate particle motion in the flow field and particle uptake by the cell via the specific and non-specific interactions. Using the model, I investigate the effects of receptor expression on the tissue targeting efficacy of finite-sized nanoparticles. My analysis reveals several interesting findings and sheds light on the mechanisms whereby specific and non-specific interactions determine cellular recognition of nanoparticles at various levels of receptor expression.

2. Material and methods

I developed a particle–cell interaction model based on the Happel model [19]. A time-adaptive Brownian dynamics algorithm [26,27] was used to simulate particle transport and particle–cell interaction. The model and simulation approach are discussed below.

2.1. Computational domain

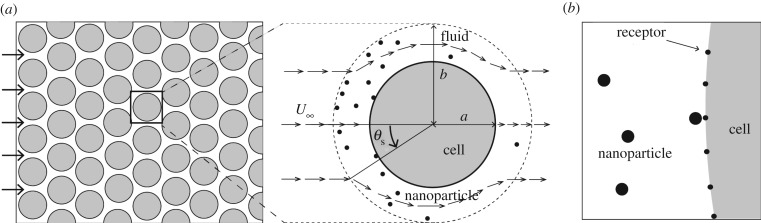
The computational domain of my model is illustrated in figure 1. The domain consists of a unit spherical cell of radius a = 10 μm and its surrounding fluid. Based on the Happel model, for a tissue with porosity ε, the thickness of the fluid surrounding the unit cell is l = a[(1 − ε)^−1/3 − 1]. I consider tissue porosity ε = 0.4 [25]. Therefore, l = 1.86 μm, and the radial distance between the centre of the cell to the periphery of the domain, b = a + l = 10.186 μm (figure 1).

Figure 1.

Illustration of the particle–cell interaction model. (a) A porous medium (left) and corresponding Happel sphere-in-cell model (right) are shown. (b) The particle–cell interaction model based on the Happel model.

Based on the Happel model, at any point (r, θ) (figure 1a), where b ≤ r ≤ a, I calculate the radial and azimuthal velocity components by using the following equations:

2.1

and

2.2

where U_∞ is the local mean fluid velocity in the tissue, K₁ = 1/K₅, K₂ = − (3 + 2ω⁵)/K₅, K₃ = (2 + 3ω⁵)/K₅, K₄ = −ω⁵/K₅, K₅ = 2 − 3ω + 3ω⁵ − 2ω⁶, ω = b/a and r^* = r/a.

2.2. Cell and nanoparticle boundary

I explicitly mark the cell boundary with receptors and bare regions, as illustrated in figure 1b. I model each receptor molecule as a small circular spot of 7.5 nm radius. The centre of the spot lies on the cell boundary. Therefore, ignoring the curvature of the cell boundary, only half of each spot is exposed to the interstitial region and therefore accessible to a particle.

I scale receptor number for the two-dimensional cell boundary. Considering N receptors on the surface of a cell in three dimensions, the equivalent number is n = (πN)^1/2. I vary n in the range 12–396, which corresponds to 45–50 000 receptors per cell in three dimensions. A larger number of receptors (n > 396) is not used because the model remains insensitive at n > 396, as will be discussed in the Results section.

I consider nanoparticles as finite-sized circles of 10 nm radius. I do not explicitly incorporate ligand molecules on the particle boundary. To purposefully favour receptor-mediated (specific) particle recognition, I consider the entire particle boundary to be reactive to a receptor. In other words, I implicitly consider the particle surface to be densely populated with ligand molecules and therefore its orientation with respect to a receptor is not important.

2.3. Adaptive Brownian dynamics

Similar to [26], I use a time-adaptive Brownian dynamics algorithm to simulate particle transport in the fluid around the cell. The sole purpose of the time-adaptive feature is to accelerate computation while capturing high-resolution details of the particle–cell interaction. My analysis involved many realizations of particle trajectories, which would be computationally too expensive without the adaptive feature. Below I briefly discuss the adaptive algorithm.

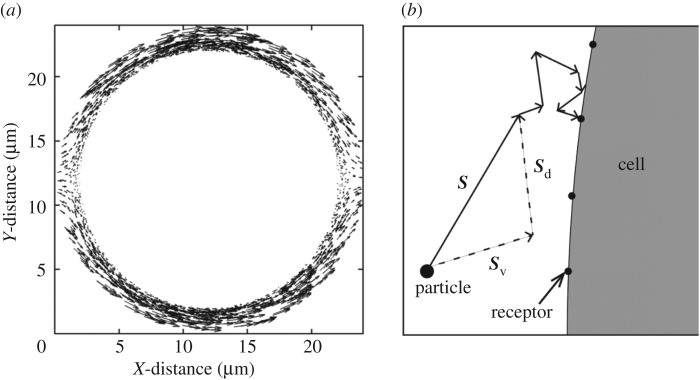
Just like in a typical Happel model, in my simulations, a particle is initiated at r = b (domain boundary) and −π/2 ≤θ_s ≤π/2. Simulation is continued until either the particle leaves the domain boundary or gets captured by the cell. In each Brownian dynamics time step Δt, a particle is advanced by a distance 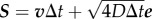, where S is displacement, v is local fluid velocity, D is particle diffusivity, and e is a unit vector in a random direction. I consider D = 10⁻⁹ cm² s⁻¹. The local fluid velocities are determined using equations (2.1) and (2.2). Figure 2a shows the velocity field around the unit cell. Figure 2b illustrates particle advancement based on the diffusion and local velocity in the flow field.

Figure 2.

Brownian dynamics simulation of particle motion. (a) Interstitial velocity field around the spherical cell calculated using equations (2.1) and (2.2). The length and direction of each arrow represent the magnitude and direction of velocity at the indicated points. (b) Particle motion in the interstitial space. The net particle displacement S in a single time step is the sum of the two vectors, S_v and S_d. These vectors represent the convective and diffusive jump of the particle, respectively. The particle takes smaller jump sizes that are adapted based on the distance from the cell boundary, as discussed in §2.3.

In the adaptive algorithm, a particle takes relatively larger steps away from the cell boundary. Near the cell boundary, it takes smaller steps to capture particle–cell interaction at the molecular scale. I impose an upper limit on the particle jump size, 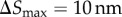, while I set a lower bound on the time step 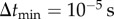. This smallest time step is applied when a particle is in the vicinity of the cell boundary, where |v| ≈ 0. Thus, the smallest jump size permitted is . Time step Δt is adapted to maintain particle jump sizes in the range 10 nm ≥| ΔS | ≥ 2 nm. This conservative limit on the particle jump size and 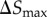are chosen for numerical accuracy because the local velocities are different at different points of the simulation domain [27].

In each Brownian dynamics step, the adaptive Δt is calculated as follows. I first evaluate l_c, the shortest distance (collision distance) between the particle boundary and the cell boundary. If 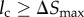, I set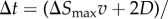 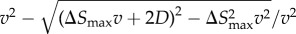, where 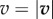is the magnitude of the local fluid velocity. However, if 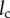, I calculate a tentative time step 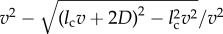. If 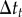, which can happen only when the particle is very near to the bare cell boundary or a receptor, I set 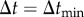. Otherwise, I set Δt = Δt_t.

2.4. Particle–cell interaction

Near the vicinity of a receptor feature or cell boundary, a particle in my simulation is advanced with subnanometre-scale steps, as discussed above. While taking such small jumps, a particle can make a contact with a receptor or the bare cell boundary. If the particle makes a contact with a receptor (specific interaction), I consider the particle is captured immediately. However, if the particle makes a contact with the bare boundary (non-specific interaction), I consider the particle is captured with probability ρ < 1. In each contact between the particle and the cell boundary, I sample a uniform random number 0 < U(0, 1) < 1. If U(0, 1) < ρ, I assume the particle is captured. Otherwise, I simply reject the particle move.

The single-collision model for particle capture by receptors may overestimate particle recognition via the specific interaction. However, as mentioned in §2.2, I purposefully favour the specific interaction (receptor targeting) to maximize the contribution from the receptor-directed targeting. On the other hand, I can change the parameter ρ between 0 and 1 to tune particle recognition via the non-specific interaction.

2.5. Targeting efficacy

Despite being a single-cell system, the Happel model can be used to evaluate parameter k in equation (1.1) using the following equation [25,28]:

2.3

In colloidal filtration theory, η_c is called unit cell collector efficiency. It measures the efficiency of the unit spherical cell to capture particles entrained in its flow field. Below I first discuss how η_c is calculated in a typical Happel model where the cell surface is featureless and homogeneous. I then explain corresponding calculation in my model to account for the specific and non-specific interaction of particles with the heterogeneous cell boundary.

In a Happel model, if a particle makes a single contact with the cell, the particle is assumed captured. However, the probability of making a contact depends on the starting angle of the particle 0≤θ_s≤π/2 (due to symmetry, −π/2 ≤θ _s ≤ 0 is simply a mirror image). A particle starting from a smaller θ_s has a higher chance to make a contact with the cell. However, even all particles starting from the same θ_s do not make a contact because of the random component (diffusion) in their motion. Therefore, for a given θ_s, the probability of a particle getting captured is less than 1. This probability, denoted as p(θ_s), can be computed from large number of Monte Carlo realizations of particle trajectories. Based on [21,29], the collector efficiency η_c is defined as

2.4

Here, 2sin(θ_s)cos(θ_s) is the weight associated with particles starting from the corresponding angle. The integration can be numerically evaluated by simulating large number of particles with starting angles 0 ≤θ_s≤π/2.

However, unlike a typical Happel model, the cell boundary in my model is heterogeneous and a particle is captured through specific (receptor-mediated) and non-specific interactions. As mentioned before, if the particle makes a contact with a receptor, the single contact leads to particle capture with probability 1. However, if the particle makes a contact with the bare cell boundary, it leads to a success with probability ρ < 1. Therefore, in my model, p(θ_s) depends on ρ and n, where n is the number of receptors on the cell boundary:

2.5

For a given ρ and n, I can evaluate η_c (equation (2.5)), and then derive the rate constant k(ρ, n) = (3(1 − ε)/2εa)η_c(ρ, n)|U_∞| (equation (2.3)). The upper limit on k(ρ, n) or η_c(ρ, n) corresponds to the condition where a single particle–cell contact results in a particle capture. This situation may arise in a hypothetical case where n = ∞ (cell surface contains infinite number of receptors) or ρ = 1. I denote corresponding k and η_c as 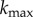and η_{c, max}, respectively. Finally, I define particle targeting efficacy by the following normalized quantity:

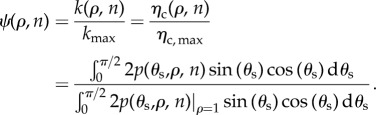2.6

Given the above definition, I can consider a few special cases. If the cell is devoid of receptors (n = 0), and particle uptake is mediated by non-specific interaction only, ψ(ρ, n)|_n=0 = α < 1. If particle capture is mediated through specific (receptor) interaction only and non-specific interaction plays no role at all (ρ = 0), then 0 < ψ(ρ, n)|_ρ=0 ≤ 1. If particle capture is mediated by both non-specific and specific interactions, α < ψ(ρ, n) ≤ 1. Finally, in order for the receptor-directed delivery to be effective, ψ(ρ, n)/α ≫1.

2.6. Model parameter values

Table 1 summarizes the model parameter values mentioned in the above sections.

Table 1.

List of model parameter values.

parameter	comment
R = 104 nm	cell radius (a typical cell size assumed)
r = 10 nm	nanoparticle radius
n = 12–396	number of receptors
rrec = 7.5 nm	radius of a receptor
ε = 0.4	tissue porosity [30]
D = 105 nm2 s−1	particle diffusion constant [30]
U∞ = 103 nm s−1	mean (bulk) fluid velocity in the tissue [30]
ρ = 0–10−4	probability of particle capture per non-specific collision
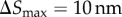	largest particle jump size
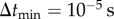	smallest time step

2.7. Code implementation

The model and simulation algorithm was written in C++. The C++ code and necessary instructions are provided in the electronic supplementary material (model.tar.gz).

3. Results

My analyses primarily focus on how variable receptor expressions may impact the tissue targeting efficacy of a nanoparticle. I consider two distinct cases. First, I consider a case where there is no non-specific particle recognition by cells; particles can be recognized only by the cell-surface receptors. Second, I consider the case where particles are recognized by both non-specific and specific interactions. Below I describe my key findings.

3.1. Targeting in the absence of non-specific recognition

I first investigated how receptor expression might impact the targeting efficacy in the absence of non-specific particle recognition by cells (ρ = 0). This is an extreme case, where the non-specific interaction does not play any role in particle uptake, and the targeting efficacy is solely determined by the level of receptor expression. In figure 3a, I show p(θ_s, ρ, n)|_ρ=0 at various levels of receptor expression (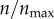). As defined in §2.5, p(θ_s, ρ, n) represents capture probability for particles with starting angle θ_s (figure 1). Each black curve in the figure represents a finite level of receptor expression, as indicated in the figure legend. The black curves are compared against the red curve, which represents a hypothetical case of infinite receptor expression (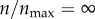). The red curve represents the maximum probability where a particle is captured in a single contact with the cell boundary.

Figure 3.

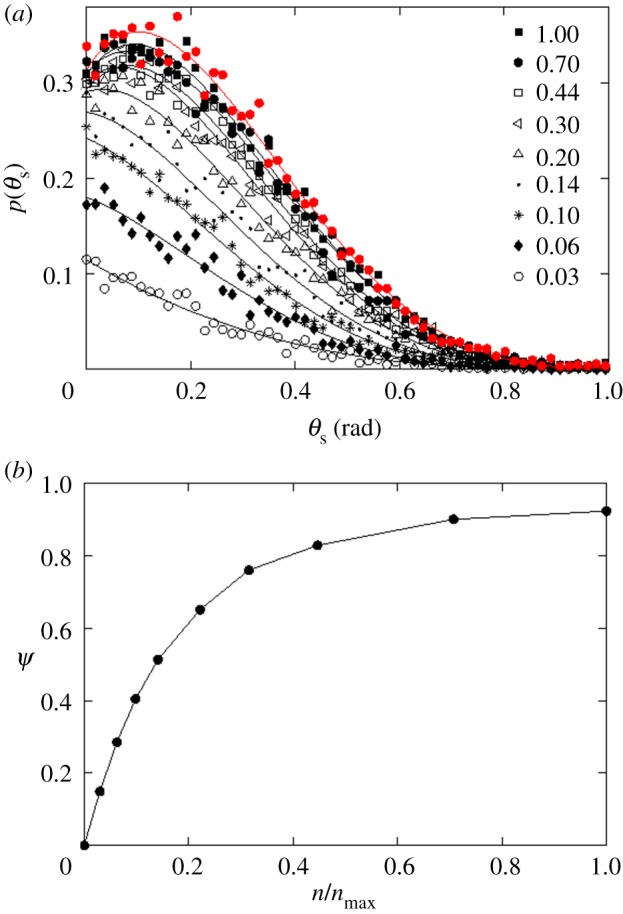
Effect of receptor expression on the targeting efficacy in the absence of non-specific particle uptake (ρ = 0). Only receptor-mediated particle uptake is allowed. (a) p(θ_s) represents the probability of capture of a particle with starting angle θ_s (figure 1). The red curve represents a hypothetical case of infinite receptor expression (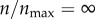). The black curves represent finite levels of receptor expression, as indicated in the legend. 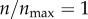correspond to 396 receptors (maximum number of receptors in the model). Each discrete point (value of p(θ_s)) is calculated from 1000 particle trajectories starting from the corresponding θ_s. The solid lines represent polynomial fits. (b) Targeting efficacy (ψ) (equation (2.6)) at different levels of receptor expression ().

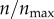The interesting thing to note in figure 3a is that 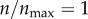and 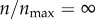(the red curve) give rise to equivalent level of particle recognition. Therefore, a further increase in 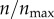beyond 1 would not change the efficiency of particle capture by the cell. As explained in §2.2, in my model, 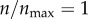represents 396 receptors on the two-dimensional cell boundary. This is equivalent to having 50 000 cell-surface receptors in three dimensions. Because the model becomes insensitive at n > 396, I used this as the maximum number of receptors in my subsequent analysis.

In figure 3b, I show targeting efficacy (ψ(ρ, n)|_ρ=0) corresponding to each level of receptor expression in figure 3a. The calculation associated with each point involves numerical evaluation of η_c(ρ, n)|_ρ=0 (equation (2.5)), and then calculation of ψ(ρ, n) (equation (2.6)). From the figure, in the range 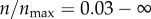, the gain in the targeting efficacy could be approximately fivefold. In my two-dimensional model, 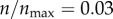corresponds to 12 receptors on the cell boundary. This is equivalent to having 45 receptors per cell in three dimensions (based on the inter-receptor distance). Importantly, in the range 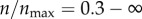(4500 to infinite number of receptors per cell), there was barely any difference in the targeting efficacy.

3.2. Effective receptor recognition of particles

According to my results in the previous section, there was no significant change in the targeting efficacy in the range 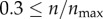(figure 3a). This was quite surprising because at 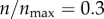(n = 119), receptors are still sparse on the cell boundary. In my model, each receptor has a radius of 7.5 nm. Thus, at this level of receptor expression, the aggregate (two-dimensional) area occupied by the receptors is only around 3% of the cell boundary. By contrast, at 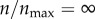, the entire cell boundary is reactive in the sense that it captures a particle in every single contact. It was not apparent how these two cases could be almost equally efficient in capturing a particle. To investigate the reason, I analysed the trajectories of individual particles in my simulation.

In figure 4a, I show trajectories of 50 individual particles. The entry point (angle) of each particle was randomly selected at r = b. From the figure, particles hitting the cell boundary made many repeated contacts and explored large patches of areas. In general, a particle initiated at a smaller θ_s was able to explore larger areas compared with a particle initiated at a larger θ_s.

Figure 4.

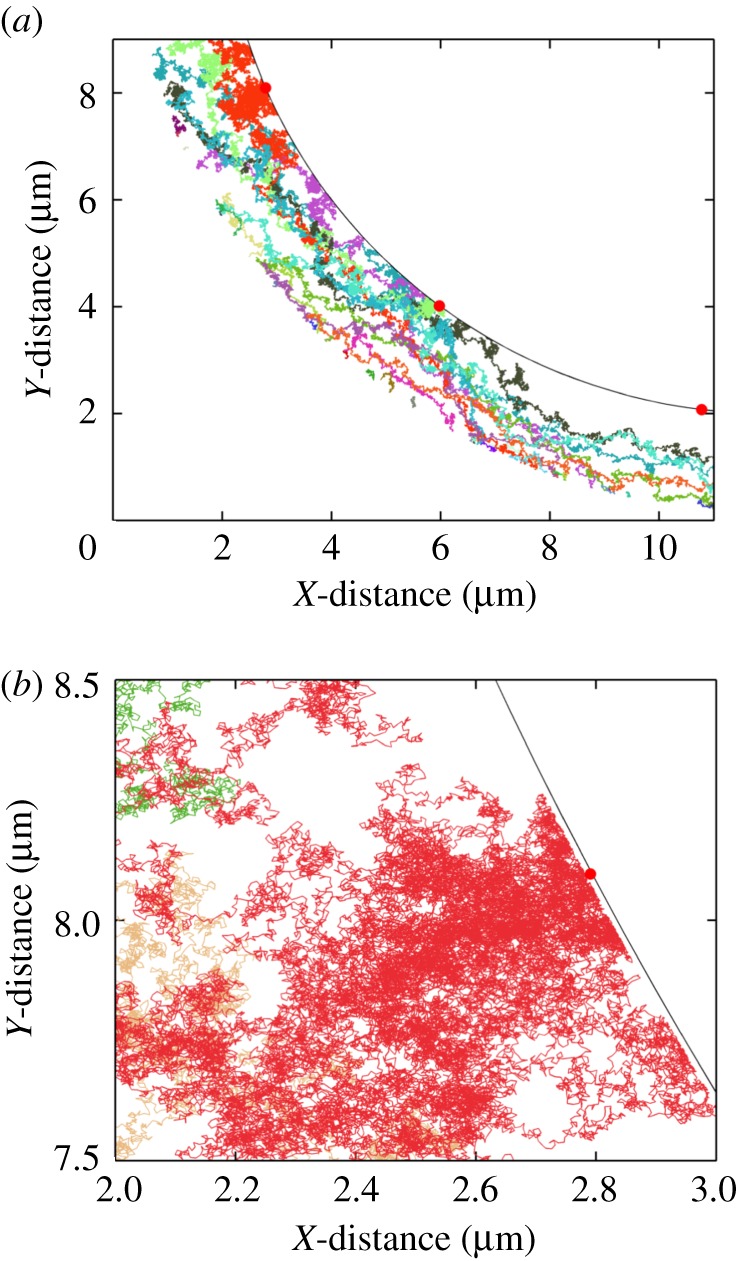
Particle trajectories in the flow field. (a) The trajectories of 50 individual particles are shown. Each colour corresponds to a distinct particle trajectory. The curved boundary represents part of the cell boundary. The red spots on this boundary represent receptor locations. (b) A zoomed-in view of a small region of (a). Simulations are done setting ρ = 0 and 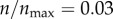(12 receptors along the cell boundary).

The result underscores the multicollision interaction between a particle and a cell, which are very different in size. To a particle, the cell boundary is a very large and almost a flat obstacle. When a particle is in the vicinity of this boundary, it can either collide or diffuse away. However, owing to the directional bias from the fluid velocity, a particle is persistently driven towards the cell boundary. This may force it to make many collisions and travel along the cell boundary to search for the sparsely populated receptors (figure 4b). In the absence of the fluid velocity and under pure diffusion, there could be a higher chance for a particle to move away from the half of the cell boundary facing the direction of the approaching particles. However, on the opposite face of the cell, smaller velocity or pure diffusion may favour particle–cell interaction.

3.3. Effects of non-specific interactions on targeting efficacy

In my analysis so far, I ignored non-specific particle recognition by setting ρ = 0. This is an extreme case where a particle never interacts with a cell without having a targeting ligand. However, this is certainly not the real scenario because the majority of the nanoparticle-mediated drug delivery experiments are based on passive targeting (without ligand attachment). Many studies indicate that tissue accumulation of passively targeted particles is comparable to that of their ligand-conjugated counterparts [11]. Therefore, for the passive targeting to be effective, a non-zero value of ρ is more realistic.

To account for a non-specific interaction, I assumed a conservative value, ρ = 0.001. This value represents my assumption of a very low-probability case where only one in every 1000 particle–cell contacts may lead to a particle capture by the cell. On the contrary, as before, I assumed every single specific (particle–receptor) contact to be productive. This assumption was made to deliberately favour the active targeting over the non-specific interaction. The small probability, ρ = 0.001, lumps together all the possibilities of non-specific particle capture, including recognition by the coated pits, non-specific membrane proteins, or electrostatic or hydrophobic interaction of the cell membrane.

In figure 5, I investigate how this value of ρ impacts the receptor targeting efficacy of a particle. In figure 5a, the same analysis as in figure 3a was performed by setting ρ = 0.001 (instead of ρ = 0 in figure 3a). The figure shows the probability distribution p(θ_s, ρ, n)|_ρ=0.001 at various levels of receptor expression, , as indicated in the figure legend. Comparing figure 5a with figure 3a, the effect arising from the difference in receptor expression is significantly reduced despite this apparently weak non-specific interaction, where a particle on average requires 1000 contacts (collisions) with the cell boundary to be captured.

Figure 5.

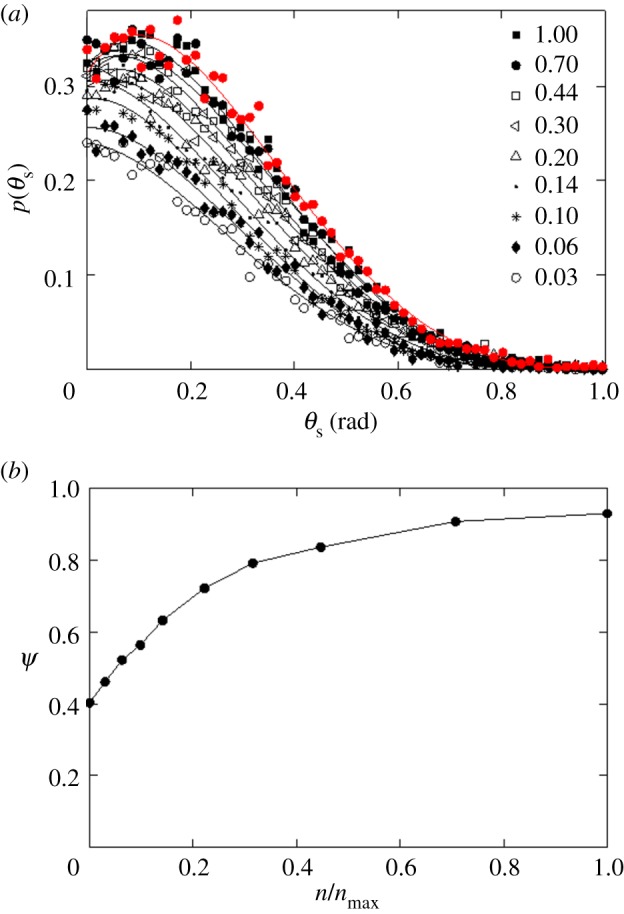
Effect of receptor expression on the targeting efficacy in the presence of non-specific particle uptake (ρ = 0.001). Both specific and non-specific particle uptake are allowed. (a) As in figure 3, p(θ_s) represents the probability of capture of a particle starting from an angle θ_s (figure 1). The red curve represents a hypothetical extreme case, where . The black curves represent finite receptor expression levels, as indicated in the legend. (b) Targeting efficacy (ψ) (equation (2.6)) at different levels of receptor expression ().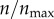

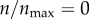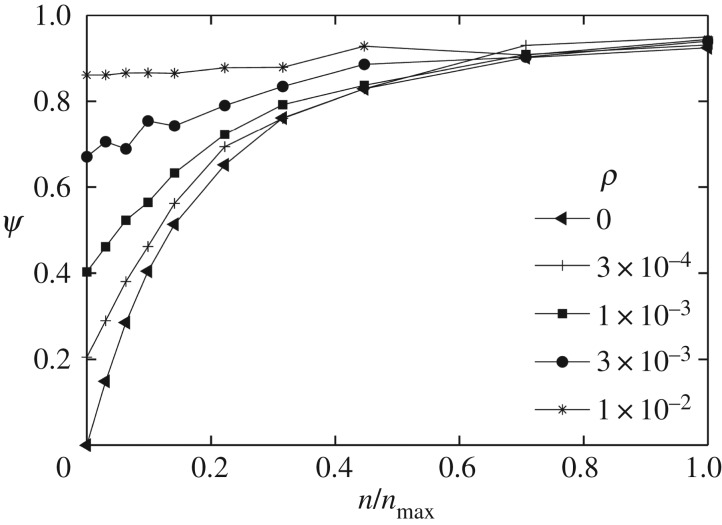
In figure 5b, I compare the targeting efficacies ψ(ρ, n)|_ρ=0.001 at different levels of receptor expression. As shown in the figure, the targeting efficacy in the absence of any receptor () was almost half of the maximum possible efficacy (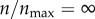). To further investigate the effects of the non-specific interaction, I compared different values of ρ in my simulations: 0, 0.0003, 0.001, 0.003 and 0.01 (figure 6). These representative values are chosen to show at what level of this probability parameter the passive and active targeting may become equivalent. The result clearly indicates that the non-specific interaction becomes the dominant mechanism of particle recognition beyond ρ = 0.003, implying a very low probability of non-specific capture (ρ) can make a significant impact on the overall targeting efficacy.

Figure 6.

Comparison of targeting efficacy at different levels of non-specific particle uptake (ρ). Each curve corresponds to a distinct value of ρ, as indicated in the figure legend.

3.4. Effects of particle size, fluid velocity and particle diffusion

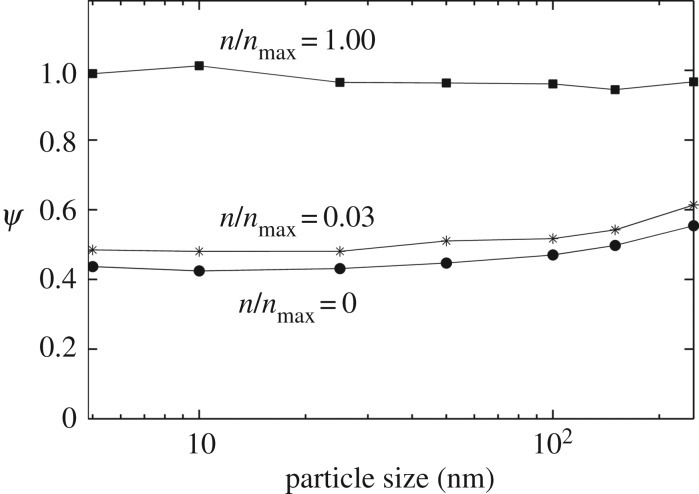
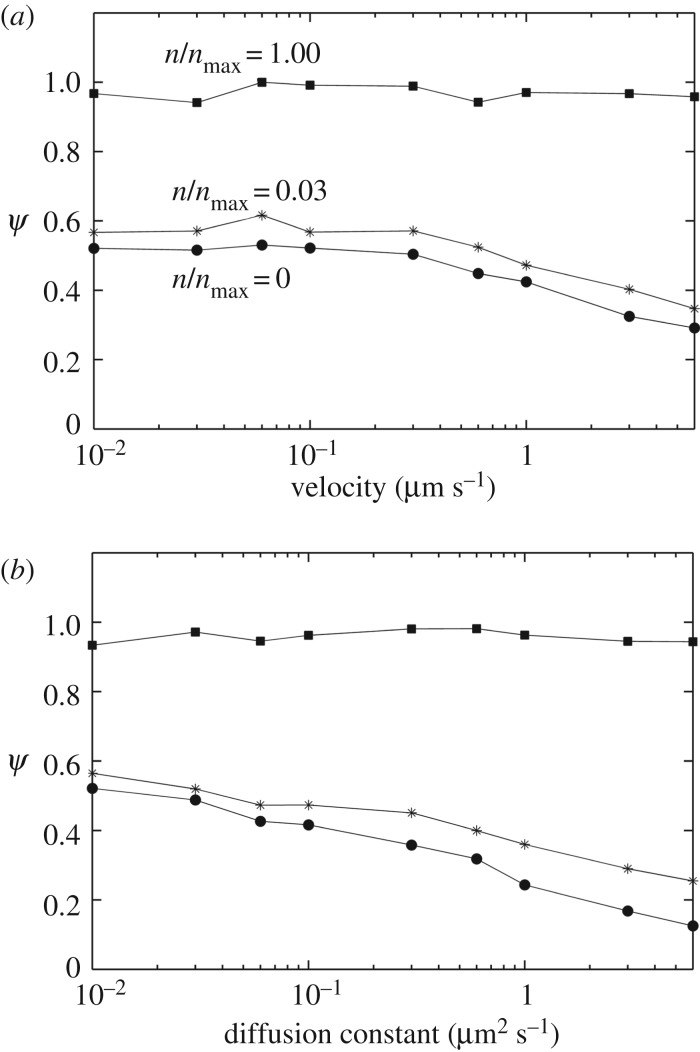
I next investigated how different parameters of the model might affect targeting in the presence of non-specific particle–cell interactions. Figure 7 shows the effect of particle size variations in my model. I varied particle size in the range 5–250 nm, and evaluated ψ for each particle size at three different receptor expression levels: 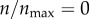, 0.03 and 1 (figure 7). For each particle size, the diffusion constant D was assumed inversely proportional to the particle radius (Einstein–Stokes equation). The 10 nm particle was assumed the base case (D = 0.1 μm² s⁻¹), and the diffusion constants of other particles were scaled according to their size. From the result, it is clear that the predictions remain insensitive to the particle size. Also, as in the default parameter case (figure 6), the difference between zero and the highest receptor expression is not significant. There is a slight increase in ψ when the particle size is increased above 100 nm.

Figure 7.

Effect of particle size on the targeting efficacy. Targeting efficacy, ψ, was evaluated for different particle sizes in the range 5–250 nm. Each curve represents a different level of receptor expression (), as indicated.

The above effect of particle size on ψ could arise for a variety of reasons. One possibility is that a large particle may explore the surface of a cell more efficiently because of the larger contact area between the particle and the cell. A recent study by Hossain et al. [31] has shown that a large particle more efficiently adheres to the arterial capillaries due to the larger overlap between the particle surface and the capillary wall. By contrast, at low velocities, a large particle becomes less efficient in adhering due to the higher dislodging drag on the particle. Such dislodging effect at higher velocities (shear) on particle–cell adherence has also been reported by Thomson et al. [32]. The other possible reason behind the slight increase in ψ with particle size might be the slower diffusion of the larger particles. A slower diffusion should permit a more efficient interaction between the particle-attached ligand molecules and cell-surface receptor proteins.

Figure 8 shows the cases where I kept particle size constant while varying the fluid velocity or particle diffusion constant. In figure 8a, I systematically changed the bulk fluid velocity U_∞ while keeping all other parameters (including the diffusion constant) fixed at the nominal values (table 1). Similarly, in figure 8b, I varied D while keeping U_∞ and all other parameters fixed at the nominal values (table 1). As shown in the figure, the targeting efficacy at the high receptor level (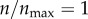) remained insensitive to the velocity or diffusion constant. However, at low receptor levels (or in the absence of receptors), there was a decrease in targeting in the high velocity and high diffusion range. These results are consistent with a recent work of Nguyen et al. [33], who have shown that nanoparticle uptake in a glioma is promoted under flow-arrest condition (hyperfusion). Based on these results, the gain from the active targeting might be relatively high in the higher interstitial fluid velocity or diffusion ranges. However, experimental measurements [34] indicate that nanoparticle diffusion in a biological tissue could be very slow and the diffusion constant could be significantly smaller than the upper range in figure 8b.

Figure 8.

Effect of bulk fluid velocity and particle diffusion rate on the targeting efficacy. (a) The bulk fluid velocity, U_∞, was varied while keeping particle diffusion constant (D) fixed at the default value (table 1). (b) The particle diffusion constant (D) was varied while keeping the bulk fluid velocity fixed at its default value (table 1). Each curve in the two panels represents a different level of receptor expression (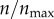), as indicated.

3.5. Targeting in the presence of non-specific recognition

I next investigated what might cause the non-specific particle–cell interaction to be so effective even at a small value of ρ. The particle trajectory analysis in figure 4 revealed that the particles may make a large number of contacts with the cell boundary. This gave us a clue to further investigate whether such multicollision interactions could lead to a large effective probability of particle capture (ρ_eff) despite a small value of ρ. For example, if a particle on average makes 1000 contacts with the cell boundary at ρ = 0.001, the effective probability of capture (ρ_eff) should be equal to 1. A further increase in ρ should make no difference in targeting efficacy.

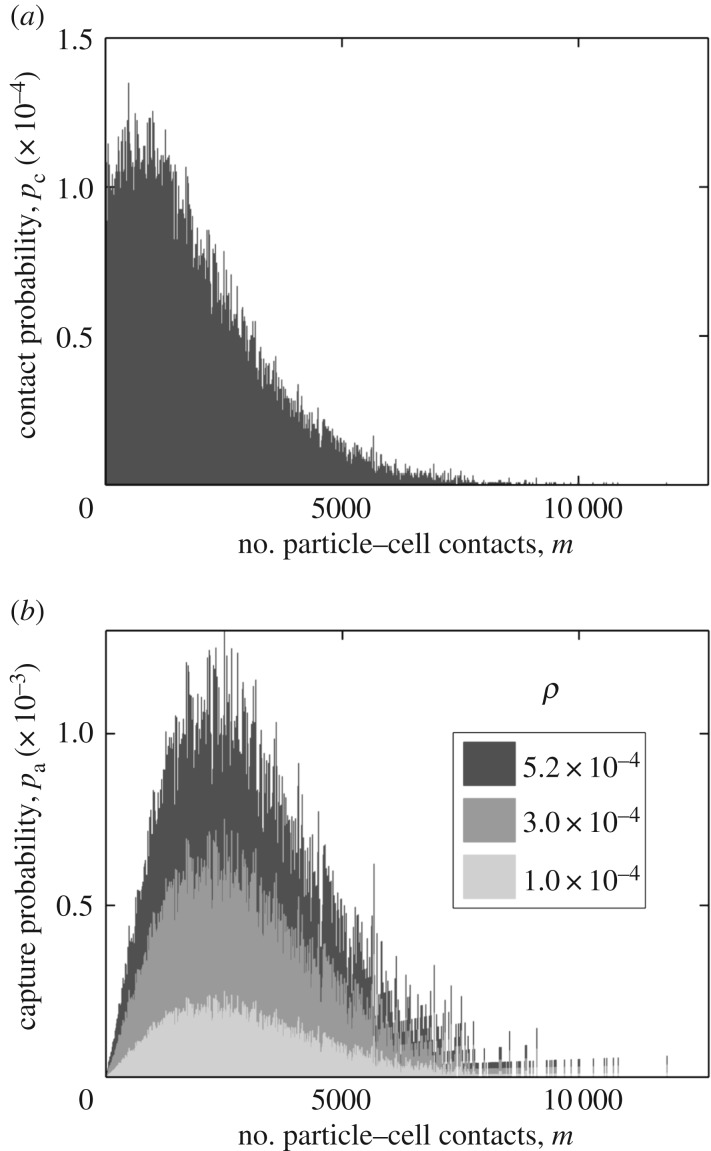
I initiated 100 000 particles from θ_s = 0 and analysed the number of contacts of these particles with the cell boundary. I set 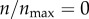and ρ = 0 so that particle can only collide with the cell boundary but never get captured by the cell. Only 32% of the particles made at least one contact with the cell boundary, while the rest of the particles were lost without making a contact. I distributed the particles making contacts into 1000 uniform bins based on the number of contacts they made. I then normalized the population size of each bin by the bin width. The resulting distribution (figure 9) is the probability distribution of number of particle–cell contacts for particles with starting angle θ_s = 0. The distribution shows that the particles make thousands of contacts with the cell boundary before escaping from the system boundary.

Figure 9.

Analysis of multicollision particle–cell interaction. (a) Distribution of number of particle–cell contacts for particles with starting angle θ_s = 0. A total of 10⁵ particles, all with starting angle θ_s = 0, were simulated considering no particle capture by the cell (ρ = 0 and 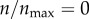). Based on the number of contacts with the cell boundary, the particles were distributed in 1000 uniform bins, and the population in each bin was normalized, as discussed in §3.5. (b) The effective probability of particle capture: p_a = ρm(pΔm), where p is the corresponding Y -axis value in (a). The probability distribution is shown for three distinct values of ρ, as indicated in the legend.

The area of the distribution in figure 9a is equal to 0.32 (the fraction of particles making contacts with the cell boundary). This area also represents the upper limit of effective capture probability, i.e. ρ_{eff, u} = 0.32. This upper limit can be achieved in a hypothetical case where every single non-specific contact results in a particle capture (ρ = 1). However, because of the multicollision interactions, it might be possible to reach this upper limit even at ρ ≪ 1. The smallest value of ρ yielding ρ_{eff, u} = 0.32 is: 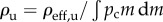, where p_c and m are the Y - and X-axes of figure 9a, respectively. My estimation led to ρ_u = 5.2 × 10⁻⁴. For any ρ greater than this value, the capture rate of particles should remain unaltered because the effective maximum capture probability cannot exceed 0.32. In figure 9b, I show the distribution of particle capture probability at ρ_u = 5.2 × 10⁻⁴ and two other values smaller than ρ. The figure shows how the multicollision particle–cell interactions contribute to the overall effective capture probability for particles with starting angle θ_s = 0.

Overall, the analysis underscores an important feature of particle–cell interaction. The multicollision interaction between a particle and cell may lead to a large effective particle capture rate despite a poor specificity. This might be a general phenomenon where the reactive bodies are too different in size.

4. Discussion

In this work, I presented a mechanistic spatio-temporal model of nanoparticle–cell interaction in a biological tissue. Using the model, I analysed the effectiveness of receptor targeting of nanoparticles. My overall analysis indicates that such strategy may not have a remarkable impact on the particle targeting efficacy. In the presence of non-specific particle recognition, the gain in the targeting efficacy from ligand attachment could be marginal. I have provided a detailed analysis of the mechanisms whereby a normal cell and a cancer cell having significantly different levels of receptor expression could recognize particles with comparable efficiencies. My analysis indicates that the size difference between a particle and a cell may enable a mobile particle to make numerous contacts with the cell surface. Such multicollision interaction could lead to a high effective rate of particle uptake despite a poor non-specific recognition.

My model does not incorporate cellular heterogeneity of a tumour microenvironment [35]. The model is based on a single-cell system assuming the tissue is homogeneous. In reality, a significant fraction of a tumour may be composed of various non-malignant cells [36] that may not express the target receptor proteins. Therefore, the aggregate cell-surface area available for non-specific interaction could be larger than what has been considered in my model. As a result, my analysis may actually underestimate non-specific recognition. Consideration of cellular heterogeneity in the model would further diminish the significance of receptor-directed targeting.

It should be noted that my model does not incorporate an explicit ligand molecule to mediate receptor interaction. Rather, the entire particle surface was assumed capable of recognizing a receptor. This consideration favoured the particle uptake via the specific (receptor-directed) interaction because every single contact between the particle and a receptor led to a capture of the particle. The implicit assumption was that the particle surface could be densely populated (to achieve efficient targeting) so that a ligand–receptor contact was possible in every contact between the particle and a receptor. In reality, ligand–receptor binding may require proper orientation of the ligand and receptor binding sites. For a finite-sized particle with sparsely populated surface ligands, steric constraints and geometrical restrictions may play important roles.

I considered particle capture an irreversible process in both specific (receptor-mediated) and non-specific particle–cell interaction. Again, the irreversible specific capture was to make the receptor-directed targeting more efficient. On the other hand, the irreversible non-specific capture accounted for the possibility of intracellular particle uptake via endocytic trafficking or other mechanisms [37,38]. The small value of ρ accounted for the numerous transient (reversible) non-specific contacts that may eventually culminate in an irreversible intracellular uptake. In the first part of my analysis (figures 3 and 4), I considered zero possibility of particle uptake via the non-specific interaction (ρ = 0). This may represent an unrealistic extreme case because numerous experimental evidence indicates that non-specific interaction accounts for an appreciable amount of particle uptake by cells [37–41]. Therefore, my subsequent analyses with a non-zero ρ in the range 10⁻⁴–10⁻² may portray a more realistic scenario. In this latter case, I found the non-specific interaction had a strong influence on particle recognition that marginalized the efficacy of receptor-directed targeting.

In my model, I consider a two-dimensional geometry. A three-dimensional form of the model would be more realistic but computationally expensive given a large number of simulations needed to generate the statistics. By proper scaling, the inter-receptor distance in my model was kept consistent with a three-dimensional system. In three dimensions, a particle would also display similar multicollision interaction, explore the two-dimensional cell surface, and avail sparsely distributed receptors. Overall, key findings and insights should not change appreciably if the dimension of the system is changed.

My study underscores the effects arising from the multi-collision interactions between two mutually reactive bodies of dissimilar sizes. The analysis in figure 9 shows that approximately one-third of the particles directly approaching a cell makes at least one contact with the cell boundary. The distribution in the figure indicates that majority of these particles hitting the cell actually make thousands of contacts due to the relative size difference between the particle and the cell. This implies a significant fraction of the entrained particles may get a chance of numerous interactions with a cell even without targeting. Such multicollision interactions may lead to a high effective rate of particle capture although there might be a very poor probability of capture in each particle–cell contact. Therefore, further gain from active targeting could be difficult. The focus should be directed to marginalizing (eliminating) the non-specific interaction. For targeting to be effective, it is necessary to ensure the non-specific recognition is minimal despite the multicollision effect.

One strategy to reduce non-specific recognition might be to encapsulate nanoparticles with biomimetic coatings derived from appropriate cell membranes. Currently, such strategies are employed to avoid immunorecognition of particles [42,43]. However, a suitable biomimetic coating may also reduce intra-tissue particle recognition and capture by healthy (non-malignant) cells. Effective particle design for active targeting, therefore, may require a proper coating as well as ligand conjugation.

The multicollision effects and non-specific recognition may also be an issue for other therapeutic agents having dimension and transport phenomena comparable to a nanoparticle. Besides nanoparticles, the targeting of a variety of antibodies is also founded upon the same rationale—differential expression of a receptor protein by cancer and non-cancer cells [44]. A careful screening of such targeting antibodies may be needed to ensure effectiveness. A small level of non-specific interaction or receptor expression by the non-malignant cells in the target tissue may compromise their targeting efficacy and therapeutic effectiveness.

It should be noted that non-specific particle–cell interactions might be governed by several factors, such as particle and cell-surface charges [45], van der Waals attraction [46], and hydrodynamic lift [47]. Explicit incorporation of these components in the model was possible. However, the exact contributions of these components should vary depending on the particle and cell. Therefore, I adopted the simpler but more general probabilistic construct where the value of ρ defines the lumped contributions from these factors in addition to the possibility of irreversible particle uptake by cells.

The approach developed in my model provides a unique capability to bridge the link between molecular-scale interaction to macroscale particle dispersion (equation (1.1)). In an earlier Happel model by Su et al. [25], the cell surface was considered featureless and homogeneous. My extended model explicitly incorporates receptor features on the cell boundary and takes into account the molecular-scale details of the particle–cell interaction. It is possible to further extend the model by incorporating particle surface attributes, including targeting ligands. Such extension will enable simulation of the transport behaviour of multivalent particles and biomolecules (ligands, antigens and growth factors) in biological tissues or porous media. Currently, only the rule-based approach provides the capability to consider site-specific details of multivalent reactive species [48,49]. However, most of the existing rule-based approaches use non-spatial graphs to define protein molecules and complexes. Therefore, the rule-based models provide limited capability to explicitly investigate the spatio-temporal effects arising from diffusion and geometry of multivalent species. Extension of my approach may enable development of realistic tissue models bridging spatio-temporal complexities at distinct time and spatial scales.

5. Conclusion

In this study, I have developed a spatio-temporal model of nanoparticle–cell interaction. Using the model, I analysed the effectiveness of receptor-directed tissue targeting of nanoparticles. My analysis indicates that a targeted nanoparticle can be barely more efficient compared with a non-targeted particle. My model indicates that non-specific interactions play a significant role in particle recognition due to the large surface area of cells available for non-specific recognition of particles. A particle having a much smaller size makes numerous contacts with the interstitial cell boundaries devoid of receptor proteins. Such multicollision interactions may allow the particle to be captured with high probability despite having a very low specificity for non-specific recognition per contact with the cell boundary.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Competing interests

The author declares no competing interest.

Funding

Research presented in this work was supported by the National Science Foundation CBET-CDS&E grant no. 1609642. No additional external funding was received to support this work. The funders had no role in the study design, data collection, analysis, decision to publish or preparation of the manuscript.