Collective regulation of cell motility using an accurate density-sensing system

Abstract

The capacity of living cells to sense their population density and to migrate accordingly is essential for the regulation of many physiological processes. However, the mechanisms used to achieve such functions are poorly known. Here, based on the analysis of multiple trajectories of vegetative Dictyostelium discoideum cells, we investigate such a system extensively. We show that the cells secrete a high-molecular-weight quorum-sensing factor (QSF) in their medium. This extracellular signal induces, in turn, a reduction of the cell movements, in particular, through the downregulation of a mode of motility with high persistence time. This response appears independent of cAMP and involves a G-protein-dependent pathway. Using a mathematical analysis of the cells' response function, we evidence a negative feedback on the QSF secretion, which unveils a powerful generic mechanism for the cells to detect when they exceed a density threshold. Altogether, our results provide a comprehensive and dynamical view of this system enabling cells in a scattered population to adapt their motion to their neighbours without physical contact.

1. Introduction

The ability of individuals to sense the presence of other members in a group is crucial for them to achieve most of their functions. In particular, it is of great interest for them not only to detect their immediate neighbours, but also to gain information about overall properties of the population such as its density. Of course this is true at the scale of metre-sized animals, including human beings, but cells also need this capacity. To achieve this function, they have developed quorum-sensing (QS) systems [1]. These consist of secreted diffusible molecules whose concentration in the extracellular medium reflects the cell density, together with a corresponding detection system at the level of single cells. Most of the known quorum-sensing factors (QSF) act to regulate the cell proliferation not only in bacteria, fungi [2] and amoeba [3], but also in higher eukaryotes. Such mechanisms could be at stake, e.g. in tumour dormancy [4] or fibrosis diseases [5]. The use of QS systems has been well described in the amoeba Dictyostelium discoideum, especially during the transition from the unicellular to the multicellular phase and the induction of development [6–11]. In the vegetative, unicellular, phase, during which the cell population exhibits logistic growth, the secreted protein AprA, which also serves as an endogenous chemorepellant [12], has been shown to inhibit proliferation at high cell densities [5,13].

We demonstrated previously that vegetative D. discoideum cells possess another density-sensing system that controls cell motility rather than cell growth. In multicellular organisms, motility is involved not only in immune response, embryonic development and neural plasticity, but also in cancer invasion and metastasis. Unicellular organisms also take advantage of this active mobility to search for food or to spread in their environment. In all these situations, adapting their motion to the collective context can be an asset for the cells, for instance to ensure efficient spreading of the colony or conversely to prevent the population from getting too scattered. We have shown previously [14] that vegetative D. discoideum cells are able to collectively regulate their motility with high sensitivity in cell density. More precisely, they make modifications in their medium, which induce an overall decrease of the motility of single cells in the population. Despite a high heterogeneity between individual cells, the observation of numerous cell trajectories evidenced a particularly marked effect on the displacements over long durations. Hypothesizing that the communication stems from the constant secretion of a QSF, an empirical relationship was found between the concentration of this unknown factor and the cells' effective diffusion constant, which measures the random motility of single cells.

Here, we further characterized the functioning of this density-sensing system. First, we confirmed that the effect of medium conditioning on motility is a generic and robust phenomenon in vegetative Dictyostelium cells that affects both the short-term cell speed and its mode of migration. Then we demonstrated that the effect indeed relies on a secreted molecule (QSF) of high-molecular weight and provided some clues about its chemical nature. We next made a quantitative analysis of the cellular response to QSF concentration: we retrieved the exponentially decaying shape of the motility–concentration relation found previously [14], with a saturation of the effect at a low-motility plateau. Yet, we also showed that the secretion is under a negative regulation loop, which could provide the cells with a very efficient density-sensing capacity. Last, we examined possible molecular players of the response to QSF. This revealed a role for the G-protein subunit Gα4 and the arrestin proteins AdcB and AdcC, suggesting that a G-protein coupled receptor (GPCR) is also involved.

2. Material and methods

2.1. Cell culture

We mainly used D. discoideum standard strain AX2. The cells were grown at 22.5°C on cell-culture-treated Petri dishes (BD Falcon, Franklin Lakes, NJ, USA) in glucose-containing HL5 medium (Formedium, Hunstanton, UK). In these conditions, the doubling time was around 9 h. Before each experiment, the cells were detached and diluted to the seeding density of 5.7 × 10³ ml⁻¹. All the mutant strains (see electronic supplementary material, table S1 [15]) were handled in the same way, except that they could differ in their doubling time.

2.2. Conditioned medium

To prepare medium containing QSF activity, cells were put in culture on a 10 cm Petri dish at a density 3 × 10³ cells ml⁻¹ in 10 ml of HL5 medium (30 000 cells initially), and allowed to grow for 48 h. Then, the medium was collected, filtered through a 0.2 μm-porous membrane and kept at 4°C until used, as the activity proved stable in these conditions. Hereafter, we refer to this medium as ‘conditioned medium’ (CM) as opposed to untreated fresh medium (FM).

2.3. Sample preparation and video microscopy

A glass slide (Marienfeld, Laud-Königshofen, Germany) was first cleaned with ethanol. Six home-made circular plastic wells (approx. 1.8 cm in diameter) were glued onto the slide using silicon joint (Loctite, Düsseldorf, Germany) and the device was sterilized under UV light for . Then, 4000 cells were transferred into the wells in 700 μl of medium and allowed to adhere at 22.5°C. After , the medium was changed to experimental medium. The cells were imaged using a slightly defocused bright-field microscope (TE2000, Nikon) at 4 × magnification and a wide-field Andor Zyla sCMOS camera. A time-lapse movie was recorded for using MicroManager software with a 60 s time-interval, while the temperature was kept constant at 22.5°C.

2.4. Characterization of the cell trajectories

2.4.1. Image processing

The cells' positions were retrieved using home-made ImageJ macros based on the ‘Find Maxima’ built-in function. The individual trajectories were then reconstructed with a squared-displacement minimization algorithm (http://site.physics.georgetown.edu/matlab/, figure 1a,b for typical examples) and the data analysed using home-made programs in Matlab (The Mathworks, Natick, MA, USA).

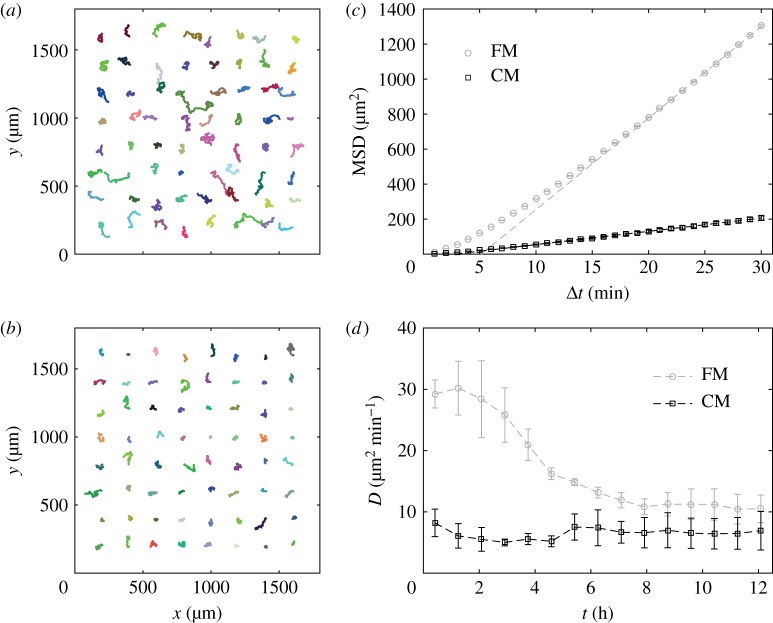
Figure 1.

The cell motility is decreased by medium conditioning. (a,b) Examples of, randomly picked up, trajectories of cells in fresh (FM, (a)) and conditioned (CM, (b)) media (trajectory duration: 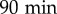). (c) MSD as a function of time for cells in FM (grey circles) or CM (black squares) and linear fits at longer durations (dashed lines). The error bars (smaller than symbol size) show the SEM of n = 156 independent experiments, with a total of approximately 25 000 trajectories in each condition. (d) Time evolution of the effective diffusion constant D, computed as the limit at large Δt (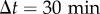) of MSD/(4Δt), for cells initially in FM (light circles) or CM (black squares). The error bars show the s.d. of n = 3 independent experiments. (Online version in colour.)

2.4.2. Diffusion constant

In the absence of external signals, the trajectory of a cell crawling on a surface is usually well described by a correlated random walk, which implies that several constants are necessary to fully characterize the motion. Over short durations (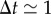 min), the movement is almost ballistic, with a linear increase of the displacement in time x(t + Δt) − x(t) = vΔt where v is the cell speed. Over long durations (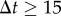min), the transport is diffusive and the mean-squared displacement (MSD) grows linearly in time as MSD(Δt) = 〈Δx²〉 = 4DΔt (figure 1c, the angle brackets 〈 · 〉 refer to average with respect to absolute time t or to the ensemble average on the population). The proportionality coefficient D is akin to a diffusion constant and hence we refer to it as the cells' ‘effective diffusion constant’ (plotted in figure 1d for both FM and CM). The effective diffusion constant was computed from the MSD as D = 〈MSD/(4Δt)〉 averaging over the trajectories of at least 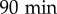with 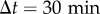and where the MSD of a single trajectory was computed as the sliding average of ∥x(t + Δt) − x(t)∥² over all (discrete) times t of the trajectory.

2.4.3. Quorum-sensing factor activity

We call the ‘relative diffusion constant’ the ratio R = D/D_FM with D_FM the diffusion constant in FM, and we define the ‘QSF activity’ as:

2.1

where R_ref is taken from a reference: when studying the response of a cell line, R comes from the studied strain in FM and CM while the reference R_ref is measured with AX2 cells; when testing the degree of QSF activity contained in a medium, R = D/D_FM and R_ref = D_CM/D_FM, yielding the alternative definition

2.2

Thanks to the robustness of the ratio R, the activity A is well adapted to quantify the amount of cellular response to CM with low sensitivity to inter-experiment or inter-strain variations of the motility. It can take values between 0 (D = D_FM) and 1 (D = D_CM). In some cases, a value outside this interval was obtained, possibly due to measurement imprecision or to insufficiently conditioned reference CM.

2.4.4. Velocity autocorrelation

The transition between the ballistic and the diffusive regimes is quantified by the velocity direction autocorrelation function (VDACF) C(Δt) = 〈u(t).u(t + Δt)〉 (where u = v/∥v∥ is the direction of motion), which measures the memory, kept after a time lag Δt, of the direction of motion exhibited at time t. In the simplest models of correlated random motion (active Brownian particles (ABPs), run-and-tumble particles (RTPs), Ornstein–Uhlenbeck (OU) process), the VDACF decreases exponentially as 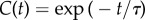with a characteristic time τ called the persistence time, and the full expression of the MSD at all times is given by the Fürth formula:

2.3

In the above models, the single exponential decay comes from a single white noise: scalar Gaussian white noise in the direction of motion for ABPs, scalar flat white noise at Poisson distributed time intervals for RTPs and vectorial Gaussian white noise in the acceleration for an OU process. Although this very simple situation may be encountered in cell trajectories, deviations of various kinds have been described lately [16–20]. Theoretically speaking, they are related to the way noise is introduced in the equations of motion. One interesting special case is when the VDACF is not a single exponential, but the sum of two exponential functions:

2.4

Generally, ϕ₁ + ϕ₂ = 1 with 0 < ϕ_1,2 < 1. The special case with ϕ₂ < 0 exists in a model applied to epithelial cells [21]. In this model, the cell velocity follows an OU process whose noise is correlated by itself coming from another OU process. The other situation, with two decaying exponential functions, may arise from two distinct populations of cells, from a memory effect in an extended OU-like model [22] or from bimodal motion [14,23,24], where cells alternate between two modes of migration with different persistence times.

2.5. Ultrafiltration

Ultrafiltration units with various cut-offs (Vivaspin 6-20, Sartorius, Germany) were first rinsed by centrifuging pure water through the membrane. The medium to be analysed was then centrifuged at 6000g until the supernatant reached a tenth of its initial volume, and both the concentrated supernatant and filtrate fractions were collected in plastic tubes (Falcon and Eppendorf). For experiments, filtrate and supernatant were assembled so that the species concentrated in the supernatant recovered their initial concentration (typically 1:9 supernatant:filtrate ratio). Both FM and CM were separated in the filtrate and supernatant, respectively, denoted FM_f and FM_s for FM and CM_f and CM_s for CM. The supernatant: filtrate mixes were made either with fractions from the same medium for ‘reconstituted’ FM and CM, or from distinct media.

2.6. Biochemical treatments

2.6.1. Phenol–chloroform extraction

FM and CM were concentrated 20 times using a 30 kDa ultrafiltration unit. The obtained fractions were split in two (‘control’ and ‘test’). The test fraction was subjected to phenol–chloroform extraction by mixing with a 1:1 phenol–chloroform mixture (1 min vortexing and centrifugation for 15 min at 2000g allowing the two phases to demix, with a white precipitate at the interface). The aqueous phase was collected and subjected to two additional extractions following the same protocol but with chloroform alone to remove the excess phenol from the aqueous phase. Finally, 1 ml of all four obtained fractions (control and test, for FM and CM) was diluted in 13 ml of deionized water and concentrated with 3 kDa ultrafiltration units to a final volume of 500 μl. The fractions were, therefore, concentrated approximately 40 times with respect to the initial FM and CM. They were all added to FM in a 1:39 volume proportion for the motility experiment.

2.6.2. Proteinase K + heat

FM and CM were incubated with 10 μg ml⁻¹ proteinase K (Sigma-Aldrich, St Louis, MO, USA) at 37°C for 2 h, then at 65°C for 20 min to inactivate the protease. Cell motility was also measured in control FM and CM (for reference D_FM and D_CM) and in FM and CM only subjected to heat (2 h at 37°C then 20 min at 65°C) in the absence of proteinase K.

2.6.3. Proteinase K + filtration

FM and CM were incubated with 10 μg ml⁻¹ proteinase K at 37°C for 2 h; then they were concentrated approximately 30 times by centrifugation at 6000g through a 30 kDa MWCO membrane to eliminate the proteinase K (M = 28 kDa) from the supernatant, which was subsequently diluted in FM_f in the same proportion as it was concentrated. Cell motility was also measured in control FM and CM (for reference D_FM and D_CM) and in FM and CM only subjected to heat, concentration and dilution in the absence of proteinase K.

2.6.4. Anion-exchange resin

One millilitre of suspended resin (Sephadex-DEAE A-25) was added to 6–10 ml of FM or CM and vortexed to ensure proper mixing. The mix was centrifuged at 1000g for 1 min and the supernatant collected, before a second decantation to completely eliminate the resin. The resulting media were used directly in parallel with non-treated (reference) FM and CM. As this treatment increased the motion even in FM due to medium depletion in anionic species, in a second experiment, the following mixes were used in a 1:1 volume ratio (the ‘a’ subscript denotes the media treated with anion-exchange resin):

• — FM_a+FM, a control to check that adding 50% of full FM restores the normal motility (i.e. 50% of the original anions are enough);

• — FM+CM, a control to check that the QSF activity is fully conserved at 50% dilution;

• — FM_a+CM, a control to check that with 50% dilution of the QSF and 50% less anions the QSF activity remains close to 1;

• — last, the test medium, FM+CM_a to check anion-depleted CM in the presence of anions from FM.

2.6.5. Cation-exchange resin

The protocol was the same as for anion-exchange resin (first experiment only) but with Sephadex-CM C-50 resin.

2.7. Statistics

Unless stated otherwise, for any observable X, hereafter 〈X〉 denotes the average of X over the trajectories of an experiment while 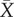denotes the average over the experiments. We used Spearman's rank correlation coefficient ρ_s with a permutation test to estimate the correlations in figure 2 (both Pearson's r and Kendall's τ gave similar trends). All the analysis was performed using Matlab's Statistical Toolbox (The MathWorks, MA, USA).

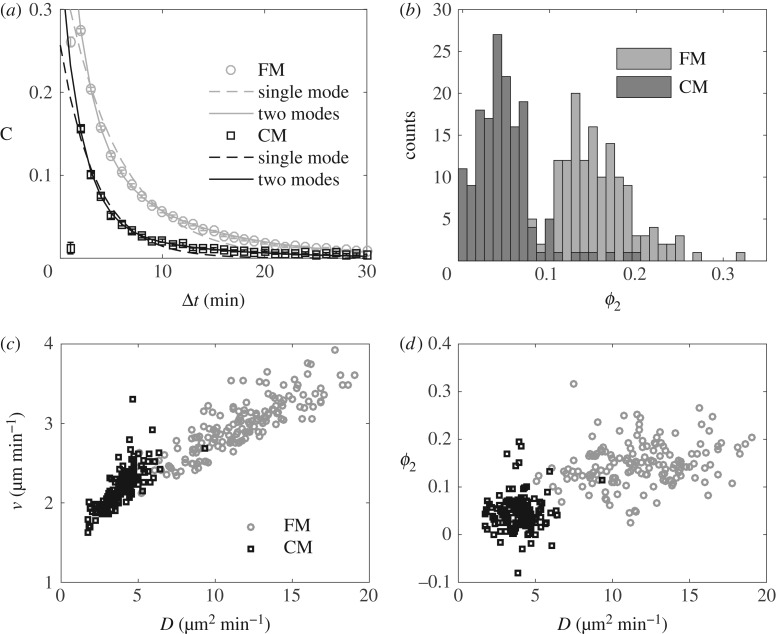
Figure 2.

Random motion with two relaxation times. (a) VDACFs of AX2 cells in FM (light circles) and CM (dark squares), and best mono-exponential (dashed lines) and bi-exponential (solid lines) fits. In both plots, the error bars (smaller than marker size) show the SEM of 156 independent experiments. (b) Distributions of ϕ₂ in FM (light grey) and CM (dark grey). (c,d) v and ϕ₂ as a function of D in both FM and HCM. In (b–d), each point or count in the histograms corresponds to one experiment.

3. Results

3.1. Medium conditioning consistently reduces cell motility

The random nature of vegetative D. discoideum motility gives rise to diffusive motion over long durations. The effective diffusion constant D is thus particularly adapted to quantify amoebal motility. Using this quantity, Golé et al. [14] evidenced that culture medium conditioned by DH1 cells harbours properties (attributed to a QSF factor) responsible for a reduction in cell motility. Here we confirm this result with the AX2 cell line (our reference ‘wild-type’ strain). To that end, we studied the trajectories obtained from all the reference experiments with AX2 cells in either FM or CM. This represents a data set of 156 independent experiments comprising approximately 25 000 trajectories in total for each condition, each single cell being tracked for 90–100 min at a 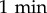interval. Given the low seeding density and the relatively short experimental time, the cells are assumed to interact neither by contact nor by secreted signals over the course of one experiment. This is confirmed by the fact that despite the relative dispersion of cell densities over the experiments—most of the values of N, the number of cells in the field of view (area 14.7 mm²), ranges from 100 to 300 (i.e. average cell–cell distance 200–400 μm)—there is no correlation between N and cell motility (electronic supplementary material, figure S1). As in our previous work with DH1 cells, we find that the MSDs in FM are larger than in medium conditioned by cells in culture (CM, figure 1a–c). The corresponding asymptotic slopes yield the effective diffusion constants, with high values D_FM in FM and low values D_CM in CM (electronic supplementary material, figure S2a). In long-term experiments (figure 1d), when the cell motility is measured over several hours, the progressive conditioning of the medium with time induces a progressive decrease of D_FM, while in already conditioned medium, D_CM remains approximately constant. This suggests that the conditioning of the medium brings the cells from a high-motility state at D_FM to a low-motility state at D_CM. Of note, the medium conditioning does not affect cell growth (electronic supplementary material, figure S2c).

Interestingly, despite a noticeable inter-experiment variability of the basal cell motility, D_FM and D_CM exhibit a strong linear correlation. We define the emergent proportionality coefficient as the ratio R = D_FM/D_CM. This ratio keeps very consistent values R = 0.34 ± 0.08 (mean ± s.d.; electronic supplementary material, figure S2b,d). To test the generality of the phenomenon, we quantified the motility of various laboratory strains of Dictyostelium in parallel with AX2. Again, despite big differences in intrinsic motility, all cell lines exposed to the same CM exhibit a similar response in terms of R (electronic supplementary material, figure S3). This shows that the regulation of the cell motility due to medium conditioning is a robust mechanism, and the ratio R is a robust feature of this mechanism.

3.2. In depth characterization of cell trajectories: medium conditioning favours a state of low persistence time

To understand which aspects of cell motion were affected by the medium conditioning, we analysed the properties of single trajectories in more detail. The plot of 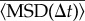shows that these trajectories fall into the class of correlated random walks (figure 1c). However, a close analysis of the shape of 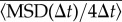reveals a divergence from the Fürth formula (electronic supplementary material, figure S4a). This is confirmed by computing the VDACF 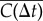(see Material and methods). Indeed, data are well fitted only by the sum of two exponential functions as in equation (2.4) (figure 2a), revealing the presence of more than one single relaxation time in the directional dynamics. Varying τ₁ and τ₂ systematically and fitting the two remaining parameters ϕ₁ and ϕ₂ for both FM and CM conditions, we find an optimum for the fit quality at 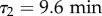and 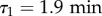, in good agreement with previous measurements [24] (see the R² landscape in electronic supplementary material, figure S5). As a consequence, it seems reasonable to set 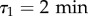and 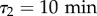in all subsequent measurements. In this framework, measuring the best fitting values of ϕ₁ and ϕ₂ allows to estimate the relative weights of both relaxation modes in the directional correlation, even without a detailed model for the motion. In particular, despite a noticeable inter-experiment variability, ϕ₂ is strikingly larger in FM than in CM (figure 2b), which translates into a higher proportion of small turn angles in the trajectories of cells in FM than in CM (electronic supplementary material, figure S6). It should be noticed that in our measurements, ϕ₁ + ϕ₂ < 1, meaning that there is a third, even faster, ‘mode 0’ in the correlation with weight ϕ₀ = 1 − (ϕ₁ + ϕ₂), which is at least partly due to noise on the position detection, and whose study is outside the scope of the present paper. Assuming the speed fluctuations are not correlated to the fluctuations in direction and the displacements due to mode 0 are negligible, one finds by integrating the VDACF (2.4):

3.1

which accounts quite correctly for the available data (electronic supplementary material, figure S4b). To sum up, the motility of the cell over longer durations of the cells quantified by D is well described as a combination of three parameters: the speed v and the relative weights ϕ₁ and ϕ₂ of modes with persistence 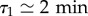and 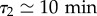, respectively. We next used this set of parameters and their correlations to quantify the effect of CM on cell motion.

Whether the QSF regulates cell speed or persistence is an important question because these two aspects of cell movement rely on partially distinct molecular mechanisms, even though they have been shown to be strongly coupled in some cases [25]. Thus, we analysed the effect of CM on 〈v〉, ϕ₁ and ϕ₂. However, none of the parameters can account alone for the change of D between FM and CM, and they all look partly correlated to these changes (figure 2c–d). Thus, we asked whether each of the constants varied rather due to the aforementioned inter-experiment variability or to the medium conditioning itself. To that end, we used Spearman's rank correlation coefficient ρ_s to estimate the correlation of a given constant X with D for all available values. Then we also measured the correlation of the values measured either only in FM—ρ^FM_s—or only in CM—ρ^CM_s—and we studied the ratios ρ^FM_s/ρ^all_s and ρ^CM_s/ρ^all_s. A ratio close to 1 indicates that the data are almost as correlated in the subgroups as in the whole set, meaning that their relation relies not only on the presence of CM but also on other exogenous parameters. A small ratio is a sign that the correlation is mainly due to regulation by the medium conditioning.

We found that v is highly correlated to D but that almost all the correlation is kept in the subgroups, showing that v is mostly affected by exogenous parameters. ϕ₁ shows a reduced correlation with D, but at least 50% is kept inside the subgroups. Conversely, while it shows similar values to ϕ₁ when all the data are considered, ϕ₂ has a much reduced correlation with D in both subgroups (table 1). This suggests that most of the changes in ϕ₂ and the related changes in D result from the regulation by the medium conditioning. Thus, in addition to changes in the short-term cellular dynamics witnessed by v and ϕ₁, the medium conditioning seems to induce an important change in the mode of motion of the cells: it reduces the amount of persistent portions in the trajectories by a factor of 3 (figure 2b).

Table 1.

Table of Spearman's rank correlation coefficients ρ_s of 〈v〉, D_comp = 〈v²〉(ϕ₁τ₁ + ϕ₂τ₂), ϕ₁ and ϕ₂ with D. The asterisks denote significance: *p < 0.001, **p < 0.0001, p > 0.1 otherwise. A small ratio in the last two columns (italics) is a clue that the correlation ρ^all_s is mainly due to the regulation by the QSF.

	ρalls	ρFMs	ρCMs	ρFMs/ρalls	ρCMs/ρalls
〈v〉	0.93**	0.84**	0.80**	0.90	0.86
Dcomp	0.93**	0.88**	0.67**	0.94	0.72
ϕ1	0.62**	0.28*	0.41**	0.46	0.66
ϕ2	0.71**	0.27*	−0.03	0.39	0.04

3.3. Medium conditioning relies on a secreted quorum-sensing factor of high-molecular weight

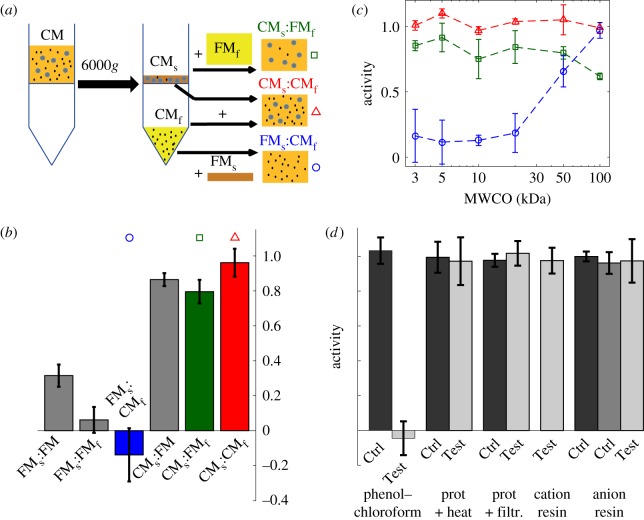
We next examined the origin of medium conditioning and its dynamics. The effect of CM on cell motility was attributed to a modication of the medium by the cells [14]. Yet, whether it relied on the secretion of a factor (QSF) as first suspected or the depletion of some constituent of the medium remained unclear. To clarify this point, we conducted ultrafiltration experiments, aiming at separating the molecules of low- and high-molecular sizes in both FM and CM. First, using a 3 kDa cut-off, we separated a supernatant fraction containing the large molecules concentrated 10 times and a filtrate containing the small molecules (figure 3a). Hereafter, we use the ‘QSF activity’ A defined in equations (2.1)–(2.2) as a fast and efficient readout to characterize the presence or amount of conditioning. We observed that a mix of supernatant from CM, diluted 10 times to restore initial concentrations of species, with filtrate from FM (CM_s:FM_f) conserved the QSF activity, while it is absent from the reverse cocktail (FM_s:CM_f, figure 3b; electronic supplementary material, figure S7). This suggests that QSF activity is carried either by a large secreted molecule present in the CM supernatant fraction, or conversely that it is due to the depletion of large molecules present in FM. To rule out the latter hypothesis, CM supernatant was added into complete FM to restore depleted molecules except for the small secreted ones (CM_s:FM). Introduction of CM_s in full FM induced a nearly maximal inhibition of motility compared with the mix FM_s:FM indicating that QSF is likely to be a secreted molecule (figure 3b).

Figure 3.

Ultrafiltration experiments show that the QSF is a large secreted molecule. (a) Principle of the ultrafiltration (example based on CM) and blend of the various fractions. (b) QSF activity for different test media. Both FM and CM have been separated in a filtrate and a supernatant (respectively, denoted by an ‘f’ and an ‘s’ subscript) using a 3 kDa cut-off, then various combinations of these fractions have been tested for QSF activity. n = 2 (FM_s:FM, CM_s:FM) and 3 for all other conditions. The symbols (and colours online) above the bars refer the corresponding curves in (c). (c) QSF activity in self- and cross-mixes of filtrate and supernatant for various pore sizes: CM_s:CM_f (triangles), CM_s:FM_f (squares), FM_s:CM_f (circles). The QSF activity switches from CM_s to CM_f at M ≃ 50 kDa (MWCO given for globular molecules; the corresponding molecular weight for a linear molecule would be 10 kDa). (d) QSF activity in media subjected to treatment with phenol–chloroform, proteinase K, cation- and anion-exchange resins. Control media (Ctrl) and treated media (Test). See Material and methods section for more details. All plots, mean ± s.d. from n ≥ 3 experiments. (Online version in colour.)

To further characterize this molecule, we varied the molecular weight cut-off. We found that QSF activity is transferred from the supernatant to the filtrate at a cut-off around 50 kDa (figure 3c). This latter value would correspond to the size of a globular molecule but should be re-interpreted at about 10 kDa in the case of a linear polymer. Of note, a small but noticeable part of the activity is lost when the small molecules of CM are replaced by those of FM (figure 3b, ‘CM_s:FM_f’ and to a lesser extent ‘CM_s:FM’). Moreover, CM filtrate alone yields reduced motility as compared to the FM filtrate (data not shown). This suggests that small molecules may also play a role in this system. However, adding FM supernatant in the CM filtrate rescues the motility of native FM (figure 3b, ‘FM_s:CM_f’), showing that this role is limited.

The CM was also subjected to various biochemical treatments to characterize the molecular properties of the QSF. We observed that QSF activity is depleted by phenol–chloroform extraction, whereas it is robust to treatment with both cation-exchange and anion-exchange resins, as well as with proteinase K and moderate heat (figure 3d). This suggests that the QSF is not heavily charged at experimental pH (approx. 6.2–6.4), and also that it does not exhibit easily accessible peptide chain so that the broad spectrum protease does not cleave it.

Thus, we expect the QSF to be a secreted molecule with a molecular weight around 50 kDa if globular, or smaller in the case of a linear chain. It could be a large carbohydrate polymer or even a lipid aggregate, but it could also contain a protein part, provided it is protected for instance by large glycans.

3.4. The secretion of the quorum-sensing factor is under negative control and provides a potentially very efficient density-sensing system

In a previous study [14], the cells were assumed to secrete QSF at a constant rate α, which enabled computation of a putative QSF concentration c up to a factor α. The response function obtained this way was correctly fitted by the following empirical relationship:

3.2

We wanted to test this hypothesis of constant α. The simple evolution equation for the concentration c can be written 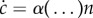, where (…) refers to unknown parameters controlling α, and n is the cell density. Note that we included no self-degradation term as we observed that QSF activity was stable in CM that was several months old. To retrieve α, the issue is to first determine the response function D(c) while making no assumption regarding the concentration: consider two conditioned media with respective concentrations c₁ and c₂. For each of them, a dilution scale is made in FM so that the dilution factor f is the volume fraction of the CM (e.g. f = 0.25 for a 1:3 CM:FM mix). Then D is computed for the two dilution scales, as a function of the dilution factor f. One should obtain two independent relations D₁(f) and D₂(f) with similar shapes. Adjusting c₁ and c₂ so that D₁(f) = D(fc₁) and D₂(f) = D(fc₂) fall on the same master curve finally yields the ratio c₁/c₂.

We applied this reasoning to the QSF. To that end, we prepared a collection of media with different levels of conditioning, as follows. Several culture dishes containing fresh HL5 medium were seeded with AX2 cells at an initial density n₀ = 3 × 10³. The time of seeding was considered t = 0. At various times t = T_i, a culture dish was picked, and the medium—conditioned for T_i—was collected and filtered. Therefore, at each time T_i corresponds one ‘medium i’ containing QSF at a concentration c(T_i, n₀) (figure 4a).

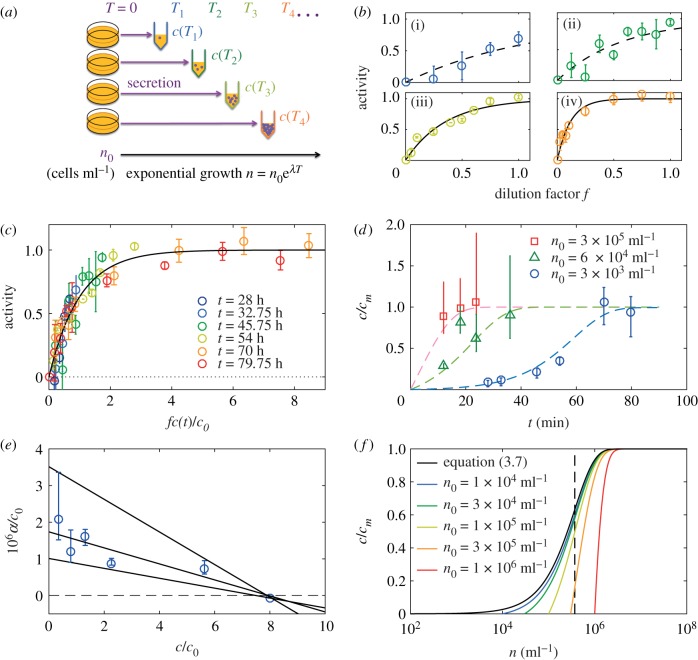
Figure 4.

The QSF secretion is under negative feedback. (a) Principle of the experiment: cell cultures are started at t = 0 in several dishes with a given cell density n₀. Then the medium is taken at various times t = T_i, so that it contains QSF at concentration c(T_i). (b(i)–b(iv)) For all media collected at different time points T_i, the activity was measured as a function of the dilution factor f. Same colours as in (c). The black lines represents the 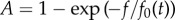fit. (c) Then all the activity curves were collapsed onto the master curve (black line) to get the relative QSF concentrations, allowing to measure c(t)/c₀ for all T_i with the definition c(t)/c₀ = 1/f₀(t). (d) Computed QSF concentration in time, starting from n₀ = 3 × 10³ ml⁻¹ (blue circles), n₀ = 6 × 10⁴ ml⁻¹ (green triangles), n₀ = 3 × 10⁵ ml⁻¹ (red squares) and theoretical predictions from equation (3.6) (dashed lines, c_m = 8c₀ for n₀ = 3 × 10³ ml⁻¹, c_m = 12c₀ for n₀ = 6 × 10⁴ and 3 × 10⁵ ml⁻¹). The error bars represent the standard deviation (n = 3 independent experiments for each point). (e) Normalized secretion rate α/c₀ as a function of the concentration, computed from the c(t) obtained with n₀ = 3 × 10³ ml⁻¹. The grey lines show a linear fit (centre) and the bounding straight lines. (f) Theoretical concentration as a function of logn in populations starting from various initial densities n₀. The system exhibits a tendency to switch fast from 0 to 1 around n^* (dashed vertical line) with a weak sensitivity to n₀ (all the curves converge fast to the limit case of equation (3.6), black line).

In a second step, the activity characteristic of each medium was built as follows. The medium i was mixed with FM so that the volume fraction of medium i was f, and the motility was measured in each medium mix with values of f varying from 0 to 1, as well as in a reference FM and CM, common to all experiments. We computed the QSF activity as in equation (2.2) and checked that it verified the relationship (3.2) (figure 4b) through

3.3

We then collapsed all the A(f, T_i) curves by fitting c(T_i), which allowed us to retrieve all concentrations c(t, n₀)—in units of c₀, like all the parameters in the following (figure 4c,d). Looking at the points from the condition n₀ = 3 × 10³ ml⁻¹, the concentration clearly saturates at a maximum value, which we define as c = c_m (figure 4d, c_m = 8c₀). This means that the secretion rate decreases over time as the cell number keeps increasing—the growth remains exponential at all times, with a doubling time t₂ = 8.5 ± 0.3 h.

To compute the secretion rate, we assumed it constant between two subsequent times T_i and T_i+1 with value α_i. Knowing that the cell density evolved as 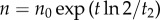, the increase in concentration is given by

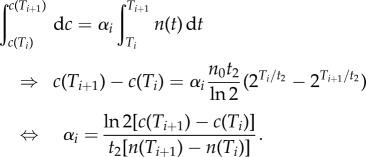3.4

We estimated α(t) and then made the approximation α((1/2)[c(T_i+1) + c(T_i)]) = α_i to obtain the α(c) relation (figure 4e). Given the obtained values, we considered the case of a linear relation α(c) = α₀(1 − c/c_m) with α₀/c₀ = 1.7 × 10⁻⁶ ml h⁻¹ and c_m = 8c₀, which is the simplest compatible model (figure 4d). Then we solved the differential equation of the QSF concentration

3.5

3.6

using this simple form for α(c) and the cells' exponential growth. The solution for c is written as:

3.7

This analytic expression represents the experimental data very well (figure 4d). In particular, repeating the experiment with two different initial cell densities n₀, this formula fits remarkably the experimental points (green, n₀ = 6 × 10⁴ and red, 3 × 10⁵ ml⁻¹) although all the parameters except c_m/c₀ (we found c_m = 12c₀ in this second experiment) were measured independently using the n₀ = 3 × 10³ ml⁻¹ data only. Thus, while the empirical response function found by Gole et al. [14] seems to describe the cellular response well, the secretion is under negative regulation, which was not accounted for before. Note that the latter effect can only be noticed with specially designed experiments. Indeed, simply measuring D without making dilutions would yield values in the plateau of low motility at all c ≥ 5c₀ without any clue whether c ∼ 5c₀ or c ≫ c₀.

More remarkably, when n is large enough compared to n₀, expression (3.6) reduces to

3.8

with n* = c_mln 2/α₀t₂ meaning that in this situation the QSF concentration depends only on the current cell density and not on the culture's past history. More precisely, c switches from 0 to c_m rapidly around n = n* = 3.7 × 10⁵ ml⁻¹ (figure 4f), a density that corresponds roughly to 30% confluence in two-dimensional culture conditions.

3.5. The response to the quorum-sensing factor involves G-protein and arrestins but not the cAMP pathway

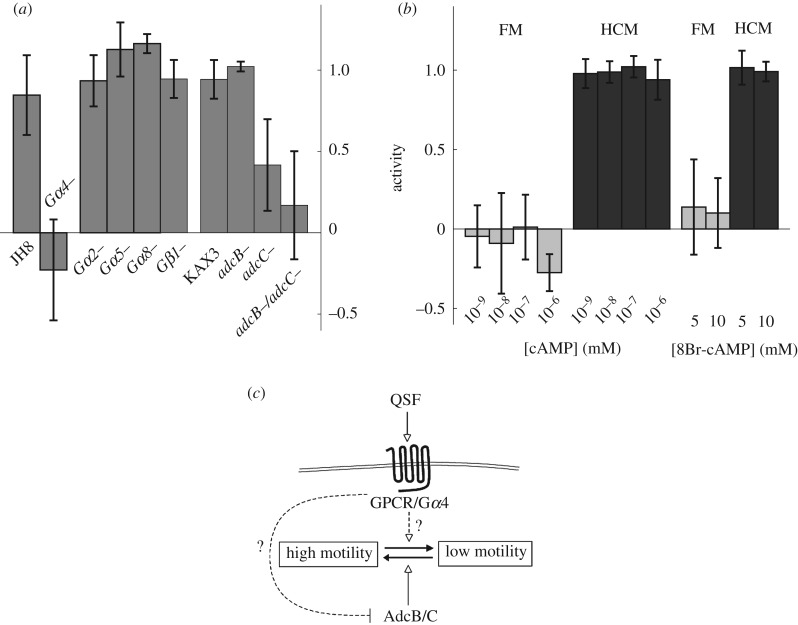
We next tried to determine actors involved in QSF sensing or downstream signalling cascades. The genome of Dictyostelium encodes a large number of heterotrimeric G-protein coupled receptors (GPCR) that could be involved in QSF detection or the subsequent response. To test this hypothesis, we analysed the motility in FM and CM of mutant cell lines disrupted for G-protein subunits (figure 5a). While Gβ1, Gα2, Gα5 and Gα8 null cells showed a normal QSF response, we found that Gα4 (gpaD) null cells exhibit a reduced response to the CM. By looking closely to the raw mean D values (electronic supplementary material, figure S8) and to the probability distribution functions (PDF, electronic supplementary material, figure S9), the motility of Gα4 null cells appears notably different from that of the parental JH8 cells in CM, suggesting that the deletion of Gα4 possibly impairs the detection of the QSF signal or the activation of downstream signalling cascades.

Figure 5.

The QSF response signalling pathway. (a) QSF activity of different strains disrupted for heterotrimeric G-proteins (Gα2, 4, 5 and 8) or arrestin family members (AdcB and AdcC), tested for their behaviour in FM or CM media. The activity was computed with expression (2.1), R_ref computed with values from control AX2 strain. For brevity, in figures, the ‘−’ (minus) sign replaces the term ‘null’. (b) QSF activity measured on AX2 cells in FM (light grey) and CM (dark grey), supplemented with various concentrations of cAMP or the cAMP analogue 8-Br-cAMP. The activity was computed with expression (2.2) using the controls in pure FM and CM. (c) Proposed model of QSF signalization: in the absence of QSF, AdcB/C are needed to maintain the cells in a high-motility state (solid arrow). When QSF molecules are present in the medium, they elicit a Gα4-dependent response, probably by binding to a G-protein-coupled receptor (GPCR). This GPCR/Gα4 complex inhibit the adcB/C-dependent pathway that promotes high-motility (dashed inhibition line), or bring the cells to a low-motility state through a distinct pathway (dashed arrow). All plots, mean ± s.d. from n ≥ 3 experiments.

We also studied mutants disrupted for two members of the arrestin family, the proteins AdcB and AdcC. Arrestins are known to interact with GPCRs and, in particular, to prevent their coupling to heterotrimeric G-proteins, thereby modulating G-protein-dependent signalling downstream of the receptors. We found that QSF activity is suppressed in the adcB/adcC double null strain, while it is only partially suppressed in adcC null cells and not in adcB null cells (figure 5a). To be more specific, we compared the motility of all the mutants to that of the parental strain KAX3 in both FM and CM. All strains exhibit the same motility in CM, but the motility in FM is reduced in the mutants—only slightly for adcB and adcC null cells, but dramatically for adcB/adcC double null cells, with values as low as in CM (see electronic supplementary material, figures S8 and S9). These results suggest that active AdcC, and AdcB to a lesser extent, are necessary to set the cells in their high-motility state. The presence of QSF might inhibit this activity of AdcB/C so that the cells exist in the low-motility state. Alternatively, the QSF response could involve other intermediates, overtaking the AdcB/C signal to reduce the cell motility.

So far, the only known target of AdcB/C is the GPCR cAR1 [26]. However, it is very likely that these proteins also regulate other receptors of this family. Though cAR1 is poorly expressed in our experimental conditions, we nonetheless tested a possible contribution of a cAMP-dependent pathway in QSF response (figure 5b). Indeed, cAMP is central to the regulation of starved D. discoideum motility, whether it be as an extracellular chemoattractant or a cytoplasmic messenger. Adding cAMP or 8-Br-cAMP (a membrane permeant analogue of cAMP) at various doses either in FM or CM did not change the motility of our vegetative cells, suggesting that cAMP-dependent pathways do not play a key role in the QSF response. The inositol-phosphate pathway does not seem to be involved in the QSF activity either, as two different plc null strains responded normally to the presence of QSF (electronic supplementary material, figure S10). Lastly, we also tested the possible contribution of the secreted protein AprA, which is a chemorepellent for vegetative D. discoideum cells [12] and which we therefore suspected at first to be the QSF. Neither AprA nor the kinase QkgA, necessary for AprA's repellent activity, seem to play a role in the QSF effect (electronic supplementary material, figure S10).

4. Discussion

Vegetative D. discoideum cells are able to condition their medium in a way that, in turn, reduces their motility as quantified by the population-averaged diffusion constant D. We showed that this effect largely relies on the production of a large QSF molecule in the external medium. This molecule has a molecular weight of about 10–50 kDa and it is robust to treatment with proteinase K, moderate heat, anion and cation-exchange resins while it is depleted by phenol–chloroform extraction. It suggests that the QSF is either a polymer or an aggregate of neutral molecules such as carbohydrates, or also possibly that it contains a protein domain decorated by large sugars. Progress in the purification of the QSF from CM together with mass spectroscopy analyses should provide a better insight into the precise nature of this molecule.

The QSF response is dramatically reduced in Gα4 null cells, suggesting that the QSF binds to a G-protein-coupled receptor (GPCR) that induces a response cascade through a G-protein. Our analysis also revealed a role for the arrestin-related proteins AdcB/C as actors in the high-motility phase. Whether AdcB/C activity is modulated by QSF and whether these well-characterized regulators of GPCR signalling and trafficking are involved in the Gα4-dependent pathway triggered by the QSF are important points that will deserve further investigation. We looked further into the possible signalling pathways, but neither the cAMP, inositol-phosphate nor AprA pathway seems to play a central role here.

We confirmed that the motility follows the QSF concentration through a nonlinear response function. By studying the QSF activity in dilution scales of media conditioned for various periods of time, we could indirectly measure the QSF concentration. We found that the secretion is itself under negative control. Using a secretion rate that decreases linearly with the concentration, we could analytically compute the concentration at all times and fit the experimental data very satisfactorily. The existence of a sharp transition around n = n* suggests that the QSF could provide the cells with a very efficient density sensing system, with good sensitivity around n*. We can reasonably guess that apart from motility, the QSF acts on other cellular functions. Interestingly, the value n* = 3.7 × 10⁵ ml⁻¹ calculated with our fitting parameters corresponds to approximately 30% confluence in two-dimensional culture. This ability to detect the transition past n* could thus be used by the cells to adapt their behaviour to a situation where the density becomes high, but still before the end of exponential growth. Note that in this part of our work, we used the motility to indirectly estimate the level of cell–cell interactions. It constitutes a step forward in the exploitation of cell motility as a tool to witness the presence of a cellular reaction to a stimuli [27].

The quantitative characterization of the cell trajectories showed that although diffusive at long durations, the dynamics was not well described at shorter durations by a random walk with simple exponential correlation, but rather that there are two timescales in the relaxation of the direction of motion. In this context, three different phenomena could lead to a decrease of D: a decrease in the speed v, a decrease in one of the persistence times or a decrease in the time spent in high-persistence mode. While the former would originate in changes in actin dynamics and adhesion turnover, the latter two would be related to the maintenance of cell polarity [15,28]. We found that both the speed and proportion of high-persistence mode were decreased in the presence of QSF, while the persistence times remained constant (figure 2b,d). It suggests that these times are inherent properties of the cells while the latter can adapt their protrusion–retraction activity and their switch frequencies between two modes of motility according to their environment. We noted that beyond the QSF regulation, the cell diffusion constant continuously varied together with the cell speed due to exogenous parameters. By contrast, the changes in D due to a regulation of the highly persistent mode of motion were only correlated to the presence of QSF. It suggests that this mode of high persistence is specifically used by the cells to react to signals from neighbouring cells. Interestingly, in a previous work [24], we have shown that this same mode of high persistence with 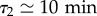could also be modulated by cell–cell contact: therefore, it appears to be a generic and fundamental element of the collective regulation of cell motility, at least in the case of D. discoideum.

At the collective level, QSF-assisted regulation of the motility could provide the cells in a scattered population with a tool for efficient collective exploration of the environment: while isolated cells may each cover a large area thanks to their high motility, such unnecessary movements can be avoided when cells are close enough to each other. In the case of Dictyostelium, this ability would be related to the optimal exploitation of nutrient resources. However, many conserved properties of motility have been first described in D. discoideum before being observed in higher organisms, and especially in leukocytes [29,30]. It is a stimulating perspective to imagine that in multicellular organisms, cell types that are dispersed in a tissue could possess a similar communication system, for instance allowing immune cells to efficiently ‘scan’ the tissues. Beyond its effect on motility, we have characterized a form of linear negative feedback on the secretion of the QSF, which is a very simple way to finely detect cell densities above a given threshold. This could actually be a very generic mechanism that various cell populations could use to adapt their behaviour relative to some critical density or density range.

Data accessibility

The raw data supporting the plots within this article can be found in the electronic supplementary material. Further lower level data and analysis codes are available upon request from the corresponding authors.

Authors' contributions

All authors designed the research. J.d.A. performed the experiments, analysed the data and wrote the manuscript. L.A. and L.M. generated the AdcB and C null cell lines. L.M. participated in the experiments on those strains. C.A. assisted in the biochemistry experiments and the cell culture. All authors commented on the data and manuscript and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

The project has been supported by the French Ministère de l'Enseignement Supérieur et de la Recherche, Université de Lyon, Université de Grenoble-Alpes and Commissariat à l'Energie Atomique (CEA). J.d.A. has been partially supported by the Fondation ARC pour la Recherche sur le Cancer and by the Programme d'Avenir Lyon-Saint Étienne. J.d.A., C.R. and J.P.R. belong to the CNRS consortium CellTiss and to the LIA ELyTLab.