The neural determinants of age-related changes in fluid intelligence: a pre-registered, longitudinal analysis in UK Biobank

Rogier A Kievit; Delia Fuhrmann; Gesa Sophia Borgeest; Ivan L Simpson-Kent; Richard N A Henson

doi:10.12688/wellcomeopenres.14241.2

. 2018 Jun 15;3:38. Originally published 2018 Apr 5. [Version 2] doi: 10.12688/wellcomeopenres.14241.2

The neural determinants of age-related changes in fluid intelligence: a pre-registered, longitudinal analysis in UK Biobank

Rogier A Kievit ^1,^a, Delia Fuhrmann ¹, Gesa Sophia Borgeest ^1,^#, Ivan L Simpson-Kent ^1,^#, Richard N A Henson ¹

PMCID: PMC5909055 PMID: 29707655

Version Changes

Revised. Amendments from Version 1

Our manuscript has been updated based on thoughtful comments from the reviewers. The main changes include additional exploration of individual item performance, using a more precise (LRT) for parameter tests, included a new figure that illustrates selective attrition, and a further discussion of the neural predictor findings,

Abstract

Background: Fluid intelligence declines with advancing age, starting in early adulthood. Within-subject declines in fluid intelligence are highly correlated with contemporaneous declines in the ability to live and function independently. To support healthy aging, the mechanisms underlying these declines need to be better understood.

Methods: In this pre-registered analysis, we applied latent growth curve modelling to investigate the neural determinants of longitudinal changes in fluid intelligence across three time points in 185,317 individuals (N=9,719 two waves, N=870 three waves) from the UK Biobank (age range: 39-73 years).

Results: We found a weak but significant effect of cross-sectional age on the mean fluid intelligence score, such that older individuals scored slightly lower. However, the mean longitudinal slope was positive, rather than negative, suggesting improvement across testing occasions. Despite the considerable sample size, the slope variance was non-significant, suggesting no reliable individual differences in change over time. This null-result is likely due to the nature of the cognitive test used. In a subset of individuals, we found that white matter microstructure (N=8839, as indexed by fractional anisotropy) and grey-matter volume (N=9931) in pre-defined regions-of-interest accounted for complementary and unique variance in mean fluid intelligence scores. The strongest effects were such that higher grey matter volume in the frontal pole and greater white matter microstructure in the posterior thalamic radiations were associated with higher fluid intelligence scores.

Conclusions: In a large preregistered analysis, we demonstrate a weak but significant negative association between age and fluid intelligence. However, we did not observe plausible longitudinal patterns, instead observing a weak increase across testing occasions, and no significant individual differences in rates of change, likely due to the suboptimal task design. Finally, we find support for our preregistered expectation that white- and grey matter make separate contributions to individual differences in fluid intelligence beyond age.

Keywords: Aging, cognitive aging, fluid intelligence, Biobank, white matter, grey matter, individual differences, structural equation modelling

Introduction

Fluid intelligence refers to the ability to solve novel problems in the absence of task-specific knowledge, and predicts important outcomes including life expectancy, expected income and work performance ( Gottfredson & Deary, 2004). Both cross-sectional (e.g. Hartshorne & Germine, 2015; Kievit et al., 2016) and longitudinal studies (e.g. Ghisletta et al., 2012; Salthouse, 2009; Schaie, 1994) have shown that advancing age is associated with a marked decrease in fluid intelligence performance. Although the precise starting point of decline is hard to estimate precisely due to cohort effects, selective attrition and enrolment and retest effects in longitudinal cohorts (e.g. Salthouse et al., 2004), estimates for the onset of decline in fluid intelligence range between the third (e.g. Park et al., 2002; Salthouse, 2009) and sixth decade of life (e.g. Schaie, 1994). Moreover, recent findings have demonstrated that within-subject decline in fluid intelligence is highly correlated with within-subject declines in the ability to live and function independently ( Tucker-Drob, 2011). The advent of large-scale neuroimaging studies has shown that neural measures can be strongly predictive of individual differences in fluid intelligence (e.g. Kievit et al., 2014; Ritchie et al., 2015). A better understanding of the neural determinants of changes in fluid intelligence is therefore necessary for improving our understanding of healthy cognitive aging, and may aid the development of early markers for individuals at risk of rapid decline. Recent innovations in multivariate models allow researchers to simultaneously estimate multiple determinants of current ability as well as changes in ability over time ( Jacobucci et al., 2018). To estimate these models with precision, large datasets are required. The UK Biobank ( Sudlow et al., 2015) is a unique resource for addressing such questions, as it includes both cognitive and neural measures on an unprecedented number of participants.

In our pre-registration, we proposed analyses of UK Biobank cognitive and brain data to a) examine the nature of age-related decline in fluid intelligence and b) model the neural determinants of this decline. The cognitive data consisted of the Biobank’s fluid intelligence scores, which were acquired in N=185,317 people (aged 39–73 years) across up to three testing occasions 2–4 years apart (though note that the majority of individuals only completed one (174,728) or two (9,719) assessments). The brain data came from a subset of approximately 10,000 individuals (white matter data, grey matter data) who underwent an MRI scan, and consisted of pre-processed measures of the integrity of major white-matter tracts (N=8839) and volume of grey matter (N=9931) in key brain regions ( Miller et al., 2016). Our preregistered analyses entailed two steps: first modelling cognitive data; second including neuroimaging predictors of cognitive abilities. More specifically, our pre-registered analyses specified the use of latent growth models ( Bauer, 2007) to model the mean and slope of age-related changes in fluid intelligence, in order to address the following questions:

1.
What is the magnitude of change in fluid intelligence across occasions, as captured by the slope of fluid intelligence?
2.
Is there significant variance associated with this slope (i.e. do people differ in their rate of change)?
3.
Is the slope linear or non-linear (i.e. does a quadratic latent growth factor capture meaningful variance above a linear factor)?
4.
Does the rate of decline (slope) depend on the level (intercept) (i.e. is age-related decline determined by current cognitive status)?
5.
Is there evidence for subgroups (growth mixture models) (i.e. do we find evidence of subgroups of individuals, differing in their baseline score or rate of change)?

On the basis of prior studies, we predicted a decline in fluid intelligence across testing occasions. We expected that the decline in fluid intelligence would be more pronounced in older individuals ( Kievit et al., 2014), and that there would be significant individual differences in the rate of change ( Ghisletta et al., 2012). We had no strong expectations about slope-intercept covariance or the presence of subgroups.

Our second set of hypotheses concerned the neural determinants of individual differences in the slope and intercept of fluid intelligence. To examine this question, we preregistered a series of analyses using Multiple Indicator Multiple Causes (MIMIC) models ( Jöreskog & Goldberger, 1975; Kievit et al., 2012) to relate the mean and slope estimates for fluid intelligence to the various brain measures, and asked:

6.
What neural properties determine the intercept and slope of fluid intelligence?
7.
Are the neural determinants of the mean (general ability) the same as those of the slope (rate of change)?
8.
Do multiple region-specific markers of neural health predict unique variance in cognitive level and slope, or does a single global marker suffice?

Based on prior work, we predicted that the mean and/or slope estimates from the latent growth models will depend in particular on complementary effects of frontal grey and white matter ( Kievit et al., 2014; Kievit et al., 2016). Moreover, we expected the slope and intercept to have similar, but non-identical multiple brain determinants, as the mechanisms that govern individual differences need not be identical to those governing within-subject change (cf. Kievit et al., 2013). We also pre-registered exploratory analyses relating possible sub-groups to factors like physical health, but given the insufficient evidence for sub-groups, we did not explore these relationships further.

Methods

Participants

The present study sample consisted of a subset of healthy middle to older-aged adults (age range at time of recruitment: 39–73 years) from the UK Biobank cohort (for more information see the Biobank website; Sudlow et al., 2015). Participants were recruited between 2006 and 2010 via the UK National Health Service. UK Biobank received ethical approval from the North West Multi-Centre Research Ethics Committee (11/NW/03820). Although a total of 502,655 participants took part in Biobank, we focus on 185,317 individuals who have data for at least one wave of fluid intelligence testing. Testing took place at 22 assessment centres across the UK with each participant completing lifestyle, demographic, health and mood questionnaires, cognitive assessments and physical measures (e.g. blood, saliva and urine samples). We here analysed fluid intelligence and neurological data downloaded in 2017. Fluid ability was measured up to three times for each participant, with intervals of approximately 2–4 years (M±SD t2-t1: 4.29±1.01 years; M±SD t3-t2: 2.56±0.84 years). There were 165,491, 20,042 and 9,167 participants at waves 1, 2, and 3, respectively (note that a subject could have their first assessment in the second wave). Despite sizeable attrition, the current dataset provides in principle sufficient power to detect any non-trivial effect(s) and enables sensitive model comparisons ( Hertzog et al., 2008). All analyses reported below can be reproduced or modified using scripts made available in the supplementary materials, namely Kievit_etal_biobank_dataprep.R (data preparation; Supplementary File 1); Kievit_etal_biobank_analysis.R (analyses and plots; Supplementary File 2); Kievitetal_GFGMM1.inp (growth mixture models in Mplus; Supplementary File 3). To acquire the raw data, one can register and apply through the central biobank portal.

Fluid ability measures

We here analysed the ‘fluid intelligence test’ included in the UK Biobank cognitive battery. The test is designed to measure “the capacity to solve problems that require logic and reasoning ability, independent of acquired knowledge” (for a complete overview of the 13 individual fluid intelligence items, please see the Biobank manual for the Fluid intelligence test). The test comprised thirteen logic and reasoning questions administered via a computer-touchscreen interface with a two-minute time limit for each question. The maximum score was 13 (one point for each correct response). Overall, the test items have a reported Cronbach alpha coefficient of 0.62 ( Hagenaars et al., 2016). No participants or observations were excluded from subsequent analyses. Raw data are shown for the fluid intelligence scores at T1 ( Figure 1, top), and a random subset of 100 individuals with 3 timepoints ( Figure 1, bottom).

Figure 1. — Bottom: A random subsample of raw fluid intelligence scores across testing occasions.

Participants who took part in all three waves (N=870) were slightly older, and had lightly higher baseline scores, than those who took part in only one or two waves (See Figure 2, top and bottom). By using all available data, under the assumption of Missing At Random (i.e. the attrition is associated with variables also included in the model) using Full Information Maximum likelihood should yield unbiased estimates (cf. Enders & Bandalos, 2001)

Figure 2. — Individuals who took part in all three waves were slightly older, and scored slightly higher on the fluid intelligence task.

Neural measures: grey and white matter components

In order to assess how individual differences in the microstructure of major white matter tracts contribute to fluid ability, we used a mean tract-based estimate of fractional anisotropy (FA) (see Miller et al., 2016, for more details on the Biobank imaging pipeline). We chose FA because previous studies of white matter in healthy aging have mostly used FA, and because FA has been shown to be a comparatively reliable metric ( Fox et al., 2012; for nuances regarding the interpretation of FA, see Jones et al., 2013 or Wandell, 2016). Note that Biobank also includes various other white matter metric of interest including diffusivity (MD), Neurite Orientation and Dispersion and others – These measures have specific strengths and weaknesses (see Cox et al., 2016, for a discussion of the merits of more novel metrics) that are beyond the remit of this manuscript. We started with 27 tracts ( Miller et al., 2016), and averaged bilateral hemispheric tracts, yielding mean FA estimates for a total of 15 tracts: acoustic radiation, anterior thalamic radiation, cingulate gyrus, parahippocampal part of cingulum, corticospinal tract, forceps major, forceps minor, inferior fronto-occipital fasciculus, inferior longitudinal fasciculus, middle cerebellar peduncle, medial lemniscus, posterior thalamic radiation, superior longitudinal fasciculus, superior thalamic radiation and uncinate fasciculus. Quality control was conducted by both automated identification of e.g. outlier slices and SNR, as well as manual inspection – For more detail, see Miller et al., 2016, online methods.

For grey matter, we selected grey matter regions based on the Parieto-Frontal Integration Theory P-FIT ( Jung & Haier, 2007). P-FIT postulates a network of cortical brain regions as the brain substrate of intelligence. The proposed network includes the dorsolateral prefrontal cortex, the inferior and superior parietal lobules, the anterior cingulate gyrus and selected areas within the temporal and occipital lobes. Recent studies have offered support for P-FIT ( Hoffman et al., 2017; Ryman et al., 2016). Following our pre-registered specification to include 10 GM regions, we selected the following 10 ROIs, bilaterally averaged: the frontal pole, superior frontal gyrus, middle frontal gyrus, inferior frontal gyrus (pars triangularis and pars opercularis subdivision), supramarginal gyrus (posterior and anterior), angular gyrus, frontal medial cortex and the cingulate gyrus.

Structural equation modelling (SEM)

Models were estimated using the Lavaan version 0.5-23.1097 ( Rosseel, 2012) package for SEM in R version 3.4.2 (Short summer) ( R Development Core Team, 2016). We used the full information maximum likelihood estimator (FIML) to use all available data and the robust maximum likelihood estimator with a Yuan-Bentler scaled test statistic (MLR) to account for violations of multivariate normality. We further assessed overall model fit via the Satorra-Bentler scaled test statistic along with the chi-square test, the root mean square error of approximation (RMSEA) with its confidence interval, the Comparative Fit Index (CFI), and the standardized root mean squared residuals (SRMR) ( Schermelleh-Engel et al., 2003). Using these indices, good fit was defined as: RMSEA (acceptable fit < 0.08, good fit < 0.05), CFI (acceptable fit 0.95 - 0.97, good fit > 0.97), SRMR (acceptable fit 0.05 - 0.10, good fit < 0.05).

Results

Fluid intelligence latent growth curve model

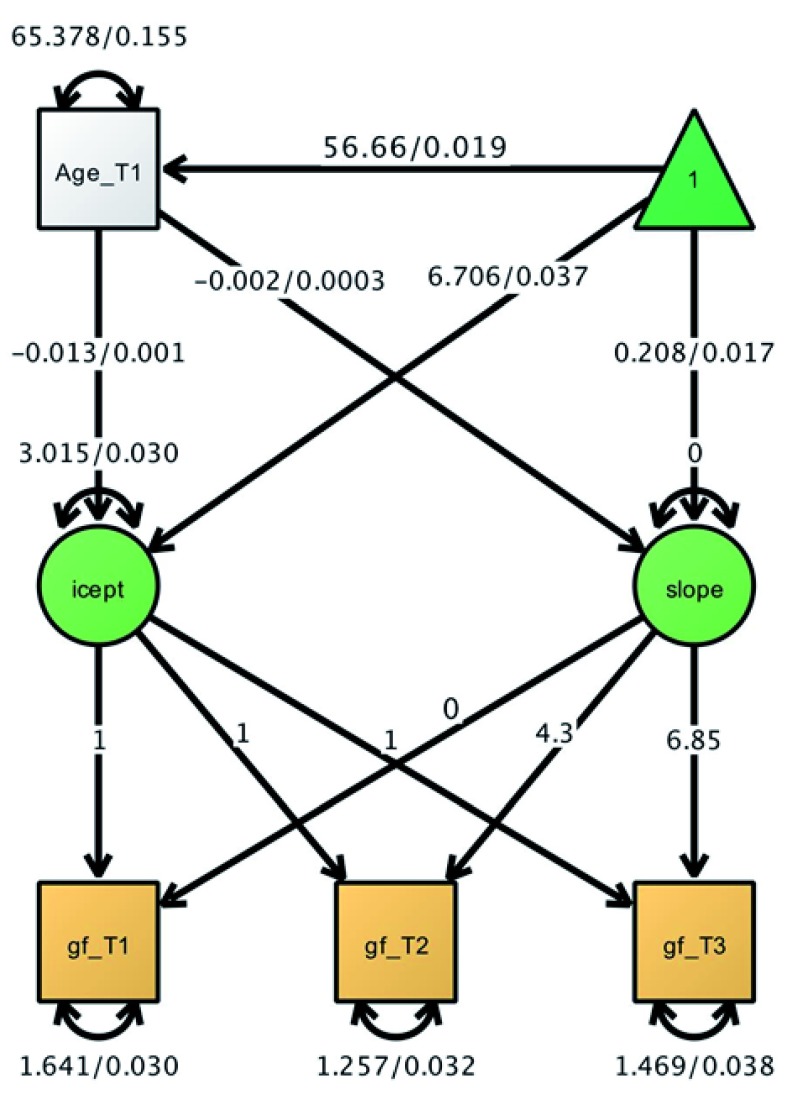
To test our pre-registered behavioural analyses, we used a latent growth curve model (LGCM), as shown in Figure 2. We fit the model to the full sample (N=185,317) with three time points, using FIML estimation to account for missingness. The slope factor loadings were constrained to the mean intervals between timepoint 1 and 2 (4.3) and 1 and 3 (6.85). This model fit the data well: χ ²(2) = 10.70, p = 0.005; RMSEA = 0.005 [0.002 - 0.008]; CFI = 0.999; SRMR = 0.006. Raw parameter estimates are shown in Figure 2. The mean score at T1 was 6.706, with a strong suggestion of individual differences (intercept variance estimate=2.955, SE=0.116, z=25.39, with a significant decrease in model fit when constraining the intercept variance: χ2(1), 549.6, p<0.0001). Higher age was associated with slightly lower intercepts (estimate= -0.013, SE= 0.001, z=-19.809, see also Figure 1A). However, this effect was very small (standardized path=-0.06), especially compared to previously reported effects (e.g. r=-0.7, Kievit et al., 2014). The pattern of results for the slopes was unexpected. First, the slope intercept (in this specification the mean change per measurement occasion) was strongly positive (estimate=0.208, SE=0.017, z=12.602), suggesting people, on average, improved over time. In other words, there was no evidence of our hypothesized within-subject age-related cognitive decline. There was a weak negative effect of age on slope (est=-0.002, SE=0.0001, z=-7.018) suggesting older individuals improved slightly less than younger adults. Most surprisingly, the slope variance was non-significant and negative (est=-0.001, SE=0.004) suggesting an improper solution. Suggesting an improper solution. A likelihood ratio test showed the slope variance could be constrained to 0 without adversely affecting model fit χ2(1), .63, p=.72). This indicates that there were no reliable indications of individual differences in change over time. Although non-significant slope variance has been reported previously for fluid intelligence over time ( Yuan et al., 2018), and improper solutions are common in random effects models ( Eager & Roy, 2017), it is nonetheless highly surprising in a sample of this magnitude. To achieve a proper solution we therefore constrained the slope variance and slope-intercept covariance to 0 (for this and future models), and refit the model, which yielded good model fit χ ²(4) = 10.88, p = 0.028; RMSEA = 0.003 [0.001 – 0.005]; CFI = 0.999; SRMR = 0.006) and showed negligible changes to other parameter estimates compared to the model without constraints (final parameters shown in Figure 2). In line with our preregistered analysis 1c, we also fit a quadratic growth model by including a quadratic growth factor with linear factor loadings squared, and imposed constraints in order to render the model identifiable (residual variances equality constrained across occasions, and linear slope variance constrained to 0 based on the linear model). However, this model too yielded an improper solution (a negative quadratic slope variance), so it cannot be interpreted with confidence.

To further examine the unexpected absence of a negative slope or reliable slope variance, we examined a set of alternative, exploratory, analytic approaches and model specifications. First, in the previous analysis we used full information maximum likelihood to analyze all individuals, despite considerable missing data. Comparable results were obtained when fitting the same models to reduced subsets of the data (e.g. only those with at least two (9,719), or all three measurements (N=870). We attempted to address two further plausible explanations for the poor quality of the longitudinal data. Firstly, we fit a second-order latent growth curve model, where fluid intelligence was measured by 13 observed indicators at every time point, imposing equal factor loadings across occasions. Such a model could appropriately weigh individual items based on the degree to which they share variance, possibly improving the purity of the fluid intelligence estimates. Although this model yielded a significant slope variance ¹, other aspects of model fit were poor, including factor loadings (mean standardized factor loading for T1=0.14), and model indices such as the CFI (0.133) and SRMR (0.150) suggested poor fit. As substantive patterns were similar to the occasion sum scores (i.e. positive slope intercept) we will continue with the first order growth model instead. In a final exploratory analysis, we reran the basic growth model with every individual item. This yielded qualitatively very similar results, with positive slopes for all items and non-significant slopes for all but one item (item 5). Closer inspection of item 5 suggested only a marginal, uncorrected benefit of freely estimating the slope variance χ2(1), 8.1, p=.004, combined with a non-significant slope intercept, and a BIC favouring the constrained slope model, together suggesting insufficient evidence to proceed with this post hoc item selection instead of the sumscore.

One likely explanation for the increase across testing occasions is the presence of practice effects (e.g. Salthouse, 2010). To address this explanation, we fit another exploratory model including an additional growth factor with factor loadings constrained to 0, 1 and 1 for the three time points. This so-called ‘boost’ factor (Hoffman et al., 2012) captures the hypothesis that test performance will show an improvement between the first and second testing occasions that is purely a practice effect. The inclusion of the boost factor rendered the slope intercept non-significant, which is compatible with the notion that the gains are most likely practice gains. However, like the quadratic model, such a more complex model is only identified by imposing a range of constraints (here including constraining the boost factor variance to 0). Moreover, despite these constraints this model yielded an improper solution and should thus be interpreted with caution. In a final exploratory analysis, we switched from an occasion-specific approach (T1, T2, T3) to an age-specific approach (scores at a given age). Although this approach yielded high proportions of missing data (as every individual will have missing data for most ages), it has been successfully applied to study cognitive aging ( Ghisletta & Lindenberger, 2003) and can allow for more convenient decomposition of retest effects. However, this approach too failed to converge. In summary, we conclude that a meaningful longitudinal signal does not exist in the repeated measures fluid intelligence task, as currently implemented in Biobank.

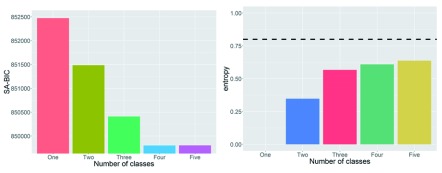
Finally, in line with our preregistered analyses (1e), we fit a series of growth mixture models to examine evidence for the presence of subgroups. For this analysis, we used Mplus (version 7.4 ( Muthén & Muthén, 2005). We fit 1 to 5 classes and examined the sample size adjusted BIC (SA-BIC) to decide on the best model. As shown in Figure 3, the SA-BIC was lowest for the four-group solution. However, further inspection of this solution suggested that evidence for subgroups was weak. Firstly, the ‘best’ solution of 4 subgroups had poor entropy (0.61, Figure 3 right panel), well below common guidelines of 0.8. This suggests subgroups were not well separated. More importantly, inspection of the slopes and intercepts showed that the four subgroups were effectively subdividing the normal distribution of the whole population into subgroups (i.e. two larger groups with an intercept/slope close to the population mean, two smaller groups with intercept/slopes closer to the upper and lower ‘edges’ of the population distribution). This pattern of results is common in growth mixture modelling ( Bauer, 2007, p. 768, Figure 3). Therefore, we conclude that there is no compelling evidence for latent subgroups with different longitudinal patterns. We now turn to our examination of the neural determinants of fluid intelligence.

Figure 3. — Plot shows beta/standard errors. gf = fluid intelligence. T=timepoint. icept= intercept.

White matter determinants of fluid intelligence

Next, in line with our second set of preregistered analyses, we fit a LGM-MIMIC model, where both the intercept and slope were regressed simultaneously on neural predictors. First, we focus on white matter. We started by testing our preregistered prediction whether the scores across tracts can be reduced to a single factor, which would suggest that a single global factor suffices (preregistration 2c), or whether individual ROIs are required. We observed that a model with a single white matter latent variable measured by all 15 tracts fit poorly (χ ²(90) = 8023.57, p < 0.001; RMSEA = 0.100 [0.099 - 0.101]; CFI = 0.957; SRMR = 0.061), replicating previous findings ( Kievit et al., 2016; Lövdén et al., 2013), and suggesting further analyses should include individual tracts. In all further models, age was included as a covariate of both intercept and slope, estimation was conducted on the full sample using FIML, and all tracts were allowed to co-vary with each other, as well as with age (not shown in figures for visual clarity).

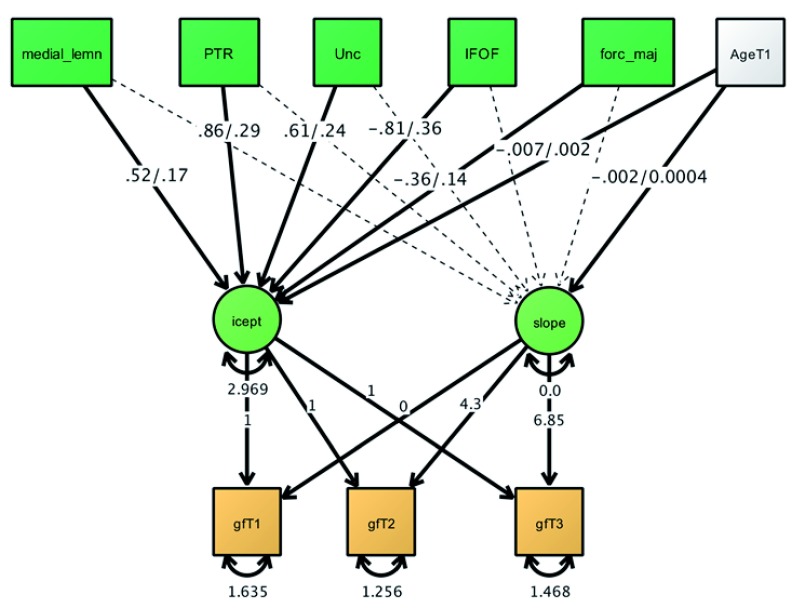
First, the full model LGM-MIMIC model fit the data well (χ ²(19) = 19.06, p = 0.453; RMSEA = 0.0001 [.000 - 0.002]; CFI = 1.000; SRMR = 0.004. In this model, the intercept of fluid ability was significantly associated with FA in five tracts, as shown in Figure 4. Jointly the tracts and age explained 2.1% of the variance in fluid intelligence, equivalent to a standardized effect of r=0.145, which is small by individual differences standards ( Gignac & Szodorai, 2016). Higher FA predicted higher fluid ability in all significant tracts apart from the forceps major and the inferior fronto-occipital fasciculus. Contrary to our expectation and previous findings, the forceps minor was not the strongest predictor of the fluid intelligence intercept ( Kievit et al., 2014, Figure 4). None of the white tracts predicted slope variance - A likelihood ratio test showed that the regression paths of the slope on the individual tracts could be constrained to 0 without adversely affecting model fit χ2(15), 17.97, p=.26. Next, we examined grey matter volume correlates of the fluid intelligence intercept.

Figure 4. — Dashed line indicates commonly accepted entropy criterion for good separation.

Grey matter determinants of fluid intelligence

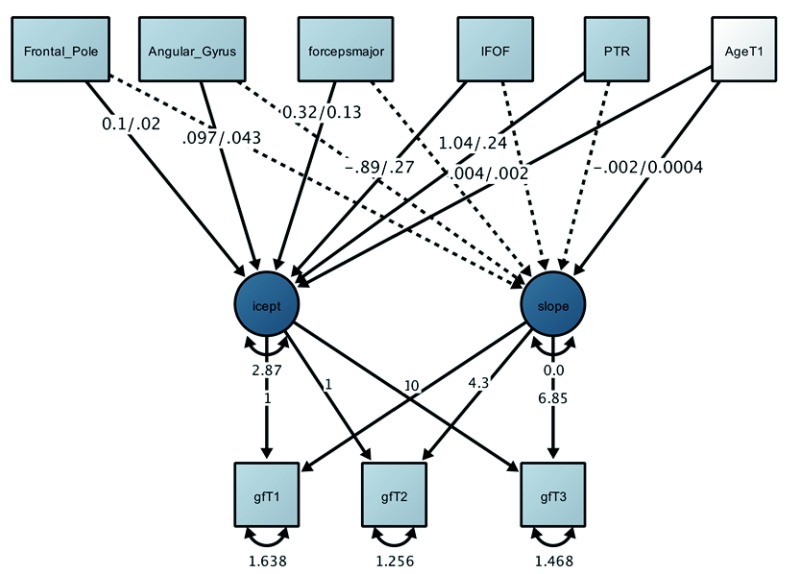
Next, we fit the same model using only estimates of grey matter volume. First, we again replicated the poor fit of a single factor model, suggesting that a global grey matter factor does not accurately reflect the population covariance structure (χ ²(35) = 7208.61, p < 0.001; RMSEA = 0.144 [0.141 - 0.146]; CFI = 0.783; SRMR = 0.071). Next, we estimated a joint LGM MIMIC model as above, which showed good model fit (χ ²(14) = 15.01, p = 0.377; RMSEA = 0.001 [0.0 - 0.002]; CFI = 1.000; SRMR = 0.003). The joint effect size of 4.5% was considerably larger than for white matter (albeit still modest). Inspection of key parameters (see Figure 5) showed that the strongest determinant of the fluid intelligence intercept was the frontal pole (r=.16), replicating our previous finding in a separate cohort ( Kievit et al., 2014, Figure 4). Two additional regions, namely the angular gyrus and the inferior frontal gyrus, explained further variance in the fluid intelligence intercept. No regions predicted slope variance - A likelihood ratio test showed the regression paths of the slope on the individual regions could be constrained to 0 without adversely affecting model fit χ2(10), 12.55, p=.24.

Figure 5. — Plot shows beta/standard errors. Non-significant tracts and tract covariances were estimated but are omitted for clarity. gF= fluid intelligence. icept= intercept. medial_lemn: medial lemniscus; PTR: posterior thalamic radiation; Unc: uncinate fasciculus; IFOF: inferior fronto-occipital fasciculus; forc_maj: forceps major.

Joint Grey matter and white matter determinants of fluid intelligence

Finally, we examined whether the grey and white matter provide complementary information about fluid intelligence, in line with our preregistered prediction. To do so, we refit the above MIMIC model, including only those white and grey matter regions that were nominally significant in the modality-specific analyses. Again, model fit was good (χ ²(14) = 16.11, p = 0.186; RMSEA = 0.001 [.0000000 - 0.003]; CFI = 1.000; SRMR = 0.004), with a joint effect size of 5.2% (intercept) variance explained. Inspection of the parameter estimates supported our a priori hypothesis regarding the intercept: grey matter volume and white matter microstructure made largely complementary contributions to individual differences in fluid intelligence. The two strongest paths were (again) grey matter in the frontal pole (r=0.16) and white matter in the posterior thalamic radiations (r=0.12). Together, these findings support our preregistered hypotheses that white matter and grey matter would provide partly complementary effects. As before, no regions or tracts predicted slope variance, χ2(10), 10.99, p=.35. As there was no meaningful slope variance, we could not address our preregistered expectation that neural determinants would be similar but distinct for intercept and slope. Contrary to our a priori hypothesis, frontal white matter was not the strongest determinant of individual differences in fluid intelligence. Instead, in the full model, the posterior thalamic radiations, a posterior tract linking the occipital lobe to the thalamus, proved most strongly predictive ( Figure 6).

Figure 6. — All paths shown are beta/standard errors. Non-significant tracts and tract covariances were estimated but are omitted for clarity.

Figure 7. — The strongest predictions are the frontal pole grey matter volume and the posterior thalamic radiations, both such that greater volume and greater Fractional Anisotropy (FA) were associated with better scores. All paths shown are beta/standard errors. Non-significant tracts and region covariances were estimated but are omitted for clarity.

Discussion

Summary of main findings

We conducted a preregistered examination of longitudinal changes in fluid intelligence in an N=185,317 subset of the Biobank cohort ( Sudlow et al., 2015). We observed a negative effect of age on the fluid intelligence intercept, consistent with other cross-sectional studies, but smaller than normally found (cf. Kievit et al., 2014). However, contrary to our expectations, our analysis of the rate of change of fluid intelligence revealed a positive rather than negative slope. In other words, rather than show decline, performance on the Biobank fluid intelligence task improved across test occasions, likely due to retest and practice effects. We also found a small negative effect of initial age on the rate of change, i.e. older people showed less improvement across time points. Convergence problems (likely due to the limited number of waves) meant that we were unable to infer whether the rates of change were best captured by a linear or quadratic model. No compelling evidence was observed for the existence of subgroups.

In a second set of analyses, we examined the neural determinants of individual differences in fluid intelligence. The absence of slope variance precluded meaningful modelling of individual differences in rate of change. In line with our expectations, we observed seven distinct and complementary contributions from individual white matter tracts. However, the effect sizes were small, and contrary to our expectations and previous work ( Kievit et al., 2014; Kievit et al., 2016), frontal white matter tracts were not among the strongest determinants of fluid abilities. The posterior thalamic radiations appeared as the strongest white matter predictor in both the white matter only model, as well as the combined grey matter/white matter model. The posterior thalamic radiations connect thalamic systems to both parietal and early visual systems. A tentative interpretation could be that parietal systems are often recruited in demanding tasks (e.g. Fedorenko et al., 2013). However, the small magnitude of the effect size, as well as the relative dearth of previous findings relating the PTR to fluid reasoning (although some weak effects have been reported, e.g. Navas-Sánchez et al., 2014), together suggest caution in interpreting this finding with confidence. Focusing on grey matter, we observed a strong, positive association between grey matter volume in the frontal pole and fluid intelligence, in line with our previous findings ( Kievit et al., 2014), and two additional smaller positive effects of the angular gyri and the inferior frontal gyrus, together explaining (alongside age) 4.5% of the intercept variance in fluid intelligence. The relatively strong association of frontal pole grey matter volume is in line with our previous work in a healthy aging cohort ( Kievit et al., 2014) as well as functional imaging findings (e.g., Kroger et al., 2002) and lesion studies (e.g. Gläscher et al., 2010). The relatively strong association of frontal pole grey matter volume is in line with our previous work in a healthy aging cohort ( Kievit et al., 2014) as well as functional imaging findings (e.g., Kroger et al., 2002) and lesion studies (e.g. Gläscher et al., 2010). Finally, a joint model of grey and white matter revealed that both neural measures made unique contributions to fluid intelligence, supporting previous findings ( Kievit et al., 2014) as well as our preregistered prediction (2c, pre-registration).

Quality of the fluid intelligence measure

A plausible explanation for both the disparity in the size of cross-sectional age effects on fluid intelligence intercept (e.g. r=-0.04 in Figure 1, versus r=-0.55 in comparable samples), as well as the absence of expected slope effects, most likely lies in the fluid intelligence task itself. First and foremost, not all items are representative of classic fluid intelligence items. For instance, item two asks ‘which number is the largest?’. This item might be best characterized as relying on crystallized knowledge, and would not usually be considered a component of fluid intelligence. It would perhaps be more appropriate in a dementia-screening task in elderly samples than in a fluid intelligence test administered in a population-representative sample. This interpretation is supported by a striking ceiling effect on this item (99.06% accuracy). Similar ceiling effects were observed for other items (94.9% for the first item). However, other items (e.g. item 3) rely on verbal analogies, which likely do require a measure of abstract reasoning abilities. Taken together, individual differences in the mean (intercept) scores likely reflect fluid abilities to some degree, but more weakly so than traditional, standardized tests. Previous work on the Biobank fluid intelligence task has characterized the nature of the test as ‘verbal-numerical reasoning’ ( Lyall et al., 2016), which is a more apt description than ‘fluid intelligence’, although arguably doesn’t cover items such as the example above. As for the longitudinal component, the relative memorability of certain items (such as the ‘largest number’ question) may help explain the absence of slope variance over time, as people are likely to provide the same answers on repeat testing occasions. Moreover, the self-paced nature of the task means that item 13 was only attempted by 4,350 out of 165,097 individuals at time point 1. Out of these participants, only 844 got the item correct, giving an overall accuracy rate of 0.5%. In short, the fluid intelligence task as currently implemented shows poor construct validity, and is vulnerable to ceiling and floor effects. Moreover, the self-paced nature (the total score reflects the number of correct items given within a 2-minute window) may exacerbate retest effects, given that remembering previous answers (right or wrong) and increased familiarity with the testing environment might lead to more items being attempted. Together, these properties may explain the absence of hypothesized longitudinal effects. Recently, Biobank has started acquiring a new fluid intelligence ‘matrix pattern completion’ task which more closely aligns with traditional psychometric tests of fluid intelligence. We expect that this novel subtest will show more robust age and neuroimaging effects.

Conclusion

Many studies, particularly in neuroimaging, are underpowered ( Button et al., 2013). The field’s effort to collect large, collaborative datasets is an important response to this scientific challenge. Biobank offers a uniquely rich, publicly-available dataset that has revolutionized the scope of large scale shared projects, and already led to numerous insights into the genetic, environmental and neural markers of healthy aging (e.g. Hagenaars et al., 2016; Miller et al., 2016; Muñoz et al., 2016). However, our current analyses of the Biobank cognitive data demonstrate that the size of the dataset cannot always overcome suboptimal data quality ( Kolossa & Kopp, 2018). Longitudinal measurements may be especially vulnerable to practical constraints in large cohorts (e.g. short administration time, ease of use of the test etc.). Further improvements in the quality of cognitive data and additional waves of longitudinal measures will likely allow for more conclusive answers about the neural determinants of age-related changes in fluid intelligence, and facilitate understanding of lifespan changes in cognitive function.

Data availability

Our analysis is based on data from the Biobank cohort, and as such cannot be attached in the raw form without violation contractual agreements. Our analyses can be reproduced (or improved) by the following three steps:

1) Create an account and enter a data access request through the Biobank portal, requesting the key variables in this manuscript (the fluid intelligence score, id 20016; the diffusion MRI tract averages for FA, id 134; and grey matter volume measures, id 110.

2) Run the script ‘Kievit_etal_biobank_dataprep.R’, provided in the supplementary materials ( Supplementary File 1). This will translate the biobank data object into an appropriately organized subset (‘Fulldat1.Rdata’ and ‘gfonly.dat’) ready for further processing.

3) Run the script Kievit_etal_biobank_analysis.R ( Supplementary File 2) on the data object (‘Fulldat1.R’) created using the ‘Kievit_etal_biobank_dataprep.R’ ( Supplementary File 1). This script will reproduce all analyses, as well as figures, reported in the above manuscript. The only exception is the growth mixture models – This can at present not be run in R. To this end, run the script Kievitetal_GFGMM1.inp ( Supplementary File 3) in Mplus, modifying the line ‘CLASSES = c (1);’ to vary the number of latent classes.

Notes

¹Note: To achieve stable model estimation convergence we had to switch the estimator from MLR to ML.

Funding Statement

This work was supported by the Wellcome Trust [107392]. This work was also conducted using the UK Biobank Resource under Application Number 23773. R.N.H. is funded by the Medical Research Council (SUAG/010 RG91365).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

[version 2; referees: 3 approved]

Supplementary material

Files allowing the replication of the presented analysis

Supplementary File 1 - Kievit_etal_biobank_dataprep.R

Click here for additional data file.^{(2.6KB, tgz)}

Supplementary File 2 – Kievit_etal_biobank_analysis.R

Click here for additional data file.^{(5.1KB, tgz)}

Supplementary File 3 – Kievitetal_GFGMM1.inp

Click here for additional data file.^{(463B, tgz)}

References

Bauer DJ: Observations on the Use of Growth Mixture Models in Psychological Research. Multivariate Behav Res. 2007;42(4):757–786. 10.1080/00273170701710338 [DOI] [Google Scholar]
Button KS, Ioannidis JP, Mokrysz C, et al. : Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci. 2013;14(5):365–76. 10.1038/nrn3475 [DOI] [PubMed] [Google Scholar]
Eager C, Roy J: Mixed Effects Models are Sometimes Terrible.2017. Reference Source [Google Scholar]
Enders CK, Bandalos DL: The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Struct Equ Modeling. 2001;8(3):430–457. 10.1207/S15328007SEM0803_5 [DOI] [Google Scholar]
Fedorenko E, Duncan J, Kanwisher N: Broad domain generality in focal regions of frontal and parietal cortex. Proc Natl Acad Sci U S A. 2013;110(41):16616–16621. 10.1073/pnas.1315235110 [DOI] [PMC free article] [PubMed] [Google Scholar]
Fox RJ, Sakaie K, Lee JC, et al. : A validation study of multicenter diffusion tensor imaging: reliability of fractional anisotropy and diffusivity values. AJNR Am J Neuroradiol. 2012;33(4):695–700. 10.3174/ajnr.A2844 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ghisletta P, Lindenberger U: Age-based structural dynamics between perceptual speed and knowledge in the Berlin Aging Study: direct evidence for ability dedifferentiation in old age. Psychol Aging. 2003;18(4):696–713. 10.1037/0882-7974.18.4.696 [DOI] [PubMed] [Google Scholar]
Ghisletta P, Rabbitt PM, Lunn M, et al. : Two thirds of the age-based changes in fluid and crystallized intelligence, perceptual speed, and memory in adulthood are shared. Intelligence. 2012;40(3):260–268. 10.1016/j.intell.2012.02.008 [DOI] [Google Scholar]
Gignac GE, Szodorai ET: Effect size guidelines for individual differences researchers. Pers Individ Dif. 2016;102:74–78. 10.1016/j.paid.2016.06.069 [DOI] [Google Scholar]
Gläscher J, Rudrauf D, Colom R, et al. : Distributed neural system for general intelligence revealed by lesion mapping. Proc Natl Acad Sci U S A. 2010;107(10):4705–4709. 10.1073/pnas.0910397107 [DOI] [PMC free article] [PubMed] [Google Scholar]
Gottfredson LS, Deary IJ: Intelligence Predicts Health and Longevity, but Why? Curr Dir Psychol Sci. 2004;13(1):1–4. 10.1111/j.0963-7214.2004.01301001.x [DOI] [Google Scholar]
Hagenaars SP, Harris SE, Davies G, et al. : Shared genetic aetiology between cognitive functions and physical and mental health in UK Biobank ( N=112 151) and 24 GWAS consortia. Mol Psychiatry. 2016;21(11):1624–1632. 10.1038/mp.2015.225 [DOI] [PMC free article] [PubMed] [Google Scholar]
Hartshorne JK, Germine LT: When does cognitive functioning peak? The asynchronous rise and fall of different cognitive abilities across the life span. Psychol Sci. 2015;26(4):433–443. 10.1177/0956797614567339 [DOI] [PMC free article] [PubMed] [Google Scholar]
Hertzog C, von Oertzen T, Ghisletta P, et al. : Evaluating the power of latent growth curve models to detect individual differences in change. Struct Equ Modeling. 2008;15(4):541–563. 10.1080/10705510802338983 [DOI] [Google Scholar]
Hoffman L, Hofer SM, Sliwinski MJ: On the confounds among retest gains and age-cohort differences in the estimation of within-person change in longitudinal studies: a simulation study. Psychol Aging. 2011;26(4):778–91. 10.1037/a0023910 [DOI] [PMC free article] [PubMed] [Google Scholar]
Hoffman P, Cox SR, Dykiert D, et al. : Brain grey and white matter predictors of verbal ability traits in older age: The Lothian Birth Cohort 1936. NeuroImage. 2017;156:394–402. 10.1016/j.neuroimage.2017.05.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
Jacobucci R, Kievit R, Brandmaier A: Variable Selection in Structural Equation Models with Regularized MIMIC Models. PsyArXiv. 2018. Reference Source [DOI] [PMC free article] [PubMed] [Google Scholar]
Jones DK, Knösche TR, Turner R: White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI. NeuroImage. 2013;73:239–254. 10.1016/j.neuroimage.2012.06.081 [DOI] [PubMed] [Google Scholar]
Jöreskog KG, Goldberger AS: Estimation of a Model with Multiple Indicators and Multiple Causes of a Single Latent Variable. J Am Stat Assoc. 1975;70(351a):631–639. 10.1080/01621459.1975.10482485 [DOI] [Google Scholar]
Jung RE, Haier RJ: The Parieto-Frontal Integration Theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci. 2007;30(2):135–87; discussion 154–87. 10.1017/S0140525X07001185 [DOI] [PubMed] [Google Scholar]
Kievit RA, Davis SW, Griffiths J, et al. : A watershed model of individual differences in fluid intelligence. Neuropsychologia. 2016;91:186–198. 10.1016/j.neuropsychologia.2016.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kievit RA, Davis SW, Mitchell DJ, et al. : Distinct aspects of frontal lobe structure mediate age-related differences in fluid intelligence and multitasking. Nat Commun. 2014;5: 5658. 10.1038/ncomms6658 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kievit RA, Frankenhuis WE, Waldorp LJ, et al. : Simpson's paradox in psychological science: a practical guide. Front Psychol. 2013;4:513. 10.3389/fpsyg.2013.00513 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kievit RA, van Rooijen H, Wicherts JM, et al. : Intelligence and the brain: A model-based approach. Cogn Neurosci. 2012;3(2):89–97. 10.1080/17588928.2011.628383 [DOI] [PubMed] [Google Scholar]
Kolossa A, Kopp B: Data quality over data quantity in computational cognitive neuroscience. NeuroImage. 2018;172:775–785. 10.1016/J.NEUROIMAGE.2018.01.005 [DOI] [PubMed] [Google Scholar]
Kroger JK, Sabb FW, Fales CL, et al. : Recruitment of anterior dorsolateral prefrontal cortex in human reasoning: a parametric study of relational complexity. Cereb Cortex. 2002;12(5):477–485. [DOI] [PubMed] [Google Scholar]
Lyall DM, Cullen B, Allerhand M, et al. : Cognitive Test Scores in UK Biobank: Data Reduction in 480,416 Participants and Longitudinal Stability in 20,346 Participants. PLoS One. 2016;11(4):e0154222. 10.1371/journal.pone.0154222 [DOI] [PMC free article] [PubMed] [Google Scholar]
Lövdén M, Laukka EJ, Rieckmann A, et al. : The dimensionality of between-person differences in white matter microstructure in old age. Hum Brain Mapp. 2013;34(6):1386–1398. 10.1002/hbm.21518 [DOI] [PMC free article] [PubMed] [Google Scholar]
Miller KL, Alfaro-Almagro F, Bangerter NK, et al. : Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat Neurosci. 2016;19(11):1523–1536. 10.1038/nn.4393 [DOI] [PMC free article] [PubMed] [Google Scholar]
Muñoz M, Pong-Wong R, Canela-Xandri O, et al. : Evaluating the contribution of genetics and familial shared environment to common disease using the UK Biobank. Nat Genet. 2016;48(9):980–3. 10.1038/ng.3618 [DOI] [PMC free article] [PubMed] [Google Scholar]
Muthén LK, Muthén BO: Mplus: Statistical analysis with latent variables: User’s guide.Los Angeles: Muthén & Muthén.2005. Reference Source [Google Scholar]
Navas-Sánchez FJ, Alemán-Gómez Y, Sánchez-Gonzalez J, et al. : White matter microstructure correlates of mathematical giftedness and intelligence quotient. Hum Brain Mapp. 2014;35(6):2619–31. 10.1002/hbm.22355 [DOI] [PMC free article] [PubMed] [Google Scholar]
Park DC, Lautenschlager G, Hedden T, et al. : Models of visuospatial and verbal memory across the adult life span. Psychol Aging. 2002;17(2):299–320. 10.1037/0882-7974.17.2.299 [DOI] [PubMed] [Google Scholar]
R Development Core Team: R: a language and environment for statistical computing.Vienna.2016. Reference Source [Google Scholar]
Ritchie SJ, Booth T, Valdés Hernández MD, et al. : Beyond a bigger brain: Multivariable structural brain imaging and intelligence. Intelligence. 2015;51:47–56. 10.1016/j.intell.2015.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
Rosseel Y: lavaan: An R Package for Structural Equation Modeling. J Stat Softw. 2012;48(2):1–36. 10.18637/jss.v048.i02 [DOI] [Google Scholar]
Ryman SG, Yeo RA, Witkiewitz K, et al. : Fronto-Parietal gray matter and white matter efficiency differentially predict intelligence in males and females. Hum Brain Mapp. 2016;37(11):4006–4016. 10.1002/hbm.23291 [DOI] [PMC free article] [PubMed] [Google Scholar]
Salthouse TA: Influence of age on practice effects in longitudinal neurocognitive change. Neuropsychology. 2010;24(5):563–72. 10.1037/a0019026 [DOI] [PMC free article] [PubMed] [Google Scholar]
Schaie KW: The course of adult intellectual development. Am Psychol. 1994;49(4):304–13. 10.1037/0003-066X.49.4.304 [DOI] [PubMed] [Google Scholar]
Schermelleh-Engel K, Moosbrugger H, Müller H: Evaluating the Fit of Structural Equation Models: Tests of Significance and Descriptive Goodness-of-Fit Measures. Methods of Psychological Research - Online. 2003;8(2):23–74. Reference Source [Google Scholar]
Sudlow C, Gallacher J, Allen N, et al. : UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015;12(3):e1001779. 10.1371/journal.pmed.1001779 [DOI] [PMC free article] [PubMed] [Google Scholar]
Stoel RD, Garre FG, Dolan C, et al. : On the likelihood ratio test in structural equation modeling when parameters are subject to boundary constraints. Psychol Methods. 2006;11(4):439–55. 10.1037/1082-989X.11.4.439 [DOI] [PubMed] [Google Scholar]
Tucker-Drob EM: Neurocognitive functions and everyday functions change together in old age. Neuropsychology. 2011;25(3):368–77. 10.1037/a0022348 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wandell BA: Clarifying Human White Matter. Annu Rev Neurosci. 2016;39:103–28. 10.1146/annurev-neuro-070815-013815 [DOI] [PubMed] [Google Scholar]
Yuan P, Voelkle MC, Raz N: Fluid intelligence and gross structural properties of the cerebral cortex in middle-aged and older adults: A multi-occasion longitudinal study. NeuroImage. 2018;172:21–30. 10.1016/j.neuroimage.2018.01.032 [DOI] [PMC free article] [PubMed] [Google Scholar]

Wellcome Open Res. 2018 Jun 29. doi: 10.21956/wellcomeopenres.15944.r33328

Referee response for version 2

Florian Schmiedek ¹

My earlier concerns and comments have been thoroughly addressed in this revised version. Changes made are all appropriate and explanations provided for not implementing some of the suggestions are clear and well comprehensible. No further queries from my side.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Wellcome Open Res. 2018 May 4. doi: 10.21956/wellcomeopenres.15497.r32843

Referee response for version 1

Florian Schmiedek ¹

This is a well-conducted set of preregistered analyses, addressing important research questions, and using an impressive longitudinal data set. While the chosen latent growth model generally is standard for analyzing questions pertaining average longitudinal change (and individual differences therein) with few measurement occasions, there are some aspects that should or could be done somewhat differently, or additionally, in my view.

1. I would refrain from attempts to model quadratic change with (at maximum) only three measurement occasions. As this was part of the pre-registration, it should be mentioned, but maybe together with a qualification that a quadratic change model is not generally identified with 3 time points and identification could only be achieved using constraints that were not specified a priori (e.g., constraining the linear slope variance to zero).

2. Similarly, I find the use of a “boost” factor problematic, as the implied assumption of retest effects only taking place between T1 and T2 is difficult to defend. Also, this model has the same identification problem as a quadratic model.

3. Power to detect individual differences in change may be larger if individual differences in the true timing of the measurement occasions would be taken into account in the models (instead of using the mean intervals). In an SEM framework, this is possible using Mplus and the TSCORES option. I would encourage trying out this modeling option and would consider it a minor deviation from the pre-registration, as it would keep with the general modeling strategy and just mean using all available information to get most precise and powerful parameter estimates.

4. In an exploratory manner, I would encourage to pursue the attempt to use measurement models for the fluid intelligence construct a bit more and reduce the set of items to those that “are representative of classic fluid intelligence items”. This may improve model fit and help model convergence, and may also increase power to detect variance in slopes. Based on a decent and time-invariant measurement model, latent change score models could also allow to model change from T1 to T2 and change from T2 to T3 separately (capturing potential quadratic change or differential retest effects). Related to this point, I would like to see a brief but complete description of all fluid intelligence items in the Methods section.

5. As the power to detect significant variance in slopes and the power to detect effects of certain moderator variables on the slope may differ, I do not think that it is precluded to test such moderation effects just because the variance in slopes turns out not to be significant. As the moderator effects pertain to pre-registered a-priori hypotheses, I would go ahead and test and report these effects (preferably using likelihood ratio tests based on model comparisons), even though the variance of slopes may not be significant.

6. Generally, the variance of the slope factor should not be evaluated with z-test, but also with likelihood ratio tests, using adjusted critical values (see Stoel et al., 2006 ¹). Implicitly, this is already done by reporting the chi2 values for models with and without the slope variance. I would fully replace the reported z and p values with the more appropriate LR test, however.

Minor points

The term “slope intercept” may be confusing. Maybe use “the regression intercept of a model with the slope factor as dependent variable” or some other explanation that helps to distinguish between “intercept” as growth factor and “intercept” as regression parameter in the MIMIC models.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

References

1. Stoel RD, Garre FG, Dolan C, van den Wittenboer G: On the likelihood ratio test in structural equation modeling when parameters are subject to boundary constraints. Psychol Methods.2006;11(4) : 10.1037/1082-989X.11.4.439 439-55 10.1037/1082-989X.11.4.439 [DOI] [PubMed] [Google Scholar]

Wellcome Open Res. 2018 May 25.

Rogier Kievit ¹

'This is a well-conducted set of preregistered analyses, addressing important research questions, and using an impressive longitudinal data set. While the chosen latent growth model generally is standard for analyzing questions pertaining average longitudinal change (and individual differences therein) with few measurement occasions, there are some aspects that should or could be done somewhat differently, or additionally, in my view.'

We thank the reviewer for their comments, which have served to strengthen the paper

We agree that we should have mentioned the necessity of constraints in the pre-registration. We had hoped to be able to model decline as a function of age rather than testing occasion which would have allowed more flexibility in this regard. We did mention this in passing in the original manuscript as follows, ‘and imposed constraints in order to render the model identifiable (residual variances equality constrained across occasions, and linear slope variance constrained to 0 based on the linear model).’ We now also include an explication of the need of constraints below in the boost factor

We agree that we should have spelled out the challenges with estimating more an additional growth factor with so few timepoints more clearly in the pre-registration, and have now explained these limitations in the revision. Conceptually, we find the boost factor intuitively plausible – The change between wave 1 and 2 would entail the familiarity with the setting, using the iPad, the time constraints etcetera. This would be much less strong between wave 2 and 3. This type of boost factor was included as a core retest mechanisms in a simulation based paper on modelling retest effects (Hoffman, L., Hofer, S. M., & Sliwinski, M. J, 2011) and was shown to have a less negative effect on the estimation on other model parameters than incremental practice effects.

This so-called ‘boost’ factor (Hoffman, Hofer, & Sliwinski, 2012) captures the hypothesis that test performance will show an improvement between the first and second testing occasions that is purely a practice effect. The inclusion of the boost factor rendered the slope intercept non-significant, which is compatible with the notion that the gains are most likely practice gains. However, like the quadratic model, such a more complex model is only identified by imposing a range of constraints (here including constraining the boost factor variance to 0). Moreover, despite these constraints this model yielded an improper solution and should thus be interpreted with caution.

We agree this is a principled and elegant manner to model these effects. However, despite increasing the EM iterations well beyond the Mplus default, this model did not converge. Nonetheless we agree it is the more principled choice so have now included it in the manuscript as follows:

Here we use the mean age interval between waves to guide the fixed factor loadings in the growth model. A more precise modelling approach is to use the individual ages at each timepoint. This is known as a ‘definition variable’ approach (Mehta & Neale), uses all the information present in the data in richer manner and can be implemented in either Mplus or OpenMx (but not yet Lavaan). However, in the present dataset this approach did not converge

In our previous manuscript we fit a full second order latent growth curve model which would allow individual items to contribute more, or less, to the latent factor. As reported this did not yield acceptable model fit nor meaningfully changed our findings. Moreover, we have now refit the models with each individual item, again yielding virtually identical results. In short we believe no meaningful signal can be extracted from these items without exhaustive data-driven subselection that may lead to overfitting.

In a final exploratory analysis, we reran the basic growth model with every individual item. This yielded qualitatively very similar results, with positive slopes for all items and non-significant slopes for all but one item (item 5). Closer inspection of item 5 suggested only a marginal, uncorrected benefit of freely estimating the slope variance χ ²(1), 8.1, p=.004, combined with a non-significant slope intercept, and a BIC favouring the constrained slope model, together suggesting insufficient evidence to proceed with this post hoc item selection instead of the sumscore.

Based on a decent and time-invariant measurement model, latent change score models could also allow to model change from T1 to T2 and change from T2 to T3 separately (capturing potential quadratic change or differential retest effects).

We agree in principle, but in practice these desiderata of the model fit and item properties seem beyond the data quality present in Biobank.

Related to this point, I would like to see a brief but complete description of all fluid intelligence items in the Methods section.

We included a link to the complete set of questionnaire items which is available online here:

https://biobank.ctsu.ox.ac.uk/crystal/docs/Fluidintelligence.pdf

We have modified the wording in the manuscript to be more explicit (as it currently only states ‘the manual’)

for a complete overview of the 13 individual fluid intelligence items, please see http://biobank.ctsu.ox.ac.uk/crystal/docs/Fluidintelligence.pdf

We agree that the significance of the slope in isolation needn’t be a guiding principle to guide the analysis of moderators. Note that all continuous predictors of slope variance in our models are still included even in the models where slope (residual) variance is constrained to 0 – in other words, all continuous neural moderators of slope were included, but proved non-significant. We now include an LRT for each relevant model, comparing one where all neural predictors of slope are freely estimated versus a model where they are constrained to 0 for white matter, grey matter and the combined model. In all case the constrained model is preferred.

None of the white tracts predicted slope variance - A likelihood ratio test showed that the regression paths of the slope on the individual tracts could be constrained to 0 without adversely affecting model fit χ ² (15), 17.97, p=.26.

No regions predicted slope variance - A likelihood ratio test showed the regression paths of the slope on the individual regions could be constrained to 0 without adversely affecting model fit χ ² (10), 12.55, p=.24.

As before, no regions or tracts predicted slope variance, χ ²(10), 10.99, p=.35.

We agree entirely. We reported the Wald test for reasons of greater familiarity to most readers, as well as slightly fewer issues of model convergence due to variance constraints, but on reflection we agree that the LR test is more appropriate and have updated this for all variance parameters.

Minor points

We agree ‘slope intercept’ can be confusing. We have clarified the first mention of this term in parentheses

First, the slope intercept (in this specification, the mean change per measurement occasion)

Wellcome Open Res. 2018 Apr 19. doi: 10.21956/wellcomeopenres.15497.r32845

Referee response for version 1

Sara Pudas ², Michael Rönnlund ¹

The study involves a pre-registered analysis, is hypothesis-driven, and seems to involve sound analyses of the data and the text is clear. Nevertheless, we have a couple of concerns in regard to the presentation and data analyses.

Introduction: The authors state that “Both cross-sectional and longitudinal studies have shown that advancing age is associated with a marked decrease in fluid intelligence starting in the third or fourth decade of life”, citing work by Hartshorne and Germine (2015) ¹ and Schaie (1994) ². However, longitudinal data in the latter article clearly indicate a higher age of onset of mean-level decline than this, for each of the Primary Mental Abilities (around age 60; see Figure 2), including Inductive reasoning, a core facet of fluid intelligence (narrowly defined). The study by Hartshorne and Germaine involved cross-sectional data. Thus, whereas cross-sectional data typically indicate decline in the third or fourth decade of life (or earlier, see Park et al., 2002 ³) actual decline at the mean level may appear later, at least as judged by the data in Schaie (1994). This is relevant to note as, from that perspective, quite a few participants in the UK biobank study (range 39-73 years) might be expected to be rather stationary in regard to mean-level fluid intelligence over a relatively short test-retest interval.

Results: Regarding attrition, did the participants who participated in 2 or 3 test waves differ from those who dropped out after the first occasion? Describing drop-out mechanisms with regards to age, gender, fluid intelligence at baseline, and potentially socio-economic factors (if such are available) may help to clarify why the average slope was positive.

Discussion: It would be informative if the authors could comment on the validity of their findings regarding gray and white matter predictors of level of fluid intelligence. Despite challenges with the task validity and psychometric properties, are the significant relationships that were observed plausible (albeit smaller in magnitude than expected)? For instance, is it reasonable that the posterior thalamic radiations had the strongest association with fluid intelligence (despite contradicting the authors own previous work)? Were the relative contributions of gray and white matter variables in line with previous literature?

The direction of the effect between two of the white matter tracts and fluid intelligence appears opposite to expectations (the forceps major and the inferior fronto-occipital fasciculus).

Minor comments:

Methods section: Please specify if the 27 white matter tracts were the total number of tracts available for this data set.

Methods section: please state whether the gray matter volumes were raw values or corrected for intracranial volume (which could have made sense given the aging-related original hypotheses)?

P. 8, the last sentence states that no regions explained significant variance in slope. But wasn’t slope variance constrained to be zero in this model?

We have read this submission. We believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

References

1. Hartshorne JK, Germine LT: When does cognitive functioning peak? The asynchronous rise and fall of different cognitive abilities across the life span. Psychol Sci.2015;26(4) : 10.1177/0956797614567339 433-43 10.1177/0956797614567339 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Schaie KW: The course of adult intellectual development. Am Psychol.1994;49(4) :304-13 [DOI] [PubMed] [Google Scholar]
3. Park DC, Lautenschlager G, Hedden T, Davidson NS, Smith AD, Smith PK: Models of visuospatial and verbal memory across the adult life span. Psychol Aging.2002;17(2) :299-320 [PubMed] [Google Scholar]

Wellcome Open Res. 2018 May 25.

Rogier Kievit ¹

We thank the reviewers for their comments, which have served to strengthen the paper

We agree that we oversimplified the state of knowledge, and did not use the optimal references to support our claim. However, it is also likely also the case that longitudinal data might underestimate within-subject decline to some degree due to retest or practice effects (e.g. Salthouse, T. A., Schroeder, D. H., & Ferrer, E. (2004), with Salthouse (2009) estimating decline to begin in the third or fourth decade. Regardless of the precise decade, we would suggest that one would not expect a slope increase or a non-significant slope variance in a sample of this age range. The rephrased section reads as follows:

Both cross-sectional (e.g. Hartshorne & Germine, 2015; Kievit et al., 2016) and longitudinal studies (e.g. Salthouse, 2009, Schaie, 1994; Ghisletta et al., 2012) have shown that advancing age is associated with a marked decrease in fluid intelligence performance. Although the precise starting point of decline is hard to estimate precisely due to cohort effects, selective attrition and enrolment and retest effects in longitudinal cohorts (e.g. Salthouse, Schroeder & Ferrer, 2004), estimates for the onset of decline in fluid intelligence range between the third (e.g. Salthouse, 2009; Park et al., 2002) and sixth decade of life (e.g. Schaie, 1994).

These participants differed slightly – those who participated in all three waves were about 6 months older on average, and had slightly higher fluid intelligence scores at T1 (see new plots in Figure 2). However, to the extent that these characteristics explain attrition (i.e. Missing At Random), our approach of full information maximum likelihood should adjust appropriately. This is confirmed by the highly similar results (non-significant slope variance, marginally positive slope) when we run the model only in those individuals who have data in all three waves. The conjunction of the results from the boost model, the task characteristics, the slight negative effect of age on slope and previous work on retest effects in longitudinal aging together strongly suggest the driving force behind the positive slope are small but significant retest effects due to increased familiarity with the task and setting, rather than a more substantively meaningful signal. We now include the below paragraphs as well as two new figures

Participants who took part in all three waves (N=870) were slightly older, and had lightly higher baseline scores, than those who took part in only one or two waves (See Figure 2A and 2B) – A common pattern of selective attrition. By using all available data, under the assumption of Missing At Random (i.e. the attrition is associated with variables also included in the model) using Full Information Maximum likelihood should yield unbiased estimates (cf. Enders & Bandalos, 2001).

The frontal pole grey matter finding is in line with previous findings from our lab as well as others – we have now clarified this as follows

The relatively strong association of frontal pole grey matter volume is in line with our previous work in a healthy aging cohort (Kievit et al. 2014) as well as functional imaging findings (e.g., Kroger et al., 2002) and lesion studies (e.g. Gläscher et al., 2010).

The absence of Forceps Minor as a strong predictor and the presence of PTR as a predictor are contrary to previous findings. We now discuss tentatively as follows:

The posterior thalamic radiations appeared as the strongest white matter predictor in both the white matter only model, as well as the combined grey matter/white matter model. The posterior thalamic radiations connect thalamic systems to both parietal and early visual systems. A tentative interpretation could be that parietal systems are often recruited in demanding tasks (e.g. Fedorenko et al, 2013). However, the small magnitude of the effect size, as well as the relative dearth of previous findings relating the PTR to fluid reasoning (although some weak effects have been reported, e.g. Navas‐Sánchez et al. 2014), together suggest caution in interpreting this finding with confidence.

The direction of the effect between two of the white matter tracts and fluid intelligence appears opposite to expectations (the forceps major and the inferior fronto-occipital fasciculus).

Indeed, this is (weakly) opposite to our and other previous findings. However, refitting the model with only each of these individual tracts (and age) removes this negative ‘effect’, so we suspect the weakly negative effects are a consequence of collinear predictors in a very large sample, rather than paths to be interpreted strongly.

Methods section: Please specify if the 27 white matter tracts were the total number of tracts available for this data set.

This was indeed the full number of tracts available – We have clarified this in the manuscript

‘We included all 27 white matter tracts in the Biobank (Miller et al., 2016),’

Methods section: please state whether the gray matter volumes were raw values or corrected for intracranial volume (which could have made sense given the aging-related original hypotheses)?

These were the raw values. Given various lines of evidence that suggest that larger overall brain volume is associated with intelligence (e.g. Gignac & Bates, 2017), we did not want to adjust in this manner (this is consistent with our previous approach, e.g. Kievit et al., 2014). Various lines of evidence suggest that total brain volume change may be a leading indicator of declines in cognitive performance (e.g. Grimm, K. J., An, Y., McArdle, J. J., Zonderman, A. B., & Resnick, S. M. (2012) which would suggest actual grey matter volume is a highly relevant measure in aging populations.

P. 8, the last sentence states that no regions explained significant variance in slope. But wasn’t slope variance constrained to be zero in this model?

Perhaps counterintuitively, constraining the slope variance effectively constrains the residual, or conditional, variance to 0, not the absolute variance– In other words, any predictors may still exert influence and be estimated as normal (although the standardized effect sizes will be artificially high). For instance, age significantly (but weakly) predicts the positive slope with identical parameter estimates regardless of the slope constraint (this is so in Mplus and Lavaan). An alternative, defensible approach would be to constrain all predictors of the slope to 0 whenever the slope variance is constrained. However, as this would gain a large number of degrees of freedom, thereby (arguably) artificially improving model fit based on purely data driven considerations, we chose against doing so.

Wellcome Open Res. 2018 Apr 19. doi: 10.21956/wellcomeopenres.15497.r32839

Referee response for version 1

Donald M Lyall ¹

This paper aimed to investigate the neural substrates of fluid intelligence, and its change across time, using participants with cognitive and brain magnetic resonance imaging (MRI) data in UK Biobank. The paper is thorough and well-written, and validly attempts to progress our understanding of this area of research. The authors found separate grey and white matter contributions to mean cognitive scores, however a major limitation related to the ‘fluid reasoning’ task itself, and its construct validity.

Is the work clearly and accurately presented and does it cite the current literature?

Yes.

Minor suggestions

You may be interested in our 2016 PLOS ONE paper ¹ where we highlighted many of the same issues discussed here with the fluid reasoning task, although at that point not including any of the participants who had completed it at MRI. We suggest an alternative title for the task – ‘verbal-numerical reasoning’ (which you may or may not agree with).

See Cox et al. ² where in n=3,513 UK Biobank participants it is suggested that 1) five specific white matter tracts are perhaps better off not included in a single FA factor - namely middle cerebellar peduncle, bilateral medial lemniscus and parahippocampal cingulum - because these had low factor loadings, 2) additional tract integrity metrics (e.g. NODDI; MD) could be informative beyond FA, and 3) there were some left vs. right hemispheric differences in FA with age, contrasting with here where values were averaged across left and right hemispheres.

Regarding the line: “We started with 27 tracts (Miller et al., 2016), and averaged bilateral hemispheric tracts, yielding mean FA estimates for a total of 15 tracts”, please elaborate on why you took this approach, vs. including more tracts.
Is the study design appropriate and is the work technically sound?

Yes.

Minor suggestions

In the section regarding white/grey-matter contributions to fluid intelligence, have you considered looking specifically at contributions to scores in participants performing it for the first time at MRI?

Did you consider people who may have developed neurological/neurodegenerative conditions across waves?

Please give more details on image quality control procedures – e.g. whether you performed anything beyond what UK Biobank have done centrally, and detail slightly more what UK Biobank have done.
Are sufficient details of methods and analysis provided to allow replication by others?

Yes. Although it is worth noting that the UK Biobank is such that firstly the number of participant scans is increasing in batches (see http://www.fmrib.ox.ac.uk/ukbiobank/), and secondly that there are sometimes participant withdrawals from the sample – so researchers who downloaded data tomorrow and ran the script might not find precisely the same results.
If applicable, is the statistical analysis and its interpretation appropriate?

Yes.

Minor suggestions

The authors refer to the ‘fluid intelligence’ task including some ‘crystal-type’ items (e.g. ‘which number is the largest’). Have you considered dropping these items from the total score? Scores on the individual items are available.
Are all the source data underlying the results available to ensure full reproducibility?

Yes. Data application must be approved and sought by researchers from UK Biobank ( http://www.ukbiobank.ac.uk/). The authors note this, and provide good directives regarding procuring the relevant data. Scripts and notes are provided.
Are the conclusions drawn adequately supported by the results?

Yes. I agree that a key limitation is the ‘poor construct validity’ of the fluid intelligence measure.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

References

1. Lyall D, Cullen B, Allerhand M, Smith D, Mackay D, Evans J, Anderson J, Fawns-Ritchie C, McIntosh A, Deary I, Pell J: Cognitive Test Scores in UK Biobank: Data Reduction in 480,416 Participants and Longitudinal Stability in 20,346 Participants. PLOS ONE.2016;11(4) : 10.1371/journal.pone.0154222 10.1371/journal.pone.0154222 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Cox S, Ritchie S, Tucker-Drob E, Liewald D, Hagenaars S, Davies G, Wardlaw J, Gale C, Bastin M, Deary I: Ageing and brain white matter structure in 3,513 UK Biobank participants. Nature Communications.2016;7: 10.1038/ncomms13629 10.1038/ncomms13629 [DOI] [PMC free article] [PubMed] [Google Scholar]

Wellcome Open Res. 2018 May 25.

Rogier Kievit ¹

1. You may be interested in our 2016 PLOS ONE paper ¹ where we highlighted many of the same issues discussed here with the fluid reasoning task, although at that point not including any of the participants who had completed it at MRI. We suggest an alternative title for the task – ‘verbal-numerical reasoning’ (which you may or may not agree with).

We agree this is a highly pertinent paper and now refer to it more explicitly. Although verbal-numerical reasoning is closer to the nature of the task, in our view, certain items do not require any reasoning at all (e.g. ‘which is the largest number’), so although closer it doesn’t cover all items. To avoid confusion we therefore maintained the Biobank nomenclature.

Previous work on the Biobank fluid intelligence task has characterized the nature of the test as ‘verbal-numerical reasoning’ (Lyall et al., 2016), which is a more apt description than ‘fluid intelligence’, although arguably doesn’t cover items such as the example above.

See Cox et al. ² where in n=3,513 UK Biobank participants it is suggested that 1) five specific white matter tracts are perhaps better off not included in a single FA factor - namely middle cerebellar peduncle, bilateral medial lemniscus and parahippocampal cingulum - because these had low factor loadings, 2) additional tract integrity metrics (e.g. NODDI; MD) could be informative beyond FA, and 3) there were some left vs. right hemispheric differences in FA with age, contrasting with here where values were averaged across left and right hemispheres.

1) In our view the global factor is a particular hypothesis, namely whether white matter integrity can be adequately captured by a single factor – In that sense, removing tracts would be a suboptimal way to answer that question. Of course if the purpose is to capture a large amount of the variance across tracts in a single summary measure then something like a PCA (e.g. Penke et al., 2012) would be appropriate, but here we wanted to specifically test whether a single factor could adequately summarize the tract covariance, and found it did not (note that one could argue the model fit of especially other metrics such as MD in the above paper below common cut offs, so even with these tracts removed one could argue there is evidence of specificity beyond the global factor).

2) We agree these metrics may be of interest for future approaches, and mention these other metrics more explicitly as possibilities in the discussion. As FA aligns with our previous cohorts (and other analyses) that inspired our pre-registered hypotheses we stuck with FA for the actual analyses. We clarify as follows

Note that Biobank also includes various other white matter metrics of interest including diffusivity (MD), Neurite Orientation and Dispersion and others – These measures have specific strengths and weaknesses (see Cox et al., 2016, for a discussion of the merits of more novel metrics) that are beyond the remit of this manuscript.

3) Regarding the line: “We started with 27 tracts (Miller et al., 2016), and averaged bilateral hemispheric tracts, yielding mean FA estimates for a total of 15 tracts”, please elaborate on why you took this approach, vs. including more tracts.

27 tracts are all the tracts in Biobank. We agree our phrasing was imprecise and could be read as suggesting a sub selection of even more tracts than 27, so we have adjusted our phrasing accordingly (another reviewer had the same query). We had no specific hypotheses regarding lateralization, and two pragmatic considerations in favour of bilateral averaging. First, inclusion of the individual tracts considerably increases the size of the covariance matrix, which can complicate estimation. Second, simultaneous inclusion of highly collinear predictors in e.g. a MIMIC model can lead to estimation problems. Moreover, in the case of highly collinear predictors, this can artificially increase the difference between the predictors (with one tract highly significant, the other non-significant) merely because they have very similar predictions.

In the section regarding white/grey-matter contributions to fluid intelligence, have you considered looking specifically at contributions to scores in participants performing it for the first time at MRI?

The prediction of the intercept score for each individual will be extremely similar to the current model which predicts fluid intelligence score intercepts.

Did you consider people who may have developed neurological/neurodegenerative conditions across waves?

We did not consider this – to the extent that a subset of participants in a cohort of this magnitude will inevitably display pre-clinical symptoms we consider that part a natural variation in a large sample and should therefore be captured. Moreover, our attempt at fitting a growth mixture model did not yield a clearly identifiable subgroup of individuals with relative rapidly decline, above and beyond what would be expected as a function of a normal population distribution of slopes.

Please give more details on image quality control procedures – e.g. whether you performed anything beyond what UK Biobank have done centrally, and detail slightly more what UK Biobank have done.

We have expanded this section as follows:

We started with 27 tracts averages as generated by Biobank

and

Quality control was conducted by both automated identification of e.g. outlier slices and SNR, as well as manual inspection – For more detail, see Miller et al. 2016, online methods.

The authors refer to the ‘fluid intelligence’ task including some ‘crystal-type’ items (e.g. ‘which number is the largest’). Have you considered dropping these items from the total score? Scores on the individual items are available.

We have now included the below

In a final exploratory analysis, we reran the basic growth model with every individual item. This yielded qualitatively very similar results, with positive (but largely non-significant) slopes for all items and non-significant slope variances for all but one item (item 5). Closer inspection of item 5 suggested only a marginal, uncorrected benefit of freely estimating the slope variance χ ²(1), 8.1, p=.004, combined with a non-significant slope intercept, and a BIC favouring the constrained-to-0 slope model, together suggesting insufficient evidence to proceed with this post hoc item selection instead of the sumscore.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file.^{(2.6KB, tgz)}

Click here for additional data file.^{(5.1KB, tgz)}

Click here for additional data file.^{(463B, tgz)}

Data Availability Statement

[ref-1] Bauer DJ: Observations on the Use of Growth Mixture Models in Psychological Research. Multivariate Behav Res. 2007;42(4):757–786. 10.1080/00273170701710338 [DOI] [Google Scholar]

[ref-2] Button KS, Ioannidis JP, Mokrysz C, et al. : Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci. 2013;14(5):365–76. 10.1038/nrn3475 [DOI] [PubMed] [Google Scholar]

[ref-3] Eager C, Roy J: Mixed Effects Models are Sometimes Terrible.2017. Reference Source [Google Scholar]

[ref-4] Enders CK, Bandalos DL: The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Struct Equ Modeling. 2001;8(3):430–457. 10.1207/S15328007SEM0803_5 [DOI] [Google Scholar]

[ref-5] Fedorenko E, Duncan J, Kanwisher N: Broad domain generality in focal regions of frontal and parietal cortex. Proc Natl Acad Sci U S A. 2013;110(41):16616–16621. 10.1073/pnas.1315235110 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-6] Fox RJ, Sakaie K, Lee JC, et al. : A validation study of multicenter diffusion tensor imaging: reliability of fractional anisotropy and diffusivity values. AJNR Am J Neuroradiol. 2012;33(4):695–700. 10.3174/ajnr.A2844 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-7] Ghisletta P, Lindenberger U: Age-based structural dynamics between perceptual speed and knowledge in the Berlin Aging Study: direct evidence for ability dedifferentiation in old age. Psychol Aging. 2003;18(4):696–713. 10.1037/0882-7974.18.4.696 [DOI] [PubMed] [Google Scholar]

[ref-8] Ghisletta P, Rabbitt PM, Lunn M, et al. : Two thirds of the age-based changes in fluid and crystallized intelligence, perceptual speed, and memory in adulthood are shared. Intelligence. 2012;40(3):260–268. 10.1016/j.intell.2012.02.008 [DOI] [Google Scholar]

[ref-9] Gignac GE, Szodorai ET: Effect size guidelines for individual differences researchers. Pers Individ Dif. 2016;102:74–78. 10.1016/j.paid.2016.06.069 [DOI] [Google Scholar]

[ref-10] Gläscher J, Rudrauf D, Colom R, et al. : Distributed neural system for general intelligence revealed by lesion mapping. Proc Natl Acad Sci U S A. 2010;107(10):4705–4709. 10.1073/pnas.0910397107 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-11] Gottfredson LS, Deary IJ: Intelligence Predicts Health and Longevity, but Why? Curr Dir Psychol Sci. 2004;13(1):1–4. 10.1111/j.0963-7214.2004.01301001.x [DOI] [Google Scholar]

[ref-12] Hagenaars SP, Harris SE, Davies G, et al. : Shared genetic aetiology between cognitive functions and physical and mental health in UK Biobank ( N=112 151) and 24 GWAS consortia. Mol Psychiatry. 2016;21(11):1624–1632. 10.1038/mp.2015.225 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-13] Hartshorne JK, Germine LT: When does cognitive functioning peak? The asynchronous rise and fall of different cognitive abilities across the life span. Psychol Sci. 2015;26(4):433–443. 10.1177/0956797614567339 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-14] Hertzog C, von Oertzen T, Ghisletta P, et al. : Evaluating the power of latent growth curve models to detect individual differences in change. Struct Equ Modeling. 2008;15(4):541–563. 10.1080/10705510802338983 [DOI] [Google Scholar]

[ref-15] Hoffman L, Hofer SM, Sliwinski MJ: On the confounds among retest gains and age-cohort differences in the estimation of within-person change in longitudinal studies: a simulation study. Psychol Aging. 2011;26(4):778–91. 10.1037/a0023910 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-16] Hoffman P, Cox SR, Dykiert D, et al. : Brain grey and white matter predictors of verbal ability traits in older age: The Lothian Birth Cohort 1936. NeuroImage. 2017;156:394–402. 10.1016/j.neuroimage.2017.05.052 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-17] Jacobucci R, Kievit R, Brandmaier A: Variable Selection in Structural Equation Models with Regularized MIMIC Models. PsyArXiv. 2018. Reference Source [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-18] Jones DK, Knösche TR, Turner R: White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI. NeuroImage. 2013;73:239–254. 10.1016/j.neuroimage.2012.06.081 [DOI] [PubMed] [Google Scholar]

[ref-19] Jöreskog KG, Goldberger AS: Estimation of a Model with Multiple Indicators and Multiple Causes of a Single Latent Variable. J Am Stat Assoc. 1975;70(351a):631–639. 10.1080/01621459.1975.10482485 [DOI] [Google Scholar]

[ref-20] Jung RE, Haier RJ: The Parieto-Frontal Integration Theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci. 2007;30(2):135–87; discussion 154–87. 10.1017/S0140525X07001185 [DOI] [PubMed] [Google Scholar]

[ref-21] Kievit RA, Davis SW, Griffiths J, et al. : A watershed model of individual differences in fluid intelligence. Neuropsychologia. 2016;91:186–198. 10.1016/j.neuropsychologia.2016.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-22] Kievit RA, Davis SW, Mitchell DJ, et al. : Distinct aspects of frontal lobe structure mediate age-related differences in fluid intelligence and multitasking. Nat Commun. 2014;5: 5658. 10.1038/ncomms6658 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-23] Kievit RA, Frankenhuis WE, Waldorp LJ, et al. : Simpson's paradox in psychological science: a practical guide. Front Psychol. 2013;4:513. 10.3389/fpsyg.2013.00513 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-24] Kievit RA, van Rooijen H, Wicherts JM, et al. : Intelligence and the brain: A model-based approach. Cogn Neurosci. 2012;3(2):89–97. 10.1080/17588928.2011.628383 [DOI] [PubMed] [Google Scholar]

[ref-25] Kolossa A, Kopp B: Data quality over data quantity in computational cognitive neuroscience. NeuroImage. 2018;172:775–785. 10.1016/J.NEUROIMAGE.2018.01.005 [DOI] [PubMed] [Google Scholar]

[ref-26] Kroger JK, Sabb FW, Fales CL, et al. : Recruitment of anterior dorsolateral prefrontal cortex in human reasoning: a parametric study of relational complexity. Cereb Cortex. 2002;12(5):477–485. [DOI] [PubMed] [Google Scholar]

[ref-27] Lyall DM, Cullen B, Allerhand M, et al. : Cognitive Test Scores in UK Biobank: Data Reduction in 480,416 Participants and Longitudinal Stability in 20,346 Participants. PLoS One. 2016;11(4):e0154222. 10.1371/journal.pone.0154222 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-28] Lövdén M, Laukka EJ, Rieckmann A, et al. : The dimensionality of between-person differences in white matter microstructure in old age. Hum Brain Mapp. 2013;34(6):1386–1398. 10.1002/hbm.21518 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-29] Miller KL, Alfaro-Almagro F, Bangerter NK, et al. : Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat Neurosci. 2016;19(11):1523–1536. 10.1038/nn.4393 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-30] Muñoz M, Pong-Wong R, Canela-Xandri O, et al. : Evaluating the contribution of genetics and familial shared environment to common disease using the UK Biobank. Nat Genet. 2016;48(9):980–3. 10.1038/ng.3618 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-31] Muthén LK, Muthén BO: Mplus: Statistical analysis with latent variables: User’s guide.Los Angeles: Muthén & Muthén.2005. Reference Source [Google Scholar]

[ref-32] Navas-Sánchez FJ, Alemán-Gómez Y, Sánchez-Gonzalez J, et al. : White matter microstructure correlates of mathematical giftedness and intelligence quotient. Hum Brain Mapp. 2014;35(6):2619–31. 10.1002/hbm.22355 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-33] Park DC, Lautenschlager G, Hedden T, et al. : Models of visuospatial and verbal memory across the adult life span. Psychol Aging. 2002;17(2):299–320. 10.1037/0882-7974.17.2.299 [DOI] [PubMed] [Google Scholar]

[ref-34] R Development Core Team: R: a language and environment for statistical computing.Vienna.2016. Reference Source [Google Scholar]

[ref-35] Ritchie SJ, Booth T, Valdés Hernández MD, et al. : Beyond a bigger brain: Multivariable structural brain imaging and intelligence. Intelligence. 2015;51:47–56. 10.1016/j.intell.2015.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-36] Rosseel Y: lavaan: An R Package for Structural Equation Modeling. J Stat Softw. 2012;48(2):1–36. 10.18637/jss.v048.i02 [DOI] [Google Scholar]

[ref-37] Ryman SG, Yeo RA, Witkiewitz K, et al. : Fronto-Parietal gray matter and white matter efficiency differentially predict intelligence in males and females. Hum Brain Mapp. 2016;37(11):4006–4016. 10.1002/hbm.23291 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-38] Salthouse TA: Influence of age on practice effects in longitudinal neurocognitive change. Neuropsychology. 2010;24(5):563–72. 10.1037/a0019026 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-39] Schaie KW: The course of adult intellectual development. Am Psychol. 1994;49(4):304–13. 10.1037/0003-066X.49.4.304 [DOI] [PubMed] [Google Scholar]

[ref-40] Schermelleh-Engel K, Moosbrugger H, Müller H: Evaluating the Fit of Structural Equation Models: Tests of Significance and Descriptive Goodness-of-Fit Measures. Methods of Psychological Research - Online. 2003;8(2):23–74. Reference Source [Google Scholar]

[ref-41] Sudlow C, Gallacher J, Allen N, et al. : UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 2015;12(3):e1001779. 10.1371/journal.pmed.1001779 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-42] Stoel RD, Garre FG, Dolan C, et al. : On the likelihood ratio test in structural equation modeling when parameters are subject to boundary constraints. Psychol Methods. 2006;11(4):439–55. 10.1037/1082-989X.11.4.439 [DOI] [PubMed] [Google Scholar]

[ref-43] Tucker-Drob EM: Neurocognitive functions and everyday functions change together in old age. Neuropsychology. 2011;25(3):368–77. 10.1037/a0022348 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-44] Wandell BA: Clarifying Human White Matter. Annu Rev Neurosci. 2016;39:103–28. 10.1146/annurev-neuro-070815-013815 [DOI] [PubMed] [Google Scholar]

[ref-45] Yuan P, Voelkle MC, Raz N: Fluid intelligence and gross structural properties of the cerebral cortex in middle-aged and older adults: A multi-occasion longitudinal study. NeuroImage. 2018;172:21–30. 10.1016/j.neuroimage.2018.01.032 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

The neural determinants of age-related changes in fluid intelligence: a pre-registered, longitudinal analysis in UK Biobank

Rogier A Kievit

Delia Fuhrmann

Gesa Sophia Borgeest

Ivan L Simpson-Kent

Richard N A Henson

Roles

Version Changes

Revised. Amendments from Version 1

Abstract

Introduction

Methods

Participants

Fluid ability measures

Figure 1. Top: Linear relation between age and fluid intelligence sumscores at Time 1 (some jitter added for visibility).

Figure 2. Intelligence intercept scores (top) and age at first testing occasion (bottom) as a function of the number of measurement occasions (one, two or three).

Neural measures: grey and white matter components

Structural equation modelling (SEM)

Results

Fluid intelligence latent growth curve model

Figure 3. Latent growth curve model for fluid intelligence sum scores across 3 occasions.

White matter determinants of fluid intelligence

Figure 4. Sample size adjusted Bayesian Information Criterion (BIC), left, and entropy (right) for 1–5 classes in a growth mixture model approach.

Grey matter determinants of fluid intelligence

Figure 5. Multiple Indicator, Multiple Causes (MIMIC) model of fluid intelligence and white matter tracts showing 5 significant predictors, jointly predicting 1.3% of the variance in gf.

Joint Grey matter and white matter determinants of fluid intelligence

Figure 6. Multiple Indicator, Multiple Causes (MIMIC) Latent Growth (LGM) model for fluid intelligence and grey matter, jointly predicting 4.5% of the variance.

Figure 7. Final Multiple Indicator, Multiple Causes (MIMIC) Latent Growth (LGM) of fluid intelligence and neural determinants (grey and white matter).

Discussion

Summary of main findings

Quality of the fluid intelligence measure

Conclusion

Data availability

Notes

Funding Statement

Supplementary material

References

Referee response for version 2

Florian Schmiedek

Roles

Referee response for version 1

Florian Schmiedek

Roles

References

Rogier Kievit

Referee response for version 1

Sara Pudas

Michael Rönnlund

Roles

References

Rogier Kievit

Referee response for version 1

Donald M Lyall

Roles

References

Rogier Kievit

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases