Impact of degree truncation on the spread of a contagious process on networks

Abstract

Understanding how person-to-person contagious processes spread through a population requires accurate information on connections between population members. However, such connectivity data, when collected via interview, is often incomplete due to partial recall, respondent fatigue or study design, e.g., fixed choice designs (FCD) truncate out-degree by limiting the number of contacts each respondent can report. Past research has shown how FCD truncation affects network properties, but its implications for predicted speed and size of spreading processes remain largely unexplored. To study the impact of degree truncation on predictions of spreading process outcomes, we generated collections of synthetic networks containing specific properties (degree distribution, degree-assortativity, clustering), and also used empirical social network data from 75 villages in Karnataka, India. We simulated FCD using various truncation thresholds and ran a susceptible-infectious-recovered (SIR) process on each network. We found that spreading processes propagated on truncated networks resulted in slower and smaller epidemics, with a sudden decrease in prediction accuracy at a level of truncation that varied by network type. Our results have implications beyond FCD to truncation due to any limited sampling from a larger network. We conclude that knowledge of network structure is important for understanding the accuracy of predictions of process spread on degree truncated networks.

Introduction

Our understanding of how disease, knowledge and many other phenomena spread through a population can often be improved by investigating the population’s social or other contact structure, which can be naturally conceptualized as a network (Newman, 2002; Pastor-Satorras et al., 2015). In the case of human populations, this contact structure is often gathered through the use of questionnaires or surveys that typically ask respondents to name some of their contacts (Burt, 1984; Holland & Leinhardt, 1973). Generating population-level network structures from such data requires one of two possible approaches (Marsden, 2005). One approach is to delineate a population of interest, interview every person in the population, and collect unique identifiers for each respondent’s contacts; this allows the mapping of the true sociocentric network within that population. The alternative is to sample the population of interest and collect information about each respondent and his or her contacts; this results in a collection of egocentric networks from that population. Either approach enables the extraction of network features that can be used to fit a graph model, such as one of the models in the family of exponential random graphs (ERGMs) (Lusher et al., 2012), which allows the subsequent generation of network graphs consistent with the fitted features of the observed networks. The features that may be extracted from egocentric networks are however quite limited, making sociocentric networks the preferred design, resources allowing.

Both egocentric and sociocentric approaches can place a considerable burden on the respondent to recall numerous contacts and describe each in detail (McCarty et al., 2007). As a result, most sample survey questionnaires, in both egocentric and sociocentric designs, limit the contacts sought from a respondent, for example by the content, intimacy level, geographic location or time frame of the relationship elucidated (Campbell & Lee, 1991). A common method is to limit the number of contacts a respondent describes. This may be done directly, e.g. by asking “who are your five closest friends with whom you regularly socialize?” It may also be done indirectly, e.g. by asking “who are the friends with whom you socialize” but then only asking follow-up questions about the first five named (Burt, 1984; Kogovsek et al., 2010). A less-common variant of the second approach is for the interviewer to ask follow-up questions on a random subset of named contacts.

All of the above approaches potentially lead to truncation of the number of observed contacts. There is longstanding concern within the sociological literature that such truncation might affect estimates of network properties, including various forms of centrality (Holland & Leinhardt, 1973). However, there are countervailing resource and data quality benefits to avoiding respondent and interviewer fatigue via truncation (McCarty et al., 2007). While investigating the effect of degree truncation on observed structural properties of networks is an important problem, substantive interest often lies in making inferences about how a dynamical process on the network, such as the spread of an infectious disease, might be affected by truncation. Surprisingly, while both the impact of degree truncation on structural properties of networks and the impact of structural properties on the spread of a dynamic process through a networked population have been investigated, the joint implications of the two processes have not yet been elucidated.

To integrate key ideas from the two corpora, we review first the literature on the impact of truncating reported contacts on structural network properties, and second the literature on the impact of structural network properties on spread dynamics, to arrive at hypotheses regarding how truncation might change expected spreading process outcomes. While our work is motivated by epidemic disease processes, our analysis should be applicable to any process that can be modeled using compartmental models of a spreading process. We test the predictions of our hypotheses with simulation models using both synthetic, structured networks, and empirically observed networks.

Spreading processes on networks can be modeled on ensembles of networks (Jenness et al., 2015), using ERGMs or in a Bayesian framework (Goyal et al., 2014). However, using this modeling approach to explore the impact of truncation would conflate two processes: the truncation process and the network generation process. In order to focus on the former, we generate multiple realizations of synthetic full-network datasets with specific network properties, and additionally utilize a collection of empirically observed sociocentric networks that can be interpreted as multiple network realizations from a larger meta-population. As a result, we are able to isolate the effect of degree truncation and explore its impact on predictions of spreading processes on networks with very different structural properties.

The impact of contact truncation on structural network properties

Limiting the number of connections (“alters”) reported by a respondent (“ego”) is known as a fixed choice design (FCD) (Holland & Leinhardt, 1973). This limitation right-censors (imposes an upper bound on) an ego’s out-degree (the number of alters nominated by an ego). In sociocentric studies out-degree truncation may in turn reduce the in-degree of others, because some true incoming ties may end up unreported due to the constraints on out-degree. Sociocentric networks are commonly analyzed as undirected networks in which an edge (or tie) exists between two nodes, i and j, if either node reports it (not least to minimize the impact of underreporting of edges). In such an undirected network, each node’s total degree will consist of the union of all in-directed and out-directed nominations. FCD causes this total degree to be lowered in some circumstances, specifically when both i and j fail to report edge e_ij between them. This can occur only when k_i and k_j are both larger than k_fc, the FCD truncation value, and thus both potentially will not report e_ij. If k_i and k_j are both larger than k_fc, then whether e_ij is observed will depend on how FCD is carried out. FCD can be conducted in two ways, as outlined above. The more-common approach of focusing on the first k_fc or fewer names reported (“weighted truncation”) is likely to lead to bias towards stronger contacts, since stronger ties are likely to be more salient to a respondent. Here e_ij is more likely to be reported if it has higher weight. This approach should thus maximize the proportion of a respondent’s social interactions that is captured. The less-common approach of drawing a random subset of all named contacts (“unweighted truncation”) will provide a broader picture of the types of contacts a respondent has – notably increasing the chance of observing weak ties – at the cost of observing a smaller proportion of the respondent’s total social interaction. Here, whether e_ij is observed depends on chance.

A body of research has highlighted the substantial impact of sampling on network structural properties (Frank, 2011; Granovetter, 1976). For example, a recent study of nine different sampling methods found substantial variability in their ability to recover four structural network characteristics (Ebbes et al., 2015). FCD is known to impact several network characteristics, but its effects depend on the structure of the complete network graph (Kossinets, 2006); we consider next some key properties (we discuss these properties in more depth in Supplementary Content 1).

Degree distribution and assortativity

FCD’s impact on the network degree distribution is almost always to reduce its mean – insofar as edges are dropped – and variance – insofar as higher-degree nodes will be forced to underreport outgoing edges, flattening the distribution. This latter effect will be strongest in degree-assortative networks, where both ends of an edge may be unable to report the connection; in contrast, in degree-disassortative networks then edges that might be censored by the high-degree end are likely to be maintained by the low-degree end (Kossinets, 2006; Vázquez & Moreno, 2003). FCD may therefore significantly affect human contact networks, which are typically somewhat degree-assortative (Newman, 2003a). Degree-assortativity itself is not systematically affected by FCD (Kossinets, 2006; Lee et al., 2006), unless individuals preferentially report stronger connections, and ties between individuals of similar degree are more likely to be strong (Louch, 2000; Marsden, 1987), in which case FCD may raise degree-assortativity.

Clustering

Local clustering can be measured in at least two different ways: (i) Triadic clustering: the mean of local clustering coefficient C_i, where C_i, is the proportion of all the possible edges between neighbors of node i that are present (Watts & Strogatz, 1998); (ii) Focal clustering: the level of global triadic closure, that is the ratio of triangles to paths of length two (Newman, 2010). Clustering can also occur at higher levels of aggregation, for example in the presence of network communities where, loosely speaking, the density of edges within a set of nodes belonging to a community is higher than the average density of edges across the whole graph (Fortunato, 2010; Porter et al., 2009). Unweighted FCD truncation should reduce clustering at the triadic and community levels as it effectively results in random edge removal. When truncation is weighted, however, FCD might lead to an increase in clustering: if within-cluster edges are stronger than others, they are more likely to be preserved.

Path lengths

In removing ties, unweighted FCD will reduce the fractional size of the largest connected component (LCC), S_LCC, and will often increase the average path length between nodes of the LCC, ℓ_LCC, insofar as the increased length between some pairs of nodes due to loss of edges is not offset by reductions in length due to peripheral nodes being dropped altogether from the LCC. These results are seen asymptotically for random and power law graphs (Fernholz & Ramachandran, 2007), and via simulation of edge removal on empirical networks (Onnela et al., 2007a). If FCD is weighted, this second factor will be stronger, as peripherally (weakly) connected nodes are preferentially dropped from the LCC.

The impact of structural network properties on spreading processes

There is a burgeoning literature on the effect of various network properties on spreading process outcomes (Barrat et al., 2008; Newman, 2002; Pastor-Satorras et al., 2015). We consider three key spreading process quantities, focusing on two aspects of an epidemic: the early stage and the final state. To simplify our analysis, we follow the tradition in this literature and focus on models that assume degree infectivity, where an infectious individual can infect all their neighbors in just one time step, rather than unit infectivity, where they can only infect one of their neighbors per time step (Staples et al., 2015).

Quantity one is the basic reproduction number, R₀, the number of new incident cases (newly infected individuals) arising from each currently infected individual in a fully-susceptible population. R₀ is defined as a function of β, the product of the probability of infection per period and the number of contacts per period, and ν, the rate at which individuals recover. In a homogeneous mass-action (i.e. fully mixed) model for an infection where recovery leads to immunity, i.e. a Susceptible-Infected-Recovered (SIR) model, R₀ = β/ν, where R₀ ≥ 1 ensures a large epidemic with non-zero probability (Hethcote, 2000). Quantity two is the initial exponential (or faster) growth rate of an epidemic, r₀. This growth rate is conceptually equal to β in the first period, but thereafter is not well-defined analytically – even in homogenous models; it is typically measured empirically as the second moment of the epidemic curve in its initial growth phase (Vynnycky & White, 2010). Quantity three is the attack rate A, the proportion of the population ever infected.

Under assumptions of population homogeneity, relatively simple solutions can be found for key network properties; however these results rarely hold with non-trivial network structure (Keeling & Eames, 2005). We consider how key structural network properties impact the above spreading process quantities (we discuss these effects in more depth in Supplementary Content 1).

Degree distribution and assortativity

R₀ can be viewed as the average number of edges through which an individual infects their neighbors across the whole period of their infectiousness, if all their neighbors are susceptible. The probability of infection for each node can, conversely, be conceptualized in terms of their degree and their neighbors’ infection statuses. The more degree-heterogeneous a network is, the higher the likelihood of a large epidemic occurring, since R₀ is a function of the first and second moments of the degree distribution (Pastor-Satorras & Vespignani, 2002).

Similarly, higher degree-assortativity increases the expected epidemic size, since the probabilistic threshold for epidemic take-off has a lower-bound of the average degree of nearest neighbors (Boguñá et al., 2003). This is intuitive, since the number of one’s neighbors bounds the number of infections one can generate. Conditional on the number of nodes and edges in a network, degree-assortative networks will have a faster initial growth rate – occurring within a dense core of high-degree nodes – but a lower attack rate – due to having longer paths to peripheral, low-degree nodes where chains of infection are more likely to die out (Gupta et al., 1989).

Clustering

For any given degree distribution, triadic clustering reduces the average number of infections each infected person causes, R_e. This reduction is due to newly-infected individuals having fewer susceptible neighbors: the contact who infected you is likely also have had the opportunity to infect your other contacts (Keeling, 2005; Miller, 2009; Molina & Stone, 2012). This will slow the epidemic growth rate r₀ since newly infected individuals in clustered networks have fewer susceptible alters (Eames, 2008), and while not lowering R₀ clustering will increase the epidemic threshold in the same manner that a fall in R₀ would (Molina & Stone, 2012).

In many networks, for a given network density, increased clustering also leads to a smaller S_LCC, which necessarily reduces the maximum possible attack rate (Newman, 2003b), although this result appears to be a by-product of clustering leading to increased degree-assortativity (Miller, 2009). Overall, cliques alone appear to have marginal effects on epidemic dynamics. However, the processes which drive clique formation – such as homophily by nodal attributes or geographic proximity – mean that networks displaying clustering also often contain topological features such as degree-assortativity or heterogeneity that do significantly affect epidemic. As a result, processes on clustered networks can look very different from those on non-clustered ones (Badham & Stocker, 2010; Molina & Stone, 2012; Volz et al., 2011).

Broader community structure acts in much the same fashion as cliques, reducing r₀ due to limited capacity to pass infection from one community to the next (Salathé & Jones, 2010), although epidemics are unhindered, or even sped up, by inter-community ties when communities are overlap (Reid & Hurley, 2011).

Path lengths

Although networks with increased ℓ_LCC will often have lower r₀, much of this effect is due simply to lower network density. For LCCs of equal density, high ℓ_LCC is likely to be due to a dense core with long peripheral arms; in such a scenario r₀ will be high once the epidemic reaches the core, but will take longer to reach all parts of the LCC (Moore & Newman, 2000). However, since random spreading processes rarely follow shortest paths between any two nodes, the shortest path typically underestimates the length of the path taken by a spreading process. Since truncation inflates the length of observed shortest paths, the shortest path seen in truncated networks may paradoxically more closely reflect actual path lengths taken than those observed in fully observed networks (Onnela & Christakis, 2012). As a result, the lower r₀ predicted from truncated networks may in fact be more accurate.

Potential impact of degree truncation on spreading processes

Based on the above results, we formulate some initial hypotheses about the likely impact of out-degree truncation on predictions of the behavior of spreading processes on the resulting network. First and foremost, truncation will reduce the number of edges in the network, since some edges are now not observed. This leads to a reduction in mean degree and is likely to increase average path lengths and reduce the size of the S_LCC ; as a result, both r₀ and A will be reduced. The reduction in r₀ may however be offset by reduced variance in degree – since out-degree variance is strictly reduced by truncation and in-degree variance is likely to drop too. Second, degree truncation by tie strength may lead to an inflation of degree-assortativity, if assortative ties are stronger on average and thus more likely to be preserved. This should lead to smaller, faster ending epidemics – especially if assortativity is created by preferentially dropping core-periphery links. Finally, degree truncation by tie strength will have an unpredictable effect on clustering – depending on the relationship between tie strength and community structure. Notably, if the two are strongly positively correlated, truncation may increase community structure as weak ties are preferentially dropped. If clustering is increased, both r₀ and A are likely to fall.

Methods

To test the above hypotheses about the impact of degree truncation on predicted spreading process outcomes, we: (1) simulated a tie-strength truncation process on a range of networks; (2) simulated a spreading process on the original (fully observed or ‘full’ network) and truncated networks a large number of times; and (3) compared spreading process outcome values for the full and truncated networks (Figure 1). In the following, we describe in detail the following: (A) the network generation process; (B) the truncation process; and (C) the spreading process.

Figure 1. Schematic of study methodology.

(1) For synthetic networks, 100 degree sequences were were generated. For the Karnataka village data, 75 empirical village datasets were used, and step 2 skipped. (2) Each degree sequence was converted into a network graph using the configuration model, and then each synthetic graph was calibrated based on target network values. (3) All networks were truncated at twice mean, mean and half mean degree. (4) 100 spreading processes were run across each full and truncated network.

A. Network structures

We considered four types of synthetic networks that we call Degree-Assortative, Triadic Clustering, Focal Clustering, and Power-Law networks, and in addition we considered networks based on empirical data (details below). The empirical social networks were collected from a stratified random sample of 46% of households in each of 75 villages in Karnataka, India, which were surveyed as part of a microfinance intervention study in 2006 (Banerjee et al., 2013a, 2013b). We defined an edge between two individuals in the sample to exist if either person reported any of the twelve types of social interaction asked about in the study.

We began synthetic network construction by generating a collection of degree sequences, where a degree sequence is a list of node degrees of a network. To generate 100 Degree-Assortative, Triadic Clustering, and Focal Clustering networks, each consisting of N = 1000 nodes, we drew 100 degree sequences of length N from a Poisson distribution P(ϕ) where ϕ = 8, as an approximation to a binomial distribution with large N. We used the configuration model to generate an initial graph realization for each degree sequence (Molloy & Reed, 1995), and then rewired the networks, edge by edge, in order to obtain a collection of calibrated networks such that each network closely matches a target value of a chosen characteristic, specifically:

1. Degree-Assortative. This was achieved by: (i) selecting two disjoint edges (u, v) and (x, y) uniformly at random; (ii) computing whether removing the two edges and replacing them with edges (u, y) and (x, v) would increase network assortativity; and if so (iii) making this change.

2. Triadic Clustering. This was achieved by: (i) choosing an ego i and two of its alters, j and k, who were not connected to one-another; (ii) adding the edge (j, k) to the network, thus forming a triangle; and (iii) removing an edge selected uniformly at random conditional on that edge not being part of a triangle, thus ensuring increased triadic clustering.

3. Focal Clustering. This was achieved by: (i) selecting three nodes i, j and k uniformly at random; (ii) adding edges (i, j), (i, k) and (j, k) if they did not already exist; (iii) choosing uniformly at random in the network the same number of edges that were just added (excluding edges (i, j), (i, k) and (j, k) in the selection); (iv) computing whether removing this second set of edges would result in a net increase in focal clustering – if so, removing them; if not, repeating steps (iii) and (iv).

We generated three versions of each type of synthetic network by calibrating assortativity, triadic clustering, and focal clustering to the minimum, median and maximum values of these quantities observed in the 75 Karnataka villages (Table 1, column 1).

Table 1.

Mean network characteristic values for empirical and calibrated synthetic networks

	Target values†	Mean degree	Variance of degrees	Gini of degrees	Degree assortativity	Modularity	Triadic clustering coefficient	Focal clustering coefficient	SLCC	ℓLCC
Karnataka villages (mean)		8.39	27.55	0.37	0.33	0.79	0.64	0.19	0.99	4.10
Synthetic networks defined by:
Degree-Assortative	r = 0.283	7.86	0.49	88.82	0.28	0.29	0.01	0.00	1.00	3.61
	r = 0.421	7.86	0.20	7.73	0.42	0.28	0.01	0.01	1.00	3.65
	r = 0.797	7.86	0.20	7.73	0.80	0.28	0.01	0.01	1.00	3.88
Triadic Clustering	c = 0.249	7.75	0.54	62.63	−0.05	0.46	0.29	0.07	0.73	3.71
	c = 0.284	7.75	0.30	18.33	−0.05	0.47	0.34	0.08	0.99	3.70
	c = 0.353	7.75	0.32	20.96	−0.06	0.50	0.43	0.09	0.99	3.69
Focal Clustering	t = 0.163	7.95	0.20	7.73	0.26	0.66	0.37	0.16	1.00	4.09
	t = 0.249	7.95	0.37	27.83	0.50	0.82	0.43	0.25	0.90	4.61
	t = 0.326	7.95	0.47	44.10	0.68	0.90	0.45	0.33	0.80	5.23
Power-Law	γ = 3	7.78	0.55	186.20	−0.04	0.36	0.04	0.02	1.00	3.35
	γ = 2.5	7.40	0.65	263.29	−0.10	0.36	0.09	0.03	0.99	3.16
	γ = 2	6.18	0.44	49.96	−0.22	0.37	0.21	0.04	0.99	3.07

S_LCC: fraction of all nodes within the largest connected component. ℓ_LCC: average path length between nodes in the LCC.

^†Target values are the minimum, median and maximum values from the 75 Karnataka village networks.

To generate Power-Law networks, the fourth type of synthetic network, we drew degree sequences from a power-law distribution P(k) ~ k^−γ, using the values 3, 2.5 and 2 for the degree exponent γ. We discarded any ungraphable sequences, i.e. those where any value greater than N – 1 = 999 was drawn. We again used the configuration model to generate an initial graph realization for each degree sequence. Note that lower values of γ are associated with degree distributions that have increasingly fat tails.

For each of the four types of synthetic networks, for each level of calibration we generated 100 independent representative networks using the above methods, for a total of 1200 networks. Mean values for a range of network characteristics for each set of 100 networks are shown in Table 1.

B. Truncation

We simulated degree truncation of the form typically seen in surveys, by placing a ceiling on the number of contacts, k_fc, that can be reported by a respondent, and then reconstructed the contact graph created from all sampled contacts. To do this, we first converted the network into a directed graph. We then selectively removed (k_i – k_fc) directed edges starting from each individual i, beginning with the edge having the smallest edge overlap value. We used edge overlap as proxy for tie strength, defined as the fraction of shared network neighbors of a connected dyad: O_ij = n_ij/[(k_i – 1) + (k_j – 1) – n_ij], where n_ij is the number of neighbors i and j have in common, and k_i and k_j are their degrees (Onnela et al., 2007b). Overlap has previously been shown to be strongly correlated with tie strength, as conjectured by the weak ties hypothesis several decades earlier (Granovetter, 1973). We were thus conducting truncation by tie strength.

We truncated at k_fc = q〈k〉, taking values of q = 0.5, 1, 2, so that the maximum out-degree of individuals was half the mean degree in the full network, the same as its mean degree, or twice its mean degree. After truncating each individual’s out-degree, we collapsed the directed graph into an undirected one based on all remaining ties. Examples of this truncation process on 20-node networks are shown in Figure 2. We measured a range of network properties for each full and truncated network, including mean degree, degree-assortativity, triadic and focal clustering, S_LCC and a measure of community clustering – normalized modularity Q_n (Newman, 2010); this last based on a graph partition for each network using the Louvain method (Blondel et al., 2008).

Figure 2. Toy examples of truncation process for different synthetic graphs.

This figure shows three graphs each containing 20 nodes and with a mean degree of approximately 5. Each was generated by calibrating a configuration-generated graph through rewiring to achieve specific target values of different network characteristics. The top row shows each calibrated graph with all edges; the bottom row shows with dotted lines those edges removed by truncating by tie strength at an out-degree of 3.

C. Spreading process

We ran a Susceptible-Infected-Recovered (SIR) model using degree infectivity on the networks defined by the per-period (per time step) probabilities β = 0.03 (the probability of an infectious individual infecting each susceptible contact) and ν = 0.05 (the probability of an infectious individual recovering). These values were not selected to mimic any particular disease, but were rather chosen to give a high probability of epidemic take-off in untruncated networks, without regularly hitting the ceiling of 100% cumulative incidence. In our networks, with a mean degree of 8, these values give a mean infectious period of 14 time steps, and an R₀ of approximately 2.8.

Each spreading process began with five initial infections, chosen uniformly at random among the nodes of a network, and each SIR model was run 100 times on the full and degree truncated variants of each of the 100 networks. We measured two categories of outcomes across all of the 10,000 runs (100 runs per network for 100 networks) of each synthetic network type (7,500 for the Karnataka village data), including results from those runs for which at least 10% of individuals were ever infected: first, time to infection of the 10^th percentile of the population (epidemic growth r₀: mean and 95% range); and second, the proportion of nodes ever infected (the attack rate A: mean and 95% range).

Results

Summary statistics for all networks at all levels of truncation are shown in Supplementary Table 1. In all networks, both synthetic and empirical, out-degree truncation consistently reduced mean degree as expected, most strongly in Power-Law and Focal Clustering networks. Truncation strongly reduced degree-assortativity in all cases except for Power-Law networks, which were already degree-disassortative, overwhelming any differences originally seen across levels of calibration; this effect was weaker for the Karnataka networks than for synthetic networks other than Power-Law. Modularity increased with truncation in all networks except for Degree-Assortative ones (which had very high initial modularity). With the exception of Power-Law and Karnataka networks, where modularity rose smoothly with increasing truncation, most of the increase only occurred once networks were truncated at half mean degree. Both triadic and focal clustering fell, and the ℓ_LCC rose, consistently with increasing truncation for all networks in which clustering was initially present.

When spreading processes were simulated on the full networks, at least 10% of the network became infected (attack rate A ≥ 10%) in almost every simulation (over 97.5%), with the exception of Degree-Assortative networks where only around 90% of simulations reached A ≥ 10% (Supplementary Table 2). Truncating networks at 2〈k〉 had almost no impact on the proportion of epidemics with A ≥ 10% for any network, but further truncation led to a sharp fall-off. At 0.5〈k〉 truncation none of the clustered network epidemics reached A ≥ 10%, and only the Power-Law networks, the Degree-Assortative networks calibrated to the lowest level of assortativity and the Karnataka networks had more than 2% of their epidemics reach the A ≥ 10% threshold.

Without truncation, 10% of all nodes were infected within 20 time steps on all networks except for the degree-assortative ones – which also showed the greatest range of initial epidemic growth rates (r₀) (Table 2). Truncation at 2〈k〉 increased r₀in all cases, but not by large amounts; however truncation at 〈k〉 raised both mean r₀ and its variance – notably in the cases of degree-assortative and triadic clustering networks (Figure 3A). For those networks in which any runs reached A ≥ 10% at 0.5〈k〉 truncation, both the mean and variance of r₀increased as networks became highly fractured.

Table 2.

Population-level outcomes amongst epidemics infecting at least 10% of the population

	No truncation		Truncation at twice mean degree		Truncation at mean degree		Truncation at half mean degree
Time to infection of 10% of population
Degree-Assortative	35.0	[20.0 – 85.0]	51.0	[27.9 – 120.9]	119.9	[67.1 – 185.0]	138.0	[81.0 – 188.0]
Triadic Clustering	17.0	[12.0 – 27.0]	22.0	[15.0 – 34.0]	61.0	[36.0 – 127.0]
Focal Clustering	18.0	[11.0 – 39.0]	32.0	[20.0 – 65.0]	96.9	[51.9 – 174.4]
Power-Law	8.0	[5.0 – 19.0]	16.9	[9.0 – 38.0]	40.0	[17.9 – 107.1]	72.9	[35.0 – 153.1]
Karnataka villages	15.0	[9.0 – 27.0]	21.0	[12.3 – 40.0]	43.0	[23.0 – 100.9]	88.4	[39.0 – 175.4]
Percentage of all individuals ever infectious
Degree-Assortative	46.6	[39.3 – 52.8]	39.5	[27.4 – 47.2]	15.2	[10.4 – 26.4]	11.5	[10.2 – 16.6]
Triadic Clustering	85.8	[83.4 – 87.9]	84.4	[81.6 – 86.7]	41.8	[18.8 – 54.1]
Focal Clustering	60.2	[55.0 – 65.0]	58.0	[51.0 – 63.2]	15.7	[10.5 – 27.4]
Power-Law	58.8	[51.5 – 65.1]	41.1	[32.6 – 48.2]	22.2	[12.6 – 30.0]	15.9	[10.6 – 27.5]
Karnataka villages	78.1	[68.9 – 83.9]	76.2	[65.6 – 82.9]	57.5	[20.1 – 70.9]	13.9	[10.3 – 24.2]
Percentage of 47,500 epidemics infecting at least 10% of the population	96.5		93.1		66.0		7.1

Figures show mean and 95% ranges for all runs from 10,000 simulations (7,500 for Karnataka villages) for which at least of 10% of individuals were ever infected. Note that the proportion of retained networks falls as the level of truncation rises (see Supplementary Table 2 for details); empty cells represent simulation types where no runs reached the 10% threshold. All network structures are those with highest network properties in each category (see Methods and Table 1).

Figure 3. Epidemic outcomes for simulation runs infecting at least 10% of the population across six network structures.

Figures show mean and 95% ranges for all runs from 10,000 simulations (7,500 for Karnataka villages) for which at least of 10% of individuals were ever infected. Simulation types are defined by out-degree truncation (Circles: no truncation; Hexagons: truncation at twice mean degree; Squares: truncation at mean degree; Triangles: truncation at half mean degree). All network structures are those with highest network properties in each category (see Methods and Table 1; full results for each network structure are available in Supplementary Figure 1 and Supplementary Figure 2). Empty lines represent simulation types where no runs reached the 10% threshold.

Network structure had a greater impact on A than on r₀, with clear differences even on full networks (Figure 3B). Truncation at 2〈k〉 had almost no impact on A except in the cases of Power-Law, and to a lesser extent Degree-Assortative, networks. However truncation at 〈k〉 leads to a mean A roughly halving for all cases except the Karnataka networks, where A only falls by about a quarter. Once truncation reached 0.5〈k〉, no network type averaged A > 16%.

Discussion

Simulating a generic spreading process on a range of networks containing different structures, we find that truncating the number of contacts that each person can report via a fixed choice design (out-degree truncation) has a substantial impact on both initial growth rates (r₀) and attack rates (A), even at the commonly used level of 〈k〉 (the mean degree of the network). Our investigations show that the level of inaccuracy introduced into predicted epidemic outcomes by a given level of truncation varied depending on the structure of the network under consideration, partly due to the impact of truncation on network properties, and partly due to the impact of network properties on process outcomes. Truncation on all network types eventually led to under-predictions of both r₀ and A, however the level of underprediction at each truncation level, and the level of truncation at which such under-prediction became substantial, varied across network types. Notably, our ability to predict process outcomes is degraded more rapidly on stylized synthetic networks than on a set of empirical social contact networks from villages in Karnataka state, India.

Central to understanding the effect of out-degree truncation on predictions of spreading process outcomes is the transition when the network becomes fragmented and the size of the largest connected component rapidly decreases. In our analyses, the Power-Law and Degree-Assortative networks showed slow declines in predicted process outcomes as truncation increased, while the loss of accuracy was more rapid for both Triadic Clustering and Focal Clustering networks – which lost fidelity early on – and the Karnataka networks – which maintained fidelity for longer (Figure 3). The speed of initial growth was notably more variable for Degree-Assortative compared to all other network types for both no truncation and truncation at 2〈k〉, reflecting the importance of the initial infection sites when networks contain both highly and lowly connected regions. This variation in findings suggests that knowledge of the structure of a network for which one wishes to predict process spread is crucial in determining the level of resources that should be placed into measuring the full extent of the network itself: locally clustered networks may require more contacts, while those with fat-tailed degree distributions may require fewer. Of course, knowing the mean out-degree of a network is a pre-requisite to determining the level of truncation that can be tolerated.

In contrast to our conjectures, in no case did truncation increase the speed of process spread. The impact of truncation in reducing the number of observed ties appeared to overwhelm all other processes, not least by affecting the network characteristics of the truncation networks: truncation at 〈k〉 led to the Degree-Assortative networks being entirely non-assortative and the Triadic Clustering and Focal Clustering networks displaying very limited clustering; only modularity appeared to be maintained or even increased as the FCD threshold was lowered – potentially because of the breakup of the network into increasingly numbers of unconnected components. Further investigation might find levels of truncation at which epidemic severity is over-estimated, but in practical terms our findings point to a consistent underestimate of speed and attack rate using data truncated by strength.

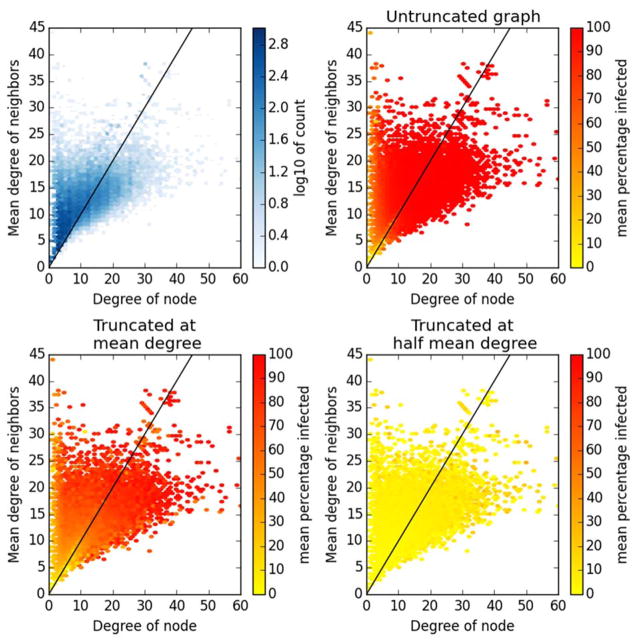
In addition to network-level outcomes, it is instructive to consider variability in outcomes at the individual level. While it is clear that individuals with higher out-degree are more likely to become infected, it is also likely that those with more-connected neighbors will become infected more often, since these connected neighbors are more likely to be infected in the first place. This association can be seen in Figure 4 for the Karnataka networks (and Supplementary Figure 3 for synthetic networks). Low degree individuals are unlikely to be infected regardless of how well-connected their neighbors are, but for our exemplar infection neighbor degree has little impact for those with own degree greater than ten (Figure 4B). As truncation increases – and has a disproportionate impact on ties dropped to higher-degree neighbors – individuals with lower mean degree neighbors are predicted to be infected less often than those with the same degree, but lower mean neighbor degree (Figure 4C and D). This effect is particularly visible at the common FCD value of 〈k〉. These findings highlight that not only can truncation impact population-level predictions of infection risk, but they may also differentially affect individual-level predictions.

Figure 4. Mean neighbor degree vs. own degree for full and truncated Karnataka village contact networks.

All plots are heatmaps, i.e. depth of color represents frequency of occurrence at the given location. A. Density of ties in full graph (log-scale); B–D: Mean proportion of all runs in which the node was infected (linear scale). The black diagonal line shows points of equal node and mean neighbor degree. In the full graph, most nodes are infected most of the time, except those with either very low degree or very low mean neighbor degree. When truncated at mean degree those with middling degree and mean neighbor degree are infected less often. When truncated at half mean degree almost no nodes are ever infected.

There are several ways in which this analysis could be extended. First, it might be informative to consider unweighted, rather than weighted, truncation. Weighted truncation is likely to minimize mis-estimation of local spreading processes, since close-knit groups are likely to be maintained at the expense of a realistic picture of cross-community connections. Unweighted truncation, in contrast, is likely to reduce the speed of process spread generally, but maintain weak ties that span structural holes in the network (Burt, 2004). Second, one could investigate spreading processes based on edge weights, or using unit infectivity. Third, it might be worthwhile to run these analyses for a wide range of truncation levels, in order to evaluate which networks have more or less rapid transitions from relatively accurate spreading process predictions to relatively inaccurate ones, and at what level of truncation these transitions occur. Such an analysis would be particularly useful in the context of a specific empirical network and spreading process, rather than in the theoretical cases presented in this paper, as a precursor to the conduct of data collection in a survey. While we have used a range of network structures and a standard spreading process, our results are limited to the cases we have considered and notably to a single level of network density, and thus investigation of other structures and processes might be worthwhile. Finally, we used only one set of transmission parameters, and thus the absolute impact of truncation may well be different for other infection processes. Nevertheless, we would not expect different transmission rates to change our central finding that network structure is an important determinant of the impact of truncation on predicted epidemic outcomes.

The ultimate goal of our analysis is to arrive at more accurate predictions of process outcomes in the context of truncated contact data, the type of data that are common in the study of infectious diseases and public health interventions. In addition to our simulation approach, there is the potential for analytic work to evaluate the level of mis-prediction likely to arise under a given level of degree truncation, for given network structures. Ultimately, this should allow for us to adjust predictions for truncation. Such an approach might use statistical or mechanistic network models to simulate full networks congruent with both the estimated rate of truncation, and observed characteristics of the truncated network; simulations could then be run on these simulated networks to predict process outcomes. As noted above, although we have framed out-degree truncation here as resulting from the adoption of FCD, our methods are agnostic to the cause of truncation. Consequently our results may generalize to settings where some other mechanism, such as social stigma in the case of self-reported sexual networks, might lead to out-degree truncation. Additionally, we have focused this work on sociocentric network data collection. Truncation and edge non-reporting may also arise within egocentric data collection, requiring the use of ERGMs or other methods to infer global network structure. While beyond the scope of this paper, investigation of the impact on epidemic prediction of degree truncation within egocentric data collection may also be of interest. Similarly, empirical networks (both sociocentric and egocentric) also often suffer missingness due to other mechanisms, such as missing nodes, reporting of non-existent alters and edges linking population members to non-members; future investigation of the impact these mechanisms – both alone and in concert with truncation – may be an important avenue of investigation in evaluating possible errors in predictions of spreading processes.

Finally, while our focus here has been on degree truncation in sociocentric studies resulting from study design, effective truncation may occur in sociocentric networks for other reasons. For example, there has been increasing research activity in the past few years into digitally mediated social networks, such as those resulting from mobile phone call and communication patterns (Blondel et al., 2015; Onnela et al., 2007a; Onnela et al., 2007b). Social networks are constructed from these data typically by aggregating longitudinal interactions over a time window of fixed length, where the features of the resulting networks are fairly sensitive to the width of the aggregation window (Krings et al., 2012). This leads to effective network degree truncation that is not a consequence of study design per se but rather is induced by the network construction process. It seems plausible that some of the insights we have obtained here, as well as some of our methods, could be translated to this research context.

Conclusion

We have shown via simulation that truncation of a network via FCD has a systematic impact on how processes are predicted to spread across this network, reducing predicted speed of epidemic take-off and the final attack rate, relative to values obtained from a fully observed network. However, the degree of impact varies strongly by the level of truncation, and we find that the transition level – at which impact on predicted process outcomes shifts from small to considerable – varies by network structure. Supplementary information on the structure of the full network – potentially estimated from past egocentric or sociocentric studies in the same or similar populations – will thus often be crucial for increasing the accuracy of predictions of process spread for truncated network data.