Abstract
Background
Recent advances in photon counting detection technology have led to significant research interest in X-ray imaging.
Objective
As a tutorial level review, this paper covers a wide range of aspects related to X-ray photon counting detector characterization.
Methods
The tutorial begins with a detailed description of the working principle and operating modes of a pixelated X-ray photon counting detector with basic architecture and detection mechanism. Currently available methods and techniques for charactering major aspects including energy response, noise floor, energy resolution, count rate performance (detector efficiency), and charge sharing effect of photon counting detectors are comprehensively reviewed. Other characterization aspects such as point spread function (PSF), line spread function (LSF), contrast transfer function (CTF), modulation transfer function (MTF), noise power spectrum (NPS), detective quantum efficiency (DQE), bias voltage, radiation damage, and polarization effect are also remarked.
Results
A cadmium telluride (CdTe) pixelated photon counting detector is employed for part of the characterization demonstration and the results are presented.
Conclusions
This review can serve as a tutorial for X-ray imaging researchers and investigators to understand, operate, characterize, and optimize photon counting detectors for a variety of applications.
Keywords: Photon counting detector, detector characterization, energy response calibration, noise floor, energy resolution, count rate performance, charge sharing effect
1. INTRODUCTION
Photon counting detectors capable of discriminating X-ray photon energies have been developed in past decades for various applications in medical imaging and material science [1–22]. Compared to energy-integrating X-ray detectors working in a current mode, photon counting detectors are operated in a pulse mode based on single event, meaning that theoretically each interaction occurred within the detection material can be processed and registered individually [23].
Three types of photon counting detectors have been developed based on the ionization radiation in gases, scintillators, and semiconductors. Gas based photon counting detectors prove their capabilities in 2D soft X-ray imaging [24, 25]. Scintillator based photon counting detectors are regarded as indirect detectors because the deposited X-ray photon energy first converts to visible light or ultraviolet radiation, which is then detected by electronic devices such as photomultiplier tubes (PMTs) through converting the light into electrical charges [23, 26, 27]. The absorption efficiency of X-ray photons in inorganic crystalline scintillators is high due to the large average atomic numbers such as in sodium iodide (NaI, Z=11/53) and bismuth germanium oxide (BGO, Z=83/32/8) [23]. Considering the high absorption efficiency and the capability of being manufactured into a large scale, inorganic scintillator based photon counting detectors are typically applied in nuclear medicine applications such as positron emission tomography (PET) [23, 28]. Conventional scintillator based detectors are also used in computed tomography (CT) scanners but are operated in current mode (energy-integrating) rather than photon counting mode (pulse mode).
Similar to gas based photon counting detectors, semiconductor based photon counting detectors directly convert X-ray photons into electrical charges, and therefore are regarded as direct detectors [28, 29]. As silicon (Si, Z=14) is a well understood semiconductor and homogeneous large Si wafers are easily available, Si has been widely used as sensor material for photon counting detector. The low atomic number of Si, however, leads to low absorption efficiency for X-rays with energies higher than a few 10keV [22, 30]. Therefore, Si is typically used for experiments at low X-ray energies (e.g. 4-25keV) [31]. This is not acceptable in low-dose medical imaging applications or hard X-ray in material science at high energy range above 30keV [31]. On one hand, a specific detector configuration approach involving multiple stacked layers of segmented detectors with varying layer thicknesses and edge illumination method are developed to improve the total absorption efficiency of silicon-based multilayer photon counting detectors [7, 32–34]. On the other hand, more X-ray absorbing materials have been developed such as cadmium telluride (CdTe, Z=48/52) and cadmium zinc telluride (CZT, Z=48/30/52) as promising materials for high absorption sensors. For example, the absorption efficiency of an 0.5mm thick CdTe sensor is 90% and 30% for X-ray energies of 40keV and 100keV, respectively [35–37], and 0.75mm thickness gives an absorption efficiency above 95% form X-ray energies up to 60keV and efficiency of 23% at 140keV [37]. Regardless of the requirement of a higher bias voltage for adequate signal charge collection and the increase of the detector cost, thicker crystal naturally improve the absorption efficiency [36]. For example, a 5mm thick CdTe detector could reach a high absorption efficiency of 82% at 150keV energy of X-ray [9]. Other compound semiconductors such as gallium arsenide (GaAs, Z=31/33) and mercuric iodide (HgI2, Z=80/53) are also under investigations [7].
Though the limitations of photon counting detection capabilities based on semiconductors are obvious due to charge sharing, lack of semiconductor crystal homogeneity exhibiting defects, and unavailability of a large field of view [31, 38], semiconductor based photon counting detectors rapidly achieve widespread applications such as in macromolecular crystallography, power diffraction, surface diffraction, phase contrast imaging, dark-field imaging, non-destructive testing (NDT) of airport luggage, and medical imaging including clinical CT, micro-CT, breast CT and K-edge CT, mammography and dental panoramic imaging [1–22, 39–46].
This paper provides a tutorial level review covering a wide range of aspects related to semiconductor based X-ray photon counting detector characterization including energy response, noise floor, energy resolution, count rate performance (detector efficiency), and charge sharing effect. Other important characterization aspects such as point spread function (PSF), line spread function (LSF), contrast transfer function (CTF), modulation transfer function (MTF), noise power spectrum (NPS), detective quantum efficiency (DQE), bias voltage, radiation damage, and polarization effect are also remarked. Part of characterizations is demonstrated by a CdTe pixelated photon counting detector. Though this tutorial is written based on pixelated X-ray photon counting detectors with basic architecture and detection mechanism with two or more parallel comparators, the description of working principle as well as operating modes, and the reviewed characterization methods and techniques are helpful for all the X-ray imaging researchers and investigators to understand, operate, characterize and optimize photon counting detectors for various applications.
2. Working principle and operating modes
The working principle and operating modes are described based on a pixelated X-ray photon counting detector with basic architecture and detection mechanism with two or more parallel channels in each pixel, other improvements and strategies regarding detecting semiconductor materials (e.g. small pixel effect, drift structures and multiple stacked layers) and ASIC readout electronics (e.g. common digital electronics, anti-charge sharing schemes, and simultaneously counting photons and integrating their energies) can be found in references [7, 47, 48].
2.1. Working principle of a pixelated photon counting detector
A typical semiconductor based photon counting detector consists of two core components: semiconductor material (e.g. Si, CdTe or CZT) with two electrodes, and application specific integrated circuits (ASICs). As seen in the schematic in Fig. 1, a single semiconductor crystal module shares a common monolithic electrode (cathode) to receive X-ray photons while pixelated electrodes are evenly distributed on the other side connecting to ASIC through bump bonding processing. 32 pixels (4×8 pixels: 4 rows and 8 columns) are formed in this crystal module and larger imaging area can be manufactured through aligning multiple modules. A reverse bias voltage is applied between two electrodes to create an external electric filed. Without loss of generality, one pixel is selected and enlarged in Fig. 1 to illustrate the process that how an X-ray photon is detected, processed, and registered.
Fig. 1.
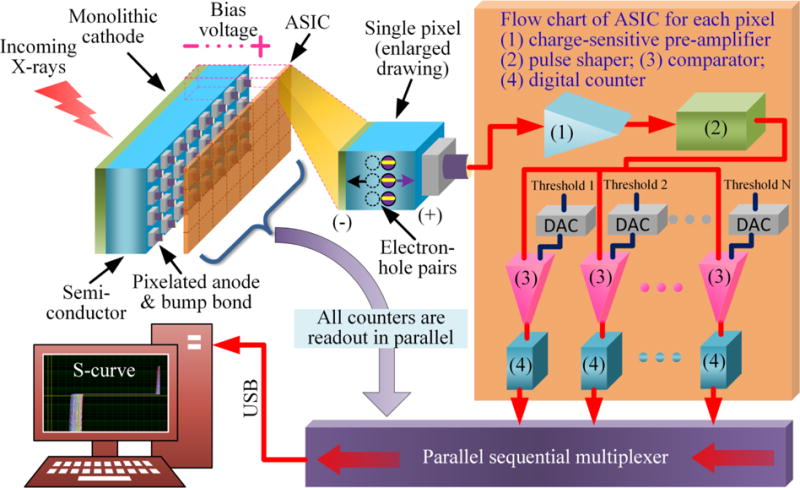
Schematic of a semiconductor based photon counting detector: each incoming X-ray photon interacts with the semiconductor material and the deposited energy generates electron-hole pairs and a transient current pulse which is then processed by so-called ASIC; a single pixel is enlarged to demonstrate how this transient current pulse is processed by an ASIC through charge-sensitive preamplifier, shaping amplifier, voltage pulse height comparators and digital counters.
When an incident X-ray photon interacts within the semiconductor material, electrical charges (electron-hole pairs) with an amount proportional to the deposited energy of the incident photon are produced and drifted towards the monolithic and pixelated electrodes separately under the influence of the externally applied electrical field [49]. During the drifting process of electron-hole pairs, a transient current is generated and then processed by the connected ASIC through one charge-sensitive preamplifier, one pulse shaper (shaping amplifier), and multiple pairs of voltage pulse height comparator and digital counter (N pairs in Fig. 1) [7].
Charge-sensitive preamplifier
Due to the proportionality between the deposited energy and the quantity of generated charges within the semiconductor, as aforementioned, the total electrical charge rather than the transient current is of utmost interest and therefore measured by a charge-sensitive preamplifier through integrating the transient current by a feedback capacitor [36, 50]. The typical input and output of a charge-sensitive preamplifier are demonstrated in Fig. 2, where the input current pulse is delivered by the charge generated from X-ray photon energy deposition, and the output signal is basically a voltage step proportional to the time integral of the input current pulse [47].
Fig. 2.
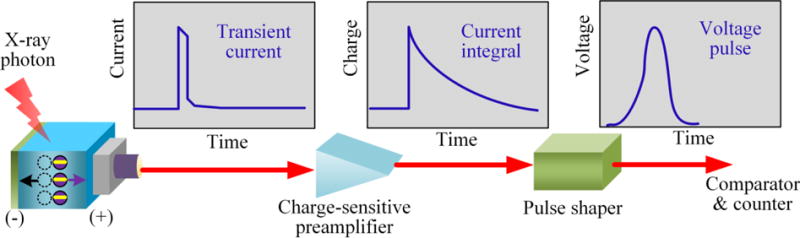
Inputs and outputs of charge-sensitive preamplifier and pulse shaper.
Pulse shaper
The pulse shaper is also called shaping amplifier, because it not only shapes the charge signals acquired from the charge-sensitive preamplifier, but also amplifies them to increase the signal intensities [50]. Moreover, the noise level generated in the preamplifier is suppressed in the pulse shaper to maximize the detection accuracy by the following procedure [10]. As a result, a shaped and amplified voltage pulse with peak amplitude proportional to the energy deposition is obtained after the pulse shaper and a typical output is shown in Fig. 2 as well.
Voltage pulse height comparator and digital counter
The voltage pulse generated by the pulse shaper is simultaneously sent to multiple voltage pulse height comparators (N comparators in Fig. 1). The pulse height (energy) thresholds for the comparators are globally programmable through digital-to-analog converter (DAC). A 3~6 bit trim-DAC (not shown in Fig. 1) is also provided for each comparator so that each global threshold can be further adjusted. The finely tuning of the global threshold for each comparator using the trim-DAC aims to compensate the pixel-to-pixel variations caused by variations of electronics. The process of compensating the pixel-to-pixel variations is called threshold equalization and will be discussed in Section 3.1 [29, 30, 35, 36, 49–52].
If the incoming voltage pulse height exceeds the threshold value, the corresponding digital counter is triggered and a count is registered. Examples for illustrating the voltage pulse processing mechanism are given when introducing two operating modes of a typical photon counting detector in Section 2.2. Note that the combination of comparator and its associated DCAs and digital counter is usually called one channel in the ASIC, and all the channels (N×4×8 channels: 4×8 pixels and N channels per pixel in Fig. 1) for the whole detector work in parallel and without interference.
2.2. Operating modes: imaging mode and scanning mode
A typical photon counting detector provides two operating modes, imaging mode for imaging purposes while scanning mode for detector characterizations. Other modes may also apply for certain pixel readout chip, yet not be introduced in details in this tutorial [38].
2.2.1. Imaging mode
Imaging mode is also called window mode or run mode. In this mode, all the thresholds (e.g. threshold 1 to N as shown in Fig. 1) for comparators are fixed values when detecting X-ray photons. A sequence with 6 voltage pulses (assuming all the pulses are distinguishable without overlapping) is given in Fig. 3 as an example to illustrate the process that how each voltage pulse is compared with the threshold and then registered in the corresponding counter. In this example, the pulse sequence is simultaneously delivered to N comparators with various pulse thresholds from threshold 1 to threshold N.
Fig. 3.
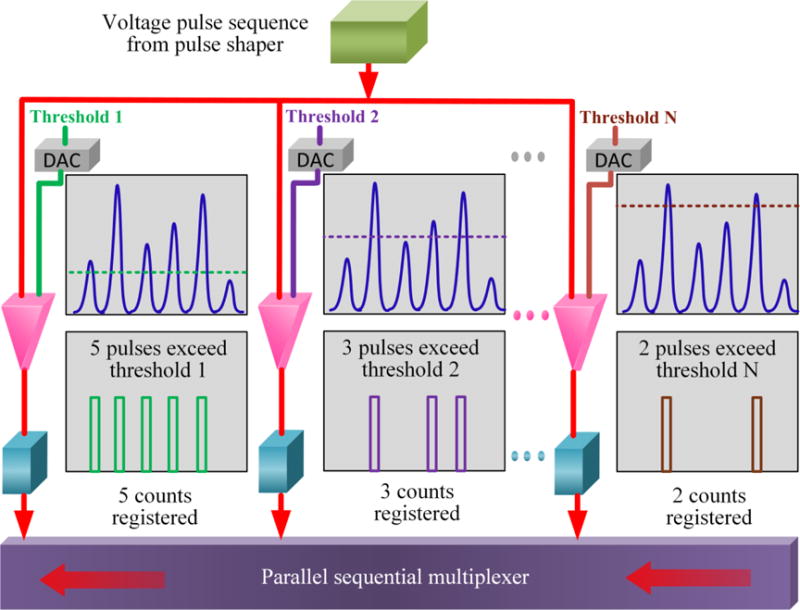
An example showing how a sequence of voltage pulses is processed and registered individually: identical voltage pulse sequence is simultaneously delivered into N channels (comparator + counter); the thresholds for N comparators are set as Threshold 1, 2, … N; each voltage pulse is compared with a threshold value and registered if the pulse height exceeds the threshold value; 5 counts are registered in counter 1, 3 counts are registered in counter 2, and similarly, 2 counts are registered in counter N.
Since 5 pulses in the sequence exceed the 1st threshold, 5 counts are registered in the 1st counter. In the meantime, 3 counts and 2 counts are registered in the 2nd and the Nth counters, respectively. The count numbers registered in between two thresholds (so-called pulse height window or energy window) can be acquired through subtracting the counts acquired in the higher threshold from the lower threshold [9, 35]. In this way, 2 counts are registered within the energy window defined by the 1st and the 2nd thresholds, 3 counts within 1st and Nth thresholds, and 1 count within the 2nd and the Nth thresholds. There is no upper bound for the Nth threshold (the highest threshold) [35]. It should be noted that the inputs of the comparators such as the preset threshold values and voltage pulse sequences to be processed are both analog signals while the outputs become digital signals in a form of binary pulse sequences in order to be registered in digital counters.
2.2.2. Scanning mode
Scanning mode is also called spectroscopic mode, threshold mode or test mode. In contrast to imaging mode with fixed threshold for a given comparator, the detector sweeps the whole pulse height (energy) range from high pulse height (high energy threshold) to low pulse height (low energy threshold) through consecutively reducing the threshold by a preset pulse height step in scanning mode [1, 9, 35]. In this way, the spectroscopic distribution (pulse height spectrum) of the incident X-ray photons can be determined. Most of the detector characterizations are performed in the scanning mode through acquiring the spectral data, as will be discussed in next section. The sweeping energy range, threshold moving step and frame time (duration of each threshold step) are adjustable for different characterization purposes. Successful spectroscopic data acquisition when the detector operates in the scanning mode highly relies on a continuous and constant exposure condition throughout the whole scanning process. In the case of utilizing a conventional poly-energetic X-ray source, for instance, the operational parameters of the source such as tube voltage, current, focal spot size and filtrations must remain constant during the continuous exposure.
An ideal example is analyzed in Fig. 4, where identical incident X-ray photons and generated voltage pulses are detected during the frame time at each threshold step. Since all the channels work in parallel as aforementioned, one channel is selected without preference to illustrate the signal processing by a specific comparator. In this example, threshold 1 (green) is the highest threshold above which 2 voltage pulses are detected and registered. Then, the threshold is reduced by a step to threshold 2 with 3 counts registered. Similarly, 5, 7, and 10 counts are registered under threshold 3, 4, and 5, respectively. Though only 5 thresholds are used in this example, hundreds of threshold may apply in a realistic photon counting detector to acquire an accurate spectral distribution.
Fig. 4.
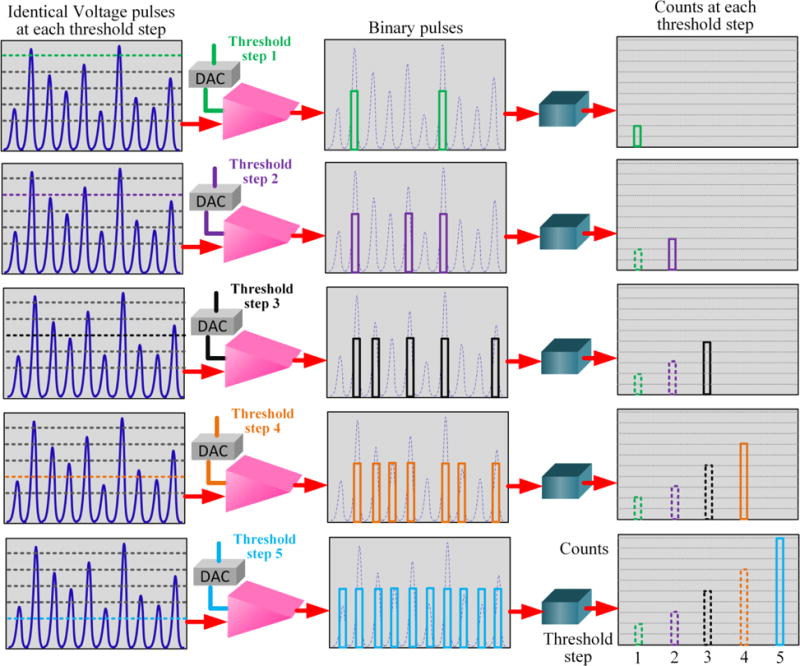
An ideal example showing that under constant and continuous exposure condition, the pulse height threshold for a specific comparator is reduced from threshold step 1 to step 5 with a constant threshold step to acquire an S-curve.
Similarly as in the imaging mode, the count numbers registered within each pulse height step can be acquired through subtracting the counts acquired in the higher threshold from its adjacent lower threshold, as shown in Fig. 5, where the curves in (b) and (c) are called integrated curve (S-curve) and differential curve (pulse height spectrum), respectively [1]. Examples of S-curves and pulse height spectra acquired using a realistic photon counting detector will be demonstrated in Section 3.
Fig. 5.
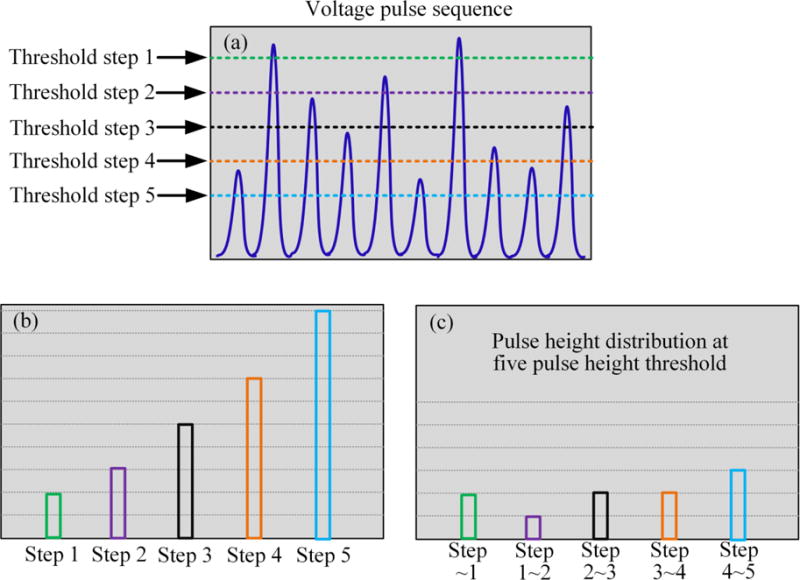
(a) Illustration of input voltage pulse sequence and five thresholds for a specific comparator, (b) S-curve, and (c) pulse height spectrum through differentiating the S-curve.
2.3. Photon counting detector utilized for demonstration
For demonstration purpose, a pixelated photon counting detector (DxRay, Inc. Northridge, CA, USA) consists of four CdTe crystals constituting dimensions of 70.4mm in length, 6.6mm in width, and 1mm in thickness is utilized. Each crystal has 64 equal pixels (4 rows and 16 columns) with an even pitch of 1.1mm × 1.65mm, and each pixel has 4 channels in its corresponding ASIC. In the imaging mode, the pulse height threshold values corresponding to 4 comparators could be set as any fixed values from 1200mV to 0mV. In the scanning mode, the highest pulse height can be set up to 1200 mV and the lowest pulse height is set within 0-400 mV. Millivolt (mV) is the unit of voltage pulse height. The threshold moving step can be set from 1mV to 10mV, and the frame time at each threshold step is adjustable from 0.1ms to 1400s.
3. Photon counting detector characterization
Currently available methods and techniques for charactering major aspects including energy response, noise floor, energy resolution, count rate performance (detector efficiency), and charge sharing effect of a photon counting detector are reviewed in this section.
3.1. Energy response calibration and pixel-to-pixel variation compensation
Photon counting detector converts each detected X-ray photon in the energy unit (keV) into a voltage pulse in the pulse height unit (mV) [49]. Energy response calibration between photon energy and pulse height in each channel is essential to characterize and compensate the detector’s pixel-to-pixel variation [53]. The generated voltage pulse height is generally proportional to the incident X-ray photon energy, but only linear up to a few tens of keV [1, 3, 54]. This is mainly because the absorption efficiency of the sensor material is non-linearly decreased with increased X-ray photon energies [31]. In order to perform the energy response calibration, multiple pairs of photon energy and pulse height are acquired by utilizing either mono-energetic X-ray and gamma-ray photons from synchrotron radiation, radioactive isotopes, and fluorescent X-rays, or polychromatic X-ray photons from laboratory X-ray sources. With constant and continuous exposure, the photon counting detector works in the scanning mode to acquire the S-curves from which the pulse height spectrum could be determined. The energy response calibration process can be repeated for all the pixels to determine the pixel-by-pixel response variations (e.g. different gains or offsets of the charge-sensitive preamplifiers [36, 49]). The process of increasing the homogeneity across a detector through finely tuning the individual trim-DAC is called threshold equalization, as discussed in Section 2.1 [29, 55].
3.1.1. Mono-energetic spectrum: synchrotron radiation
Synchrotron radiation is an ideal candidate for energy response calibration because it emanates mono-energetic X-rays whose photon energy can be freely adjusted by using so-called monochromators while maintaining a very narrow energy bandwidth [16, 30, 31, 55]. Also, since the beam size can be collimated to a very small size in a micrometer level which is far less than the typical pixel size in a photon counting detector, it could potentially minimize the effect of charge sharing (will be discussed later) through hitting the center of the investigated pixel [31]. In this method, multiple distinct incident energies within the detector’s operational energy range are selected. For example, eight energies ranging from 25keV to 60keV in a step of 5keV are employed for the energy response calibration of a detector operated up to 80keV [15]. Under constant flux condition for any selected energy, the detector is operated in the scanning mode to obtain S-curves, from which the corresponding pulse height spectra are derived through performing a threshold-by-threshold differentiation. The derived pulse height spectra are generally broadened rather than only occupying a single pulse height value due to incomplete charge collection caused by charge-sharing effect. Through fitting with a Gaussian function for each derived pulse height spectrum, multiple pairs of the pulse height at the photo peak in the fitted spectrum and the incident X-ray photon with known energy are acquired. In order to effectively avoid the spectral distortion caused by pile-up effect, the photon flux (incident count rate) must be limited to a certain level, such as 105 photon pixel−1s−1 or less [15, 31, 55]. The reduction of photon flux can be achieved through placing aluminum/copper attenuator slabs with sufficient thickness into the synchrotron radiation beam [29, 55, 56].
Though synchrotron radiation provides excellent calibration results due to its mono-energetic X-ray emission with freely adjusted energy levels and very narrow energy bandwidth, it has prohibitive problems of limited accessibility for most conventional imaging laboratories. Also, the synchrotron beam is relatively small that requires the detector perpendicular to the beam to be translated to cover all the pixels, in an effort to determine the energy response variations for all the pixels [55].
3.1.2. Mono-energetic spectrum: radioactive isotopes
Compared to synchrotron radiation with limited accessibility, radioactive isotopes are more readily available in conventional imaging laboratories. During the radioactive decay process, X-ray or gamma-ray photons which are characteristics for different types of radioactive isotopes are continuously emitted in a form of mono-energetic spectrum. Thus, radioactive isotopes can also be used for detector energy response calibration purpose [3]. Since the emitted energies from radioactive isotopes can’t be freely adjusted as in a synchrotron, the radioactive isotopes for calibrating different detectors must be carefully selected. Popularly utilized radioactive isotopes include 99mTc (140keV) [3], 133Ba (80keV) [57], 57Co (122keV) [36, 57–60], 109Cd (22.1keV and 88keV) [3, 57, 59], 241Am (59.6keV) [3, 36, 57–61], 153Gd (41.5keV), 55Fe (5.9keV). Under constant exposure for any selected radioactive isotope, the detector is operated in the same way as using synchrotron radiation to obtain S-curves, differentiated pulse height spectra, and photo peaks in the fitted Gaussian functions.
However, the acquired pulse height and photon energy pairs utilizing radioactive isotopes are generally not sufficient to perform a comprehensive energy response calibration due to a limited selection of isotopes. Therefore, radioactive isotopes are commonly used in combination with synchrotron radiation [55], laboratory X-ray sources [58] or fluorescent escape peaks from the semiconductor material [55] for detector calibration purposes, or solely for determining the energy resolution. Another disadvantage is that it may be a time-consuming process due to the generally low activities of common radioactive isotopes, especially for a detector with large imaging area. Highly active radioactive isotopes can be available with special permission but result in more safety and storage issues.
3.1.3. Mono-energetic spectrum: X-ray fluorescence (XRF)
XRF is the third option for detector energy response calibration based on mono-energetic spectrum. In order to produce mono-energetic fluorescent X-rays, a fluorescent target with high atomic number (Z) is illuminated by high energy X-rays or gamma-rays from either radioactive isotopes [51, 53, 62] or laboratory X-ray sources [33, 63–66]. When the energy of the incident photons exceeds the binding energy (e.g. K-edge) of the electron in the inner shell (K-shell), this electron is ejected from its original shell, leaving a vacancy which is immediately occupied by a second electron with a higher energy from an outer shell. During this process, the excess energy caused by electron transition is released by either XRF or Auger electron emission. The emitted fluorescent X-rays have discrete energies which are characteristics for different fluorescent targets due to their specific atomic structures (or different Z). In order to properly generate multiple energy response calibration pairs between photon energy and pulse height, the fluorescent targets should be purposely selected. Regularly utilized fluorescent targets and their K-edge binding energies, Kα and Kβ emission energies are listed in Table. 1, in which some elements are in powder or liquid formats and stored in separate containers [65].
Table. 1.
| Fluorescent target | Cu | Zn | Ge | Br | Rb | Zr | Nb | Mo | Pd | Ag | Cd | In |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Atomic number (Z) | 29 | 30 | 32 | 35 | 37 | 40 | 41 | 42 | 46 | 47 | 48 | 49 |
| K-edge (keV) | 9.0 | 9.7 | 11.1 | 13.5 | 15.2 | 18.0 | 19.0 | 20.0 | 24.4 | 25.5 | 26.7 | 27.9 |
| Kα (keV) | 8.0 | 8.6 | 9.9 | 11.9 | 13.4 | 15.8 | 16.6 | 17.5 | 21.1 | 22.1 | 23.1 | 24.1 |
| Kβ (keV) | 8.9 | 9.6 | 11.0 | 13.3 | 15.0 | 17.7 | 18.6 | 19.6 | 23.8 | 24.9 | 26.1 | 27.3 |
|
| ||||||||||||
| Fluorescent target | Sn | I | Ba | Ce | Gd | Tb | Ho | Hf | W | Au | Pb | U |
|
| ||||||||||||
| Atomic number (Z) | 50 | 53 | 56 | 58 | 64 | 65 | 67 | 72 | 74 | 79 | 82 | 92 |
| K-edge (keV) | 29.2 | 33.2 | 37.4 | 40.4 | 50.2 | 52.0 | 55.6 | 65.4 | 69.5 | 80.7 | 88.0 | 116 |
| Kα (keV) | 25.1 | 28.5 | 32.0 | 34.5 | 42.7 | 44.1 | 47.1 | 55.2 | 58.7 | 67.9 | 73.9 | 96.5 |
| Kβ (keV) | 28.5 | 32.3 | 36.4 | 39.3 | 48.7 | 50.3 | 53.8 | 63.1 | 67.1 | 77.8 | 84.7 | 111 |
In contrast to using synchrotron radiation or radioactive isotopes that the detector is directly illuminated, the excitation source (laboratory X-ray source or radioactive isotope) and the detector are generally placed perpendicularly to each other in the method using XRF [64], both facing to the fluorescent targets. This experimental setup could significantly improve the fluorescence-to-scatter ratio (FSR) [65]. Other experimental strategies such as excitation filtration selection, excitation and emission beam collimation and detection angle optimization may also be applied to further improve the FSR [33, 65, 67–70]. Under constant illumination of any selected fluorescent target, the detector is operated in the same way as using synchrotron radiation and radioactive isotopes to obtain S-curves, differentiated pulse height spectra, and photo peak in the fitted Gaussian functions.
Though the calibration method with XRF has less concerns regarding the accessibility as using synchrotron radiation and safety issue as using radioactive isotopes, it has the following limitations: 1) Regarding Kα fluorescence line in Table. 1, the Kα energy of each fluorescent target is determined as the average of Kα2 and Kα1 energies. When the fluorescent target has a Z less than around 70, typically these two sub-fluorescence lines are too close to be separated even with a spectrometer with high energy resolution, let alone the use of a photon counting detector with a relatively lower energy resolution in several keVs [33, 64]. For Z>70, in contrast, both of these two sub-fluorescence lines can be clearly distinguished with high energy resolution spectrometers, but this is not the case with a photon counting detector. In short, for almost all the fluorescent targets in Table. 1, only a single Kα fluorescent peak contributed by both Kα2 and Kα1 can be detected by the photon counting detector. Since the fluorescent intensity determined by radiative rates are different for Kα2 and Kα1 fluorescent emissions, a single Gaussian function fitting of the differentiated spectrum may not locate the precise pulse height value corresponding to the averaged Kα energy, thus reducing the calibration accuracy. 2) Regarding Kβ fluorescent line in Table. 1, similarly, the Kβ energy of each fluorescent target is determined as the average of Kβ1 and Kβ3 energies. Due to the relatively low energy resolution in a photon counting detector, only a single Kβ fluorescent peak is detected, resulting in the same issue as using the Kα fluorescence line. Moreover, the broadened Kβ peak is subject to be affected by the high energy tail from the Kα peak due to high fluorescent intensity ratio of Kα/Kβ, thus also limiting the calibration accuracy using the Kβ fluorescence line [35]. 3) According to Table. 1, the possible calibration range is from 8keV (Cu) to 110keV (U) for stable fluorescent materials, which is not sufficient for calibrating photon counting detectors working up to 150keV in diagnostic imaging [65].
3.1.4. Poly-energetic spectrum: laboratory X-ray sources
The detector energy response can be also calibrated with a laboratory X-ray source generating X-rays in a ploy-energetic spectrum. Several approaches utilizing different features in a ploy-energetic spectrum have been proposed for the calibration purpose. All the X-ray spectra utilized in this section are generated by an online tool for the simulation of X-ray spectra, and the tool itself is based on algorithms developed by John M. Boone [71] and on X-ray attenuation data provided by the National Institute of Standards and Technology (NIST) [72].
Characteristic peaks
In this method, the characteristic emission peaks corresponding to the anode target material in the output spectrum are utilized. Similarly in XRF, characteristic X-rays with discrete energies are produced when the kinetic energy of the accelerating electrons exceeds the target’s K-edge binding energy. The output spectra with characteristic peaks from two popularly used targets (W at 100kVp and Mo at 40kVp) are demonstrated in Fig. 6, where Kα and Kβ represent the combinations of their sub-fluorescence lines. Under ideal condition and assuming a linear detector response, two pairs of known photon energy and measured pulse height may be acquired [35].
Fig. 6.
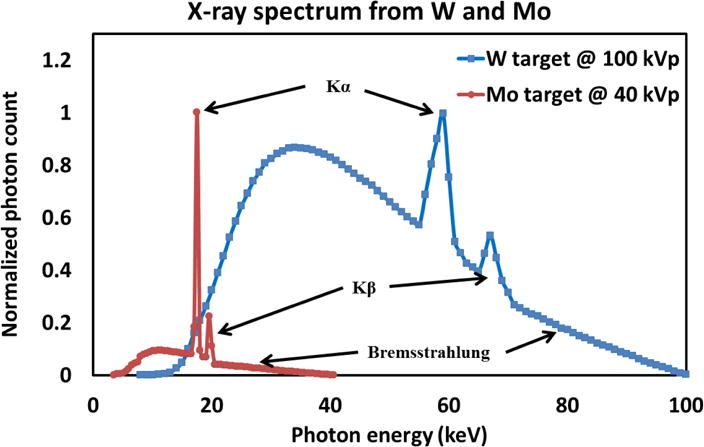
Two spectra with characteristic peaks from W at 100kVp and Mo at 40kVp; the continuous spectra under characteristic peaks are called bremsstrahlung.
This method itself, however, is not sufficient because: 1) similarly in XRF, all the characteristic peaks are composed by two sub-fluorescence peaks; 2) characteristic peaks from K-shell with strong fluorescence intensities only appear when the applied voltage accelerates electrons to a kinetic energy higher than the K-edge binding energy [35]; 3) limited photon energy and pulse height pairs may not fully characterize the detector energy response within the whole operating energy range. Therefore, this method is more suitable to verify the calibration results acquired by using other methods.
Maximum energies (endpoints in spectra)
It has been known that the applied voltage determines the electrons’ kinetic energy, which further determines the maximum photon energy generated by an X-ray source, as shown in Fig. 7 [71]. Therefore, through gradually increasing the applied voltage (maximum photon energy) and locating the pulse height value at the endpoint in the acquired pulse height spectrum (or S-curve), multiple pairs of photon energy and pulse height can be theoretically acquired for detector energy response calibration [1, 35, 54, 58].
Fig. 7.
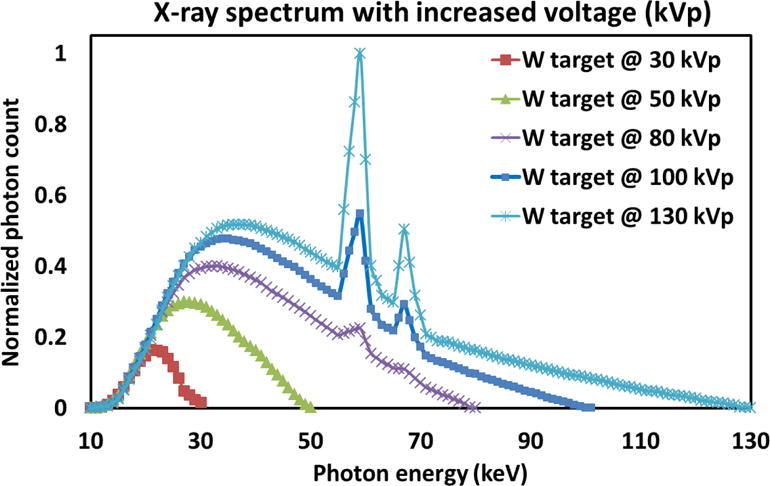
Five spectra acquired under voltages of 30, 50, 80, 100 and 130kVp; the maximum photon energy in each spectrum is determined by the applied voltage.
The challenge for this method is how to accurately determine the endpoint in the acquired pulse height spectrum. A fraction of counts with pulse height higher than the theoretical maximum value are always recorded due to the pile-up effect, even with limited incident photon flux. One feasible scheme is first to locate the maximum counts in a specific pulse height spectrum, and find two pulse height values whose count numbers correspond to 20% and 10% of the maximum counts on the side with higher energy. Then, through linearly extrapolating these two count numbers to be crossed with the pulse height axis, the pulse height corresponding to the maximum X-ray photon energy can be determined [58]. Note that the maximum counts should be derived from the continuous bremsstrahlung rather than from characteristic peaks (e.g. the pulse height spectrum acquired from an X-ray tube with W tungsten and high voltage, as shown in Fig. 7). This method will be performed in Section 3.1.6 for demonstration.
Spectral peak energy (maximum count)
In this method, the spectral peak energy corresponding to the maximum count number, which can be easily modulated by adjusting the applied voltage (kVp) and adding additional filtrations with different thickness/material, is utilized to perform the detector energy response calibration [71, 73], as shown in Fig. 8.
Fig. 8.
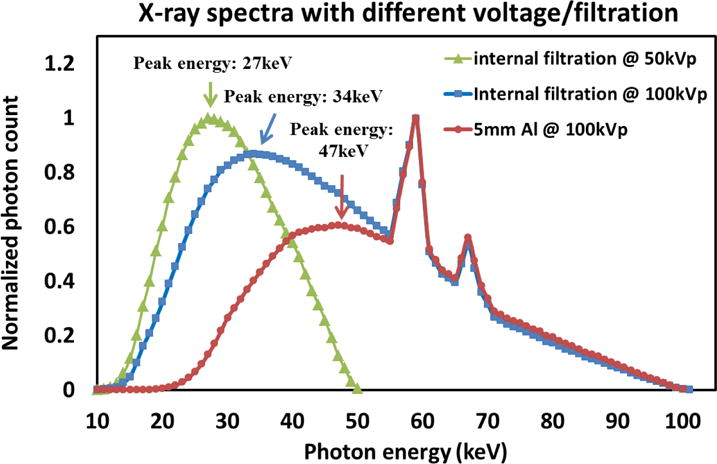
Three spectra acquired under different voltages and filtrations, indicating the peak energy can be adjusted by selecting different voltages and filtrations.
This method is typically performed in four steps: 1) selecting various combinations of applied voltage and additional filtration, so that multiple spectra with different peak energies within the detector’s operational energy range can be obtained; 2) measuring the X-ray spectra using a high energy resolution spectrometer which is newly calibrated to determine the peak energy value (unit: keV) of each spectrum; 3) irradiating the photon counting detector in a distance that all the pixels are covered simultaneously and the incident photon flux is low to avoid the pile-up effect; 4) each detected S-curve is smoothed and differentiated to obtain the pulse height spectrum, from which the pulse height corresponding to the spectral peak energy is located. Similarly in using the previous method, the maximum energy should be acquired from the continuous bremsstrahlung under all the situations.
These three methods introduced above using characteristic peaks, maximum energies and peak energies are generally applied in combination either to calibrate or to verify the calibration accuracy. Energy response calibration of a photon counting detector using a laboratory X-ray source becomes more and more attractive since it would be more practical and easily accessible than using synchrotron radiation, radioactive isotopes, or fluorescent targets (XRF) in most conventional X-ray imaging groups.
3.1.5. Other methods using poly/mono-energetic spectrum
Other methods are also developed for energy response calibration and threshold equalization using either poly-energetic or mono-energetic X-ray beams. For example, noise floor, which will be discussed in Section 3.2 can be used for threshold equalization [52, 74]. A method making a full use of the whole poly-energetic spectrum rather than using single or multiple spectral characteristic features is developed [49]. This method involves the adjustment of a simulated spectrum of deposited energies to a measured pulse height spectrum. Since the model is established based on a linear relationship between the detected pulse height and the actual incident photon energy, necessary modification of the regression model is required for calibrating photon counting detectors with a nonlinear response to photon energies.
Another method uses a parameter based model for the energy calibration and concludes on the optimal parameters of the model by finding the best correlation between the measured pulse-height spectrum and multiple synthetic pulse-height spectra which are constructed with different sets of calibration parameters [75]. The capability of resolving the K-edges of certain high Z materials shows the potential to develop a convenient alternative for energy response calibration with a polychromatic X-ray source [35].
3.1.6. Energy response calibration demonstration
The second method (maximum energy) using a laboratory X-ray source is applied to demonstrate the energy response calibration procedure and result. In this demonstration, none additional filtrations or collimations applied between the X-ray tube (L8121-03, Hamamatsu photonics, Hamamatsu, Japan) and the photon counting detector described in Section 2.2.3, except for the X-ray tube exit and the detector entrance windows. The detector is placed in front of the X-ray tube with a distance of 1650mm from the X-ray focal spot. In order to maintain a low but constant incident photon flux to avoid the possible pile-up effects, the X-ray tube voltage and current settings are selected as below: (40kVp, 150μA), (50kVp, 100μA), (60kVp, 85μA), (70kVp, 60μA), (80kVp, 60μA), (90kVp, 55μA), (100kVp, 50μA), (110kVp, 45μA), (120kVp, 40μA), (130kVp, 29μA), (140kVp, 25μA), and (150kVp, 20μA) [35]. Under each exposure condition, the detector works in the scanning mode through sweeping the pulse height threshold from 1000mV down to 200mV with a decrement of 2mV and a frame time of 500ms. The sweeping process can be repeated several times for each X-ray tube setting to acquire the average. For this specific photon counting detector with 256 pixels and 4 channels per pixel, 1024 S-curves are synthesized from the count data acquired by 1024 comparators.
Without loss of generality, the acquired S-curves from one channel in a certain pixel under different X-ray tube voltages from 40kVp to 150kVp are shown in Fig. 9 (a). Sudden increases of the photon counts registered at low pulse height, especially with lower voltages, can be observed due to the presence of electrical noise [1]. The determination of noise floor to eliminate the noise will be specifically introduced in Section 3.2. Assuming that the noise floor is determined as 270mV, data from 270mV to 1000mV in each S-curve are then fitted by a sum of three Gaussian functions. A fitting example of the S-curve acquired under 100kVp and 50μA is shown in Fig. 9 (b). The fitted curve is then differentiated to derive the pulse height spectrum, as indicated in Fig. 9 (b) as well.
Fig. 9.
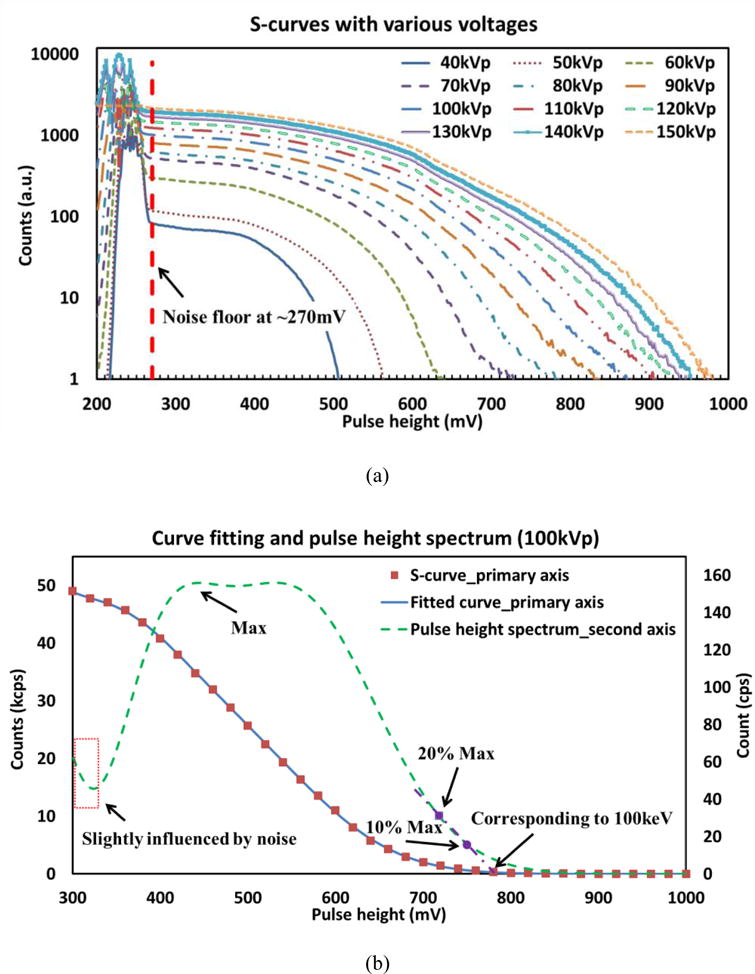
(a) S-curves acquired under X-ray tube voltages from 40kVp to 150kVp and noise floor determined at around 270mV; (b) An example showing the curve fitting and differentiation computation under 100kVp and the determination of pulse height value corresponding to the maximum photon energy.
In the derived pulse height spectrum, the maximum photon counts and its 20% and 10% values on the higher energy side are located to determine the pulse height value corresponding to 100keV. With all determined photon energy and pulse height pairs, the detector energy response can be calibrated through least square fitting these pairs with a sum of two exponential functions, as indicated in Fig. 10, where the detector responses to X-ray photon energies are linearly up to around 80keV.
Fig. 10.
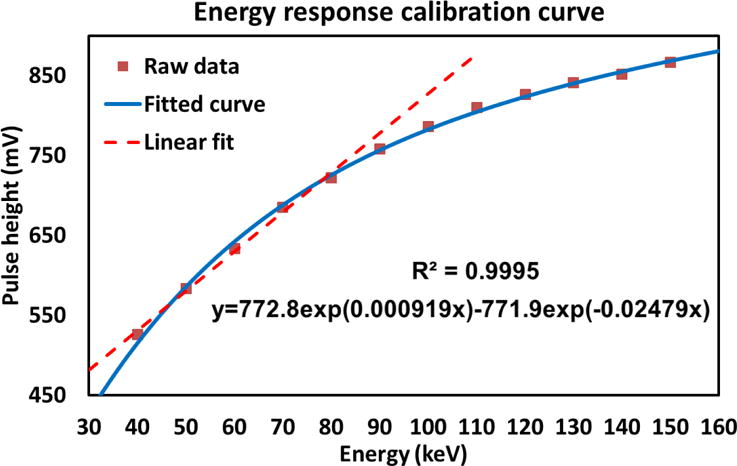
Energy response calibration curve using a sum of two exponential functions.
Other functions used to characterize the energy response are given in Eq. (1) and (2), where E is the photon energy, H is the measured pulse height, and c1, c2, c3, d1, d2, d3, d4, and d5 are parameters determined by the calibration pairs [1, 3, 58]:
| (1) |
| (2) |
3.2. Noise floor determination
Unlike energy-integrating detector, photon counting detector can effectively separate electrical noise from useful X-ray signals since the noise generally affects X-ray signals with lower energies in a detected pulse height spectrum (or an S-curve) [35]. Therefore, it is necessary to determine a proper pulse height threshold at the upper bound of noise level, so-called noise floor, above which only X-ray signals are recorded. Subjective and objective methods have been proposed to determine the noise floor.
3.2.1. Subjective observation
In this method, the noise floor is determined through observing the sudden increase of the photon counts in a detected S-curve (low pulse height part). This effect has been noticed in Fig. 9 (a) especially under lower voltages. The significant increase of X-ray photon counts is due to the presence of electrical noise below the noise floor [3, 76]. It is noteworthy that in order to reflect the presence of electrical noise, the total counts registered under an S-curve should be much less than the noise level [1]. For example, it is very difficult to subjectively locate the noise floor using the S-curve acquired under voltage of 150kVp in Fig. 9 (a). Subjective observation of noise floor can be also performed using synchrotron radiation and radioactive isotopes [10, 57].
3.2.2. Objective comparison
The noise floor can be also objectively determined by multiple measurements (e.g. 20 times) under certain exposure condition and calculation of the mean and the variance within each pulse height step [58]. It would be expected that the mean and the variance are comparable (e.g. less than 10%) above the noise floor, indicating that the measurements obey a Poisson distribution. On the other hand, the mean and the variance are significantly different for the counts acquired below the noise floor, demonstrating the presence of electrical noise. The mean and the variance of 12 measurements performed under identical condition of 80kVp and 60μA are demonstrated in Fig. 11, data being collected using the photon counting detector described in Section 2.3. Significant difference between the mean and the variance is presented in the comparison, based on which the noise floor can be determined as 270~280mV.
Fig. 11.
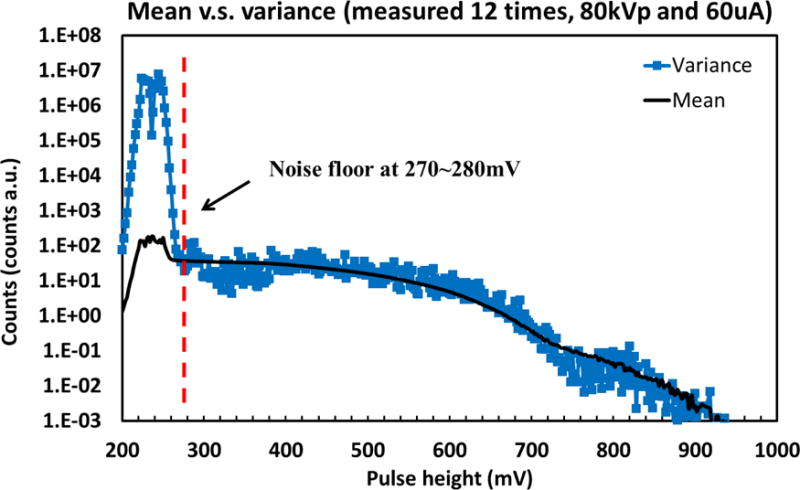
Comparison between mean and variance: S-curve measured under 80kVp and 60uA for 12 times, showing that the mean and the variance are comparable above 280mV (noise floor) while significant difference exists below the noise floor.
3.3. Energy resolution
Energy resolution is a very important parameter to describe the ability of an energy resolved detector to separate photons with different energies. It is indicated by the width of the resultant peak in a pulse height spectrum when the detector is illuminated by mono-energetic photons emanating from synchrotron radiation or radioactive isotopes [1, 36, 54, 57–61, 76]. Therefore the characterization of energy resolution can be performed together with detector energy response calibration. The peak usually obeys a Gaussian distribution and its width is measured as the full width at half maximum (FWHM). Energy resolution can be derived through dividing the FWHM by the energy corresponding to the maximum of the peak, as in Eq. (3), where R is the energy resolution at energy E and is the FWHM in energy unit [1, 23, 50]. A schematic showing how to calculate the energy resolution is illustrated in Fig. 12.
| (3) |
Fig. 12.
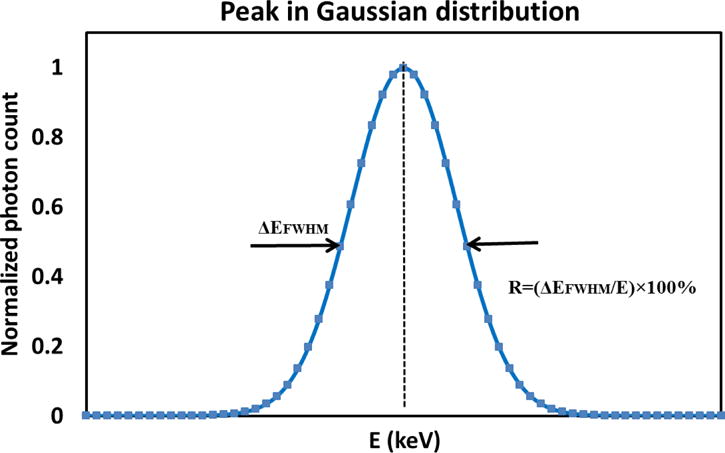
Schematic showing how to calculate the energy resolution.
XRF is also employed to calculate the energy resolution, but encounters the same difficulty as calibrating the detector energy response that the summation of sub-fluorescence peaks further broadens the detected peak, which would underestimate the energy resolution [33]. The characteristic X-ray peaks from a poly-energetic X-ray spectrum can be theoretically applied for determining the energy resolution as well. This method, however, requires a higher characteristic-to-bremsstrahlung ratio and proper estimation and removal of the bremsstrahlung background before applying Eq. (3) for energy resolution. Considering the accessibility and accuracy of determining energy resolution, radioactive isotopes are regarded as the best candidates and popularly utilized in practice.
The determination of energy resolution can be significantly influenced by charge sharing effect and pile-up effect, as will be remarked in Section 4. The requirement of the energy resolution for a given photon counting detector relies on its specific applications. A lower energy resolution (e.g. ~10%) may be sufficient for dual energy applications since the separation of two energy thresholds are relatively large [58]. Other imaging applications such as K-edge CT imaging or XRF imaging, in contrast, may need higher energy resolutions [14, 15, 58, 77].
3.4. Count rate performance (dynamic range) and detector efficiency
3.4.1. Mathematical model description
Due to pile-up effect and dead time (τ) loss, the linearity between the detected photon rate and the incident photon rate gradually lacks with increased photon fluxes [1, 7, 78]. It is very important to determine the linearity range and maximum detectable photon rate for a given photon counting detector to justify its proper applications [63]. Two mathematical models are generally used to describe the detector’s count rate performance: non-paralyzable and paralyzable models. In non-paralyzable model, the event occurred within the dead time of the former event doesn’t extend the dead time; on the contrary, the dead time extends by the following event arrived within its dead time in paralyzable mode. An example with 4 events in Fig. 13 is illustrated to describe the difference between these two models. Once the first event detected, the detector becomes inactive for duration of dead time and goes back to an active state then. The detector becomes inactive again when detecting the second event, of which the consequent dead time is not affected by the third event in the non-paralyzable model, but extends duration of dead time starting from the arriving point of the third event in the paralyzable model. Since the detector is active before detecting the fourth event in the non-paralyzable model, the fourth event can be detected and registered. In contrast, the fourth event further extends the dead time of the third event, resulting losses of both of the third and the fourth events.
Fig. 13.
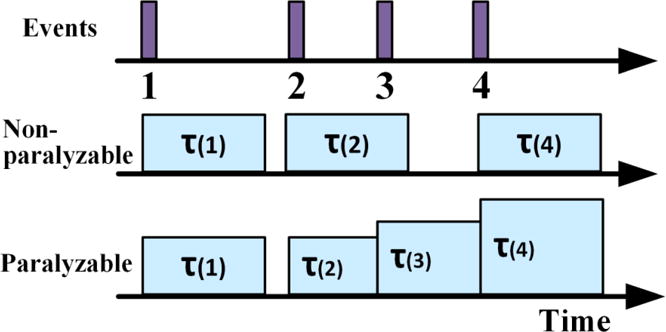
An example with 4 events used to illustrate the difference between non-paralyzable and paralyzable models.
In reality, two or more nearly simultaneously incident photons may be regarded as a single event with a higher energy, resulting in not only dead time losses, but also a distortion of the recorded pulse height spectrum [7, 58]. Understanding of the spectral distortion caused by pileup effects (peak and tail pileup) under high X-ray flux and the corresponding compensation methods using analytical model and Monte Carlo simulation are important to make full use of the spectral information provided by photon counting detectors [2, 29, 79–81]. Detailed description regarding the compensation methods, however, is quite beyond the scope of this tutorial and has been comprehensively introduced elsewhere [4, 58, 79, 80].
In order to characterize the count rate performance, the detector needs to be illuminated by various incident photon fluxes, which can be achieved using synchrotron radiation through adding additional filtrations with different thickness [31], or laboratory X-ray sources through adjusting the current under certain voltage [1, 3, 4, 50, 54, 57, 58, 60, 61, 63, 76] or using additional filtrations [78]. In either way, the recorded count rate Arec and the incident count rate Ainc are connected by P(Aincτ), the probability of the counts being recorded, in Eq. (4).
| (4) |
P(Aincτ) is defined in Eq. (5) and (6) for non-paralyzable and paralyzable models, respectively [3, 4, 10, 59, 61, 76].
| (5) |
| (6) |
In the condition of using a laboratory X-ray source, the incident count rate (Ainc) is assumed to be proportional to the X-ray tube current (I) in Eq. (7), where k is the proportionality constant.
| (7) |
Substituting Eqs. (4) and (7) into Eqs. (5) and (6) and performing several formula transformations, the following expressions in Eqs. (8) and (9) are derived, where k and τ can be obtained by a least-square method using (1/Arec) and (1/I) for non-paralyzable model while using (Arec/I) and [exp(-I)] for paralyzable model.
| (8) |
| (9) |
3.4.2. Demonstration for count rate performance and detector efficiency
The same X-ray source used for detector energy response calibration is applied in the demonstration of characterizing the detector photon count performance and detection efficiency. The distance between the X-ray tube and the photon counting detector is reduced to 380mm. The X-ray tube voltage is fixed as 70kVp, while the current settings are varied as 2, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100, 125, 150, 175, 200, 250, 300, 350, 400, 450, and 500μA to acquire various incident count rates. Data are collected by sweeping the threshold pulse height range from 1000mV to 200mV with a decrement step of 2mV, but a shorter frame time of 10ms. Each sweeping process is repeated 10 times for each current setting and their average is used for further processing. One channel of a typical pixel is used to evaluate the count rate performance and the maximum values in the acquired S-curves. The count numbers right above the noise floor determined in Section 3.2 are extracted to determine the relation between Arec and Ainc.
After eliminating the noise data below the determined noise floor of 270mV, the recorded photon count rates are plotted against various X-ray tube current settings, as shown in Fig. 14 (a). It can be seen that the linear response of incident count rate is up to around 450kcps (kilo counts per second), while the maximum rate could reach 760kcps with proper correction, beyond which, however, the detector starts to be paralyzable. Using the data acquired from 2μA to 100μA and Eqs. (5) and (6), non-paralyzable and paralyzable models are applied to characterize the detector efficiency and calculate the proportionality constant (k) and the dead time (τ). The calculated results are k=18.53kcps/μA and τ=647.22ns, and k=18.23kcps/μA and τ=448.48ns for non-paralyzable and paralyzable models, respectively. As indicated in Fig. 14 (b), both non-paralyzable and paralyzable models agree well with the measurements up to the maximum detectable rate, and the detector behaves in-between of two models after around 200μA. Also, the probability of events being recorded shown in Fig. 14 (c) demonstrates that, within the linear range, both probabilities derived by two models are above 0.8, which is regarded as a minimum probability among the nuclear medicine community when operating a photon counting detector [19].
Fig. 14.
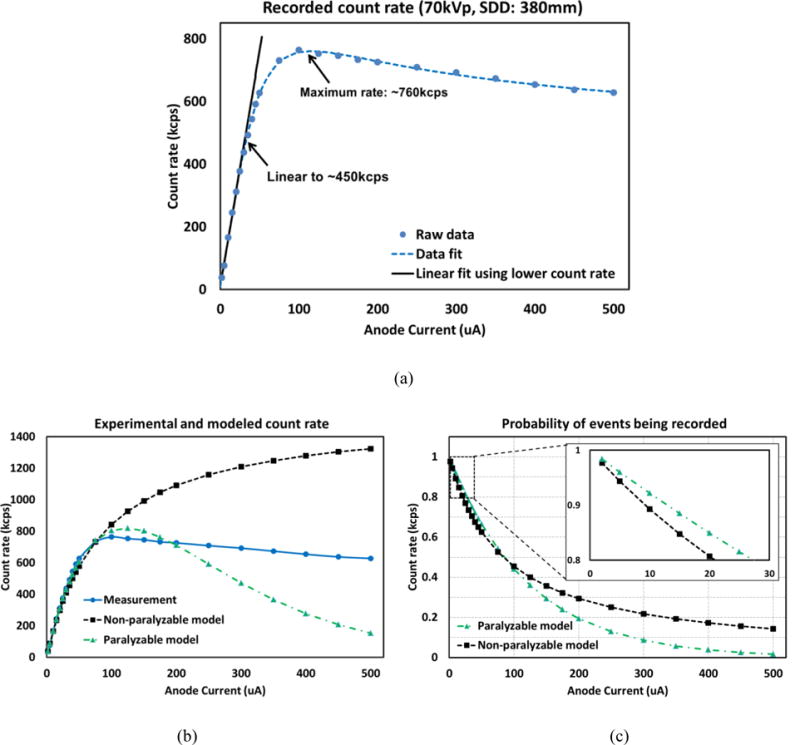
(a) Recorded count rate with respect to various X-ray tube setting with fixed X-ray tube voltage of 70kVp and source-to-detector of 380mm; (b) Comparison curves among the experiments and using two models; (c) Probabilities of events being recorded (predicted by two theoretical models).
3.5. Charge sharing effect
Charge sharing effect is almost unavoidable in photon counting detector because the radiation semiconductor is electrically, rather than physically, pixelated. The charge cloud generated from each X-ray interaction spreads laterally when it drifts toward the electrode, resulting in a sharing of induced current signals by multiple neighboring pixels. This sharing effect is further exacerbated by other processes such as energetic photoelectrons and characteristic X-rays [35]. Charge sharing effect is more pronounced for small pixels, especially less than 0.5mm and can be effectively reduced through utilizing large pixels or by post-treatment algorithms such as summing signals from several adjacent pixels at the expense of reducing spatial resolution [38]. Decreasing the thickness of the detection material is also a possible solution to reduce charge sharing effect, yet leads to a reduction of absorption efficiency.
Without properly setting the pulse height threshold, the incoming X-ray photon may be double counted if its generated charges are shared by two or more pixels. Therefore, for photon counting detector with a single threshold and small pixels, the threshold is suggested to set as half the incident photon energy, in an effort to avoid the double counting of X-rays [82]. This tutorial discusses how to subjectively and objectively observe and evaluate the charge sharing effect for a given photon counting detector.
3.5.1. Subjective observation
As aforementioned, the charges generated by an interaction in one pixel are partially shared by its adjacent pixels, thus reducing the detected pulse height compared to the original value corresponding to the deposited X-ray photon energy. Therefore, when the photon counting detector is illuminated by X-rays or gamma rays in the form of mono-energetic spectrum, a low-energy tail can be observed beside the detected pulse height peak [1, 55]. The low-energy tail exhibits stronger for those with small pixels and high insufficient charge collection [10, 36, 64, 66]. This observation is generally performed with energy response calibration and energy resolution determination using synchrotron radiation, radioactive isotopes and XRF with fluorescent materials. Note that charge sharing is an important influencing factor on energy resolution reduction and spectral distortion [38].
3.5.2. Experimental evaluation
Charge sharing effect can be also experimentally evaluated through utilizing a very narrow pencil-beam with sufficient X-ray photon flux, which is typically acquired from synchrotron radiation. During the evaluation, at least two pixels are probed by the pencil-beam in a small step equal to or smaller than the pencil-beam size in both vertical and horizontal directions [29, 83]. Then, a sensitivity map of the investigated pixels in a precision equal to or smaller than the pencil-beam size can be reconstructed based on the probing data. The schematic of probing and reconstruction process demonstrated in Fig. 15 provides the responses from adjacent pixels to a particular pixel through charge sharing effect. In Fig. 15, two adjacent pixels are probed with 49 probes each, showing that charge sharing effect is less concerned at the center of the pixel and becomes significant at the boundary between two pixels and the corners where four pixels share the charges.
Fig. 15.
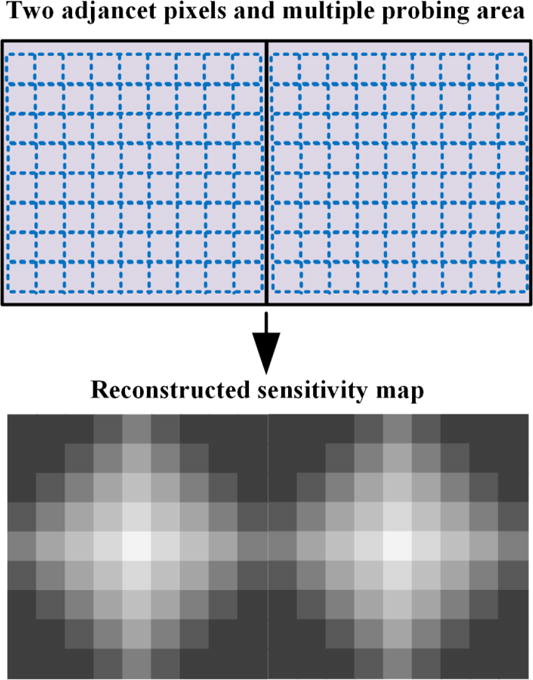
A schematic demonstrating the process of experimentally evaluating charge sharing effect using a very narrow pencil-beam from synchrotron radiation.
3.5.3. Empirical modeling
A simple model assuming a 2D isotropic Gaussian dispersion of the measured charges at the electrodes is proposed to investigate the charge sharing effect [35]. In this model, the charge cloud modeled by 2D Gaussian is centered at the location where the electron-hole pairs are generated. The shared energy is represented by the underlying area of the Gaussian dispersion spreading into the neighboring pixels while the left energy is detected by the incident pixel in which the interaction occurs. Three steps are adopted to determine the parameters for the modeled Gaussian function: 1) Measuring ideal incident spectra using a high energy resolution spectrometer from a poly-energetic X-ray tube; 2) Distorting these ideal spectra with the above charge sharing model and energy resolution model through convoluting with an energy-independent Gaussian; 3) Applying different combinations of the values for the charge sharing dispersion (FHWM) and the energy resolution to the distorted spectra and comparing them with the directly measured spectra using the photon counting detector, with respect to the width of the characteristic X-ray peaks and low energy range in the spectra. Details regarding this empirical modeling and its limitations refer to [35].
3.5.4. Numerical calculations
As mentioned above, the charge sharing effect is mainly influenced by three factors, namely photoelectron range, characteristic X-ray emission and carrier diffusion, and each factor can be numerically estimated as below [59].
Photoelectron range
When the incident X-ray photon is absorbed by photoelectric effect, a photoelectron is produced and then travels in the detection material generating electron-hole pairs before its complete dissipation. The traveling distance of the generated photoelectron is called photoelectron range which can be derived from NIST database [35, 84].
Characteristic X-ray emission
Characteristic (fluorescent) X-rays are emitted following the photoelectric effect due to the electron transition from an outer shell to an inner shell. The emission energy is equal to the binding energy difference between these two shells. These characteristic X-rays can exit the material resulting in a complete energy loss, remain in the original pixel regarding as either two separate counts with lower energies or a single count similar to pulse pile-up effect, or be absorbed by neighboring pixels. The energies of characteristic X-rays (K-shell) for typically utilized semiconductors and their mean free path (MFP) determined as the reciprocal of the linear attenuation coefficient are estimated and listed in Table. 2 [23, 35, 85, 86].
Table. 2.
Characteristic X-ray energies and mean free path.
| Fluorescent target | Si | Zn | Ga | As | Cd | Te | I | Hg |
|---|---|---|---|---|---|---|---|---|
| Atomic number (Z) | 14 | 30 | 31 | 33 | 48 | 52 | 53 | 80 |
| Kα (keV) | 1.7 | 8.6 | 9.2 | 10.5 | 23.1 | 27.3 | 28.4 | 69.8 |
| MFL for Kα (μm) | – | ~6.5 | ~50 | ~55 | ~75 | ~55 | ~91 | ~15747 |
| Kβ (keV) | 1.8 | 9.6 | 10.3 | 11.7 | 26.1 | 31.0 | 32.6 | 80.0 |
| MFL for Kβ (μm) | – | ~12 | ~55 | ~21 | ~55 | ~86 | ~118 | ~37606 |
Charge carrier diffusion
As discussed in Section 2.1, electrical charges drift towards the monolithic and pixelated electrodes separately under the influence of the externally applied electrical field. The generated charge cloud, however, increases its size during the drifting process. The average charge dispersion ( ) is associated with the detection material thickness ( ), operation temperature ( ), the bias voltage ( ), and linear attenuation coefficient ( ) under incident energy of E, as described in Eq. (10), where k is the Boltzmann constant and e is the electrical charge. Details regarding the derivation of this equation can refer to [35, 72, 87].
| (10) |
For the photon counting detector used for demonstration in this tutorial, the parameters used for calculating the average charge dispersion are: T=300K, KT/e=0.026V, d=1mm, V=400V and , and the maximum charge dispersion is less than 12μm, which is negligible compared to the pixel size of 1.1mm.
4. Remarks and conclusion
This tutorial covers the basic working principle and operating modes of a photon counting detector in Section 2, followed by a review of several aspects for detector characterization including energy response, noise floor, energy resolution, count rate performance (detector efficiency), and charge sharing effect in Section 3.
As introduced in Section 2.1, the working principle and operating modes are illustrated using a pixelated X-ray photon counting detector with basic architecture and detection mechanism with two or more parallel channels in each pixel. Photon counting detectors with specific data readout mechanism involving only one channel per pixel are also developed, in an effort to effectively reject the intrinsic electrical noise and low-energy fluorescence photons, and avoid double counting of low-energy photons due to charge sharing [16, 30, 52]. Also, two or more pulse shapers may be employed for certain photon counting counters to improve the counting efficiency [30]. The digital counter in certain photon counting detectors is designed to be gateable, meaning that the time duration of detecting X-rays can be defined by electrical digital signals (e.g. electrical shutter) [30]. This specific design provides the potential to synchronize the photon counting detector with radiation source. Another specific strategy to improve the data processing mechanism is to split the digital counter into two parts: counting part and readout part. In this way, the detector can continuously count the voltage pulses while reading out the counting number, thus minimizing the readout time but reducing the dynamic range [30].
The noise floor can be determined subjectively or objectively and the minimum threshold is suggested to set above the threshold. In real practice, however, the determination of the minimum pulse height also takes into consideration of charge sharing effect to avoid double counting of the shared X-ray photons, which is particularly important for photon counting detector with only one threshold, as discussed above. On the other hand, a simple pulse pileup rejection method is suggested to set the highest threshold at an energy corresponding to the X-ray tube voltage in photon counting detectors with multiple energy thresholds [35]. Since only the counts with energy higher than the threshold are registered, the counts in the corresponding digital counter with highest threshold can be regarded as pileup pulses only and therefore are discarded.
The measurement of energy resolution should be performed under reasonably low photon flux, but it is necessary to investigate the influence of high photon flux on energy resolution reduction, for instance in CT system [56]. For certain photon counting detector designed for operating under high photon flux, the use of conventional X-ray sources may not be sufficient to evaluate the performance towards very high flux regime and therefore intense synchrotron radiation should be utilized. A strategy of reducing the pixel size has been employed to mitigate the high photon flux when the photon counting detector is designed for CT imaging. A comparison between the unit of photons per second per mm2 and that of photons per second per pixel has been given in [7]. This method can theoretically reduce the photon rate per pixel but tend to increase the charge sharing effect, distort the detected spectrum, and reduce the energy resolution [56]. Therefore, a tradeoff between the effective photon count rate and the pixel size must be carefully balanced. With identical semiconductor material and thickness, larger pixel size leads to less charge sharing, as in human patient imaging in which the pixel sizes are usually in the order of 0.3mm or larger. Due to the requirement of high spatial resolution, the pixels are typical smaller in small animal imaging and material research [55].
Other evaluation parameters such as PSF, LSF, CTF, MTF, NPS, and DQE are also of great importance to characterize photon counting detectors. Though the related methods and techniques are similar to those used for characterizing energy-integrating detectors in general X-ray imaging systems and have been extensively investigated in literatures [29, 88–108], the differences are obvious. For example, evaluations in photon counting detectors can be performed with various energy windows investigating the dependence of detector performance on photon energies. Also, for evaluations related to the noise, the minimum pulse height threshold can be set above the noise floor determined in Section 3.2, thus removing the influence from electrical noise and dark current. In addition, the influence of charge sharing on the evaluation parameters should be taken into consideration [19, 29, 36, 38]. Methods specifically developed for characterizing photon counting detectors with respect to imaging performance can be found in [55, 66, 107–109].
For most given photon counting detectors, the optimal bias voltage which is associated with the detector material and thickness has been suggested [62]. According to the investigation performed for bias voltages of 200, 300, 400 and 500V for different pixel sizes, the optimal bias voltage should maximize the charge collection efficiency and guarantee a stable leakage current [31, 55]. Fast data processing and readout are important not only to reduce the pile-up effect but to speed up experiments in order to avoid radiation damage in the sample and increase the experimental throughput [16]. Polarization effect caused by insufficient transport properties of the semiconductor detection materials is also characterized especially for photon counting detector working for a long duration of time, because the polarization effect may cause imaging defects and count rate instabilities [7, 31, 59]. This effect can be effectively reduced through automatically and periodically resetting the applied bias voltage [31].
In conclusion, this tutorial reviews the methods and techniques for characterizing important aspects of a semiconductor based X-ray photon counting detector including energy response, noise floor, energy resolution, count rate performance (detector efficiency), and charge sharing effect, and gives remarks on other important characterization aspects such as PSF, LSF, CTF, MTF, NPS, DQE, bias voltage, radiation damage, and polarization effect. It can be a useful reference for all the X-ray imaging researchers to understand, operate, characterize, and optimize photon counting detectors in their future investigations.
Fig. 16.
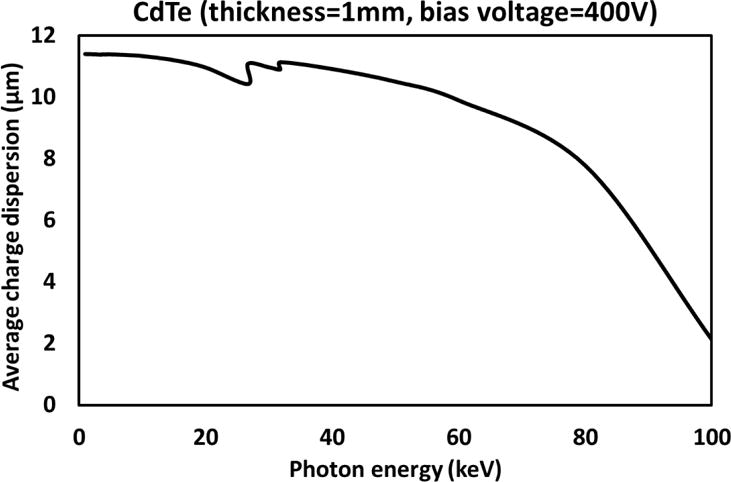
Average charge dispersion with respect to detected X-ray photon energy of the photon counting detector used for demonstration.
Acknowledgments
This research is supported in part by a grant from the University of Oklahoma Charles and Peggy Stephenson Cancer Center funded by the Oklahoma Tobacco Settlement Endowment Trust, and supported in part by NIH under grant R01 CA193378. The authors would like to acknowledge the support of the Charles and Jean Smith Chair endowment fund as well.
References
- 1.Barber WC, et al. Characterization of a novel photon counting detector for clinical CT: count rate, energy resolution, and noise performance. Proc SPIE 7258, Medical Imaging. 2009 [Google Scholar]
- 2.Taguchi K, et al. Enabling photon counting clinical X-ray CT. Nuclear Science Symposium Conference (NSS/MIC) 2009 [Google Scholar]
- 3.Cammin J, et al. A tabletop clinical x-ray CT scanner with energy-resolving photon counting detectors. Proc SPIE 7961, Medical Imaging. 2011 [Google Scholar]
- 4.Cammin J, et al. Compensation of nonlinear distortions in photon-counting spectral CT: deadtime loss, spectral response, and beam hardening effects. Proc SPIE 8313, Medical Imaging. 2012 [Google Scholar]
- 5.Kobayashi T, et al. Accuracy of linear attenuation coefficients measured with a photon counting CT system. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2012 [Google Scholar]
- 6.Kaibuki F, Matsumoto M, Ogawa K. Evaluation of CT images in the very low x-ray exposure with a photon counting detector with a CdTe semiconductor. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2013 [Google Scholar]
- 7.Taguchi K, Iwanczyk JS. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Medical Physics. 2013;40(10):100901. doi: 10.1118/1.4820371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee S, Choi Y-N, Kim H-J. A simulation study of high-resolution x-ray computed tomography imaging using irregular sampling with a photon-counting detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2013;726:175–180. [Google Scholar]
- 9.Tomita Y, et al. X-ray color scanner with multiple energy differentiate capability. Nuclear Science Symposium Conference. 2004 [Google Scholar]
- 10.Steadman R, et al. ChromAIX: Fast photon-counting ASIC for Spectral Computed Tomography. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2011;648(Supplement 1):S211–S215. doi: 10.1016/j.nima.2010.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kraft E, et al. Counting and Integrating Readout for Direct Conversion X-ray Imaging: Concept, Realization and First Prototype Measurements. IEEE Transactions on Nuclear Science. 2007;54(2):383–390. [Google Scholar]
- 12.Atak H, Shikhaliev PM. Photon counting x-ray imaging with K-edge filtered x-rays: A simulation study. Medical Physics. 2016;43(3):1385–1400. doi: 10.1118/1.4941742. [DOI] [PubMed] [Google Scholar]
- 13.Silkwood JD, Matthews KL, Shikhaliev PM. Photon counting spectral breast CT: Effect of adaptive filtration on CT numbers, noise, and contrast to noise ratio. Medical Physics. 2013;40(5):051905. doi: 10.1118/1.4800504. [DOI] [PubMed] [Google Scholar]
- 14.Roessl E, Proksa R. K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors. Physics in Medicine and Biology. 2007;52(15):4679. doi: 10.1088/0031-9155/52/15/020. [DOI] [PubMed] [Google Scholar]
- 15.Schlomka JP, et al. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Physics in Medicine and Biology. 2008;53(15):4031. doi: 10.1088/0031-9155/53/15/002. [DOI] [PubMed] [Google Scholar]
- 16.Kraft P, et al. Characterization and Calibration of PILATUS Detectors. IEEE Transactions on Nuclear Science. 2009;56(3):758–764. [Google Scholar]
- 17.Kanai Y, et al. Diagnosis of Periodontitis with the Energy Information in Dental Panoramic Image. In: Long M, editor. World Congress on Medical Physics and Biomedical Engineering May 26-31, 2012, Beijing, China. Springer Berlin Heidelberg; Berlin, Heidelberg: 2013. pp. 1117–1120. [Google Scholar]
- 18.Langlais R, et al. The cadmium telluride photon counting sensor in panoramic radiology: gray value separation and its potential application for bone density evaluation. Oral Surgery, Oral Medicine, Oral Pathology and Oral Radiology. 2015;120(5):636–643. doi: 10.1016/j.oooo.2015.07.002. [DOI] [PubMed] [Google Scholar]
- 19.Yu Z, et al. Evaluation of conventional imaging performance in a research whole-body CT system with a photon-counting detector array. Physics in Medicine and Biology. 2016;61(4):1572. doi: 10.1088/0031-9155/61/4/1572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alessio AM, MacDonald LR. Quantitative material characterization from multi-energy photon counting CT. Medical Physics. 2013;40(3):031108. doi: 10.1118/1.4790692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Maji T, et al. Material decomposition using a singular value decomposition method. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2013 [Google Scholar]
- 22.Niwa N, et al. Breast Imaging: 12th International Workshop, IWDM 2014, Gifu City, Japan, June 29 – July 2, 2014 Proceedings. Springer International Publishing; Cham: 2014. Development of Mammography System Using CdTe Photon Counting Detector for Exposure Dose Reduction; pp. 468–474. [Google Scholar]
- 23.J Bushberg JS, Leidholdt M, Jr, Boone J. The Essential Physics of Medical Imaging. Third. Lippincott Williams & Wilkins; 2012. [Google Scholar]
- 24.Pacella D, Bellazzini R, Finkenthal M. Energy resolved two-dimensional soft x-ray radiography with a micropattern gas detector. Review of Scientific Instruments. 2006;77(4):043702. [Google Scholar]
- 25.Pacella D, et al. X-VUV spectroscopic imaging with a micropattern gas detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2003;508(3):414–424. [Google Scholar]
- 26.Martin N. Scintillation detectors for X-rays. Measurement Science and Technology. 2006;17(4):R37. [Google Scholar]
- 27.Mikerov V, et al. Multi-Energy X-ray Sensors Based on Pixilated Scintillator. IEEE Transactions on Nuclear Science. 2013;60(2):963–967. [Google Scholar]
- 28.Prekas G, et al. Direct and indirect detectors for X-ray photon counting systems. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2011 [Google Scholar]
- 29.Ponchut C, et al. Evaluation of a photon-counting hybrid pixel detector array with a synchrotron X-ray source. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2002;484(1–3):396–406. [Google Scholar]
- 30.Bergamaschi A, et al. The MYTHEN detector for X-ray powder diffraction experiments at the Swiss Light Source. Journal of Synchrotron Radiation. 2010;17(5):653–668. doi: 10.1107/S0909049510026051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ruat M, Ponchut C. Characterization of a Pixelated CdTe X-Ray Detector Using the Timepix Photon-Counting Readout Chip. IEEE Transactions on Nuclear Science. 2012;59(5):2392–2401. [Google Scholar]
- 32.Cho HM, et al. Characteristic performance evaluation of a photon counting Si strip detector for low dose spectral breast CT imaging. Medical Physics. 2014;41(9):091903. doi: 10.1118/1.4892174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ding H, et al. Characterization of energy response for photon-counting detectors using x-ray fluorescence. Medical Physics. 2014;41(12):121902. doi: 10.1118/1.4900820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Xu C, et al. Performance characterization of a silicon strip detector for spectral computed tomography utilizing a laser testing system. Proc SPIE 7961, Medical Imaging. 2011 [Google Scholar]
- 35.Wang X, et al. MicroCT with energy-resolved photon-counting detectors. Physics in Medicine and Biology. 2011;56(9):2791. doi: 10.1088/0031-9155/56/9/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Spartiotis K, et al. A photon counting CdTe gamma- and X-ray camera. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2005;550(1–2):267–277. doi: 10.1016/j.nima.2009.02.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Locker M, et al. Single photon counting X-ray imaging with Si and CdTe single chip pixel detectors and multichip pixel modules. IEEE Transactions on Nuclear Science. 2004;51(4):1717–1723. [Google Scholar]
- 38.Llopart X, et al. Timepix, a 65k programmable pixel readout chip for arrival time, energy and/or photon counting measurements. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2007;581(1–2):485–494. [Google Scholar]
- 39.Song J, Liu QH, Johnson GA, Badea CT. Sparseness prior based iterative image reconstruction for retrospectively gated cardiac micro-CT. Medical Physics. 2007;34:4476. doi: 10.1118/1.2795830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yu L, Liu X, McCollough CH. Pre-reconstruction three-material decomposition in dual-energy CT. SPIE Medical Imaging, Int Society for Optics and Photonics. 2009;7258:72583V. [Google Scholar]
- 41.Yu Z, et al. Initial results from a prototype whole-body photon-counting computed tomography system. Proc SPIE 9412, Medical Imaging. 2015 doi: 10.1117/12.2082739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gutjahr R, et al. Human Imaging With Photon Counting–Based Computed Tomography at Clinical Dose Levels: Contrast-to-Noise Ratio and Cadaver Studies. Investigative Radiology. 2016;51(7):421–429. doi: 10.1097/RLI.0000000000000251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kalender WA, et al. Technical feasibility proof for high-resolution low-dose photon-counting CT of the breast. European Radiology. 2016:1–6. doi: 10.1007/s00330-016-4459-3. [DOI] [PubMed] [Google Scholar]
- 44.Pourmorteza A, et al. Abdominal Imaging with Contrast-enhanced Photon-counting CT: First Human Experience. Radiology. 2016;279(1):239–245. doi: 10.1148/radiol.2016152601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ren L, et al. Optimized acquisition time for x-ray fluorescence imaging of gold nanoparticles: a preliminary study using photon counting detector. Proc SPIE 9709, Biophotonics and Immune Responses XI. 2016 [Google Scholar]
- 46.Yu Z, et al. How Low Can We Go in Radiation Dose for the Data-Completion Scan on a Research Whole-Body Photon-Counting Computed Tomography System. Journal of Computer Assisted Tomography. 2016;40(4):663–670. doi: 10.1097/RCT.0000000000000412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhang Q, et al. Progress in the Development of CdZnTe Unipolar Detectors for Different Anode Geometries and Data Corrections. Sensors. 2013;13(2):2447. doi: 10.3390/s130202447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ballabriga R, et al. Review of hybrid pixel detector readout ASICs for spectroscopic X-ray imaging. Journal of Instrumentation. 2016;11(01):P01007. [Google Scholar]
- 49.Liu X, et al. Energy Calibration of a Silicon-Strip Detector for Photon-Counting Spectral CT by Direct Usage of the X-ray Tube Spectrum. IEEE Transactions on Nuclear Science. 2015;62(1):68–75. [Google Scholar]
- 50.Iwanczyk JS, et al. Photon Counting Energy Dispersive Detector Arrays for X-ray Imaging. IEEE Transactions on Nuclear Science. 2009;56(3):535–542. doi: 10.1109/TNS.2009.2013709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Procz S, et al. Optimization of Medipix-2 Threshold Masks for Spectroscopic X-Ray Imaging. IEEE Transactions on Nuclear Science. 2009;56(4):1795–1799. [Google Scholar]
- 52.Uher J, Jakubek J. Equalization of Medipix2 imaging detector energy thresholds using measurement of polychromatic X-ray beam attenuation. Journal of Instrumentation. 2011;6(11):C11012. [Google Scholar]
- 53.Bates R, et al. Performance of an energy resolving X-ray pixel detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2002;477(1–3):161–165. [Google Scholar]
- 54.Barber WC, et al. Large area photon counting X-ray imaging arrays for clinical dual-energy applications. Nuclear Science Symposium Conference. 2009 [Google Scholar]
- 55.Thomas K, et al. Imaging properties of small-pixel spectroscopic x-ray detectors based on cadmium telluride sensors. Physics in Medicine and Biology. 2012;57(21):6743. doi: 10.1088/0031-9155/57/21/6743. [DOI] [PubMed] [Google Scholar]
- 56.Xu C, et al. Energy resolution of a segmented silicon strip detector for photon-counting spectral CT. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2013;715:11–17. [Google Scholar]
- 57.Barber WC, et al. Energy dispersive CdTe and CdZnTe detectors for spectral clinical CT and NDT applications. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2015;784:531–537. doi: 10.1016/j.nima.2014.10.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Taguchi K, et al. Modeling the performance of a photon counting x-ray detector for CT: Energy response and pulse pileup effects. Medical Physics. 2011;38(2):1089–1102. doi: 10.1118/1.3539602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Abbene L, Gerardi G, Principato F. Digital performance improvements of a CdTe pixel detector for high flux energy-resolved X-ray imaging. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2015;777:54–62. [Google Scholar]
- 60.Ogawa K, et al. Development of an energy-binned photon-counting detector for X-ray and gamma-ray imaging. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2012;664(1):29–37. [Google Scholar]
- 61.Abbene L, Gerardi G. High-rate dead-time corrections in a general purpose digital pulse processing system. Journal of Synchrotron Radiation. 2015;22(5):1190–1201. doi: 10.1107/S1600577515013776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jakubek J. Precise energy calibration of pixel detector working in time-over-threshold mode. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2011;633(Supplement 1):S262–S266. [Google Scholar]
- 63.Ballabriga R, et al. Characterization of the Medipix3 pixel readout chip. Journal of Instrumentation. 2011;6(01):C01052. [Google Scholar]
- 64.Uher J, Harvey G, Jakubek J. X-ray fluorescence imaging with the Medipix2 single-photon counting detector. Nuclear Science Symposium Conference Record. 2010 [Google Scholar]
- 65.Cho HM, et al. Energy response calibration of photon-counting detectors using x-ray fluorescence: a feasibility study. Physics in Medicine and Biology. 2014;59(23):7211. doi: 10.1088/0031-9155/59/23/7211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Campbell-Ricketts T, Das M. Direct spectral recovery using X-ray fluorescence measurements for material decomposition applications using photon counting spectral X-ray detectors. Proc SPIE 9033, Medical Imaging. 2014 [Google Scholar]
- 67.Ren L, et al. Detection of posteriorly located breast tumors using gold nanoparticles: a breast-mimicking phantom study. Journal of X-ray science and technology. 2014;22(6):785–796. doi: 10.3233/XST-140463. [DOI] [PubMed] [Google Scholar]
- 68.Ren L, et al. Background estimation methods for quantitative x-ray fluorescence analysis of gold nanoparticles in biomedical applications. Proc SPIE 8944, Biophotonics and Immune Responses IX. 2014 [Google Scholar]
- 69.Ren L, et al. Three-dimensional x-ray fluorescence mapping of a gold nanoparticle-loaded phantom. Medical Physics. 2014;41(3):031902. doi: 10.1118/1.4863510. [DOI] [PubMed] [Google Scholar]
- 70.Ren L, et al. Method for determining the modulation transfer function of X-ray fluorescence mapping system. Optics Express. 2014;22(18):21199–21213. doi: 10.1364/OE.22.021199. [DOI] [PubMed] [Google Scholar]
- 71.Boone JM, Seibert JA. An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV. Medical Physics. 1997;24(11):1661–1670. doi: 10.1118/1.597953. [DOI] [PubMed] [Google Scholar]
- 72.Hubbell JH, Seltzer SM. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients 1 keV to 20 MeV for elements Z= 1 to 92 and 48 additional substances of dosimetric interest. National Inst. of Standards and Technology-PL; Gaithersburg, MD United States: 1995. Ionizing Radiation Div. [Google Scholar]
- 73.Youn H, et al. Energy calibration of energy-resolved photon-counting pixel detectors using laboratory polychromatic x-ray beams. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2014;760:79–85. [Google Scholar]
- 74.Tlustos L, et al. Imaging properties of the Medipix2 system exploiting single and dual energy thresholds. Nuclear Science Symposium Conference. 2004 [Google Scholar]
- 75.Maier D, Limousin O. Energy calibration via correlation. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2016;812:43–49. [Google Scholar]
- 76.Tomita Y, et al. X-ray color scanner with multiple energy discrimination capability. Proc SPIE 5922, Hard X-Ray and Gamma-Ray Detector Physics VII. 2005 [Google Scholar]
- 77.Matsumoto M, Kaibuki F, Ogawa K. K-edge imaging with a photon counting CT system. Nuclear Science Symposium and Medical Imaging Conference. 2013 [Google Scholar]
- 78.Cho HM, et al. The effects of photon flux on energy spectra and imaging characteristics in a photon-counting x-ray detector. Physics in Medicine and Biology. 2013;58(14):4865. doi: 10.1088/0031-9155/58/14/4865. [DOI] [PubMed] [Google Scholar]
- 79.Taguchi K, et al. An analytical model of the effects of pulse pileup on the energy spectrum recorded by energy resolved photon counting x-ray detectors. Medical Physics. 2010;37(8):3957–3969. doi: 10.1118/1.3429056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Taguchi K, et al. Pulse pileup statistics for energy sensitive photon counting detectors with pulse height analysis. Proc SPIE 8313, Medical Imaging. 2012 [Google Scholar]
- 81.Roessl E, Daerr H, Proksa R. A Fourier approach to pulse pile-up in photon-counting x-ray detectors. Medical Physics. 2016;43(3):1295–1298. doi: 10.1118/1.4941743. [DOI] [PubMed] [Google Scholar]
- 82.Broennimann C, et al. The PILATUS 1M detector. Journal of Synchrotron Radiation. 2006;13(2):120–130. doi: 10.1107/S0909049505038665. [DOI] [PubMed] [Google Scholar]
- 83.Marinho F, Akiba K. A GEANT4 based simulation for pixelated X-ray hybrid detectors. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2015;772:50–51. [Google Scholar]
- 84.Berger MJ, et al. Stopping-power and range tables for electrons, protons, and helium ions. NIST Physics Laboratory; 1998. [Google Scholar]
- 85.Using XRAYLIB, C. et al. XRAYLIB tables (X-ray fluorescence cross-section) 2003 [Google Scholar]
- 86.Brunetti A, et al. A library for X-ray–matter interaction cross sections for X-ray fluorescence applications. Spectrochimica Acta Part B: Atomic Spectroscopy. 2004;59(10–11):1725–1731. [Google Scholar]
- 87.Knoll GF. Radiation detection and measurement. John Wiley & Sons; 2010. [Google Scholar]
- 88.Wu D, et al. Characterization of a high-energy in-line phase contrast tomosynthesis prototype. Medical Physics. 2015;42(5):2404–2420. doi: 10.1118/1.4917227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Wu D, et al. DQE characterization of a high-energy in-line phase contrast prototype under different kVp and beam filtration. Proc SPIE 9324, Biophotonics and Immune Responses X. 2015 [Google Scholar]
- 90.Ghani MU, et al. Investigation of spatial resolution characteristics of an in vivo microcomputed tomography system. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2016;807:129–136. doi: 10.1016/j.nima.2015.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Ghani MU, et al. Characterization of operating parameters of an in vivo micro CT system. Proc SPIE 9709, Biophotonics and Immune Responses XI. 2016 [Google Scholar]
- 92.Zhou Z, et al. Monotone spline regression for accurate MTF measurement at low frequencies. Optics Express. 2014;22(19):22446–22455. doi: 10.1364/OE.22.022446. [DOI] [PubMed] [Google Scholar]
- 93.Wong MD, Zhang D, Liu H. Step by step analysis toward optimal MTF algorithm using an edge test device. Journal of X-ray science and technology. 2009;17(1):1–15. doi: 10.3233/XST-2009-0210. [DOI] [PubMed] [Google Scholar]
- 94.Zhang D, et al. Imaging characteristics of a high resolution computed radiography system. Journal of X-ray science and technology. 2006;14(4):273–282. [Google Scholar]
- 95.Zhou Z, et al. Improving the accuracy of MTF measurement at low frequencies based on oversampled edge spread function deconvolution. Journal of X-ray science and technology. 2015;23(4):517–529. doi: 10.3233/XST-150506. [DOI] [PubMed] [Google Scholar]
- 96.Zhang D, Liu H, Wu X. DQE analysis on a dual detector phase x-ray imaging system. Physics in Medicine and Biology. 2008;53(18):5165. doi: 10.1088/0031-9155/53/18/021. [DOI] [PubMed] [Google Scholar]
- 97.Ghani MU, et al. Noise Power Characteristics of a Micro–Computed Tomography System. Journal of Computer Assisted Tomography. 2017;41(1):82–89. doi: 10.1097/RCT.0000000000000483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Liu H, Fajardo LL, Penny BC. Signal-to-noise ratio and detective quantum efficiency analysis of optically coupled CCD mammography imaging systems. Academic Radiology. 1996;3(10):799–805. doi: 10.1016/s1076-6332(96)80269-8. [DOI] [PubMed] [Google Scholar]
- 99.Jiang H, Chen WR, Liu H. Techniques to improve the accuracy and to reduce the variance in noise power spectrum measurement. IEEE Transactions on Biomedical Engineering. 2002;49(11):1270–1278. doi: 10.1109/TBME.2002.804595. [DOI] [PubMed] [Google Scholar]
- 100.Ouandji F, et al. Characterization of a CCD-based digital x-ray imaging system for small-animal studies: properties of spatial resolution. Applied Optics. 2002;41(13):2420–2427. doi: 10.1364/ao.41.002420. [DOI] [PubMed] [Google Scholar]
- 101.Zhang D, et al. Preliminary Feasibility Study of an In-line Phase Contrast X-Ray Imaging Prototype. IEEE Transactions on Biomedical Engineering. 2008;55(9):2249–2257. doi: 10.1109/TBME.2008.919136. [DOI] [PubMed] [Google Scholar]
- 102.Wu X, Wong MD, Deans AE, Liu H. X-ray diagnostic techniques, in. In: Vo-Dinh T, editor. Biomedical Photonics Handbook, Vol II : Biomedical Diagnostics. CRC Press; 2015. pp. 415–451. [Google Scholar]
- 103.Dammann H. Model MTF for Conventional X-ray Imaging Systems. Optica Acta: International Journal of Optics. 1977;24(4):385–390. [Google Scholar]
- 104.Kozyrev EA, Kuper KE, Lemzyakov AG, Petrozhitskiy AV, Popov AS. Performance and Characterization of CsI: Tl thin Films for X-ray Imaging Application. Physics Procedia. 2016;84:245. [Google Scholar]
- 105.Duan Y, et al. Non-uniform sampling knife-edge method for camera modulation transfer function measurement. Proc SPIE 10023, Optical Metrology and Inspection for Industrial Applications IV. 2016 [Google Scholar]
- 106.Ghani MU, et al. Characterization of continuous and pulsed emission modes of a hybrid micro focus x-ray source for medical imaging applications. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2017;853:70–77. doi: 10.1016/j.nima.2017.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Tanguay J, et al. Detective quantum efficiency of photon-counting x-ray detectors. Medical Physics. 2015;42(1):491–509. doi: 10.1118/1.4903503. [DOI] [PubMed] [Google Scholar]
- 108.Michel T, et al. A fundamental method to determine the signal-to-noise ratio (SNR) and detective quantum efficiency (DQE) for a photon counting pixel detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2006;568(2):799–802. [Google Scholar]
- 109.Ponchut C. Characterization of X-ray area detectors for synchrotron beamlines. Journal of Synchrotron Radiation. 2006;13(2):195–203. doi: 10.1107/S0909049505034278. [DOI] [PubMed] [Google Scholar]


