Peptide Solubility Limits: Backbone and Side-Chain Interactions

Abstract

We calculate the solubility limit of pentapeptides in water by simulating the phase separation in an oversaturated aqueous solution. The solubility limit order followed by our model peptides (GGRGG > GGDGG > GGGGG > GGVGG > GGQGG > GGNGG > GGFGG) is found to be the same as that reported for amino acid monomers from experiment (R > D > G > V > Q > N > F). Investigation of dynamical properties of peptides shows that the higher the solubility of a peptide is, the lower the time spent by the peptide in the aggregated cluster is. We also demonstrate that fluctuations in conformation and hydration number of peptide in monomeric form are correlated with the solubility of the peptide. We considered energetic mechanisms and dynamical properties of interbackbone CO–CO and CO···HN interactions. Our results confirm that CO–CO interactions more than the interbackbone H-bonds are important in peptide self-assembly and association. Further, we find that the stability of H-bonded peptide pairs arises mainly from coexisting CO–CO and CO···HN interactions.

Graphical Abstract

INTRODUCTION

Solubility is an important factor which drives a range of chemical and biological phenomena.¹ The solubility limit of a solute is defined by the concentration of the solution at saturation. In such a solution both the free energy of solvation as well as the effective interactions among solutes determine the properties of the system including conformations and phase behavior. Cellular cytoplasm is a concentrated, crowded mixture with many components near their solubility limits.² The phase behaviors of proteins and protein–RNA mixtures establish the formation and activity of nonenveloped organelles, also referred to as membraneless organelles or biomolecular condensates, in cells.^3,4 These structures are known to play a role in the regulation of many biological processes.

Aggregation of proteins and peptides, driven by solubility, has been shown to share molecular mechanisms similar to the collapse of the polypeptide chain.^5,6 Many efforts have been made to understand the role of side-chains in the collapse and folding of proteins.^7–9 The role of the backbone in this process is understood to be of similar importance to that of the side-chains from transfer free energy measurements.¹⁰ A number of experimental and theoretical efforts have worked to parse the effects of the side-chains from the backbone.^11,12 The backbone has often been modeled as either an alanine or a glycine chain.¹³ Here we use oligoglycine as our reference to understand the effect that various side-chains have on the solubility limit of peptides in solution.

Although the free energy of hydration is more favorable for dilute solutions of longer oligoglycines, they collapse in water to unstructured globules.^6,14–17 Experimentally, the solubility of oligoglycines in water reduces with length.¹⁸ This suggests that self-association of backbone amide (CONH) groups and backbone–water interactions are enhanced at different rates with respect to the length of the peptide leading to backbone collapse. Simulation was employed recently to model the saturation concentration of pentaglycine in water.⁵ The purpose of the present study is to extend solubility limit modeling to aid in the interpretation of side-chain effects on peptide aggregation.

Here, we probe the role of various interactions involving backbone and side-chains involved in aggregation and hence solubility of peptides. Backbone hydrogen bonding (H-bonding) interactions have long been proposed to control collapse of proteins into their folded states.^19,20 Interactions that govern peptide molecular recognition via aggregation and protein collapse share similar features. Significant numbers of H-bonds are observed in the reported well-ordered structures produced from self-assembly of oligoglycines (polyglycines I and II).^21,22 In polyglycine I which resembles a β-structure, each chain forms H-bonds with neighboring parallel or antiparallel chains.²¹ Similarly, oligoglycine chains are parallel and hexagonally packed in polyglycine II crystals, and each of these chains forms a single H-bond with each of its six identical neighbors.²² Because of competition with water molecules in a solution, a reduction in the contribution of H-bonds to the stability of peptide clusters is expected in water as observed in simulations of pentaglycines in water.⁵ We note that each H-bond between amide groups in water has been shown to contribute 1–2 kcal/mol favorably of free energy which is significantly less than the contribution (>3 kcal/mol) upon burial and dehydration.^23–31

In addition to backbone H-bonds, other dipolar interactions among groups in the main-chain occur as well. Backbone interactions between dipoles, especially of the carbonyl groups, CO–CO, with a contact distance less than 4 Å are common in helices and β-sheets.^32,33 These contacts arise from interactions between the carbonyl (CO) dipoles,^34,35 and have been ascribed to the so-called n → π* interaction.^36–43 In classical terms, the attraction between the oppositely charged atoms is given angular dependence by excluded volume and the like charge repulsions which constitute a major part of the amide dipole–dipole interactions.^32,43,44 It has been argued that interactions between CO groups modulate conformations of peptides, peptoids, and related small molecules.^{32–41,44–48} Relevant to these findings, perturbation theory (IMPT) applied to a perpendicular propanone dimer shows that the attractive energy of a nonbonded CO–CO interaction is comparable to the CO···HN H-bond in water.⁴⁹ In their computational analyses of helices and β-sheets in native proteins, Maccallum et al. found that CO–CO interactions are occasionally more attractive than CO···HN H-bonds, and backbone H-bonds usually deviate from linearity and adopt a geometry that maximizes the favorable CO–CO interaction.³²

Collapsed states as well as the aggregated structure of oligoglycines in water have been found to have more numerous CO–CO interactions than backbone H-bonds.^5,6,15,17 Such systems are quite disordered compared to folded proteins or crystalline peptides. Despite the high abundance of short-range CO–CO interactions and their similarity in magnitude of attractive strength to H-bonds in water, they have received less attention in protein folding research relative to that of H-bonds due to the central importance of secondary structure. Motivated by the necessity of understanding the nature of backbone CO–CO and CO···HN interactions and their relative importance in self-association of backbone amide groups, we present an analysis of these interactions for a variety of concentrated peptide solutions.

Side-chains play important roles in the solubility of a peptide as well as protein folding.^10,50 As in the case of oligoglycines, the solubility limit of an amino acid in water cannot be predicted from its hydration free energy alone; an amino acid with more favorable dilute solution hydration free energy is not necessarily more soluble in water. For example, despite its much more favorable hydration free energy, Gln is less soluble than Val in water.^50–54 Some glycine-rich proteins have been found to exhibit globular-like conformations⁵⁵ but without a hydrophobic side-chain core. These systems violate the premise that folding is driven by the hydrophobic side-chains gravitating to the interior, avoiding the solvent, but rather highlights our hypothesis that folding is a cooperative and correlated process between the solute–solvent and solute–solute enthalpic and entropic energies. The backbone dihedrals, the solute inter- and intramolecular interactions, including the H-bond network, and the solute–solvent interactions work with or against each other to drive the system to a collapsed or folded state. We conduct our investigation on model pentaglycines substituted with six different amino acid side-chains using unsubstituted pentaglycine as a reference. Structural, energetic, and dynamical properties of various interactions involving backbone and side-chains are investigated to probe the nature of these interactions and their relative importance in self-assembly of our model peptides. Preferential interaction coefficients and transfer free energies have also been used to decipher protein and peptide interactions in unfolding and aggregation,^56,57 but have not been included as part of this study.

The rest of this study is organized into three sections. After the description of the systems, models, and methods employed in this study, we present the results obtained from simulations. We first address aggregation and the solubility limit of our model peptides in water. Stability of peptides in the aggregated cluster as well as in saturated solution are compared thereafter. This is followed by a presentation of structural, energetic, and dynamic properties. We summarize the findings and draw our conclusions in the last section.

MODELS AND METHODS

We wish to interpret the side-chain effects on the solubility of pentapeptides and to understand the role of various interactions involving backbone and side-chains behind aggregation. To consider the solubility limit of peptides, we performed MD simulations of peptides with uncharged sequences GGGGG, GGNGG, GGQGG, GGVGG, and GGFGG, as well as charged side-chains GGRGG and GGDGG denoted here, respectively, as gly, asn, gln, val, phe, arg, and asp at finite concentration in explicit water. The peptides were initially built in extended conformation with the ends capped with acetyl (CH₃CO) and N-methyl (NHCH₃) groups using the AMBER⁵⁸ software package. There were 625 peptides and ~90 000 water molecules then arranged on a lattice in a cubic box (see Table SI-I for overview of simulations) giving a total concentration of around 0.3 M, which is expected to be well above the solubility limit. For those with charged side-chains, arg and asp, we included 0.1 M NaCl and neutralizing ions. Due to the nature of the systems with net charge, some analyses (e.g., dipole correlations, etc.) are only performed and compared for the uncharged side-chains chosen.

Our protocol to avoid the metastable parts of the phase diagram and kinetic traps follows our previous work.⁵ After energy minimization, simulations were performed first in the isothermal–isobaric (NpT) ensemble for 2 ns with targeted temperature and pressure of 300 K and 1 atm, respectively, and then in the canonical (NVT) ensemble for 1 ns with the average box volume obtained from the last 1 ns of the previous NpT simulation run. Finally, 140 ns of MD trajectories were generated in the microcanonical (NVE) ensemble, the last 40 ns of which were considered for equilibrium analysis. This choice of ensemble in a large system ensures that thermostats and barostats are not affecting the phase behavior.

The NAMD⁵⁹ package was employed. The simulations used the TIP3P⁶⁰ water with the peptide forces described by the AMBER ff12SB force field. We employed an integration time step of 2 fs and a spherical cutoff distance of 12 Å for nonbonding interactions. The long-range electrostatic interactions were treated with the particle mesh Ewald method. All bonds involving hydrogen were constrained using the SHAKE algorithm.

In earlier work in this laboratory⁶¹ a comparative analysis of force fields for short, Gly₃, and long, Gly₁₀, peptides in solution as a function of three all-atom molecular mechanics force fields was performed. Those long simulations, 300 ns and 1 μs, for 2 different peptide lengths allowed evaluation of the structural metrics, such as the end-to-end distance, radius of gyration, and the distribution of conformations to be evaluated as a function of force field. The results showed different structural tendencies based on the force field. In particular, the CHARMM 36 (C36) force field tended to produce more extended conformations. Others have discussed the ability of the molecular mechanics force field to represent the protein–solvent interactions, in particular those of intrinsically disordered systems.^62–66 These involve modifications to existing terms, use of alternate solvent parameters, or entirely new force field parameter sets. In this study we are not comparing the force field parameters but, instead, choose to evaluate the details of aggregation using one of the commonly used molecular mechanics force fields.

RESULTS AND DISCUSSION

Solubility Limit of Peptides

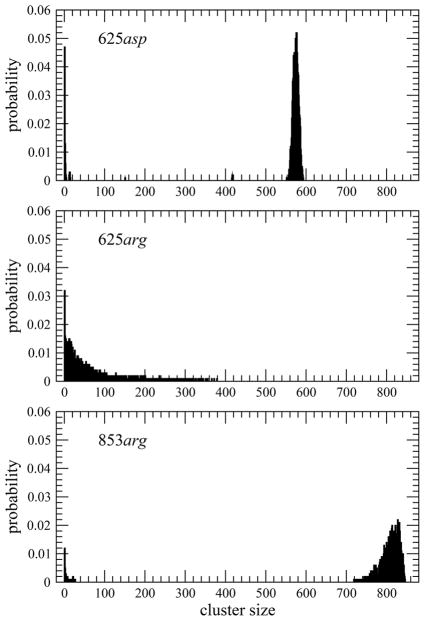
All of the uncharged systems studied spontaneously phase separated in tens of nanoseconds from initiation, similar to our previous study of GGGGG using the CHARMM potential.⁵ After the saturated solution was equilibrated, we performed clustering analyses of our model peptides. A cutoff distance of 4 Å between heavy atoms of different peptides was applied for this clustering. The time-averaged, bimodal distribution of the peptides in clusters of different sizes, shown in Figure 1, demonstrates the presence of the expected phase separation. All systems had a dilute phase with a few peptide monomers and small clusters (up to 5) along with a concentrated phase of large clusters of size greater than 570. As expected, the phase separated systems avoid clusters of intermediate sizes when far from metastability.

Figure 1.

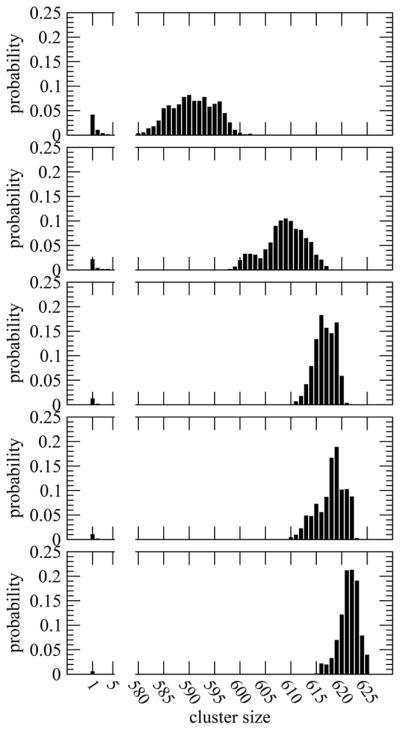
Probability (normalized to one) of finding uncharged peptides in clusters of different sizes for systems gly, val, gln, asn, and phe (from top to bottom, respectively).

Our simulations display the effects of side-chains in peptide aggregation. We find that, in the case of gly, the average number of peptide monomers in the saturated solution is around 26, and clusters in the concentrated phase average 590.7 ± 0.8. For the other uncharged compounds we find peptide aggregation increases and the solubility limit decreases in the presence of the side-chains chosen. We note that these span a range of classical hydrophobicity scales.⁶⁷ The number of monomers or small clusters with these side-chains decreases, and the distribution shifts in favor of large clusters. The average size of the large uncharged cluster is greatest in the phe system, 621.4 ± 0.4. The cluster size is slightly higher for asn (618.0 ± 0.6) than that for gln (616.7 ± 0.4) which, in turn, is higher than that for val (608.8 ± 0.9).

For the charged systems arg and asp, we tried the same procedure. We found that the asp system followed the expected phase separation pattern of the uncharged side-chain solutions. The arg system did not. We expected it to be more soluble, but we had issues with metastability and the system did not phase separate after 200 ns. This was reminiscent of what was seen in an earlier simulation with a solution of the gly system roughly 10 times more dilute,⁵ while above the solubility limit the metastability issues led to no discernible phase separation in 200 ns. This is evident in Figure 2. Thus, for arg we raised the initial concentration by more than a third to include 853 arg peptides. This system phase separated and produced stable averages without further issues.

Figure 2.

Probability (normalized to 1) of finding charged peptides in clusters of different sizes. In the top two panels, both systems had 625 GGXGG peptides. The failure of the arg system to clearly phase separate led us to increase the initial concentration to 853 GGRGG peptides shown in the bottom panel.

The large cluster formed by the solutes after phase separation is often continuous across the periodic boundary box (Figure SI-1). This arrangement, which is stable due to interpeptide interactions, is similar to that seen in the aggregation of hydrophobic particles and other phase separations.^68,69 Each solution here separates into organic-rich and water-rich (peptide saturated) phases (Figure SI-1). The peptide concentration in the saturated solution was measured by subtracting the number of peptides in the large cluster from the total divided by the solvent excluded volume remaining after removing that cluster. We used the software package DAlpha-ball⁷⁰ to compute solvent excluded volume of the large cluster.

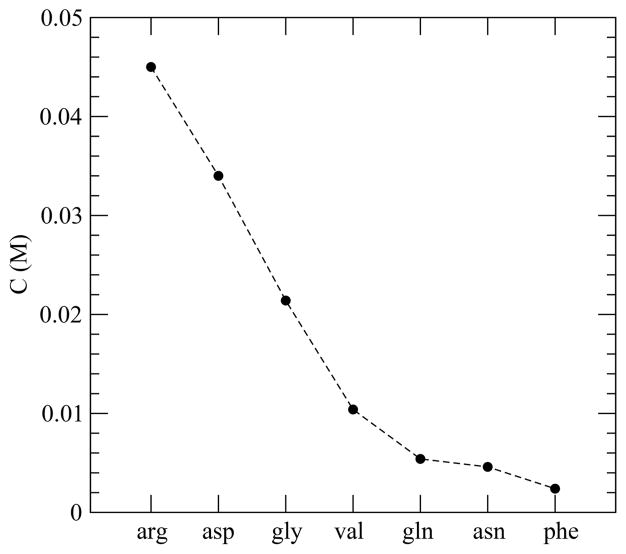
In Figure 3, we present the concentration of peptides in the saturated solution or the solubility limit for each system. For pentaglycine, we find that the concentration of the saturated solution is 0.021 ± 0.001 M, which is higher than that measured (0.016 ± 0.003 M) with another force field previously.⁵ The experimentally¹⁸ measured solubility of pentaglycine is 0.005 M at pH 5.4 and temperature 298.15 K which is 4 times lower than the force field dependent estimate here. We remark that none of the current force fields were parametrized to fit this property, nor were they parameterized at pH values comparable to experimental ones.

Figure 3.

Peptide concentration in saturated solution for all the systems studied.

As expected, the amount of peptide in the saturated solution, or in other words the solubility of the peptide, decreases in the presence of nonpolar side-chains relative to gly and increases for those systems studied with charge. For instance, we find that substitution of a H-atom in a glycine unit with a benzyl (C₆H₅CH₂–) group causes more reduction in solubility than that with an iso-propyl ((CH₃)₂CH₂–) group. That is in agreement with the experimental finding that aqueous solubility of amino acid molecules decreases on enhancing the nonpolar portion.^53,54 Beyond classically hydrophobic residues, we also find that substitution of a glycine unit with an asparagine or a glutamine, both of which have polar side-chains, also gives a solubility less than gly. The charged side-chains produce a strong increase in solubility over the gly system. Overall, solubility of our model peptides follows an order (arg > asp > gly > val > gln > asn > phe) which is the experimental aqueous solubility of amino acid molecules.^50,53,54

Stability of Peptides in Organic-Rich and Water-Rich Phases

Each monomer in the peptide saturated water-rich phase has 40–45 (depending on the peptide considered) water molecules within 4 Å of peptide heavy atoms (see Figure SI-3). Considering the neutral side-chain systems, computation of the total stabilization energy of each monomer arising from its interaction energies with these water molecules suggests a trend (gln > asn > phe > gly > val) for the systems studied which is similar to the trend in solvation free energy of neutral Gly, Val, Gln, Asn, and Phe units in water as reported from Monte Carlo simulations.⁵¹ In a more recent free energy simulation study of N-acetyl-X-methylamide amino acids, Boresch and co-workers observed a slightly altered trend in dilute solution solvation free energy with Gln > Asn > Gly > Phe > Val.⁵² The solvation free energy values and their ordering in these previous studies^51,52 were found to depend strongly on whether they were capped or zwitterionic. These results in light of the current study indicate how solvation free energy is only one factor determining the solubility limit and phase behavior.

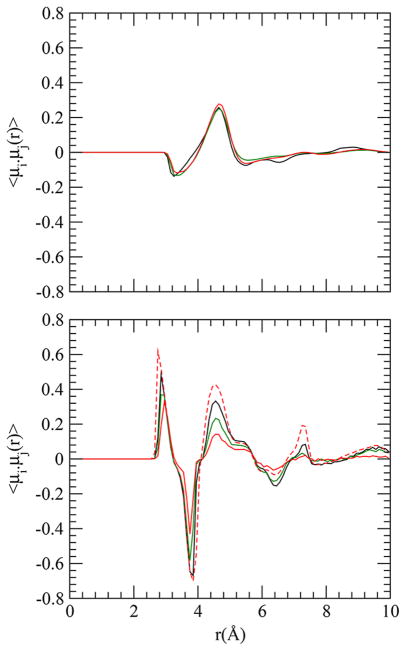
We considered both intramolecular and intermolecular correlations between amides. Previous simulations showed a distinctive correlation between amide dipoles within an oligoglycine with a strong positive correlation (parallel dipoles) near 3 Å and a strong negative correlation (antiparallel dipoles) near 4 Å.^5,6 Such distinctive correlations arise from constraints created by bonded peptide backbone and hence should be dependent on conformational fluctuation of the peptide. We computed the correlation between amide dipoles i and j at a distance r, 〈μ_i·μ_j(r)〉, similarly to that described previously.⁵

The curves for pentaglycine (both intrapeptide and interpeptide), presented in Figure 4, are very similar to those found for another force field.⁵ However, the intrapeptide correlation declines with larger uncharged side-chains; the correlation almost vanishes in the case of F-substituted pentaglycine. Larger uncharged side-chain substitution reduces the conformational space available in solution. The trend of decreasing correlation gly < val < gln < asn < phe is similar to that of aggregation propensity of the peptides studied. Also, in line with the expectation that conformational fluctuation of a peptide decreases on moving from monomeric form to a large cluster, we find that the intrapeptide dipole correlation is stronger for a peptide in the cluster than that in monomeric form (Figure 4).

Figure 4.

Interpeptide (top) and intrapeptide (bottom) dipole correlations as a function of distance in systems gly (black), gln (green), and phe (red). Solid and dashed lines in the bottom panel are, respectively, for monomeric peptides and for all peptides in the system (in the cluster as well as in saturated solution).

The behavior of the hydration layer for the uncharged peptides was examined by calculating a water number fluctuation function, N_w(t), for isolated monomers and peptides in the organic-rich phase. The function was defined as

$$N_{\mathrm{w}}(t)=\frac{\langle n_{\mathrm{w}}(t)\rangle -\langle n_{\mathrm{w}}\rangle }{\langle n_{\mathrm{w}}\rangle }$$ (1)

where n_w(t) represents the number of waters of hydration (contact waters) at time t and n_w is the average number of hydration water. The average hydration number at time t and for the entire simulation was estimated separately for peptides in clusters and in monomeric form. A cutoff distance of 4 Å between peptide heavy atoms and water oxygen was used to define a water molecule in the hydration layer.

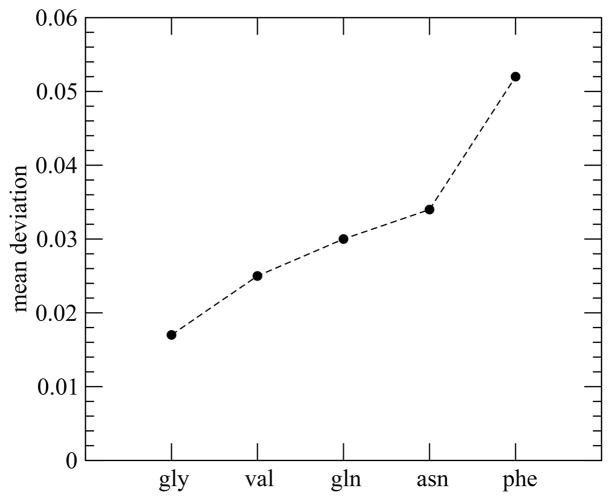
The uncharged side-chain differences affect the fluctuation in hydration number of monomeric peptides (Figure SI-2). The greater the fluctuation in the hydration number is, the higher the aggregation propensity of the peptide is. Fluctuation of N_w(t) for phe, the highest among the peptides studied, is nearly 3 times that for pentaglycine. This is in accord with modern theories of the hydrophobic effect related to the fluctuation of the first solvation shell water.^71,72 We note that the order for the fluctuations (Figure 5) is the same as that for the solubility limits but has differences with many hydrophobicity scales.^67,73 These findings are also in accord with previous work on the hydration layer of helices facilitating the actin binding process of protein HP-36.⁷⁴

Figure 5.

Mean deviation of water number fluctuation function.

The interaction energy of an uncharged peptide with a water does not depend strongly on size of the cluster to which the peptide belongs although the total stabilization energy from water does (Figure SI-3). However, because clustering increases the local density of peptides, the total energetic gain from interpeptide interactions increases significantly in a large cluster. This stabilization is higher in magnitude than the energetic loss from the reduction in the number of water molecules interacting directly with a tagged peptide in large cluster. We find a decrease in energy of 26–35 kcal/mol on moving from its monomeric state to a large cluster, which provides a noteworthy energetic contribution to peptide clustering.

We calculated a free energy change, ΔG_s, for peptides between the saturated solution and the large cluster using the relation ΔG_s = −RT ln K_s, where K_s is the equilibrium constant defined as

$$K_{\mathrm{s}}=\frac{[\text{LC}]}{[\text{SS}]}$$ (2)

In this definition, [LC] and [SS] represent molar concentrations of peptides in the large clusters and saturated solution, respectively. The estimated values of K_s and ΔG_s for the uncharged systems are in Table 1. Since we are well beyond the solubility limit, peptide aggregation is spontaneous and favored in all the systems studied. The relative stability of the cluster is smallest for gly and greatest for phe. We find the relative cluster stability of the uncharged peptides to be gly < val < gln < asn < phe.

Table 1.

Cluster Stability^a

system	Ks	ΔGs	τ	non	noff
gly	17.2	−1.7	965	77.8	77.9
val	37.6	−2.2	1314	55.3	55.6
gln	74.3	−2.6	1416	26.2	26.2
asn	88.3	−2.7	1665	23.7	23.8
phe	172.6	−3.1	1703	23.1	23.0

^aK_s, ΔG_s, and τ represent, respectively, equilibrium constant, relative stability of large cluster (in kcal/mol), and lifetime (in ps) of a peptide in large cluster. n_on and n_off, respectively, are the number of peptides that reach and leave the cluster per nanosecond.

During the simulations, a cluster changes its size by collecting or releasing one or more monomers. Therefore, following Rashke et al.,⁶⁸ we compute the free energy (ΔG_m) of formation of a cluster of size n + 1 (S_n+1) by addition of a monomer (S₁) to a cluster of size n (S_n) using the relation $K_{\mathrm{m}}=\frac{[{\mathrm{S}}_{n+1}]C_0}{[{\mathrm{S}}_n][{\mathrm{S}}_1]}={\mathrm{e}}^{-1/RT\mathrm{\Delta }{G}_{\mathrm{m}}}$ where K_m is the equilibrium constant for the monomer addition process and C₀ is the reference state. Figure 6 presents the average molar concentration of each cluster used in the free energy of cluster formation. We find that formation of a large cluster is more favorable than that of a dimer or trimer. On average, the free energy of formation of a large cluster of pentaglycine by monomer addition is around −2.6 kcal/mol. The cluster formation becomes more favorable for the uncharged substituted pentaglycines. The average free energy of cluster formation is −3.0 kcal/mol in val, −3.3 kcal/mol in gln, −3.6 kcal/mol in asn, and −3.8 kcal/mol in phe.

Figure 6.

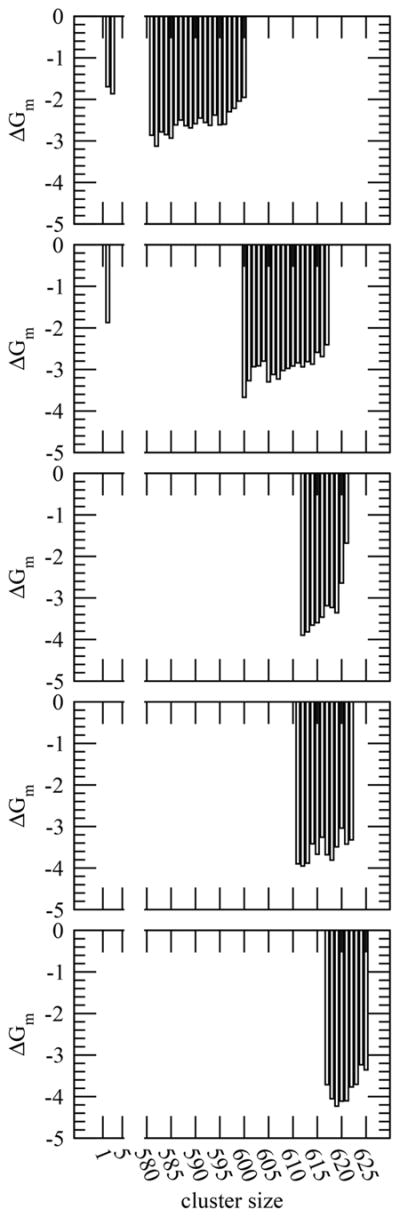
Free energy (in kcal/mol) of cluster formation by monomer addition for systems gly, val, gln, asn, and phe (from top to bottom, respectively). Clusters with very low concentrations are excluded in the free energy calculations.

Dynamical Properties of Peptide Clusters

To compare the kinetic stability of our model uncharged peptide clusters, we calculated the average lifetime of a peptide in a large cluster as well as the flux to leave the cluster. This would be complicated by charge neutrality for the charged systems, and so, we restrict the analysis to the neutral solutes. We use a survival function, S(t), to calculate lifetime.

$$S(t)=\frac{\langle h(0)H(t)\rangle }{\langle h(0)\rangle }$$ (3)

In this relation, the variable h is equal to unity when the tagged peptide makes contact with a large cluster and is zero otherwise. The other variable H takes a value of unity if the tagged peptide remains continuously connected to the large cluster to time t and is zero otherwise.

In all the neutral systems studied, the survival function decays rapidly during the initial periods. However, there are some peptides that remain in the large cluster for almost 40 ns before leaving or exchanging with those in solution. We find that the relaxation of the function for our neutral peptides is the fastest for gly and the slowest in system phe, indicating relative kinetic stability. We show in Table 1 the average lifetime of a peptide in the large cluster as estimated by time integration of S(t). For the neutral system it can be seen that gly spends the shortest time in the large cluster, whereas time spent by phe is nearly 2 times longer. This is further reflected in the average number of peptides that leave the cluster per nanosecond (n_off). We find that n_off is at a maximum for gly and at a minimum for phe (Table 1), despite the presence of the smallest cluster in the former and the largest cluster in the latter. As a check of equilibrium, the number of peptides that leave the cluster per nanosecond was found to be essentially equal to the number of peptides that join the cluster per nanosecond (n_on).

Interactions on Neutral Peptide Aggregation

To develop an assessment of forces that stabilize the large cluster formed by our model peptides, we investigated structural, energetic, and dynamical properties of CO–CO and CO···HN H-bonding interactions. Following earlier work,⁷⁵ a H-bond was identified by imposing cutoff distances for N–O and O–H (of 3.4 and 2.4 Å, respectively, here), and a simultaneous cutoff angle (of 45°) for H–N–O. We considered that a CO–CO interaction exists if the O–C separation does not exceed 4 Å. The stabilization energies of a backbone CO involved in either CO–CO or CO···HN H-bonding interactions are simply obtained from the nonbonded energy function.

Only the CO-to-CO and CO-to-NH interactions (rather than the whole peptide moiety) were used to calculate stabilization energy. Note that H-bond strength in the DSSP algorithm⁷⁶ for assigning protein secondary structure elements is measured by considering only CO-to-NH interactions as in our study, but instead of employing the full nonbonded potential, it employs only the electrostatic part and hence overestimates attraction between close oppositely charged atoms. Finally, the average lifetimes of these interactions were computed by time integration of the survival function, S(t), as defined in eq 3. The variable h in this case is equal to unity when the tagged CO–CO or CO···HN pair exists and is zero otherwise. The other variable H takes a value of unity if the tagged pair remains continuously paired to time t and is zero otherwise.

In all the systems studied, the number of H-bonds formed by a peptide with surrounding peptides with this definition is 1.9–2.4 with the current potential model (Table SI–II). With a different potential and H-bond definition, previous studies found that number to be around 2 for the aggregation of pentaglycines.⁵ A β_10–40 peptide collapse in water has been found to be driven by a small number of H-bonds.⁷⁷ Given that pentapeptides with the blocking groups could make 6 donor and 6 acceptor H-bonds by either definition, the number found in these relatively unstructured clusters is far less than that expected from maximally H-bonded regular structures familiar from secondary structural elements.

We find that the number of CO–CO interactions as defined here is more than twice the number of H-bonds. It is notable here that, for a strict cutoff distance of 3.6 Å, which is the reported³² average distance between C- and O-atoms of H-bonded CONH groups in α-helices and antiparallel β-sheets (a criteria which dismisses half the distribution), the number of CO–CO interactions is close to the number of H-bonds as obtained from our highly relaxed H-bond definition. While this finding could give the impression that all of these short COCO interactions are an inevitable consequence of H-bonds between CONH pairs, our data in Table 2 clearly suggest that short CO–CO interactions do exist even in the absence of H-bonds. This shows the importance of CO–CO interactions in aggregation of our model peptides. As expected, side-chains sterically reduce the ability of backbone carbonyls to interact with other groups. The formation of a H-bond gives about 1.4 kcal/mol energetic stabilization (Table SI–II). This value, which is much lower than the attractive strength of a H-bond in the gas phase, agrees well with the generally accepted strength of a H-bond in water (1–2 kcal/mol).^23–31,78 On the other hand, the CO–CO backbone interaction gives an energetic stabilization of 1.8 kcal/mol in system gly, and the gain increases slightly more in the presence of side-chains. Notably, using IMPT on a perpendicular propanone dimer, Allen et al. obtained an attractive energy of 1.8 kcal/mol for CO–CO interactions at a C–O separation of 3.02 Å.⁴⁹

Table 2.

Probability (p) of Observing Backbone CO in Different Groups Considered and Their Lifetime (τ) and Energetic Stability (E) in System gly^a

	gCO	gOH	gCOH	gfree
p	0.267 (0.134)	0.013 (0.168)	0.349 (0.194)	0.371 (0.504)
E (kcal/mol)	−7.276	−5.938	−8.557	−7.063
τ (fs)	126	29	235

^aNumbers within parentheses are for O–C cutoff distance of 3.6 Å. For other systems, see Supporting Information.

We find that a CO–CO contact relaxes relatively slowly (Figure SI-4) and thus has a longer lifetime (Table SI–II) than a H-bond. Other work found that collapsed states of oligoglycines in water are stabilized by the more numerous CO–CO interactions than H-bonds.^6,15,17 Similarly, short CO–CO contacts are common in proteins,^32,33 and these interactions alter conformational preferences of peptides, peptoids, and other related small molecules.^{32–41,44–48}

Coexisting CO–CO and CO···HN Interactions in Neutral Systems

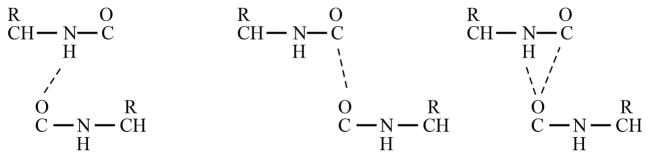
We now decompose backbone carbonyl interactions into four different groups, g_i, based on the type of interbackbone interactions the considered O-atom makes: (a) CO–CO interaction exists but not a H-bond (g_CO), (b) H-bond exists but not a CO–CO interaction (g_OH), (c) CO–CO and H-bonding interactions exist simultaneously (g_COH), and (d) neither CO–CO nor H-bonding interactions exists (g_free). This classification is illustrated in Figure 7.

Figure 7.

Decomposition of backbone CO into different groups based on the interbackbone interactions. Left: a H-bond exists but not a CO–CO interaction (group g_OH). Middle: a CO–CO interaction exists but not a H-bond (group g_CO). Right: CO–CO and H-bonding interactions exist simultaneously (group g_COH).

Table 2 presents the probability of observing the classified interaction groups for gly. We find a significant number of backbone COs that interact directly with identical neighbors but do not form H-bonds (g_CO). Among the backbone carbonyls involved in CO–CO interactions, ~60% simultaneously form interbackbone H-bonds. With these conventions, the relative population of backbone carbonyls that form H-bonds without interacting directly with identical neighbors (g_OH) is negligible, <2%. Of the backbone carbonyls that form H-bonds, more than 94% interact simultaneously with neighboring carbonyls (g_COH) as well. Propensities of the interactions have previously been observed in computational and crystallographic analyses of protein α-helices and β-sheets.^32,33

The energetic contribution of backbone carbonyls to the stability was calculated by considering CO group interactions (with C–O separation less than 4 Å), NH, C_α groups, and water. The survival function, S(t), used to compute lifetime is similar to that defined in eq 3. The variable h in this case is equal to unity when the tagged CO belongs to the particular group considered and is zero otherwise. The other variable H takes a value of unity if the tagged CO remains continuously in the same considered group to time t and is zero otherwise.

Figure SI-9 displays the relaxation of S(t), and the estimated lifetimes are listed in Table 2. We observe dramatic differences in the relaxation behavior of S(t) for the three groups considered. The survival function for group g_OH decays at a much faster rate. A backbone CO belonging to this group has the shortest lifetime (~30 fs), suggesting that a H-bond without any contribution from the CO–CO interaction in these unstructured systems is not kinetically very stable. Relaxation of S(t) for group g_CO is noticeably slower than that for group g_OH, resulting in a longer (~4 times) lifetime for the former. Among the groups considered, relaxation is the slowest for interaction group g_COH. It is clear that a backbone CO is the most stable in g_COH and the least stable in g_OH with an energy difference of more than 2.4 kcal/mol. Interestingly, the energy of a backbone carbonyl in g_OH is less favorable than that in g_free by more than 0.8 kcal/mol. On the other hand, the stability of a carbonyl is slightly higher in g_CO than that in g_free. Thus, consideration of Figure SI-9 and Table 2 suggests that the coexistence of the CO–CO contact is correlated with survival of a backbone H-bond. A backbone CO in g_CO provides some stability to the cluster, holding the peptides together in a large cluster for some time without any help from a H-bond. Nonetheless, the coexistence of H-bonds and CO–CO interactions increases stability.

Water interacts significantly with the backbone carbonyls with a maximum in g_free for gly of 6.8 kcal/mol and minimum in g_COH of only ~1.3 kcal/mol. Importantly, it is not only the obvious reduction in number of water molecules near backbone carbonyls in g_COH but also the decreased strength of interactions between them that cause the significant reduction (Figure SI-5).

In Table 3, we present structural, energetic, and dynamical properties of CO–CO and CO···HN interactions for backbone COs in different groups to demonstrate the influence of neighboring groups on these interactions. The survival function, S(t), used here is similar to that defined in eq 3. The variable h is equal to unity when the tagged CO–CO or CO···HN interaction exists with backbone CO belonging to the particular group considered and is zero otherwise. The other variable H takes a value of unity if the tagged CO–CO or CO···HN interaction remains continuous in the same considered group to time t and is zero otherwise.

Table 3.

Decomposition of Interpeptide CO-to-CO and CO-to-HN Interactions into Groups g_CO, g_OH, and g_COH in System gly^a

	CO–CO			CO···HN
	gCO	gOH	gCOH	gCO	gOH	gCOH
n	1.298	0	1.772	0	1.013	1.098
E	−1.422		−1.988		−1.507	−1.437
τ	99		153		29	195

^aFor other systems, see Supporting Information. n, E, and τ represent, respectively, number, energy (in kcal/mol), and lifetime (in fs) of interactions.

We see that backbone COs that form H-bonds gain more stability through interactions with identical groups than do backbone COs with no H-bonds (g_CO). Slower relaxation of CO–CO interactions in g_COH as compared to that in g_CO is also noticed (Figure SI-6). Additionally, for a backbone CO in g_COH, the energetic stabilization from a CO–CO interaction is higher than that from a H-bond. Total energetic stabilization of backbone COs from CO–CO interactions is higher than that from H-bonding interactions by more than 2 times.

In agreement with previous suggestions that backbone H-bonds in α-helices and β-sheets usually deviate from linearity to maximize favorable backbone CO–CO interaction,³² our simulations capture slight destabilization (by ~0.1 kcal/mol) of H-bonds on moving from g_OH to g_COH. The relaxation of H-bonds slows down noticeably with coexisting CO–CO interactions (Figure SI-6). This dynamic slowing is a reflection of the stability of a backbone CO in g_COH as compared to that in g_OH and indicates the advantage of coexisting CO–CO interactions for survival of a backbone H-bond. It is notable here that the much faster relaxation of H-bonds in g_OH as compared to that of CO–CO contacts in g_CO causes the differential relaxation behaviors of CO–CO and CO···HN interactions, shown in Figure SI-4.

Figure 8 shows the probability of an interacting carbonyl converting from one group state to another. Table 4 presents the pairwise energies for CO–CO and CO···HN interactions prior to conversion from one group to another. A backbone carbonyl almost always converts to either g_COH or g_free both from groups g_CO and g_OH. The rate of conversion from g_OH is much faster than that from g_CO (Table SI–V).

Figure 8.

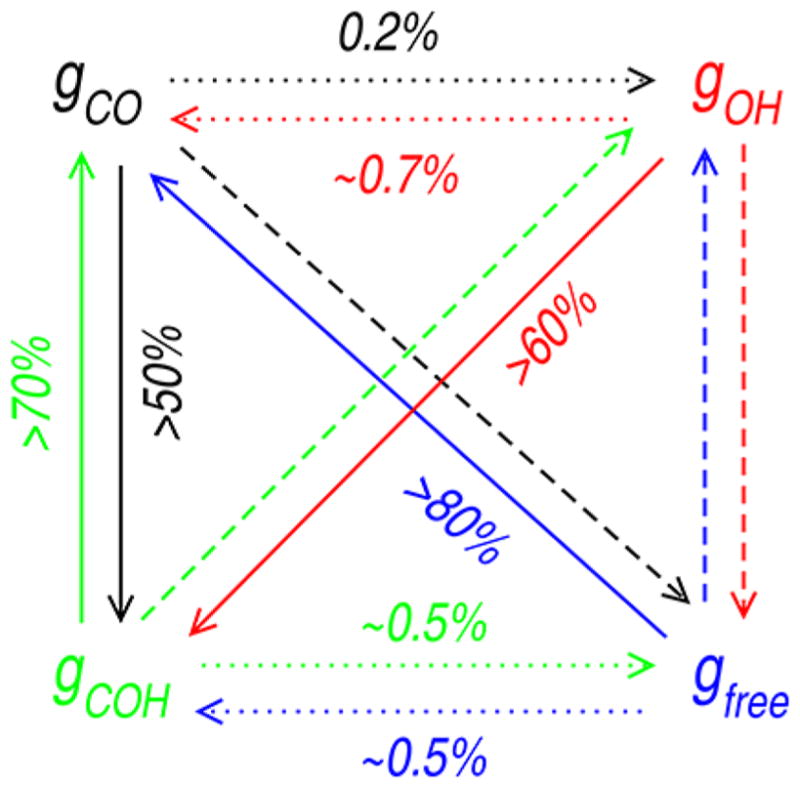
Schematic representation of probability of conversion of backbone CO from one group to another. Probability is at a maximum for the solid line and at a minimum for the dotted line. For details, see Table SI–V.

Table 4.

Interaction Energy (in kcal/mol) for CO–CO and CO···HN Interactions Prior to Conversion from Groups g_CO, g_OH, and g_COH to Other Groups in System gly^a

	to ↓	from →
		gCO	gOH	gCOH
CO–CO	gCO			−1.912
	gOH	−1.408		−1.680
	gCOH	−1.909
	gfree	−0.877		−1.425
CO···HN	gCO		−1.143	−0.704
	gOH			−1.616
	gCOH		−1.622
	gfree		−1.168	−1.302

^aFor other systems, see Figure SI-8.

We find that not only is the probability of conversion from g_COH to g_OH significantly lower than that to g_CO but also the time needed is noticeably shorter for conversion to the latter, indicating a shorter time required to break the H-bond than that to break the CO–CO contact for a backbone CO in g_COH (Table SI–V). It is also important to note that a backbone CO that is free in solution (g_free) shows a much higher (more than 4 times) preference to interact with another backbone CO than with backbone NH. We find the CO–CO interaction initiates the formation of a new H-bond. On the other hand, although a H-bond between backbone amide groups can lead to the formation of a new CO–CO contact, the effect is less significant.

Not surprisingly, the choice of cutoff distance influences these findings. We note that a reduction of O–C cutoff distance from 4.0 to 3.6 Å (the average) (a) increases probability of conversion from g_CO to g_free, g_OH to g_COH, g_COH to g_OH, and g_free to g_OH, and (b) decreases the probability of conversion from g_CO to g_COH, g_OH to g_free, g_COH to g_CO, and g_free to g_CO (data not presented).

To understand the geometric criteria for conversion of a backbone CO from g_COH to either g_CO or g_OH, we considered the CO–CO and CO···HN distances as well as the CO–C and CO···H angles in system gly when backbone CO interacts simultaneously with NH and identical groups in the main-chain of surrounding peptides. For CO–CO interactions, we find that the mean contact distance (d_OC) is 3.6 Å and the mean CO–C contact angle (θ_OC) is 129°. The mean value of d_OC found here is essentially the same as the reported average distance between C and O-atoms of H-bonded CONH groups in proteins (3.6 Å for α-helices and antiparallel β-sheets and 3.7 Å for parallel β-sheets).³² We find that disruption of CO–CO contacts leading to conversion of backbone CO from g_COH to g_OH is expected for CO–CO contact distances more than 3.8 Å or CO–C contact angles less than 120°.

For H-bonds, the calculated mean distance (d_OH) and the mean CO–H contact angle (θ_OH) are 2.0 Å and 138°, respectively. In the region d_OH ≃ 1.9 Å and 110° ≤ θ_OH ≤ 170°, contribution of CO···HN interaction to stability of backbone CO in g_COH is at a maximum (>1.6 kcal/mol). A higher frequency of H-bond disruption leading to conversion of backbone CO from g_COH to g_CO is expected for a H-bond distance of more than 2.2 Å or for a CO···H contact angle less than 100°.

Interactions of Uncharged Side-Chains

To probe the interactions of side-chains in the large cluster, we consider the radial distributions among side-chains and the backbone about side-chains (Figure SI-7). We find that the side-chain Asn shows the highest tendency to interact directly with the backbone. From the location of the first peak (<3 Å), most of these noncovalent interactions between side-chain and backbone in asn can be assigned to H-bonding interactions. The tendency of the iso-propyl group in Val to interact directly is the lowest both with the backbone and side-chains. We also find a close packing of phenyl rings in the arrangement of peptides. Among the uncharged side-chains considered, the benzyl group in Phe shows the highest tendency to cluster. Interactions between phenyl groups are common in proteins, and the high tendency of aromatic groups to be surrounded by identical groups in solution is often considered to drive protein folding. Our calculations also show that the angle between the ring planes of interacting phenyl pair is usually ~90°. In other words, phenyl groups prefer to interact perpendicularly which is in accord with solution,⁷⁹ crystal structures of benzene (Cambridge database), and analyses of proteins.⁸⁰

To further characterize the interactions of side-chains in asn and gln, we find that side-chain N interacts more with backbone O of other peptides than does side-chain O with backbone N (Figure SI-7). The number of interpeptide H-bonds between side-chain N and backbone O in the large cluster is more than 2 times higher than that between side-chain O and backbone N. The probability of a side-chain to form H-bonds with side-chains is significantly lower than with a backbone. This is due in part to the much higher population of backbone H-bonding sites than those of side-chains. We find the side-chain O of Asn interacts more than that of Gln with backbone N of same peptide, whereas it is the side-chain N of Gln that interacts more than that of Asn with backbone oxygens of the same peptide.

Comparison between Charged and Uncharged Aggregates

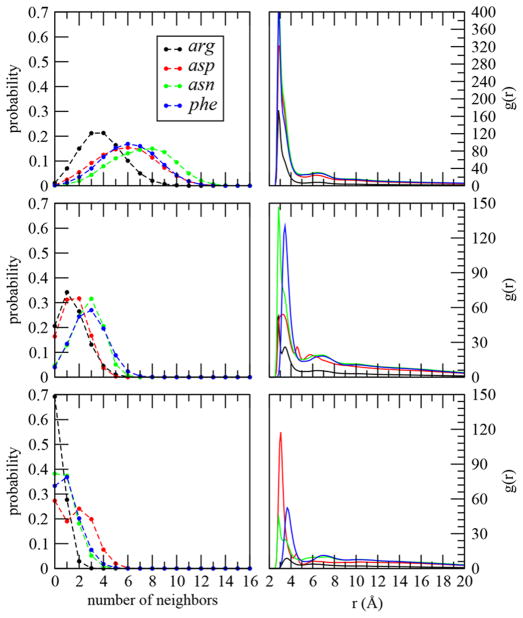
The mechanism of association leading to phase separation depends on the chemical nature of the side-chain. In Figure 9 we compare our acidic, asp, and basic, arg, peptides with both polar, asn, and nonpolar, phe, systems. The interactions both among and between side-chains and backbone in the phase separated cluster can be characterized in different ways. On the left side of Figure 9 we show the backbone–backbone, side-chain–backbone and side-chain–side-chain probability of neighbors within 4 Å. On the right-hand side are the corresponding radial distribution functions. As expected the backbones of the pentapeptides can have contacts with a more substantial number of other backbones than with side-chains. The side-chain–side-chain neighbor distribution is the narrowest.

Figure 9.

Comparison between charged and uncharged peptide associations. Left: Probability distribution of the number of backbone within 4 Å of backbone (top), backbone within 4 Å of a side-chain (middle), and side-chain within 4 Å of a side-chain (bottom) for peptides in the large cluster. Right: Site–site radial distribution functions (based on shortest heavy atom distance) between the heavy atoms of peptide backbones (top), between the heavy atoms of peptide side-chains and backbones (middle), and between the heavy atoms of peptide side-chains (bottom) for peptides in the large cluster.

The cationic and anionic side-chains cluster quite differently. The arg system generally interacts with fewer partners regardless of whether they are backbone or side-chain. Interestingly, we find asp to make more side-chain to side-chain contacts than the other systems. Proteins are known to hold like charged groups together in active sites for catalysis,⁸¹ but here we do not have any polymer architecture leading to constraint. Accounting for differences in side-chain volume we see more similarity between the uncharged groups than the charged ones.

CONCLUSION

We analyzed the effect of side-chains on aggregation/association of peptides by directly calculating the solubility limit of classical molecular models. Spontaneous aggregation separated the solution into organic-rich and peptide saturated water-rich phases. Correlated with the changes in peptide aggregation were the fluctuations in the waters of the first hydration shell. It was found that the greater the fluctuations are, the higher the aggregation propensity of the peptide is, which is reflected in modern theories of hydrophobicity.^71,72,82,83 However, we note that our fluctuation trend also predicted the clustering propensity of Asn and Gln side-chains which are classically hydrophilic. Yet, these residues are well-known to play a role in peptide aggregation (plaque forming) diseases.^84,85

Our preliminary assessment of forces that hold the disordered peptides together in aggregates showed a greater contribution of CO–CO interactions than that of H-bonds. The relative importance of CO–CO and H-bonding interactions in peptide aggregation was then examined closely by decomposing backbone CO into different interactions the considered O-atom made. Backbone COs that participate in H-bonding interactions with backbone NH are almost always surrounded by other CO groups from the main-chains.

Our simulations also captured the high tendency of the benzyl group in Phe to be surrounded by identical groups in solution, the tendency often considered to be the driving force of protein folding. In contrast, the tendency of the side-chain –CONH₂ group in Asn and Gln, which readily aggregate with a low solubility limit, was not seen to form a significant number of H-bonds with identical groups. Instead, the side-chain N was observed forming H-bonds mainly with the backbone.

The H-bond has long been considered to be the most important contributor to forces that hold backbone amide groups together and stabilize proteins in their folded states. Disordered systems such as the peptides considered here show different behaviors. Our study suggests that a backbone amide pair in a disordered peptide connected by a H-bond gains maximum energetic and dynamic stability only if the pair can make use of other CO–CO interactions as well. Our results thus bring clarity to the role of CO–CO interaction in formation and stability of disordered peptide aggregates. Extended to unstructured proteins, backbone H-bonds are unlikely to form or survive for a long time without surrounding backbone carbonyls.