Abstract
Interstitial photodynamic therapy has shown promising results in the treatment of locally advanced head and neck cancer. In this therapy, systemic administration of a light-sensitive drug is followed by insertion of multiple laser fibers to illuminate the tumor and its margins. Image-based pretreatment planning is employed in order to deliver a sufficient light dose to the complex locally advanced head-and-neck cancer anatomy, in order to meet clinical requirements. Unfortunately, the tumor may deform between pretreatment imaging for the purpose of planning and intraoperative imaging when the plan is executed. Tumor deformation may result from the mechanical forces applied by the light fibers and variation of the patient’s posture. Pretreatment planning is frequently done with the assistance of computed tomography or magnetic resonance imaging in an outpatient suite, while treatment monitoring and control typically uses ultrasound imaging due to considerations of costs and availability in the operation room. This article presents a computational method designed to bridge the gap between the 2 imaging events by taking a tumor geometry, reconstructed during preplanning, and by following the displacement of fiducial markers, which are initially placed during the preplanning procedure. The deformed tumor shape is predicted by solving an inverse problem, seeking for the forces that would have resulted in the corresponding fiducial marker displacements. The computational method is studied on spheres of variable sizes and demonstrated on computed tomography reconstructed locally advanced head and neck cancer model. Results of this study demonstrate an average error of less than 1 mm in predicting the deformed tumor shape, where 1 mm is typically the order of uncertainty in distance measurements using magnetic resonance imaging or computed tomography imaging and high-quality ultrasound imaging. This study further demonstrates that the deformed shape can be calculated in a few seconds, making the proposed method clinically relevant.
Keywords: interstitial photodynamic therapy, head and neck cancer, tumor deformation, shape reconstruction, optimization
Introduction
Clinical studies have reported success in using interstitial photodynamic therapy (I-PDT) for the purpose of palliative treatment of refractory locally advanced head and neck squamous cell carcinoma (LAHNC).1–6 Interstitial photodynamic therapy is a binary treatment consisting of a systemic administration of a light-sensitive drug (photosensitizer [PS]) that is activated to generate reactive oxygen species to destroy the tumor.7,8 The light is delivered through an array of laser fibers embedded in transparent catheters, which are inserted into the target tumor under image guidance. The number and location of the fibers are typically determined by the tumor size and location. In I-PDT, the challenge is to ensure that all regions of the tumor and its margins receive a prescribed light dose.
Treatment planning and dosimetry systems have been developed and used to administer I-PDT in the treatment of prostate cancer.9–13 Davidson et al presented a system known as “TOOKAD vascular targeted photodynamic therapy for prostate cancer.”9 Swartling et al presented a somewhat similar system (known as iDose) for the same cancer treatment.10 Both systems were tested in clinical studies. Li and Zhu presented a dosimetry system and treatment planning for calculating light fluence in a heterogeneous prostate.14 However, this model applies only to a single heterogeneous and nondeformed geometry. Karakullukcu et al used modified brachytherapy techniques for treatment planning of I-PDT in patients with LAHNC.5,6 The plan has been shown useful in assisting physicians in decision-making related to the number of fibers to be used, but it does not calculate the light fluence distribution. Baran and Foster developed a treatment planning that uses a graphics processing unit–enhanced Monte Carlo simulations to model the delivery of light in near real time, in tissue volumes representing head and neck (HN) tumors.15,16 Oakley et al recently presented a treatment planning using finite element method (FEM), designed specifically to simulate light propagation in geometries that accurately mimics LAHNC.17
The common I-PDT treatment approach combines 2 imaging modalities in subsequent stages. In the first stage, the tumor shape is reconstructed by means of diagnostic computed tomography (CT) or magnetic resonance imaging (MRI). The 3-dimensional (3-D) imaging data are utilized for evaluation of the extent of the disease. The reconstructed shape is then used for treatment preplanning, which could be assisted by computational means. The ultimate goal of the preplan is to maximize illumination within the tumor and its margins, also known as the clinical target volume. In the second stage, light sources (laser probes) are localized under ultrasound (US) imaging according to the preplan. Here, US imaging is further used for intraoperative monitoring and control. These 2 stages are typically performed days apart, which create 2 inherent challenges: (1) registration of the US image with the CT- or MRI-reconstructed shape, which was used for preplanning, and (2) tumor deformation between the 2 stages associated with patient posture variations, possibly with tumor growth if the 2 stages are performed too far apart, and deformation due to the insertion of the laser probes.
In previous studies, clinicians and researchers combined FEM and a diffusion model of cancer growth in order to predict the evolving tumor shape after CT or MRI.18–20 Such routines assume the mechanical properties of materials to be constant in the interstitial environment, which may be unrealistic in many cases due to the geometric complexity of the tumor and nonuniform mechanical properties of the tissues surrounding the tumor. Pure geometric approach based on data mining and regression analysis has also been proposed21; however, such methods may not well represent the physics of the problem. Thus, an approach that can capture the mechanical interaction between the tumor and its interstitial environment will likely produce preferable predictive results.
One possible approach to register the intraoperative US image with the image-based preplan for HN cancer is to integrate fiducial markers (FMs), similar to those used to guide radiotherapy in prostate cancer treatment.22–24 Prior works in medical imaging have demonstrated the viability of automated FM tracking methods with high computational efficiency, robustness, and accuracy.25 Thus, in our context, it is reasonable to assume more than 10 FMs could be traced robustly and accurately in real-time settings. The relative orientation (positioning) and relative displacements of FMs would then be available through the observed FM locations. Here, the relative orientation of the FMs could be used for shape registration, while the relative displacement between the FMs can be used to evaluate the shape deformation. In the absence of tumor deformation, FM-based registration is essentially a geometric minimization problem. The outstanding question is which mathematical model was used to evaluate shape deformation when significant relative displacement between FM is also present. The current study addresses this question for the benefit of I-PDT in patients with LAHNC.
Methods
Our goal is to predict the deformed shape of the tumor given (1) an initial shape of a tumor, (2) a set of initial FM locations, and (3) measured displacements of FMs due to tumor deformation between 2 imaging events. Toward this goal, we use a physically based computational model where we first predict the external force field on the tumor surface using the observed FM displacements as displacement boundary conditions (Integration of FMs Constraints into FEM section). Using the predicted force field, we then compute the deformed shape of the tumor using an FEM.
The problem of determining the external force field from the FM displacements leads to an underdetermined set of equations. Hence, there exists no unique force field solution that produces the observed FM displacements. To regularize the problem, we impose a smoothness term to our force field calculations using the bi-Laplacian operator that minimizes the variation of the force field over the tumor surface (Force-Field Smoothness section). With this formulation, computing the deformed shape of the tumor becomes a quadratic constrained optimization problem (Optimization Formulation section).
Integration of FMs Constraints Into FEM
We developed our solution based on a linear FEM with linear tetrahedral elements and an isotropic material model. However, hyperelastic and heterogeneous elastic material model may potentially result in a better outcome in deformation prediction, if one would only know the most appropriate constitutive law and all its properties. Given the available information and as a proof of concept, the chosen FEM scheme is deemed adequate. Although these choices facilitate the development of the following mathematical model, our approach can be readily used with other element types and high-order blending functions as well as anisotropic materials. Only the construction of the stiffness matrix (described below) would be altered in those cases.
Given a tetrahedral mesh model Ω of the tumor, the local stiffness matrix ke for element e is constructed as26:
| 1 |
where Ve is volume of the tetrahedron, Be, is the 6 × 12 strain matrix computed from the rest positions of the tetrahedron’s vertices, and c is the 6 × 6 material constant matrix derived from the Young modulus and Poisson ratio of the material.
Suppose Ω has n vertices with each vertex v ∈ ℝ3 encoding the x, y, and z position coordinates. We obtain a 3n × 3n sparse global stiffness matrix K by assembling the local stiffness matrices ke. A system of linear equations mapping the nodal displacements to the corresponding external forces is then established as follows:
| 2 |
In our context, the primary cause of tumor deformation is the change in human posture between lying on the imaging device table and the operation table during I-PDT. The deformation of the tumor is thus caused primarily by the change in the interface forces between the tumor and its surrounding tissues. As such, we model the tumor to deform only due to the external forces on its surface nodes. All interior nodes are set to have unconstrained (free) displacements with no external forces. Hence, their corresponding entries in f is equal to 0, while their displacements are to be computed. We rearrange the rows of the global stiffness matrix K into 2 submatrices (upper stiffness matrix) and (lower stiffness matrix):
| 3 |
where the nonzero entries in Ku and Kl pertain to the surface nodes and interior nodes of the tumor, respectively. Note that if K and f are row-shifted consistently, x remains unaltered. In our problem, we aim to predict the tumor’s deformation using the final positions of several FMs. Suppose we have FMs on t nodes of the mesh model (these can be on the surface, in the interior of the tumor, or in both regions). Let be a binary indicator matrix. Each row of D encodes one of the FMs by placing a value of 1 for the corresponding x, y, and z column indices of the node having the FM, and a 0 value otherwise. The corresponding FM displacement constraints are given by:
| 4 |
where is the measured (known) displacement vector of the FMs. By concatenating Equations 3 and 4, we obtain the system of linear equations governing our model:
| 5 |
Force Field Smoothness
Both x and fu are unknown in Equation 5. In order to obtain a unique solution in this underdetermined system, we regularize the problem by preferring a smooth solution to fu such that local variations in fu are minimized. Instead of assuming uniformity of surrounding tissue material in previous literatures,18–20 our approach focuses on the interstitial forces between the tumor and its surrounding tissue. This choice is based on the observation that a tumor’s surrounding tissues would generally induce pressure areas on the tumor, rather than inducing discrete force points. We formulate this preference by minimizing the bi-Laplacian27 of fu, computed over the surface nodes of the tumor model Ω. We employ the cotangent-weighted discretized Laplacian operator as described by Crane et al.28 By following the sequence of nodal indices in K, the discretized Laplace operator can be assembled into a symmetric matrix L with high sparsity.
To account for the size variations across the surface triangles, we normalize each row of the Laplacian matrix L by the corresponding vertex’s area29:
| 6 |
where aj is the area of triangle j adjacent to vertex vi. We prefer the per-vertex area in Equation 6 because the per-triangle area is more efficient to compute than Voronoi region created in the dual graph.30 Additionally, the distributed force field on the edges and faces of the elements in the pressure will be converted to per-vertex forces in our finite element formulation, and thus, the choice of per-vertex area normalization is also consistent with the finite element discretization.
To facilitate conversion between pressure area and nodal forces in FEM computation, we assemble an inverse mass matrix Mj such that when Mj is multiplied by a column vector of the computed Laplacian, where the Laplacian is normalized correspondingly. Assume that there are u nodes on the tumor surface, Mj is a u × u diagonal matrix, with diagonal entries equal to the inverse of corresponding per-vertex area:
| 7 |
Optimization Formulation
The interstitial forces on the surface of the tumor can be conveniently decomposed into 3 scalar functions fux, fuy, and fuz over the surface nodes. The Laplacian of fux is calculated as:
| 8 |
where fux, Kux, and xx are the x components of the force vector, stiffness matrix, and displacement vector of surface nodes, and Mj and Lj are the corresponding inverse mass matrix and cotangent-weighted Laplacian matrix operating on fux.
Using the bi-Laplacian term , the smoothness of fux can be enforced by minimizing the following functional:
| 9 |
Note that in this form, the explicit dependency on fux has been removed by replacing fux with . This allows xx to be the only unknown to be computed. In a similar way, the smoothness of fuy and fuz can be encoded in . We concatenate and rearrange Mj and Lj into a global inverse mass matrix and a Laplacian matrix by following the pattern of how fu is assembled from fux, fuy, and fuz.
Finally, we formulate our deformation prediction process as a quadratic programming optimization problem as:
| 10 |
where . In this formulation, the displacement vector x is the only unknown variable. The constraints ensure that (1) the displacements of FMs exactly match the measured FMs using imaging technology and (2) there are no external forces on the internal nodes. A key advantage of this formulation is that the solution can be achieved quickly by using the interior point algorithm31 for a quadratic programming problems, as K* is a symmetric matrix with high sparsity.
Evaluation Approach and Performance Metrics
To evaluate our method, we use the following methodology:
Given a 3-D digital tumor model (synthetic or real), place FMs randomly on its surface/inside its volume.
Apply point forces to the surface nodes based on a known continuous force field.
Using a commercial FEA package (Abaqus in our case), solve the full-scale solid mechanics deformation problem according to the applied forces and displacement boundary conditions and compute the FMs’ displacements—we call this deformed model the benchmark.
Use the computed FM displacements as input to our algorithm to predict the applied force field and the tumor deformation—we call the outcome the prediction model.
Compare the prediction against the benchmark using several performance metrics as explained below.
Repeat the above process for a varying number of FMs and their placements and report outcomes over multiple runs.
We tested our approach on 2 spherical models with diameters of 3 and 8 cm and a diagnostic CT scanned tumor model acquired from the Roswell Park Cancer Institute. The dimensions of the spherical models are reflective of the typical range of tumors encountered in HN cancers, which is taken from the minimum of and maximum dimension of our CT scanned tumor model. Table 1 lists the parameters used in our evaluations, which were selected for the purpose of demonstrating a proof of concept for our method. Note that the tumor properties in 32 are given for a brain tumor and are used here in the absence of LAHNC-specific properties. We will explore parameter optimization in future studies.
Table 1.
Geometric Parameters of the Tetrahedral Mesh Models Used in the Current Study.
The number of vertices and elements in the sphere and tumor models are chosen such that (1) the shapes possess appropriate degrees of freedom for realistic deformations and (2) the 2 models exhibit differences in complexity to allow a comparison of the computational cost. For the 2 sphere models (3 and 8 cm), the topology is identical, which allows an identification of the impact of geometric size on our approach.
Sphere Model
To create the benchmark deformations, we sample each component of the interstitial force vector on a node from a sinusoidal force field:
| 11 |
where the 3 components of force fi on vertex i are sine functions defined on the node’s position vector vi, Sj is a sign term that controls the direction of the force component in the j direction; Am is the force amplitude (N), and ω is the spatial frequency (m−1). A sinusoidal force distribution model is infinitely differentiable, which ensures continuity with respect to the change in nodal positions, while the resulting forces are well bounded. Additionally, the frequency term allows us to control the spatial rate of change of the force field, thereby allowing us to simulate different levels of pressure undulations over the tumor surface.
Ideally, we desire to create benchmark deformations with smoothly varying external forces on the surface nodes. However, this is hard to achieve due to the difficulty in controlling the reaction forces on the nodes that have been anchored (ie, zero displacements) to prevent rigid body motions. If 3 surface nodes are anchored and a sinusoidal force field is applied on the remaining surface nodes, the reaction forces on the fixed nodes are likely to be far different from the forces on their immediate neighbors. This discrepancy would result in unrealistic forces around the anchor nodes. To mitigate this possibility, we randomly select 3 internal nodes to be anchored in our benchmarks. Although this choice may induce discontinuities in the deformation gradient inside the tumor (hence adversely affecting the predicted accuracy), it nonetheless allows the creation of a smooth force field over the tumor surface.
Tumor Model
We use an HN tumor model reconstructed from MRI (Figure 1).
Figure 1.
Original tumor model (blue) reconstructed from magnetic resonance imaging (MRI) and the resulting finite elements tumor model created for testing.
In this study, we aim to simulate a bending of the tumor by first applying the forces on 3 surface nodes as shown in Figure 2A. We apply 0.1 N on each of the 2 ends and −0.2 N in the middle—along the x axis. To create a force field, we apply implicit fairing on the initial forces as described in the study by Desbrun et al.33 The final force field for this benchmark is shown in Figure 2B. Given the material properties, this force model and the magnitudes simulate a realistic bending behavior representative of real tumors.
Figure 2.
Scaled initial force and smoothed force fields.
Performance Metrics
As discussed below, we use the following 3 metrics to compare our predictions against the benchmarks: (1) absolute and relative forces, (2) absolute and relative displacement, and (3) displacement offset.
- Absolute and relative force difference over the tumor surface (, respectively)
12 13
where are the absolute and relative difference in the force vectors computed at node i, respectively. These force vectors are defined over the surface nodes of the tumor only. Here, is the L2 norm operator. normalized by the scale of the benchmark force at the same vertex.
Absolute and relative displacement difference over the tumor ( and , respectively)
| 14 |
| 15 |
where are the absolute and relative difference in the displacement vectors at node i. These displacement vectors are computed over all the nodes of the tumor (surface and interior combined).
Displacement offset over the tumor surface (Oi)
| 16 |
where Oi is the signed displacement offset at node i, which encodes the difference between the deformed nodal positions for the benchmark and our prediction, while si determines whether the predicted vertex position falls inside or outside of the benchmark surface. This is a conservative approach to how much the predicted model deviates from the benchmark, since it tends to overestimate the actual offset, as it computes the difference per corresponding vertex pairs rather than point-to-surface distance.
Modeling the Impact of Tumor Deformation on the Light Dose
We employed our previously published FEM approach to calculate light distribution within an LAHNC model generated from CT scanning of a patient amenable to I-PDT.17 The respective simulations and analyses were conducted with Comsol 5.2a (Comsol Inc, Burlington, Massachusetts). A detailed description of this computation method is provided in the study by Oakley et al. In the current study, we utilized our model to compute the light dose distribution in the tumor models as shown in Figure 2. The light propagation simulations were performed for laser settings of 630 nm and 400 mW/cm, which are typical setting for I-PDT with a PS that is being used in clinical settings in the United States.
Results and Discussion
Sphere Model
We induce a deformation that squeezes the sphere around z = 0 plane and stretch it at its 2 poles along the z axis. Thus, the sign term in Equation 11, Sj, is set to be +1 on the z axis and −1 on the other 2, simulating tension in the z direction and compression in the x and y directions. The resulting force vector field is shown in Figure 3A for the 3-cm sphere subject to . The FMs are randomly chosen from the internal nodes. Because we apply the same loading model (Equation 11), the shape of the force field for the 8-cm case sphere is very similar to that of the 3-cm case sphere. Any discrepancies are due to the differences in the size of the spheres, which affect the vertex positions on the spheres, hence the force magnitudes.
Figure 3.
A, Benchmark model: Force vectors on the surface nodes (green arrows) and fixed nodes with their reaction forces (black) for a 3 cm sphere. B, Prediction model: Force prediction result of a 10 fiducial markers (FMs) case with predicted forces (red arrows), 10 FMs (blue circles), and reaction forces (black). Note that the prediction force field matches the benchmark force field well.
The predicted force distribution on the 3-cm sphere is shown in Figure 3B for 10 FMs, for example. A comparison between the tumor deformation for the benchmark (green) and our prediction (red) is shown in Figure 4.
Figure 4.
Visualizing the deformed models for the benchmark (green) and prediction (red) with fiducial marker (FMs, blue circles) in 3 cm case. Note that the predicted deformation matches the benchmark deformation well.
The absolute and relative differences in the nodal force vectors (sorted) are shown in Figure 5.
Figure 5.
Sorted absolute (blue) and relative (orange) difference () in the forces between the benchmark and prediction on surface nodes for the 3 cm case.
The absolute and relative differences in displacements (sorted) for the 3 cm case are shown in Figure 6. The displacement offsets are shown in Figure 7.
Figure 6.
Sorted absolute (blue) and relative (orange) difference in displacement () for the 3 cm case.
Figure 7.
Displacement offset O of surface nodes for the 3 cm case.
The difference between the benchmark and predicted forces on certain nodes can be relatively large (maximum relative force difference of around 40% in Figure 5). However, a close inspection of the nodal displacements (Figure 6), especially the surface offset (Figure 7), reveals that the deformation differences between the benchmark and the prediction are in fact quite small. As a point of reference, the maximum offset in the prediction model is about 0.5 mm, while the typical US imaging resolution is of the order of 1 mm. The results are encouraging as we are primarily concerned about the final deformed shape rather than the actual forces that caused that deformation.
Our formulation computes the deformed shape of the tumor by ensuring that the FMs are matched perfectly (equality constraints in Equations 4 and 5) by assuming the presence of a smoothly varying—but unknown—external force field. In our approach, the true recovery of the benchmark force field is not critical, as there could be arbitrarily many different force fields giving rise to the same FM displacements. Our approach, thus, computes a unique force field that enables the FM displacements to be matched perfectly, while ensuring the Laplacian of the force field, which can be thought of the second-order spatial derivative of the force field, vanishes giving rise to a smooth force field. Although the benchmark force fields we applied as well as the force fields that would normally be encountered in reality would not necessarily exhibit this precise property, the Laplace energy minimization helps our approach to produce a viable force field that ensures the FM displacements are matched perfectly. In fact, the displacement field is rather only weakly sensitive to the precise values of the force field as evidenced with our results (very good match in displacement prediction even with large force prediction errors). Therefore, the 10% to 40% nodal force error is quite tolerable with minimal impact on the nodal displacements.
The model could be improved with more FMs or by optimizing the placement of the FMs in our approach (Summary and Conclusion section). Beyond this improvement, and without any additional input to the system, any shape recovery method has to make assumptions about the force field, thereby likely resulting in deviations from the benchmark forces.
To the best of our knowledge, there exists no prior information regarding the magnitudes of the forces that develop in the real interstitial environment of tumors. Hence, to gain a better understanding of the robustness of our approach to the variations in the force field as well as to the variations in tumor size, we test our algorithm on the 2 sphere models with varying force fields that can induce significant deformations under US imaging. For each pair of diameter and Am, we average the results of 10 independent runs to mitigate the error induced by the selection of FMs. The results are shown in Table 2 for experiments involving 10 FMs for each case. Among all the test cases, the 8-cm sphere model with yields the largest prediction error. Thus, the increase in the tumor size and the force field magnitude may result in a lower prediction accuracy. Nonetheless, the maximum offset (0.7 mm) is still smaller than the typical US imaging resolution of 1 mm.
Table 2.
Quality of the Tumor Shape Prediction Results, Averaged Over 10 Runs for Each of Randomally Distributed 10 FMs.a
| Case | Am | 0.1 N | 0.05 N | 0.01 N | |
|---|---|---|---|---|---|
| 3 cm | %) | Mean | . (26.5%) | . (24.5%) | . (24.0%) |
| Max | (41.8%) | (44.8%) | (32.0%) | ||
| mm (, %) | Mean | (1.5%) | (3.0%) | (1.3%) | |
| Max | (38.7%) | (107%) | (41.2%) | ||
| O, mm | Max | ||||
| x, mm | Max | ||||
| 8 cm | , N (, %) | Mean | (25.6%) | (21.5%) | (13.9%) |
| Max | (48.0%) | (48.9%) | (30.1%) | ||
| mm (, %) | Mean | (2.3%) | (2.93%) | (1.6%) | |
| Max | (56.0%) | (79.6%) | (20.9%) | ||
| O, mm | Max | ||||
| x, mm | Max | ||||
Abbreviations: FM, fiducial marker; max, maximum.
aThe performance metrics are computed as described in section “Performance Metrics.”
We conduct parametric studies on the key factors that may affect the accuracy of our prediction algorithm: the number of FMs and the spatial rate of force distribution.
Number of FMs
Figure 8 shows how the number of FMs affects the prediction accuracy of our algorithm in the 3-cm sphere case (). The mean relative difference in displacements descends quickly from over 40% to less than 3% when the number of FMs increases from 5 to 10. Although future clinical studies will be necessary, we believe 10 to 20 FMs will be satisfactory (and physically feasible) in the vast majority of real treatment procedures. For test cases with more than 10 FMs, the mean relative difference in displacements vanishes, as desirably more constraints are imposed by the FMs.
Figure 8.
Mean relative difference (%) in nodal displacements versus the number of fiducial markers (FMs, 3 cm, ). The error bars indicate one standard deviation among results of 10 runs subject to similar conditions and randomly distributed FMs.
For a given number of FMs, the error bars in Figure 8 indicate the 1 standard deviation (SD) in over 10 runs of our algorithm with random placement of the FMs. The results for the lower number of FMs indicate that the variation can be significant. This observation implies an opportunity for a strategic placement of the FMs on the tumor rather than a random placement. However, we defer FM placement optimization to a future study. As the number of FMs increases, the variation in the results vanishes, which means that a strategic placement is no longer critical in these cases.
The current study focuses on a proof of concept for a newly developed algorithm, while leaving an optimization scheme for practical applications to a later stage. An advanced optimization stage would naturally include the best FM placement, such that a minimal number of FMs can be used. Recall that a random initial placement strategy for FMs is applied at this stage, which may result in a large number of FMs. Nonetheless, it can be observed from Figure 8 that the mean relative difference error in the current nonoptimized system decreases below 2% for 10 FMs or more. This 2% error is translated, on average, to 0.015 mm in tracing the tumor contour in an absolute scale. In general, a lower number of FMs may be used for applications that permit even lower accuracy.
Spatial rate of change of the force field
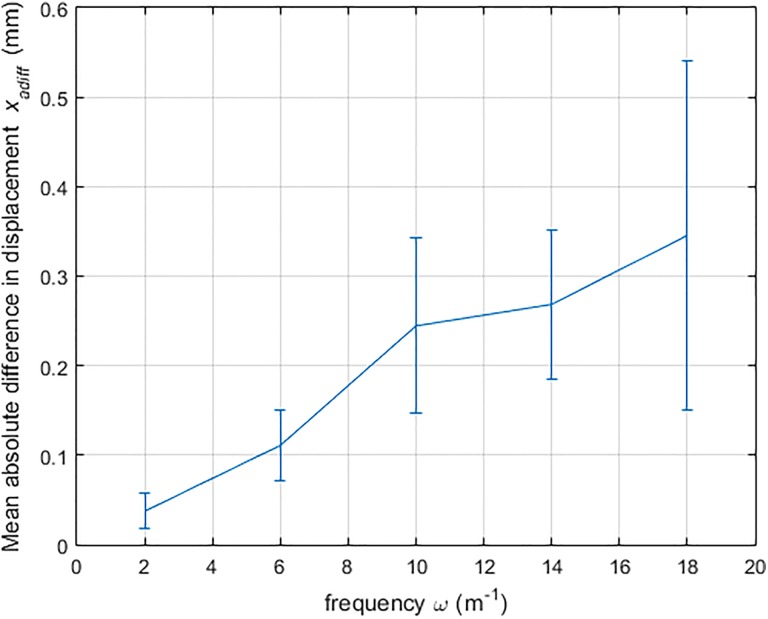
This study aims to understand the effect of the force field frequency on the prediction results. Higher frequencies represent rapidly changing forces over the tumor model, whereas lower frequencies represent small rates of spatial changes in the force field. By varying the spatial frequency ω of the sinusoidal function (ie, the pressure area), the spatial rate of change in the force field can be adjusted. As shown in Figure 9, the prediction results are more accurate for small ω value, which reflects a slow rate of force changes. In I-PDT, the rate of change of the force field on the tumor surface is expected to be low, as the deformation is generally caused by the simple motion of the patient.
Figure 9.
Average relative difference in nodal displacements xadiff with respect to change in spatial frequencies ω (3 cm, # fiducial marker [FM] = 10, ). The error bars indicate the one standard deviation of the results from 10 runs.
Tumor Model
The results of our force prediction method with 10 FMs are shown in Figure 10A. In the benchmark, we model the force field to have only an x component (Figure 2). As our algorithm enforces smoothness on the predicted force field and is unaware of the benchmark force model, the prediction results in a force field with all 3 components (dominant magnitudes in x and minor magnitudes in y and z, as expected). We visualize the benchmark and the predicted force field with a color map on their x components as shown in Figures 11 and 12. By comparison, the predicted force field differs considerably compared to the benchmark. This discrepancy is due to the slender nature of the specific tumor analyzed, where pushing on the tumor from the right side will produce qualitatively similar results as pulling it from its left side, hence creating a duality in the solution. Thus, in our prediction, the force field points in the negative x direction on both sides of the middle part and the opposite on the 2 ends. Despite the difference between the predicted force field and the benchmark, the prediction of the displacement field is quite accurate, with the maximum offset on the surface still being within the US imaging resolution as shown in Table 3. It follows that our approach is able to predict the tumor deformation with high accuracy.
Figure 10.
A, Predicted force field. B, Comparison of deformed shapes of the benchmark (green) and prediction (red).
Figure 11.
View of the force field’s x component in benchmark (left) and prediction (right) looking down +y direction.
Figure 12.
View of the force field’s x component in benchmark (left) and prediction (right) looking down −y direction.
Table 3.
Averaged Prediction Results on Tumor Case (10 Runs).a
| , N () | Mean | |
| Max | ||
| , mm (, %) | Mean | |
| Max | ||
| O, mm | Max(abs) | |
| x, mm | Max |
Abbreviation: max, maximum.
aThe performance metrics are computed as described in section “Performance Metrics.”
Our computational benchmark and prediction methods are decoupled except for the fact that: (1) we use FEA with linear elements in both cases and (2) the material properties are assumed to be known and identical in the benchmark and the prediction models. This model could readily be extended quadratic or higher order shape functions, but the level of dependency would remain the same. During prediction, our method has no knowledge of the force field used for the benchmark creation and only takes as input the displacement of the FMs.
This study has been performed on a ×64 machine with 2.7 GHz Intel i7 processor and 16 GB of 1600 MHz DDR3 L onboard memory. Our algorithm is implemented with Matlab R2015a. The average run time for our algorithm is 1.3 seconds for the sphere model (coarse-mesh) and 5.5 seconds for the tumor model (fine-mesh). These run times indicate that our algorithm can be clinically relevant.
Light dose distributions
Figure 13 Illustrates the effect of 10% tumor deformation on light dose distribution for the optical properties listed in Table 4. Consistent with the locations of the applied forces, we evaluated the impact of deformation on the dose–volume histograms (DVHs) in 3 different regions. Dose–volume histograms representative of the percentage of the tumor volume and surface area that receives at least 100 J/cm2 were calculated for PDT with Photofrin, which has an excitation at 630 nm. The maximum differences in the DVHs between the nondeformed and the deformed tumor are listed in Table 5.
Figure 13.
Illustration of the effect 10% tumor deformation on light dose distribution: (A) region break down for the tumor model before deformation consistent with the applied forces, (B) light dose distribution according to preplan on the undeformed tumor, (C) deformed regions, and (D) light dose distribution calculations after the tumor has been deformed while maintaining the preplan light probes layout; the dashed line represents the tumor contour before deformation.
Table 4.
Optical Properties.
| Free space wavelength | 630 nm |
| Absorption coefficient | 20 (1/m) |
| Scattering coefficient | 2777 (1/m) |
| Reduced scattering coefficient | 500 (1/m) |
| Tissue optical anisotropy factor, g | 0.82 |
| Tissue refractive index | 1.37 |
| Optical diffusion coefficient | 1.4 × 105 m2/s |
Table 5.
Maximum Difference Between the Pre- and Postdeformation Tumor Model Dose–Volume Histograms.
| Percent of Surface Area That Receives >100 J/cm2 | Percent of Volume That Receives >100 J/cm2 | |
|---|---|---|
| Region 1 | 1.47% | 5.43% |
| Region 2 | 2.19% | 0.99% |
| Region 3 | 3.11% | 1.94% |
It is well established that it is critical to treat tumor margins for disease control in HN cancer,34,35 where its surface is a part of these margins. The simulated light dose distributions for deformed tumor varies by up to 5.4% from its predeformed shape (Table 5). Closer inspection of Figure 13B and D indicates how the effect on local margins may far exceed these regional values, where the dashed red line display the predeformed tumor contour on the specific plane. For example, the lower light probe in region 3 has shifted 5 mm to the left due to tumor deformation, which means an increase in internal margins of 5 mm right to the same light probe, which is a significant undertreated area. Consistently, this deformation caused an increase in 5 mm to the external margins left to this light probe, which may cause undo damage to surrounding tissues, such as blood vessels. A similar effect is displayed in region 1. If the deformed shape could be predicted in real time, which would facilitate intraoperative plan modifications, the I-PDT effect to the tumor margins could be improved.
It is noted that the tumor model was deformed by a modest rate of 10% and only in 1 plane. More significant deformations in 2 or more directions, including twisting as the neck is positioned for easy light probe insertion, may increase the global values listed in Table 5. The effect of such more complex deformations on the tumor’s margins is now under investigation.
Finally, while tumor deformation is assumed due to posture change and anatomy constraints in the current study, this study did not take into account possible additional deformation due to the insertion of light fibers into the target area. The reason for the latter assumption is that the light fiber is small in diameter, has a sharp pointed tip, and is inserted into the target region through an x–y placement grid after the tumor has already been deformed due to posture changes. Nonetheless, additional tumor deformation due to fiber insertion may be taken into account without affecting the proposed method, computation framework, or the validity of the proof of concept.
Summary and Conclusion
We propose an optimization method that uses the tracked positions of a set of FMs for reconstructing the deformed shape of HN tumors. In addition to the constraints imposed by the FMs, the smoothness of the force field on the tumor’s surface is used as an objective as a way to compute a unique force field and hence tumor deformations. The force field smoothness is formulated as a bi-Laplacian term in objective function, and thus the prediction can be achieved at interactive rates by using sparse quadratic programming solver. Despite the relative large error in the prediction of the nodal forces, the prediction accuracy in terms of nodal displacements is highly encouraging (below typical US imaging resolution) in both the sphere and the real tumor cases. Future work will involve extending our formulation to nonlinear FEM and validating our approach against physical experiments. Additionally, an interesting area of investigation includes optimizing the placement of the FMs given the 3-D tumor model. We have shown that FM placement optimization may be particularly useful when only a handful of FMs are available.
The simulation of light dose distributions in the pre- and post-deformed tumor showed that the tumor surface is likely to receive a light dose that is up to 5.4% different than the planned dose (see Table 5). It is well established that it is critical to treat tumor margins for disease control in HN cancer.34,35 The tumor surface is part of the margin. Thus, it would be important to assure that the prescribed light dose is delivered to the surface of the deformed tumor.
Our current results indicate that a real-time computational prediction of a tumor’s deformed shape using only US-tracked FMs is feasible using standard personal computers. We believe our methodology may pave the way for a novel clinical technique for the real-time shape reconstruction and tracking for HN tumors in I-PDT. Additional studies are required to evaluate the impact of tumor deformation on the response to I-PDT.
Acknowledgments
The authors thank Prof Stelian Coros and Dr M. Ersin Yumer for useful discussions.
Abbreviations
- CT
computed tomography
- 3-D
3-dimensional
- DVH
dose–volume histogram
- FEM
finite element method
- FM
fiducial marker
- HN
head and neck
- I-PDT
interstitial photodynamic therapy
- LAHNC
locally advanced head and neck squamous cell carcinoma
- MRI
magnetic resonance imaging
- PS
photosensitizer
- SD
standard deviation
- US
ultrasound
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This study was supported in part by National Cancer Institute grants R01 CA193610 to G. Shafirstein.
References
- 1. Jäger HR, Taylor MN, Theodossy T, Hopper C. MR imaging-guided interstitial photodynamic laser therapy for advanced head and neck tumors. AJNR Am J Neuroradiol. 2005;26(5):1193–1200. [PMC free article] [PubMed] [Google Scholar]
- 2. Jerjes W, Upile T, Akram S, Hopper C. The surgical palliation of advanced head and neck cancer using photodynamic therapy. Clin Oncol. 2010;22(9):785–791. doi:10.1016/j.clon.2010.07.001. [DOI] [PubMed] [Google Scholar]
- 3. Jerjes W, Upile T, Alexander Mosse C, et al. Prospective evaluation of 110 patients following ultrasound-guided photodynamic therapy for deep seated pathologies. Photodiagnosis Photodyn Ther. 2011;8(4):297–306. doi:10.1016/j.pdpdt.2011.08.002. [DOI] [PubMed] [Google Scholar]
- 4. Lou P-J, Jäger HR, Jones L, Theodossy T, Bown SG, Hopper C. Interstitial photodynamic therapy as salvage treatment for recurrent head and neck cancer. Br J Cancer. 2004;91(3):441–446. doi:10.1038/sj.bjc.6601993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Karakullukcu B, van Veen RLP, Aans JB, et al. MR and CT based treatment planning for mTHPC mediated interstitial photodynamic therapy of head and neck cancer: description of the method. Lasers Surg Med. 2013;45(8):517–523. doi:10.1002/lsm.22174. [DOI] [PubMed] [Google Scholar]
- 6. Karakullukcu B, Nyst HJ, van Veen RL, et al. mTHPC mediated interstitial photodynamic therapy of recurrent nonmetastatic base of tongue cancers: development of a new method. Head Neck. 2012;34(11):1597–1606. doi:10.1002/hed.21969. [DOI] [PubMed] [Google Scholar]
- 7. Agostinis P, Berg K, Cengel KA, et al. Photodynamic therapy of cancer: an update. CA Cancer J Clin. 2011;61(4):250–281. doi:10.3322/caac.20114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Wilson BC, Patterson MS. The physics, biophysics and technology of photodynamic therapy. Phys Med Biol. 2008;53(9): R61 doi:10.1088/0031-9155/53/9/R01. [DOI] [PubMed] [Google Scholar]
- 9. Davidson SRH, Weersink RA, Haider MA, et al. Treatment planning and dose analysis for interstitial photodynamic therapy of prostate cancer. Phys Med Biol. 2009;54(8):2293 doi:10.1088/0031-9155/54/8/003. [DOI] [PubMed] [Google Scholar]
- 10. Swartling J, Axelsson J, Ahlgren G, et al. System for interstitial photodynamic therapy with online dosimetry: first clinical experiences of prostate cancer. J Biomed Opt. 2010;15(5):05800 3-058003-9. doi:10.1117/1.3495720. [DOI] [PubMed] [Google Scholar]
- 11. Johansson A, Axelsson J, Andersson-Engels S, Swartling J. Realtime light dosimetry software tools for interstitial photodynamic therapy of the human prostate. Med Phys. 2007;34(11):4309–4321. doi:10.1118/1.2790585. [DOI] [PubMed] [Google Scholar]
- 12. Finlay JC, Zhu TC, Dimofte A, et al. Interstitial fluorescence spectroscopy in the human prostate during motexafin lutetium-mediated photodynamic therapy. Photochem Photobiol. 2006;82(5):1270–1278. doi:10.1562/2005-10-04-RA-711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Du K, Mick R, Busch M, et al. Preliminary results of interstitial motexafin lutetium-mediated PDT for prostate cancer. Lasers Surg Med. 2006;38(5):427–434. doi:10.1002/lsm.20341. [DOI] [PubMed] [Google Scholar]
- 14. Li J, Zhu TC. Determination of in vivo light fluence distribution in a heterogeneous prostate during photodynamic therapy. Phys Med Biol. 2008;53(8):2103–2114. doi:10.1088/0031-9155/53/8/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Baran TM, Foster TH, Nazareth DP. Image-guided treatment planning and dosimetry for interstitial photodynamic therapy In: Biomedical Optics and 3-D Imaging (2012), Paper JM3A.17. Optical Society of America; 2012: JM3A.17. doi:10.1364/BIOMED.2012.JM3A.17. [Google Scholar]
- 16. Baran TM, Foster TH. Comparison of flat cleaved and cylindrical diffusing fibers as treatment sources for interstitial photodynamic therapy. Med Phys. 2014;41(2):022701 doi:10.1118/1.4862078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Oakley E, Wrazen B, Bellnier DA, Syed Y, Arshad H, Shafirstein G. A new finite element approach for near real-time simulation of light propagation in locally advanced head and neck tumors. Lasers Surg Med. 2015;47(1):60–67. doi:10.1002/lsm.22313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Wong KCL, Summers R, Kebebew E, Yao J. Tumor growth prediction with hyperelastic biomechanical model, physiological data fusion, and nonlinear optimization In: Golland P, Hata N, Barillot C, Hornegger J, Howe R, eds. Medical Image Computing and Computer-Assisted Intervention—MICCAI 2014. Lecture Notes in Computer Science Springer International Publishing; 2014:25–32. doi:10.1007/978-3-319-10470-6_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Clatz O, Sermesant M, Bondiau P-Y, et al. Realistic simulation of the 3D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Trans Med Imaging. 2005;24(10):1334–1346. doi:10.1109/TMI.2005.857217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Chen X, Summers R, Yao J. FEM-based 3-D tumor growth prediction for kidney tumor. IEEE Trans Biomed Eng. 2011;58(3):463–467. doi:10.1109/TBME.2010.2089522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kamrani A, Azimi M. Geometrical analysis and predictive modeling of head and neck tumors. In: 2014 World Automation Congress (WAC); 2014:1–5. doi:10.1109/WAC.2014.6935641. [Google Scholar]
- 22. Gill S, Li J, Thomas J, et al. Patient-reported complications from fiducial marker implantation for prostate image-guided radiotherapy. Br J Radiol. 2012;85(1015):1011–1017. doi:10.1259/bjr/68127917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Ng M, Brown E, Williams A, Chao M, Lawrentschuk N, Chee R. Fiducial markers and spacers in prostate radiotherapy: current applications. BJU Int. 2014;113(suppl 2):13–20. doi:10.1111/bju.12624. [DOI] [PubMed] [Google Scholar]
- 24. Cendales R, Torres F, Arbelaez J, Gaitan A, Vasquez J, Bobadilla I. Displacements of fiducial markers in patients with prostate cancer treated with image guided radiotherapy: a single-institution descriptive study. Rep Pract Oncol Radiother. 2015;20(1):38–42. doi:10.1016/j.rpor.2014.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Oliveira FPM, Tavares JMRS. Medical image registration: a review. Comput Methods Biomech Biomed Engin. 2014;17(2):73–93. doi:10.1080/10255842.2012.670855. [DOI] [PubMed] [Google Scholar]
- 26. Bathe K-J. Finite Element Procedures. Prentice Hall; 1996. [Google Scholar]
- 27. Rosenberg S. The Laplacian on a Riemannian Manifold: An Introduction to Analysis on Manifolds. Cambridge: Cambridge University Press; 1997. http://ebooks.cambridge.org/ref/id/CBO9780511623783. Accessed June 1, 2016. [Google Scholar]
- 28. Crane K, de Goes F, Desbrun M, Schröder P. Digital geometry processing with discrete exterior calculus In: ACM SIGGRAPH 2013 Courses. SIGGRAPH ‘13 New York, NY: ACM; 2013:Article 7:1-7:126. doi:10.1145/2504435.2504442. [Google Scholar]
- 29. Pinkall U, Juni SD, Polthier K. Computing discrete minimal surfaces and their conjugates. Exp Math. 1993;2:15–36. [Google Scholar]
- 30. de Berg M, Cheong O, van Kreveld M, Overmars M. Computational Geometry: Algorithms and Applications. 3rd ed Santa Clara, CA: Springer-Verlag Telos; 2008. [Google Scholar]
- 31. Potra FA, Wright SJ. Interior-point methods. J Comput Appl Math. 2000;124(1-2):281–302. doi:10.1016/S0377-0427(00)00433-7. [Google Scholar]
- 32. Drakopoulos F, Chrisochoides NP. A parallel adaptive physics-based non-rigid registration framework for brain tumor resection In: Zhang YJ, Tavares JMRS, eds. Computational Modeling of Objects Presented in Images. Fundamentals, Methods, and Applications. Lecture Notes in Computer Science Springer International Publishing; 2014:57–68. doi:10.1007/978-3-319-09994-1_6. [Google Scholar]
- 33. Desbrun M, Meyer M, Schröder P, Barr AH. Implicit fairing of irregular meshes using diffusion and curvature flow. Poster presented at: Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH ‘99 New York, NY: ACM Press/Addison-Wesley Publishing Co; 1999:317–324. doi:10.1145/311535.311576. [Google Scholar]
- 34. Baddour HM, Magliocca KR, Chen AY. The importance of margins in head and neck cancer. J Surg Oncol. 2016;113(3):248–255. doi:10.1002/jso.24134. [DOI] [PubMed] [Google Scholar]
- 35. Bittermann G, Ermer M, Voss P, et al. Comparison of virtual and titanium clip marking of tumour resection margins for improved radiation planning in head and neck cancer surgery. Int J Oral Maxillofac Surg. 2015;44(12):1468–1473. doi:10.1016/j.ijom.2015.07.013. [DOI] [PubMed] [Google Scholar]