Multimodal Teaching Analytics: Automated Extraction of Orchestration Graphs from Wearable Sensor Data

Abstract

The pedagogical modelling of everyday classroom practice is an interesting kind of evidence, both for educational research and teachers’ own professional development. This paper explores the usage of wearable sensors and machine learning techniques to automatically extract orchestration graphs (teaching activities and their social plane over time), on a dataset of 12 classroom sessions enacted by two different teachers in different classroom settings. The dataset included mobile eye-tracking as well as audiovisual and accelerometry data from sensors worn by the teacher. We evaluated both time-independent and time-aware models, achieving median F1 scores of about 0.7-0.8 on leave-one-session-out k-fold cross-validation. Although these results show the feasibility of this approach, they also highlight the need for larger datasets, recorded in a wider variety of classroom settings, to provide automated tagging of classroom practice that can be used in everyday practice across multiple teachers.

Introduction

Teacher facilitation is a crucial element in the learning outcomes of many technology-enhanced learning (TEL) situations in formal settings. This importance has been highlighted by educational research efforts in naturalistic settings, including inquiry-based learning experiences (e.g., Kirschner et al. 2006), computer-supported collaborative writing (e.g., Onrubia & Engel 2012), and many others. Indeed, the understanding of specific problems and phenomena that arise in the implementation of educational innovations in authentic settings (also known as ‘orchestration’) is considered one of the foremost challenges in the field of TEL (Fischer et al. 2014; Roschelle et al. 2013).

The inquiry into classroom practice and classroom management (regardless of whether it is for research, or for practitioners’ own professional development) is known to be difficult, due to classrooms’ immediacy and unpredictability (even in settings without a technological component, see Doyle 1977). Even today, this investigation requires either the observation or recording of real classroom situations, often followed by manual coding of the recordings (Cortina et al. 2015; Wolff et al. 2015). However, this kind of approaches have obvious limitations in terms of the scale and frequency at which they can be applied. This can also be seen as a cause for the reported lack of evidence used in reflection-based teacher professional development approaches (Marcos et al. 2011).

However, recent advances and affordability of sensor and computation technologies may help in the automation of some of this tasks (as shown by, e.g., Donnelly et al. 2017; ref. anonymized for review) in ecologically valid conditions and in unobtrusive ways, leading to multimodal approaches to teaching analytics (Vatrapu 2012).

In this paper, we build upon previous preliminary work on the feasibility of using wearable sensors to extract both the moment-to-moment teaching activity and the social plane of interaction (ref. anonymized for review). More concretely, we recorded a multimodal dataset of 12 classroom lessons performed by two different teachers, in a variety of situations. We then used different machine learning models (both time-independent and with an emphasis on time structure), to explore more deeply the possibilities of this kind of approach. To understand the potential generalizability of our findings, we trained and evaluated both personalized (i.e., trained on just one specific teacher) and general models (aimed at working across teachers).

The next section offers an overview of related work in the field of multimodal teaching analytics, followed by the description of our study’s context, methodology and results. Finally, we discuss several implications of the study in terms of tradeoffs and guidelines for future research and technology design in the area.

Related Work

Teaching Analytics for Research and Reflection

Teacher facilitation is considered a challenging and critical aspect for effective learning (Fischer et al. 2014). Both educational researchers and practitioners have paid special attention to this process, using different data gathering methods such as classroom observations, audio and video recordings, student feedback, or teacher self-reflections. These methods, however, present obvious limitations in terms of scalability, since they often require manual processing which is time-consuming and error-prone (Cortina et al. 2015; Marcos et al. 2011; Wolff et al. 2015). In that sense, the application of automated analytics to these tasks could be tremendously beneficial, even if they also require a certain amount of manual labeling of data to kick-start such automation (see initial prototypes in this direction, like Fong et al. 2016).

Teaching analytics is often conceived as the subset of learning analytics (LA) devoted to help teachers understand learning and teaching processes (Vatrapu 2012). Although this definition considers both learning and teaching processes as objects of analysis, most research in this area collects data about the student learning/behavior, to provide feedback to the teacher. This is apparent, for instance, from the “Towards Theory and Practice of Teaching Analytics workshop” and the “International Workshop on Teaching Analytics” organized in 2012–2016.

Most of the research focusing on teaching practice analyses teacher-generated artifacts, such as the lesson plans. These proposals make use of digital representations of the plan, e.g., in the shape of a learning design (Mor et al. 2015; Sergis & Sampson 2017), or based on learning environment structure (Rebholz et al. 2012; Vozniuk et al. 2015). However, sometimes the lesson plan is not followed as envisioned, or details of the plan influencing the learning process may have not been described (if the plan is ever formalized at all). Fewer studies follow a bottom-up approach, attempting the characterization of the actual enactment of the lesson, often in very specific kinds of settings, e.g., examining teachers’ tool usage patterns (Xu & Recker 2012), through explicit audience-provided feedback during lectures (Rivera-Pelayo et al. 2013), or through the analysis of the reasoning behind expert teacher assessments (Gauthier 2013).

As it often happens in other LA areas, most current teaching analytics research focuses exclusively on data available in a virtual environment, or provided ad-hoc by participants (e.g., questionnaires) (Rodríguez-Triana et al. 2015). This reveals a common limitation of our field: we tend to focus on spaces where there is an abundance of data, not where most of the learning actually occurs (also known as the “streetlamp effect”, Freedman 2010).

To address this limitation in face-to face learning scenarios, recent works use alternative data sources (e.g., audio recordings in live classrooms) to characterize automatically teachers’ instructional strategies. For instance, Donnelly et al. (2016) use such audio data to recognize among five different kinds of teaching activities. The same authors (2017) used similar data to distinguish questions from non-questions in teacher classroom discourse.

Multimodal Analytics and Professional Activity Detection

This emergent trend to complement easily available digital traces with data captured from the physical world has been labeled multimodal learning analytics (MMLA). Typical examples of MMLA include text-based and graphic-based content, speech, gesture and electro-dermal activation (Blikstein & Worsley 2016; Ochoa & Worsley 2016). For instance, Ochoa et al. (2013) used video, audio and pen stroke information to discriminate between expert and non-expert students solving mathematical problems. In the area of professional development there is also room for MMLA solutions, by using sensors in the workplace (e.g., inserted in patient manikins used for healthcare training, see Martinez-Maldonado et al. 2017).

In terms of data processing, the initial forays into MMLA used relatively simple machine learning algorithms to build models of the phenomena under study (Ochoa et al. 2013). However, more recently deep and recurrent neural networks have shown promising capabilities, outperforming previous results in dealing with rich multimodal data in areas like facial expression recognition (Kim et al. 2015) or speech recognition, both in lab settings and even in the wild (Dhall et al. 2015).

Modelling Classroom Events: Orchestration Graphs

Multimodal approaches to analyze teaching or learning processes in the physical world are not yet widespread. Isolated examples include the iKlassroom conceptual proposal (Vatrapu et al. 2013), which features a map of the classroom to help contextualize real-time data about the learners in a lecture. Also in university settings, unobtrusive computer vision approaches to assess student attention from their posture and other behavioral cues have been applied (Raca & Dillenbourg 2013). Albeit solutions that model student actions and information exist, studies that characterize teacher practice in the classroom using MMLA are scarce, and novel ways of meaningfully characterizing teacher practice are needed. But, why is such modeling of teaching beneficial from an educational perspective, and what pedagogically-meaningful aspects can be modeled automatically?

Reviews of literature about teacher reflection in professional development highlight that very often such reflection is insufficiently based on actual evidence about daily practice (Marcos et al. 2011). The observation and characterization of teaching activities (e.g., Flanders 1970; Fogarty et al. 1983; Prieto et al. 2011) and the specification of social planes of teacher-student interaction (Vygotsky 1978; Richards & Farrell 2011) are two of the most aspects examined, and they are also the focus in instructional design practice (especially, of collaborative learning, see Dillenbourg & Jermann 2007). Hence, it can be especially useful to track deviations between the intended instruction and the actual classroom enactment (see Lockyer et al. 2013 and other work on the value of aligning learning design and learning analytics), as the focus not only of educational research, but also teacher professional development.

These two aspects (teaching activites and social levels) are also present in the notion of teaching practice as an orchestration process, i.e., “productively coordinating supportive interventions across multiple learning activities occurring at multiple social levels” (Dillenbourg et al. 2009). Graphical and computational representations of a lesson’s orchestration can be made, sometimes named ‘orchestration graphs’ (Dillenbourg 2015). This kind of graph, representing activities over time horizontally, and social plane (individual, group, or whole-class) vertically, can be used to express instructional designs (Dillenbourg 2015) or even the improvised actions during lesson enactment (Prieto et al. 2011).

Following this same formalism (the orchestration graph), in our previous work (ref. anonymized for review) we explored the automatic extraction of orchestration graphs from a multimodal dataset gathered from only one teacher, classroom space and a single instructional design. In this paper, we apply more advanced machine learning techniques to an extended version of this dataset. In particular, we focus on the fact that classroom practice (and its orchestration graph representation) is sequential in nature, and that the events occurring at different points in a lesson are not likely to be independent of each other. We aim to explore these temporal relationships (as captured by multiple data sources) in different ways, an aspect seldom explored in multimodal learning and teaching analytics literature, which often uses time-independent machine learning models (e.g., the decision trees used by Ochoa et al. 2013).

Modelling Orchestration Graphs of Using a Multimodal Dataset

Study Context

The current study is part of a long-term collaboration between a local school and our research lab, with the aim of modelling and supporting teacher orchestration in technology-enhanced classrooms. As part of our exploration of how multimodal sensor data could be used for teacher reflection in professional development, we recorded eight lessons from a single school teacher, and two of her cohorts of students aged 11–12 years old. These eight sessions covered four different kinds of mathematics lessons, from the taking of a math test, to a collaborative investigation of certain properties of numbers (situations 2-5, see Table 1). Each of these four kinds of lessons was enacted with the two cohorts (hence, pairs of sessions shared a common instructional design, but differed in the students involved and the concrete classroom events).

Table 1.

Main contextual characteristics of the 12 classroom sessions of our multimodal dataset.

Situation	Sit.1	Sit.2	Sit.3	Sit.4	Sit.5
Nr. recorded sessions	4	2	2	2	2
Student cohorts	A, B, C, D	E, F	E, F	E, F	E, F
Nr. students	19–21 (each)	19–21 (each)	17 (each)	18–20 (each)	19–21 (each)
Teacher	T1 (novice)	T2 (expert)	T2 (expert)	T2 (expert)	T2 (expert)
Lesson length	32–38 mins	16–32 mins	43–44 mins	41–50 mins	47–49 mins
Topic	Geometry and coordinate systems	Numbers	Numbers	Numbers	Numbers
Dynamic	Collaborative/competitive game-based	Collaborative inquiry-based	Worksheet	Collaborative/competitive game-based	Test
Classroom technology	Tabletops, Wall display	Wall display, pen/paper	Wall display, pen/paper	Pen/paper	Pen/paper

To complement these recordings made in the same classroom space with a single teacher, we recorded four additional math lessons with a different teacher in a completely different space (see Figure 1), during the course of an open doors day in our lab. Four different cohorts of local school children went over the activities of a game-based lesson using tangible tabletop computers, facilitated by a novice teacher-researcher (situation 1 in Table 1).

Figure 1.

The two different classroom spaces where the dataset was recorded. School classroom (teacher T2, right) and open doors day multi-tabletop classroom (teacher T1, left).

Methodology

Data gathering

During each of the aforementioned twelve sessions, the teacher was equipped with eye-tracking glasses and a smartphone. The SMI eye-tracking glasses collected gaze data at 60 Hz (binocular gaze). They also recorded the teacher’s subjective video (24 FPS, HD resolution) and audio streams. The smartphone included an application that recorded 3-axis accelerometer signals, thus tracking the teacher’s movement in the classroom.

We hypothesized that, by combining the features extracted from these four sources (eye-tracking, video, audio and accelerometer), we would be able to model the simple yet pedagogically-meaningful formalism of the orchestration graph (Dillenbourg 2015), thus proving the feasibility of this approach to support future teacher reflection and researcher tools.

Data pre-processing and feature extraction

The four aforementioned data sources were manually aligned. Then, in order to bring these data sources with different sampling rates into a common level of granularity, we partitioned each of them into 10-second episodes using a sliding windows with an overlap of 5 seconds. Such window length was chosen on the basis of our initial work in orchestration graph extraction (ref. anonymized for review), in which 10-second windows lead to better model performance, and also was more adequate for the manual coding of episodes (as it is often hard to assign a single activity or social plane to a 1-second piece of video, especially when transitioning between actions, or to assign a single label to a 30-second-long piece of teacher action). From each of these 10-second windows (or episodes, from now on), features were extracted:

• From the eye-tracking data, 10 commonly-used features were extracted, including pupillary data (e.g., pupil diameter mean and standard deviation in each episode) and eye movement data (e.g., saccade speed or fixation duration).

• From the accelerometer data, 140 features were extracted, including means, variations and 30-coefficient FFT spectrum of the three accelerometer axes, as well as means, variations and FFT of the accelerometer jerk (related to the energy spent in the movement).

• From the audio data, 6405 features were extracted using the openSMILE audio processing toolkit (http://audeering.com/technology/opensmile/). The features extracted included both high-level constructs (e.g., emotion detection predictions) as well as low-level features of the spectrum, energy, etc. of each episode (commonly used in audio data mining and machine learning challenges).

• From the video data, 1000 features were extracted, using a pre-trained deep convolutional neural network. More concretely, one frame extracted from each episode was input to a the VGG-19 network (Simonyan & Zisserman 2014). The output prediction vector was taken as video-related features. The network output can be considered as a semantic summary of what the teacher was seeing.

Aside from these extracted features, the audio/video of the session was manually video-coded to obtain the ground truth of the orchestration graph. More concretely, each episode was tagged with one of five mutually-exclusive teaching activities, according to the teacher’s most immediate intent during the episode (in upper case, the labels used in Figure 5):

• EXPlanation, that is, the teacher delivering content in lecture style,

• MONitoring, checking around the classroom while students work on a task,

• REPairs, in which the teacher answers to a student question or doubt,

• QUEstioning, in which it is the teacher who tries to assess the student(s) knowledge orally, and

• Other activities not included above.

Figure 5.

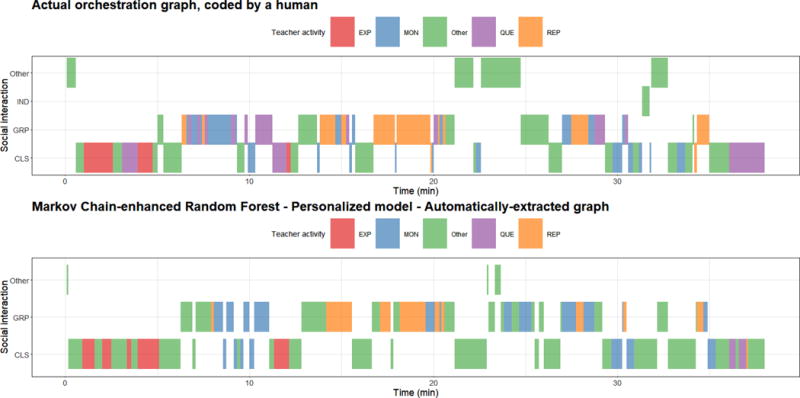
Example graphical representation of the human-labeled and automatically-extracted orchestration graphs of a session, resulting from the personalized Markov Chain-enhanced random forest models for teaching activity and social plane (median F1 scores of 0.74 and 0.83, respectively).

This categorization schema was derived from previous observational studies of classroom activities and routines (such as Fogarty et al. 1983; Prieto et al. 2011), as well as classroom observation schemas (concretely, the Flanders Interaction Analysis Categories, see Flanders 1970). These initial literature-driven categories were then refined with the help of participant teachers (i.e., what kinds of classroom activities were interesting for them) during a participatory preparation phase of the experiments.

Similarly, each episode was tagged as containing interactions at INDividual, small-GRouP or CLaSs-wide social planes, or other plane of interaction (i.e., not socially relevant, or no social interaction). As mentioned before, these social plane categories were derived from Vygotsky’s socio-constructivist theories (1978), and is often included in instructional design (Dillenbourg & Jermann 2007) and classroom observation schemes (e.g., Richards & Farrell 2011).

It is also important to note that the inclusion of an ‘other’ category (i.e., the episode is not interesting) in both orchestration graph dimensions makes the accurate automatic extraction much more difficult, but has great practical importance: our models and potential future applications should be able to tell the interesting episodes from the non-interesting ones, which may cover a wide array of events and occurrences (this code is not present in most previous work such as ref. anonymized for review).

Hence, at the end of this process we had a dataset comprising a total of 5561 episodes from the twelve sessions, and each episode was characterized by a total of 7555 features from four data sources. Furthermore, each episode had been assigned a teaching activity and a social plane of interaction code, thus forming the target orchestration graph to be extracted. Figure 2 shows the distribution of codes for both target variables, including a noticeable class imbalance.

Figure 2.

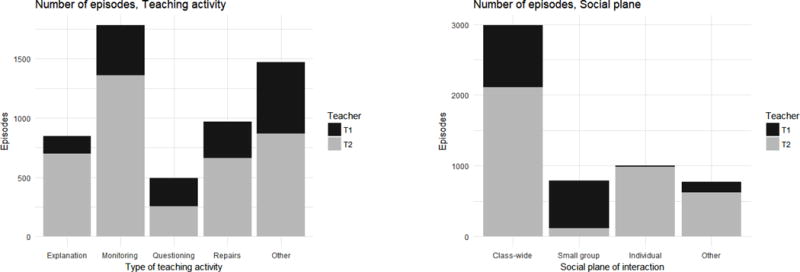
Distribution of codes for the (human-labeled) ground truth used to detect teaching activities and social planes of interaction. The two colors denote the participant teacher that generated them.

Model training and evaluation

From a machine learning point of view, we can express the automatic extraction of orchestration graphs as two parallel classification tasks (one to deduce the teaching activity, another to guess the social plane of interaction), to be predicted for each episode from the same pool of features. We trained different kinds of machine learning models: a) personalized models, trained and tuned for use by a single teacher; and b) general models, aimed at working across multiple teachers. In order to assess how well these models perform in circumstances different than those in which they were trained, we performed k-fold cross validations (in which data is partitioned in k contiguous segments, training the model with k-1 segments and testing its performance on the remaining one - repeating the process k times). We took each classroom session as the basic, natural unit for partition (as every session, even ones with a similar instructional design, had different students and different classroom events):

• To evaluate personalized models, we trained the model on N-1 sessions of a single teacher (N being 4 for the novice teacher T1, and 8 for the expert teacher T2, see Table 1), and tested the model on the remaining session (leave-one-session-out).

• On the other hand, general models were tested using a similar leave-one-session-out schema (i.e., training on 11 of the sessions available from both teachers, and testing on the remaining session).

The motivation behind such an evaluation framework to position different models within the bias-variance spectrum (see Kidzinski et al. 2016 for a similar discussion in the context of MOOC learning analytics). We can either aim at very general features and a generalizable model across the population, or very specific features and a model that only generalizes to the same individuals. Given our limited dataset, in this study we explore more exhaustively the bias side of the spectrum, and only provide initial indications of how much our models can generalize across the population. In order to compare models against each other, we have used the median F1 scores (to avoid misleading results that using plain accuracy would provide, due to the ground truth’s class imbalance; also, to more easily place ourselves within similar related work on teaching activity extraction, such as Donnelly et al. 2016).

Following our initial exploration of this approach (ref. anonymized for review), we have trained and evaluated different kinds of models, including both time-independent (i.e., that considers and classifies each episode in isolation) and time-aware models that account for the ordered sequence of events/episodes in time. Among the different models we explored, we chose to prime performance over interpretability, leading to the use of several ‘black box’ models (like random forests or neural networks). This was motivated by the fact that we aim at automating a task that is relatively easy to perform by a human (deciding what is the teacher’s immediate intent at a certain point in the lesson), rather than deepening our understanding of classroom orchestration or how such extraction is performed per se.

Finally, as it is common in many MMLA efforts (e.g., Ochoa et al. 2013), we also explore the added value of different data sources (and data source combinations) or types of features, in order to guide future research and technology design in this area. However, for brevity’s sake, in the results below we do not detail all the models and combinations of data sources explored; only the most effective or interesting ones are mentioned.

Technical implementation details

The aligning and pre-processing of the data, accelerometer and eye-tracking feature extraction, as well as most of the data models and their evaluation have been implemented in R, using standard packages such as ‘randomForest’ or ‘e1071’ (for support vector machines). The video feature extraction has been performed using the Lua implementation of VGG-19, while the audio feature extraction has been done using the openSMILE toolkit. The neural network models described below have been implemented using the Keras library (in Python). The source code for the aforementioned processing and modelling is available at <<to be released upon paper acceptance>>.

Personalized Models for Orchestration Graph Extraction

One potential scenario for future applications of orchestration graphs extraction, is the personal use by practitioners (e.g., for reflection-based teacher professional development). These models could be trained and tuned over long periods of time for a single teacher, for increased accuracy. With the machine learning models described below, we explore the following questions: “how effective can be a model trained/tuned for a single teacher?” and “what are the most informative data sources and features when building this kind of models?”

Time-independent Models

Several families of time-independent classification algorithms were tested with the present dataset. Among those, random forests proved to have the most robust performance, both on predicting the teaching activity and the social plane of interaction. Random forests also performed comparatively well with different combinations of data sources. As an alternative to this relatively complex ensemble model acting on a high-dimensional dataset, we tried also lower-complexity ones, like support vector machines (SVMs) with a radial kernel, operating on a selection of the 100 uncorrelated features that most varied across the target variable. To perform this feature ranking, we used Cohen’s d (a metric of effect size, see Cohen 1977) against the target variable (teaching activity or social plane) as a proxy for the potential predictive value of the feature.

As we can see in Figure 3, the random forest model achieved median F1 scores of around 0.7 in extracting the teaching activity, reaching F1=0.8 for the social plane of interaction. Interestingly, the lower-complexity SVM alternative also performed at similar levels, even outperforming the random forest in predicting both the teaching activity and social plane (median F1=0.72 and 0.813, respectively).

Figure 3.

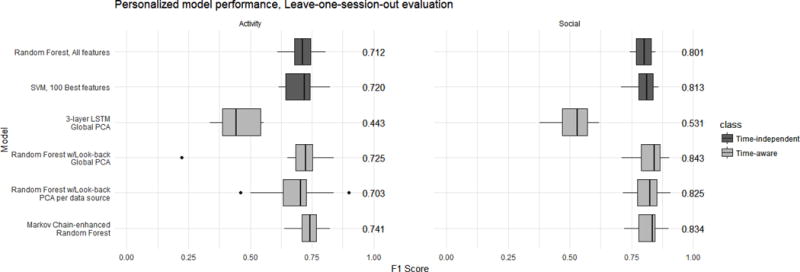
Boxplot representation (median and inter-quartile range) of the evaluation results (F1 scores) for the top personalized models trained, in a leave-one-session-out k-fold cross-validation. Numbers to the right of the boxplots indicate the exact median value of the F1 scores.

As for the relative value of the different data sources and their features, audio was the most informative source across the board (average F1=0.702 and 0.787, respectively), with a combination of audio/accelerometer features ranking among the best time-independent models to predict teaching activity (avg. F1=0.717).

Despite being considered a ‘black box’ algorithm, random forests also can provide a measure of the relative importance of features. As we can see in Table 2, certain eye-tracking and accelerometer features are often ranked among the most influential, although the rest of the table is largely dominated by the (much more numerous) audio features.

Table 2.

Feature importance of the multimodal dataset: features most often appearing among the 10 most important variables in the (time-independent) random forest model, trained using all data sources’ features

Target variable		Activity	Social
Feature	Data source	Nr. appearances (out of 16)	Nr. appearances (out of 16)
Mean pupil diameter	eyetracking	15	13
Mean x-axis value	accelerometer	3	7
Median jerk value	accelerometer	0	8
audSpec_Rfilt_sma.21._flatness	audio	4	2
audSpec_Rfilt_sma.19._percentile1.0	audio	3	3
audspec_lengthL1norm_sma_flatness	audio	2	4

Modelling Time Using Look-back

As a first (rather naive) approach to exploiting the time structure of classroom events, we can use the features in the immediately previous episodes as additional inputs for our models, accounting for the fact that what happens right now is partially determined by what happened some moments ago. We trained random forest models by feeding them with both the current features and those from the previous nine episodes (‘look-back’ strategy). In order to avert the curse of dimensionality (we would have 10 times more features than in the original model, while the number of training samples would remain the same), a principal component analysis (PCA) was performed to reduce the number of features to 100, before the look-back. As an alternative, and to avoid the over-representation of audio features in this PCA, we also performed an even more drastic dimensionality reduction separately to each data source, to a total of 45 features before the look-back.

Figure 3 summarizes the results: we can see that this naive time-aware model in fact outperforms the time-independent ones in both extraction tasks, performing especially well regarding the prediction of social planes (F1=0.843).

Although the features after the PCA transformation are even harder to interpret than the original ones, we can use the random forests’ variable importance to explore the relative value of the different data sources and the look-back (time) component, in the models’ predictions. Table 3 shows that not only the current audio features are important in the predictions; also, the same component up to 3 episodes before (i.e., 15 seconds before), and previous eye-tracking data, have a large influence in the models’ predictions.

Table 3.

Feature importance of the multimodal dataset: features most often appearing among the 10 most important variables in the (time-aware) personalized look-back random forest model, trained from all data sources (using separate PCA components per data source)

Target variable		Activity	Social
Feature	Data source	Nr. appearances (out of 16)	Nr. appearances (out of 16)
PCA comp.1 (curr)	audio	16	16
PCA comp.1 (t-1)	audio	16	16
PCA comp.1 (t-2)	audio	16	14
PCA comp.3 (t-1)	audio	12	16
PCA comp.1 (t-3)	audio	16	7
PCA comp.2 (t-1)	eyetracking	2	10

Modelling Time Using Markov Chains

Another approach to modelling the time structure of the classroom orchestration graphs can be made by modelling the transitions between the different teaching activities and social planes of interaction, as two different Markov processes. We can thus train Markov Chains to calculate the probability of the teacher transitioning from one teaching activity (or social plane) to a different one (or to keep doing the same one). These transition probabilities can then be used to tune the results of a time-independent model to make them more similar to the observed classroom behavior (e.g., making the stay in the same teaching activity or social plane more probable than other transitions).

As we can see in Figure 3, the personalized models that used this approach outperformed all other models in the prediction of teaching activity (median F1=0.741), even if they failed to beat the performance of the look-back strategy for social plane of interaction.

Modelling Time Using Recurrent Neural Networks (RNNs)

Although the look-back and Markov Chain approaches to modelling time already provided a certain boost in performance, they failed to account for longer-term (or more sophisticated) dependences between the data at different moments in time. For instance, if the teacher is lecturing, momentarily jumps to a repair activity prompted by a student question, but later comes back to the explanation. To capture these long-term dependences, we can train models that are able to learn when to remember/forget past data, such as recurrent neural networks (RNNs). Concretely, long short-term memory networks (LSTMs) are especially designed for this purpose, and have been used successfully in many machine learning challenges recently.

We trained LSTMs with different architectures, ranging from 1-3 layers and different amounts of cells per layer (32-200), as well as dropout regularization to avoid overfitting (given the relatively small dataset available). However, as we can see in the example of Figure 3, these personalized models did not perform as well as the previously presented ones (median F1 scores around 0.4-0.5).

General Models for Orchestration Graph Extraction

The previous section illustrated how machine learning models can be built to extract the orchestration graph for the classroom practice of a single teacher. However, can we also build models that are able to extract an orchestration graph reliably across the radically different classroom realities of multiple teachers? This question is explored below, also using a leave-one-session-out k-fold cross-validation schema.

Time-independent Models

Machine learning algorithms from multiple families were trained for the extraction of orchestration graphs, including random forests and SVMs applied on a selection of features, and using different combinations of data sources. The results of evaluating these general models are summarized in Figure 4.

Figure 4.

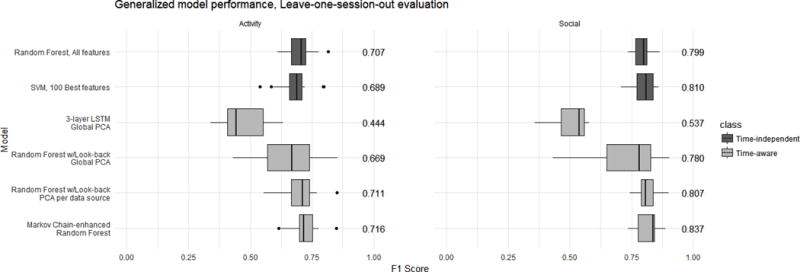
Boxplot representation (median and inter-quartile range) of the evaluation results (F1 scores) for the top generalized models trained, in a leave-one-session-out k-fold cross-validation. Numbers to the right of the boxplots indicate the exact median value of the F1 scores.

The performance of these general time-independent models on leave-one-session-out evaluations is inferior to that of the personalized models, as expected (e.g., for a random forest, median F1=0.707 and 0.799, respectively). Regarding the predictive value of the different data sources and features, again audio was the most predictive one (mean F1=0.702 and 0.765, respectively), even if the random forests’ variable importance also feature very often the mean pupil diameter as a top variable (not shown here for brevity).

Modelling Time Using Look-back

We can again try to model the short-term time dependences between different features by using look-back, over the dataset whose dimensionality has been reduced using PCA. In this case (Figure 4), the performance is only improved in the case of predicting teaching activity using separate PCA per data source (median F1=0.711). The importance of the different PCA components and their previous states also showed predominance of audio features and their previous states, as well as certain eye-tracking components (not shown for brevity).

Modelling Time Using Markov Chains

We can also try the same Markov Chain enhancement to calculate the probability of transitioning from one teaching activity or social plane to another (this time across multiple teachers), in order to enhance the predictions of our time-independent general models.

As we can see in Figure 4, the general models that used this approach outperformed all other general models in the prediction of teaching activity (even if only slightly, median F1=0.716), achieving a noticeable gain in performance for the prediction of social plane of interaction across teachers (median F1=0.837).

Modelling Time using Recurrent Neural Networks (RNNs)

Finally, we also tried to model longer-term time structure and relationships between features in general models through LSTM recurrent neural networks. As we can see in Figure 4, such models were not very successful either, performing quite poorly under the leave-one-session-out evaluation schema (F1 in the range of 0.4-0.5).

Discussion

In summary, the results from our evaluation of personalized and general models to automatically extract orchestration graphs highlight the fact that machine learning models can be successfully trained with such multimodal sensor data, using relatively low-level features. Our results show a comparable or superior performance to recent related work in the automatic tagging of classroom events, like Donnelly et al.’s (2016; 2017), which report F1 scores around 0.6-0.7 in similar tasks (although such performance values cannot be compared directly due to the differences in the tasks and datasets used).

Our results underline the current state of multimodal learning and teaching analytics: the reported accuracies when working with sensor and other unstructured sources of data (around 60-80%, see Morency et al. 2013; Chahuara et al. 2016; Dhall et al. 2015) represents considerable progress in the latest years, but is still far from the performance that end users would expect from commercially-deployable solutions. To illustrate this point, we can see the graphical comparison between human-labeled and automatically-extracted orchestration graphs in Figure 5: albeit the overall balance of teaching activities and social planes may be preserved, noticeable differences are visible to the naked eye. This is in part due to the fact that this graph represents two simultaneous classification tasks and hence, even with relatively high F1 scores, there is a fair chance that at any point in time either the teaching activity or the social plane will have been misclassified.

Our results also illustrate the different tradeoffs that researchers and technology designers in this area need to take into account:

• Bias vs. variance tradeoff: in this paper we illustrate two kinds of models that can be built across the bias-variance spectrum, ones more specific and others more generalizable. The range of best model performances reported here (F1 scores between 0.44 and 0.84) give an idea of what we can expect from current multimodal teaching analytics models, which in turn may condition the kinds of applications and usage dynamics that are feasible for these models (e.g., in long-term personalization vs. generally ready-to-use).

• Computational cost and latency vs. performance: we have explored models with varying levels of complexity, both in terms of training and prediction. Although the most common usages of the presented models in research and professional development are performed post-hoc without strict time limitations, our results with simpler feature sets and comparatively “cheap” SVM models, also open the door to real-time applications of these models, with little reduction in model performance.

• Data gathering costs vs. benefits: the gathering of the dataset used in the present paper was rather costly, in terms of hardware, setup time and researcher effort. Although this arrangement provided us with higher-quality data, we could also observe how less costly data sources (like audio or accelerometer) are already quite effective by themselves. This tradeoff, together with the issue of data ownership and the handling of potentially sensitive personal data (e.g., video recordings), have prompted researchers to recently propose approaches in which students or teachers collect and own the multimodal data (Domínguez et al. 2015).

• High- vs. low-interpretability models and features (and the curse of dimensionality): in this paper, contrary to other works in the area (e.g., Donnelly et al. 2017), we have chosen to use multimodal features with relatively low interpretability (as opposed to, e.g., analyzing the automated transcription of what the teacher says, which can be easily interpreted). This is again a tradeoff: highly interpretable features may enable higher performance levels and more advanced analyses, but also make the approach more fragile in terms of what languages or local cultures it is applicable to. Related to this issue is the “curse of dimensionality” (e.g., the fact that we had more low-level audio features than we had samples in the dataset), which can be a problem when training many machine learning models. Our use of ensemble models (e.g., random forests that include 500 decision trees using 86 features each), or explicit strategies like PCA or simple feature ranking/selection enabled us to deal with this problem with relatively little impact on the performance of the models.

• Efficiency vs. effectiveness in measuring model performance: our choice of F1 as the scoring metric to compare and judge the models is not the only possible choice, although it is an efficient one favored by many researchers in the area (as it is also more impervious to class imbalances in the dataset). Other target users (such as teachers) may find more effective the use of other metrics like accuracy, which are easier to grasp and visualize.

• Data fusion and tooling: the data fusion strategy used (at the feature extraction level) is not the only possible one when dealing with disparate sources of data, and such choice may also impact the performance of the resulting models (Worsley 2014). This choice is also limited by the tooling available to the multimodal analytics researcher, as there is still no widely accepted standard or toolkit for convenient data fusion and pre-processing.

Aside from these tradeoffs (ubiquitous in current multimodal analytics), our results are mainly constrained by the limitations in the scale and variety of the dataset used, especially in terms of the number of teachers and classroom settings covered. Other, more rigorous kinds of evaluation could also be possible (e.g., leave-one-kind-of-situation-out, or leave-one-teacher-out), and would give a better idea of the real-world performance of these approaches. However, our current dataset (with only two teachers and five different kinds of classroom situations) is too limited to apply these evaluation schemes effectively. Indeed, our current results should not be understood as blanket statements (e.g., that LSTMs perform worse than look-back random forests), as such comparisons depend largely on the selected feature set, model hyperparameters and architectures, but very especially on the size of the (human-labeled) training dataset. In this paper we have tried to explore the machine learning space for the problem at hand in multiple directions, rather than greedily striving for the smallest fraction of F1 score (e.g., by ensembling some of the most successful models presented here).

These limitations and tradeoffs also illuminate the most promising paths for future work in this research direction, which include the collection of a larger and more varied multimodal classroom dataset, using more cost-effective, predictive and privacy-friendly sources (e.g., accelerometer and audio, or even others like indoor location or depth sensors). This data gathering effort should be made eventually available to (or jointly gathered with) the MMLA research community.