Improving the power to establish clinical similarity in a Phase 3 efficacy trial by incorporating prior evidence of analytical and pharmacokinetic similarity

Abstract

To improve patients’ access to safe and effective biological medicines, abbreviated licensure pathways for biosimilar and interchangeable biological products have been established in the US, Europe, and other countries around the world. The US Food and Drug Administration and European Medicines Agency have published various guidance documents on the development and approval of biosimilars, which recommend a “totality-of-the-evidence” approach with a stepwise process to demonstrate biosimilarity. The approach relies on comprehensive comparability studies ranging from analytical and nonclinical studies to clinical pharmacokinetic/pharmacodynamic (PK/PD) and efficacy studies. A clinical efficacy study may be necessary to address residual uncertainty about the biosimilarity of the proposed product to the reference product and support a demonstration that there are no clinically meaningful differences. In this article, we propose a statistical strategy that takes into account the similarity evidence from analytical assessments and PK studies in the design and analysis of the clinical efficacy study in order to address residual uncertainty and enhance statistical power and precision. We assume that if the proposed biosimilar product and the reference product are shown to be highly similar with respect to the analytical and PK parameters, then they should also be similar with respect to the efficacy parameters. We show that the proposed methods provide correct control of the type I error and improve the power and precision of the efficacy study upon the standard analysis that disregards the prior evidence. We confirm and illustrate the theoretical results through simulation studies based on the biosimilars development experience of many different products.

1. Introduction

A biological medicine is a large molecule derived from living cells (Dranitsaris et al., 2013). As the patents for a large number of biological products have already expired or are due to expire, there is an increasing interest from both the biopharmaceutical industry and the regulatory agencies in the development and approval of biosimilars (Noaiseh and Moreland, 2013; Ventola, 2013). The US Food and Drug Administration (FDA) defines a biosimilar as a product that is highly similar to the reference innovator product notwithstanding minor differences in clinically inactive components and with no clinically meaningful differences between the proposed biosimilar and the reference innovator product (US Food and Drug Administration, 2015a). Differences in cell lines and manufacturing processes make it impossible for biological products to be replicated exactly. Thus, the requirements to demonstrate similarity of biological products are different from those of demonstrating bioequivalence for generic small-molecule drug products that have an identical chemical structure.

To improve patients’ access to safe and effective biological medicines, an abbreviated licensure pathway for biosimilar and interchangeable biological products was established under section 351 (k) of the Public Health Service Act in the US. Similar legal pathways for approval of biosimilars were established in the European and other countries around the world. Various guidance documents have been published by health authorities regarding the development and approval of biosimilars. The FDA (2015a, 2015b, 2015c, 2016a) and European Medicines Agency (2014) issued guidance documents that recommend a “totality-of-evidence” approach to assess biosimilarity with a stepwise process. The approach relies on comprehensive comparability studies with the reference product, progressing from analytical and nonclinical studies to clinical pharmacokinetic (PK) and pharmacodynamic (PD) studies (if there are relevant PD measures), and then to clinical efficacy studies. The analytical studies compare structural and functional characterization between the proposed biosimilar and the reference product. This serves as the foundation for a demonstration of biosimilarity. If there is residual uncertainty about biosimilarity after conducting analytical studies, animal testing, and clinical PK/PD studies, then clinical efficacy studies may be needed to adequately address that uncertainty, so as to support a demonstration that there are no clinically meaningful differences.

In light of the regulatory guidelines, it is strongly desirable to incorporate the prior knowledge of similarity or degree of uncertainty directly into the design and analysis of the clinical efficacy study. In general, the more similar the analytical and particularly the functional evaluations of the proposed biosimilar to the reference product are, the less residual uncertainty about biosimilarity there is to be addressed through the clinical studies. In addition, it is useful to incorporate PK similarity evidence to further reduce residual uncertainty and support a demonstration of no clinically meaningful differences.

In this article, we propose a statistical strategy that uses the analytical and PK similarity evidence from structural and functional characterization and phase 1 PK studies to reduce the sample size and enhance the power for a Phase 3 biosimilar efficacy study. Our assumption is that if the proposed biosimilar product and the reference product are highly similar with respect to the analytical and phase 1 PK parameters, then they should also be similar with respect to the Phase 3 efficacy parameter. This strategy is in line with the FDA’s guidance on the stepwise process and the totality-of-the-evidence approach to establish similarity. No such methods have been published, although there is a large body of literature on bioequivalence (e.g., Chow and Liu, 2008).

The rest of this article is organized as follows. In Section 2, we describe the proposed methods to incorporate the prior evidence of similarity (e.g., analytical and PK similarity) to improve the power of equivalence test and the precision of parameter estimation for a Phase 3 efficacy similarity study. We consider both the scenarios of a single source and multiple sources of prior similarity evidence. In Section 3, we conduct simulation studies to evaluate the proposed methods in realistic settings. Specifically, we show that the proposed methods preserve the type I error and enhance the power and estimation precision as opposed to disregarding the prior evidence when designing and analyzing the biosimilar clinical efficacy study. We also investigate the impact of the strength of analytical similarity on the proposed methods and show that combining the evidence from analytical and PK similarity can boost the power in the Phase 3 study. We provide some concluding remarks in Section 4.We relegate all theoretical details to appendices.

2. Methods

2.1. Incorporating single source of prior similarity evidence

Suppose that the parameter of interest in the prior evidence is θ, which may be a functional assessment for the mechanism of action, such as the primary receptor binding (particularly, tumor necrosis factor or TNF α binding) and antibody-dependent cellular cytotoxicity, in analytical studies or the logarithm of area under the curve (AUC) in the PK study. Suppose also that the parameter of interest in the Phase 3 trial is p, which is typically the response rate. Let (θ_T, p_T) and (θ_R, p_R) denote the values of (θ, p) for the biosimilar product to be tested and the reference product, respectively.

In the prior study, we test the null hypothesis

$$H_0^{(1)}:{\theta }_T-{\theta }_R<L^{\prime }or{\theta }_T-{\theta }_R>U^{\prime }$$

against the alternative hypothesis

$$H_a^{(1)}:L^{\prime }\le {\theta }_T-{\theta }_R\le U^{\prime },$$

where L′ ≤ 0 ≤ U′ are two specific margins. If, for example, θ is the logarithm of AUC, then L′ = −U′ = log(0.8). In the Phase 3 efficacy trial, we test the null hypothesis

$$H_0^{(3)}:log\frac{p_T}{p_R}<Lorlog\frac{p_T}{p_R}>U$$

against the alternative hypothesis

$$H_a^{(3)}:L\le log\frac{p_T}{p_R}\le U,$$

where L ≤ 0 ≤ U are two specific margins. Typically, U and L are symmetric around 0, i.e., U = −L.

If there is strong empirical evidence that θ_T and θ_R are similar, then we wish to leverage this information when demonstrating the similarity between p_T and p_R in the Phase 3 trial. There are several challenges in formalizing this strategy. First, the parameters θ and p have different scales of measurement. Secondly, it is unclear how to efficiently incorporate the evidence about similarity from the prior study into the design and analysis of the Phase 3 study without making strong assumptions about the relationship between the parameters of the two studies. Lastly, because the prior evidence is empirical, we need to account for its randomness when incorporating it into the design and analysis of the Phase 3 study in order to control the overall type I error.

To address the first challenge, we rescale the parameters in the prior study and the Phase 3 study by defining a relative similarity measurement (RSM), which is the ratio between the absolute difference of the proposed biosimilar product and the reference product and the range of the margins. That is, the RSMs for the prior study and the Phase 3 study are defined as

$${\mathit{RSM}}_1=\frac{\mid {\theta }_T-{\theta }_R\mid }{\mid U^{\prime }-L^{\prime }\mid },{\mathit{RSM}}_3=\frac{\mid log{p}_T-log{p}_R\mid }{\mid U-L\mid },$$

respectively. Because RSM is a relative difference and thus has no unit, RSM₁ and RSM₃ are comparable. Furthermore, if the two products are similar within the margin, then RSM takes a value in [0, 1].

To address the second challenge, we impose a structural assumption on the relationship between RSM₁ and RSM₃, under which there exists a known positive constant c₁ such that

$$\mathrm{i}f{\mathit{RSM}}_1<c_1,\mathrm{t}\mathit{hen}{\mathit{RSM}}_3<\frac{max\{\mid L\mid ,\mid U\mid \}}{\mid U-L\mid }.$$ (1)

Thus, if the relative similarity in the prior study is within the bound c₁, then the difference between the two products in the Phase 3 study should be within the margins. In other words, very similar performance between the two products in the parameter of the prior study renders evidence that the two products perform similarly with respect to the Phase 3 parameter. However, we do not specify any functional relationship between RSM₁ and RSM₃ but rather how the alternative hypothesis in the Phase 3 study is related to a bound for the relative similarity in the prior study. This structural assumption is minimal for the purpose of hypothesis testing. Clearly, the constant c₁ governs how much information is borrowed from the prior study. Specifying a reasonable c₁ requires some biological knowledge about the relationship between RSM₁ and RSM₃. For example, if we believe that RSM₁ is proportional to RSM₃, then for the case that L = −U, the structural assumption holds with c₁ = RSM₁/(2RSM₃).

To address the last challenge, we must take into account the fact that there is some positive probability that the similarity evidence of RSM₁ < c₁ can be wrong when we construct the rejection region for hypothesis testing in the Phase 3 study. We propose to appropriately allocate the type I error as follows. Suppose that the overall type I error is set to α and that the null hypothesis that the two products are not similar holds for the Phase 3 study. We can reject the null hypothesis under one of two scenarios: (1) the empirical evidence in the prior study concludes that RSM₁ < c₁, such that the structural assumption leads to the conclusion that the two products are similar with respect to the Phase 3 parameter; and (2) the empirical evidence in the Phase 3 study indicates that the two products are similar. Thus, to control the overall type I error at α, we will control the error for case (1) to be under α₁ (0 ≤ α₁ ≤ α) while controlling the error for case (2) to be under (α − α₁). We provide a formal derivation and justification in Appendix A.

Note that, in the design stage, α₁ in the type I error spending needs to be specified before the Phase 3 study. We propose to search for the optimal α₁ such that the power under the alternative hypothesis in the Phase 3 study is maximized at the design stage. We show in Appendix B how to find this optimal α₁. After the Phase 3 study is completed, the ideas for using the structural assumption and error spending can be used to refine the confidence interval in the Phase 3 study at the analysis stage, where the error of using the prior evidence can be either fixed beforehand or determined in a data-adaptive manner. The details are provided in Appendix C.

2.2. Incorporating multiple sources of prior similarity evidence

We now extend the proposed methods to combine multiple sources of similarity evidence from, for example, analytical assessments and phase 1 PK studies. Suppose that there are K sources of similarity evidence. For k = 1, …, K, the parameters for the proposed biosimilar product and the reference product in the kth source of evidence are denoted by θ_Tk and θ_Rk, respectively, and the corresponding margins are denoted by $L_k^{\prime }$ and $U_k^{\prime }$. To combine the K sources of evidence, we define a weighted similarity metric

$${\mathit{RSM}}_1=\left|\sum _{k=1}^K{w}_k\frac{{\theta }_{Tk}-{\theta }_{Rk}}{{U^{\prime }}_k-{L^{\prime }}_k}\right|,$$

where w₁, …, w_K are pre-specified weights such that ${\sum }_{k=1}^K{w}_k=1$. With this definition of RSM₁, the structural assumption is again given in (1).

If we define

$${\theta }_T=\sum _{k=1}^K{w}_k{\theta }_{Tk}/(U_k^{\prime }-L_k^{\prime }),{\theta }_R=\sum _{k=1}^K{w}_k{\theta }_{Rk}/(U_k^{\prime }-L_k^{\prime })$$

and set L′ = ≤0.5 and U′ = 0.5, then RSM₁ = |θ_T − θ_R|/|U′ − L′|. Thus, the design and analysis procedures described in section “Incorporating single source of prior similarity evidence” can be applied to multiple sources of prior evidence by treating θ_T and θ_R as the single parameter for the prior evidence. The implementation requires knowledge of the covariances between the estimators of (θ_T1, …, θ_TK)^T and (θ_R1, …, θ_RK)^T if the parameters are estimated from the same study. If the two sets of parameters pertain to analytical assessments and the PK study, then the covariance is zero.

The weights w_k reflect the importance of each source of prior evidence. If one of the w_k is 1 and the rest are 0, then we recover the set-up of one source of similarity evidence described in section “Incorporating single source of prior similarity evidence”. The weights should be chosen on the basis of scientific knowledge, such as the extent of similarity in primary and secondary functions, together with overall structural/functional similarity. As functional tests are considered to be highly correlated with efficacy, more weights should be given to analytical similarity results than to PK similarity results. It is desirable to explore a range of values for the weights.

3 Numerical studies

3.1 Type I error and power

We conducted simulation studies to examine the performance of the proposed methods in practical situations. The first simulation study was designed to assess the type I error when the Phase 3 null hypothesis holds, and the second simulation study was designed to assess the power gain of the proposed method over the standard method that does not use the prior information. In both simulation studies, we simulated n₁ = 50 subjects from each treatment arm in the prior study and n₃ = 300 from each treatment arm in the Phase 3 study. We varied the threshold c₁ from 0.1 to 0.8 in a grid size 0.1. For each combination of simulation parameters, we set the number of replicates to 10,000.

In the first simulation study, we set the parameter value for the reference product in the prior study as θ_R = 5 and set the two margins as L′ = −U′ = log(0.8). In addition, we set the response rates for the two products in Phase 3 as p_R = 0.4 and p_T = 0.75p_R. We let the two margins for Phase 3 be L = −U = log(0.75), such that the Phase 3 null hypothesis holds. Since the structural assumption must hold, the parameter value for the proposed biosimilar product, θ_T, should satisfy RSM₁ ≥ c₁. We particularly chose RSM₁ = 1.25c₁ by setting θ_T = 1.25c₁(U′ − L′) + θ_R. Thus, we generated n₁ measurements from N(θ_R, 0.11²) for the reference product and from N(θ_T, 0.1²) for the proposed biosimilar product. In Phase 3, we generated n₃ binary responses from Bernoulli(p_R) for the reference product and from Bernoulli(p_T) for the proposed biosimilar product.

In the second simulation study, we adopted the same simulation set-up but let p_T = p_R = 0.4 and θ_T be 0.75c₁(U′ − L′) + θ_R. The latter condition guarantees that the structural assumption is satisfied under the alternative hypothesis $H_a^{(3)}$. With n₃ = 300, the power of the Phase 3 trial is 80% at α = 0.05.

For each simulated data set, we applied the method described in Appendix A to obtain the rejection region at the significance level of α = 5%. We set α₁/α to 0, 0.2, or 0.4. Clearly, α₁ = 0 is equivalent to using the Phase 3 data only. We also applied the method described in Appendix B with 1 million Monte Carlo samples to obtain the optimal type I error for using the prior evidence, ${\alpha }_1^{\mathit{opt}}$. Finally, we used the method described in Appendix C to construct the 90% confidence intervals for log(p_T/p_R) corresponding to different choices of α₁.

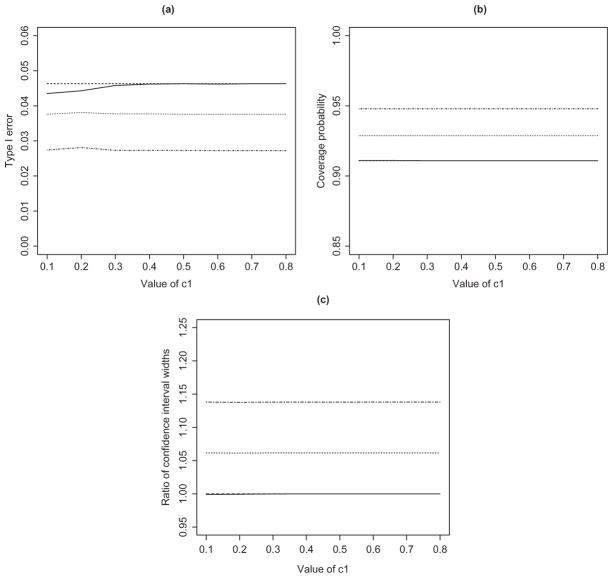
Figure 1 displays the results from the first simulation study, including the empirical type I error at the 5% significance level, the coverage probability of the 90% confidence interval, and the relative width of the 90% confidence interval based on different α₁ over that of using the Phase 3 data only. Clearly, the type I error rates for all the methods are below the nominal significance level for all values of c₁, and the coverage probabilities of the confidence intervals are all above the nominal level of 90%. Using a pre-specified value of α₁ tends to yield conservative type I error and wider confidence intervals. By contrast, the proposed method based on the optimal choice of α₁ provides accurate control of the type I error and the tightest confidence intervals. For the particular parameter set-up in this simulation, the method based on α^opt performs very similarly to the method using the Phase 3 data only because the value of α^opt turns out to be close to 0. This is due to the fact that p_T = p_R, such that the Phase 3 data almost possess sufficient power to reject the null hypothesis.

Figure 1.

Simulation results under the null hypothesis: (a) type I error of the equivalence test; (b) coverage probability of the 90% confidence interval; and (c) ratio of the widths of the confidence intervals with versus without the prior evidence. The solid, dashed, dotted, and dot-dashed curves pertain to ${\alpha }_1^{\mathit{opt}}$, α₁ = 0, α₁ = 0.2α, and α₁ = 0.4α, respectively. The solid and dashed curves are indistinguishable.

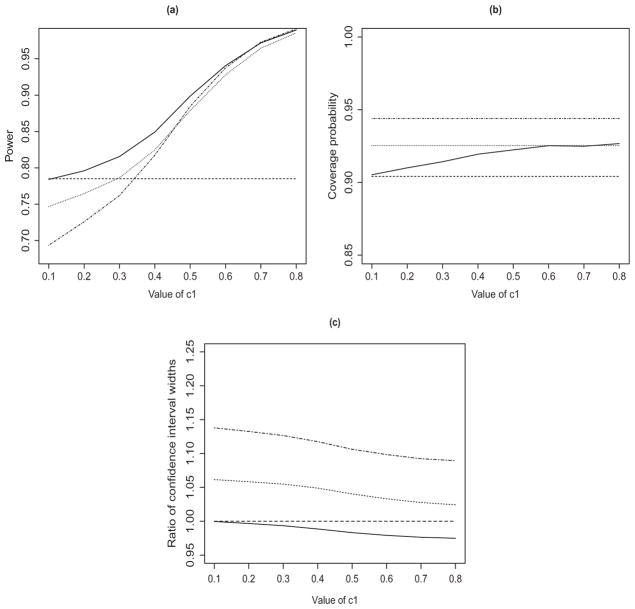
Figure 2 displays the results from the second simulation study. The proposed method based on α^opt has the highest power and the shortest confidence intervals for all choices of c₁. The power increases and the confidence interval becomes narrower as c₁ increases. Thus, using the prior evidence through the structural assumption in an optimal way leads to higher power and more accurate estimation for the Phase 3 study.

Figure 2.

Simulation results under the alternative hypothesis: (a) power of the equivalence test; (b) coverage probability of the 90% confidence interval; and (c) ratio of the widths of the confidence intervals with versus without the prior evidence. The solid, dashed, dotted, and dot-dashed curves pertain to ${\alpha }_1^{\mathit{opt}}$, α₁ = 0, α₁ = 0.2α, and α₁ = 0.4α, respectively.

3.2 Impact of the strength of analytical similarity evidence

It is worthwhile to investigate how the strength of the prior evidence may impact the Phase 3 study in our approach. The strength mostly depends on the extent of similarity in the prior study. Thus, we conducted a simulation study to evaluate the power and estimation results for the Phase 3 study after incorporating the evidence from analytical assessments, where the extent of similarity varies in terms of the variability or the difference pertaining to a functional test (e.g., TNFα binding affinity) between the proposed biosimilar product and the reference product. Specifically, we generated 10 measurements from N(1.08 + δ, σ²) for the reference product and 10 measurements from N(1.08, σ²) for the proposed biosimilar product. Clearly, the larger the value of δ or σ is, the weaker the evidence is. We let L′ = −U′ = −0.1497. For Phase 3, we set p_T = p_R = 0.85 and set the margins for p_T − p_R as L = −U = −0.15. We set the type I error at 0.05 and restricted α₁ to be less than 0.01 so as to avoid the situation in which the analytical evidence is sufficient to conclude the success of Phase 3. We first fixed δ = 0.04 and varied σ in order to assess the impact of the variability of the measurements. We then fixed σ = 0.09 and varied δ in order to assess the impact of the actual product difference in analytical assessments.

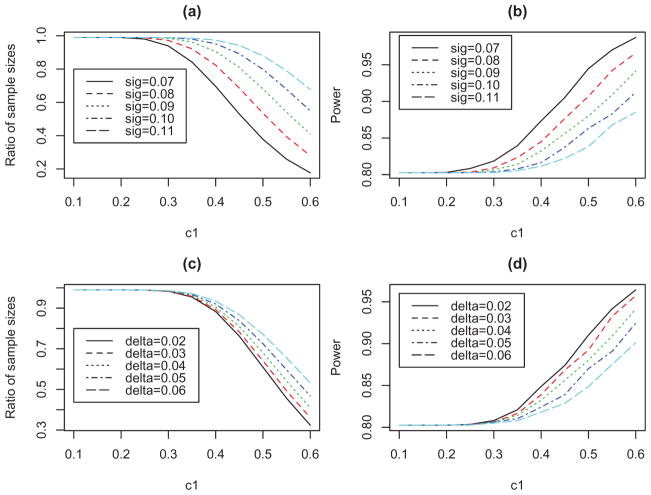
If the prior evidence is not used, then the sample size of 98 per arm is required to achieve the power of 80%. Figure 3(a) displays the ratio of the sample size for using the analytical evidence to the sample size for not using the prior evidence (i.e., 98) under five different values of σ. To determine the sample size, we searched over a wide range of sample sizes to obtain the smallest sample size such that the power calculated in Appendix B was at least 80%. Figure 3(b) displays the power of the proposed method for analyzing the Phase 3 data. The strength of the analytical evidence, characterized by σ, has strong impact on the results. For example, under c₁ = 0.4, the value of σ = 0.07 reduces the sample size from 98 to about 69, and even with the reduced sample size, the average power is increased from 80% to 87%. Figure 3(c) and (d) show the ratio of the sample sizes and the power when the difference between the two products, δ, changes. The conclusion is similar: the smaller the value of δ is (i.e., the stronger the analytical similarity is), the more gain we achieve for both the design and the analysis of the Phase 3 study.

Figure 3.

Simulation results for using the analytical assessment evidence in both designing and analyzing the Phase 3 study: (a) and (c) show the ratio of the sample sizes in the Phase 3 study to achieve the power of 80% when the prior evidence is used versus when it is not used; and (b) and (d) show the power of the proposed equivalence test in analyzing the Phase 3 data.

3.3 Impact of analytical and PK similarity evidence

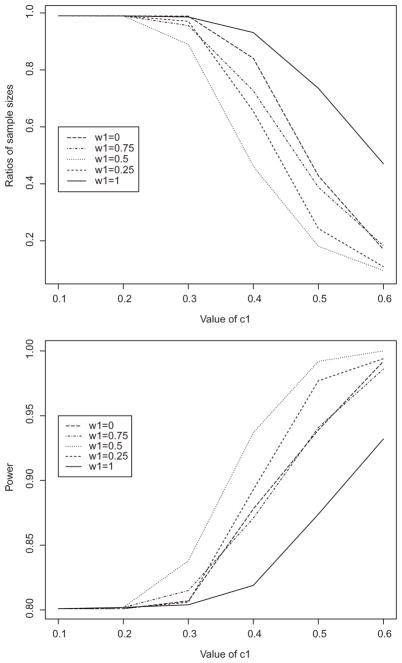
In this simulation study, we combined two sources of similarity evidence, one from analytical assessments and one from a phase 1 PK study, and evaluated their impact on the sample size and power of a future Phase 3 efficacy study. For the first source, we generated comparative measurements from N(1.08, 0.089²) for the proposed biosimilar product and from N(1.12, 0.1²) for the reference product based on the established functional similarity (US Food and Drug Administration, 2016b). The corresponding margins were $L_1^{\prime }=-U_1^{\prime }=-0.1497$. The parameter in the second source is the logarithm of the AUC in a PK study (Yoo et al., 2017). We generated 45 observation on the logarithm of the AUC for the reference product from N(8.9099, 0.3²) and 96 observations for the proposed biosimilar product from N(8.9668, 0.3²), and we set $L_2^{\prime }=-U_2^{\prime }=log(0.8)$. For the Phase 3 study, we set p_T = p_R = 0.85, and the margins of their equivalence were L = −U = −0.15. We used the proposed method to combine these two sources of similarity evidence. The two sources were derived from independent studies, so the parameter estimators are uncorrelated. We varied the weight for the analytic evidence, i.e., w₁, from 1 to 0, in order to examine the impact of the contribution from each evidence. Again, we set α₁ to be at most 0.01. As shown in Figure 4, adding PK similarity evidence (i.e., setting w₁ < 1) further reduces the sample size and increases the study power as compared to using analytical similarity evidence alone (i.e., w₁ = 1). When c₁ = 0.4 and the desired power is 0.85, the candidate values of w₁ are 0.25, 0.5, and 0.75. Since the analytic similarity is deemed the most relevant to the clinical outcome, the best choice of the weight would be w₁ = 0.75.

Figure 4.

Simulation results for combining both analytical and PK similarity evidence: (a) ratio of the sample sizes in the Phase 3 study to achieve the power of 80% when the prior evidence is used versus when it is not used; and (b) power of the proposed equivalence test in analyzing the Phase 3 data.

4 Discussion

We have developed a simple and effective strategy to reduce the sample size and improve the power and estimation for the Phase 3 efficacy trial of biosimilars by leveraging the prior similarity evidence from multiple sources such as analytical assessments and PK studies. Our approach hinges on the structural assumption, under which strong evidence for similarity in the parameters of prior studies implies similarity in the Phase 3 parameter. This assumption is a qualitative rather than a functional relationship between the two similarity measures.

From a Bayesian point of view, the structural assumption can be regarded as a prior distribution for the two similarity measures. The corresponding prior is qualitative. We may use a more continuous prior distribution by assuming that RSM₃/RSM₁ − 1~N(0, σ²), which is equivalent to a ridge penalty for (RSM₃/RSM₁ − 1)². The hyperparameter σ² plays the role of c₁ to govern how much prior similarity evidence is used to reinforce the Phase 3 trial. The continuous prior/penalty is computationally easier to handle than the discrete prior. However, it is not desirable to constrain the parameters when RSM₃ is far from RSM₁.

The choice of c₁ is a critical aspect of the proposed methods. We recommend to determine c₁ using the evidence on related products with approved indications. For example, for an infliximab biosimilar product approved by the FDA in 2016, the analytical similarity (as measured by TNFα binding affinity) yields the difference between the reference and test products as 2.59% with the margins of −7.04% and 7.04%, and the clinical similarity as measured by ACR20 yields the difference of 2% with the margins of −15% and 15% (Yoo et al., 2017). For a biosimilar later approved by the FDA for similar indications, the analytical similarity is −3.6% with the margins of −14.97% and 14.97%, and the clinical similarity is −0.4% with the margins of −12% and 12% (US Food and Drug Administration, 2016b). Thus, the ratio RSM₁/RSM₃ is estimated at 2.76 for the first study and at 7.46 for the second study. This empirical evidence suggests that c₁, which is chosen as half of this ratio to satisfy the structural assumption, can be as large as 1.3. In addition to empirical evidence, it is worthwhile to conduct sensitivity analysis to examine the power over a range of values for c₁ when designing a new Phase 3 study and when analyzing data after the study is completed.

If the prespecified value of c₁ is not small, the prior evidence may be strong enough to reject the Phase 3 null hypothesis, such that there is no need to run the Phase 3 study. To reduce the likelihood of this scenario, we may, as in the numerical studies, restrict α₁ to be within a certain threshold, such that we will use only the prior evidence when RSM₁ < c₁ is supported by prior studies with very high probability. The optimal error spending may be different between the design stage and the analysis stage, as the former aims to maximize power whereas the latter aims to construct the narrowest confidence interval that depends on the empirical data in the Phase 3 study. This difference was observed in our numerical studies.

We have assumed that the endpoint for the Phase 3 efficacy study is a binary response. We can easily extend our methods to a time-to-event endpoint. The null hypothesis will then pertain to the hazard ratio instead of the ratio of the two response rates.

The FDA recommended a tier approach to statistical analysis based on a critically risk ranking as described by Tsong et al. (2017). For the attributes with the highest risk to clinical outcomes (Tier 1), which include assays that evaluate clinically relevant mechanisms of action of the product, a demonstration of statistical equivalence is required. Specifically, the equivalence is demonstrated if the confidence interval for the difference in the mean between the proposed biosimilar product and the reference product is fully contained within the equivalence acceptance region. For the quality attributes with lower risk ranking (Tier 2), the similarity is assessed by comparing the individual results of the proposed biosimilar product with a quality range based on the mean and standard deviation of the reference product dataset. Finally, for the quality attributes with the lowest risk ranking and those that do not deliver quantitative results (Tier 3), the similarity is assessed qualitatively by using raw data and graphical comparisons.

The methods proposed in this article can be applied directly to the quantitative similarity evidence from Tier 1 quality attributes, as illustrated in sections “Impact of the strength of analytical similarity evidence” and “Impact of analytical and PK similarity evidence”. The proposed methods can also be applied to the similarity evidence from Tier 2 attributes by treating the quality range as the margin. However, the requirement to show similarity for Tier 2 quality attributes is different from the rigorous bio-equivalence test described in this article, so the use of the proposed methods to incorporate the similarity evidence from Tier 2 attributes may require further consideration. For Tier 3 quality attributes whose similarity evidence is qualitative, the proposed methods cannot be directly applied. Since Tier 2 and Tier 3 quality attributes have low or no risk to patients, the proposed methods remain a viable approach to efficiently leverage the prior analytical similarity information from Tier 1 attributes for the design and analysis of a biosimilar clinical study.

In the proposed methods, weights are introduced to combine multiple sources of similarity evidence. As with any weighted statistical methods, the choice of the weights is challenging, and the weights should reflect the importance of each source of the prior evidence. Since functional attributes are most relevant to clinical outcomes, we recommend that more weights be given to the functional similarity evidence, especially the Tier 1 functional attributes. In addition, the weights should be reference-drug specific and be determined according to the scientific knowledge about the relevance of the prior evidence (from structural, functional, and PK studies) on the clinical outcomes for the reference product. Ultimately, the acceptable values for weights become a negotiating point between the sponsor and regulatory agencies, and it will be up to regulatory agencies to decide whether the same approach to design a clinical similarity study should be implemented by different biosimilar applicants.

Appendix A. Rejection Region for Hypothesis Testing in the Phase 3 Study

First, we construct a rejection region based on the prior evidence data such that the type I error to reject the null hypothesis $H_0^{\ast }:{\mathit{RSM}}_1\ge c_1$ is controlled at α₁. Specifically, let θ̂_T and θ̂_R denote the estimators of θ_T and θ_R, and let ${\widehat{\sigma }}_T^2$ and ${\widehat{\sigma }}_R^2$ denote the corresponding variance estimators. Write δ₁ = θ_T − θ_R and δ̂₁ = θ̂_T − θ̂_R. Then δ̂₁ is approximately normal with mean δ₁ and variance ${\widehat{v}}_1^2={\widehat{\sigma }}_T^2+{\widehat{\sigma }}_R^2$. Thus,

$$P\left({\widehat{\delta }}_1-{\widehat{v}}_1{z}_{1-{\alpha }_1/2}\le {\delta }_1\le {\widehat{\delta }}_1+{\widehat{v}}_1{z}_{1-{\alpha }_1/2}\right)=1-{\alpha }_1,$$

where z_p is the 100p th percentile of the standard normal distribution. It follows that

$$P(\mid {\delta }_1\mid \le {\widehat{Z}}_{{\alpha }_1})\ge 1-{\alpha }_1,$$

where

$${\widehat{Z}}_{{\alpha }_1}=max\left(|{\widehat{\delta }}_1-{\widehat{v}}_1{z}_{1-{\alpha }_1/2}\mid ,\mid {\widehat{\delta }}_1+{\widehat{v}}_1{z}_{1-{\alpha }_1/2}|\right).$$ (2)

That is, [0, Ẑ_α1/|U′ − L′|] is a (1 − α₁)100% confidence interval for RSM₁. Hence, we reject $H_0^{\ast }$ when c₁ is within this interval, i.e., Ẑ_α1 ≤ c₁|U′ ≤ L′|. This rejection region has the type I error of α₁.

Second, we construct a rejection region based on the Phase 3 data such that the type I error is controlled at α₃. This can be achieved by using the standard equivalence test. Define δ₃ = log p_T/p_R and δ̂₃ = log p̂_T/p̂_R. We estimate the variance of δ̂₃ by ${\widehat{v}}_3^2={\widehat{p}}_T(1-{\widehat{p}}_T)/(n_T{\widehat{p}}_T^2)+{\widehat{p}}_R(1-{\widehat{p}}_R)/(n_R{\widehat{p}}_R^2)$, where n_T and n_R are the sample sizes for the proposed biosimilar product and the reference product, respectively, in the Phase 3 study. Clearly, δ̂₃ is approximately normal with mean δ₃ and variance ${\widehat{v}}_3^2$. Thus, a (1 − 2α₃)100% confidence interval for δ₃ is[L̂_α3, Û_α3], where

$${\widehat{L}}_{{\alpha }_3}={\widehat{\delta }}_3-{\widehat{v}}_3{z}_{1-{\alpha }_3},{\widehat{U}}_{{\alpha }_3}={\widehat{\delta }}_3+{\widehat{v}}_3{z}_{1-{\alpha }_3}.$$

Hence, we reject $H_0^{(3)}$ if [L̂_α3, Û_α3] is contained in [L,U]. This rejection region controls the type I error at the level of α₃. Combining the above two regions and setting α₃ = α − α₁, we obtain the overall rejection rule for $H_0^{(3)}$

$$A_{{\alpha }_1}=I([{\widehat{L}}_{\alpha -{\alpha }_1},{\widehat{U}}_{\alpha -{\alpha }_1}]\subset [L,U]or{\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid ).$$

Suppose that the null hypothesis $H_0^{(3)}$ holds. Then the structural assumption implies that the null hypothesis $H_0^{\ast }$ also holds. Thus,

$$\begin{gathered} P(A_{{\alpha }_1}=1)\le P([{\widehat{L}}_{\alpha -{\alpha }_1},{\widehat{U}}_{\alpha -{\alpha }_1}]\subset [L,U])+P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid ) \\ \le (\alpha -{\alpha }_1)+{\alpha }_1=\alpha . \end{gathered}$$

In other words, the overall probability of rejection is no larger than α under $H_0^{(3)}$.

Appendix B. Optimal Type I Error Spending

Under the alternative hypothesis $H_a^{(3)}$, the probability of no rejection is

$$\begin{gathered} P(L>{\widehat{L}}_{\alpha -{\alpha }_1}or{\widehat{U}}_{\alpha -{\alpha }_1}>U)P({\widehat{Z}}_{{\alpha }_1}\ge c_1\mid U^{\prime }-L^{\prime }\mid ) \\ \le \left\{\mathit{\Phi }\left(\frac{L-{\delta }_3}{v_3}-z_{\alpha -{\alpha }_1}\right)+\mathit{\Phi }\left(-\frac{U-{\delta }_3}{v_3}-z_{\alpha -{\alpha }_1}\right)\right\} \\ \times P\left(max\left\{\left|N(0,1)-z_{1-{\alpha }_1/2}+\frac{{\delta }_1}{v_1}\right|,\left|N(0,1)+z_{1-{\alpha }_1/2}+\frac{{\delta }_1}{v_1}\right|\right\}\ge \frac{c_1\mid U^{\prime }-L^{\prime }\mid }{v_1}\right), \end{gathered}$$

where N(0, 1) denotes a standard normal random variable, Φ is the standard-normal distribution function, and ν₁ and ν₃ are obtained from ν̂₁ and ν̂₃, respectively, by replacing the parameter estimators with the true parameter values. Denote the right side of the above inequality by G(α₁). We then search over α₁ ∈ [0, α] such that the power 1 − G(α₁) is maximized. Note that 1 − G(0) is the power without using the prior evidence.

We construct the optimal rejection region as follows:

• Step 1. We obtain θ̂_T, θ̂_R and (δ̂₁, ν̂₁) using the prior study data.

• Step 2. We obtain δ₃ = log p_T/p_R and ν₃ under $H_a^{(3)}$.

• Step 3. We search over a grid of α₁ in [0, α] to evaluate G(α₁), where δ₁ and ν₁ are replaced by δ̂₁ and ν̂₁, respectively. In particular, the probabilities in G(α₁) are calculated by Monte Carlo simulation.

• Step 4. We determine ${\alpha }_1^{\mathit{opt}}$ which maximizes 1 − G(α₁), such that we reject $H_0^{(3)}$ using $A_{{\alpha }_1^{\mathit{opt}}}$.

Appendix C. Refined Confidence Region in the Phase 3 Study Using the Prior Evidence

The idea of using the prior information for hypothesis testing in the Phase 3 study can be extended to obtain a narrower confidence interval for δ₃. To construct a (1 − 2α)100% confidence interval (corresponding to the hypothesis testing for equivalence with the type I error α), we split α into α₁ and (α − α₁). Using the prior evidence, we calculate Ẑ_α1 as before such that P(|δ₁| ≤ Ẑ_α1) ≥ 1 − α₁. Thus, if RSM₁ ≥ c₁, then

$$P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid )\le P({\widehat{Z}}_{{\alpha }_1}\le \mid {\delta }_1\mid )\le {\alpha }_1.$$

Using the Phase 3 data, we construct a (1 − 2α + 2α₁)100% confidence interval for δ₃ as (L̂_α−α1, Û_α−α1), such that

$$P({\delta }_3\le {\widehat{L}}_{\alpha -{\alpha }_1})\le \alpha -{\alpha }_1,({\delta }_3\ge {\widehat{U}}_{\alpha -{\alpha }_1})\le \alpha -{\alpha }_1.$$

By combining the above two confidence intervals, we obtain

$$[{\widehat{L}}_f,{\widehat{U}}_f]=\{\begin{array}{ll}[{\widehat{L}}_{\alpha -{\alpha }_1},{\widehat{U}}_{\alpha -{\alpha }_1}]\hfill & if{\widehat{Z}}_{{\alpha }_1}>c_1\mid \widehat{U}-L^{\prime }\mid \hfill \\ [{\widehat{L}}_{\alpha -{\alpha }_1}\vee L,{\widehat{U}}_{\alpha -{\alpha }_1}\wedge U]\hfill & \mathit{otherwise}\hfill \end{array}$$

where a ∨ b = max (a, b), and a ∧ b = min(a, b). If α₁ = 0, then [L̂_f, Û_f] reduces to [L̂_α, Û_α], which is the confidence interval based on the Phase 3 data only.

To see why the proposed confidence interval has the correct coverage, we note that

$$\begin{gathered} P({\delta }_3\le {\widehat{L}}_f)=P({\delta }_3\le {\widehat{L}}_{\alpha -{\alpha }_1},{\widehat{Z}}_{{\alpha }_1}>c_1\mid U^{\prime }-L^{\prime }\mid )+P({\delta }_3\le {\widehat{L}}_{\alpha -{\alpha }_1}\vee L,{\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid ) \\ \le (\alpha -{\alpha }_1)P({\widehat{Z}}_{{\alpha }_1}>c_1\mid U^{\prime }-L^{\prime }\mid )+P({\delta }_3\le {\widehat{L}}_{\alpha -{\alpha }_1}or{\delta }_3\le L)P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid ). \end{gathered}$$

We consider the second term on the right side. If δ₃ > L, then this probability is less than

$$P({\delta }_3\le {\widehat{L}}_{\alpha -{\alpha }_1})P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid )\le (\alpha -{\alpha }_1)P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid ).$$

If δ₃ ≤ L, then since the structural assumption implies that RSM₁ > c₁ and thus |δ₁| > Ẑ_α1, this probability is less than

$$P({\widehat{Z}}_{{\alpha }_1}\le c_1\mid U^{\prime }-L^{\prime }\mid )\le P({\widehat{Z}}_{{\alpha }_1}\le \mid {\delta }_1\mid )\le {\alpha }_1.$$

In either case,

$$P({\delta }_3\le {\widehat{L}}_f)\le \alpha .$$

Likewise, we conclude that P(δ₃ ≥ Û_f) ≤ α. That is, [L̂_f, Û_f] is a valid (1 − 2α)-confidence interval for δ₃. We can search for the optimal α₁ such that the resulting confidence interval has the shortest length.

Remark 1

If we use the confidence interval to perform the hypothesis test by rejecting $H_0^{(3)}$ when [L̂_f, Û_f] ⊂ [L,U], then we reject $H_0^{(3)}$ when either Ẑ_α1 ≤ c₁|U′ − L′| or [L̂_α−α1, Û_α−α1] ⊂ [L,U]. This is exactly the rejection region described in Appendix A.

Remark 2

When analyzing the Phase 3 data, we may adjust for covariates through a log-linear regression model:

$$logp={\delta }_{3}G+{\xi }^{\mathrm{T}}X,$$

where G is the indicator for the proposed biosimilar product versus the reference product, and X is the set of covariates including the unit component.