Skip to main content
PMC home page
Astrobiology logoLink to Astrobiology
. 2018 Apr 1;18(4):419–430. doi: 10.1089/ast.2016.1615

Replication of Simulated Prebiotic Amphiphilic Vesicles in a Finite Environment Exhibits Complex Behavior That Includes High Progeny Variability and Competition

Don L Armstrong 1,,2, Doron Lancet 3, Raphael Zidovetzki 2,✉
PMCID: PMC5910049  PMID: 29634319

Abstract

We studied the simulated replication and growth of prebiotic vesicles composed of 140 phospholipids and cholesterol using our R-GARD (Real Graded Autocatalysis Replication Domain) formalism that utilizes currently extant lipids that have known rate constants of lipid-vesicle interactions from published experimental data. R-GARD normally modifies kinetic parameters of lipid-vesicle interactions based on vesicle composition and properties. Our original R-GARD model tracked the growth and division of one vesicle at a time in an environment with unlimited lipids at a constant concentration. We explore here a modified model where vesicles compete for a finite supply of lipids. We observed that vesicles exhibit complex behavior including initial fast unrestricted growth, followed by intervesicle competition for diminishing resources, then a second growth burst driven by better-adapted vesicles, and ending with a final steady state. Furthermore, in simulations without kinetic parameter modifications (“invariant kinetics”), the initial replication was an order of magnitude slower, and vesicles' composition variability at the final steady state was much lower. The complex kinetic behavior was not observed either in the previously published R-GARD simulations or in additional simulations presented here with only one lipid component. This demonstrates that both a finite environment (inducing selection) and multiple components (providing variation for selection to act upon) are crucial for portraying evolution-like behavior. Such properties can improve survival in a changing environment by increasing the ability of early protocellular entities to respond to rapid environmental fluctuations likely present during abiogenesis both on Earth and possibly on other planets. This in silico simulation predicts that a relatively simple in vitro chemical system containing only lipid molecules might exhibit properties that are relevant to prebiotic processes. Key Words: Phospholipid vesicles—Prebiotic compartments—Prebiotic vesicle competition—Prebiotic vesicle variability. Astrobiology 18, 419–430.

1. Introduction

One of the first questions of early evolution is when a specific form of information transfer emerged: “What came first?” The “RNA World” hypothesis suggests that the presence of informational biopolymers such as RNA was an absolute requirement for information transfer and life's emergence. RNA is hypothesized to be the information molecule because RNA not only has the capacity of storing and replicating sequence-based (genetic or linear) information by a templating mechanism but also can catalyze reactions (Joyce, 2002; Copley et al., 2007). It has been further suggested that, after the emergence of RNA-based biopolymers, RNA was sequestered into compartments, isolating RNA from the environment, thereby protecting the informational molecules, and potentially leading to cellular life (Joyce, 2002; Copley et al., 2007).

An alternative, “Lipid World” hypothesis (Segré et al., 2001a), suggests that amphiphile aggregates were sufficient by themselves to provide both compartmentalization and storage and transfer of compositional molecular information to subsequent generations during early abiogenesis. As postulated by Segré et al. (2000), this happens via compositional inheritance in multicomponent lipid vesicles to future generations brought about by growth-split cycles governed by mutual catalysis (Segré et al., 2001b). The origin of these amphiphiles is also under debate, with hypotheses including both terrestrial and extraterrestrial sources (Deamer, 1985; Deamer and Pashley, 1989; Cronin, 1998; Hanczyc et al., 2003; Bada, 2004; Thomas and Rana, 2007; Georgiou and Deamer, 2014; Mayer et al., 2015). The question of how compositional inheritance in lipid assemblies transitions to polynucleotide-based inheritance is still wide open (Shenhav et al., 2005). A third hypothesis suggests that compartmentalization emerged independently of information, and these two branches of evolution merged at some later date (Pulselli et al., 2009; Regis, 2009). Such a development is less improbable than simultaneous emergence of both compartments and information-carrying polymers (Pulselli et al., 2009). This view is supported by experimental findings that vesicles can grow and self-reproduce (Berclaz et al., 2001). In a computational model, Fellermann and Solé (2007) argued that a dividing, cell-like structure can be composed of only a metabolism-container coupled system. This allows natural selection to be applied to an experimental system of self-reproducing vesicles (Božič and Svetina, 2004, 2007; Svetina, 2012) in terms of Oparin's principles, where simple self-replicating vesicles predate cells driven by informational molecules such as RNA, unknown at that time (Oparin, 1936). An alternative hypothesis suggests that a common chemistry generated precursors to all three components (compartmentalization, information, and metabolism) (Budin and Szostak, 2011; Blain and Szostak, 2014; Patel et al., 2015).

The GARD model employed in our simulations is a formalism that follows the dynamic fate of amphiphile assemblies and enables asking specific questions about their capacities to portray certain life-like attributes. Early GARD simulations did not commit to a specific amphiphile chemistry (Segré et al., 2001). In our previous study (Armstrong et al., 2011), we invoked realistic amphiphilic molecules in our simulations, while considering which specific building blocks are best suited for simulations. Fatty acids are much simpler and more easily envisaged as prebiotic components (Segré et al., 2001a). Whether phospholipids were present in the early prebiotic period is still a matter of debate. The possibility of prebiotically synthesized phospholipids was suggested by Hargreaves et al. (1977), but current consensus considers the early presence of phospholipids unlikely (Pohorille and Deamer, 2009). However, the importance of phospholipids in later evolution is indisputable, and there is much more thermodynamic and kinetic data available on phospholipids as compared with fatty acids, which is important for constructing a reasonable kinetic formalism from empirically derived parameters. Finally, when considering a role for GARD-invoked amphiphile structures as potential compartments, the fact that phospholipid vesicles are less leaky than those composed of fatty acids played a role in our decision.

In our previous publication (Armstrong et al., 2011), we advanced a novel formalism based on a semi-empirical approach where data from published kinetic interactions of today's phospholipids with bilayer lipid vesicles of diverse compositions and properties were utilized to simulate the progression of such a vesicle system in the environment of infinite availability of lipid monomers. In contrast to most previous modeling and experimental studies that use amphiphile systems of limited number of components, we used a system that includes four classes of phospholipids: phosphatidylethanolamine (PE), phosphatidylserine (PS), phosphatidylcholine (PC), and sphingomyelin (SM), and cholesterol (CHOL), with a variety of acyl chain lengths and unsaturation levels comprising altogether 141 different lipid components. This component heterogeneity is much more realistic and can lead to different outcomes than simple systems with more limited numbers of component types (Szostak, 2011; Budin et al., 2014). Nonlipid molecules present in the prebiotic milieu are likely to have influenced vesicle growth (see Adamala and Szostak, 2013), and future formalisms may include them.

In the present work, we extend our previous formalism to an environment of finite resources and examine the kinetics and properties of the resultant phospholipid vesicle system. These properties include high variability of vesicle composition and properties, critical importance of compositional heterogeneity, and vesicle-vesicle competition for diminishing resources. Additionally, these results inform efforts to construct de novo cells, as they predict the composition of cell membranes that will be stable given a particular environmental milieu.

2. Materials and Methods

2.1. Lipid vesicle simulations

Simulations of lipid vesicles were carried out by using a simulation environment that follows the kinetic parameters of our previous work (Armstrong et al., 2011), as described in the Supplementary Material (available at http://online.liebertpub.com/doi/suppl/10.1089/ast.2016.1615), with two important modifications. First, the environment consisted of a limited number of lipid molecules (4.096 × 107) for all 141 lipid types with a total environmental concentration of 1.41 × 10−8 M in a fixed volume. Lipids in the environment were depleted or added to as lipids entered or left vesicles during the simulation, but the total number of lipid molecules in the simulation remained constant. Second, all vesicles were tracked in the simulation, enabling vesicles to compete with each other for finite resources. Simulations ran for 300–1000 s and generally progressed to an average of 12 generations, with on the order of 2048 vesicles in each simulation at the end. The simulation environment noted the starting and ending vesicles for each division and stored the state of every vesicle every min(5 × 2⌊i/50⌋, 50) iterations, where i is the current iteration number. Vesicles divided once they reached 20,000 lipid molecules, and lipids in the parent vesicle were randomly assorted between each of the two progeny vesicles. Vesicle reproduction upon doubling was previously suggested as a result of mild shear forces acting on the growing vesicles (Zhu and Szostak, 2009; Budin and Szostak, 2011; Szostak, 2011). Such mild shear forces induce division without loss of the content and are common in natural environments (Zhu and Szostak, 2009).

It has been demonstrated, by using various experimental systems, that vesicles can grow and divide autonomously (Wick et al., 1995; Hanczyc et al., 2003; Takakura et al., 2003, 2004; Thomas and Rana, 2007; Toyota et al., 2008).

The rate of incorporation (or removal) of each lipid component into (or from) a vesicle is dependent upon the lipid's environmental concentration, base kinetic rate parameters, the average properties (curvature, charge, unsaturation, length, complex formation) of the vesicle into which the lipid is entering or leaving, the surface area of the vesicle, and the properties of that particular lipid molecule (length, type, unsaturation). For complete details of the kinetic formalism, see the Supplementary Material and Armstrong et al. (2011).

The simulations were carried out on a cluster in parallel using code written in Perl.

2.2. Plots and summary statistics

The states of the environment and vesicles were collected into an SQLite database, extracted using R scripts, and then plotted using ggplot2. Summary statistics were calculated by using linear least-squares models and t tests as appropriate.

3. Results

The simulations presented here are based on the R-GARD (Real Graded Autocatalysis Replication Domain) equation (Supplementary Material and Eq. 1), providing a quantitative description for the principle that kinetic parameters for lipid entry and exit depend on the current composition of vesicles they join. In this study, the simulations started with one seeded vesicle, and all progenies from each division were followed. The environment started with enough lipid material for 4096 lipid vesicles with average of 10,000 lipid molecules per vesicle (4.096 × 107 lipid molecules overall).

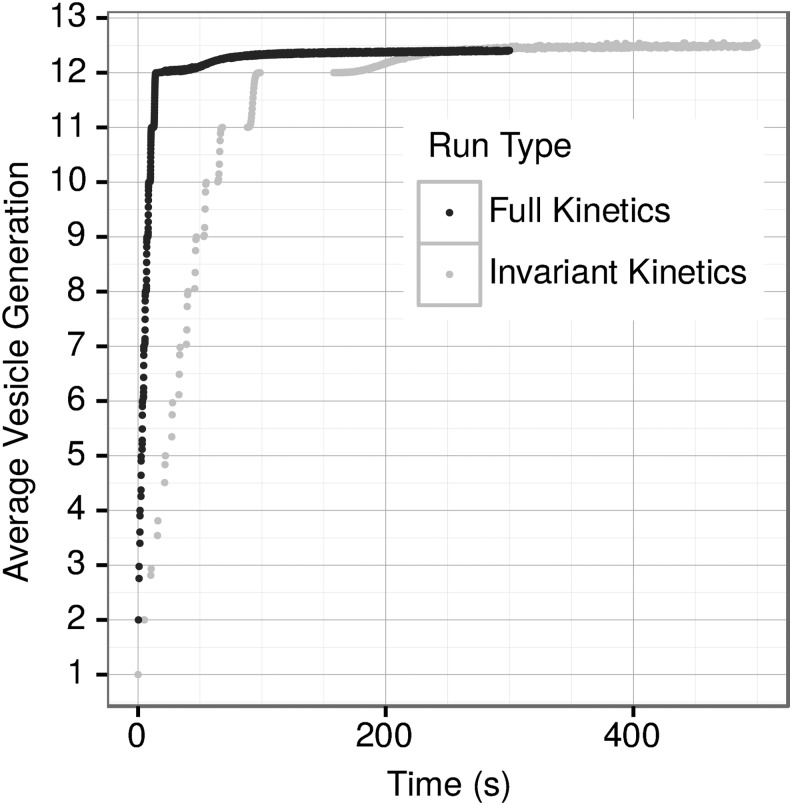
The average age in generations of all vesicles in the simulation when run with “full kinetics” (modification of lipid kinetics by the properties of the vesicles into which the lipids are entering or leaving) or with “invariant kinetics” (where the rates are not modified by the vesicle composition and properties) is shown in Fig. 1, which represents an average of multiple runs. Vesicles whose properties affect kinetic parameters grow and divide approximately an order of magnitude more rapidly than vesicles without modification due to vesicle properties. This is further illustrated in Table 1.

FIG. 1.

FIG. 1.

Open in a new tab

Average number of generations over time for full and invariant kinetics for multiple runs.

Table 1.

Average Times for Vesicles to Reach an Average of 12 Generations in Simulations with Full Kinetics and Invariant Kinetics with All Lipids (All), and Missing a Single Lipid Type (e.g., No CHOL)

Formalism Lipid types Time (s) SD Runs
Full kinetics All 17.6 0.68 20
No CHOL 34.6 9.52 6
No PC 35.4 7.86 6
No PE 22.5 1.76 6
No PS 22.1 1.03 6
No SM 13.7 0.21 6
Invariant kinetics All 164.3 3.57 16
No CHOL 267.5 2.69 6
No PC 162.5 5.45 6
No PE 138.0 2.26 6
No PS 157.9 2.83 20
No SM 155.6 4.17 6
Open in a new tab

Vesicles take 17.6 ± 0.7 s to reach an average generation of 12 in the full kinetics simulations, whereas vesicles take 164.3 ± 3.6 s in the invariant kinetics runs (Table 1). To explore unequal availability of different lipids, we ran the simulations without one lipid class (that is, without one PC, PE, PS, SM, or CHOL). Omitting CHOL decreases the time necessary to reach an average generation of 12 with full kinetics but increases the time by a factor of 2 with invariant kinetics (Table 1). Conversely, omitting PC increases the time to reach an average generation of 12 with full kinetics but has the opposite effect with invariant kinetics. Only minor effects on the overall time to reach an average generation of 12 were observed in cases of omitting PS, PE, or SM from the environment (Table 1).

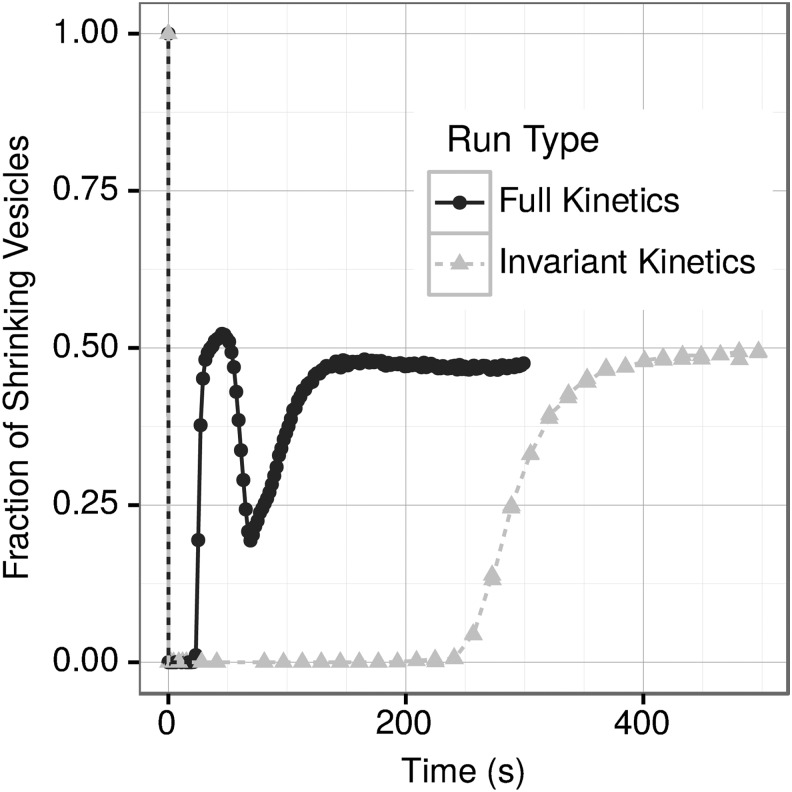
When our formalism was applied to a finite environment, we expected to find that vesicles with compositions that had less favorable kinetics would lose lipids to the environment. Those lipids lost to the environment would then be incorporated by vesicles with compositions that resulted in more favorable kinetics, providing evidence for competition among the vesicles. Figure 2 shows the fraction of vesicles that are shrinking over the total number of vesicles at a given time point in simulations with (“full kinetics”) and without (“invariant kinetics”)—an impact of vesicle properties upon kinetics. In both types of simulation, the initial vesicle shrinks slightly as a few lipids with high kb are shed; then all vesicles in the simulation begin growing (0–15 s for full kinetics, 0–230 s for invariant kinetics, Fig. 2). After the initial shrinkage of the seed vesicle, the behavior of “full kinetics” is very different from that of the “invariant kinetics” simulations.

FIG. 2.

FIG. 2.

Open in a new tab

Average fraction of vesicles that are shrinking over time for the full and invariant kinetics simulations for multiple runs.

In simulations with full kinetics, a few distinct phases of the vesicle growth and division can be discerned (Fig. 2). After initial shrinkage, vesicles undergo an unrestricted growth phase until about 15 s. At this point, the depletion of free lipids from the environment results in an increase in the number of vesicles that are actually shrinking (15–47 s), until the number of shrinking vesicles is larger than the number of growing ones (Fig. 2, 47 s peak). However, at the same time, a significant proportion of the vesicles (approximately 45% at 47 s) are growing by incorporating the lipid molecules released by the shrinking vesicles, thus demonstrating competition among the vesicles for diminishing resources. The second growth phase (in this case due to the reduced fraction of the shrinking vesicles) occurs at 47–70 s. After 70 s, the system progresses toward the final steady state, reached at 170 s. The invariant kinetics formalism exhibits a simple kinetics behavior: unrestricted growth (0–230 s), transition to steady state (230–450 s), and steady state, reached at 450 s (Fig. 2).

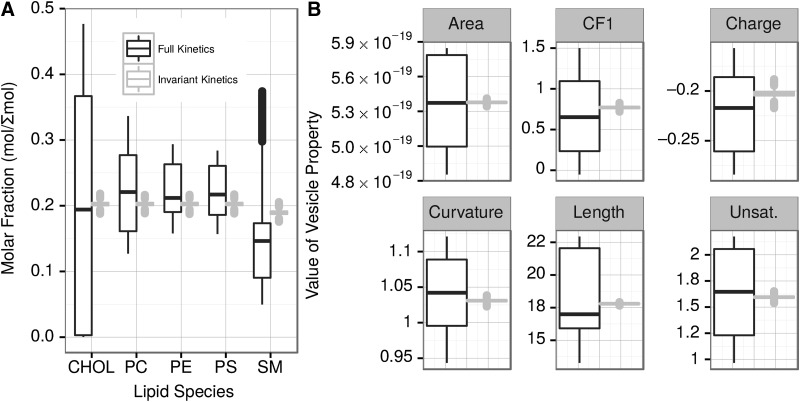
Importantly, both vesicle composition and the resulting properties exhibit much higher variability in the full kinetics simulations (Fig. 3). Removing one lipid type from the environment in most cases did not result in significant changes; however, removing SM results in the second growth burst being much less pronounced (not shown).

FIG. 3.

FIG. 3.

Open in a new tab

The molar fractions and variabilities of the vesicle lipid compositions (A) and values and variabilities of vesicle properties (B) with (full kinetics) and without (invariant kinetics) kinetic modifications at the end of the simulation for 20 full kinetics simulations and 16 invariant kinetics simulations. Area is shown in m2; the other properties are unitless.

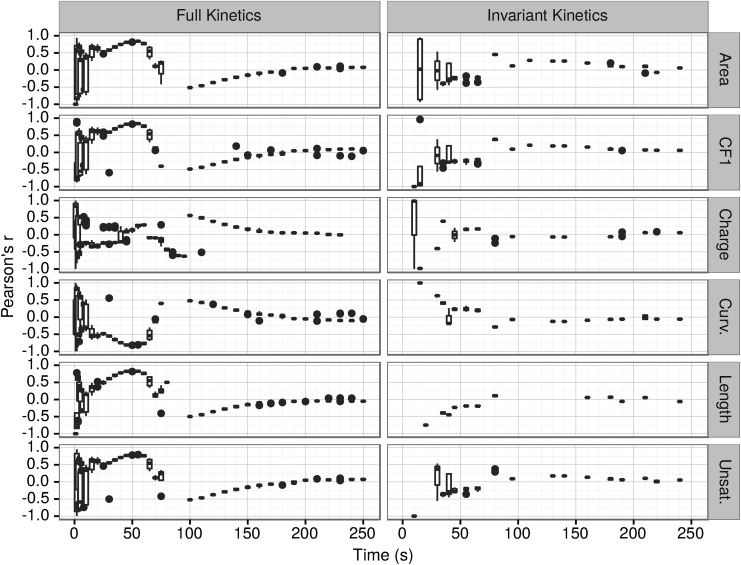
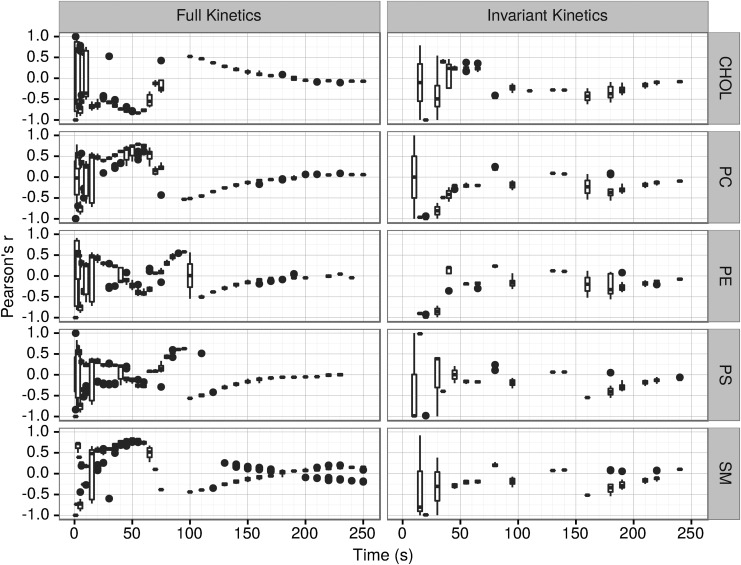
The complexity of the kinetic rate modifying equations (Supplementary Material and Armstrong et al., 2011) results in an accordingly complex correlation of vesicle growth with the vesicle composition and properties. Pearson correlation analysis of the time-dependent correlation of the vesicles' growth with their composition and properties (Figs. 4 and 5) mostly corresponds with growth and shrinkage phases identified on Fig. 2.

FIG. 4.

FIG. 4.

Open in a new tab

Pearson's r correlations between vesicle growth and vesicle properties.

FIG. 5.

FIG. 5.

Open in a new tab

Pearson's r correlations between vesicle growth and lipid types.

Distribution of the Pearson's product-moment correlation coefficient of significant (p ≤ 0.05) correlations between the rate of growth or shrinkage Inline graphic and the properties of that vesicle over time for 10 full kinetics and 10 invariant kinetics simulations are shown on Fig. 4. In the full kinetics simulations, the correlations are relatively random for all vesicle properties (Fig. 4) and lipid classes (Fig. 5) in the first 20 s, with some simulations of the same variables showing positive correlation and others showing negative correlation as evidenced by the width of the distribution of values of PC at those times. In the time period between 35 and 70 s, more consistent correlations are seen throughout each simulation.

In the case of full kinetics, we observed in this time period (35–70 s) a strong positive correlation of the vesicle growth with the vesicle's length, unsaturation, area, and CF1 (Fig. 4, Table 2).

Table 2.

Correlation of Vesicle Growth with Lipid Classes and Vesicle Properties at 51 s

  p Pearson's r Adjusted r2
Charge 1.86 × 10−5 0.18 0.03
Length 2.89 × 10−52 0.85 0.72
Unsaturation 6.23 × 10−40 0.82 0.67
Area 2.23 × 10−60 0.85 0.72
Curvature 2.45 × 10−68 −0.85 0.72
CF1 1.07 × 10−67 0.85 0.73
CHOL 1.60 × 10−53 −0.84 0.71
PE 9.61 × 10−13 −0.33 0.10
PS 1.86 × 10−5 −0.18 0.03
PC 1.63 × 10−39 0.77 0.60
SM 1.85 × 10−64 0.84 0.70
Open in a new tab

Conversely, curvature is negatively correlated with the vesicle growth (Figs. 4 and 6 and Table 2). Similarly, in most cases (PC, PS, SM), in the competition phase growth is positively correlated with the amount of lipid type in the vesicle (Fig. 5). However, this correlation is much less pronounced in the case of PE and is negative in the case of CHOL. In full kinetics after about 120–130 s, the correlations become too small (|r| < 0.2) to be meaningful.

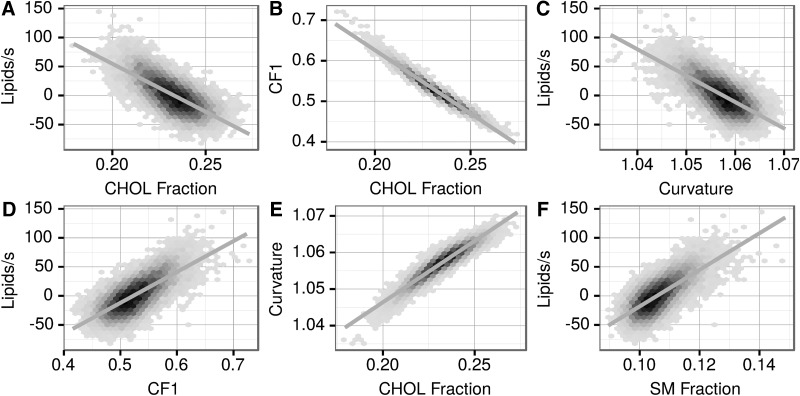
FIG. 6.

FIG. 6.

Open in a new tab

Correlation of the rate of growing or shrinkage of the vesicles at 37 s in lipids per second (competition/shrinking vesicles phase) with selected lipid classes and properties of the vesicles.

Correlation of selected lipid types and properties with vesicle growth is shown on Fig. 6. Such correlations serve to understand the basic promoters and inhibitors of the vesicle growth.

Since CF1 is positively (Fig. 6D), and curvature negatively (Fig. 6C), correlated with growth, negative correlation with growth was expected and observed with the CHOL content (Fig. 6A). More typically and straightforwardly, the increased amount of a lipid correlated with growth (Fig. 6F).

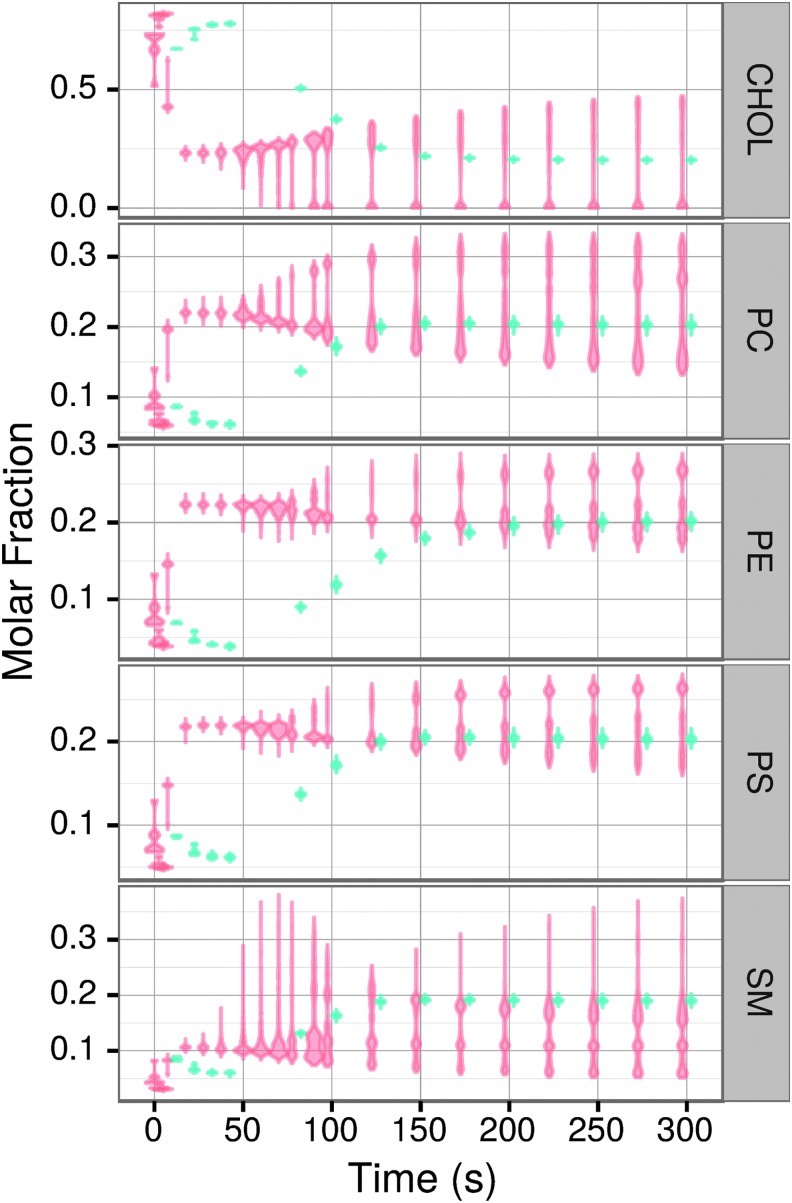
The changes in lipid composition and properties of the vesicles over time are shown in Figs. 7 and 8, respectively. A prominent feature for every lipid type is a much higher variability in vesicle composition at the final steady state in the full kinetics as compared to the invariant kinetics simulations. For example, CHOL molecular fractions range from nearly 0 in some vesicles to 0.5 in others in the full kinetics simulations, whereas the invariant kinetics simulations have all a CHOL fraction of 0.2 with only a small variation (Fig. 7). Other lipid types show more complicated distributions. Thus, in the full kinetics simulations, PC ranges from a molar ratio of approximately 0.13 to 0.35 in the steady state, but the molar ratios are not normally distributed about a mean: the allowed concentrations instead consist of three superimposed normal distributions at times greater than 130 s. As expected, given the changes in distribution of the molar ratios of lipid types over time, the distribution of the properties of vesicles shows similar complex patterns. Invariant kinetics simulations exhibit little variance in the distribution of vesicle composition (Fig. 7) or of vesicle properties (Fig. 8). Full kinetics simulations display a more complex behavior with the most prominent and important difference from invariant kinetics being an order of magnitude higher variability of the vesicles' composition and the resulting properties. In invariant kinetics simulations steady state is more slowly, consistent with the data shown in Fig. 1. Early in the simulation, vesicles are rich in CHOL because of its high kf. With time, all lipids in both the full and invariant kinetics converge to steady state values of about 0.2 mol/fraction, reflecting the corresponding ratios in the environment.

FIG. 7.

FIG. 7.

Open in a new tab

Violin plots of the time-dependent distribution of the fraction of lipid types contained within vesicles in full (orange) and invariant (blue) kinetics simulations.

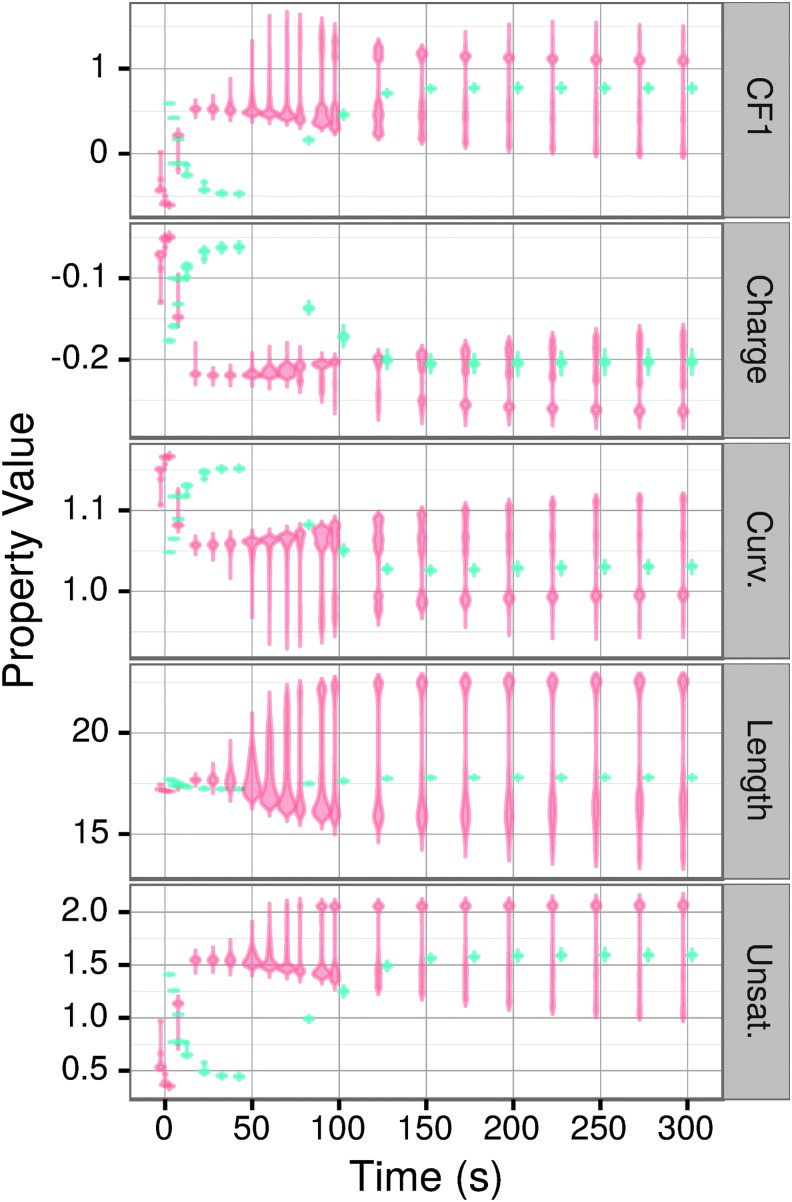
FIG. 8.

FIG. 8.

Open in a new tab

Violin plots of the time-dependent distribution of the properties of the vesicles in full (orange) and invariant (blue) kinetics simulations.

Accordingly, the properties' behavior corresponds to that of the lipid (or lipids) most prominently expressing a particular property. Charge is directly related to the concentration of PS, and its distribution mirrors that of PS; thus, at the start when the concentration of PS in the vesicles is relatively low (Fig. 7), the negative charge is low, too (Fig. 8). Curvature is primarily a function of the concentrations of CHOL, SM, and PS, and most closely follows the concentration of CHOL. This is also reflected in Fig. 8, where the curvature increases at the beginning as a consequence of the high CHOL fraction. In the case of CF1, we observed high initial CHOL concentration (CF1 = −1) and low initial SM concentration (CF1 = 3) (Fig. 7) that corresponded with initial low values of CF1 for vesicles (Fig. 8). The formalism preferentially selects for vesicles with similar-length lipids, and because CHOL only comes in one length, vesicles with higher CHOL content at early times preferentially contain lipids with lengths near 18 (Fig. 8). And finally, CHOL unsaturation of zero is reflected by the decrease of unsaturation at the beginning (Fig. 8).

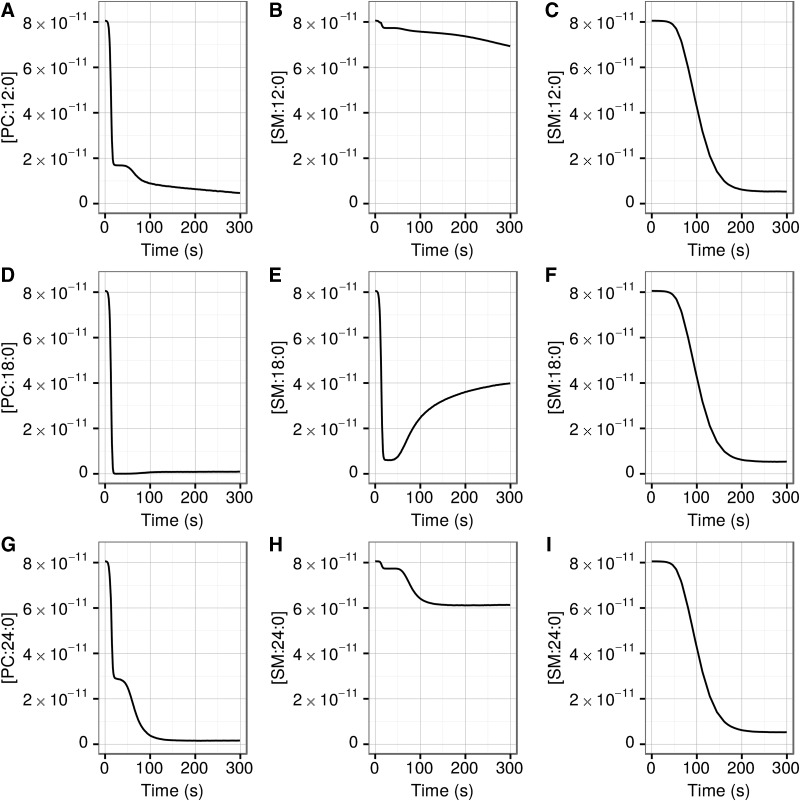
Time dependencies of the environment concentrations of full kinetics saturated PC (left) and SM (middle column) of the complete range of lengths, and of invariant kinetics SM (right), are shown in Fig. 9. All other lipids in the invariant kinetics simulations exhibited behavior similar to that of SM. Whereas SM in the invariant kinetics mode exhibits classic kinetics behavior, the behaviors of PC and, especially, SM in the full kinetics mode are considerably more complex. The first phase, unrestricted growth, is reflected by sharp decreases of all lipids in the environment. In most full kinetics cases, the next, competition/shrinking vesicle, phase (15–47 s) is reflected by a plateau of the environmental lipid concentrations, followed by further decrease corresponding to renewed lipid consumption by the vesicles. The plateau also corresponds to the increased fraction of the shrinking vesicles (Fig. 2). Some lipids (e.g., PC 18:0, Fig. 9D) exhibit little or no plateau, because they were almost completely absorbed by the vesicles during the unrestricted growth phase due to their high kf.

FIG. 9.

FIG. 9.

Open in a new tab

Time dependence of the environmental concentrations of selected lipids. Y axes are concentrations in M. Left and middle columns: full kinetics; right column: invariant kinetics simulations.

Some SM components exhibit interesting behavior (see Fig. 9E) where they are released by vesicles into the environment after the first 50 s, corresponding to the competition/second growth burst. This is due to the large kb of SM, which dominates the kfadj for all SM that do not match the average length of the vesicle. All other lipids exhibit behavior similar to PC. The final consequence of high kb is that all other non-SM lipids are virtually completely consumed by the vesicles (see Fig. 9A, 9D, 9G for PC), but much of SM remains in the environment (Fig. 9B, 9E, 9H).

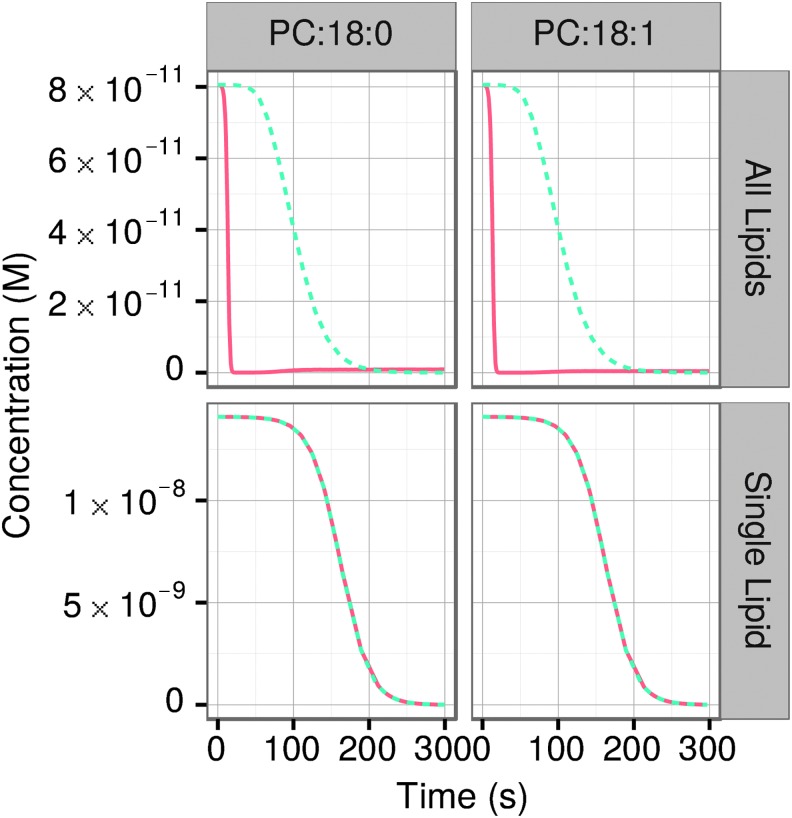
We have further investigated the role of lipid component heterogeneity in the complex behavior of the lipid system at full kinetics. When only one component is present, the resulting kinetics are essentially identical for full and invariant kinetics at all times, in contrast with the multicomponent runs (Fig. 10). Schrum et al. (2010) pointed out that prebiotic vesicles were likely composed of complex mixtures of amphiphiles and noted that amphiphilic molecules found in meteorites (Deamer, 1985; Deamer and Pashley, 1989) and those synthesized under simulated prebiotic conditions (McCollom et al., 1999; Dworkin et al., 2001; Rushdi and Simoneit, 2001) are highly heterogeneous.

FIG. 10.

FIG. 10.

Open in a new tab

The role of lipid heterogeneity. Comparison of runs with all lipids or a single lipid (i.e., DOPC or DPPC) and full (orange solid line) or invariant (blue dotted line) kinetics.

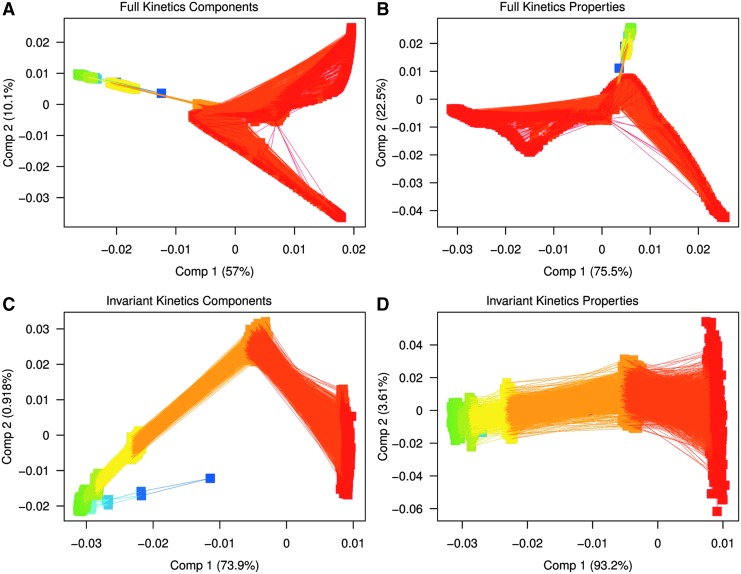
The principal components analysis (PCA) plots (Fig. 11) also demonstrate higher variability of both vesicle properties and compositions in the case of full kinetics. This is the best seen in the variation along the first two components occupied by the final generation (in red) of full kinetics for the lipid components (range of 0.03 in component 1 and 0.06 in component 2 for full kinetics [Fig. 11A] vs. essentially constant in component 1 and 0.03 in component 2 for invariant kinetics [Fig. 11C]). Similarly, in the case of vesicle properties, the variation for component 1 for full kinetics is 0.055 (Fig. 11B), as compared to the essentially constant at 0.01 for the invariant kinetics (Fig. 11D). Component 2 in the full kinetics properties varies by 0.05 (Fig. 11B), and in the invariant kinetics by 0.1 (Fig. 11D), agreeing with Figs. 7 and 8 that demonstrate high variability of the composition and properties of the vesicles in the full kinetics mode.

FIG. 11.

FIG. 11.

Open in a new tab

PCA plots of lipid components (A, C) and properties (B, D) for full (A, B) and invariant (C, D) kinetics. The color scheme progresses from the first generations (blue to green) to the last (red).

4. Discussion

In this study, we have extended our formalism, which includes modification of kinetic parameters of lipid monomer–vesicle interaction by the composition and the resulting properties of the vesicles (Armstrong et al., 2011) to an environment with finite resources. Competition for finite resources among vesicles introduces selective pressure, which, in combination with the kinetic formalism, is entirely responsible for the behavior of vesicles in this system.

Extensive comparisons of the full kinetics and invariant kinetics formalisms demonstrate crucial differences, essential for considering this relatively simple lipid vesicle system as a model of the prebiotic evolution. Specifically, we found that in the full kinetics system vesicles replicate almost an order of magnitude faster than in the invariant kinetics system. Furthermore, whereas the invariant kinetics system exhibits simple classical behavior of initial growth, followed by decay to final steady state as the resources diminish, the behavior of the full kinetics system is much more complex and exhibits the following distinct phases.

(1) Unrestricted growth phase until about 15 s. This phase is similar to the general behavior of the system with unlimited resources described in our previous publication (Armstrong et al., 2011). (2) Inter-vesicle competition phases. (2.1) Shrinking vesicles. The depletion of free lipids in the environment results in an increase in the fraction of vesicles that are actually shrinking at 15–47 s, until the number of shrinking vesicles is larger than the number of growing ones. Since most of the resources at this point are consumed, the vesicles that are growing are obtaining material from other, shrinking vesicles. (2.2) Second growth burst (in this case due to the reduced fraction of shrinking vesicles) occurs at 47–70 s. (3) Decay to steady state, 70–170 s, and (4) Final steady state, reached at ∼170 s. In contrast, the invariant kinetics formalism results in a simple “classical” kinetics behavior: unrestricted growth (0–230 s), decay to steady state (230–450 s), and finally steady state (reached at 450 s).

Our formalism, which is based on the modification of the kinetic rates by the compositions and thus the properties of the vesicles, differs in essential aspects from previously published studies. A computational system to study the structural properties and dynamic behavior of lipid vesicle populations was developed by Mavelli and Ruiz-Mirazo (2010) and tested experimentally. There are some substantial differences with our formalism. We seed the simulations with one vesicle, as compared to 50 vesicles as described by Mavelli and Ruiz-Mirazo (2010). This allowed us to simulate the entire course of a vesicle population from a single vesicle to the maximal number of 4096 vesicles. In the process, we demonstrated that appreciable vesicle compositional variability is spontaneously generated even when initiating the simulation with only one composition, stemming from stochastic factors in the vesicle division as a “natural” built-in variability generator. Using terminology of Damer and Deamer (2015), in our case “Each vesicle represents a protocell, an ‘experiment’ in a natural version of combinatorial chemistry.” Damer and Deamer (2015) also considered cycles of hydration and dehydration, whereas in our system a constant excess of water is present. Finally, in our formalism, kinetics strongly depends on the vesicle structure, whereas the only bilayer structure parameter taken into account by Mavelli and Ruiz-Mirazo (2010) was elastic/bending state of the membrane as a result of osmotic stress.

One of the most distinguishing processes we identified that is relevant for evolution is intervesicle competition. Vesicle competition was also demonstrated experimentally by Shirt-Ediss et al. (2014) where vesicles were “stealing” lipids from each other as a function of their lipid composition and membrane asymmetry. Shirt-Ediss et al. (2014) did account for lipid composition by altering the kinetic rates of lipid monomers that enter and leave vesicles, although in a way different from ours. The “direct effect” described by Shirt-Ediss et al. (2014) makes a general assumption that the acyl tails of phospholipids have a high affinity for packing closer to each other and increasing bilayer order, thus making the exit of the simple lipids more difficult, which is also explicitly included in our formalism. In addition to this, we also take into account a number of other effects, including charge, shape, complex formation, and the degree of unsaturation of the phospholipids (Armstrong et al., 2011, and Supplementary Material).

Competition between vesicles was also previously experimentally observed among fatty acid vesicles prepared under different physical conditions, for example, swollen or isotonic (Chen et al., 2004), again different from our system where the simulations start with one vesicle and competition is observed among its progenies. Chen et al. (2004) showed that vesicles with high internal osmotic pressure (caused in that particular case by incorporated RNA or sucrose) can acquire lipids from isotonic vesicles. However, their system included at most two membrane lipid components. In geological settings, a phase of crowded protocells enables competition and selection similar to the behavior of the lipid vesicle system in our simulations (Damer, 2016).

We have concentrated on resource availability in this study because it is one of the main factors that determines the population dynamics (Pekkonen et al., 2013). Our results emphasize the critical importance of heterogeneity in lipid component types. In our previous study, we noted the importance of such heterogeneity for high variability of the vesicles under the conditions of unlimited resources (Armstrong et al., 2011). In the current study, we demonstrate that systems composed of only one lipid type replicate much slower and do not exhibit the complex behavior that is observed with multicomponent lipid mixtures, including an absence of different phases, such as vesicle shrinking/lipid redistribution, second growth burst phase, and vesicle competition among progenies. Indeed our simulations with only one lipid component present gave results identical for both full and invariant kinetics. An approach that allows a certain degree of heterogeneity—“controlled complexity”—is more realistic and potentially more useful for the prebiotic studies than oversimplified homogeneous systems (Szostak, 2011).

Based on the observation that the inclusion of phospholipids into fatty acid vesicles results in the combined vesicles acquiring material faster and losing it slower, Budin and Szostak (2011) suggested that the “evolution of phospholipid membranes could thus have been a deterministic outcome of intrinsic physical processes and a key driving force for early cellular evolution.” However, because the properties of a vesicle are necessarily determined by its composition, which can change rapidly, vesicles transmit their compositional information content to subsequent generations with much more stochasticity than template-directed processes, such as RNA replication. Furthermore, the full kinetics system grew an order of magnitude faster than the invariant kinetics system. Finally, multicomponent vesicles grow almost an order of magnitude faster than simple vesicles with only one component, thus providing a selective advantage (under competition) for including multiple complementary components.

Our analyses explore two antipodal cases: in one, the rates of lipid joining and leaving do depend on vesicle composition; in another, they do not. We show that only in the first case a complex chain of events is observed along the time axis (complex kinetics), including intervesicle competition for diminishing resources and a growth burst driven by better-adapted vesicles, a behavior that is similar to evolution in later forms of early life. In contrast, replication is much slower and vesicle variability is smaller in simulations where vesicle composition does not alter kinetic parameters. Both replication speed and variability between vesicles are determinants of evolutionary behavior. All of these findings become clearer in the present paper, which explores for the first time the effects on GARD evolutionary dynamics in an environment with a finite supply of lipids.

Some of the main conclusions of our in silico results are testable experimentally. Among them, changes in the environmental concentrations of lipids (Fig. 9) where there are distinct qualitative and quantitative differences between the full and invariant kinetics formalisms, including in the most interesting manifestation: the consumption followed by a partial release back to the environment of some lipid constituents, the most pronounced with SM. Furthermore, the importance of a large number of component types for replication speed can be tested by comparing behaviors of a simple one-component system with a multicomponent one to see which system incorporates lipids more rapidly. We predict that a single-component system will behave similarly to the invariant kinetics one (cf. Fig. 10). Perhaps the most interesting phenomenon predicted here is a large proportion of shrinking vesicles at specific stages of the process. The growth or shrinkage of vesicles can be directly observed, for example, by using a membrane-staining fluorescent dye and time-lapse confocal microscopy, as described by Hardy et al. (2015). The conditions used can be adjusted to correspond to the specific questions asked, for example to the physical environment of conditions on the prebiotic Earth.

In summary, utilizing this formalism where the kinetics constants are affected by the vesicle composition and properties, we have demonstrated in silico that a lipid vesicle system of a high number of component types, composed of extant phospholipids and cholesterol, exhibits prebiotic properties such as replication, competition, and high variability of vesicle composition and properties, which are critical for evolution. These in silico predictions are amenable to testing by physical experiment. In addition to physical experiments, future developments of this model include the addition of biopolymers that can interact with the simulated membranes and external selective pressures, such as thermal stress, hydration cycles, and ion availability.

Supplementary Material

Supplemental data
Supp_Data.pdf (421.2KB, pdf)

Abbreviations Used

CHOL

cholesterol

PC

phosphatidylcholine

PCA

principal components analysis

PE

phosphatidylethanolamine

PS

phosphatidylserine

R-GARD

Real Graded Autocatalysis Replication Domain

SM

sphingomyelin

Acknowledgments

We acknowledge support from The Morris Belkin Visiting Professorship to R.Z., and from the Minerva Center for Life under Extreme Planetary Conditions, both at the Weizmann Institute of Science.

Author Disclosure Statement

No competing financial interests exist.

References

  1. Adamala K. and Szostak J.W. (2013) Competition between model protocells driven by an encapsulated catalyst. Nat Chem 5:495–501 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Armstrong D.L., Markovitch O., Zidovetzki R., and Lancet D. (2011) Replication of simulated prebiotic amphiphile vesicles controlled by experimental lipid physicochemical properties. Phys Biol 8, doi: 10.1088/1478-3975/8/6/066001 [DOI] [PubMed] [Google Scholar]
  3. Bada J.L. (2004) How life began on Earth: a status report. Earth Planet Sci Lett 226:1–15 [Google Scholar]
  4. Berclaz N., Muller M., Walde P., and Luisi P.L. (2001) Growth and transformation of vesicles studied by ferritin labeling and cryotransmission electron microscopy. J Phys Chem B 105:1056–1064 [Google Scholar]
  5. Blain J.C. and Szostak J.W. (2014) Progress toward synthetic cells. Annu Rev Biochem 83:615–640 [DOI] [PubMed] [Google Scholar]
  6. Božič B. and Svetina S. (2004) A relationship between membrane properties forms the basis of a selectivity mechanism for vesicle self-reproduction. Eur Biophys J 33:565–571 [DOI] [PubMed] [Google Scholar]
  7. Božič B. and Svetina S. (2007) Vesicle self-reproduction: the involvement of membrane hydraulic and solute permeabilities. Eur Phys J E Soft Matter 24:79–90 [DOI] [PubMed] [Google Scholar]
  8. Budin I. and Szostak J.W. (2011) Physical effects underlying the transition from primitive to modern cell membranes. Proc Natl Acad Sci USA 108:5249–5254 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Budin I., Prwyes N., Zhang N., and Szostak J.W. (2014) Chain-length heterogeneity allows for the assembly of fatty acid vesicles in dilute solutions. Biophys J 107:1582–1590 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chen I.A., Roberts R.W., and Szostak J.W. (2004) The emergence of competition between model protocells. Science 305:1474–1476 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Copley S.D., Smith E., and Morowitz H.J. (2007) The origin of the RNA world: co-evolution of genes and metabolism. Bioorg Chem 35:430–443 [DOI] [PubMed] [Google Scholar]
  12. Cronin J.R. (1998) Clues from the origin of the Solar System: meteorites. In The Molecular Origin of Life: Assembling Pieces of the Puzzle, edited by Andre B., Cambridge University Press, Cambridge, UK, pp 119–146 [Google Scholar]
  13. Damer B. (2016) A field trip to the Archaean in search of Darwin's warm little pond. Life (Basel) 6, doi: 10.3390/life6020021 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Damer B. and Deamer D. (2015) Coupled phases and combinatorial selection in fluctuating hydrothermal pools: a scenario to guide experimental approaches to the origin of cellular life. Life (Basel) 13:872–887 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Deamer D.W. (1985) Boundary structures are formed by organic compounds of the Murchinson carbonaceous chondrites. Nature 317:792–794 [Google Scholar]
  16. Deamer D.W. and Pashley R.M. (1989) Amphiphilic components of the Murchinson carbonaceous chondrite: surface properties and membrane formation. Orig Life Evol Biosph 19:21–38 [DOI] [PubMed] [Google Scholar]
  17. Dworkin J., Deamer D., Sandford S., and Allamandola L. (2001) Self-assembling amphiphilic molecules: Synthesis in simulated interstellar/precometary ices. Proc Natl Acad Sci U S A 98:815–819 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fellermann H. and Solé R.V. (2007) Minimal model of self-replicating nanocells: a physically embodied information-free scenario. Philos Trans R Soc Lond B Biol Sci 362:1803–1811 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Georgiou C.D. and Deamer D.W. (2014) Lipids as universal biomarkers of extraterrestrial life. Astrobiology 14:541–549 [DOI] [PubMed] [Google Scholar]
  20. Hanczyc M.M., Fujikawa S.M., and Szostak J.W. (2003) Experimental models of primitive cellular compartments: encapsulation, growth, and division. Science 302:618–622 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hardy M.D., Yang J., Selimkhanov J., Cole C.M., Tsimring L.S., and Devaraj N.K. (2015) Self-reproducing catalyst drives repeated phospholipid synthesis and membrane growth. Proc Natl Acad Sci USA 112:8187–8192 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hargreaves W.R., Mulvihill S.J., and Deamer D.W. (1977) Synthesis of phophospholipids and membranes in prebiotic conditions. Nature 266:78–80 [DOI] [PubMed] [Google Scholar]
  23. Joyce G.F. (2002) The antiquity of RNA-based evolution. Nature 418:214–221 [DOI] [PubMed] [Google Scholar]
  24. Mavelli F. and Ruiz-Mirazo K. (2010) ENVIRONMENT: a computational platform to stochastically simulate reacting and self-reproducing lipid compartments. Phys Biol 7, doi: 10.1088/1478-3975/7/3/036002 [DOI] [PubMed] [Google Scholar]
  25. Mayer C., Schreiber U., and Dávila M.J. (2015) Periodic vesicle formation in tectonic fault zones—an ideal scenario for molecular evolution. Orig Life Evol Biosph 45:139–148 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. McCollom T.M., Ritter G., and Simoneit B.R. (1999) Lipid synthesis under hydrothermal conditions by Fischer-Tropsch-type reactions. Orig Life Evol Biosph 29:153–166 [DOI] [PubMed] [Google Scholar]
  27. Oparin A.I. (1936) The Origin of Life, Macmillan, New York [Google Scholar]
  28. Patel B.H., Percivalle C., Ritson D.J., Duffy C.D., and Sutherland J.D. (2015) Common origins of RNA, protein and lipid precursors in a cyanosulfidic protometabolism. Nat Chem 7:301–307 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pekkonen M., Ketola T., and Laakso J.T. (2013) Resource availability and competition shape the evolution of survival and growth ability in a bacterial community. PLoS One 8, doi: 10.1371/journal.pone.0076471 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pohorille A. and Deamer D. (2009) Self-assembly and function of primitive cell membranes. Res Microbiol 160:449–456 [DOI] [PubMed] [Google Scholar]
  31. Pulselli R.M., Simoncini E., and Tiezzi E. (2009) Self-organization in dissipative structures: a thermodynamic theory for the emergence of prebiotic cells and their epigenetic evolution. Biosystems 3:237–241 [DOI] [PubMed] [Google Scholar]
  32. Regis E. (2009) What is Life? Investigating the Nature of Life in the Age of Synthetic Biology, Oxford University Press, Oxford, UK [Google Scholar]
  33. Rushdi A.I. and Simoneit B.R. (2001) Lipid formation by aqueous Fischer-Tropsch-type synthesis over a temperature range of 100 to 400 degrees C. Orig Life Evol Biosph 31:103–118 [DOI] [PubMed] [Google Scholar]
  34. Schrum J.P., Zhu T.F., and Szostak J.W. (2010) The origins of cellular life. Cold Spring Harb Perspect Biol 2, doi: 10.1101/cshperspect.a002212 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Segré D., Ben-Eli D., and Lancet D. (2000) Compositional genomes: prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc Natl Acad Sci USA 97:4112–4117 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Segré D., Ben-Eli D., Deamer D.W., and Lancet D. (2001a) The lipid world. Orig Life Evol Biosph 31:119–145 [DOI] [PubMed] [Google Scholar]
  37. Segré D., Shenhav B., Kafri R., and Lancet D. (2001b) The molecular roots of compositional inheritance. J Theor Biol 213:481–491 [DOI] [PubMed] [Google Scholar]
  38. Shenhav B., Bar-Even A., Kafri R., and Lancet D. (2005) Polymer GARD: computer simulation of covalent bond formation in reproducing molecular assemblies. Orig Life Evol Biosph 35:111–133 [DOI] [PubMed] [Google Scholar]
  39. Shirt-Ediss B., Ruiz-Mirazo K., Mavelli F., and Solé R.V. (2014) Modelling lipid competition dynamics in heterogeneous protocell populations. Sci Rep 4, doi: 10.1038/srep05675 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Svetina S. (2012) Cellular life could have emerged from properties of vesicles. Orig Life Evol Biosph 42:483–486 [DOI] [PubMed] [Google Scholar]
  41. Szostak J.W. (2011) An optimal degree of physical and chemical heterogeneity for the origin of life? Philos Trans R Soc Lond B Biol Sci 366:2894–2901 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Takakura K., Toyota T., and Sugawara T. (2003) A novel system of self-reproducing giant vesicles. J Am Chem Soc 125:8134–8140 [DOI] [PubMed] [Google Scholar]
  43. Takakura K., Toyota T., and Sugawara T. (2004) A novel system of self-reproducing giant vesicles. J Am Chem Soc 125:8134–8140 [DOI] [PubMed] [Google Scholar]
  44. Thomas J.A. and Rana F.R. (2007) The influence of environmental conditions, lipid composition, and phase behavior on the origin of cell membranes. Orig Life Evol Biosph 37:267–285 [DOI] [PubMed] [Google Scholar]
  45. Toyota T., Takakura K., Kageyama Y., Kurihara K., Maru N., Ohnuma K., Kaneko K., and Sugawara T. (2008) Population study of sizes and components of self-reproducing giant multilamellar vesicles. Langmuir 24:3037–3044 [DOI] [PubMed] [Google Scholar]
  46. Wick R., Walde P., and Luisi P.L. (1995) Light microscopic investigations of the autocatalytic self-reproduction of giant vesicles. J Am Chem Soc 117:1435–1436 [Google Scholar]
  47. Zhu T.F. and Szostak J.W. (2009) Coupled growth and division of model protocell membranes. J Am Chem Soc 131:5705–5713 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Data.pdf (421.2KB, pdf)

Articles from Astrobiology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES