Abstract
Approximately 1% of all babies are born with some form of congenital heart defect. Many serious forms of CHD can now be surgically corrected after birth, which has lead to improved survival into adulthood. However, many patients require serial monitoring to evaluate progression of heart failure and determine timing of interventions. Accurate multidimensional quantification of regional heart shape and function are required for characterizing these patients. A computational atlas of single ventricle and biventricular heart shape and function enables quantification of remodeling in terms of z-scores in relation to specific reference populations. Progression of disease can then be monitored effectively by longitudinal evaluation of z-scores. A biomechanical analysis of cardiac function in relation to population variation enables investigation of the underlying mechanisms for developing pathology. Here, we summarize recent progress in this field, with examples in single ventricle and biventricular congenital pathologies.
Keywords: congenital heart disease, patient specific modeling, atlas based analysis
Introduction
Congenital heart disease is found in up to 1% of live births, and ranks among the most common birth defects [1]. The more severe types have traditionally had high infant mortality; however, improved surgical interventions have led to an increasing population of adults surviving with CHD [2]. Common types of CHD include coarctation of the aorta, tetralogy of Fallot, and transposition of the great arteries (both congenitally and surgically corrected). CHD lesions leading to a dominant single ventricle (e.g. hypoplastic left heart syndrome or hypoplastic right heart syndrome) are often ameliorated using a Fontan procedure, in which blood is diverted to the lungs without passing through the heart. Thus CHD encompasses a range of cardiac defects, which lead to different types of biventricular or single ventricle morphologies. Regular monitoring of the status of heart shape and function is often required in patients to determine the progression of disease. Sequelae often include heart failure involving the left, right, or both ventricles and the timing of interventions (e.g. valve repairs) is critical to patient care. Early intervention may lead to unnecessary complications while late interventions risk deterioration into heart failure.
Cardiovascular magnetic resonance (CMR) imaging is the current gold standard for patient evaluation in CHD and many other cardiovascular diseases [2]. The lack of ionizing radiation makes CMR ideal for serial longitudinal evaluations of patients, both for monitoring the progression of disease and for timing surgical interventions. For example patients with tetralogy of Fallot often develop right ventricular eccentric hypertrophy due to excessive volume overload. Postponement of pulmonary valve implantation may risk unrecoverable adverse remodelling leading to eventual heart failure. However, valve replacement does not lead to improved function in some patients [3], and premature valve implantation risks further interventions such as valve replacement [4]. In single ventricle pathologies, the adult population is expected to grow by 60% in the next 10 years [5]. A registry of patients has reported 42% of the recorded deaths were patients aged 20–30 [6].
Standard methods of analysis include quantification of right and left ventricular mass and volumes, including stroke volume and ejection fraction. For example the decision to implant a pulmonary valve in tetralogy of Fallot is often made on the basis of end-diastolic right ventricular volume, indexed to body habitus. However, modern imaging techniques enable detailed regional analysis of function, resulting in multidimensional measures of shape and motion. An atlas of heart morphology and function is a spatio-temporal map of a specific patient or a population of patients, referred to a common coordinate system. Methods derived from computational anatomy can then be applied to derive quantitative measures of patient specific performance relative to a population, and to quantify progression of disease. This paper reviews recent advanced in the application of atlas-based analysis methods to the evaluation of patients with congenital heart disease. We show how customization of generic templates enables fast interactive analysis of biventricular function in a range of pathologies. Also, we apply finite element analysis to single ventricle shapes drawn from an atlas of Fontan repair patients and illustrate how simulations of biomechanics can aid understanding of how single ventricle morphology impacts cardiac function.
Overview of Methods for Atlas Construction
Imaging Cardiac Function
Cardiac MRI is able to image all parts of the heart without the need for acoustic windows, and does not utilize ionizing radiation. Left and right ventricular mass and volumes are highly accurate and reproducible, with low inter-scan error. Disadvantages of MRI are that patients with implanted electronic devices are generally contraindicated, and children often require anesthesia. However, new advances in image acquisition are beginning to provide diagnostic data in these cases [7–9]. The current standard protocol for analysis of regional and global function requires segmentation of the epicardial and endocardial boundaries of the heart from 2D cine CMR image data. Typically, multiple short and long axis 2D cine acquisitions are performed during breath-hold. Typical imaging parameters include 60° flip angle, TR 30ms, TE 1.6ms, 6mm slice thickness, 360×360mm field of view, 256×208 image matrix, and 20–30 reconstructed frames [10]. However, the substantial slice thickness (5–10mm) leads to partial voluming near the apex and base, increasing the error in boundary placement on short axis cine images [11,12]. Several custom long axis scans must therefore also be planned through the inflow and outflow tracts of both ventricles to locate the four valves (if present), as well as the apex [13]. Three-dimensional cine acquisitions are now becoming available, which avoids the partial voluming problem and the need for planning multiple orientations [14]. At present, these typically require lengthy imaging protocols during which the breathing pattern and heart rate must be highly regular. However, recent advances in accelerated imaging show promise for reconstruction of three-dimensional cine images using gated or free-breathing self gating protocols [15].
Image Analysis
Ventricular volume and mass is typically calculated by contouring inner and outer boundaries in 2D image series acquired in the short axis orientation (a process known as segmentation), and summing volumes from slice to slice. Segmentation of the images is time-consuming and prone to error; however, automated methods are now becoming more widespread [16,17]. Recently, machine-learning algorithms are now enabling fully automated analysis of contours in each slice [18–20]. These methods require training with a significant number of cases with manual ground truth. However, contours can vary between laboratories and care must be taken to ensure the method is trained using several observers [21]. Figure 1 shows short and long axis CMR images their relationship in 3D space.
Figure 1.
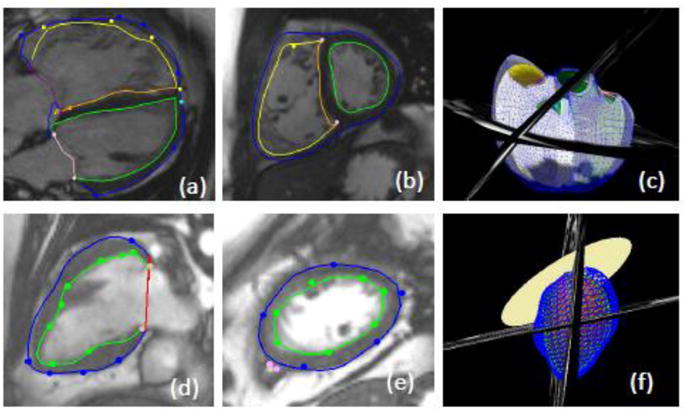
Cardiac magnetic resonance images with epicardial and endocardial contours. a) long axis view b) short axis view and c) 3D biventricular model of a patient with tetralogy of Fallot. d) long axis view e) short axis view and f) 3D single ventricle model.
Model Based Analysis
Shape and motion information for multiple slices and frames can be integrated by the customization of a geometric model of heart shape and function to the image data. Model-based analysis of cardiac function has a long history [22,23]. If contours are available (either through manual or automatic segmentation), a 3D surface mesh can be customized to the segmented contours in each slice using optimization [24] or registration [25] techniques. Several groups have employed subdivision surface models (similar to computer graphics animations) to map heart shape [26–28]. One advantage of subdivision surface models is that resolution and continuity in the mesh can be locally controlled using computational rules rather than explicit constraints. In CHD patients, Morcos et al. [29,30] used a subdivision surface model to reconstruct 3D RV geometries from CMR manually traced images. A marked regional change in RV function, with reduced basal function but augmented apical function, was found in tetralogy of Fallot patients compared with controls using a regional motion analysis. Although global measures of RV function such as tricuspid annular plane systolic excursion and RV ejection fraction have shown clinical utility for characterizing global function, more detailed information can be obtained from the local variations in function available using the surface model. The inclusion of long axis slices with short axis orientations improved the accuracy of the surfaces in patients with transposition of the great arteries [31], and enabled shape models to be constructed in Ebstien’s anomaly [32], capturing large variations in the tricuspid valve size and location.
Finite Element Guide Point Modelling
Finite element modeling is a numerical procedure used to solve problems of mechanics, electrophysiological activity, and fluid flow in engineering applications. Finite element models of cardiac function enable estimation of wall stress, muscle stiffness properties, fluid structure interaction, and predict response to resynchronization therapy [33]. Finite element models have also been used to interactively customize models to patient geometry and motion, through a procedure called guide-point modeling. The model represents the beating heart surfaces as a patchwork of splines (elements) connected at nodes, with constrained continuity of shape and motion. These models were initially applied to biplane coronary cineangiograms [34] and extended to quantify right and left ventricular interaction in mitral regurgitation [35]. In the guide-point modeling procedure, a real time interactive optimization process is employed to iteratively customize the finite element model to user-defined surface guide points, as well as computer generated edge features and feature tracking to deform the model from frame to frame (non-rigid registration) [36]. Initially validated in the left ventricle [37], the method has been extended to biventricular models and validated in CHD patients [38]. The model is customized by least squares optimization of the surface locations to landmarks provided interactively on short and long axis cine images. Using these methods, all four valves can be included (if present). The mass and volume of both ventricles can be obtained, new pathological shapes can be generated which are not already in the database, and all frames in the cine sequence analyzed, resulting in 3D+time motion of the surfaces and valves, and thereby the basal extent of the ventricles, throughout the cardiac cycle. In this method, individual contours of each image are not required since they are provided by the intersections of the model with the image plane. Figure 1 shows short and long axis images and the model-image intersections, together with a 3D view of the model and the image planes.
Atlas-Based Image Analysis
The customization of a geometric model also establishes a coordinate system, fixed to the model, which is transported to each individual heart during the customization process. Once a model has been customized to one patient’s images, it can be used as a template for subsequent customizations. The template image data can be matched to the target image data by optimizing a similarity function, typically using non-rigid registration [39]. Over a large number of templates, an average template can be computed iteratively by successive registration of volumetric images [40].
Once sufficient templates have been constructed, the statistical properties of the population of models can be used to assist the customization process [41]. In one method, principal component analysis (PCA) is applied to a population of shape models, typically using a consistent sampling of points which correspond to the same anatomical location in each patient. Active shape models [42] and active appearance models [43] enable identification of patient specific geometry as a combination of atlas shapes. Given a variety of templates, multi-atlas segmentation can be used to find the best local matching templates, which are then propagated to the target image, and the associated labels are then fused to achieve a consensus contour [44].
Atlas-based statistical models have shown promise in the evaluation of patients with CHD. In one method known as knowledge-based reconstruction, the patient customization is performed using a linear combination of database templates [45]. Using a database of ~60 sub-systemic RV geometries, this method provides accurate and rapid analysis of right ventricular volumes in patients with tetralogy of Fallot, and after arterial switch operation for dextro-transposition of the great arteries [46,47]. In patients with transposition of the great arteries after atrial switch, the right ventricle was dilated and more spherical than controls, with reduced basal regional function relative to patients with congenitally corrected transposition of the great arteries [48]. One limitation of these methods is that the target case may not be adequately represented by a linear combination of template cases. One area of future research is the joint estimation of shape and the underlying statistical shape model using a data driven approach [28]. Stebbing et al. [28] used a subdivision surface parameterization to optimize the basis of heart shapes needed for accurate shape delineation, and could be used to automatically update the statistical model while analyzing new cases.
Atlas-Based Shape analysis
Principal component analysis (PCA), an unsupervised dimension reduction analysis method, was used in the Multi-Ethnic Study of Atherosclerosis to investigate relationships between traditional risk factors (smoking, hypertension, diabetes etc) and cardiac shape and function in approximately 2000 volunteers [24]. Projection of patient-specific geometry onto the orthogonal PCA modes provides z-scores associated with the main modes of variation. These show more sensitive relationships with risk factors [24] and to disease [49] than traditional mass and volume measures. Supervised dimension reduction methods such as information-maximizing component analysis enable optimal classification of distributions between patient groups [50]. Partial least squares optimization methods (another form of supervised dimension reduction) were used to derive orthogonal modes based on clinical remodelling indices with known prognostic value [51].
Another class of statistical methods is mass univariate regression analysis. This has been used to determine sub-clinical relationships between wall thickness distributions and systolic blood pressure [52] and bio-impedance body composition [53]. Similar methods have shown links with SNPs associated with hypertrophy identified from GWAS studies [54]. Recently, these methods have also identified relationship between titin truncation variants and eccentric remodeling patterns in the healthy population [55].
Finite element biomechanical analysis
Although modern medical imaging methods can provide detailed information on the morphology and function of the heart under different conditions, investigation of the underlying mechanisms leading to heart failure requires knowledge of biomechanical quantities such as stress and compliance. Currently, these are impossible to determine directly, and mathematical modeling techniques are required to estimate biophysical parameters from the data available. Finite element models of stress, material properties and activation show promise in this area. Computational physiological models have been used to provide personalized estimates of contraction force, stiffness and activation parameters [56]. Typically, biophysical parameters are iteratively optimized to match the imaged shape and motion [57]. Recently, community benchmark studies have provided valuable validation of code and methods[58] [59]. These methods enable estimation of regional wall stress, contractility, relaxation parameters and ventricular stiffness [33,60]. Similar methods can also be applied in the right ventricle. In one preliminary study, right ventricular wall stress was the best measure for predicting better outcomes after pulmonary valve replacement in tetralogy of Fallot patients [61].
Case Studies: Construction of Biventricular and Single Ventricle CHD Atlases
Preliminary results are presented to illustrate the applications of atlas-based computational analysis in CHD.
Template Generation and Customization
An initial study into the feasibility of guide-point modeling in biventricular CHD patients was described in [38]. The method was validated against ex-vivo sheep heart for LV and RV mass and against manual contours in 17 patients, showing good precision but some bias in LV and RV mass. The method was improved in [62] with validation in 60 patients (35 male, aged 23 ± 13 years, 29 tetralogy of Fallot, 9 transposition of the great arteries, 7 coarctation of the aorta, and 14 other including bicuspid aortic valve and pulmonary atresia). In these studies, a single template derived from a normal biventricular anatomy was customized to each patient. Given multiple templates representing a variety of common biventricular geometries, the shape-specific template closest to the patient’s geometry can be customized, thereby reducing the time required for patient specific modeling. One case was excluded due to incorrect gating of the images, reducing the number of cases to 59. Ethical approval for this study was obtained from the Northern X Ethics Committee of New Zealand.
In order to generate a set of shape-specific templates, we recruited and scanned 24 CHD patients with a wide range of pathologies and biventricular shapes with ethical approval obtained from the Health and Disability Ethics Committee of New Zealand. This dataset contains 4 cases of dextro-transposition of the great arteries, 1 case of congenitally corrected transposition of the great arteries, 1 case of Ebstien’s abnormality, 2 cases of bicuspid aortic valve, 2 cases of double outlet right ventricle, 2 cases of Marfans syndrome, 1 case of congenital aortic stenosis, 2 cases of coartaction of the aorta, and 6 cases of tetralogy of Fallot. A single frame high resolution 3D image of the heart was obtained during diastasis, using a respiratory and cardiac gated gradient recalled echo (GRE) sequence on a 3T MRI scanner (Siemens Skyra; Siemens Healthcare, Erlangen, Germany): TE = 1.4ms, TR = 350ms, voxel size = 1.5 × 1.5 × 1.5mm and flip angle = 20°. In our experiments, we chose three types of CHD biventricular morphology, in order to capture a range of geometries. These scans were independent to the 59 cases used to create the atlas.
To illustrate the shape-specific template generation process, we chose three different geometries commonly seen in biventricular CHD patients (Figure 2). These three characteristic shapes spanned a variety of pathologies: i) LV dominant, where the LV forms the apex of the heart (Figure 2(a)); ii) RV dominant, where the RV forms the apex of the heart (Figure 2(b)); and iii) double apex, where both LV and RV have a separate distinct apex (Figure 2(c)). These were not dependent on a particular CHD type; rather, they reflect remodelling due to pressure and volume overload.
Figure 2.
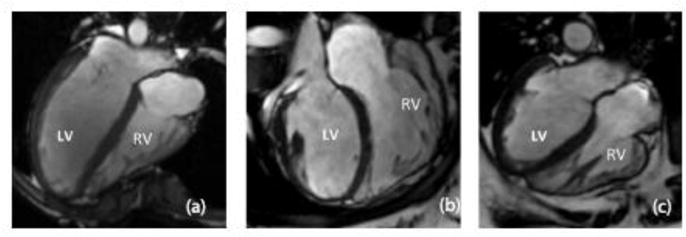
Four chamber ED frames from three participants showing the three shapes identified. (a) LV dominant, (b) RV dominant (c) double apex. The images are from three participants with, (a) Dextro-Transposition of the great arteries, (b) tetralogy of Fallot, and (c) a ventricular septal defect and coarctation of the aorta.
The method of Gonzales et al. [63] was extended to generate the shape-specific templates (Figure 3, steps 1–4). Contours were manually drawn on all slices using ITK-snap (www.itksnap.org) [64]. Finite element nodes were placed on the surfaces using Blender (www.blender.org), connecting nodes to construct hexahedral elements [63]. The resulting bi-linear elements were then subdivided using a Li-Kobbelt subdivision surface method to obtain an interpolating bi-cubic surface that was continuous in position and derivative in all areas, and approximately continuous at the extraordinary nodes [63]. The RV dominant template was created from the 3D CMR dataset of a 24 year old female with tetralogy of Fallot. The double apex template was created from the 3D CMR dataset of a 45 year old female with coarctation of the aorta and a ventricular septal defect. The resulting templates are shown in Figure 4. Each template was generated using the same number of nodes and the same element connections. This was done to ensure that all templates had the same topology so that population shape analyses, such as principal component analysis, can be performed over many cases.
Figure 3.
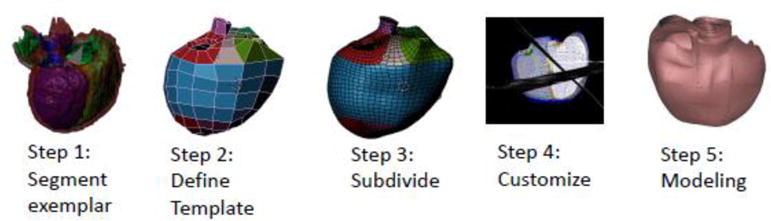
Pipeline for creating new CHD specific templates and patient specific models. Step 1: 3D CMR data is segmented; Step 2: Notes in the template are defined; Step 3: Subdivision surface give the shape-specific template; Step 4: the template is interactively customized to short and long axis cine images in each frame; Step 5: finite element models are generated for biomechanical analysis.
Figure 4.
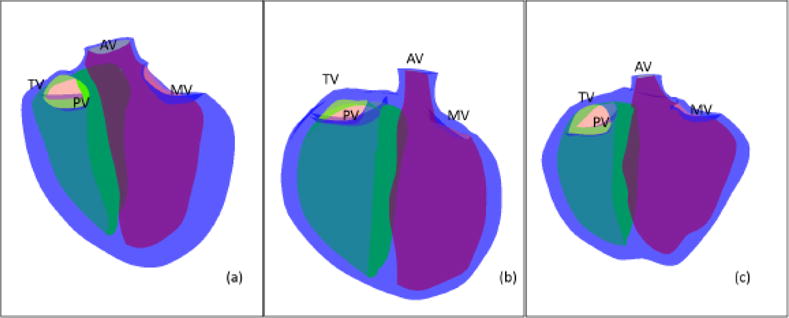
The shape-specific templates. (a) LV dominant, (b) RV dominant and (c) is double apex. The LV is shown in green, the RV in yellow the biventricular epicardial surface is in blue. MV-mitral valve, AV-aortic valve, TV-tricuspid valve and PV-pulmonary valve.
Shape-specific templates could then be customized to the patient’s cine images using guide-point modeling, resulting in patient-specific quantification of biventricular morphology. Briefly, the template was registered to the images using a small number of fiducial landmarks placed on the four valves (if present) and epicardial apex. Interactively-placed guide-points on the epicardial and endocardial surfaces on the short or long axis images were then used to deform the finite element model using least squares minimization. Non-rigid registration methods were used to track image features from frame to frame, in order to propagate the model contours to each frame in the cine sequence [36]. This process resulted in a four dimensional (4D, being 3D plus time) patient-specific time-varying model in an interactive workflow.
Atlas Based Biventricular analysis
A biventricular atlas was created from the 59 patients described above. Figure 5 shows the first three principal components of the ED atlas ranked by the amount of variance explained. Mode 1 shows changes in the relative RV and LV size (ie as the RV gets larger the LV gets smaller), the shape of the apex, and transitions from the right dominant shape at the 5th percentile to the LV dominant shape at the 95th percentile. Mode 2 in the ED atlas shows changes in size of both ventricles. In Mode 3 shows changes in the overall longitudinal dimension of the ventricles, giving a more spherical biventricular shape. The first 3 modes described 50% of the variation in the dataset and the first 10 described 80% of the variation. The amount of each mode present in a specific patient can be calculated by projection of the patient geometry onto the mode shape, giving rise to quantitative z-scores (0 for the mean, 1 for one standard deviation from the mean, etc).
Figure 5.
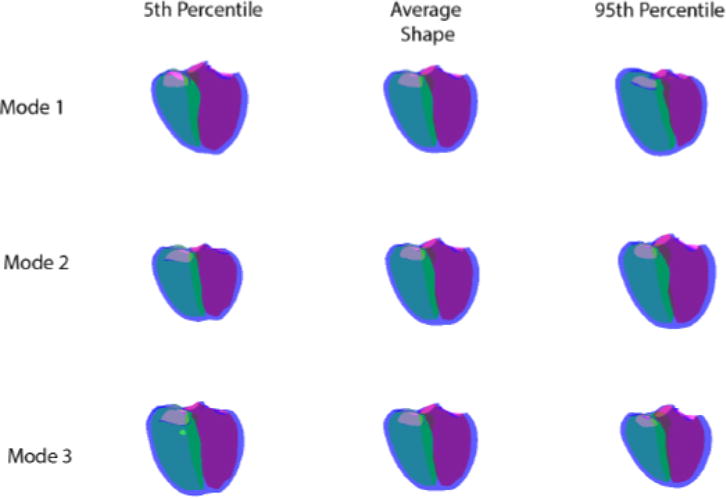
The first three modes of the ED atlas. The left hand column shows the 5th percentile, the middle column the average shape and the right hand column the 95th percentile. The LV is shown in pink, the RV in green and the biventricular epicardium in blue.
Single Ventricle Analysis
An atlas of 42 single ventricle cases was generated from the cardiac atlas database, comprising cases which were listed as having undergone a Fontan procedure or having a condition which was a single ventricle physiology and were accessed to have a left ventricle (with ethical approval obtained from the Health and Disability Ethics Committee of New Zealand). The MRI scans used to create the single ventricle atlas were independent to the datasets already described in this paper. The images were acquired on a Siemens 1.5T Avanto and the average age of participants is 15 ± 9.1years. Size variation due to height was removed using linear regression [24]. This method allows for size due to height to be removed while retaining difference in size related to other factors. The top row of Figure 6 shows the average shape at ED and ES. The first mode of the ED atlas was mainly associated with variation in size. This mode explained 23% of the total variance in the dataset.
Figure 6.
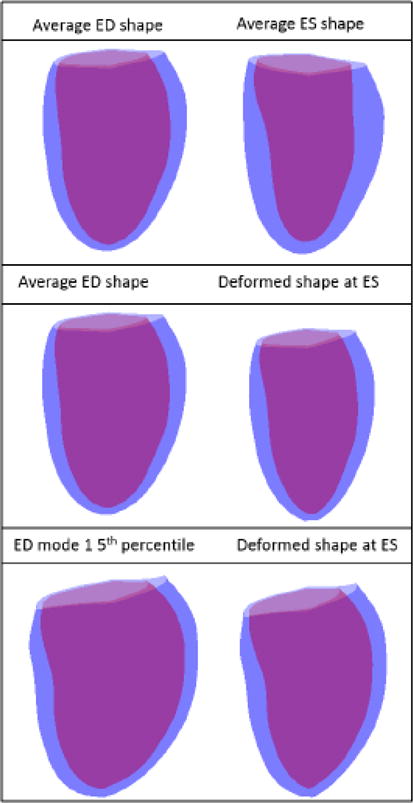
Top: The average shapes at ED and ES for the Fontan dataset. Middle: Average ED shape and the resulting deformed ES shape. Bottom: 5th percentile of mode 1 and the resulting deformed ES shape.
Finite element biomechanical analysis
A finite element model of ventricular biomechanics was used to investigate the relationships between observed variations in end-diastolic shape and variations in ventricular systolic regional wall motions. The end-diastolic geometry was varied to determine the contributions of specific variations in shape to observed variations in systolic function. In the left ventricle of Fontan patients with a systemic left ventricle, average left ventricular end-diastolic shape from the atlas-based analysis was used to create finite element meshes for the biomechanical analysis. A finite element model derived from the average ED Fontan atlas was subjected to ventricular pressures on the endocardial surface corresponding to estimated average LVESP, and the length-dependent tension in the model was modified until the measured mean end-systolic volume was reached [65]. To test how the variation in ED shape of the Fontan patients can explain the observed variation in the atlas-based model ES modes, the initial model geometry was replaced with the average ED shape of the Fontan patients except for shape mode 1, which was adjusted to represent the 5th percentile of the atlas shape distribution. The process of endocardial pressure loading and active tension generation in the finite element model was repeated with the same material properties and activation model parameters.
Figure 6 shows the undeformed and deformed finite element model. The average ED model had a volume of 88.7ml and the deformed model had a volume of 54.6ml. The 5th percentile ED shape model had a volume of 130.5ml and the deformed model had an ESV of 82ml.
Discussion and Conclusions
Although analysis of biventricular and single ventricle function with CMR has been time-consuming and complex in the past, new methods including machine learning, image registration and 3D modeling enables fast and accurate quantification of heart shape and function in congenital heart disease. Rapid customization of shape-specific templates can be performed interactively in a time compatible with a clinical workflow. A major advantage of this method is the inclusion of all four valves and long axis slices. The customization method allows generation of new shapes outside the range spanned by previously analyzed cases.
The patient specific modeling method demonstrated in this paper was able to provide patient specific clinical indices of function quickly (each 4D model took less than 1 hour with some analysts reporting a 20 minute analysis time). It also demonstrated a flexibility to create atlases directly from these models in under 10 minutes, which in the future could provide clinicians with information about how a patient’s heart shape is changing relative to their population (eg other patients with tetralogy of Fallot). The method is still somewhat dependent on the observer’s ability to correctly define boundaries, although this will be assisted in the future with machine learning algorithms.
A statistical atlas of CHD shape variation can be computed from a population of customized shape models. These population atlases enable characterization of the distribution of shape and function in particular cohorts. Individual patient status can be quantified using z-scores showing similarity or differences relative to the population. In the future this method can be used to quantify longitudinal changes in biventricular morphology to assess shape changes in individual patients over time. Although these results are preliminary, the biventricular atlas suggests that the major modes or shape change involve relative dilatation of the right ventricle with respect to the left, overall heart size (not explained by height), sphericalization. Right heart size is indicative of adverse remodelling, and is currently used as the criteria to determine the timing of pulmonary valve replacement [3]. Overall heart size has been linked to adverse events in population studies [66] and sphericalization of heart geometry is also linked with adverse outcomes [67].
As the tool creates a personalized finite element model, it will be possible in the future for biomechanical and electrophysiology models to be created from the 4D patient specific models [68]. Preliminary results shown here illustrate how atlases of CHD shape and function can be used in conjunction with biomechanical models to evaluate underlying mechanisms of the progression to heart failure in different types of disease.
In conclusion, atlas-based analysis of CHD has the potential to be a powerful comparative tool that can be used to prognosticate and improve outcomes. Future work is needed to evaluate which atlas-based measures best determine timing of intervention and future events. Longitudinal studies with large numbers of patients are required for these studies. Since CHD is relatively rare (compared with other heart disease such as myocardial infarction), large scale data pooling studies are required which combine patient studies from many institutions in a standard analysis framework. Also, there is a need to obtain normative data on healthy children, from birth to adulthood. Almost all large cohort studies to date have been in adults, leading to a gap in our knowledge on normal growth and development. A substantial study of children using MRI would significantly aid the quantification of individual and group differences in CHD.
Acknowledgments
This study was funded by NIH grants 1R01HL121754 to ADM, JHO and AAY and 8P41GM103426 (the Biomedical Computation Resource) to ADM. KG received funding from the Greenlane Research and Education fund and AS received funding from the National Heart Foundation of New Zealand.
Footnotes
Ethics
All human studies were approved by the appropriate ethics committees and have therefore been performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki and its later amendments. All persons gave their informed consent prior to their inclusion in the study. Details that might disclose the identity of the subjects under study have been omitted.
Competing interests
ADM and JHO are a co-founders of, and have an equity interest in Insilicomed, Inc., and serve on the scientific advisory board. ADM is a co-founder of Vektor Medical, Inc., and serves on the scientific advisory board. Some of their research grants, including those acknowledged here, have been identified for conflict of interest management based on the overall scope of the project and its potential benefit to Insilicomed, Inc. The authors are required to disclose this relationship in publications acknowledging the grant support, however the research subject and findings reported here did not involve the company in any way and have no relationship whatsoever to the business activities or scientific interests of the company. The terms of this arrangement have been reviewed and approved by the University of California San Diego in accordance with its conflict of interest policies. The other authors have no competing interests to declare.
References
- 1.Marelli AJ, Mackie AS, Ionescu-Ittu R, Rahme E, Pilote L. Congenital heart disease in the general population: changing prevalence and age distribution. Circulation. 2007;115(2):163–172. doi: 10.1161/CIRCULATIONAHA.106.627224. doi:CIRCULATIONAHA.106.627224 [pii] [DOI] [PubMed] [Google Scholar]
- 2.Roest AA, de Roos A. Imaging of patients with congenital heart disease. [Review] Nat Rev Cardiol. 2012;9(2):101–115. doi: 10.1038/nrcardio.2011.162. [DOI] [PubMed] [Google Scholar]
- 3.Geva T. Repaired tetralogy of Fallot: the roles of cardiovascular magnetic resonance in evaluating pathophysiology and for pulmonary valve replacement decision support. J Cardiovasc Magn Reson. 2011;13:9. doi: 10.1186/1532-429X-13-9. pii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McKenzie ED, Khan MS, Dietzman TW, Guzman-Pruneda FA, Samayoa AX, Liou A, et al. Surgical pulmonary valve replacement: a benchmark for outcomes comparisons. J Thorac Cardiovasc Surg. 2014;148(4):1450–1453. doi: 10.1016/j.jtcvs.2014.02.060. [DOI] [PubMed] [Google Scholar]
- 5.Coats L, O’Connor S, Wren C, O’Sullivan J. The single-ventricle patient population: a current and future concern a population-based study in the North of England. [Research Support, Non-U.S. Gov’t] Heart. 2014;100(17):1348–1353. doi: 10.1136/heartjnl-2013-305336. [DOI] [PubMed] [Google Scholar]
- 6.Iyengar AJ, Winlaw DS, Galati JC, Gentles TL, Weintraub RG, Justo RN, et al. The Australia and New Zealand Fontan Registry: description and initial results from the first population-based Fontan registry. Intern Med J. 2014;44(2):148–155. doi: 10.1111/imj.12318. [DOI] [PubMed] [Google Scholar]
- 7.Kalb B, Indik JH, Ott P, Martin DR. MRI of patients with implanted cardiac devices. [Review] J Magn Reson Imaging. 2017 doi: 10.1002/jmri.25824. [DOI] [PubMed] [Google Scholar]
- 8.Kharabish A, Mkrtchyan N, Meierhofer C, Martinoff S, Ewert P, Stern H, et al. Cardiovascular magnetic resonance is successfully feasible in many patients aged 3 to 8years without general anesthesia or sedation. [Comparative Study] J Clin Anesth. 2016;34:11–14. doi: 10.1016/j.jclinane.2016.02.048. [DOI] [PubMed] [Google Scholar]
- 9.Olivieri L, Cross R, O’Brien KJ, Xue H, Kellman P, Hansen MS. Free-breathing motion-corrected late-gadolinium-enhancement imaging improves image quality in children. Pediatr Radiol. 2016;46(7):983–990. doi: 10.1007/s00247-016-3553-7. [DOI] [PubMed] [Google Scholar]
- 10.Schulz-Menger J, Bluemke DA, Bremerich J, Flamm SD, Fogel MA, Friedrich MG, et al. Standardized image interpretation and post processing in cardiovascular magnetic resonance: Society for Cardiovascular Magnetic Resonance (SCMR) board of trustees task force on standardized post processing. J Cardiovasc Magn Reson. 2013;15:35. doi: 10.1186/1532-429X-15-35. pii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hudsmith LE, Petersen SE, Francis JM, Robson MD, Neubauer S. Normal human left and right ventricular and left atrial dimensions using steady state free precession magnetic resonance imaging. J Cardiovasc Magn Reson. 2005;7(5):775–782. doi: 10.1080/10976640500295516. [DOI] [PubMed] [Google Scholar]
- 12.Pattynama PM, Lamb HJ, Van der Velde EA, Van der Geest RJ, Van der Wall EE, De Roos A. Reproducibility of MRI-derived measurements of right ventricular volumes and myocardial mass. Magn Reson Imaging. 1995;13(1):53–63. doi: 10.1016/0730-725x(94)00076-f. pii. [DOI] [PubMed] [Google Scholar]
- 13.Mooij CF, de Wit CJ, Graham DA, Powell AJ, Geva T. Reproducibility of MRI measurements of right ventricular size and function in patients with normal and dilated ventricles. J Magn Reson Imaging. 2008;28(1):67–73. doi: 10.1002/jmri.21407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nguyen KL, Han F, Zhou Z, Brunengraber DZ, Ayad I, Levi DS, et al. 4D MUSIC CMR: value-based imaging of neonates and infants with congenital heart disease. J Cardiovasc Magn Reson. 2017;19(1):40. doi: 10.1186/s12968-017-0352-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feng L, Coppo S, Piccini D, Yerly J, Lim RP, Masci PG, et al. 5D whole-heart sparse MRI. Magn Reson Med. 2017 doi: 10.1002/mrm.26745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Peng P, Lekadir K, Gooya A, Shao L, Petersen SE, Frangi AF. A review of heart chamber segmentation for structural and functional analysis using cardiac magnetic resonance imaging. MAGMA. 2016;29(2):155–195. doi: 10.1007/s10334-015-0521-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Petitjean C, Dacher JN. A review of segmentation methods in short axis cardiac MR images. Med Image Anal. 2011;15(2):169–184. doi: 10.1016/j.media.2010.12.004. pii. [DOI] [PubMed] [Google Scholar]
- 18.Avendi MR, Kheradvar A, Jafarkhani H. A combined deep-learning and deformable-model approach to fully automatic segmentation of the left ventricle in cardiac MRI. [Research Support, Non-U.S. Gov’t] Med Image Anal. 2016;30:108–119. doi: 10.1016/j.media.2016.01.005. [DOI] [PubMed] [Google Scholar]
- 19.Tan LK, Liew YM, Lim E, McLaughlin RA. Convolutional neural network regression for short-axis left ventricle segmentation in cardiac cine MR sequences. Med Image Anal. 2017;39:78–86. doi: 10.1016/j.media.2017.04.002. [DOI] [PubMed] [Google Scholar]
- 20.Avendi MR, Kheradvar A, Jafarkhani H. Automatic segmentation of the right ventricle from cardiac MRI using a learning-based approach. Magn Reson Med. 2017 doi: 10.1002/mrm.26631. [DOI] [PubMed] [Google Scholar]
- 21.Suinesiaputra A, Bluemke DA, Cowan BR, Friedrich MG, Kramer CM, Kwong R, et al. Quantification of LV function and mass by cardiovascular magnetic resonance: multi-center variability and consensus contours. [Research Support, N.I.H., Extramural] J Cardiovasc Magn Reson. 2015;17(1):63. doi: 10.1186/s12968-015-0170-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Frangi AF, Niessen WJ, Viergever MA. Three-dimensional modeling for functional analysis of cardiac images: a review. IEEE Trans Med Imaging. 2001;20(1):2–25. doi: 10.1109/42.906421. [DOI] [PubMed] [Google Scholar]
- 23.Young AA, Frangi AF. Computational cardiac atlases: from patient to population and back. Exp Physiol. 2009;94(5):578–596. doi: 10.1113/expphysiol.2008.044081. doi:expphysiol.2008.044081 [pii] [DOI] [PubMed] [Google Scholar]
- 24.Medrano-Gracia P, Cowan BR, Ambale-Venkatesh B, Bluemke DA, Eng J, Finn JP, et al. Left ventricular shape variation in asymptomatic populations: The Multi-Ethnic Study of Atherosclerosis. Journal of Cardiovascular Magnetic Resonance. 2014;16:56. doi: 10.1186/s12968-014-0056-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lamata P, Niederer S, Nordsletten D, Barber DC, Roy I, Hose DR, et al. An accurate, fast and robust method to generate patient-specific cubic Hermite meshes. Med Image Anal. 2011;15(6):801–813. doi: 10.1016/j.media.2011.06.010. pii. [DOI] [PubMed] [Google Scholar]
- 26.Sheehan FH, Bolson EL, Martin RW, Bashein G, McDonald J. Quantitative three dimensional echocardiography: Methodology, validation, and clinical applications. In: Wells WM, Colchester A, Delp S, editors. Medical Image Computing and Computer-Assisted Intervention — MICCAI’98. Springer; 1998. [Google Scholar]
- 27.Chandrashekara R, Mohiaddin R, Razavi R, Rueckert D. Nonrigid image registration with subdivision lattices: application to cardiac MR image analysis. Med Image Comput Comput Assist Interv. 2007;10(Pt 1):335–342. doi: 10.1007/978-3-540-75757-3_41. [DOI] [PubMed] [Google Scholar]
- 28.Stebbing RV, Namburete AI, Upton R, Leeson P, Noble JA. Data-driven shape parameterization for segmentation of the right ventricle from 3D+t echocardiography. Med Image Anal. 2015;21(1):29–39. doi: 10.1016/j.media.2014.12.002. [DOI] [PubMed] [Google Scholar]
- 29.Morcos P, Vick GW, 3rd, Sahn DJ, Jerosch-Herold M, Shurman A, Sheehan FH. Correlation of right ventricular ejection fraction and tricuspid annular plane systolic excursion in tetralogy of Fallot by magnetic resonance imaging. Int J Cardiovasc Imaging. 2009;25(3):263–270. doi: 10.1007/s10554-008-9387-0. [DOI] [PubMed] [Google Scholar]
- 30.Morcos M, Sheehan FH. Regional right ventricular wall motion in tetralogy of fallot: a three dimensional analysis. Int J Cardiovasc Imaging. 2013;29(5):1051–1058. doi: 10.1007/s10554-012-0178-2. [DOI] [PubMed] [Google Scholar]
- 31.Moroseos T, Mitsumori L, Kerwin WS, Sahn DJ, Helbing WA, Kilner PJ, et al. Comparison of Simpson’s method and three-dimensional reconstruction for measurement of right ventricular volume in patients with complete or corrected transposition of the great arteries. Am J Cardiol. 2010;105(11):1603–1609. doi: 10.1016/j.amjcard.2010.01.025. [DOI] [PubMed] [Google Scholar]
- 32.Lee CM, Sheehan FH, Bouzas B, Chen SS, Gatzoulis MA, Kilner PJ. The shape and function of the right ventricle in Ebstein’s anomaly. Int J Cardiol. 2013;167(3):704–710. doi: 10.1016/j.ijcard.2012.03.062. [DOI] [PubMed] [Google Scholar]
- 33.Chabiniok R, Wang VY, Hadjicharalambous M, Asner L, Lee J, Sermesant M, et al. Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: ventricular cardiac mechanics. Interface Focus. 2016;6:20150083. doi: 10.1098/rsfs.2015.0083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Young AA, Hunter PJ, Smaill BH. Estimation of epicardial strain using the motions of coronary bifurcations in biplane cineangiography. IEEE Trans Biomed Eng. 1992;39(5):526–531. doi: 10.1109/10.135547. [DOI] [PubMed] [Google Scholar]
- 35.Young AA, Orr R, Smaill BH, Dell’Italia LJ. Three-dimensional changes in left and right ventricular geometry in chronic mitral regurgitation. Am J Physiol. 1996;271(6 Pt 2):H2689–2700. doi: 10.1152/ajpheart.1996.271.6.H2689. [DOI] [PubMed] [Google Scholar]
- 36.Li B, Liu Y, Occleshaw CJ, Cowan BR, Young AA. In-line automated tracking for ventricular function with magnetic resonance imaging. JACC Cardiovasc Imaging. 2010;3(8):860–866. doi: 10.1016/j.jcmg.2010.04.013. pii. [DOI] [PubMed] [Google Scholar]
- 37.Young AA, Cowan BR, Thrupp SF, Hedley WJ, Dell’Italia LJ. Left ventricular mass and volume: fast calculation with guide-point modeling on MR images. Radiology. 2000;216(2):597–602. doi: 10.1148/radiology.216.2.r00au14597. [DOI] [PubMed] [Google Scholar]
- 38.Gilbert K, Lam HI, Pontre B, Cowan BR, Occleshaw CJ, Liu JY, et al. An interactive tool for rapid biventricular analysis of congenital heart disease. Clin Physiol Funct Imaging. 2017;37(4):413–420. doi: 10.1111/cpf.12319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Peyrat JM, Delingette H, Sermesant M, Xu C, Ayache N. Registration of 4D cardiac CT sequences under trajectory constraints with multichannel diffeomorphic demons. [Research Support, Non-U.S. Gov’t] IEEE Trans Med Imaging. 2010;29(7):1351–1368. doi: 10.1109/TMI.2009.2038908. [DOI] [PubMed] [Google Scholar]
- 40.Bai W, Shi W, de Marvao A, Dawes TJ, O’Regan DP, Cook SA, et al. A bi-ventricular cardiac atlas built from 1000+ high resolution MR images of healthy subjects and an analysis of shape and motion. [Research Support, Non-U.S. Gov’t] Med Image Anal. 2015;26(1):133–145. doi: 10.1016/j.media.2015.08.009. [DOI] [PubMed] [Google Scholar]
- 41.Chandrashekara R, Rao A, Sanchez-Ortiz GI, Mohiaddin RH, Rueckert D. Construction of a statistical model for cardiac motion analysis using nonrigid image registration. Inf Process Med Imaging. 2003;18:599–610. doi: 10.1007/978-3-540-45087-0_50. [DOI] [PubMed] [Google Scholar]
- 42.Cootes TF, Hill A, Taylor CF, Halsam J. The use of active shape models for locating structures in medical images. Image and Vision Computing. 1994;12(6):355–366. [Google Scholar]
- 43.Mitchell SC, Bosch JG, Lelieveldt BP, van der Geest RJ, Reiber JH, Sonka M. 3-D active appearance models: segmentation of cardiac MR and ultrasound images. IEEE Trans Med Imaging. 2002;21(9):1167–1178. doi: 10.1109/TMI.2002.804425. [DOI] [PubMed] [Google Scholar]
- 44.Bai W, Shi W, Ledig C, Rueckert D. Multi-atlas segmentation with augmented features for cardiac MR images. Med Image Anal. 2015;19(1):98–109. doi: 10.1016/j.media.2014.09.005. [DOI] [PubMed] [Google Scholar]
- 45.Sheehan FH, Kilner PJ, Sahn DJ, Vick GW, 3rd, Stout KK, Ge S, et al. Accuracy of knowledge-based reconstruction for measurement of right ventricular volume and function in patients with tetralogy of Fallot. Am J Cardiol. 2010;105(7):993–999. doi: 10.1016/j.amjcard.2009.11.032. [DOI] [PubMed] [Google Scholar]
- 46.Nyns EC, Dragulescu A, Yoo SJ, Grosse-Wortmann L. Evaluation of knowledge-based reconstruction for magnetic resonance volumetry of the right ventricle in tetralogy of Fallot. [Observational Study] Pediatr Radiol. 2014;44(12):1532–1540. doi: 10.1007/s00247-014-3042-9. [DOI] [PubMed] [Google Scholar]
- 47.Nyns EC, Dragulescu A, Yoo SJ, Grosse-Wortmann L. Evaluation of knowledge-based reconstruction for magnetic resonance volumetry of the right ventricle after arterial switch operation for dextro-transposition of the great arteries. Int J Cardiovasc Imaging. 2016;32(9):1415–1423. doi: 10.1007/s10554-016-0921-1. [DOI] [PubMed] [Google Scholar]
- 48.Morcos M, Kilner PJ, Sahn DJ, Litt HI, Valsangiacomo-Buechel ER, Sheehan FH. Comparison of systemic right ventricular function in transposition of the great arteries after atrial switch and congenitally corrected transposition of the great arteries. Int J Cardiovasc Imaging. 2017 doi: 10.1007/s10554-017-1201-4. [DOI] [PubMed] [Google Scholar]
- 49.Zhang X, Cowan BR, Bluemcke DA, Finn JP, Fonseca CG, Kadish AH, et al. Atlas-based quantification of cardiac remodeling due to myocardial infarction. PLoS One. 2014;9(10):e110243. doi: 10.1371/journal.pone.0110243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang X, Ambale-Venkatesh B, Bluemcke DA, Cowan BR, Finn JP, Fonseca CG, et al. Information maximizing component analysis of left ventricular remodeling due to myocardial infarction. Journal of Translational Medicine. 2015;13(343) doi: 10.1186/s12967-015-0709-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhang X, Medrano-Gracia P, Ambale-Venkatesh B, Bluemke DA, Cowan BR, Finn JP, et al. Orthogonal decomposition of left ventricular remodelling in myocardial infarction. Gigascience. 2017 doi: 10.1093/gigascience/gix005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.de Marvao A, Dawes TJ, Shi W, Durighel G, Rueckert D, Cook SA, et al. Precursors of Hypertensive Heart Phenotype Develop in Healthy Adults: A High-Resolution 3D MRI Study. [Research Support, Non-U.S. Gov’t] JACC Cardiovasc Imaging. 2015;8(11):1260–1269. doi: 10.1016/j.jcmg.2015.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Corden B, de Marvao A, Dawes TJ, Shi W, Rueckert D, Cook SA, et al. Relationship between body composition and left ventricular geometry using three dimensional cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2016;18(1):32. doi: 10.1186/s12968-016-0251-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Biffi C, de Marvao A, Attard MI, Dawes TJW, Whiffin N, Bai W, et al. Three-dimensional Cardiovascular Imaging-Genetics: A Mass Univariate Framework. Bioinformatics. 2017 doi: 10.1093/bioinformatics/btx552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schafer S, de Marvao A, Adami E, Fiedler LR, Ng B, Khin E, et al. Titin-truncating variants affect heart function in disease cohorts and the general population. [Comparative Study] Nat Genet. 2017;49(1):46–53. doi: 10.1038/ng.3719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Marchesseau S, Delingette H, Sermesant M, Cabrera-Lozoya R, Tobon-Gomez C, Moireau P, et al. Personalization of a cardiac electromechanical model using reduced order unscented Kalman filtering from regional volumes. [Research Support, Non-U.S. Gov’t] Med Image Anal. 2013;17(7):816–829. doi: 10.1016/j.media.2013.04.012. [DOI] [PubMed] [Google Scholar]
- 57.Wang VY, Lam HI, Ennis DB, Cowan BR, Young AA, Nash MP. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Med Image Anal. 2009;13(5):773–784. doi: 10.1016/j.media.2009.07.006. pii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Land S, Gurev V, Arens S, Augustin CM, Baron L, Blake R, et al. Verification of cardiac mechanics software: benchmark problems and solutions for testing active and passive material behaviour. Proc R Soc A. 2015;471(2184) doi: 10.1098/rspa.2015.0641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Niederer SA, Kerfoot E, Benson AP, Bernabeu MO, Bernus O, Bradley C, et al. Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos Trans A Math Phys Eng Sci. 2011;369(1954):4331–4351. doi: 10.1098/rsta.2011.0139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wang VY, Nielsen PM, Nash MP. Image-Based Predictive Modeling of Heart Mechanics. Annu Rev Biomed Eng. 2015;17:351–383. doi: 10.1146/annurev-bioeng-071114-040609. [DOI] [PubMed] [Google Scholar]
- 61.Tang D, Yang C, Del Nido PJ, Zuo H, Rathod RH, Huang X, et al. Mechanical stress is associated with right ventricular response to pulmonary valve replacement in patients with repaired tetralogy of Fallot. J Thorac Cardiovasc Surg. 2016;151(3):687–694 e683. doi: 10.1016/j.jtcvs.2015.09.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gilbert K, Pontre B, Occleshaw CJ, Cowan BR, Suinesiaputra A, Young AA. 4D modelling for rapid assessment of biventricular function in congenital heart disease. Int J Cardiovasc Imaging. 2017 doi: 10.1007/s10554-017-1236-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gonzales MJ, Sturgeon G, Krishnamurthy A, Hake J, Jonas R, Stark P, et al. A three-dimensional finite element model of human atrial anatomy: new methods for cubic Hermite meshes with extraordinary vertices. Med Image Anal. 2013;17(5):525–537. doi: 10.1016/j.media.2013.03.005. pii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Contijoch F, Witschey WR, Rogers K, Rears H, Hansen M, Yushkevich P, et al. User-initialized active contour segmentation and golden-angle real-time cardiovascular magnetic resonance enable accurate assessment of LV function in patients with sinus rhythm and arrhythmias. J Cardiovasc Magn Reson. 2015;17:37. doi: 10.1186/s12968-015-0146-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lumens J, Delhaas T, Kirn B, Arts T. Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. [Research Support, Non-U.S. Gov’t] Ann Biomed Eng. 2009;37(11):2234–2255. doi: 10.1007/s10439-009-9774-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bluemke DA, Kronmal RA, Lima JA, Liu K, Olson J, Burke GL, et al. The relationship of left ventricular mass and geometry to incident cardiovascular events: the MESA (Multi-Ethnic Study of Atherosclerosis) study. J Am Coll Cardiol. 2008;52(25):2148–2155. doi: 10.1016/j.jacc.2008.09.014. pii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ambale-Venkatesh B, Yoneyama K, Sharma RK, Ohyama Y, Wu CO, Burke GL, et al. Left ventricular shape predicts different types of cardiovascular events in the general population. Heart. 2016 doi: 10.1136/heartjnl-2016-310052. [DOI] [PubMed] [Google Scholar]
- 68.Villongco CT, Krummen DE, Omens JH, McCulloch AD. Non-invasive, model-based measures of ventricular electrical dyssynchrony for predicting CRT outcomes. Europace. 2016;18(suppl 4):iv104–iv112. doi: 10.1093/europace/euw356. [DOI] [PMC free article] [PubMed] [Google Scholar]


