Quantifying Axonal Responses in Patient-Specific Models of Subthalamic Deep Brain Stimulation

Abstract

Medical imaging has played a major role in defining the general anatomical targets for deep brain stimulation (DBS) therapies. However, specifics on the underlying brain circuitry that is directly modulated by DBS electric fields remain relatively undefined. Detailed biophysical modeling of DBS provides an approach to quantify the theoretical responses to stimulation at the cellular level, and has established a key role for axonal activation in the therapeutic mechanisms of DBS. Estimates of DBS-induced axonal activation can then be coupled with advances in defining the structural connectome of the human brain to provide insight into the modulated brain circuitry and possible correlations with clinical outcomes. These pathway-activation models (PAMs) represent powerful tools for DBS research, but the theoretical predictions are highly dependent upon the underlying assumptions of the particular modeling strategy used to create the PAM. In general, three types of PAMs are used to estimate activation: 1) field-cable (FC) models, 2) driving force (DF) models, and 3) volume of tissue activated (VTA) models. FC models represent the “gold standard” for analysis but at the cost of extreme technical demands and computational resources. Consequently, DF and VTA PAMs, derived from simplified FC models, are typically used in clinical research studies, but the relative accuracy of these implementations is unknown. Therefore, we performed a head-to-head comparison of the different PAMs, specifically evaluating DBS of three different axonal pathways in the subthalamic region. The DF PAM was markedly more accurate than the VTA PAMs, but none of these simplified models were able to match the results of the patient-specific FC PAM across all pathways and combinations of stimulus parameters. These results highlight the limitations of using simplified predictors to estimate axonal stimulation and emphasize the need for novel algorithms that are both biophysically realistic and computationally simple.

1. Introduction

Deep brain stimulation (DBS) is an established clinical therapy for a range of neurological disorders. The most common application is subthalamic DBS for the treatment of Parkinson’s disease (PD). Advanced medical imaging and decades of clinical experience have helped identify anatomical targets for therapeutic stimulation in the subthalamic region [e.g. Saint-Cyr et al., 2002; Herzog et al., 2004; Nowinski et al., 2005; Butson et al., 2011; Welter et al., 2014; Eisenstein et al., 2014]. However, there is still little to no clinical consensus on the specific neural elements (and/or axonal pathways) that are necessary and sufficient for evoking therapeutic effects when stimulated [Hamel et al., 2017].

Patient-specific computational models are tools to study the underlying effects of DBS and evaluate different stimulation paradigms [McIntyre et al., 2007]. They allow for noninvasive quantitative characterization of the theoretical response of various neural elements to a wide range of stimulation settings. Recently, patient-specific DBS models have been used in combination with explicit representations of axonal pathways, typically derived from tractography, to evaluate possible stimulation correlations with symptom improvement or side effects [Chaturvedi et al., 2010]. These pathway-activation models (PAMs) leverage advances in the scientific documentation of the human brain structural connectome, and now represent a burgeoning subfield of DBS research we call connectomic DBS modeling. In particular, subthalamic DBS has already been the focus of numerous PAM studies [e.g. Coenen et al., 2011; Chaturvedi et al., 2012; Groppa et al., 2014; Sweet et al., 2014; Accolla et al., 2016; Vanegas-Arroyave et al., 2016; Gunalan et al., 2017; Horn et al., 2017; Akram et al., 2017]. However, the various PAM analyses have employed a wide range of different methods without much in the way of documentation or validation of their accuracy.

There are currently three general classes of methods for estimating the response of axonal pathways to DBS: 1) field-cable (FC) methods, 2) driving force (DF) methods, and 3) volume of tissue activated (VTA) methods. FC methods are the most detailed and technically demanding, explicitly modeling the electric field, axonal trajectories, and transmembrane ion channels responsible for action potential initiation in response to extracellular stimuli [McNeal, 1976; Gunalan et al., 2017]. DF methods represent a 1-degree simplification of FC methods, requiring calculation of the electric field but simplifying estimation of the transmembrane response to substantially speed up the simulations [Warman et al., 1992; Peterson et al., 2011]. VTA methods represent a 2-degree simplification of FC methods, reducing calculations of the electric field and axonal response into a generic algorithm that is the fastest and easiest to implement [Butson and McIntyre, 2006; Chaturvedi et al., 2013]. Each method has inherent limitations, but FC methods represent the “gold standard” for comparison because the DF and VTA methods are derivative formulations.

Numerous academic software tools have been created to help facilitate the use of PAMs by clinical DBS researchers [e.g. Miocinovic et al., 2007; Horn and Kuhn, 2015; Lauro et al., 2016; Noecker et al., 2017]. However, these tools hide non-expert users from the technical details of the PAM methodology and tend to rely on numerous simplifications to generate their results, which subsequently have unknown implications on the conclusions reached. This technical issue within the field of connectomic DBS modeling is exacerbated by the lack of direct comparisons of different methods for estimating axonal responses to electrical stimulation [Chaturvedi et al., 2010; Howell and McIntyre, 2017]. Therefore, the goal of this study was to perform a head-to-head comparison of different methods for estimating axonal activation, specifically evaluating DBS of three different axonal pathways in the subthalamic region.

2. Methods

2.1. Patient-specific model of subthalamic DBS

The technical details and methodology for constructing the patient-specific DBS models are described in prior works [Howell and McIntyre, 2016; Howell and McIntyre, 2017; Gunalan et al., 2017] and summarized below. We hypothesized that the assumptions and simplifications inherent in DF and VTA PAMs would generate markedly different results when compared to FC PAMs. We used the most detailed patient-specific foundation for DBS modeling currently available to perform our analysis [Gunalan et al., 2017], and attempted to minimize sources of variance between comparison of methods. We used the FC PAM, one DF PAM [Peterson et al., 2011] and three VTA PAMs [Chaturvedi et al., 2013; Madler and Coenen, 2012; Astrom et al., 2015] to estimate the activation thresholds of individual axons within three different pathways coursing through the subthalamic region. Our pathways of interest were the internal capsule fibers of passage (IC), hyperdirect pathway (HDP), and cerebellothalamic tract (CbTT).

2.1.1. Patient data

Collection of all patient data for this study was approved by the University of Minnesota Institutional Review Board. Pre-operative T1-weighted (T1W), T2-weighted (T2W), susceptibility-weighted (SW), and diffusion-weighted (DW) images were obtained on a 7T magnetic resonance imaging (MRI) system (Magnex Scientific, UK) [Duchin et al., 2012; Gunalan et al., 2017]. A pre-operative T1W image was also acquired on a 1.5T Siemens Magnetom Espree. These MRI data were used to create the anatomical model of the patient. A post-operative CT image (Biograph64 Sensation, Siemens) was obtained approximately 1 month after surgery and used to define the location of the implanted DBS electrode.

2.1.2. Image processing

The DW images were corrected for distortions from eddy currents using FSL’s eddy tool and from magnetic field inhomogeneities using FSL’s topup tool. We registered all images to the T1W image using Advanced Normalization Tools or FSL’s image registration tool, flirt [Jenkinson and Smith, 2001; Jenkinson et al., 2002]. FSL’s brain extraction tool, bet [Smith, 2002], was used to isolate the brain from the 1.5T T1W image, and subsequently, we used FSL’s automated segmentation tool, fast [Zhang et al., 2001], to subdivide the brain image into grey matter, white matter, and cerebrospinal fluid (CSF). The locations of bone and other soft tissues (e.g. fat and muscle) were approximated using a detailed single-patient atlas named MIDA [Iacono et al., 2015]. A linear mapping was calculated by using flirt with 12 degrees of freedom to coregister the grey matter, white matter, and CSF tissue types in the MIDA image to those in the patient’s T1W image, and the affine transformation was used to warp the MIDA masks of the non-brain regions into the patient’s T1W space [Gunalan et al., 2017].

Manual segmentation of subcortical nuclei (putamen, globus pallidus, subthalamic nucleus, substantia nigra, red nucleus) was performed with Seg3D. As no image had adequate contrast for thalamic segmentation, we fit the thalamic atlas developed by Krauth et al. [2010] to the 1.5T T1W image in Cicerone [Miocinovic et al., 2007]. Freesurfer’s recon tool was used to segment the ipsilateral CSF and contralateral cerebral hemisphere from the 1.5T T1W image [Fischl et al., 2012].

2.1.3. Streamline reconstruction

We reconstructed three pathways for our analysis: internal capsule fibers of passage (IC), hyperdirect pathway (HDP), and cerebellothalamic tract (CbTT) (Figure 1). IC and HDP are comprised of layer V pyramidal cells that project corticofugal axons from the motor cortex, through the internal capsule, and terminate in the brainstem/spinal cord. The HDP is distinct from the IC in that it gives off a collateral from the corticofugal axon to the STN [Nambu et al., 2002; Kita and Kita, 2012; Haynes and Haber, 2013]. The CbTT originates from the dentate and interposed nuclei of the cerebellum, passes through the superior cerebellar peduncle, and terminates in the ventral lateral posteroventral (VLpv) thalamic nucleus [Gallay et al., 2008].

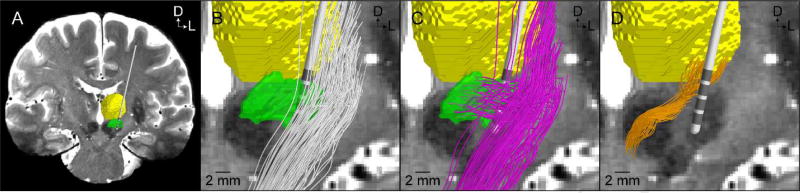
Figure 1.

Patient-specific axonal pathways. (A) A coronal view of the 7T T2-weighted magnetic resonance image along with overlaid representations of the DBS lead (Medtronic model 3389), thalamus (yellow), and subthalamic nucleus (green). Representative population of 100 streamlines of the: (B) internal capsule fibers of passage (white streamlines), (C) hyperdirect pathway (pink streamlines), and (D) cerebellothalamic tract (orange streamlines). Axes: D = dorsal, L = lateral.

The IC, HDP, and CbTT each represent pathways of substantial clinical interest in the subthalamic region for DBS studies. Stimulation of the IC is commonly associated with motor contraction side effects of subthalamic DBS [Tommasi et al., 2008; Mahlknecht et al., 2017]. Stimulation of the HDP is thought to be a major contributor to the therapeutic effects of subthalamic DBS [Walker et al., 2012; Sanders and Jaeger, 2016]. Stimulation of the CbTT is considered therapeutic for the control of tremor [Coenen et al., 2011; Groppa et al., 2014; Sweet et al., 2014], but has also been implicated in the generation of speech disturbance side effects [Astrom et al., 2010; Tripoliti et al., 2014].

We used the probabilistic tractography toolbox in FSL to reconstruct the IC, HDP, and CbTT pathways. Diffusion parameters were fit using bedpostx, and streamlines were generated with probtrackx. We saved only those streamlines that originated in the seed mask, terminated in the target mask(s), and avoided the exclusion masks (as well as the patient-specific DBS electrode position). We fit a smoothing spline to the tractography-generated streamlines to create the axonal trajectories used in our simulations (Figures 1 and S1).

The streamlines of the IC were generated from a seed region (with 100 seeds per voxel) that resided in the white matter lateral to the STN, between the thalamus and lenticular nucleus. Streamlines connected a target mask in the cerebral peduncle of the midbrain to another target mask superior to the seed mask [Gunalan et al., 2017], while avoiding the ipsilateral thalamus, globus pallidus, putamen, substantia nigra, red nucleus, CSF, DBS lead, and contralateral cerebral hemisphere. This process resulted in 13,219 streamlines, from which we randomly subsampled 1,000 to represent the IC. The corticofugal streamlines of the HDP were constructed by randomly subsampling another 1,000 samples from the IC population. Then for each axon of the HDP, we constructed a collateral that branched from a node of Ranvier along the corticofugal axon and terminated within the STN [Kang and Lowery, 2014; Gunalan et al., 2017].

The streamlines of the CbTT were generated from a seed mask within the contralateral superior cerebellar peduncle (with 2,000 seeds per voxel) (Figure S1). Streamlines decussated, then passed through a waypoint mask between the red nucleus and subthalamic nucleus, and terminated within the VLpv thalamic nucleus (Figure S1) [Gallay et al., 2008], while avoiding the ipsilateral globus pallidus, substantia nigra, subthalamic nucleus, ventral lateral anterior (VLa) thalamic nucleus, ventral posterior lateral (VPL) thalamic nucleus, CSF, DBS lead, and contralateral cerebral hemisphere. Additionally, we excluded streamlines that traveled superior to the VLpv thalamic nucleus. Applying these constraints resulted in 1,662 streamlines, from which we randomly subsampled 1,000 for creation of our CbTT. We then extended these CbTT streamlines up into the VLpv, using a weighting of the average their trajectory, so they did not simply terminate at the ventral border of the thalamus.

2.1.4. Volume conductor

The volume conductor of the head consisted of three domains (Figure 2). Domain 1 consisted of encapsulation tissue delineated by the internal boundary representing the implanted Medtronic model 3389 lead and the outer surface of a 0.5 mm thick uniform layer surrounding the lead. Domain 2 consisted of brain tissue delineated by the outer boundaries of the encapsulation tissue and the surface of the brain. Domain 3 was delineated by the outer boundaries of the brain and the scalp.

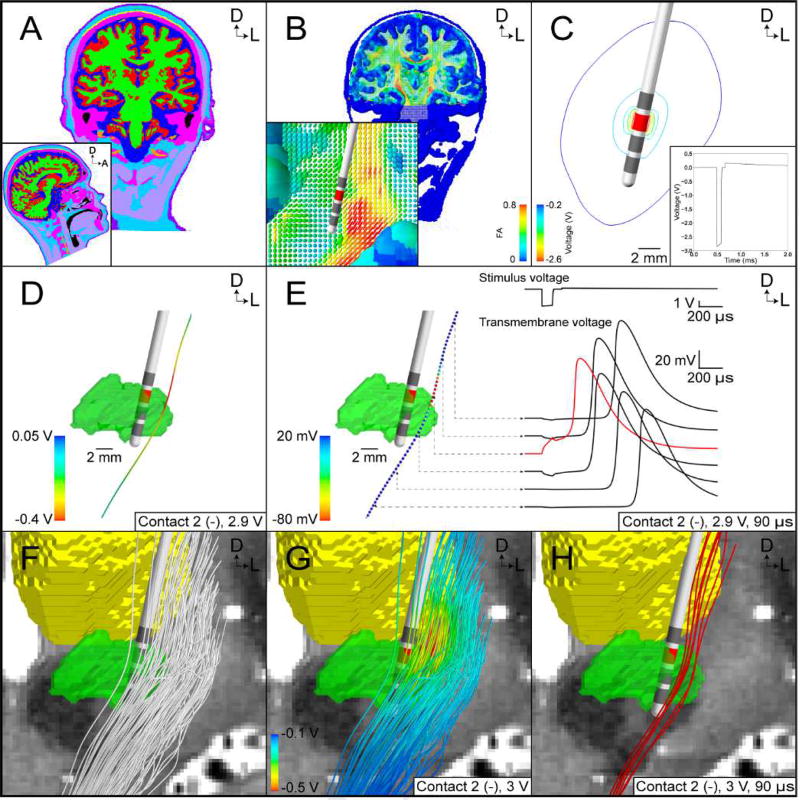
Figure 2.

FC PAM of subthalamic DBS. (A) Tissue-type segmentation (grey matter – red, white matter – green, cerebrospinal fluid – dark blue, muscle – light purple, tendon – yellow, bone – pink, fat – light blue, skin – dark purple, intervertebral disks – not visible, blood – orange, air – black). (B) Conductivity tensors colored according to their fractional anisotropy (FA). (C) Isolines of the potential distribution generated by the Medtronic model 3389 lead (active contact – red). Inset. Stimulus waveform at the electrode-tissue interface. (D) Extracellular potentials interpolated along a tractography-generated streamline. (E) Multi-compartment cable model of an axon is stimulated with a suprathreshold stimulus from D. (Right) Stimulus waveform and transmembrane voltage response at select nodes of Ranvier (red line - node of action potential initiation). (F) Subsample of 100 axons representing the internal capsule fibers of passage. (G) Potential distribution used to stimulate the axon models. (H) Red axons generated action potentials in response to the stimulus.

We constructed a conductivity tensor field for the entire head volume in the patient’s T1W space. Each voxel was categorized into 1 of 11 different types of tissues (Figure 2A), each with its own corresponding effective conductivity [Gunalan et al., 2017]. Within the brain volume, FSL’s dtifit tool was used to fit a single tensor to the signal in each voxel of the patient’s DW image, and the diffusion tensors (Ds) in DW space were warped to T1W space. Anisotropic conductivity tensors used in the patient model were a scaled version of D. We used the load preservation approach to generate impedance values that agreed with expected impedances measured in subthalamic DBS [Howell and McIntyre, 2016]. Because D was only used within the boundaries of the patient’s brain (i.e. domain 2), conductivity tensors within the brain were modeled as anisotropic, whereas the conductivity tensors outside the brain (i.e. in domain 3) were modeled as isotropic.

We used COMSOL (version 5.1) to construct tetrahedral meshes for the head model. The mesh was refined with an especially high nodal density within a 30-mm cubic region surrounding the tip of the modeled DBS lead. Elements within domain 1, the encapsulation tissue, were assigned an isotropic conductivity of 0.07 S/m, which falls within the range of previously reported values [Grill and Mortimer, 1994] and was chosen so that the load of the modeled head matched that measured from the patient by the Medtronic programming device [Gunalan et al., 2017]. Elements in domains 2 and 3, the brain and non-brain domains, respectively, were assigned conductivity tensors based on their proximity to the nearest neighbor in the tensor field defined by the structured rectangular grid in the patient’s T1W space. The complete head model consisted of 1,429,416 total tetrahedral elements and 6,524,354 nodes in the finite element mesh.

For stimulation configurations where the implantable stimulator was intended to be the return electrode (i.e. monopolar configurations), we defined Dirichlet boundary conditions of 1 V at the active contact(s), and 0 V at the neck. Inactive contacts were treated as ideal conductors and modeled using Robin boundary conditions that specified two conditions, per contact: all potentials within the contact were equal in value, and the net current flow through the surface of the contact was 0 A. Neumann boundary conditions of 0 A/mm² were used to model the electrode shaft and scalp surface (minus the neck) as perfect insulators. In stimulation configurations where the return and source were both electrode contacts (i.e. bipolar configurations), the base of the neck was insulated.

The potential field in the volume conductor at the onset of the stimulus was calculated by using the finite element method (FEM) to solve numerically Laplace’s equation for conductive media:

$$\nabla ·(\sum ·\nabla \mathrm{\Phi })=0$$ (1)

, where Σ is the tensor conductivity field. The variation of the potentials over time was approximated by multiplying Equation 1 with the time-varying voltage drop across the tissue in an equivalent circuit model of the implanted DBS system [Gunalan et al., 2017]. Although this approximation ignores the dispersion of time constants generated by nonuniform current densities [Howell et al., 2014], it is an accurate approximation at the frequencies considered in DBS [Howell and McIntyre, 2016].

2.1.5. Cable model of axons

Multi-compartment cable models of axons were constructed and solved in the NEURON simulation environment (version 7.3). We started with the MRG axon model [McIntyre et al., 2002] and modified some of the geometrical parameters to better reflect central nervous system axons [Howell and McIntyre, 2016]. We defined the diameter of the hyperdirect collateral as a fraction (1/3.1) of the diameter of the corticofugal axon [Hongo et al., 1987; Struijk et al., 1992; Grill et al., 2008]. We used the streamlines generated from tractography (Section 2.1.3) to define the axonal trajectories in the volume conductor. We interpolated the extracellular potentials at the coordinates of the centers of the compartments in the cable models and used the extracellular mechanism in NEURON to stimulate the modeled axons [McNeal, 1976; Gunalan et al., 2017] (Figure 2). For a given electrode configuration and stimulus pulse width, we used a binary search algorithm to determine the threshold stimulus amplitude for action potential generation to within 0.01 V. An axon was deemed activated when it responded “one-to-one” with the stimulus frequency. The combination of the electric field from the volume conductor and axonal responses from the multi-compartment cable models represent the results of the FC PAM (Figure 2).

2.2. DF PAM

Simulating the nonlinear response of axons in an FC PAM is a time-consuming process. Therefore, incentives exist for estimating the axonal response using predictive algorithms. Charge flow throughout an axon is modeled with the cable equation, where the driving force (DF) approximates the effects of the extracellular potentials on the neural membrane [McNeal, 1976]. Warman et al. [1992] demonstrated that a weighted version of the DF could be used to calculate the steady-state response of a passive cable in response to an extracellular stimulus, and that passive response could be used to estimate the threshold for activation in the corresponding nonlinear axon model. However, it is not possible to determine a priori the critical steady-state response that corresponds to the threshold for activation in the nonlinear axon model. Therefore, DF-based predictors are capable of reducing computation time and achieving relatively high accuracy in most situations, but require extensive parameterization steps [Moffitt et al., 2004]. In this study, we elected to analyze the most recent iteration of a DF-based predictor [Peterson et al., 2011], which we refer to as DF-Peterson.

2.2.1. DF-Peterson

Peterson et al. [2011] estimated stimulation thresholds based on two metrics: the maximum magnitude of the stimulus potentials (Φ_e) across the axon and the weighted sum of Δ²Φ_e across the nodes of Ranvier (NoRs), which they refer to as a modified driving force (MDF),

$$\mathit{\text{MDF}}=\sum _{i=-n}^n{w}_i(\mathit{\text{PW}},D){\Delta }^2{\Phi }_{e,i}$$ (2)

$${\Delta }^2{\Phi }_{e,i}={\Phi }_{e,i-1}-2{\Phi }_{e,i}+{\Phi }_{e,i+1}$$ (3)

, where i is a relative index denoting the NoR where Δ²Φ_e is maximal, w_i is a weighting term at the i^th adjacent NoR for a given stimulus pulse width (PW) and axon diameter (D), and n is the number of adjacent nodes. Peterson et al. [2011] ignored n > 10 because these weights were negligible compared to the more proximal nodes. The calculation of the weights is summarized in the Section A of the Supplementary Text.

Development of the DF-Peterson algorithm can be summarized in two phases: In the first phase, vectors of artificial applied potentials were constructed without the use of a volume conductor. They began by defining values for Φ_e,0 and Δ²Φ_e,0, which, by construction, were located at the middle NoR of the axons modeled by Peterson et al. [2011]. Assuming Φ_e,−1 = Φ_e,+1, (3) was used to define Φ_e,−1 and Φ_e,+1. The remaining nodal potentials were then set to decay so that the first derivatives were zero at the ends of the axons, and a fitted spline was used to define the potentials at all internodal compartments. This process was repeated, constructing vectors of artificial applied potentials for various different combinations of Φ_e,0 and Δ²Φ_e,0, and (2) was used to calculate an MDF for each vector of potentials.

In the second phase, simulations were conducted in NEURON to determine which vectors of potentials from the previous phase evoked action potentials in the modeled axon [McIntyre et al., 2002]. The threshold MDF was defined as the smallest MDF for a given Φ_e,0 whose corresponding potentials directly activated the axon. The threshold MDFs for all values of Φ_e,0 at a given PW and D were summarized in a lookup table, and phases 1 and 2 were repeated for various combinations of PW and D. PWs ranged from 20 µs to 10 ms, and Ds ranged from 4 µm to 20 µm. We refer to the threshold Φ_e,0 and threshold MDF as Φ_e,0,th and MDF_th, respectively.

Peterson et al. [2011] provide the data for implementing their predictor in Tables S1 and S3 of their supplement. We calculated weights at their unspecified combinations of D and PW using bilinear interpolation, and nearest neighbor extrapolation was used to estimate MDF_th at Φ_e,0,th > 500 mV (Section B of Supplementary Text). We also used a fitted spline to approximate the continuous relationship between Φ_e,0,th and MDF_th. Stimulation thresholds at a given D and PW were calculated as follows (Figure 3). First, for a given axon, we sampled Φ_e at the NoRs generated with the patient-specific volume conductor (Figure 3A/B), and then we determined where Δ²Φ_e was maximal; this NoR, which could be any node along the length of the axon, was designated as i = 0. The potential at this NoR was defined as Φ_e,0,unit, and we used (2) to calculate the corresponding MDF_unit, where “unit” designates that values were calculated at an applied voltage of 1 V. Then, Φ_e,0 and MDF were calculated by multiplying Φ_e,0,unit and MDF_unit by a scalar, respectively. The stimulation threshold voltage was the smallest scalar multiple that when applied to Φ_e,0,unit generated an Φ_e,0 whose corresponding MDF was ≥ MDF_th (Figure 3C/D).

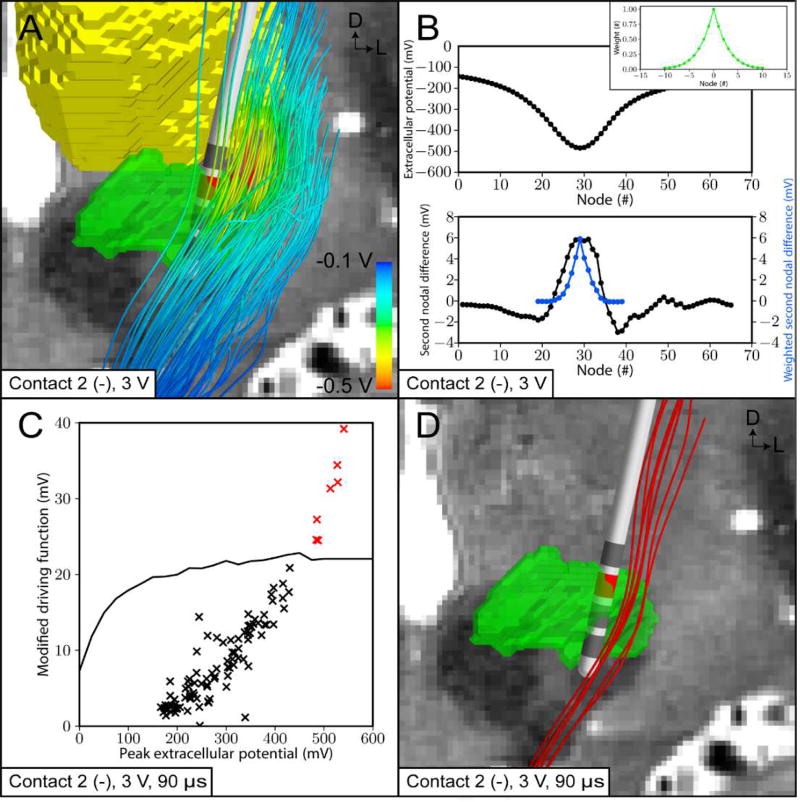
Figure 3.

DF PAM of subthalamic DBS. (A) Extracellular potentials (Φ_e) calculated from the patient-specific volume conductor (3 V, contact 2 [−]) were interpolated along 100 internal capsule fibers of passage. (B) (Top) Φ_e at the nodes of Ranvier along an example axon. (Bottom) Second differences of Φ_e (black line) and weighted second differences of Φ_e (blue line). (Inset) Corresponding weights for weighted second difference calculation (green line). (C) Peterson et al. [2011] threshold modified driving force (MDF_th) values as a function of the maximum extracellular potential (Φ_e,0) (black line). Patient-specific axons with a MDF that lie above the threshold curve are classified as active (red cross). (D) Red axons are categorized as activated by the stimulus.

For the HDP, we calculated the thresholds in a piecewise manner. We calculated the MDF_unit along the main body of the corticofugal axon separately from the MDF_unit along the collateral projecting to the STN. We then used the larger of the two MDF_unit to calculate thresholds as described above.

2.3. VTA PAMs

Another way to simplify DBS modeling is to use a predictor to estimate the nonlinear relationship between the parameters of stimulation and the spatial extent over which axons are activated. The typical approach is to use an ellipsoidal volume, commonly referred to as a volume of tissue activated (VTA) [Butson and McIntyre, 2006]. VTA PAMs are derived from highly simplified FC models, where a DBS lead is placed in an isotropic volume conductor and used to estimate the extent of activation of straight axons oriented perpendicular to the electrode shaft (Figure 4A). Simulations are conducted to assess which axons are directly activated for various stimulation settings and circumscribing ellipsoids are used to approximate the region of activation. This section describes three common implementations of VTA PAMs (Figure 4). We defined the stimulation threshold for direct activation of an axon as the minimum voltage amplitude needed to generate a VTA that intersects the respective streamline for a given axon diameter, stimulus pulse width, and electrode configuration (Figure 4C).

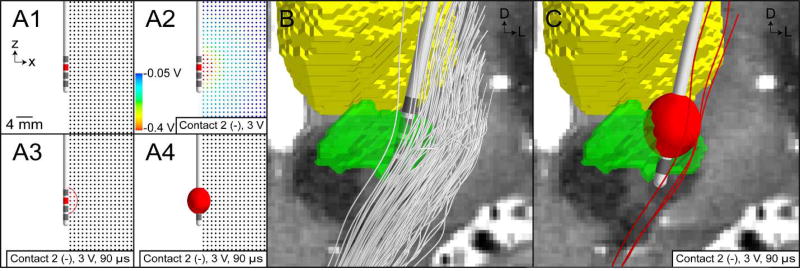
Figure 4.

VTA PAM for subthalamic DBS. (A) Illustrative example of training a VTA algorithm with an axisymmetric model of DBS. (A1) Multi-compartment cable models of straight axons perpendicular to the electrode are modeled. (A2) The potential distribution from a volume conductor model with isotropic and homogeneous conductivities is used to stimulate the model axons. (A3) Those axons that are activated by stimulation are shown as red. A circumscribing ellipse is then used to characterize the spatial extent of activation. (A4) The ellipse is then extruded about the electrode shaft to create an ellipsoid volume. (B) Trajectories of internal capsule fibers of passage are generated using probabilistic tractography. (C) VTA mapped to the patient-specific location of the DBS electrode, and the trajectories of axons that intersect the VTA are categorized as active (red streamlines).

2.3.1. VTA-Chaturvedi

Chaturvedi et al. [2013] used a series of ellipsoids to approximate the planar regions of activation, and then used an artificial neural network (ANN) to predict the relationship between a set of input parameters (described below), and the center and radii of the ellipsoids, which were the output of the ANN. We refer to this VTA PAM as VTA-Chaturvedi. This predictor represents the latest advancement of the original concepts developed by Butson and McIntyre [2006] and is capable of predicting the VTA for multipolar electrode configurations and multiple axon diameters.

Given an electrode configuration, an electrode/access resistance (R_a), a stimulus amplitude ≤ 10 V, a PW between 60 µs and 450 µs, and axon diameter of 2 µm, 5.7 µm, or 10 µm; we generated an ellipsoid or set of ellipsoids based on the radii and center coordinates output from the ANN. The VTAs were then used to estimate which axons in the IC, HDP, and CbTT pathways were activated by quantifying the intersection of individual streamlines with the VTA (Figure 4). The VTA-Chaturvedi predictor is currently employed by the StimVision software tool [Noecker et al., 2017].

2.3.2. VTA-Madler

Madler and Coenen [2012] began with digital reconstructions of ellipsoidal VTAs originally calculated by Butson et al. [2006], and the lateral radius of each ellipsoid, which is the radius transverse to the electrode shaft’s axis, was used to define a corresponding spherical VTA. Next, they used a fitted second-order bivariate polynomial to approximate the relationship between the applied voltage, the nominal dependent variable, and two nominal independent variables, the radius of the spherical VTA and R_a. Coefficients that altered the output of the predictor by < 1% were dropped, thereby allowing the radius of the spherical VTA to be expressed as a closed-form function of the applied voltage and R_a. We refer to this bivariate quadratic predictor as VTA-Madler.

VTA-Madler can be used for a range of R_a, namely between 741 Ω and 1244 Ω, but the data used to fit the predictor only reflects one combination of PW and D; more specifically, PW = 90 µs and D = 5.7 µm. Therefore, this predictor is very limited compared to the other more flexible predictors. The VTA-Madler predictor is currently employed by the DBSproc software tool [Lauro et al., 2016].

2.3.3. VTA-Astrom

Astrom et al. [2015] constructed VTAs based on the magnitude of the electric field (E_T). For a given combination of PW and D, E_T was calculated at the location in the grid where the furthest perpendicular axon was activated, and this process was repeated (at a given PW and D) across a number of stimulation amplitudes. The effective nominal threshold, or E_T,th, was the median threshold E_T across all the stimulus amplitudes. The VTA, then, was the minimum ellipsoidal volume circumscribing the volume delineated in the bulk tissue where E were ≥ E_T,th. We refer to this predictor as VTA-Astrom.

Astrom et al. [2015] provide a table summarizing E_T,th for PWs between 30 µs and 120 µs and Ds between 2 µm and 7.5 µm. Because only values for E_T,th were provided, we constructed the simplified axisymmetric volume conductor model used in their work. The conductivity of the bulk tissue and scar were set to 0.2 S/m and 0.1 S/m, respectively, which yielded an R_a that matched their reported value of 1 kΩ. We then changed the encapsulation layer conductivity from 0.1 S/m to 0.0625 S/m, yielding an R_a of 1.37 kΩ, that matched the R_a in our patient-specific model, and we used the axisymmetric model to calculate the VTAs described above. For combinations of PW and D that were not provided in the tables, we estimated E_T,th by using a fitted bivariate decaying rational function to interpolate and extrapolate values (Figure S2). The concept of E_T,th-based VTAs are currently employed by the Lead-DBS software tool [Horn et al., 2017].

One important note is that VTA-Astrom is based on a myelinated single-cable axon model whose ion channels and geometry are different than that of the double-cable model used in the FC PAM. The results of the former better match the latter when their axon diameters are 3.5 µm and 5.7 µm, respectively [Astrom et al., 2015]. To match better VTA-Astrom with the FC PAM, we reduced the axon diameter by a factor of 0.6140 (i.e., 3.5/5.7) when analyzing a subset of the axonal responses with VTA-Astrom (Figure S6).

Of the three VTA PAMs considered in this work, only VTA-Astrom can be paired with a de novo volume conductor electric field to estimate a patient-specific VTA. Therefore, we also used the magnitude of the electric field from the patient-specific volume conductor model (Section 2.1.4) and thresholded it at the E_T,th of 0.142 V/mm (90 µs, 3.5 µm) [Astrom et al., 2015]. We called this model variant VTA-Astrom* and the resulting non-symmetric isosurfaces were used to calculate the stimulation thresholds for each axon as described above (Figure S6).

2.4. Analyses

Stimulation thresholds were calculated for all 1,000 axons in each pathway (IC, HDP, CbTT) using the most advanced methods currently available for patient-specific modeling of DBS (Section 2.1, Figure 2) [Gunalan et al., 2017]. We defined thresholds from the FC PAM as our gold standard and evaluated the ability of the simplified predictor functions to estimate the thresholds of each axon. We omitted those axons from our analyses that initiated action potentials from the distal nodes of Ranvier along the main body of the axon, as calculated with the FC PAM. This resulted in 933, 983, and 1,000 axons for the IC, HDP, and CbTT, respectively. We defined absolute error in the voltage stimulation threshold (V_th) as V_th,Predictor-V_th,FC. Axons with V_th,FC > 10 V or V_th,Predictor > 10 V were omitted from the stimulus threshold error calculations, as these stimulation amplitudes are not relevant to clinical DBS (Table S1).

Using the threshold amplitude calculations, we created recruitment curves at a 0.1 V step size. For a given pathway, each axon was randomly clustered into 100 populations of 1000 axons in a bootstrapping manner (with replacement), to quantify the effects of variability in the distribution of the axon trajectories. The average and standard deviation of the number of activated axons for the 100 populations in response to a stimulation amplitude are presented in the recruitment curves.

The vast majority of axons in the CNS have fiber diameters below 4 µm [Liewald et al., 2014; Aboitiz et al., 1992], except pyramidal axons whose diameters, although predominantly between 2 µm and 4 µm, can range up to 12 µm [Firmin et al., 2014]. Nonetheless, it is the largest diameter axons that dominate the response to electrical stimulation due to their low stimulation thresholds [McNeal, 1976]. Therefore, our analysis focuses on a fiber diameter of 5.7 µm and a pulse width of 90 µs. These parameters also represent the basis for most VTA algorithms currently in use. However, because a wide range of fiber diameters and pulse widths are relevant to clinical DBS, we incorporated a broader range of comparisons where possible.

3. Results

We constructed a detailed patient-specific model of subthalamic DBS and used it to evaluate a range of different methods for estimating axonal response. The FC PAM, which incorporated the latest advances in biophysical modeling of DBS [Gunalan et al., 2017], served as our gold standard, and we compared those results to the estimations of four predictive algorithms. Some of the predictors were unable to simulate all of the combinations of stimulus pulse widths, electrode configurations, and axon diameters investigated in this study. Therefore, an absence of results in the figures indicates that the corresponding predictor could not evaluate thresholds for that given set of parameters. The model parameters used to develop each predictor are summarized in Table 1.

Table 1.

Predictive algorithms and the parameters for which they were developed.

Predictor	Amplitude (V)	Pulse width (µs)	Frequency (Hz)	Configuration	Electrode impedance (Ω)	Axon diameter (µm)
DF-Peterson	N/Aa	20 – 10,000	Single pulseb	N/Aa	N/Aa	4.0 – 20.0
VTA-Chaturvedi	≤ 10	60, 90, 120, 150, 180, 210, 450	130c	Monopolar, Bipolar, Tripolar, Quadripolar	Low (0–749), Medium (750–1250), High (1251+)	2.0, 5.7, 7.3, 8.7, 10.0
VTA-Madler	1–10	90	130c	Monopolar	Low (741), Medium (1003), High (1244)	5.7
VTA-Astrom	1–5 (step 0.5)	30, 60, 90, 120	Single pulsec	Monopolar	1000	2.0 – 7.5 (step 0.5)d

^aPredictor was developed for a peak extracellular potential along an axon.

^bSquare, monophasic pulse.

^cRepresentative of the stimulation waveform output from a Medtronic pulse generator.

^dAxon diameter to internodal distance relationship is different than the other predictors.

3.1. Errors in stimulation thresholds

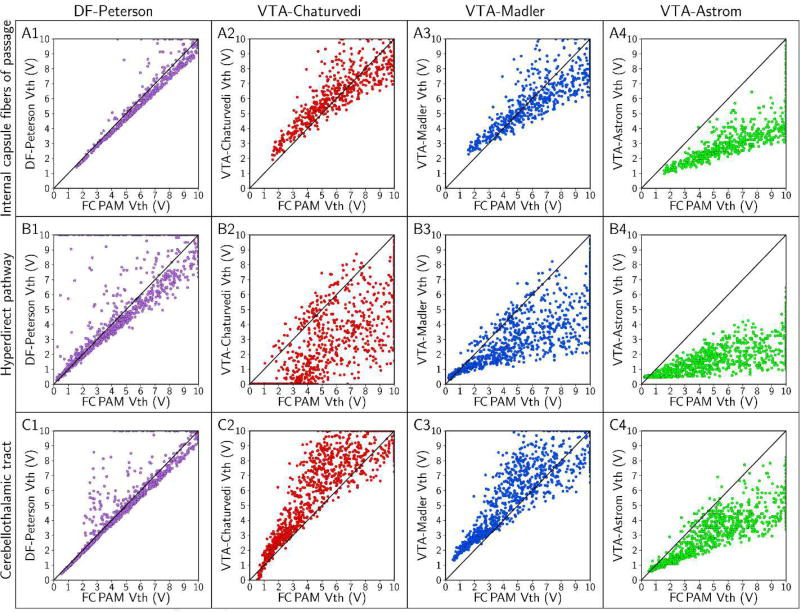
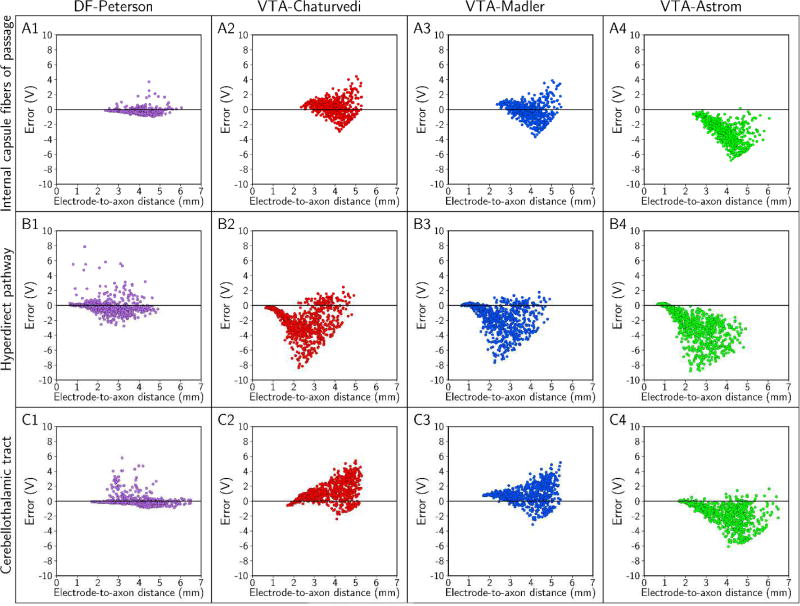
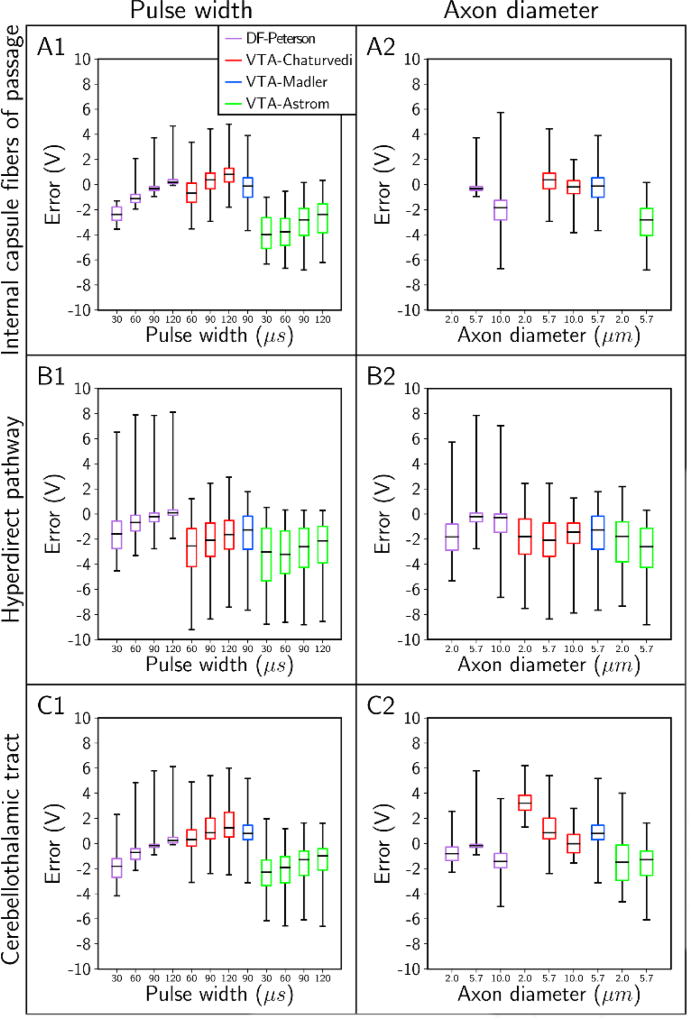
Absolute errors in the predicted stimulation thresholds had systematic trends. Errors generally increased with increasing stimulus amplitude, and errors in estimating the stimulation thresholds of the HDP were markedly greater than the errors in estimating thresholds of the IC and CbTT (Figures 5 and 6). However, the order of magnitude of the absolute errors was not the same across the different predictors (Figure 7). We observed the largest errors with VTA-Astrom, which had median errors between −1 V and −4 V. In addition, pairing VTA-Astrom with the electric field from the patient-specific volume conductor (VTA-Astrom*) did not improve its performance (Figure S6). The next most accurate predictors were VTA-Chaturvedi and VTA-Madler, with median errors of between −3 V and 3 V. DF-Peterson was the most accurate, with median errors of between −3 V and 1 V. No predictor was accurate enough to limit errors to within 1 V across all stimulus pulse widths, electrode configurations, and axon diameters tested (Figure 7).

Figure 5.

Axon-to-axon comparison of threshold stimulus amplitude (V_th) with FC, DF, and VTA PAMs. We used a stimulus pulse width of 90 µs and a monopolar cathodic electrode configuration (contact 2 [−] and case [+]) to stimulate axons with diameters of 5.7 µm. The rows denote results for the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract; and there is one column for each of the four predictors. In this plot, we set axons with V_th > 10 V as 10 V, so that all axons representing a pathway can be visualized in the field of view.

Figure 6.

Errors in the threshold stimulus amplitude as a function of the electrode-to-axon distance. Each column pertains to one predictor, and errors were calculated for the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. In this analysis, the stimulus pulse width was 90 µs; contact 2 was the cathode (−), the case was the anode (+), and the axon diameter was 5.7 µm.

Figure 7.

Absolute errors in the stimulation thresholds for a variety of stimulus pulse widths and axon diameters. We started with a stimulus pulse width of 90 µs, a monopolar electrode configuration of contact 2 (−) and case (+), and an axon diameter of 5.7 µm; and we varied each parameter individually. The absolute error in the stimulation threshold for each predictor is plotted for the different pulse widths (column 1), and axon diameters (column 2). Rows denote results for the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. Note: data was omitted when all stimulation thresholds were > 10 V.

Given that the DF and VTA PAMs were derived from relatively simple models of stimulation (Figures 3 and 4), we expected to find inherent biases in their results as described above. The biases in the VTA PAMs are likely due to disparities in the decay and shape of the extracellular potentials between the simple volume conductor model (Figure 4A2) and the highly detailed patient-specific volume conductor (Figure 2C), as well as the nonlinear trajectory of the axonal pathways (Section 4.1). In addition, the bias in VTA-Astrom to underestimate the stimulation thresholds is likely because of the simplified axon model used to generate this predictor (Figure S6) (Section 2.3.3).

The tendency for DF-Peterson to markedly overestimate the activation thresholds at smaller pulse widths and larger axon diameters could be explained by discrepancies between Δ²Φ_e in the training and test data sets. The artificial potentials used to stimulate axons in the work by Peterson et al. [2011] had Δ²Φ_e that were depolarizing to within five nodes of the node of excitation, whereas Δ²Φ_e in the anisotropic and heterogeneous volume conductor produced Δ²Φ_e that were sometimes largely hyperpolarizing much closer to the node of excitation (Figures S7 and S8). Thus, in cases where DF-Peterson performed poorly, the predicted MDF curves underestimated the true threshold MDF.

Despite DF-Peterson being developed from an even more simplified volume conductor than that of the VTA PAMs, it was more accurate overall. DF predictors are a 1-degree simplification from FC models, whereas VTA predictors are a 2-degree simplification. As such, DF predictors performed better because they are able to take advantage of both the patient-specific extracellular potentials and the actual axonal trajectories in their threshold predictions.

3.2. Errors in pathway recruitment

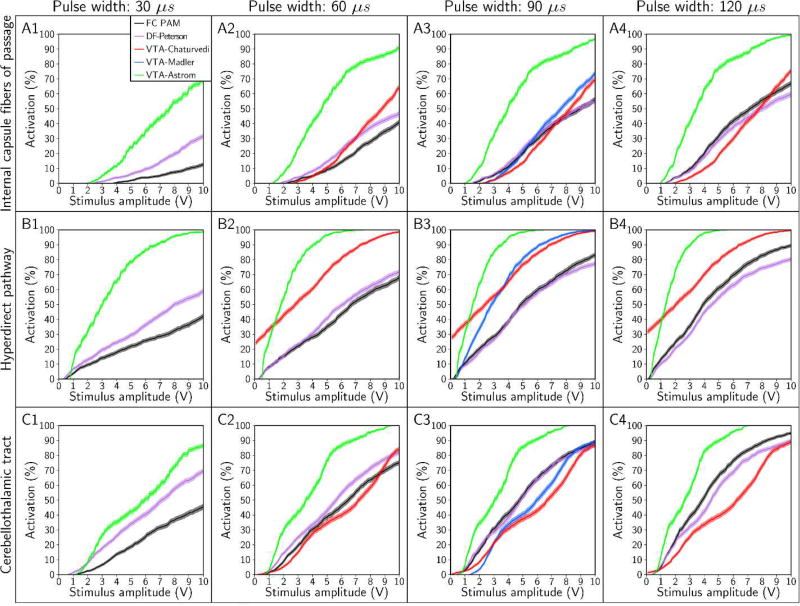
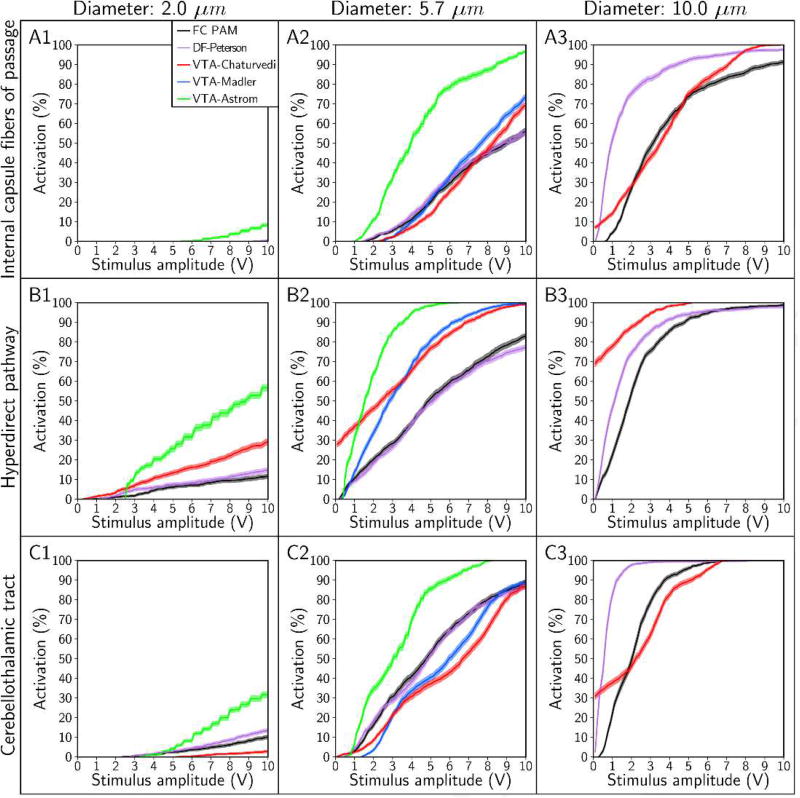
Although the four predictors were unable to estimate accurately the stimulation thresholds of individual axons, the predictors could still, in some cases, accurately predict the percent activation of a given pathway (Figures 8 and 9). We first designated a predictor as accurate if it estimated the percent activation of a given pathway to within 5% accuracy (on an absolute scale) at amplitudes of ≤ 10 V (Table 2). VTA-Astrom, because of its large bias in underestimating V_th, overestimated the percent activation of all pathways, regardless of the choice of stimulus pulse width (Figure 8) or axon diameter (Figure 9). VTA-Madler and VTA-Chaturvedi were also inaccurate for all of the cases tested. DF-Peterson, although more accurate than all the VTA PAMs, still only satisfied our criterion for accuracy in 4 of the 18 cases.

Figure 8.

Recruitment curves generated with the FC, DF, and VTA PAMs for stimulus pulse widths of 30 µs, 60 µs, 90 µs, and 120 µs. Recruitment curves were calculated for the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. The electrode configuration was contact 2 (−), case (+) and axon diameter was 5.7 µm.

Figure 9.

Recruitment curves generated with the FC, DF, and VTA PAMs for axon diameters of 2 µm, 5.7 µm, and 10 µm. Recruitment curves were calculated for the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. The stimulus pulse width was 90 µs and electrode configuration was contact 2 (−), case (+).

Table 2.

Maximum absolute difference in percent activation between each predictor and the FC PAM, for the range of 0–10 Volts. This analysis is based on the data presented in the recruitment curves in Figures 8 and 9. ‘-’ signifies that the predictor was not developed for the pulse width and axon diameter combination and ‘X’ signifies that the FC PAM predicted 0% activation for the entire range. Data is presented for the internal capsule fibers of passage (IC), hyperdirect pathway (HDP), and cerebellothalamic tract (CbTT).

Axon diameter (µm)	Pulse width (µs)	DF-Peterson			VTA-Chaturvedi			VTA-Madler			VTA-Astrom
		IC	HDP	CbTT	IC	HDP	CbTT	IC	HDP	CbTT	IC	HDP	CbTT
2.0	90	X	3.3	3.7	X	17.4	7.4	---------	---------	---------	X	45.4	22.2
5.7	30	19.2	17.9	24.1	---------	---------	---------	---------	---------	---------	56.6	63.9	42.5
5.7	60	10.0	7.7	9.5	23.5	38.7	9.0	---------	---------	---------	58.6	62.7	41.9
5.7	90	3.3	5.7	4.0	13.5	28.7	22.4	17.8	31.1	15.5	50.4	58.1	34.7
5.7	120	7.3	9.6	10.3	13.6	32.1	29.9	---------	---------	---------	46.4	55.4	30.7
10.0	90	53.6	25.9	60.7	11.3	69.1	32.8	---------	---------	---------	---------	---------	---------

If we relaxed our criterion for accuracy to a maximum absolute error of 10%, we observed that DF-Peterson could satisfy 11 of the 18 cases, VTA-Chaturvedi could satisfy 2 of the 18 cases, and VTA-Astrom remained inaccurate in all cases. DF-Peterson was the only PAM accurate enough to capture the monotonic trends of the recruitment curves in most cases. However, given that clinical/behavioral effects are typically noted at pathway activation levels beginning at ~10% [Chaturvedi et al., 2010; Gunalan et al., 2017], it is unclear if a 10% error tolerance is acceptable for clinical DBS research analyses.

4. Discussion

The goal of this study was to evaluate the relative accuracy of different methodologies for estimating axonal pathway activation in clinical DBS. We found that algorithms derived from simplified FC models have substantial limitations in their predictive capabilities, especially VTA-based predictors which are commonly used in clinical DBS research. Despite matching model parameters, VTA PAMs had activation thresholds errors on the order of volts, which translates to mis-estimates of the extent of activation on the order of millimeters. Errors of this magnitude will likely impact correlations attempting to link VTA models with structural connectome results. Nonetheless, there exists a great scientific and clinical need to characterize the axonal pathways directly modulated by DBS, as well as their anatomical connections. Therefore, future connectomic DBS studies should require far greater attention to the technical details of the stimulation modeling strategy being used, as well as appropriate selection of a method that has the quantitative accuracy necessary for the desired analysis to be performed.

4.1. Pathway-activation models

Patient-specific DBS models utilizing anatomically and electrically accurate volume conductor models and multi-compartment cable neuron models represent the most scientifically advanced tools for simulating the effects of DBS [Gunalan et al., 2017]. However, these FC PAMs are so technically demanding to implement that their use in clinical research studies is greatly limited. They require massive processing power, as well as extensive proficiency in neuroimaging, electromagnetics, and numerical methods. Possibly the limitations of FC PAMs could be overcome via centralized computational resources and cloud-based dissemination strategies (e.g. CranialCloud [D’Haese et al., 2015]). However, the current alternative is to use predictors derived from simplified DBS models, which impose various assumptions to speed up the simulations and reduce the complexity of implementation. DF PAMs represent a 1-degree simplification from FC PAMs, whereas VTA PAMs are a 2-degree simplification. Therefore, it is not surprising that the DF PAMs performed better than the VTA PAMs in our analyses (Figure 5, S3, S4, S5). While DF PAMs are exceptionally faster than FC PAMs, they still require constructing a volume conductor model, making them only moderately easier to implement than a FC PAM and thereby not widely used. On the other hand, VTA PAMs can be reduced to a simple ellipsoid overlaid onto the patient imaging data, making them widely used in clinical DBS research.

The ease of implementing VTA PAMs facilitates their use in DBS software tools designed to enable patient-specific analyses [Horn and Kuhn, 2015; Lauro et al., 2016; Noecker et al., 2017]. However, the simplifying assumptions and methodology used to create VTA PAMs can dramatically affect the subsequent predictions (Figure 5). VTA-based methods are the product of two major simplifications. First, VTAs are derived from volume conductor models with a homogenous and isotropic tissue medium (Figure 4). Second, with a VTA-based method, the axonal trajectories are assumed to be perfectly straight and perpendicular to the electrode shaft (Figure 4A). These two simplifications impart symmetry in the model that generates a smooth and continuous “strength-distance” relationship (Figure S3). However, more realistic DBS models generate substantial scatter in stimulation thresholds as a function of electrode-to-axon distance [Chaturvedi et al., 2010]. As a result, the corresponding fit of the VTA PAM to pathway recruitment is primarily dictated by how well it approximates the mean of the thresholds as a function of distance (Figure S3). In addition, VTA PAMs tend to do better simulating the response of relatively straight pathways, but have more difficulty when the pathway trajectory is tortuous or branching (Figures S3, S4, S5).

In general, we found that VTA PAMs performed relatively poorly when placed into a patients-pecific context. However, if an appropriate method (i.e. VTA-Chaturvedi) is being used to estimate activation of an appropriate pathway (i.e. IC) at typical stimulation parameter settings (i.e. 60 µs, <5 V), it can perform very well (i.e. 1.9% error) (Table S2). Nonetheless, those particular instances are somewhat limited, and our results reinforce the need to apply PAMs with care when using simplified algorithms or software tools that shield users from the technical details of the underlying model.

Unfortunately, simplified PAMs have not been used with care in the recent clinical DBS literature. They have been extended far beyond their design capabilities to perform analyses that are likely unsound. One glaring example is the use of activation volume tractography (AVT) (Figure 10). AVT defines an activation volume around a DBS electrode contact, uses the voxels contained within that volume as seeds for tractography, and then attempts to define connectivity between the VTA and different brain regions. However, this method, especially when applied in a grey matter region, actually violates numerous assumptions inherent to VTA-based methods [Butson and McIntyre, 2006]. In addition, blindly relying on tractography from a seed region to define connectivity is known to generate a great deal of false positive/negative results [Behrens et al., 2007; Morris et al., 2008; Thomas et al., 2014].

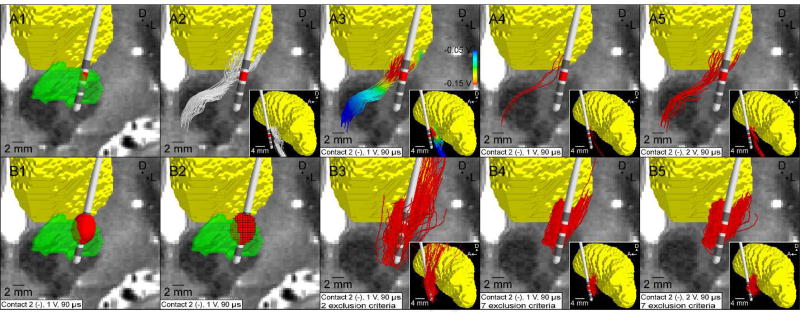
Figure 10.

Activation volume tractography (AVT) of the cerebellothalamic tract. (A) FC PAM. (A1) T2-weighted image with overlaid DBS electrode (subthalamic nucleus - green, thalamus - yellow). (A2) Subsample of 100 streamlines representing the cerebellothalamic tract. (A3) Potentials from the volume conductor model interpolated along the streamlines. (A4) Axons activated by a 1 V stimulus (2.9 ± 0.5%). (A5) Axons activated by a 2 V stimulus (16.3 ± 1.1%). (B) AVT. For clarity, only 10% of the streamlines generated are displayed. (B1) VTA-Chaturvedi predictor for a 1 V stimulus. (B2) Voxelized VTA. (B3) Streamlines originating from the VTA shown in B2, terminating in the VLpv thalamus, and avoiding CSF and the contralateral cerebral hemisphere (16.0%). (B4) The same as B3 except subject to the same exclusion constraints used in the FC PAM (13.7%) (Section 2.1.3). (B5) The same as B4 except for a 2 V VTA (15.1%). The same model parameters were used for both the FC PAM and AVT: pulse width = 90 µs; pulse frequency = 130 Hz; electrode configuration = contact 2 (−) and case (+); axon diameter = 5.7 µm.

As an example of AVT and its shortcomings, we used AVT (with VTA-Chaturvedi) to evaluate thalamic connectivity and compared it to the corresponding FC PAM estimation of CbTT activation (Figure 10 and Section C in Supplementary Text). Not only did the percent activation predicted by the two algorithms not align, but the spatial trajectory of the resulting pathways were markedly different. Discrepancies with AVT were exacerbated even further when only excluding tracts that intersected the CSF or passed into the contralateral cerebral hemisphere, which is consistent with the tractography exclusion criteria typically used in clinical DBS research using AVT (Figure 10B3). For example, aberrant streamlines from AVT passed above the thalamus before terminating in the VLpv (Figure 10B3). Therefore, we have found that minimizing the potential for erroneous results requires first the construction of the pathways of interest with appropriate anatomical constraints, and then the application of the stimulation predictor to estimate theoretical activation of the predefined pathways.

One application where AVT may be slightly more accurate is when it is used explicitly within large white matter pathways. Examples include DBS clinical research applications focused on neuropsychiatric targets such as the anterior limb of internal capsule or the subcallosal cingulate white matter. For example, AVT from the subcallosal cingulate white matter generates predictions [Riva-Posse et al., 2017] that are qualitatively consistent with predictions from a patient-specific FC PAM [Lujan et al., 2013]. Nonetheless, AVT is likely not generalizable to all white matter regions, and we recommend that AVT methodology should not be used in future DBS research.

4.2. Limitations

The major limitation of this study is that an experimental ground truth for model comparison does not currently exist. The patient-specific FC PAM that we used as our gold standard is the most detailed and advanced computational model of DBS ever created. However, while aspects of that model, such as the volume conductor and cable model, can be validated and constrained by experimental data [McIntyre et al., 2002; Miocinovic et al., 2009], the output predictions of pathway activation cannot be measured with current experimental techniques. It is possible to perform indirect measurements that can be used to evaluate model predictions, with electromyography (EMG) measurements corresponding to IC activation being the most easily attainable [Chaturvedi et al., 2010]. As such, recent clinical interest in using EMG to better characterize activation of the IC during subthalamic DBS [e.g. Mahlknecht et al., 2017; Bally et al., 2017], or cortically evoked potentials from HDP antidromic activation [e.g. Walker et al., 2012], represent excellent opportunities for the DBS modeling and clinical communities to converge on analyses that would be mutually beneficial.

This study analyzed four different predictors, which only represents a subset of the different VTA and DF PAMs that are currently available. We chose VTA-Chaturvedi because it is more accurate and generalizable than previous VTA methods [Chaturvedi et al., 2013]. VTA-Madler and VTA-Astrom were chosen because they are being utilized by a broader community of researchers studying DBS [e.g. Vanegas-Arroyave et al., 2016; Horn et al., 2017]. And, we chose DF-Peterson because it is the most accurate and generalizable DF-based method currently available [Peterson et al., 2011]. Another relevant consideration is that certain VTA predictors can be adapted to use patient-specific voltage distribution data to define the activation volume [Butson et al., 2007]. This could theoretically improve their accuracy by transitioning the method from a 2-degree to a 1-degree simplification. However, our attempts to employ such a strategy with VTA-Astrom did not improve its performance (Figure S6). Therefore, our analyses, although not exhaustive, likely provides a best-case assessment of the current predictive algorithms versus patient-specific FC PAMs.

Finally, a group of important limitations associated with modeling DBS are the substantial errors that can arise from image co-registration [Klein et al., 2009], imprecise localization of the DBS electrode in a post-operative CT [Hemm et al., 2009], general ambiguity of tractography [Thomas et al., 2014], and uncertainty in various parameters used to define the patient-specific volume conductor model [Miocinovic et al., 2009; Howell and McIntyre, 2016]. However, by using the same underlying imaging data and model parameters for all of our simulations, we were able to hold these general errors constant and focus on quantifying the errors that come about from using a predictive algorithm in place of a full patient-specific FC PAM. Nonetheless, it should be noted that these general errors do come into play when connectomic DBS analyses are performed across a population of subjects, and compound when attempting to map population results into an atlas space.

4.3. Future directions

Patient-specific DWI data suffers from a lack of spatial resolution that brings into question the anatomical accuracy of tractographic reconstructions of axonal pathways. As the field of connectomic DBS modeling evolves, polarized light imaging (PLI) may provide a better overall foundation for the creation of human axonal pathway models [Reckfort et al., 2015]. Although PLI requires post-mortem tissue, the micron-resolution vector maps can provide exceptional detail for the creation of a human PLI-based pathway atlas. Such an atlas could then be coregistered to a patient’s MRI for use in connectomic DBS modeling. The main negative of this approach would be the assumption that the fitted PLI atlas would be a better approximation of the axonal pathways than DWI-based reconstructions derived from the patient’s own imaging data. However, we suspect that the anatomical realism of the PLI atlas would be superior to the false negative/positive limitations of tractography.

Connectomic DBS models hold promise for augmenting the interpretation of brain network modulation induced by stimulation. However, PAMs only provide estimates of the brain network connections that are being activated. Those activated connections then impose excitatory and/or inhibitory synaptic influences on the larger brain network which remain difficult to understand [McIntyre and Anderson, 2016]. In turn, analyzing the network dynamics induced by DBS requires a different kind of model system that is designed to simulate the oscillatory activity of interconnected groups of neurons [Rubin and Terman, 2004; Hauptmann and Tass, 2007]. PAM results should represent the stimulation inputs to DBS network models, specifically driving activity in the various pathways at representative percentages [Hahn and McIntyre, 2010] and conduction delays [Esfahani et al., 2016]. We propose that integration of pathway activation results with dynamical network analysis has great potential to accelerate the clinical optimization of novel stimulation paradigms [Tass et al., 2012].

5. Conclusions

Predictive algorithms that estimate the neural response to DBS do simplify the process of patient-specific pathway-activation modeling, but those simplifications come at the cost of a substantial decline in predictive accuracy. When parameters such as stimulus pulse width, electrode configuration, and axon diameter are matched, VTA-based methods offer a coarse estimate of the extent of activation but are subject to errors on the order of millimeters. Thus, current versions of these algorithms are likely not suitable for defining correlations between clinical metrics and stimulation of specific axonal pathways. While that same caveat probably applies to currently available DF-based methods, their general framework, with some additional customization for DBS studies, does hold promise for accurately estimating the percent activation of individual axonal pathways within a patient-specific context. Therefore, future connectomic DBS studies looking to strike a balance between model tractability and accuracy should transition away from VTA-based analyses and focus on developing and using DF-based tools.