Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Aug 1.
Published in final edited form as: Magn Reson Med. 2017 Dec 28;80(2):474–479. doi: 10.1002/mrm.27044

Simultaneous editing of GABA and glutathione at 7T using semi-LASER localization

Muhammad G Saleh 1,2, Mark Mikkelsen 1,2, Georg Oeltzschner 1,2, Kimberly L Chan 1,2,3, Adam Berrington 1,2, Peter B Barker 1,2, Richard A E Edden 1,2,*
PMCID: PMC5910225  NIHMSID: NIHMS930901  PMID: 29285783

Abstract

Purpose

To demonstrate simultaneous editing of the two most commonly edited and overlapping signals, γ-aminobutyric acid (GABA) and glutathione (GSH), with Hadamard encoding and reconstruction of MEGA-edited spectroscopy (HERMES) using sLASER localization at 7T.

Methods

Density matrix simulations of HERMES at 7T were carried out and compared to phantom experiments. Additional phantom experiments were performed to characterize the TE-dependent modulation of GABA- and GSH-edited HERMES spectra at TE of 80–160 ms. In vivo experiments were performed in ten healthy volunteers, comparing HERMES (11 min) to sequentially acquired MEGA-sLASER detection of GABA and GSH (2 × 11 min).

Results

Simulations of HERMES show GABA- and GSH-edited spectra with negligible levels of crosstalk, and give modest agreement with phantom spectra. The TE series of GABA- and GSH-edited HERMES spectra modulate as a result of T2 relaxation and coupling evolution, with GABA showing a stronger TE-dependence. In vivo HERMES experiments show well-edited GABA and GSH signals. Measured concentrations are not statistically different between HERMES and MEGA-sLASER for GABA (1. 051 ± 0.254 i.u. and 1.053 ± 0.248 i.u, P > 0.985) or GSH (0.300 ± 0.091 i.u. and 0.302 ± 0.093 i.u, P > 0.940).

Conclusion

Simulated, phantom and in vivo measurements of HERMES show excellent segregation of GABA- and GSH-edited signals, and excellent agreement with separately acquired MEGA-sLASER data. HERMES allows two-fold acceleration of editing while maintaining spectral quality compared to sequentially acquired MEGA-sLASER measurements.

Keywords: HERMES, semi-LASER, GABA, GSH, 7T, editing

Introduction

Proton magnetic resonance spectroscopy (1H-MRS) is a valuable tool for investigating a broad range of neurological disorders and diseases (1). In vivo measurements of lower-concentration metabolites are challenging due to low signal-to-noise ratios (SNR) and overlap with signals from more concentrated metabolites, such as N-acetylaspartate (NAA), creatine (Cr) and choline (Cho). Edited MRS can overcome these challenges, particularly for detection of the inhibitory neurotransmitter γ-aminobutyric acid (GABA) and the antioxidant glutathione (GSH). Both metabolites are of interest in several neurological disorders, including amyotrophic lateral sclerosis (2,3), Parkinson’s disease (4,5) and schizophrenia (6,7).

Both GABA and GSH are most commonly detected at a magnetic field strength (B0) of 3–4T (8–10) using a J-difference editing technique (11). J-difference editing at higher field strengths has two major advantages, despite the challenges of shorter T2 relaxation times: higher intrinsic SNR due to increased equilibrium polarization (12) and increased editing pulse selectivity for a given finite pulse duration due to increased spectral dispersion.

A major drawback of ultra-high-field MR is transmit radiofrequency field (B1) inhomogeneity, resulting in losses of signal (13,14) and poorer spatial localization. Moreover, the attainable peak value of B1 does not scale with B0 due to hardware and specific absorption rate (SAR) constraints, limiting the bandwidth of conventional amplitude-modulated slice-selective RF pulses and increasing the chemical shift displacement error (CSDE), further impacting localization, exacerbating spatially dependent scalar-coupling evolution, and reducing editing efficiency (15,16). These challenges can be mitigated by using frequency-modulated adiabatic RF pulses that are less sensitive to B1 inhomogeneity, have larger bandwidth relative to conventional RF pulses and produce uniform and sharp slice profiles (17,18). Thus, single-voxel spectroscopy at 7T is widely performed using semi-localization by adiabatic selective refocusing (sLASER, (14)) localization. Recent work has demonstrated spatially accurate and efficient editing at 7T by implementing MEGA editing pulses within sLASER localization to give the MEGA-sLASER sequence (19,20).

A significant drawback of MEGA-sLASER is that it usually selectively edits only one metabolite at a time. Since spectral editing is usually applied to lower-concentration compounds, such as GSH and GABA, relatively long acquisition times are necessary, limiting both the numbers of brain regions and metabolites that can be studied within the time constraints of an MR exam. Recently, the Hadamard Encoding and Reconstruction of MEGA-Edited Spectroscopy (HERMES) technique was implemented to edit more than one metabolite within a single MR exam (21–23) using PRESS localization (24) at 3T. Here, we demonstrate through simulations and phantom and in vivo experiments that HERMES can be used to simultaneously and separately edit GABA and GSH at 7T with sLASER localization.

Methods

Phantom and in vivo data were acquired on a Philips Achieva 7T scanner using a head coil with dual-channel transmit (with peak B1 = 15 μT) and 32-channel receive capabilities.

HERMES-sLASER of GABA and GSH

The HERMES-sLASER experiment, as shown in Figure 1, can be understood as two MEGA-sLASER experiments performed at the same time using an orthogonal editing scheme. HERMES of GABA and GSH consists of four sub-experiments (A, B, C and D), where editing pulses are applied to: both GABA and GSH simultaneously (A: ONGABA = 1.9 ppm, ONGSH = 4.56 ppm); GABA only (B: ONGABA, OFFGSH); GSH only (C: OFFGABA, ONGSH); or neither (D: OFFGABA, OFFGSH) (23). For sub-experiments B and C, a sinc-Gaussian editing pulse was used to invert a single frequency. For sub-experiment A, a dual-lobe cosine-sinc-Gaussian editing pulse was used, generated by multiplying sinc-Gaussian editing pulse by 2cos(πΔΩ(t−τp/2)), where ΔΩ is the frequency difference between 4.56 and 1.9 ppm (796 Hz at 7T) and τp is the editing pulse duration. Sub-experiment D does not require an editing pulse; thus, a single-lobe editing pulse was instead applied at 7.46 ppm.

Figure 1.

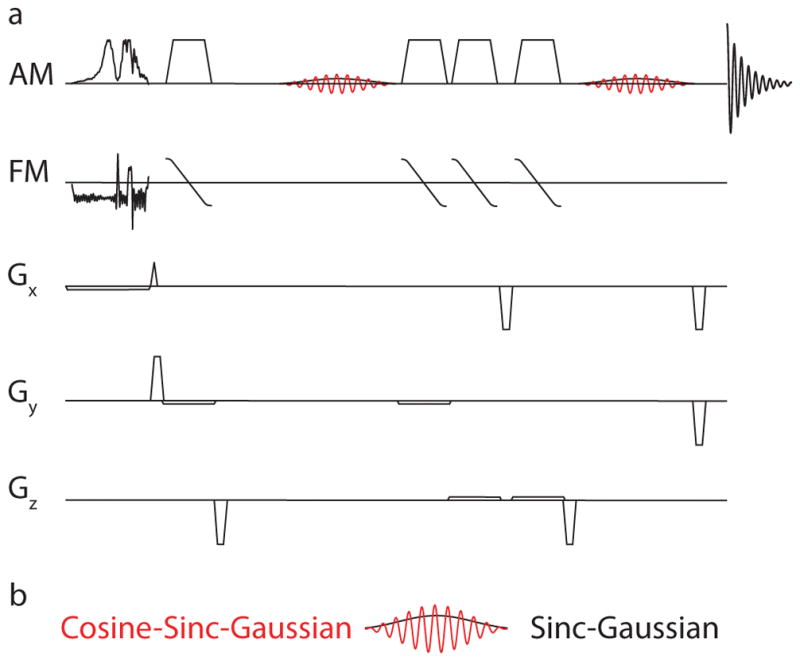
Figure 1

Open in a new tab

Pulse sequence diagram for HERMES using sLASER for localization. a) Excitation was performed using frequency-modulated pulse. Refocusing was performed, using two pairs of broadband adiabatic pulses (OIT pulses) with amplitude and frequency modulation (AM and FM). b) Editing is performed using dual-lobe (cosine-sinc-Gaussian) and single-lobe (sinc-Gaussian) editing pulses. Gx, Gy and Gz: Gradients in the x, y and z directions.

The Hadamard combination of sub-experiments A+B-C-D yields the GABA-edited spectrum. The Hadamard combination of sub-experiments A-B+C-D yields the GSH-edited spectrum. The duration and bandwidth of each editing lobe at FWHM of both the sinc-Gaussian and cosine-sinc-Gaussian editing pulses were 15 ms and 83 Hz, respectively. A broadband amplitude- and frequency-modulated excitation pulse (fremex05) (25) with a bandwidth of 4.73 kHz and a duration of 8.77 ms was used. Pairs of adiabatic 180° pulses (26) each with a sweep width of 5 kHz and a duration of 5.23 ms were used for refocusing.

Simulations

Density matrix simulations of the GSH-cysteine and GABA spin systems were performed using FID-A (27) at 7T for nominal voxel dimensions of 3×3 cm2. Both sLASER and HERMES-sLASER simulations were performed, assuming ideal excitation and shaped refocusing and editing pulses (bandwidths as above).

In order to validate the GSH spin system parameters and the simulation approach used, a TE series of (unedited) sLASER simulations was performed, using: 1. chemical shifts and coupling constants derived from (28), simulating a spatial location at the voxel center; 2. chemical shifts and coupling constants derived from (29) at the voxel center; 3. chemical shifts and coupling constants derived from (28) on a 19×19 two-dimensional spatial array, as in reference (13); and 4. chemical shifts and coupling constants derived from (29) on the same spatial array. Spatially resolved simulations were performed in the dimensions defined by the refocusing pulses spanning 3.2×3.2 cm2. The spectral pattern that is acquired experimentally is the sum over the entire voxel, and only spatially resolved simulations can capture the spatial inhomogeneity of coupling evolution. Simulations were performed at TEs ranging from 35 to 160 ms in 5-ms increments using the following parameters at each position within the array: vector size of 8192; spectral width of 5 kHz; simulated linewidth of 2 Hz; additional line broadening using a 3-Hz exponential filter. Transverse relaxation was simulated for T2 of 70 ms.

HERMES simulations were performed at the voxel center using spin parameters from (29) for GSH and (13) for GABA. The simulation parameters were the same as for the sLASER TE series, except only TE 80 ms was considered and no additional line broadening was performed.

Phantom experiments

Two phantoms were prepared at room temperature (25°C) with pH of 7.2 in phosphate-buffered solution containing 1.5 g/L NaN3: 20 mM GSH only and 20 mM GABA and 20 mM GSH. Unedited TE-dependence was investigated in the GSH-only phantom using a sLASER sequence with the following parameters: TR 3000 ms; TEs 35–160 ms in 5-ms increments; 5 kHz spectral width; 27 cm3 voxel; 16 averages per TE; and VAPOR water suppression. The phantom spectra were plotted point-by-point against the simulations (with T2 decay removed from both to consider all TEs equally), and Pearson correlation coefficients were calculated.

In the GABA+GSH phantom, the HERMES-sLASER experiment was performed with the same acquisition parameters for a TE of 80 ms. An additional set of HERMES scans was performed to investigate the TE-dependent behavior of GABA- and GSH-edited spectra for TEs ranging from 80 to 160 ms in 10-ms increments. Adiabatic pulses had 3-kHz sweep width and peak B1 of 13 μT.

In vivo experiments

Ten healthy adults (5 females, age: (mean ± SD) 30.0 ± 3.9 years) were scanned with approval of the local Institutional review board after giving informed consent to participate.

HERMES, GABA-edited MEGA-sLASER and GSH-edited MEGA-sLASER data were acquired in each participant from a single 27 cm3 voxel positioned in the midline parietal region. All in vivo experiments were conducted using the same acquisition parameters as for the phantom experiments: TE = 80 ms; 224 total averages, i.e., 56 averages for each sub-experiment in HERMES and 112 edit-ON and 112 edit-OFF averages for each (GABA, or GSH) MEGA-sLASER scan. The scan duration of each acquisition was about 11 min.

Post-processing

In vivo data were analyzed using Gannet (30), a MATLAB-based (The MathWorks, Natick, MA, USA) software package, modified from the original published version to incorporate support for 7T and HERMES multiplexed editing. Data were apodized using a 1-Hz exponential function. A multi-step frequency-and-phase correction (FPC) method was implemented to reduce subtraction artifacts in the final edited spectra. First, each dataset was segregated into the four sub-experiment sets for HERMES (A, B, C and D) and the two sub-experiment sets for MEGA-sLASER (ON and OFF). Within each sub-experiment set, frequency/phase offsets were estimated using spectral registration (31). Second, the distributions of the estimated frequency/phase offsets for each sub-experiment set were then modeled using a Cauchy probability density function, after which the center parameter of the fitted model was subtracted from the previously estimated frequency/phase offsets. Third, residual frequency offsets were corrected in the frequency domain by aligning the Cr peak maxima to 3.0 ppm. Finally, a residual zero-order phase correction was applied by fitting the phase of Cho and Cr signals in the sum spectrum with a model of two Lorentzian lineshapes. Subsequent to frequency alignment, additional apodization using 4-Hz exponential function was applied and the edited GABA and GSH peaks were then quantified. The GABA-edited signal was modeled with a Gaussian function with a non-linear baseline. The GSH-edited signal was modeled with four Gaussian functions with a linear baseline. GABA and GSH levels were quantified relative to the unsuppressed water signal from the same volume, assuming an MR-visible tissue water concentration of 35.75 mol/l and editing efficiencies of 0.5 for GABA and 0.36 for GSH. A paired, two-tailed t-test was calculated to determine statistical differences in GABA and GSH measurements from the two editing schemes.

Results

Simulated and phantom TE series

GSH density matrix simulations and phantom spectra are overlaid (Supporting Fig. S1). Simulations using the spin system parameters from (28) do not agree closely with phantom data, particularly at 45–65 ms, 90–110 ms and 135–160 ms. Simulations using the spin system parameters from (29) show somewhat better agreement, but with discrepancies remaining at TEs of 40–60 ms and 95–125 ms. Simulations using these spin system parameters over the entire voxel show improvements especially apparent at TEs of 60 ms and longer, however agreement is still not perfect.

In quantitative terms, the R2 of the correlation between phantom spectra (with T2 weighting removed) and the four simulations was 0.17 for the old spin system parameters for both the voxel center and the full voxel (Supporting Fig. S2). This improved to 0.36 with the new spin system parameters at the voxel center, and 0.6 for the full voxel.

Simulated and phantom HERMES experiments

Density matrix simulations and phantom experiments of GABA and GSH HERMES are shown in Figure 2, using the GSH-cysteine spin system parameters from (29). Simulated sub-experiments A–D show the intended pattern of modulation across the four sub-experiments. The Hadamard combinations of the simulated experiments result in GABA- and GSH-edited spectra with negligible levels of crosstalk.

Figure 2.

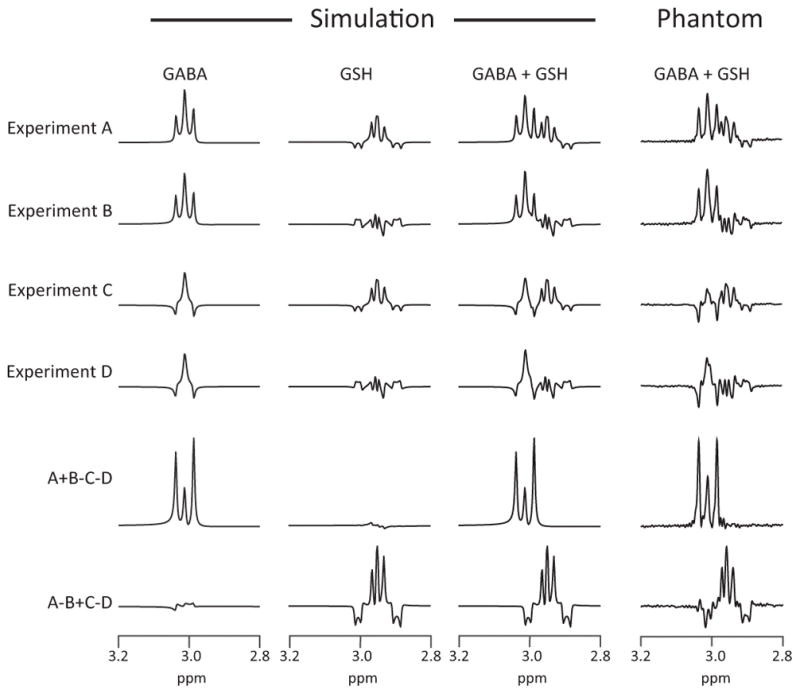
Figure 2

Open in a new tab

Simulated and phantom experiments of HERMES-sLASER of GABA and GSH. Phantoms contained both GABA and GSH. Sub-experiment A: ONGABA, ONGSH; sub-experiment B: ONGABA, OFFGSH; sub-experiment C: OFFGABA, ONGSH; sub-experiment D: OFFGABA, OFFGSH.

The TE-dependence of GABA- and GSH-edited HERMES-sLASER phantom spectra are shown in Figure 3. The intensity and multiplet pattern of edited signals change with TE as a result of T2 relaxation and coupling evolution. It is apparent that GABA editing is improved at shorter TEs, while the GSH signal is relatively similar between 80 and 140 ms (32). Shorter in vivo T2s would further bias TE-dependence toward short TEs.

Figure 3.

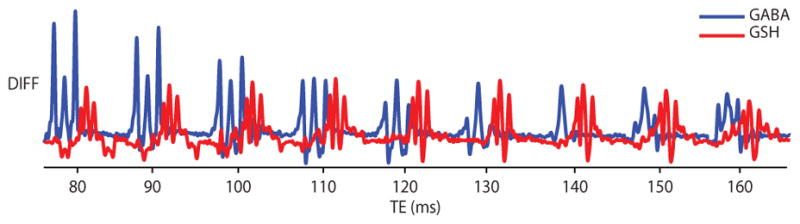
Figure 3

Open in a new tab

TE-dependent scalar coupling evolution using HERMES-sLASER from the phantom with both GABA (blue) and GSH (red) at TEs of 80–160 ms in 10-ms increments. At each TE, the multiplets are plotted from 2.85 to 3.05 ppm. DIFF: difference spectra.

HERMES and MEGA-sLASER spectra were successfully acquired in vivo in all ten volunteers (Figure 4). The HERMES editing scheme shows well-separated GSH and GABA signals in every volunteer. In terms of line shape, linewidth and amplitude, HERMES spectra are in agreement with sequentially acquired MEGA-sLASER spectra. The GABA concentrations in institutional units (i.u.) are 1.051 ± 0.254 and 1.053 ± 0.248 from HERMES and MEGA-sLASER, respectively. The GSH concentrations in i.u. are 0.300 ± 0.091 and 0.302 ± 0.093 from HERMES and MEGA-sLASER, respectively. The concentrations from the two editing schemes are not statistically different for both GABA (P = 0.985) and GSH (P = 0.940).

Figure 4.

Figure 4

Open in a new tab

In vivo GABA- and GSH-edited spectra acquired using HERMES (black) overlaid with sequentially acquired MEGA-sLASER spectra (red).

Discussion

Simultaneous editing of GABA and GSH is possible at ultra-high-field using sLASER localization. To our knowledge, this represents the first implementation of HERMES within the sLASER pulse sequence (an approach that would also be effective at 3T) and the first implementation of HERMES editing at 7T. HERMES halves the total effective acquisition time compared to currently available MEGA-sLASER editing of two metabolites sequentially.

Single-voxel localization at 3T is most commonly achieved by the PRESS pulse sequence. Moving from 3T to 7T, attainable peak B1 levels do not scale up with B0, leading to substantially increased CSDE. Peak achievable B1 levels are volunteer-dependent and B1 inhomogeneity is also substantially poorer, making B1 calibration more important and more challenging. For this reason, many 7T studies have relied on STEAM localization (33), which has higher pulse bandwidth and lower sensitivity to B1 calibration errors, in spite of the 50% SNR penalty of stimulated (compared to spin) echoes. The shorter minimum TEs of STEAM are important given the more rapid transverse relaxation seen at 7T (34). However, the advantages of sLASER at 7T are increasingly being recognized: full signal compared to STEAM; substantially reduced CSDE; and less B1 sensitivity compared to PRESS (14). The behavior of coupled spin systems in the STEAM sequence is complex and MEGA-STEAM has never been widely adopted, so for this study, HERMES editing was implemented within the sLASER sequence.

Simulation and phantom experiments of HERMES at 7T show excellent segregation of signals into GABA- and GSH-edited spectra, with excellent spectral quality and low levels of crosstalk. TE series of edited spectra demonstrate that GABA evolves significantly between TEs of 80–160 ms, while GSH demonstrates much less evolution. In GABA, it is a triplet-like coupling that is being edited (with maximal theoretical editing efficiency around 70 ms), while in GSH, it is a doublet (with maximal editing efficiency around 140 ms). The choice of an TE of 80 ms struck a balance between these two, with awareness of short in vivo T2s (< 100 ms (35)) and the fact that neither coupling nor transverse relaxation occur uninterrupted for the full TE in the sLASER sequence.

One particularly challenging aspect of this implementation was achieving agreement between simulations and phantom HERMES experiments for GSH. Simulations of unedited GSH disagree with the phantom experiments at several TEs using the widely available spin parameters from (28), but improve with modest differences when simulated using new spin system parameters (29). It is striking how much improvement is achieved with only minor changes to the parameters; the chemical shift difference between the germinal cysteine protons changes by 0.01 ppm and the couplings change by under 0.5 Hz. This issue is 7T-specific, as previous simulations of GSH at 3T were successful (23), because the chemical shift difference between the two spins of the detected signal is very close to the coupling between them, both ~14 Hz. At 7T, the GSH-cysteine multiplet is highly impacted by strong coupling, with coupling becoming weaker at greater separations and spins becoming increasingly equivalent at smaller separations. Although this GSH-7T clash is particularly harsh, it does underline the fact that there are limitations to the accuracy of published sets of spin system parameters. It should also be noted that chemical shifts are weakly temperature-dependent, and in the case of strongly coupled spin systems, this can impact the behavior of coupled multiplets. Since the phantom spectra were acquired at room (and not physiological) temperature, the spin system behavior may not match the expected in vivo behavior or tabulated values (36). Linear-combination modeling of short-TE spectra is increasingly performed with simulated, rather than experimentally acquired basis sets, and the ongoing refinement of spin system parameters is an important work.

J-difference editing is sensitive to B0 field drift caused by scanner instability and/or subject motion. Drift can cause editing pulses to be applied at the wrong frequency, reducing the efficacy of the technique. This problem of field drift can be mitigated by implementing prospective motion and B0 correction techniques during acquisition (37,38). Drift can also result in subtraction artifacts in the difference spectra, with Cr subtraction artifacts particularly impacting quantification of GABA and GSH. These residual signals can be substantially reduced using post-acquisition FPC strategies (31). The HERMES subspectra share fewer commonalities: GSHON scans impact the residual water signal, while GABAON scans impact the NAA signal, making most FPC strategies ineffective. In this study, subspectra were aligned using a new multi-step FPC technique, which resulted in well-edited spectra, although some residual Cho artifacts were still visible in some of the GSH-edited spectra. Further work to improve FPC post-processing is still ongoing.

We have performed the simulations using a 19x19 matrix covering an area only slightly larger than the voxel, corresponding to 17x17 simulations within the voxel itself, as in previous work (13). Higher spatial resolution might further improve agreement between simulations and phantom spectra (39). Another limitation of this study is that the peak B1 value (15 μT) was lower compared to previous studies (40). Hardware enhancements would allow increases in peak B1 and improvements in the performance of the adiabatic pulses. Further enhancements can be achieved by incorporating adiabatic pulses with increased bandwidth, such as frequency offset corrected inversion pulses, which have been shown to reduce CSDE and improve editing efficiency (41).

Conclusions

HERMES can simultaneously measure GABA and GSH at 7T using sLASER localization in half the scan time compared to sequentially acquired conventional MEGA-sLASER editing without any loss in spectral quality. HERMES allows excellent segregation of edited signals with negligible crosstalk.

Supplementary Material

Supp info

Supporting Figure S1: Comparison of simulated and phantom sLASER TE series of the GSH-cysteine spin system. Simulation (red) overlaid with phantom (blue) experiments for TEs ranging from 35 ms to 160 ms. The phantom experiments were performed on the GSH-only phantom. Simulations are weighted by an exponential T2 factor. ‘Old’ spin parameters are form (28), while ‘New’ spin parameters are from (29).

Supporting Figure S2: Point-by-point scatterplots of the phantom spectra against the four simulated spectra (T2 relaxation weighting removed).

Acknowledgments

This work was supported by NIH grants R01 EB023963 and P41EB015909.

References

  • 1.Bonavita S, Di Salle F, Tedeschi G. Proton MRS in neurological disorders. Eur J Radiol. 1999;30:125–131. doi: 10.1016/s0720-048x(99)00051-0. [DOI] [PubMed] [Google Scholar]
  • 2.Foerster B, Callaghan B, Petrou M, Edden R, Chenevert T, Feldman E. Decreased motor cortex γ-aminobutyric acid in amyotrophic lateral sclerosis. Neurology. 2012;78:1596–1600. doi: 10.1212/WNL.0b013e3182563b57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Weiduschat N, Mao X, Hupf J, Armstrong N, Kang G, Lange D, Mitsumoto H, Shungu D. Motor cortex glutathione deficit in ALS measured in vivo with the J-editing technique. Neuroscience letters. 2014;570:102–107. doi: 10.1016/j.neulet.2014.04.020. [DOI] [PubMed] [Google Scholar]
  • 4.Olanow C. An introduction to the free radical hypothesis in Parkinson’s disease. Ann Neurol. 1992;32:S2–S9. doi: 10.1002/ana.410320703. [DOI] [PubMed] [Google Scholar]
  • 5.Öz G, Terpstra M, Tkáč I, Aia P, Lowary J, Tuite PJ, Gruetter R. Proton MRS of the unilateral substantia nigra in the human brain at 4 tesla: detection of high GABA concentrations. Magn Reson Med. 2006;55:296–301. doi: 10.1002/mrm.20761. [DOI] [PubMed] [Google Scholar]
  • 6.Shetty AK, Bates A. Potential of GABA-ergic cell therapy for schizophrenia, neuropathic pain, and Alzheimer’s and Parkinson’s diseases. Brain Res. 2016;1638:74–87. doi: 10.1016/j.brainres.2015.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Shungu DC. N-acetylcysteine for the treatment of glutathione deficiency and oxidative stress in schizophrenia. Biol Psychiatry. 2012;71:937–938. doi: 10.1016/j.biopsych.2012.03.025. [DOI] [PubMed] [Google Scholar]
  • 8.Harris AD, Saleh MG, Edden RA. Edited 1H magnetic resonance spectroscopy in vivo: Methods and metabolites. Magn Reson Med. 2017;77:1377–1389. doi: 10.1002/mrm.26619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Mullins PG, McGonigle DJ, O’Gorman RL, Puts NA, Vidyasagar R, Evans CJ, Edden RA Cardiff Symposium on MRSoG. Current practice in the use of MEGA-PRESS spectroscopy for the detection of GABA. Neuroimage. 2014;86:43–52. doi: 10.1016/j.neuroimage.2012.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Terpstra M, Henry PG, Gruetter R. Measurement of reduced glutathione (GSH) in human brain using LCModel analysis of difference-edited spectra. Magn Reson Med. 2003;50:19–23. doi: 10.1002/mrm.10499. [DOI] [PubMed] [Google Scholar]
  • 11.Mescher M, Merkle H, Kirsch J, Garwood M, Gruetter R. Simultaneous in vivo spectral editing and water suppression. NMR Biomed. 1998;11:266–272. doi: 10.1002/(sici)1099-1492(199810)11:6<266::aid-nbm530>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
  • 12.Otazo R, Mueller B, Ugurbil K, Wald L, Posse S. Signal-to-noise ratio and spectral linewidth improvements between 1. 5 and 7 Tesla in proton echo-planar spectroscopic imaging. Magn Reson Med. 2006;56:1200–1210. doi: 10.1002/mrm.21067. [DOI] [PubMed] [Google Scholar]
  • 13.Near J, Evans CJ, Puts NA, Barker PB, Edden RA. J-difference editing of gamma-aminobutyric acid (GABA): simulated and experimental multiplet patterns. Magn Reson Med. 2013;70:1183–1191. doi: 10.1002/mrm.24572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Scheenen TW, Klomp DW, Wijnen JP, Heerschap A. Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magn Reson Med. 2008;59:1–6. doi: 10.1002/mrm.21302. [DOI] [PubMed] [Google Scholar]
  • 15.Edden RA, Barker PB. Spatial effects in the detection of γ-aminobutyric acid: Improved sensitivity at high fields using inner volume saturation. Magn Reson Med. 2007;58:1276–1282. doi: 10.1002/mrm.21383. [DOI] [PubMed] [Google Scholar]
  • 16.Mao J, Mareci T, Andrew E. Experimental study of optimal selective 180 radiofrequency pulses. Journal of Magnetic Resonance (1969) 1988;79:1–10. [Google Scholar]
  • 17.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
  • 18.Tannús A, Garwood M. Adiabatic pulses. NMR Biomed. 1997;10:423–434. doi: 10.1002/(sici)1099-1492(199712)10:8<423::aid-nbm488>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
  • 19.Andreychenko A, Boer VO, Arteaga de Castro CS, Luijten PR, Klomp DW. Efficient spectral editing at 7 T: GABA detection with MEGA-sLASER. Magn Reson Med. 2012;68:1018–1025. doi: 10.1002/mrm.24131. [DOI] [PubMed] [Google Scholar]
  • 20.Prinsen H, de Graaf RA, Mason GF, Pelletier D, Juchem C. Reproducibility measurement of glutathione, GABA, and glutamate: Towards in vivo neurochemical profiling of multiple sclerosis with MR spectroscopy at 7T. J Magn Reson Imaging. 2017;45:187–198. doi: 10.1002/jmri.25356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Chan KL, Puts NA, Schar M, Barker PB, Edden RA. HERMES: Hadamard encoding and reconstruction of MEGA-edited spectroscopy. Magn Reson Med. 2016;76:11–19. doi: 10.1002/mrm.26233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Chan KL, Saleh MG, Oeltzschner G, Barker PB, Edden RA. Simultaneous measurement of Aspartate, NAA, and NAAG using HERMES spectral editing at 3 Tesla. Neuroimage. 2017;155:587–593. doi: 10.1016/j.neuroimage.2017.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Saleh MG, Oeltzschner G, Chan KL, Puts NA, Mikkelsen M, Schär M, Harris AD, Edden RA. Simultaneous edited MRS of GABA and glutathione. Neuroimage. 2016;15:576–582. doi: 10.1016/j.neuroimage.2016.07.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Bottomley PA. Spatial localization in NMR spectroscopy in vivo. Proc Natl Acad Sci U S A. 1987;508:333–348. doi: 10.1111/j.1749-6632.1987.tb32915.x. [DOI] [PubMed] [Google Scholar]
  • 25.Henning A, Fuchs A, Murdoch JB, Boesiger P. Slice-selective FID acquisition, localized by outer volume suppression (FIDLOVS) for 1H-MRSI of the human brain at 7 T with minimal signal loss. NMR Biomed. 2009;22:683–696. doi: 10.1002/nbm.1366. [DOI] [PubMed] [Google Scholar]
  • 26.Rosenfeld D, Zur Y. A new adiabatic inversion pulse. Magn Reson Med. 1996;36:124–136. doi: 10.1002/mrm.1910360121. [DOI] [PubMed] [Google Scholar]
  • 27.Simpson R, Devenyi GA, Jezzard P, Hennessy TJ, Near J. Advanced processing and simulation of MRS data using the FID appliance (FID-A)—An open source, MATLAB-based toolkit. Magn Reson Med. 2017;77:23–33. doi: 10.1002/mrm.26091. [DOI] [PubMed] [Google Scholar]
  • 28.Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR Biomed. 2000;13:129–153. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
  • 29.Tkac I. Refinement of simulated basis set for LCModel analysis. Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 1624. [Google Scholar]
  • 30.Edden RA, Puts NA, Harris AD, Barker PB, Evans CJ. Gannet: A batch-processing tool for the quantitative analysis of gamma-aminobutyric acid–edited MR spectroscopy spectra. J Magn Reson Imaging. 2014;40:1445–1452. doi: 10.1002/jmri.24478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Near J, Edden R, Evans CJ, Paquin R, Harris A, Jezzard P. Frequency and phase drift correction of magnetic resonance spectroscopy data by spectral registration in the time domain. Magn Reson Med. 2015;73:44–50. doi: 10.1002/mrm.25094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Chan KL, Puts NA, Snoussi K, Harris AD, Barker PB, Edden RA. Echo time optimization for J-difference editing of glutathione at 3T. Magn Reson Med. 2016 doi: 10.1002/mrm.26122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Frahm J, Merboldt K-D, Hänicke W. Localized proton spectroscopy using stimulated echoes. Journal of Magnetic Resonance (1969) 1987;72:502–508. [Google Scholar]
  • 34.Moonen CT, Kienlin MV, Van Zijl P, Cohen J, Gillen J, Daly P, Wolf G. Comparison of single-shot localization methods (steam and press) for In vivo proton NMR spectroscopy. NMR Biomed. 1989;2:201–208. doi: 10.1002/nbm.1940020506. [DOI] [PubMed] [Google Scholar]
  • 35.Intrapiromkul J, Zhu H, Cheng Y, Barker PB, Edden RA. Determining the in vivo transverse relaxation time of GABA in the human brain at 7T. J Magn Reson Imaging. 2013;38:1224–1229. doi: 10.1002/jmri.23979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Wermter FC, Mitschke N, Bock C, Dreher W. Temperature dependence of 1H NMR chemical shifts and its influence on estimated metabolite concentrations. Magn Reson Mater Phy. 2017:1–12. doi: 10.1007/s10334-017-0642-z. [DOI] [PubMed] [Google Scholar]
  • 37.Edden RA, Oeltzschner G, Harris AD, Puts NA, Chan KL, Boer VO, Schär M, Barker PB. Prospective frequency correction for macromolecule-suppressed GABA editing at 3T. J Magn Reson Imaging. 2016;44:1474–1482. doi: 10.1002/jmri.25304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Saleh MG, Alhamud A, Near J, Kouwe AJ, Meintjes EM. Volumetric navigated MEGA-SPECIAL for real-time motion and shim corrected GABA editing. NMR Biomed. 2016;29:248–255. doi: 10.1002/nbm.3454. [DOI] [PubMed] [Google Scholar]
  • 39.Maudsley AA, Govindaraju V, Young K, Aygula ZK, Pattany PM, Soher BJ, Matson GB. Numerical simulation of PRESS localized MR spectroscopy. J Magn Reson. 2005;173:54–63. doi: 10.1016/j.jmr.2004.11.018. [DOI] [PubMed] [Google Scholar]
  • 40.Andronesi OC, Ramadan S, Ratai E-M, Jennings D, Mountford CE, Sorensen AG. Spectroscopic imaging with improved gradient modulated constant adiabaticity pulses on high-field clinical scanners. J Magn Reson. 2010;203:283–293. doi: 10.1016/j.jmr.2010.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Arteaga de Castro CS, Boer VO, Andreychenko A, Wijnen JP, van der Heide UA, Luijten PR, Klomp DW. Improved efficiency on editing MRS of lactate and gamma-aminobutyric acid by inclusion of frequency offset corrected inversion pulses at high fields. NMR Biomed. 2013;26:1213–1219. doi: 10.1002/nbm.2937. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp info

Supporting Figure S1: Comparison of simulated and phantom sLASER TE series of the GSH-cysteine spin system. Simulation (red) overlaid with phantom (blue) experiments for TEs ranging from 35 ms to 160 ms. The phantom experiments were performed on the GSH-only phantom. Simulations are weighted by an exponential T2 factor. ‘Old’ spin parameters are form (28), while ‘New’ spin parameters are from (29).

Supporting Figure S2: Point-by-point scatterplots of the phantom spectra against the four simulated spectra (T2 relaxation weighting removed).

NIHMS930901-supplement-Supp_info.docx (1.4MB, docx)

RESOURCES