Abstract
Purpose
To develop parallel imaging techniques that simultaneously exploit coil sensitivity encoding, image phase prior information, similarities across multiple images and complementary k-space sampling for highly accelerated data acquisition.
Methods
We introduce Joint Virtual Coil (JVC-) GRAPPA to jointly reconstruct data acquired with different contrast preparations, and show its application in 2D, 3D and Simultaneous Multi-Slice (SMS) acquisitions. We extend the joint parallel imaging concept to exploit limited support and smooth phase constraints through Joint (J-) LORAKS formulation. J-LORAKS allows joint parallel imaging from limited auto-calibration signal (ACS) region, as well as permitting partial Fourier sampling and calibrationless reconstruction.
Results
We demonstrate highly accelerated 2D bSSFP with phase-cycling, SMS multi-echo spin echo, 3D multi-echo MPRAGE and multi-echo GRE acquisitions in vivo. Compared to conventional GRAPPA, proposed joint acquisition/reconstruction techniques provide more than 2-fold reduction in reconstruction error.
Conclusion
JVC-GRAPPA takes advantage of additional spatial encoding from phase information and image similarity, and employs different sampling patterns across acquisitions. J-LORAKS achieves a more parsimonious low rank representation of local k-space by considering multiple images as additional coils. Both approaches provide dramatic improvement in artifact and noise mitigation over conventional single-contrast parallel imaging reconstruction.
Keywords: Parallel imaging, virtual coil, simultaneous multi-slice, partial Fourier, GRAPPA, LORAKS
INTRODUCTION
Magnetic Resonance (MR) data acquisition routinely involves image acquisition at multiple echoes or phase-cycles to obtain complementary information. Multi-echo acquisition finds important applications in T2 and T2* relaxation time mapping (1–4), water/fat imaging (5–8), and reduction of field inhomogeneity related distortion (9). Although enabling numerous applications, achieving whole-brain coverage with high-resolution multi-echo imaging is encoding intensive, leading to excessive scan times.
Another application where multiple images are acquired and combined is balanced steady state free precession (bSSFP). Despite being an SNR efficient sequence with unique T2/T1 contrast, bSSFP suffers from image banding artifacts due its sensitivity to B0 field inhomogeneity. To mitigate these artifacts, multiple images with different RF phase-cycling can be acquired (10,11). This scheme shifts the location of the banding artifacts in each acquisition, so that the phase-cycled images can be combined through e.g. maximum intensity projection (MIP) to eliminate the artifacts. However, collecting multiple phase-cycles increases the scan time and counteracts the inherent efficiency of bSSFP.
Faster acquisitions are possible using receiver encoding, e.g. with sensitivity encoding (12) or generalized auto-calibrating partially parallel acquisitions (GRAPPA) (13). While parallel imaging allows acceleration along one phase encoding direction in 2D acquisitions, undersampling can be flexibly distributed between two axes (phase encoding and partition/slice direction) in 3D (14,15) and SMS imaging (16–20) to achieve higher accelerations.
Parallel imaging can be combined with compressed sensing to exploit sparsity/low-rank properties (21–24), and can be augmented with the Virtual Coil (VC) concept to provide additional spatial encoding using image phase prior information (25–27). On the other hand, LORAKS has been introduced as a novel method that can harness image phase smoothness and limited spatial support, and relies on local low rank properties of k-space to estimate missing data (28). Its extension to parallel imaging also allows utilization of coil sensitivity encoding (29,30). Earlier applications of low rank prior in k- or image-space have also permitted calibrationless parallel imaging (28,29,31–34).
These approaches have been designed to utilize coil sensitivity encoding and prior information to reconstruct a single contrast, without exploiting potential similarities/differences across multiple images. Within the SENSE framework (12), joint reconstruction across echoes/contrasts can be performed by exploiting joint sparse (35–39) (in this context, we use “joint reconstruction” to refer to approaches that couple the reconstruction of multiple images of the same anatomy (37,40)). However, compared to regularized SENSE per single image (41,42), exploiting similarities at the regularization level was seen to provide a small improvement (43). Joint reconstruction at the receiver encoding level could serve as a better alternative to coupling the images at the regularization stage. Such approaches include k-t GRAPPA (44,45), joint reconstruction of multiple shots in echo-planar diffusion imaging (46,47), k-space interpolation across all echoes in a gradient and spin echo (GRASE) acquisition (48,49), or across multiple gradient echoes for temperature mapping (50). Moreover, transmit inhomogeneity at ultra-high field can be mitigated by acquiring multiple images with different excitation modes, which are then jointly reconstructed in the TIAMO approach (51).
Recent advances in multi-shot diffusion imaging also perform joint reconstruction (46,47). These techniques aim to reconstruct a single, high-resolution k-space by merging data from multiple acquisitions while avoiding motion artifacts. Liu et al. (52) made use of self-navigated trajectories to estimate motion-induced shot-to-shot phase variations. Inverse reconstruction (53) instead solves for the complex-valued diffusion images in each shot separately. The phase information of each shot is then used as additional coil sensitivity variation to jointly reconstruct a combined, real-valued diffusion image with data from all shots. Similarly, MUSE estimates the phase variation of each shot using regularization, then solves a general model incorporating data from all shots and the calculated phase information (54). GRAPPA-based realigned kernel techniques (46,47) embed these phase variations into GRAPPA kernels estimated from additional navigators, which are then used for jointly reconstructing multi-shot data. The goal of such Joint-GRAPPA DWI techniques is to reduce the sensitivity to mismatches between navigator and image echoes.
MUSSELS is a new approach for phase-calibration-free multi-shot DWI reconstruction (55). This considers the multi-shot images to have the same contrast, but allow for slowly varying phase across the shots. These constraints are modeled with an annihilating k-space filter (55–60), which is learned during the structured low-rank recovery of the missing data.
While multi-shot DW images have the same contrast except for phase discrepancies, we instead focus on joint reconstruction to treat a broader class of applications, where the acquisitions are made with multiple contrasts/echoes/cycles. Rather than improved combination of multiple shots, we are targeting higher acceleration rates. For this, we propose a general framework for joint reconstruction. We reformulate the joint reconstruction problem as an extension of parallel imaging, and employ existing components such as GRAPPA, LORAKS, and virtual coils as our building blocks. We also extend the scope, performance and application space of these techniques. In designing our joint parallel imaging approaches, our hypothesis was that joint reconstruction would allow us to accelerate multi-contrast acquisitions further than currently possible with conventional parallel imaging.
To this end, we introduce the Joint Virtual Coil (JVC) technique wherein multiple echoes/cycles are reconstructed jointly under the GRAPPA framework. This combines and extends k-t (44,45), realigned GRAPPA (46,47) and TIAMO (51) approaches with the VC concept (25,26) to permit highly accelerated 2D, 3D and SMS acquisitions. JVC-GRAPPA allows all channels from all image contrasts to contribute to the reconstruction of a particular channel, and employs VC to convert image phase information into additional spatial encoding. Data were undersampled with shifts in the k-space sampling pattern across echoes/cycles to provide complementary k-space coverage and improve reconstruction.
We further extend the joint parallel imaging concept to exploit limited support and smooth phase constraints through Joint (J-) LORAKS formulation. J-LORAKS achieves a more parsimonious low rank representation of local k-space by considering multi-contrast images as additional coils, and allows reconstruction from limited ACS region. J-LORAKS seamlessly incorporates partial Fourier sampling into joint parallel imaging and permits improved calibrationless parallel imaging through joint reconstruction.
Herein, we demonstrate our joint parallel imaging concept in 2D phase-cycled bSSFP, 3D ME-MPRAGE (9,61) multi-echo gradient-echo (ME-GRE), and SMS multi-echo spin-echo imaging. We have reported initial versions of this work as abstracts (62,63), where we have shown the application of joint GRAPPA and SPIRiT (21) in reconstructing phase-cycled bSSFP with 2D and SMS encoding. Herein, we have extended this initial version with the addition of VC concept, J-LORAKS formalism that admits arbitrary sampling patterns including partial Fourier and CAIPI (14), calibrationless reconstruction, and application to multi-echo acquisitions. We also note the elegant profile-encoding by Ilicak et al. that independently developed joint parallel imaging reconstruction for phase-cycled bSSFP (64,65), which was also extended to multi-echo acquisition in a recent abstract (66).
Accompanying Matlab code that reproduces our results is submitted as supplementary material and can also be downloaded from: http://bit.ly/2sY1FJT
METHODS
RECONSTRUCTION ALGORITHMS
GRAPPA, JVC-GRAPPA and J-LORAKS were implemented and compared for a number of imaging cases/applications. All experiments used 16 compressed channels with singular value decomposition (SVD) coil compression for faster reconstruction (67,68). ACS regions used for calibration were included in the final reconstruction for improved SNR and fidelity. Partial Fourier experiments made use of coil-by-coil projection onto convex sets (POCS) processing (69–71) following GRAPPA reconstruction. Experiments were performed on a workstation with 64 Intel Xeon CPU’s and 256 GB memory running Matlab 8.0 (Mathworks, Natick, MA). Details of various reconstructions are provided below.
GRAPPA and Slice GRAPPA
Kernel estimation for conventional parallel imaging reconstruction using GRAPPA (13) and Slice GRAPPA (16) was regularized with Tikhonov penalty, and kernel sizes and regularization parameters were selected to minimize root mean squared error (RMSE) relative to the fully sampled data. Slice GRAPPA made use of signal leakage constraint (72) to minimize crosstalk between reconstructed slices.
JVC-GRAPPA and JVC Slice GRAPPA
JVC-GRAPPA creates additional channels by treating data from other echoes/cycles as extra coils. In addition to stacking all contrasts in the coil axis, virtual coil concept is employed to further double the number of channels. Starting with Nc coils in each of the Ne echoes, we end up having 2 × Nc × Ne total number of channels for joint reconstruction. For example, using typical numbers Nc = 16 and Ne = 4, the number of coils reach 128, and the amount of kernels that need to be estimated escalates rapidly since this scales with the square of the channel count.
To address this, we follow (26) and perform an iterative procedure where an initial Joint-GRAPPA is performed without virtual coils. This way, the entire k-space of the interim reconstruction becomes available for calibration of JVC kernels. We limit the number of JVC iterations to 4, since the gain diminishes after the first couple of iterations (26). In addition to providing ample sample points for kernel estimation, such large calibration region is also better at capturing high-resolution image phase information into the kernels of the virtual coils, thus preventing structured aliasing artifacts (26). During reconstruction, two different Tikhonov regularization parameters were used for the initial Joint (λinit) and the latter JVC (λlatter) kernel calibrations to further optimize RMSE in the face of increasing calibration region.
To provide complementary frequency information, k-space sampling patterns of the individual echoes/cycles were shifted with respect to each other. Partial Fourier sampling was also explored in 2D, 3D and SMS acquisition settings. This, however, has prevented the use of VC concept because missing portion of virtual coil k-space due to partial Fourier would be otherwise used for reconstructing the actual coil k-space based on conjugate symmetry. As such, partial Fourier experiments made use of Joint (J-) GRAPPA only, without the aid of virtual coils. Similarly, all contrasts were constrained to use the same partial Fourier sampling direction in the J-GRAPPA reconstructions. To increase the amount of available k-space region for kernel calibration, J-GRAPPA also used an iterative scheme with 4 iterations. The initial step used the ACS data to train kernels and generate an interim reconstruction. The following iteration was then able to utilize the k-space of this interim data and re-train kernels with a larger calibration region. Again, two different Tikhonov regularization parameters could be used for the initial and latter iterations.
Both regularization parameters, kernel sizes and k-space staggering amounts were optimized to minimize RMSE in joint reconstruction.
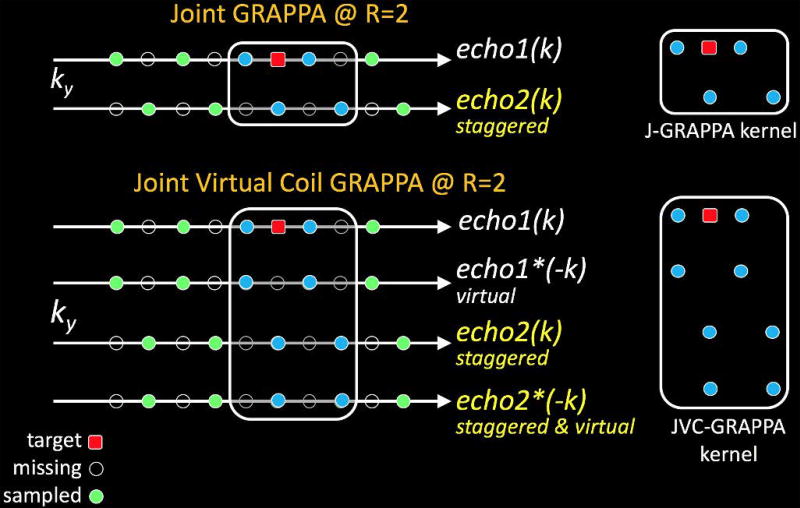
Fig1 provides a depiction of Joint and Joint Virtual Coil GRAPPA reconstructions, ignoring coil and readout axes for simplicity.
Fig1.
Joint GRAPPA fits kernels across contrasts and employs staggered k-space sampling to improve parallel imaging capability. Joint Virtual Coil GRAPPA further employs extra phase information provided by virtual coils to synthesize the target k-space signal.
Autocalibrating J-LORAKS
J-LORAKS also stacks data from all contrasts in the channel axis, and makes use of image phase information by creating virtual coils. It enforces local k-space neighborhoods, now extended across all echoes/cycles in the coil dimension, to have low rank during the reconstruction. There are two parameters associated with this constraint; the neighborhood size and the target rank of the local k-space matrices, which were optimized to reduce RMSE. Since J-LORAKS admits arbitrary sampling patterns, staggering across contrasts, 2D-CAIPI controlled aliasing as well as using different partial Fourier undersampling (e.g. +k or –k) for each image were explored. While many LORAKS publications solve non-convex matrix completion problems and are compatible with calibrationless data, substantial computational accelerations are possible when ACS data is present. Specifically, the autocalibrated LORAKS framework learns the nullspace properties of the k-space matrices prior to image reconstruction, and then uses the learned nullspace to formulate image reconstruction as a simple linear least squares problem that can be solved efficiently (73). Autocalibrating J-LORAKS reconstruction was performed using preconditioned conjugate gradient (pcg) with 50 iterations for all cases, apart from partial Fourier experiments which employed 100 iterations to ensure successful completion of k-space. Unlike GRAPPA, this also obviated the need for a sequential POCS reconstruction for partial Fourier sampling. For SMS image reconstruction, autocalibrated J-LORAKS was implemented using the SMS framework for LORAKS (74).
Calibrationless J-LORAKS
In calibrationless J-LORAKS, we assume that no ACS data are available, and thus solve the non-convex matrix completion problems described in (28,29) instead of the simpler least-squares problem associated with the autocalibrated case. To reduce reconstruction time, we first reconstruct a central subregion of the k-space data, and then use that as quasi-ACS data to enable autocalibrated J-LORAKS reconstruction of progressively larger k-space regions until the entire region has been covered. Since the quasi-ACS data may have imperfections, we then use the autocalibrated results as an initialization for the original non-convex optimization problem. The neighborhood size and the matrix rank were tuned to optimize RMSE. The number of maximum iterations were set to 1000.
DATA ACQUISITION AND COMPARISON CASES
The performances of various reconstruction algorithms were compared for 2D phase-cycled bSSFP, 3D ME-MPRAGE, SMS multi-echo spin-echo and calibrationless 3D ME-GRE imaging. Imaging parameters and comparison scenarios are described in detail below.
2D Phase-Cycled bSSFP
Data Acquisition
A single abdominal slice of a volunteer was imaged with bSSFP on a 3T Siemens Skyra system. Four phase-cycles (0, π/2, π, 3π/2) were collected during a single breath-hold to minimize motion. Parameters were: field of view (FOV) = 380×380 mm2, matrix size = 160×160, slice thickness = 5 mm, repetition time (TR) = 3.3 ms, echo time (TE) = 1.54 ms, flip angle = 37°, bandwidth = 822 Hz/pixel, using 34-channel chest/spine coil reception.
Image Reconstruction at 6-fold acceleration
Fully-sampled data were retrospectively undersampled by R=6×1-fold with a uniform sampling pattern. The three reconstruction methods used 20 lines of ACS data for kernel calibration.
For J-LORAKS, using an ACS size smaller than 20 lines was also explored, and the calibration region was reduced until J-LORAKS had similar RMSE performance as JVC-GRAPPA from 20 lines of calibration data. 50 pcg iterations were used in these reconstructions.
The sampling pattern was shifted by Δky = {0,1,2,3} samples between the four phase-cycles to provide complementary k-space coverage in the JVC-GRAPPA and J-LORAKS reconstructions.
For comparison, VC-GRAPPA without joint reconstruction was also performed. As an alternative to k-space based parallel imaging, Tikhonov-regularized SENSE reconstruction with ESPIRiT coil sensitivity estimation (75) was also explored. Both the regularization parameter and the threshold for sensitivity mask size were optimized to reduce RMSE.
Image Reconstruction at 7-fold acceleration
To explore even higher acceleration rates where conventional parallel imaging would break down, we further pushed the undersampling rate to R=7×1. We also tested the combination of uniform R=6×1-fold undersampling and partial Fourier acquisition, while keeping the number of sampled points the same as the R=7×1-fold case. For this, the required partial Fourier amount to achieve the same number of phase encoding lines, including the ACS data, was 7/8.
Combination of J-GRAPPA and POCS was used for reconstructing the data at R=6×1-fold undersampling with 7/8 partial Fourier. Following parallel imaging reconstruction, the missing portion of k-space due to partial Fourier sampling was completed with 100 iterations of POCS.
J-LORAKS with 7/8 partial sampling and R=6×1-fold uniform acceleration employed 100 pcg iterations to ensure successful completion of partially sampled k-space.
3D Multi-Echo MPRAGE
Data Acquisition
A volunteer was scanned with a Siemens 3T Skyra system using a fully-sampled ME-MPRAGE sequence at 1 mm3 resolution with FOV = 256×240×192 mm3. Salient parameters were: TR = 2530 ms, inversion time (TI) = 1100 ms, four echos were sampled at TE’s = {1.7, 3.6, 5.4, 7.3} ms, flip angle = 7°, and bandwidth = 651 Hz/pixel. A Siemens 32 channel head coil was used for reception.
Image Reconstruction at 12-fold acceleration
A single slice along the readout direction was selected out of the 3D dataset, and was retrospectively undersampled along the two phase encoding axes by R=4×3. Performance of the reconstruction methods was compared using an ACS region size of 24×24.
The sampling pattern was shifted by (Δky, Δkz) = (2,2) in the second, by (4,4) in the third, and by (6,6) samples in the fourth echo relative to the first TE to provide complementary k-space coverage. In addition to such complementary sampling, J-LORAKS also employed a different 2D-CAIPI sampling pattern (14) for each TE to better distribute aliasing. These were designed according to (Ry=4, ∆=0) for TE1, (Ry=4, ∆=1) for TE2, (Ry=4, ∆=2) for TE3 and (Ry=4, ∆=3) for TE4.
Iterative VC-GRAPPA without joint reconstruction and Tikhonov-regularized SENSE were also performed for each echo individually.
Image Reconstruction at 16-fold acceleration
To push the acceleration even further, we compared R=4×4 uniform sampling against R=4×3-fold acceleration combined with partial Fourier sampling in both phase encoding axes. The required partial sampling amount to keep the acquired number of sampled points the same was 6/8, distributed among ky and kz.
Partial Fourier cases were reconstructed using J-GRAPPA with POCS as well as J-LORAKS. J-GRAPPA was constrained to use the same partial Fourier sampling direction, whereas J-LORAKS used a different partial Fourier mask for each echo, rotated by 90° in each image, to provide complementary information.
SMS Multi-Echo TSE
Data Acquisition
A volunteer was scanned with a Siemens 3T Prisma system using a fully-sampled 2D multi-echo turbo spin echo (TSE) sequence. The imaging parameters were, FOV = 240×240, matrix size = 256×256, slice thickness = 4 mm, slice gap = 12.8 mm, number of slices = 10, number of echoes = 6, TR = 4 sec, TE’s = {12, 25, 50, 62, 87, 99} ms, echo train length (ETL) = 3, and bandwidth = 260 Hz/pixel. A Siemens 32 channel product head coil was used for reception.
Image Reconstruction at MB-10 acceleration
The separately encoded 10 slices were retrospectively collapsed to simulate an MB-10 acquisition. Slice unaliasing performance of conventional and JVC Slice GRAPPA as well as Joint SMS LORAKS were compared using 24 lines of ACS data.
Image Reconstruction at MB-10 acceleration with 6/8 partial Fourier
The same MB-10 experiment was performed using an additional 6/8 in-plane partial Fourier acceleration. Since VC concept is not applicable with partial Fourier due to asymmetric sampling, joint parallel imaging was performed with Joint Slice GRAPPA, without virtual coils. 100 iterations of POCS were utilized to estimate the missing data due to partial sampling following conventional and Joint Slice GRAPPA reconstruction.
Unlike the Joint Slice GRAPPA case, J-SMS-LORAKS still used virtual coils and did not require POCS to implement phase-constrained partial Fourier reconstruction.
Calibrationless: 3D Multi-Echo Gradient-Echo
Data Acquisition
A volunteer was scanned using Siemens 3T Skyra system to collect 3D ME-GRE data. The imaging parameters were, FOV = 240×240×192, matrix size = 160×160×128, TR = 23 ms, TE’s = {3, 7, 11, 15, 19} ms, flip angle = 15° and bandwidth = 496 Hz/pixel using a Siemens 32 channel head array.
Image Reconstruction at 4-fold acceleration
A single slice along the readout was taken out from 3D k-space data. Then, it was retrospectively undersampled with R=4 fold calibrationless Poisson random sampling pattern in 2D. The performance was compared between conventional single contrast LORAKS and the proposed multi-contrast J-LORAKS in terms of reconstruction of the individual echoes, as well as the R2* parameter maps. Echo images were coil combined with the RSoS method, and parameter mapping was performed by taking the logarithm of the echo images and fitting a line in each voxel. The negative slope of the fitted line yielded the R2* value in that voxel. To ensure realistic parameter maps, a non-negativity constraint on the R2* values was applied using the lsqnonneg function in Matlab.
RESULTS
A quick summary of reconstruction results is provided in Table 2, in which the RMSE performance of the methods under consideration are compared.
Table2.
Comparison of GRAPPA and the proposed joint reconstruction algorithms, where the results in Figs 2–7 are summarized.
|
|
||||
|---|---|---|---|---|
| RMSE% | ||||
|
|
||||
| (Slice) GRAPPA |
JVC (Slice) GRAPPA |
Joint (Slice) GRAPPA & POCS |
Joint (SMS) LORAKS |
|
| Phase-cycled bSSFP @ R=6 | 13.3% | 7.1% | – | 6.5% |
| Phase-cycled bSSFP @ R=7 | 19.0% | 10.7% | 9.2% | 8.0% |
|
| ||||
| ME-MPRAGE @ R=12 | 10.3% | 6.4% | – | 6.8% |
| ME-MPRAGE @ R=16 | 14.8% | 7.8% | 8.5% | 7.9% |
|
| ||||
| ME-TSE @ MB=10 | 5.1% | 3.6% | – | 3.3% |
| ME TSE @ MB=10 & PF=6/8 | 6.0% | – | 4.9% | 3.7% |
2D Phase-Cycled bSSFP
Image Reconstruction at 6-fold acceleration
Optimal parameters for conventional GRAPPA were, kernel size = 7×3 and regularization parameter λ = 10−8. Best RMSE in JVC-GRAPPA was obtained with 5×3 kernels and an initial Joint-GRAPPA reconstruction using regularization parameter λinit = 3×10−8, which was increased to λlatter = 3×10−6 in the subsequent JVC iterations. For J-LORAKS, best results were obtained with a k-space neighborhood radius of 2 voxels and rank constraint = 600.
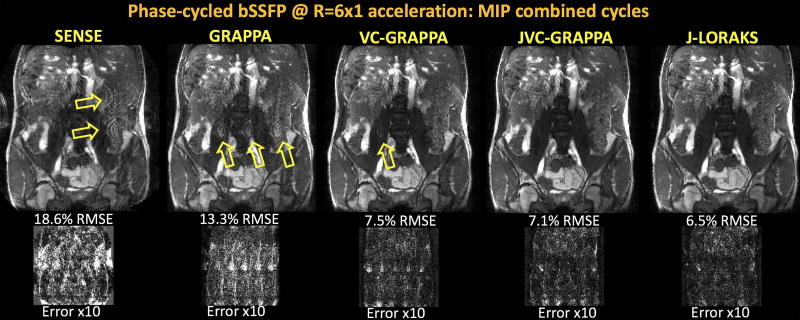
Fig2 compares the reconstruction results, where the phase-cycle images were combined with MIP. Conventional GRAPPA suffered from aliasing artifacts (yellow arrows) and noise amplification and yielded 13.3% RMSE. Image quality and noise suppression were improved with JVC-GRAPPA, and reconstruction error was reduced to 7.1%. J-LORAKS provided more than 2-fold RMSE improvement (6.5%) over conventional GRAPPA using the same calibration region size of 20 lines. Even with a more stringent calibration region of 16 lines, J-LORAKS had similar performance as JVC-GRAPPA that used 20 ACS lines, (7.1% RMSE, not shown). Fig2 provides further comparison against SENSE (18.6% RMSE) and VC-GRAPPA (7.5% RMSE) methods, which reconstructed each phase-cycle image separately.
Fig2.
Maximum intensity projection combination of phase-cycled bSSFP reconstructions with four cycles at R=6x1-fold acceleration. Conventional SENSE and GRAPPA suffered from noise amplification and aliasing artifacts, leading to 18.6% and 13.3% RMSE, respectively. VC-GRAPPA made use of image phase information to improve the reconstruction with 7.5% RMSE. JVC-GRAPPA jointly reconstructed the phase-cycles with staggered k-space sampling and mitigated noise and aliasing with 7.1% error. J-LORAKS further improved the image quality and RMSE performance (6.5%). Even when using a more limited calibration region of 16 samples, J-LORAKS was able to yield similar performance as JVC-GRAPPA using 20 lines of ACS (7.1% RMSE, not shown).
Supporting Fig S1 demonstrates the individual phase-cycles and the sampling patterns, where the improvement in noise reduction thanks to joint parallel imaging is more apparent. Yellow arrows point to more subtle aliasing artifacts in JVC-GRAPPA, which were better mitigated in the J-LORAKS reconstruction.
Image Reconstruction at 7-fold acceleration
Optimal kernel size and regularization parameters at R=7×1-fold acceleration were 7×3 and λ = 3×10−8 for conventional GRAPPA, and 3×3, λinit = 3×10−8 and λlatter = 3×10−6 for JVC-GRAPPA.
At R=6×1-fold undersampling with 7/8 partial Fourier, the optimal parameters for J-GRAPPA and POCS were, 3×3 kernel size, λinit = 3×10−8 and λlatter = 3×10−7. J-LORAKS used a local neighborhood of 2 voxels and rank constraint = 600.
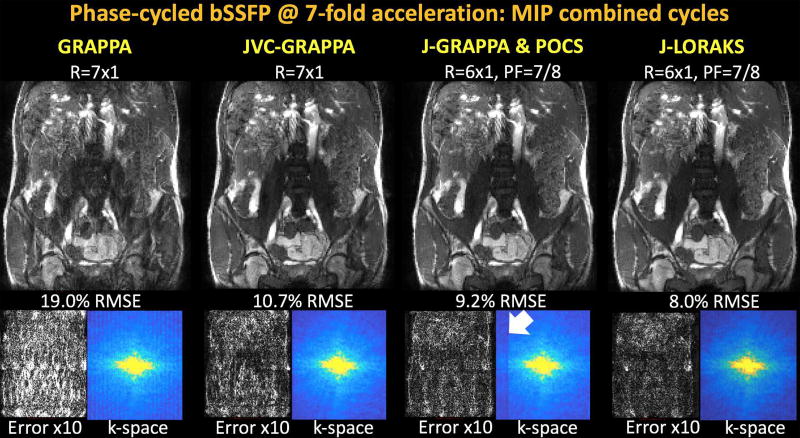
Fig3 shows reconstructed MIPs, error images as well as the k-spaces of the first phase-cycle reconstructed data. Conventional GRAPPA broke down at such high acceleration with 19.0% RMSE, while JVC-GRAPPA demonstrated better artifact and noise mitigation and yielded 10.7% error. At the same net acceleration factor, the combination of 6-fold uniform and 7/8-fold partial Fourier undersampling returned 9.2% RMSE with J-GRAPPA and POCS. The portion of k-space that was completed with POCS appeared underestimated (white arrow). J-LORAKS had the best RMSE performance with 8.0%, and mitigated this underestimation problem.
Fig3.
Phase-cycled bSSFP with 7-fold total acceleration. Conventional GRAPPA broke down at such high acceleration factor, and had 19.0% error with severe aliasing artifacts and noise amplification. JVC-GRAPPA was able to mitigate some of these artifacts, but still yielded a large error of 10.7%. Combination of 6-fold uniform and 7/8 partial Fourier sampling provided the same 7-fold net acceleration. In this setting, virtual coil concept was not applicable in Joint GRAPPA. Its combination with POCS reconstruction led to 9.2% RMSE and some signal underestimation in k-space (white arrow). J-LORAKS was able to outperform all methods with 8.0% error, and was more successful in completing the partially sampled k-space without the need for an additional POCS step.
3D Multi-Echo MPRAGE
Image Reconstruction at 12-fold acceleration
The kernel size that yielded the best RMSE was 3×3 for both conventional and JVC-GRAPPA. Optimal Tikhonov parameter for conventional GRAPPA was λ = 7×10−6. For initial Joint GRAPPA reconstruction, regularization parameter was λinit = 2×10−7, and for the following JVC iterations optimal parameter was λlatter = 2×10−6.
J-LORAKS obtained optimal performance using a k-space neighborhood of radius = 1 and rank constraint of 300, with 50 pcg iterations.
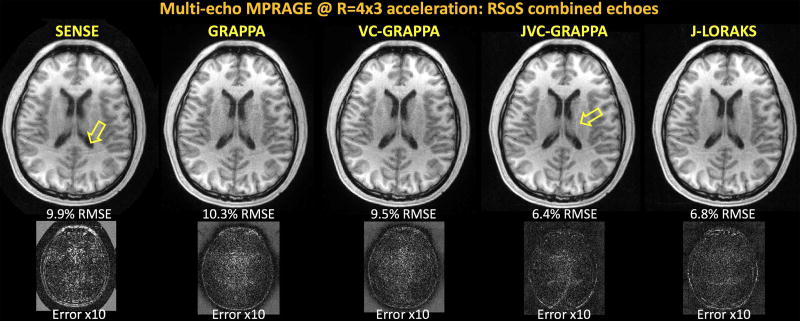
RSoS combined echoes from the three reconstruction techniques are compared in Fig4. GRAPPA suffered from noise amplification especially in the middle of the FOV (more visible in Supporting Fig S2 where each echo is shown separately). The RMSE of conventional reconstruction was 10.3%, and this was reduced to 6.4% with JVC-GRAPPA. Despite substantially mitigating noise amplification, JVC suffered from a structured aliasing artifact (yellow arrow). This was eliminated in the J-LORAKS reconstruction, with similar noise mitigation and RMSE performance (6.8%). Fig4 also presents comparisons against SENSE and VC-GRAPPA reconstructions that were performed for each echo separately.
Fig4.
Root-sum-of-squares combination of multi-echo MPRAGE reconstructions with four echoes and R=4x3-fold acceleration. Regularized SENSE reconstruction suffered from structured artifacts with 9.9% error. Conventional GRAPPA had noise amplification especially in the middle of the field of view with 10.3% RMSE. VC-GRAPPA provided minor improvement to yield 9.5% error. JVC-GRAPPA mitigated this and reduced the error to 6.4%, but at the expense of some structured aliasing artifact (yellow arrow). J-LORAKS provided a cleaner image with reduced noise amplification and 6.8% error.
Supporting Fig S2 demonstrates the staggered sampling patterns and the individual echoes’ reconstructions, where the noise mitigation difference between the conventional and joint techniques can be better appreciated.
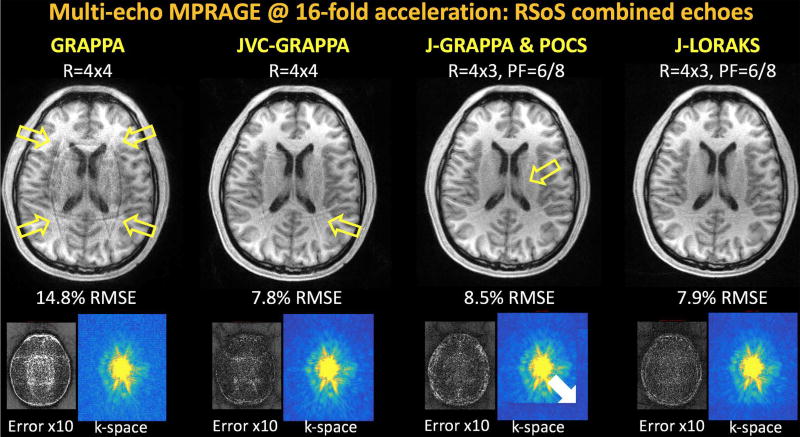
Image Reconstruction at 16-fold acceleration
Conventional and JVC-GRAPPA used kernels of size 3×3. Optimal RMSE’s were achieved using λ = 2×10−5 for conventional GRAPPA, and λinit = 2×10−7, λlatter = 7×10−6 for JVC reconstruction.
For the partial Fourier cases, optimal parameters were λinit = 2×10−7, λlatter = 2×10−6 for J-GRAPPA, and neighborhood radius = 1, rank constraint = 300, and 100 pcg iterations for J-LORAKS.
At this high acceleration factor, conventional GRAPPA demonstrated severe aliasing artifacts and noise amplification (Fig5), with an RMSE of 14.8%. JVC-GRAPPA partially mitigated these issues with an error of 7.8%, but some aliasing artifacts were still visible. Combination of J-GRAPPA and POCS used R=4×3 uniform and 6/8 partial Fourier undersampling to achieve the same net acceleration factor. Despite an overall improvement in artifact reduction, partially sampled k-space suffered from underestimation (white arrow) and some structured aliasing artifacts were present (yellow arrow). J-LORAKS was able to further address these issues to provide a cleaner reconstruction with an RMSE of 7.9%.
Fig5.
Multi-echo MPRAGE reconstruction at 16-fold total acceleration. Conventional GRAPPA broke down at this high acceleration factor, yielding 14.8% error. JVC-GRAPPA managed to mitigate most of the structured artifacts and noise amplification, with 7.8% RMSE and some residual aliasing artifacts (yellow arrow). At the same net acceleration factor, the combination of R=4x3 uniform undersampling and 6/8 partial Fourier sampling was explored. Combination of J-GRAPPA and POCS had 8.5% error, underestimation in partially sampled k-space (white arrow), and structured artifact (yellow arrow). J-LORAKS was able to provide an improved reconstruction with 7.9% RMSE and more successfully completed partial k-space data.
SMS Multi-Echo Spin-Echo
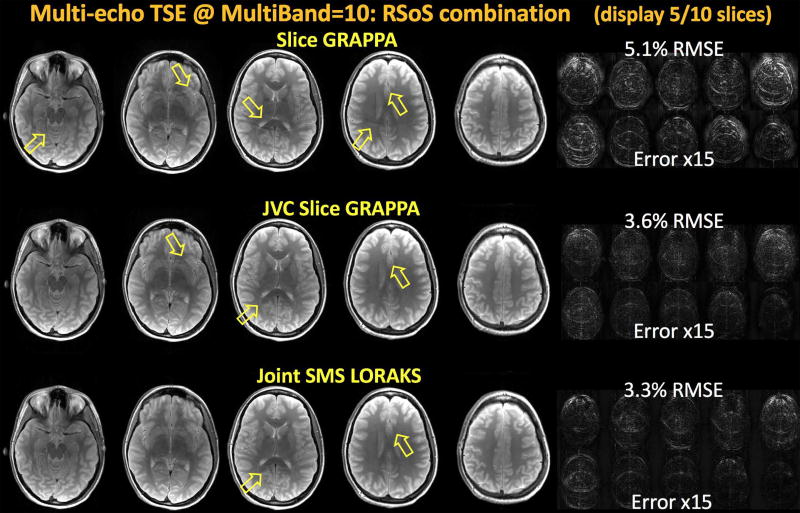
Image Reconstruction at MB-10 acceleration
FOV shift between slices was optimized to yield the best RMSE and was found to be FOV/4.
Optimal kernel size and Tikhonov regularization parameter for conventional Slice GRAPPA were 9×9 and 10−6. These were selected as 7×7 and 10−7 for JVC Slice GRAPPA.
The parameters chosen for J-SMS-LORAKS were neighborhood radius = 3 (which lead to circle diameter 7), rank r = 1000, with regularization parameter λ = 10−5.
RSoS combination of reconstructed echoes are shown in Fig6. Conventional Slice GRAPPA yielded 5.1% error and exhibited structured aliasing artifacts (yellow arrows). JVC Slice GRAPPA partially mitigated these artifacts as well as reducing the noise amplification (better appreciated in Supporting Fig S3 where individual echo images are shown). While the RMSE was reduced to 3.6%, some structured artifacts were present (yellow arrows). J-SMS-LORAKS was more successful at artifact mitigation, as well as at RMSE performance (3.3%).
Fig6.
Multi-echo Turbo Spin Echo reconstruction with six echoes and Simultaneous MultiSlice acceleration (displaying 5 out of 10 slices). Root-sum-of-squares combination of the echoes using MultiBand=10 acceleration are depicted. Conventional Slice GRAPPA with signal leakage constrained yielded 5.1% error and structured aliasing artifacts (yellow arrows). JVC Slice GRAPPA obtained a reduced RMSE of 3.6% with better noise suppression and artifact mitigation. However, some aliasing artifacts were still visible. Joint SMS LORAKS provided the lowest error 3.3% with better artifact suppression.
Whereas Fig6 displays only 5 out of 10 reconstructed slices, the entire 10-slice reconstruction can be viewed in Supporting Fig S4.
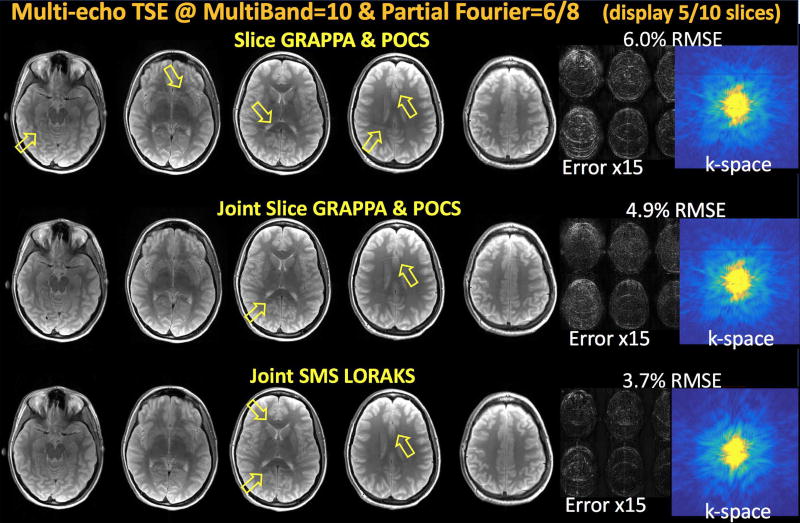
Image Reconstruction at MB-10 acceleration with 6/8 partial Fourier
All reconstruction parameters for the three methods were the same as the previous MB-10 experiment.
Reconstruction results, error images and k-space data of the first echo are compared in Fig7. Slice GRAPPA followed by POCS processing returned 6.0% error with aliasing artifacts as pointed by yellow arrows. Due to asymmetric k-space sampling, VC concept could not be exploited in Joint Slice GRAPPA. As such, the reconstruction was performed without the aid of virtual coils, and sequential POCS processing was applied to estimate the partially sampled portion. Despite the reduction in RMSE to 4.9%, some residual aliasing artifacts were still present (yellow arrows). Apart from the readout line at the edge of the partial Fourier sampling mask, POCS completed portion did not appear to be underestimated. This is because the background phase is minimal for spin-echo data, unlike the bSSFP and MPRAGE cases.
Fig7.
Multi-echo Turbo Spin Echo reconstruction with MultiBand=10 acceleration and 6/8 partial Fourier sampling (displaying 5 out of 10 slices). Combination of Slice GRAPPA and POCS had 6.0% RMSE with visible aliasing artifacts and some k-space discontinuity at the partial Fourier transition line. Joint Slice GRAPPA was not able to utilize virtual coil concept, and required POCS post-processing to estimate partially sampled data. This combination led to 4.9% error with some reconstruction artifacts and minor k-space discontinuity. Joint SMS LORAKS did employ virtual coils, and incorporated partial Fourier reconstruction without the need for POCS processing. This allowed 3.7% RMSE performance, while not being able to fully mitigate aliasing artifacts at such high acceleration factor (yellow arrows).
J-SMS-LORAKS attained the best RMSE performance (3.7%), with some structured aliasing artifacts at such high acceleration (yellow arrows). Estimated k-space appeared smooth, and devoid of discontinuity or underestimation problems.
For display purposes, Fig7 shows only 5 out of 10 slices reconstructed in this MB10 experiment. The entire array of 10 slices can be viewed in Supporting Fig S5.
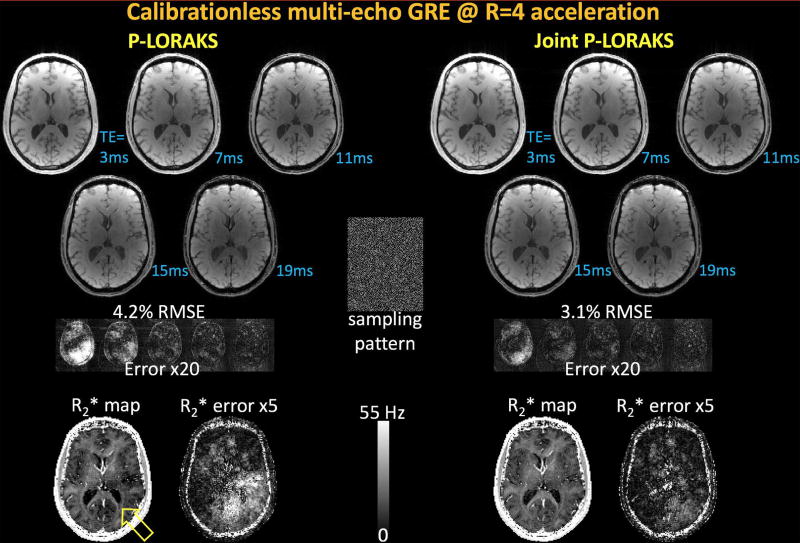
Calibrationless: 3D Multi-Echo Gradient-Echo
The parameters were tuned to minimize RMSE, where neighborhood radius = 3 for both cases, and the matrix rank r = 50 for single contrast and r = 300 for multi-contrast LORAKS. While both reconstructions were devoid of visible artifacts, observing the error maps in Fig8 revealed a signal bias especially in the early echoes of the conventional LORAKS results. These were reflected in the estimated R2* parameter maps, where J-LORAKS mitigated the underestimation problem that single-LORAKS suffered from (yellow arrow). The reconstruction errors were 4.2% and 3.1% for the two algorithms.
Fig8.
Calibrationless multi-echo gradient-echo reconstruction at R=4-fold pseudo-random acceleration. Single-contrast calibrationless LORAKS yielded 4.2% error with underestimation in the R2* parameter map (yellow arrow). This is likely caused by the signal drop in the early echoes as can be better seen in the error maps. Joint calibrationless LORAKS had an improved RMSE performance of 3.1%, and mitigated the signal dropout problem in both the individual echoes and the estimated parameter map.
DISCUSSION
We presented joint parallel imaging acquisition/reconstruction approaches that exploit similarities between multi-contrast images, as well as complementary sampling and image phase priors to provide dramatic improvements over conventional techniques for highly accelerated acquisitions. JVC-GRAPPA made this possible by converting intensity and phase differences across images into extra spatial encoding and utilizing the VC concept. J-LORAKS, sought to achieve local k-space matrices with lower rank because of the added redundancy from the multiple images stacked along the coil axis. Proposed joint reconstruction techniques thus enabled acceleration rates beyond the capability of conventional parallel imaging, while mitigating aliasing artifacts and reducing noise amplification.
JVC-GRAPPA is a straightforward extension of GRAPPA, where multi-contrast images are stacked in the coil axis with staggered k-space sampling and iterative VC reconstruction. J-LORAKS addresses two main limitations of JVC-GRAPPA: (i) it allows arbitrary sampling patterns, and (ii) can work with parsimonious ACS size or even without calibration. We took advantage of (i) by using different sampling patterns in each contrast, as well as exploiting VC concept despite partial Fourier sampling. Mitigating drawback (ii) is especially important at high acceleration rates, where the span of GRAPPA kernels can be very large. At R=7-fold acceleration with a small kernel size of 3 samples, GRAPPA kernels would already span a 15-sample distance in k-space. With small ACS sizes, it becomes difficult to extract sufficient amount of training data because we can only slide such a large 15-sample window in k-space by a few samples. This also constrains the size of the GRAPPA kernel, e.g. we would need 30 ACS lines to be able to fit a 5-sample kernel.
In terms of reconstruction time, both algorithms perform similarly with a small advantage for J-LORAKS. Points where JVC-GRAPPA might be advantageous are its simplicity in implementation and less memory usage than J-LORAKS. Overall, J-LORAKS is superior to JVC-GRAPPA in most aspects, except for the relative ease of exporting it to online reconstruction platforms.
Joint reconstruction of calibrationless dataset showed advantages in RMSE (Fig8), which could be further improved using different sampling patterns across the echoes. In most conventional exams, calibration signal can be acquired by fully-sampling the k-space center, or by using a separate acquisition e.g. a low-resolution GRE. Since such separate calibration information is cheap, Cartesian acquisitions for high-resolution structural imaging may not benefit from calibrationless reconstruction.
There are, however, applications where a rapid separate acquisition may not provide suitable calibration information, or an integrated ACS region with Nyquist-sampling may be disadvantageous. For instance, inconsistencies between the separate ACS data and the accelerated functional imaging acquisition can reduce the temporal SNR (76), and it is not practical to have an integrated calibration region in echo planar trajectories. Dynamic imaging could be another domain where calibrationless reconstruction could be impactful (33), since coil sensitivity information is subject to change due to motion and it is costly to sample ACS data over time. Despite having potential applications, increased computational burden and the reduction in the achievable acceleration are some of the trade-offs in calibrationless imaging.
Because SENSE-based reconstruction does not introduce coupling between different contrasts, we have chosen to employ GRAPPA and LORAKS in joint reconstruction. However, we have combined SENSE and LORAKS in our earlier work (30), and recently improved on this by combining LORAKS with k-space parallel imaging constraints in (58,59). In particular, (58) provides a comparison of SENSE-based LORAKS versus autocalibrating LORAKS, where the latter has a clear advantage.
We think that VC-GRAPPA can be modified to allow partial Fourier reconstruction. Similar to the way that the GRAPPA kernel needs to change for each distinct local sampling pattern, we would need to apply a different GRAPPA kernel for the asymmetrically sampled region compared to the kernel used for the symmetric region. This kernel for the asymmetric region would employ only the actual k-space during the training and reconstruction stages. For simplicity, we used J-GRAPPA without VC in partial Fourier experiments. The impact of not using VC can be appreciated by comparing Figs6&7. With JVC Slice GRAPPA, reconstruction error reduced by 42% compared to Slice GRAPPA (Fig6, no partial-Fourier case). With Joint Slice GRAPPA (Fig7, 6/8 partial-Fourier, no VC) the improvement was 22%. With J-LORAKS, the phase prior constraint is better incorporated into the reconstruction for partial Fourier acquisition to provide a 62% reduction compared to standard GRAPPA reconstruction. Please also see Supporting Information for further discussion on partial Fourier sampling in specific acquisitions. We have also explored using VC concept without joint reconstruction in Supplementary Figs S2&4. This has provided improvement over conventional GRAPPA/SENSE, but failed to reach the quality of the proposed joint reconstruction algorithms.
Shifted sampling patterns are helpful in providing increased collective frequency coverage. In the bSSFP experiments at R=6-fold acceleration (Fig2), JVC-GRAPPA would have yielded 8.4% RMSE if all phase-cycles were using the same undersampling pattern, compared to the optimal 7.1% with the staggered acquisition. For J-LORAKS, the reconstruction error would have increased to 7.0%, as opposed to the optimal 6.5% RMSE. These indicate that complementary undersampling is aiding the joint reconstruction, but both algorithms are robust to changes in the sampling strategy, with small degradation in the RMSE performance (less than 20%). Table 1 report the same analysis for MPRAGE reconstruction, where both techniques are seen to be robust to changes in the staggering amount (less than 15% degradation without shifts).
Table1.
Performance analysis of 12-fold accelerated JVC-GRAPPA and J-LORAKS reconstructions for multi-echo MPRAGE acquisition with different k-space staggering amounts across echoes.
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE(JVC-GRAPPA): MPRAGE @ R=12 | RMSE(J-LORAKS): MPRAGE @ R=12 | ||||||||
|
|
|
||||||||
| ∆kz | ∆kz | ||||||||
|
|
|
||||||||
| 0 | 1 | 2 | 0 | 1 | 2 | ||||
|
|
|
||||||||
| ∆ky | 0 | 7.3% | 6.7% | 6.7% | ∆ky | 0 | 7.1% | 6.8% | 6.8% |
| 1 | 6.6% | 6.6% | 6.6% | 1 | 7.0% | 6.8% | 6.8% | ||
| 2 | 6.4% | 6.4% | 6.4% | 2 | 7.0% | 6.8% | 6.8% | ||
Because it stacks data from all image contrasts into the channel axis and also creates virtual coils, JVC-GRAPPA requires larger amount of calibration data as the number of kernels scale with the square of the channel count. This problem is exacerbated by shifted sampling, as the staggered JVC kernels span a larger k-space extent which is more difficult to fit in the ACS region. This is addressed in part by the iterative approach, which uses the reconstructed k-space to re-train the kernels. Increasing the size of calibration region however lengthens the reconstruction time, since the calibration matrix that needs to be inverted grows in size. J-LORAKS addresses this second limitation of large ACS requirement as well, and is capable of outperforming JVC-GRAPPA even when it uses a smaller calibration region size (Fig1).
The reconstruction errors in the 2D and 3D acquisition experiments include some contribution from the intrinsic √R SNR penalty. This stems from the data undersampling that reduces the total noise averaging window of the images. Such √R penalty does not impact SMS acquisition in practice, since SMS k-space data are not undersampled and each slice experiences the same noise averaging benefit as the MB-1 case. However, because we have simulated SMS acceleration by collapsing separately acquired slices, our results are actually impacted by √MB = √10 noise penalty in Figs6&7. Since the actual SMS experiment would not have been affected by this additional noise, the RMSE levels would have been lower. Nonetheless, it would not be possible to eliminate the additional factor of √(4/3) SNR penalty due to partial Fourier undersampling in Fig7.
Limitations
We have employed different regularization parameters for kernel training in the initial Joint-GRAPPA reconstruction and the following JVC iterations for optimal RMSE. It is possible to use the same Tikhonov parameters for the two steps without a large drop in the performance. For instance, using λinit = λlatter = 3×10−8 in Fig2 led to an RMSE of 7.7%, which is slightly higher than the optimal JVC performance (7.1%). Automatic parameter selection algorithms could further help address this limitation (77,78).
Another drawback in the joint parallel imaging reconstruction is the increased reconstruction time. For the results presented in Fig2, computation time for the four phase-cycles was 6 sec for GRAPPA, 6.8 min for JVC-GRAPPA, and 5.4 min for J-LORAKS. We think that there are several ways to reduce this 50-fold gap in performance. We have used SVD coil compression in the current experiments. More advanced compression techniques such as Geometric Coil Compression (79) would permit higher compression rates. Secondly, JVC-GRAPPA uses the entire k-space to re-train kernels in the latter iterations. This calibration size could be restricted to a smaller portion of k-space to reduce the calibration time, at the cost of increasing the condition number of the matrix inversion. Rather than applying these large number of JVC kernels via convolution in k-space, an image space version could be implemented with a simple elementwise multiplication. Finally, the number of pcg iterations in J-LORAKS could be reduced to reach a better compromise between speed and accuracy.
A further limitation of the joint reconstruction is potential motion between scans. While multi-echo acquisitions do not suffer from this drawback, phase-cycled bSSFP could be impacted by potential mismatches across cycles. Since JVC-GRAPPA employs low-resolution kernels for data interpolation, we expect this technique to be resilient against small amounts of motion. In the presence of larger mismatches, an initial GRAPPA could be applied on each phase-cycle independently, followed by retrospective motion correction and JVC-GRAPPA or J-LORAKS processing. The higher acceleration factors that can be achieved with joint reconstruction could also help mitigate some of the involuntary motion.
Extensions
A potential extension to the proposed joint parallel imaging techniques could be the addition of joint sparse regularization (36,43). This extension would easily fit within SPIRiT (21) or LORAKS (28) frameworks. For JVC-GRAPPA, sparsity enforcing priors could be used either during kernel calibration (80) or reconstruction (23).
Another application where joint parallel imaging could be powerful is single-shot diffusion imaging, where multiple diffusion volumes at neighboring q-space positions could be jointly reconstructed.
Supplementary Material
Supporting Fig S1. Individual bSSFP phase-cycle images at R=6-fold acceleration. K-space sampling patterns are indicated below each phase-cycle. Conventional GRAPPA incurred noise amplification and structured aliasing artifacts with 13.3% RMSE. These were largely mitigated in JVC-GRAPPA with 7.1% error, while some subtle artifacts remained (yellow arrows). J-LORAKS further improved the image quality to yield 6.5% RMSE.
Supporting Fig S2. Individual echoes from the R=12-fold accelerated ME-MPRAGE reconstruction. GRAPPA with uniform sampling led to substantial noise amplification and 10.3% error. JVC-GRAPPA used staggered sampling across echoes, reduced the noise amplification and improved the RMSE to 6.4%, but suffered from some structured aliasing artifacts (yellow arrows). J-LORAKS explored the use of different CAIPI sampling patterns to mitigate both noise amplification and aliasing artifacts, with similar RMSE performance (6.8%).
Supporting Fig S3. Individual echoes from SMS multi-echo TSE reconstruction at MB-10 acceleration. Slice GRAPPA achieved 5.1% RMSE and suffered from noise amplification and aliasing artifacts (yellow arrows), which became less apparent at the later echoes due to relaxation. JVC Slice GRAPPA was able to mitigate the noise amplification, but some of the visible aliasing artifacts remained (3.6% RMSE). Joint SMS Loraks further improved the image quality and attained the lowest reconstruction error of 3.3%.
Supporting Fig S4. Multi-echo SMS TSE results at MB-10 acceleration, displaying all 10 slices from the three reconstruction techniques.
Supporting Fig S5. Multi-echo SMS TSE results at MB-10 acceleration and 6/8 Partial Fourier sampling. In addition to all 10 of the reconstructed slices, corresponding error images and k-space representation are displayed for the three algorithms.
Acknowledgments
We acknowledge grant support from NIH NINDS grant number R24 MH10609603 and NIBIB R01 EB02061302, R01 EB019437, P41 EB015896 and R21 EB02295102.
References
- 1.Ben-Eliezer N, Sodickson D, Block K. Rapid and accurate T2 mapping from multi–spin-echo data using Bloch-simulation-based reconstruction. Magn. Reson. Med. 2015;73.2:809–817. doi: 10.1002/mrm.25156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sumpf T, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo. MRI. J. Magn. Reson. Imaging. 2011;34.2:420–428. doi: 10.1002/jmri.22634. [DOI] [PubMed] [Google Scholar]
- 3.Wu B, Li W, Avram AV, Gho S-M, Liu C. Fast and tissue-optimized mapping of magnetic susceptibility and T2* with multi-echo and multi-shot spirals. Neuroimage. 2012;59:297–305. doi: 10.1016/j.neuroimage.2011.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Poser B, Versluis M, Hoogduin J, Norris DG. BOLD contrast sensitivity enhancement and artifact reduction with multiecho EPI: parallel-acquired inhomogeneity-desensitized fMRI. Magn. Reson. Med. 2006;55.6:1227–1235. doi: 10.1002/mrm.20900. [DOI] [PubMed] [Google Scholar]
- 5.Reeder S, McKenzie C, Pineda A, Yu H, Shimakawa A, Brau AC, Hargreaves BA, Gold GE, Brittain JH. Water–fat separation with IDEAL gradient-echo imaging. J. Magn. Reson. Imaging. 2007;25.3:644–652. doi: 10.1002/jmri.20831. [DOI] [PubMed] [Google Scholar]
- 6.Yu H, McKenzie C, Shimakawa A, Vu A, Brau AC, Beatty P, Pineda A, Brittain JH, Reeder S. Multiecho reconstruction for simultaneous water-fat decomposition and T2* estimation. J. Magn. Reson. Imaging. 2007;26.4:1153–1161. doi: 10.1002/jmri.21090. [DOI] [PubMed] [Google Scholar]
- 7.Glover G. Multipoint Dixon technique for water and fat proton and susceptibility imaging. J. Magn. Reson. Imaging. 1991;1.5:521–530. doi: 10.1002/jmri.1880010504. [DOI] [PubMed] [Google Scholar]
- 8.Dixon W. Simple proton spectroscopic imaging. Radiology. 1984;153.1:189–194. doi: 10.1148/radiology.153.1.6089263. [DOI] [PubMed] [Google Scholar]
- 9.van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage. 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Miller KL, Smith SM, Jezzard P, Pauly JM. High-resolution FMRI at 1.5T using balanced SSFP. Magn. Reson. Med. 2006;55:161–170. doi: 10.1002/mrm.20753. [DOI] [PubMed] [Google Scholar]
- 11.Lee J, Dumoulin S, Saritas E, Glover G, Wandell B, Nishimura D, Pauly J. Full-brain coverage and high-resolution imaging capabilities of passband b-SSFP fMRI at 3T. Magn. Reson. Med. 2008;59.5:1099–1110. doi: 10.1002/mrm.21576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 13.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn. Reson. Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 14.Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA) Magn. Reson. Med. 2006;55:549–556. doi: 10.1002/mrm.20787. [DOI] [PubMed] [Google Scholar]
- 15.Brenner D, Stirnberg R, Pracht ED, Stöcker T. Two-dimensional accelerated MP-RAGE imaging with flexible linear reordering. Magn. Reson. Mater. Physics, Biol. Med. 2014;27:455–462. doi: 10.1007/s10334-014-0430-y. [DOI] [PubMed] [Google Scholar]
- 16.Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med. 2012;67:1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 2005;53:684–691. doi: 10.1002/mrm.20401. [DOI] [PubMed] [Google Scholar]
- 18.Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging. 2001;13:313–317. doi: 10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 19.Stäb D, Ritter CO, Breuer FA, Weng AM, Hahn D, Köstler H. CAIPIRINHA accelerated SSFP imaging. Magn. Reson. Med. 2011;65:157–164. doi: 10.1002/mrm.22600. [DOI] [PubMed] [Google Scholar]
- 20.Wang Y, Shao X, Martin T, Moeller S, Yacoub E, Wang DJJ. Phase-cycled simultaneous multislice balanced SSFP imaging with CAIPIRINHA for efficient banding reduction. Magn. Reson. Med. 2016;76.6:1764–1774. doi: 10.1002/mrm.26076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010;64:457–471. doi: 10.1002/mrm.22428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Otazo R, Candès E, Sodickson D. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med. 2015;73.3:1125–1136. doi: 10.1002/mrm.25240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Weller DS, Polimeni JR, Grady L, Wald LL, Adalsteinsson E, Goyal VK. Denoising sparse images from GRAPPA using the nullspace method. Magn. Reson. Med. 2012;68:1176–1189. doi: 10.1002/mrm.24116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 2009;62:1574–1584. doi: 10.1002/mrm.22161. [DOI] [PubMed] [Google Scholar]
- 25.Blaimer M, Gutberlet M, Kellman P, Breuer F, Kostler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med. 2009;61:93–102. doi: 10.1002/mrm.21652. [DOI] [PubMed] [Google Scholar]
- 26.Blaimer M, Heim M, Neumann D, Jakob P, Kannengiesser SA, Breuer F. Comparison of phase-constrained parallel MRI approaches: Analogies and differences. Magn. Reson. Med. 2016;75:1086–1099. doi: 10.1002/mrm.25685. [DOI] [PubMed] [Google Scholar]
- 27.Blaimer M, Choli M, Jakob P, Griswold MA, Breuer FA. Multiband phase-constrained parallel MRI. Magn. Reson. Med. 2013;69:974–980. doi: 10.1002/mrm.24685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Haldar JP. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans. Med. Imaging. 2014;33:668–681. doi: 10.1109/TMI.2013.2293974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 2016;75:1499–1514. doi: 10.1002/mrm.25717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kim T, Setsompop K, Haldar J. LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration. Magn. Reson. Med. 2017;77:1021–1035. doi: 10.1002/mrm.26182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lustig M, Elad M, Pauly JM. Calibrationless Parallel Imaging Reconstruction by Structured Low-Rank Matrix Completion; Proceedings of the 18th Annual Meeting ISMRM; 2010. p. 2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Trzasko J, Manduca A. Calibrationless parallel MRI using CLEAR; Conference Record of the Forty Fifth Asilomar Conference; 2011. pp. 75–79. [Google Scholar]
- 33.Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 2014;72:959–970. doi: 10.1002/mrm.24997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jin K, Lee D, Ye J. A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix. IEEE Trans. Comput. 2016;2:480–495. [Google Scholar]
- 35.Gong E, Huang F, Ying K, Wu W, Wang S, Yuan C. PROMISE: Parallel-imaging and compressed-sensing reconstruction of multicontrast imaging using SharablE information. Magn. Reson. Med. 2015;73:523–535. doi: 10.1002/mrm.25142. [DOI] [PubMed] [Google Scholar]
- 36.Knoll F, Holler M, Koesters T, Otazo R, Bredies K, Sodickson D. Joint MR-PET reconstruction using a multi-channel image regularizer. IEEE Trans. Med. Imaging. 2017;36:1–16. doi: 10.1109/TMI.2016.2564989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haldar JP, Zhi-Pei Liang. Joint reconstruction of noisy high-resolution MR image sequences; 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE; 2008. pp. 752–755. [DOI] [Google Scholar]
- 38.Haldar JP, Wedeen VJ, Nezamzadeh M, Dai G, Weiner MW, Schuff N, Liang Z-P. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn. Reson. Med. 2013;69:277–289. doi: 10.1002/mrm.24229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bilgic B, Goyal VK, Adalsteinsson E. Multi-contrast reconstruction with Bayesian compressed sensing. Magn. Reson. Med. 2011;66 doi: 10.1002/mrm.22956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang Y, Fessler JA, Clinthorne NH, Rogers WL. Experimental evaluation for joint estimation approach; 1996 IEEE Nuclear Science Symposium. Conference Record. Vol. 3. IEEE; pp. 1623–1627. [DOI] [Google Scholar]
- 41.Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007;57:1086–1098. doi: 10.1002/mrm.21236. [DOI] [PubMed] [Google Scholar]
- 42.Liu B, King K, Steckner M, Xie J, Sheng J, Ying L. Regularized sensitivity encoding (SENSE) reconstruction using bregman iterations. Magn. Reson. Med. 2009;61:145–152. doi: 10.1002/mrm.21799. [DOI] [PubMed] [Google Scholar]
- 43.Chatnuntawech I, Martin A, Bilgic B, Setsompop K, Adalsteinsson E, Schiavi E. Vectorial total generalized variation for accelerated multi-channel multi-contrast MRI. Magn. Reson. Imaging. 2016;34:1161–1170. doi: 10.1016/j.mri.2016.05.014. [DOI] [PubMed] [Google Scholar]
- 44.Huang F, Akao J, Vijayakumar S, Duensing GR, Limkeman M. k-t GRAPPA: Ak-space implementation for dynamic MRI with high reduction factor. Magn. Reson. Med. 2005;54:1172–1184. doi: 10.1002/mrm.20641. [DOI] [PubMed] [Google Scholar]
- 45.Jung B, Ullmann P, Honal M, Bauer S, Hennig J, Markl M. Parallel MRI with extended and averaged GRAPPA kernels (PEAK-GRAPPA): Optimized spatiotemporal dynamic imaging. J. Magn. Reson. Imaging. 2008;28:1226–1232. doi: 10.1002/jmri.21561. [DOI] [PubMed] [Google Scholar]
- 46.Liu W, Zhao X, Ma Y, Tang X, Gao J-H. DWI using navigated interleaved multishot EPI with realigned GRAPPA reconstruction. Magn. Reson. Med. 2016;75:280–286. doi: 10.1002/mrm.25586. [DOI] [PubMed] [Google Scholar]
- 47.Ma X, Zhang Z, Dai E, Guo H. Improved multi-shot diffusion imaging using GRAPPA with a compact kernel. Neuroimage. 2016;138:88–99. doi: 10.1016/j.neuroimage.2016.05.079. [DOI] [PubMed] [Google Scholar]
- 48.Kim H, Kim D-H, Sohn C-H, Park J. Rapid chemical shift encoding with single-acquisition single-slab 3D GRASE. Magn. Reson. Med. 2017 doi: 10.1002/mrm.26595. [DOI] [PubMed] [Google Scholar]
- 49.Kim H, Kim D-H, Park J. Variable-flip-angle single-slab 3D GRASE imaging with phase-independent image reconstruction. Magn. Reson. Med. 2015;73:1041–1052. doi: 10.1002/mrm.25223. [DOI] [PubMed] [Google Scholar]
- 50.Chen F, Shi X, Chen S, Johnson E, Chen B. Accelerated model-based proton resonance frequency shift temperature mapping using echo-based GRAPPA reconstruction. Magn. Reson. Imaging. 2015;33.2:240–245. doi: 10.1016/j.mri.2014.10.006. [DOI] [PubMed] [Google Scholar]
- 51.Orzada S, Maderwald S, Poser B, Bitz AK, Quick HH, Ladd ME. RF excitation using time interleaved acquisition of modes (TIAMO) to address B1 inhomogeneity in high-field MRI. Magn. Reson. Med. 2010;64:327–333. doi: 10.1002/mrm.22527. [DOI] [PubMed] [Google Scholar]
- 52.Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn. Reson. Med. 2005;54:1412–1422. doi: 10.1002/mrm.20706. [DOI] [PubMed] [Google Scholar]
- 53.Uecker M, Karaus A, Frahm J. Inverse reconstruction method for segmented multishot diffusion-weighted MRI with multiple coils. Magn. Reson. Med. 2009;62:1342–1348. doi: 10.1002/mrm.22126. [DOI] [PubMed] [Google Scholar]
- 54.Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE) Neuroimage. 2013;72:41–47. doi: 10.1016/J.NEUROIMAGE.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS) Magn. Reson. Med. 2017;78:494–507. doi: 10.1002/mrm.26382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lee D, Jin KH, Kim EY, Park S-H, Ye JC. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA) Magn. Reson. Med. 2016;76:1848–1864. doi: 10.1002/mrm.26081. [DOI] [PubMed] [Google Scholar]
- 57.Lee J, Jin KH, Ye JC. Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA) Magn. Reson. Med. 2016;76:1775–1789. doi: 10.1002/mrm.26077. [DOI] [PubMed] [Google Scholar]
- 58.Lobos RA, Kim TH, Hoge WS, Haldar JP. Navigator-free EPI Ghost Correction with Structured Low-Rank Matrix Models: New Theory and Methods. 2017 doi: 10.1109/TMI.2018.2822053. doi: https://arxiv.org/abs/1708.05095. [DOI] [PMC free article] [PubMed]
- 59.RA L, TH K, WS H, JP H. Navigator-free EPI ghost correction using low-rank matrix modeling: Theoretical insights and practical improvements; Proceedings of the 25th Annual Meeting ISMRM; 2017. p. 449. [Google Scholar]
- 60.Mani M, Magnotta V, Kelley D, Jacob M. Comprehensive reconstruction of multi-shot multi-channel diffusion data using mussels; 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE; 2016. pp. 1107–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mugler JP, Brookeman JR. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE) Magn. Reson. Med. 1990;15:152–157. doi: 10.1002/mrm.1910150117. [DOI] [PubMed] [Google Scholar]
- 62.Bilgic B, Witzel T, Bhat H, Wald LL, Setsompop K. International Society for Magnetic Resonance in Medicine 25th Scientific Meeting. Hawaii, USA: 2017. Joint Reconstruction of Phase-Cycled Balanced SSFP with Constrained Parallel Imaging; p. 441. [Google Scholar]
- 63.Bilgic B, Witzel T, Bhat H, Wald LL, Setsompop K. ESMRMB 33rd Scientific Meeting. Vienna, AT: 2016. Joint Reconstruction for Phase-Cycled Balanced SSFP. p. late breaking abstracts. [Google Scholar]
- 64.Ilicak E, Senel LK, Biyik E, Çukur T. Profile-encoding reconstruction for multiple-acquisition balanced steady-state free precession imaging. Magn. Reson. Med. 2016 doi: 10.1002/mrm.26507. [DOI] [PubMed] [Google Scholar]
- 65.Ilicak E, Çukur T. International Society for Magnetic Resonance in Medicine 25th Scientific Meeting. Hawaii, USA: 2017. Parameter-Free Profile Encoding Reconstruction for Multiple-Acquisition BSSFP Imaging; p. 571. [DOI] [PubMed] [Google Scholar]
- 66.Kilic T, Ilicak E, Çukur T, Saritas E. International Society for Magnetic Resonance in Medicine 25th Scientific Meeting. Hawaii, USA: 2017. Improved SPIRiT Operator for Joint Reconstruction of Multiple T2-Weighted Images; p. 5165. [Google Scholar]
- 67.Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn. Reson. Imaging. 2008;26:133–141. doi: 10.1016/j.mri.2007.04.010. [DOI] [PubMed] [Google Scholar]
- 68.Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn. Reson. Med. 2007;57:1131–1139. doi: 10.1002/mrm.21237. [DOI] [PubMed] [Google Scholar]
- 69.Liang Z, Lauterbur P. Principles of magnetic resonance imaging: a signal processing perspective. SPIE Optical Engineering Press; 2000. [Google Scholar]
- 70.Haacke E, Lindskogj E, Lin W. A fast, iterative, partial-Fourier technique capable of local phase recovery. J. Magn. Reson. 1991 [Google Scholar]
- 71.Cuppen J, Est A van Reducing MR imaging time by one-sided reconstruction. Magn. Reson. Imaging. 1987;5.6:526–527. [Google Scholar]
- 72.Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn. Reson. Med. 2014;72:93–102. doi: 10.1002/mrm.24898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Haldar JP. Autocalibrated loraks for fast constrained MRI reconstruction; 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). IEEE; 2015. pp. 910–913. [DOI] [Google Scholar]
- 74.Kim TH, Haldar JP. SMS-LORAKS: Calibrationless simultaneous multislice MRI using low-rank matrix modeling; 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). IEEE; 2015. pp. 323–326. [DOI] [Google Scholar]
- 75.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Polimeni JR, Bhat H, Witzel T, Benner T, Feiweier T, Inati SJ, Renvall V, Heberlein K, Wald LL. Reducing sensitivity losses due to respiration and motion in accelerated echo planar imaging by reordering the autocalibration data acquisition. Magn. Reson. Med. 2016;75:665–679. doi: 10.1002/mrm.25628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Candes EJ, Sing-Long CA, Trzasko JD. Unbiased Risk Estimates for Singular Value Thresholding and Spectral Estimators. IEEE Trans. Signal Process. 2013;61:4643–4657. doi: 10.1109/TSP.2013.2270464. [DOI] [Google Scholar]
- 78.Weller DS, Ramani S, Nielsen J-F, Fessler JA. Monte Carlo SURE-based parameter selection for parallel magnetic resonance imaging reconstruction. Magn. Reson. Med. 2014;71:1760–1770. doi: 10.1002/mrm.24840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–582. doi: 10.1002/mrm.24267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Weller DS, Polimeni JR, Grady L, Wald LL, Adalsteinsson E, Goyal VK. Sparsity-Promoting Calibration for GRAPPA Accelerated Parallel MRI Reconstruction. IEEE Trans. Med. Imaging. 2013;32:1325–1335. doi: 10.1109/TMI.2013.2256923. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Fig S1. Individual bSSFP phase-cycle images at R=6-fold acceleration. K-space sampling patterns are indicated below each phase-cycle. Conventional GRAPPA incurred noise amplification and structured aliasing artifacts with 13.3% RMSE. These were largely mitigated in JVC-GRAPPA with 7.1% error, while some subtle artifacts remained (yellow arrows). J-LORAKS further improved the image quality to yield 6.5% RMSE.
Supporting Fig S2. Individual echoes from the R=12-fold accelerated ME-MPRAGE reconstruction. GRAPPA with uniform sampling led to substantial noise amplification and 10.3% error. JVC-GRAPPA used staggered sampling across echoes, reduced the noise amplification and improved the RMSE to 6.4%, but suffered from some structured aliasing artifacts (yellow arrows). J-LORAKS explored the use of different CAIPI sampling patterns to mitigate both noise amplification and aliasing artifacts, with similar RMSE performance (6.8%).
Supporting Fig S3. Individual echoes from SMS multi-echo TSE reconstruction at MB-10 acceleration. Slice GRAPPA achieved 5.1% RMSE and suffered from noise amplification and aliasing artifacts (yellow arrows), which became less apparent at the later echoes due to relaxation. JVC Slice GRAPPA was able to mitigate the noise amplification, but some of the visible aliasing artifacts remained (3.6% RMSE). Joint SMS Loraks further improved the image quality and attained the lowest reconstruction error of 3.3%.
Supporting Fig S4. Multi-echo SMS TSE results at MB-10 acceleration, displaying all 10 slices from the three reconstruction techniques.
Supporting Fig S5. Multi-echo SMS TSE results at MB-10 acceleration and 6/8 Partial Fourier sampling. In addition to all 10 of the reconstructed slices, corresponding error images and k-space representation are displayed for the three algorithms.