Noise Properties of Proton Density Fat Fraction Estimated Using Chemical Shift Encoded MRI

Abstract

Purpose

The purpose of this work is to characterize the noise distribution of proton density fat fraction (PDFF) measured using chemical shift encoded magnetic resonance imaging (CSE-MRI), and to provide alternative strategies to reduce bias in PDFF estimation.

Theory

We derived the probability density function for PDFF estimated using CSE-MRI and found it to exhibit an asymmetric noise distribution that contributes to signal-to-noise (SNR) dependent bias.

Methods

To study PDFF noise bias we performed (at 1.5T) numerical simulations, phantom acquisitions, and a retrospective in vivo experiment. In each experiment, we compared the performance of three statistics (mean, median, and maximum likelihood estimator (MLE)) in estimating the PDFF in a region of interest.

Results

We demonstrated the presence of the asymmetric noise distribution in simulations, phantoms, and in vivo. In each experiment we demonstrated that both the median and proposed MLE statistics outperformed the mean statistic in mitigating noise related bias for low SNR acquisitions.

Conclusions

Characterization of the noise distribution of PDFF estimated using CSE-MRI enabled new strategies based on median and MLE statistics to mitigate noise-related bias for accurate PDFF measurement from a region of interest. Such strategies are important for quantitative CSE-MRI applications that typically operate in low SNR regimes.

Introduction

Proton density fat fraction (PDFF) is a fundamental property of tissue that reflects tissue triglyceride concentration. CSE-MRI methods have used PDFF to quantify triglyceride content in many organs, including the liver, pancreas, thymus, bone marrow, white and brown adipose tissue, skeletal muscle, and heart (1). In the liver specifically, abnormal accumulation of intracellular triglycerides within hepatocytes (ie: hepatic steatosis) is the earliest and hallmark feature of non-alcoholic fatty liver disease (NAFLD). NAFLD afflicts an estimated 30% of the population in developed countries, including up to 100 million people in the United States and approximately 10% of people in developing countries (2–4). There is a growing and urgent need for early and non-invasive biomarkers of NAFLD, including accurate quantification of low liver fat content.

Chemical shift encoded magnetic resonance imaging (CSE-MRI) methods are emerging as well-validated, quantitative biomarkers of tissue triglyceride content (5–8). When all relevant confounders such as T1 bias (9), T2* decay (10–12), spectral complexity of fat (11,12), eddy currents (13,14), and bias related to Rician noise distribution in magnitude estimates of water and fat (9) have been addressed, CSE-MRI methods provide an accurate and precise estimate of PDFF.

Recent studies also underscore the need for both accurate and precise PDFF measurements, particularly at low PDFF values (0-20%) (5,6,15,16). In particular, Nasr et al found a 47% improvement (from 53% to 100%) in the sensitivity of PDFF for diagnosis of hepatic steatosis by decreasing the PDFF cut-off value by just 2% (from 5% to 3%) (16). Further, Rehm et al demonstrated that a hepatic PDFF threshold of 3.0% was highly predictive of the presence of the metabolic syndrome in adolescent girls (5). These results demonstrate that clinically relevant thresholds may be much lower than previously known (5). Any small bias in the accuracy of PDFF estimation may have significant impact on the ability of CSE-MRI to diagnose clinically relevant disease. With sufficient signal-to-noise ratio (SNR), CSE-MRI provides accurate and reproducible PDFF measurements in the liver (17,18). Motosugi et al reports SNRs near 20 for a typical 3D CSE-MRI acquisition in the liver with voxel size 35mm³ (18). Accounting for acquisition time differences, this corresponds to SNRs in the range of 5-10 for a typical sequential 2D CSE-MRI acquisition, which is commonly used in rapid imaging applications and described in greater detail in the Methods section. However, clinically accurate and precise PDFF measurements from magnitude images are confounded at low SNR values by a noise bias that occurs primarily at low (<≈20%) and high (>≈80%) PDFF values (9). In these PDFF maps, the mean value of voxels from a region of interest (ROI) would not reflect the true PDFF of the tissue, but would instead be biased. Liu et al proposed and validated two methods, “magnitude discrimination” and “phase-constrained,” that reduced this noise bias by addressing the effects of Rician distributed noise created by the magnitude operator (9). As we show below, however, an additional source of SNR related bias occurs, even when using the approaches described by Liu et al.

In a more recent study, Holmes et al characterized the accuracy of current noise bias correction techniques (9,19). At low SNR, a persistent empirical bias in PDFF estimation was observed even after the effects of Rician distributed noise had been address. This will affect emerging applications that inherently suffer from a lack of SNR, such as highly accelerated breath-hold acquisitions, acquisitions in the presence of concomitant iron overload, or rapid free-breathing sequential acquisitions. Furthermore, the compounded effects of the low flip angle needed to remove T1 bias, parallel imaging, and simultaneous corrections for R2* confounder effects, decrease the SNR performance of CSE-MRI acquisitions. Thus, methods to reduce bias in low SNR PDFF maps could benefit a wide range of CSE-MRI protocols.

Therefore, the purpose of this work is to perform a rigorous characterization of the noise distribution of PDFF and to propose and validate alternative strategies to mitigate the bias in PDFF estimation. A complete statistical model of PDFF (as estimated by CSE-MRI) will be derived and used to explain and mitigate persistent noise-related bias in PDFF maps. Furthermore, the median and MLE statistics are proposed as alternatives to the conventional mean statistic for low SNR CSE-MRI applications, in order to mitigate noise-related bias for an accurate PDFF measurement from an ROI.

Theory

CSE-MRI techniques allow accurate and robust signal quantification from multi-echo acquisitions by estimating unknown parameters of a signal model (9,11–13). In our work, we use the spoiled gradient recalled signal model proposed by Yu et al (11,20,21):

$$s\left(n;\theta \right)=({\rho }_w+{\rho }_f{{\displaystyle \sum }}_{p=1}^P{\alpha }_p{e}^{i2\pi f_p{t}_n})e^{i\varphi }{e}^{i\psi t_n}{e}^{-R_2^{\ast }{t}_n}.$$ [1]

Where $\theta =\{{\rho }_w, {\rho }_f, \varphi , \psi ,R_2^{\ast }\}$ is the set of unknown signal parameters to be estimated. Specifically, ${\rho }_w$ and ${\rho }_f$ are the real-valued signals from water and fat, respectively; $\varphi$ is the initial phase for the fat and water signals; and $\psi$ is the magnetic field inhomogeneity map. Additionally, ${\alpha }_p$ and $f_p$ are the corresponding relative amplitudes and frequencies of the P peak spectral model of fat, here chosen as 6 (22); and $t_n$ is the echo time.

Many CSE-MRI algorithms use nonlinear least squares (NLSQ) to determine estimates of the unknown signal parameters that best fit (in the least-squares sense) the acquired data. Our work focuses on CSE-MRI that uses either of two types of NLSQ algorithms, complex fitting and mixed fitting (developed for robustness to phase errors), both described in (13). Our work uses complex fitting NLSQ for simulations and mixed fitting NLSQ for phantom and in vivo acquisitions.

Once the unknown signal parameters have been estimated ( $\widehat{\theta }=\{{\widehat{\rho }}_w,{\widehat{\rho }}_f, \widehat{\varphi }, \widehat{\psi },{\widehat{R}}_2^{\ast }\}$), an estimate of PDFF ( $\widehat{\eta }$) is calculated as:

$$\widehat{\eta }=\frac{{\widehat{\rho }}_f}{{\widehat{\rho }}_f+{\widehat{\rho }}_w}.$$ [2]

This formulation of PDFF stems from the phase constrained method described by Liu et al (9). By assuming that the phase of water and fat within a voxel are equal at TE = 0 (i.e.: $\varphi$ in Eq. 1), PDFF can be estimated as a real variable (Eq. 2) from complex data. This is a reasonable assumption that accurately reflects the physics of spoiled gradient echo pulse sequence acquisitions (9).

After data acquisition and image reconstruction, the standard workflow of PDFF analysis proceeds to ROI analysis. Typical ROI analysis consists of selecting an ROI and then calculating a statistical description (e.g. mean, median, etc.) of the encompassed voxels of the PDFF map.

Noise in the multi-echo acquisition propagates to noise in the CSE-MRI estimates of fat and water ( ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ respectively). Therefore, PDFF maps are subject to a form of structured noise dependent on the noise distributions of ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$. Our work models ${\widehat{\rho }}_f\text{ and }{\widehat{\rho }}_w$as correlated Gaussian random variables with correlation coefficient λ_FW, means μ_F and μ_W, and standard deviations σ_F and σ_W, respectively. This modeling assumption follows from two characteristics of least squares theory. The first characteristic states that under conditions of Gaussian noise, linear least squares estimators are also normally distributed (23). Although our signal model is nonlinear, the fat and water signals themselves are linear elements within the nonlinear signal equation. While NLSQ estimators are not always distributed normally under non-asymptotic conditions, the second characteristic states that under certain requirements, NLSQ estimators are asymptotically normally distributed (23). Although CSE-MRI acquires a finite number of echoes, this asymptotic behavior provides added rationalization for employing the linear least squares result in our nonlinear least squares solution.

By modeling ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ as correlated Gaussian random variables, we were able to derive the previously uncharacterized structure of PDFF noise and understand the bias observed in its ROI analysis. This characterization of the noise distribution of PDFF is model-dependent and this work uses the model as described by Eqs. 1 and 2. However, this analysis remains generally applicable to a variety of CSE-MRI PDFF mapping applications provided that PDFF is calculated according to Eq. 2 and that ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ can be modeled as Gaussian random variables (an assumption tested in this work, see the Methods section below for both complex and mixed fitting NLSQ algorithms). Extending on the work of Fieller and Hinkley (24), we have determined (derivation provided in Supplementary Material, Appendix A) that the noise of CSE-MRI estimated PDFF (Eq. 2) has the following probability density function (PDF):

$$Pr\left(\widehat{\eta }=z\right)=\frac{b\left(z\right)d\left(z\right)}{\sqrt{2\pi }{\sigma }_F{\sigma }_Y{a}^3\left(z\right)}\left[\mathrm{\Phi }\left(\frac{\mathrm{b}\left(\mathrm{z}\right)}{a\left(z\right)\sqrt{1-{\lambda }_{FY}^2}}\right)-\mathrm{\Phi }\left(-\frac{\mathrm{b}\left(\mathrm{z}\right)}{a\left(z\right)\sqrt{1-{\lambda }_{FY}^2}}\right)\right]+\frac{\sqrt{1-{\lambda }_{FY}^2}}{\pi {\sigma }_F{\sigma }_Y{a}^2\left(z\right)}{e}^{\frac{-c}{2\left(1-{\lambda }_{FY}^2\right)}}$$ [3]

where

$$a\left(z\right)=\sqrt{\frac{z^2}{{\sigma }_F^2}-\frac{2z{\lambda }_{FY}}{{\sigma }_F{\sigma }_Y}+\frac{1}{{\sigma }_Y^2}}$$

$$b\left(z\right)=\frac{z{\mu }_F}{{\sigma }_F^2}-\frac{{\lambda }_{FY}\left({\mu }_F+{\mu }_{Y}z\right)}{{\sigma }_F{\sigma }_Y}+\frac{{\mu }_Y}{{\sigma }_Y^2}$$

$$c=\frac{{\mu }_F^2}{{\sigma }_F^2}-\frac{2{\mu }_F{\mu }_Y{\lambda }_{FY}}{{\sigma }_F{\sigma }_Y}+\frac{{\mu }_Y^2}{{\sigma }_Y^2}$$

$$d\left(z\right)=e^{\frac{b^2\left(z\right)-c{a}^2\left(z\right)}{2\left(1-{\lambda }_{FY}^2\right)a^2\left(z\right)}}$$

$$\mathrm{\Phi }\left(\mathrm{\lambda }\right)=\frac{1}{\sqrt{2\pi }}{{\displaystyle \int }}_{-\infty }^{\lambda }{e}^{\frac{-{\tau }^2}{2}}d\tau$$

$${\mu }_Y={\mu }_F+{\mu }_W$$

$${\sigma }_Y=\sqrt{{\sigma }_F^2+{\sigma }_W^2+2{\sigma }_F{\sigma }_W{\lambda }_{FW}}$$

$${\lambda }_{FY}=\frac{{\sigma }_F^2+{\sigma }_F{\sigma }_W{\lambda }_{FW}}{{\sigma }_F\sqrt{{\sigma }_F^2+{\sigma }_W^2+2{\sigma }_F{\sigma }_W{\lambda }_{FW}}}$$

Figure 1 contains plots of this derived distribution for two cases of PDFF (η=0% and 100%) over a range of SNR values (SNR=3, 5, 10, and 15). A key property of this distribution is that, at low SNR, it is asymmetric with a distinct heavy-tailed feature at both low and high PDFF values. In ROI analysis, this asymmetry explains the biased distribution of voxels observed in PDFF maps that can skew measurements. This ties in with a second key property, specifically, that computer-aided results (Maple 2016.2 Maplesoft, a division of Waterloo Maple Inc., Waterloo, Ontario) demonstrated that this distribution has an undefined expectation. The combination of heavy-tailed asymmetry and undefined moments is indicative of potentially unstable and unreliable sample means and variances (25), which helps to explain the bias observed in averaging PDFF ROI values.

Figure 1.

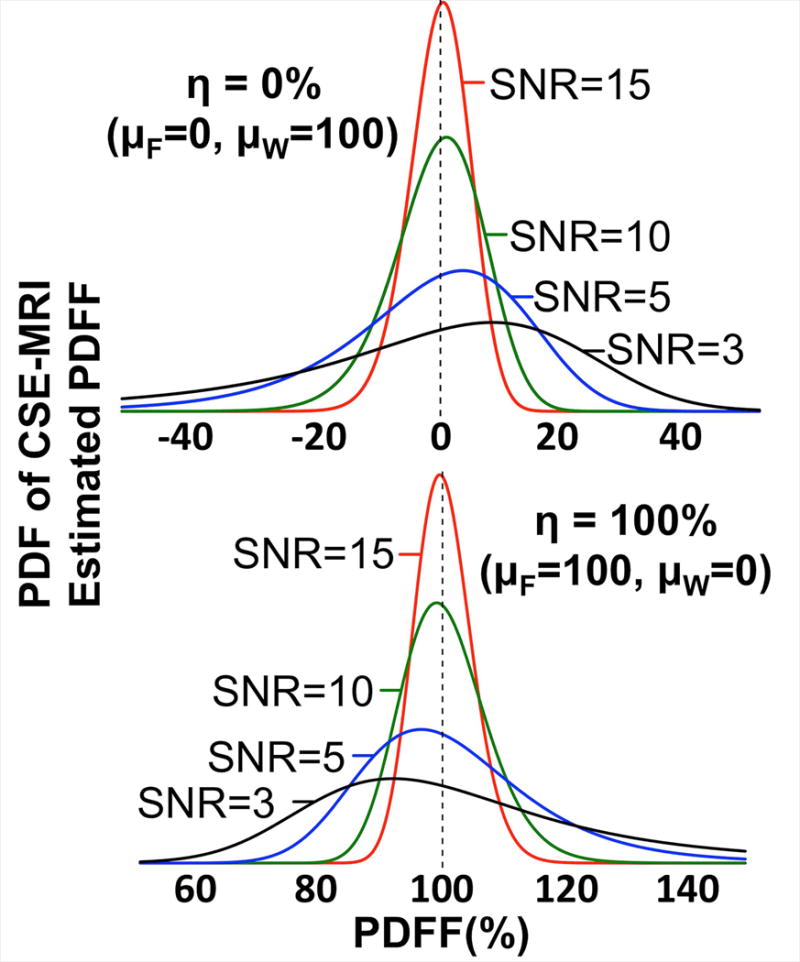
The probability density function of CSE-MRI estimated PDFF becomes increasingly asymmetric as SNR decreases. These plots show the derived noise distribution of PDFF over a range of SNR values. μ_F and μ_W, shown in each plot, were adjusted to select the true PDFF (η). λ_FW, σ_F, and σ_W (here shown with λ_FW=0.0, σ_F=σ_W) were adjusted to modulate the SNR (as approximated by SNR = (μ_F+μ_W)/(σ_F²+σ_W²+2σ_Fσ_Wλ_FW)^1/2). While these plots show λ_FW=0.0, it should be noted that the distribution remains asymmetric as λ_FW is varied.

Another important property of this distribution is its high SNR approximation. In his work on the ratio of Gaussian random variables, Hinkley (24) showed that as the probability that the random variable in the denominator is greater than zero approaches unity, then the cumulative density function (CDF) will approach a shifted and scaled standard normal CDF. In our work, these conditions are satisfied when $\frac{{\mu }_Y}{{\sigma }_Y}\to \infty$ (i.e. high SNR). This means that the probability density function of PDFF from a high SNR acquisition could be reasonably approximated as a Gaussian distribution. Under these conditions, using the sample mean for ROI analysis in PDFF maps should not result in a sizable bias.

Strategies to Account for Noise-related Bias in PDFF Estimation

The remainder of this will paper will focus on the methods, results, and conclusions of simulations, phantom experiments and in vivo human acquisitions designed to study the theoretical predictions given in this section. However, we specifically evaluated three statistics for their use in PDFF map ROI analysis, which we will enumerate here before advancing to their use in subsequent experiments:

1. Mean. All published reports describing PDFF measured using CSE-MRI use the mean statistic as part of their analysis. We study it as a reference by which to compare alternative strategies.

2. Median. The median exhibits known robustness to outlying data (26). We study it because the heavy-tailed asymmetry of the PDFF noise distribution can be viewed as outlying data to the true PDFF value.

3. Maximum Likelihood Estimator (MLE). This approach uses maximum likelihood estimation to fit the distribution of PDFF values from an ROI to the PDF derived above. In practice, the MLE reduces to an optimization problem and is formulated as:

   $${\widehat{\theta }}_{\mathit{MLE}}=\underset{\theta }{\text{argmin}}\{-{\displaystyle \sum }_{\lambda \epsilon \mathrm{\Lambda }}\log \left(\text{Pr}\left(\widehat{\eta }=\lambda ;\theta \right)\right)\}.$$ [4]
   Where $\theta =\left\{{\mu }_F,{\mu }_W,{\sigma }_F,{\sigma }_W,{\rho }_{FW}\right\}$ represents the parameter vector, Λ the set of all PDFF values in an ROI, λ a single PDFF value from Λ, and Pr( $\widehat{\eta }$=λ; θ) the probability density function given by Eq. 3 with parameters θ. The solution to this formulation returns ${\widehat{\theta }}_{\mathit{MLE}}$, the vector containing the parameters most likely to fit the measured data to the theoretical distribution. The components of ${\widehat{\theta }}_{\mathit{MLE}}$ can then be used to give an estimate of the true PDFF value of the ROI:

   $${\widehat{\eta }}_{\mathit{MLE}}=\frac{{\mu }_{F,\mathit{MLE}}}{{\mu }_{F,\mathit{MLE}}+{\mu }_{W,\mathit{MLE}}}$$ [5]

   In the experiments of the following sections, we used an implementation of the Nelder-Mead algorithm to perform the MLE minimization given by Eq. 4 (27,28)

Methods

Modeling ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ as Gaussian Random Variables

In this experiment, designed to test the assumption that ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ can be modeled as Gaussian random variables, CSE-MRI data were simulated for a given PDFF value according to Eq. 1 with parameters including 6 echoes, TE₁=1.2ms, ΔTE=2.0ms, and B₀=1.5T. Zero-mean complex Gaussian noise, with standard deviation ${\sigma }_{\mathit{noise}}$, was added to the signal to reflect a specific SNR (SNR = $\frac{{\rho }_w+{\rho }_f}{{\sigma }_{\mathit{noise}}}$). 100,000 repetitions of complex fitting NLSQ were performed to obtain 100,000 estimates of fat and water at a specified SNR. These estimates were broken up into 10,000 sets of 100 fat and water estimates and each set was tested for normality using the Sharpiro-Wilk test (29). This process was repeated for all possible combinations of PDFF=0%, 50%, 100% and SNR=3, 5, 15. An alpha level (significance level) of 0.05 was selected for the Shapiro-Wilk tests. Finally, the experiment was repeated using the mixed fitting NLSQ algorithm (13).

Effect of Statistics in ROI Analysis on Bias

The following four subsections and their experiments are aimed to validate our theoretical work by analyzing the ability of the three statistics listed above to accurately estimate the true PDFF value of an ROI of uniform PDFF. First, the water phantom experiment will look for the presence of the derived heavy-tailed distribution in a simple setup where the true PDFF (0%) is known with certainty. The simulations and phantom experiments that follow compare the performance of the three statistics over the entire range of PDFF (0-100%). The final subsection describes proof of concept experiments designed to compare the performance of the three statistics in vivo.

Water Phantom Experiment

Four acquisitions of a 10-cm diameter cylindrical phantom filled with distilled water (true PDFF=0%) doped with NiCl₂ (Quadrature Lower Extremity Phantom, P/N #14246, IGC – Medical Advances, Milwaukee, WI) were acquired on a 1.5T clinical MRI system (Signa HDxt, GE Healthcare, Waukesha, WI) with a single channel quadrature head coil. All acquisitions were performed with a multi-echo 3D spoiled gradient echo pulse sequence, with the following parameters: 21×14.7cm field of view and 256×180 matrix for 0.82×0.82mm in-plane resolution, 1.7mm slice thickness, 6 echoes in one TR using a flyback readout with TE₁=1.9ms and ∆TE=3.3ms, BW=±142.86kHz, and number of signal averages=1. The flip angles (varied to modify the SNR) were 3°, 5°, 10°, and 20°. As there is no fat in this phantom, the use of T1 weighting will not lead to T1 related bias in the estimated PDFF.

SNR was measured empirically in the real data of the first of the complex echo images using two ROIs as the average signal over the standard deviation of the noise. A mixed magnitude/complex fitting method (13) was used to estimate parametric maps of fat and water which were then used to calculate PDFF maps. In each PDFF map, an ROI of approximately 11,000 pixels was drawn and the mean, median and MLE statistics were used to compute a PDFF estimate, which was then compared to the true PDFF value (0%).

Numerical Simulations

The accuracy and precision of three statistics (mean, median, MLE) were assessed using two sets of Monte-Carlo simulations. In the first set, a large number of repetitions were performed allowing the evaluation of each statistic in a case where the noise distribution was well represented. In the second set, repeated calculations of each statistic were performed on ROIs allowing the evaluation of each statistic in a case that more closely replicates a typical acquisition.

In a first set of numerical simulations, complex-valued CSE-MRI data were simulated for a given PDFF value according to the signal equation shown in Eq. 1 with parameters including 6 echoes with TE₁=1.2ms and ΔTE=2.0ms, and B₀=1.5T (13). Zero-mean complex Gaussian noise, with standard deviation ${\sigma }_{\mathit{noise}}$, was added to the signal to reflect a specific SNR (SNR = $\frac{{\rho }_w+{\rho }_f}{{\sigma }_{\mathit{noise}}}$). Complex fitting NLSQ of the signal equation (Eq. 1) and PDFF calculation (Eq. 2) of 10,000 repetitions were performed. This process was repeated for each PDFF-SNR pair over a range of PDFF (0-100%) and SNR values (1–30). The mean, median, and MLE of each set of 10,000 PDFF estimates were taken and compared to the true PDFF value.

In the second set of numerical simulations, a 2D CSE-MRI numerical phantom, with 20 regions of varying PDFF values, was simulated according to the signal equation given in Eq. 1 with parameters including 6 echoes in one TR with TE₁=1.2ms and ΔTE=2.0ms, optimized for B₀=1.5T (13). Gaussian noise was added and a NLSQ complex fitting algorithm was used to estimate fat and water maps from complex valued data based on the signal equation (Eq. 1). A PDFF map was then calculated from the estimated fat and water maps according to Eq. 2. ROIs of approximately 220 pixels were then drawn in the each of the 20 regions of varying PDFF (0-100%) and the mean, median, and MLE statistics were calculated for each ROI. These estimates were then compared against the underlying PDFF value of each ROI. This process was repeated 200 times for each SNR value (SNR=3 and SNR=5).

Fat-Water Phantom Experiments

The phantom experiments were designed to replicate the second set of numerical simulations. Three 2D-CSE-MRI acquisitions in an agar-based fat-water phantom (30) containing multiple vials with varying PDFF concentration (0-100%) were performed on a 1.5T MRI (Optima MR450W, GE Healthcare, Waukesha, WI) using a single-channel quadrature head coil. The first two acquisitions acquired 100 repetitions of an axial slice at SNR=3 and SNR=5 (calculated empirically using the correction factor described by Henkelman (31) for a single channel coil). The third acquisition was a single repetition of the same axial slice acquired as a reference with approximate SNR=70. All acquisitions employed flyback readouts in a single TR. Scan parameters can be seen in Table 1.

Table 1.

Fat-Water Phantom Acquisition Parameters.

Measured SNR	FOV	Matrix (pixels)	In-Plane Resolution	Slice Thickness	Number of Echoes	TE1	ΔTE	Flip Angle	BW	NSA
3	24×9.6cm2	256×102	0.9×0.9mm2	4mm	6	2.1ms	2.5ms	5°	±125kHz	1
5	24×9.6cm2	256×102	0.9×0.9mm2	8mm	6	2ms	2.4ms	5°	±125kHz	1
70	24×9.6cm2	256×102	0.9×0.9mm2	10mm	6	2ms	2.4ms	5°	±125kHz	100

For all acquisitions, the confounder-corrected NLSQ mixed fitting CSE-MRI algorithm (13), using the same signal model of Eq. 1, was used to reconstruct PDFF maps from the acquired data. Estimates from ROIs of approximately 310 voxels drawn within each of the 11 vials of the PDFF maps were taken and compared to the SNR=70 case. If fat/water swaps were encountered during ROI analysis, those particular ROIs were excluded to avoid the confounding effects of fat/water swaps on the comparison of the three ROI statistics.

In Vivo Experiment

Retrospective data from a previously reported study (32) were reanalyzed for the purpose of evaluating the performance of the three ROI statistics (mean, median, MLE). Briefly, the acquisition was performed on a 1.5T clinical MRI system (Optima MR450W, GE Healthcare, Waukesha, WI) using a 32-channel phased array torso coil (Neocoil, Pewaukee, WI). In each patient, images of the liver were acquired using a 2D sequential CSE-MRI sequence (32) and a 3D CSE-MRI sequence (33). In contrast to a typical interleaved acquisition, where all of the slices for a particular phase encode are acquired before moving to the subsequent phase encode, a sequential acquisition strategy acquires all phase encode lines for a particular slice before moving on to the next slice. This sequential acquisition strategy gains improved motion robustness at the expense of SNR. Additionally, single voxel magnetic resonance spectroscopy (MRS) was acquired in the right lobe of the liver. Both the image and MRS data were reconstructed offline and the same confounder corrected mixed fitting method (13) was used to generate PDFF maps. ROIs, corresponding to the location of the MRS voxel, were drawn in the higher SNR (3D CSE-MRI) and lower SNR (2D sequential CSE-MRI) PDFF maps. SNR values were measured in the magnitude first echo images of each dataset as the average signal over the standard deviation of the noise within an ROI co-localized with the MRS voxel.

Co-localization of the MRS voxel in the 3D CSE-MRI and MRS acquisitions was processed automatically as both were recorded during end-expiration breath holds. A trained radiologist assisted in the co-localization of the MRS voxel in the 2D CSE-MRI acquisition. ROI area in the 3D CSE-MRI PDFF maps ranged between 60-70 pixels, while the ROI areas in the 2D CSE-MRI PDFF maps were approximately 50 pixels. Three cases (low, moderate, and high levels of liver fat) were selected. Mean, median, and MLE estimates of PDFF were calculated from the ROIs of each case and then compared between the high and low SNR acquisitions and against MRS-PDFF.

Results

Modeling ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$ as Gaussian Random Variables

Results of the Shapiro-Wilk tests for the complex fitting NLSQ algorithm, summarized in Table 2, indicate more significant P-values (indicating not enough evidence to reject normality) with increasing SNR in both CSE-MRI estimates of fat and water. Near unity W-statistic averages suggest substantial Gaussian behavior at all PDFF-SNR pairs, and all average P-values exceeded the 0.05 alpha threshold, although some median P-values did not. Additionally, Figure 2 shows plots of the distributions of the 100,000 simulated fat and water estimates for each PDFF-SNR pair with best-fit Gaussian curves overlaid. Nearly identical results were recorded for the mixed fitting NLSQ algorithm (shown in Supporting Table S1 and Supporting Figure S2).

Table 2.

Shapiro-Wilk Test Results for Complex Nonlinear Least Squares Fitting

	PDFF	SNR	Average P-value	Median P-value	Average W-Statistic
Fat	0%	3	0.38	0.32	0.98
		5	0.48	0.48	0.99
		10	0.49	0.49	0.99
		15	0.49	0.49	0.99
	50%	3	0.08	0.00	0.94
		5	0.19	0.07	0.97
		10	0.39	0.35	0.98
		15	0.44	0.42	0.98
	100%	3	0.18	0.05	0.96
		5	0.36	0.29	0.98
		10	0.46	0.45	0.99
		15	0.49	0.49	0.99
Water	0%	3	0.30	0.21	0.98
		5	0.42	0.38	0.98
		10	0.47	0.46	0.99
		15	0.49	0.49	0.99
	50%	3	0.05	0.00	0.94
		5	0.18	0.06	0.97
		10	0.39	0.35	0.98
		15	0.44	0.42	0.99
	100%	3	0.07	0.00	0.92
		5	0.35	0.28	0.98
		10	0.48	0.48	0.99
		15	0.49	0.48	0.99

Low P-values (<0.05) indicate evidence against normality. Higher p-values indicate that there is not enough evidence to reject normality.

W-Statistic values near 1 are indicative of normally distributed data.

Figure 2.

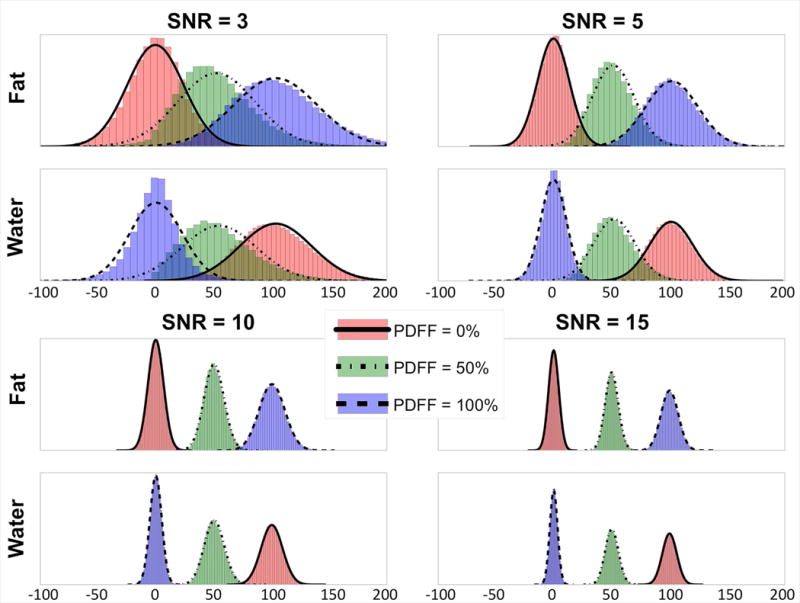
The noise distributions of separated water and fat signals closely follow a Gaussian distribution, particularly at higher SNR and lower PDFF. In this simulated example, the distributions of all three PDFF values appear strongly Gaussian at SNR=10 and 15 for both fat and water signals. Further, the noise distributions for water and fat signals at very low SNR (SNR=3) appear more Gaussian for PDFF=0% than for either PDFF=50% or 100%. For this simulation 100,000 individual CSE-MRI pixel simulations were performed for each SNR/PDFF pair over a range of SNR (3,5,10,15) and PDFF values (0%, 50%, 100%). For each SNR/PDFF pair, the histograms of the resulting estimates of fat and water were plotted along with their respective Gaussian best-fit curves. Note that outliers outside the range of −100 to 200 were excluded.

Effect of Statistics on Bias in ROI Analysis

Water Phantom Experiment

The noise distributions of PDFF estimations were observed in a water phantom at different SNRs ranging from 5 to 28 (Figure 3). The noise distributions became increasingly asymmetric as SNR decreased, providing verification of a theoretically derived property of the PDFF noise distribution. The asymmetric noise distribution at low SNR (i.e. SNR=5 and SNR=8) caused a bias in the mean PDFF statistic. This bias was reduced when a median or MLE PDFF statistic was used.

Figure 3.

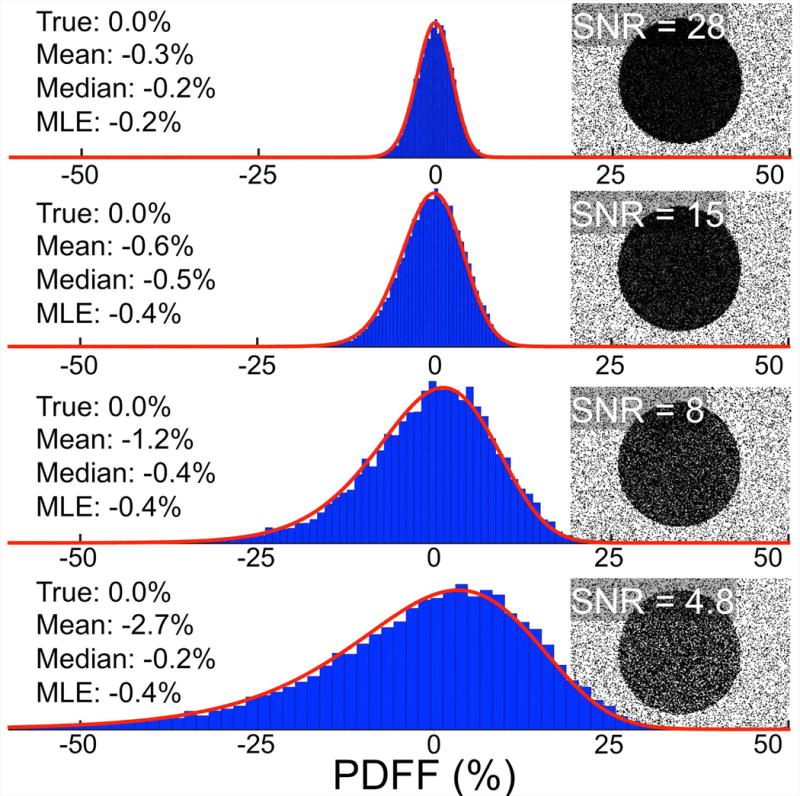
The noise distribution of PDFF estimation, as shown in a water phantom, becomes more asymmetric as SNR decreases. The heavy-tailed asymmetry of the distribution (seen clearly in the SNR=4.8 histogram) is a preliminary indicator that PDFF estimates obtained by averaging may be biased. Shown are histograms and corresponding PDFF Maps from sequential 3D CSE-MRI acquisitions of a water phantom (PDFF=0%). The blue bars of the histogram represent roughly 11,000 pixel values taken from within the water region of the PDFF map. The red line is the MLE fitting of the derived PDFF noise distribution.

Numerical Simulations

Figure 4 shows the bias in the PDFF estimate of the mean, median, and MLE statistics over a range of SNR and PDFF in the case where the noise distribution is well sampled. The results show that the median and MLE statistics provide accurate estimates of the PDFF across all PDFF even at low SNR values where the mean statistic is biased. It should be noted that these large-sample results reflect a best-case situation that is atypical for in vivo applications.

Figure 4.

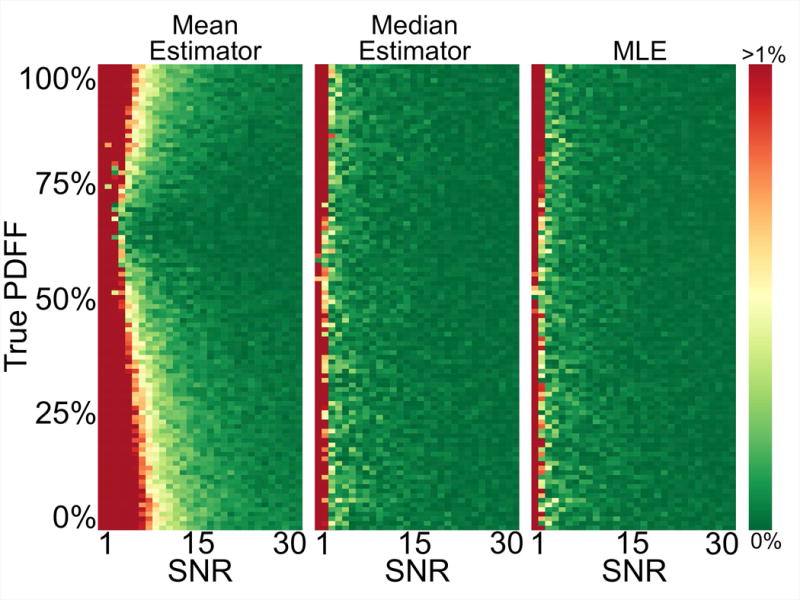
Median and MLE estimators provide accurate PDFF quantification even at very low SNRs, where the mean estimator is biased. Each rectangular pixel represents the result of using the mean, median, or MLE estimator, respectively, on the equivalent of an ROI of roughly 10,000 pixels of a particular PDFF at a specified SNR. The colors map the absolute error of the estimators from 0% to a capped error of 1%.

Figure 5 shows the bias and precision of the mean, median, and MLE statistics in the case where the noise distribution is sampled with the number of voxels contained in a more typical ROI thereby simulating the conditions of a ROI analysis. At both SNR=3 and SNR=5, substantial PDFF dependent bias was observed with the mean statistic. The median and MLE statistics mitigate this bias.

Figure 5.

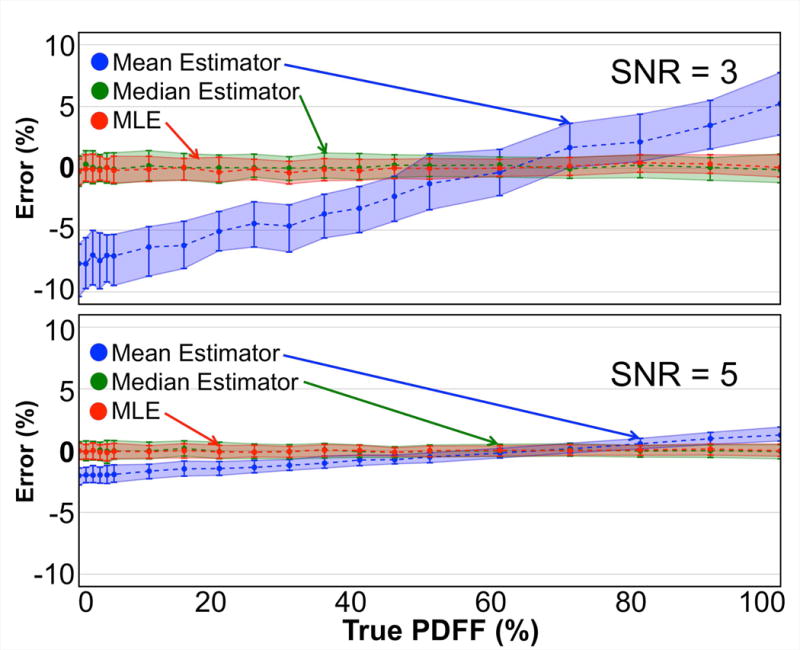
In simulation, the mean of an ROI in a PDFF map tends to underestimate low PDFF values and overestimate high PDFF values. In contrast, note the apparent unbiased quality of both the median and MLE in determining an estimate of the true PDFF. Each point represents a statistical analysis (median, 25^th and 75^th percentiles) of the PDFF estimation error of the three estimators on 200 noisy realizations of a simulated ROI. Signed absolute errors are plotted.

Linear regression analysis of the second set of numerical simulations (shown in Supporting Fig. S3) showed the median and MLE statistics to be better predictors of true PDFF at both SNR=3 and SNR=5. In the SNR=3 case, the mean statistic was shown to exhibit a strong bias (intercept=−17.7%) and large variability (R²=0.01). The variability in the mean statistic was greatly reduced in the SNR=5 case (R²=0.99, matching the median and MLE), but bias remained (intercept=−2.1% compared to 0% and −0.1% of the median and MLE statistics, respectively).

Phantom Experiments

Figure 6 shows the bias and precision of the mean, median, and MLE statistics from PDFF map ROI analysis of fat-water phantom acquisitions. Consistent with the simulated results, the median and MLE estimates outperform the mean statistic for PDFF estimation. Our analysis found 4 ROIs with fat/water swaps in the SNR=3 case, which were then removed from our calculations.

Figure 6.

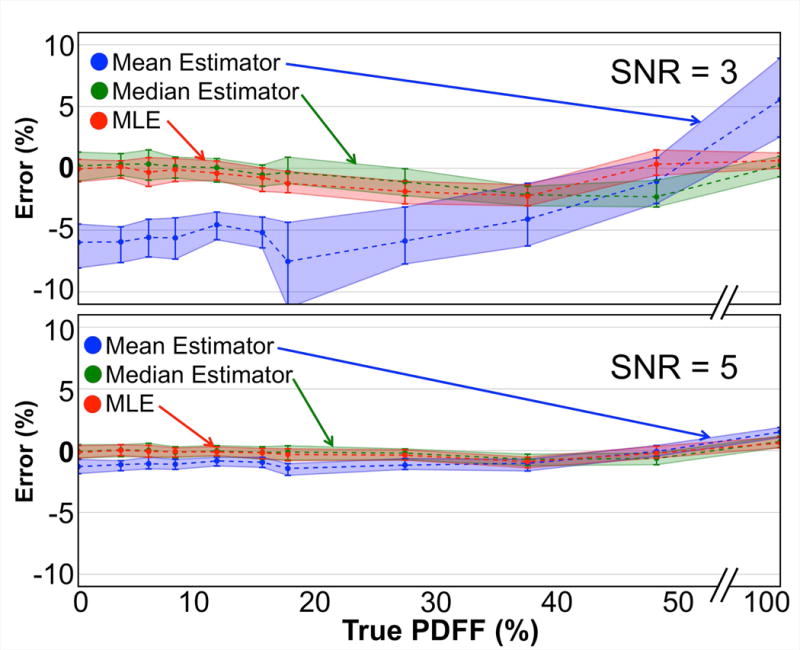
Consistent with the results of the simulated data, in phantom acquisitions the mean underestimates low PDFF values and overestimates high PDFF values in ROIs, while both the median and the MLE remain largely unbiased. Two sets (SNR=3 and 5) of 100 back-to-back CSE-MRI acquisitions of an axial slice of a PDFF phantom containing 11 vials of varying PDFF values were compared against a high-SNR acquisition (SNR=70). Each point represents a statistical analysis (median, 25^th and 75^th percentiles) of the error of the three estimators on 100 corresponding ROIs. Signed absolute errors are plotted.

Linear regression analysis (again shown in Supporting Fig. S3) showed the mean statistic to be a poor predictor of true PDFF in the lowest SNR regime (SNR=3) with a slope=1.2, intercept=−6.4% and R²=0.18. At the same SNR, the median and MLE statistics were much more predictive of true PDFF with slopes=0.99 and 0.99, intercepts=−0.3% and −0.7% and R²=0.99 and 0.99, respectively. At SNR=5, linear regression showed improved performance of the mean statistic (slope=1.0, intercept=−1.5%, R²=0.99) with the median and MLE statistics exhibiting similar slopes and R² values, but with intercepts closer to 0%.

In Vivo Experiments

Finally, composite PDFF estimates were made in three in vivo cases. SNR ranged from 5-7 in the conventional 2D sequential CSE-MRI maps and from 10-15 in the 3D CSE-MRI maps. Using the median or MLE statistics in ROI analysis of the three cases of low, medium, and high liver fat content patients, yielded average PDFF estimation improvements of 1.7%, 1.1%, and 1.2%, respectively, when compared to MRS. The calculated ROI statistics for each of the three in vivo cases are shown in Figure 7.

Figure 7.

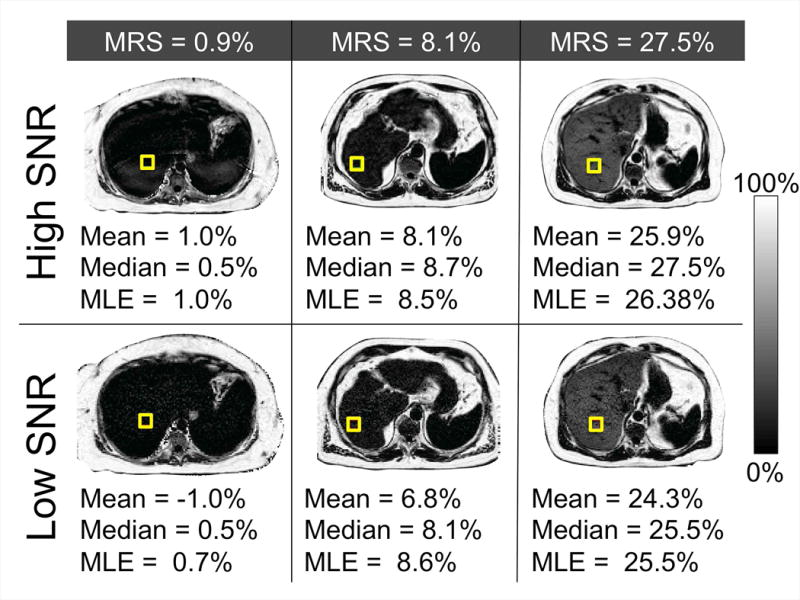
In vivo, the median and MLE ROI statistics of the lower SNR acquisitions return more accurate composite PDFF measurements than the mean when compared against the MRS PDFF values. Specifically, median and MLE statistics in the lower SNR PDFF maps (2D sequential CSE-MRI) made average estimation improvements over the mean of 1.7%, 1.1%, and 1.2%, respectively, when compared to MRS. As expected, mean, median, and MLE estimates show reduced bias in the higher SNR PDFF maps (3D CSE-MRI).

Discussion

In this work we have successfully characterized the noise distribution of PDFF as quantified using CSE-MRI, and have provided a closed form expression of its probability density function. We demonstrated that this SNR- and PDFF-dependent asymmetric noise distribution leads to bias when measuring the average value of an ROI placed in a low SNR PDFF map. To address this, we provided two strategies that mitigated noise-related bias in PDFF estimation. We showed that fitting ROI voxel values to the derived PDFF noise distribution (using the MLE) or using the median improved the accuracy of PDFF ROI analysis in simulation and in phantom acquisitions.

Our derivation began by modeling the estimated fat and water signal components ( ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$, respectively) of CSE-MRI as Gaussian. We verified this assumption in digital simulations and phantom experiments at 1.5T. Given that the physics of CSE-MRI is fundamentally the same as at 3.0T and the fact that PDFF estimation is independent of field strength (8,34), it is likely that the results from this work also extends to 3.0T, although further work would be needed to demonstrate this rigorously. Using this model, we were able to derive a closed form expression for the PDFF noise distribution. In this work, we do not claim to have characterized the non-asymptotic behavior of ${\widehat{\rho }}_f$ and ${\widehat{\rho }}_w$, but rather, we recognize that the premise of correlated Gaussian random variables provided a good foundation for characterizing the PDFF noise distribution. Additionally, our analysis employed a signal equation (Eq. 1) that required estimating fat and water before calculating PDFF (Eq. 2); however, PDFF can be estimated directly by rewriting this signal equation as a function of PDFF multiplied by a scaling factor as shown by Horng et al (35). In an analysis not presented in this paper, we determined that the distributions of PDFF estimates for either formulation of the signal equation share identical distributions and biases and that both are characterized by the derived distribution presented in this work.

We have shown that the distribution of PDFF values in ROI analysis, and accompanying bias, depends strongly on the SNR of the underlying source data. Specifically, we have demonstrated that the bias is reduced as SNR increases. To that end, we generally recommend a minimum SNR of 10 when using the mean statistic in PDFF ROI analysis to ensure absolute errors less than 1%; however, we recognize that this requirement could vary based on the application and need for accuracy. The derived distribution of the noise of PDFF, combined with the results of this work, should be a powerful tool in determining application specific SNR thresholds. Future work is required to validate this guideline for various in vivo circumstances.

Viewed in the context of current literature, this work extends on the work done by Liu et al. The “magnitude discrimination” method described by Liu et al resulted in a large reduction of noise bias in comparison to the original approach that used magnitude estimates of fat and water signals to calculate PDFF maps (9). However, as the use of CSE-MRI techniques has expanded into applications that utilize low SNR acquisitions (due to breath-hold limitations, low flip angle needed to remove T1 bias, parallel imaging, and simultaneous corrections for R2* confounder effects, etc.), substantial noise dependent bias is still observed. Our study derived, from first principles, the underlying statistical noise model of PDFF estimation and thus characterized the previously undescribed source of PDFF bias. From that characterization we were able to propose strategies that reduce bias in PDFF ROI analysis. The results of this study highlight the importance of understanding the noise distribution of parametric maps where quantitative measurements are taken, particularly in low SNR acquisitions. Similar analysis, involving MLE statistics, could be applied to a wide range of currently accepted MR biomarkers.

Our study had several limitations. First, this manuscript is focused on characterizing the noise distribution of PDFF and validating improved estimation techniques using simulations and phantom acquisitions. For this reason, the in vivo analysis was limited in number and focused exclusively in the liver. As noted in the introduction, PDFF can be used to quantify triglyceride content in many organs, not just the liver. Therefore, subsequent work will examine the effect of noise dependent bias in PDFF in both the liver and other organ systems. For our purposes, the in vivo experiment included served as a proof of concept for the application of the techniques described in this paper to be applied in vivo. The relatively minor bias observed in the mean statistics of the low SNR images in this experiment is consistent with what we would expect based on the SNR measurements and suggests that the median and MLE would still effectively reduce bias in even lower SNR acquisitions. Future studies are being planned to perform rigorous clinical evaluation of these strategies in vivo to determine their performance in CSE-MRI acquisition and PDFF reconstruction protocols and to study their SNR requirements.

Our study was also limited in comparing of the performance of the median and MLE statistics. Both the median and MLE statistics resulted in improved PDFF ROI analysis estimation accuracy and stability compared to the mean statistic; however, the relative performance between the median and MLE statistics remains unclear. While a single calculation of an MLE algorithm can estimate PDFF quickly (we averaged less than one second per ROI for ROIs of approximately 500 pixels), it requires special and specific programming. The median, on the other hand, is a simple calculation, which is functionally present in many analysis software packages. The convenience of the median statistic, coupled with the inability of our current work to distinguish their relative performance, would suggest that it is preferable over the MLE in practice.

There is some precedent to using the median instead of the mean in ROI analysis, and past MRI studies have used the median to report values in ROI analysis (36–38). More specifically, Holmes et al made the observation that the median would better represent the non-Gaussian distribution observed in PDFF (19). We note that use of the median statistic does not negate the importance of understanding the underlying statistical model. Future work may reveal a more optimal estimation method based on the statistical modeling or fully assess the relative performance of the median and MLE statistics.

In contrast to other noise performance studies for CSE-MRI, this work has largely ignored the effects of echo time choices. Optimization of echo times can be used to maximize SNR performance. We recognize that the choice of echo times plays an important role in determining the bias of PDFF; however, our work has largely relied on that effect being encompassed by SNR. Future work will examine the role, if any, that echo time selection could have on noise related PDFF bias. Our simulations used the echo times suggested by Hernando et al (13) for optimizing SNR performance. However, we note that we used a phase constrained signal equation and therefore it is possible that our choice of echo times may be non-optimal. An additional limitation of our work was that the choice of echo times used for simulations did not precisely match those for our phantom experiments. While we anticipate this discrepancy should have a negligible effect on our results, a more careful analysis of the impact of echo times on noise related PDFF bias is needed.

In all numerical simulations, NLSQ estimates were performed with a complex fitting method (see Hernando et al (13) for comparison of fitting methods). Complex fitting is the preferable choice given our signal model (Eq. 1) and definition of PDFF (Eq. 2); however, in phantom acquisitions we found the mixed complex/magnitude fitting (13) to produce PDFF estimates (mean, median, and MLE) with less bias than those that resulted from a purely complex fitting. Mixed fitting algorithms are almost equivalent to a pure complex fitting algorithm, but they ignore the phase on the first echo of multi-echo acquisitions to avoid bias created by the presence of eddy currents (13). We hypothesize that this may be why the mixed fitting performed better in our phantom experiments. As the in vivo experiment is mainly proof of concept, we also used the mixed complex/magnitude fitting to be consistent with the phantom acquisitions.

Magnitude fitting is another method for computing NLSQ. Magnitude fitting is common, but leads to a known SNR reduction in the resultant fat and water maps (13). Preliminary magnitude fitting simulations, not presented in this paper, indicate significant P-values and high W-statistics from Sharpiro-Wilk tests (29) performed on the estimated fat and water maps, suggesting Gaussian behavior. As this was the only assumption required to characterize the PDFF distribution, it follows that the same statistical analysis could apply to PDFF maps generated using a magnitude fitting method. However, the methods presented in this paper correct bias in estimated PDFF maps, not bias in the fat and water maps. Therefore, should the estimated fat or water maps incur a bias as a result of magnitude fitting, then the mean, median, and MLE statistics in the PDFF map would all yield inaccurate results. Future work is being planned to study more closely the effects of fitting methods on the PDFF noise distribution.

In conclusion, this work provides improved characterization of the noise distribution of PDFF estimated using CSE-MRI. This characterization enabled the development of new strategies for mitigating SNR dependent noise-related bias in PDFF maps. These strategies may have important application in emerging CSE-MRI fat quantification techniques that operate at low SNR.

Supplementary Material

Supp info

Supporting Table S1: Shapiro-Wilk Test Results for mixed fitting NLSQ. Low P-values (<0.05) indicate evidence against normality. Higher P-values indicate that there is not enough evidence to reject normality. W-Statistic values near 1 are indicative of normally distributed data.

Supporting Figure S2: Distribution plots for mixed fitting NLSQ. The noise distributions of water and fat signals estimated by mixed fitting NLSQ closely follow a Gaussian distribution, particularly at higher SNR and lower PDFF. Similar to complex fitting NLSQ CSE-MRI (see Figure 2), the distributions of all three PDFF values appear strongly Gaussian at SNR=10 and 15 for both fat and water signals. Further, the noise distributions for water and fat signals at very low SNR (SNR=3) appear more Gaussian for PDFF=0% than for either PDFF=50% or 100%. For this simulation 100,000 individual mixed fitting NLSQ CSE-MRI pixel simulations were performed for each SNR/PDFF pair over a range of SNR (3,5,10,15) and PDFF values (0%, 50%, 100%). For each SNR/PDFF pair, the histograms of the resulting estimates of fat and water were plotted along with their respective Gaussian best-fit curves. Note that outliers outside the range of −100 to 200 were excluded.

Supporting Figure S3: Linear regression analysis of numerical and phantom experiments. Linear regression analysis reveals reduced bias and lower variability of the median and MLE statistics compared to the mean, especially when SNR=3. Each point represents the mean, median, or MLE of an ROI at the specified SNR and true PDFF. The solid line is the linear fit of the data whose accompanying function and R² value is given in each plot. The dashed line (often covered by the solid line) represents the perfect predictor (y=x and R²=1).

Appendix A: Derivation of the probability density function of PDFF.