Significance
Investigations of the free-living nematode Caenorhabditis elegans give powerful insights into fundamental biological processes that are conserved across species. Locomotion of this model organism is used to assess muscular and neural defects and score impacts of genetic mutations and pharmacological interventions. Existing analyses of the nematode gait have been focused on 2D locomotion, and 3D motion remains largely unexplored. We identify and mathematically describe a unique 3D behavioral pattern in burrowing and swimming—a roll maneuver—which, in combination with 2D turns, allows the nematode to explore bulk media. Our results provide important insights into 3D neuromuscular actuation and may be used to develop better assays for locomotion phenotype analysis.
Keywords: Caenorhabdtis elegans, undulatory locomotion, 3D gait, maneuverability, behavior
Abstract
Locomotion of the nematode Caenorhabditis elegans is a key observable used in investigations ranging from behavior to neuroscience to aging. However, while the natural environment of this model organism is 3D, quantitative investigations of its locomotion have been mostly limited to 2D motion. Here, we present a quantitative analysis of how the nematode reorients itself in 3D media. We identify a unique behavioral state of C. elegans—a roll maneuver—which is an essential component of 3D locomotion in burrowing and swimming. The rolls, associated with nonzero torsion of the nematode body, result in rotation of the plane of dorsoventral body undulations about the symmetry axis of the trajectory. When combined with planar turns in a new undulation plane, the rolls allow the nematode to reorient its body in any direction, thus enabling complete exploration of 3D space. The rolls observed in swimming are much faster than the ones in burrowing; we show that this difference stems from a purely hydrodynamic enhancement mechanism and not from a gait change or an increase in the body torsion. This result demonstrates that hydrodynamic viscous forces can enhance 3D reorientation in undulatory locomotion, in contrast to known hydrodynamic hindrance of both forward motion and planar turns.
Investigations of locomotion of the nematode Caenorhabditis elegans can provide a wealth of knowledge on physiology, muscle biology, and neural control of movement and behavior. Locomotion depends on muscular strength (1–3), neuromuscular coordination (4, 5), and processing of information from sensory inputs (6, 7). Locomotory readouts are thus extensively used to quantify effects of genetic mutations (8–10), exercise, nutrition, and environmental factors (11–17) and to evaluate pharmacological impacts (18, 19).
In its natural environment (soil rich in decaying organic matter), C. elegans interacts with a complex 3D surrounding medium that includes soft organic materials and rainwater (20, 21). Most studies of nematode locomotion, however, have focused on 2D motion (22–32), and little effort has been made to characterize worm motility in 3D environments.
Only recently was 3D burrowing motion of C. elegans in soft substrates stereoscopically imaged (33) and a statistical analysis of basic locomotory parameters reported (34); it was also shown that a burrowing nematode can reorient itself in response to external stimuli (34, 35). Furthermore, feasibility of using 3D motion to assess genetic mutations (36) and to identify muscular dystrophy (34) was experimentally demonstrated.
Such 3D methods of scoring C. elegans locomotory behavior can achieve better sensitivity than screens based on 2D observations alone. However, unleashing the full potential of these promising techniques requires complementary efforts to identify specific behavioral patterns associated with 3D reorientation maneuvers. A thorough quantitative understanding of 3D gait geometry and mechanics is also important for gaining insights into mechanisms of neuromuscular actuation of body movements and for development of next-generation software packages for automated tracking and analysis of nematode behavior.
Active Spatial Reorientation Maneuvers of C. elegans: Planar Turns and 3D Rolls
In our investigation of 3D locomotion of C. elegans in bulk media we focus on active body reorientation, in contrast to recently studied passive changes of locomotion direction produced by interactions of the nematode body with obstacles (37), boundaries (30), and/or external flow (31). Active reorientation maneuvers (29) have received, so far, much less attention, despite their importance for search behavior, chemotaxis, thermotaxis, and escape response.
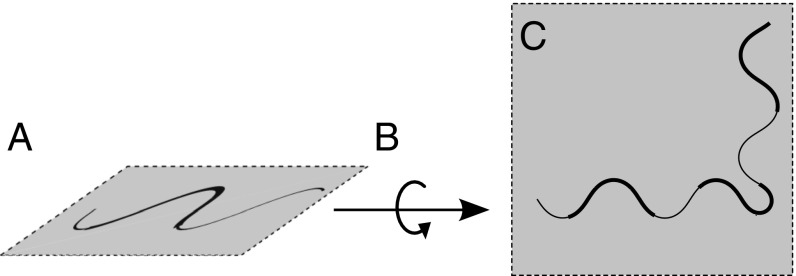
As illustrated in Fig. 1 for a swimming nematode (also corresponding Movies S1 and S2), C. elegans can reorient its body by combining 2D turns in the plane of dorsoventral undulations with 3D roll maneuvers that result in axial rotation of the undulation plane. Turns in 2D are executed by asymmetrically altering the amplitude of planar body undulations (28, 29, 34, 38), whereas rolls require nonplanar body postures. Our geometricalanalysis (presented in Torsional Roll Is a Unique 3D Behavioral State) of available stereoscopic nematode images (33) demonstrates that turns and rolls can also be observed for nematodes burrowing in soft gel-like media.
Fig. 1.
Typical reorientation maneuvers of swimming C. elegans. Shown are time-lapse images of a swimming C. elegans (A) performing a 2D turn and (B) rapidly switching the plane of undulations in a 3D roll maneuver. The nematode moves from right to left in both A and B. The arrows in B indicate the location of the ovary, helping to identify the nematode body orientation. (Magnification: 1.6×.)
A combination of planar turns and 3D rolls allows C. elegans to reorient itself in any direction (schematically depicted in Fig. 2), whereas 2D turning maneuvers alone [e.g., turns (6), loop/ turns (28, 33, 39), and pirouettes (40)] restrict nematode movements to one plane. Thus, the roll maneuvers identified in this work constitute an important behavioral state; this crucial locomotion component enables C. elegans to explore 3D media in search for optimal environmental conditions.
Fig. 2.
Schematic illustrating nematode reorientation in 3D. The worm (A) undulates in the initial plane of motion, (B) executes a roll maneuver, and (C) performs a planar turn in the new plane of motion.
Movie S1 and video images shown in Fig. 1A [and our prior study (29)] reveal that planar turns in swimming are shallower than no-slip turns in crawling or burrowing (analogous to the reduced forward progression in swimming). In contrast, swimming rolls (Movie S2 and Fig. 1B) can be significantly more rapid than those found for burrowing. The effectiveness of turn and roll maneuvers in burrowing and swimming is assessed by solving equations of motion for the nematode body moving in gels and fluids. Our calculations show that the same hydrodynamic resistance forces that reduce the swimming velocity (29, 41, 42) and planar turn angles (29) significantly enhance the roll rotation rate. This counterintuitive result of our theoretical analysis agrees well with experimental observations.
The geometry of 3D nematode motion is significantly more involved than planar geometry. Therefore, to faithfully identify and interpret specific locomotory behavioral patterns of C. elegans and understand hydrodynamic mechanisms of enhancement of the roll maneuvers, we need adequate tools for describing body postures. To explain the geometry of nematode movements in 3D, we thus generalize the recently proposed piecewise harmonic curvature (PHC) model of planar nematode gait (28, 29) by introducing the curve torsion to the gait description.
Geometrical Description of 3D Nematode Gait
Three-Dimensional Nematode Gait Can Be Described Using Curvature and Torsion of the Nematode Body.
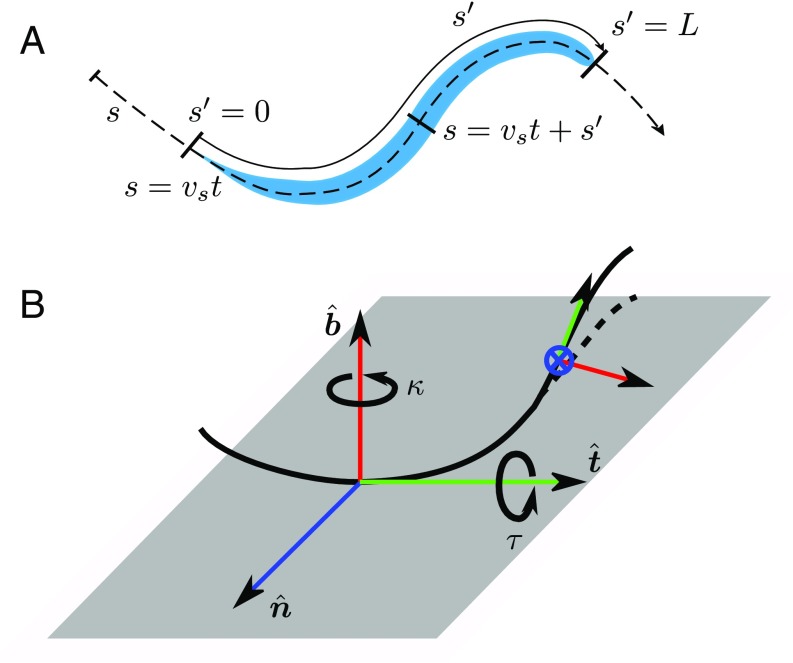
Since the body of C. elegans is highly elongated, its postures can be faithfully represented by the body centerline (22, 28, 38, 42–44). In 3D the centerline configuration at time is described by the local worm curvature and torsion , where is the arc-length coordinate along the body (Fig. 3A).
Fig. 3.
Description of body postures and trails of C. elegans in 3D. (A) Definition of the trail coordinate and the worm coordinate . (B) Rotation of the Serret–Frenet basis as it moves along the curve. The curvature is associated with rotation around the binormal unit vector ; deformations resulting from nonzero curvature thus occur in the – plane. Torsion is associated with rotation around the tangent unit vector ; a nonzero torsion results in out-of-plane curve deformation, because the local deformation plane changes its orientation.
The body configuration can be reconstructed from the curvature and torsion functions, and , by solving the Serret–Frenet equations (45)
| [1a] |
| [1b] |
| [1c] |
with the boundary condition corresponding to a given position and orientation of the nematode tail or head. Here , , and are the normal, tangent, and binormal unit vectors at a local position along the nematode body. The curvature and torsion correspond to rotation of the Serret–Frenet basis about the binormal and tangent directions; the geometrical interpretation of these parameters is illustrated in Fig. 3B. In what follows we analyze the curvature and torsion of the nematode body to identify behavioral patterns of C. elegans moving in 3D.
Curvature and Torsion Waveform Is Similar in Motion With and Without Transverse Slip.
Due to large transverse mechanical resistance provided by the environment, burrowing or crawling C. elegans often move with no transverse slip of body segments. Therefore, all segments follow a single curvilinear trail. The trail geometry can be described using the trail curvature and torsion, and , where is the arc-length coordinate measured from the beginning of the trail. Since at any given time the configuration of the nematode body coincides with a trail segment (Fig. 3A), the worm curvature and torsion and trail curvature and torsion are directly related,
| [2a] |
| [2b] |
where , and is the worm velocity along the trail. Accordingly, the curvature and torsion waves propagate along the nematode body without changing their waveform.
In fluid media where transverse slip does occur, and the nematode body segments do not follow the same path because of their transverse displacements, the worm curvature and torsion functions and are not geometrically constrained to obey the propagating-wave relations, Eq. 2. Nonetheless, our earlier analysis of the 2D gait of C. elegans swimming in water indicates that even in a fluid environment the curvature-wave relation, Eq. 2a, is preserved with good accuracy (28), despite a significant transverse motion. Since this behavior is a signature of the proprioceptive coupling (4) that allows the nematode to maintain properly formed propulsive body undulations in media with different mechanical properties, we assume that the curvature and torsion propagating-wave relations, Eq. 2, are satisfied both in no-slip burrowing and in 3D swimming. Moreover, as discussed below, the waveform and of body undulations is essentially the same in different media (although the wavelength of the undulations varies).
Key Elements of 2D Locomotion
Since identification of 3D behavioral patterns of C. elegans relies on prior understanding of planar locomotion, we summarize here the relevant key results of our previous studies of the geometry of 2D motion (28, 29, 46).
Harmonic Curvature Undulations Describe a Variety of Elementary Body Postures.
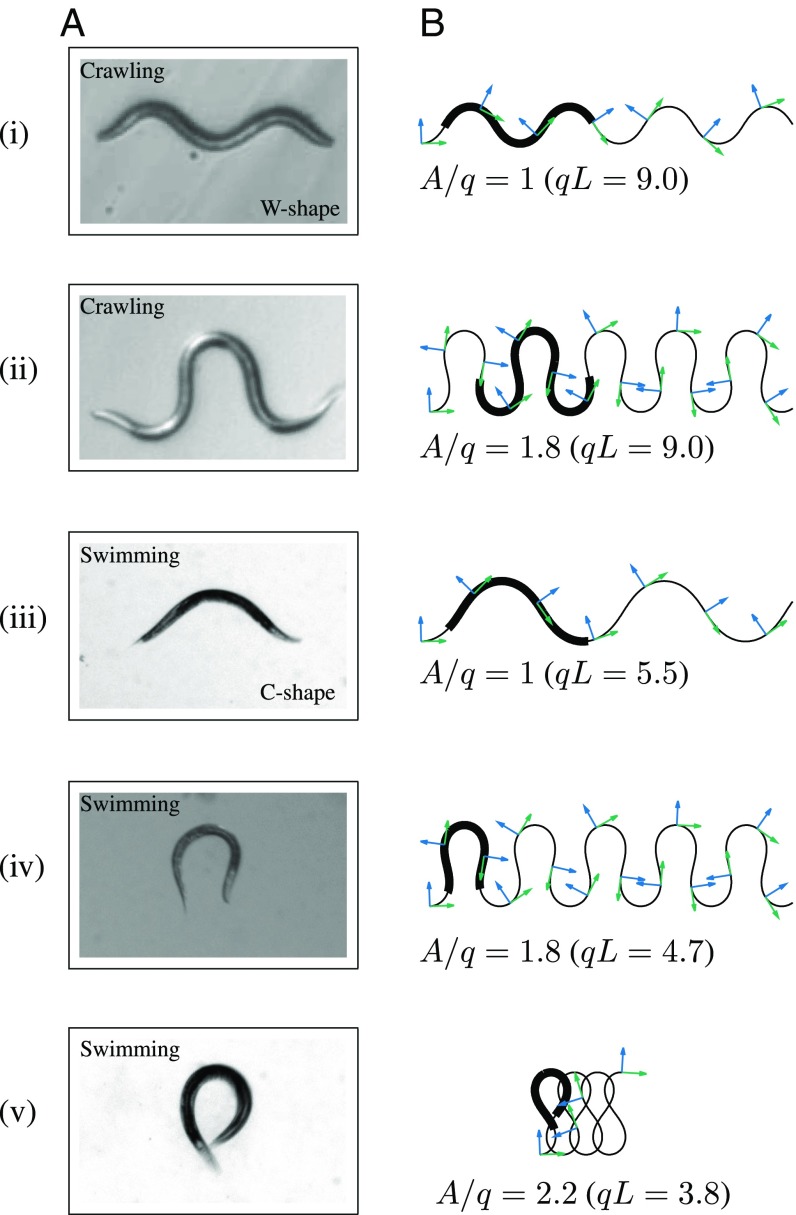
In 2D environments, C. elegans generally restrict their locomotion patterns to dorsoventral planar undulations. A quantitative analysis presented in our previous work (28) shows that a variety of planar nematode body postures can be accurately described by the harmonic curvature function
| [3] |
where is the wave amplitude, is the wavevector, and is the phase angle.
Fig. 4 shows some typical crawling and swimming 2D postures that can be represented by the harmonic curvature. Typical crawling and swimming body configurations associated with forward motion are characterized by moderate values of the dimensionless amplitude (Fig. 4 A, i and iii and B, i and iii); higher amplitudes correspond to commonly observed shapes (Fig. 4 A, ii and iv and B, ii and iv) and loops (Fig. 4 A, v and B, v). The distinction between swimming and crawling postures stems primarily from a difference in normalized wavelength ; swimming C-shaped postures generally exhibit larger compared with crawling (25) and burrowing (34) W-shaped postures.
Fig. 4.
Elementary body shapes of C. elegans in crawling and swimming. (A) Video images of crawling and swimming C. elegans. (Magnification: 1.6×.) (B) Family of approximately matching curves reproduced from harmonic curvature, Eq. 3, for normalized amplitude as labeled. The green and blue arrows are the unit tangent and normal vectors, respectively. The body of a nematode moving along the curves is represented by thick line segments of normalized length .
Two-Dimensional Turns Are Associated with Harmonic Mode Transitions.
A moving C. elegans does not maintain a single harmonic-curvature mode; instead, it stochastically varies mode parameters, which results in changes of the moving direction. A quantitative analysis of crawling trajectories (28) indicates that entire trails of crawling C. elegans can be accurately represented by the harmonic function, Eq. 3, with discontinuously varying wave parameters , , and between harmonic-curvature intervals. In this PHC representation sharp turns associated with strongly curved or loop body postures correspond to harmonic-curvature intervals characterized by a large normalized curvature amplitude .
Three-Dimensional Torsional Roll Maneuvers in No-Slip Burrowing
C. elegans burrowing through a soft gel-like substrate (such as agar) often move without transverse slip of the body with respect to the surrounding medium, because the finite yield stress of the gel prevents transverse displacements. In this section we consider no-slip 3D locomotion along a curvilinear path carved in the gel.
Recently Beron et al. (34) and Vidal-Gadea et al. (35) investigated nonplanar motion of C. elegans in a gel showing that the nematode can actively reorient itself in 3D in response to external stimuli. While they measured the frequency of out-of-plane changes of direction, their studies have not supplied sufficient data for unambiguous identification of stereotyped behavioral patterns associated with 3D reorientation maneuvers. Quantitative data on 3D nematode shapes and motion have been provided by Kwon et al. (33), who presented stereoscopic images of 3D burrowing C. elegans. Our thorough analysis of these images allows us to identify a specific behavioral pattern—the roll maneuver—that the nematode uses in 3D locomotion.
One-Mode Roll Maneuver: Nonzero Torsion Results in Rotation of the Undulation Plane.
Before we proceed to our analysis of the observed 3D nematode gait, we first examine the effect of nonzero torsion on harmonic-curvature undulations. Fig. 5A shows numerical solutions of Serret–Frenet equations for a curve with harmonic curvature, Eq. 3, and constant torsion
| [4] |
The results are shown for the default curvature-wave amplitude and several values of the torsion .
Fig. 5.
The effect of nonzero torsion on body postures and no-slip trails. (A) Curves defined by the harmonic curvature (normalized amplitude ) and constant torsion (normalized magnitude as labeled). The green, blue, and red arrows are the unit tangent, normal, and binormal vectors, respectively. A, Left shows projection of nematode trajectories on the – plane, where the direction of travel is along the axis. A, Right shows – projections of the respective trajectories. The green and red circles represent the initial and final points of the trajectories. (B) The torsional roll-rotation rate per undulation period (in degrees) vs. normalized body torsion for one-mode torsional roll with harmonic-curvature amplitude as labeled. (C) A crawling nematode undergoing a nonplanar body deformation. The lifted body segment is indicated by the arrow. Reprinted with permission from ref. 47; www.sciencedirect.com/science/journal/09252312. The thick line segment shown for in A represents a nematode shape approximately matching the image depicted in C.
The plots indicate that for moderate values of , the undulatory character of nematode motion is preserved, and the undulation plane rotates when the nematode moves forward. Geometrically, this torsion-induced reorientation stems from the rotation of the deformation plane – about the tangent vector when the Serret–Frenet basis moves along the nematode trail (schematically depicted in Fig. 3B). We call the gait defined by Eqs. 3 and 4 a (one-mode) torsional roll. The results of our calculations for the roll-rotation rate per undulation period are presented in Fig. 5B.
First, we point out that a calculated body configuration depicted by the thick line segment in Fig. 5A (for ) resembles the reported (47) nonplanar posture of a crawling nematode that lifts a body segment from the underlying agar surface; the reported image (47) is reproduced in Fig. 5C. Second, our detailed analysis of stereoscopic images (33) of a burrowing nematode, discussed next, demonstrates that C. elegans use the torsional-roll maneuver for 3D reorientation.
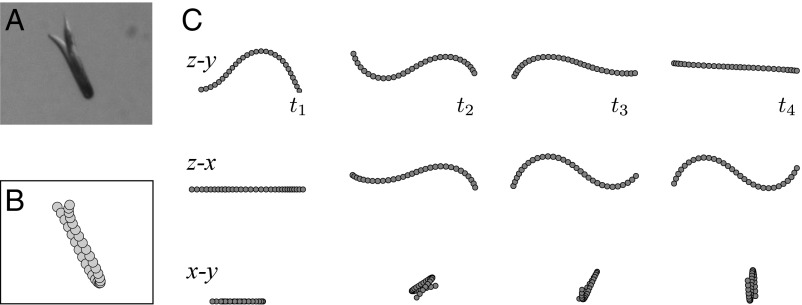
The Three-Mode Torsional Roll Model Accurately Describes Observed 3D Motion of Burrowing C. elegans.
The video images reproduced from ref. 33 (Fig. 6A) show that during its forward motion the depicted nematode is gradually changing the orientation of the plane of undulations, consistent with the general shape of the constant-torsion lines shown in Fig. 5A. In the initial frame of Fig. 6A the entire nematode body undulates in the – plane, which indicates that at time the roll maneuver has not yet started. Subsequently, the nematode begins the roll maneuver, and an increasing portion of the body-wave plane is reorienting. At time , the anterior part is already significantly reoriented (by ), but the undulations in the posterior portion still remain oriented in the – plane.
Fig. 6.
Torsional roll of a burrowing C. elegans. (A) Stereoscopic images of a wild-type C. elegans burrowing in gelatin (image reprinted from ref. 33). (B) A matching time-lapse set of simulated postures of a nematode performing a three-mode torsional roll, Eq. 5. The simulation parameters are curvature amplitude , worm length , torsion , and torsional-mode length . Similar to the experimental images, the calculated postures are equally spaced in time. The region of nonzero torsion is shaded in blue.
To describe the observed behavior, we introduce a three-mode torsional-roll model,
| [5] |
where for and the nematode undergoes planar undulations, and it performs the roll only in the spatiotemporal interval of finite length . During the entire three-mode roll maneuver, the body undulations are described by a single harmonic-curvature mode, Eq. 3, and the propagating body curvature and torsion waves are given by Eq. 2.
Torsional Roll Is a Unique 3D Behavioral State.
As shown in Fig. 6, our three-mode roll model, Eq. 5, is in excellent agreement with the stereoscopic nematode-tracking images by Kwon et al. (33). All key features of the nematode gait are correctly reproduced for the entire 2-s time interval, including the fact that an increasing part of the body undergoes the roll, but the rest remains planar. The calculated body postures shown in Fig. 6B were obtained from a single continuous simulation; these are not separate fits to individual body postures. Our model faithfully describes the entire behavioral pattern (a 3D roll). We conclude that we have identified and mathematically described a unique behavioral state of C. elegans.
Maneuverability of Swimming C. elegans in Bulk Fluids
In environments with different mechanical properties typical body postures of C. elegans are distinct because the undulation wavelength differs relative to the body length (Fig. 4); however, the harmonic-curvature undulation waveform described by Eqs. 1–3 is preserved (28). In particular, the geometrical similarity between the swimming and crawling gaits is corroborated by the important observation by Fang-Yen et al. (25) that the wavelength of undulations in swimming continuously decreases with increasing fluid viscosity, and in highly viscous fluids the swimming gait is very similar to the crawling gait. Thus, fluid viscosity affects the undulation wavelength, but the waveform is unaffected.
Swimming Trajectories Depend on the Gait Geometry and Hydrodynamic Force and Torque Balance.
Based on the above observations, we conclude that the gait description developed in the previous sections to elucidate no-slip locomotion yields a suitable framework for inquiry into the mechanics of reorientation maneuvers of swimming C. elegans. Accordingly, we assume that the waveform Eq. 2 of the propagating curvature and torsion is maintained in fluids, and we decompose the motion of a swimming nematode into the geometrical component i and dynamical component ii, where i is the progression along the curvilinear path determined by the curvature and torsion functions and , and ii is the rigid-body translation and rotation resulting from the hydrodynamic force and torque balance on the entire nematode body.
Due to the presence of the translational and rotational motion ii, the trajectories of swimming nematodes differ from those of crawling/burrowing nematodes using the same sequence of body postures and moving along a no-slip path. Moreover, in swimming the trajectories depend not only on the form of the curvature and torsion waves, but also on the normalized undulation wavelength , whereas the no-slip path i is independent of this parameter.
The above decomposition into i and ii is particularly useful in the linear creeping-flow regime (considered here), because in this case there are no inertial effects, and the total hydrodynamic force and torque can be evaluated by superposing the forces and torques associated with the component velocities i and ii. Our bead-based technique for calculating hydrodynamic forces acting on a nematode is described in Materials and Methods and in our previous study of 2D undulatory locomotion (29).
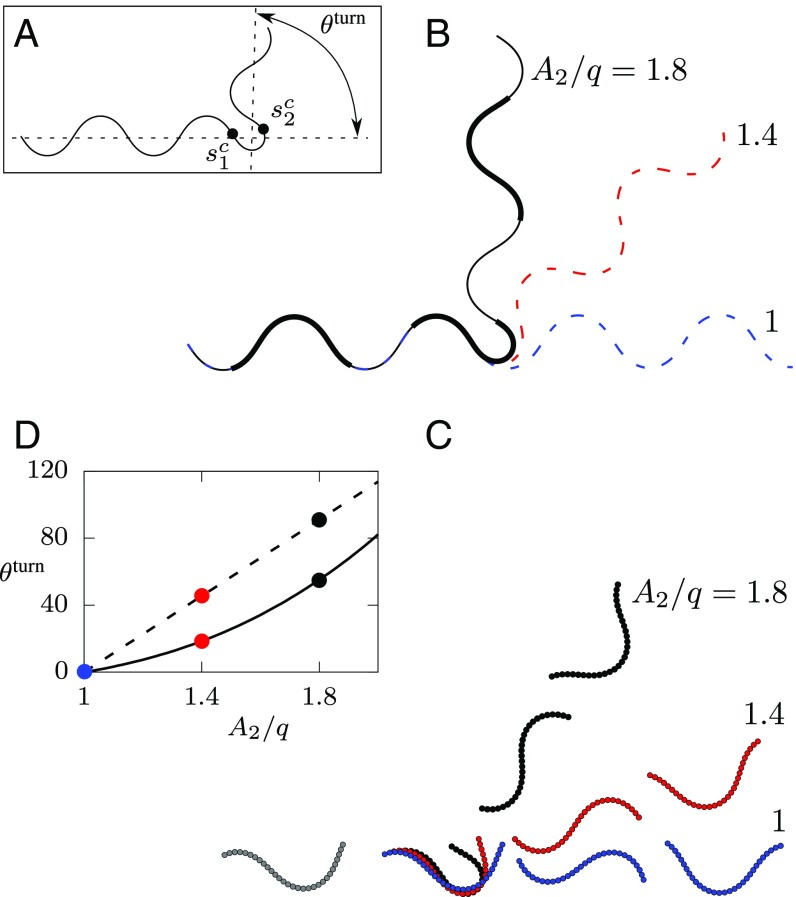
Planar Turn Angles in Swimming Are Reduced Compared with No-Slip Motion.
As shown in Fig. 1A and the corresponding Movie S1, crawling and swimming nematodes perform planar turns by asymmetrically increasing their undulation amplitude for short time intervals. To assess the effectiveness of such turning maneuvers, we consider three-mode PHC turns,
| [6] |
in which the nematode initially moves using the default locomotion mode with the amplitude , then at a position switches to the turning mode with a higher amplitude , and finally at a position returns to the default locomotion mode (Fig. 7A). For simplicity, we focus on maneuvers in which only the amplitude of the harmonic curvature varies.
Fig. 7.
Effectiveness of three-mode planar turns in crawling/burrowing and swimming. (A) Definition of the turn angle and positions of the turn mode-switching points and for the PHC maneuvers shown. We use , , and default mode amplitude for all calculations shown. (B) Three-mode planar turn trajectories and snapshots of body postures (thick trail segments, ) for a nematode crawling/burrowing without transverse slip and with turning-mode amplitude as labeled. (C) A sequence of simulation snapshots of a swimming C-shaped nematode () performing a three-mode PHC turn, with the turning mode amplitude as labeled. (D) Comparison of the dependence of the turn angle (in degrees) on the turning-mode amplitude for motion without transverse slip (dashed line) and swimming (solid line). The three circles for each case correspond to the shown trajectories and snapshots.
Fig. 7 presents a comparison between calculated trajectories for nematodes executing a three-mode planar turn in crawling/burrowing without transverse slip (Fig. 7B) and swimming (Fig. 7C). The swimming nematodes undergo the same sequence of body postures as the crawling/burrowing ones, but their corresponding trajectories differ because of the translational and rotational velocity component ii that is present only in swimming. Fig. 7D shows the dependence of the turn angle on the turning-mode amplitude for both cases. Consistent with the experimental results (Fig. 1A and Movie S1), the turn angles in swimming are relatively shallow, as a result of the hydrodynamically induced rotation.
The swimming angles are always significantly smaller than the corresponding angles for crawling (or burrowing); this hydrodynamic hindrance is especially pronounced for small turning-mode amplitudes. A swimming nematode usually needs to perform several turns to significantly change its locomotion direction. A typical case of such a combined multimode turning maneuver is presented in Movie S1, which shows a turn of a swimming wild-type C. elegans along with a matching hydrodynamic simulation.
Roll Rotation Rate in Swimming Is Increased Compared with No-Slip Motion.
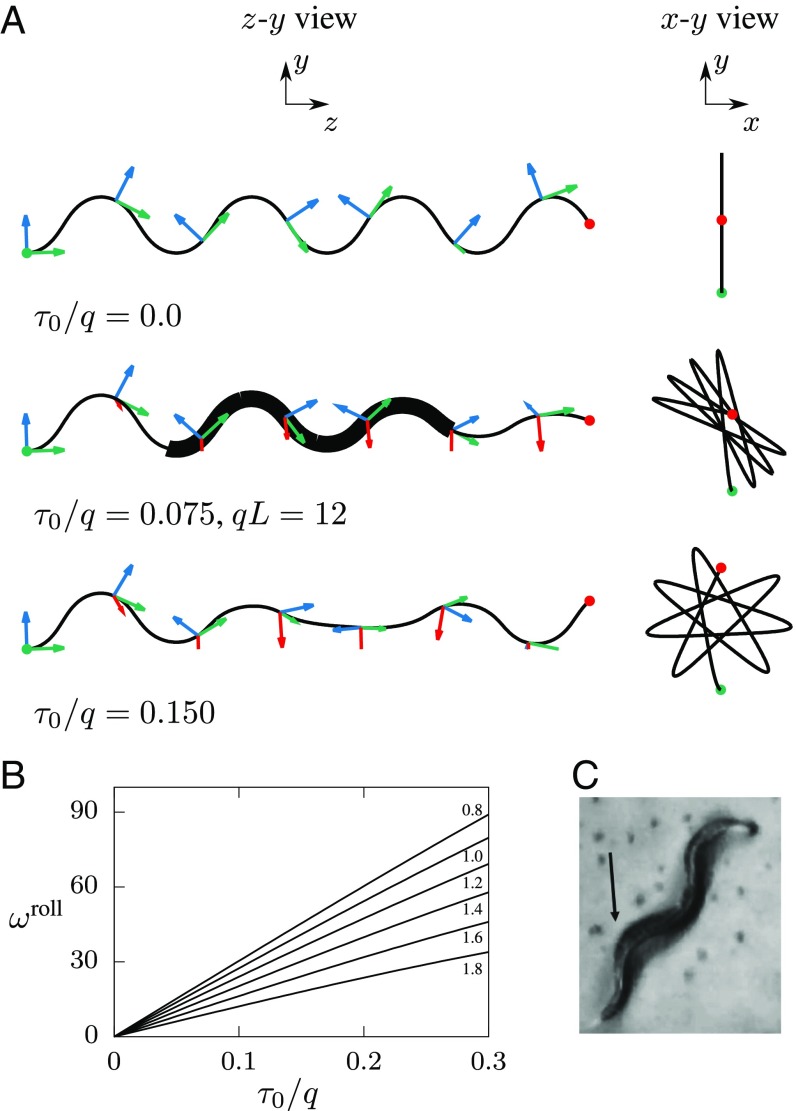
As shown in Fig. 1B and the corresponding Movie S2, a swimming nematode can quickly change the plane of undulations by performing a roll maneuver. Our experimental observations indicate that a roll by 90° often occurs in one undulation period, and faster rolls are not unusual. This rotation is much more rapid than the rotation observed in burrowing (Fig. 6).
Our images of swimming C. elegans undergoing undulation-plane reorientation indicate that the nematode body postures are nonplanar, similar to the corresponding behavior in burrowing. These 3D swimming postures closely resemble the torsional-roll configurations defined by Eqs. 3 and 4, as depicted in Fig. 8 A and B. While the out-of-plane deformation of the nematode body shown in Fig. 8A seems quite small, our hydrodynamic simulations indicate that even such a relatively minor out-of-plane torsional distortion can result in a rapid reorientation of the undulation plane.
Fig. 8.
Three-mode torsional roll of a swimming C. elegans. (A and B) A recorded nonplanar body posture (A) and a matching calculated body shape (B) with harmonic curvature and constant torsion. Normalized curvature amplitude , wavevector , and torsion (which is equivalent to ). (Magnification: 1.6×.) (C) Stereoscopic views of a simulated nematode performing a three-mode swimming roll maneuver (projection planes as labeled). At times and the nematode performs planar undulations; at and it performs a roll with gait parameters corresponding to the posture shown in B; the total length of the torsional roll mode is . The roll results in a change of the undulation plane by .
Such rapid axial reorientation is illustrated by the hydrodynamic simulations of three-mode roll maneuvers presented in Fig. 8C and in Movie S3. In both cases the nematode undergoes a roll rotation of in less than one period of undulations, in agreement with our experimental observations.
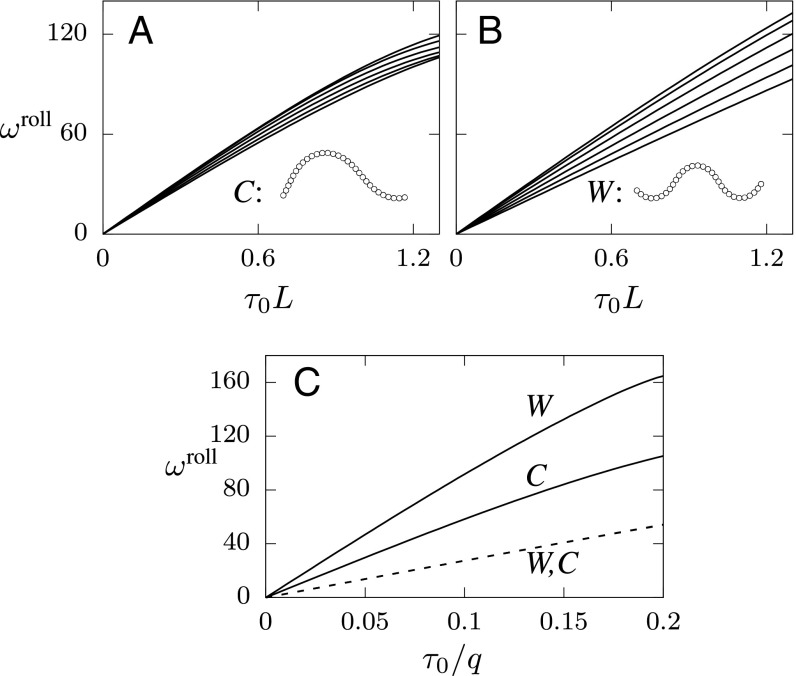
The effectiveness of roll reorientation in fluids is quantitatively assessed in Fig. 9A for C-shaped gait and in Fig. 9B for W-shaped gait in terms of the roll rotation rate per undulation period. Since the hydrodynamic component of the rolling rate is affected by the nematode length , the results are shown versus , that is, the torsion normalized by . Similar to the corresponding result for the no-slip roll of a burrowing nematode (Fig. 5B), the roll rotation rate in swimming decreases with the normalized curvature-wave amplitude . However, the relation between and the torsion is nonlinear, and the dependence on the normalized undulation amplitude is significantly weaker, due to hydrodynamic effects. The roll rotation for C-shaped and W-shaped gaits has a similar magnitude for given values of and .
Fig. 9.
Hydrodynamic enhancement of roll rotation rate. (A and B) The roll rotation rate per undulation (in degrees) in swimming is shown vs. normalized body torsion , for normalized curvature-wave amplitude (from above) for (A) C-shaped (q) and (B) W-shaped (q) swimming nematodes. Examples of nematode shapes are shown in respective Insets. (C) Comparison of roll rotation rate per undulation period, (in degrees), between nematodes performing one-mode roll in swimming (solid lines) and burrowing (dashed lines), shown vs. normalized magnitude of body torsion . Results are presented for C-shaped and W-shaped gaits (as labeled) and normalized harmonic-curvature amplitude .
A Comparison of Roll Rotation Rate in Burrowing and Swimming Provides Evidence for a Significant Hydrodynamic Enhancement.
To directly compare the swimming roll rotation rate shown in Fig. 9 A and B with the corresponding purely geometrical no-slip result (Fig. 5B), the swimming and no-slip simulation data are replotted in Fig. 9C using the same scaling of the torsion for both datasets. The results indicate that hydrodynamic forces in swimming can enhance the rotation rate in a very significant way. Compared with the values in the no-slip burrowing case (for the same sequence of nematode body motions), the roll rotation rate in swimming increases by a factor ranging from approximately 2 (for C-shaped gait) to even 3 (for W-shaped gait). For example, a swimming nematode using a W-shaped gait [e.g., C. elegans swimming in a highly viscous dextran solution (25)] would rotate at a rate per undulation period for body torsion . A burrowing nematode with a similar gait (e.g., Fig. 6) would have a rotation rate of only .
The Mechanisms of Hydrodynamic Hindrance and Enhancement
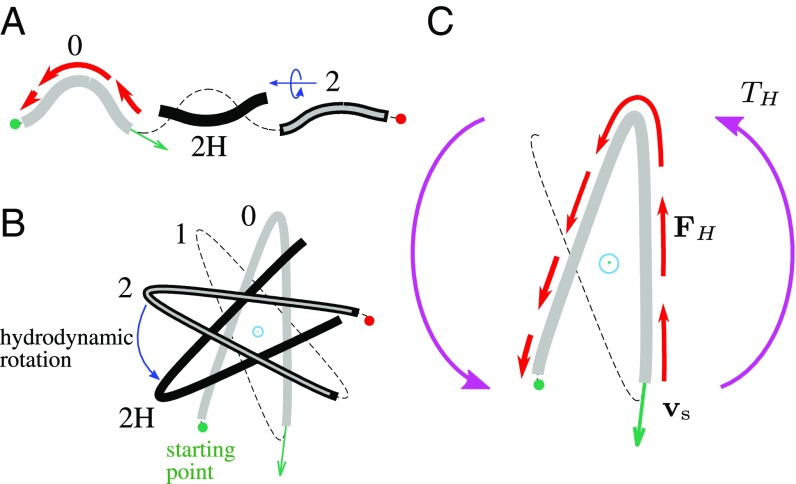
As illustrated in Figs. 10 and 11, both the hindrance of planar locomotion and the 3D roll enhancement result from the longitudinal resistance forces (acting parallel to local body segments). These longitudinal resistance forces counteract the propulsive transverse forces that drive the nematode forward when the undulatory wave propagates backward along the body. In burrowing, the longitudinal resistance is too weak (compared with the transverse resistance) to produce any significant body displacements; thus the nematode moves along the purely geometrical no-slip path i, defined by the curvature and torsion wave. In swimming, the force and torque associated with the longitudinal resistance produce additional translation and rotation of the nematode body ii (indicated by blue arrows in Figs. 10 and 11).
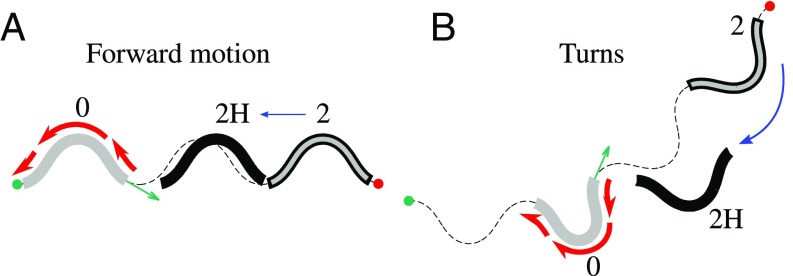
Fig. 10.
Mechanism of hydrodynamic hindrance of planar motion. A and B show no-slip paths (thin dashed line) and nematode positions (thick lines) in no-slip crawling/burrowing and swimming. The initial body configurations (0) are marked by the thick gray line. The body configurations after two undulation periods, marked with 2, are shown in no-slip crawling/burrowing by the gray line with black border and the corresponding body configurations in swimming (2H) by a thick black line. In forward locomotion (A), the longitudinal hydrodynamic resistance (indicated for the initial configuration by red arrows) produces a net hydrodynamic force causing backward nematode displacement (indicated by the blue arrow); it slows the nematode down. Similarly, during a planar turn (B) the net hydrodynamic torque produces rotation that reduces the overall turn angle of the nematode.
Fig. 11.
Mechanism of hydrodynamic enhancement of axial roll rotation. A shows a side view and B and C a front view of nematode trajectories in a roll maneuver. The labeling convention follows that of Fig. 10. In B and C the axis of motion (toward the viewer) is indicated by the symbol . In forward locomotion (A) the longitudinal hydrodynamic resistance (red arrows) slows the nematode down. During the torsional roll (B and C), the net torque (magenta arrows in C) associated with (red arrows) produces hydrodynamic rotation (blue arrow in B) in the same direction as the geometrical rotation of the undulation plane (progression ).
Force and Torque Associated with Longitudinal Hydrodynamic Resistance Hinder Forward Motion and 2D Turns.
In forward locomotion, the longitudinal resistance force always acts in the direction opposite to the direction of nematode motion (Fig. 10A). In swimming this force thus results in reduction of locomotion velocity (29, 41). Similarly, the torque acting on the nematode body undergoing a deep asymmetric undulation during a planar turn is oriented opposite to the turn direction, thus hindering the turn (Fig. 10B).
Axial Torque Produced by the Longitudinal Hydrodynamic Resistance Enhances Roll Rotation.
The analysis of the effect of hydrodynamic interactions in torsional roll is more subtle. To elucidate the interplay of the gait geometry and the longitudinal hydrodynamic friction, we show two views of the nematode trajectory: the side view (Fig. 11A) and the front view (Fig. 11 B and C). Fig. 11 indicates that, as a result of torsional distortion of the nematode body, the undulation plane in no-slip motion [i.e., along the path i before the hydrodynamic displacement ii is included] gradually changes its orientation. Therefore, it can be observed that the trajectory spirals around its axis (Fig. 11B).
In the projections of the no-slip path shown in Fig. 11 B and C, the nematode moves in the clockwise direction around the trajectory axis (which points toward the viewer). In contrast, the undulation plane geometrically rotates anticlockwise (determined from the orientation of this plane in subsequent periods). This anticlockwise rotation of the undulation plane arises from the star-like topology of the calculated path projection.
The clockwise nematode motion produces the oppositely oriented hydrodynamically induced resistance (Fig. 11C), which in our example results in an anticlockwise axial torque and the corresponding hydrodynamic rotation of the nematode in the anticlockwise direction about the trajectory axis. Since the geometrical and hydrodynamic contributions to have the same orientation (anticlockwise in the particular case analyzed), they add up, which leads to a significant enhancement of the roll rotation in swimming, consistent with our experimental observations and the numerical results shown in Fig. 9C.
Discussion
Torsional Roll Is a Unique Behavioral State That Is Essential for 3D Locomotion.
Based on our investigation of available stereoscopic images and other experimental evidence, we have shown that C. elegans explore their 3D environment by combining planar turns with roll reorientation maneuvers. The rolls, during which the undulation plane of the worm rotates about the trajectory axis, constitute an important previously unrecognized behavioral pattern that is an essential component of 3D locomotion.
To identify the roll maneuvers and describe their geometry, we have developed a mathematical representation of the 3D nematode gait. According to our analysis, the roll maneuvers combine harmonic curvature with a piecewise constant torsion that causes the undulation-plane reorientation. Our 3D model of roll maneuvers faithfully reproduces all key geometrical features of the observed roll behavior of a burrowing nematode and, when integrated with appropriate hydrodynamic calculations, replicates a rapid roll rotation observed in swimming. We have provided a physical explanation of this unexpected hydrodynamic enhancement effect in the 3D roll maneuver.
Our modeling approach provides a powerful tool for investigating 3D locomotion of C. elegans, including initiation and execution of behavioral patterns associated with 3D reorientation. For example, our techniques can be applied to analyze chemotaxis strategies and escape responses, as well as to evaluate the effect of nematode health and age on locomotory abilities. In Application to Chemotaxis we describe a proof-of-concept calculation showing that the nematode can use a combination of turn and roll reorientation maneuvers to efficiently chemotax in 3D environments. To illustrate typical maneuvers in 3D space, we present two examples of numerical simulations of a nematode performing multiple turns and rolls (Movie S4 for burrowing and Movie S5 for swimming).
Our analysis reveals that both the burrowing and swimming rolls involve a similar pattern of nematode movements defined by a curvature wave with nonzero torsion. Several recent experimental studies showed that the nematode gait is not significantly affected by the rheological properties of the suspending medium (48–51), for the system parameters investigated. Such results were documented for viscoelastic fluids (48), shear-thinning fluids (50), and entangled polymeric solutions (49). For nematodes swimming in a shear-thinning suspension (51), a moderate increase in the head-bending angle was observed, but even in this case, the overall form of undulations remained similar to the waveform observed in Newtonian fluids. Based on the above wide spectrum of systems in which rheological properties of the suspending medium do not affect the locomotory undulation pattern, we conclude that the same simple undulation waveform likely occurs for C. elegans moving in a variety of complex media present in its natural environment. Moreover, since roll maneuvers provide effective 3D reorientation and do not require complicated patterns of body actuation, we anticipate that similar rolls are performed by other undulatory burrowers and swimmers.
Torsional Roll Maneuvers Help Sedimented Adult Nematodes Maintain Swimming Capabilities.
Trajectories of swimming C. elegans are affected not only by active actuation but also by buoyancy forces. During the larval stages of development and for nematodes swimming in highly viscous aqueous solutions of organic matter (common in C. elegans habitat) the effect of buoyancy is negligible. Adult nematodes swimming in water, however, tend to settle down toward the bottom of the pool and reside close to the bottom surface, following its topology (52). As shown by Yuan et al. (52), the worms remain suspended due to the upward force that results from continuous head collisions with the bottom wall when the nematode body undulates in an approximately vertical plane.
In our experiments, we find that during this near-the-bottom locomotion, nematodes perform frequent rolls (one roll of about 90° per several undulation periods), with the frequency similar to the roll frequency in a bulk fluid. The rolls allow the worms to repeatedly attain approximately vertical orientation of the undulation plane (Movie S6). Such a vertical orientation is necessary for the sedimenting worms to be able to generate the upward resuspending force through collisions with the bottom. We thus conclude that the roll maneuvers are used by C. elegans not only to change the direction of motion in 3D, but also to remain suspended near the bottom surface and, therefore, to maintain the swimming behavior in the presence of significant buoyancy forces.
Muscular System of C. elegans Is Compatible with 3D Body Actuation, but Neural Control Mechanism Is Unknown.
As an important application of this study, our results may shed light on subtle aspects of neuromuscular control of 3D locomotion of C. elegans. Body movements of C. elegans are actuated by a coordinated action of four quadrants of body muscles, which are arranged into double rows that span the entire nematode length (53). While this muscle anatomy is compatible with 3D body actuation, it is less clear how the neural system can activate differential muscle contractions needed to generate 3D body deformations out of the dorsoventral undulation plane.
According to a detailed map of neural connections in C. elegans (53–55), the head and neck body muscles are innervated by the nerve ring motor neurons, which synapse onto cells in individual quadrants (and thus are capable to actuate each quadrant individually). In contrast, the remaining body muscles are innervated only by the ventral-cord motor neurons, which synapse onto muscles of either two ventral or two dorsal quadrants, consistent with 2D actuation.
Based on this topology of neural connections, it is generally assumed that only the head and neck segments can perform 3D motion. However, the stereoscopic experiments by Kwon et al. (33) clearly show that burrowing nematodes can adopt a variety of 3D postures. The images clearly show that the entire body undergoes out-of-plane deformations. In the swimming case the evidence is less conclusive because stereoscopic images are not yet available. Nonetheless, 2D images of swimming nematodes (such as the one shown in Fig. 8A) agree with our 3D body posture model.
Our hydrodynamic calculations of the roll dynamics further support a conclusion that the entire nematode body participates in generating the roll motion. We find that the torsional wave propagating throughout the entire body length can produce a 90° roll in less than one undulation period, consistent with rolls observed in our laboratory experiments using wild-type C. elegans. In contrast, a stroke in which only the head and neck segments are displaced out of the undulation plane produces significantly weaker rolls. The results of these additional simulations are presented in Analysis of a Roll Resulting from Out-of-Plane Displacements of the Nematode Head.
We hypothesize that the generation of a nonzero torsion in the posterior part of the nematode body involves a 3D proprioceptive feedback, which enables propagation of the torsional wave from the head segment in the posterior direction. The existence of 2D proprioceptive feedback in C. elegans and its important role in generation of a planar undulation wave have been demonstrated by Wen et al. (4). Based on this result and building on their observation that individual neurons of C. elegans may have a high degree of functional complexity, we conjecture that 3D proprioception may give rise to asymmetric neural signals and differential muscular contractions that are needed to achieve well-controlled out-of-plane body movements during the torsional roll.
We note that current evidence is not sufficient to rule out a passive, purely mechanical origin of propagation of 3D deformations along the portion of the nematode body outside the head and neck regions. In particular, the body shapes observed during burrowing (33) can, in principle, be generated by 3D actuation of the head and neck muscles, with the rest of the body passively sliding along the tunnel carved by the nematode head. Such motion, however, would be inefficient, especially in media with low-yield stress, in which transverse forces needed to passively deform the nematode body would result in undesirable transverse slip.
Since C. elegans has a four-quadrant muscle arrangement that is anatomically capable of generating 3D body deformations, we expect that there is a compatible neuromuscular-control system that allows the nematode to fully use this (existing) muscle structure. Further analyses of 3D locomotion of C. elegans will help determine whether such a control system exists and how it may actuate the nematode body.
Materials and Methods
Imaging of Swimming Nematodes Performing Rolls and Turns in Water.
Wild-type C. elegans were used to record the 3D swimming. Worms were cultured in a nematode growth medium plate seeded with the bacteria Escherichia coli OP50 at 20 °C. A liquid pool was created for the swimming assay by adding 5–7 mL of M9 buffer into a 60-mm Petri dish. The pool height was 2 mm. The surface of the Petri dish was treated with 5% Pluoronic F127 for 5 min before adding M9 buffer. Individual young adults were manually transferred into a liquid pool of M9 buffer, using a worm pick. Swimming episodes were recorded at 30 frames per second using an SVSI camera and Zeiss Stemi 2000-C stereo microscope imaging system at 1.6× magnification with a pixel resolution of 0.21 pixels/m. All imaging was carried out in a food-free environment at 20 °C.
Assessing Buoyancy Effects in 3D Swimming.
A mixed culture of worms (L1–L3 larvae and adults) was used to observe the voluntary 3D movement of sedimenting nematodes in water and in 10% dextran solution (Dextran 2000 from Leuconostoc spp.) of viscosity 50.2 cP at 20 °C. Settling of a mixed worm population was observed in a BrandTech Macro Cuvette. Worms were washed from a plate and concentrated in 200 L of M9 solution. In each experiment, 50 L of the worm solution (50–100 worms) was added at the top surface of the fluid in the cuvette and allowed to settle under the influence of gravity. Worms were recorded for the entire settling path (4.5 cm).
We observed that in water the sedimentation velocity of adult worms was comparable to the active swimming velocity, and the nematodes settled toward the bottom of the cuvette. In contrast, many larvae did not settle and remained in the top layer of fluid even after 10 min. In the dextran solution the settling velocity was negligible for both adults and larvae. Nematodes changed the undulation plane using roll maneuvers every 2 to 3 undulations. The rate of planar turns was much slower (10 undulations per turn, consistent with results from ref. 34). No evidence of gravity-induced passive reorientations was found in either experiment; therefore we conclude that the effect of buoyancy forces on reorientation maneuvers is negligible.
Description of Planar Nematode Postures.
Based on our prior quantitative analysis of nematode shapes (28), in our turn and roll-rotation angle calculations we use for the W-shaped basic crawling/burrowing gait and for the C-shaped swimming gait. These values are within the range of wavelength variability reported in ref. 25. Since in crawling and burrowing without transverse slip the resistance forces are of the same magnitude, we assume that the 3D burrowing and crawling gaits have similar parameter values, consistent with the available experimental images of burrowing C. elegans (33).
Modeling of Nematode Hydrodynamics.
In our numerical simulations of swimming nematodes we use a 3D generalization of the bead-based model introduced in ref. 29. Accordingly, a swimming nematode is represented as an active chain of hydrodynamically coupled spherical beads arranged along the nematode centerline. As the configuration of a chain submerged in a viscous fluid evolves, the beads move with the linear and angular velocities
| [7] |
| [8] |
which are decomposed into the active and passive components.
The active linear velocity corresponds to the sliding motion of the bead along the curve defined by the curvature and torsion waves, Eq. 2,
| [9] |
where is the unit tangent vector at the position of bead , and is the velocity of the curvature wave propagating along the nematode body. The active angular bead velocity
| [10] |
depends on the curvature , torsion , and the binormal unit vector at the bead position . The angular velocity Eq. 10 mimics the rotational motion of individual segments of the deforming nematode body. As explained in our previous paper (29), neglecting the active rotational contribution results in an overprediction of nematode swimming speed, especially for large .
The passive linear and angular velocities of individual beads,
| [11] |
| [12] |
are associated with the rigid-body translation and rotation of the entire chain. The hydrodynamic torque, chain velocity , and bead positions are evaluated relative to a prescribed center of rotation of the chain.
The linear and angular chain velocities and are determined from the hydrodynamic force and torque balance,
| [13] |
where and are the active torque and force required to produce the prescribed chain motion, Eqs. 9 and 10, and are translational () and rotational () hydrodynamic resistance tensors of the chain at a current configuration.
Expressions for the active force , active torque , and the hydrodynamic resistance tensors in terms of the hydrodynamic resistance and mobility tensors of a system of hydrodynamically coupled beads are given in ref. 29. The calculations presented in our paper were performed using a generalized Rotne–Prager–Yamakawa (RPY) approximation (56) for multiparticle hydrodynamic interactions. A limited set of calculations was also performed using a more accurate but computationally more expensive Hydromultipole algorithm (57); for our current problem, the RPY approximation produces fairly accurate results. The nematode body was modeled using a chain of beads. We note that in an independent study Berman et al. (42) also used a hydrodynamic bead-based model to investigate undulatory swimming of a nematode.
Evaluation of the Roll Rotation Rate.
The single-mode roll rotation rate per period of undulations, , was determined from the angle between the binormal vectors at and .
Supplementary Material
Acknowledgments
We thank Dr. N. J. Szewczyk and Dr. M. Driscoll for useful discussions. A.B. acknowledges financial support from NSF Grant CBET 1059745 and a Texas Tech University Doctoral Dissertation Completion Fellowship. J.B. was partially supported by NSF Grant CBET 1603627. S.A.V. and M.R. acknowledge partial support from Grants NIH 1R21AG050503-01 and NASA NNX15AL16G.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1706754115/-/DCSupplemental.
References
- 1.Ghanbari A, et al. A micropillar-based on-chip system for continuous force measurement of C. elegans. J Micromech Microeng. 2012;22:095009. [Google Scholar]
- 2.Johari S, Nock V, Alkaisi MM, Wang W. On-chip analysis of C. elegans muscular forces and locomotion patterns in microstructured environments. Lab Chip. 2013;13:1699–1707. doi: 10.1039/c3lc41403e. [DOI] [PubMed] [Google Scholar]
- 3.Etheridge T, et al. The integrin-adhesome is required to maintain muscle structure, mitochondrial ATP production, and movement forces in Caenorhabditis elegans. FASEB J. 2015;29:1235–1246. doi: 10.1096/fj.14-259119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wen Q, et al. Proprioceptive coupling within motor neurons drives C. elegans forward locomotion. Neuron. 2012;76:750–761. doi: 10.1016/j.neuron.2012.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stirman JN, et al. Real-time multimodal optical control of neurons and muscles in freely behaving Caenorhabditis elegans. Nat Methods. 2011;8:153–159. doi: 10.1038/nmeth.1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gray JM, Hill JJ, Bargmann CI. A circuit for navigation in Caenorhabditis elegans. Proc Natl Acad Sci USA. 2005;102:3184–3191. doi: 10.1073/pnas.0409009101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kocabas A, Shen CH, Guo ZV, Ramanathan S. Controlling interneuron activity in Caenorhabditis elegans to evoke chemotactic behaviour. Nature. 2012;490:273–277. doi: 10.1038/nature11431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sznitman J, Purohit PK, Krajacic P, Lamitina T, Arratia PE. Material properties of Caenorhabditis elegans swimming at low Reynolds number. Biophys J. 2010;98:617–626. doi: 10.1016/j.bpj.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brown AEX, Yemini EI, Grundy LJ, Jucikas T, Schafer WR. A dictionary of behavioral motifs reveals clusters of genes affecting Caenorhabditis elegans locomotion. Proc Natl Acad Sci USA. 2013;110:791–796. doi: 10.1073/pnas.1211447110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Restif C, et al. CeleST: Computer vision software for quantitative analysis of C. elegans swim behavior reveals novel features of locomotion. PLoS Comput Biol. 2014;10:e1003702. doi: 10.1371/journal.pcbi.1003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lanza IR, et al. Endurance exercise as a countermeasure for aging. Diabetes. 2009;57:2933–2942. doi: 10.2337/db08-0349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lanza IR, Nair KS. Muscle mitochondrial changes with aging and exercise. Am J Clin Nutr. 2009;89:467S–471S. doi: 10.3945/ajcn.2008.26717D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Greer EL, Brunet A. Different dietary restriction regimens extend lifespan by both independent and overlapping genetic pathways in C. elegans. Aging Cell. 2009;8:113–127. doi: 10.1111/j.1474-9726.2009.00459.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chinsomboon J, et al. The transcriptional coactivator PGC-1 mediates exercise-induced angiogenesis in skeletal muscle. Proc Natl Acad Sci USA. 2009;106:21401–21406. doi: 10.1073/pnas.0909131106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kenyon CJ. The genetics of ageing. Nature. 2010;464:504–512. doi: 10.1038/nature08980. [DOI] [PubMed] [Google Scholar]
- 16.Fernandez-Marcos PJ, Auwerx J. Regulation of PGC-1, a nodal regulator of mitochondrial biogenesis. Am J Clin Nutr. 2011;93:884S–890S. doi: 10.3945/ajcn.110.001917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chuang HS, Kuo WJ, Lee CL, Chu IH, Chen CS. Exercise in an electrotactic flow chamber ameliorates age-related degeneration in Caenorhabditis elegans. Sci Rep. 2016;6:28064. doi: 10.1038/srep28064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Artal-Sanz M, de Jong L, Tavernarakis N. Caenorhabditis elegans: A versatile platform for drug discovery. Biotechnol J. 2006;1:1405–1418. doi: 10.1002/biot.200600176. [DOI] [PubMed] [Google Scholar]
- 19.Omura DT, Clark DA, Samuel ADT, Horvitz HR. Dopamine signaling is essential for precise rates of locomotion by C. elegans. PLoS One. 2012;7:e38649. doi: 10.1371/journal.pone.0038649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Voorhies W, Fuchs J, Thomas S. The longevity of Caenorhabditis elegans in soil. Biol Lett. 2005;1:247–249. doi: 10.1098/rsbl.2004.0278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Frezal L, Felix M. The natural history of model organisms: C. elegans outside the petri dish. eLife. 2015;4:e05849. doi: 10.7554/eLife.05849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stephens GJ, Johnson-Kerner B, Bialek W, Ryu WS. Dimensionality and dynamics in the behavior of C. elegans. PLoS Comput Biol. 2008;4:e1000028. doi: 10.1371/journal.pcbi.1000028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Berri S, Boyle JH, Tassieri M, Hope IA, Cohen N. Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait. HFSP J. 2009;3:186–193. doi: 10.2976/1.3082260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cohen N, Boyle JH. Swimming at low Reynolds number: A beginners guide to undulatory locomotion. Contemp Phys. 2010;51:103–123. [Google Scholar]
- 25.Fang-Yen C, et al. Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc Natl Acad Sci USA. 2010;107:20323–20328. doi: 10.1073/pnas.1003016107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sznitman J, Shen X, Purohit PK, Arratia PE. The effects of fluid viscosity on the kinematics and material properties of C. elegans swimming at low Reynolds number. Exp Mech. 2010;50:1303–1311. [Google Scholar]
- 27.Stephens GJ, de Mesquita MB, Ryu WS, Bialek W. Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans. Proc Natl Acad Sci USA. 2011;108:7286–7289. doi: 10.1073/pnas.1007868108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Padmanabhan V, et al. Locomotion of C. elegans: A piecewise-harmonic curvature representation of nematode behavior. PLoS One. 2012;7:e40121. doi: 10.1371/journal.pone.0040121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bilbao A, Wajnryb E, Vanapalli SA, Blawzdziewicz J. Nematode locomotion in unconfined and confined fluids. Phys Fluids. 2013;25:081902. [Google Scholar]
- 30.Yuan J, Raizen DM, Bau HH. A hydrodynamic mechanism for attraction of undulatory microswimmers to surfaces (bordertaxis) J R Soc Interface. 2015;12:20150227. doi: 10.1098/rsif.2015.0227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yuan J, Raizen DM, Bau HH. Propensity of undulatory swimmers, such as worms, to go against the flow. Proc Natl Acad Sci USA. 2015;112:3606–3611. doi: 10.1073/pnas.1424962112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Montenegro-Johnson TD, Gagnon DA, Arratia PE, Lauga E. Flow analysis of the low Reynolds number swimmer C. elegans. Phys Rev Fluids. 2016;1:053202. [Google Scholar]
- 33.Kwon N, Pyo J, Lee S, Je J. 3-D worm tracker for freely moving C. elegans. PLoS One. 2013;8:e57484. doi: 10.1371/journal.pone.0057484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Beron C, et al. The burrowing behavior of the nematode Caenorhabditis elegans: A new assay for the study of neuromuscular disorders. Genes Brain Behav. 2015;14:357–368. doi: 10.1111/gbb.12217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vidal-Gadea A, et al. Magnetosensitive neurons mediate geomagnetic orientation in Caenorhabditis elegans. eLife. 2015;4:e07493. doi: 10.7554/eLife.07493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kwon N, Hwang AB, You YJ, Lee SJV, Je JH. Dissection of C. elegans behavioral genetics in 3-D environments. Sci Rep. 2015;5:9564. doi: 10.1038/srep09564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Majmudar T, Keaveny E, Zhang J, Shelley M. Experiments and theory of undulatory locomotion in a simple structured medium. J R Soc Interface. 2012;9:1809–1823. doi: 10.1098/rsif.2011.0856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kim D, Park S, Mahadevan L, Shin JH. The shallow turn of a worm. J Exp Biol. 2011;214:1554–1559. doi: 10.1242/jeb.052092. [DOI] [PubMed] [Google Scholar]
- 39.Broekmans OD, Rodgers JB, Ryu WS, Stephens GJ. Resolving coiled shapes reveals new reorientation behaviors in C. elegans. eLife. 2016;5:e17227. doi: 10.7554/eLife.17227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Albrecht DR, Bargmann CI. High-content behavioral analysis of Caenorhabditis elegans in precise spatiotemporal chemical environments. Nat Methods. 2011;8:599–605. doi: 10.1038/nmeth.1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gray J. Undulatory propulsion. J Cell Sci. 1953;94:551–578. [Google Scholar]
- 42.Berman RS, Kenneth O, Sznitman J, Leshansky AM. Undulatory locomotion of finite filaments: Lessons from C. elegans. New J Phys. 2013;15:075022. [Google Scholar]
- 43.Sznitman J, Shen X, Sznitman R, Arratia PE. Propulsive force measurements and flow behavior of undulatory swimmers at low Reynolds number. Phys Fluids. 2010;22:12901. [Google Scholar]
- 44.Husson SJ, Costa WS, Schmitt C, Gottschalk A. Keeping track of worm trackers. WormBook. 2013 doi: 10.1895/wormbook.1.156.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stoker J. Differential Geometry. Wiley; New York: 1969. [Google Scholar]
- 46.Bilbao A. 2016. Modeling the locomotion of Caenorhabditis elegans: Undulatory propulsion and maneuverability in fluids. PhD thesis (Texas Tech University, Lubbock, TX)
- 47.Deng X, Xu J. A 3d undulatory locomotion model inspired by C. elegans through DNN approach. Neurocomputing. 2014;131:248–264. [Google Scholar]
- 48.Shen XN, Arratia PE. Undulatory swimming in viscoelastic fluids. Phys Rev Lett. 2011;106:208101. doi: 10.1103/PhysRevLett.106.208101. [DOI] [PubMed] [Google Scholar]
- 49.Gagnon DA, Shen XN, Arratia PE. Undulatory swimming in fluids with polymer networks. EPL. 2013;104:14004. [Google Scholar]
- 50.Gagnon DA, Keim NC, Arratia PE. Undulatory swimming in shear-thinning fluids: Experiments with Caenorhabditis elegans. J Fluid Mech. 2014;758:R3. [Google Scholar]
- 51.Park JS, Kim D, Shin JH, Weitz DA. Efficient nematode swimming in a shear thinning colloidal suspension. Soft Matter. 2016;12:1892–1897. doi: 10.1039/c5sm01824b. [DOI] [PubMed] [Google Scholar]
- 52.Yuan J, Ko H, Raizen DM, Bau HH. Terrain following and applications: Caenorhabditis elegans swims along the floor using a bump and undulate strategy. J R Soc Interface. 2016;13:20160612. doi: 10.1098/rsif.2016.0612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Altun ZF, Hall DH. Muscle system, somatic muscle. WormAtlas. 2009 doi: 10.3908/wormatlas.1.7. [DOI] [Google Scholar]
- 54.White JG, Southgate E, Thomson JN, Brenner S. The structure of the nervous-system of the nematode Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci. 1986;314:1–340. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
- 55.Ugural AC, Fenster SK. C. elegans II. 2nd Ed Cold Spring Harbor Lab Press; Cold Spring Harbor, NY: 1997. [Google Scholar]
- 56.Wajnryb E, Mizerski KA, Zuk PJ, Szymczak P. Generalization of the Rotne-Prager-Yamakawa mobility and shear disturbance tensors. J Fluid Mech. 2013;731:R3. [Google Scholar]
- 57.Cichocki B, Felderhof BU, Hinsen K, Wajnryb E, Bławzdziewicz J. Friction and mobility of many spheres in Stokes flow. J Chem Phys. 1994;100:3780–3790. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.