Significance
The reasons why aquatic mammals exhibit larger average sizes than their terrestrial relatives have long been debated. Most previous hypotheses have focused on releases from terrestrial constraints on large sizes. Through the analysis of mammal size distributions, we find the aquatic realm imposes stronger constraints on body size than does the terrestrial realm, driving and confining aquatic mammals to larger sizes. Calculations of energy intake and demand as a function of body size indicate heat loss imposes a strong lower bound on size, whereas the scaling of feeding rate versus metabolic rate imposes a constraint on maximum size. Rather than freeing animals from body size constraints, living in water appears to impose stronger selective pressures than does living on land.
Keywords: body mass, Ornstein–Uhlenbeck, metabolism, phylogenetic comparative methods, Mammalia
Abstract
Four extant lineages of mammals have invaded and diversified in the water: Sirenia, Cetacea, Pinnipedia, and Lutrinae. Most of these aquatic clades are larger bodied, on average, than their closest land-dwelling relatives, but the extent to which potential ecological, biomechanical, and physiological controls contributed to this pattern remains untested quantitatively. Here, we use previously published data on the body masses of 3,859 living and 2,999 fossil mammal species to examine the evolutionary trajectories of body size in aquatic mammals through both comparative phylogenetic analysis and examination of the fossil record. Both methods indicate that the evolution of an aquatic lifestyle is driving three of the four extant aquatic mammal clades toward a size attractor at ∼500 kg. The existence of this body size attractor and the relatively rapid selection toward, and limited deviation from, this attractor rule out most hypothesized drivers of size increase. These three independent body size increases and a shared aquatic optimum size are consistent with control by differences in the scaling of energetic intake and cost functions with body size between the terrestrial and aquatic realms. Under this energetic model, thermoregulatory costs constrain minimum size, whereas limitations on feeding efficiency constrain maximum size. The optimum size occurs at an intermediate value where thermoregulatory costs are low but feeding efficiency remains high. Rather than being released from size pressures, water-dwelling mammals are driven and confined to larger body sizes by the strict energetic demands of the aquatic medium.
Most mammal species live on land, but the largest mammals inhabit the ocean (1). The same is true of reptiles and arthropods (2–4). Aquatic and terrestrial habitats clearly impose differing selective pressures on body size. However, the quantitative study of body size evolution in mammals and other diverse animal clades typically focuses on either terrestrial or aquatic clades independently (e.g., refs. 5–9). Consequently, the extent to which the rate, magnitude, and outcome of size change associated with habitat transitions are shared among clades remains unknown. This gap in knowledge leaves open the question of whether the apparently common phenomenon of size increase associated with the adoption of an aquatic lifestyle reflects idiosyncratic responses of individual clades versus a common response to shared constraints.
Identifying the causes of size increase in aquatic mammalian clades requires information not only on the differences in current mean size between terrestrial and aquatic sister groups but also on the variance about these differing means and the value of the mean size, given sufficient evolutionary time for the size distribution to reach equilibrium. Here, we quantify these parameters for four independent terrestrial-aquatic transitions in mammals within a phylogenetic context to quantify how the shift to aquatic habitat has impacted the rate, magnitude, and directionality of body size evolution.
Several hypotheses have been put forward to explain why mammals living in water are larger, on average, than their closest terrestrial relatives, including theories regarding diet, neutral buoyancy, habitat area, protein availability, and thermoregulation (10–21). Although each of these theories predicts that mammalian clades entering the water will increase in average size, these theories differ in their predictions for how such a size change is achieved. More specifically, they differ in their predictions both about the rate of evolution toward the new, larger average size as well as the variance of the aquatic size distribution relative to its terrestrial sister group (22).
The Ornstein–Uhlenbeck (OU) process (23) represents a model of adaptive evolution appropriate to the question of size evolution across a transition in habitat, where the change of body mass, X, over time, t, is the result of the interactions between the body mass optimum, θ, the strength of selection toward the optimum, α, the intensity of random drift away from the optimum, σ, and white noise, B:
| [1] |
Under this framework, the mean body mass (E) of the clade is expected to approach the optimum asymptotically following an exponential trajectory (24) (Eq. 2). The variance (Var) of the size distribution also converges exponentially on a value related to the strength of selection (α) and the intensity of random drift (σ) (24) (Eq. 3):
| [2] |
| [3] |
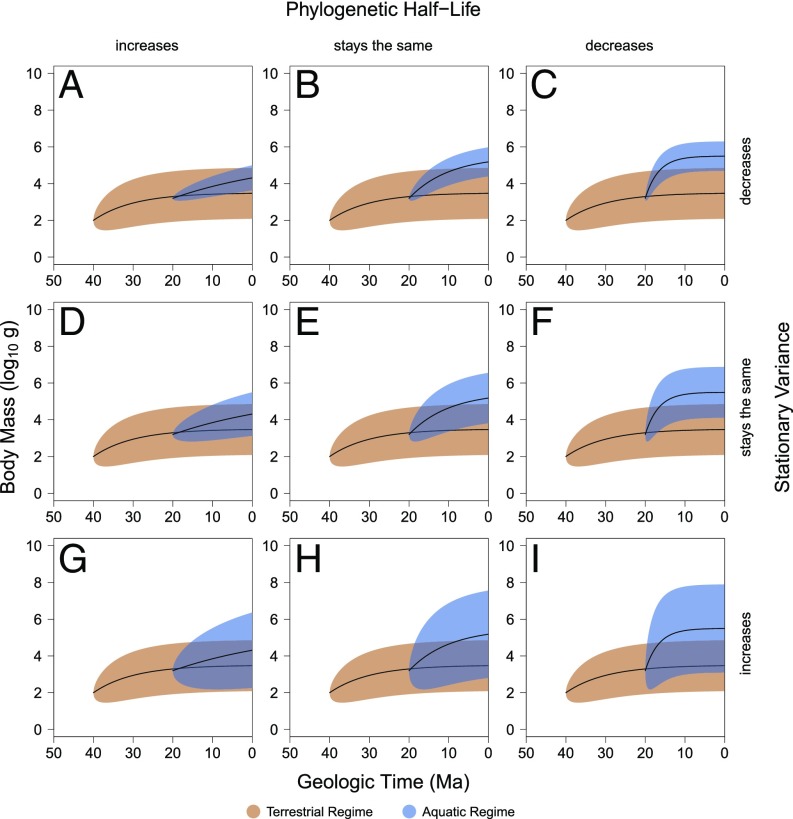
From this basic model of selective evolution, one can also calculate the phylogenetic half-life [ln(2)/α], which represents the time it takes to evolve halfway toward the optimum, as well as the stationary variance (σ2/2α), which represents the expected variance when the process is at equilibrium. Under this model, increases in body size can occur in nine discrete ways (Fig. 1). In each of the illustrated hypothetical scenarios, a clade is originally in the terrestrial adaptive regime with an optimal body mass of ∼3 kg, but a subclade then enters the aquatic adaptive regime with an optimal body mass of ∼300 kg. However, upon entering the aquatic realm, the subclade can also experience null, positive, or negative changes in the phylogenetic half-life and stationary variance. Consequently, the combined pattern of change in the optimum, phylogenetic half-life, and stationary variance can be used to distinguish among potential causes of size change following habitat transition.
Fig. 1.
Idealized theoretical scenarios in which body mass optimum increases. Nine different scenarios are illustrated in which the optimal body mass of a clade increases when it transitions from the terrestrial regime to the aquatic regime. These scenarios represent combinations of discrete threefold increases and/or decreases in the phylogenetic half-life (PHL) and stationary variance (SV) upon a clade entering the aquatic regime. In all scenarios, the optimum, PHL, and SV of the terrestrial regime are 3.5, 7.0, and 0.5, respectively, and the optimum of the aquatic regime is 5.5. A, D, and G show an increase in PHF; B, E, and F show no change in PHL; and C, F, and I show a decrease in PHL. A–C show a decrease in SV; D–F show no change in SV; and G–I show an increase in SV. The protein availability, neutral buoyancy, and habitat area hypotheses predict any of G, H, or I. The thermoregulation hypothesis predicts B, C, E, or F.
Each of the previously proposed hypotheses for increase in mean size maps onto only a subset of these nine possibilities, providing a means of testing among potential driving mechanisms and even for identifying contributions from multiple processes. The diet hypothesis predicts that herbivores are often larger than closely related carnivores due to a greater metabolic demand (8, 25). This potential effect of diet is particularly important in clades where the aquatic members have changed feeding mode. If, for example, a group of terrestrial carnivores evolved into aquatic herbivores, this hypothesis would predict an increase in body size based on the change in feeding mode but no particular change in stationary variance or phylogenetic half-life (Fig. 1E). The neutral buoyancy hypothesis predicts a release from terrestrial constraints that should result in an increase in the stationary variance (11–16) (Fig. 1 G–I). The protein availability hypothesis similarly predicts a release from energetic constraint on maximum size, enabling larger maximum sizes in the oceans, and ultimately increasing the stationary variance (17, 18, 24) (Fig. 1 G–I). The habitat area hypothesis predicts that larger habitats in the aquatic realm will allow mammals to expand to larger sizes, which also results in an increase in stationary variance (8, 20, 21, 25–28) (Fig. 1 G–I). Finally, the thermoregulation hypothesis predicts that terrestrial mammals that enter the water should encounter selection toward larger body sizes, not merely a release from smaller sizes, which should result in an equal or decreased phylogenetic half-life and/or an equal or decreased stationary variance (10) (Fig. 1 B, C, E, and F).
Here, we use previously compiled body size data for extant and fossil mammal species to perform phylogenetic comparative analyses and fossil time series analyses to estimate these body size dynamics across the four evolutionary transitions between land and water within modern mammals. We then use these estimates to test among the various previously mooted hypotheses for the large sizes of aquatic mammals.
Results and Discussion
Best Models.
The best-supported phylogenetic models for size evolution in Afrotheria, Artiodactyla, and Caniformia indicate separate size optima for terrestrial versus aquatic habitats (Dataset S1). For Musteloidea, the best-fitting models treat body size evolution as simple Brownian motion, with no trend toward an optimal size (Dataset S1).
Body Mass Optima.
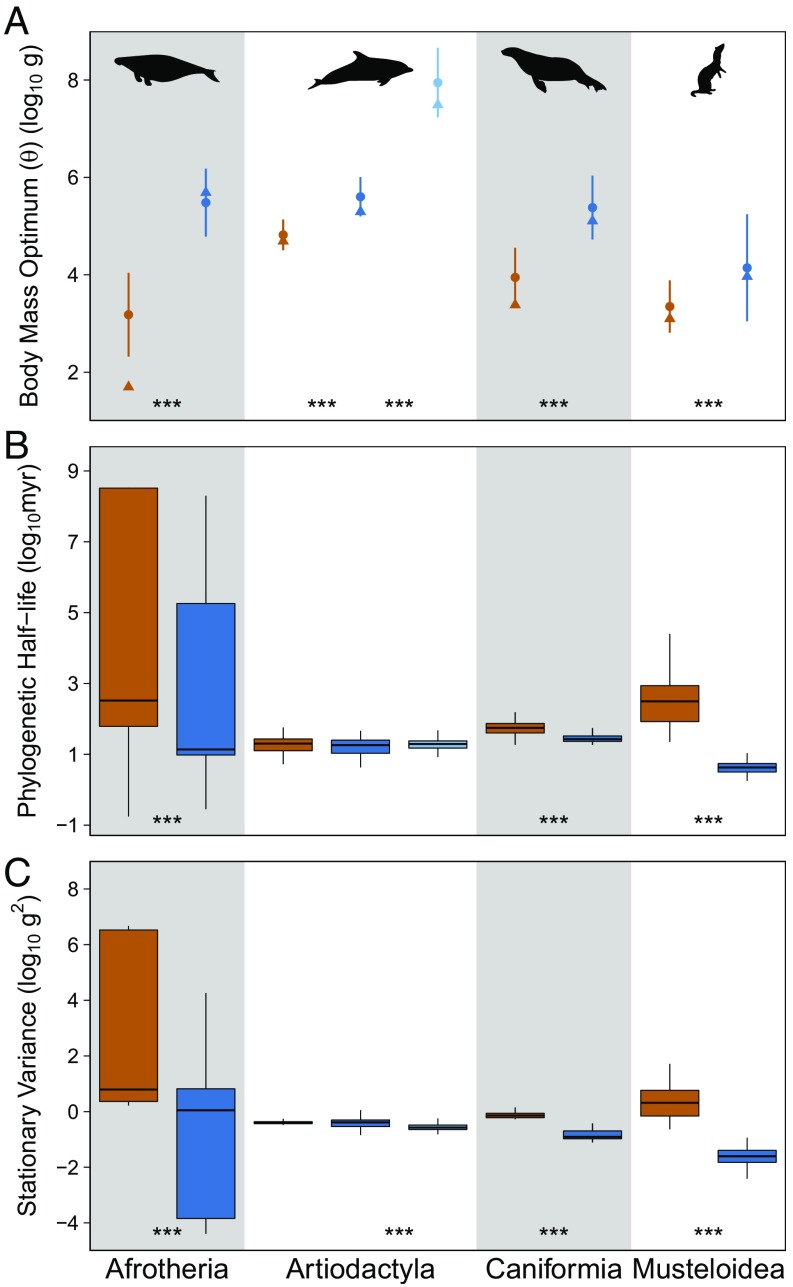
Pairwise tests between all of the estimated body mass optima indicate that they are statistically distinct from one another (Mann–Whitney test, P < 0.001). However, despite the substantial differences between the terrestrial optima of Afrotheria, Artiodactyla, and Caniformia, the estimated aquatic body mass optima for these three groups with evidence for separate aquatic body mass optima are much closer to one another (Afrotheria: 5.48, Artiodactyla: 5.60, and Caniformia: 5.38) than they are to any of their respective terrestrial optima (Afrotheria: 3.18, Artiodactyla: 4.82, and Caniformia: 3.95), implying convergence on a body mass attractor near 500 kg (Fig. 2A). Furthermore, the optimum for Mysticeti is higher than that of any of the other analyzed groups. The estimated aquatic optimum for Musteloidea does not mirror the dramatic increase of the other three clades (Fig. 2A). This sustained small size of aquatic mustelids could indicate the presence of a second attractor at a smaller mass of roughly 10 kg or competitive exclusion from the 500-kg attractor. One potential interpretation is that this finding reflects the semiaquatic nature of most otters, which causes them to be under a combination of aquatic and terrestrial selective forces. Testing this possibility is not feasible, however, because there exists only one fully aquatic otter species.
Fig. 2.
Plots of estimated body mass optima (A), phylogenetic half-lives (B), and stationary variances (C) by clade and habitat type, illustrating the statistically larger optimal body masses, equal or decreased phylogenetic half-lives, and equal or decreased stationary variance for aquatic mammals relative to their terrestrial sister groups. Optima (θ) are reported as weighted means with 2σ confidence intervals of model-averaged values (●) and are accompanied by median modern body masses (▲). Phylogenetic half-lives [ln(2)/α] and stationary variances (σ2/2α) are reported as box plots of model-averaged values. Color coding refers to habitat regime (orange, terrestrial; dark blue, toothed aquatic; light blue, baleen aquatic). Symbols at the bottom of the plots represent significance of results of pairwise Mann–Whitney tests (0 < *** < 0.001 < ** < 0.01 < * < 0.05 < . < 0.1).
OU models fit to the fossil time series of aquatic members of each of the four clades of interest produce optimal body mass estimates that overlap with the estimates of the phylogenetic modeling (Fig. S3 and Dataset S1). However, the confidence intervals for the paleoTS (Analyze Paleontological Time-Series) estimates span multiple orders of magnitude for Sirenia and Pinnipedia. These large confidence intervals are most likely due to the very linear trends of these two groups (Fig. S3), causing poor inference of the future plateaus implied by an OU model. The use of binned data for the paleoTS analyses may also be contributing to this uncertainty due to the loss of time resolution. Furthermore, while the use of fossil specimens and measurements may give a more complete picture of body size changes through time, the paleoTS software is designed specifically for use with ancestor-descendant sequences and accounts for the auto-correlation of adjacent points in the time series but does not account for the varied dependence of measurements to one another in a single time bin or across time bins (29, 30). This factor could also help to explain the decrease in statistical power when using paleoTS.
Phylogenetic Half-Life and Stationary Variance.
Phylogenetic half-life and stationary variance estimates for the aquatic regimes were consistently less than or equal to those of the terrestrial regimes across all four clades (Fig. 2 B and C, corresponding to Fig. 1 B, C, E, and F). Together, these parameter estimates indicate equivalent or decreased body size disparity and equivalent or increased strength of selection upon the transition into the aquatic habitat. The convergence of these three aquatic mammal clades in such a manner suggests that living in the aquatic realm, more than merely enabling large size, imposes a strong selective pressure toward larger body sizes while simultaneously imposing tighter constraints on size variation than those present in the terrestrial realm, potentially for reasons that are shared across clades.
Previous Explanations for Larger Size.
Most previously proposed explanations for mammal size increase in aquatic habitats are either incompatible with the results of this analysis or at least incomplete in explaining the pattern. Hypotheses regarding neutral buoyancy, increased protein availability, and increased habitat area all predict a release from terrestrial constraints, which should result in an increase in the stationary variance (8, 11–18, 20, 21, 24–28) (Fig. 1 G–I). However, the results above show no support for increased stationary variance upon entering the aquatic realm. The diet hypothesis predicts that herbivores are often larger than closely related carnivores (8, 25). For the optimal size of a group to increase, this would require some or all of the aquatic members to convert from carnivory to herbivory. However, most aquatic mammals are carnivores, and the only herbivorous aquatic mammals evolved from herbivorous terrestrial ancestors. Therefore, diet shift does not serve as a unifying explanation for the convergence of these three groups. Finally, the thermoregulatory differences between land and water (10) should cause selection toward larger body sizes, not merely a release from smaller sizes, which would manifest as equal or decreased phylogenetic half-lives and/or stationary variance (Fig. 1 B, C, E, and F), both of which are indicated by our results. Therefore, selective pressures from thermoregulatory requirements can explain convergent increases in minimum size across these groups. However, the thermoregulatory hypothesis only partially explains the observed patterns. Thermoregulatory costs scale roughly to the 1/4 power of body size and should most strongly impact the smallest end of the aquatic size distribution. They do not fully explain the optimum or maximum sizes of aquatic mammals.
An Energetic Model to Explain Size Dynamics.
An expansion of the thermoregulatory hypothesis toward a more general energetic explanation of mammal body size distributions helps to account for changes not only in minimum size but also in the calculated optimum and stationary variance as well as the observed maximum size and skewness of the aquatic size distribution. This expanded energetic model is similar to the models of energy use as a function of body size that have been applied to explain size distributions of other groups (31–35). In this model, surplus energy, E, for an organism is the energy used for growth, reproduction, and behaviors that demand energy beyond basal metabolism. We take this to be the difference between the intake of chemical energy by feeding, F, and the expenditure of this energy by basal metabolism, M, and heat loss to the environment, H:
| [4] |
Estimates to calibrate each of these parameters in detail for all aquatic mammals are not available. However, a plausibility test calibrated to parameter values measured on phocids illustrates the potential for this conceptual approach to be developed into a fully quantitative model. For purposes of illustration, we used the empirical feeding rate of adult Phocidae, in watts (36), where m is mass in kilograms:
| [5] |
Next, we used an empirical basal metabolic rate for adult Phocidae, in watts (37):
| [6] |
Finally, we calculated the heat loss term as the rate of heat loss, in watts, for a cylindrical body with an effective constant blubber thickness (38, 39), where L is the length of the mammal in meters, b is the fraction of the total body mass that is blubber, k is the blubber conductivity, and ΔT is the temperature difference between the water and the mammal’s internal temperature:
| [7] |
Ryg et al. (38) report a common value of 0.2 for blubber conductivity and an average ΔT of 30 °C, Watts et al. (39) report a value of 0.29 for blubber proportion in Phocidae, and Kshatriya and Blake (40) report an allometric relationship in aquatic mammals between length, in meters, and mass, in kilograms, such that:
| [8] |
Combined, this yields an equation to estimate heat loss, in watts:
| [9] |
Therefore, as an illustration of plausibility of an energetic model to explain body size dynamics, the energy surplus of a generalized Phocid, in watts, is represented by:
| [10] |
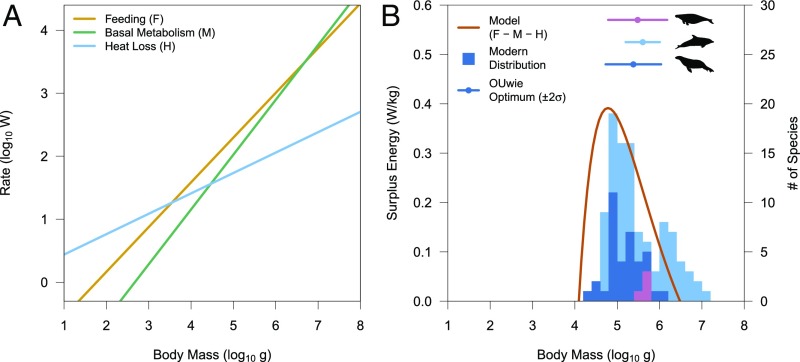
The independent components (F, M, and H) of this model lead to a calculated energy surplus as a function of body mass that corresponds closely to the observed mean and calculated optimum values for marine mammal clades and also predicts the observed right skewness of the size distributions (Fig. 3). Furthermore, the predicted distribution based on energetics closely matches the observed minimum and maximum sizes of pinnipeds, the clade for which the model was parameterized. We have intentionally standardized the energy surplus by body mass in this case because this surplus is ultimately used for growth and/or reproduction (31), both of which are size-dependent. Therefore, maximizing the energy surplus in watts per kilogram rather than in watts provides an organism the greatest opportunity to invest in these facets.
Fig. 3.
Plot of a plausible energetics model (B) and its components (A) that predicts the estimated optimal body masses and modern distributions of aquatic mammals. Components of energetics model with respect to body mass (A) and comparison of energetics model calculation with stacked modern aquatic mammal body mass distributions and estimated OUwie optima for Sirenia, Odontoceti, and Pinnipedia, respectively (B), are shown. The surplus energy curve predicts the OUwie optima and modern distributions.
This energetic model for fitness as a function of size in marine mammals successfully explains not only the increase in mean size but also the observed increase in constraint on size relative to terrestrial sister groups. Due to the increased energetic cost of living in water below body temperature (the H component), the minimum possible size of an aquatic endotherm is more than three orders of magnitude larger than the minimum possible size of an otherwise similar endotherm on land (10). Therefore, terrestrial mammals that enter the water encounter selection toward larger body sizes, not merely a release from smaller sizes. In addition, basal metabolism exceeds the rate of feeding at larger sizes due to differences in allometric scaling exponents, imposing a selective pressure from energy metabolism against size increase at larger body masses. The similarities in the size distributions among toothed aquatic mammals suggest that among-clade differences in the mass-feeding relationship are comparatively minor.
Changes in the slope and/or intercept of the relationship between body mass and feeding rate associated with the evolution of baleen can account for the shift toward even larger sizes in baleen whales. This shift in the energetic constraints on size evolution may be the result of an increase in feeding efficiency in baleen whales compared with their toothed relatives, due to the evolution of new foraging strategies, particularly filter-feeding and lunge feeding (41–43). For example, modifying the feeding function presented in Eq. 5 to an exponent of 0.78 (versus 0.71) results in a surplus energy distribution that maintains a peak around the optima of the three toothed aquatic groups but also includes the largest sizes of the baleen whales (Fig. S4). This hypothetical relationship does not explain the absence of extant baleen whales at smaller sizes, suggesting that this feeding mode also leads to poor competitiveness with toothed relatives (or other taxa) at smaller sizes or modifies the scaling of feeding with respect to body mass in more complex ways than addressed by the model above. The fact that extreme gigantism in baleen whales is a fairly recent phenomenon, within the last 10 My, relative to the evolution of baleen further suggests that the amount and spatial distribution of food resources further determine the viability of this feeding mechanism (44, 45).
Through the combination of heat loss and feeding constraints, an energetic model for body size evolution in aquatic mammals predicts equal or decreased phylogenetic half-lives and stationary variances on evolutionary time scales (Fig. 1 B, C, E, and F), both of which are indicated by the distributions of body sizes across living and fossil aquatic mammals. Because all aquatic mammals share these energetic constraints, they can explain the rapid, convergent evolution toward larger optimal body sizes across toothed Sirenia, Cetacea, and Pinnipedia, despite differences in the body size attractors displayed by their terrestrial sister groups.
Conclusion
Whereas the aquatic medium has been argued to release animals from constraints on body size through mechanisms such as habitat area and neutral buoyancy (10–21), comparative analysis of fossil and living mammals demonstrates that the aquatic realm actually imposes tighter constraints on size evolution in aquatic mammals than in their land-dwelling relatives. Three of the four mammal clades living in aquatic environments have evolved toward larger optimal body masses than their terrestrial counterparts. Moreover, these three clades have evolved independently toward a shared body mass attractor of ∼500 kg, coupled with increased rates of evolution and decreased variance. Many previous hypotheses for mammalian body size increase in aquatic habitats fail to account for these additional body size dynamics. By contrast, an energetic cost model incorporating size-dependent functions for food intake and costs from basic energy metabolism and thermoregulation accounts for the observed combination of increase in body size, decrease in variance, and increase in evolutionary rate. Parameterizing the energetic model using data from phocids also predicts the observed lower and upper bounds of the distribution as well as the observed right skewness of the distribution. Therefore, the convergence of aquatic mammal clades on a body mass optimum near 500 kg appears to reflect the shared constraints of allometric scaling of thermoregulation, basal metabolic rate, and feeding potential with body size for toothed mammals. Rather than being released from size pressures, they are driven and confined to larger body sizes by the strict demands of the aquatic medium.
Data and Methods
We compiled body masses for 3,859 extant and 2,999 fossil mammal species from existing datasets (5–7, 46–53; www.helsinki.fi/science/now/) that, in aggregate, cover ∼70% of extant mammalian species and 25% of accepted extinct species (Figs. S1 and S2). We replaced synonymous taxonomic names with the accepted canonical names using the Global Biodiversity Information Facility (GBIF) Backbone Taxonomy (https://www.gbif.org/), accessed using the R package rgbif (54, 55). When multiple measurements existed, we calculated the mean and SE. When only a single measurement existed, we randomly sampled a SE from the calculated SEs of the other members of the species’ family or, if none existed, of the species’ order.
We combined binary habitat assignments (coded as marine/nonmarine) from the GBIF and categorical habitat assignments (coded as terrestrial/marine/brackish/freshwater) from the World Register of Marine Species to create a habitat assignment for each species coded as aquatic/nonaquatic (https://www.gbif.org/; www.marinespecies.org). We resolved ambiguous habitats for fossil species using “life habit” assignments from the Paleobiology Database and the primary literature. Ultimately, we excluded 273 species from further analysis because their habitat affinities remained ambiguous after these searches.
We downloaded the stratigraphic ranges of all mammal species with fossil records using the Paleobiology Database Data Service v.1.1 on November 8, 2016 (https://paleobiodb.org/data1.1/taxa/list.txt?name=Mammalia&rel=all_children&show=app&rank=species&status=senior&limit=15000). We excluded all species that lacked a stage-resolved stratigraphic range. This culling procedure yielded a set of 3,099 species that could be used for time series analyses.
We used the time-calibrated supertree of extant mammalian species for all analyses requiring a phylogenetic framework (56, 57). We used a sample of 100 trees from the posterior distribution of a Bayesian birth-death polytomy resolver for all analyses (58). Although this approach is not a perfect substitute for a fully resolved tree (59), it allows us to randomly sample over the different resolved forms of the supertree for the analyses discussed below. The supertree includes 3,832 of the species in our database.
We tested the influence of habitat on body size evolution using generalized OU process modeling (23, 60, 61) (Eqs. 1–3), as has been used in previous studies (25, 62). These OU models contain three parameters describing the evolution of body size over time: the primary optimum of body size (θ), the rate of stochastic evolution away from the optimum (σ2), and the strength of selection toward the optimum (α). The hypothetical trait value that distinguishes stabilizing and directional selection from Brownian motion is θ. This value is assumed to be constant through time for a given selective regime and represents the average value reached by an infinite number of populations descended from a single ancestor, also referred to herein as the attractor. The parameter σ2 is a constant measure of the stochastic evolution within a selective regime. Under a Brownian motion model (where α = 0), σ2 is also known as the Brownian motion rate parameter. The parameter α is a measure of how quickly a lineage within a given selective regime reaches θ. If α is large, the selective pressure of living in a given selective regime has a much stronger effect on the trait value than the phylogenetic history, whereas if α is small, the phylogenetic constraints are relatively strong. Together, the parameters σ2 and α determine the trait disparity within a selective regime.
We performed all tree manipulations and statistical analyses using the R software environment (54). Using the R package OUwie (63), we fit seven different OU models in which one, two, or all three of these parameters were estimated for the entirety of a clade and separately for members of the two habitat types, terrestrial and aquatic. In each analysis, these parameters are optimized to best fit the given model’s predictions to the known body sizes of the extant species while also taking into account the known measurement error. The BM1 model fits a single Brownian motion model to the entire clade, estimating only the σ2 parameter. The BMS model fits separate Brownian motion models to terrestrial and aquatic members within the clade, estimating σ2 separately for each selective regime. The OU1 model fits a single OU model to the entire clade, estimating the single values for the θ, σ2, and α parameters over the entire phylogeny. The OUM model, in addition to estimating σ2 and α for the entire clade, estimates θ separately for each selective regime. The OUMV model builds on the OUM model, allowing σ2 to vary across selective regimes but holding α constant across the entire clade. Meanwhile, the OUMA model allows α to vary across selective regimes but holds σ2 constant across the entire clade. The most complex model, OUMVA, allows all three parameters to vary between terrestrial and aquatic selective regimes. It is assumed that all parameter space is theoretically biologically valid.
We fit these models across the Afrotheria, Artiodactyla, Caniformia, and Musteloidea clades using a set of 100 resolved Mammalia phylogenies (discussed above) to test the independent evolutions of aquatic life habit in mammals. In this modeling process, the time-scaled phylogeny is used to estimate the amount of time that exists since the divergence of a set of species (t in Eqs. 1–3). Lutrinae (otters) were excluded from the Caniformia analyses because they are the aquatic clade of interest in the Musteloidea analyses. The ancestral habitat conditions required by the OUwie R package and function were reconstructed using the ace function from the R package ape (64). The state with the highest marginal likelihood was assigned at each node. The ape package was also used for tree manipulation (e.g., tip removal, clade isolation). Through preliminary analyses, we found that dropping the estimated root parameter (θ0) (i.e., setting root.station = TRUE) within the OUwie function helped to stabilize the parameter estimates. With positive alpha values, the weight of the information in the analysis becomes skewed toward the present and the root estimate carries very little weight, causing it to be a difficult parameter to estimate and causing stabilization problems downstream. Dropping this parameter therefore assumes that the root was within the distribution of the ancestral regime (in this case, the terrestrial regime in all analyses: θ0 = θt). Furthermore, due to the key innovations of baleen and ram feeding in baleen whales and the definite impact this evolutionary innovation has on their body size (41), we have separated Cetacea into two regimes, corresponding to Mysticeti and Odontoceti. Including this split in the analyses resulted in a very small decrease in the optimum for toothed whales and improved likelihood support compared with a two-regime model.
We determined the relative support for each model for each tree using weighted Akaike information criterion (AIC) values, corrected for sample sizes, hereafter referred to as AICc weights (65, 66). In all AICc weight calculations, the sample size is taken to be the total number of tips within the clade of interest (61). To account for the various degrees of support for the different models and for the inclusion of different parameters in each of the models, we calculated model-averaged parameter estimates using the formulae presented by Burnham and Anderson (65). Because the θ parameter estimates for the BM1 and BMS models represent the estimated body size at the root, not necessarily the optimal body size, these models were not included in the model-averaging process.
To compare these phylogenetic (extant) results with fossil data, we used the fossil mammal ranges in our database to compute time series consisting of species body size means and variances for 1-My time bins for Sirenia, Pinnipedia, Odontoceti, and Lutrinae. We then fit OU models to these time series using the R package paleoTS (67–69). We used the joint parameterization methods in the log-likelihood function to account for auto-correlation among samples (29).
Supplementary Material
Acknowledgments
We thank J. Beaulieu and G. Hunt for insightful conversations about their software and for accommodating feature requests. We thank S. K. Lyons for sharing fossil mammal body size estimates. We are grateful to two anonymous reviewers for providing very helpful comments on earlier versions of this manuscript.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. N.D.P. is a guest editor invited by the Editorial Board.
Data deposition: The code and data for all analyses are available at BitBucket (https://bitbucket.org/wgearty/body-size-analyses/).
See Commentary on page 3995.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1712629115/-/DCSupplemental.
References
- 1.Smith FA, Lyons SK. How big should a mammal be? A macroecological look at mammalian body size over space and time. Philos Trans R Soc Lond B Biol Sci. 2011;366:2364–2378. doi: 10.1098/rstb.2011.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nicholls EL, Manabe M. Giant ichthyosaurs of the Triassic—A new species of Shonisaurus from the Pardonet formation (Norian: Late Triassic) of British Columbia. J Vertebr Paleontol. 2004;24:838–849. [Google Scholar]
- 3.Lingham-Soliar T. Anatomy and functional morphology of the largest marine reptile known, Mosasaurus hoffmanni (Mosasauridae, Reptilia) from the upper Cretaceous, upper Maastrichtian of The Netherlands. Philos Trans R Soc B. 1995;347:155–172. [Google Scholar]
- 4.Braddy SJ, Poschmann M, Tetlie OE. Giant claw reveals the largest ever arthropod. Biol Lett. 2008;4:106–109. doi: 10.1098/rsbl.2007.0491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Churchill M, Clementz MT, Kohno N. Cope’s rule and the evolution of body size in Pinnipedimorpha (Mammalia: Carnivora) Evolution. 2015;69:201–215. doi: 10.1111/evo.12560. [DOI] [PubMed] [Google Scholar]
- 6.Montgomery SH, et al. The evolutionary history of cetacean brain and body size. Evolution. 2013;67:3339–3353. doi: 10.1111/evo.12197. [DOI] [PubMed] [Google Scholar]
- 7.Tomiya S. Body size and extinction risk in terrestrial mammals above the species level. Am Nat. 2013;182:E196–E214. doi: 10.1086/673489. [DOI] [PubMed] [Google Scholar]
- 8.Smith FA, et al. The evolution of maximum body size of terrestrial mammals. Science. 2010;330:1216–1219. doi: 10.1126/science.1194830. [DOI] [PubMed] [Google Scholar]
- 9.Saarinen JJ, et al. Patterns of maximum body size evolution in Cenozoic land mammals: Eco-evolutionary processes and abiotic forcing. Proc Biol Sci. 2014;281:20132049. doi: 10.1098/rspb.2013.2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Downhower JF, Bulmer LS. Calculating just how small a whale can be. Nature. 1988;335:675. [Google Scholar]
- 11.Anderson JF, Hermann R, Prange HD. Scaling of supportive tissue mass. Q Rev Biol. 1979;54:139–148. [Google Scholar]
- 12.Schmidt-Nielsen K. Scaling: Why Is Animal Size So Important? Cambridge Univ Press; Cambridge, UK: 1984. [Google Scholar]
- 13.Reynolds W, Karlotski W. The allometric relationship of skeleton weight to body weight in teleost fishes: A preliminary comparison with birds and mammals. Copeia. 1977;1977:160–163. [Google Scholar]
- 14.Prange H, Anderson J, Rahn H. Scaling of skeletal mass to body mass in birds and mammals. Am Nat. 1979;113:103–122. [Google Scholar]
- 15.Schmidt-Nielsen K. Locomotion: Energy cost of swimming, flying, and running. Science. 1971;177:222–228. doi: 10.1126/science.177.4045.222. [DOI] [PubMed] [Google Scholar]
- 16.Williams TM. The evolution of cost efficient swimming in marine mammals: Limits to energetic optimization. Philos Trans R Soc B. 1999;354:193–201. [Google Scholar]
- 17.Tucker MA, Rogers TL. Examining predator-prey body size, trophic level and body mass across marine and terrestrial mammals. Proc Biol Sci. 2014;281:20142103. doi: 10.1098/rspb.2014.2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shurin JB, Gruner DS, Hillebrand H. All wet or dried up? Real differences between aquatic and terrestrial food webs. Proc Biol Sci. 2006;273:1–9. doi: 10.1098/rspb.2005.3377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Burness GP, Diamond J, Flannery T. Dinosaurs, dragons, and dwarfs: The evolution of maximal body size. Proc Natl Acad Sci USA. 2001;98:14518–14523. doi: 10.1073/pnas.251548698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tucker MA, Ord TJ, Rogers TL. Evolutionary predictors of mammalian home range size: Body mass, diet and the environment. Glob Ecol Biogeogr. 2014;23:1105–1114. [Google Scholar]
- 21.Pawar S, Dell AI, Savage VM. Dimensionality of consumer search space drives trophic interaction strengths. Nature. 2012;486:485–489. doi: 10.1038/nature11131. [DOI] [PubMed] [Google Scholar]
- 22.Jablonski D. Body-size evolution in Cretaceous molluscs and the status of Cope’s rule. Nature. 1997;385:250–252. [Google Scholar]
- 23.Hansen TF. Stabilizing selection and the comparative analysis of adaptation. Evolution. 1997;51:1341–1351. doi: 10.1111/j.1558-5646.1997.tb01457.x. [DOI] [PubMed] [Google Scholar]
- 24.Hansen TF, Pienaar J, Orzack SH. A comparative method for studying adaptation to a randomly evolving environment. Evolution. 2008;62:1965–1977. doi: 10.1111/j.1558-5646.2008.00412.x. [DOI] [PubMed] [Google Scholar]
- 25.Price SA, Hopkins SSB. The macroevolutionary relationship between diet and body mass across mammals. Biol J Linn Soc Lond. 2015;115:173–184. [Google Scholar]
- 26.McClain CR, Gullett T, Jackson-Ricketts J, Unmack PJ. Increased energy promotes size-based niche availability in marine mollusks. Evolution. 2012;66:2204–2215. doi: 10.1111/j.1558-5646.2012.01580.x. [DOI] [PubMed] [Google Scholar]
- 27.Marquet PA, Taper ML. On size and area: Patterns of mammalian body size extremes across landmasses. Evol Ecol. 1998;12:127–139. [Google Scholar]
- 28.Smith FA, et al. Similarity of mammalian body size across the taxonomic hierarchy and across space and time. Am Nat. 2004;163:672–691. doi: 10.1086/382898. [DOI] [PubMed] [Google Scholar]
- 29.Hunt G, Bell MA, Travis MP. Evolution toward a new adaptive optimum: Phenotypic evolution in a fossil stickleback lineage. Evolution. 2008;62:700–710. doi: 10.1111/j.1558-5646.2007.00310.x. [DOI] [PubMed] [Google Scholar]
- 30.Hunt G, Carrano M. Models and methods for analyzing phenotypic evolution in lineages and clades. Spec Pap Pal Soc. 2010;16:245–269. [Google Scholar]
- 31.Sebens KP. Energetic constraints, size gradients, and size limits in benthic marine invertebrates. Integr Comp Biol. 2002;42:853–861. doi: 10.1093/icb/42.4.853. [DOI] [PubMed] [Google Scholar]
- 32.Sebens KP. The energetics of asexual reproduction and colony formation in benthic marine invertebrates. Am Zool. 1979;19:683–699. [Google Scholar]
- 33.Case TJ. Optimal body size and an animal’s diet. Acta Biotheor. 1979;28:54–69. doi: 10.1007/BF00054680. [DOI] [PubMed] [Google Scholar]
- 34.Rex MA, Etter RJ. Bathymetric patterns of body size: Implications for deep-sea biodiversity. Deep Sea Res Part II. 1998;45:103–127. [Google Scholar]
- 35.Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. Toward a metabolic theory of ecology. Ecology. 2004;85:1771–1789. [Google Scholar]
- 36.Innes S, Lavigne DM, Earle WM, Kovacs KM. Feeding rates of seals and whales. J Anim Ecol. 1987;56:115. [Google Scholar]
- 37.Lavigne DM, et al. Metabolic rates of seals and whales. Can J Zool. 1986;64:279–284. [Google Scholar]
- 38.Ryg M, Smith TG, Øritsland NA. Thermal significance of the topographical distribution of blubber in ringed seals (Phoca hispida) Can J Fish Aquat Sci. 1988;45:985–992. [Google Scholar]
- 39.Watts P, Hansen S, Lavigne DM. Models of heat loss by marine mammals: Thermoregulation below the zone of irrelevance. J Theor Biol. 1993;163:505–525. [Google Scholar]
- 40.Kshatriya M, Blake RW. Theoretical model of migration energetics in the blue whale, Balaenoptera musculus. J Theor Biol. 1988;133:479–498. [Google Scholar]
- 41.Goldbogen JA, et al. How baleen whales feed: The biomechanics of engulfment and filtration. Annu Rev Mar Sci. 2017;9:367–386. doi: 10.1146/annurev-marine-122414-033905. [DOI] [PubMed] [Google Scholar]
- 42.Goldbogen JA, et al. Mechanics, hydrodynamics and energetics of blue whale lunge feeding: Efficiency dependence on krill density. J Exp Biol. 2011;214:131–146. doi: 10.1242/jeb.048157. [DOI] [PubMed] [Google Scholar]
- 43.Potvin J, Goldbogen JA, Shadwick RE. Metabolic expenditures of lunge feeding rorquals across scale: Implications for the evolution of filter feeding and the limits to maximum body size. PLoS One. 2012;7:e44854. doi: 10.1371/journal.pone.0044854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Slater GJ, Goldbogen JA, Pyenson ND. Independent evolution of baleen whale gigantism linked to Plio-Pleistocene ocean dynamics. Proc Biol Sci. 2017;284:20170546. doi: 10.1098/rspb.2017.0546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pyenson ND, Vermeij GJ. The rise of ocean giants: Maximum body size in Cenozoic marine mammals as an indicator for productivity in the Pacific and Atlantic Oceans. Biol Lett. 2016;12:20160186. doi: 10.1098/rsbl.2016.0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ernest SKM. Life history characteristics of placental nonvolant mammals. Ecology. 2008;84:3402. [Google Scholar]
- 47.Heim NA, Knope ML, Schaal EK, Wang SC, Payne JL. Animal evolution. Cope’s rule in the evolution of marine animals. Science. 2015;347:867–870. doi: 10.1126/science.1260065. [DOI] [PubMed] [Google Scholar]
- 48.Jones KE, et al. PanTHERIA: A species-level database of life history, ecology, and geography of extant and recently extinct mammals. Ecology. 2009;90:2648. [Google Scholar]
- 49.Smith FA, et al. Body mass of late quaternary mammals. Ecology. 2003;84:3403. [Google Scholar]
- 50.Schwartz GT, Rasmussen DT, Smith RJ. Body-size diversity and community structure of fossil hyracoids. J Mammal. 1995;76:1088–1099. [Google Scholar]
- 51.Christiansen P. Body size in proboscideans, with notes on elephant metabolism. Zool J Linn Soc. 2004;140:523–549. [Google Scholar]
- 52.Sarko DK, Domning DP, Marino L, Reep RL. Estimating body size of fossil sirenians. Mar Mamm Sci. 2010;26:937–959. [Google Scholar]
- 53.Alroy J. Cope’s rule and the dynamics of body mass evolution in North American fossil mammals. Science. 1998;280:731–734. doi: 10.1126/science.280.5364.731. [DOI] [PubMed] [Google Scholar]
- 54.R Core Team 2016 R: A Language and Environment for Statistical Computing Version 3.3.2. Available at www.r-project.org/. Accessed November 8, 2016.
- 55.Chamberlain S, Ram K, Barve V, Mcglinn D. 2015 rgbif: Interface to the Global Biodiversity Information Facility API Version 0.9.7. Available at https://github.com/ropensci/rgbif. Accessed November 8, 2016.
- 56.Bininda-Emonds ORP, et al. The delayed rise of present-day mammals. Nature. 2007;446:507–512. doi: 10.1038/nature05634. [DOI] [PubMed] [Google Scholar]
- 57.Fritz SA, Bininda-Emonds ORP, Purvis A. Geographical variation in predictors of mammalian extinction risk: Big is bad, but only in the tropics. Ecol Lett. 2009;12:538–549. doi: 10.1111/j.1461-0248.2009.01307.x. [DOI] [PubMed] [Google Scholar]
- 58.Kuhn TS, Mooers AØ, Thomas GH. A simple polytomy resolver for dated phylogenies. Methods Ecol Evol. 2011;2:427–436. [Google Scholar]
- 59.Rabosky DL. No substitute for real data: A cautionary note on the use of phylogenies from birth-death polytomy resolvers for downstream comparative analyses. Evolution. 2015;69:3207–3216. doi: 10.1111/evo.12817. [DOI] [PubMed] [Google Scholar]
- 60.Beaulieu JM, Jhwueng D-C, Boettiger C, O’Meara BC. Modeling stabilizing selection: Expanding the Ornstein-Uhlenbeck model of adaptive evolution. Evolution. 2012;66:2369–2383. doi: 10.1111/j.1558-5646.2012.01619.x. [DOI] [PubMed] [Google Scholar]
- 61.Butler M, King A. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. Am Nat. 2004;164:683–695. doi: 10.1086/426002. [DOI] [PubMed] [Google Scholar]
- 62.Benson RBJ, Frigot RA, Goswami A, Andres B, Butler RJ. Competition and constraint drove Cope’s rule in the evolution of giant flying reptiles. Nat Commun. 2014;5:3567. doi: 10.1038/ncomms4567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Beaulieu JM, O’Meara B. 2016 OUwie: Analysis of Evolutionary Rates in an OU Framework Version 1.50. Available at cran.r-project.org/package=OUwie. Accessed November 8, 2016.
- 64.Paradis E, Claude J, Strimmer K. APE: Analyses of phylogenetics and evolution in R language. Bioinformatics. 2004;20:289–290. doi: 10.1093/bioinformatics/btg412. [DOI] [PubMed] [Google Scholar]
- 65.Burnham KP, Anderson DR. Model Selection and Multimodel Inference. Springer; New York: 2002. [Google Scholar]
- 66.Sugiura N. Further analysts of the data by Akaike’s information criterion and the finite corrections. Commun Stat Theory Methods. 1987;7:13–26. [Google Scholar]
- 67.Hunt G, Roy K. Climate change, body size evolution, and Cope’s rule in deep-sea ostracodes. Proc Natl Acad Sci USA. 2006;103:1347–1352. doi: 10.1073/pnas.0510550103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hunt G, Hopkins MJ, Lidgard S. Simple versus complex models of trait evolution and stasis as a response to environmental change. Proc Natl Acad Sci USA. 2015;112:4885–4890. doi: 10.1073/pnas.1403662111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hunt MG. 2015 paleoTS: Analyze Paleontological Time-Series. R package Version 0.5-1. Available at https://cran.r-project.org/package=paleoTS. Accessed November 8, 2016.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.