Significance
Notch signaling and hemodynamics are widely known to regulate arterial morphogenesis, remodeling, and homeostasis. Recent studies suggest that Notch signaling and mechanics interact in vascular remodeling, but the impact on vascular homeostasis is still unclear. Here, using a computational–experimental approach, we show that expression of Notch ligands, receptors, and target genes are down-regulated with mechanical strain. Incorporation of these results in a computational model of the arterial wall reveals that this mechanosensitivity leads to a sudden transition from synthetic toward contractile smooth muscle cells at a certain wall thickness, which varies per arterial location and closely agrees with reported anatomical data. This result provides an explanation for how mechanical forces can regulate arterial morphogenesis and homeostasis through Notch signaling.
Keywords: mechanosensitivity, Notch, Jagged, homeostasis
Abstract
Hemodynamic forces and Notch signaling are both known as key regulators of arterial remodeling and homeostasis. However, how these two factors integrate in vascular morphogenesis and homeostasis is unclear. Here, we combined experiments and modeling to evaluate the impact of the integration of mechanics and Notch signaling on vascular homeostasis. Vascular smooth muscle cells (VSMCs) were cyclically stretched on flexible membranes, as quantified via video tracking, demonstrating that the expression of Jagged1, Notch3, and target genes was down-regulated with strain. The data were incorporated in a computational framework of Notch signaling in the vascular wall, where the mechanical load was defined by the vascular geometry and blood pressure. Upon increasing wall thickness, the model predicted a switch-type behavior of the Notch signaling state with a steep transition of synthetic toward contractile VSMCs at a certain transition thickness. These thicknesses varied per investigated arterial location and were in good agreement with human anatomical data, thereby suggesting that the Notch response to hemodynamics plays an important role in the establishment of vascular homeostasis.
Arteries generally have a trilayered structure, consisting of a monolayer of endothelial cells (ECs) on the luminal side, multiple lamellae of vascular smooth muscle cells (VSMCs) in the middle, and a layer of connective tissue and fibroblasts in the outer layer. The relative and absolute thickness of each layer depends on the location in the vascular tree (1, 2). In a healthy homeostatic state, VSMCs demonstrate the contractile phenotype, which is crucial for regulating vascular tone and overall vascular functionality (3, 4). Upon alterations in the hemodynamic environment, VSMCs have the capacity to dedifferentiate into the synthetic phenotype to induce vascular growth and remodeling and restore the equilibrium configuration (5, 6). Understanding how this phenotypic plasticity of VSMCs is influenced/regulated by hemodynamic stimuli is essential for understanding healthy vascular development and pathogenesis.
It is generally accepted that mechanical factors play a pivotal role in vascular morphogenesis and adaptation. A central hypothesis is that both processes occur to obtain or maintain mechanical homeostasis (7–11). However, the biological mechanisms that regulate mechanical homeostasis are poorly understood due to the complex and dynamic interplay between mechanics and tissue adaptation, and the spatial heterogeneity of the processes involved. In the context of phenotypic plasticity of VSMCs, it is unclear how mechanical cues interact with the responsible signaling pathways, and what the potential impact of these interactions is on the establishment and preservation of vascular homeostasis, that is, when VSMCs express the contractile phenotype.
The Notch signaling pathway is also known as a key regulator of multiple aspects of cardiovascular morphogenesis (12–16). Notch signaling is initiated by the interaction between the Notch receptors (Notch1 to Notch4) and ligands, Delta (Dll) or Jagged, presented on the cell membrane of juxtaposed cells (17). Notch plays a critical role in homeostasis and remodeling of the vascular wall (12–16), where VSMCs mainly express receptors Notch1, Notch2, and Notch3, and the ligand Jagged1, whereas ECs express the ligands Jagged1, Dll4, and to some extent in remodeling vasculature Dll1 (18, 19). Endothelial Jagged typically activates Notch in neighboring VSMCs, which subsequently induces propagation of Jagged–Notch signaling throughout the VSMC lamellae through the process of lateral induction (14, 20). The propagation of Notch signaling is crucial for regulating VSMC phenotype throughout the vascular wall, and hence is a critical phenomenon for inducing differentiation of the complete VSMC layer toward the homeostatic contractile phenotype (14).
Collectively, previous observations suggest that mechanical factors and Notch signaling strongly affect vascular morphogenesis and homeostasis. In fact, as Notch activation is force-dependent and links to the cytoskeleton, a key mechanosensor of the cell (21–29), it can be anticipated that Notch signaling and mechanics are interdependent. We hypothesize that mechanosensitivity of the Notch signaling pathway might be a key biological mechanism responsible for mechanical homeostasis. The studies published to date indeed point to an interrelation between Notch signaling and mechanics (29–32), but are inconclusive as to the potential implications of this interdependency on vascular morphogenesis and homeostasis. Due to the complex, dynamic interactions between mechanics, Notch signaling, and the vascular architecture, computational modeling is required to predict and understand the impact of mechanosensitivity of Notch signaling on the differentiation state of VSMCs and vascular homeostasis.
Here, we have integrated experimental studies with computational modeling to obtain an understanding of how mechanics (e.g., stress and strain as experienced by VSMCs during hemodynamic loading) and Jagged–Notch signaling integrate in the establishment of vascular homeostasis. Our experimental data confirm that the expression of Notch3, Jagged1, and Notch target genes in VSMCs decreases with the degree of mechanical strain imposed onto the cells. Translation of these findings into a computational model of Jagged–Notch signaling in the vascular wall reveals that the onset of VSMC differentiation depends on the thickness of the VSMC layer. Strikingly, a switch-type behavior with a clear transition thickness between predominantly synthetic and contractile VSMCs was predicted, which likely represents a homeostatic mechanical state. This homeostatic thickness arising from the mechanosensitivity of Jagged–Notch signaling was predicted to be different for different locations in the vascular tree, and in close agreement with the actual differences in human arterial wall thickness observed in vivo. These findings therefore support our hypothesis that mechanosensitivity of Notch signaling plays an important role in the establishment of vascular homeostasis.
Results
Expression Levels of Jagged1 and Notch3 by VSMCs Decrease with Mechanical Strain.
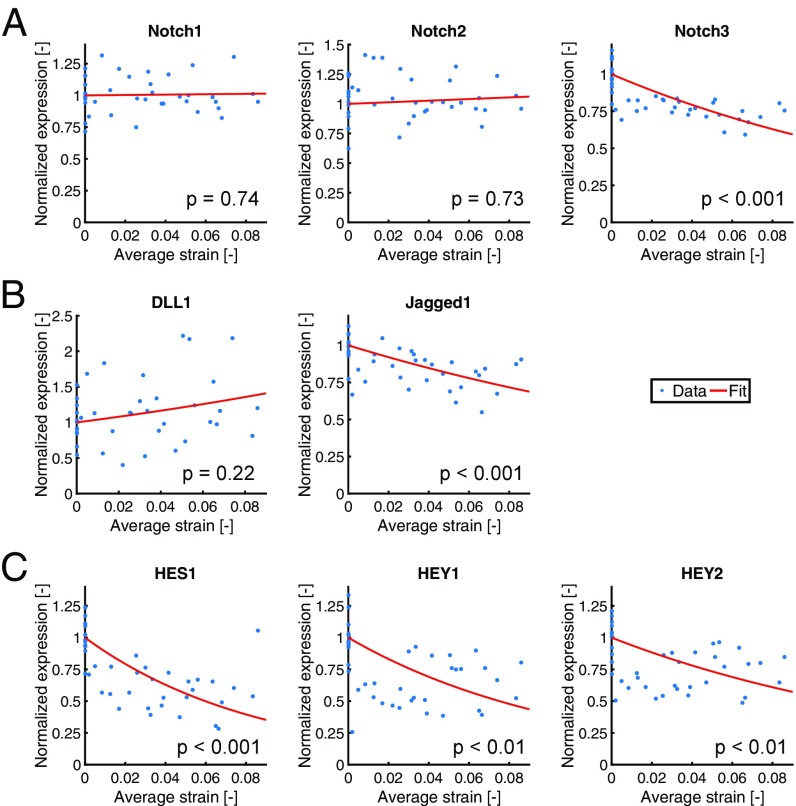
To investigate the response of Notch signaling to mechanical stimuli, we performed mechanical stretch experiments. VSMCs were stretched radially for 24 h, and analyzed for Notch receptor and ligand mRNA expression, as well as for the downstream target genes HES, HEY1, and HEY2. We imposed strains between 1% and 9% onto the VSMCS, and quantified the strain per sample by Global Digital Image Correlation (GDIC) (Fig. 1). Of the Notch receptors, only Notch3 showed a strain-induced decrease (Fig. 2A and Table 1). The only ligand with a significant strain-induced expression reduction was Jagged1 (Fig. 2B and Table 1). Interestingly, the Notch target genes HES1, HEY1, and HEY2 all displayed stronger strain-responsive down-regulation than the Notch receptors and ligands, implying a nonlinear relation between the mechanosensitivity of Notch component expression and their downstream target genes (Fig. 2C and Table 1).
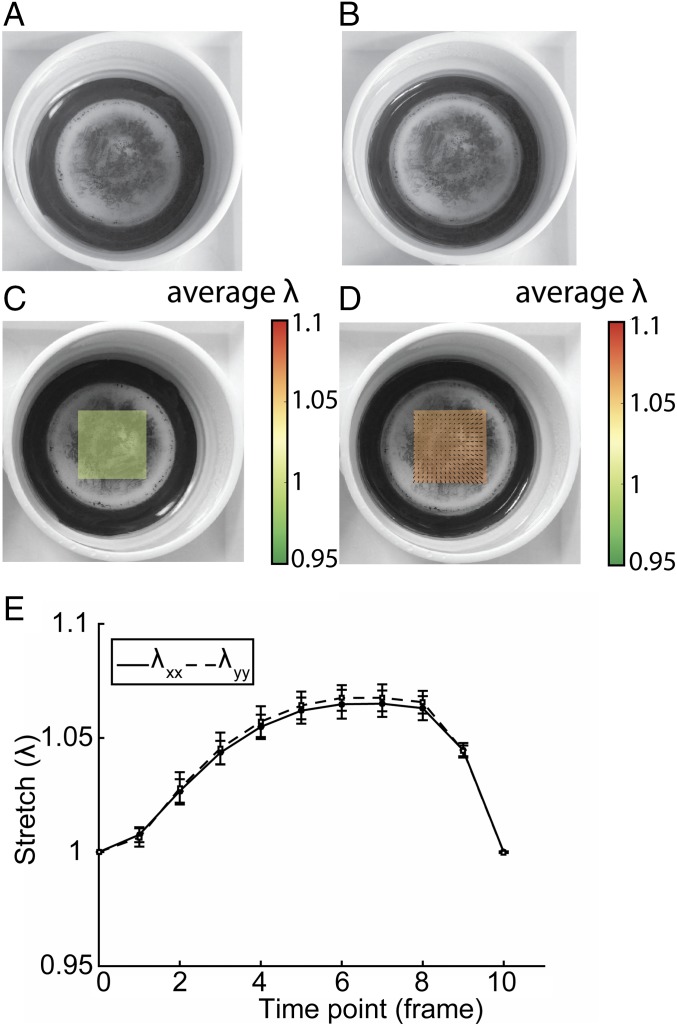
Fig. 1.
Stretch applied to each sample was quantified using video recording. Bottom surfaces of the flexible membranes were marked with graphite for tracking, and frames at (A) minimal and (B) maximal displacement were extracted. Analysis by GDIC resulted in the displacement field and corresponding stretch () at (C) minimal and (D) maximal displacement. (E) Per cycle, 10 frames were analyzed to determine the maximal stretch.
Fig. 2.
Gene expression levels of (A) Notch receptors, (B) ligands, and (C) target genes as a function of the strain imposed on the VSMCs and normalized with respect to gene expression levels in the absence of strain. Red lines indicate the fits through the data, and values correspond to the significance level of the Spearman correlation coefficient.
Table 1.
Effect of strain on expression levels of Notch receptors, ligands, and target genes
| Parameter | Notch1 | Notch2 | Notch3 | DLL1 | Jagged1 | HES1 | HEY1 | HEY2 |
| Spearman correlation coefficient | −0.05 | −0.06 | 0.75 | 0.20 | 0.61 | 0.65 | 0.47 | 0.40 |
| value | 0.74 | 0.73 | 0.001 | 0.22 | 0.001 | 0.001 | 0.01 | 0.01 |
| A [−] | 0.15 | 0.66 | −5.79 | 3.81 | −4.17 | −11.59 | −9.22 | −6.19 |
Significant correlations (P <0.05) are indicated in italic. Parameter A, defining the strength of mechanosensitivity, followed from fitting the experimental data with the exponential function y = exp(Ax) (parameters included in model indicated in bold).
To quantify the mechanosensitivity of the mRNA levels of VSMCs, exponential curves of the form were fitted through the data (Fig. 2 and Table 1), and served as input for the computational model. Here, is the normalized expression level compared with the absence of strain, is the average Green–Lagrange strain imposed on the VSMCs, and represents the strength of mechanosensitivity (gene-specific).
A Computational Model to Predict Notch Signaling in the Vascular Wall.
To understand and predict the potential implications of mechanosensitivity of the Notch signaling pathway in vascular adaptation and homeostasis, we developed a computational framework by building on the earlier theoretical works devised by Sprinzak et al. (33) and Boareto et al. (34) that predict the dynamics of the Notch signaling pathway in juxtaposed cells. As these frameworks have been described and analyzed extensively before, here we only describe the fundamental principles of the framework. The mathematical treatment is provided in Materials and Methods.
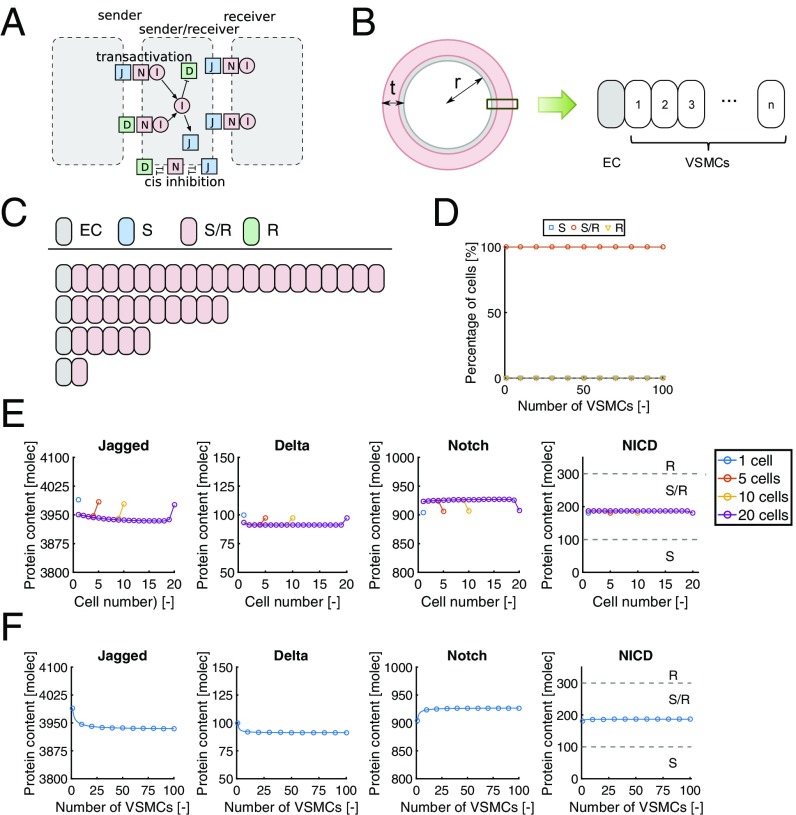
Briefly, the model of Boareto et al. (34) includes the cis and trans interactions of both the ligands Delta and Jagged with the receptor Notch (Fig. 3A), where cis interactions are defined as interactions between ligands and receptors within the same cell and trans interactions constitute the interactions between ligands and receptors located on different cells (33, 35–37). Cis interactions are assumed to lead to degradation of both the interacting ligands and receptors. Although cis inhibition does not need to be symmetric (35), inactivation of the Notch receptor is well known, and inhibition of Notch alone leads to similar predictions in terms of cell state as mutual inhibition (Fig. S1). Trans interactions induce a cleavage of the Notch receptor and the release of the Notch IntraCellular Domain (NICD) in the receiving cell. Since NICD is translocated to the nucleus to activate Notch target genes (33, 35–37), the NICD content is used in the model to define the state of the cell as either a Sender (S, low NICD levels), a Receiver (R, high NICD levels), or a hybrid Sender/Receiver state (S/R, NICD levels in between S and R) (34). Delta–Notch and Jagged–Notch interactions affect the cell state in different manners, due to the fact that NICD suppresses Delta and activates Jagged and Notch expressions. Consequently, Delta–Notch signaling typically induces the adoption of distinct states of adjacent cells in the vascular system (38), whereas Jagged–Notch signaling leads to the adoption of similar cell states (14, 39). The effect of intracellular Fringe on the binding affinity of Notch with either Jagged or Delta was not considered in the present study, as the role and regulation of Fringes in VSMCs are unclear. Moreover, the inclusion of Fringe as proposed by Boareto et al. (34) would not lead to notable differences in results with the current parameter settings, as Delta expression is extremely low compared with Jagged expression, and Fringe affects cis and trans interactions in a similar way (Fig. S2).
Fig. 3.
(A) Schematic representation of the protein interactions included in the theoretical framework. (B) Geometry specifications in the 1D modeling approach. Predicted (C) individual and (D) percentages of cell states for different wall thicknesses. Predicted (E) individual and (F) average protein contents for different wall thicknesses. molec, number of molecules.
As our experimental data only concerned VSMCs, we restricted our numerical predictions to Notch signaling in muscular arteries where VSMCs are the dominant component. We considered a 1D cross-section of the vascular wall, consisting of one EC on the luminal side, and multiple layers of VSMCs toward the outer end of the vessel (Fig. 3B). For the VSMCs, we adopted the same parameter values as in Boareto et al. (34), except for the expression of Delta, which was set to a low value in correspondence with experimental observations (18). The EC was included, as its Jagged content is hypothesized to provide the kickoff for the lateral induction of Jagged–Notch signaling (14, 20). The EC Jagged content was assumed to be constant with time and equal to the average Jagged content in VSMCs as predicted by the computational model. In line with the hypothesized mechanism for lateral induction (14, 20), the Jagged distribution in VSMCs was hypothesized to be polarized toward the neighboring VSMC. In this way, the model intrinsically incorporates the two modes of Jagged–Notch signaling where NICD levels of VSMCs close to the EC depend on the EC Jagged content (first mode), and VSMC NICD levels farther away from the EC primarily depend on the VSMC Jagged contents (second mode). Differences in Jagged content between the EC and VSMCs may thus lead to different degrees of signaling within the arterial wall (Fig. S3). In terms of defining the cell state of VSMCs, we adopted the same thresholds as in Boareto et al. (34), where NICD levels of <100 molecules represent the S state, levels of >300 molecules represent the R state, and levels in between those thresholds are assumed to represent the S/R state. Related to the physiological context, the S state of VSMCs was assumed to correspond to the synthetic phenotype, and the S/R state represents the quiescent, contractile phenotype corresponding with the homeostatic state (40). To confirm that our VSMCs do show Notch activity-dependent contractility markers, we exposed VSMCs to Jagged1, resulting in Notch target gene production, Notch3 and Jagged1 induction, and SMA production (Fig. S4).
We first performed simulations without the incorporation of mechanosensitivity, to obtain a general understanding of the process of lateral induction of Jagged–Notch signaling in the vascular wall without mechanosensitivity. Simulations with different wall thicknesses [1 to 100 VSMC layers corresponding with a media thickness of 0.01 mm to 1 mm (41)] revealed that the S/R state is predicted by the model for all VSMCs regardless of the adopted wall thickness (Fig. 3 C and D). This suggests that, with the current model assumptions, the number of cells in the signaling cascade does not affect the equilibrium state of individual cells, so, in other words, there is no spatial limit for the lateral induction process. Consequently, there appears to be no preference for a vessel to adopt any specific wall thickness, as all situations would lead to homeostasis, that is, all cells have the contractile phenotype. Our result therefore indicates that there would be no stimulus for continued development in response to changes in hemodynamics or during morphogenesis, as the homeostatic contractile state is already present from the start.
The signaling cascade and subsequent equilibrium states of the VSMCs in the simulations depend on the Jagged, Delta, Notch, and NICD contents in each cell. At equilibrium, the protein levels of individual cells were fairly homogeneous throughout the vascular wall, with only minor spatial variations in protein contents near both ends of the vessel (Fig. 3E). Jagged was predicted to be the most abundant protein in VSMCs, with Notch contents being fourfold lower than Jagged. Delta was hardly present, and the NICD content was well within the S/R range. Additionally, the average protein contents in the wall hardly varied with wall thickness (Fig. 3F). Minor variations were only predicted for the lower range of thicknesses, which can be explained by boundary effects that diminish with increasing wall thickness. Altogether, these predictions with a 1D framework suggest that the VSMC state and presence of homeostasis do not directly depend on wall thickness, as there appears to be no spatial limit for the feed-forward of Jagged–Notch signaling via lateral induction.
Mechanosensitivity of Jagged–Notch Signaling Is Predicted to Induce a Switch-Type Behavior in Vascular Homeostasis.
From the principle of force equilibrium, it can be derived that the average circumferential stress in an artery satisfies Laplace’s law, where the stress is expressed as a function of the pressure applied to the luminal side of the vascular wall, and the radius and wall thickness of the artery (41). As stress and strain are related via constitutive relations, it follows that strain-dependent gene expressions of the Notch signaling pathway may affect the states of VSMCs in the arterial wall, depending on its geometry and hemodynamic conditions. To investigate these potential implications of Notch mechanosensitivity on vascular homeostasis, we incorporated the experimentally observed relations between gene expressions and strain into our computational framework, if a significant correlation between gene expression and strain was found (Notch3 and Jagged1). For this, a simplified approach was adopted by assuming a linear relation between stress and strain to translate the experimental strains into the estimated stresses in the computational model (see Materials and Methods for details).
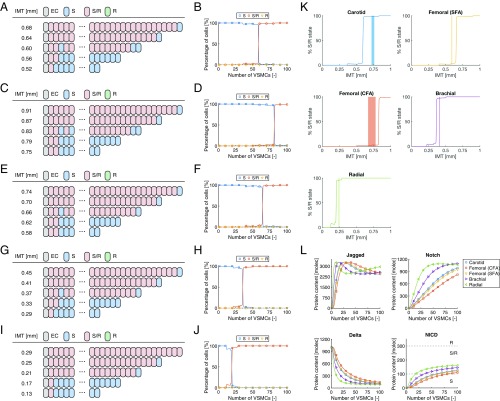
We used quantitative information on arterial geometry [internal radius and intima-media thickness (IMT)] and in vivo strains as reported for the carotid artery to estimate this relationship between in vivo stresses and strains, where we discriminated between relatively young and older subjects, as different ranges of IMT were found depending on the age of the subjects (Table S1). Next, simulations were performed for different types of arteries featuring different luminal sizes and wall thicknesses (Table S1) to understand how mechanical factors may affect vascular homeostasis depending on the artery of interest, based on the identified stress–strain relationships for relatively young and older subjects. For each artery, we assumed that the systolic pressure equaled 16 kPa (common systolic brachial artery pressure) and set the lumen radius to the average value reported in the literature (Table S1). Wall thickness was varied between 1 and 100 VSMCs for each case to vary the mechanical state in the model and predict its effect on vascular homeostasis, meaning that the IMT in the model varied between 0.02 mm and 1.01 mm (assuming that the EC and VSMCs have a thickness of 0.01 mm).
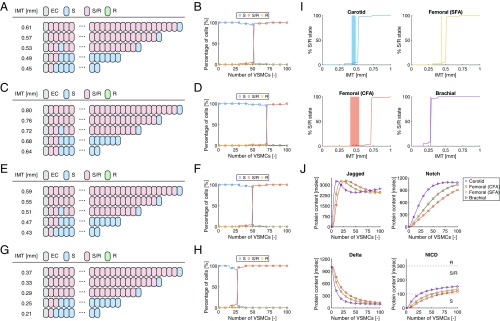
When the stress–strain relationship and radii reported for the carotid artery, common femoral artery (CFA), superficial femoral artery (SFA), and brachial artery of relatively young subjects were used, the model predicted that all VSMCs adopt the S state in case of extremely low wall thicknesses, whereas the S/R state was predicted at high wall thicknesses (Fig. 4 A–H). The R state was not predicted in any of the investigated situations. More specifically, at relatively low wall thicknesses for each artery, either none or only the first one or two VSMCs on the luminal side of the arterial wall were predicted to adopt the S/R state as a result of EC Jagged signaling, indicating that lateral induction is inhibited in these situations due to the reduced Notch and Jagged expression by VSMCs in response to high mechanical stress. Strikingly, this inhibition of lateral induction was suddenly resolved upon reaching a certain transition thickness, leading to the adoption of the S/R state in (almost) all of the VSMCs beyond this thickness. The model therefore suggests that sensitivity of the Notch signaling pathway appears to induce a switch-type behavior regarding the presence of vascular homeostasis, depending on the wall thickness and corresponding mechanical state of the artery. Importantly, this predicted transition thickness varied across the investigated arteries, in line with their differences in luminal radius, and was in close agreement with the IMT values of human subjects reported in the literature (Fig. 4I), where the best and worst correspondences were found for the brachial artery (predicted transition thickness of 0.29 mm vs. a measured IMT of 0.28 mm) and the CFA (predicted transition thickness of 0.72 mm vs. measured IMT values of 0.41 to 0.54 mm), respectively (Fig. 4I and Table S1).
Fig. 4.
Predictions of Notch signaling in the vascular wall using the stress–strain relationship derived for relatively young individuals. Individual and percentages of cell states for different wall thicknesses of the (A and B) carotid artery, (C and D) CFA, (E and F) SFA, and (G and H) brachial artery. (I) Percentage of S/R state VSMCs in the model (solid lines) in comparison with the reported range of IMT values for different arteries (shaded areas; see Table S1). (J) Average protein contents as a function of wall thickness as predicted for the different arteries. A, C, E, and G represent the results of individual simulations, where alternating cell states may randomly occur around the transition thickness as slightly varying NICD levels are close to the S-S/R threshold. B, D, F, H, I, and J are based on the results averaged over 25 simulations. molec, number of molecules.
Regarding the average protein levels of the VSMCs as a function of wall thickness, Notch and Jagged were almost absent at low wall thicknesses, due to the reduced protein expressions (Fig. 4J). The absence of Notch inherently resulted in an absence of NICD and the establishment of a certain Delta level. An increase in wall thickness was associated with a steep increase in both Notch and Jagged contents that varied per artery depending on its mechanical conditions. Within the investigated range of wall thicknesses, Notch levels appeared to rise monotonically with wall thickness, where a stabilization in Notch content occurred at high thicknesses in the situation of the brachial artery. Jagged levels all decreased after the steep initial increase, followed by either a stabilization in the case of the carotid artery, CFA, and SFA or a subsequent increase in Jagged content in the case of the brachial artery. The changes in Notch and Jagged with increasing wall thickness resulted in a decrease in Delta contents due to Delta–Notch signaling, and an increase in NICD levels primarily due to Jagged–Notch signaling. The threshold NICD content that discriminates between S and S/R states was reached at different wall thicknesses for each artery, which explains the differences in predicted transition thickness across the different investigated arteries.
Using the stress–strain relationships and average lumen radii of the older subjects resulted in a similar switch-type behavior in terms of vascular homeostasis (Fig. 5 A–J). The transition thicknesses in these situations are generally higher compared with the cases where the data for relatively young subjects were incorporated, and again in good agreement with the reported IMT values in the literature (Fig. 5K). Here, the best and worst correspondences were found for the brachial artery (predicted transition thickness of 0.37 mm vs. a measured IMT of 0.41 mm) and the carotid artery (predicted transition thickness of 0.60 mm vs. measured IMT values of 0.72 to 0.76 mm), respectively (Fig. 5K and Table S1). As only the quantitative relationship between stress and strain was different here, the protein levels followed similar patterns as in Fig. 4, with Notch and particularly Jagged levels rising quickly upon an increase in wall thickness due to the decrease in mechanical stress and corresponding increase in Jagged and Notch production rates (Fig. 5L). In addition, within the investigated range of wall thicknesses, Notch levels in the radial artery appeared to decrease slightly after the initial increase upon increasing wall thickness, and the Jagged content in the same artery exhibited a steady increase at high wall thicknesses.
Fig. 5.
Predictions of Notch signaling in the vascular wall using the stress–strain relationship derived for older individuals. Individual and percentages of cell states for different wall thicknesses of the (A and B) carotid artery, (C and D) CFA, (E and F) SFA, (G and H) brachial, and (I and J) radial artery. (K) Percentage of S/R state VSMCs in the model (solid lines) in comparison with the reported range of IMT values for different arteries (shaded areas; see Table S1). (L) Average protein contents as a function of wall thickness as predicted for the different arteries. A, C, E, G, and I represent the results of individual simulations, where alternating cell states may randomly occur around the transition thickness as slightly varying NICD levels are close to the S-S/R threshold. B, D, F, H, J, K, and L are based on the results averaged over 25 simulations. molec, number of molecules.
Collectively, these predictions reveal that mechanosensitivity of Jagged–Notch signaling leads to a switch-type behavior in vascular homeostasis, where the transition thickness varies between different arteries due to differences in lumen radius. Interestingly, these transition thicknesses correspond fairly well with the reported IMT values of the different arteries, suggesting that Jagged–Notch mechanosensitivity may be one of the important biological mechanisms responsible for establishing physiological wall thicknesses and vascular homeostasis.
Magnitude of Transition Thickness Mainly Depends on Mechanosensitivity of Notch.
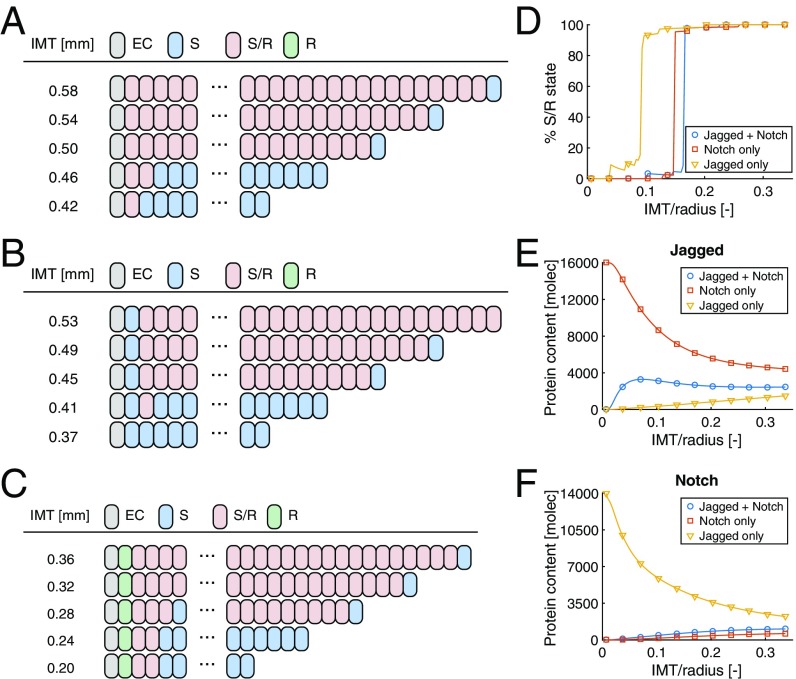
To evaluate the potential necessity of having both stress-/strain-dependent production rates of Jagged and Notch, we performed simulations with the included mechanosensitivity of either Jagged or Notch, in comparison with having mechanosensitivity of both protein production rates. As the qualitative impact is independent of the choice of the stress–strain relationship (young vs. old) and the actual lumen radius, we used the stress–strain coupling assumed for young individuals and adopted an arbitrary radius of 3 mm for these simulations while presenting the variations in wall thickness in a normalized form as IMT/radius (Fig. 6).
Fig. 6.
Predictions with mechanosensitivity of (A) both Jagged and Notch, (B) only Notch, and (C) only Jagged. (D) Percentage of VSMCs with the S/R state as a function of relative wall thickness. Average (E) Jagged and (F) Notch contents as a function of relative wall thickness. molec, number of molecules.
As in Mechanosensitivity of Jagged–Notch Signaling, including the mechanosensitivity of both Jagged and Notch results in an S state for all VSMCs at low wall thicknesses, except for the first one or two VSMCs adjacent to the EC, with a sudden transition toward a predominantly S/R state beyond the transition thickness (Fig. 6A). Elimination of the mechanosensitivity of Jagged preserves this switch-type behavior in terms of cell fate, although a minor (10%) decrease in transition thickness was predicted (Fig. 6 B and D) due to the relatively high Jagged levels that lead to more cis and trans interactions with Notch, and ultimately lower Notch contents (Fig. 6 E and F). The combination of lower Notch and higher Jagged contents results in preservation of the S/R state in most of the VSMCs, except for the cell adjacent to the EC due to the exposure to the original (i.e., lower) EC Jagged content.
Elimination of Notch mechanosensitivity was predicted to preserve the switch-type behavior as well, although its elimination has a more notable effect (44% decrease) on the predicted transition thickness (Fig. 6 C and D). In contrast to the elimination of Jagged mechanosensitivity, here the reduction in transition thickness is resulting from considerable increases in Notch levels upon eliminating Notch mechanosensitivity, which leads to increased signaling and a notable decrease in Jagged contents (Fig. 6 E and F). Also in this case, the S/R state is preserved for almost all VSMCs except for the one adjacent to the EC. Since the EC Jagged content is higher than the Jagged content of the VSMCs, here the increased Notch content leads to the adoption of the R state (Fig. 6C).
Taken together, these simulations suggest that the switch-type behavior of Jagged–Notch signaling as a result of mechanosensitivity not only follows from the combined decreases in Jagged and Notch production rate with strain but also from the individual reductions in production rate of either Jagged or Notch. Importantly, the magnitude of the predicted transition stretch, which corresponds fairly well to the reported IMT values in the literature, appears to primarily depend on mechanosensitivity of the Notch production rate.
Discussion
Mechanistic understanding of vascular remodeling and homeostasis is required to understand healthy vascular morphogenesis and pathologies, and provide design guidelines in vascular tissue engineering. One of the major challenges is the integration of complex cellular processes and changes in mechanical conditions into predictive and robust models of physiology and pathophysiology. Here, we have developed a computational model of muscular arteries that incorporates mechanics and cell–cell signaling related to homeostasis. Our experimental data demonstrate that expression of Notch signaling components is controlled by mechanical stimuli, and incorporating these findings into the computational model reveals that mechanics and Notch signaling integrate in the control of vascular morphogenesis and homeostasis.
We quantified the expression of Notch ligands, receptors, and target genes in VSMCs over a range of strains. The quantification of strains in individual samples accommodated variability within the setup, and enabled the fitting of a strain response curve to the imposed strain range. We used exponential curves to fit the gene expressions that resulted in best fits for the majority of genes that were significantly changed. The experimentally determined mechanosensitivity of Notch3 and Jagged1 was translated into the mechanosensitivity of the protein production rates in the computational model. Interestingly, Dll1 demonstrated a nonsignificant increase in expression levels with strain. An increase in Dll1 expression is to be expected with the observed decrease in expression of Notch target genes. The absence of significance is likely due to the low absolute Dll1 expression levels in VSMCs (18). Of note, we did not take into account regulatory steps that can occur during mRNA-to-protein conversion. These steps can be relevant in Notch signaling, as not in all cases do protein levels follow mRNA expression. Especially when regulation of this conversion is also mechanosensitive, this will need to be taken into account in future improvements of the model.
Computational modeling was used to evaluate the potential impact of the experimentally observed reduction in gene expression levels of Jagged1 and Notch3 on vascular homeostasis. Our computational framework was an adapted version of the earlier models developed by Sprinzak et al. (33) and Boareto et al. (34), and allowed for predicting the cis and trans interactions of Jagged and Delta with Notch and their subsequent effects on the individual production rates. As a first step, a relatively simple 1D approach was adopted where an EC was connected to multiple layers of VSMCs that communicated with each other. The experimentally derived relations between Jagged1 and Notch3 gene expressions of VSMCs and strain informed the production rates in the model via assumed relations between stress and strain.
As the aim of the current study was to explore the potential impact of the integration of mechanics and Notch signaling in the establishment of vascular homeostasis, we deliberately used a relatively simple computational approach to study the general consequences of the experimental observations for vascular structures. One of the limitations of the current framework is the relatively simple treatment of vascular mechanics. The average stress could be calculated from Laplace’s law, the vascular geometry, and pressure conditions, but the translation of this stress to the strain measured in the experiments was less straightforward. The linear stress–strain relation that was currently assumed based on the in vivo estimation of stresses and strains in carotid arteries is not representing the well-known nonlinear material response of cardiovascular tissues. Additionally, potential spatial heterogeneities in mechanical state (e.g., larger strains near the lumen than on the outer side) were not taken into account. In future studies, the current framework should therefore be coupled to 2D/3D macroscopic mechanical models to more accurately capture the local (variations in) stresses and strains in vascular tissue, e.g., using multiscale frameworks (42–44). Other limitations include the fact that we defined cell states in the model using the original NICD thresholds proposed in Boareto et al. (34), which may not necessarily be representative for VSMCs, and our assumption that the EC Jagged content is insensitive to mechanical cues. Particularly, the latter assumption may need adjustments, as fluid shear stress acting on ECs is known to be of vital importance for vascular remodeling (45). Future studies should elucidate whether and how these assumptions need to be adapted.
Both Notch3 and Jagged1 as well as the downstream target genes HES1, HEY1, and HEY2 demonstrated a down-regulation upon applied strain (Fig. 2). Interestingly, the target genes showed a stronger reduction with strain, implying that the different genes measured may be dependent on different upstream interactions with other activating signaling pathways that have a different mechanosensitivity. On the other hand, there may be further posttranslational steps in Notch activation that are mechanosensitive and can further enhance the activating effect upon the Notch target genes. Jagged1 mediated activation is specifically interesting in this, as it shows catch bond behavior (23). Moreover, we found strain-dependent inhibition of Notch3 and Jagged1 expression, but not for Notch1 or Notch2. This differential sensitivity of Notch receptors to cell stretch can cause different cell fates under different hemodynamic conditions. Notch2 and Notch3 have opposing effects on cell proliferation and survival, and similar mechanisms may be in place for regulation of the contractile fate (46). Strain sensitivity of Notch1 expression in VSMCs has been reported before (31), but this may reflect distinct responses of VSMCs of different origin, and does also result in a general down-regulation of Notch activity upon strain. As VSMCs have a heterogeneous developmental origin (47), and expression of specific Notch proteins is highly dependent on the developmental origin of a tissue, other mechanosensitive behavior may also occur. Specific physiological versus pathological strain (48) and Notch signaling dose may result in more complex outcomes in cell phenotype, e.g., through HEY1/2 mediated feedback loops inhibiting contractility, that may become activated at higher levels of Notch activation (49). Additionally, cross-talk with other signaling pathways occurs, such as with platelet-derived growth factor (PDGF) signaling, a known inducer of VSMC proliferation and migration. Notch activation induces expression of PDGF receptor (PDGFR-) in VSMCs, whereas subsequent PDGF induction leads to down-regulation of both Notch3 and PDGFR- (50, 51). This could, in future refinements, be included in the model.
Without including the observed decrease in expression levels of Jagged1 and Notch3 in the model, our predictions suggest that there is no spatial limit for lateral induction of Jagged–Notch signaling in the vascular wall. Consequently, vascular homeostasis would be independent of wall thickness and mechanical conditions, which implies that there would be no preference for adopting any specific wall thickness. This result does not match with in vivo observations where mutations or elimination of Jagged1 or Notch3 have been confirmed to induce considerable changes in vascular geometry and differentiation status (52, 53). Including the mechanosensitivity of Jagged and Notch in the model based on our in vitro data resulted in a switch-type behavior with a steep transition of primarily synthetic (S) toward contractile (S/R) VSMCs at a certain wall thickness. Importantly, the magnitude of this transition thickness varied per artery and agreed remarkably well with IMT values of different arteries as quantified in vivo. These predictions therefore suggest that Jagged–Notch signaling may be a key mechanism in the establishment of vascular morphogenesis and homeostasis. Our predictions further indicated that this switch-type nature of Jagged–Notch signaling arises from the individual reductions of both Jagged and Notch production with strain, although the magnitude of the transition thickness is primarily determined via Notch mechanosensitivity. Obviously, future studies should investigate whether manipulations of other components of the Notch signaling pathway could induce a similar behavior. For example, changes in the strength of cis interactions could affect the signaling state and thereby the presence of homeostasis as well (Fig. S5). Still, the results of the present study indicate that mechanosensitivity of Jagged and Notch production rates by themselves are sufficient to induce this switch-type behavior.
The data, therefore, suggest that the mechanosensitivity of Notch regulates a phenotypic switch in VSMCs, where the Notch dose determines the VSMC phenotype. This is in line with the dose sensitivity of the pathway and explains how Notch signaling facilitates cell fate decisions and drives context-dependent tissue patterning (33) and homeostasis. The data also indicate that some Notch components might be more sensitive and exhibit a stronger power over phenotypic decisions in the vessel wall, and that in-depth knowledge of the function of individual Notch components and the Notch profiles in different developmental and disease settings is needed. Importantly, the data highlight that in-depth knowledge of the interplay between mechanics and Notch status is important for rational targeting of Notch in vascular morphogenesis, pathologies, and regeneration, and emphasize the need for mechanical tuning in tissue engineering to remain within certain strain/stress thresholds to obtain proper maturation and establish functional tissue homeostasis. The model and future developments thereof can also provide new insights into previously unexplained mutant behaviors linked to vascular disease, e.g., Alagille (Jagged1) and Cadasil (Notch3).
Taken together, we presented a first attempt to model the complex interactions between cell signaling and mechanics in vascular morphogenesis and homeostasis. We integrated experimental data and modeling and included quantitative analyses of the mechanosensitivity of the Notch signaling pathway. The model certainly has a number of simplifications and limitations as outlined above, but nevertheless constitutes a promising first approach to reveal the impact of the integration of mechanics and Notch signaling informed by experimental data, and suggests the presence of a switch-type behavior of Jagged–Notch signaling in establishing arterial homeostasis.
Materials and Methods
Cell Culture.
Coronary artery smooth muscle cells were cultured in 231 medium supplemented with smooth muscle growth serum (Gibco). Culture took place in humidified, 5% CO2 air at 37 ∘C. Cells were passaged when 80 to 90% confluent, and used in experiments at passage 5 to 7.
Stretch Experiment.
Uncoated Bioflex six-well plates (Flexcell) were coated with 2.2 g/cm2 of bovine fibronectin (Alpha Aesar) on 2.5 cm2 in the center of the well. The rest of the well surface was treated with 1% pluronic F127 (Sigma) in PBS for 1 h at room temperature to prevent aspecific adhesion. Cells were seeded at a density of 20.000 cells per cm2 and were left to attach overnight. Medium was refreshed the next morning. The plates were mounted on circular 25-mm posts and stretched with the Flexcell system at 1 Hz for 24 h.
Stretch Quantification.
The displacement of each well was tracked by marking the membranes with graphite and recording displacement with a camera. Displacement of each stretched well was analyzed by using GDIC software (54–56). The deformation gradient tensor was determined via fitting a polynomial function to the images (10 frames per second). Subsequently, the Green–Lagrange strain was calculated from with as the deformation gradient tensor and as the identity tensor. Eigenvalues of the strain per well were calculated and averaged to obtain a representative measure of the applied strain per well during the experiment.
cDNA Synthesis.
RNA was isolated by Trizol (Invitrogen) as per manufacturers’ protocol and stored at −80 ∘C until further processing. Concentrations and purity of RNA were measured by nanodrop, with concentrations ranging from 60 ng/L to 270 ng/L; 200 ng of RNA was converted into cDNA in a reaction containing 8 ng/L of RNA, 50 mM Tris (pH 8.3), 75 mM KCl, 3 mM MgCl2, 0.5 mM dNTPs (Invitrogen), 2 ng/L of random hexamers (Promega), 10 mM dithiothreitol, and 100 U Moloney murine leukemia virus reverse transcriptase (Invitrogen). cDNA was synthesized on a C1000 thermal cycler (Bio-Rad).
qPCR Analysis.
The produced cDNA was used as a template in a real-time quantitative polymerase chain reaction (qPCR). cDNA samples were cycled in 10-L reactions by a C1000 thermal cycler (Bio-Rad) measured by a CFX 384 real-time system. Reactions contained 2.5 ng of RNA converted into cDNA as template and 0.2 M of forward and reverse primers in iQ SYBR Green Supermix (#170-8886; Bio-Rad). Primers were designed to target separate exons of the transcripts of interest and to generate 50- to 150-bp-long amplicons. Amplification efficiencies and dissociation curves of all primers were verified using a 2.5-ng to 78-pg dilution series of RNA converted to cDNA, and the amplicon product size was verified on an agarose gel, with verification of a nontemplate control. Specifications of primers are given in Table S2. The qPCR program consisted of an incubation of 3 min at 95 ∘C, followed by 40 cycles of 20 s at 95 ∘C, 20 s at 60 ∘C, and 30 s at 72 ∘C. After these cycles, a dissociation curve was made by ramping from 65 ∘C to 95 ∘C to test for correct dissociation peaks. The qPCR curves were analyzed in the Bio-Rad CFX v2.0 software. As reference genes, we used noncommercial primers targeting GAPDH and AluJ-repeats, and commercial primers targeting ATP and B2M (Primer Design). Quantification cycles (Cqs) were determined by thresholding at 100 relative fluorescence units after baseline correction, within the exponential part of the curve. Baseline and threshold determination were performed per primer pair. The Cq values were normalized for the reference genes by relative quantification (57).
Computational Framework of Jagged–Delta–Notch Signaling.
To analyze and predict the dynamics of Notch signaling in the vascular wall, we adopted a 1D approach with one EC on the luminal side of the wall and multiple layers of VSMCs (with cell 1 adjacent to the EC) toward the outer end. The relevant protein levels (Notch, Jagged, Delta, and NICD) were predicted for every individual cell and allowed to interact with neighboring cells on both sides of each cell. Specifically, the changes of the Notch (), Delta (), Jagged (), and NICD () contents in cell with time were described by the following differential equations (34):
| [1] |
| [2] |
| [3] |
| [4] |
Here, , , and represent the production rates of Notch, Jagged, and Delta, respectively, which were assumed to be constant without mechanosensitivity. The strength of cis and trans interactions is governed by parameters and , respectively, and the degradation of the proteins is described by parameter in case of the transmembrane proteins Notch, Delta, and Jagged, and by in case of NICD. The activation (Jagged, Notch) or suppression (Delta) of the production rates upon signaling is described by shifted Hill functions for which the general form is given by (34)
| [5] |
| [6] |
| [7] |
where parameter defines the maximum fold change in production rate ( for activation and for suppression), and parameters and define the transition point and sensitivity of the change in production rate as a function of the NICD content, respectively.
The trans interactions occur with proteins located on the membranes of neighboring cells. Notch and Delta were assumed to be distributed equally over the cell membrane, where half of the amount is available for binding with each of its neighbors. Hence, the external Delta content for cell that is available for Delta–Notch signaling is given by
| [8] |
and the available external Notch content for Delta–Notch signaling equals
| [9] |
Jagged–Notch signaling was modeled in a different way compared with the earlier work of Boareto et al. (34), due to the assumption that Jagged clusters on the outer side of VSMCs in any mechanically stimulated (i.e., in vivo) situation (14, 20). As a result of this assumption, the external Jagged content that cell can interact with is provided only by the cell on the luminal side of the VSMC,
| [10] |
Another consequence of the polarized clustering is that the Jagged proteins can only interact with the Notch proteins of the cell on the outer side of cell . In analogy with the homogeneous distribution of Notch and the external Notch content for Delta–Notch signaling, we assumed that only half of the Notch content of the outer neighbor is available for interaction with the Jagged proteins of cell ,
| [11] |
The parameter values that regulate the dynamics of Jagged–Delta–Notch signaling in VSMCs were all adopted from Boareto et al. (34), except for the Delta production rate that was set to an arbitrarily low value as Delta expression has been reported to be low for VSMCs (18) (Table 2). For the EC, only the Jagged content was described, as this serves as kickoff for the lateral induction process (14, 20). For this, a constant value was assumed equal to the average predicted Jagged content in the VSMCs in absence of mechanical stimuli (Table 2). A similar sensitivity analysis as in Boareto et al. (34) was performed to assess the robustness of the model with its current assumptions and parameter settings (Fig. S6A). The changes in NICD levels in response to 10% variations in parameter values are in the same range as those of the original model (34).
Table 2.
Parameter values used in the computational framework
| Parameter | Value |
| 1,400 h−1 | |
| 100 h−1 | |
| 1,600 h−1 | |
| 5 10 h−1 | |
| 2.5 10 h−1 | |
| 0.1 h−1 | |
| 0.5 h−1 | |
| 2.0 | |
| 0.0 | |
| 2.0 | |
| 2.0 | |
| 2.0 | |
| 5.0 | |
| 200 |
With regard to the initial conditions, the protein levels for each cell were randomly chosen between 0 and 6,000 molecules for Jagged, Delta, and Notch, and between 0 and 600 molecules for NICD (34). The wall thickness was varied between 1 and 100 VSMCs, representing a range of media thicknesses of 0.01 mm to 1 mm (41). The differential equations were solved for 0 250 h (equilibrium was established in all cases) using an explicit time integration scheme with a time step of 0.01 h. Simulations were repeated 25 times for each thickness with different (random) initial conditions.
Including Mechanosensitivity in the Computational Framework.
The production rates of Jagged and Notch were adapted as follows to incorporate the experimentally observed decreases in gene expression:
| [12] |
| [13] |
Here, and represent the default production rates without including mechanosensitivity (Table 2), and are the fitted parameters defining the decrease in gene expression of Jagged1 and Notch3, respectively, with strain, and is the average circumferential stress in the vascular wall as calculated with Laplace’s law,
| [14] |
with as the pressure, as the internal (lumen) radius, and as the wall thickness (i.e., IMT in our simulations). Parameters and are the average physiological in vivo strain and stress (either for young or old individuals), where the strain was obtained from the literature (Table S1) and the stress was estimated from the pressure and measured IMT (Table S1). A sensitivity analysis with 10% variations in parameter values indicated that the predicted transition thickness is relatively insensitive to the parameters associated with mechanosensitivity of Notch signaling, implying that minor changes in any of the introduced parameters as identified from experiments would not induce dramatic changes in predicted homeostatic thickness (Fig. S6 B and C).
Data Availability.
All data, protocols, and numerical code have been stored at SURFdrive, a personal cloud storage service for the Dutch education and research community (https://surfdrive.surf.nl/files/index.php/s/Yel6AZFu78dvy25).
Supplementary Material
Acknowledgments
We acknowledge funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement 654513 (to S.L.), the European Union’s Seventh Framework Programme under Grant Agreement 604514 (ImaValve) (to S.L., O.M.J.A.S., C.V.C.B., and C.M.S.), and the Netherlands CardioVascular Research Initiative CVON2012-01 (to S.L., C.V.C.B., and C.M.S.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: All data, protocols, and numerical code have been stored at SURFdrive (available at https://surfdrive.surf.nl/files/index.php/s/Yel6AZFu78dvy25).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1715277115/-/DCSupplemental.
References
- 1.Boron WF, Boulpaep EL. 2012. Medical Physiology (Saunders, Philadelphia). updated Ed. [Google Scholar]
- 2.Mescher A. Junqueira’s Basic Histology: Text and Atlas. 12th Ed McGraw Hill Med; New York: 2009. [Google Scholar]
- 3.Turner SR, MacDonald JA. Novel contributions of the smoothelin-like 1 protein in vascular smooth muscle contraction and its potential involvement in myogenic tone. Microcirculation. 2014;21:249–258. doi: 10.1111/micc.12108. [DOI] [PubMed] [Google Scholar]
- 4.Ye GJ, Nesmith AP, Parker KK. The role of mechanotransduction on vascular smooth muscle myocytes’ [corrected] cytoskeleton and contractile function. Anat Rec (Hoboken) 2014;297:1758–1769. doi: 10.1002/ar.22983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Halayko AJ, Solway J. Molecular mechanisms of phenotypic plasticity in smooth muscle cells. J Appl Physiol. 2001;90:358–368. doi: 10.1152/jappl.2001.90.1.358. [DOI] [PubMed] [Google Scholar]
- 6.Rensen SS, Doevendans PA, van Eys GJ. Regulation and characteristics of vascular smooth muscle cell phenotypic diversity. Neth Heart J. 2007;15:100–108. doi: 10.1007/BF03085963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cyron CJ, Humphrey JD. Vascular homeostasis and the concept of mechanobiological stability. Int J Eng Sci. 2014;85:203–223. doi: 10.1016/j.ijengsci.2014.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cyron CJ, Humphrey JD. Growth and remodeling of load-bearing biological soft tissues. Meccanica. 2017;52:645–664. doi: 10.1007/s11012-016-0472-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochem Biophys. 2008;50:53–78. doi: 10.1007/s12013-007-9002-3. [DOI] [PubMed] [Google Scholar]
- 10.Humphrey JD, Dufresne ER, Schwartz MA. Mechanotransduction and extracellular matrix homeostasis. Nat Rev Mol Cell Biol. 2014;15:802–812. doi: 10.1038/nrm3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mammoto T, Mammoto A, Ingber DE. Mechanobiology and developmental control. Annu Rev Cell Dev Biol. 2013;29:27–61. doi: 10.1146/annurev-cellbio-101512-122340. [DOI] [PubMed] [Google Scholar]
- 12.Fouillade C, Monet-Lepretre M, Baron-Menguy C, Joutel A. Notch signalling in smooth muscle cells during development and disease. Cardiovasc Res. 2012;95:138–146. doi: 10.1093/cvr/cvs019. [DOI] [PubMed] [Google Scholar]
- 13.Gridley T. Notch signaling in the vasculature. Curr Top Dev Biol. 2010;92:277–309. doi: 10.1016/S0070-2153(10)92009-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Manderfield LJ, et al. Notch activation of Jagged1 contributes to the assembly of the arterial wall. Circulation. 2012;125:314–323. doi: 10.1161/CIRCULATIONAHA.111.047159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.de la Pompa JL, Epstein JA. Coordinating tissue interactions: Notch signaling in cardiac development and disease. Dev Cell. 2012;22:244–254. doi: 10.1016/j.devcel.2012.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rostama B, Peterson SM, Vary CP, Liaw L. Notch signal integration in the vasculature during remodeling. Vascul Pharmacol. 2014;63:97–104. doi: 10.1016/j.vph.2014.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hori K, Sen A, Artavanis-Tsakonas S. Notch signaling at a glance. J Cell Sci. 2013;126:2135–2140. doi: 10.1242/jcs.127308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Baeten JT, Lilly B. Notch signaling in vascular smooth muscle cells. Adv Pharmacol. 2017;78:351–382. doi: 10.1016/bs.apha.2016.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boucher J, Gridley T, Liaw L. Molecular pathways of notch signaling in vascular smooth muscle cells. Front Physiol. 2012;3:81. doi: 10.3389/fphys.2012.00081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hoglund VJ, Majesky MW. Patterning the artery wall by lateral induction of Notch signaling. Circulation. 2012;125:212–215. doi: 10.1161/CIRCULATIONAHA.111.075937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chowdhury F, et al. Defining single molecular forces required for Notch activation using Nano Yoyo. Nano Lett. 2016;16:3892–3897. doi: 10.1021/acs.nanolett.6b01403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee J, et al. 4-Dimensional light-sheet microscopy to elucidate shear stress modulation of cardiac trabeculation. J Clin Invest. 2016;126:1679–1690. doi: 10.1172/JCI83496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Luca VC, et al. Notch-Jagged complex structure implicates a catch bond in tuning ligand sensitivity. Science. 2017;355:1320–1324. doi: 10.1126/science.aaf9739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Meloty-Kapella L, Shergill B, Kuon J, Botvinick E, Weinmaster G. Notch ligand endocytosis generates mechanical pulling force dependent on dynamin, epsins, and actin. Dev Cell. 2012;22:1299–1312. doi: 10.1016/j.devcel.2012.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ramasamy SK, et al. Blood flow controls bone vascular function and osteogenesis. Nat Commun. 2016;7:13601. doi: 10.1038/ncomms13601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Samsa LA, et al. Cardiac contraction activates endocardial Notch signaling to modulate chamber maturation in zebrafish. Development. 2015;142:4080–4091. doi: 10.1242/dev.125724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shergill B, Meloty-Kapella L, Musse AA, Weinmaster G, Botvinick E. Optical tweezers studies on Notch: Single-molecule interaction strength is independent of ligand endocytosis. Dev Cell. 2012;22:1313–1320. doi: 10.1016/j.devcel.2012.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang X, Ha T. Defining single molecular forces required to activate integrin and Notch signaling. Science. 2013;340:991–994. doi: 10.1126/science.1231041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Watson O, et al. Blood flow suppresses vascular Notch signalling via dll4 and is required for angiogenesis in response to hypoxic signalling. Cardiovasc Res. 2013;100:252–261. doi: 10.1093/cvr/cvt170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Masumura T, Yamamoto K, Shimizu N, Obi S, Ando J. Shear stress increases expression of the arterial endothelial marker ephrinB2 in murine ES cells via the VEGF-Notch signaling pathways. Arterioscler Thromb Vasc Biol. 2009;29:2125–2131. doi: 10.1161/ATVBAHA.109.193185. [DOI] [PubMed] [Google Scholar]
- 31.Morrow D, et al. Cyclic strain inhibits Notch receptor signaling in vascular smooth muscle cells in vitro. Circ Res. 2005;96:567–575. doi: 10.1161/01.RES.0000159182.98874.43. [DOI] [PubMed] [Google Scholar]
- 32.Tu J, Li Y, Hu Z. Notch1 and 4 signaling responds to an increasing vascular wall shear stress in a rat model of arteriovenous malformations. Biomed Res Int. 2014;2014:368082. doi: 10.1155/2014/368082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sprinzak D, et al. Cis-interactions between Notch and Delta generate mutually exclusive signalling states. Nature. 2010;465:86–90. doi: 10.1038/nature08959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Boareto M, et al. Jagged-Delta asymmetry in Notch signaling can give rise to a Sender/Receiver hybrid phenotype. Proc Natl Acad Sci USA. 2015;112:E402–409. doi: 10.1073/pnas.1416287112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.del Álamo D, Rouault H, Schweisguth F. Mechanism and significance of cis-inhibition in Notch signalling. Curr Biol. 2011;21:R40–47. doi: 10.1016/j.cub.2010.10.034. [DOI] [PubMed] [Google Scholar]
- 36.LeBon L, Lee TV, Sprinzak D, Jafar-Nejad H, Elowitz MB. Fringe proteins modulate Notch-ligand cis and trans interactions to specify signaling states. Elife. 2014;3:e02950. doi: 10.7554/eLife.02950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Palmer WH, Jia D, Deng WM. Cis-interactions between Notch and its ligands block ligand-independent Notch activity. Elife. 2014;3:e04415. doi: 10.7554/eLife.04415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hellström M, et al. Dll4 signalling through Notch1 regulates formation of tip cells during angiogenesis. Nature. 2007;445:776–780. doi: 10.1038/nature05571. [DOI] [PubMed] [Google Scholar]
- 39.Benedito R, et al. The notch ligands Dll4 and Jagged1 have opposing effects on angiogenesis. Cell. 2009;137:1124–1135. doi: 10.1016/j.cell.2009.03.025. [DOI] [PubMed] [Google Scholar]
- 40.Doi H, et al. Jagged1-selective notch signaling induces smooth muscle differentiation via a RBP-Jkappa-dependent pathway. J Biol Chem. 2006;281:28555–28564. doi: 10.1074/jbc.M602749200. [DOI] [PubMed] [Google Scholar]
- 41.Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer; New York: 2002. [Google Scholar]
- 42.Rouillard AD, Holmes JW. Coupled agent-based and finite-element models for predicting scar structure following myocardial infarction. Prog Biophys Mol Biol. 2014;115:235–243. doi: 10.1016/j.pbiomolbio.2014.06.010. [DOI] [PubMed] [Google Scholar]
- 43.Thorne BC, Hayenga HN, Humphrey JD, Peirce SM. Toward a multi-scale computational model of arterial adaptation in hypertension: Verification of a multi-cell agent based model. Front Physiol. 2011;2:20. doi: 10.3389/fphys.2011.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zahedmanesh H, Lally C. A multiscale mechanobiological modelling framework using agent-based models and finite element analysis: Application to vascular tissue engineering. Biomech Model Mechanobiol. 2012;11:363–377. doi: 10.1007/s10237-011-0316-0. [DOI] [PubMed] [Google Scholar]
- 45.Baeyens N, et al. Vascular remodeling is governed by a VEGFR3-dependent fluid shear stress set point. Elife. 2015;4:e04645. doi: 10.7554/eLife.04645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Baeten JT, Lilly B. Differential regulation of NOTCH2 and NOTCH3 contribute to their unique functions in vascular smooth muscle cells. J Biol Chem. 2015;290:16226–16237. doi: 10.1074/jbc.M115.655548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Majesky MW. Developmental basis of vascular smooth muscle diversity. Arterioscler Thromb Vasc Biol. 2007;27:1248–1258. doi: 10.1161/ATVBAHA.107.141069. [DOI] [PubMed] [Google Scholar]
- 48.Williams B. Mechanical influences on vascular smooth muscle cell function. J Hypertens. 1998;16:1921–1929. doi: 10.1097/00004872-199816121-00011. [DOI] [PubMed] [Google Scholar]
- 49.Basu S, Proweller A. Autoregulatory control of smooth muscle myosin light chain kinase promoter by Notch signaling. J Biol Chem. 2016;291:2988–2999. doi: 10.1074/jbc.M115.679803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Campos AH, Wang W, Pollman MJ, Gibbons GH. Determinants of Notch-3 receptor expression and signaling in vascular smooth muscle cells: Implications in cell-cycle regulation. Circ Res. 2002;91:999–1006. doi: 10.1161/01.res.0000044944.99984.25. [DOI] [PubMed] [Google Scholar]
- 51.Jin S, et al. Notch signaling regulates platelet-derived growth factor receptor-beta expression in vascular smooth muscle cells. Circ Res. 2008;102:1483–1491. doi: 10.1161/CIRCRESAHA.107.167965. [DOI] [PubMed] [Google Scholar]
- 52.Domenga V, et al. Notch3 is required for arterial identity and maturation of vascular smooth muscle cells. Genes Dev. 2004;18:2730–2735. doi: 10.1101/gad.308904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.High FA, et al. Endothelial expression of the Notch ligand Jagged1 is required for vascular smooth muscle development. Proc Natl Acad Sci USA. 2008;105:1955–1959. doi: 10.1073/pnas.0709663105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hild F, Roux S. Comparison of local and global approaches to digital image correlation. Exp Mech. 2012;52:1503–1519. [Google Scholar]
- 55.Neggers J, Hoefnagels JPM, Hild F, Roux S, Geers MGD. Direct stress-strain measurements from bulged membranes using topography image correlation. Exp Mech. 2014;54:717–727. [Google Scholar]
- 56.Neggers J, Blaysat B, Hoefnagels JPM, Geers MGD. On image gradients in digital image correlation. Int J Num Meth Eng. 2016;105:243–260. [Google Scholar]
- 57.Pfaffl MW. A new mathematical model for relative quantification in real-time RT-PCR. Nucleic Acids Res. 2001;29:e45. doi: 10.1093/nar/29.9.e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data, protocols, and numerical code have been stored at SURFdrive, a personal cloud storage service for the Dutch education and research community (https://surfdrive.surf.nl/files/index.php/s/Yel6AZFu78dvy25).