Significance
Traveling waves describe diverse natural phenomena from crystal growth in physics to range expansions in biology. Two classes of waves exist with very different properties: pulled and pushed. Pulled waves are driven by high growth rates at the expansion edge, where the number of organisms is small and fluctuations are large. In contrast, fluctuations are suppressed in pushed waves because the region of maximal growth is shifted toward the population bulk. Although it is commonly believed that expansions are either pulled or pushed, we found an intermediate class of waves with bulk-driven growth, but exceedingly large fluctuations. These waves are unusual because their properties are controlled by both the leading edge and the bulk of the front.
Keywords: invasion, range expansion, diversity loss, Allee effect, reaction–diffusion
Abstract
Epidemics, flame propagation, and cardiac rhythms are classic examples of reaction–diffusion waves that describe a switch from one alternative state to another. Only two types of waves are known: pulled, driven by the leading edge, and pushed, driven by the bulk of the wave. Here, we report a distinct class of semipushed waves for which both the bulk and the leading edge contribute to the dynamics. These hybrid waves have the kinetics of pushed waves, but exhibit giant fluctuations similar to pulled waves. The transitions between pulled, semipushed, and fully pushed waves occur at universal ratios of the wave velocity to the Fisher velocity. We derive these results in the context of a species invading a new habitat by examining front diffusion, rate of diversity loss, and fluctuation-induced corrections to the expansion velocity. All three quantities decrease as a power law of the population density with the same exponent. We analytically calculate this exponent, taking into account the fluctuations in the shape of the wave front. For fully pushed waves, the exponent is −1, consistent with the central limit theorem. In semipushed waves, however, the fluctuations average out much more slowly, and the exponent approaches 0 toward the transition to pulled waves. As a result, a rapid loss of genetic diversity and large fluctuations in the position of the front occur, even for populations with cooperative growth and other forms of an Allee effect. The evolutionary outcome of spatial spreading in such populations could therefore be less predictable than previously thought.
Wave-like phenomena are ubiquitous in nature and have been extensively studied across many disciplines. In physics, traveling waves describe chemical reactions, kinetics of phase transitions, and fluid flow (1–8). In biology, traveling waves describe invasions, disease outbreaks, and spatial processes in physiology and development (9–20). Even nonspatial phenomena such as Darwinian evolution and dynamics on networks can be successfully modeled by waves propagating in more abstract spaces such as fitness (20–25).
The wide range of applications stimulated substantial effort to develop a general theory of traveling waves that is now commonly used to understand, predict, and control spreading phenomena (1, 9, 14, 16, 17, 20, 26, 27). A major achievement of this theory was the division of traveling waves into two classes with very different properties (1, 6, 9, 26, 28–33). The first class contains waves that are “pulled” forward by the dynamics at the leading edge. Kinetics of pulled waves are independent from the nonlinearities behind the front, but extremely sensitive to noise and external perturbations (1, 29, 34). In contrast, the waves in the second class are resilient to fluctuations and are “pushed” forward by the nonlinear dynamics behind the wave front.
Fluctuations in traveling waves arise due to the randomness associated with discrete events such chemical reaction or births and deaths. This microscopic stochasticity manifests in many macroscopic properties of the wave, including its velocity, the diffusive wandering of the front position, and the loss of genetic diversity (33, 35–38). For pulled waves, these quantities have been intensely studied because they show an apparent violation of the central limit theorem (1, 25, 29, 30, 33–37, 39, 40). Naively, one might expect that fluctuations self-average, and their variance is, therefore, inversely proportional to the population density. Instead, the strength of fluctuations in pulled waves has only a logarithmic dependence on the population density. This weak dependence is now completely understood and is explained by the extreme sensitivity of pulled waves to the dynamics at the front (1, 33, 37, 40).
A complete understanding is, however, lacking for fluctuations in pushed waves (1, 25, 29–31, 34–36). Since pushed waves are driven by the dynamics at the bulk of the wave front, it is reasonable to expect that the central limit theorem holds, and fluctuations decrease as one over the population density . Consistent with this expectation, the scaling was theoretically derived both for the effective diffusion constant of the front (38) and for the rate of diversity loss (35). Numerical simulations confirmed the scaling for the diffusion constant (41), but showed a much weaker dependence for the rate of diversity loss (35). Ref. 41, however, considered only propagation into a metastable state, while ref. 35 analyzed only one particular choice of the nonlinear growth function. As a result, it is not clear whether the effective diffusion constant and the rate of diversity loss behave differently, or if there are two distinct types of dynamics within the class of pushed waves.
The latter possibility was anticipated by the analysis of how the wave velocity changes if one sets the growth rate to zero below a certain population density (31). This study found that the velocity correction scales as a power law of the growth-rate cutoff with a continuously varying exponent. If the cutoff was a faithful approximation of fluctuations at the front, this result would suggest that the central limit theorem does not apply to pushed waves. Stochastic simulations, however, were not carried out in ref. 31 to test this prediction.
Together, previous findings highlight the need to characterize the dynamics of pushed waves more thoroughly. Here, we develop a unified theoretical approach to fluctuations in reaction–diffusion waves and show how to handle divergences and cutoffs that typically arise in analytical calculations. Theoretical predictions are tested against extensive numerical simulations. In simulations, we vary the model parameters to tune the propagation dynamics from pulled to pushed and determine how the front diffusion, diversity loss, and wave velocity depend on the population density. Our main result is that the simple pulled vs. pushed classification does not hold. Instead, there are three distinct classes of traveling waves. Only one of these classes shows weak fluctuations consistent with the central limit theorem. The other two classes exhibit large fluctuations because they are very sensitive to the dynamics at the leading edge of the wave front.
Model
Traveling waves occur when a transport mechanism couples dynamics at different spatial locations. The nature of these wave-generating processes could be very different and ranges from reactions and diffusion in chemistry to growth and dispersal in ecology. The simplest and most widely used model of a reaction–diffusion wave * is the generalized Fisher–Kolmogorov equation:
| [1] |
which, in the context of ecology, describes how a species colonizes a new habitat (1, 9, 42–44). Here, is the population density of the species, is the dispersal rate, and is the density-dependent per capita growth rate. The last term accounts for demographic fluctuations: is a Gaussian white noise, and quantifies the strength of demographic fluctuations. In simple birth–death models, is a constant, but we allow for an arbitrary dependence on provided that . The origin of the noise term and its effects on the wave dynamics are further discussed in SI Appendix, section IV.
Pulled waves occur when is maximal at small ; for example, when the growth is logistic: (1, 9). Here, is the growth rate at low densities, and is the carrying capacity that sets the population density behind the front. For pulled waves, the expansion dynamics are controlled by the very tip of the front, where the organisms not only grow at the fastest rate, but also have an unhindered access to the uncolonized territories. As a result, the expansion velocity is independent of the functional form of and is given by the celebrated result due to Fisher, Kolmogorov et al., and Skellam (42–44):
| [2] |
Eq. 2, to which we refer as the Fisher velocity, can be defined for any model with even when the expansion is not pulled. We show below that provides a useful baseline for comparing different types of waves.
Pushed waves occur when a species grows best at intermediate population densities (1, 9). Such nonmonotonic behavior of arises through a diverse set of mechanisms and is known as an Allee effect in ecology (45, 46). Most common causes of an Allee effect are cooperative feeding, collective defense against predators, and the difficulty in finding mates at low population densities (47–50). The velocity of pushed waves is always greater than Fisher’s prediction and depends on all aspects of the functional form of (1, 9).
Allee effects are typically described by adding a cooperative term to the logistic equation:
| [3] |
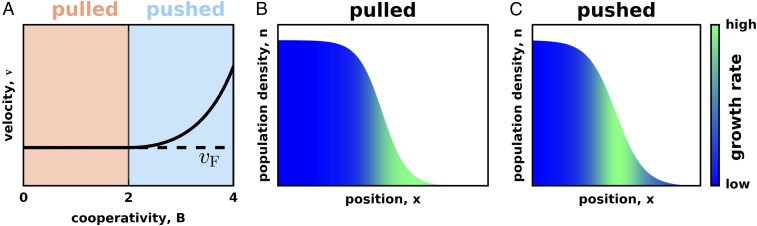
where is the strength of cooperativity. For this model, the exact solutions are known for the expansion velocity and the population density profile; SI Appendix, section II and refs. 9, 51, and 52. For , expansions are pulled, and the expansion velocity equals , which is independent of . That is, cooperativity does not always increase the expansion velocity, even though it always increases the growth rates at high densities. For , expansions are pushed, and increases with . Fig. 1A illustrates this transition from pulled to pushed waves as cooperativity is increased. In Materials and Methods and SI Appendix, section II, we also present several alternative models of an Allee effect and show that our conclusions do not depend on a particular choice of .
Fig. 1.
Waves transition from pulled to pushed as growth becomes more cooperative. (A) The expansion velocity as a function of cooperativity for the growth rate specified by Eq. 3. For low cooperativity, expansions are pulled, and their velocity equals the Fisher velocity. Beyond the critical value of , expansions become pushed, and their velocity exceeds . (B and C) Note that the region of high growth is at the leading edge of the front in pulled waves (B), but in the interior of the front in pushed waves (C). This difference is due to the dependence of the growth rate on the population density. For low cooperativity, the growth rate is maximal at low population densities, but, for high cooperativity, the growth rate is maximal at intermediate population densities. In all images, the exact solution of Eq. 1 is plotted; for B and C; and in B, and and in C.
Increasing the value of cooperativity beyond not only makes the expansion faster, but also shifts the region of high growth from the tip to the interior of the expansion front (Fig. 1 B and C). This shift is the most fundamental difference between pulled and pushed waves because it indicates the transition from a wave being pulled by its leading edge to a wave being pushed by its bulk growth.
The edge-dominated dynamics make pulled waves extremely sensitive to the vagaries of reproduction, death, and dispersal (1, 29, 33, 34). Indeed, the number of organisms at the leading edge is always small, so strong number fluctuations are expected, even in populations with a large carrying capacity, . These fluctuation affect both physical properties, such as the shape and position of the wave front, and evolutionary properties, such as the genetic diversity of the expanding population.† Consistent with these expectations, experiments with pulled waves reported an unusual roughness of the expansion front (6) and a rapid loss of genetic diversity (53, 54).
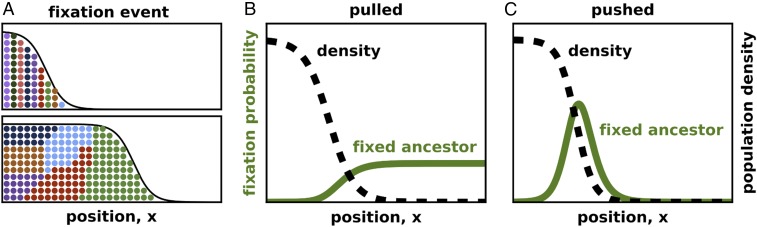
The transition from pulled to pushed dynamics is also evident in the number of organisms that trace their ancestry to the leading edge vs. the bulk of the front. The expected number of descendants has been determined for any spatial position along the front for both pulled and pushed waves (35, 36, 55, 56). For pulled waves, only the very tip of the expansion contributes to future generations. On the contrary, the organisms at the leading edge leave few progeny in pushed waves, and the population descends primarily from the organisms in the region of high growth. This shift in the spatial patterns of ancestry has a profound effect on species evolution. In pulled waves, only mutations near the very edge of the expansion have an appreciable fixation probability, but the entire expansion front contributes to evolution in pushed waves (Fig. 2).
Fig. 2.
Ancestral lineages occupy distinct locations in pulled and pushed waves. A illustrates the fixation of a particular genotype. Initially, a unique and heritable color was assigned to every organism to visualize its ancestral lineage. There are no fitness differences in the population, so fixations are caused by genetic drift. B and C show the probability that the fixed genotype was initially present at a specific position in the reference frame comoving with the expansion. The transition from pulled to pushed waves is marked by a shift in the fixation probability from the tip to the interior of the expansion front. This shift indicates that most ancestral lineages are focused at the leading edge in pulled waves, but near the middle of the front in pushed waves. The fixation probabilities were computed analytically, following refs. 35 and 36, as described in SI Appendix, section III. We used for both B and C; and in B, and and in C.
Fixation probabilities and, more generally, the dynamics of heritable markers provide an important window into the internal dynamics of a reaction–diffusion wave (55). When the markers are neutral, i.e., they do not affect the growth and dispersal of the agents, the relative abundance of the markers changes only stochastically. In population genetics, such random changes in the genotype frequencies are known as genetic drift. To describe genetic drift mathematically, we introduce the relative fraction of one of the genotypes in the population . The dynamics of follow from Eq. 1 and are derived in SI Appendix, section III (see also refs. 55, 57, and 58). The result reads
| [4] |
where is the strength of genetic drift.
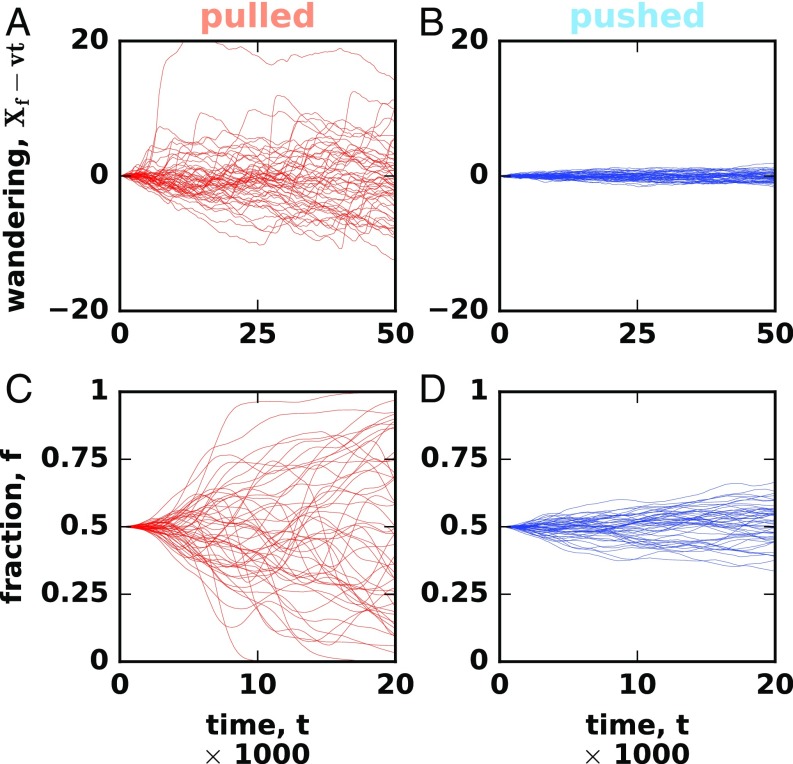
Eq. 4 preserves the expectation value of , but the variance of increases with time until one of the absorbing states is reached. The two absorbing states are and , which correspond to the extinction and fixation of a particular genotype, respectively. The fluctuations of and front position are shown in Fig. 3. Both quantities show an order of magnitude differences between pulled and pushed waves, even though the corresponding change in cooperativity is quite small.
Fig. 3.
Fluctuations are much stronger in pulled than in pushed waves. A and B compare front wandering between pulled (A) and pushed (B) expansions. Each line shows the position of the front in a single simulation relative to the mean overall simulations in the plot. C and D compares the strength of genetic drift between pulled (C) and pushed (D) expansions. We started the simulations with two neutral genotypes equally distributed throughout the front and then tracked how the fraction of one of the genotypes changes with time. This fraction was computed from 300 patches centered on to exclude the fluctuations well behind the expansion front.
Although the difference between pulled and pushed waves seems well-established, little is known about the transition between the two types of behavior. In particular, it is not clear how increasing the nonlinearity of transforms the patterns of fluctuations and other properties of a traveling wave. To answer this question, we solved Eqs. 1 and 4 numerically. Specifically, our simulations described the dynamics of both the population density and the relative abundance of two neutral genotypes. The former was used to estimate the fluctuations in the position of the front, and the latter was used to quantify the decay rate of genetic diversity. In simulations, the species expanded in a one-dimensional array of habitable patches connected by dispersal between the nearest neighbors. Each time step consisted of a deterministic dispersal and growth followed by random sampling to simulate demographic fluctuations and genetic drift (Materials and Methods and SI Appendix, section XIII). By increasing the cooperativity of the growth rate, we observed a clear transition from pulled () to pushed () waves accompanied by a dramatic reduction in fluctuations; Fig. 3.
Results
Fluctuations provide an easy readout of the internal dynamics in a traveling wave, so we decided to determine how they change as a function of cooperativity. Because the magnitude of the fluctuations also depends on the population density, we looked for a qualitative change in this dependence while varying . In particular, we aimed to determine whether population dynamics change gradually or discontinuously at the transition between pulled and pushed waves.
Spatial Wandering of the Front.
We first examined the fluctuations of the front position in the comoving reference frame. The position of the front was defined as the total population size in the colonized space normalized by the carrying capacity . As expected (1, 33, 34, 38), performed a random walk due to demographic fluctuations in addition to the average motion with a constant velocity (Fig. 3 A and B). For both pulled and pushed waves, the variance of grew linearly in time (Fig. 4A), i.e., the front wandering was diffusive and could be quantified by an effective diffusion constant .
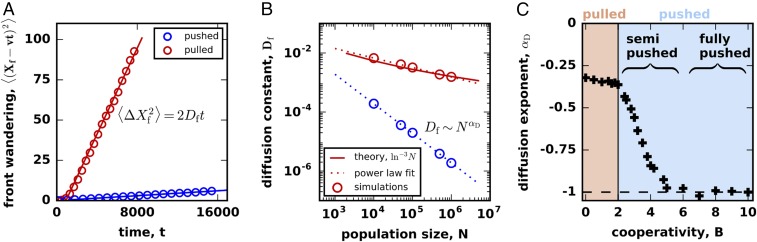
Fig. 4.
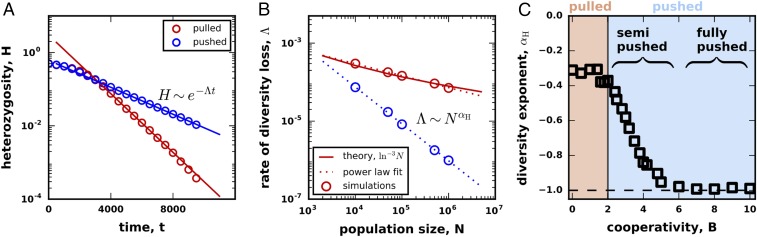
Front wandering identifies two classes of pushed waves. (A) Fluctuations in the front position can be described by simple diffusion for both pulled and pushed waves. (B) The front diffusion is caused by the number fluctuations, so the effective diffusion constant, , decreases with the carrying capacity, . For pulled waves, (33), while, for pushed waves, can decrease much faster as (38). We quantify the scaling of with by the exponent equal to the slope on the log–log plot shown. The overlap of the two red lines highlights the fact that, even though should equal for pulled waves, the limited range of results in a different value of . (C) The dependence of the scaling exponent on cooperativity identifies two distinct classes of pushed waves.
The magnitude of the front wandering is expected to depend strongly on the type of the expansion (1, 33, 34, 38). For pulled waves, ref. 33 found that , but a very different scaling was predicted for certain pushed waves (38); Fig. 4B. Given that pulled and pushed waves belong to distinct universality classes, it is easy to assume that the transition between the two scaling regimens should be discontinuous (1, 33–36, 38). This assumption, however, has not been carefully investigated, and we hypothesized that there could be an intermediate regime with . From simulations, we computed how changes with and indeed found that pushed waves have intermediate values of between and when (SI Appendix, Fig. S3).
The dependence of the scaling exponent on the value of cooperativity is shown in Fig. 4C. For large , we found that is constant and equal to , which is consistent with previous work (38). Below a critical value of cooperativity, however, the exponent continually changes with toward . The critical cooperativity is much larger than the transition point between pulled and pushed waves, so the change in the scaling occurs within the class of pushed waves. This transition divides pushed waves into two subclasses, which we termed fully pushed and semipushed waves. For pulled waves, we found that is independent of , but our estimate of deviated slightly from the expected value due to the finite range of in the simulations (compare and fits in Fig. 4B).
Loss of Genetic Diversity.
Our analysis of the front wandering showed that pushed waves consist of two classes with a very different response to demographic fluctuations. To determine whether this difference extends to other properties of expansions, we turned to genetic drift, a different process that describes fluctuations in the genetic composition of the front. Genetic drift occurs even in the absence of front wandering (SI Appendix, section III and ref. 59), so these two properties are largely independent from each other and capture complementary aspects related to physical and evolutionary dynamics in traveling waves.‡
We quantified genetic fluctuations by the rate at which genetic diversity is lost during an expansion. The simulations were started in a diverse state with each habitable patch containing an equal number of two neutral genotypes. As the expansion proceeded, the relative fractions of the genotypes fluctuated, and eventually one of them was lost from the expansion front (Fig. 3C). To capture the loss of diversity, we computed the average heterozygosity , defined as the probability to sample two different genotypes at the front. Mathematically, equals the average of , where is the fraction of one of the genotypes in an array of patches comoving with the front, and the averaging is done over independent realizations. Consistent with previous work (33, 35), we found that the heterozygosity decays exponentially at long times: for both pulled and pushed waves (Fig. 5A). Therefore, the rate was used to measure the strength of genetic drift across all values of cooperativity.
Fig. 5.
Genetic diversity is lost at different rates in pulled, semipushed, and fully pushed waves. (A) The average heterozygosity, , is a measure of diversity equal to the probability to sample two distinct genotypes in the population. For both pulled and pushed expansions, the decay of genetic diversity is exponential in time: , so we used to measure the strength of genetic drift. (B) Genetic drift decreases with . For pulled waves, (33), while, for fully pushed waves, we predict that ; see Eq. 5. To quantify the dependence of on , we fit . The dashed red line shows that even though should equal for pulled waves, the limited range of results in a different value of . (C) The dependence of the scaling exponent on cooperativity identifies the same three classes of waves as in Fig. 4C; the transitions between the classes occur at the same values of .
By analogy with the front wandering, we reasoned that would scales as for large , and would serve as an effective “order parameter” that distinguishes different classes of traveling waves. Indeed, ref. 33 showed that for pulled waves, i.e., the expected is zero. Although no conclusive results have been reported for pushed waves, the work on adaptation waves in fitness space suggests for fully pushed waves (25). Our simulations confirmed both of these predictions (Fig. 5B) and showed scaling for all values of cooperativity.
The dependence of on shows that genetic fluctuations follow exactly the same pattern as the front wandering (Fig. 5C). In particular, both exponents undergo a simultaneous transition from to a continual dependence on as cooperativity is decreased. Thus, genetic fluctuations also become large as waves switch from fully pushed to semipushed. In the region of pulled waves, and are independent of , but their values deviate from the theoretical expectation due to the finite range of explored in the simulations. Overall, the consistent behavior of the fluctuations in the position and composition of the front strongly suggest the existence of two classes of pushed waves, each with a distinct set of properties.
The Origin of Semipushed Waves.
We next sought an analytical argument that can explain the origin of the giant fluctuations in semipushed waves. In SI Appendix, sections VI and VIII, we explain and extend the approaches from refs. 35 and 38 to compute and using a perturbation expansion in . The main results are
| [5] |
Here, primes denote derivatives; is the coordinate in the reference frame comoving with the expansion; is the normalized population density profile in the steady state; is the expansion velocity; is the dispersal rate as in Eq. 1; and and are the strength of demographic fluctuations and genetic drift, which in general could be different (SI Appendix, section III).
The scaling that we observed for fully pushed waves is readily apparent from Eq. 5. The prefactors of account for the dependence of microscopic fluctuations on the carrying capacity, and the ratios of the integrals describe the relative contribution of the different locations within the wave front.
For fully pushed waves, the integrands in Eq. 5 vanish both in the bulk and at the leading edge, so and are controlled by the number of organisms within the wave front. Hence, the scaling can be viewed as a manifestation of the central limit theorem, which predicts that the variance in the position and genetic diversity of the front should be inversely proportional to the effective population size of the front. To test this theory, we calculated the integrals in Eq. 5 analytically for the model specified by Eq. 3; SI Appendix, sections VI and VIII. These exact results show excellent agreement with our simulations (SI Appendix, Fig. S4) and thus confirm the validity of the perturbation approach for fully pushed waves.
Why does the scaling break down in semipushed waves? We found that the integrals in the numerators in Eq. 5 become more and more dominated by large as cooperativity decreases, and, at a critical value of , they diverge. To pinpoint this transition, we determined the behavior of for large by linearizing Eq. 1 for small population densities:
| [6] |
where we replaced by and shifted into the reference frame comoving with the front. Eq. 6 is linear, so the population density decreases exponentially at the front as . The value of is obtained by substituting this exponential form into Eq. 6 and is given by with as in Eq. 2 (SI Appendix, sections II and IX). From the asymptotic behavior of , it is clear that the integrands in the numerators in Eq. 5 scale as , and the integrals diverge when . The integrals in the denominators converge for all pushed waves.
The divergence condition can be stated more clearly by expressing in terms of and then solving for the critical velocity . From this calculation, we found that the transition from fully pushed to semipushed waves occurs at a universal ratio of the expansion velocity to the linear spreading velocity :
| [7] |
This result does not rely on Eq. 3 and holds for any model of cooperative growth.
The ratio increases with cooperativity and serves as a model-independent metric of the extent to which a wave is pushed. Eq. 7 and the results below further show that this metric is universal, i.e., different models with the same have the same patterns of fluctuations. We can then classify all reaction–diffusion waves using this metric. Pulled waves correspond to the special point of . When , waves are semipushed, and fully pushed waves occur when . Fully pushed waves also occur when ; SI Appendix, section X. Such situations are called propagation into metastable state in physics (1) and strong Allee effect in ecology (47). Because the growth rate at the front is negative, does not exist, and the expansion proceeds only due to the growth in the bulk, where the fluctuations are small.
Properties of Semipushed Waves.
Although the perturbation theory breaks down for , we can nevertheless estimate the scaling exponents and by imposing an appropriate cutoff in the integrals in Eq. 5. One reasonable choice of the cutoff is , which ensures that there is no growth in patches that have fewer than one organism. In SI Appendix, section IX, we show that this cutoff is appropriate for deterministic fronts with , but a different cutoff is needed for fluctuating fronts with .
The need for a different cutoff had been recognized for a long time both from simulations (31) and theoretical considerations (33). However, a method to compute the cutoff has been developed only recently. For pulled waves, the correct value of the cutoff was obtained in ref. 37 by using a nonstandard moment-closure approximation for Eq. 1. We extended this method to pushed waves and found that the integrals should be cut off when falls below ; SI Appendix, section IX. Note that the value of the cutoff depends not only on the absolute number of organisms, but also on the shape and velocity of the front. This dependence arises because population dynamics are much more sensitive to the rare excursions of the front ahead of its deterministic position than to the local fluctuations of the population density; SI Appendix, section IX and ref. 33. Since front excursions occur into typically unoccupied regions, we find that and, therefore, genetic drift and front wandering are stronger than one would expect from .
Upon applying the correct cutoff to Eq. 5, we find that the fluctuations in semipushed waves have a power-law dependence on with a nontrivial exponent between and . The exponent is the same for both and and depends only on . Overall, our theoretical results can be summarized as follows
| [8] |
In the case of pulled waves, our cutoff-based calculation not only predicts the correct values of , but also reproduces the expected scaling (SI Appendix, section X).
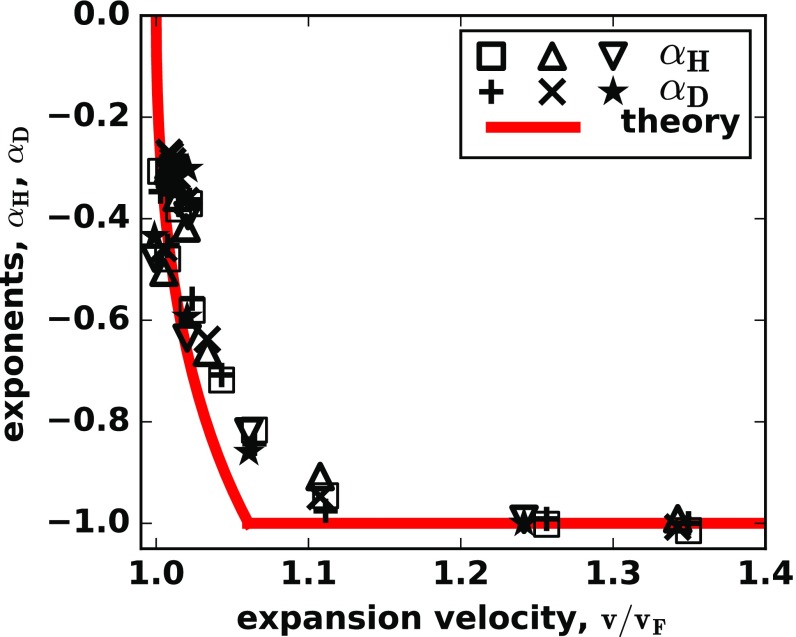
To test the validity of the cutoff approach, we compared its predictions to the simulations of Eq. 3 and two other models of cooperative growth; Fig. 6, Materials and Methods, and SI Appendix, Fig. S5. The simulations confirm that the values of and are equal to each other and depend only on . Moreover, there is a reasonable quantitative agreement between the theory and the data, given the errors in and due to the finite range of in our simulations.
Fig. 6.
The universal transition from semipushed to fully pushed waves. For three different models on an Allee effect, the scaling exponents for the heterozygosity and front diffusion collapse on the same curve when plotted as a function of . Thus, serves as a universal metric that quantifies the effects of cooperativity and separates semipushed from fully pushed waves. We used squares and plus signs for the model specified by Eq. 3, triangles and crosses for the model specified by Eq. 9, inverted triangles and stars for the model specified by Eq. 10, and the red line for the theoretical prediction from Eq. 5.
The success of the cutoff-based calculation leads to the following conclusion about the dynamics in semipushed waves: The fluctuations are controlled only by the very tip of the front, while the growth and ancestry are controlled by the front bulk (Figs. 1C and 2C). Thus, the counterintuitive behavior of semipushed waves originates from the spatial segregation of different processes within a wave front. This segregation is not present in either pulled or fully pushed waves and signifies a new state of the internal dynamics in a traveling wave.
Corrections to the Expansion Velocity due to Demographic Fluctuations.
Finally, we examined how the expansion velocity depends on the strength of demographic fluctuations. To quantify this dependence, we computed , the difference between the actual wave velocity and the deterministic wave velocity obtained by setting in Eq. 1. The perturbation theory in shows that with equal to (SI Appendix, section VII). Thus, we predict scaling for fully pushed waves and a weaker power-law dependence for semipushed waves with the exponent given by Eq. 8§. Our simulations agreed with these results (SI Appendix, Fig. S6) and, therefore, provided further support for the existence of two distinct classes of pushed waves.
Historically, corrections to wave velocity have been used to test the theories of fluctuating fronts (1, 31, 34). For pulled waves, the scaling was first obtained by using the growth-rate cutoff (39). This calculation yielded the right answer because the correct value of the cutoff reduces to in the limit of pulled waves.¶ It is then natural to expect that the approach based on the cutoff must fail for pushed waves. Indeed, Kessler et al. (31) extended the cutoff-based approach to pushed wave and obtained results quite different from what we report here. They analyzed deterministic fronts and imposed a fixed growth-rate cutoff. Upon setting the value of this cutoff to , one obtains that changes continuously from to as cooperativity increases. Thus, for some values of cooperativity, the decrease with is faster than would be expected from the central limit theorem. This clearly indicates that fluctuations rather than the modification of the growth rates play the dominant role. In SI Appendix, section X, we show that the approach of ref. 31 supplemented with the correct value of the cutoff captures the dependence of on for semipushed waves. We also explain why this approach does not apply to fully pushed waves, in which is not sensitive to the growth dynamics at the expansion edge, but is instead controlled by the fluctuations throughout the wave front. There, we also provides a detailed comparison of the rate of diversity loss in fluctuating vs. deterministic fronts (SI Appendix, section X and Figs. S7, S8, and S9).
Discussion
Spatially extended systems often change through a wave-like process. In reaction–diffusion systems, two types of waves have been known for a long time: pulled and pushed. Pulled waves are driven by the dynamics at the leading edge, and all their properties can be obtained by linearizing the equations of motion. In contrast, the kinetics of pushed waves are determined by nonlinear reaction processes. The distinction between pulled and pushed waves has been further supported by recent work on the evolutionary dynamics during range expansions (35, 36). In pulled waves, mutations spread only if they occur at the expansion edge, but the entire front contributes to adaptation in pushed waves.
A natural conclusion from the previous work is that all aspects of the wave behavior are determined by whether the wave is pulled or pushed. Here, we challenged this view by reporting how fluctuation patterns change as the growth of a species becomes more nonlinear. Our main finding is that both front wandering (a physical property) and genetic drift (an evolutionary property) show identical behavior with increasing nonlinearity and undergo two phase transitions. The first phase transition is the classic transition between pulled and pushed waves. The second phase transition separates pushed waves into two distinct subclasses, which we termed fully pushed and semipushed waves.
The differences between the three wave classes can be understood from the spatial distribution of population dynamics. The transition from pulled to semipushed waves is marked by a shift of growth and ancestry from the edge to the bulk of the front (SI Appendix, Fig. S2). In pulled waves, the expansion velocity is determined only by the growth rate at the expansion edge, while the velocity of semipushed waves depends on the growth rates throughout the front. Similarly, all organisms descend from the individuals right at the edge of the front in pulled, but not in semipushed waves, where any organism at the front has a nonzero probability to become the sole ancestor of the future generations. The transition from semipushed to fully pushed waves is marked by an additional change in the spatial pattern of fluctuations. In fully pushed waves, the wandering of the front arises due to the fluctuations in the shape of the entire wave front. Similarly, genetic drift at all regions of the wave front contributes to the overall fluctuations in genotype frequencies. The dynamics of semipushed waves are different: Both the bulk processes and rare excursions of the leading edge control the rate of diversity loss and front wandering. As a result, semipushed waves possess characteristics of both pulled and pushed expansions and require analysis that relies on neither linearization of the reaction–diffusion equation nor an effective averaging within the wave front.
The shift of the fluctuations from the front to the bulk of the wave front explains the different scalings of fluctuations with the population density, . In fully pushed waves, fluctuations obey the central limit theorem and decrease with the carrying capacity as . This simple behavior arises because all processes are localized in a region behind the front. The number of organisms in this region grows linearly with , so the variance of the fluctuations scales as . The central limit theorem seems not to apply to semipushed waves, for which we observed a nontrivial power-law scaling with variable exponents. The new scaling reflects the balance between the large fluctuations at the leading edge and the localization of the growth and ancestry processes behind the front. The departure from the scaling is the strongest in pulled waves, where all processes localize at the tip of the front. Since the number of organisms at the leading edge is always close to , the fluctuations are very large and decrease only logarithmically with the population size.
The different scalings of fluctuations with population density may reflect the different structure of genealogies in pulled, semipushed, and fully pushed waves. Although little is known about the structure of genealogies in the context of range expansions, we can nevertheless propose a conjecture based on an analogy with evolutionary waves in fitness space. Similar to range expansions, evolutionary waves are described by a one-dimensional reaction–diffusion equation, where the role of dispersal is assumed by mutations, which take populations to neighboring regions of the fitness space. The growth rate in evolutionary waves, however, depends not only on the local population density, but also on the location itself because the location of an organism is its fitness. Despite this important difference, evolutionary waves and range expansions have striking similarities. Some evolutionary waves driven by frequent adaptive mutations are similar to pulled waves because their velocity is controlled by the dynamics at the wave edge, and their rate of diversity loss scales as (21, 22, 24, 25, 33, 60, 61). Approximately neutral evolution is in turn similar to pushed waves because its dynamics is controlled by the entire population, and the rate of diversity loss scales as (25, 62). The transition between these two regimes is not fully understood (25, 62), and range expansions might provide a simpler context in which to approach this problem.
Based on the above similarity and the known structure of genealogies in evolutionary waves, it has been conjectured that genealogies in pulled waves are described by the Bolthausen–Sznitman coalescent with multiple mergers (24, 25, 60–66). For fully pushed waves, we conjecture that their genealogies are described by the standard Kingman coalescent with pairwise merges. The Kingman coalescent was rigorously derived for well-mixed populations with arbitrary complex demographic structure (64), so it is natural to expect that it should apply to fully pushed waves, where all of the dynamics occur in a well-defined region within the wave front. The structure of genealogies in semipushed waves is likely to be intermediate and could be similar to that of a coalescent with multiple mergers (25, 66). Although these conjectures are in line with the results for evolutionary waves (25, 62, 62, 63), their applicability to range expansions requires further study. Given that genealogies can be readily inferred from population sequencing, they could provide a convenient method to identify the class of a wave and characterize the pattern of fluctuations.
Our analysis of diversity loss and front wandering also revealed surprising universality in pushed waves. Because pushed waves are nonlinear, their velocity and front shape depend on all aspects of the growth rate, and it is natural to assume that there are as many types of pushed waves as there are nonlinear growth functions. Contrary to this expectation, we showed that many consequences of nonlinearities can be captured by a single dimensionless parameter . This ratio was first used to distinguish pulled and pushed waves, but we found that also determines the transition from semipushed to fully pushed waves and the magnitude of the fluctuations. We therefore suggest that could be a useful and possibly universal metric of the extent to which an expansion is pushed. Such a metric is needed to compare dynamics in different ecosystems and could play an important role in connecting the theory to empirical studies that can measure sufficiently accurately.
In most ecological studies, however, the measurements of both the observed and the Fisher velocities have substantial uncertainty. Our results caution against the common practice of using the approximate equality of and to conclude that the invasion is pulled. The transition to fully pushed waves occurs at , which is very close to the regime of pulled waves . Therefore, expansions with velocities that are only a few percent greater than could behave very differently from pulled waves, e.g., have orders-of-magnitude lower rates of diversity loss. Given that Allee effects arise via a large number of mechanisms and are usually difficult to detect (47, 48, 67), it is possible that many expansions thought to be pulled based on are actually semipushed or even fully pushed. The utility of for distinguishing pulled from semipushed waves could, therefore, be limited to systems where accurate measurements are possible such as waves in physical systems or in well-controlled experimental populations. Identifying fully pushed waves based on the velocity ratio is, however, more straightforward because substantially greater than unambiguously signals that the wave is fully pushed and that the fluctuations are weak.
The somewhat narrow range of velocity ratios for semipushed waves, , does not imply that semipushed waves are rare. Indeed, the entire class of pulled waves is mapped to a single point even though a large number of growth functions lead to pulled expansions. For the growth function in Eq. 3, pulled and semipushed waves occupy equally sized regions in the parameter space: for pulled and for semipushed waves. We examined several other models of cooperative growth in SI Appendix, section XII and Fig. S1), including the one that describes the observed transition from pulled to pushed waves in an experimental yeast population (32). For all models, we found that pulled, semipushed, and fully pushed waves occupy regions in the parameter space that have comparable size. Thus, all three classes of waves should be readily observable in cooperatively growing populations.
Conclusions
Despite the critical role that evolution plays in biological invasions (10, 18, 27, 68–74), only a handful of studies have examined the link between genetic diversity and species ecology in this context (35, 36, 56, 59). The main result of the previous work is that Allee effects reduce genetic drift and preserve diversity. This conclusion, however, was reached without systematically varying the strength on the Allee effect in simulations and was often motivated by the behavior of the fixation probabilities rather than the diversity itself. Our findings not only provide firm analytical and numerical support for the previous results, but also demonstrate that the simple picture of reduced fluctuations in pushed waves does not accurately reflect the entire complexity of the eco-evolutionary feedback in traveling waves. In particular, we showed that the strength of genetic drift varies greatly between semipushed and fully pushed waves. As a result, even a large Allee effect that makes the expansion pushed could be insufficient to substantially slow down the rate of diversity loss.
Beyond specific applications in the evolution and ecology of expanding populations, our work provides an important conceptual advance in the theory of fluctuations in reaction–diffusion waves. We showed that there are three distinct classes of traveling waves and developed a unified approach to describe their fluctuations. In fully pushed waves, fluctuations throughout the entire wave front contribute to the population dynamics. In contrast, the behavior of pulled and semipushed waves is largely controlled by rare front excursions, which can be captured by an effective cutoff at low population densities. Both the contribution of the dynamics at the leading edge and the value of the cutoff depend on the ratio of the wave velocity to the Fisher velocity. This dependence explains the transition from giant, , fluctuations in pulled waves to regular fluctuations in fully pushed waves. Extensions of our analytical approach could potentially be useful in other settings, where one needs to describe stochastic dynamics of nonlinear waves.
Materials and Methods
The simulations in Figs. 3–5 were carried out for the growth model defined by Eq. 3. In Fig. 6, we also used two other growth models to demonstrate that our results do not depend on the choice of . These growth models are specified by the following equations:
| [9] |
and
| [10] |
where is the carrying capacity, sets the time scale of growth, and is the Allee threshold, which could assume both positive and negative values; SI Appendix, section II.
We simulated range expansions of two neutral genotypes in a one-dimensional habitat modeled by an array of patches separated by distance ; the time was discretized in steps of duration . Thus, the abundance of each genotype was represented as , where is the index of the genotype, and and are integer multiples of and . Each time step, we updated the abundance of both genotypes simultaneously by drawing from a multinomial distribution with trials and probability to sample genotype . The values of reflected the expected abundances of the genotypes following dispersal and growth:
| [11] |
where is the total population density after dispersal. Note that in patches, where the population density is less than the carrying capacity.
In the continuum limit, when and , our model becomes equivalent to Eq. 1 for the population density and to Eq. 4 for the relative fraction of the two genotypes with , , and . For simplicity, we set both and to in all of our simulations. We used and for all simulations, unless noted otherwise. These values were chosen to minimize the effects of discreteness of space and time while preserving computational efficiency.
Supplementary Material
Acknowledgments
We thank Jeff Gore and Saurabh Gandhi for useful discussions. This work was supported by Simons Foundation Grants 409704 (to K.S.K.) and 327934 (to O.H.); by the Boston University startup fund (K.S.K.); and National Science Foundation Career Award 1555330 (to O.H.). Simulations were carried out on the Boston University Shared Computing Cluster.
Footnotes
The authors declare no conflict of interest.
*Throughout the paper, we use the term reaction–diffusion wave to describe propagating fronts that connect two states with different population densities. Reaction–diffusion models, especially with several components, also describe more intricate phenomena such as periodic waves, spatiotemporal chaos, and pulse propagation. While some of our results could be useful in these more general settings, our theory and numerical simulations are limited to regular fronts only.
†We refer to genetic drift and genetic diversity as an evolutionary property because they occur only in systems where agents can be assigned heritable labels. In contrast, front wandering occurs in any physical system and can be quantified even when all agents are indistinguishable as is the case in chemical processes.
‡Front wandering and genetic drift are in general coupled because both arise due to the randomness of birth and death. The two processes are, however, not identical because the fluctuations in the total population density could differ from the fluctuations in the relative frequency of the genotypes. For example, in the standard Wright–Fisher model, only genetic drift is present since the total population size is fixed; see SI Appendix, section III for further details.
§Note that, for pulled waves, , which is different from the scaling of and (33, 37). All three quantities, however, scale identically with for semipushed and fully pushed waves.
¶For pulled waves, depends on , so any power-law dependence of on leads to the same scaling with . The coefficient of proportionality between and is, however, also universal, and the correct value is obtained only for .
This article is a PNAS Direct Submission.
Data deposition: Code, data, and scripts for this work have been deposited at https://github.com/gbirzu/pulled_pushed_waves.git.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1715737115/-/DCSupplemental.
References
- 1.Van Saarloos W. Front propagation into unstable states. Phys Rep. 2003;386:29–222. [Google Scholar]
- 2.Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Rev Mod Phys. 1993;65:851–1112. [Google Scholar]
- 3.Aranson IS, Kramer L. The world of the complex Ginzburg-Landau equation. Rev Mod Phys. 2002;74:99–143. [Google Scholar]
- 4.Sachdev PL. Nonlinear Diffusive Waves. Cambridge Univ Press; Cambridge, UK: 1987. [Google Scholar]
- 5.Barenblatt GI. Scaling, Self-Similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics. Vol 14 Cambridge Univ Press; Cambridge, UK: 1996. [Google Scholar]
- 6.Douglas JF, Efimenko K, Fischer DA, Phelan FR, Genzer J. Propagating waves of self-assembly in organosilane monolayers. Proc Natl Acad Sci USA. 2007;104:10324–10329. doi: 10.1073/pnas.0703620104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fox JM, Whitesides GM. Warning signals for eruptive events in spreading fires. Proc Natl Acad Sci USA. 2015;112:2378–2383. doi: 10.1073/pnas.1417043112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ramaswamy S, Toner J, Prost J. Nonequilibrium fluctuations, traveling waves, and instabilities in active membranes. Phys Rev Lett. 2000;84:3494–3497. doi: 10.1103/PhysRevLett.84.3494. [DOI] [PubMed] [Google Scholar]
- 9.Murray JD. Mathematical Biology. Springer; New York: 2003. [Google Scholar]
- 10.Korolev KS. Evolution arrests invasions of cooperative populations. Phys Rev Lett. 2015;115:208104. doi: 10.1103/PhysRevLett.115.208104. [DOI] [PubMed] [Google Scholar]
- 11.Nelson P. Biological Physics. WH Freeman; New York: 2004. [Google Scholar]
- 12.Takamatsu T, Wier W. Calcium waves in mammalian heart: Quantification of origin, magnitude, waveform, and velocity. FASEB J. 1990;4:1519–1525. doi: 10.1096/fasebj.4.5.2307330. [DOI] [PubMed] [Google Scholar]
- 13.Chang JB, Ferrell JE., Jr Mitotic trigger waves and the spatial coordination of the Xenopus cell cycle. Nature. 2013;500:603–607. doi: 10.1038/nature12321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ishihara K, Korolev KS, Mitchison TJ. Physical basis of large microtubule aster growth. eLife. 2016;5:e19145. doi: 10.7554/eLife.19145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pálsson E, et al. Selection for spiral waves in the social amoebae dictyostelium. Proc Natl Acad Sci USA. 1997;94:13719–13723. doi: 10.1073/pnas.94.25.13719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hastings A, et al. The spatial spread of invasions: New developments in theory and evidence. Ecol Lett. 2005;8:91–101. [Google Scholar]
- 17.Fagan WF, Lewis MA, Neubert MG, Van Den Driessche P. Invasion theory and biological control. Ecol Lett. 2002;5:148–157. [Google Scholar]
- 18.Bocedi G, Pe’er G, Heikkinen RK, Matsinos Y, Travis JM. Projecting species’ range expansion dynamics: Sources of systematic biases when scaling up patterns and processes. Methods Ecol Evol. 2012;3:1008–1018. [Google Scholar]
- 19.Hallatschek O, Korolev K. Fisher waves in the strong noise limit. Phys Rev Lett. 2009;103:108103. doi: 10.1103/PhysRevLett.103.108103. [DOI] [PubMed] [Google Scholar]
- 20.Brockmann D, Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
- 21.Tsimring LS, Levine H, Kessler DA. RNA virus evolution via a fitness-space model. Phys Rev Lett. 1996;76:4440–4443. doi: 10.1103/PhysRevLett.76.4440. [DOI] [PubMed] [Google Scholar]
- 22.Rouzine IM, Wakeley J, Coffin JM. The solitary wave of asexual evolution. Proc Natl Acad Sci USA. 2003;100:587–592. doi: 10.1073/pnas.242719299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Good BH, Rouzine IM, Balick DJ, Hallatschek O, Desai MM. Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc Natl Acad Sci USA. 2012;109:4950–4955. doi: 10.1073/pnas.1119910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Neher RA, Hallatschek O. Genealogies of rapidly adapting populations. Proc Natl Acad Sci USA. 2013;110:437–442. doi: 10.1073/pnas.1213113110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brunet É, Derrida B. How genealogies are affected by the speed of evolution. Philos Mag. 2012;92:255–271. [Google Scholar]
- 26.Lewis MA. Finding the sweet spot for invasion theory. Proc Natl Acad Sci USA. 2016;113:6819–6820. doi: 10.1073/pnas.1606665113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tanaka H, Stone HA, Nelson DR. 2017. Spatial gene drives and pushed genetic waves. bioRxiv:10.1101/126722. [DOI] [PMC free article] [PubMed]
- 28.Stokes A. On two types of moving front in quasilinear diffusion. Math Biosci. 1976;31:307–315. [Google Scholar]
- 29.Paquette G, Chen LY, Goldenfeld N, Oono Y. Structural stability and renormalization group for propagating fronts. Phys Rev Lett. 1994;72:76–79. doi: 10.1103/PhysRevLett.72.76. [DOI] [PubMed] [Google Scholar]
- 30.Kessler DA, Levine H. Velocity selection in dendritic growth. Phys Rev B. 1986;33:7867–7870. doi: 10.1103/physrevb.33.7867. [DOI] [PubMed] [Google Scholar]
- 31.Kessler DA, Ner Z, Sander LM. Front propagation: Precursors, cutoffs, and structural stability. Phys Rev E. 1998;58:107–114. [Google Scholar]
- 32.Gandhi SR, Yurtsev EA, Korolev KS, Gore J. Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population. Proc Natl Acad Sci USA. 2016;113:6922–6927. doi: 10.1073/pnas.1521056113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Brunet E, Derrida B, Mueller A, Munier S. Phenomenological theory giving the full statistics of the position of fluctuating pulled fronts. Phys Rev E. 2006;73:056126. doi: 10.1103/PhysRevE.73.056126. [DOI] [PubMed] [Google Scholar]
- 34.Panja D. Effects of fluctuations on propagating fronts. Phys Rep. 2004;393:87–174. [Google Scholar]
- 35.Hallatschek O, Nelson DR. Gene surfing in expanding populations. Theor Popul Biol. 2008;73:158–170. doi: 10.1016/j.tpb.2007.08.008. [DOI] [PubMed] [Google Scholar]
- 36.Roques L, Garnier J, Hamel F, Klein EK. Allee effect promotes diversity in traveling waves of colonization. Proc Natl Acad Sci USA. 2012;109:8828–8833. doi: 10.1073/pnas.1201695109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hallatschek O. The noisy edge of traveling waves. Proc Natl Acad Sci USA. 2011;108:1783–1787. doi: 10.1073/pnas.1013529108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Meerson B, Sasorov PV, Kaplan Y. Velocity fluctuations of population fronts propagating into metastable states. Phys Rev E. 2011;84:011147. doi: 10.1103/PhysRevE.84.011147. [DOI] [PubMed] [Google Scholar]
- 39.Brunet E, Derrida B. Shift in the velocity of a front due to a cutoff. Phys Rev E. 1997;56:2597–2604. [Google Scholar]
- 40.Hallatschek O, Geyrhofer L. Collective fluctuations in the dynamics of adaptation and other traveling waves. Genetics. 2016;202:1201–1227. doi: 10.1534/genetics.115.181271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Khain E, Meerson B. Velocity fluctuations of noisy reaction fronts propagating into a metastable state. J Phys A Math Theor. 2013;46:125002. [Google Scholar]
- 42.Fisher RA. The wave of advance of advantageous genes. Ann Eugen. 1937;7:355–369. [Google Scholar]
- 43.Kolmogorov AN, Petrovsky N, Piscounov NS. A study of the equation of diffusion with increase in the quantity of matter, and its application to a biological problem. Mosc Univ Bull Mathematics. 1937;1:1–25. [Google Scholar]
- 44.Skellam JG. Random dispersal in theoretical populations. Biometrika. 1951:196–218. [PubMed] [Google Scholar]
- 45.Lewis M, Kareiva P. Allee dynamics and the spread of invading organisms. Theor Popul Biol. 1993;43:141–158. [Google Scholar]
- 46.Veit RR, Lewis MA. Dispersal, population growth, and the allee effect: Dynamics of the house finch invasion of eastern north America. Am Nat. 1996;148:255–274. [Google Scholar]
- 47.Courchamp F, Clutton-Brock T, Grenfell B. Inverse density dependence and the Allee effect. Trends Ecol Evol. 1999;14:405–410. doi: 10.1016/s0169-5347(99)01683-3. [DOI] [PubMed] [Google Scholar]
- 48.Kramer AM, Dennis B, Liebhold AM, Drake JM. The evidence for allee effects. Popul Ecol. 2009;51:341–354. [Google Scholar]
- 49.Dai L, Vorselen D, Korolev KS, Gore J. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science. 2012;336:1175–1177. doi: 10.1126/science.1219805. [DOI] [PubMed] [Google Scholar]
- 50.Tobin PC, et al. The role of allee effects in gypsy moth, lymantria dispar (l.), invasions. Popul Ecol. 2009;51:373–384. [Google Scholar]
- 51.Aronson DG, Weinberger HG. Nonlinear Diffusion in Population Genetics, Combustion and Nerve Propagation Lectures Notes Math. Vol 446. Springer; New York: 1975. pp. 5–49. [Google Scholar]
- 52.Fife PC, McLeod JB. The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch Ration Mech Anal. 1977;65:335–361. [Google Scholar]
- 53.Hallatschek O, Hersen P, Ramanathan S, Nelson DR. Genetic drift at expanding frontiers promotes gene segregation. Proc Natl Acad Sci USA. 2007;104:19926–19930. doi: 10.1073/pnas.0710150104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Korolev KS, Xavier JB, Nelson DR, Foster KR. A quantitative test of population genetics using spatiogenetic patterns in bacterial colonies. Am Nat. 2011;178:538–552. doi: 10.1086/661897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Vlad MO, Cavalli-Sforza LL, Ross J. Enhanced (hydrodynamic) transport induced by population growth in reaction–diffusion systems with application to population genetics. Proc Natl Acad Sci USA. 2004;101:10249–10253. doi: 10.1073/pnas.0403419101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Marculis NG, Lui R, Lewis MA. Neutral genetic patterns for expanding populations with nonoverlapping generations. Bull Math Biol. 2017;79:828–852. doi: 10.1007/s11538-017-0256-7. [DOI] [PubMed] [Google Scholar]
- 57.Constable GW, McKane AJ. Models of genetic drift as limiting forms of the Lotka-Volterra competition model. Phys Rev Lett. 2015;114:038101. doi: 10.1103/PhysRevLett.114.038101. [DOI] [PubMed] [Google Scholar]
- 58.Korolev KS, Avlund M, Hallatschek O, Nelson DR. Genetic demixing and evolution in linear stepping stone models. Rev Mod Phys. 2010;82:1691–1718. doi: 10.1103/RevModPhys.82.1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Nullmeier J, Hallatschek O. The coalescent in boundary-limited range expansions. Evolution. 2013;67:1307–1320. doi: 10.1111/evo.12037. [DOI] [PubMed] [Google Scholar]
- 60.Neher RA, Kessinger TA, Shraiman BI. Coalescence and genetic diversity in sexual populations under selection. Proc Natl Acad Sci USA. 2013;110:15836–15841. doi: 10.1073/pnas.1309697110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Desai MM, Walczak AM, Fisher DS. Genetic diversity and the structure of genealogies in rapidly adapting populations. Genetics. 2013;193:565–585. doi: 10.1534/genetics.112.147157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Good BH, Walczak AM, Neher RA, Desai MM. Genetic diversity in the interference selection limit. PLoS Genet. 2014;10:e1004222. doi: 10.1371/journal.pgen.1004222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Brunet É, Derrida B, Mueller AH, Munier S. Effect of selection on ancestry: An exactly soluble case and its phenomenological generalization. Phys Rev E. 2007;76:041104. doi: 10.1103/PhysRevE.76.041104. [DOI] [PubMed] [Google Scholar]
- 64.Kingman JFC. The coalescent. Stochastic Process Appl. 1982;13:235–248. [Google Scholar]
- 65.Wakeley J. Coalescent Theory. Roberts & Company; Greenwood Village, CO: 2009. [Google Scholar]
- 66.Berestycki N. Recent progress in coalescent theory. Ensaios Matematicos. 2009;16:1–193. [Google Scholar]
- 67.Berec L, Angulo E, Courchamp F. Multiple Allee effects and population management. Trends Ecol Evol. 2007;22:185–191. doi: 10.1016/j.tree.2006.12.002. [DOI] [PubMed] [Google Scholar]
- 68.Pateman RM, Hill JK, Roy DB, Fox R, Thomas CD. Temperature-dependent alterations in host use drive rapid range expansion in a butterfly. Science. 2012;336:1028–1030. doi: 10.1126/science.1216980. [DOI] [PubMed] [Google Scholar]
- 69.Roman J, Darling JA. Paradox lost: Genetic diversity and the success of aquatic invasions. Trends Ecol Evol. 2007;22:454–464. doi: 10.1016/j.tree.2007.07.002. [DOI] [PubMed] [Google Scholar]
- 70.Lee CE. Evolutionary genetics of invasive species. Trends Ecol Evol. 2002;17:386–391. [Google Scholar]
- 71.Dlugosch K, Parker I. Founding events in species invasions: Genetic variation, adaptive evolution, and the role of multiple introductions. Mol Ecol. 2008;17:431–449. doi: 10.1111/j.1365-294X.2007.03538.x. [DOI] [PubMed] [Google Scholar]
- 72.Shine R, Brown GP, Phillips BL. An evolutionary process that assembles phenotypes through space rather than through time. Proc Natl Acad Sci USA. 2011;108:5708–5711. doi: 10.1073/pnas.1018989108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Phillips BL, Brown GP, Greenlees M, Webb JK, Shine R. Rapid expansion of the cane toad (Bufo marinus) invasion front in tropical Australia. Austral Ecol. 2007;32:169–176. [Google Scholar]
- 74.Gray ME, Sappington TW, Miller NJ, Moeser J, Bohn MO. Adaptation and invasiveness of western corn rootworm: Intensifying research on a worsening pest. Annu Rev Entomol. 2009;54:303–321. doi: 10.1146/annurev.ento.54.110807.090434. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.