Abstract
Functional connectivity analysis is an essential tool for understanding brain function. Previous studies showed that brain regions are functionally connected through low-frequency signals both within the default mode network (DMN) and task networks. However, no studies have directly compared the time scale (frequency) properties of network connectivity during task versus rest, or examined how they relate to task performance. Here, using fMRI data collected from sixty-eight subjects at rest and during a stop signal task, we addressed this issue with a novel functional connectivity measure based on detrended partial cross-correlation analysis (DPCCA). DPCCA has the advantage of quantifying correlations between two variables in different time scales while controlling for the influence of other variables. The results showed that the time scales of within-network connectivity of the DMN and task networks are modulated in opposite directions across rest and task, with the time scale increased during rest vs. task in the DMN and vice versa in task networks. In regions of interest analysis, the within-network connectivity time scale of the pre-supplementary motor area – a medial prefrontal cortical structure of the task network critical to proactive inhibitory control – correlated inversely with Barratt impulsivity and stop signal reaction time. Together, these findings demonstrate that time scale properties of brain networks may vary across mental states and provide evidence in support of a role of low frequency fluctuations of BOLD signals in behavioral control.
Keywords: resting state, stop-signal task, functional connectivity, DPCCA, multiple time scales, preSMA
1. Introduction
Connectivity analysis is an important tool to understanding brain functions at rest or during task challenges. Greicius and colleagues observed that the so-called default mode regions (Raichle et al., 2001), which deactivated during task challenges, were functionally connected during a resting state, forming the default mode network (DMN) (Greicius et al., 2003). A later study showed that task regions responding to external events were also functionally connected at rest (Smith et al., 2009), echoing an earlier report of motor cortical blood oxygenation level dependent (BOLD) signals connected at low frequency during rest (Biswal et al., 1995). These observations raise the question whether low frequency fluctuations (more persistent and of longer time scale) of BOLD signals may play a role in orchestrating not only the DMN but also task-related networks in response to behavioral challenges. That is, a substantial body of work supports that the DMN and task networks are connected during rest (Biswal et al., 1995; Smith et al., 2009; Zhang and Raichle, 2010; Buckner et al., 2011; Yeo et al., 2011); however, it is unclear whether the temporal scales of the functional connectivities of these networks differ between rest and task challenges and whether these differences may influence task performance.
Recent studies have focused on the dynamic nature of functional connectivity (Hutchison et al., 2013b; Calhoun et al., 2014; Preti et al., 2016; Shine et al., 2016; Bassett and Sporns, 2017). Dynamic functional connectivity may index changes in macroscopic neural patterns underlying aging (Hutchison and Morton, 2015), consciousness (Hutchison et al., 2013a; Keilholz et al., 2013), and cognitive task performance (Jia et al., 2014; Madhyastha et al., 2015; Shine et al., 2016). The sliding window method is widely used to examine dynamic connectivity, although it is somewhat arbitrary to determine the window size (Hutchison et al., 2013b; Preti et al., 2016) and the choice of a fixed window length limits the analysis to the frequency range below the window period. Further, information about connectivity time scale proves critical to analyses based on sliding windows (Calhoun et al., 2014; Hindriks et al., 2016). For instance, with simulated data Hindriks and colleagues showed that the probability of connectivity detection varies as a function of the window length, and its maximum is approximately at 1/3 of the characteristic time scale of correlation (Hindriks et al., 2016). Alternative to the sliding-windows methods are time-frequency methods, popular in EEG and MEG analyses (Le Van Quyen and Bragin, 2007; Roach and Mathalon, 2008). Recent work has applied wavelet transform coherence (WTC) approaches to examine the temporal variability in connectivity between nodes of the DMN during rest (Chang and Glover, 2010; Yaesoubi et al., 2015). WTC methods can be used to analyze the coherence and phase lag between two time series as a function of both time and frequency (Torrence and Compo, 1998).
Many studies examined functional connectivity in distinct frequency bands (Achard et al., 2008; You et al., 2012; Kalcher et al., 2014; Thompson and Fransson, 2015), including work showing varying topological network properties (Salvador et al., 2005; Qian et al., 2015a). These approaches allowed contrasting predominantly low-frequency fluctuations of cortical regions with high-frequency fluctuations of subcortical regions (Kalcher et al., 2014), and showed that the integration (within nodes) and segregation (between nodes) of large-scale networks operate at different time scales (Thompson and Fransson, 2015). On the other hand, the choice of frequency bands is arbitrary, and may impact the results. Regional interactions are likely not restricted to a binary range (low versus high) or a particular frequency band, and it remains open how to characterize network interactions that operate in a continuous range of frequencies. In this context, time-frequency analysis based on wavelets methods helps in quantifying dynamic functional connectivity across distinct time periods (Chang and Glover, 2010; Yaesoubi et al., 2015). The drawback of wavelet analyses involves the complex process of selecting the appropriate wavelet shapes and parameters (Zhang et al., 2016). Additionally, it does not provide a way to control for the influence of third variables, an issue of central importance to disambiguating network connectivity.
In sum, despite a wealth of connectivity studies, none to our knowledge have directly compared the time scale (frequency) properties of network connectivity during rest versus task. We sought to address this gap in research by examining the fMRI data of the same individuals collected at rest and during a cognitive task, using a novel functional connectivity measure based on detrended partial cross correlation analysis (DPCCA) (Ide et al., 2017). DPCCA (Qian et al., 2015b; Yuan et al., 2015) is an extended version of detrended cross-correlation analysis (Podobnik and Stanley, 2008; Kristoufek, 2014), developed initially in physics and econometrics to model correlations among non-stationary time series of complex systems. DPCCA quantifies correlations between two variables in different time-scales, while controlling for the influence of other variables (i.e., partial correlations). The correlation in activity between two brain regions can vary according to different time scales, as demonstrated by previous scale-free and wavelet analyses of BOLD signals (Park et al., 2010; You et al., 2012; Ciuciu et al., 2014; Zhang et al., 2016). Distinguishing connectivity at a short and long-time scale thus helps to elucidate transient vs. sustained interaction between brain regions. Although the DPCCA is not a dynamic functional connectivity measure, it can inform the size of the sliding windows used to compute the dynamic measures. We posited that functional interactions among task networks and DMN transpire at different signal frequencies and these neural features are related to task performance.
2. Material and Methods
2.1 Subjects and informed consent
Study participants were recruited from the greater New Haven, CT area. All were free of major medical illness, past or present neurological and psychiatric illnesses including substance use disorders [DSM-IV (First et al., 1995)]. Individuals who were currently using any psychotropic medications or tested positive for illicit substances in urine toxicology were not invited to participate. All subjects signed a written informed consent, in accordance to a protocol approved by the Yale Human Investigation Committee. In total, 71 healthy adults participated in four 10-minute sessions of a stop signal task (SST) and a 10-minute resting session during fMRI. Three subjects were excluded because of excessive head movements (Section 4.2) and data from the remaining 68 individuals (36 women; age 32.7 ± 13.2 years) were included in the analyses. Participants were also assessed with the Barratt Impulsivity Scale (BIS-11, (Patton et al., 1995)) for impulsive personality trait, which is known to be associated with deficits in response inhibition (Farr et al., 2012; Weidacker et al., 2017).
2.2 Behavioral task and performance measures
In resting state, participants were asked to relax but stay awake with eyes closed. For behavioral task we employed a stop-signal paradigm (Logan et al., 1984; Li et al., 2006; Hendrick et al., 2010; Li et al., 2010; Ide and Li, 2011b; Farr et al., 2012; Winkler et al., 2012; Hu et al., 2014). Go and stop trials were randomly intermixed in presentation each about 75% and 25% of the time and with an inter-trial interval of 2 s. A small dot appeared on the screen to engage attention at the beginning of a trial. After a randomized fore-period between 1 and 5 s, drawn from a uniform distribution, the dot turned into a circle (the “go” signal), prompting the subjects to quickly press a button. The circle vanished at a button press or after 1 s had elapsed, whichever came first, and the trial terminated. A premature button press prior to the appearance of the circle also terminated the trial. On a stop trial, an additional “X,” the “stop” signal, appeared after and replaced the go signal, and instructed participants to withhold their response. Similar to go trials, a stop trial terminated at button press or 1 s after the appearance of the stop signal. Failure to withhold the go response for the 1-s period constituted a stop error. The stop signal delay (SSD) – the time interval between go and stop signals – started at 200 ms and was adjusted according to a staircase procedure, increasing and decreasing by 67 ms each for a successful and failed stop (Levitt, 1971). Subjects were instructed to respond to the go signal quickly while keeping in mind that a stop signal could come up occasionally. The staircase procedure ensured that subjects would succeed in withholding their response in approximately half of the stop trials.
We computed a critical SSD that represents the time delay between go and stop signals that a subject would need to succeed in 50% of the stop trials (Levitt, 1971). Specifically, SSDs across trials were grouped into runs, with each run defined as a monotonically increasing or decreasing series. We derived a mid-run estimate by taking the middle SSD (or average of the two middle SSDs when there was an even number of SSDs) of every second run. The critical SSD was computed by taking the mean of all mid-run SSDs. It was reported that, except for experiments with a small number of trials (less than 30), the mid-run estimate was close to the maximum likelihood estimate of X50 (50% positive response; i.e., 50% SS in the SST, (Wetherill et al., 1966)). The stop signal reaction time (SSRT) was computed by subtracting the critical SSD from the median go trial RT (Logan, 1994). The SSRT represents the time required to successfully withhold a motor response in half of the stop trials and reflects the capacity of response inhibition.
2.3 Image acquisition and preprocessing
All imaging data were collected in the same 3T Siemens Trio scanner. Each scan comprised four 10-min runs of the SST and one 10-min run of rest. Functional blood oxygen level dependent (BOLD) signals were acquired with a single-shot gradient echo echo-planar imaging (EPI) sequence, with 32 axial slices parallel to the AC-PC line covering the whole brain, using published parameters: TR=2000 ms, TE=25 ms, bandwidth=2004 Hz/pixel, flip angle=85°, FOV=220×220 mm2, matrix=64×64, slice thickness=4 mm and no gap. A high-resolution 3D structural image (MPRAGE; 1 mm resolution) was also obtained for anatomical co-registration.
Functional MRI data was preprocessed with Statistical Parametric Mapping 12 (SPM12) (Wellcome Department of Imaging Neuroscience, University College London, U.K.). Images from the first five TRs at the beginning of each trial were discarded to enable the signal to achieve steady-state equilibrium between RF pulsing and relaxation. Images of each individual subject were first corrected for slice timing, realigned (motion-corrected) (Andersson et al., 2001; Hutton et al., 2002). A mean functional image volume was constructed for each subject for each run from the realigned image volumes. The anatomical images (T1-weighted) were co-registered to the mean functional image, and normalized to an MNI (Montreal Neurological Institute) template with affine registration followed by nonlinear transformation using a unified segmentation and registration framework (Ashburner and Friston, 2005). The normalization parameters determined for the anatomical volume were then applied to the corresponding functional image volumes for each subject.
2.4 Head motion evaluation
As extensively investigated in (Van Dijk et al., 2012), micro head motion (>0.1mm) is an important source of spurious correlations in resting state functional connectivity analysis. Therefore, we evaluated head motion using methods proposed by Power and colleagues (Power et al., 2012). Unlike previous work (Smyser et al., 2010; Power et al., 2012; Tomasi and Volkow, 2012), we did not “scrub” the data because we were interested in the time scale properties of connectivity and removing time points jeopardized the computation of detrended partial cross-correlation. Therefore, we addressed head motion by excluding subjects with movements over a threshold. For every time point t, we computed the framewise displacement given by the expression FD (t) = |Δdx (t)| + |Δdy (t) | + |Δdz (t) | + r |α (t) | + r |β (t) | + r |γ (t) |, where (dx,dy,dz) and (α,β,γ) – the translation and rotation realignment parameters from SPM12 – and r = 50mm – a constant that approximates the mean distance between center of MNI space and the cortex – were used to transform rotations into displacements (Power et al., 2012). The second head movement metric computed was the root mean square variance (DVARS) of the differences in % BOLD intensity I (t) between consecutive time points across brain voxels: , where the brackets indicate the mean across brain voxels. As with previous work (Power et al., 2012; Tomasi and Volkow, 2012), time points that exceeded FD(t)>0.5mm or DVARS(t)>0.5% were considered significant and, as a result, we removed 3 (out of 71) individuals who presented severe head movements (time points removed >25%). Head movement parameters were used as nuisance variables during time series extraction to account for potential spurious connectivities (Van Dijk et al., 2012).
2.5 Functional nodes and time series extraction
Region of interest (ROI) or nodes were defined according to the Yale functional brain atlas comprising 268 regions covering the whole brain (Shen et al., 2013). In this atlas constructed from fMRI data of 79 healthy subjects, each “node” was optimized to contain voxels with similar resting state time series. In additional analysis, we focused on the pre-supplementary motor area (preSMA), which responds to proactive inhibitory control (Hu et al., 2015), as an ROI and examined how preSMA connectivity relates to Barratt impulsivity score and SSRT across subjects. For each node, time-series were extracted by averaging over voxels and preprocessed to reduce spurious BOLD variances that were unlikely to reflect neuronal activity (Rombouts et al., 2003; Fox et al., 2005; Fair et al., 2007; Fox and Raichle, 2007). The sources of spurious variance were removed through linear regression by including the signal from the ventricular system, white matter, and whole brain, in addition to the six parameters obtained by rigid body head motion correction. First-order derivatives of the whole brain, ventricular and white matter signals were also included in the regression.
2.6 Detrended partial cross-correlation analysis (DPCCA)
DPCCA (Qian et al., 2015b; Yuan et al., 2015) builds on detrended cross-correlation analysis (Podobnik and Stanley, 2008; Kristoufek, 2014) and quantifies correlations between two variables in different time-scales, while controlling for the influence of other variables (i.e., partial correlations). Briefly, given two time series {xa(t)}, {xb(t)} ∈ X (t), where X (t) ∈ ℝm, m is the total number of time series, t= 1, 2, …, N time points, DPCCA is computed by the expression:
| (1) |
where s is the time scale and each term Ca,b (s) is estimated by inverting the matrix of coefficients ρ (s). This step is analogous to partial correlation computation. Each element ρa,b (s) ∈ ρ (s) is the so-called detrended cross-correlation analysis (DCCA) coefficient (Kristoufek, 2014). DCCA coefficient combines detrended cross correlation analysis (Podobnik and Stanley, 2008) with the detrended fluctuation analysis (DFA) (Kantelhardt et al., 2002) first used to study power-law properties of non-stationary time series.
Given two time series {x},{y} ∈ X (t) (indices omitted for simplicity) with N time points and time scale s, the DCCA coefficient is given by Equation 2:
| (2) |
where the numerator is the average of detrended variance, and the denominators represent the covariances of N − s + windows (partial sums), as estimated by Equations 3 and 4:
| (3) |
| (4) |
Finally, the partial sums are obtained with sliding windows across the integrated time series and . For each j-th time window with size s, detrended covariance and variance are computed according to Equations 5 and 6:
| (5) |
| (6) |
where and are polynomial fits of time trends. We used a linear fit as originally proposed (Kristoufek, 2014). In this way, with DPCCA, we quantified partial correlations among time series with varying levels of non-stationarity.
Statistical significance of DPCCA measures were estimated by customized nonparametric tests as proposed in (Smith et al., 2011), where empirical null distributions of connectivity were constructed with randomly shuffled time series across subjects and regions, for multiple time scales. Briefly, Figure 1 shows a sample DPCCA profile for a simulated BOLD data set. With the temporal profile of correlation, we were able to identify a peak DPCCA value (DPCCAmax) in association with a particular time scale (smax). Thus, DPCCAmax quantifies the magnitude of connectivity at the time scale smax. In this work, we only considered positive DPCCAmax values, because the functional implications of negative correlations (anticorrelated networks) remain actively debated (Fox et al., 2009; Murphy et al., 2009; Chai et al., 2012; Liang et al., 2012). Validation of DPCCA as a measure of functional connectivity can be found in (Ide et al., 2017). shade represents the standard deviation; and dashed lines are 95% confidence intervals (CI) estimated from the empirical null dataset. Peak time scale smax=10s. Details are available in (Ide et al., 2017).
Figure 1.
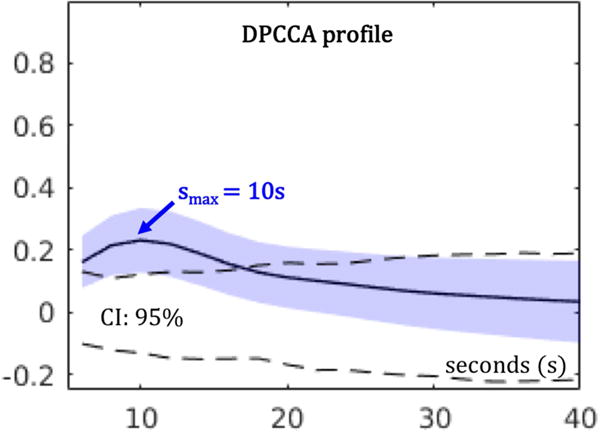
Illustration of a sample DPCCA profile. Given simulated BOLD time series, DPCCA coefficients were computed for different time scales ranging from 6 to 40 s (18 time points spaced by 2 s). Solid line represents the average across 100 simulated data sets; blue shade represents the standard deviation; and dashed lines are 95% confidence intervals (CI) estimated from the empirical null dataset. Peak time scale smax=10s. Details are available in (Ide et al., 2017).
In the current analyses, we examined time scales ranging from 6 to 40 s, covering most of the frequency spectrum of resting state (Thompson and Fransson, 2015) and partially of fast event interactions (average trial duration = 5.7 s in the stop signal task). We chose 6 s as the lower time scale limit in order to allow quadratic interpolations in Equations 5 and 6, which required 3 time points with the sample period TR=2 s.
3. Results
3.1 Functional connectivity: Rest versus task
With 268 nodes (Figure 2a), we computed the pairwise DPCCA profiles each for rest and task, and extracted the connectivity matrix of peak DPCCA values. Figure 2b shows connectivity matrices thresholded at the 90th percentile (i.e. 10% most significant connections). The use of percentiles guaranteed the same number of connections in the matrices, a common practice for group comparison (Bassett et al., 2008) or characterization of individuals’ connectivity fingerprint (Finn et al., 2015) in network analysis. To investigate the peak connectivity of all 35,778 possible connections (combination of 268 nodes), we computed the average correlation (DPCCAmax) of connections among nodes both within (In) and between (Out) networks. We focused on eight networks, each defined by a set of nodes that are functionally connected (Finn et al., 2015), and for each network obtained 2 average values: DPCCAmax(In) and DPCCAmax(Out). The eight networks are defined using the same clustering algorithm used to delineate the 268 nodes (Shen et al., 2013), and are named according to their correspondence to existing resting-state networks (Finn et al., 2015), including the medial frontal (MF), frontoparietal (FP), default-mode (DMN), subcortical-cerebellum (SubCB) as well as the motor (Mot) and the visual (Vis 1-3) networks. In order to parametrically compare the rest and task networks, we Fisher-z transformed connectivity matrix and removed the mean to eliminate baseline differences. Table 1 summarizes the results of all peak connectivity strengths and the statistics of paired t tests (rest vs. task). Except for DPCCAmax(In) of the Vis1 network, all connectivity strengths increased in task vs. rest. DPCCAmax were higher for task as compared to rest for the within-network or “In” connectivity of the SubCB network (p=8.5e-08), and for between-network or “Out” connectivity of the MF, FP, Vis1 and Vis3 networks (p=7.8e-03, 2.8e-04, 0,01 and 7.7e-0.3, respectively), with the results of SubCB and FP networks reaching significance at a corrected threshold [p=0.05/(2×8)=0.0031].
Figure 2.
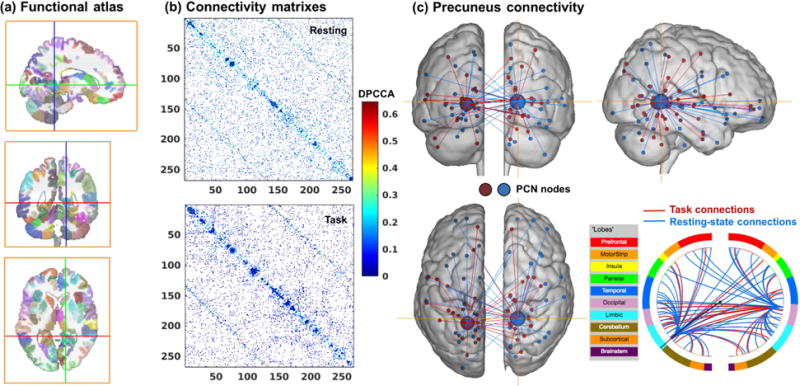
(a) Yale functional brain atlas of 268 nodes covering the whole-brain (Shen et al., 2013). (b) Connectivity matrix of the 268 nodes, given by the DPCCAmax values thresholded at 90% percentile for rest and task. (c) Ventral precuneus connections as an example to illustrate network connectivity. In the circle plot, lines indicate the ‘networks’ to which precuneus nodes are connected.
Table 1.
Average peak connectivity for within (In) and between (Out) network connections, during task and rest.
| Network | MF | FP | DMN | SubCB | Mot | Vis1 | Vis2 | Vis3 |
|---|---|---|---|---|---|---|---|---|
| DPCCAmax (In) Task | 0.052 ±0.015 | 0.063 ±0.014 | 0.118 ±0.023 | 0.064 ±0.010 | 0.053 ±0.012 | 0.083 ±0.015 | 0.099 ±0.027 | 0.068 ±0.024 |
| DPCCAmax (In) Rest | 0.049± 0.030 | 0.059± 0.028 | 0.112 ±0.040 | 0.052 ±0.015 | 0.049 ±0.020 | 0.090 ±0.030 | 0.088 ±0.051 | 0.066 ±0.041 |
| Paired t-test p | 0.324 | 0.228 | 0.298 | 8.5e-08* | 0.181 | 0.076 | 0.075 | 0.770 |
| DPCCAmax (Out) Task | 0.022 ±0.012 | 0.024 ±0.010 | 0.023 ±0.011 | 0.018 ±0.008 | 0.018 ±0.010 | 0.021 ±0.014 | 0.035 ±0.016 | 0.027 ±0.013 |
| DPCCAmax (Out) Rest | 0.016 ±0.018 | 0.016 ±0.017 | 0.018 ±0.018 | 0.017 ±0.013 | 0.016 ±0.018 | 0.015 ±0.023 | 0.026 ±0.025 | 0.019 ±0.019 |
| Paired t-test p | 7.8e-03 | 2.8e-04* | 0.034 | 0.365 | 0.473 | 0.094 | 0.010 | 7.7e-03 |
Note: The eight networks are medial frontal (MF), frontoparietal (FP), default-mode (DMN), subcortical-cerebellum (SubCB), motor (Mot) and visual areas (Vis1-3). MF: medial superior frontal and inferior frontal gyri, dorsal anterior cingulate, middle temporal lobes; FP: orbitofrontal and middle frontal gyri, dorsolateral cortex, angular gyrus and inferior temporal; SubCB: thalamus, caudate, putamen, insula, hippocampus, brain stem and cerebellum; Mot: post- and precentral regions, supplementary motor area, middle cingulate and superior temporal lobe; Vis1: cuneus, calcarine, lingual; Vis2: middle occipital, cerebellum Crus1; Vis3: inferior and middle occipital, inferior and superior parietal and fusiform. All DPCCAmax values are mean ± standard deviation. P values <0.05 are in bold
indicates values that survive Bonferroni correction for multiple comparisons.
3.2 Time scale of peak connectivity: Rest versus task
To investigate the time scale of peak connectivity we computed the average peak time scale (smax) of connections among nodes both within (In) and between (Out) the eight networks. Thus, for each of the eight networks, we obtained 2 averages: smax(In) and smax(Out). Average time scales of peak connectivity for rest and task are shown in Figure 3. The smax(In) of the medial frontal (MF) and frontoparietal (FP) networks were greater during task versus rest (both p’s<0.05). In contrast, the smax(In) of the DMN were greater during rest as compared to task (p<0.05). For “between network” or “Out” connectivity, Vis3 network showed higher smax(Out) during task as compared to rest (p<0.005).
Figure 3.
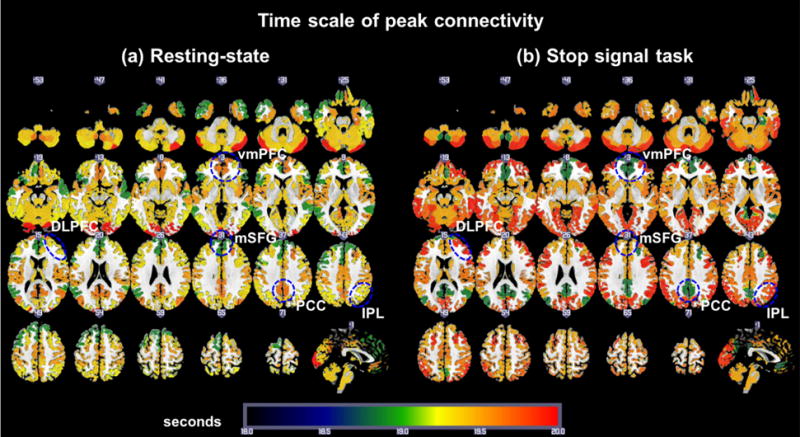
Average time scales of the peak connectivity within each one of the eight functional networks (“In” network connectivity). (a) Map of smax(In) during rest. (b) Map of smax(In) during the stop signal task. vmPFC: ventromedial prefrontal cortex (DMN); PCC: posterior cingulate cortex (DMN); mSFG: medial superior frontal gyrus (MF network, including the presupplementary motor area), DLPFC: dorsolateral prefrontal cortex (FP network); and IPL: inferior parietal lobule (FP network).
For within-network (In) connectivity, smax of both MF and FP networks increased and smax of DMN decreased during task as compared to test. We computed the smax(In) by combining MF and FP and performed an analysis of variance (ANOVA) with two factors: network (MF+FP) vs. DMN and condition rest vs. task. The results showed that there was a significant interaction (p<0.001), with the smax(In) decreased (delta = −0.56) in the MF+FP networks and increased (delta = 0.95) in the DMN for rest as compared to task. Table 2 summarizes the results of all smax and the statistics of paired t tests of rest vs. task as well as the ANOVA of (MF+FP vs. DMN) × (Task vs. Rest).
Table 2.
Average peak time scales for within (In) and between (Out) network connections, during task and rest.
| Network | MF | FP | DMN | SubCB | Mot | Vis1 | Vis2 | Vis3 |
|---|---|---|---|---|---|---|---|---|
| smax (In) Task | 19.49 ± 1.43 | 19.96 ± 1.63 | 18.75 ± 2.40 | 19.47 ± 0.78 | 19.65 ± 1.01 | 19.84 ± 1.67 | 19.95 ± 3.14 | 19.68 ± 2.11 |
| smax (In) Rest | 18.96 ±1.39 | 19.37 ± 1.65 | 19.70 ± 2.64 | 19.41 ± 0.94 | 19.52 ± 0.99 | 19.33 ± 1.95 | 20.19 ± 2.94 | 19.20 ± 2.45 |
| Paired t-test p | 0.0441 | 0.0386 | 0.0148 | 0.6622 | 0.4657 | 0.1432 | 0.6198 | 0.2093 |
| smax (Out) Task | 19.35 ±0.76 | 19.53 ± 0.85 | 19.23 ± 1.20 | 19.39 ± 0.76 | 19.44 ± 0.86 | 19.29 ± 1.37 | 19.51 ± 1.39 | 19.62 ± 1.19 |
| smax (Out) Rest | 19.35 ±1.02 | 19.41 ± 0.97 | 19.27 ± 1.13 | 19.26 ± 0.88 | 19.23 ± 1.06 | 19.12 ± 1.57 | 19.36 ± 1.74 | 19.06 ± 1.13 |
| Paired t-test p | 0.9711 | 0.4547 | 0.8120 | 0.3085 | 0.2296 | 0.4963 | 0.5625 | 0.0047 |
| smax (In): ANOVA p (MF+FP/DMN × Task/Rest) | ||||||||
| MF+FP/DMN | 0.3751 | |||||||
| Task/Rest | 0.3413 | |||||||
| Interaction | 0.0009* | |||||||
Note: The eight networks are medial frontal (MF), frontoparietal (FP), default-mode (DMN), subcortical-cerebellum (SubCB), motor (Mot) and visual areas (Vis1-3). All smax values are mean ± standard deviation. p-values <0.05 are in bold
indicates values that survive Bonferroni correction for multiple comparisons.
3.3 Validation across different connectivity thresholds
In network analysis, patterns of connectivity as well as graph properties are affected by the choice of the connection strength threshold (Wang et al., 2011), and there is no trivial solution for the selection of a single optimal threshold (Bordier et al., 2017). Therefore, a common practice in comparing connectivities between groups or conditions involves the use of a range of thresholds (Bassett et al., 2008). Further, the use of percentiles ensured that the number of connections is the same across groups or conditions. To evaluate whether the results as presented in Table 2 were robust, we computed and compared the smax for different connectivity thresholds, ranging from 80% to 99% (i.e., less to more sparse networks). Figure 4 shows the smax during rest and task as well as the statistics for different thresholds. Average peak time scales smax were consistently higher in the DMN than in the MF and FP networks during rest as compared to task, across thresholds. Variability of the smax estimates increased significantly at greater than 95%.
Figure 4.
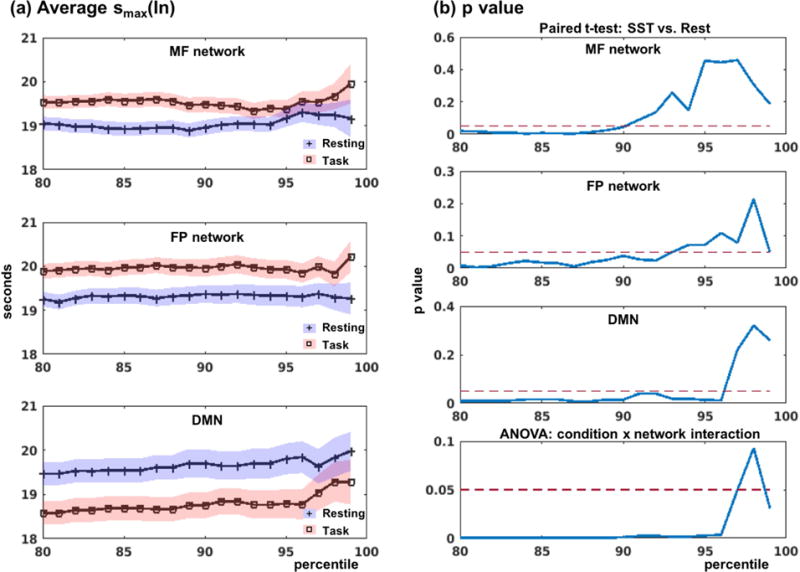
Comparison of peak time scales of within network connectivity or smax(In). (a) Average smax for resting and task conditions within MF, FP and DMN. Blue and red shades represent the standard error of the mean for resting and task conditions, respectively. (b) Paired t-test (task vs. rest) results for each network, and the interaction effects (two-way ANOVA: task vs. rest × MF+FP vs. DMN).
3.4 Connectivity and task performance
As shown earlier, within-network (In) connectivity of the SubCB network and between-network (Out) connectivity of the FP network increased in DPCCAmax during the stop signal task as compared to rest (paired t-test, p=8.5e-08 and p=2.8e-04, respectively). Additionally, the task networks (FP+MF) increased in smax(In) during the task, as compared to the DMN during the rest (ANOVA, interaction effect, p=0.0009). These differences were significant at a corrected threshold. On the other hand, none of the DPCCAmax or smax of the MF, FP, DMN or SubCB within- or between-network connectivities were correlated with BIS score or SSRT at a corrected threshold.
To further investigate whether connectivity strength or time scale may be associated with task performance, we focused on the pre-supplementary motor area (preSMA, Figure 5a), a MF network structure widely implicated in impulse control (Duann et al., 2009; Hu et al., 2015). We computed the DPCCAmax and smax averaged across 6 nodes within the preSMA and cross-correlated the connectivity measures with impulsivity (total BIS score) and stop signal reaction time (SSRT). Neither impulsivity nor response inhibition correlated with DPCCAmax(In) (p’s > 0.8) but both correlated negatively with smax(In) (Figure 5b and 5c).
Figure 5.
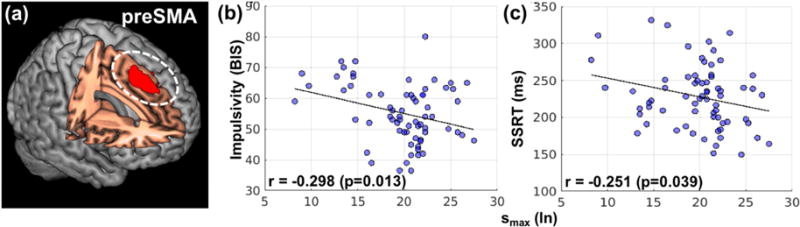
Association between task performance and the connectivity of the pre-supplementary motor area (preSMA). (a) Cluster of the preSMA as identified from a recent work on proactive control and response inhibition (Hu et al., 2015). (b, c) Increased time scale of “within- preSMA” connectivity is associated with decreased impulsivity and improved inhibition performance (decreased SSRT).
3.5 Head motion and functional connectivity
Consistent with a recent work (Huijbers et al., 2017), we also observed increased head motion during resting-state as compared to task performance. Both FD and DVARS were increased during rest as compared to task conditions: FD = 0.177±0.091 vs. 0.140±0.061; DVARS = 0.221±0.051 vs. 0.210±0.039 (paired t-test: p=2.5e-07 and p=0.018, respectively). Therefore, we examined for potential association between these movement metrics and the connectivity measures DPCCAmax and smax for each one of the eight networks. None of the DPCCAmax(Out) and DPCCAmax(In) were correlated with FD or DVARS for the 8 networks (all p’s > 0.08). Importantly, among the three networks (MF, FP and DMN) with significant differences in smax(In) (Table 2), there were no correlations between FD/DVARS and smax(In) (all p’s > 0.10), suggesting that it was unlikely that the connectivity differences resulted from head motion. Further, we included FD and DVARS as covariates in a covariance analysis and confirmed that the interaction effect MF+FP/DMN × Task/Rest of smax(In) remained significant (p<0.0048).
4. Discussion
4.1 Connectivity strength and time scale: Rest versus task
The connection strength (DPCCAmax) within the SubCB network and out of the MF, FP and Vis3 networks were increased during task as compared to rest (Table 1), broadly consistent with our previous reports of co-activation and connectivity of these networks during response inhibition (Li et al., 2006; Li et al., 2008a; Duann et al., 2009), error detection (Li et al., 2008c; Hendrick et al., 2010), and post-error slowing (Li et al., 2008b; Ide and Li, 2011a; Ide and Li, 2011b). For instance, the SubCB network comprises the cerebellum and caudate, both responding to response inhibition (Li et al., 2008a), as well as the thalamus and brain stem, forming a cortical-pontine-cerebellar-thalamic circuit to support post-error behavioral adjustment in the SST (Ide and Li, 2011a).
The connectivity time scale smax(In) of the DMN was higher during rest as compared to task, whereas the smax(In) of task networks (MF+FP) was higher during task as compared to rest (Table 2). This interaction was strong (ANOVA, p=0.0009), indicating longer-range (increased time scale or more sustained) functional connections within the DMN regions during rest and within the MF+FP regions during task. Higher connectivity time scale within the DMN during rest as compared to task supports the observation that the DMN manifests predominantly for low-frequency BOLD fluctuations (Greicius et al., 2009). Higher connectivity time scale within the MF and FP networks during task as compared to rest highlights low-frequency task network connections (“spontaneous” activity) that may conduce to task performance. These results are consistent with previous report of increased within-network connectivity of the DMN and FP network each for lower and higher frequencies during rest (Thompson and Fransson, 2015). In an earlier fMRI study with participants performing a button-press paradigm intermixed with resting periods, left and right motor cortices synchronized activities both during rest and task, in association with inter-trial variability in button press strength (Fox et al., 2007). Authors suggested that spontaneous low-frequency fluctuations during rest reflect synchronized neuronal activity that persists during task performance. In a more recent study, using held-out regions and individuals, activity or information flow (spread of activation amplitudes between brain locations) (Laughlin and Sejnowski, 2003) of functional connectivity maps during rest successfully predicted average activations during seven different cognitive tasks (Cole et al., 2016). The current findings add to this literature by associating task exposure with longer connectivity time scale within task networks.
Notably, the MF and FP increased in strength for between-network or Out connectivity, but increased in time scales for within-network or In connectivity, during task as compared to rest. In contrast, for the DMN, increased strength of Out connectivity was accompanied by decreased time scale of In connectivity, during task as compared to rest. Thus, the DMN showed longer-lasting within-network connectivity during rest, but stronger between-network connectivity during task performance, in support of engagement of the DMN in task execution via connection with task networks. For instance, the connectivity of the posterior cingulate cortex (PCC) with the left superior frontal gyrus increased, in link with faster reaction times, during finger movement, as compared to rest (Vatansever et al., 2015). The concurrent changes of task networks and DMN perhaps reflect more efficient global information transmission and systems integration to support task performance (Di et al., 2013). The current finding thus add to this literature by elucidating the connectivity time scales of the DMN and task networks under task challenges. More studies are needed to examine whether the opposing patterns in connectivity time scales of the DMN and task networks applies to other behavioral conditions and reflects a general organizing principle of functional connectivity. Likewise, whether persistent (lower frequency) within-network connectivity is related to increased brain activity as measured by BOLD signals remains to be confirmed in future work.
4.2 Connectivity time scale: association with behavior
By examining the smax specifically of the presupplementary motor area (preSMA), we showed that longer connectivity time scale within this medial prefrontal cortical structure is associated with better impulse control, as reflected in lower BIS score and shorter SSRT. That is, the low-frequency connections within the preSMA support proactive inhibitory control and related behavioral trait of the individuals (Krieghoff et al., 2009; Criaud and Boulinguez, 2013; Rae et al., 2014; Ritterband-Rosenbaum et al., 2014). As the preSMA increases in BOLD signals in response to proactive control (Hu et al., 2015), this finding suggested a relationship between within-network connectivity time scale and BOLD signal strength in regional responses. Many clinical conditions implicate dysfunctional impulse control and impulsivity represents a target for behavioral and pharmacological therapy (Friederich et al., 2013; Jahanshahi et al., 2015). Thus, the current findings may shed new light on a neural process of impulse control disorder (Yu et al., 2015).
4.3 Methodological considerations and limitations
One needs to consider whether the current findings simply reflect the temporal profiles of the task events in the SST. Frequency characteristics of the task data are unlikely to be influenced or biased by the frequency characteristics of the task paradigm because of two reasons. First, the average connectivity peak time scale is higher for task than resting conditions in the task-related networks (MF: 19.49/FP: 19.96 vs. MF: 18.96/FP: 19.37, respectively, Table 2), whereas the trial duration averaged at 5.7 s in the SST, suggesting that it is highly unlikely that the temporal profiles of task events biased the peak time scale toward the upper frequency range. Second, stimuli are randomly generated in the SST, ruling out the possibility of a systematic influence on a particular frequency. An additional issue concerns whether the co-activation patterns in the task data can really be considered connectivity as opposed to co-activation. Although one cannot completely exclude the possibility of interaction between co-activation patterns and functional connectivity, the following consideration suggests that these are distinct neural processes. In the SST, on average 75% of the trials were go success (GS) trials and thus the co-activation of the “GS regions” occurred with an average period of 7.6 s, which would drive the peak time scale to the lower frequency end. On the other hand, we did not observe any differences in peak time for the motor network between task and rest conditions (Table 2). Thus, co-activation is likely not systematically driving the peak time scale of functional connectivity.
Unlike coherence connectivity methods (Sun et al., 2004; Yaesoubi et al., 2015), DPCCA quantifies the frequency characteristics at a discrete resolution of 2 s, whereas with coherence methods, one would be able to precisely define the characteristic frequency within a continuous range. Additionally, coherence methods provide phase information of functional connectivity, thus quantifying the time delay of interaction among brain regions. The impact of these analytical features on functional connectivity metrics remain to be clarified.
Brain network analysis suggested that topological graph properties are dependent on the threshold used to generate the connectivity matrix, presenting a critical issue in comparison between groups or conditions (van Wijk et al., 2010; van den Heuvel et al., 2017). On the other hand, studies have documented the reproducibility of graph properties across different thresholds (Telesford et al., 2010; Telesford et al., 2013). Here, we showed that the differences in time scale smax between rest and task were significant across a large range of connectivity thresholds (Figure 4).
Further, recent work highlighted the dynamic nature of functional connectivity (Hutchison et al., 2013b; Calhoun et al., 2014; Preti et al., 2016; Shine et al., 2016; Bassett and Sporns, 2017). Although we did not consider the dynamics of connectivity, this could be addressed by examining the temporal evolution of DPCCA (TDCCA), where the evolution of partial correlations is estimated on multiple time scales (Yuan et al., 2016).
4.4 Conclusions
In summary, using DPCCA, we characterize the time scale of brain network interactions during rest and the stop signal task. We showed that the connectivities were of longer time scale within the task networks during task performance as compared to rest. In contrast, connectivity occurred at longer time scale within the default mode network during rest as compared to task. Longer time scales of within-network connectivity of a task region were associated with better inhibition performance and decreased impulsivity, in support of a role of low frequency fluctuations of BOLD signals in behavioral control. These findings suggest the importance of examining transient versus sustained interaction between network regions in unraveling brain function.
Acknowledgments
This study is supported by NIH grants DA023248 and DA026990 and NSF grant BCS1309260. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We have disclosed all research support and do not have conflicts of interest in the current work.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Achard S, Bassett DS, Meyer-Lindenberg A, Bullmore E. Fractal connectivity of long-memory networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;77:036104. doi: 10.1103/PhysRevE.77.036104. [DOI] [PubMed] [Google Scholar]
- Andersson JL, Hutton C, Ashburner J, Turner R, Friston K. Modeling geometric deformations in EPI time series. Neuroimage. 2001;13:903–919. doi: 10.1006/nimg.2001.0746. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Sporns O. Network neuroscience. Nat Neurosci. 2017;20:353–364. doi: 10.1038/nn.4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, Meyer-Lindenberg A. Hierarchical organization of human cortical networks in health and schizophrenia. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2008;28:9239–9248. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bordier C, Nicolini C, Bifone A. Graph Analysis and Modularity of Brain Functional Connectivity Networks: Searching for the Optimal Threshold. Frontiers in neuroscience. 2017;11:441. doi: 10.3389/fnins.2017.00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Krienen FM, Castellanos A, Diaz JC, Yeo BT. The organization of the human cerebellum estimated by intrinsic functional connectivity. Journal of neurophysiology. 2011;106:2322–2345. doi: 10.1152/jn.00339.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Miller R, Pearlson G, Adali T. The chronnectome: time-varying connectivity networks as the next frontier in fMRI data discovery. Neuron. 2014;84:262–274. doi: 10.1016/j.neuron.2014.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chai XJ, Castanon AN, Ongur D, Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. Neuroimage. 2012;59:1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage. 2010;50:81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Ito T, Bassett DS, Schultz DH. Activity flow over resting-state networks shapes cognitive task activations. Nat Neurosci. 2016;19:1718–1726. doi: 10.1038/nn.4406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Criaud M, Boulinguez P. Have we been asking the right questions when assessing response inhibition in go/no-go tasks with fMRI? A meta-analysis and critical review. Neurosci Biobehav Rev. 2013;37:11–23. doi: 10.1016/j.neubiorev.2012.11.003. [DOI] [PubMed] [Google Scholar]
- Di X, Gohel S, Kim EH, Biswal BB. Task vs. rest-different network configurations between the coactivation and the resting-state brain networks. Front Hum Neurosci. 2013;7:493. doi: 10.3389/fnhum.2013.00493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duann JR, Ide JS, Luo X, Li CS. Functional connectivity delineates distinct roles of the inferior frontal cortex and presupplementary motor area in stop signal inhibition. J Neurosci. 2009;29:10171–10179. doi: 10.1523/JNEUROSCI.1300-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Schlaggar BL, Cohen AL, Miezin FM, Dosenbach NU, Wenger KK, Fox MD, Snyder AZ, Raichle ME, Petersen SE. A method for using blocked and event-related fMRI data to study “resting state” functional connectivity. Neuroimage. 2007;35:396–405. doi: 10.1016/j.neuroimage.2006.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farr OM, Hu S, Zhang S, Li CS. Decreased saliency processing as a neural measure of Barratt impulsivity in healthy adults. Neuroimage. 2012;63:1070–1077. doi: 10.1016/j.neuroimage.2012.07.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci. 2015;18:1664–1671. doi: 10.1038/nn.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- First M, Spitzer R, Williams J, Gibbon M. Structured Clinical Interview for DSM-IV (SCID) Washington DC: American Psychiatric Association; 1995. [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Raichle ME. Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron. 2007;56:171–184. doi: 10.1016/j.neuron.2007.08.023. [DOI] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. Journal of neurophysiology. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friederich HC, Wu M, Simon JJ, Herzog W. Neurocircuit function in eating disorders. Int J Eat Disord. 2013;46:425–432. doi: 10.1002/eat.22099. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF. Resting-State Functional Connectivity Reflects Structural Connectivity in the Default Mode Network. Cerebral cortex. 2009;19:72–78. doi: 10.1093/cercor/bhn059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrick OM, Ide JS, Luo X, Li CS. Dissociable processes of cognitive control during error and non-error conflicts: a study of the stop signal task. PloS one. 2010;5:e13155. doi: 10.1371/journal.pone.0013155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindriks R, Adhikari MH, Murayama Y, Ganzetti M, Mantini D, Logothetis NK, Deco G. Can sliding-window correlations reveal dynamic functional connectivity in resting-state fMRI? Neuroimage. 2016;127:242–256. doi: 10.1016/j.neuroimage.2015.11.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu S, Tseng YC, Winkler AD, Li CS. Neural bases of individual variation in decision time. Hum Brain Mapp. 2014;35:2531–2542. doi: 10.1002/hbm.22347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu S, Ide JS, Zhang S, Li CS. Anticipating conflict: Neural correlates of a Bayesian belief and its motor consequence. Neuroimage. 2015;119:286–295. doi: 10.1016/j.neuroimage.2015.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huijbers W, Van Dijk KR, Boenniger MM, Stirnberg R, Breteler MM. Less head motion during MRI under task than resting-state conditions. Neuroimage. 2017;147:111–120. doi: 10.1016/j.neuroimage.2016.12.002. [DOI] [PubMed] [Google Scholar]
- Hutchison RM, Morton JB. Tracking the Brain’s Functional Coupling Dynamics over Development. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2015;35:6849–6859. doi: 10.1523/JNEUROSCI.4638-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS. Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp. 2013a;34:2154–2177. doi: 10.1002/hbm.22058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez-Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage. 2013b;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutton C, Bork A, Josephs O, Deichmann R, Ashburner J, Turner R. Image distortion correction in fMRI: A quantitative evaluation. Neuroimage. 2002;16:217–240. doi: 10.1006/nimg.2001.1054. [DOI] [PubMed] [Google Scholar]
- Ide JS, Li CS. A cerebellar thalamic cortical circuit for error-related cognitive control. NeuroImage. 2011a;54:455–464. doi: 10.1016/j.neuroimage.2010.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ide JS, Li CSR. Error-Related Functional Connectivity of the Habenula in Humans. Frontiers in Human Neuroscience. 2011b;5 doi: 10.3389/fnhum.2011.00025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ide JS, Cappabianco FA, Faria FA, Li CS-R. Neural Information Processing Systems (NIPS) Long Beach, CA: 2017. Detrended Partial Cross Correlation for Brain Connectivity Analysis. (in press) [Google Scholar]
- Jahanshahi M, Obeso I, Baunez C, Alegre M, Krack P. Parkinson’s disease, the subthalamic nucleus, inhibition, and impulsivity. Mov Disord. 2015;30:128–140. doi: 10.1002/mds.26049. [DOI] [PubMed] [Google Scholar]
- Jia H, Hu X, Deshpande G. Behavioral relevance of the dynamics of the functional brain connectome. Brain connectivity. 2014;4:741–759. doi: 10.1089/brain.2014.0300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalcher K, Boubela RN, Huf W, Bartova L, Kronnerwetter C, Derntl B, Pezawas L, Filzmoser P, Nasel C, Moser E, Margulies D. The Spectral Diversity of Resting-State Fluctuations in the Human Brain. PloS one. 2014;9 doi: 10.1371/journal.pone.0093375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantelhardt JW, Zschiegner SA, Koscielny-Bunde E, Havlin S, Bunde A, Stanley HE. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A. 2002;316:87–114. [Google Scholar]
- Keilholz SD, Magnuson ME, Pan WJ, Willis M, Thompson GJ. Dynamic properties of functional connectivity in the rodent. Brain connectivity. 2013;3:31–40. doi: 10.1089/brain.2012.0115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krieghoff V, Brass M, Prinz W, Waszak F. Dissociating what and when of intentional actions. Front Hum Neurosci. 2009;3:3. doi: 10.3389/neuro.09.003.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristoufek L. Measuring correlations between non-stationary series with DCCA coefficient. Physica A. 2014;402:291–298. [Google Scholar]
- Laughlin SB, Sejnowski TJ. Communication in neuronal networks. Science. 2003;301:1870–1874. doi: 10.1126/science.1089662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Van Quyen M, Bragin A. Analysis of dynamic brain oscillations: methodological advances. Trends Neurosci. 2007;30:365–373. doi: 10.1016/j.tins.2007.05.006. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49(Suppl 2):467. + [PubMed] [Google Scholar]
- Li CS, Huang C, Constable RT, Sinha R. Imaging response inhibition in a stop-signal task: neural correlates independent of signal monitoring and post-response processing. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2006;26:186–192. doi: 10.1523/JNEUROSCI.3741-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Yan P, Sinha R, Lee TW. Subcortical processes of motor response inhibition during a stop signal task. Neuroimage. 2008a;41:1352–1363. doi: 10.1016/j.neuroimage.2008.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Huang C, Yan P, Paliwal P, Constable RT, Sinha R. Neural correlates of post-error slowing during a stop signal task: a functional magnetic resonance imaging study. Journal of cognitive neuroscience. 2008b;20:1021–1029. doi: 10.1162/jocn.2008.20071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Yan P, Chao HH, Sinha R, Paliwal P, Constable RT, Zhang S, Lee TW. Error-specific medial cortical and subcortical activity during the stop signal task: a functional magnetic resonance imaging study. Neuroscience. 2008c;155:1142–1151. doi: 10.1016/j.neuroscience.2008.06.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Luo X, Sinha R, Rounsaville BJ, Carroll KM, Malison RT, Ding YS, Zhang S, Ide JS. Increased error-related thalamic activity during early compared to late cocaine abstinence. Drug Alcohol Depend. 2010;109:181–189. doi: 10.1016/j.drugalcdep.2010.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Z, King J, Zhang N. Anticorrelated resting-state functional connectivity in awake rat brain. Neuroimage. 2012;59:1190–1199. doi: 10.1016/j.neuroimage.2011.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logan GD. On the ability to inhibit thought and action: A user’s guide to the stop signal paradigm. In: Dagenbach D, Carr TH, editors. Inhibitory Processes in Attention, Memory and Language. San Diego: Academic Press; 1994. pp. 189–239. [Google Scholar]
- Logan GD, Cowan WB, Davis KA. On the ability to inhibit simple and choice reaction time responses: a model and a method. J Exp Psychol Hum Percept Perform. 1984;10:276–291. doi: 10.1037//0096-1523.10.2.276. [DOI] [PubMed] [Google Scholar]
- Madhyastha TM, Askren MK, Boord P, Grabowski TJ. Dynamic connectivity at rest predicts attention task performance. Brain connectivity. 2015;5:45–59. doi: 10.1089/brain.2014.0248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patton JH, Stanford MS, Barratt ES. Factor structure of the Barratt impulsiveness scale. J Clin Psychol. 1995;51:768–774. doi: 10.1002/1097-4679(199511)51:6<768::aid-jclp2270510607>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- Podobnik B, Stanley HE. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series. Phys Rev Lett. 2008;100:084102. doi: 10.1103/PhysRevLett.100.084102. [DOI] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preti MG, Bolton TA, Van De Ville D. The dynamic functional connectome: State-of-the-art and perspectives. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.12.061. [DOI] [PubMed] [Google Scholar]
- Qian L, Zhang Y, Zheng L, Shang Y, Gao JH, Liu Y. Frequency dependent topological patterns of resting-state brain networks. PloS one. 2015a;10:e0124681. doi: 10.1371/journal.pone.0124681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian XY, Liu YM, Jiang ZQ, Podobnik B, Zhou WX, Stanley HE. Detrended partial cross-correlation analysis of two nonstationary time series influenced by common external forces. Phys Rev E Stat Nonlin Soft Matter Phys. 2015b;91:062816. doi: 10.1103/PhysRevE.91.062816. [DOI] [PubMed] [Google Scholar]
- Rae CL, Hughes LE, Weaver C, Anderson MC, Rowe JB. Selection and stopping in voluntary action: a meta-analysis and combined fMRI study. Neuroimage. 2014;86:381–391. doi: 10.1016/j.neuroimage.2013.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci U S A. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritterband-Rosenbaum A, Karabanov AN, Christensen MS, Nielsen JB. 10 Hz rTMS over right parietal cortex alters sense of agency during self-controlled movements. Front Hum Neurosci. 2014;8:471. doi: 10.3389/fnhum.2014.00471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach BJ, Mathalon DH. Event-related EEG time-frequency analysis: an overview of measures and an analysis of early gamma band phase locking in schizophrenia. Schizophr Bull. 2008;34:907–926. doi: 10.1093/schbul/sbn093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rombouts SA, Stam CJ, Kuijer JP, Scheltens P, Barkhof F. Identifying confounds to increase specificity during a “no task condition”. Evidence for hippocampal connectivity using fMRI. Neuroimage. 2003;20:1236–1245. doi: 10.1016/S1053-8119(03)00386-0. [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci. 2005;360:937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Tokoglu F, Papademetris X, Constable RT. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage. 2013;82:403–415. doi: 10.1016/j.neuroimage.2013.05.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shine JM, Bissett PG, Bell PT, Koyejo O, Balsters JH, Gorgolewski KJ, Moodie CA, Poldrack RA. The Dynamics of Functional Brain Networks: Integrated Network States during Cognitive Task Performance. Neuron. 2016;92:544–554. doi: 10.1016/j.neuron.2016.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. Network modelling methods for FMRI. Neuroimage. 2011;54:875–891. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. Proc Natl Acad Sci U S A. 2009;106:13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyser CD, Inder TE, Shimony JS, Hill JE, Degnan AJ, Snyder AZ, Neil JJ. Longitudinal analysis of neural network development in preterm infants. Cerebral cortex. 2010;20:2852–2862. doi: 10.1093/cercor/bhq035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun FT, Miller LM, D’Esposito M. Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage. 2004;21:647–658. doi: 10.1016/j.neuroimage.2003.09.056. [DOI] [PubMed] [Google Scholar]
- Telesford QK, Burdette JH, Laurienti PJ. An exploration of graph metric reproducibility in complex brain networks. Frontiers in neuroscience. 2013;7:67. doi: 10.3389/fnins.2013.00067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telesford QK, Morgan AR, Hayasaka S, Simpson SL, Barret W, Kraft RA, Mozolic JL, Laurienti PJ. Reproducibility of graph metrics in FMRI networks. Front Neuroinform. 2010;4:117. doi: 10.3389/fninf.2010.00117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson WH, Fransson P. The frequency dimension of fMRI dynamic connectivity: Network connectivity, functional hubs and integration in the resting brain. Neuroimage. 2015;121:227–242. doi: 10.1016/j.neuroimage.2015.07.022. [DOI] [PubMed] [Google Scholar]
- Tomasi D, Volkow ND. Functional Connectivity of Substantia Nigra and Ventral Tegmental Area: Maturation During Adolescence and Effects of ADHD. Cerebral cortex. 2012 doi: 10.1093/cercor/bhs382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrence C, Compo GP. A practical guide to wavelet analysis. B Am Meteorol Soc. 1998;79:61–78. [Google Scholar]
- van den Heuvel MP, de Lange SC, Zalesky A, Seguin C, Yeo BTT, Schmidt R. Proportional thresholding in resting-state fMRI functional connectivity networks and consequences for patient-control connectome studies: Issues and recommendations. Neuroimage. 2017;152:437–449. doi: 10.1016/j.neuroimage.2017.02.005. [DOI] [PubMed] [Google Scholar]
- Van Dijk KR, Sabuncu MR, Buckner RL. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wijk BC, Stam CJ, Daffertshofer A. Comparing brain networks of different size and connectivity density using graph theory. PloS one. 2010;5:e13701. doi: 10.1371/journal.pone.0013701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vatansever D, Menon DK, Manktelow AE, Sahakian BJ, Stamatakis EA. Default mode network connectivity during task execution. Neuroimage. 2015;122:96–104. doi: 10.1016/j.neuroimage.2015.07.053. [DOI] [PubMed] [Google Scholar]
- Wang JH, Zuo XN, Gohel S, Milham MP, Biswal BB, He Y. Graph theoretical analysis of functional brain networks: test-retest evaluation on short- and long-term resting-state functional MRI data. PloS one. 2011;6:e21976. doi: 10.1371/journal.pone.0021976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weidacker K, Snowden RJ, Boy F, Johnston SJ. Response inhibition in the parametric Go/No-Go task in psychopathic offenders. Psychiatry research. 2017;250:256–263. doi: 10.1016/j.psychres.2017.01.083. [DOI] [PubMed] [Google Scholar]
- Wetherill GB, Chen H, Vasudeva RB. Sequential estimation of quantal response curves: A new method of estimation. Biometrika. 1966;53:439–454. [Google Scholar]
- Winkler AD, Hu S, Li CS. The influence of risky and conservative mental sets on cerebral activations of cognitive control. International journal of psychophysiology: official journal of the International Organization of Psychophysiology. 2012 doi: 10.1016/j.ijpsycho.2012.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaesoubi M, Allen EA, Miller RL, Calhoun VD. Dynamic coherence analysis of resting fMRI data to jointly capture state-based phase, frequency, and time-domain information. Neuroimage. 2015;120:133–142. doi: 10.1016/j.neuroimage.2015.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zollei L, Polimeni JR, Fischl B, Liu H, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of neurophysiology. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You WS, Achard S, Stadler J, Bruckner B, Seiffert U. Fractal analysis of resting state functional connectivity of the brain. Ieee Ijcnn 2012 [Google Scholar]
- Yu J, Tseng P, Hung DL, Wu SW, Juan CH. Brain stimulation improves cognitive control by modulating medial-frontal activity and preSMA-vmPFC functional connectivity. Human brain mapping. 2015;36:4004–4015. doi: 10.1002/hbm.22893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan N, Xoplaki E, Zhu C, Luterbacher J. A novel way to detect correlations on multi-time scales, with temporal evolution and for multi-variables. Sci Rep. 2016;6:27707. doi: 10.1038/srep27707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan N, Fu Z, Zhang H, Piao L, Xoplaki E, Luterbacher J. Detrended partial-cross-correlation analysis: a new method for analyzing correlations in complex system. Scientific reports. 2015;5:8143. doi: 10.1038/srep08143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Raichle ME. Disease and the brain’s dark energy. Nat Rev Neurol. 2010;6:15–28. doi: 10.1038/nrneurol.2009.198. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Telesford QK, Giusti C, Lim KO, Bassett DS. Choosing Wavelet Methods, Filters, and Lengths for Functional Brain Network Construction. PloS one. 2016;11:e0157243. doi: 10.1371/journal.pone.0157243. [DOI] [PMC free article] [PubMed] [Google Scholar]


