Dynamic fMRI Networks Predict Success in a Behavioral Weight Loss Program among Older Adults

Abstract

More than one-third of adults in the United States are obese, with a higher prevalence among older adults. Obesity among older adults is a major cause of physical dysfunction, hypertension, diabetes, and coronary heart diseases. Many people who engage in lifestyle weight loss interventions fail to reach targeted goals for weight loss, and most will regain what was lost within 1–2 years following cessation of treatment. This variability in treatment efficacy suggests that there are important phenotypes predictive of success with intentional weight loss that could lead to tailored treatment regimen, an idea that is consistent with the concept of precision-based medicine. Although the identification of biochemical and metabolic phenotypes are one potential direction of research, neurobiological measures may prove useful as substantial behavioral change is necessary to achieve success in a lifestyle intervention. In the present study, we use dynamic brain networks from functional magnetic resonance imaging (fMRI) data to prospectively identify individuals most likely to succeed in a behavioral weight loss intervention. Brain imaging was performed in overweight or obese older adults (age: 65–79 years) who participated in an 18-month lifestyle weight loss intervention. Machine learning and functional brain networks were combined to produce multivariate prediction models. The prediction accuracy exceeded 95%, suggesting that there exists a consistent pattern of connectivity which correctly predicts success with weight loss at the individual level. Connectivity patterns that contributed to the prediction consisted of complex multivariate network components that substantially overlapped with known brain networks that are associated with behavior emergence, self-regulation, body awareness, and the sensory features of food. Future work on independent datasets and diverse populations is needed to corroborate our findings. Additionally, we believe that efforts can begin to examine whether these models have clinical utility in tailoring treatment.

1. Introduction

Obesity and its adverse health effects are highly prevalent and uniquely problematic among older adults (65+ years) (Flegal et al., 2012). Obesity is associated with declines in physical functioning, the primary driver of disability and loss of independence with aging (Mathus-Vliegen et al., 2012). Unfortunately, although effective lifestyle weight loss interventions in overweight and obese adults produce mean weight loss in the range of 5–10% of baseline weight (Rejeski et al., 2011), there is considerable variability in how much people lose (Curioni and Lourenco, 2005; MacLean et al., 2011). In fact, understanding potential phenotypes for success in behavioral weight loss has been identified as a critical area for research by the National Institutes of Health (http://1.usa.gov/1VCI7pA). In the present study, we used baseline (pre-intervention) functional magnetic resonance imaging (fMRI) dynamic networks as a biomarker to identify those older adults that exhibited the greatest success in an 18-month behavioral weight loss intervention.

Although knowledge about nutrition and physical activity is essential to behavioral weight loss, arguably more important are the self-regulatory skills and motivation required to enact needed behavior change (Rejeski et al., 2008; Wing, 2002). Consistent with this perspective are studies showing that high self-efficacy for regulating eating behavior, the ability to manage stress, and motivation to lose weight are positively associated with better initial weight loss and weight maintenance (Elfhag and Rössner, 2005; Williams et al., 1996). More relevant to the current study are data showing that brain activity in neural networks including the hippocampus/amygdala, dorsal striatum, orbitofrontal, prefrontal and anterior cingulate cortices has been shown to be important in overeating and food craving (Berridge et al., 2010; Rothemund et al., 2007; Stice et al., 2013). Specific to behavioral weight loss treatment, we have observed that following an overnight fast, global connectivity of hubs located in the insula, superior temporal pole, limbic regions, and anterior cingulate cortex (ACC) during pre-intervention resting state fMRI (rs-fMRI) was correlated with weight loss 18-months later (Paolini et al., 2015).

Despite the growing emphasis on complex brain networks in the neuroscience literature (Bullmore and Sporns, 2009), most weight loss studies have focused on specific brain regions (Stice et al., 2013; Volkow et al., 2011) rather than integrated networks. However, we would argue that multiple regions of the brain are involved in eating behavior, and that these regions interact in complex patterns with one another. Moreover, there has recently been growing interest in quantifying dynamic brain connections (Hutchison et al., 2013) rather than relying on measures of static connectivity, as brain networks intrinsically change over time due to varying physiological states (Barnes et al., 2009; Deshpande et al., 2006), even in a task-free environment (Chang and Glover, 2010). Thus, we believe it is vital that studies examine whole-brain dynamic networks (Allen et al., 2014; Hutchison et al., 2013), to understand how interacting brain areas contribute to obesity and weight loss.

In contrast to univariate statistical methods commonly used when examining region-based group differences in fMRI data, multivariate machine learning classification algorithms aim to discover a multivariate discriminatory pattern between groups. The machine learning algorithms are first trained with a subset of the data or with a specific training dataset. Once trained, these algorithms are used to predict an outcome or to classify test individuals (Mokhtari et al., 2016; Richiardi et al., 2013; Shahnazian et al., 2012). Multivariate pattern analysis is potentially capable of capturing complex interactions of distant brain sites that is not possible using pairwise connectivity analysis (Richiardi et al., 2013). This methodology allows for single-subject analyses where each participant can be classified rather than group-level summary outcomes such as brain maps of population differences.

The current study aimed to discover multivariate brain connectivity patterns in overweight/obese older adults following an overnight fast that might predict success with a behavioral weight loss intervention. We studied participants in a fasted state because food restraint is a contributing factor to failure with self-regulation of eating behavior (Fedoroff et al., 2003; Fedoroff et al., 1997; Polivy et al., 2005), and variability in body weight (Heatherton et al., 1991). The ability to self-regulate caloric intake is central to intentional weight loss interventions. We believe that deficits in self-regulation are apparent in both automatic and control-based brain networks. We performed a prospective study in which baseline fMRI, baseline weight, and the weight following an 18-month lifestyle intervention were recorded. Here, we brought together dynamic brain networks and classification models for prospectively predicting the weight loss success of older adults who were overweight or obese, and had a documented history of cardiometabolic dysfunction. Given that multivariate prediction models can be used to perform treatment outcome predictions at the individual level, this study could help to provide critical groundwork to personalize weight loss interventions for patients based on individual brain networks.

2. Material and methods

2.1. Participants

Data collection for this study was completed in 2013. A sample of 66 individuals (ages: 60–79 years) were recruited as an ancillary study to the Cooperative Lifestyle Intervention Program-II (CLIP-II) trial (Marsh et al., 2013). Participants were required to be either overweight or obese (BMI ≥ 28 kg/m² but < 42 kg/m²). Additional inclusion criteria involved having a documented history of either cardiovascular disease (CVD) or metabolic syndrome (MetS), low level of physical activity (less than 60 minutes of moderate physical activity per week), and mobility disability (having difficulty to complete daily physical tasks). All participants signed an informed consent/HIPAA authorization form. The study protocol was approved by the Wake Forest University School of Medicine institutional review board (IRB).

Major exclusion criteria included having a binge eating disorder, high alcoholic intake, a resting blood pressure > 160/100mmHg, a fasting blood glucose ≥ 140mg/dL, diagnosis of type 1 or type 2 diabetes and insulin therapy, significant visual or hearing impairments, sever systemic diseases (for instance diagnosis of Parkinson’s disease, and chronic liver disease), or abnormal health conditions which disable individuals to successfully complete the required study protocol.

Of 66 participants, 2 individuals did not meet eligibility to be randomized in the trial, 2 individuals withdrew from the study because of claustrophobia during magnetic resonance imaging (MRI), and 4 participants withdrew during the first 6-months of intervention for health reasons. Six additional individuals withdrew from the study after the 6-month intensive phase of intervention. Thus, a final sample size of 52 participants (female: 39, male: 13, mean age: 67.62) was used in this analysis. For greater details regarding the data used in this study, refer to (Marsh et al., 2013; Rejeski et al., 2017).

2.2. Lifestyle interventions

The CLIP II trial was designed with three different 18-month lifestyle weight loss interventions, including a diet only weight loss condition (WL), WL plus aerobic exercise training (WL+AT), or WL plus resistance exercise training (WL+RT). Participants were required to complete three 6-month phases during the intervention: 1) intensive (months 1–6), 2) transition (months 7–12), and 3) maintenance (months 13–18) phases. Participants were instructed to regulate their food intake, so that the rate of weekly weight loss was approximately 0.3 kg, and eventually after completing the intervention BMI to be decreased 7–10%. The goals of the transition phase varied between subjects based on intensive phase performance. During the maintenance phase, the major focus was on maintaining the weight loss that has been achieved. Participants assigned to the WL+AT group were required to walk on an indoor cushioned track at the YMCA. The intensity of walking was moderate, 4 days/week, with the goal toward 45 minutes/session. Participants were encouraged to walk at home as well. Participants assigned to the WL+RT intervention were required to perform strength training exercises 4 days/week. Participants completed 3 sets of 10–12 repetitions on 8 machines with initial resistance determined from 1 repetition maximum (RM) testing (Goal of 75% of 1RM). For greater details, refer to (Marsh et al., 2013; Rejeski et al., 2017).

2.3. MRI scanning protocol

MRI data was collected using a Siemens MAGNETOM SKYRA 3T MRI Scanner with Tim + Dot Technology. Participants were required to undergo an overnight fast, and were only allowed to consume water after midnight. The scans occurred in the early morning (between 8 am and 11 am) following the overnight fast. Each individual participated in a scanning session which included anatomical imaging, two rs-fMRI series, and a food visualization fMRI series between the two rs-fMRI, with each series consisting of 157 images. During the rs-fMRI, participants were instructed to relax, not think of anything particular and view a cross sign on the rear projection screen. The food visualization task was designed as alternatively representing four of each participant’s favorite food words on an MR-compatible rear projection screen; each word for 30 s. Participants were instructed to imagine the food with all five senses for the entire time that the food word was on the screen. For the current study, only the first resting state and the food visualization fMRI scans were examined. T1 structural images were acquired in the sagittal plane using a single-shot 3D MPRAGE GRAPPA2 sequence (TR = 2.3 s, TE = 2.9 ms, TI= 900 ms, flip angle = 9°, resolution = 1 × 1 × 1 mm). Functional BOLD imaging or T2*-weighted imaging were performed using a single-shot echo-planar imaging sequence (TR = 2.0 s, TE = 25ms, flip angle = 75, resolution = 3.5×3.5×5.0 mm).

2.4. Image processing

Statistical parametric mapping 12 (SPM12) software and advanced normalization tools (ANTS) were used to preprocess images. The SPM12 segmentation was used to parcellate the T1 images to gray matter, white matter, cerebrospinal fluid (CSF), bone, soft tissue, and air/background. High dimensional image warping was performed using ANTS symmetric diffeomorphic normalization (Avants et al., 2011), to obtain the deformation transformation map from the native space of each subject to Colin27 average brain template (Holmes et al., 1998).

The first 10 images of functional scans were discarded to assure fMRI signal equilibration. This resulted in fMRI time series with 147 time points. Functional scans were slice-time corrected, and then realigned to the first volume. Functional scans of each study participant were coregisterd with the same participant’s T1 structural data, to assure that they were aligned. The resulting fMRI time series were then band-pass filtered (0.009–0.08 Hz) to filter out physiological noise and low-frequency drifts (Biswal et al., 1995). Finally, confounding signals, including 6 rigid-body transformation parameters generated through the realignment process and 3 mean tissue signals (whole-brain, white matter, and CSF) were regressed out of the functional data. The mask of segmented tissues, created by SPM12 segmentation, was used to extract the mean tissue signals from fMRI data.

The inverse of the deformation field resulting from ANTS registration was applied to transform a functional brain atlas (Shen et al., 2013) to each subject’s native brain space. Unlike anatomical brain atlases which may integrate functionally different areas into one region (Tzourio-Mazoyer et al., 2002), the functional atlas used in the present study parcellates brain into finer functionally distinct unites; 268 regions versus 90 regions of automated anatomical labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002). Finally, the resulting atlas in the native space of each study participant was used to extract the mean time series of each region for that individual. It is noteworthy that networks were created and analyzed in native space to limit manipulation and interpolation of the fMRI time series.

2.5. Functional network creation

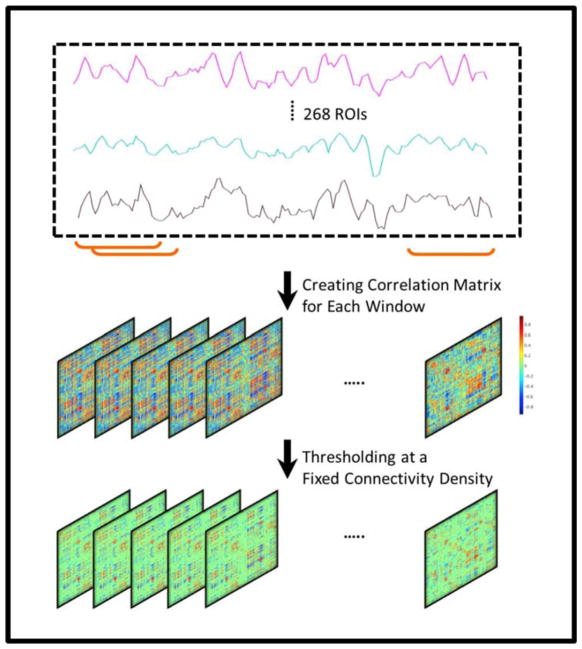
In this study, we used the sliding window technique to account for dynamic alterations associated with functional brain connectivity (Allen et al., 2014). For the sliding window method, a time window of fixed length W was selected and time points within that window were used to compute pairwise Pearson correlation coefficients. The window was then moved across the time and a matrix of correlation coefficients was computed for each shift. For each subject, connectivity data was then represented by a 3^rd-order tensor ℭ ∈ ℝ^N×N×T, where the first and second modes were connectivity and the third mode was time. Here, N = 268 was the number of regions of interest (ROIs), and T = T′ − W + 1, with T′ = 147, was the length of the preprocessed time series. For instance, the entry 𝔠_ijt, i, j ∈ {1, …, N}, t ∈ {1, 2, …, T} of the tensor ℭ denoted the functional connectivity between regions O_i and O_j at time window t. No self-connections was allowed.

We varied the window size from 61TRs to 101TRs in increments of 10TRs (where TR = 2 seconds), to capture dynamic changes of functional connectivity in different frequency ranges, and examine sensitivity of the prediction model to the window size alterations. In order to prevent adding the spurious fluctuations associated with intrinsic changes of fMRI time series to the dynamic connectivity computations, the window size should be greater than 1/f_min (Leonardi and Van De Ville, 2015), where f_min is the lowest frequency of the fMRI time series. As mentioned above, the time series were band-pass filtered at 0.009–0.08 Hz. Thus, in our study the minimum length of window size could be 56 time points (or equivalently 56TRs). To assure passing the lowest value for the window size, the lower limit for window size search range was set at 61 time points. Moreover, the odd length of the window allowed centered sliding window analysis, as it used a symmetric window at each time point. On the other hand, as the window size increases, the dynamic connectivity estimation approaches the static connectivity. Therefore, we limited the search range with the upper bound of 101 time points. To maintain the highest possible temporal resolution, the shift size was set at 1TR throughout the analysis.

To reduce the computational burden, as well as to generate sparse networks with the strong connections retained, the magnitude of correlation tensor was thresholded. It has been shown (Garrison et al., 2015) that proportional threshodling strategies (e.g. consistent connectivity density) provide more stable network measures compared with absolute thresholding methods (e.g. statistical significance criterion indicated with p-value < 0.05). Thus, in this study, the connectivity tensors were thresholded such that a certain percentage of the high-strength connections was preserved for each subject at each time window. The sign of connections was preserved in the thresholded connectivity tensor. After thresholding, the resulting networks were checked for the fragmentation into multiple subnetworks, and no fragmented network was observed throughout our analysis. To examine the prediction performance consistency versus connectivity density threshold, a density range of 10–30% with increments of 5% was examined. Fig. 1 shows a schematic representation of dynamic connectivity tensor creation.

Fig. 1.

Dynamic connectivity tensor creation procedure using sliding window technique, for which a window of fixed length is used to split the fMRI time series. For each split, a connectivity matrix is then constructed using pairwise Pearson correlation analysis. By concatenating the resulting matrices, a 3^rd-order connectivity tensor is created for each participant. A thresholding value is chosen to remove weak connections, such that for each individual and at each time window a fixed percentage (e.g. 10%) of the total connections is maintained.

2.6. Connectivity tensor rank reduction using HOSVD

Each connection of the resulting brain network can be considered as a feature or equivalently an axis of the feature space that could contribute to distinguishing study populations. In the current study, the brain networks with 268 nodes have a potential of over 35,000 connections that could serve as features. To avoid including noisy contents which potentially results in low generalization power of the prediction model, the feature space dimension, or rank of the connectivity network data was reduced prior to being used in the multivariate model.

For the cases where datasets are represented with matrices (2^nd-order tensors), one popular technique is to perform singular value decomposition (SVD) to obtain a summarized presentation of the data, and mitigating the high dimensionality issue (Klema and Laub, 1980; Leonardi et al., 2013). As mentioned above, each feature is represented by an axis/dimension in the feature space; SVD identifies combined features (new axes) as a linear combination of the original features. The new features are called singular vectors or principal axes. The singular vectors are ordered regarding the amount of the data variance that they represent, with the first singular vector as the highest-ordered. Additionally, the variability along each singular vector is computed, namely singular values. The main idea of rank reduction analysis using SVD is to project the data along the R highest-ordered singular vectors such that a certain percent of data variance could be preserved.

In the current study, tensor-based higher-order SVD (HOSVD) (De Lathauwer et al., 2000) was used to reduce the dimensionality of connectivity tensors. HOSVD decomposes a tensor 𝒜 ∈ ℝ^{d₁×…×d_p} to a core tensor 𝒢 ∈ ℝ^{d₁×…×d_p} consisting of singular values, and column spaces U⁽ⁿ⁾, n ∈ {1, 2, …, p}, each consisting of singular vectors in a specific mode. HOSVD preserves the information embedded in the structured tensors by computing singular vectors in each mode (connectivity, time and participants in this study) separately, in conjunction with their corresponding singular values. In the present study, the connectivity tensors, ℭ ∈ ℝ^N×N×T, were concatenated across the M_Trn training samples to create a 4^th-order connectivity tensor 𝒞 ∈ ℝ^{N×N×T×M_Trn}. According to the HOSVD model, 𝒞_Trn can be decomposed as

$${\mathcal{C}}_{\mathit{Trn}}=\mathcal{G}{\times }_1{\mathbf{U}}^{(1)}{\times }_2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}{\times }_4{\mathbf{U}}^{(4)}$$ (1)

where ×_n denotes the n-mode tensor-matrix product. ${\mathbf{U}}^{(n)}=[{\mathbf{u}}_1^{(n)}{\mathbf{u}}_2^{(n)}\cdots {\mathbf{u}}_{d_n}^{(n)}]\in {ℝ}^{d_n\times d_n}$ is the singular vector matrix (or column space) in the n-th mode, where d₁ = d₂ = N, d₃ = T and d₄ = M_Trn. The vector ${\mathbf{u}}_i^{(n)}\in {ℝ}^{d_n\times 1}$, i ∈ {1, 2, …, d_n}, is the i-th singular vector in the n-th mode. As brain connectivity matrix for each subject at each time is symmetric, U⁽¹⁾ and U⁽²⁾ are theoretically equal. 𝒢 ∈ ℝ^{N×N×T×M_Trn} is the core tensor with orthogonal sub-tensors, ${\mathcal{G}}_k^{(n)}$, and corresponding ordered Frobenius norms, ${\sigma }_k^{(n)}=\Vert {\mathcal{G}}_k^{(n)}\Vert$, where sub-tensors ${\mathcal{G}}_k^{(n)}$ are obtained by fixing the n-th index of 𝒢 at k ∈ {1, 2, …, d_n}, while the other indices are free. For instance, for a 3^rd-order tensor, orthogonality means that different horizontal matrices of the tensor (where the first index is kept fixed, while the two other indices are free) are mutually orthogonal. In other words, the inner product of every pair of the horizontal matrices is zero. Furthermore, the same rule applies to different frontal and vertical matrices as well. The same notion is generalized to nth-order tensors, n > 3, where orthogonal matrices are substituted with orthogonal subtensors. Details on the tensor algebra relevant to this project are provided in the Appendix A.

As the norm of the sub-tensors ${\sigma }_k^{(n)}=\Vert {\mathcal{G}}_k^{(n)}\Vert$, k ∈ {1, 2, …, d_n}, are in descending order, one can take advantage of the truncated version of the core tensor to reduce the rank of the connectivity tensors (De Lathauwer et al., 2000; Rabusseau and Kadri, 2016). The optimal solution of the truncated decomposition of the tensor 𝒞_Trn ∈ ℝ^{N×N×T×M_trn} is obtained when the core tensor is in the hypercube form, 𝒢_r ∈ ℝ^R×R×R×R where R ≤ min{N, N, T, M_Trn} (Chen and Saad, 2009). It is shown that in such a decomposition the diagonal entries of the core tensor are maximized (Chen and Saad, 2009). In this study, R was first set at M_Trn = 42. However, since 85% of the total variance was captured by the first 21 singular vectors, ultimately rank R = 21 was chosen for the final analyses throughout the study. Please refer to Fig. B.1 (Appendix B), to see the supporting data regarding rank reduction.

According to the definitions provided in the Appendix A, each entry c_ijkl, of the connectivity tensor, 𝒞_Trn, is obtained as below

$$c_{\mathit{ijkl}}=\sum _{\mathit{pqrs}}{u}_{ip}^{(1)}{u}_{jq}^{(2)}{u}_{kr}^{(3)}{u}_{ls}^{(4)}{ℊ}_{\mathit{pqrs}}=\sum _{\mathit{pqrs}}\left(u_{ip}^{(1)}{u}_{jq}^{(2)}\right){ℊ}_{\mathit{pqrs}}\left(u_{kr}^{(3)}{u}_{ls}^{(4)}\right)$$ (2)

where $u_{ij}^{(n)}$ indicates the entry (i, j) of U⁽ⁿ⁾, and ℊ_pqrs is the entry (p, q, r, s) of the core tensor 𝒢. The Eq. (2) can be rewritten in the matrix multiplication form as below

$${\mathbf{C}}_{\mathit{Trn}}=({\mathbf{U}}^{(1)}\otimes {\mathbf{U}}^{(2)})\mathbf{G}{({\mathbf{U}}^{(3)}\otimes {\mathbf{U}}^{(4)})}^T\in {ℝ}^{N^2\times T{M}_{\mathit{trn}}}$$ (3)

where C_Trn ∈ ℝ^N2×TM_Trn and G ∈ ℝ^N2×TM_Trn are the reshaped format of the tensor 𝒞_Trn ∈ ℝ^{N×N×T×M_Trn}, and 𝒢 ∈ ℝ^{N×N×T×M_Trn}, respectively. Using the truncated version of HOSVD, while only the R highest ranked singular vectors are kept in each mode, we can approximate the connectivity matrix, C_Trn, as below

$${\stackrel{\sim }{\mathbf{C}}}_{\mathit{Trn}}=\left({\mathbf{U}}_r^{(1)}\otimes {\mathbf{U}}_r^{(2)}\right){\mathbf{G}}_r{\left({\mathbf{U}}_r^{(3)}\otimes {\mathbf{U}}_r^{(4)}\right)}^T$$ (4)

where C̃_Trn ∈ ℝ^N2×TM_Trn is the reconstructed connectivity matrix using the R highest-ordered singular vectors, subscript r denotes reduced-rank, G_r ∈ ℝ^R2×R2, ${\mathbf{U}}_r^{(1)}\in {ℝ}^{N\times R},{\mathbf{U}}_r^{(2)}\in {ℝ}^{T\times R},{\mathbf{U}}_r^{(3)}\in {ℝ}^{T\times R}$ and ${\mathbf{U}}_r^{(4)}\in {ℝ}^{M_{\mathit{Trn}}\times R}$. It should be noted that only the training samples were used in finding the singular vectors. Therefore, the projection of the training samples onto the reduced rank connectivity space, ${\mathbf{U}}_r^{(1)}\otimes {\mathbf{U}}_r^{(2)}$, can be represented by

$${\mathbf{C}}_{\mathit{rTrn}}={\mathbf{G}}_r{\left({\mathbf{U}}_r^{(3)}\otimes {\mathbf{U}}_r^{(4)}\right)}^T$$ (5)

where C_rTrn ∈ ℝ^R2×TM_Trn presents the reduced-rank connectivity networks of the training samples, which are reshaped to the tensor format as 𝒞_rTrn ∈ ℝ^{R×R×T×M_Trn}, prior to being used in the prediction model. Consequently, with the reduced-rank connectivity space represented by ${\mathbf{U}}_r^{(1)}\otimes {\mathbf{U}}_r^{(2)}$, and the reshaped version of the test samples connectivity tensors C_Tst ∈ ℝ^N2×TM_Tst, the dimensionality of the test samples can be reduced through

$${\mathbf{C}}_{\mathit{rTst}}={\left({\mathbf{U}}_r^{(1)}\otimes {\mathbf{U}}_r^{(2)}\right)}^{-1}{\mathbf{C}}_{\mathit{Tst}}$$ (6)

where C_rTst ∈ ℝ^R2×TM_Tst is the reduced-rank connectivity networks of these samples that are reshaped to the tensor format 𝒞_rTst ∈ ℝ^{R×R×T×M_Tst} before testing the predictive model. The resulting reduced-rank connectivity tensors of the training samples 𝒞_rTrn ∈ ℝ^{R×R×T×M_Trn} and the test samples 𝒞_rTst ∈ ℝ^{R×R×T×M_Tst} were finally averaged across time to obtain an R × R summarized representation of the connectivity tensor for each participant. Eventually, the dimension of the new feature vector representation was R².

It is also worth mentioning that by having principal vectors in the reduced-rank connectome space ${\mathbf{U}}_r^{(1)}=\left[{\mathbf{u}}_1^{(1)},{\mathbf{u}}_2^{(1)},\dots ,{\mathbf{u}}_R^{(1)}\right]\in {ℝ}^{N\times R}$, connectivity network components FC_ij ∈ ℝ^N×N associated with the singular vectors i and j, are obtained through the outer product of the corresponding vectors, i.e. $F{C}_{ij}={\mathbf{u}}_i^{(1)}{\left({\mathbf{u}}_j^{(1)}\right)}^T$. Nevertheless, as previously mentioned, in the HOSVD estimation, the diagonal entries of the core tensor are maximized. Hence, the connectivity components, FC_ij, where i = j, should carry the highest level of information. In this study, only these components are then presented.

This analysis was conducted independently for the resting state and food visualization task. The resulting low-rank connectivity networks were used in a linear SVM model (Cortes and Vapnik, 1995). LIBSVM toolbox was used to implement support vector classification (Chang and Lin, 2011).

2.7. Assessing prediction performance

The sample set was split to the low- and high-weight loss groups using the median of the weight change percentage [(weight after 18 months – baseline weight)/baseline weight × 100]. The performance of the models was evaluated using random sub-sampling cross validation approach, for which 52 samples were randomly permuted, the first 21 samples from each group (low- and high-weight loss groups) were assigned to the training set and the remaining to the test set (5 samples from each group). Thus, in each permutation, training and test sets consisted of 42 and 10 samples, respectively. It should be noted that before running the prediction model, 100 random permutations of the participants were recorded, and the same permutations of training and test participants were used for all the analyses of this study. Prediction performance measures were evaluated as the average of the resulting scores across the 100 permutations (or validation folds).

The grouping label of sample i was set as [a_i1, a_i2], with a_i1 = 1 and a_i2 = 0 for the low weight loss group, and vice versa for the high weight loss group. The label predicted for the test sample i, [ $a_{i1}^{\prime },a_{i2}^{\prime }$], was not a binary array. In other words, $a_{i1}^{\prime }$ and $a_{i2}^{\prime }$ indicate the probability of belongingness of the test sample i to the group 1 and 2, respectively. The label array [ $a_{i1}^{\prime },a_{i2}^{\prime }$] was then binarized, to determine the grouping label of each sample. Equivalently, subject i was assigned to the low weight loss group, [a_i1, a_i2] = [1, 0], if $a_{i1}^{\prime }>a_{i2}^{\prime }$, and to the high weight loss group, [a_i1, a_i2] = [0, 1], if $a_{i1}^{\prime }<a_{i2}^{\prime }$. The probability of belongingness of each sample to either of the groups was estimated as suggested in (Chang and Lin, 2011).

We estimated cross entropy (CE) of the prediction model that quantified how the predicted probabilities (prior to binarizing) were close to the real binary labels. In other words, a high accuracy might not always imply a highly confident decision regarding grouping assignments, characterized by low CE. For instance, a sample with grouping probability [0.49, 0.51] is assigned to the high weight loss group, while there is not a high confidence margin in this prediction. CE was then defined as below

$$\text{CE}=-\frac{1}{M_{\mathit{tst}}}\sum _i^{M_{\mathit{tst}}}\sum _d^D(a_{id}ln(a_{id}^{\prime })+(1-a_{id})ln(1-a_{id}^{\prime }))$$ (7)

where D denotes the number of groups (2 in this study), M_tst indicates the number of test samples, and a_id and $a_{id}^{\prime }$ denote real and predicted probability of belongingness of the test sample i to the group d, respectively. For a perfect probability prediction CE is 0, and for a chance level probability, i.e. $a_{id}^{\prime }=0.5$, CE is D ln 2.

For each validation fold, the accuracy, sensitivity and specificity of the model were determined using the test samples as below

$$\begin{gathered} \text{Accuracy}=\frac{\text{Number}\text{of}\text{correctly}\text{classified}\text{samples}}{\text{Total}\text{number}\text{of}\text{samples}}\times 100 \\ \text{Sensitivity}=\frac{\text{Number}\text{of}\text{correctly}\text{classified}\text{samples}\text{from}\text{the}\text{low}\text{weight}\text{loss}\text{group}}{\text{Total}\text{number}\text{of}\text{low}\text{weight}\text{loss}\text{group}\text{samples}}\times 100 \\ \text{Specificity}=\frac{\text{Number}\text{of}\text{correctly}\text{classified}\text{samples}\text{from}\text{the}\text{high}\text{weight}\text{loss}\text{group}}{\text{Total}\text{number}\text{of}\text{high}\text{weight}\text{loss}\text{group}\text{samples}}\times 100 \end{gathered}$$ (8)

3. Results

3.1. Weight loss and hunger ratings following the overnight fast in the study sample

Within the entire sample, the mean (SD) baseline weight was 93.28 (12.80) kg, and the percent weight loss was 8.41 (7.14)%. The mean percent weight loss for those below the median was 2.87% (95%CI = 1.41, 4.33), while it was 13.96% (95%CI = 11.86, 16.05) for those above the median. These group differences reflect a poor and successful outcome for weight loss treatment, a conclusion that is in agreement with the clinically significant threshold of 5% established by The Obesity Society (TOS), since the loss of 5% or more has been associated with positive health consequences (Jensen et al., 2014). At the time of entering the scanner, the group was in the state of moderate hunger as evident by hunger ratings acquired using a 100 point VAS scale: Mean (95%CI) for hunger scale = 56.56 (48.30, 64.63). For greater details of the descriptive and clinical data, refer to Table B.1 (Appendix B) and the existing publications using this dataset (Mokhtari et al., 2016; Rejeski et al., 2017).

3.2. Prediction performance of the dynamic brain networks

The networks of the resting state and food cue task were used in separate prediction analyses. There was no significant difference in the prediction accuracy between resting-state and food-cue task; hence, the remainder of the manuscript focuses on resting-state data with detailed results for the food-cue task being presented in Fig. B.2.

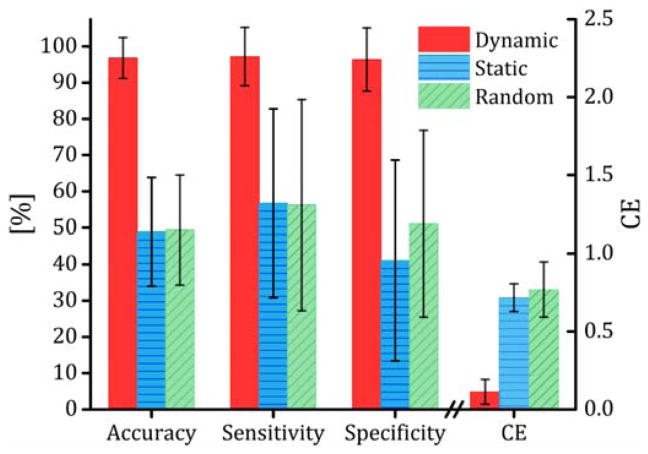
Direct comparisons were made between the dynamic networks, static networks and dynamic networks with random grouping assignment. The dynamic connectivity networks were created using a sliding window with length of 61 time points and connectivity density of 10%. A single static connectivity matrix was also generated for each participant using the entire fMRI time series and thresholded at a density of 10%. For the networks with random grouping assignments, the labels of the 52 samples were randomly permuted and the resulting randomly assigned samples were used in the same rank reduction and prediction algorithms with the same 100 random subsampling cross validation folds. The entire random grouping assignment analysis was repeated 10 times and the average performance across the 10 runs was used. These networks were also created with a window size of 61 time points and a density of 10%. Fig. 2 contrasts the prediction performance measures from the different connectivity networks. The dynamic model exhibited the best performance with an average accuracy (SD) of 96.80% (5.67). The static networks resulted in a prediction accuracy of 48.90% (14.90). The prediction accuracy of the random grouping model was 49.40% (16.00) over the 10 runs; its correct prediction rate failed to exceed 70% in any of the validation folds.

Fig. 2.

Prediction performance, quanitified using accuracy (rate of correct prediction), sensitivity (rate of correct prediction for low-weight loss group), specificity (rate of correct prediction for high-weight loss group) and CE (a measure of prediction error defined as the difference between the prediction grouping probabilities and the real grouping labels, see section 2.7 for detailed definitions) for the dynamic and static connectivity and random grouping analysis. Dynamic connectivity tensors were constructed using a sliding window length of 61 time points and theresholded at connectivity density of 10%. No sliding window was used to make the static netowork; the entire fMRI time series was used to compute a single pairwise correlation matrix for the static networks. For the random grouping analysis, the particpants’ labels were randomly permuted. HOSVD was used to reduce the networks’ rank, HOSVD linearly decomposes the dynamic connectivity tensors to a set of linearly independent (equivalently orthogonal) dynamic connectivity components. To identify the components, HOSVD maximizes the amount of variance captured by the components.

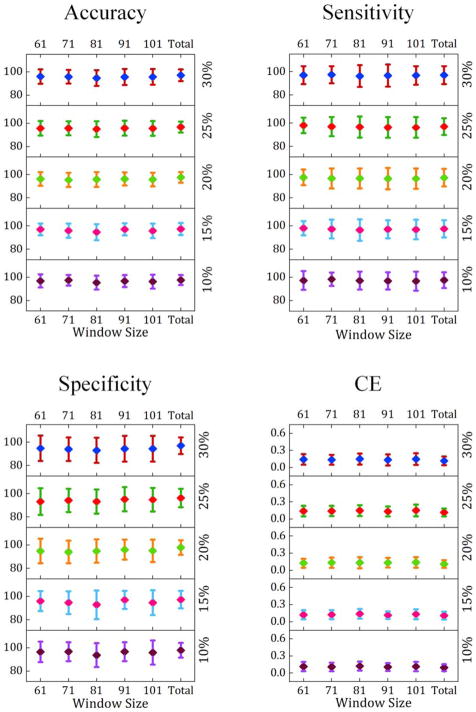
Fig. 3 contrasts the prediction performance measures for the dynamic networks across different window sizes and different connectivity density thresholds. As shown on the right vertical axis, to explore how different density thresholds can affect prediction performance, a search range of 10 to 30% with 5% increments was examined. Similarly, prediction performance was evaluated with different window sizes ranging from 61 to 101 time points with 10 time points increments. To utilize information across a wider range of connectivity fluctuation frequencies, for each participant, a “Total” score was generated by concatenating the low-rank networks estimated for the same participant across all window sizes.

Fig. 3.

Prediction performance measures [mean with error bars reflecting ±SD across 100 validation folds] of the SVM model estimated for different window sizes and different connectivity density thresholds. The numbers on the left vertical axis of each figure illustrate the prediction performance values, and the numbers on the right side indicate connectivity density thresholding values.

Results from a two-factor (window size and density) repeated measures analysis of variance (ANOVA) test with significance level of 0.05 showed that window size was a significant factor in the prediction performance measures including accuracy, specificity and cross entropy (p-value < 0.05). In addition, connectivity density was significantly associated with accuracy, specificity and cross entropy (p-value < 0.05). However, the interaction of window size and density was not significantly associated with the performance measures (p-value > 0.05). Further, multiple comparison tests were performed to identify which pairs of window sizes and density values contributed to the significant difference in the prediction performance (see Fig. B.3). As indicated in Fig. B.3 (a), the model integrating networks from different window sizes, namely “Total”, significantly outperformed the models trained and tested using a single window size for the data. Additionally, a connectivity density of 10% resulted in significantly lower cross entropy (Fig. B.3 (b)).

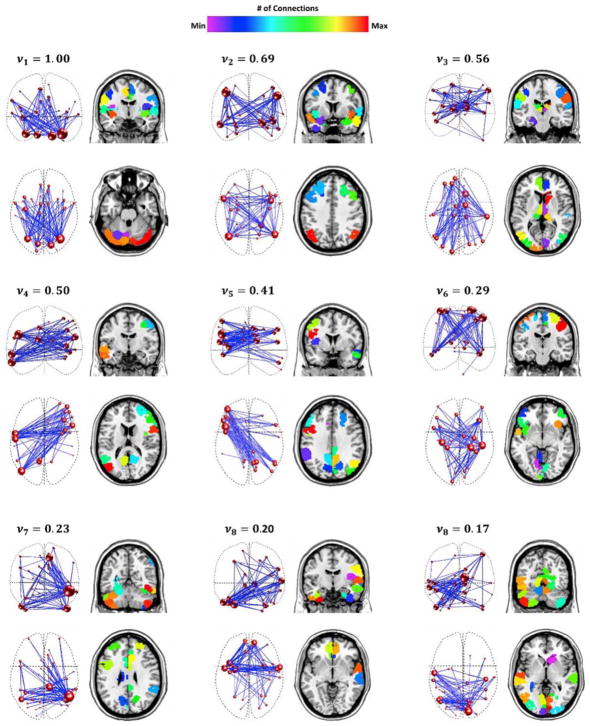
3.3. Connectivity principal components of the dynamic connectivity networks

The 9 highest-ranked connectivity singular vectors captured ~81% of the variance of the reduced-rank data. Each singular vector identified by HOSVD represents a connectivity pattern, namely connectivity principal components. Fig. 4 shows the principle components described by the 9 highest-ordered singular vectors, averaged over 100 validation folds. The amount of the variance carried by each component (equivalent to the corresponding singular value squared), normalized to the first singular vector variance, and averaged over 100 cross-validation folds, is shown on the top of that component. There were no qualitative differences between the network components generated using different window sizes. Due to space limitation and for simplicity, we only present the network components created with a window size of 61 time points and a density of 10%. For interested readers, the network components were provided in Appendix C as an Excel file, each sheet shows the connections (edges) of a specific component as a set of node pairs and corresponding weights. The number of each node is determined based on its label in the functional atlas (Shen et al., 2013). Only the connections located in the 99th percentile of the connection strength distribution are shown for each component.

Fig. 4.

The connectivity principal components revealed by HOSVD. For each component, the left column displays a network-based representation and the right column shows the individual nodes in their anatomical locations. Each network component is a collection of nodes and edges that captures the greatest amount of variance across time and within individuals. The size of each node is directly related to its number of connections. The variance explained by each component, v_i, where i indicates the component index, is noted on the top of the same component’s graph. For each component, the variance was computed as the square of the corresponding singular value normalized by the first singular value, that was finally averaged across 100 validation folds.

Given that these components represent the complex patterns that emerge from temporally high level interactions between single connections, they should be viewed as whole connectivity components, rather than sets of independent connections between regions. Nevertheless, it is noteworthy that the network components contain brain connections that are hypothesized to be involved in many aspects of eating behavior and behavioral change skills necessary for successful weight loss (Rothemund et al., 2007; Stice et al., 2013; Volkow et al., 2008). The components were made up of the following interconnected regions:

1. Dorsal insula, basal ganglia, anterior cingulate, and cerebellum

2. Attention network and limbic regions such as amygdala, hippocampus and inferior insula

3. Right caudate, visual cortex, motor and sensory regions, thalamus, medial prefrontal and dorsolateral prefrontal cortices

4. Left posterior cingulate/precuneus, left temporal pole and right ventrolateral prefrontal cortex

5. Right posterior cingulate/precuneus, right temporal pole and left ventrolateral prefrontal cortex

6. Bilateral anterior insula, bilateral inferior frontal, and early visual and primary motor cortices

7. Entire cingulate gyrus, lateral visual cortex and frontal poles

8. Orbitofrontal cortex, temporal poles and parietal regions

9. Visual cortex and cerebellum

As mentioned above, to provide a clearer visualization of the network components, only connections located in the 99^th percentile of the connection strength distribution are shown for each component. Thus, the images in Fig. 4 were selected to highlight the key regions that might contribute to the classification of successful weight loss. Note that the connections shown in this figure do not represent simple temporal correlation between the regions. Rather, connections between two regions indicate a complex coupling between the connections of those two regions across time and within individual participants.

The SVM model exploits an optimum parametrized linear combination of the features to build the maximum-margin hyperplane between the two groups (Cortes and Vapnik, 1995). A parameter is assigned to each feature that represents the weight of the same feature in the linear maximum-margin separation. Thus, for the reduced-rank connectivity data ∈ ℝ^21×21, the parameters, also known as the weights, can be represented with the matrix W ∈ ℝ^21×21. The strength of parameter matrix |W| ∈ ℝ^21×21, averaged over 100 permutations, is illustrated in Fig. 5(a). The diagonal entry, w_ii i ∈ {1, 2, …, 21}, represents the weight of the principal component i. The off-diagonal entry, w_ij i, j ∈ {1, 2, …, 21}, i ≠ j, represents the weight assigned to the interaction of principal components i and j. As apparent in the diagonal entries, the weights, as a measure of principal components discriminatory power, decrease as the order of the components decreases. Moreover, it shows that overall the diagonal elements are substantially stronger than the off-diagonal entries in the corresponding row and column. In other words, the individual principal networks, play a significant role in discriminating the groups whereas the interaction between principal components contributes much less. To clarify this point, Fig. 5(b) and 5(c) depict the average and standard deviation of the diagonal entries and the cumulative weight associated with each principal component (equivalently row-wise sum of the matrix |W|).

Fig. 5.

(a) Strength of SVM weight matrix, |W| ∈ ℝ^21×21, averaged over 100 validation folds, (b) average weights on the diagonal entries of the SVM weight matrix |W| ∈ ℝ^21×21, (c) average of row-wise sum of the matrix |W| ∈ ℝ^21×21.

4. Discussion

This study involved an examination of whether functional brain networks of older, obese adults assessed in a fasted state prior to randomization to intentional weight loss could be used to predict success with weight loss 18-month after initiation of treatment. Evaluating functional brain networks following an overnight fast was a critical feature of the study design in that periods of food restraint result in nutritional deficits that trigger hunger and hence food consumption (Fedoroff et al., 2003; Fedoroff et al., 1997; Polivy et al., 2005). In line with Kavanagh and colleagues’ (Kavanagh et al., 2005) Elaborated Intrusion Theory of Desire, the motivation to eat is driven by both unconscious and conscious processes. Moreover, physiological deficits, created by manipulations such as food restraint, trigger cravings for food and challenge self-regulatory capacities (Fedoroff et al., 2003; Fedoroff et al., 1997; Polivy et al., 2005). Indeed, we have observed this pattern of response in our prior work with food restraint (Rejeski et al., 2010). Consistent with our study hypothesis, we found that HOSVD in combination with machine learning applied to pre-treatment functional brain networks generated from resting-state scans resulted in network components that were highly accurate (>95%) in predicting 18-month weight loss.

There is growing consensus that self-regulatory skills and the motivation required to follow-through with behavior change (Rejeski et al., 2008; Wing, 2002) are vital for successful weight loss or adopting any new health behavior. Whereas weight loss research in neuroscience has focused on specific regions of interest (Stice et al., 2013), the current methodology is highly innovative in that we used HOSVD in conjunction with machine learning to identify patterns of multivariate connectivity across the whole brain that effectively discriminated between individuals who either exceeded or failed to exceed the 5% weight loss criterion that defines success with intentional weight loss. Furthermore, the network components used in the predictive model have at least three important implications. First, they could assist in the development of a comprehensive neural-based theory of intentional weight loss, since studies involving specific regions of interest are restrictive and ignore the inherent complexity of the brain. Indeed, recent comprehensive reviews of research into obesity suggest that a whole brain approach is warranted (Stice et al., 2013). Second, a broader view of dynamic brain networks could lead to the development of new treatment options. These options could complement or improve upon current behavioral methods for weight management which largely rely on conscious, decision based theories (Wing, 2002). And third, we believe that a more comprehensive understanding of neural networks involved in successful weight management could lead to the tailoring of treatment consistent with precision-based models of medicine. It is unlikely that “one size fits all” when it comes to implementing strategies for promoting health behavior change. Because the analytic approach in the current investigation relied on multivariate relationships across the whole brain, prior to discussing key brain networks illuminated by these analyses, we first want to emphasize what the phenotypic characterizations can and cannot tell us.

As noted above, the predictive analyses combined HOSVD with machine learning to identify patterns of multivariate connectivity that were effective in discriminating between individuals who either exceeded or failed to exceed the 5% criterion for successful weight loss. The multivariate patterns indicate that, as opposed to specific regions of interest, complex connectivity patterns between widespread areas of the brain are key to understanding intentional weight loss. This finding is vital when attempting to gain a mechanistic understanding of the network components that contribute to successful weight loss. The network components cannot be dissected and interpreted as individual brain regions or individual connections between brain regions. It is the entire connectivity pattern of the network components that was essential to effective classification.

The results clearly demonstrated that dynamic network analyses were successful at predicting weight loss whereas static network analyses were not. This means that a series of networks that evolved over time was necessary to discriminate between the weight loss groups. Each component (see Fig. 4) represents a brain subnetwork that accounts for variability in connectivity across the groups. The expression of each component varies over time (see Fig. B.4) in each individual participant. The machine learning algorithm was able to identify spatio-temporal patterns that distinguished the high from low weight loss groups. This does not simply translate to a given component being more or less likely to be connected in the high or low weight loss groups. Rather, the temporal profile of the network components and the interaction between the temporal dynamics of the components distinguished the study populations. Due to the fact that the multivariate pattern spans many interacting spatial and temporal dimensions, it is not possible to simply identify a single discriminant feature for the two groups. The complex pattern is what discriminated between the two groups and it required a machine learning algorithm to identify that pattern in high dimensional space.

With these caveats in mind, 9 principal components captured in excess of 80% of dynamic connectivity variance. Consistent with Kavanagh and colleagues’ (Kavanagh et al., 2005) Elaborated Intrusion Theory of Desire, these components underscore that effective self-regulation involves both unconscious processes—sensory, motor, cognitive and affective—that are likely responsible for the intrusive quality of food craving as well as conscious processes—both cognitive and emotional—that serve to elaborate on these intrusive cues to promote consumption. Although we want to reemphasize the importance of interpreting each network as a whole component, and not as distinct regions of interests, the implication of regional interactions in each component is briefly discussed below.

Component 1 represents a network that is dominated by interactions between the cerebellum, lateral sensorimotor areas (including face, mouth, and throat), posterior insula, mid-anterior cingulate cortex, as well as the early visual cortex. Given this connectivity pattern, the component 1 may play an active role in higher-order cognitive processing, e.g. self-regulation and goal-directed behaviors for optimizing context-appropriate performance (Imamizu and Kawato, 2009; Schmahmann, 1991, 1996; Stoodley, 2012; Stoodley et al., 2012), feeding behavior (Zhu and Wang, 2008; Zhu et al., 2006), and voluntary movement commands (Daskalakis et al., 2004; Guye et al., 2003).

A bilateral interacting pattern between the executive attention network and hedonic/goal directed network including the amygdala, hippocampus and inferior insula was found to serve as the core for component 2. We postulate that this network component represents the process of top-down control that the attention network projects onto the limbic regions known to be important in goal-oriented behavior (Dosenbach et al., 2008; Hopfinger et al., 2000). Altered connectivity within this network component could adversely affect inhibitory control processing and consequently lead to altered behavioral regulation (Volkow et al., 2008). Interestingly connections between the control and reward/motivation networks are known to play a central role in regulating food consumption (Brooks et al., 2012; Volkow et al., 2011).

Component 3 represents a sensory network that involves extensive connectivity with the visual cortex, thalamus, caudate, ACC, medial prefrontal cortex (MPFC) and dorsal lateral prefrontal cortex (DLPFC). While the ACC, MPFC and DLPFC are known to be associated with salience and the rewarding qualities of sensory input (Ridderinkhof et al., 2004; Rogers et al., 2004), the DLPFC also plays a key role in working memory.

The importance and complexity of elaboration and inhibition to intentional weight loss is evident in network components 4–8. The presence of an interacting pattern consisting of the left temporal pole, right ventrolateral prefrontal (RVLPF) and posterior cingulate cortices defines component 4 as an important network in cognitive elaboration/inhibition (Levy and Wagner, 2011; Noesselt et al., 2007). Interestingly, the structure of network component 4 was also present in network component 5, albeit with opposite laterality. Network component 5 includes emotional elaboration/delayed discounting network comprising the interactions between right temporal pole and left ventrolateral prefrontal cortex (LVLPFC) (McClure et al., 2004).

Network component 6 represents communication between the bilateral anterior insula, bilateral inferior frontal areas, early visual areas, and superior and medial motor cortex. This network component can be considered influential in self-regulatory processes involving emotional awareness and inhibition (Rueda et al., 2004), whereas network component 7 captures interactions between inferior temporal areas and the posterior cingulate cortex, key elements of the resting state brain default mode network (DMN) (Bluhm et al., 2007; Uddin et al., 2009).

The 8th network component includes high-level interactions between temporal poles, anterior cingulate, and orbital frontal cortices. This component resembles the hot state brain network of appetite (HBN-A) -including insula, anterior cingulate cortex (ACC), superior temporal pole (STP), amygdala and the parahippocampal gyrus- (Paolini et al., 2014; Paolini et al., 2015) that was found to be an important control-based network contributing to the prediction of weight loss in prior work (Paolini et al., 2015).

Finally, network component 9 is dominated by connections between the visual cortex and the cerebellum. In general, we posit that the appearance of the interactions between visual cortex and cerebellum in this dedicated network component, underscores the powerful role that visual imagery and embodied long term memory play in the desire for food and hence the strength of self-regulatory capacities. In fact, the role of visual imagery in food craving is a topic that has attracted considerable attention (Bullins et al., 2013; Harvey et al., 2005; Kemps and Tiggemann, 2010; Kemps et al., 2008; Tiggemann and Kemps, 2005). Not surprisingly, visual imagery and other body related/sensory inputs are core features of Kavanagh and colleagues’ Elaborated Intrusion Theory of Desire (Kavanagh et al., 2005).

Despite the strengths of the current method in classifying intervention success and the role that this model played in elucidating the complex, whole brain connectivity involved in intentional weight loss, the study is not without limitations. First, the sample size was small and involved a relatively homogeneous group of overweight/obese older adults with metabolic syndrome and/or cardiovascular disease (CVD). We are aware that the extra-ordinary prediction accuracy in this study could be artificially inflated by these factors. There is a need to replicate these findings with larger independent samples. Given the complexity of the data and technique, we expect that the prediction performance will fall off some, when using independent samples. Nevertheless, in real-life applications, even a prediction performance of ~60% could significantly impact medical decisions. Second, although sex has been identified as a determinant of brain function and self-regulation (Cosgrove et al., 2007; Kimura, 1992; Rolls et al., 1991), we did not find that sex was an important consideration in the success of classifying who was likely to fail or succeed at weight loss. It is possible that in a larger more heterogeneous sample of men and women, classification accuracy could be compromised if sex was ignored. The same could be said for age, race and other potentially important moderating variables that do compromise the external validity of these results. Third, previous studies have shown that overeating and consequently obesity can occur in the absence of hunger (Faith et al., 2006; Fisher and Birch, 2002; Hill et al., 1991). In the current study, baseline fMRI scans were acquired in a physiological state of hunger following an overnight fast, and the successful weight loss performance was prospectively predicted using the resulting dynamic connectivity networks. However, we did not compare fasted and sated treatment conditions. This topic is certainly worthy of study in subsequent research.

Finally, there are at least two other important areas of study that deserve attention. First, if one prescribes an intervention based on the multivariate connectivity patterns, will this lead to an improved outcome? In other words, although this study shows that there are well-defined network components that are useful in predicting weight loss success, the current study does not tell us whether these components can be modified in a manner that changes the outcome for those who failed. In addition to this limitation in interpreting the component networks, one should also keep in mind that the interaction of individual characteristics and intervention type could make the interpretation of network components even more challenging. A second and related issue is that, although this is the first step toward specifying weight loss treatment at individual level, separate models should be generated for each specific intervention of conceptual interest to demonstrate its efficacy, eventually developing a clinical paradigm in which individuals could be matched to highly specific behavioral and/or pharmacological interventions. In other words, if we had sufficient sample sizes (e.g. 200 participants) for different interventions, we could construct a separate model for each specific intervention to identify phenotypes that are predictive of success. The probability of successful weight loss for each future patient would then be estimated with all the resulting models based on their brain phenotypes. The intervention associated with the model resulting in the highest probability would then be assigned to that patient. In this way, we can extend the proposed idea in this paper to a personalized medicine paradigm.

5. Conclusions

In summary, the current study offers an exciting new frontier for behavioral neuroscience in that it demonstrates the utility of studying connectivity across the whole brain as opposed to focusing on limited regions of interest. Although the study sample was relatively homogeneous, obesity is a major factor in the high rates of metabolic syndrome and/or CVD as people age and creates an enormous burden on public health. The combined use of HOSVD with machine learning was highly effective at using baseline dynamic fMRI networks to identity participants who were likely to either succeed or fail at intentional weight loss 18-months after the initiation of treatment. This is a novel and highly innovative approach to identifying phenotypes that are best suited for current behavioral weight loss interventions and offers guidance for tailoring treatment, a research priority at the National Institutes of Health. For example, it may well be that individuals who most closely resemble the phenotype of those who were successful with our intervention, could be effectively treated with less intensive behavioral therapy. This has important implications for public health. Moreover, we believe the 9 components that accounted for over 80% of the variance of the data will serve as an impetus for theory development in future exploratory studies that aim to investigate baseline brain functional characteristics as predictive phenotypes of obesity treatment success.

Appendix A. Tensor Algebra Details

A tensor 𝒜 ∈ ℝ^{d₁×…×d_p} can be represented by a multidimensional array (𝒜_i1,…,ip: i_n ∈ {1, 2, …, d_n}, n ∈ {1, …, p}). The n-mode fibers of the 𝒜 are the vectors obtained by letting the n-th index to change while the remaining indices are fixed, e. g. 𝒜:,_i1,…,ip ∈ ℝ^d₁×1 represents the 1-mode fiber of 𝒜. The n-mode matrix of 𝒜, A_(n) ∈ ℝ^{d_n×d₁d₁…d_n−1d_n+1…d_p} is constructed by stacking n-mode fibers of 𝒜 as columns. The vectorization form of the tensor 𝒜 ∈ ℝ^{d₁×…×d_p} is defined as vec(𝒜) = vec(A₍₁₎). The inner product between two same-size tensors 𝒜 and ℬ is defined by 〈𝒜, ℬ〉 = 〈vec(𝒜), vec(ℬ)〉, and the Ferobinus norm of 𝒜 is defined as ${\Vert \mathcal{A}\Vert }_F^2=\langle \mathcal{A},\mathcal{A}\rangle$.

The n-mode matrix product of the tensor 𝒜 with a matrix X ∈ ℝ^m×d_n, shown with the symbol ×_n, is defined by the relationship below

$$\mathcal{Y}=\mathcal{A}{\times }_{n}X\iff Y_{(n)}=X{A}_{(n)}$$ (A.1)

where the tensor 𝒴 ∈ ℝ^{d₁×d₁×…×d_n−1×m×d_n+1×…×d_p}. The n-mode rank of 𝒜 is defined as the rank of n-mode matricization of the tensor denoted by A_(n), rank_n(𝒜) = rank(A_(n)), that represents the dimension of the space spanned by the n-mode fibers of the tensor. The multilinear rank of the tensor 𝒜, denoted by rank(𝒜), is the tuple of the n-mode ranks of 𝒜, denoted by rank(𝒜) = (R₁, … R_p) where R_n = rank_n(𝒜), n ∈ {1, 2, … p}. It is written that rank(𝒜) ≤ (S₁, …, S_p) whenever rank₁(𝒜) ≤ S₁, rank₁(𝒜) ≤ S₂, …, rank_p(𝒜) ≤ S_p.

Having these basic definitions established, according to the higher order singular value decomposition (HOSVD), the tensor 𝒜 can be decomposed as below

$$\mathcal{A}=\mathcal{G}{\times }_1{\mathbf{U}}^{(1)}{\times }_2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}\times \dots {\times }_p{\mathbf{U}}^{(p)}$$ (A.2)

where 𝒢 ∈ ℝ^{d₁×…×d_p} is the core tensor with orthogonal subtensors, ${\mathbf{G}}_k^{(n)}$, and corresponding ordered Frobenius norms ${\sigma }_k^{(n)}={\Vert {\mathbf{G}}_k^{(n)}\Vert }_F^2$. The subtensor ${\mathbf{G}}_k^{(n)}$ is obtained by fixing the n-th index of 𝒢 at k ∈ {1, 2, … d_n}, n ∈ {1, 2, …, p}, while the other indices are free. ${\mathbf{U}}^{(n)}=[{\mathbf{u}}_1^{(n)}{\mathbf{u}}_2^{(n)}\cdots {\mathbf{u}}_{d_n}^{(n)}]\in {ℝ}^{d_n\times R_n}$ is a unitary matrix, ${\mathbf{U}}_i^T{\mathbf{U}}_i=\mathbf{I}$, and represents the singular vectors in the n-th mode.

According to the tensor rank definition provided above, the number of parameters needed to fully represent the tensor 𝒜 using HOSVD should be equal or smaller than d₁d₂ … . d_p. Finding the optimum decomposition of the tensor 𝒜, with the multilinear rank (R₁, R₂, … R_p) ≤ (d₁, d₂, … ., d_p) is a very hard and time consuming problem. In practice, truncated HOSVD algorithm provides a good approximation of the multilinear tensor decomposition (Rabusseau and Kadri, 2016). For the truncated HOSVD, only the l_n singular vectors with the largest singular values (λ_k, k ∈ {0, 1, … d_n}) within n-th mode are chosen to reconstruct the data, that results in a retained variance percent of ${\sum }_{k=1}^{l_n}{\lambda }_k^2/{\sum }_{k=1}^{d_n}{\lambda }_k^2\times 100$ in that mode. Furthermore, it has also been proved (Chen and Saad, 2009) that there exists an optimal solution for the tensor-based low rank decomposition problem when R₁ = R₂ = ··· = R_p ≤ min(d₁, d₂, … ., d_p).