Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 14;9(4):783–789. doi: 10.1021/acschemneuro.7b00409

Thermodynamics of Amyloid-β Fibril Elongation: Atomistic Details of the Transition State

Roberto A Rodriguez †,*, Liao Y Chen †,*, Germán Plascencia-Villa †, George Perry ‡
PMCID: PMC5911799  PMID: 29239603

Abstract

graphic file with name cn-2017-00409x_0008.jpg

Amyloid-β (Aβ) fibrils and plaques are one of the hallmarks of Alzheimer’s disease. While the kinetics of fibrillar growth of Aβ have been extensively studied, several vital questions remain. In particular, the atomistic origins of the Arrhenius barrier observed in experiments have not been elucidated. Employing the familiar thermodynamic integration method, we have directly simulated the dissociation of an Aβ(15–40) (D23N mutant) peptide from the surface of a filament along its most probable path (MPP) using all-atom molecular dynamics. This allows for a direct calculation of the free energy profile along the MPP, revealing a multipeak energetic barrier between the free peptide state and the aggregated state. By definition of the MPP, this simulated unbinding process represents the reverse of the physical elongation pathway, allowing us to draw biophysically relevant conclusions from the simulation data. Analyzing the detailed atomistic interactions along the MPP, we identify the atomistic origins of these peaks as resulting from the dock-lock mechanism of filament elongation. Careful analysis of the dynamics of filament elongation could prove key to the development of novel therapeutic strategies for amyloid-related diseases.

Keywords: Amyloid-beta, molecular dynamics, transition state, fibril elongation, protein interactions, hydrophobic contacts

Introduction

The presence of abnormal fibrillar aggregates of amyloid species in the brain is associated with the development of neurodegenerative diseases such as Alzheimer’s (AD), Parkinson’s, and Huntington’s.1−3 Amyloid-beta (Aβ) peptides in Alzheimer’s are produced from the cleavage of amyloid-β precursor protein (AβPP) via sequential cleavage by β and γ-secretases. While the exact pathogenic role of amyloid-β aggregating into senile plaques is still not well-understood, fibrillar associations of Aβ have emerged as key neurotoxic species in Alzheimer’s disease affected brain areas such as the hippocampus, cerebral cortex, and amygdala.

The aggregation and elongation processes of amyloid-β fibrils have been previously studied in kinetics experiments.4−11 On the basis of such, a two-step process for fibril elongation has been proposed, commonly known as the dock-lock mechanism. In this paradigm, first a free Aβ peptide rapidly adheres (docking) to a mature preformed fibril, followed by a slower second step where a rearrangement of the incoming peptide occurs into the ordered fibrillar shape (locking).5,6,10 From kinetics experiments, this process is known to follow the Arrhenius equation with an associated energetic barrier. Detailed molecular analysis of this binding process of Aβ fibrils is crucial for the better understanding of protein aggregation processes into neurotoxic species in AD, identification of key residues/domains involved in fibrillation of Aβ, and the design of potential inhibitors of fibrillar growth.

Molecular dynamics (MD) simulations have proven a valuable and precise tool to elucidate details in complement to experimental studies on Aβ kinetics. The dynamics of fibril aggregation have been simulated at various levels of resolution by coarse-grained,12−17 implicit water,18,19 and hybrid models.20 All-atom simulations have typically been restricted to short peptides,21−23 although some longer peptides have been studied recently on this level.24−26 Recent work has also studied the free energy landscape as a function of peptide number.14 The long time scales, elucidated by kinetics experiments, involved in the aggregation process present a major hurdle for atomistic simulations of fibril elongation. In addition, the atomistic origins of the Arrhenius barrier observed in experiments4−11 have not been explained in the current literature. Such all-atom simulations are necessary for a detailed molecular picture of the elongation process and for the determination of the relevant thermodynamic parameters.

In the present study, we have simulated the elongation process of Aβ using all-atom molecular dynamics. By conducting (slow) steered molecular dynamics (SMD) experiments coupled with the thermodynamic integration method, we simulated the process of dissociating a monomeric peptide from a mature amyloid-β filament. By relaxing the dissociated peptide at each step of the unbinding pathway (similar to the gentlest ascent algorithm27), we have directly sampled the most probable path (MPP) of fibril growth under the imposed SMD constraints. Evaluating the Gibbs free energy (the potential of mean force,28 PMF) along the MPP yielded a multipeak activation barrier consistent with the kinetics experiments of the current literature. Analysis of the detailed atomistic interactions along the MPP allowed us to identify the origins of the Arrhenius barriers as related to the dock-lock mechanism of Aβ fibril elongation.

Results and Discussion

We have simulated an Aβ peptide unbinding event from an amyloid filament by steering a monomer along its MPP. We computed the PMF along the MPP, revealing a multipeak energetic barrier separating the dissociated state from the aggregated state. In what follows, we elucidate the origins of this barrier via atomistic analyses of the Aβ peptide-filament system along the unbinding pathway.

Atomistic Origins of the Energetic Barrier

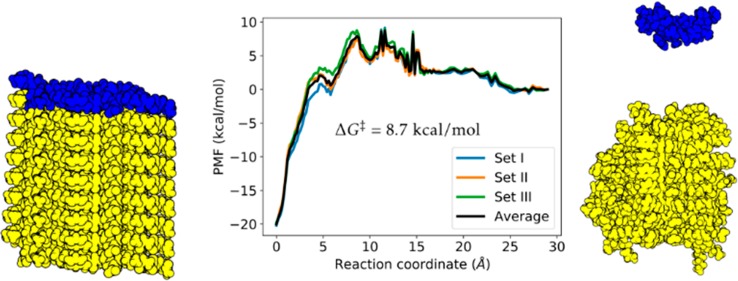
The key findings of the present work are shown in Figure 1. Our calculations indicate the presence of a multipeak energetic barrier along the unbinding pathway, showing at least three characteristic peaks along the reaction coordinate (hereafter referred to as RC or as P0s displacement interchangeably). The estimated Arrhenius barrier was 8.7 ± 1.4 kcal/mol above the dissociated state (average of three sets of simulations, uncertainty is the largest standard deviation). The overall energetic barrier obtained from the simulations of the system along the Aβ filament elongation pathway is in agreement with the experimental results of Hasegawa and co-workers, who estimated the energetic barrier to be approximately 10 kcal/mol for wild-type Aβ40.29 Recently, Young et al.30 measured the elongation barrier for the wild-type Aβ42 to be 11.2 kcal/mol. Thus, our result of 8.7 kcal/mol for the D23N Iowa mutant isoform of Aβ40 agrees with the existent experimental measurements.

Figure 1.

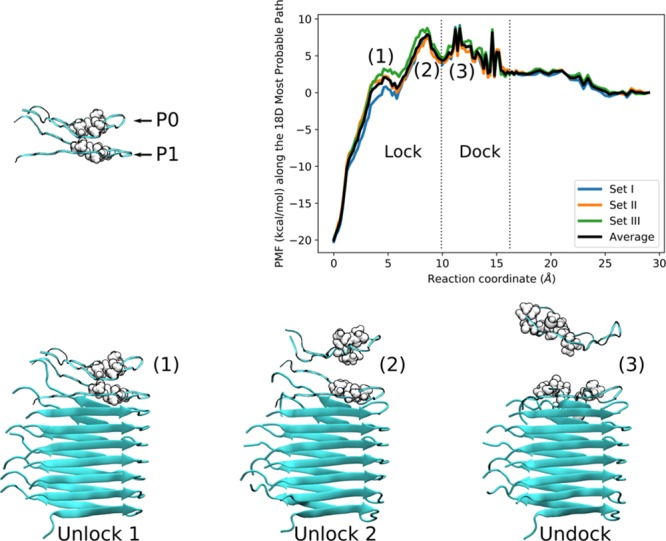
Figure 1

Open in a new tab

Top: Free energy of elongation along the most probable path (MPP) with dock-lock steps identified. Bottom: Snapshots of the dissociation process corresponding to the three different peaks in the free energy profile. Note how during the unlocking steps the N- and C-termini of P0 and P1 are still tightly interacting, whereas during the undocking step they break away from each other. All molecular graphics in this work were rendered with VMD.38

Free energy profiles along the elongation pathway have been computed previously. Schwierz et al.24 computed a monotonic profile involving only a one-dimensional PMF, in contrast to our 18-dimensional profile, which could help to explain why their PMF does not exhibit a barrier. Our computational strategy allows us to directly probe the most probable path, which yields the Arrhenius barriers along the elongation pathway, in agreement with experimental reports. The free energy computed by Gurry and Stultz19 exhibits a barrier of approximately 4 kcal/mol in the locking regime, most likely due to their choice to restrain the coordinates of the topmost layer (P1) of the aggregate. Our simulations indicate that the dynamically fluctuating hydrophobic interactions between P0 and P1 are critical for the elongation process of Aβ fibrils.

An additional parameter of interest is the elongation rate (k+) for monomer addition. Our computed barrier allows us to estimate k+ as

graphic file with name cn-2017-00409x_m001.jpg 1

where the diffusion rate for monomer addition has been estimated24 to be 3 × 109 M–1 s–1, Ea is the Arrhenius barrier, kB is the Boltzmann constant, and T is the temperature (298 K in our simulations). This yields an estimate for k+ of 1.2 × 103 M–1 s–1, in contrast with Young et al.’s30 experimental value of 9.3 × 105 M–1 s–1 for Aβ42. The discrepancy between these values is due to our neglect of the entropic contributions to the elongation rate (see the computational details in the Methods and in the Supporting Information).

To elucidate the atomistic basis for the barrier, we analyzed the main hydrophobic contacts between the steered peptide (P0) and the nearest strand in the aggregate (P1) (Figure 1). Figure 2 shows a snapshot along the steering path. In what follows, we use filament/aggregate interchangeably to refer to an organized layer of Aβ peptides (P1–P8 in Figure 2). As evidenced by the proximity between P0 and P1 during the first two displacement peaks, these states may be assigned to the locking step of filament elongation kinetics.5,6,10 In contrast, the definite separation during the third displacement peak is consistent with the docking step. Thus, our simulations are in agreement with the experimental results as well as with the template-dependent dock-lock mechanism of Aβ elongation.

Figure 2.

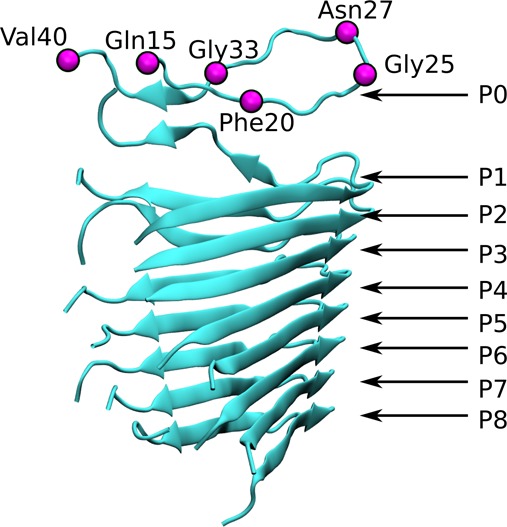
Figure 2

Open in a new tab

Snapshot of the steering pathway with the steered alpha carbons shown as magenta-colored spheres. The numbering used to refer to the peptides constituting the filament is indicated.

Hydrophobic Interactions Promote Assembly of Aβ Filaments

Which residues of Aβ are essential for the transition from a free peptide to the well-packed elongated filament? To answer this, we studied the hydrophobic interactions between P0 and P1. We monitored the α carbon (Cα) distances between the corresponding hydrophobic residues in P0 and P1, (e.g., the distance between P0-Val36-Cα and P1-Val36-Cα) as a function of P0s displacement. Clusters of hydrophobic residues have been suggested to stabilize Aβ filament structure.31 In addition, mutations of specific residues such as Glu22 into hydrophobic residues have been found to increase the aggregation of Aβ as a function of the mutation’s hydrophobicity.14,32 We identified three distinct elongation stages involving three sets of hydrophobic residues. The first set of residues included Ala30, Ile31, and Ile32, which initially showed stable Cα–Cα distances until RC reached a value of 5 Å (Figure 3), consistent with the first peak in the free energy profile. The second peak in the free energy profile can be identified with residues Ala21, Ala30, and Ile32 (Figure 4). Ala21 presented a particularly abrupt increment in the Cα–Cα distance at RC ∼ 9 Å, in conjunction with transitions in the Cα–Cα distances of Ala30 and Ile32, which had already contributed to the first peak (Figure 3). The third peak (Figure 5), corresponding to the undock step resulted from the overall contribution of hydrophobic amino acids in the C-terminus of Aβ: Leu34, Met35, Val36, Val39, and Val40. Our results indicated that the Cα distances of this third group transitioned abruptly at RC around 12–13 Å, which we attribute to a breakage of the associated hydrophobic contacts among the residues that provide stability and promote the well-organized assembly of Aβ filaments. Of this last set, Leu34, Met35, and Val36 had been identified as being highly flexible by solid state 2H NMR line shape experiments.33 In particular, this NMR study identified Val36 as having the highest conformational variability for the Iowa mutant, which agrees with our results. Snapshots of the three elongation stages are shown in Figure 1, bottom. Trajectory movies showing snapshots centered around these peaks and highlighting the residues involved are available in the Supporting Information as Movies 1, 2, and 3.

Figure 3.

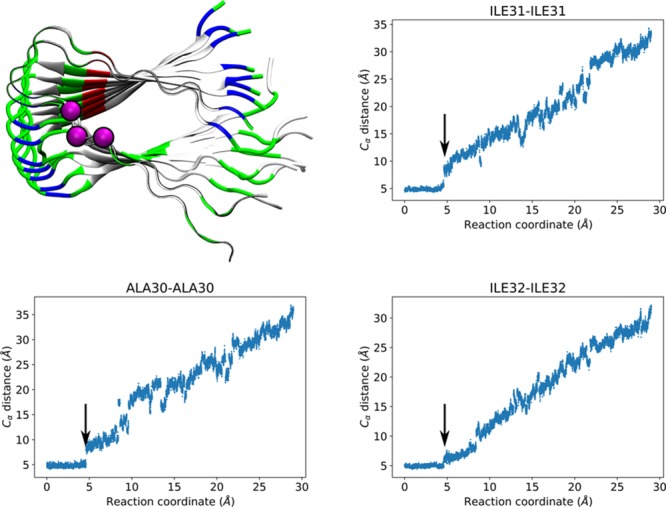
Figure 3

Open in a new tab

Residues involved in the first peak of the PMF. Top left: Alpha carbons of Ala30, Ile31, and Ile32 represented as magenta-colored spheres. P0 and P1 are shown as ribbons colored by residue type (white for hydrophobic, green for hydrophilic, blue for positively charged, and red for negatively charged), while the rest of the peptides are shown in cartoon representation colored by residue type. Top right, bottom left and right: Distance between corresponding alpha carbons of P0 and P1 as a function of the reaction coordinate. Arrows highlight the transition, occurring at displacements consistent with the first peak.

Figure 4.

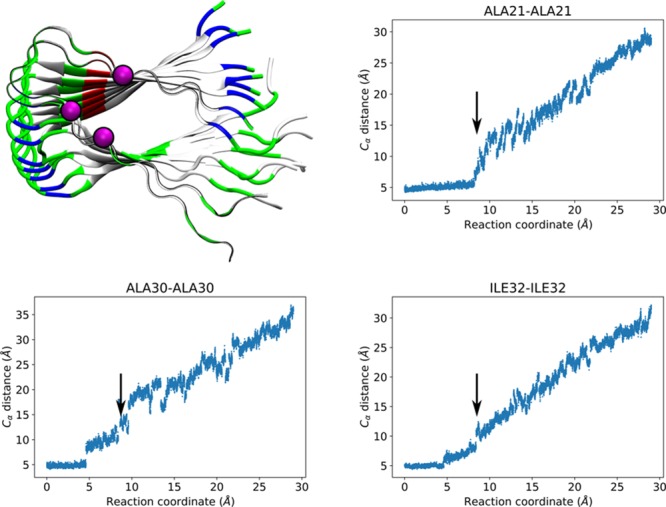
Figure 4

Open in a new tab

Residues involved in the second peak of the PMF. Top left: Alpha carbons of Ala21, Ala30, Ile32 represented as magenta-colored spheres. P0 and P1 are shown as ribbons colored by residue type (white for hydrophobic, green for hydrophilic, blue for positively charged, and red for negatively charged) while the rest of the peptides are shown in cartoon representation colored by residue type. Top right, bottom left and right: Distance between corresponding alpha carbons of P0 and P1 as a function of the reaction coordinate. Arrows highlight the transition, occurring at displacements consistent with the second peak.

Figure 5.

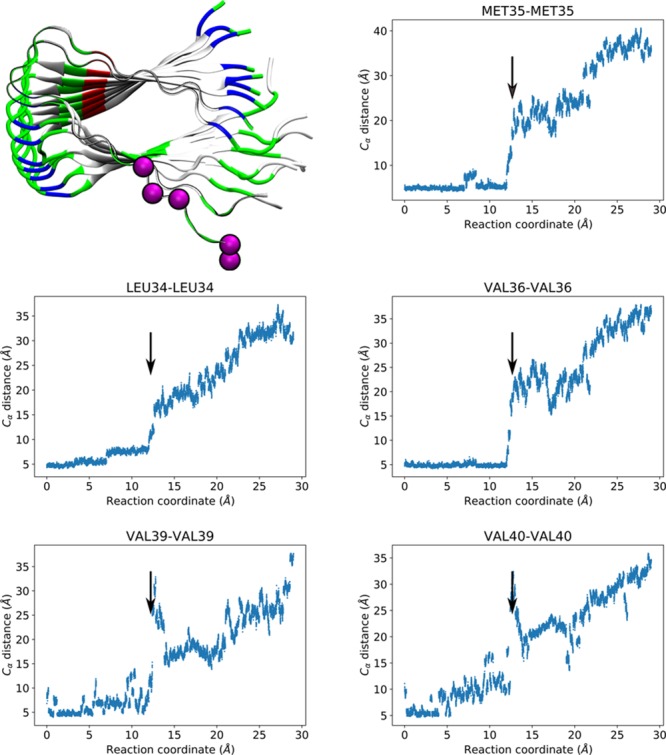
Figure 5

Open in a new tab

Residues involved in the third peak of the PMF. Top left: Alpha carbons of Leu34, Met35, Val36, Val39, and Val40 represented as magenta-colored spheres. P0 and P1 are shown as ribbons colored by residue type (white for hydrophobic, green for hydrophilic, blue for positively charged, and red for negatively charged), while the rest of the peptides are shown in cartoon representation colored by residue type. Top right, bottom left and right: Distance between corresponding alpha carbons of P0 and P1 as a function of the reaction coordinate. Arrows highlight the transition, occurring at displacements consistent with the third peak.

Recently, Mason et al.34 studied the self-assembly of phenylalanine dimers and found that they exhibit remarkably similar activation parameters compared to full-length Aβ42. The importance of these residues in the assembly of Aβ filaments has been recognized in multiple studies.35,36 Our metric of measuring the corresponding Cα distances between hydrophobic residues of P0 and P1 did not reveal the same abrupt transitions for Phe19, Phe20 as it did for the residues in Figures 3–5. However, the aromatic interactions between these residues are still significant for the peptide–aggregate interactions. In Figure S4 in the Supporting Information, we show the Cα–Cα distances between P0 and P1 for every pair of hydrophobic residues of the Aβ15–40 atomic model as a function of the reaction coordinate.

Our simulations indicate that the C-terminal hydrophobic residues are responsible for the initial docking stage. In contrast, previous studies19,20,37 have identified the central hydrophobic core as the initial point of attachment. In the study by Gurry et al.19 and the work by Han et al.,20 both groups positionally restrained the atoms of the core filament. We, on the other hand, only fixed the alpha carbons on P4 (Figure 2), which allows us to capture the dynamics between the incoming monomer (P0) and the topmost layer of the aggregate (P1). Recently, Bacci et al.37 used advanced sampling techniques to probe the monomer-filament interactions that give rise to the slow locking pathways. Our findings are in complement to theirs since our study focused on the Arrhenius barrier for elongation rather than the complex conformational rearrangement that accompanies the slower aggregation steps of Aβ. In addition, our findings on the importance of the dynamics of P1 for elongation are consistent with the study by Bacci et al., which also illustrated the role of the penultimate peptide in the elongation process.37

Release of Water Molecules from Filaments

Aβ is generated by endoproteolysis of AβPP, a Type I transmembrane protein of 695–770 amino acids. The fragment corresponding to Aβ is part of the transmembrane domain, originally located in a hydrophobic environment of the cell membrane. Upon release of Aβ, it can exist in multiple assembly states (monomer, oligomers, protofilaments and filaments). The filament assembly process is complex, nucleation-dependent and the mechanism driving this process is not well-understood.39 In the aggregate state, the P0–P1 interface is essentially devoid of water molecules.23,24 Our simulations along the unbinding pathway showed that a hydration layer begins to form around P0 and over the exposed surface of the aggregate. Figure 6 shows the number of water molecules (Nw) within 5 Å of P0 or the aggregate as a function of the reaction coordinate. A trajectory movie showing the formation of a hydration layer as the peptide transverses the binding pathway is available in the Supporting Information as Movie 4. We highlight that these water molecules are located outside the inner filament. Interestingly, a recent report37 suggests that protofibril-internal waters do not contribute to the elongation process. In the neurodegenerative context, the opposite phenomenon occurs, where the incoming or newly formed Aβ monomers or dimers are fully hydrated (in the cerebrospinal fluid) and will achieve a dry interface state directly related to the approach distance to the filament template. This assembly process is repeated until the formation of mature fibers, diffuse plaques and neuritic plaques in the affected areas of the brain. Hydrophobic residues of Aβ mediate specific interactions that direct the self-assembly and are sufficient to promote Aβ aggregation as confirmed through site specific mutation variants of Aβ.40 Taken together, these results confirm the importance of hydrophobic residues in the aggregation mechanism.

Figure 6.

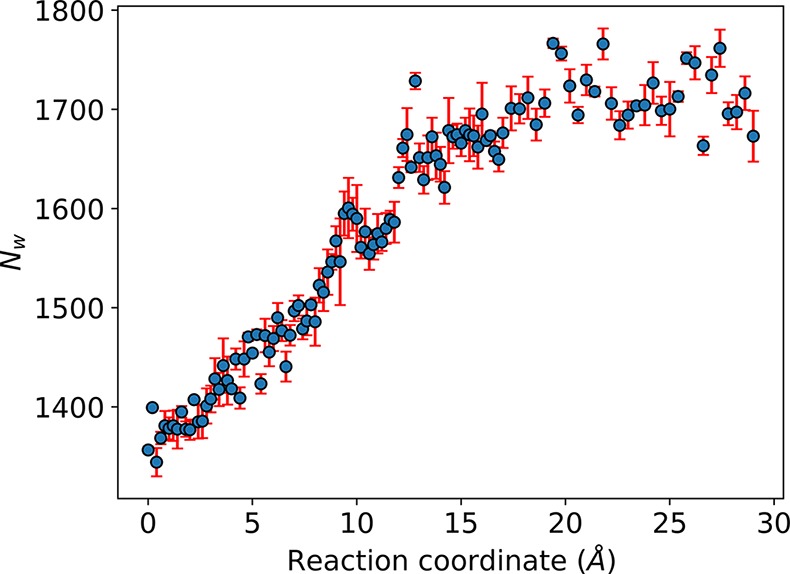
Figure 6

Open in a new tab

Waters surrounding the Aβ-peptide–filament system as a function of the reaction coordinate. Waters were considered to surround the system if their oxygen atoms were within 5 Å of either P0 or the filament. Error bars are standard deviations from the three sets used to calculate the free energy profiles in Figure 1.

Thermodynamics of Elongation

Additional insight into the origin of the energetic barriers of Aβ elongation is possible from analyses of the system’s enthalpy. For a better understanding of the individual thermodynamic contributions, we decomposed the total enthalpy into various components: solvent–P0 (SP), aggregate–P0 (AP), P0–P0 (PP), aggregate–aggregate (AA), solvent–solvent (SS), and solvent–aggregate (SA). These individual contributions can be further dissected into bonded and nonbonded interactions, the latter of which consist of electrostatics and van der Waals (vdW) interactions. The relevant hydrophobic contacts identified in Figures 3–5 are primarily based on vdW interactions, which are distance-dependent and are weakened as P0 undergoes the corresponding unlocking/undocking steps. As P0 is progressively exposed to the solvent, we expect the vdW interactions between the solvent and P0 to increase. Figure 7 shows the total, the vdW, and the electrostatic interactions between the solvent and P0 as well as between the aggregate and P0 as a function of P0s displacement. Note how the displacement at which the vdW plot rapidly increases (for SP) is consistent with the transition states of Figure 1. Similar decompositions for the peptide–peptide, aggregate–aggregate, solvent–aggregate, and solvent–solvent subsystems are shown in Figures S2 and S3 in the Supporting Information. It should be noted that, while the computation of the free energy profile is robust, the decomposed interactions are much less so. This is, in part, a consequence of the limited sample space molecular dynamics simulations can probe. Figure 7 thus reveals qualitatively consistent trends with our robust PMF results in Figure 1, but have limited quantitatively predictive power.

Figure 7.

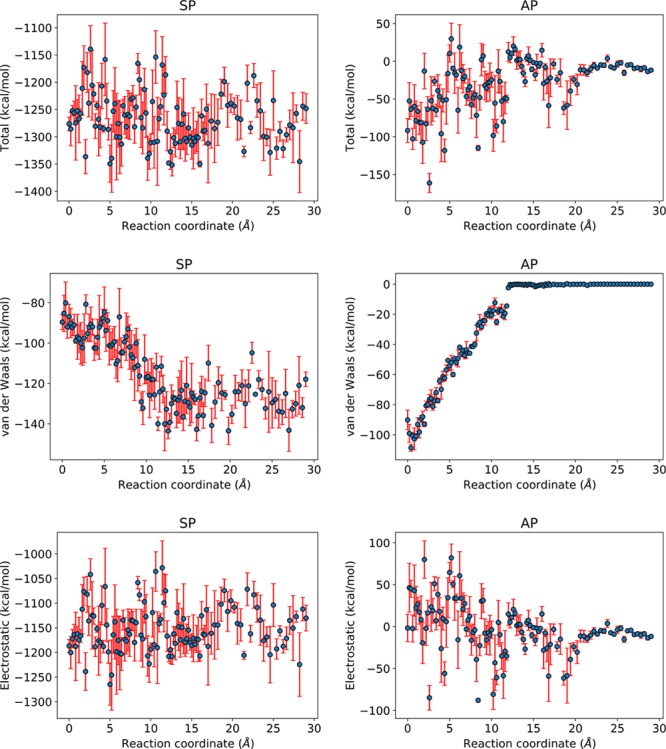
Figure 7

Open in a new tab

Energetics between the solvent and the peptide (SP) and the aggregate and the peptide (AP) along the binding pathway. Left column: Total, vdW, and electrostatic interaction along the binding pathway for SP. Right column: Total, vdW, and electrostatic interaction along the binding pathway for AP. The rapid transitions and subsequent relaxations in the vdW plots are consistent with the free energy profile of Figure 1. In particular, the subtle jumps at displacements ∼9 and ∼12 Å in the AP vdW plot are consistent with those of Figures 3 and 4.

The elongation steps present in our results involve dynamical fluctuations between the incoming monomer (P0) and the topmost layer of the filament (P1). In particular, P1 undergoes significant structural changes in order to “welcome” P0 onto the preformed filament. Dynamics similar to these have been described previously, e.g., Bacci et al.37 identified multiple putative docking states associated with increased disorder at the filament tip. The consistency between our decomposed enthalpies and the fluctuations between P0 and P1, quantified by their hydrophobic Cα-Cα distances (Figures 3–5), serves to corroborate our proposed atomistic mechanism of filament elongation.

In summation, we simulated an elongation event for the D23N “Iowa” mutant of Aβ15–40 by steering six α carbons on the odd end of the filament. By equilibrating the system under the steering constraints, we determined the overall free energy of the system along the 18-dimensional (6 × 3 degrees of freedom) most probable binding path. Our results show a free energy barrier (8.7 kcal/mol) consistent with experimental results showing that the elongation of Aβ is an activated process.

Along the elongation pathway, we found three distinguishable peaks in the free energy profile. Our analyses indicate that the origins of these peaks follow from the relevant hydrophobic interactions between the steered Aβ peptide and the template filament. The aggregation mechanism showed significant similarities to the dock-lock mechanism of filament elongation. Initially, a set of hydrophobic contacts from the C-terminus of the Aβ filament “docks” the incoming peptide to the preformed filament template, after which additional interactions “lock” it in place. This process also releases water molecules that were part of the hydration shell of the Aβ peptide and the exposed filament surface.

Analyzing the energetics of our system reveals consistent trends with the hydrophobic interactions we identified along the elongation pathway. By decomposing the total enthalpy of the system into pair contributions and further dissecting these into bonded and nonbonded interactions, it was possible to identify distinct transitions in the van der Waals interaction energies between the steered Aβ peptide and the solvent, as well as between the steered Aβ peptide and the Aβ filament at reaction coordinate values of ∼5, 9, and 12 Å, consistent with the transition states in the free energy profile. The specific identification and classification of individual contributions of hydrophobic amino acids to the self-assembly process of Aβ peptides provides valuable information on the most critical and reactive sites triggering the formation/stabilization of Aβ filaments. This information may open opportunities for the design of novel diagnostic or therapeutic compounds that specifically target these active subdomains in Aβ.

Methods

System Preparation and Equilibrium Dynamics

The starting point for our simulations was the NMR structure for the in-register, parallel, D23N Iowa mutant of Aβ15–40 filaments (PDB ID: 2MPZ) determined by Sgourakis et al.41 We extracted a single filament/aggregate (Figure 2) from the trimeric structure (chains A, D, G, J, M, P, S, V, Y) and fully solvated it by adding water molecules (TIP3P42) in a box with dimensions of 80 × 80 × 100 Å3. Then, we added counterions to neutralize the system and set the NaCl concentration to 150 mM, mimicking the physiological conditions of the cerebrospinal fluid (ionic strength and pH). We used NAMD 2.1243 in conjunction with the CHARMM3644 force field for the equilibrium simulations. We optimized the structure in the isobaric–isothermal (NPT) ensemble for 10 ps after which we equilibrated the system for 22 ns. We used the Nosé–Hoover barostat with a piston target of 1 bar. We also used Langevin dynamics with a friction coefficient γ of 5/ps for the thermal control. For electrostatics calculations, we used periodic boundary conditions with the particle-mesh Ewald method (with grid points of 128 × 128 × 128). We used a time step of 1 fs for bonded interactions, 2 fs for short-range nonbonded interactions, and 4 fs for long-range nonbonded interactions.

Sampling the Transition States of Aβ

Starting from the final state of the equilibrium simulations, we steered the alpha carbons of residues Gln15, Phe20, Gly25, Asn27, Gly33, and Val40 (the collective positions of which will be denoted as R = {r15,r20,r25,r27,r33,r40}, where rj denotes the position vector of residue j’s α carbon) of the odd tip (peptide P0) of the Aβ filament as shown in Figure 2. We steered the alpha carbons (R) along the filament axis at a rate of 2.5 Å/ns. We chose as our reaction coordinate the center of mass displacement of R along the filament axis (that is, if we define the center of mass position rcm as 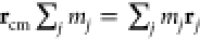Inline graphic, then the reaction coordinate is the component of rcm along the filament axis) with respect to the initial configuration. Each steering segment was followed by 4 ns of relaxation in the degrees of freedom orthogonal to the reaction coordinate (by disallowing fluctuations of the steered alpha carbons). This is similar to the gentlest ascent algorithm of Crippen and Scheraga.27 Restricting the movement of the alpha carbons is also necessary to ensure each subsequent steering section is continuous with the previous one, that is, the configuration of the steered carbons at the end of section j is identical to the one at the beginning of section j + 1. We divided the dissociation pathway into 115 sections, the first 85 of which were 0.2 Å in length, while the remaining covered 0.4 Å each. The choice of atoms to steer is guided by how well they represent the overall position and orientation of the peptide. Different choices may lead to convergence issues for the free energy profile. Additional details regarding the PMF computation can be found in the Supporting Information.

To calculate the Gibbs free energy (ΔG or the PMF) as a function of P0s displacement, we employed thermodynamic integration. First, we equilibrated the resulting states at the end of each steering section for an additional 2 ns (for a total initial equilibration of 6 ns because of the initial 4 ns between each steering segment). Second, we conducted three independent 1 ns long samplings for the mean force acting on the steered atoms, where each data set was used as the input for the next one, i.e., the first set was sampled for 6 + 1 ns (discarding 6 ns), the second one for 6 + 1 + 1 ns (discarding 7 ns) and the third set was sampled for 6 + 1 + 1 + 1 ns (discarding 8 ns). This was done to improve the statistics of our results as well as to test the convergence of the method used. The positions of the steered alpha carbons were not allowed to fluctuate during this sampling, but the forces acting on them were recorded during the course of the simulations. By integrating over the mean force on the steered atoms, we are effectively calculating the thermodynamic integral along the 18-dimensional curve defined by the displacement of the 3 × 6 degrees of freedom of the steered atoms in the phase space. If the steering speed is low enough and/or the system has been equilibrated enough, the steering pathway will be near the MPP of the physically feasible unbinding pathway (the reverse of which represents the physical binding pathway). In addition, the free energy profile calculated from each set will converge to a common value, as seen in Figure 1. Two nonconverged trials, with initial equilibrations at each steering section of 4 and 5 ns, respectively, are shown in Figure S1 in the Supporting Information.

Acknowledgments

The authors acknowledge the computing resources provided by the Texas Advanced Computing Center (TACC) at the University of Texas at Austin.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acschemneuro.7b00409.

  • Convergence of the free energy profiles, nonbonded energy decomposition of the P0–P0, aggregate–aggregate, solvent–aggregate, and solvent–solvent subcategories, α carbon distances for hydrophobic residues of P0 and P1, and details on PMF computation (PDF)

  • Trajectory around the first peak of the free energy profile, highlighting the residues of Figure 3 (AVI)

  • Trajectory around the second peak of the free energy profile, highlighting the residues of Figure 4 (AVI)

  • Trajectory around the third peak of the free energy profile, highlighting the residues of Figure 5 (AVI)

  • Trajectory of the unbinding pathway showing the hydration layer around the aggregate–P0 system (AVI)

Author Contributions

R.A.R and L.Y.C. conducted molecular dynamics simulations and analyzed data. All authors contributed to the manuscript.

This work was supported by the NIH (GM121275), the Semmes Foundation, the Lowe Foundation, and the Alzheimer’s Association (AARFD 17-529742).

The authors declare no competing financial interest.

Supplementary Material

cn7b00409_si_001.pdf (1.1MB, pdf)
cn7b00409_si_002.avi (1.1MB, avi)
cn7b00409_si_003.avi (839.7KB, avi)
cn7b00409_si_004.avi (875.4KB, avi)
cn7b00409_si_005.avi (4.6MB, avi)

References

  1. Dauer W.; Przedborski S. (2003) Parkinson’s disease: Mechanisms and models. Neuron 39, 889–909. 10.1016/S0896-6273(03)00568-3. [DOI] [PubMed] [Google Scholar]
  2. DiFiglia M.; Sapp E.; Chase K. O.; Davies S. W.; Bates G. P.; Vonsattel J. P.; Aronin N. (1997) Aggregation of huntingtin in neuronal intranuclear inclusions and dystrophic neurites in brain. Science 277, 1990–1993. 10.1126/science.277.5334.1990. [DOI] [PubMed] [Google Scholar]
  3. Hardy J.; Selkoe D. J. (2002) Medicine - The amyloid hypothesis of Alzheimer’s disease: Progress and problems on the road to therapeutics. Science 297, 353–356. 10.1126/science.1072994. [DOI] [PubMed] [Google Scholar]
  4. Kusumoto Y.; Lomakin A.; Teplow D. B.; Benedek G. B. (1998) Temperature dependence of amyloid beta-protein fibrillization. Proc. Natl. Acad. Sci. U. S. A. 95, 12277–12282. 10.1073/pnas.95.21.12277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Esler W. P.; Stimson E. R.; Jennings J. M.; Vinters H. V.; Ghilardi J. R.; Lee J. P.; Mantyh P. W.; Maggio J. E. (2000) Alzheimer’s disease amyloid propagation by a template-dependent dock-lock mechanism. Biochemistry 39, 6288–6295. 10.1021/bi992933h. [DOI] [PubMed] [Google Scholar]
  6. Cannon M. J.; Williams A. D.; Wetzel R.; Myszka D. G. (2004) Kinetic analysis of beta-amyloid fibril elongation. Anal. Biochem. 328, 67–75. 10.1016/j.ab.2004.01.014. [DOI] [PubMed] [Google Scholar]
  7. O’Nuallain B.; Shivaprasad S.; Kheterpal I.; Wetzel R. (2005) Thermodynamics of A beta(1–40) amyloid fibril elongation. Biochemistry 44, 12709–12718. 10.1021/bi050927h. [DOI] [PubMed] [Google Scholar]
  8. Ban T.; Yamaguchi K.; Goto Y. (2006) Direct observation of amyloid fibril growth, propagation, and adaptation. Acc. Chem. Res. 39, 663–670. 10.1021/ar050074l. [DOI] [PubMed] [Google Scholar]
  9. Buell A. K.; Dhulesia A.; White D. A.; Knowles T. P. J.; Dobson C. M.; Welland M. E. (2012) Detailed Analysis of the Energy Barriers for Amyloid Fibril Growth. Angew. Chem., Int. Ed. 51, 5247–5251. 10.1002/anie.201108040. [DOI] [PubMed] [Google Scholar]
  10. Qiang W.; Kelley K.; Tycko R. (2013) Polymorph-Specific Kinetics and Thermodynamics of beta-Amyloid Fibril Growth. J. Am. Chem. Soc. 135, 6860–6871. 10.1021/ja311963f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cohen S. I. A.; Linse S.; Luheshi L. M.; Hellstrand E.; White D. A.; Rajah L.; Otzen D. E.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2013) Proliferation of amyloid-beta 42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. U. S. A. 110, 9758–9763. 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Rojas A.; Maisuradze N.; Kachlishvili K.; Scheraga H. A.; Maisuradze G. G. (2017) Elucidating Important Sites and the Mechanism for Amyloid Fibril Formation by Coarse-Grained Molecular Dynamics. ACS Chem. Neurosci. 8, 201–209. 10.1021/acschemneuro.6b00331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Sasmal S.; Schwierz N.; Head-Gordon T. (2016) Mechanism of Nucleation and Growth of Aβ40 Fibrils from All-Atom and Coarse-Grained Simulations. J. Phys. Chem. B 120, 12088–12097. 10.1021/acs.jpcb.6b09655. [DOI] [PubMed] [Google Scholar]
  14. Zheng W.; Tsai M.-Y.; Chen M.; Wolynes P. G. (2016) Exploring the aggregation free energy landscape of the amyloid-β protein (1–40). Proc. Natl. Acad. Sci. U. S. A. 113, 11835–11840. 10.1073/pnas.1612362113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wu C.; Shea J.-E. (2011) Coarse-grained models for protein aggregation. Curr. Opin. Struct. Biol. 21, 209–220. 10.1016/j.sbi.2011.02.002. [DOI] [PubMed] [Google Scholar]
  16. Fawzi N. L.; Kohlstedt K. L.; Okabe Y.; Head-Gordon T. (2008) Protofibril assemblies of the arctic, dutch, and flemish mutants of the Alzheimer’s A beta(1–40) peptide. Biophys. J. 94, 2007–2016. 10.1529/biophysj.107.121467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fawzi N. L.; Okabe Y.; Yap E.-H.; Head-Gordon T. (2007) Determining the critical nucleus and mechanism of fibril elongation of the Alzheimer’s A beta(1–40) peptide. J. Mol. Biol. 365, 535–550. 10.1016/j.jmb.2006.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Takeda T.; Klimov D. K. (2009) Replica Exchange Simulations of the Thermodynamics of A beta Fibril Growth. Biophys. J. 96, 442–452. 10.1016/j.bpj.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gurry T.; Stultz C. M. (2014) Mechanism of Amyloid-beta Fibril Elongation. Biochemistry 53, 6981–6991. 10.1021/bi500695g. [DOI] [PubMed] [Google Scholar]
  20. Han W.; Schulten K. (2014) Fibril Elongation by A beta(17–42): Kinetic Network Analysis of Hybrid-Resolution Molecular Dynamics Simulations. J. Am. Chem. Soc. 136, 12450–12460. 10.1021/ja507002p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. O’Brien E. P.; Okamoto Y.; Straub J. E.; Brooks B. R.; Thirumalai D. (2009) Thermodynamic Perspective on the Dock-Lock Growth Mechanism of Amyloid Fibrils. J. Phys. Chem. B 113, 14421–14430. 10.1021/jp9050098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Santini S.; Mousseau N.; Derreumaux P. (2004) In silico assembly of Alzheimer’s A beta(16–22) peptide into beta-sheets. J. Am. Chem. Soc. 126, 11509–11516. 10.1021/ja047286i. [DOI] [PubMed] [Google Scholar]
  23. Nguyen P. H.; Li M. S.; Stock G.; Straub J. E.; Thirumalai D. (2007) Monomer adds to preformed structured oligomers of A beta-peptides by a two-stage dock-lock mechanism. Proc. Natl. Acad. Sci. U. S. A. 104, 111–116. 10.1073/pnas.0607440104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schwierz N.; Frost C. V.; Geissler P. L.; Zacharias M. (2016) Dynamics of Seeded Aβ40-Fibril Growth from Atomistic Molecular Dynamics Simulations: Kinetic Trapping and Reduced Water Mobility in the Locking Step. J. Am. Chem. Soc. 138, 527–539. 10.1021/jacs.5b08717. [DOI] [PubMed] [Google Scholar]
  25. Schwierz N.; Frost C. V.; Geissler P. L.; Zacharias M. (2017) From Aβ Filament to Fibril: Molecular Mechanism of Surface-Activated Secondary Nucleation from All-Atom MD Simulations. J. Phys. Chem. B 121, 671. 10.1021/acs.jpcb.6b10189. [DOI] [PubMed] [Google Scholar]
  26. Rodriguez R. A.; Chen L. Y.; Plascencia-Villa G.; Perry G. (2017) Elongation affinity, activation barrier, and stability of Aβ42 oligomers/fibrils in physiological saline. Biochem. Biophys. Res. Commun. 487, 444–449. 10.1016/j.bbrc.2017.04.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Crippen G. M.; Scheraga H. A. (1971) Minimization of polypeptide energy: XI. The method of gentlest ascent. Arch. Biochem. Biophys. 144, 462–466. 10.1016/0003-9861(71)90349-3. [DOI] [PubMed] [Google Scholar]
  28. Kirkwood J. G. (1935) Statistical mechanics of fluid mixtures. J. Chem. Phys. 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  29. Hasegawa K.; Ono K.; Yamada M.; Naiki H. (2002) Kinetic Modeling and Determination of Reaction Constants of Alzheimer’s β-Amyloid Fibril Extension and Dissociation Using Surface Plasmon Resonance. Biochemistry 41, 13489–13498. 10.1021/bi020369w. [DOI] [PubMed] [Google Scholar]
  30. Young L. J.; Kaminski Schierle G. S.; Kaminski C. F. (2017) Imaging Aβ(1–42) fibril elongation reveals strongly polarised growth and growth incompetent states. Phys. Chem. Chem. Phys. 19, 27987–27996. 10.1039/C7CP03412A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Gremer L.; Schölzel D.; Schenk C.; Reinartz E.; Labahn J.; Ravelli R. B. G.; Tusche M.; Lopez-Iglesias C.; Hoyer W.; Heise H.; Willbold D.; Schröder G. F. (2017) Fibril structure of amyloid-β(1–42) by cryoelectron microscopy. Science 358, 116. 10.1126/science.aao2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Päiviö A.; Jarvet J.; Gräslund A.; Lannfelt L.; Westlind-Danielsson A. (2004) Unique Physicochemical Profile of β-Amyloid Peptide Variant Aβ1–40E22G Protofibrils: Conceivable Neuropathogen in Arctic Mutant Carriers. J. Mol. Biol. 339, 145–159. 10.1016/j.jmb.2004.03.028. [DOI] [PubMed] [Google Scholar]
  33. Vugmeyster L.; Clark M. A.; Falconer I. B.; Ostrovsky D.; Gantz D.; Qiang W.; Hoatson G. L. (2016) Flexibility and Solvation of Amyloid-β Hydrophobic Core. J. Biol. Chem. 291, 18484–18495. 10.1074/jbc.M116.740530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mason T. O.; Michaels T. C. T.; Levin A.; Dobson C. M.; Gazit E.; Knowles T. P. J.; Buell A. K. (2017) Thermodynamics of Polypeptide Supramolecular Assembly in the Short-Chain Limit. J. Am. Chem. Soc. 139, 16134–16142. 10.1021/jacs.7b00229. [DOI] [PubMed] [Google Scholar]
  35. Gazit E. (2007) Self Assembly of Short Aromatic Peptides into Amyloid Fibrils and Related Nanostructures. Prion 1, 32–35. 10.4161/pri.1.1.4095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Genji M.; Yano Y.; Hoshino M.; Matsuzaki K. (2017) Aromaticity of Phenylalanine Residues Is Essential for Amyloid Formation by Alzheimer’s Amyloid β-Peptide. Chem. Pharm. Bull. 65, 668–673. 10.1248/cpb.c17-00203. [DOI] [PubMed] [Google Scholar]
  37. Bacci M.; Vymětal J.; Mihajlovic M.; Caflisch A.; Vitalis A. (2017) Amyloid β Fibril Elongation by Monomers Involves Disorder at the Tip. J. Chem. Theory Comput. 13, 5117–5130. 10.1021/acs.jctc.7b00662. [DOI] [PubMed] [Google Scholar]
  38. Humphrey W.; Dalke A.; Schulten K. (1996) VMD: Visual molecular dynamics. J. Mol. Graphics 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  39. LaFerla F. M.; Green K. N.; Oddo S. (2007) Intracellular amyloid-beta in Alzheimer’s disease. Nat. Rev. Neurosci. 8, 499–509. 10.1038/nrn2168. [DOI] [PubMed] [Google Scholar]
  40. Kim W.; Hecht M. H. (2006) Generic hydrophobic residues are sufficient to promote aggregation of the Alzheimer’s Aβ42 peptide. Proc. Natl. Acad. Sci. U. S. A. 103, 15824–15829. 10.1073/pnas.0605629103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sgourakis N. G.; Yau W. M.; Qiang W. (2015) Modeling an in-register, parallel ″Iowa″ Aβ fibril structure using solid-state NMR data from labeled samples with Rosetta. Structure 23, 216–227. 10.1016/j.str.2014.10.022. [DOI] [PubMed] [Google Scholar]
  42. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. (1983) Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  43. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. (2005) Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. (2012) Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cn7b00409_si_001.pdf (1.1MB, pdf)
cn7b00409_si_002.avi (1.1MB, avi)
cn7b00409_si_003.avi (839.7KB, avi)
cn7b00409_si_004.avi (875.4KB, avi)
cn7b00409_si_005.avi (4.6MB, avi)

Articles from ACS Chemical Neuroscience are provided here courtesy of American Chemical Society

RESOURCES