Benchmarking NLDAS-2 Soil Moisture and Evapotranspiration to Separate Uncertainty Contributions

Abstract

Model benchmarking allows us to separate uncertainty in model predictions caused by model inputs from uncertainty due to model structural error. We extend this method with a “large-sample” approach (using data from multiple field sites) to measure prediction uncertainty caused by errors in (i) forcing data, (ii) model parameters, and (iii) model structure, and use it to compare the efficiency of soil moisture state and evapotranspiration flux predictions made by the four land surface models in the North American Land Data Assimilation System Phase 2 (NLDAS-2). Parameters dominated uncertainty in soil moisture estimates and forcing data dominated uncertainty in evapotranspiration estimates; however, the models themselves used only a fraction of the information available to them. This means that there is significant potential to improve all three components of the NLDAS-2 system. In particular, continued work toward refining the parameter maps and look-up tables, the forcing data measurement and processing, and also the land surface models themselves, has potential to result in improved estimates of surface mass and energy balances.

1. Introduction

Abramowitz et al. (2008) found that statistical models out-perform physics-based models at estimating land surface states and fluxes, and concluded that land surface models are not able to fully utilize information in forcing data. Gong et al. (2013) provided a theoretical explanation for this result, and also showed how to measure both the underutilization of available information by a particular model as well as the extent to which the information available from forcing data was unable to resolve the total uncertainty about the predicted phenomena. That is, they separated uncertainty due to forcing data from uncertainty due to imperfect models.

Dynamical systems models, however, are composed of three primary components (Gupta & Nearing, 2014): model structures are descriptions of and solvers for hypotheses about the governing behavior of a certain class of dynamical systems, model parameters describe details of individual members of that class of systems, and forcing data are measurements of the time-dependent boundary conditions of each prediction scenario. Gong et al.’s analysis did not distinguish between uncertainties that are due to a mis-parameterized model from those due to a misspecified model structure, and we propose that this distinction is important for directing model development and efforts to both quantify and reduce uncertainty.

The problem of segregating these three sources of uncertainty has been studied extensively (e.g., Keenan et al., 2012, Montanari & Koutsoyiannis, 2012, Schoniger et al., 2015, Liu & Gupta, 2007, Kavetski et al., 2006, Draper, 1995, Oberkampf et al., 2002, Wilby & Harris, 2006, Poulin et al., 2011, Clark et al., 2011). Almost ubiquitously, the methods that have been applied to this problem are based on the chain rule of probability theory (Liu & Gupta, 2007). These methods ignore model structural error completely (e.g., Keenan et al., 2012), require sampling a priori distributions over model structures (e.g., Clark et al., 2011), or rely on distributions derived from model residuals (e.g., Montanari & Koutsoyiannis, 2012). In all cases, results are conditional on the proposed model structure(s). Multi-model ensembles allow us to assess the sensitivity of predictions to a choice between different model structures, but they do not facilitate true uncertainty attribution or partitioning. Specifically, any distribution (prior or posterior) over potential model parameters and/or structures is necessarily degenerate (Nearing et al., 2015), and sampling from or integrating over such distributions does not facilitate uncertainty estimates that approach any true value.

Gong et al.’s (2013) theoretical development fundamentally solved this problem. They first measured the amount of information contained in the forcing data – that is, the total amount of information available for the model to translate into predictions¹ – and then showed that this represents an upper bound on the performance of any model (not just the model being evaluated). Deviation between a given model’s actual performance and this upper bound represents uncertainty due to errors in that model. The upper bound can – in theory – be estimated using an asymptotically accurate empirical regression (e.g., Cybenko, 1989, Wand & Jones, 1994). That is, estimates and attributions of uncertainty produced by this method approach correct values as the amount of evaluation data increases – something that is not true for any method that relies on sampling from degenerate distributions over models.

In this paper, we extend Gong et al.’s analysis of information use efficiency to consider model parameters. We do this by using a “large-sample” approach (Gupta et al., 2013) that requires field data from a number of sites. Formally, this is an example of model benchmarking (Abramowitz, 2005). A benchmark consists of (i) a specific reference value for (ii) a particular performance metric that is computed against (iii) a specific data set. Benchmarks have been used extensively to test land surface models (e.g., van den Hurk et al., 2011; Best et al., 2011; Abramowitz, 2012; Best et al., 2015). They allow for direct and consistent comparisons between different models, and although it has been argued that they can be developed to highlight potential model deficiencies (Luo et al., 2012), there is no systematic method for doing so (see discussion by Beck et al., 2009). What we propose is a systematic benchmarking strategy that at least lets us evaluate whether the problems with land surface model predictions are due primarily to forcings, parameters, or structures.

We applied the proposed strategy to benchmark the four land surface models that constitute the second phase of the North American Land Data Assimilation System (NLDAS-2; Xia et al., 2012a, Xia et al., 2012b), which is a continental-scale ensemble land modeling and data assimilation system. The structure of the paper is as follows. A brief and general theory of model performance metrics is given in the Appendix, along with an explanation of the basic concept of information-theoretic benchmarking. The strategy is general enough to be applicable to any dynamical systems model. The remainder of the main text describes the application of this theory to the NLDAS-2. Methods are given in Section 2 and results in Section 3. Section 4 offers a discussion both about the strengths and limitations of information-theoretic benchmarking in general, and also about how the results can be interpreted in context of our application to NLDAS-2.

2. Methods

2.1. NLDAS-2

The NLDAS-2 produces distributed hydrometeorological products over CONUS used primarily for drought assessment and NWP initialization. NLDAS-2 is the second generation of the NLDAS, which became operational at the National Center for Environmental Protection in 2014. Xia et al. (2012b) provided extensive details about the NLDAS-2 models, forcing data, and parameters, and so we will present only a brief summary here. NLDAS-2 runs four land surface models over a North American domain (125° to 67° W, 25° to 53° N) at 1/8° resolution: (1) Noah, (2) Mosaic, (3) the Sacramento Soil Moisture Accounting (SAC-SMA) model, and (4) the Variable Infiltration Capacity (VIC) model. Noah and Mosaic run at a 15-minute timestep whereas SAC-SMA and VIC run at an hourly timestep; however, all produce hourly time-averaged output of soil moisture in various soil layers and evapotranspiration at the surface. Mosaic has three soil layers with depths of 10 cm, 30 cm, and 160 cm. Noah uses four soil layers with depths of 10 cm, 30 cm, 60 cm, and 100 cm. SAC-SMA uses conceptual water storage zones that are post-processed to produce soil moisture values at the depths of the Noah soil layers. VIC uses a 10 cm surface soil layer and two deeper layers with variable soil depths. Here we are concerned with estimating surface and root-zone (top 100 cm) soil moistures. The former is taken to be the moisture content of the top 10 cm (top layer of each model), and the latter as the depth-weighted average over the top 100 cm of the soil column.

Atmospheric data from the North American Regional Reanalysis (NARR), which is natively at 32 km spatial resolution and 3 h temporal resolution, is interpolated to the 15 minute and 1/8° resolution required by NLDAS-2. NLDAS-2 forcing also includes several observational datasets including a daily gage-based precipitation, which is temporally disaggregated to hourly using a number of different data sources, as well as satellite-derived shortwave radiation used for bias-correction. A lapse-rate correction between the NARR grid elevation and the NLDAS grid elevation was also applied to several NLDAS-2 surface meteorological forcing variables. NLDAS forcings consist of eight variables: 2 m air temperature (K), 2 m specific humidity (kg kg⁻¹), 10 m zonal and meridional wind speed (m s⁻¹), surface pressure (kPa), hourly-integrated precipitation (kg m⁻²), and incoming longwave and shortwave radiation (W m⁻²). All models act only on the total windspeed, and in this study we also used only the net radiation (sum of shortwave and longwave) so that a total of six forcing variables were considered at each timestep.

Parameters used by each model are listed in Table 1. The vegetation and soil classes are categorical variables and are therefore unsuitable for using as regressors in our benchmarks. The vegetation classification indices were mapped onto a five-dimensional real-valued parameter set using the UMD classification system (Hansen et al., 2000). These real-valued vegetation parameters included optimum transpiration air temperature (called topt in the Noah model and literature), a radiation stress parameter (rgl), maximum and minimum stomatal resistances (rsmax and rsmin), and a parameter used in the calculation of vapor pressure deficit (hs). Similarly, the soil classification indices were mapped for use in NLDAS-2 model to soil hydraulic parameters: porosity, field capacity, wilting point, a Clapp-Hornberger type exponent, saturated matric potential, and saturated conductivity. These mappings from class indices to real-valued parameters ensured that similar parameter values generally indicated similar phenomenological behavior. In addition, certain models use one or two time-dependent parameters: monthly climatology of greenness fraction, quarterly albedo climatology, and monthly leaf area index (LAI). These were each interpolated to the model timestep and so had different values at each timestep.

Table 1.

Parameters used by the NLDAS-2 LSMs

Parameter	Mosaic	Noah	SAC- SMA	VIC
Monthly GVF(a)	X	X
Snow-Free Albedo(a)		X
Monthly LAI(a)	X			X
Vegetation Class	X	X	X	X
Soil Class(b)	X	X	X	X
Maximum Snow Albedo		X
Max/Min GVF		X
Average Soil Temperature				X
3-Layer Porosity(c)	X			X
3-Layer Soil Depths				X
3-Layer Bulk Density				X
3-Layer Soil Density				X
3-Layer Residual Moisture				X
3-Layer Wilting Point(c)	X			X
3-layer Saturated Conductivity				X
Slope Type		X
Deep Soil Temperature(d)		X		X

^aLinearly interpolated to the timestep.

^bMapped to soil hydraulic parameters.

^cMosaic uses a different 3-layer porosity and wilting point than VIC.

^dNoah and VIC use different deep soil temperature values.

2.2. Benchmarks

As mentioned in the introduction, a model benchmark consists of three components: a particular data set, a particular performance metric, and a particular reference value for that metric. The following subsections describe these three components of our benchmark analysis of NLDAS-2.

2.2.1. Benchmark Data Set

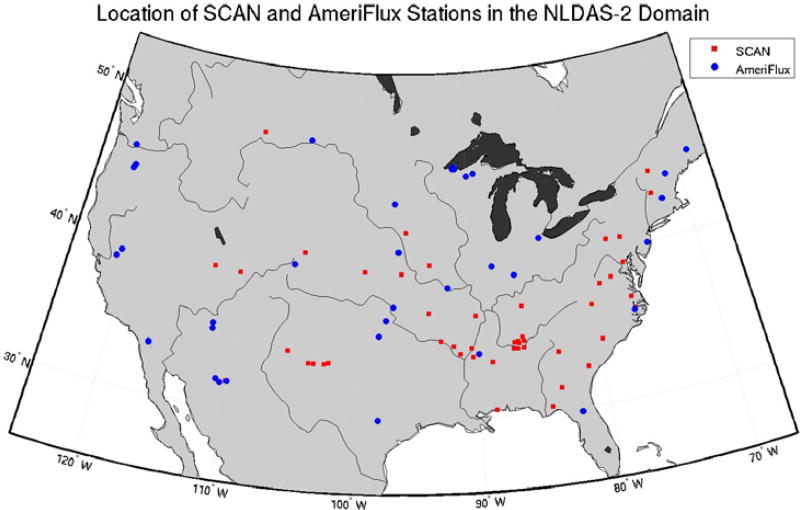
As was done by Kumar et al. (2014) and Xia et al. (2014a), we evaluated the NLDAS-2 models against quality controlled hourly soil moisture observations from the Soil Climate Analysis Network (SCAN). Although there are over one hundred operational SCAN sites, we used only those forty-nine sites with at least two years worth of complete hourly data during the period of 2001–2011. These sites are distributed throughout the NLDAS-2 domain (Figure 1). The SCAN data have measurement depths of 5 cm, 10 cm, 20.3 cm, 51 cm, and 101.6 cm (2, 4, 8, 20, and 40 inches), and were quality controlled (Liu et al. 2011) and depth averaged to 10 cm and 100 cm to match the surface and root-zone depth-weighted model estimates.

Figure 1.

Location of the SCAN and AmeriFlux stations used in this study. Each SCAN station contributed two year’s worth of hourly measurements (17,520) and each AmeriFlux station contributed four thousand hourly measurements to the training of the model regressions.

For evapotranspiration (ET), we used level 3 station data from the AmeriFlux network (Baldocchi et al., 2001). We used only those fifty sites that had at least four thousand timesteps worth of hourly data during the period 2001–2011. The AmeriFlux network was also used by Mo et al. (2011) and by Xia et al. (2014b) for evaluation of the NLDAS-2 models, and a gridded flux dataset from Jung et al. (2009), based on the same station data, was used by Peters-Lidard et al. (2011) to assess the impact on ET estimates of soil moisture data assimilation in the NLDAS framework.

2.2.2. Benchmark Metrics and Reference Values

Nearing & Gupta (2015) provide a brief overview of the theory of model performance metrics, and the general formula for a performance metric is given in the Appendix. All performance metrics measure some aspect (either quantity or quality) of the information content of model predictions, and the metric that we propose here uses this fact explicitly.

The basic strategy for measuring uncertainty due to model errors is to first measure the amount of information available in model inputs (forcing data and parameters) and then to subtract the information that is contained in model predictions. The latter is always less than the former since the model is never perfect, and this difference measures uncertainty (i.e., lack of complete information) that is due to model error (Nearing & Gupta, 2015). This requires that we measure information (and uncertainty) using a metric that behaves so that the total quantity of information available from two independent sources is the sum of the information available from either source. The only type of metric that meets this requirement is based on Shannon’s (1948) entropy, so we use this standard definition of information and accordingly measure uncertainty as (conditional) entropy (the Appendix contains further explanation).

To segregate the three sources of uncertainty (forcings, parameters, structures), we require three reference values. The first is the total entropy of the benchmark observations, which is notated as H(z) where z represents observations. Strictly speaking, H(z) is the amount of uncertainty that one has when drawing randomly from the available historical record, and this is equivalent, at least in the context of the benchmark data set, to the amount of information necessary to make accurate and precise predictions of the benchmark observations. Note that H(z) is calculated using all benchmark observations at all sites simultaneously, since the total uncertainty prior to adding any information from forcing data, parameters, or models includes no distinction between sites.

The second reference value measures information about the benchmark observations contained in model forcing data. This is notated as I(z; u) where I is the Mutual Information Function (Cover & Thomas, 1991; Chapter 2), and u represents the forcing data. Mutual information is the amount of entropy of either variable that is resolvable given knowledge of the other variable. For example, H(z|u) is the entropy (uncertainty) in the benchmark observations conditional on the forcing data, and is equal to the difference between total prior uncertainty less the information content of the forcing data: H(z|u) = H(z) − I(z; u). This difference, H(z|u), measures uncertainty that is due to errors or incompleteness in the forcing data.

Our third reference value is the total amount of information about the benchmark observations that is contained in the forcing data plus model parameters. This is notated as I(z; u, θ) where θ represents model parameters. As discussed in the introduction, θ is what differentiates between applications of a particular model to different dynamical systems (in this case, as applied at different SCAN or AmeriFlux sites), and it is important to understand that I(z; u) describes the relationship between forcing data and observations at a particular site, whereas I(z; u, θ) considers how the relationship between model forcings and benchmark observations varies between sites, and how much the model parameters can tell us about this inter-site variation. The following subsection (Section 2.2.3) describes how to deal with this subtlety when calculating these reference values, however for now the somewhat counterintuitive result is that it is always the case that I(z; u) is always greater than I(z; u, θ), since no set of model parameters can ever be expected to fully and accurately describe differences between field sites.

Finally, the actual benchmark performance metric is the total information available in model predictions y^ℳ, and is notated I(z; y^ℳ). Because of the Data Processing Inequality (see Appendix, as well as Gong et al., 2013), these four quantities will always obey the following hierarchy:

$$\mathrm{H}(\mathbf{z})\ge \mathrm{I}(\mathbf{z};\mathbf{u})\ge \mathrm{I}(\mathbf{z};\mathbf{u},\mathbf{\theta })\ge \mathrm{I}(\mathbf{z};{\mathbf{y}}^{ℳ}).$$ (1)

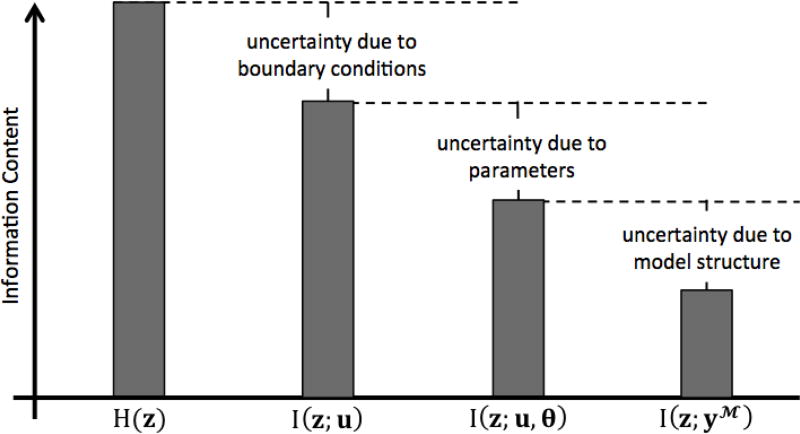
Furthermore, since Shannon information is additive, the differences between each of these ordered quantities represent the contribution to total uncertainty due to each model component. This is illustrated in Figure 2, which is adapted from Gong et al. (2013) to include parameters. The total uncertainty in the model predictions is H(z) − I(z; y^ℳ), and the portions of this total uncertainty that are due to forcing data, parameters, and model structure are H(z) − I(z; u), I(z; u) − I(z; u, θ), and I(z; u, θ) − I(z; y^ℳ) respectively.

Figure 2.

A conceptual diagram of uncertainty decomposition using Shannon information. H(z) represents the total uncertainty (entropy) in the benchmark observations. I(z; u) represents the amount of information about the benchmark observations that is available from the forcing data. Uncertainty due to forcing data is the difference between the total entropy and the information available in the forcing data. The information in the parameters plus forcing data is I(z; u, θ), and I(z; u, θ) < I(z; u) due to errors in the parameters. I(z; y^ℳ) is the total information available from the model and I(z; y^ℳ) < I(z; u, θ) due to model structural error. This figure is adapted from (Gong et al., 2013).

The above differences that measure uncertainty contributions can be reformulated as efficiency metrics. The efficiency of the forcing data is simply the fraction of resolvable entropy:

$${ℰ}_{\mathrm{u}}=\frac{\mathrm{I}(\mathbf{z};\mathbf{u})}{\mathrm{H}(\mathbf{z})}.$$ (2.1)

The efficiency of the model parameters to interpret information in forcing data independent of any particular model structure is:

$${ℰ}_{\mathrm{\theta }}=\frac{\mathrm{I}(\mathbf{z};\mathbf{u},\mathbf{\theta })}{\mathrm{I}(\mathbf{z};\mathbf{u})},$$ (2.2)

and the efficiency of any particular model structure at interpreting all of the available information (in forcing data and parameters) is:

$${ℰ}_{ℳ}=\frac{\mathrm{I}(\mathbf{z};{\mathbf{y}}^{\mathit{ℳ}})}{\mathrm{I}(\mathbf{z};\mathbf{u},\mathbf{\theta })}.$$ (2.3)

In summary, the benchmark performance metric that we use is Shannon’s mutual information function, I(z; y^ℳ), which measures the decrease in entropy (uncertainty) due to running the model. To decompose prediction uncertainty into its constituent components due to forcing data, parameters, and the model structure we require three benchmark reference values: H(z), I(z; u), and I(z; u, θ). These reference values represent a series of decreasing upper bounds on model performance, and appropriate differences between the performance metric and these reference values partition uncertainties. Similarly, appropriate ratios, given in equations (2), measure the efficiency of each model component at utilizing available information.

2.2.3. Calculating Information Metrics

Calculating the first reference value, H(z), is relatively straightforward. There are many ways to numerically estimate entropy and mutual information (Paninski, 2003), and here we used maximum likelihood estimators. A histogram was constructed using all N observations of a particular quantity (10 cm soil moisture, 100 cm soil moisture, or ET from all sites), and the first reference value was:

$$\mathrm{H}(\mathbf{z})=-\sum _{i=1}^B\frac{n_i}{N}\text{ln}\left(\frac{n_i}{N}\right)$$ (3.1)

where n_i is the histogram count for the i^th of B bins. The histogram bin-width determines the effective precision of the benchmark measurements, and we used a bin-width of 0.01 m³ m⁻³ (1% volumetric water content) for soil moisture and 5 W m⁻² for ET.

Similarly, the benchmark performance metric, I(z; y^ℳ), is also straightforward to calculate. In this case, a joint histogram was estimated using all observations and model predictions at all sites, and the joint entropy was calculated as:

$$\mathrm{H}(\mathbf{z},{\mathbf{y}}^{ℳ})=\sum _{i=1}^B\sum _{j=1}^B\frac{n_{i,j}}{N}\text{ln}\left(\frac{n_{i,j}}{N}\right).$$ (3.2)

We used square histogram bins so that the effective precision of the benchmark measurements and model predictions was the same, and for convenience we notate the same number of bins (B) in both dimensions. The entropy of the model predictions was calculated in a way identical to equation (3.1), and mutual information was:

$$\mathrm{I}(\mathbf{z};{\mathbf{y}}^{ℳ})=\mathrm{H}(\mathbf{z})+\mathrm{H}({\mathbf{y}}^{ℳ})-\mathrm{H}(\mathbf{z},{\mathbf{y}}^{ℳ}).$$ (3.3)

The other two intermediate reference values, I(z; u) and I(z; u, θ), are more complicated. The forcing data u was very high-dimensional because the system effectively acts on all past forcing data, therefore it is impossible to estimate mutual information using a histogram as above. To reduce the dimensionality of the problem we trained a separate regression of the form ${ℛ}_{\mathrm{i}}^{\mathrm{u}}:\left\{{\mathbf{u}}_{1:t,i}\right\}\to \left\{{\mathbf{z}}_{t,i}\right\}$ for each individual site where the site is indexed by i. That is, we used the benchmark observations from a particular site to train an empirical regression that mapped a (necessarily truncated) time-history of forcing data onto predictions ${\mathrm{y}}_{t,i}^{\mathrm{u}}={ℛ}_i^{\mathrm{u}}({\mathbf{u}}_{t-s:t,i})$. The reference value was then estimated as I(z; u) ≈ I(z; y^u) where I(z; y^u) was calculated according to equations (3) using all y^u data from all sites simultaneously. Even though a separate ${ℛ}_{\mathrm{i}}^{\mathrm{u}}$ regression was trained at each site, we did not calculate site-specific reference values.

As described in the Appendix, the ${ℛ}_i^{\mathrm{u}}$ regressions are actually kernel density estimators of the conditional probability density P(z_t,i|u_1:t,i), and to the extent that these estimators are asymptotically complete (i.e., they approach the true functional relationships between u and z at individual sites in the limit of infinite training data), I(z; y^u) approaches the true benchmark reference value.

I(z; u, θ) was estimated in a similar way; however, to account for the role of parameters in representing differences between sites, a single regression ℛ^u,θ: {u_1:t, θ} → {z_t} was trained using data from all sites simultaneously. This regression was used to produce estimates ${\mathrm{y}}_t^{\mathrm{u},\mathrm{\theta }}={ℛ}^{\mathrm{u},\mathrm{\theta }}({\mathbf{u}}_{t-s:t},\mathbf{\theta })$ at all sites, and these data were then used to estimate I(z; y^u,θ) according to equation (3).

It is important to point out that we did not use a split-record training/prediction for either the ${ℛ}_i^{\mathrm{u}}$ regressions at each site, nor for the ℛ^u,θ regressions trained with data from all sites simultaneously. This is because our goal was to measure the amount of information in the regressors (forcing data, parameters), rather than to develop a model that could be used to make future predictions. The amount of information in each set of regressors is determined completely by the injectivity of the regression mapping. That is, if the functional mapping from a particular set of regressors onto benchmark observations preserves distinctness, then those regressors provide complete information about the diagnostics – they are able to completely resolve H(z). If there is error or incompleteness in the forcing data or parameters data, or if these data are otherwise insufficient to distinguish between distinct system behavior (i.e., the system is truly stochastic or it is random up to the limit of the information in regressors), then the regressors lack complete information and therefore contribute to prediction uncertainty. For this method to work we must have sufficient data to identify this type of redundancy, and like all model evaluation exercises, the results are only as representative as the evaluation data.

2.2.4. Training the Regressions

A separate ${ℛ}_i^{\mathrm{u}}$ regression was trained at each site, so that in the soil moisture case there were ninety-eight (49 × 2) separate ${ℛ}_i^{\mathrm{u}}$ regressions, and in the ET case there were fifty separate ${ℛ}_i^{\mathrm{u}}$ regressions. In contrast, a single ℛ^u,θ regression was trained separately for each observation type and for each LSM (because the LSMs used different parameter sets) on data from all sites so that there were a total of twelve separate ℛ^u,θ regressions (10 cm soil moisture, 100 cm soil moisture, and ET for each of Noah, Mosaic, SAC-SMA, and VIC).

We used sparse Gaussian processes (SPGPs; Snelson & Ghahramani, 2006), which are kernel density emulators of differentiable functions. SPGPs are computationally efficient and very general in the class of functions that they can emulate. SPGPs use a stationary anisotropic squared exponential kernel (see Rasmussen & Williams, 2006 chapter 4) that we call an Automatic Relevance Determination kernel (ARD) for reasons that are described presently. Because the land surface responds differently during rain events than it does during dry-down, we trained two separate SPGPs for each observation variable to act on timesteps (1) during and (2) between rain events. Thus each ${ℛ}_i^{\mathrm{u}}$ and ℛ^u,θ regression consisted of two separate SPGPs.

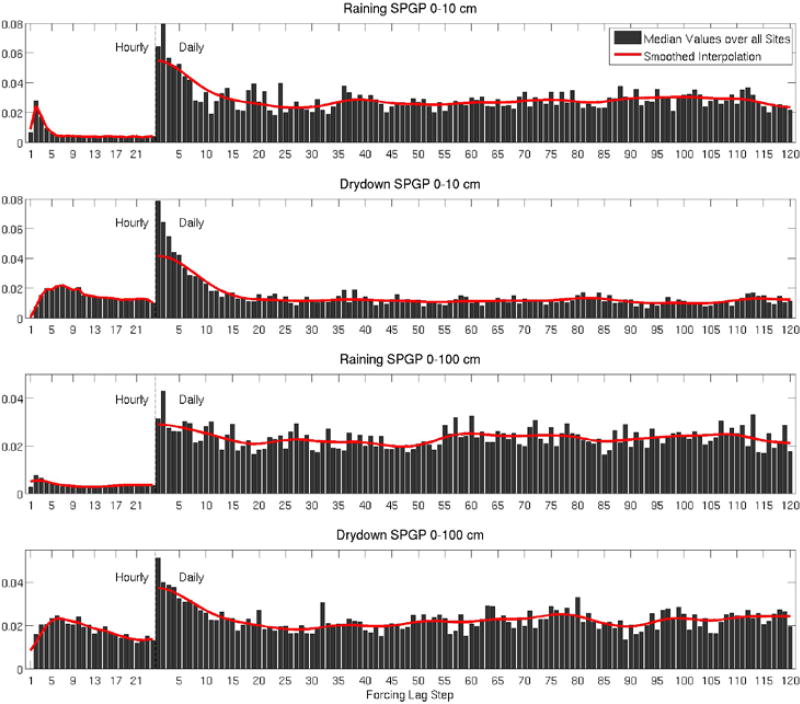
Because the NLDAS-2 models effectively act on all past forcing data, it was necessary for the regressions to act on lagged forcings. We used hourly-lagged forcings from the fifteen hours previous to time t plus daily averaged (or aggregated in the case of precipitation) forcings for the twenty-five days prior to that. These lag periods were chosen based on an analysis of the sensitivity of the SPGPs. The anisotropic ARD kernel assigns a separate correlation length to each input dimension in the set of regressors (Neil, 1993), and the correlation lengths of the ARD kernel were chosen as the maximum likelihood estimates conditional on the training data. Higher a posteriori correlation lengths (lower inverse correlation lengths) correspond to input dimensions to which the SPGP is less sensitive, which is why this type of kernel is sometimes called an Automatic Relevance Determination kernel – because it provides native estimates of the relative (nonlinear and nonparameteric) sensitivity to each regressor. We chose lag-periods for the forcing data that reflect the memory of the soil moisture at these sites. To do this, we trained rainy and dry SPGPs at all sites using only precipitation data over a lag period of twenty-four hours plus one hundred and twenty days. We then truncated the lag hourly and daily lag periods where the mean a posteriori correlation lengths stabilized at a constant value: fifteen hourly lags and twenty-five daily lags. This is illustrated in Figure 3. Since soil moisture is the unique long-term control on ET, we used the same lag period for ET as for soil moisture.

Figure 3.

Median ARD inverse correlation lengths from soil moisture SPGPs trained at each site using only lagged precipitation data. Inverse correlation lengths indicate a posteriori sensitivity to each dimension of the input data. The hourly inputs approach a minimum value around fifteen lag periods at the 100 cm depth and the daily inputs approach a minimum at around twenty-five lag periods at the 10 cm depth. This indicates that these lag periods are generally sufficient to capture the information from forcing data that is available to the SPGPs. All benchmark SPGPs were trained with these lag periods.

Because of the time lagged regressors, each SPGP for rainy timesteps in the ${ℛ}_i^{\mathrm{u}}$ regressions acted on two hundred and forty forcing inputs, and each SPGP for dry timesteps acted on two hundred and thirty-nine forcing data inputs (the latter did not consider the zero rain condition at the current time t). Similarly, the wet and dry SPGPs that constituted the ℛ^u,θ regressions acted on the same forcing data, plus the number parameter inputs necessary for each model (a separate ℛ^u,θ regression was trained for each of the four NLDAS-2 land surface models). Each ${ℛ}_i^{\mathrm{u}}$ regression for SCAN soil moisture was trained using two years worth of data (17,520 data points), and each ℛ^u,θ SCAN regression was trained on one hundred thousand data points selected randomly from the 49 × 17,520 = 858,480 available. The ${ℛ}_i^{\mathrm{u}}$ ET regressions were trained on four thousand data points and the ℛ^u,θ ET regressions were trained on one hundred thousand of the 50 × 4,000 = 200,000 available. All ${ℛ}_i^{\mathrm{u}}$ SPGPs used one thousand pseudo-inputs (see Snelson and Ghahramani, 2006 for an explanation of pseudo-inputs), and all ℛ^u,θ SPGPs used two thousand pseudo-inputs.

3. Results

3.1. Soil Moisture

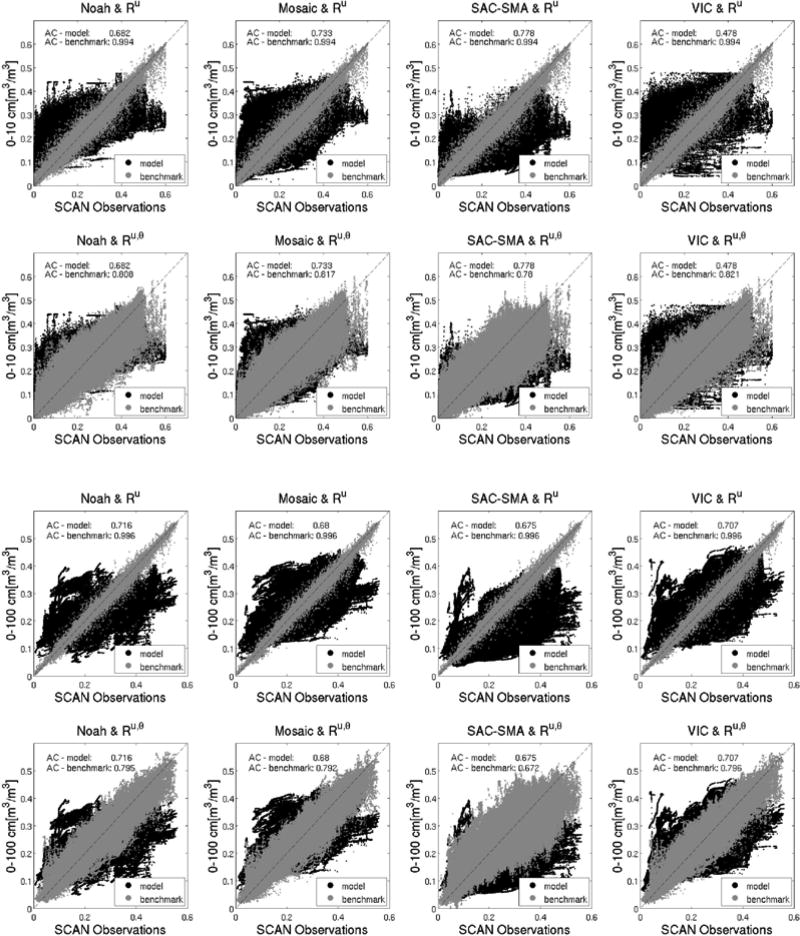
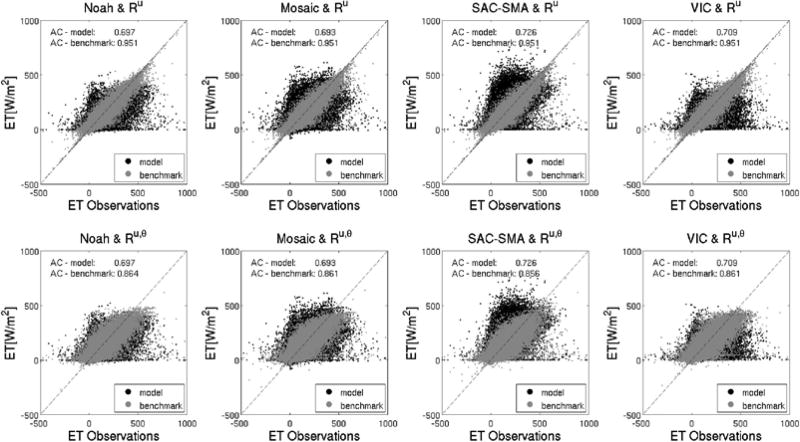
Figure 4 compares the model and benchmark estimates of soil moisture with SCAN observations, and also provides anomaly correlations for the model estimates, which for Noah were very similar to those presented by Kumar et al. (2014). The spread of the benchmark estimates around the 1:1 line represents uncertainty that was unresolvable given the input data – this occurred when we were unable to construct an injective mapping from inputs to observations. This happened, for example, near the high range of the soil moisture observations, which indicates that the forcing data was not representative of the largest rainfall events at these measurements sites. This might be due to localized precipitation events that are not always captured by the 1/8° forcing data, and is an example of the type of lack of representativeness that is captured by this information analysis – the forcing data simply lacks this type of information.

Figure 4.

Scatterplots of soil moisture observations and estimates made by the NLDAS-2 models (black) and by the benchmarks (gray) in both soil layers (top two rows for surface soil moisture; bottom two rows for top 100 cm soil moisture). The ${ℛ}_i^{\mathrm{u}}$ regressions (first and third rows) act on the forcing data only and the ℛ^u,θ regressions (second and fourth rows) act on forcing data plus parameters. The mean anomaly correlations over all sites are listed on each subplot.

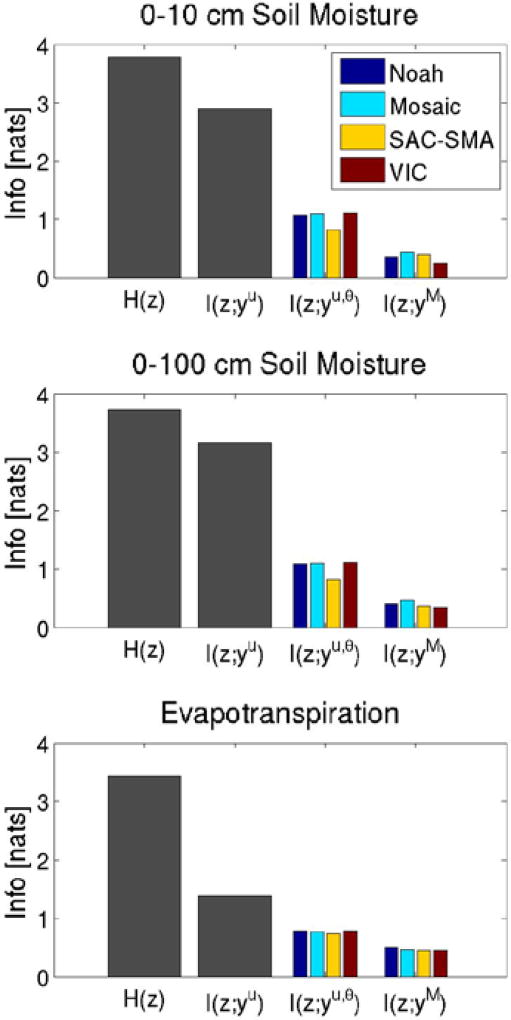
It is clear from these scatterplots that the models did not use all available information in the forcing data. In concordance with Abramowitz et al.’s (2008) empirical results and Gong et al.’s (2013) theory, the statistical models here outperformed the physics-based models. This is not at all surprising considering that the regressions were trained on the benchmark data set, which – to re-emphasize – is necessary for this particular type of analysis. Figure 5 reproduces the conceptual diagram from Figure 2 using the data from this study, and directly compares the three benchmark reference values with the values of benchmark performance metric. Table 2 lists the fractions of total uncertainty, i.e., H(z) − I(z; y^ℳ), that were due to each model component, and Table 3 lists the efficiency metrics calculated according to equations (2).

Figure 5.

The fraction of total uncertainty in soil moisture estimates contributed by each model component. These plots are conceptually identical to Figure 2 except that these use real data.

Table 2.

Fractions of total uncertainty due to forcings, parameters, and structures.

		Soil Moisture		ET
		10 cm	100 cm
Forcings	Noah	0.26	0.17	0.69
	Mosaic	0.26	0.17	0.69
	SAC-SMA	0.26	0.17	0.68
	VIC	0.25	0.17	0.68
Parameters	Noah	0.53	0.52	0.20
	Mosaic	0.54	0.54	0.21
	SAC-SMA	0.62	0.70	0.22
	VIC	0.51	0.51	0.20
Structures	Noah	0.21	0.31	0.10
	Mosaic	0.20	0.29	0.11
	SAC-SMA	0.12	0.14	0.10
	VIC	0.24	0.32	0.11

Table 3.

Efficiency of forcings, parameters and structures according to equations (2).

		Soil Moisture		ET
		10 cm	100 cm
Forcings		0.77	0.85	0.40
Parameters	Noah	0.37	0.45	0.57
	Mosaic	0.38	0.45	0.56
	SAC-SMA	0.28	0.26	0.53
	VIC	0.38	0.45	0.56
Structures	Noah	0.33	0.28	0.62
	Mosaic	0.40	0.34	0.60
	SAC-SMA	0.49	0.44	0.60
	VIC	0.22	0.24	0.57

The total uncertainty in each set of model predictions was generally about 90% of the total entropy of the benchmark observations (this was similar for all four land surface models and can be inferred from Figure 5). Forcing data accounted for about a quarter of this total uncertainty related to soil moisture near the surface (10 cm), and about one sixth of total uncertainty in the 100 cm observations (Table 2). The difference is expected since the surface soil moisture responds more dynamically to the system boundary conditions, and so errors in measurements of those boundary conditions will have a larger effect in predicting the near-surface response.

In all cases except SAC-SMA, parameters accounted for about half of total uncertainty in both soil layers, however for SAC-SMA this percentage was higher, at sixty and seventy percent for the two soil depths respectively (Table 2). Similarly, the efficiencies of the different parameter sets were relatively low – below forty-five percent in all cases and below thirty percent for SAC-SMA (Table 3). SAC-SMA parameters are a strict subset of the others, so it is not surprising that this set contained less information. In general, these results indicate that the greatest potential for improvement to NLDAS-2 simulations of soil moisture would come from improving the parameter sets.

Although the total uncertainty in all model predictions was similar, the model structures themselves performed very differently. Overall, VIC performed the worst and was able to use less than a quarter of the information available to it, while SAC-SMA was able to use almost half (Table 3). SAC-SMA had less information to work with (from parameters; Figure 5), but it was better at using what it had. The obvious extension of this analysis would measure which of the parameters that were not used by SAC-SMA are the most important, and then determine how SAC-SMA might consider the processes represented by these missing parameters. It is interesting to notice that the model structure that performed the best, SAC-SMA, was an uncalibrated conceptual model, whereas Noah, Mosaic, and VIC are ostensibly physics-based (and VIC parameters were calibrated).

The primary takeaway from these results is that there is significant room to improve both the NLDAS-2 models and parameter sets, but that the highest return on investment, in terms of predicting soil moisture, will likely come from looking at the parameters. This type of information-based analysis could easily be extended to look at the relative value of individual parameters.

3.2. Evapotranspiration

Figure 6 compares the model and benchmark estimates of ET with AmeriFlux observations. Again, the spread in the benchmark estimates is indicative of substantial unresolvable uncertainty given the various input data. Figure 5 again plots the ET reference values and values of the ET performance metrics. Related to ET, forcing data accounted for about two thirds of total uncertainty in the predictions from all four models (Table 2). Parameters accounted for about one fifth of total uncertainty, and model structures only accounted for about ten percent. In all three cases, the fractions of ET uncertainty due to different components were essentially the same between the four models. Related to efficiency, the forcing data was able to resolve less than half of total uncertainty in the benchmark observations, and the parameters and structures generally had efficiencies between fifty and sixty percent, with the efficiencies of the models being slightly higher (Table 3). Again, the ET efficiencies were similar among all four models and their respective parameter sets.

Figure 6.

Scatterplots of ET observations and estimates made by the NLDAS-2 models (black) and by the benchmark estimates (grey). The ${ℛ}_i^{\mathrm{u}}$ regressions (first row) act on the forcing data only and the ℛ^u,θ regressions (second row) act on forcing data plus parameters. The mean anomaly correlations over all sites are listed on each subplot.

4. Discussion

The purpose of this paper is two-fold. First, we want to demonstrate (and expand) information-theoretic benchmarking as a way to quantify contributions to uncertainty in dynamical model predictions without relying on degenerate priors or on specific model structures. Second, we used this strategy to measure the potential for improving various aspects of the continental-scale hydrologic modeling system, NLDAS-2.

Related to NLDAS-2 specifically, we found significant potential to improve all parts of the modeling system. Parameters contributed the most uncertainty to soil moisture estimates, and forcing data contributed the majority of uncertainty to evapotranspiration estimates, however the models themselves used only a fraction of the information that was available to them. Differences between the soil moisture and ET results and those from the soil moisture experiments highlight that model adequacy (Gupta et al., 2012) depends very much on the specific purpose of the model (in this case, the “purpose” indicates what variable we are particularly interested in predicting with the model). As mentioned above, an information use efficiency analysis like this one could easily be extended not only to look at the information content of individual parameters, but also of individual process components of a model by using a modular modeling system (e.g., Clark et al., 2011). We therefore expect that this study will serve as a foundation for a diagnostic approach to both assessing and improving model performance – again in a way that does not rely on simply comparing a priori models. The ideas presented here also will guide the development and evaluation of the next phase of NLDAS, which will be at a finer spatial scale, and include updated physics in the land-surface models, data assimilation of remotely-sensed water states, improved model parameters, and higher-quality forcings through improved model forcings.

Related to benchmarking theory in general, there have recently been a number of large-scale initiatives to compare, benchmark, and evaluate the land surface models used for hydrological, ecological, and weather and climate prediction (e.g., van den Hurk et al., 2011, Best et al., 2015), however we argue that those efforts have not exploited the full power of model benchmarking. The most exciting aspect of the benchmarking concept seems to be its ability to help us understand and measure factors that limit model performance. Specifically, benchmarking’s ability to assign (approximating) upper bounds on the potential to improve various components of the modeling system. As we mentioned earlier, essentially all existing methods for quantifying uncertainty rely on a priori distributions over model structures, and because such distributions are necessarily incomplete, there is no way for such analyses to give approximating estimates of uncertainty. What we outline here can provide such estimates. It is often at least theoretically possible to use regressions that asymptotically approximate the true relationship between model inputs and outputs (Cybenko, 1989).

The caveat here is that although this type of benchmarking-based uncertainty analysis solves the problem of degenerate priors, the problem of finite evaluation data remains. We can argue that information-theoretic benchmarking allows us to produce asymptotic estimates of uncertainty, but since we will only ever have access to a finite number of benchmark observations, the best we can ever hope to do in terms of uncertainty partitioning (using any available method) is to estimate uncertainty in the context of whatever data we have available. We can certainly extrapolate any uncertainty estimates into the future (e.g., Montanari & Koutsoyiannis, 2012), but there is no guarantee that such extrapolations will be correct. Information-theoretic benchmarking does not solve this problem. All model evaluation exercises necessarily ask the question “what information does the model provide about the available observations?” Such is the nature of inductive reasoning.

Similarly, although it is possible to explicitly consider error in the benchmark observations during uncertainty partitioning (Nearing & Gupta, 2015), any estimate of this observation error ultimately and necessarily constitutes part of the model that we are evaluating (Nearing et al, 2015). The only thing that we can ever assess during any type of model evaluation (in fact, during any application of the scientific method) is whether a given model (including all probabilistic components) is able to reproduce various instrument readings with certain accuracy and precision. Like any other type of uncertainty analysis, benchmarking is fully capable of testing models that do include models of instrument error and representativeness.

The obvious open question is about how to use this to fix our models. It seems that the method proposed here might, at least theoretically, help to address the question in certain respects. To better understand the relationship between individual model parameters and model structures, we could use an ℛ^u,θ type regression that acts only on a single model parameter to measure the amount of information contained in that parameter, and then measure the ability of a given model structure to extract information from that parameter by running the model many times at all sites using random samples of the other parameters and calculating something like ℰ_ℳ(θ_i) = I (z; y^ℳ(u, θ_i)) / I(z; u, θ_i). This would tell us whether a model is making efficient use of a single parameter, but not whether that parameter itself is a good representation of differences between any real dynamical systems. It would also be interesting to know whether the model is most sensitive (in a traditional sense) to the same parameters that contain the most information. Additionally, if we had sufficient and appropriate evaluation data we could use a deconstructed model or set of models, like what was proposed by Clark et al. (2015), to measure the ability of any individual model process representation to use the information made available to it via other model processes, parameter, and boundary conditions.

To summarize, Earth scientists are collecting ever-increasing amounts of data from a growing number of field sites and remote sensing platforms. This data is typically not cheap, and we expect that it will be valuable to understand the extent to which we are able to fully utilize this investment – i.e., by using it to characterize and model biogeophysical relationships. Hydrologic prediction in particular seems to be a data limited endeavor. Our ability to apply our knowledge of watershed physics is limited by unresolved heterogeneity in the systems at different scales (Blöschl & Sivapalan, 1995), and we see here that this difficulty manifests in our data and parameters. Our ability to resolve prediction problems will, to a large extent, be dependent on our ability to collect and make use of observational data, and one part of this puzzle involves understanding the extents to which (1) our current data is insufficient, and (2) our current data is underutilized. Model benchmarking has the potential to help distinguish these two issues.

Appendix

A General Description of Model Performance Metrics

We begin with five things: (1) a (probabilistic) model ℳ with (2) parameter values θ ∈ ℝ_dθ, acts on (3) measurements of time-dependent boundary conditions u_t ∈ ℝ_du to produce (4) time-dependent estimates or predictions ${\mathbf{y}}_t^{ℳ}\in {ℝ}_{{\mathrm{d}}_{\mathrm{z}}}$ of phenomena that are observed by (5) z_t ∈ ℝ_dz. A deterministic model is simply a delta distribution, however even when we use a deterministic model we always treat the answer as a statistic of some distribution that is typically implied by some performance metric (Weijs et al., 2010). Invariably, during model evaluation, the model implies a distribution over the observation z_t that we notate P(z|y^ℳ).

Further, we use the word information to refer to the change in a probability distribution due to conditioning on a model or data (see discussion by Jaynes, 2003, and also, but somewhat less importantly, by Edwards, 1984). Since probabilities are multiplicative, the effect that new information has on our current state of knowledge about what we expect to observe is given by the ratio:

$$\frac{\mathrm{P}(\mathbf{z}|{\mathbf{y}}^{ℳ})}{\mathrm{P}(\mathbf{z})}$$ (A.1)

where P(z) is our prior knowledge about the observations before running the model. In most cases, P(z) will be an empirical distribution derived from past observations of the same phenomenon (see Nearing & Gupta, 2015 for a discussion).

Information is defined by equation (A.1), measuring this information (i.e., collapsing the ratio to a scalar) requires integrating. The information contributed by a model to any set of predictions is measured by integrating this ratio, so that the most general expression for any measure of the information contained in model predictions y^ℳ about observations z is:

$${\mathrm{E}}_{\mathrm{z}}\left[f\right(\frac{\mathrm{P}(\mathbf{z}|{\mathbf{y}}^{ℳ})}{\mathrm{P}(\mathbf{z})}\left)\right].$$ (A.2.1)

The integration in the expected value operator is over the range of possibilities for the value of the observation. Most standard performance metrics (e.g., bias, MS, and ρ) take this form (see Appendix of Nearing & Gupta, 2015). The f function is essentially a utility function, and can be thought of, in a very informal way, as defining the question that we want to answer about the observations.

Since y^ℳ is a transformation of u_1:t and θ (via model ℳ), any information measure where f is monotone and convex, is bounded by (Ziv and Zakai, 1973):

$${\mathrm{E}}_{\mathrm{z}}\left[f\right(\frac{\mathrm{P}(\mathbf{z}|{\mathbf{y}}^{\mathit{ℳ}})}{\mathrm{P}(\mathbf{z})}\left)\right]\le {\mathrm{E}}_{\mathrm{z}}\left[f\right(\frac{\mathrm{P}(\mathbf{z}|\mathbf{u},\mathbf{\theta })}{\mathrm{P}(\mathbf{z})}\left)\right].$$ (A.3)

Equation (A.3) is called the Data Processing Inequality, and represents the reference value for our benchmark.

Shannon (1948) showed that the only function f that results in an additive measure of information that takes the form of equation (A.2.1) is f(․) = − log_b(․), where b is any base. As described presently, we require an additive measure, so the performance metric for our benchmark takes the form of equation (A.2.1) and uses the natural log as the integrating function. We therefore measure entropy H and mutual information I in units nats in the usual way, as:

$$\mathrm{H}(\mathbf{z})={\mathrm{E}}_{\mathrm{z}}[-\text{ln}(\mathrm{P}(\mathbf{z}))]\text{ and}$$ (A.2.2)

$$\mathrm{I}(\mathbf{z};\xi )={\mathrm{E}}_{\mathrm{z}|\xi }[-\text{ln}(\frac{\mathrm{P}(\mathbf{z}|\xi )}{\mathrm{P}(\mathbf{z})}\left)\right],$$ (A.2.3)

respectively, where ξ is a placeholder for any variable that informs us about the observations (e.g., u, θ, y^ℳ).

Because it is necessary to have a model to translate the information contained in u and θ into information about the observations z, the challenge in applying this benchmark is to estimate P(z_t|u_1:t, θ). This conditional probability distribution can be estimated using some form of kernel density function (Cybenko, 1989, Rasmussen & Williams, 2006, Wand & Jones, 1994), which creates a mapping function ℛ^u,θ: {u_1:t, θ} → {z_t}, where the "ℛ" stands for regression to indicate that this is fundamentally a generative approach to estimating probability distributions (see Nearing et al, 2013 for a discussion). The regression estimates are ${\mathbf{y}}_t^{\mathrm{u},\mathrm{\theta }}\in {ℝ}^{{\mathrm{d}}_{\mathrm{z}}}$. To the extent that this regression is asymptotically complete (i.e., it approaches the true functional relationship between {u, θ} and z), an approximation of the right-hand side of equation (A.3) approaches the benchmark reference value.