 Two calculated structures of the [Fe4N(CO)12]3– CO2 reduction electrocatalyst in its twice reduced state connected by a CO dissociation pathway are studied.
Two calculated structures of the [Fe4N(CO)12]3– CO2 reduction electrocatalyst in its twice reduced state connected by a CO dissociation pathway are studied.
Abstract
The CO2 reduction electrocatalyst [Fe4N(CO)12]– (abbrev. 1–) reduces CO2 to HCO2– in a two-electron, one-proton catalytic cycle. Here, we employ ab initio calculations to estimate the first two redox potentials of 1– and explore the pathway of a side reaction involving CO dissociation from 13–. Using the BP86 density functional approximation, the redox potentials were computed with a root mean squared error of 0.15 V with respect to experimental data. High temperature Born–Oppenheimer molecular dynamics was employed to discover a reaction pathway of CO dissociation from 13– with a reaction energy of +10.6 kcal mol–1 and an activation energy of 18.8 kcal mol–1; including harmonic free energy terms, this yields ΔGsep = 1.4 kcal mol–1 for fully separated species and ΔG‡ = +17.4 kcal mol–1, indicating CO dissociation is energetically accessible at ambient conditions. The analogous dissociation pathway from 12– has a reaction energy of 22.1 kcal mol–1 and an activation energy of 22.4 kcal mol–1 (ΔGsep = 12.8 kcal mol–1, ΔG‡ = +18.1 kcal mol–1). Our computed harmonic vibrational analysis of [Fe4N(CO)11]3– or 23– reveals a distinct CO-stretching peak red-shifted from the main CO-stretching band, pointing to a possible vibrational signature of dissociation. Multi-reference CASSCF calculations are used to check the assumptions of the density functional approximations that were used to obtain the majority of the results.
Introduction
The development of economically viable technologies for reducing the CO2 concentration in Earth’s atmosphere is one of the global environmental problems that we must solve in the near future. One of the major research fields in modern chemistry is the development of CO2 capture, utilization, and storage strategies. Electrochemical CO2 reduction has been studied as a CO2 utilization technique, which can provide us with the possibility to produce useful products from CO2.
The discovery of CO2 reduction electrocatalysts represents a significant advance in CO2 utilization.1 Certain metallic electrodes have been reported to have catalytic activity for carbon dioxide reduction; Hori reported the formation of hydrocarbons and alcohols in the electrochemical reduction of carbon dioxide at copper electrodes in aqueous solution and discussed the reaction mechanism in 1989.2 In recent years, several metal and metal dichalcogenide nanostructured catalysts with high surface areas have been proposed as promising candidates for electrocatalysts for the CO2 reduction.3–8 In addition to the heterogeneous catalysts, a number of molecular catalysts have also been investigated for CO2 reduction and reviewed in several papers.9–11
In 2011, Rail and Berben found that an Earth-abundant metal complex, first described by Muetterties and coworkers12,13 and denoted as [Fe4N(CO)12]– or 1– in its resting state, can act as a selective electrocatalyst for CO2 reduction to formate in aqueous solution.14 The preference of the catalyst for hydrogen evolution vs. CO2 reduction can be adjusted by tuning the strength of the acid used as a proton donor. An isoelectronic compound, [Fe4C(CO)12]2–, was found to be a catalyst for hydrogen evolution only.15 In more recent work, Taheri and Berben further characterized the CO2 reduction mechanism and proposed the reduced hydride H-1– as a key reaction intermediate.16 The hydricity, or hydride donor ability of H-1– was proposed as a thermodynamic predictor of the selectivity for hydrogen evolution or CO2 reduction; a free energy window was proposed to explain the activity of 1– for CO2 reduction, as opposed to its isoelectronic analogues.
[Fe4N(CO)12]– is experimentally known to undergo two reduction events. When 1– is electrochemically reduced to 13–, slow CO dissociation from the cluster is observed, resulting in the [Fe4N(CO)11]3– or 23– species; the catalytic activity of this species is unknown but presumed to be inactive. In an accompanying experimental work, the X-ray crystal structure of 23– is reported.17 Simulations that uncover the mechanisms of side reactions are important to the overall strategy for designing molecular catalysts which are resistant to them. In this respect, this article describes the redox properties and CO dissociation pathway of this complex using computational quantum chemistry to complement the experimental findings and provide atomic-resolution insights.
The use of density functional theory (DFT) to study the electronic properties of metal carbonyl clusters has precedent in the literature. In particular, Schaefer and coworkers have produced a series of studies on the structures and metal–metal bonding of iron carbonyls and their derivatives.18–37 Several other groups have also carried out DFT studies for geometry optimization and vibrational frequency analysis of iron carbonyl complexes.38–41 Presumably, the strong fields from the CO ligands promote a low-spin and single-reference electronic state, making DFT a qualitatively appropriate method for studying these otherwise daunting multi-center inorganic clusters. Likewise, the application of DFT and solvent models for calculating redox potentials is well established.42–44 On the other hand, we are not aware of any theoretical studies that have investigated the redox properties and reactivity of 1; the significant metal–metal bonding and variation of charge states in this cluster may pose significant challenges for the density functional approximation and solvent model. For this reason, it is vital to compare calculated observables with experimental data where available.
In this theoretical study, we characterize the structures and energetics of the series of redox states: 10, 1–, 12–, and 13–, and provide mechanistic insight into the CO dissociation side reaction: 13– → 23– + CO. Our calculations of the one-electron reduction potentials show close agreement with the experimentally measured values and provide some evidence that the BP86 density functional approximation45,46 performs more accurately for this system than the hybrid B3LYP functional.47 The dissociation pathway was found using high temperature ab initio molecular dynamics and relaxed to the minimum energy path to calculate the activation barrier.48 The calculations predict a structure of 23– in remarkable agreement with the X-ray crystal structure that was determined concurrently,17 lending further confidence to the level of theory used in this study. We also compare the CO dissociation barrier height to the analogous reaction after only one reduction event: 12– → 22– + CO, and show that dissociation from this electronic state is energetically uphill, though the activation free energy of CO dissociation is similar in both states. Our usage of DFT approximations is checked using natural orbital occupation numbers from multi-reference complete active space self-consistent field (CASSCF) calculations at key geometries.49,50
Computational methods and results
1. Redox potential calculations
We evaluated the relative free energies between the redox intermediates 10, 1–, 12–, and 13– using unrestricted Kohn–Sham DFT51 with the implicit solvent environment, conductor-like screening model (COSMO)52 for comparison to experimentally determined redox potentials. These calculations were carried out using the TeraChem software, which uses graphics processing units to accelerate the computation of the Coulomb and exchange matrices,53–55 effective core potentials (ECPs),56,57 and solvent response58 that appear in the SCF calculation. A recently developed geometry optimization method using translation-rotation internal coordinates was employed to accelerate the energy minimization calculations.59G = Gsolv + HSCF + ZPE + Htr,rot,vib – TStr,rot,vibΔG = Gred. – Gox. = –FE0
Geometry optimization was used to derive the self-consistent field (SCF) electronic energy together with the solvation free energy. Vibrational frequency calculations were used to derive the zero point energy and Gibbs free energy within the harmonic approximation. To calculate the relative redox potential, we took the differences of the free energies of the redox pairs and subtracted the absolute potential of the reference electrode, which is 4.67 V for the saturated calomel electrode (SCE). This value is based on the absolute potential of the NHE, which was determined by Reiss and Heller to be 4.43 V,60 although this quantity is difficult to measure and values in the range of 4.2–4.7 V have been reported in the literature.61
We tested the dependence of the results on the choice of DFT approximation by performing calculations using three functionals: the BP86 gradient corrected semi-local functional,45,46 the B3LYP hybrid functional,47 and the PBE0 hybrid functional.62 Previous studies have noted that BP86 may perform more reliably than B3LYP in the study of the compounds in this paper.63,64 We also investigated whether adding diffuse basis functions affects the calculation results, because previous gas phase DFT studies suggest that diffuse basis functions are needed for the description of anions.65–67 For light elements (H, C, N, and O) we used the def2-TZVP triple-valence Gaussian basis set68,69 with f and higher angular momentum functions removed, denoted as def2-TZVP(-f). For the iron atoms we used either the LANL08 or LANL08+ basis set/ECP combination,70 which differ by the addition of a diffuse d angular momentum function in the latter. We further tested the effects of adding a minimal set of diffuse functions on light elements.71 The combined basis sets are called def2-TZVP(-f)-LTZ, def2-TZVP(-f)-LTZ+, and ma-def2-TZVP(-f)-LTZ+. Finally, since the cyclic voltammetry experiments to measure the redox potentials were carried out in a MeCN/H2O (95 : 5) solvent, we also conducted the calculations employing the dielectric constants of water (78.4) and MeCN (37.5). From Tables 1 and 2, we concluded that the system has a minor dependence on the choice of basis set and solvent, while the functional dependence is significant. The BP86 functional gave closer agreement with experimental results (root-mean-square error, RMSE < 0.2 V) than the B3LYP and PBE0 hybrid functionals (RMSE > 0.4 V); the improved agreement is not due to shifting the absolute electrode potential, because the BP86 RMSE is still much lower than the other two functionals with the average gap subtracted out. Overall, the combination of the BP86 functional, the def2-TZVP(-f)-LTZ+ basis, and the dielectric constant of water yields good agreement with experimental data, with a RMSE of 0.15 V. The relatively high accuracy of BP86 (compared to hybrid functionals) for this system is consistent with previously published DFT studies of 3d transition metal containing complexes.63 To check the possible higher spin multiplicities for each state of the catalyst, we also calculated the energies of the higher spin multiplicities for each redox state (triplet and quintet for even-electron systems, quartet and sextet for odd-electron systems) and found that increasing the spin multiplicity significantly increases the total energy by over 10 kcal mol–1 (ESI Table S1†). From these findings we conclude that higher spin multiplicities do not participate in the redox chemistry and reaction pathways in this paper.
Table 1. Functional dependence of the redox potential calculation and comparison with the experimentally determined redox potentials. The BP86 results are shown in bold as they are judged to be the most reliable from the present data and literature precedent.
| def2-TZVP(-f)_LTZ+/water (V) |
||||
| 1 0/1– | 1 1–/2– | 1 2–/3– | RMSE | |
| Exp | >0.2 | –1.23 | –1.60 | |
| B3LYP | –0.13 | –1.37 | –2.07 | 0.42 |
| PBE0 | –0.26 | –1.42 | –2.19 | 0.50 |
| BP86 | +0.37 | –1.16 | –1.54 | 0.15 |
Table 2. Addition of diffuse functions and solvent dependence of the redox potential calculation. The line shown in bold is identical to the bold line in Table 1 .
| BP86/water (V) |
||||
| 1 0/1– | 1 1–/2– | 1 2–/3– | RMSE | |
| Exp | >0.20 | –1.23 | –1.60 | |
| def2-TZVP(-f)_LTZ | +0.42 | –1.24 | –1.54 | 0.15 |
| def2-TZVP(-f)_LTZ+ | +0.37 | –1.16 | –1.54 | 0.15 |
| Ma-def2-TZVP(-f)_LTZ+ | +0.38 | –1.18 | –1.43 | 0.19 |
| BP86/acetonitrile (V) |
||||
| 1 0/1– | 1 1–/2– | 1 2–/3– | RMSE | |
| Exp | >0.20 | –1.23 | –1.60 | |
| def2-TZVP(-f)_LTZ | +0.41 | –1.30 | –1.62 | 0.14 |
| def2-TZVP(-f)_LTZ+ | +0.34 | –1.22 | –1.64 | 0.13 |
| Ma-def2-TZVP(-f)_LTZ+ | +0.39 | –1.27 | –1.55 | 0.15 |
2. Computational discovery of dissociation pathways by ab initio molecular dynamics
We used ab initio molecular dynamics (AIMD) to explore the chemical and structural rearrangements of Fe4N(CO)12 in its different electronic states. In the Born–Oppenheimer MD (BOMD) framework, the motion of atoms is simulated by applying the nuclear gradients of the energy as classical forces to the atoms, and then accelerating the atoms along the force vectors using Newton’s second law. In order for the simulations to broadly sample the chemical space and discover many reaction pathways while keeping the computational cost affordable, accelerated sampling techniques are needed to cross over potential barriers more rapidly.72–77 In this study, we simply ran unbiased AIMD at elevated temperatures to accelerate the sampling. A velocity Verlet integrator was used with a time step of 1.0 fs. A Langevin thermostat was used with the equilibrium temperature set to 1000 K and a collision frequency of 1.0 ps–1. Several simulations were started from the energy minimized structures of 12– and 13–, as well as from the protonated isoelectronic species, i.e. H-11– and H-12–. These simulations used the B3LYP functional and a hybrid basis set combining 6-31G*78 for light elements and the LANL2DZ basis set/ECP for Fe,79 abbreviated as 6-31G*-LDZ.
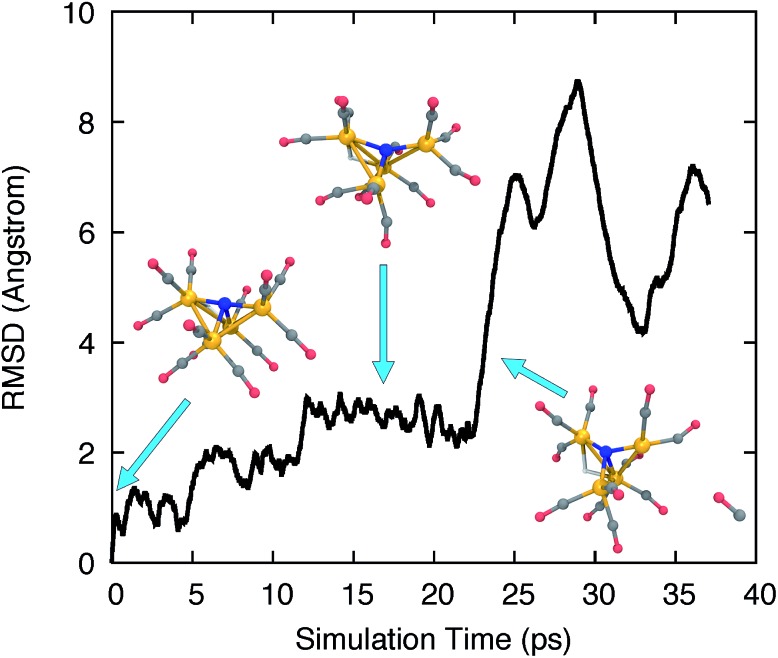
The AIMD trajectories at elevated temperatures feature highly fluxional behavior of the CO ligands. Fig. 1 shows the all-atom root-mean-square deviation (RMSD) of the trajectory frames to the initial structure, and several trajectory snapshots of the simulation of H-11–. The RMSD rapidly reaches 1 Å after 1000 simulation steps (1 ps) and increases steadily over the course of ∼15 ps to almost 3 Å as larger geometric rearrangements take place. The conformational changes include the concerted rotation of multiple CO groups bonded to the same iron atom (analogous to torsion about a single bond), as well as the exchange of CO ligands on different iron atoms. At frame 22 500, we observed a significant increase of the RMSD to >6 Å, where a CO ligand dissociated from the cluster. The distance between the dissociated CO and the catalyst molecule continued to increase until the simulation was terminated at frame 37 000.
Fig. 1. RMSD time series to the initial optimized structure for a high temperature AIMD simulation of H-11–. Several trajectory snapshots are shown, along with blue arrows indicating their corresponding simulation time. Fe, orange; C, grey; N, blue; O, red; H, white.
3. Characterization of optimized structures
The AIMD simulation explores the potential landscape very broadly, but a closer examination of the optimized structures and barriers is needed to assess the feasibility of the discovered pathways under experimental conditions. We focused on trajectory frames numbered 22 000–22 390, where the CO is observed to dissociate from the complex, and optimized a total of 40 trajectory frames evenly spaced by 10 frames (i.e. spanning 400 simulation time steps). The proton was deleted from the trajectory frames prior to optimization. The charge and spin multiplicity of the twice-reduced state were set to –3 and 1, respectively, prompted by CASSCF (8,8) calculations that indicated that the lowest-energy state is a closed shell singlet.
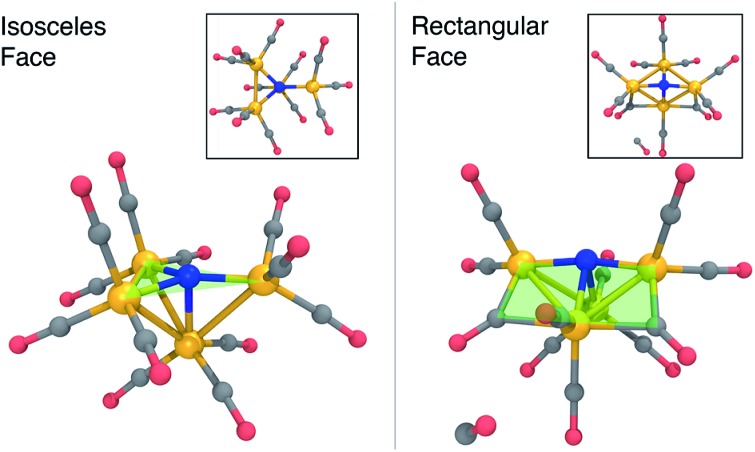
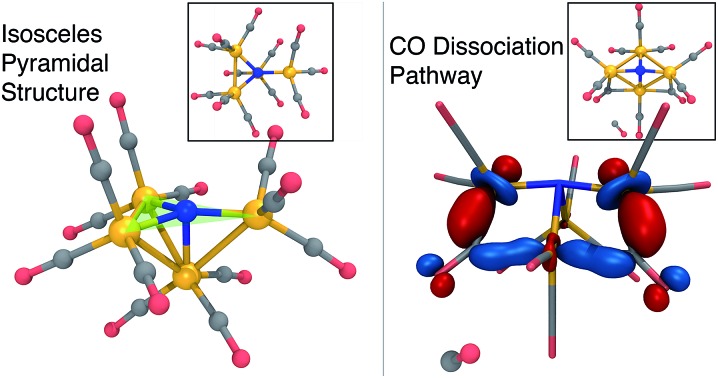
Fig. 2 summarizes the main results when the cluster is optimized in the –3 charge, singlet electronic state. The lowest energy structure (Fig. 2, left) is close to Cs-symmetric with a single mirror plane; the Fe atoms surround the central N in an isosceles trigonal pyramidal arrangement. The central N is nearly in the plane made by three iron atoms, with three in-plane Fe–N–Fe angles of 137, 137, and 84 degrees, summing up to 358 degrees. The other three Fe–N–Fe angles are between 85 and 90 degrees. Each Fe atom has three CO ligands with a tight distribution of Fe–C distances ranging from 1.74–1.77 Å; the ab initio bond order (BO) indices computed using Mayer’s method80 range from 1.05 to 1.25, indicating single bond order.
Fig. 2. Optimized structures of 13– (left) and 23– + CO (right) at the B3LYP/6-31G*-LANL2DZ level of theory, before and after CO dissociation. The structures are characterized by a nearly planar isosceles triangular face (left) and a rectangular face (right) that contain the nitrogen atom. Fe, orange; C, grey; N, blue; O, red; H, white.
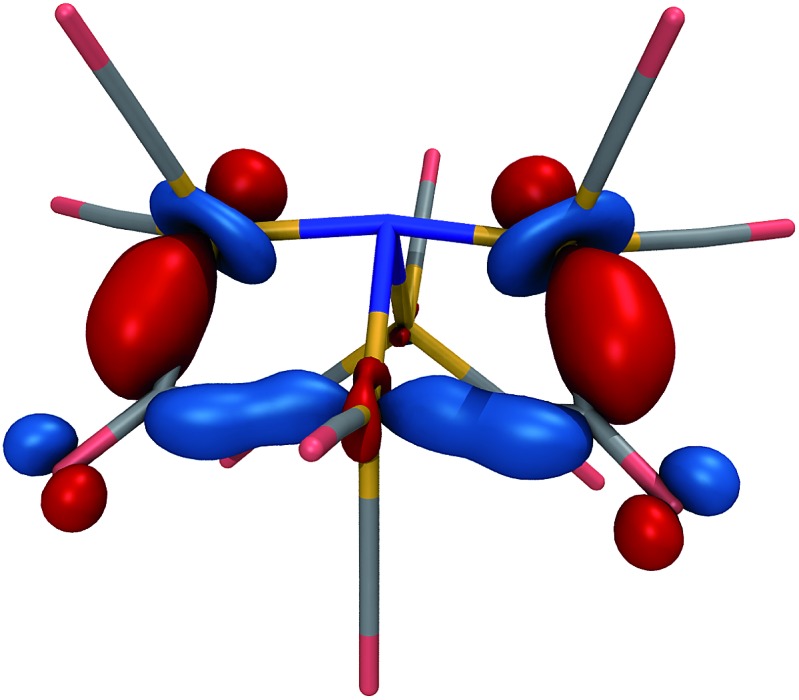
The lowest-energy structure with a dissociated CO ligand (Fig. 2, right) features two CO ligands bridging a pair of Fe atoms. The three Fe atoms, central nitrogen, and two bridging carbons form nearly a planar rectangle, with Fe–N–Fe and C–Fe–C angles of 168 and 174 degrees, respectively. The cluster is also nearly Cs-symmetric with a single mirror plane. Moreover, the bridging CO ligands have significantly larger Fe–C distances of 1.83 Å (left and right edges of rectangle) and 2.08 Å (bottom edge). The increased lengths of the Fe–C bonds along the bottom edge of the rectangle suggest that they possess a different electronic character; indeed, these two bonds have ab initio bond orders of 0.55, which are almost exactly half of the others. Our interpretation is that the C–Fe–C is a three-center two-electron bond, which compensates for the two σ-electrons that are lost in the dissociation process. To support this interpretation, Fig. 3 shows a doubly-occupied CASSCF (8,8) optimized molecular orbital that shows significant electron delocalization across the C–Fe–C bond; this is the only orbital we observed that possesses bonding character for these atoms. A comparison of the optimized structure with the experimentally determined X-ray crystal structure17 revealed an excellent agreement of 0.13 Å RMSD, lending confidence to the accuracy of the theoretical methods used; the calculations were performed without knowledge of the crystal structure, and the comparison was only performed later. The experimental crystal structure also contains three Na+ counterions that further stabilize the 23– structure; these were not included in the present calculations.
Fig. 3. Optimized, doubly-occupied molecular orbital of 23– at the CASSCF(8,8)/6-31G*-LANL2DZ level of theory, indicating a delocalized bond that connects the three Fe centers and two bridging C atoms in the foreground. The orbital is plotted with an isosurface value of 0.07.
To assess the possibility that 2 may be a catalyst for CO2 reduction, we computed redox potentials of the 20/2–, 2–/22–, and 22–/23– couples in analogy to 1. Our computed potentials are +0.30, –0.45, and –1.05 V vs. SCE, respectively. Because all of these potentials are more positive than the applied potential for electrocatalysis, we do not think these species are participating redox intermediates in the main CO2 reduction reaction.
4. Calculation of barrier heights of CO dissociation
The AIMD simulation that discovered the dissociation pathway is a good starting point for estimating the activation barrier separating the initial and final states. An initial reaction pathway is obtained by concatenating the MD trajectory frames with the output frames from the geometry optimization. From these structures, an “initial chain” of 21 equally spaced frames is selected. Because the initial chain may contain kinks that interfere with the convergence of reaction path optimization methods, we performed an initial smoothing by minimizing an elastic band energy function that depends solely on internal coordinate displacements. The resulting “smoothed chain” is free of kinks and has a shorter arc length than the initial chain, and is input into a nudged elastic band (NEB) calculation. The NEB uses a climbing image approach to ensure the highest-energy structure is as close as possible to the true transition state.
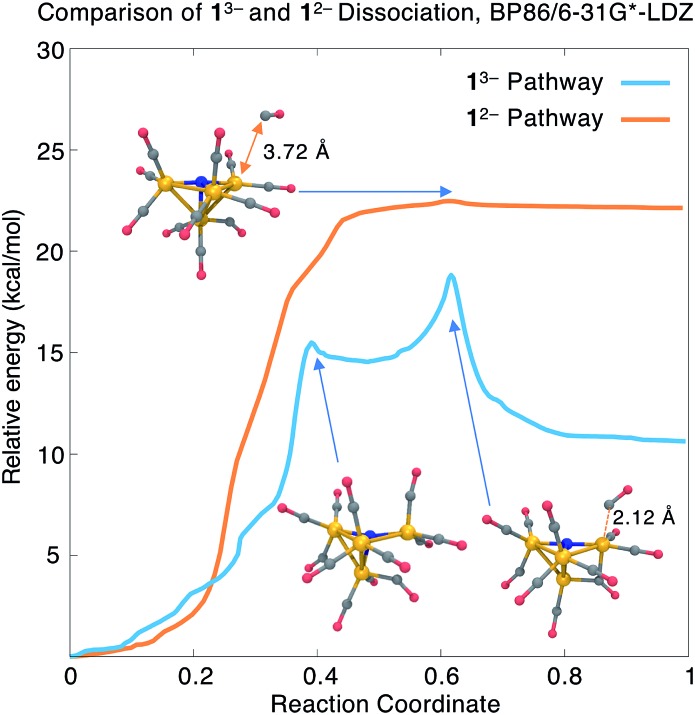
The transition state estimate from the NEB is input into a calculation of the ab initio Hessian, followed by a geometry optimization to precisely locate the transition state structure; we then verify, using a second Hessian calculation, that the optimized structure has only one imaginary vibrational frequency. Finally, an intrinsic reaction coordinate (IRC) calculation follows the energy downhill in the forward and backward directions of the imaginary vibrational mode to provide a continuous path connecting the TS and energy minima. The TS optimization and IRC calculations were performed in the Q-Chem software package81, with input parameters that reproduce the TeraChem total energies to within 0.0005 a.u. (<0.5 kcal mol–1). We provide harmonic free energy corrections at the transition state and final geometries, as well as reaction energies and free energies with the dissociated species completely separated. Our main results in this section are summarized in Fig. 4 and the first four rows of Table 3.
Fig. 4. Comparison of relative energies along the CO dissociation coordinate from 13– and 12–, calculated using BP86/6-31G*-LDZ. The Fe–C distance for the dissociating CO ligand is highlighted. Fe, orange; C, grey; N, blue; O, red; H, white.
Table 3. Relative energies and free energies (via harmonic approximation) for CO dissociation from 13– and 12–. Each group of four rows refers to calculations performed using a different DFT approximation. In the fourth row of each group, energies and free energies are calculated as a sum of the separated species in the product. All energies are reported in kcal mol–1.
| Structure |
1
3– → 23– + CO |
1
2– → 22– + CO |
||
| ΔE | ΔG | ΔE | ΔG | |
| Optimized IRC at BP86/6-31G*-LDZ | ||||
| Initial | 0.0 | 0.0 | 0.0 | 0.0 |
| TS | 18.8 | 17.4 | 22.4 | 18.1 |
| Final | 10.6 | 7.2 | 22.1 | 16.3 |
| Separated | 13.3 | 1.4 | 25.2 | 12.8 |
| Optimized IRC at M06-L/6-31G*-LDZ | ||||
| Initial | 0.0 | 0.0 | 0.0 | 0.0 |
| TS | 20.1 | 18.3 | — | — |
| Final | 11.0 | 7.6 | — | — |
| Separated | 15.9 | 3.6 | 22.9 | 12.9 |
| Optimized IRC at B3LYP/6-31G*-LDZ | ||||
| Initial | 0.0 | 0.0 | 0.0 | 0.0 |
| TS | 25.3 | 23.1 | 25.2 | 16.5 |
| Final | 12.2 | 7.8 | 24.9 | 14.7 |
| Separated | 14.8 | 3.3 | 27.2 | 11.5 |
| Optimized IRC at M06/6-31G*-LDZ | ||||
| Initial | 0.0 | 0.0 | 0.0 | 0.0 |
| TS | 23.5 | 22.5 | — | — |
| Final | 11.1 | 9.9 | — | — |
| Separated | 15.6 | 4.2 | 21.9 | 10.0 |
The blue curve in Fig. 4 shows the total energy for CO dissociation from 13– along the BP86/6-31G*-LDZ optimized reaction coordinate. The first part of the path involves a torsional motion of six CO ligands, allowing the two highlighted Fe–C distances to come into closer contact. An intermediate is found with a relative energy of ΔE1 = +14.5 kcal mol–1 and an activation barrier of Ea1 = +15.5 kcal mol–1; the structure contains an additional Fe–C bond (distance = 2.09 Å; BO = 0.63). The second transition state has energy Ea = +18.8 kcal mol–1 (ΔG‡ = 17.4 kcal mol–1) and has the CO ligand beginning to dissociate from the cluster; this is followed by a relatively flat energy basin where the two newly formed Fe–C bonds (the three-center bond) become equal in length. The final CO-dissociated structure gives a reaction energy ΔE = +10.6 kcal mol–1 (ΔG = +7.2 kcal mol–1). We also computed the reaction energy by treating the products as completely separate species and obtained ΔEsep = 13.3 kcal mol–1 (ΔGsep = +1.4 kcal mol–1). The higher value of ΔEsep is attributed to dissociating intramolecular interactions, and the lower value of ΔGsep to the translational and rotational entropy of separated dissociation products. The slightly uphill ΔG and moderate ΔG‡ values indicate that this mechanism may be operative for forming the experimentally observed 23– species.
We also investigated CO dissociation from the 12– electronic state; because dissociation is not observed from 12– in the experimental studies, we presume that the calculated thermodynamic and/or kinetic parameters should be less favourable compared to 13–. In searching for the reaction energies and activation barriers for the 12– state, we proceeded from the same initial structures from the AIMD trajectory; the charge and spin multiplicity were set to –2 and 2, respectively. Our BP86 calculations found an uphill and nearly barrierless dissociation pathway (orange curve in Fig. 4) with ΔE = 22.1 kcal mol–1 and Ea = 22.5 kcal mol–1 (ΔG = +16.6 kcal mol–1; ΔG‡ = 18.1 kcal mol–1). The reaction energy calculated using separated species as the products is ΔE = 25.2 kcal mol–1 (ΔG = 12.8 kcal mol–1).
Comparison of the dissociation pathways from 13–vs.12– gives reaction free energies of ΔG = +7.2 vs. +16.3 kcal mol–1; with separated product species, ΔGsep = +1.4 vs. +12.8 kcal mol–1. These values indicate that CO dissociation from 12– is thermodynamically less favourable than from 13–, consistent with the experimental findings. On the other hand, although the energy barrier for 13– is lower than for 12– (ΔE = 18.8 vs. 22.4 kcal mol–1), the calculated activation free energies are nearly the same (ΔG‡ = 17.4 vs. 18.1 kcal mol–1). Comparison of the overall shape of the dissociation curve shows some other important differences: whereas the 13– pathway has two clearly defined barriers and an intermediate, the 12– pathway is nearly barrierless, which indicates that tunnelling effects may play a significant role in determining the reaction rate.82 In summary, CO dissociation from 12– is found to be thermodynamically less favourable, but more detailed reaction rate and free energy calculations may be needed to accurately compare the kinetics of these two pathways.
5. Validation of electronic structure method
The veracity of our predictions regarding CO dissociation rests upon the choice of method. In this section we provide some justifications for our use of DFT in general, and the BP86/6-31G*-LDZ level of theory in particular. Our comparison tests include four DFT approximations (BP86, B3LYP, the meta-GGA functional M06-L83, and the hybrid meta-GGA M06 84). Whereas the first two functionals contain minimal empiricism, the latter two functionals contain 30+ parameters fitted to databases of diverse molecular properties. Optimized IRCs from 13– and 12– were computed using all four functionals in the 6-31G*-LDZ basis (Table 3). We also tested for basis set effects in the BP86 and B3LYP calculations by comparing a smaller double-zeta basis 6-31G*-LDZ (6-31G* for main group, LANL2DZ for Fe) and a larger triple-zeta basis TZVP-LTZ (TZVP85,86 for main group, LANL2TZ for Fe). ΔE and Ea in the large basis set were estimated by taking differences in single-point energies along the small basis optimized pathway following the IRCMax approach.87 Our results for comparing BP86 vs. B3LYP and the basis set effects in the 13– dissociation pathway are shown in ESI Table S2 and ESI Fig. S4.† 88
In all of our results, we found that increasing the basis set size has a relatively small effect. In the BP86/TZVP-LTZ calculations of CO dissociation from 13–, ΔE is essentially unchanged from the 6-31G*-LDZ result (10.6 kcal mol–1); Ea is slightly lower at 18.3 kcal mol–1. For the 12– pathway, BP86/TZVP-LTZ predicts a slightly higher value of ΔE = 22.7 kcal mol–1, and there is no energy maximum on the pathway; this is perhaps not surprising, given the nearly barrierless dissociation curve. In the B3LYP/TZVP-LTZ calculations, the ΔE and Ea values changed by <1 kcal mol–1 compared to the corresponding B3LYP/6-31G*-LDZ values. The choice of DFT functional has a more significant impact. B3LYP/6-31G*-LDZ predicts ΔE = 12.2 kcal mol–1 and Ea = 25.3 kcal mol–1 for CO dissociation from 13–; notably, Ea is 6 kcal mol–1 higher than in BP86. Despite differences in the barrier height, the structures along the 13– IRCs are highly similar for both functionals, as evidenced by the B3LYP single-point calculations along the BP86 optimized pathway and vice versa (ESI Table S2†).
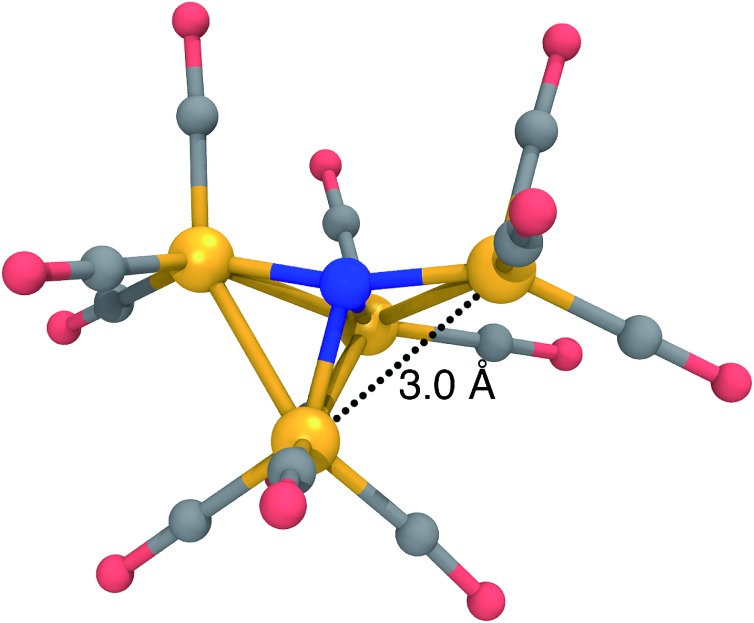
The most significant DFT functional dependence is seen in the 12– dissociation pathway. For the reactant (12–) structure, B3LYP predicts a pyramidal structure with an isosceles triangular base, almost identical to the structure of 13– in Fig. 2, left. On the other hand, BP86 predicts a “crooked butterfly” structure (Fig. 5) that is closer to the 1– resting state; the largest Fe–N–Fe angle is 165 degrees, and one of the Fe–Fe distances is elongated to 3.01 Å (the other Fe–Fe distances are between 2.55 and 2.65 Å). These structures are only stable on the potential surfaces of their respective functionals, as a BP86 optimization started from the B3LYP-optimized structure leads to the BP86 minimum and vice versa. Clearly, a more objective measure is needed to determine which DFT approximation is more appropriate for this system.
Fig. 5. Optimized structure of 12– at the BP86/6-31G*-LANL2DZ level of theory, characterized by a “crooked butterfly” structure with a single elongated Fe–Fe distance of 3.0 Å. Fe, orange; C, grey; N, blue; O, red; H, white.
The differences in BP86 vs. B3LYP in the 12– state originate from the electronic character of the ground state Kohn–Sham (KS) wavefunction. We computed the expectation value of the squared total spin operator S2 to measure any deviations of the KS wavefunction from a pure doublet (ESI Fig. S5†). Along the BP86 pathway, the S2 value of the BP86 KS wavefunction is stable around 0.77, close to the value of 0.75 for a pure doublet; on the other hand, the B3LYP wavefunction has higher S2 values, ranging from 0.84 to 1.08, indicating a higher degree of spin contamination. The spin contamination is even greater along the B3LYP IRC, where the B3LYP wavefunction has a S2 value close to 2.0 at the dissociated state. BP86 also predicts S2 values around 1.6–1.7 for these structures, indicating a broken symmetry KS wavefunction, containing more than one unpaired electron.
The significant spin contamination along the B3LYP IRC for 12– points to a multi-reference ground state that is not well described by a KS determinant. To investigate this further, we carried out single-point CASSCF calculations at the initial, TS, and final geometries along the CO dissociation pathway for both the 13– and 12– IRCs calculated using BP86 and B3LYP. These calculations employ the same 6-31G*-LDZ basis set as the DFT calculations, and active spaces of (4,6) and (3,6) were used for all states from the 13– and 12– state pathways, respectively. These calculations were carried out in the ORCA software package.89,90 CASSCF-optimized molecular orbitals for all 12 critical points are provided in the ESI.†
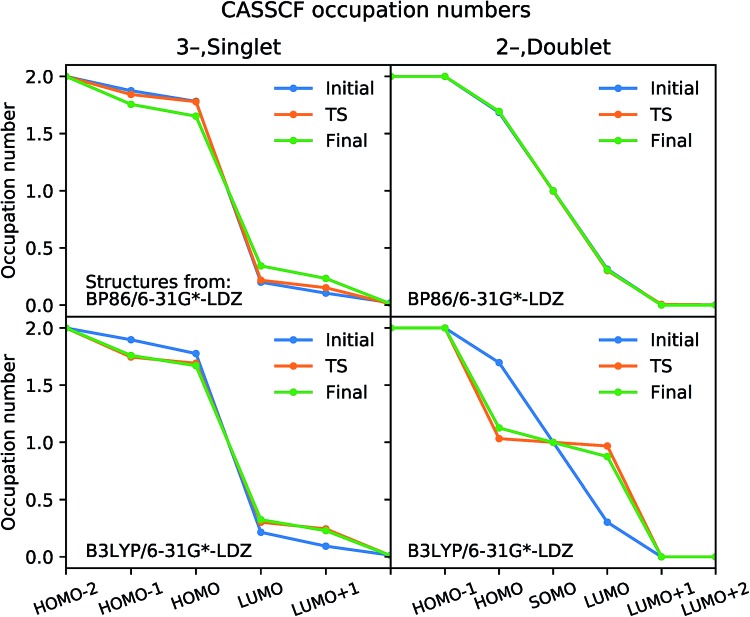
The optimized CASSCF molecular orbitals are very close to the natural orbitals that diagonalize the density matrix; the eigenvalues are within 10–4 of the diagonal elements, and off-diagonal elements are all <10–4. The natural orbital occupation numbers for initial, TS, and final structures optimized using B3LYP and BP86 are plotted in Fig. 6; the more the occupation numbers deviate from 2.0 and 0.0 (for occupied and virtual orbitals), the greater the multi-reference character. Our analysis for 13– shows that the natural orbitals at the “frontier” have occupation numbers in the range of 1.9–1.7 and 0.1–0.2. The variations in these values are small when comparing the initial, TS, and final structures, indicating that there is no qualitative change in the electronic character along the reaction pathway. Moreover, none of the natural orbitals have occupation numbers near 1.0, which is a hallmark of wavefunctions that display strong multi-reference character; this is the case for diradicals and the homolytic dissociation of N2.49
Fig. 6. Natural orbital occupation numbers calculated from CASSCF. The input geometries are from the IRCs of CO dissociation from 13– (left) and 12– (right) optimized using BP86 (top) and B3LYP (bottom). Active spaces of (4,6) and (3,6) were used for all structures from 13– and 12–, respectively.
For CO dissociation from 12–, the CASSCF calculations using BP86-optimized structures show a similar pattern to 13–, except a singly-occupied molecular orbital is present. On the other hand, a major change in the electronic character is seen for the B3LYP-optimized structures. The TS and final structures have occupation numbers close to 1.0 in three orbitals, indicating strong ground state multi-reference character; this result agrees with the spin contamination observed in the DFT wavefunctions for the same structures. When comparing the BP86 and B3LYP functionals, only the BP86-optimized structures have CASSCF ground states with consistent electronic character; we thus conclude that BP86 gives the more reliable result overall.
We also calculated reaction energies and activation energies of the reactions using the M06 and M06-L functionals to confirm the accuracy of BP86 for this system (Table 3). These calculations were performed in Q-Chem 5.0. We could not find a TS structure for CO dissociation from 12– using these functionals, again possibly owing to the nearly barrierless dissociation curve. The M06-L results are in close agreement with BP86, which is reasonable given that both functionals contain no Hartree–Fock (HF) exchange; spin contamination along the BP86-optimized 12– dissociation pathway is low, with S2 = 0.79–0.80. The M06 results are closer to B3LYP, perhaps because both functionals contain a similar amount of HF exchange (28% vs. 20%). M06 also shows similar amounts of spin contamination to B3LYP along both the BP86-optimized and B3LYP-optimized 12– dissociation pathways.
6. Calculated vibrational analyses
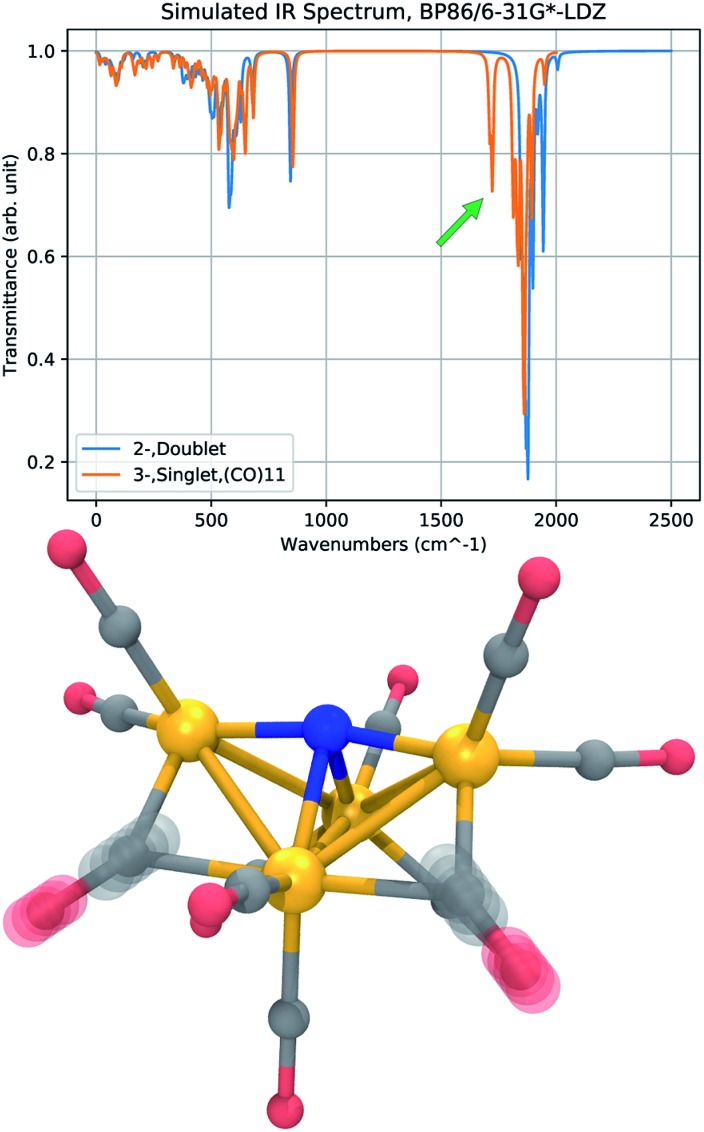
Infrared (IR) absorption spectra provide a meaningful connection between theory and experiment; a harmonic vibrational analysis calculation provides a series of frequencies and intensities that may be converted to a simulated spectrum by applying artificial broadening to each absorption peak. The results of two frequency calculations are shown in Fig. 7, where we compare the IR absorption peaks of 12– and 23–, the presumed initial and final states of the CO dissociation. The approximate spectra cannot accurately reproduce the widths of the experimental peaks, and only the shift in the peak positions, or the appearance of new peaks, is meaningful. The most notable feature in the spectrum of 23– is a new peak that appears in a region red-shifted from the main CO-stretching band by about 150 cm–1. The vibrational mode of this peak corresponds to CO-stretching of the bridging CO ligands. The reduced frequency indicates a slightly lower force constant in the CO bond of the bridging ligands that donate more electron density to the Fe centers. This red-shifted stretching peak may be used as a vibrational signature of CO dissociation.
Fig. 7. Comparison of vibrational spectra calculated at the BP86/6-31G*-LDZ level for 12– (blue) and 23– (orange). The IR spectrum of 23– has a distinct peak red-shifted from the main band of CO-stretches by about 150 cm–1 (green arrow), corresponding to a symmetric and antisymmetric stretch of the bridging CO ligands (bottom). An artificial Lorentzian broadening of 10 cm–1 is used.
Conclusions
In this study, we calculated the redox properties of the CO2 reduction electrocatalyst [Fe4N(CO)12]3– (1–) and investigated the possibility of CO dissociation from the twice-reduced state, 13–. Our calculated redox potentials show close agreement with experimentally measured values. The structure of the product of CO dissociation (23–) was predicted and found to be in close agreement with the experimental X-ray crystal structure. The CO dissociation pathway from 13– is energetically accessible under ambient conditions (in kcal mol–1: ΔE = +10.6, Ea = 18.8; ΔGsep = +1.4, ΔG‡ = +17.4). The analogous CO dissociation from 12– has a higher reaction energy and similar activation free energy (in kcal mol–1: ΔE = 22.1, Ea = 22.4; ΔGsep = +12.8, ΔG‡ = +18.1) with a nearly barrierless dissociation curve. Vibrational analysis of 23– shows a distinct CO-stretching peak red-shifted from the main CO-stretching band, indicating a possible vibrational signature of CO dissociation. Our calculations indicate that the BP86 semi-local functional gives more reliable results than the B3LYP hybrid functional in the study of this system. Future studies will focus on the potentially important role of counterions in stabilizing redox intermediates, as well as the strong solvent dependence in the selectivity of this catalyst for H2 evolution vs. CO2 reduction.
Conflicts of interest
There are no conflicts to declare.
Acknowledgments
L. A. Berben is grateful to the Department of Energy Office of Science for support from award number DE-SC0016395; L.-P. Wang and Y. Qiu acknowledge a gift from Walt Disney Imagineering. H. Jang acknowledges support from the ACS Petroleum Research Fund, award number 58158-DNI6. We would like to thank Atefeh Taheri, Tobias Sherbow and Natalia Loewen for helpful discussions.
Footnotes
†Electronic supplementary information (ESI) available: XYZ coordinates of energy minimized and transition state structures reported in this paper, as well as wavefunction analyses of CO dissociation from 12–. See DOI: 10.1039/c7sc04342b
References
- Senftle T. P., Carter E. A. Acc. Chem. Res. 2017;50:472–475. doi: 10.1021/acs.accounts.6b00479. [DOI] [PubMed] [Google Scholar]
- Hori Y., Murata A., Takahashi R. J. Chem. Soc., Faraday Trans. 1. 1989;85:2309–2326. [Google Scholar]
- Feng X., Jiang K., Fan S., Kanan M. W. J. Am. Chem. Soc. 2015;137:4606–4609. doi: 10.1021/ja5130513. [DOI] [PubMed] [Google Scholar]
- Min X., Kanan M. W. J. Am. Chem. Soc. 2015;137:4701–4708. doi: 10.1021/ja511890h. [DOI] [PubMed] [Google Scholar]
- Asadi M., Kim K., Liu C., Addepalli A. V., Abbasi P., Yasaei P., Phillips P., Behranginia A., Cerrato J. M., Haasch R., Zapol P., Kumar B., Klie R. F., Abiade J., Curtiss L. A., Salehi-Khojin A. Science. 2016;353:467. doi: 10.1126/science.aaf4767. [DOI] [PubMed] [Google Scholar]
- Kauffman D. R., Alfonso D., Matranga C., Qian H., Jin R. J. Am. Chem. Soc. 2012;134:10237–10243. doi: 10.1021/ja303259q. [DOI] [PubMed] [Google Scholar]
- Zhang S., Kang P., Meyer T. J. J. Am. Chem. Soc. 2014;136:1734–1737. doi: 10.1021/ja4113885. [DOI] [PubMed] [Google Scholar]
- Rosen J., Hutchings G. S., Lu Q., Rivera S., Zhou Y., Vlachos D. G., Jiao F. ACS Catal. 2015;5:4293–4299. [Google Scholar]
- Savéant J.-M. Chem. Rev. 2008;108:2348–2378. doi: 10.1021/cr068079z. [DOI] [PubMed] [Google Scholar]
- Benson E. E., Kubiak C. P., Sathrum A. J., Smieja J. M. Chem. Soc. Rev. 2009;38:89–99. doi: 10.1039/b804323j. [DOI] [PubMed] [Google Scholar]
- Costentin C., Robert M., Saveant J.-M. Chem. Soc. Rev. 2013;42:2423–2436. doi: 10.1039/c2cs35360a. [DOI] [PubMed] [Google Scholar]
- Tachikawa M., Muetterties E. L. J. Am. Chem. Soc. 1980;102:4541–4542. [Google Scholar]
- Tachikawa M., Stein J., Muetterties E. L., Teller R. G., Beno M. A., Gebert E., Williams J. M. J. Am. Chem. Soc. 1980;102:6648–6649. [Google Scholar]
- Rail M. D., Berben L. A. J. Am. Chem. Soc. 2011;133:18577–18579. doi: 10.1021/ja208312t. [DOI] [PubMed] [Google Scholar]
- Nguyen A. D., Rail M. D., Shanmugam M., Fettinger J. C., Berben L. A. Inorg. Chem. 2013;52:12847–12854. doi: 10.1021/ic4023882. [DOI] [PubMed] [Google Scholar]
- Taheri A., Thompson E. J., Fettinger J. C., Berben L. A. ACS Catal. 2015;5:7140–7151. [Google Scholar]
- Taheri A., Cluff D. B., Berben L. A. Organometallics. 2017 doi: 10.1021/acs.organomet.7b00824. [DOI] [Google Scholar]
- Wang H., Xie Y., King R. B., Schaefer H. F. Inorg. Chem. 2006;45:3384–3392. doi: 10.1021/ic051613l. [DOI] [PubMed] [Google Scholar]
- Wang H., Xie Y., King R. B., Schaefer H. F. Organometallics. 2008;27:3113–3123. [Google Scholar]
- Wang H., Xie Y., King R. B., Schaefer H. F. Inorg. Chem. 2008;47:3045–3055. doi: 10.1021/ic702077s. [DOI] [PubMed] [Google Scholar]
- Zhang Z., Li Q.-s., Xie Y., King R. B., Schaefer H. F. Inorg. Chem. 2009;48:6167–6177. doi: 10.1021/ic900518s. [DOI] [PubMed] [Google Scholar]
- Zhang Z., Li Q.-s., Xie Y., King R. B., Schaefer H. F. Inorg. Chem. 2009;48:1974–1988. doi: 10.1021/ic8016276. [DOI] [PubMed] [Google Scholar]
- Wang H., Sun Z., Xie Y., King R. B., Schaefer H. F. Organometallics. 2010;29:630–641. [Google Scholar]
- Xu L., Li Q.-s., Xie Y., King R. B., Schaefer H. F. Inorg. Chem. 2010;49:1046–1055. doi: 10.1021/ic901964f. [DOI] [PubMed] [Google Scholar]
- Xu L., Li Q.-s., King R. B., Schaefer H. F. Organometallics. 2011;30:5084–5087. [Google Scholar]
- Zeng Y., Wang S., Feng H., Xie Y., King R. B., Schaefer III H. F. New J. Chem. 2011;35:920–929. [Google Scholar]
- Chen J., Chen S., Zhong L., Hao F., Xie Y., Bruce King R., Schaefer III H. F. Theor. Chem. Acc. 2012;131:1090. [Google Scholar]
- Zhang Z., Li Q.-s., King R. B., Schaefer H. F. Eur. J. Inorg. Chem. 2012;2012:1104–1113. [Google Scholar]
- Fan Q., Feng H., Sun W., Xie Y., King R. B., Schaefer H. F. Organometallics. 2012;31:3610–3619. [Google Scholar]
- Jin R., Chen X., Du Q., Feng H., Xie Y., King R. B., Schaefer H. F. Organometallics. 2012;31:5005–5017. [Google Scholar]
- Jin R., Chen X., Du Q., Feng H., Xie Y., King R. B., Schaefer H. F. RSC Adv. 2016;6:82661–82668. [Google Scholar]
- Gong X., Zhu L., Yang J., Gao X., Li Q.-s., Xie Y., King R. B., Schaefer III H. F. New J. Chem. 2014;38:3762–3769. [Google Scholar]
- Li H., Feng H., Sun W., Xie Y., King R. B., Schaefer H. F. Organometallics. 2013;32:88–94. [Google Scholar]
- Li G., Zhou L., Zhai X., Li Q.-s., Xie Y., King R. B., Schaefer III H. F. New J. Chem. 2013;37:3294–3302. [Google Scholar]
- Deng J., Li Q.-s., Xie Y., King R. B., Schaefer I. H. F. New J. Chem. 2013;37:2902–2910. [Google Scholar]
- Shi T. T., Li Q.-S., Xie Y., King R. B., Schaefer III H. F. New J. Chem. 2010;34:208–214. [Google Scholar]
- Wang H., Xie Y., King R. B., Schaefer H. F. J. Am. Chem. Soc. 2006;128:11376–11384. doi: 10.1021/ja055223+. [DOI] [PubMed] [Google Scholar]
- Wang G., Cui J., Chi C., Zhou X., Li Z. H., Xing X., Zhou M. Chem. Sci. 2012;3:3272–3279. [Google Scholar]
- Chi C., Cui J., Li Z. H., Xing X., Wang G., Zhou M. Chem. Sci. 2012;3:1698–1706. [Google Scholar]
- Mirmohades M., Pullen S., Stein M., Maji S., Ott S., Hammarström L., Lomoth R. J. Am. Chem. Soc. 2014;136:17366–17369. doi: 10.1021/ja5085817. [DOI] [PubMed] [Google Scholar]
- Kuppuswamy S., Wofford J. D., Joseph C., Xie Z.-L., Ali A. K., Lynch V. M., Lindahl P. A., Rose M. J. Inorg. Chem. 2017;56:5998–6012. doi: 10.1021/acs.inorgchem.7b00741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baik M. H., Friesner R. A. J. Phys. Chem. A. 2002;106:7407–7412. [Google Scholar]
- Marenich A. V., Ho J. M., Coote M. L., Cramer C. J., Truhlar D. G. Phys. Chem. Chem. Phys. 2014;16:15068–15106. doi: 10.1039/c4cp01572j. [DOI] [PubMed] [Google Scholar]
- Wang L. P., Van Voorhis T. J. Chem. Theory Comput. 2012;8:610–617. doi: 10.1021/ct200340x. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Phys. Rev. A: At., Mol., Opt. Phys. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Phys. Rev. B: Condens. Matter Mater. Phys. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- Becke A. D. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- Wang L.-P., McGibbon R. T., Pande V. S., Martinez T. J. J. Chem. Theory Comput. 2016;12:638–649. doi: 10.1021/acs.jctc.5b00830. [DOI] [PubMed] [Google Scholar]
- Gordon M. S., Schmidt M. W., Chaban G. M., Glaesemann K. R., Stevens W. J., Gonzalez C. J. Chem. Phys. 1999;110:4199–4207. [Google Scholar]
- Pulay P., Hamilton T. P. J. Chem. Phys. 1988;88:4926–4933. [Google Scholar]
- Parr R. G., Yang W. Annu. Rev. Phys. Chem. 1995;46:701–728. doi: 10.1146/annurev.pc.46.100195.003413. [DOI] [PubMed] [Google Scholar]
- Klamt A. J. Phys. Chem. 1995;99:2224–2235. [Google Scholar]
- Ufimtsev I. S., Martinez T. J. J. Chem. Theory Comput. 2008;4:222–231. doi: 10.1021/ct700268q. [DOI] [PubMed] [Google Scholar]
- Ufimtsev I. S., Martinez T. J. J. Chem. Theory Comput. 2009;5:2619–2628. doi: 10.1021/ct9003004. [DOI] [PubMed] [Google Scholar]
- Ufimtsev I. S., Martinez T. J. J. Chem. Theory Comput. 2009;5:1004–1015. doi: 10.1021/ct800526s. [DOI] [PubMed] [Google Scholar]
- Song C. C., Wang L. P., Sachse T., Preiss J., Presselt M., Martinez T. J. J. Chem. Phys. 2015;143:014114. doi: 10.1063/1.4922844. [DOI] [PubMed] [Google Scholar]
- Song C. C., Wang L. P., Martinez T. J. J. Chem. Theory Comput. 2016;12:92–106. doi: 10.1021/acs.jctc.5b00790. [DOI] [PubMed] [Google Scholar]
- Liu F., Luehr N., Kulik H. J., Martinez T. J. J. Chem. Theory Comput. 2015;11:3131–3144. doi: 10.1021/acs.jctc.5b00370. [DOI] [PubMed] [Google Scholar]
- Wang L. P., Song C. C. J. Chem. Phys. 2016;144:214108. doi: 10.1063/1.4952956. [DOI] [PubMed] [Google Scholar]
- Reiss H., Heller A. J. Phys. Chem. 1985;89:4207–4213. [Google Scholar]
- Donald W. A., Leib R. D., O’Brien J. T., Bush M. F., Williams E. R. J. Am. Chem. Soc. 2008;130:3371–3381. doi: 10.1021/ja073946i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adamo C., Barone V. J. Chem. Phys. 1999;110:6158–6170. [Google Scholar]
- Furche F., Perdew J. P. J. Chem. Phys. 2006;124:044103. doi: 10.1063/1.2162161. [DOI] [PubMed] [Google Scholar]
- Cramer C. J., Truhlar D. G. Phys. Chem. Chem. Phys. 2009;11:10757–10816. doi: 10.1039/b907148b. [DOI] [PubMed] [Google Scholar]
- Galbraith J. M., Schaefer H. F. J. Chem. Phys. 1996;105:862–864. [Google Scholar]
- Jarcki A. A., Davidson E. R. Chem. Phys. Lett. 1999;300:44–52. [Google Scholar]
- Jensen F. J. Chem. Theory Comput. 2010;6:2726–2735. doi: 10.1021/ct1003324. [DOI] [PubMed] [Google Scholar]
- Weigend F., Ahlrichs R. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Weigend F. Phys. Chem. Chem. Phys. 2006;8:1057–1065. doi: 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- Roy L. E., Hay P. J., Martin R. L. J. Chem. Theory Comput. 2008;4:1029–1031. doi: 10.1021/ct8000409. [DOI] [PubMed] [Google Scholar]
- Zheng J., Xu X., Truhlar D. G. Theor. Chem. Acc. 2011;128:295–305. [Google Scholar]
- Laio A., Parrinello M. Proc. Natl. Acad. Sci. U. S. A. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaendtner J., Bonomi M. J. Chem. Theory Comput. 2015;11:5062–5067. doi: 10.1021/acs.jctc.5b00846. [DOI] [PubMed] [Google Scholar]
- Pietrucci F., Andreoni W. Phys. Rev. Lett. 2011;107:085504. doi: 10.1103/PhysRevLett.107.085504. [DOI] [PubMed] [Google Scholar]
- Wang L.-P., Titov A., McGibbon R., Liu F., Pande V. S., Martínez T. J. Nat. Chem. 2014;6:1044–1048. doi: 10.1038/nchem.2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L., Zhao Q., Jensen K. F., Kulik H. J. J. Phys. Chem. C. 2016;120:2472–2483. [Google Scholar]
- Goldman N., Reed E. J., Fried L. E., William Kuo I. F., Maiti A. Nat. Chem. 2010;2:949–954. doi: 10.1038/nchem.827. [DOI] [PubMed] [Google Scholar]
- Hehre W. J., Ditchfield R., Pople J. A. J. Chem. Phys. 1972;56:2257–2261. [Google Scholar]
- Hay P. J., Wadt W. R. J. Chem. Phys. 1985;82:299–310. [Google Scholar]
- Mayer I. J. Comput. Chem. 2007;28:204–221. doi: 10.1002/jcc.20494. [DOI] [PubMed] [Google Scholar]
- Shao Y., Gan Z., Epifanovsky E., Gilbert A. T. B., Wormit M., Kussmann J., Lange A. W., Behn A., Deng J., Feng X., Ghosh D., Goldey M., Horn P. R., Jacobson L. D., Kaliman I., Khaliullin R. Z., Kuś T., Landau A., Liu J., Proynov E. I., Rhee Y. M., Richard R. M., Rohrdanz M. A., Steele R. P., Sundstrom E. J., Woodcock H. L., Zimmerman P. M., Zuev D., Albrecht B., Alguire E., Austin B., Beran G. J. O., Bernard Y. A., Berquist E., Brandhorst K., Bravaya K. B., Brown S. T., Casanova D., Chang C.-M., Chen Y., Chien S. H., Closser K. D., Crittenden D. L., Diedenhofen M., DiStasio R. A., Do H., Dutoi A. D., Edgar R. G., Fatehi S., Fusti-Molnar L., Ghysels A., Golubeva-Zadorozhnaya A., Gomes J., Hanson-Heine M. W. D., Harbach P. H. P., Hauser A. W., Hohenstein E. G., Holden Z. C., Jagau T.-C., Ji H., Kaduk B., Khistyaev K., Kim J., Kim J., King R. A., Klunzinger P., Kosenkov D., Kowalczyk T., Krauter C. M., Lao K. U., Laurent A. D., Lawler K. V., Levchenko S. V., Lin C. Y., Liu F., Livshits E., Lochan R. C., Luenser A., Manohar P., Manzer S. F., Mao S.-P., Mardirossian N., Marenich A. V., Maurer S. A., Mayhall N. J., Neuscamman E., Oana C. M., Olivares-Amaya R., O’Neill D. P., Parkhill J. A., Perrine T. M., Peverati R., Prociuk A., Rehn D. R., Rosta E., Russ N. J., Sharada S. M., Sharma S., Small D. W., Sodt A., Stein T., Stück D., Su Y.-C., Thom A. J. W., Tsuchimochi T., Vanovschi V., Vogt L., Vydrov O., Wang T., Watson M. A., Wenzel J., White A., Williams C. F., Yang J., Yeganeh S., Yost S. R., You Z.-Q., Zhang I. Y., Zhang X., Zhao Y., Brooks B. R., Chan G. K. L., Chipman D. M., Cramer C. J., Goddard W. A., Gordon M. S., Hehre W. J., Klamt A., Schaefer H. F., Schmidt M. W., Sherrill C. D., Truhlar D. G., Warshel A., Xu X., Aspuru-Guzik A., Baer R., Bell A. T., Besley N. A., Chai J.-D., Dreuw A., Dunietz B. D., Furlani T. R., Gwaltney S. R., Hsu C.-P., Jung Y., Kong J., Lambrecht D. S., Liang W., Ochsenfeld C., Rassolov V. A., Slipchenko L. V., Subotnik J. E., Van Voorhis T., Herbert J. M., Krylov A. I., Gill P. M. W., Head-Gordon M. Mol. Phys. 2015;113:184–215. [Google Scholar]
- Bozkaya U., Turney J. M., Yamaguchi Y., Schaefer H. F. J. Chem. Phys. 2012;136(16):164303. doi: 10.1063/1.4704895. [DOI] [PubMed] [Google Scholar]
- Zhao Y., Truhlar D. G. J. Chem. Phys. 2006;125:194101. doi: 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
- Zhao Y., Truhlar D. G. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- Schäfer A., Huber C., Ahlrichs R. J. Chem. Phys. 1994;100:5829–5835. [Google Scholar]
- Schäfer A., Horn H., Ahlrichs R. J. Chem. Phys. 1992;97:2571–2577. [Google Scholar]
- Malick D. K., Petersson G. A., Montgomery J. A. J. Chem. Phys. 1998;108:5704–5713. [Google Scholar]
- Malick D. K., Petersson G. A., Montgomery J. A. J. Chem. Phys. 1998;108:5704–5713. [Google Scholar]
- Schweinfurth D., Sommer M. G., Atanasov M., Demeshko S., Hohloch S., Meyer F., Neese F., Sarkar B. J. Am. Chem. Soc. 2015;137:1993–2005. doi: 10.1021/ja512232f. [DOI] [PubMed] [Google Scholar]
- Neese F. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:73–78. [Google Scholar]