Analysis of Cancer Gene Expression Data with an Assisted Robust Marker Identification Approach

Abstract

Gene expression studies have been playing a critical role in cancer research. Despite tremendous effort, the analysis results are still often unsatisfactory, because of the weak signals and high data dimensionality. Analysis is often further challenged by the long-tailed distributions of the outcome variables. In recent multidimensional studies, data have been collected on gene expressions as well as their regulators (for example, copy number alterations, methylation, and microRNAs), which can provide additional information on the associations between gene expressions and cancer outcomes. In this study, we develop an ARMI (Assisted Robust Marker Identification) approach for analyzing cancer studies with measurements on gene expressions as well as regulators. The proposed approach borrows information from regulators and can be more effective than analyzing gene expression data alone. A robust objective function is adopted to accommodate long-tailed distributions. Marker identification is effectively realized using penalization. The proposed approach has an intuitive formulation and is computationally much affordable. Simulation shows its satisfactory performance under a variety of settings. TCGA (The Cancer Genome Atlas) data on melanoma and lung cancer are analyzed, which leads to biologically plausible marker identification and superior prediction.

1 Introduction

For many cancer outcomes/phenotypes, profiling studies have been extensively conducted, searching for omics markers which may assist in diagnosis, treatment selection, and prediction of prognosis paths. Gene expression (GE) studies have been having a pivotal role in cancer research. Compared to some other types of omics measurements (for example, DNA methylation, mutations, and microRNAs), gene expressions are at the downstream and “closer” to cancer outcomes. Measurements on proteins and metabolisms, which are at the downstream of GEs, are often insufficiently collected. For the outcomes and phenotypes of many cancer types, recent studies show that GEs have prediction performance superior to the other omics measurements (Zhao et al. 2015; Jiang et al. 2016). In addition, a large amount of cancer GE data are available at TCGA, GEO, and other databases, which facilitates testing new analysis methods, conducting secondary analysis, and making new discoveries cost-effectively.

Consider a study with n subjects, each with an outcome/phenotype and p GE measurements. Let y = (y₁, …, y_n)′ be the vector of outcome variable and X = (X₁, …, X_p) be the n × p matrix of GEs. As a representative example, consider the popular case with a continuous outcome and linear modeling. Accommodating other types of outcomes will be discussed later. Consider

$$y=X\beta +\epsilon ,$$ (1)

where β is the p-vector of unknown regression coefficients and ε = (ε₁, …, ε_n)′ is the vector of random errors. With proper normalization, the intercept is omitted.

In a typical cancer GE study, the number of subjects is usually smaller (sometimes much smaller) than the number of GEs. Thus, regularization is usually needed in model estimation. In addition, out of a large number of GEs measured, only a small subset is expected to be cancer-associated. Marker identification, which facilitates interpretation, modeling, and practical utilization, is generally conducted along with estimation. A large number of techniques have been developed for regularized estimation and marker identification. Among them, penalization has been popular because of its satisfactory numerical and statistical properties (Ma and Huang 2008). Under the penalization framework, the estimate is defined as the minimizer of the following objective function:

$$\frac{1}{n}{\Vert y-X\beta \Vert }_2^2+\mathit{pen}(\beta ),$$ (2)

where pen(·) is the penalty function. The most popular penalty is perhaps Lasso, with alternatives including SCAD, MCP, bridge, and others.

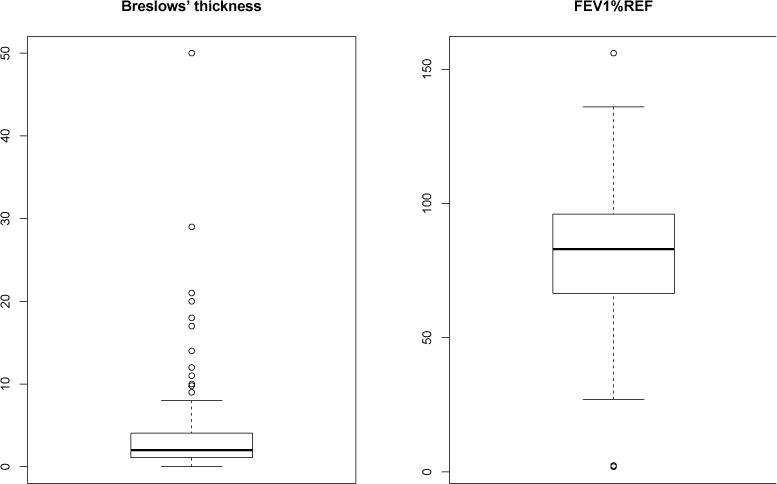
Quite a few cancer GE studies have been conducted under the penalized analysis framework, with various goodness-of-fit and penalty functions. Despite great successes, in practice, the analysis in (2) still often generates unsatisfactory results, which may be attributable to the following factors. Most GE signals are moderate to small, and most of the existing cancer omics studies have small sample sizes. As a result, there is not enough “information” to make reliable discoveries. In practice, long-tailed distributions of the outcome variables are not rare. This can be caused by multiple reasons. Some clinical outcomes have skewed distributions in nature. In addition, measurement error and human mistakes can happen, and data extracted from medical records are not always reliable (Fall et al. 2008; Bowman 2011). Such data contaminations can lead to long-tailed distributions. Most cancer GE studies cannot afford conducting rigorous patient selection, and seemingly similar patients can have different cancer subtypes. In this case, data on the major subtypes can be viewed as “contaminated” by those on the smaller subtypes. For the datasets analyzed in this article, we plot the outcome variables in Figure 1, where we can clearly see the long tails. For a continuous outcome variable, the commonly adopted least squared estimation in (2) cannot effectively accommodate long-tailed distributions (or data contamination). One possible solution is to transform the outcome variable first (some more details in data analysis). However, the transformation function needs to be properly selected, which is not a simple task. In addition, the transformed outcome may be not as interpretable as the original one. Similar problems exist for other types of outcome variables. In this article, we will directly address the aforementioned problems which are commonly encountered in cancer gene expression studies.

Figure 1.

Histograms of the outcome variables for the SKCM (left) and LUAD (right) data.

The levels of GEs are regulated by multiple types of regulators including for example copy number alteration (CNA), methylation, and microRNA. With the regulation relationship, the regulators contain information on the relevancy of GEs. To more intuitively demonstrate the idea, consider the simplified scenario where each GE is only regulated by one CNA, and the regulation relationship is strong. Consider two (GE, CNA) pairs. The first pair has (GE, CNA) effects on a cancer outcome equal to (1, 0.01), and the second pair has effects (0.7, 0.6). If we only look at the GE data, then the first GE will be identified as having a stronger association with the outcome. However, considering the regulation, the first GE is possibly a false positive, as the finding is not supported by its regulator, while the second GE is more likely to be truly associated. In this study, our goal is to take advantage of information in regulators so as to more accurately identify GE signals. The proposed analysis is made possible by the recent multidimensional studies such as TCGA (The Cancer Genome Atlas) which collect data on GEs as well as regulators on the same subjects. A few recent studies have collectively analyzed data on GEs and their regulators. For example, Shi et al. (2015) studies the regulations of GEs by regulators. Zhao et al. (2014) develops an additive strategy and integrates GE and regulator data in model building. Wang et al. (2013) and Zhu et al. (2016) decompose GEs using regulator information and allow different GE components to behave differently in cancer models. The analysis paradigm in this study is fundamentally different from that of the aforementioned studies. Specifically, it differs from Shi et al. (2015) and some others by developing a model for a cancer outcome/phenotype. The main goal is to identify GE markers, not multiple types of omics markers as in Zhao et al. (2014). Different from the decomposition in Wang et al. (2013) and Zhu et al. (2016), GEs are considered as a whole, which facilitates interpretation. In the literature, the most relevant study is perhaps Gross and Tibshirani (2015), which develops the collaborative regression method and encourages two types of omics measurements to explain similar variations in outcome. However, the collaborative regression method does not explicitly account for the regulation relationship, which, as shown in our numerical study, may lead to inferior results. In addition, it is noted that in all these aforementioned studies, “standard” estimation, which cannot accommodate long-tailed distributions (or contamination), is adopted.

To accommodate long-tailed outcome distributions (or data contamination), we adopt robust estimation. In GE studies, robust estimation has been adopted but is still rather limited (Wu and Ma 2015). To the best of our knowledge, it has not been used in contexts similar to the present analysis. For some long-tailed distributions, transformations such as logarithm may be sufficient from a statistical perspective but may complicate interpretation, since the models are not on the original scale. For other distributions, simple and satisfactory transformations may not exist. In contrast, robust estimation can provide a more broadly applicable solution.

In this article, we develop an ARMI (Assisted Robust Marker Identification) approach for analyzing cancer GE studies. With the assistance of GE regulators, the proposed approach can more accurately identify GE markers than those that analyze GE data alone. Unlike the collaborative regression and others, it explicitly accounts for the regulation relationship between GEs and regulators and can have superior numerical performance. With robustness, it can accommodate data distributions that are not appropriate for simple models and/or estimations. Overall, this study provides a practically more effective way for analyzing cancer GE data.

2 Methods

2.1 Data and model settings

Consider the data settings described in the previous section and model (1). For comparability, we normalize the data matrix such that ${\Vert X_j\Vert }_2^2=n$ for j = 1, …, p. With the least squared estimation in (2), it needs to be assumed that ε_j has mean zero and a finite variance. To accommodate long-tailed distributions, we adopt robust estimation and only assume that ε_j has median zero, but no variance assumption is made. This weaker error assumption makes the proposed approach more broadly applicable. More details are presented in Appendix.

For each subject, assume that measurements are also available on q regulators of GEs. The regulators can be CNAs, methylation, mutations, microRNAs, and others. When there are multiple types of regulators, for example q₁ CNAs and q₂ methylation, we stack the measurements together and create the q = q₁ + q₂-vector of regulator measurements. This approach, although may be a little crude, has been shown to be effective (Zhu et al. 2016). Further discussions are also provided in our simulation study. Denote Z = (Z₁, …, Z_q) as the n × q data matrix of regulators. With normalization, Z_k has mean zero and ${\Vert Z_k\Vert }_2^2=n$ for k = 1, …, q. For modeling the relationship between GEs and regulators, following Shi et al. (2015) and others, we consider

$$X=Z\eta +W,$$ (3)

where η is the q × p matrix of unknown regression coefficients and represents the “transition” from regulators to GEs. Denote the true value of η as η₀. W = (W₁, …, W_p) is an n × p matrix and accommodates both “random errors” as well as regulation mechanisms not measured. The expression level of a specific gene is only affected by a small number of regulators (that is, η₀ is sparse). However, the set of regulators and strengths of their effects are unknown, posing a variable selection and regularized estimation problem.

Remarks

Linear models have been assumed. For datasets analyzed in this article, we graphically examine the relationships between outcomes and GEs and between GEs and CNAs. Representative plots are provided in Figure 1 (Appendix), which suggest that linear modeling is reasonable. For continuous outcomes and GEs, linear modeling has been extensively adopted in the literature. Examples include Wang et al. (2013), Gross and Tibshirani (2014), Park et al. (2007), and others. For GEs and their regulators, examples of linear modeling include Kim et al. (2009), Peng et al. (2010), Wang et al. (2014), Shi et al. (2015) and many others. Extending the proposed approach to other models is in principle possible but expected to be challenging. We postpone such pursuit to future research.

2.2 ARMI

With models (1) and (3), we have

$$y=X\beta +\epsilon =Z\eta \beta +e=Z\mathrm{\gamma }+e,$$ (4)

where e = Wβ + ε. An interpretation of this model is that there are important regulators that are associated with the cancer outcome. Motivated by similar considerations, studies have been conducted, directly linking CNAs, methylation, microRNAs, and others with cancer outcomes.

Another interpretation/utilization of (4) is that important (cancer-associated) regulators regulate important GEs, which then contribute to the cancer outcome. Motivated by this consideration, we proposed borrowing information from important regulators to assist in identifying important GEs so as to improve accuracy. Specifically, we propose the ARMI estimate as

$$(\widehat{\beta },\widehat{\mathrm{\gamma }})=\underset{\beta ,\mathrm{\gamma }}{\arg \text{min}}\left\{\frac{1}{n}{\Vert y-X\beta \Vert }_1+\frac{1}{n}{\Vert y-Z\mathrm{\gamma }\Vert }_1+{\mathrm{\lambda }}_1{\Vert \beta \Vert }_1+{\mathrm{\lambda }}_2{\Vert \mathrm{\gamma }\Vert }_1+{\mathrm{\lambda }}_3{\Vert {\eta }_0\beta -\mathrm{\gamma }\Vert }_1\right\}.$$ (5)

λ₁, λ₂, and λ₃ are tuning parameters. GEs corresponding to the nonzero components of $\widehat{\beta }$ are identified as associated with the cancer outcome.

The ARMI approach has been motivated by the following considerations. In (5), when λ₃ = 0, it reduces to two separate penalized regressions for the outcome variable, with one on GEs and the other on regulators. With the sparsity of both β and η, γ is also expected to be sparse. Thus, a penalized estimation and selection is sensible. The robust LAD (least absolute deviation) loss function, which is a special case of the popular quantile regression, is adopted to accommodate long-tailed distributions (and/or contamination). Interestingly, it has been suggested that for high-dimensional data, even without long-tailed distributions, the ℓ₁ distance may provide a better measure than the commonly adopted ℓ₂ (Aggarwal et al. 2001). For regularized estimation and marker identification, we adopt the popular Lasso penalty. We note that many other penalties, for example SCAD and MCP, are also applicable here. Lasso is adopted for its outstanding numerical properties. Another consideration is that “consistently” adopting the ℓ₁ norm considerably simplies computation. The most significant advancement is the introduction of penalty λ₃‖η₀β – γ‖₁. GEs and their regulators are connected by (3). The new penalty promotes the similarity of η₀β and γ. The intuition is that the estimation of β and hence marker identification can be improved by borrowing information from γ.

Shrinking the differences between regression coefficients and promoting their similarity have been considered in the literature. Popular examples include the fused penalization and Laplacian penalization (Shi et al. 2015). For a specific coefficient, the fused penalization penalizes its differences with two adjacent ones. It demands a spatial adjacency structure, which is not present in our analysis. The Laplacian penalization approach imposes ℓ₂ penalties and is usually built on correlations. The most significant difference of the present analysis is that β and γ correspond to different types of omics measurements. They can have different dimensions, are not directly comparable, and demand the involvement of the transition matrix η₀. It is insensible to directly take the difference of β and γ or compute the pairwise correlations between GEs and regulators.

In practice, η₀ is unknown. In (5), we replace it with its estimate which is defined as

$$\widehat{\eta }=\underset{\eta }{\arg \text{min}}\left\{\frac{1}{n}{\Vert X-Z_{\eta }\Vert }_F^2+{\mathrm{\lambda }}_4{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{k=1}^q\left|{\eta }_{j}k\right|}}\right\},$$ (6)

where ‖·‖_F is the Frobenius norm, and η_jk is the (j, k)th element of η. In (6), the ℓ₂ loss is adopted as no obvious long-tailed distributions (or contamination) are spotted in X. It can be replaced by other loss functions if necessary. The Lasso penalty is imposed again for regularized estimation and selection.

Compared to the “benchmark” approach which corresponds to λ₂ = λ₃ = 0 in (5) and others, the ARMI approach involves more parameters. However, it is still expected that if the regulators contain information on GEs, which is most likely to be the case given extensive biological evidences, GE marker identification can benefit from borrowing information. On the other hand, if GEs and regulators are actually not related, then η₀ = 0, and $\widehat{\eta }\approx 0$. When η₀ = 0, λ₃‖η₀β – γ‖₁ reduces to another Lasso penalty for γ. Data-dependently adjusting λ₂ and λ₃ can ensure no “double penalization” for γ.

In Appendix, we rigorously establish that the ARMI estimate enjoys the much desired consistency properties under high-dimensional settings, which provides it a solid statistical ground and may make it preferred over alternative approaches that do not have a strong statistical support.

2.3 Computation

Estimation in (6) is standard Lasso and can be efficiently realized using the existing algorithms and software packages (such as glmnet and ncvreg in R). Although a large number of Lasso estimates need to be computed, as computation can be carried out in a highly parallel manner, the cost is very affordable.

With all norms being ℓ₁, optimization in (5) can be effectively realized using linear programming. Define α = (y − Xβ)/n, π = (y − Zγ)/n, and $\tau =\widehat{\eta }\beta -\mathrm{\gamma }$. Let α_±, β_±, γ_±, π_±, and τ_± be the positive/negative parts of α, β, γ, π, and τ, respectively. For two vectors a and b with the same length, if a_i = b_i for all index i, we denote this element-wise equivalency as a =_e b. Similarly, if a_i ≥ b_i for all i, denote the element-wise greater than or equal to relationship as a ≥_e b. Minimizing the objective function in (5) is equivalent to minimizing

$${\alpha }_{+}+{\alpha }_{-}+{\pi }_{+}+{\pi }_{-}+{\mathrm{\lambda }}_1{\beta }_{+}+{\mathrm{\lambda }}_1{\beta }_{-}+{\mathrm{\lambda }}_2{\mathrm{\gamma }}_{+}+{\mathrm{\lambda }}_2{\mathrm{\gamma }}_{-}+{\mathrm{\lambda }}_3{\tau }_{+}+{\mathrm{\lambda }}_3{\tau }_{-},$$ (7)

subject to the constraints

$$\begin{gathered} {\alpha }_{+}-{\alpha }_{-}{=}_e[y-X({\beta }_{+}-{\beta }_{-})]/n, \\ {\pi }_{+}-{\pi }_{-}{=}_e[y-Z({\mathrm{\gamma }}_{+}-{\mathrm{\gamma }}_{-})]/n, \\ {\tau }_{+}-{\tau }_{-}{=}_e\widehat{\eta }({\beta }_{+}-{\beta }_{-})-({\mathrm{\gamma }}_{+}-{\mathrm{\gamma }}_{-}), \\ {\alpha }_{\pm },{\beta }_{\pm },{\mathrm{\gamma }}_{\pm },{\pi }_{\pm },{\tau }_{\pm }{\ge }_{e}0. \end{gathered}$$

This linear programming optimization is very fast. For example, for a simulated dataset with n = 200 and p = q = 500 (more details below) and fixed $\widehat{\eta }$, we compute the solutions under 50(λ₁) × 50(λ₂) × 10(λ₃) tuning parameter values. Computation is accomplished within 6 seconds using a laptop with standard configurations.

The ARMI approach involves two steps. In both steps, the tuning parameters can be selected using many approaches. In numerical study, we adopt cross validation (CV). As the computational cost is really low, it is feasible to search for the optimal values of multiple tunings simultaneously. To facilitate applications beyond this study, we have developed R code which is available at https://github.com/shuanggema. The code can be easily modified for other analysis.

3 Simulation

Simulation is conducted to assess the performance of ARMI. In addition, as a reference, we also consider the following alternatives.

• Alt.1: Consider the estimate

  $${\widehat{\beta }}^{\mathit{LassoX}}=\arg \text{min}\left\{\frac{1}{n}{\Vert y-X\beta \Vert }_2^2+\mathrm{\lambda }{\Vert \beta \Vert }_1\right\}.$$ (8)

  This is the benchmark Lasso approach, involves X only, and adopts the popular least squared loss.
• Alt.2: Consider the estimate

  $${\widehat{\beta }}^{\mathit{LassoXZ}}=\arg \text{min}\left\{\frac{1}{n}{\Vert y-X\beta -Z\mathrm{\gamma }\Vert }_2^2+\mathrm{\lambda }({\Vert \beta \Vert }_1+{\Vert \mathrm{\gamma }\Vert }_1)\right\}.$$ (9)

  This approach models the outcome directly as a function of X and Z and adopts the least squared loss and Lasso penalized estimation.
• Alt.3: The ARMI approach, Alt.1, and Alt.2 all conduct the joint analysis of multiple GEs. A popular family of approaches conducts marginal analysis. Specifically, for j = 1, …, p, consider the estimate

  $${\widehat{\beta }}_j^{m\arg }=\arg \text{min}\left\{\frac{1}{n}{\Vert y-X_j{\beta }_j\Vert }_2^2\right\}.$$ (10)

  Note that this is a one-dimensional estimation problem and does not require penalization. A p-value is obtained for each ${\widehat{\beta }}_j^{\mathit{marg}}$. GEs with the smallest p-values are identified as important.

• Alt.4: Consider the collaborative regression approach developed in Gross and Tibshirani (2015). This approach also analyzes both GEs and regulators. It encourages the two components to explain similar variations in the outcome variable. Different from ARMI, there is no explicit account for the regulation relationship (and hence no involvement of η).

A special case of ARMI with λ₃ = 0. This approach conducts the “LAD loss + Lasso penalization” analysis of GE data.

The ARMI and alternative approaches all involve tuning parameters. For Alt.3, the p-value cutoff for significance can be viewed as a tuning. Focusing on specific tuning parameter values may not generate a comprehensive picture. To tackle this problem, we adopt the ROC (Receiver Operating Characteristic) approach, which considers a set of tuning parameter values, evaluates identification at each value, and uses the ROC-based measures for evaluation. This evaluation approach has been extensively adopted in the literature. In our simulation, the AUC (area under the ROC curve) is adopted as the overall identification accuracy measure. ARMI has the additional tuning λ₃, which is directly relevant to the estimation of β. To make it more comparable to the alternatives, for each λ₁ value, we select λ₃ using CV. We have also examined this ROC-based evaluation for a grid of (λ₁, λ₂, λ₃) values and obtained similar results.

Three simulation settings are considered, with multiple scenarios under each setting. Under Setting I and II, there is one type of regulator. Under Setting III, there are two types of regulators. Specifically, under Setting I, data are generated under the models assumed above, and so the effects of regulators on outcome are completely captured by GEs, and GEs do not have “unregulated effects”. Under Setting II, GEs and regulators have overlapping effects as well as independent effects. Note that under this setting, the proposed models and approach are mis-specified. Thus this setting can serve as a test of sensitivity. It has been motivated by the following considerations. First in some studies, there may be regulators of GEs not measured (that is, the measurements are “incomplete”). Thus some GE signals cannot be explained by the measured regulators. Second, methylation and possibly other regulators may directly affect proteins and hence cancer outcomes not through GEs. Under Setting III, there are two types of regulators, and one type of regulator is regulated by the other. Other setup is similar to under Setting I. This setting is designed to accommodate possible complex interconnections among regulators as well as different data characteristics of different types of regulators. In analysis, we stack the two types of regulator measurements together and create a longer vector of regulators.

Setting I

Data are generated as follows. (a) Z_n×q is generated from MVN(0, Σ_q(ρ₁)) – a multivariate normal distribution with mean zero and covariance ${\sum }_q{({\rho }_1)}_{i,j}={\rho }_1^{|i-j|}$ if ρ₁ ≠ 0, and Σ_q(ρ₁) = I if ρ₁ = 0 – and then kept fixed. W has distribution MVN(0, Σ_p(ρ₂)). Consider different levels of correlation with (ρ₁, ρ₂) = {(0, 0), (0.8, 0), (0.8, 0.8)}. (b) For matrix η, consider three structures. (b.1) A block diagonal structure with block size three and the blocks equal to J and −J alternatively. J is the 3 × 3 matrix with all elements equal to 1. (b.2) A diagonal structure with all diagonal elements equal to 1. (b.3) A “milky-way” structure. The diagonal elements are all equal to 1. A small portion (8%) of the off-diagonal elements are randomly generated from Unif(−0.4, 0.4). Their positions are randomly simulated. (c) Consider the outcome generating model $y=X\beta +\sigma \stackrel{\sim }{\epsilon }$. Consider two noise levels with σ = 2 and 5. For $\stackrel{\sim }{\epsilon }$, consider three scenarios with (E1) N(0, 1), (E2) t(3), and (E3) a mixture of standard normal (70%) and Cauchy (30%). Among them, E2 has long tails, while E3 is a representative of contamination. (d) For β₀, the first six elements are equal to 0.5, the next six are equal to −0.5, and the rest are equal to 0. The value of γ₀ is computed from β₀ and η₀. (e) Set n = 200 and (p, q) = (500, 500). Here we note that, although bigger than n, the value of p may not seem “dramatic”. Whole-genome studies may have a much higher dimensionality. However to improve analysis reliability, it is a common practice to focus on a smaller set of genes, which can be selected biologically or statistically. It is noted that even with moderate p and q, the number of parameters involved is still much larger than n.

AUCs are computed based on 200 replicates. Results under the block-diagonal η are shown in Table 1, and those under the diagonal and milky-way structures are shown in Tables 4 and 5 (Appendix). It is observed that ARMI has competitive performance across the whole spectrum of simulation. For some simple cases, all approaches have satisfactory performance. For example in the first row of Table 1, all approaches can precisely identify the true signals. For more difficult cases, the advantage of ARMI gets prominent. For example in the last row of Table 1, with tunings selected using CV, ARMI has AUC 0.855. For the special case of ARMI with λ₃ = 0, the AUC value is 0.78. The four other alternatives have the largest AUC 0.629. It is interesting to note that although Alt.2 and the collaborative regression also jointly analyze GEs and regulators and borrow information, without explicitly accounting for the regulation relationship, they have inferior performance.

Table 1.

Simulation I with block-diagonal η: mean (sd) of AUC (×100).

σ	ε	ρ1	ρ2	Alt.1	Alt.2	Alt.3	Alt.4	ARMI (λ3 =)
								0	CV
2	E1	0	0	100(0)	100(0)	99.8(0.9)	100(0)	100(0)	100(0)
2	E1	0.8	0	100(0)	100(0.1)	86.5(8.7)	100(0)	99.8(0.1)	99.9(0.1)
2	E1	0.8	0.8	98.7(2.4)	96.9(4.1)	88.7(9.9)	99.4(1)	96.6(4.4)	98(2.8)
2	E2	0	0	98.1(5.6)	97.8(6.7)	99(4.3)	98(6.1)	100(0)	100(0)
2	E2	0.8	0	98.3(5.1)	95.5(7.7)	83.4(11)	98.9(4)	99.5(1)	99.8(0.3)
2	E2	0.8	0.8	92(5.3)	90.2(5.7)	87.7(11.8)	93.2(5.1)	94.8(4)	96.6(3.1)
2	E3	0	0	76.4(16.8)	76.1(15.2)	84.3(18.5)	77.5(17.4)	96.6(11.3)	97.3(11.2)
2	E3	0.8	0	78.3(17.8)	74.8(16.4)	73.9(14.9)	80.5(18.2)	97(11.1)	97(11.1)
2	E3	0.8	0.8	68.5(12.8)	69.2(15.4)	74.1(21.8)	69.9(13.9)	92.3(11.4)	94.9(11)
5	E1	0	0	96.9(3)	96.3(3.1)	99.9(0.4)	97.3(2.6)	96.1(4.4)	98.8(1.5)
5	E1	0.8	0	95.9(3.7)	91.2(6.3)	80.2(13.8)	97.2(3.1)	93.4(4.7)	97.6(2.1)
5	E1	0.8	0.8	83.1(7.2)	82.4(6.5)	91.2(8.8)	84.7(6)	81.9(5.5)	89.7(3.5)
5	E2	0	0	83.9(7)	82.2(8.2)	95(6.1)	85.9(7.3)	91.9(5.9)	97.7(2.6)
5	E2	0.8	0	82.5(7.7)	75.8(7.2)	78.7(10.4)	85.6(6.9)	90(4.8)	95.5(2.8)
5	E2	0.8	0.8	74.6(5)	74.2(7.1)	82.1(9.2)	75.7(5.6)	78.4(6.2)	87.3(5.7)
5	E3	0	0	61.2(11.7)	61.6(11.4)	72.1(15.7)	61.7(12)	88.7(7.7)	96.6(3.3)
5	E3	0.8	0	60(10.4)	57(10.1)	59.1(15.7)	60.1(11)	84.5(10.7)	89(11.8)
5	E3	0.8	0.8	58.4(10.1)	57.8(11.1)	62.9(21.3)	58.1(10.2)	78(8.7)	85.5(10)

Setting II

The setups are largely similar to those under Setting I. The differences are as follows. (a) We first generate the η matrix in the same way as under Setting I. Then we set the last ten rows equal to 0. Correspondingly, the last ten GEs are not regulated. (b) The outcome generating model (4) is revised as

$$y=X_{1,\dots ,490}{\beta }_{1,\dots ,490}+X_{491,\dots ,500}{\beta }_{491,\dots ,500}+Z_{491,\dots ,500}{\mathrm{\gamma }}_{491,\dots ,500}+\epsilon ,$$

where, with a slight abuse of notation, the subscripts are the components’ indexes. In this model, the first term is the same as under Setting I and represents the overlapping signals. The second term X_491,…,500β_491,…,500 represents the contributions of GEs (to the outcome) that are not regulated. The third term Z_491,…,500γ_491,…,500 reflects the contributions of regulators (to the outcome) that are not captured by GEs. The first 490 components of β and γ are the same as under Setting I. For the last ten components, β_491,…,500 = (.4, 0, 0, 0, 0, 0, – .5, 0, 0, 0)′, and γ_491,…,500 = (.5, 0, 0, 0, 0 – .5, 0, 0, 0, 0)′. That is, out of a total of sixteen signals, four are “misspecified” in that they do not fit the proposed models.

The AUC results are summarized in Tables 6, 7, and 8 (Appendix). As can be expected, with mis-specification, ARMI does not perform as good as under Setting I. However, it still performs similar to or better than the alternatives. For example, in the last row of Table 6 (Appendix), ARMI has AUC 0.752 when the tunings are selected using CV. The special case of ARMI with λ₃ = 0 has AUC 0.723. The four other alternatives have the best AUC 0.613. This set of simulation suggests that with a moderate model mis-specification, the ARMI approach still has satisfactory performance.

Setting III

Data are generated as follows. (a) There are two types of GE regulators, Z₁ and Z₂, with dimensions q₁ and q₂, respectively. We first generate Z₁ in a similar way as for Z under Setting I. (b) Z₂ is then generated from $Z_2=\xi Z_1+\stackrel{\sim }{W}$, where ξ and $\stackrel{\sim }{W}$ are generated similarly to η and W under Setting I. To differentiate Z₂ from Z₁, $\stackrel{\sim }{W}$ is generated such that conditional on Z₁, Z₂ has a t-distribution with degree of freedom 4. (c) Z is then generated by stacking Z₁ and Z₂ together. It is noted that the two components of Z are interconnected and have different distributions. (d) X and the outcome variable are generated similarly as under Setting I. (e) Set n = 200, p = 300, and q₁ = q₂ = 300.

The results are summarized in Tables 9, 10, and 11 (Appendix). The observed patterns as similar to those under the previous settings. The ARMI approach has competitive or superior performance under a variety of scenarios with different regulations between Z₁ and Z₂, between Z and X, and between X and the outcome variable.

4 Data analysis

4.1 Analysis of SKCM data

We analyze the TCGA data on SKCM (skin cutaneous melanoma). Data are downloaded from the TCGA website and contain records on 295 SKCM patients. In this analysis, we search for gene expressions in the cell cycle pathway that are associated with Breslow thickness. Breslow thickness is a clinically important variable and has been extensively examined in etiology and prognosis studies. Its measure is available for 221 (74.9%) out of 295 subjects. Research has been conducted, looking for the omics determinants of Breslow thickness. For example, studies have detected and validated the positive correlation between the expression of gene NRP2 and Breslow thickness. In principle, it is possible to conduct a whole-genome analysis. Here to improve analysis reliability, we conduct a more focused analysis on the cell cycle pathway, which plays a critical role in melanoma.

Measurements are available on GEs and multiple types of regulators. In this analysis, we focus on CNAs. Compared to other types of regulators (for example microRNAs), the regulations between GEs and CNAs are more clearly defined. With the assistance of GO (Gene Ontology) and the annotation package in GSEA (www.broadinstitute.org/gsea), we identify 177 GEs and 177 CNAs belonging to the cell cycle pathway. We conduct a light processing and remove subjects with a high rate of missing measurements as well as highly correlated GE (CNA) measurements. The data used for downstream analysis contain 176 GE and 137 CNA measurements on 208 subjects. We examine the distribution of Brewslow thickness (Figure 1), where we can clearly see a long right tail. We also conduct exploratory analysis and graphically examine the associations between the outcome and GEs and between GEs and CNAs. Plots in Figure 2 (Appendix) suggest that linear modeling is reasonable (more plots have been examined and omitted here).

We analyze data using the ARMI and alternative approaches. Beyond the four alternatives considered in simulation, we also apply Alt.5, which first conducts the logarithm transformation of the outcome variable and then applies Lasso for selection and estimation. The logarithm transformation is perhaps the simplest among all transformations and can accommodate the long right tail to a great extent. In Figure 3 (Appendix), we show the correlations between GEs and CNAs, which clearly show that they are interconnected. In addition, we also plot the estimated η matrix. The final analysis results using different approaches are shown in Table 2. With ARMI, the strongest signals (largest coefficients) are identified as genes EREG and GAS1. Epiregulin (EREG) has been found to be overexpressed in melanoma cells and has a delayed impact on tumor progression and the onset of apoptosis. Growth arrest-specific 1 (GAS1) has been identified as a novel melanoma metastasis suppressor gene. These two genes also rank in the top with the alternatives, suggesting the reliability of findings. Using ARMI, other biologically plausible findings include the tumor suppressor gene RUNX3, tissue-specific regulation gene CDK2, XPC which enhances melanoma photocarcinogenesis, and MAPK12 which has been found as playing a critical role in a variety of cancers. The alternatives are also able to make some interesting findings. But they miss some important ones for example gene CDK2, whose copy number and gene expression have been used to identify deregulation of melanoma cells at the transcriptional level.

Table 2.

Analysis of SKCM data: GEs identified using different methods. Estimated coefficients for Alt.1, Alt.2, Alt.4, Alt.5, and ARMI and p-values for Alt.3.

	Alt.f	Alt. 2	Alt.3	Alt. 4	Alt. 5	ARMI
TTK	−0.40	−0.58	6E-02	−0.21	−0.06	0.21
CITED2			1E-07
MAP2K6	0.30	0.39
UHRF2	0.01			−0.01
TIMELESS				0.00
AL0X15B	0.06				0.01	0.06
TBRG1						−0.27
CDK5R1	0.19				0.07
CDK5R2					−0.05
NEK2			2E-01
HUS1	0.24			0.07
UHMK1						−0.11
HEXIM1			2E-01
NPM2	0.22	0.02		0.01	0.08
CDC123	−0.21	−0.26		−0.17
RUNX3	0.34	0.25	1E-01	0.15	−0.00	0.43
BMP2			1E-06
SMAD3	1.35	1.45	1E-01	0.29	0.18
GAS1	−0.65	−0.83	6E-02	−0.09	−0.07	−1.04
CDKN1C	−0.55	−0.69	1E-01	−0.14	−0.11	−0.13
NBN					−0.06	−0.32
CCNT1						0.28
CDT1					−0.11	−0.68
TRIAP1			2E-01
PRMT5					0.01
TGFA			7E-12
CDK5RAP3	0.34			0.05
CDK10						0.07
FANCG	−0.33			−0.11	−0.10	−0.43
MYC	0.32	0.51		0.16
SERTAD1			8E-02
DLG1			2E-01
ZW10						0.37
KHDRBS1		−0.15				−0.07
CCNK			6E-02
TP53	0.26			0.09
NUSAP1			9E-02
UBE2C					0.03	0.26
NEK11						−0.22
CDK2		0.02		0.02	0.03	0.35
EIF4G2						−0.58
DHRS2	0.91	0.89	7E-02	0.30	0.08
PPM1G						0.03
XPC						0.12
EREG	3.40	3.40	5E-24	1.54	0.18	3.32
BTG4	0.38	0.41	1E-07	0.07	0.07	0.64
BTG3	0.52	0.42	1E-02	0.11	0.08
ERN1				−0.03
BUB1B	−0.11	−0.08	6E-02		0.02	0.18
FOXC1			1E-01
PPP1R15A					0.16
ING4			5E-02
HCFC1	0.85	0.60		0.22	0.16
ASNS					−0.02
BCCIP	0.04	−0.18		−0.00
TMEM8B	−0.36		2E-01	−0.04	−0.09
BUB1					−0.08	−0.36
TBX3	−0.39	−0.30			−0.04	−0.21
CDKN3	−0.46
CDC25C			1E-01
MAPK12						−0.16
EPGN			2E-01
CKS2						−0.06
HPGD	0.65	0.72		0.18	0.13	0.27

The differences in findings of different approaches are summarized in Table 12 (Appendix). To better comprehend their difference/similarity, we compute the RV-coefficients between the identified GEs of any two approaches. The RV-coefficient (Smilde et al. 2009) measures the common information of two matrices (data matrices of GEs identified by two different approaches in our analysis), with a larger value indicating higher similarity. It is observed that findings of different approaches have moderate overlaps. To complement the identification analysis and also to provide an indirect support, we conduct a cross-validation based prediction analysis. Note that with Alt.3, after the top markers are identified, a second-step fitting is needed to generate a prediction model. With Alt.5, the results need to be transformed back to the original scale. The predicted median absolute error (PMAE), defined as $\mathit{median}(|y_i-{\widehat{y}}_i|)$ where ${\widehat{y}}_i$ is the predicted value for the ith subject, is used for prediction evaluation. The PMAEs are 1.904 (Alt.1), 1.912 (Alt.2), 2.006 (Alt.3), 1.902 (Alt.4), 1.713 (Alt.5), and 1.228 (ARMI), respectively, with ARMI having a significant advantage in prediction. We also compute the prediction mean squared errors (PMSE), which takes values 16.138 (Alt.1), 14.607 (Alt.2), 21.781 (Alt.3), 17.528 (Alt.4), 26.524 (Alt.5), and 10.093 (ARMI), respectively.

4.2 Analysis of LUAD data

We analyze TCGA data on lung adenocarcinoma (LUAD). The analysis strategy and procedure are similar to those for the SKCM data. The outcome variable of interest is FEV1 (forced expiratory volume in one second), which quantifies reduced lung function and has been extensively utilized in lung cancer research and clinics. In analysis, we are specifically interested in the apoptosis pathway, which has been functionally related to lung function reduction. With the same processing as in the previous section, the analyzed data contain 231 LUAD patients with 337 GE and 246 CNA measurements.

The distribution of outcome (Figure 1), graphical exploratory analysis (Figure 2, Appendix), and correlation analysis (Figure 3, Appendix) lead to similar observations as for the SKCM data. The GEs identified by different approaches are shown in Table 3. ARMI generates biologically plausible findings by identifying a handful of genes that have been established as strongly associated with LUAD. For example, it detects a strong negative association between FEV1 and gene NOTCH2, which is associated with the progression of early-stage LUAD and a more aggressive phenotype at advanced stages. Other notable findings include genes VCP (Valosin-containing protein), BCL2L10 and BCL2L2 (which encode the antiapoptotic BCL-2 proteins), PRKCA (protein kinase C alpha), and HDAC3 (histone deacetylases). Among them, genes VCP and BCL2L10 are identified only by ARMI, which also identifies important tumor suppressors including genes BECN1 (Beclinl protein) and MOAP-1 (Modulator of apoptosis 1). The summary in Table 12 (Appendix) suggests that the findings of different approaches have moderate overlap. Prediction evaluation is conducted. The PMAEs are 12.553 (Alt.1), 12.134 (Alt.2), 13.881 (Alt.3), 15.387 (Alt.4), 16.965 (Alt.5), and 10.232 (ARMI), respectively. The PMSEs are 535.279 (Alt.1), 603.148 (Alt.2), 525.273 (Alt.3), 567.523 (Alt.4), 691.905 (Alt.5), and 481.051 (ARMI), respectively. Again it is observed that the ARMI approach has superior prediction.

Table 3.

Analysis of LUAD data: GEs identified using different methods. Estimated coefficients for Alt.1, Alt.2, Alt.4, Alt.5, and ARMI and p-values for Alt.3.

	Alt.1	Alt.2	Alt.3	Alt.4	Alt.5	ARMI
SNCA	−5.56	−4.89	2E-02	−1.23	−0.14
CUL3				0.57
FAS				−1.64
CUL1						−1.83
BCL2L10						−2.07
IFNB1						−2.77
MAPK8			1E-02
UNC13B						−2.41
SIVA1	−0.27	0.78	1E-02	0.50
TNFRSF6B					−0.06
BCL2L2	−1.28	−2.14			−0.04	−2.59
CD74	2.49	2.70	3E-02		0.02
BECN1						1.20
TAX1BP1	−1.64				−0.04
CIDEC				−0.49
N0TCH2	−0.86		3E-02			−1.02
ВFAR						0.64
EI24	−2.41	−2.15	2E-02
NUAK2				0.60
PTEN				−0.32
T0P2A			2E-02			1.63
DHCR24	2.56	1.95	2E-02			1.44
CDK1	−3.14	−3.84	5E-04		−0.04	−4.54
NDUFA13			2E-02			0.25
JMY	−1.63	−2.78	7E-03		−0.05	−3.47
BCL6	−1.67			−0.45
AATF						−0.83
IL3	2.90		3E-02
IL6	−1.14	−1.61		−0.19
BIRC3				−0.13
TP73					0.06
CBX4	−1.97
PMAIP1	−1.96	−2.40	1E-02		−0.13
TNFSF12			2E-02		0.04
TGFB2					−0.09
TDGF1	1.73	2.11
ZNF443	1.90	2.63	6E-03		0.05
DAP				0.26
MX1	1.07					4.22
NUDT2				−1.28		−0.52
SOCS2	−5.15			−1.53
STK4			3E-02	−1.52		−1.12
HSPB1					−0.03
ERC1			2E-02			−0.95
GCLC					−0.06
TRAF7	−3.80	−3.64	3E-02	−0.25	−0.05
HDAC3						0.85
VCP						−1.50
DEDD				0.18
ACVR1B					−0.06
CASP3	3.14	3.37			0.08
CASP9	1.84			0.14
BOK	5.12	3.99	4E-03	0.26	0.08	1.84
PRKCA	−2.20	−2.31	2E-02			−2.53
CYCS			3E-02
IFI16					0.06
DAPK2			2E-02
DAPK1						4.87
ERN2					−0.08
ACVR1				0.50
TNFRSF25					−0.07
UTP11L					0.07	2.18
MOAP1			8E-03			0.35
NF1					−0.03
SAP30BP				0.10
SON						1.32
MPO	−3.62	−3.75	8E-03	−0.78	−0.09	−2.57
PPP1R13B			1E-02	0.90		3.04

5 Discussion

Identifying GEs important for outcomes and constructing cancer models is an important task. Taking advantage of recent cancer studies that collect data on both GEs and their regulators, in this article, we have developed an assisted analysis method, which uses regulator information to assist penalized analysis of GE data. The analysis strategy differs significantly from that of the existing GE and multidimensional omics data analysis. Specifically, this study is the first to explicitly incorporate the regulation relationship in estimation. Another advancement is the adoption of LAD loss to accommodate long-tailed outcome distributions and contamination. The proposed approach has an intuitive formulation, belongs to the popular penalization framework, and can be effectively realized. The development of R code facilitates future applications. We have established that, under mild conditions, the ARMI approach has the well desired consistency properties under high-dimensional settings, which provides a strong support and may make it preferred over the alternatives. In simulation, when the assumed models are satisfied, ARMI clearly outperforms the alternatives. It is comforting to observe that it still has competitive performance when the models are moderately violated. In addition, simulation suggests that the improved identification accuracy results from both information borrowing and robust estimation. In the analysis of TCGA data on melanoma and lung cancer, biologically plausible findings are made. The improved prediction provides an indirect support to the marker identification results.

This study can be potentially extended in multiple aspects. We have conducted gene-based analysis. In future studies, it may be of interest to extend and conduct for example pathway-based analysis. We have considered continuous outcome data and linear modeling, which match data analyzed in this article. For other types of data and models (for example, survival data and an exponential model), it is also possible to construct robust loss functions. Carefully examining the ARMI approach suggests that the penalized estimation and selection is relatively “independent” of the loss function. Thus the proposed analysis strategy can be potentially applied to other outcome data and models. GEs are regulated by multiple types of regulators. In our methodological development, we have focused on a single vector of Z. When there are two or more types of regulators, we have proposed stacking them together – this strategy has been proposed and applied in the literature. Our simulation Setting III suggests that ARMI has satisfactory performance with this strategy. We do realize that this strategy can be overly simplified. It is still being explored how to more effectively model GEs and interconnected regulators. The proposed approach will be extended once such modeling becomes available. Our main interest is on GEs, and the regulators serve as a “tool” to improve GE analysis. However, to be prudent, we have also briefly examined $\widehat{\mathrm{\gamma }}$ and observed satisfactory numerical properties (details omitted). In simulation, we have compared against the most relevant alternatives. The analysis of data with multidimensional omics measurements is a fast moving field. It can be of interest to expand the comparison in the near future. Data analysis serves as a proof of concept and demonstrates the satisfactory performance of ARMI. We study the two pathways because of their significant roles in the two cancers. In principle, ARMI can be applied to conduct whole-genome analysis. However, as with other joint analysis approaches, there is a concern on the stability of findings, and hence such an analysis is not pursued.