Intramolecular Interactions Overcome Hydration to Drive the Collapse Transition of Gly₁₅

Abstract

Simulations and experiments show oligo-glycines, polypeptides lacking any side chains, can collapse in water. We assess the hydration thermodynamics of this collapse by calculating the hydration free energy at each of the end points of the reaction coordinate, here taken as the end-to-end distance (r) in the chain. To examine the role of the various conformations for a given r, we study the conditional distribution, P(R_g|r), of the radius of gyration for a given value of r. The free energy change versus R_g, −k_BT ln P(R_g|r), is found to vary more gently compared to the corresponding variation in the excess hydration free energy. Using this observation within a multistate generalization of the potential distribution theorem, we calculate a tight upper bound for the hydration free energy of the peptide for a given r. On this basis, we find that peptide hydration greatly favors the expanded state of the chain, despite primitive hydrophobic effects favoring chain collapse. The net free energy of collapse is seen to be a delicate balance between opposing intrapeptide and hydration effects, with intrapeptide contributions favoring collapse.

Graphical Abstract

INTRODUCTION

The concept of hydrophobic hydration, the tendency of apolar solutes to disfavor the aqueous phase, is commonly accepted as providing the driving force for proteins to fold.^1–4 However, this rationalization cannot explain previous experimental^5,6 and simulation^7,8 observations that oligoglycine, only mildly hydrophobic by some accounts,^9,10 also collapses into a set of nonspecific structures in liquid water.

Experimental studies on the collapse of (Gly)_n and the closely related (GlySer)_n polypeptides have attributed the collapse to the formation of intramolecular hydrogen bonds.^5,6 However, an earlier simulation study has suggested that collapse is unlikely to be driven solely by intramolecular hydrogen bonding.⁷ They have instead postulated that the unfavorable cost of creating a cavity to accommodate the peptide drives the collapse, a picture that is synonymous with hydrophobicity driven collapse. More recent work has implicated the charge ordering and the favorable correlation between the CO groups of the peptide as an important determinant in oligoglycine collapse.^11,12 A rigorous analysis of hydration effects in folding of Gly₁₅ would clarify the responsible driving forces.

Here we explore the hydration thermodynamics of Gly₁₅ collapse using the regularization approach to free energy calculations.^13,14 This approach makes possible the facile calculation of free energies of hydration of polypeptides and proteins in all-atom simulations,^14–17 and most importantly for this study, we obtain a direct quantification of the hydrophilic and hydrophobic contributions to hydration.^16,17 We complement these studies with an evaluation of the excess enthalpy and entropy of hydration as well.^16,17 Our results show that, in contrast to the usual paradigm of water aiding the folding process by decreasing the mutual solubility of the peptide units comprising the polypeptide chain, hydration drives unfolding in this peptide; importantly, intrapeptide van der Waals and electrostatic interactions are critical in driving Gly₁₅ to collapse.

THEORY

The calculation of μ^ex and its entropic Ts^ex and enthalpic h^ex components follows earlier work.^15–17 Here we briefly review the basic ideas for completeness.

Formally, from the potential distribution theorem,^18,19 the chemical potential is given by βμ^ex = ln〈e^βε〉, where the averaging is over the solute–solvent binding energy (ε) distribution P(ε). As usual, β = 1/k_BT, with T being the temperature and k_B the Boltzmann constant. However, in simulations, it is not possible to resolve P(ε) well enough, especially in the high-ε region that is dominated by short-range repulsion, to ensure a converged statistical average of e^βε. To address this problem, we introduce an auxiliary field ϕ(r; λ) to regularize²⁰ the statistical problem of calculating μ^ex from the potential distribution theorem. The field ϕ(r; λ) serves to move the solvent away from the solute, thereby tempering the solute–solvent binding energy. The conditional distribution P(ε|ϕ) is always better behaved than P(ε), and in calculations, we adjust λ, the range of the field, such that P(ε|ϕ) is Gaussian.

With the introduction of the field, we have^13–17

$$\beta {\mu }^{\text{ex}}=\underset{\text{chemistry}}{\underbrace{ln{x}_0[\varphi ]}}-\underset{\text{packing}}{\underbrace{ln{p}_0[\varphi ]}}+\underset{\text{long-range}}{\underbrace{\beta {\mu }^{\text{ex}}[P(\epsilon \mid \varphi )]}}$$ (1)

the quasichemical organization of the potential distribution theorem.^19,21,22 (Note that the individual components are functionals of the applied external field.) The packing and chemistry contributions are the proximal solvent contributions that are added back to the long-range, regularized problem to complete the calculation.

The packing contribution measures the free energy to create a cavity to accommodate the peptide and is a measure of primitive hydrophobic effects,^23,24 i.e., hydrophobic hydration of an ideal hydrophobe. The chemistry contribution captures the role of solute attractive interactions with solvent in the hydration layer extending up to a distance λ from the center of the nearest heavy atom. The long-range contribution is the free energy of interaction between the peptide and the solvent when solvent is excluded from the hydration layer. The chemistry plus long-range contribution describes the total hydrophilic contributions to hydration.

The packing and chemistry contributions in our calculations are based on a soft cavity. The soft-cavity packing estimate is a lower bound to the hard-cavity estimate that is used in theoretical discussions of hydrophobic hydration. Conversely, the soft-cavity chemistry estimate is an upper bound to the hard-cavity estimate. The soft-cavity estimate can be easily corrected to give the hard-cavity result.¹³ However, we do not pursue those corrections here, because the balance of packing plus chemistry is expected to be relatively insensitive to the boundary being hard or soft. Thus, we will use the soft-cavity packing result as a measure of primitive hydrophobic effects.

We find that λ ≈ 5 Å ensures that the conditional binding energy distribution is Gaussian to a good approximation. (Please see Supporting Information Figure S1 for an example.) We denote this range as λ_G. The largest value of λ, labeled λ_SE, for which the chemistry contribution is zero has a special meaning. It demarcates the domain which is excluded to the solvent. For the given force field and solute geometry, this surface is uniquely defined.¹⁷ We find that λ_SE ≈ 3 Å. With this choice, eq 1 can be rearranged as

$$\beta {\mu }^{\text{ex}}=\underset{\text{renormalized}\text{chemistry}}{\underbrace{ln\left[x_0({\lambda }_{\mathrm{G}})\frac{p_0({\lambda }_{\text{SE}})}{p_0({\lambda }_{\mathrm{G}})}\right]}}-\underset{\text{SE}\text{packing}}{\underbrace{ln{p}_0({\lambda }_{\text{SE}})}}+\underset{\text{long-range}}{\underbrace{\beta {\mu }^{\text{ex}}[P(\epsilon \mid {\lambda }_{\mathrm{G}})]}}$$ (2)

To be concise, in eq 2, the various quasi-components are shown as functions of the range parameter. Thus, for example, x₀(λ_G) ≡ x₀[ϕ(λ_G)]. The term identified as renormalized chemistry has the following physical meaning. It is the work done to move the solvent interface a distance λ_G away from the solute relative to the case when the only role played by the solute is to exclude solvent up to λ_SE. This term explicates the role of short-range solute–solvent attractive interactions on hydration. Interestingly, the range between λ_SE = 3 Å and λ_G = 5 Å corresponds to the first hydration shell for a methane carbon²⁰ and is an approximate descriptor of the first hydration shell of groups containing nitrogen and oxygen heavy atoms.

Entropy and enthalpy of hydration

The excess entropy of hydration is given by¹⁶

$$\begin{gathered} T{s}^{\text{ex}}=E^{\text{ex}}-k{T}^2{\alpha }_p+p(\langle V^{\text{ex}}\rangle +kT{\kappa }_T)-{\mu }^{\text{ex}} \\ \approx E_{\text{sw}}+E_{\text{reorg}}-{\mu }^{\text{ex}} \end{gathered}$$ (3)

where κ_T is the isothermal compressibility of the solvent, α_p is the thermal expansivity of the solvent, and 〈V^ex〉 is the excess volume of hydration, and in writing the second line of the equation, we have ignored the small contribution from all of these terms. The average excess energy of hydration, E^ex, is the sum of the average solute–water interaction energy E_sw and E_reorg, the reorganization energy. The latter is given by the change in the average potential energy of the solvent in the solute–solvent system minus that in the neat solvent system. (Note that solute–solvent interactions are not counted as part of E_reorg.) Ignoring pressure–volume effects, the excess enthalpy of hydration is h^ex = E^ex.

COMPUTATIONAL DETAILS

Gly₁₅ was constructed with an acetylated (ACE) N-terminus and n-methyl-amide (NME) C-terminus capped ends and solvated in a box containing 13358 CHARMM-modified TIP3P^25,26 water molecules. The peptide is described by the CHARMM22 force field with the CMAP corrections.^27,28 As an aside, we note that we have previously studied the force field dependence of the properties of oligo-glycines in solution.²⁹ While the structural ensembles were found to differ, the solvation thermodynamics of short (2–5 residue) glycine peptides³⁰ is considerably less sensitive to the differences between CHARMM³¹ and AMBER³² force fields. Further, the collapse transition of Gly₁₅, which is of principal interest here, is also seen with the OPLS-AA force field.⁷ Thus, while the precise balance of hydration and intrapeptide interaction explored in this work could depend somewhat on the force field, the overall trends are expected to be independent of force field biases.

The starting equilibrated configuration was obtained from the earlier study by Karandur, Harris, and Pettitt,^12,33 where in the initial equilibration phase the system was simulated at a temperature of 300 K and a pressure of 1 atm using, respectively, a Langevin thermostat and a Langevin barostat.³⁴ (The equilibrated system is a cube of edge length ≈ 73.5 Å.) We note that we maintained the simulation parameters as in the earlier study. Specifically, the barostat piston period was 100 fs and the decay time was 50 fs. The decay constant of the thermostat was 4 ps⁻¹. The SHAKE algorithm was used to constrain the geometry of water molecules and fix the bond between hydrogens and parent heavy atoms. Lennard-Jones interactions were terminated at 12.00 Å by smoothly switching to zero starting at 10.0 Å. Electrostatic interactions were treated with the particle mesh Ewald method with a grid spacing of 1.0 Å. In contrast to the earlier study,¹² here we use a 2.0 fs time step. In vacuo calculations for peptide provided the vacuum reference. These in vacuo simulations lasted at least 25 ns with a 1 fs time step. The decay constant of the thermostat was 10 ps⁻¹.

To calculate the potential of mean force (PMF), W(r), where the order parameter r is the distance between the terminal carbon atoms of the Gly₁₅ peptide, we first obtained one frame each with r ∈ (30, 40) Å (domain L40), r ∈ (25, 35) Å (domain L35), and r ∈ (20, 30) Å (domain L30) from the earlier simulations.¹² Then, the PMFs in the respective domains were obtained using the adaptive-bias force (ABF) technique.^35,36 Briefly, in the ABF approach, the order parameter is binned in windows of width 0.1 Å. As the simulation evolves, we accumulate statistics of counts of the order parameter in each bin. Using these counts, initial biasing forces are estimated that encourage a uniform sampling of the order parameter in the chosen domain. As the simulation progresses, the distribution of r and hence also the biasing forces are updated. The biasing force serves to cancel the force due to the underlying free energy surface (the quantity of interest), thereby encouraging a more uniform sampling of the order parameter. From the converged biasing forces, it is straightforward to reconstruct the W(r).

For each domain, ABF simulations spanned 26 ns. The first 16 ns was set aside for equilibration, during which time we monitored the evolution of the biasing forces (Supporting Information, section S.III). Then, the gradients of W(r) obtained at the end of 18, 20, 22, 24, and 26 ns were averaged. The biasing forces from the overlapping segments in L30 and L35 were averaged. The L30–L35 average and forces from L40 were then averaged to construct the gradient of W(r) in the entire domain r ∈ [20, 40] Å. During the averaging process, we also calculate the standard error of the mean forces. The gradient was then numerically integrated (a trapezoidal rule suffices) to obtain W(r) from r = 20.1 Å to r = 39.9 Å. (For the in vacuo ABF simulation, we follow a similar procedure with gradients obtained at the end of 10, 15, 20, and 25 ns.) The final standard errors of the mean forces (and hence also the PMF) were obtained using standard variance addition rules.

The potential energy of the peptide (in the solvent) as a function of r was obtained from the last 4 ns of the ABF trajectory. These energies are sorted and binned in windows of width 0.1 Å along r. For the potential energy calculation, we used structures only from L40 and L30 simulations.

Please note that Supporting Information section S.I provides the documentation of the methods used to calculate the hydration free energy; section S.II provides the documentation of the approach to assess the hydration enthalpy; and section S.III provides additional details pertinent to ABF, including examples of the evolution of biasing forces.

RESULTS

Free energy of chain compaction

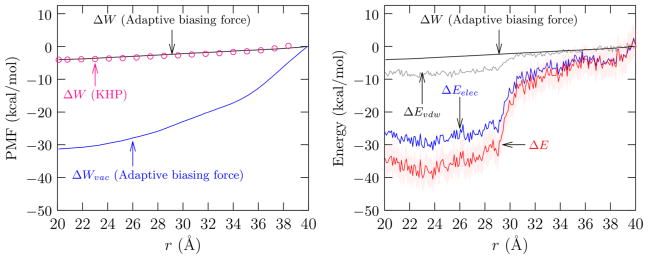
Figure 1 shows the potential of mean force (PMF) between the terminal carbon atoms of the Gly₁₅. As r decreases from 40 to 20 Å, the radius of gyration of the peptide changes from about 13 Å to about 6 Å, indicating that the polypeptide adopts a compact configuration as r decreases. Note also the excellent agreement between results obtained using the ABF procedure and the earlier study¹² where the probability distribution along the folding coordinate was obtained using over 100 ns of unbiased simulations. There the authors had used NVE simulations in the production phase to avoid any potential thermostatting artifacts. However, in a separate study,³³ they found that using a thermostat did not change the results.

Figure 1.

Left panel: PMF, ΔW(r), relative to r = 40 Å for Gly₁₅ folding in the domain r ∈ [20, 40] Å. The PMF obtained from ABF is shown as a solid black line; the statistical uncertainty is below 0.1 kcal/mol (1σ) and is not shown. ○, ΔW (KHP), PMF obtained independently by Karandur, Harris, and Pettitt¹² from large-scale unbiased sampling. Right panel: The change in the internal energy ΔE (red line) and its electrostatic (blue) and van der Waals (gray) contributions for the solvated peptide. Peptide conformations from only the L30 and L40 domains were used in calculating the internal energies. The internal energies are sorted and binned according to r. The light red shading indicates the 2σ standard error of the mean. The contributions from dihedral and angle terms of the force field are negligible on the scale of the graph.

Figure 1 shows that chain compaction is favored by a free energy change of approximately −4 kcal/mol. Observe that there is an intrinsic drive for the peptide chain to collapse, as is clearly seen in the potential of mean force for chain compaction obtained in the absence of the solvent (ΔW_vac). Qualitatively, the same trend can also be inferred from the large intrapeptide energy change accompanying chain compaction (Figure 1, right panel).

Hydration thermodynamics

We next consider the analysis of hydration effects. To parse the effect of hydration, we write

$$\mathrm{\Delta }W=\mathrm{\Delta }{W}_{\text{vac}}+\mathrm{\Delta }{W}_{\text{ss}}$$ (4)

where ΔW_ss accounts for all of the hydration effects. Here ΔW_ss = μ^ex(r = 20.1) − μ^ex(r = 39.9), where μ^ex(r) is the hydration free energy of the polypeptide with the constraint that the end-to-end distance is r. To estimate μ^ex(r), we first classify the ensemble of conformations satisfying the constraint r by the radius of gyration R_g. For a given r, denoting the excess chemical potential of a specific conformation R_g by μ^ex(R_g|r), the multistate generalization^{19,21,22,37–39} of the chemical potential μ^ex (r) gives

$$\beta {\mu }^{\text{ex}}(r)=ln{\int }_{R_{\mathrm{g}}}{\mathrm{e}}^{\beta {\mu }^{\text{ex}}(R_{\mathrm{g}}\mid r)}P(R_{\mathrm{g}}\mid r)\mathrm{d}{R}_{\mathrm{g}}$$ (5)

where the integration is over all of the conformations (classified according to R_g) that satisfy the constraint of fixed r. P(R_g|r) dR_g is the probability of finding a conformation in the range [R_g, R_g + dR_g] given the constraint r.

Constructing μ^ex(r) by calculating μ^ex(R_g|r) for an ensemble of configurations is a challenging task, but much progress can be made using eq 5 and some physically realistic assumptions. Note that hydration free energy calculations for several different conformations of Gly₁₅ show that μ^ex for a given conformation is negative (Figure 2). This negative μ^ex is also consistent with explicit hydration free energy calculations on shorter polyglycines^15,16 and is as expected based on hydration free energy calculations of other homogeneous peptides of varying chain lengths (up to about 10); for example, see refs 17 and 40–44.

Figure 2.

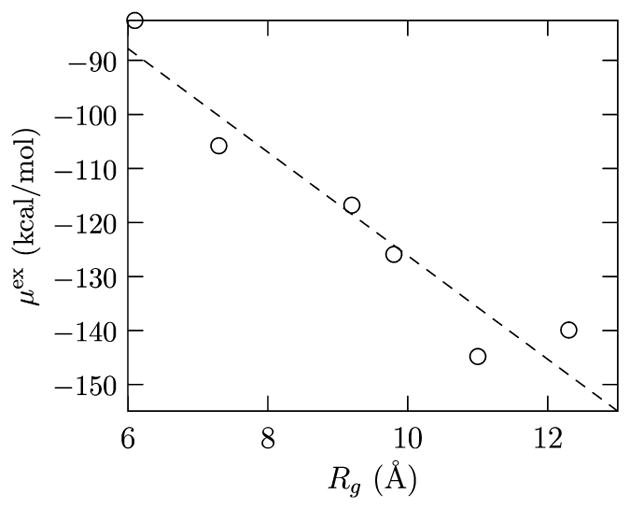
Hydration free energy values for several Gly₁₅ conformations for R_g values of interest in the present study. All calculations are based on all-atom simulations and the regularization approach. The linear fit is solely to indicate that on average μ^ex decreases with increasing R_g, i.e., as more of the chain is exposed to the solvent.

Since μ^ex(R_g|r) < 0, it is clear that μ^ex(r) must be bounded from above by the least negative and from below by the most negative hydration free energy. Further, since μ^ex(R_g|r) decreases with increasing R_g, i.e., with increasing solvent exposure of the backbone, we can infer that, for a given r, the hydration free energy μ^ex(R_g|r) for the most collapsed conformation is expected to be least negative. Denoting the most collapsed conformation by $R_{\mathrm{g}}^{\ast }$, we thus expect $[{\mu }^{\text{ex}}(R_{\mathrm{g}}\mid r)-{\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r)]\le 0$ and thus

$$\begin{gathered} \beta {\mu }^{\text{ex}}(r)=\beta {\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r)+ln{\int }_{R_{\mathrm{g}}}{\mathrm{e}}^{\beta [{\mu }^{\text{ex}}(R_{\mathrm{g}}\mid r)-{\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r)]}P(R_{\mathrm{g}}\mid r)\mathrm{d}{R}_{\mathrm{g}} \\ \le \beta {\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r) \end{gathered}$$ (6)

For using eq 6, we first obtained two structures satisfying r = 39.9 Å and r = 20.1 Å, respectively, from the ABF trajectory. (We find a structure that is within 0.05 Å of the target distance and then adjust r.) Subsequently, these peptide configurations were centered and rotated such that the end-to-end vector is along the principal diagonal of the simulation cell. With the terminal carbon atoms fixed in space, we sampled conformations of the peptide from 2 ns of production.

Analysis of the distribution of R_g for r = 20.1 and 39.9 Å shows that $P(R_{\mathrm{g}}^{\ast }\mid r)\approx e^{-2}$ relative to the most probable R̄_g, i.e., $-k_{\mathrm{B}}Tln[P(R_{\mathrm{g}}^{\ast }\mid r)/P({\overline{R}}_{\mathrm{g}}\mid r)]\approx 2k_{\mathrm{B}}T$ (Figure 3). However, for the same increase in R_g, about 1 Å, the hydration free energy decreases by O(17k_BT) (Figure 2). Because of the exponential dependence of the free energy on $[{\mu }^{\text{ex}}(R_{\mathrm{g}}\mid r)-{\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r)]<0$ which decreases sharply relative to the growth in P(R_g|r), we expect the upper bound to itself be a fair approximation to the required free energy. (See also ref 39 for a similar argument in the context of ion hydration.) Thus, we expect that the hydration contribution in eq 4 can be approximated as

Figure 3.

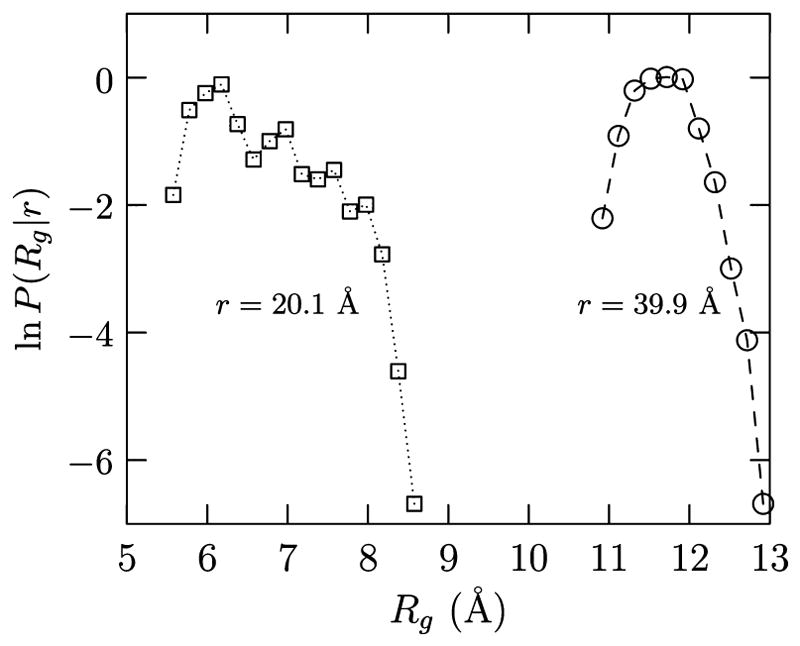
Probability distribution of R_g values for the specified end-to-end distances. For r = 20.1 Å, the R_g of the most collapsed conformation is 5.5 Å, and for r = 39.9 Å, the R_g of the most collapsed conformation is 10.8 Å. These R_g values fall slightly to the left of the leftmost point shown in the plot.

$$\begin{gathered} \mathrm{\Delta }{W}_{\text{ss}}={\mu }^{\text{ex}}[r=20.1\mathrm{A}]-{\mu }^{\text{ex}}[r=39.9\mathrm{A}] \\ \approx {\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r=20.1\mathrm{A})-{\mu }^{\text{ex}}(R_{\mathrm{g}}^{\ast }\mid r=39.9\mathrm{A}) \end{gathered}$$ (7)

For the ( $R_{\mathrm{g}}^{\ast }\mid r=20.1$) and ( $R_{\mathrm{g}}^{\ast }\mid r=39.9$) structures, we find the hydration free energy, μ^ex, using the regularization approach^13–16 discussed above. Table 1 collects the results of the hydration analysis, and it is clear that the calculated value of the free energy of collapse is in reasonable accord with the value obtained using the ABF procedure (Figure 1).

Table 1.

Hydration and Intrapeptide Interaction Contributions in the Collapse of Gly₁₅ from r = 39.9 Å to r = 20.1 Å

quantity	(kcal/mol)
ΔWvac (ABF)	−31.3
ΔWss	25.5 ± 2
ΔW (calc.)	−5.8 ± 2
ΔW (ABF)	−4.0

^aΔW_ss is based on eq 7. ΔW (calc.) = ΔW_ss + W_vac is the value of the free energy of collapse using the calculated hydration free energy; ΔW (ABF) is the corresponding value from Figure 1. We ignore the statistical uncertainty of about 0.2 kcal/mol in the ABF results.

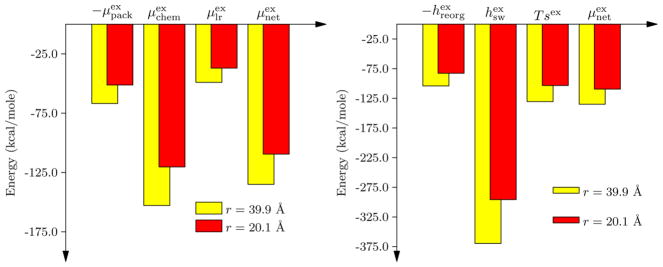
Analyzing ΔW_ss shows that the packing contribution, a measure of primitive hydrophobic effects,^23,24 does favor chain compaction, as is expected (Figure 4). However, this packing contribution is approximately balanced by the long-range contributions that favor chain unfolding. The remaining hydrophilic, chemistry contribution which reflects the role of favorable solute interactions with the solvent in the first hydration shell is nearly twice the magnitude of the packing contribution and favors chain unfolding. Thus, in classical terms, hydrophilic effects overwhelm hydrophobic effects to shift the balance to the unfolded state.

Figure 4.

Left panel: The hydration free energy and its components based on the quasichemical decomposition.^{13–16,19,22} Right panel: Decomposition of the hydration free energy change into enthalpic and entropic contributions. The enthalpy of hydration is further separated into a solvent reorganization and solute–solvent interaction parts.

Mirroring the packing contribution, the energetic cost to reorganize the solvent around a cavity ( $h_{\text{reorg}}^{\text{ex}}$) favors chain compaction, as does the entropy of hydration. However, favorable solute–water interactions reflected in $h_{\text{sw}}^{\text{ex}}$ greatly favor chain expansion. This observation suggests that the backbone must play a substantial role in protein folding, consistent with previous suggestions to this effect.^45–47

CONCLUSIONS

We examined the free energy, enthalpy, and entropy of hydration in the collapse transition of the Gly₁₅ peptide. The free energy of hydration was calculated using the quasichemical theory of solutions. Within the theory, the hydration free energy is naturally partitioned into contributions from attractive (hydrophilic) interactions and packing (primitive hydrophobic) effects, i.e., hydrophobic effects associated with the hydration of a cavity (an ideal hydrophobe). The attractive interactions are further partitioned into short-range attractive interactions, arising from the interaction between the peptide and the solvent in the first hydration shell, and long-range attractive interactions, arising from the interaction between the peptide and the solvent outside the first shell. We also quantified the enthalpy of hydration, which is given by the sum of solute–solvent and solvent reorganization contributions.

Our analysis shows that hydration disfavors compaction of the Gly₁₅ chain. We find that, although the gain due to primitive hydrophobic effects favors chain compaction, the loss of attractive interactions between the solvent and the solute upon compaction decidedly opposes this transition. These trends are confirmed by an analysis of enthalpic effects, which reveal that, although reorganization of the solvent molecules around the solute favors chain compaction, solute–solvent attractive interactions dominate. These results are similar to what we found earlier in the coil-to-helix transition and helix–helix assembly of a deca-alanine peptide.¹⁷ There, too, we found that solute–solvent attractive interactions favor the expanded, coil state in the coil-to-helix transition and the disassembly of the helix-pair in the helix–helix complex.

We expect the trends noted for Gly₁₅ to hold for longer polyglycines investigated in experiments⁶ and computer simulations.¹² Importantly, analysis by Karandur et al.¹² of Gly₁₅ and Gly₂₅ shows that these peptides undergo a collapse transition that is opposed by hydration, which they quantified on the basis of average peptide–solvent interaction energies, but favored by intramolecular effects. The nature of the intramolecular interactions leading to the collapse is an important question, but we do not pursue a detailed analysis here and refer the reader to the forthcoming work by Sharma and Pettitt (in preparation).

The net balance between intramolecular interactions and hydration is such that intramolecular contributions win by a small margin and drive the collapse of the peptide. Liquid water is both a good solvent for the hydration of the peptide unit^15,41 and also a poor solvent from the perspective of folding, as the hydration effects lose in comparison to intrapeptide interactions.

Our earlier study on the coil-to-helix transition and helix–helix pairing in a deca-alanine peptide and the present study on an archetype of an intrinsically disordered peptide both lead to the finding that intramolecular interactions provide an intrinsic drive for polypeptides to form a compact structure and that contributions to the hydration thermodynamics from solute–solvent attractive interactions can serve to suppress this trend. Further, an emerging body of work on prototypical hydrophobes such as methane,²⁰ argon,⁴⁸ and larger alkanes^44,49–51 shows that solute–solvent attractive interactions can temper hydrophobic association. This suggests that “hydrophilic hydration and the intramolecular interactions are as important as, if not more important than, the hydrophobic effects”¹⁷ in determining the structure of peptides and proteins. Evaluating the thermodynamic and kinetic consequences of this hypothesis in a wider class of proteins and solvents using a variety of force fields remains a challenge for future studies.