Longitudinal Genotype-Phenotype Association Study via Temporal Structure Auto-Learning Predictive Model

Abstract

With rapid progress in high-throughput genotyping and neuroimaging, imaging genetics has gained significant attention in the research of complex brain disorders, such as Alzheimer’s Disease (AD). The genotype-phenotype association study using imaging genetic data has the potential to reveal genetic basis and biological mechanism of brain structure and function. AD is a progressive neurodegenerative disease, thus, it is crucial to look into the relations between SNPs and longitudinal variations of neuroimaging phenotypes. Although some machine learning models were newly presented to capture the longitudinal patterns in genotype-phenotype association study, most of them required fixed longitudinal structures of prediction tasks and could not automatically learn the interrelations among longitudinal prediction tasks. To address this challenge, we proposed a novel temporal structure auto-learning model to automatically uncover longitudinal genotype-phenotype interrelations and utilized such interrelated structures to enhance phenotype prediction in the meantime. We conducted longitudinal phenotype prediction experiments on the ADNI cohort including 3,123 SNPs and 2 types of biomarkers, VBM and FreeSurfer. Empirical results demonstrated advantages of our proposed model over the counterparts. Moreover, available literature was identified for our top selected SNPs, which demonstrated the rationality of our prediction results. An executable program is available online at https://github.com/littleq1991/sparse_lowRank_regression.

1 Introduction

As the most prevalent and severe type of neurodegenerative disorder, Alzheimer’s Disease (AD) strongly impacts human’s memory, thinking and behavior [1]. This disease is characterized by progressive impairment of memory and other cognitive abilities, triggered by the damage of neurons [2]. AD usually progresses along a temporal continuum, initially from a preclinical stage, subsequently to mild cognitive impairment (MCI) and ultimately deteriorating to AD [3]. According to [4], AD is the 6th leading cause of death in the United States. Every 66 seconds, there is someone in the United States developing AD. Up until 2016, an estimate of 5.4 million individuals in the United States are living with AD, while the number worldwide is about 44 million. To make matters worse, if no breakthrough discovered, the world will see a more striking increase in these numbers in near future.

With all these facts, AD has gained its growing attention in this day and age. Current consensus underscores the need of understanding the genetic causes of AD, with which to achieve the goal of stoping or slowing down disease progression [5]. Recent advances in neuroimaging and microbiology have provided a helping hand for exploring the associations among genes, brain structure and behavior [6]. Meanwhile, rapid developments in high-throughput genotyping have enabled the measurement of hundreds of thousands of, or even more than one million single nucleotide polymorphisms (SNPs) simultaneously [7]. These progresses have facilitated the pullulation of imaging genetics, which holds great promise for better understanding complex neurobiological systems.

In imaging genetics, an emerging strategy to facilitate identification of susceptibility genes for disorders like AD is to evaluate genetic variation using outcome-relevant biomarkers as quantitative traits (QTs). The association studies between genetic variations and imaging measures usually maintain an obvious advantage over case-control studies, as QTs are quantitative measures with the ability of increasing statistical power four to eight fold and decreasing required sample size to a large extent [8]. Numerous works have been reported to identify genetic factors impacting imaging phenotypes of biomedical importance [9–11].

In the genotype-phenotype association study, we can denote our inputs in the matrix format as follows: the SNP matrix X ∈ ℝ^d×n (n is the number or samples, d is the number of SNPs) and the imaging phenotype matrices Y = [Y₁, Y₂, …, Y_T] ∈ ℝ^n×cT (c is the number of QTs, T is the number of time points, and Y_t ∈ ℝ^n×c is the phenotype matrix at time t). The goal is to find the weight matrix W = [W₁, W₂, …, W_T] ∈ ℝ^d×cT, which properly reflect the relations between SNPs and QTs and capture a subset of SNPs responsible for phenotype prediction at the same time. If we treat the prediction of one phenotype at one time point as a task, then the association study between genotypes with multiple longitudinal phenotypes can be seen as a multi-task learning problem.

Conventional strategies [12–14], which perform standard regression at all time points, are equivalent to carrying out regression at individual time point separately, thus ignore the longitudinal variations of brain phenotypes. Since AD is a progressive disorder and imaging phenotype is a quantitative reflect of its neurodegenerative status, prediction tasks at various time points can be reasonably assumed related. For a certain QT, its value at different time may be correlated, while distinct QTs at a certain time may also retain some mutual influence. To excavate correlations among longitudinal prediction tasks, several multi-task models were proposed on the basis of sparse learning [15, 16]. The main idea of these models is to exert trace norm on the entire parameter matrix, such that the common subspace globally shared by different prediction tasks can be extracted.

However, longitudinal prediction tasks are interrelated as different groups, not as a whole. Existing methods cannot find the task interrelations properly. It is intractable to discover such task group structure. One straightforward way of capturing such interrelated groups is to conduct clustering analysis and extract the group structure as a preprocessing step. Nevertheless, such a heuristic step is independent to the entire longitudinal learning model, thus the detected group structures are not optimal for the longitudinal learning. To bridge this gap, we propose a novel temporal structure auto-learning low-rank predictive model to simultaneously uncover the interrelations among different prediction tasks and utilize the learned interrelated structures to enhance phenotype prediction.

Notations

In this paper, matrices are all written as uppercase letters while vectors as bold lower case letters. For a matrix M ∈ ℝ^d×n, its i-th row and j-th column are denoted by mⁱ, m_j respectively, while its ij-th element is written as m_ij or M(i, j). For a positive value p, the ℓ_2,p-norm of M is defined as ${\Vert M\Vert }_{2,p}={({\sum }_{i=1}^d{({\sum }_{j=1}^n{m}_{\mathit{\text{ij}}}^2)}^{\frac{p}{2}})}^{\frac{1}{p}}={({\sum }_{i=1}^d{({\Vert {\mathbf{m}}^i\Vert }_2)}^p)}^{\frac{1}{p}}$.

2 Temporal Structure Auto-Learning Predictive Model

2.1 Illustration of Our Idea

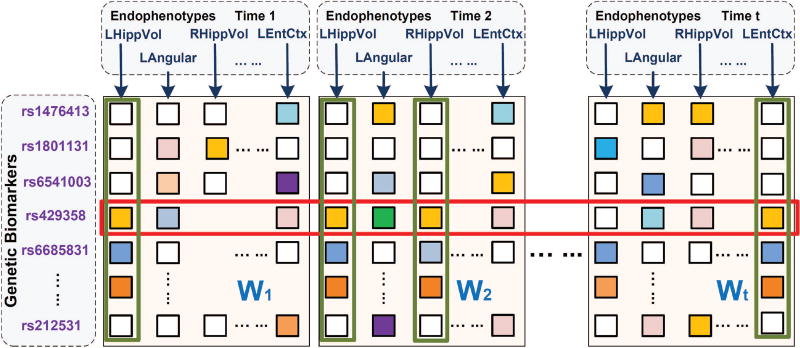
Our main purpose is to construct a model to simultaneously detect the latent group structure of longitudinal phenotype prediction tasks and study SNP associations across all endophenotypes. As is shown in Fig. 1, the four phenotypes marked by the green rectangles have similar distributions and are very likely to be correlated. However, previous models are not capable of capturing such interlinked structures in different task groups. In our model, we expect to uncover such latent subspaces in different groups via low-rank constraints. Meanwhile, the SNP loci marked by the red rectangle, rs429358, appears to be predominant for most response variables. Correspondingly, we impose a sparsity constraint to pick it out. In consequence, our model should be able to capture the group structure within the prediction tasks and utilize this information to select prominent SNPs across the relevant phenotypes. In the next subsection, we will elaborate how to translate these ideas into the new learning model.

Fig. 1.

Illustration of our temporal structure auto-learning regression model. In this figure, parameter matrices at different time points are arranged in the column order. Four tasks marked out by green rectangles obey similar patterns thus have high interrelations while one SNP loci rs429358 enclosed by a red rectangle appears to be correlated with most phenotypes. Our model is meant to uncover the group information among all prediction tasks along the time continuum, i.e., cluster the phenotypes in the same latent subspace (phenotypes marked out by green rectangles) into the same group and meanwhile discover genetic biomarkers responsible for most prediction tasks (SNPs marked out by red rectangles).

2.2 New Objective Function

To discover the group structure of phenotype prediction tasks, we introduce and optimize a group index matrix set Q. Suppose the tasks come from g groups, then we have Q = {Q₁, Q₂, …, Q_g}, where Q_i is a diagonal matrix and Q_i ∈ {0, 1}^cT×cT. For each Q_i, (Q_i)_(k,k) = 1 means the k-th feature belongs to the i-th group while (Q_i)_(k,k) = 0 means not. To avoid overlap of subspaces, we maintain the constraint that ${\sum }_{i=1}^g{Q}_i=I$.

On the other hand, since SNPs are often correlated and have an overlap in impacting phenotypes, we impose low-rank constraint to uncover the common subspaces shared by prediction tasks. The traditional method to impose low-rank constraint is minimizing trace norm, which is a convex relaxation of rank minimization problem. However, trace norm is not an ideal approximation of the rank minimization. Here, we use the Schatten p-norm regularization term instead, which approximates the rank minimization better than trace norm [17]. The definition of Schatten p-norm of a matrix M ∈ ℝ^m×n is:

$${\Vert M\Vert }_{S_p}={(\mathit{\text{Tr}}({(M^{T}M)}^{\frac{p}{2}}))}^{\frac{1}{p}}={(\sum _{i=1}^{\text{min}\{m,n\}}{\sigma }_i^p)}^{\frac{1}{p}},$$ (1)

where σ_i is the i-th singular value of M. Specially, when p = 1, the Schatten p-norm of M is exactly the trace norm since ${\Vert M\Vert }_{\ast }={\Vert M\Vert }_{S_1}=\mathit{\text{Tr}}({(M^{T}M)}^{\frac{1}{2}})=\sum _{i=1}^{\text{min}\{m,n\}}{\sigma }_i$. As we recall, the rank of M can be denoted as $\mathit{\text{rank}}(M)={\sum }_{i=1}^{\text{min}\{m,n\}}{\sigma }_i^0$, where 0⁰ = 0. Thus, when 0 < p < 1, Schatten p-norm is a better low-rank regularization than trace norm.

Moreover, since we intend to integrate the SNP selection procedure across multiple learning tasks, here we impose a sparsity constraint. One possible approach is ℓ_2,1-norm regularization [18], which is popularly utilized owing to its convex property. However, the real data usually don’t satisfy the RIP condition, thus the solution of ℓ_2,1-norm may not be sparse enough. See [19, 20] for details. To solve this problem, in our model, we resort to a stricter sparsity constraint, ℓ_2,0+-norm, which is defined as follows:

$${\Vert M\Vert }_{2,q}={(\sum _{i=1}^d{(\sum _{j=1}^n{m}_{\mathit{\text{ij}}}^2)}^{\frac{q}{2}})}^{\frac{1}{q}}={(\sum _{i=1}^d{({\Vert {\mathbf{m}}^i\Vert }_2)}^q)}^{\frac{1}{q}},$$

where q is a positive value. Similarly to the previous discussion, when 0 < q < 1, ℓ_2,0+-norm can achieve a more sparse solution than ℓ_2,1 norm.

All in all, we propose a new temporal structure auto-learning model:

$$\underset{W,{Q_i|}_{i=1}^g}{\text{min}}{\Vert X^{T}W-Y\Vert }_F^2+{\gamma }_1\sum _{i=1}^g{({\Vert {\mathit{\text{WQ}}}_i\Vert }_{S_p}^p)}^k+{\gamma }_2{\Vert W\Vert }_{2,0+},$$ (2)

$$s.t.{Q_i|}_{i=1}^g\in {\{0,1\}}^{\mathit{\text{cT}}\times \mathit{\text{cT}}},\sum _{i=1}^g{Q}_i=I.$$

In Eq. (2), we adopt the k-power of Schatten p-norm to make our model more robust. The use of parameter k will be articulated in Section 4. Since it is difficult to solve the proposed new non-convex and non-smooth objective, in the next section we propose a novel alternating optimization method for Problem (2).

3 Optimization Algorithm

In this section, we first introduce an optimization algorithm for general problems with Problem (2) being a special case, and then discuss the detailed optimization steps of Problem (2).

Lemma 1

Let g_i(x) denote a general function over x, where x can be a scalar, vector or matrix, then we can claim:

When δ → 0, The optimization problem

$$\underset{x\in 𝒞}{\text{min}}f(x)+\sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x))}^{\frac{p}{2}})$$

is equivalent to

$$\underset{x\in 𝒞}{\text{min}}f(x)+\sum _i\mathit{\text{Tr}}(g_i^T(x)g_i(x)D_i),\mathit{\text{ where }}{D}_i=\frac{p}{2}{(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}}.$$ (3)

Proof

When δ → 0, it’s apparent that the optimization problem

$$\underset{x\in 𝒞}{\text{min}}f(x)+\sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})$$ (4)

will reduce to

$$\underset{x\in 𝒞}{\text{min}}f(x)+\sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x))}^{\frac{p}{2}}).$$ (5)

So we turn the non-smooth Problem (5) to the smooth Problem (4) where δ is fairly small.

The Lagrangian function of Problem (4) is:

$$ℒ(x,\lambda )=f(x)+\sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})-r(x,\lambda ),$$ (6)

where r(x, λ) is a Lagrangian term for the domain constraint x ∈ 𝒞. Take derivative w.r.t. x and set it to zero, we have:

$$f\prime (x)+\sum _i\frac{\partial \mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})}{\partial x}-\frac{\partial r(x,\lambda )}{\partial x}=0.$$ (7)

Based on the chain rule [21], Eq. (7) can be rewritten as:

$$f\prime (x)+\sum _i\frac{\mathit{\text{tr }}(2\frac{p}{2}{(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}}{g}_i^T(x)\partial g_i(x))}{\partial x}-\frac{\partial r(x,\lambda )}{\partial x}=0.$$ (8)

According to the Karush-Kuhn-Tucker conditions [22], if we can find a solution x that satisfies Eq. (8), then we usually find a local/global optimal solution to Problem (4). However, it is intractable to directly find the solution x that satisfies Eq. (8). Here we come up with a strategy as follows:

If we define $D_i=\frac{p}{2}{(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}}$ as a given constant, then Eq. (8) can be reduced to

$$f\prime (x)+\sum _i\frac{\mathit{\text{tr }}(2D_i{g}_i^T(x)\partial g_i(x))}{\partial x}-\frac{\partial r(x,\lambda )}{\partial x}=0.$$ (9)

Based on the chain rule [21], the optimal solution x* of Eq. (9) is also an optimal solution to the following problem:

$$\underset{x\in 𝒞}{\text{min}}f(x)+\sum _i\mathit{\text{Tr}}(g_i^T(x)g_i(x)D_i).$$ (10)

Based on this observation, we can first guess a solution x, next calculate D_i based on the current solution x, and then update the current solution x by the optimal solution of Problem (10) on the basis of the calculated D_i. We can iteratively perform this procedure until it converges.

According to Lemma 1 and the property of Q_i that $Q_i{Q}_i^T=Q_i$, Problem (2) is equivalent to:

$$\underset{W,{Q_i|}_{i=1}^g}{\text{min}}{\Vert X^{T}W-Y\Vert }_F^2+{\gamma }_1\sum _{i=1}^g\mathit{\text{Tr}}({\mathit{\text{WQ}}}_i{W}^T{D}_i)+{\gamma }_2\mathit{\text{Tr}}({\mathit{\text{WW}}}^{T}B)$$ (11)

$$s.t.{Q_i|}_{i=1}^g\in {\{0,1\}}^{\mathit{\text{cT}}\times \mathit{\text{cT}}},\sum _{i=1}^g{Q}_i=I,$$

where D_i is defined as:

$$D_i=\frac{\mathit{\text{kp}}}{2}{({\Vert {\mathit{\text{WQ}}}_i\Vert }_{S_p}^p)}^{k-1}{({\mathit{\text{WQ}}}_i{W}^T+{\delta }_{1}I)}^{\frac{p-2}{2}},$$ (12)

and B is defined as a diagonal matrix with the l-th diagonal element to be:

$$b_{\mathit{\text{ll}}}=\frac{q}{2}{({\mathbf{w}}^l{({\mathbf{w}}^l)}^T+{\delta }_{2}I)}^{\frac{q-2}{2}},$$ (13)

and δ₁ and δ₂ are two fairly small parameters close to zero.

We can solve Problem (11) via alternating optimization.

The first step is fixing W and solving Q, then Problem (11) becomes:

$$\underset{{Q_i|}_{i=1}^g}{\text{min}}\sum _{i=1}^g\mathit{\text{Tr}}((W^T{D}_{i}W)Q_i)s.t.{Q_i|}_{i=1}^g\in {\{0,1\}}^{\mathit{\text{cT}}\times \mathit{\text{cT}}},\sum _{i=1}^g{Q}_i=I.$$

Let A_i = W^TD_iW, then the solution of each Q_i is as follows:

$$Q_i(k,k)=\{\begin{array}{cc}\hfill 1,\hfill & \hfill i=\text{arg }\underset{j}{\text{min}}{A}_j(k,k)\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}$$ (14)

The second step is fixing Q and solving W. Problem (11) becomes:

$$\underset{W}{\text{min}}{\Vert X^{T}W-Y\Vert }_F^2+{\gamma }_1\sum _{i=1}^g\mathit{\text{Tr}}({\mathit{\text{WQ}}}_i{W}^T{D}_i)+{\gamma }_2\mathit{\text{Tr}}({\mathit{\text{WW}}}^{T}B),$$

which can be further decoupled for each column of W as follows:

$$\underset{{\mathbf{w}}_k}{\text{min}}{\Vert X^T{\mathbf{w}}_k-{\mathbf{y}}_k\Vert }_2^2+{\gamma }_1\sum _{i=1}^g(Q_i(k,k){\mathbf{w}}_k^T{D}_i{\mathbf{w}}_k)+{\gamma }_2{\mathbf{w}}_k^{T}B{\mathbf{w}}_k.$$

Taking derivative w.r.t. w_k in the above problem and set it to zero, we get:

$${\mathbf{w}}_k={({\mathit{\text{XX}}}^T+{\gamma }_1(\sum _{i=1}^g{Q}_i(k,k)D_i)+{\gamma }_{2}B)}^{-1}X{\mathbf{y}}_k.$$ (15)

We can iteratively update D, Q, B and W with the alternative steps mentioned above and the algorithm for Problem (11) is summarized in Algorithm 1.

Convergence analysis

Our algorithm uses the alternating optimization method to update variables, whose convergence has already been proved in [23]. As for the newly proposed reweighted algorithm, we will provide its convergence proof in Appendix A. In our model, variables in each iteration has a closed form solution and can be computed fairly fast. In most cases, our method converges within 10 iterations.

4 Discussion of Parameters

In our model, we introduced several parameters to make it more general and adaptive to various circumstances. Here we analyze the functionality of each parameter in detail.

In Problem (2), parameter p and q are norm parameters proposed for the two regularization terms. For p, it adjusts the stringency of the low-rank constraint. As analyzed in Section 3, Schatten p-norm makes a stricter low-rank constraint than trace norm when 0 < p < 1. The closer p is to 0, the more rigorous low-rank constraint the regularization term ${\Vert M\Vert }_{S_p}^p$ imposes. The rationale is similar for parameter q. The ℓ_2,0+-norm is a better approximation of ℓ_2,0-norm than ℓ_2,1-norm when q lies in the range of (0, 1), thus makes our learned parameter matrix more sparse.

Algorithm 1.

Algorithm to solve problem (11).

Input:

SNP matrix X ∈ ℝd×n, longitudinal phenotype matrix Y = [Y1 Y2 … YT] where ${Y_t|}_{t=1}^T\in {ℝ}^{n\times c}$, parameter δ1 = 10−12 and δ2 = 10−12, number of groups g.

Output:

Weight matrix W = [W1 W2 … WT] where ${W_t|}_{t=1}^T\in {ℝ}^{d\times c}$ and g different group matrices ${Q_i|}_{i=1}^g\in {ℝ}^{\mathit{\text{cT}}\times \mathit{\text{cT}}}$ which groups the tasks into exactly g subspaces.

Initialize W by the optimal solution to the ridge regression problem: $\underset{W}{\text{min}}{\Vert W^{T}X-Y\Vert }_F^2+{\Vert W\Vert }_F^2$

Initialize Q matrices randomly

while not converge do

1. Update D according to the definition in Eq. (12).

2. Update Q according to the solution in Eq. (14)

3. Update B according to the definition in Eq. (13).

4. Update W, where the solution to the k-th column of W is displayed in Eq. (15).

end while

In the low rank regularization term ${\Vert M\Vert }_{S_p}^p$, when p is small, the number of local solutions becomes more thus lead our model (2) to be more sensitive to outliers. Under this condition, we use k-power of this term as ${({\Vert M\Vert }_{S_p}^p)}^k$ to make our model robust. According to experimental experience, the value of k can be determined in the range of [2, 3].

The parameters γ₁ and γ₂ are proposed to balance the importance of two regularization terms. Larger γ₁ lead to more attention on the low-rank constraint while larger γ₂ lays more emphasis on the sparse structure. These two parameters can be adjusted to accommodate different cases.

In our empirical section, we didn’t make too much effort on tuning these parameters. Instead, in fairness to other comparing methods, we just simply set each parameters to a reasonable value. Though these parameters brought about great challenges in solving our optimization problem, they make our model more flexible and adaptive to different settings and conditions.

5 Experimental Results

In this section, we evaluate the prediction performance of our proposed method using both synthetic and real data. Our goal is to uncover the latent subspace structure of the prediction tasks and meanwhile select a subset of SNPs responsible for their variation.

5.1 Experiments on Synthetic Data

First of all, we utilize synthetic data to illustrate the effectiveness of our model. Our synthetic data is composed of 30 features and 3 groups of tasks from 4 different time points. Each group includes 4 tasks, who are identical to each other up to a scaling. After we generated weight matrix W in this way, we constructed a random X including 10000 samples and get Y according to Y = X^TW.

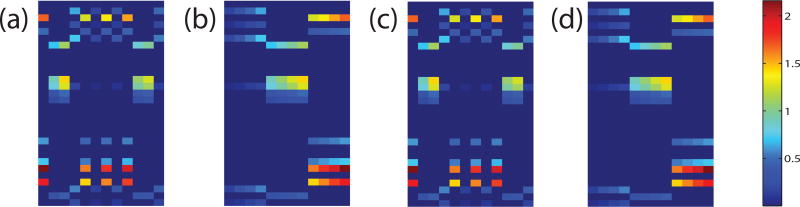
Fig. 2(a) shows the original W_o matrix, where weight matrices in different time points are arranged in a column order. According to the construction process of W_o, tasks in W_o should form three low-rank subspaces. For easier visualizing this low-rank structure, we reshuffled tasks in W_o by putting tasks in the same group together and formed Fig. 2(b). Now the low-rank structure within the synthetic data can be easily detected, where every four columns in Fig. 2(b) make a low-rank subspace. We applied our method to this synthetic data and plotted our learned W matrix in Fig. 2(c). To evaluate the structure of W, we did the rearrangement likewise. By comparing Fig. 2(b) and Fig. 2(d), we note that our method has successfully uncover the group structure of the synthetic data and recovered the parameter matrix W in an accurate way.

Fig. 2.

Visualization of the synthetic parameter matrix W. Columns of W denote 12 prediction tasks from 4 different time points, while rows of W correspond to 30 features. These 12 tasks are equally divided into 3 groups, where tasks in the same group are identical to each other up to a scaling factor. (a) The original weight matrix W_o. (b) Rearrangement of columns in W_o by putting tasks in the same group together, such that the low-rank structure of W_o is more clear. (c) The learned W matrix by our model. (d) Rearrangement of W learned by our model.

5.2 Experimental Settings on Real Benchmark Data

In the following we evaluate our method on real benchmark datasets. We compare our method with all the counterparts discussed in the introduction section, which are: multivariate Linear Regression (LR), multivariate Ridge Regression (RR), Multi-Task Trace-norm regression (MTT) [24], Multi-Task ℓ_2,1-norm Regression (MTL21) [25] and their combination (MTT+L21) [15, 16].

In our pre-experiments, we found the performance of our method to be relatively stable with parameters in the reasonable range (data not shown). For simplicity, we set γ₁ = 1, γ₂ = 1, p = 0.8, q = 0.1, and k = 2.5 without tuning. The definition and reasonable range of these parameters has been discussed in Section 4.

As the evaluation metric, we reported the root mean square error (RMSE) and correlation coefficient (CorCoe) between the predicted and actual scores in out-of-sample prediction. In our experiment, the RMSE was normalized by the Frobenius norm of the ground truth matrix. Better performance relates with lower RMSE or higher CorCoe value. We utilized the 5-fold cross validation technique and reported the average RMSE and CorCoe on these 5 trials for each method.

5.3 Description of ADNI Data

Data used in this work were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). One goal of ADNI is to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. For up-to-date information, see www.adni-info.org. The genotype data [26] of all non-Hispanic Caucasian participants from the ADNI Phase 1 cohort were used here. They were genotyped using the Human 610-Quad BeadChip. Among all the SNPs, only SNPs, within the boundary of ±20K base pairs of the 153 AD candidate genes listed on the AlzGene database (www.alzgene.org) as of 4/18/2011 [27], were selected after the standard quality control (QC) and imputation steps. The QC criteria for the SNP data include (1) call rate check per subject and per SNP marker, (2) gender check, (3) sibling pair identification, (4) the Hardy-Weinberg equilibrium test, (5) marker removal by the minor allele frequency and (6) population stratification. As the second preprocessing step, the QC’ed SNPs were imputed using the MaCH software [28] to estimate the missing genotypes. As a result, our analyses included 3,576 SNPs extracted from 153 genes (boundary: ±20KB) using the ANNOVAR annotation (http://www.openbioinformatics.org/annovar/).

Two widely employed automated MRI analysis techniques were used to process and extract imaging phenotypes from scans of ADNI participants as previously described [11]. First, Voxel-Based Morphometry (VBM) [29] was performed to define global gray matter (GM) density maps and extract local GM density values for 90 target regions. Second, automated parcellation via FreeSurfer V4 [30] was conducted to define volumetric and cortical thickness values for 90 regions of interest (ROIs) and to extract total intracranial volume (ICV). Further details are available in [11]. All these measures were adjusted for the baseline ICV using the regression weights derived from the healthy control (HC) participants. The time points examined in this study for imaging markers included baseline (BL), Month 6 (M6), Month 12 (M12) and Month 24 (M24). All the participants with no missing BL/M6/M12/M24 MRI measurements were included in this study, including 96 AD samples, and 219 MCI samples and 174 health control (HC) samples.

5.4 Performance Comparison on ADNI Cohort

Here we assessed the ability of our method to predict a set of imaging biomarkers via genetic variations. We tracked the process along the time axis and intended to uncover the latent subspace structure maintained by phenotypes and meanwhile capture a subset of SNPs influencing the phenotypes in a certain subspace.

We examined the cases where the number of selected SNPs were {30, 40, …, 80}. The experimental results are summarized in Table 1 and 2. We observe that our method consistently outperforms other methods in most cases. The reasons go as follows: multivariate regression and ridge regression assumed the imaging features at different time points to be independent, thus didn’t consider the correlations within. Their neglects of the interrelations among the data was detrimental to their prediction performance.

Table 1.

Biomarker “VBM” and “FreeSurfer” (upper table for “VBM”, lower table for “FreeSurfer”) prediction comparison via root mean square error (RMSE) measurement with different number of selected SNPs. Better performance corresponds to lower RMSE.

# of SNPs	LR	RR	MTT	MTL21	MTT+L21	OURS
30	0.9277±0.0122	0.9278±0.0122	0.9270±0.0135	0.9278±0.0122	0.9276±0.0126	0.9266±0.0124
40	0.9106±0.0147	0.9100±0.0146	0.9099±0.0141	0.9100±0.0146	0.9099±0.0141	0.9061±0.0087
50	0.8914±0.0177	0.8916±0.0176	0.8934±0.0159	0.8916±0.0176	0.8919±0.0176	0.8913±0.0084
60	0.8843±0.0216	0.8846±0.0216	0.8831±0.0192	0.8846±0.0216	0.8848±0.0215	0.8726±0.0051
70	0.8661±0.0204	0.8663±0.0203	0.8675±0.0211	0.8663±0.0203	0.8666±0.0202	0.8615±0.0045
80	0.8509±0.0250	0.8503±0.0244	0.8500±0.0242	0.8503±0.0244	0.8500±0.0242	0.8482±0.0042
30	0.9667±0.0145	0.9664±0.0145	0.9667±0.0145	0.9664±0.0145	0.9664±0.0146	0.9558±0.0147
40	0.9569±0.0113	0.9569±0.0112	0.9569±0.0113	0.9569±0.0112	0.9569±0.0114	0.9436±0.0113
50	0.9502±0.0141	0.9503±0.0141	0.9502±0.0141	0.9503±0.0141	0.9503±0.0142	0.9350±0.0143
60	0.9416±0.0106	0.9417±0.0106	0.9416±0.0106	0.9417±0.0106	0.9415±0.0107	0.9234±0.0106
70	0.9319±0.0105	0.9316±0.0105	0.9319±0.0105	0.9316±0.0105	0.9321±0.0106	0.9096±0.0106
80	0.9246±0.0093	0.9247±0.0093	0.9246±0.0093	0.9247±0.0093	0.9247±0.0094	0.9012±0.0094

Table 2.

Biomarker “VBM” and “FreeSurfer” (upper table for “VBM”, lower table for “FreeSurfer”) prediction comparison via correlation coefficient (CorCoe) measurement with different number of selected SNPs. Better performance corresponds to higher CorCoe.

# of SNPs	LR	RR	MTT	MTL21	MTT+L21	OURS
30	0.4186±0.0092	0.4180±0.0098	0.4232±0.0088	0.4180±0.0098	0.4216±0.0077	0.6193±0.0177
40	0.4284±0.0163	0.4282±0.0166	0.4333±0.0181	0.4282±0.0166	0.4312±0.0157	0.6294±0.0071
50	0.4476±0.0395	0.4470±0.0400	0.4526±0.0384	0.4470±0.0400	0.4508±0.0385	0.6362±0.0094
60	0.4477±0.0391	0.4471±0.0397	0.4513±0.0388	0.4471±0.0397	0.4510±0.0380	0.6435±0.0196
70	0.4502±0.0345	0.4490±0.0356	0.4547±0.0335	0.4490±0.0356	0.4529±0.0339	0.6460±0.0129
80	0.4467±0.0287	0.4470±0.0286	0.4514±0.0271	0.4470±0.0286	0.4508±0.0268	0.6521±0.0083
30	0.9007±0.0145	0.9008±0.0145	0.9007±0.0145	0.9008±0.0145	0.9010±0.0146	0.9019±0.0147
40	0.9049±0.0113	0.9051±0.0112	0.9049±0.0113	0.9051±0.0112	0.9052±0.0114	0.9060±0.0113
50	0.9045±0.0141	0.9046±0.0141	0.9045±0.0141	0.9046±0.0141	0.9048±0.0142	0.9057±0.0143
60	0.9079±0.0106	0.9080±0.0106	0.9079±0.0106	0.9080±0.0106	0.9081±0.0107	0.9089±0.0106
70	0.9094±0.0105	0.9096±0.0105	0.9094±0.0105	0.9096±0.0105	0.9097±0.0106	0.9106±0.0106
80	0.9114±0.0093	0.9115±0.0093	0.9114±0.0093	0.9115±0.0093	0.9117±0.0094	0.9124±0.0094

As for MTTrace, MTL21 and their combination MTTrace+MTL21, even though they take into account the inner connection information of imaging phenotypes, they simply constrain all phenotypes to a global space thus cannot handle the possible group structure therein. That is why they may overweigh the standard methods in some cases, but cannot outperform our proposed method. As for our proposed method, not only did we capture the latent structure among the longitudinal phenotypes, but we also selected a set of responsible SNPs at the same time. All in all, our model can capture SNPs responsible for some but not necessarily all imaging phenotypes along the time continuum, which save more effective information in the prediction.

5.5 Identification of Top Selected SNPs

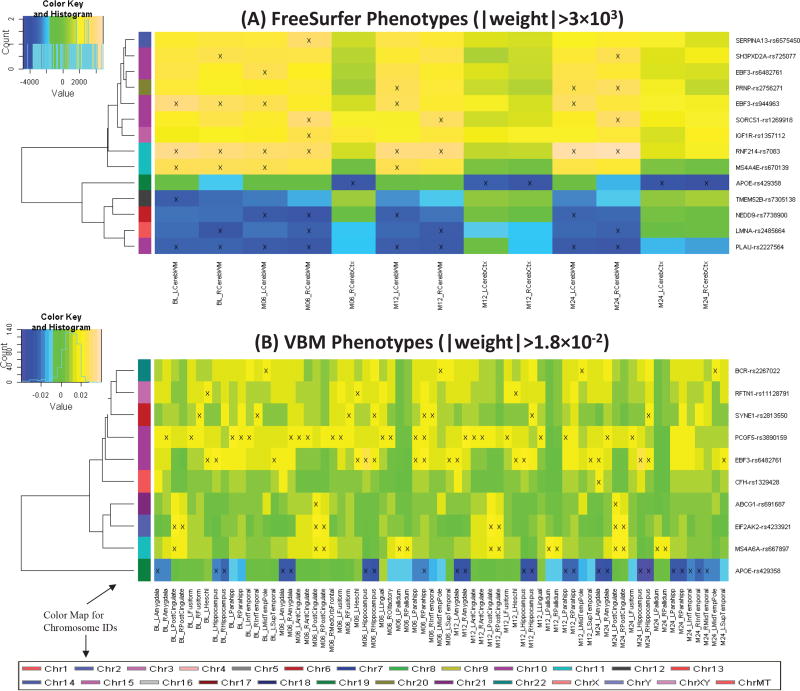
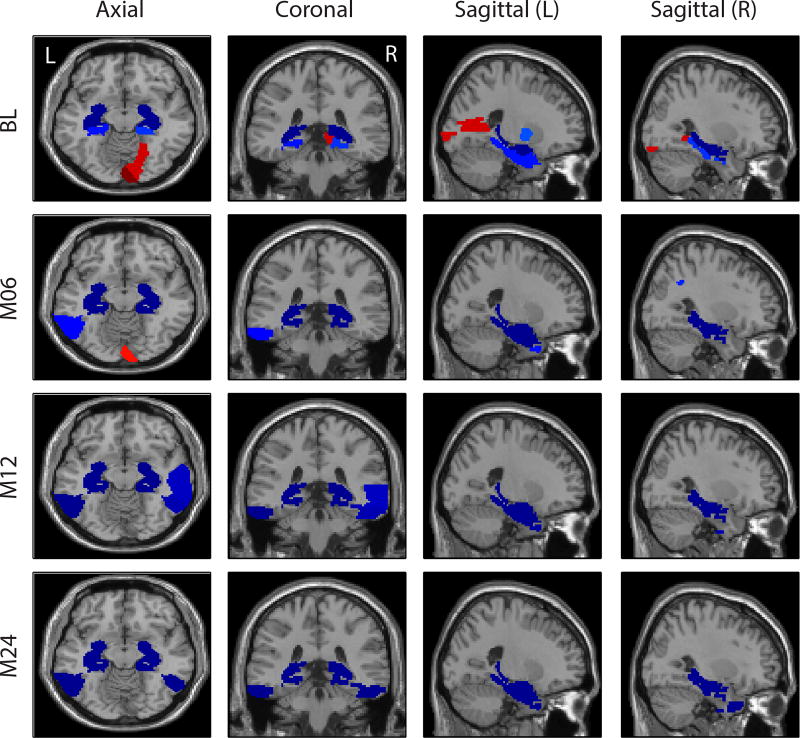
Shown in Fig. 3 are the heat maps of top regression weights between imaging QTs and SNPs. APOE-rs429358, the well-known major AD risk factor, demonstrated relatively strong predictive power in both analysis: (1) In FreeSurfer analysis, it predicts mainly the cerebral cortex volume at M06, M12 and M24. (2) In VBM analysis, it predicts the GM densities of amygdala, hippocampus, and parahippocampal gyrus at multiple time points (Fig. 4). Both patterns are reassuring, since APOE-rs429358 and atrophy patterns of the entire cortex as well as medial temporal regions (including amygdala, hippocampus, and parahippocampal gyrus) are all highly associated with AD.

Fig. 3.

Heat maps of top regression weights between quantitative traits (QTs) and SNPs filtered by a user-specified weight threshold: (A) FreeSurfer QTs and (B) VBM QTs. Weights from each regression analysis are color-mapped and displayed in the heat maps. Heat map blocks labeled with “x” reach the weight threshold. Only top SNPs and QTs are included in the heat maps, and so each row (SNP) and column (QT) have at least one “x” block. Dendrograms derived from hierarchical clustering are plotted for SNPs. The color bar on the left side of the heat map codes the chromosome IDs for the corresponding SNPs.

Fig. 4.

Top 10 weights of APOE-rs429358 mapped on the brain for the VBM analysis.

In addition, APOE-rs429358 has been shown to be related to medial temporal lobe atrophy [31], hippocampal atrophy [32] and cortical atrophy [33]. Variants within membrane-spanning 4-domains subfamily A (MS4A) gene cluster are some other recently discovered AD risk factors [34]. Our analysis also demonstrated their associations with imaging QTs: (1) MS4A4E-rs670139 predicts cerebral white matter volume at BL, M06 and M12; and (2) MS4A6A-rs667897 predicts GM densities of posterior cingulate and pallidum at almost all time points. Another interesting finding is EBF3-rs482761, which is identified in both analyses: (1) In FreeSurfer analysis, it predicts left cerebral white matter volume at M06; and (2) in VBM analysis, it predicts GM densities of left Heschl’s gyri, left superior temporal gyri, hippocampus, left amygdala at multiple time points. EBF3 (early B-cell factor 3) is a protein-coding gene and has been associated with neurogenesis and glioblastoma. In general, both FreeSurfer and VBM analyses picked up similar regions across different time points. These identified imaging genomic associations warrant further investigation in independent cohorts. If replicated, these findings can potentially contribute to biomarker discovery for diagnosis and drug design.

6 Conclusions

In this paper, we proposed a novel temporal structure auto-learning model to study the associations between genetic variations and longitudinal imaging phenotypes. Our model can simultaneously uncover the interrelation structures existing in different prediction tasks and utilize such learned interrelated structures to enhance the feature learning model. Moreover, we utilized the Schatten p-norm to extract the common subspace shared by the prediction tasks. Our new model is applied to ADNI cohort for neuroimaging phenotypes prediction via SNPs. We conducted experiments on both synthetic and real benchmark data. Empirical results validated the effectiveness of our model by demonstrating the improved prediction performance compared with related methods. In real data analysis, we also identified a set of interesting and biologically meaningful imaging genomic associations, showing the potential for biomarker discovery in disease diagnosis and drug design.

Appendix A

Convergence proof of Reweighted Method in Algorithm 1

Before proving convergence of the reweighted algorithm shown in Lemma 1, we first introduce several lemmas:

Lemma 2

For any σ > 0, the following inequality holds when 0 < p ≤ 2:

$$\frac{p}{2}\sigma -{\sigma }^{\frac{p}{2}}+\frac{2-p}{2}\ge 0.$$ (16)

Proof

Denote $f(\sigma )=p\sigma -2{\sigma }^{\frac{p}{2}}+2-p$, we have the following derivatives:

$$f\prime (\sigma )=p(1-{\sigma }^{\frac{p-2}{2}}),\text{ and }f″(\sigma )=\frac{p(2-p)}{2}{\sigma }_i^{\frac{p-4}{2}}.$$

Obviously, when σ > 0 and 0 < p ≤ 2, then f″(σ) ≥ 0 and σ = 1 is the only point that f′(σ) = 0. Note that f(1) = 0, thus when σ > 0 and 0 < p ≤ 2, then f(σ) ≥ 0, which indicates Eq. (16).

Lemma 3 ([35])

For any positive definite matrices M̃, M with the same size, suppose the eigen-decomposition M̃ = U ΣU^T, M = V ΛV^T, where the eigenvalues in Σ is in increasing order and the eigenvalues in Λ is in decreasing order. Then the following inequality holds:

$$\mathit{\text{Tr}}(\stackrel{\sim }{M}M)\ge \mathit{\text{Tr}}(\mathit{\sum }\Lambda ).$$ (17)

Lemma 4

For any positive definite matrices M̃, M with the same size, the following inequality holds when 0 < p ≤ 2:

$$\mathit{\text{Tr}}({\stackrel{\sim }{M}}^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})\le \mathit{\text{Tr}}(M^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}({\mathit{\text{MM}}}^{\frac{p-2}{2}}).$$ (18)

Proof

For any σ > 0, λ > 0 and 0 < p ≤ 2, according to Lemma 2 we have $\frac{p}{2}(\frac{\sigma }{\lambda })-{(\frac{\sigma }{\lambda })}^{\frac{p}{2}}+\frac{2-p}{2}\ge 0$, which indicates

$$\frac{p}{2}\sigma {\lambda }^{\frac{p-2}{2}}-{\sigma }^{\frac{p}{2}}+\frac{2-p}{2}{\lambda }^{\frac{p}{2}}\ge 0.$$ (19)

Suppose the eigen-decomposition M̃ = U ΣU^T, M = V ΛV^T, where the eigenvalues in Σ is in increasing order and the eigenvalues in Λ is in decreasing order. According to Eq. (19), we have

$$\frac{p}{2}\mathit{\text{Tr}}(\mathit{\sum }{\Lambda }^{\frac{p-2}{2}})-\mathit{\text{Tr}}({\mathit{\sum }}^{\frac{p}{2}})+\frac{2-p}{2}\mathit{\text{Tr}}({\Lambda }^{\frac{p}{2}})\ge 0,$$ (20)

and according to Lemma 3 we have

$$\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})-\frac{p}{2}\mathit{\text{Tr}}(\mathit{\sum }{\Lambda }^{\frac{p-2}{2}})\ge 0,$$ (21)

$$\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})-\mathit{\text{Tr}}({\mathit{\sum }}^{\frac{p}{2}})+\frac{2-p}{2}\mathit{\text{Tr}}({\Lambda }^{\frac{p}{2}})\ge 0.$$

Note that $\mathit{\text{Tr}}({\stackrel{\sim }{M}}^{\frac{p}{2}})=\mathit{\text{Tr}}({\mathit{\sum }}^{\frac{p}{2}})$ and $\mathit{\text{Tr}}(M^{\frac{p}{2}})=\mathit{\text{Tr}}({\Lambda }^{\frac{p}{2}})$, so we have

$$\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})-\mathit{\text{Tr}}({\stackrel{\sim }{M}}^{\frac{p}{2}})+\frac{2-p}{2}\mathit{\text{Tr}}(M^{\frac{p}{2}})\ge 0\Rightarrow \mathit{\text{Tr}}({\stackrel{\sim }{M}}^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})\le \frac{2-p}{2}\mathit{\text{Tr}}(M^{\frac{p}{2}})\Rightarrow \mathit{\text{Tr}}({\stackrel{\sim }{M}}^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}(\stackrel{\sim }{M}{M}^{\frac{p-2}{2}})\le \mathit{\text{Tr}}(M^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}({\mathit{\text{MM}}}^{\frac{p-2}{2}}),$$

which completes the proof.

As a result, we have the following theorem:

Theorem 1

The reweighted algorithm shown in Lemma 1, which optimizes Problem (3) instead of Problem (4), will monotonically decrease the objective of Problem (4) in each iteration until the algorithm converges.

Proof

In Problem (3), suppose the updated x is x̃. Thus we know

$$f(\stackrel{\sim }{x})+\sum _i\mathit{\text{Tr}}(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})D_i)\le f(x)+\sum _i\mathit{\text{Tr}}(g_i^T(x)g_i(x)D_i),$$ (22)

where the equality holds when and only when the algorithm converges.

For each i, according to Lemma 4, we have

$$\mathit{\text{Tr}}({(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})+\delta I)}^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x}){(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}})\le \mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})-\frac{p}{2}\mathit{\text{Tr}}(g_i^T(x)g_i(x){(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}}).$$ (23)

Note that $D_i=\frac{p}{2}{(g_i^T(x)g_i(x)+\delta I)}^{\frac{p-2}{2}}$, so for each i we have

$$\mathit{\text{Tr}}({(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})+\delta I)}^{\frac{p}{2}})-\mathit{\text{Tr}}(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})D_i)\le \mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})-\mathit{\text{Tr}}(g_i^T(x)g_i(x)D_i).$$ (24)

Then we have

$$\sum _i\mathit{\text{Tr}}({(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})+\delta I)}^{\frac{p}{2}})-\sum _i\mathit{\text{Tr}}(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})D_i)\le \sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}})-\sum _i\mathit{\text{Tr}}(g_i^T(x)g_i(x)D_i).$$ (25)

Summing Eq. (22) and Eq. (25) in the two sides, we arrive at

$$f(\stackrel{\sim }{x})+\sum _i\mathit{\text{Tr}}({(g_i^T(\stackrel{\sim }{x})g_i(\stackrel{\sim }{x})+\delta I)}^{\frac{p}{2}})\le f(x)+\sum _i\mathit{\text{Tr}}({(g_i^T(x)g_i(x)+\delta I)}^{\frac{p}{2}}).$$ (26)

Note that the equality in Eq. (26) holds only when the algorithm converges. Thus the reweighted algorithm shown in Lemma 1 will monotonically decrease the objective of Problem (4) in each iteration until the algorithm converges.