Abstract
Background and Purpose
Functional selectivity describes the ability of ligands to differentially regulate multiple signalling pathways when coupled to a single receptor, and the operational model is commonly used to analyse these data. Here, we assess the mathematical properties of the operational model and evaluate the outcomes of fixing parameters on model performance.
Experimental Approach
The operational model was evaluated using both a mathematical identifiability analysis and simulation.
Key Results
Mathematical analysis revealed that the parameters R0 and KE were not independently identifiable which can be solved by considering their ratio, τ. The ratio parameter, τ, was often imprecisely estimated when only functional assay data were available and generally only the transduction coefficient R ( ) could be estimated precisely. The general operational model (that includes baseline and the Hill coefficient) required either the parameters Em or KA to be fixed. The normalization process largely cancelled out the mean error of the calculated Δlog (R) caused by fixing these parameters. From this analysis, it was determined that we can avoid the need for a full agonist ligand to be included in an experiment to determine Δlog (R).
Conclusion and Implications
This analysis has provided a ready‐to‐use understanding of current methods for quantifying functional selectivity. It showed that current methods are generally tolerant to fixing parameters. A new method was proposed that removes the need for including a high efficacy ligand in any given experiment, which allows application to large‐scale screening to identify compounds with desirable features of functional selectivity.
Abbreviations
- RSE
relative standard error
- SSE
stochastic simulation estimation
Introduction
Ever since the earliest description of receptor–ligand interactions (Clark, 1926), attempts to develop a reliable method for their quantification have been made. The Emax model provides an empirical justification for the concentration–response relationship. It makes the assumption that the effect of the ligand is directly proportional to receptor occupancy; that is to say, maximal response can only be achieved with maximal receptor occupancy (Clarke and Bond, 1998). The operational model relaxes this assumption by incorporating an (unobserved) empirical transducer function to convert occupancy into effect (Black and Leff, 1983), which allows the effect to represent a potential cascade of cellular or tissue signalling. This can explain the ‘receptor reserve’ phenomenon, that is, stimulation of only a fraction of the whole receptor population elicits an apparent maximal response. Furthermore, incorporation of the transducer function also allows the investigator to create a link directly from ligand concentration to response without the need to formally incorporate ligand binding as a necessary intermediary step. In this sense, the operational model is a ‘middle‐out’ strategy in receptor theory which keeps the balance between model simplicity and mechanistic insight. Here, the equation for the operational model (Equation (1)), in the same style as Equation 5 from the original paper (Black and Leff, 1983), is given:
| (1) |
In the operational model described by Black and Leff, there are two key parameters: τ and KA. This is a re‐parameterization (of Equation (1) here) by Black and Leff which they present in their Equation 6 (shown in this paper in Equation (5)). The transducer ratio parameter, τ ( ), encompasses receptor density (R0) and the stimulus coupling efficiency (KE). KA is an implicit parameter in the model that accounts for ligand binding but is not specifically estimated in their work. In more recent developments, the operational model has been generalized into several variants, such as the conformation‐based operational model (Roche et al., 2013) and the operational model with constitutive activity (Slack and Hall, 2012). Among these variants, the general operational model (Equation (2)) is the most widely used model that accounts for non‐zero basal (Basal), non‐unity Hill slope factor (n) and estimable maximal system response (Em) (van der Westhuizen et al., 2014). Furthermore, it is evident within the operational model framework that the classical concepts of ‘full agonism’ and ‘partial agonism’ need further examination, as such classifications are made on the combination of ligand attributes and how efficiently the system transduces the stimulus into effect (Kenakin, 2014). It is possible that one single ligand may appear to be a full agonist in an efficient transduction system but a partial agonist in a less efficient transduction system.
Recently, interest has arisen in the ability of ligands to differentially regulate different signalling pathways when coupled to a single receptor; a concept termed functional selectivity (Urban et al., 2007). The need to link ligand concentration to response at (now) multiple pathways has rejuvenated interest in the operational model. In such studies, it is common to consider a single composite parameter, R, in quantifying a ligand's effect on a pathway. This parameter is defined as the ratio and is termed the transduction coefficient. It is derived from an application of the operational model to simultaneously account for both affinity and efficacy of a ligand (Kenakin and Miller, 2010). Because the system itself will complicate interpretation of this composite parameter (e.g. system bias and observation bias), it is necessary to normalize R to a reference ligand, yielding the normalized transduction coefficient Δ log (R) (Kenakin et al., 2012). Finally, as the goal of the analysis is to consider how a ligand may bias the response to a particular pathway, it is convention to further normalize the transduction coefficient for one pathway to another, thereby providing a single metric to encapsulate the relative effect of a ligand on a pathway of interest compared to a reference pathway. The additional normalization leads to the now widely used metric ΔΔ log (R) (Kenakin et al., 2012).
In this work, we explore the mathematical and statistical properties of the operational and the general operational model in relation to parameter estimation, which is termed identifiability analysis. A model that contains one or more parameters that are not able to be estimated (given perfect data) is termed not identifiable. In other words, identifiability analysis answers the question of whether there is a unique solution for the parameters of a mathematical model based on its structure and also the experimental design (Shivva et al., 2013; Lavielle and Aarons, 2016). This concept is more commonly considered in pharmacokinetic studies where, for instance, it is known that if you only administer a drug orally to an individual, then the parameter absolute bioavailability (F) cannot be estimated (as it requires both intravenous and oral administration to provide the data for this parameter). As such, this parameter is said to be not identifiable. When model parameters are not identifiable, this means that there are an infinite number of solutions for the model parameters that can fit the data equally well. This causes the parameters of the model to be imprecisely estimated and potentially misrepresent the data. Identifiability issues are also present in pharmacological experiments, but these properties are less well explored. The concept of identifiability is divided into two types: (i) structural identifiability and (ii) deterministic identifiability (sometimes also termed pragmatic identifiability). Structural identifiability is a formal mathematical technique to determine whether a parameter can be uniquely estimated given perfect data (data that contain no error of any type – e.g. no assay error) (Bellman and Åström, 1970). Deterministic identifiability addresses the degree of precision with which a parameter can be estimated based on typical experimental data (Guedj et al., 2007). These concepts are naturally hierarchical, such that if a model is not structurally identifiable, then it cannot be applied to any data and one or more parameters will need to be either fixed or merged into a composite parameter (the latter is analogous to fixing one of the parameters to a null value; e.g. 0 or 1). Once a model is structurally identifiable, then the lower hierarchy, deterministic identifiability, yields knowledge about how well it can be estimated by a given experiment. These concepts are critical in understanding how a model can represent a given set of experimental data.
Application of the operational model to describe the responses elicited by a ligand in multiple pathways is known to result in issues with mathematical identifiability of the model (Kenakin et al., 2012; van der Westhuizen et al., 2014). It should be noted that application of the operational model does not explicitly include ligand binding and considers a single pathway from a single ligand at a time (hence the need for normalization). It is, in theory, possible to apply a general equilibrium model that encompasses all pathways simultaneously that would obviate some of these mathematical issues, but this is beyond the scope of this work.
The overarching aim of this paper is to provide a ready‐to‐use understanding of the application of the operational model for quantifying functional selectivity. This encompasses three specific objectives: (i) to systematically assess the identifiability (structural and deterministic) of both the operational model and the general operational model; (ii) to evaluate the effects of parameter mis‐specification on the quantification of ligand bias; and (iii) to assess whether we can relax the need for the presence of a full agonist to quantify ligand bias.
Methods
The methods are described in two parts. In the first part, the technical details of the methodology are provided as they relate to both structural and deterministic identifiability as well as simulation estimation methods. In the second part, methods are provided for each of the three aims.
Part 1
Structural identifiability analysis
This type of identifiability determines whether a unique set of parameter values exist within the model, given perfect data. If this is not true, then the model is said to be not identifiable. This means that the model parameters cannot be estimated in its current form and a parameter (or parameters) will need to be fixed. The structural identifiability analysis followed the processes developed in previous work (Shivva et al., 2013). The Population OPTimal design for Identifiability (POPT_I), a MATLAB‐based software (available at http://www.otago.ac.nz/pharmacometrics/downloads/index.html), was used for the assessment of structural identifiability. Brief details of the application of this method are provided here for completeness. In this work, two necessary criteria for claiming a structurally identifiable, fixed‐effect model were adopted: (i) there was a continuous linear log–log relationship between the log of the determinant of Fisher information matrix (MF) and the log of the random noise; (ii) the determinant should approach infinity as residual variance approaches zero (Shivva et al., 2013). The values for the random noise log(σ2) were the same for all analyses, −7, −6, −5, −4, −3, −2, −1, 0, 1 and 2.
Deterministic identifiability analysis
Deterministic identifiability is concerned with the precision of parameter estimation. The relative magnitude of the SE is an indication of the precision of the parameter estimates and is amenable to the experimental design. The SE value can be obtained either theoretically, via the Fisher information matrix (MF), or they can be obtained after a data set has been analysed using standard software (such as GraphPad Prism®). Technically, these are termed the expected SE or the observed SE values respectively. Both methods to calculate the SE values give very similar results. Irrespective of the method used to calculate the SE values, large values are a measure of uncertainty in the parameter values that (if large enough) may yield a claim that the model is not deterministically identifiable. In this work, in order to alleviate the need to generate and analyse data, we use the information matrix (MF) and calculate the expected SE values. Hence, it is straightforward (with appropriate software) to calculate the expected SE values for any model given any potential experimental design without having to do the experiment. For convenience, we express the SE value for a parameter as its value relative to the parameter value (in order to normalize to scale). This is termed relative SE (RSE) which we show as per cent. Values greater than 50% are suggestive of potential problems with deterministic identifiability.
Briefly, and for completeness, the SE values are calculated as the square root of the diagonal elements of the inverse of the MF. The MF can be calculated as the product of the sensitivity matrices weighted by the residual error. In this work, optimal design software PFIM (Bazzoli et al., 2010), available at http://www.pfim.biostat.fr/, was used to calculate the MF and provide the expected SE values.
Stochastic simulation and estimation (SSE)
Outline of stochastic simulation estimation (SSE) unit
In practice, the slope factor n is commonly added to improve curve fitting. Hence, we intend to explore a range of values of n to assess their influence on the results of this analysis. We tried an exact numerical evaluation, but it became unfeasible (this failure is shown in the Supporting Information). A more general method involving simulating data and estimating the model parameters was therefore used. This is termed stochastic simulation and estimation (SSE). Practically, this method requires the data to be simulated with random error (aka ‘experimental noise’), termed stochastic simulation, and then estimated using an appropriate software application. It is common to use SSE methods when the model is too complicated to perform exact mathematical analyses. Both the simulation (SSE) method and exact calculation (when possible) provide equivalent answers and interpretations.
The SSE methods in this work were used to assess the influence of mis‐specification of parameter values (i.e. when the parameters were fixed to something other than their true value). Each SSE unit consists of three steps: dataset simulation, parameter estimation and analysis of the results. In the simulation step, based on the given parameter values and study design, pseudo‐experimental data were generated from the general operational model (Equation (2)) using R version 3.0.2 (http://www.r-project.org/) within Rstudio IDE Version 0.98.490 (http://www.rstudio.com/). In total, there were 1000 replicates. In each replicate, two concentration–response curves corresponding to a pair of reference and test ligands were generated with random error. Then, in the estimation step, each replicate was analysed in GraphPad Prism (v7.0; GraphPad Software, La Jolla, CA, USA) following usual estimation methods (van der Westhuizen et al., 2014). R code for stochastic simulation and GraphPad Prism code for batch analysis are included in the Supporting Information. In the post‐estimation analysis step, the normalized transduction coefficient (Δ log (R)) value was calculated for each replicate by taking the difference of log(R) between reference and test ligand. For the final outcome of each SSE unit, only the results from the replicates with successful estimation were included and contributed to calculation of the median and 95% confidence intervals (CI) for log(R) and Δ log (R).
Criteria for successful estimation
A successful estimation was defined as not ambiguous estimates of the parameter log (R) for the pair of ligands in a replicate. The term ambiguous is a term coined by Prism to describe the case that the parameters cannot be precisely estimated. This is akin to defining the parameters as not deterministically identifiable. Such parameters are marked in Prism with a ‘~’ before the best fit values. Ambiguous values were omitted from further computation. The successful estimation rate was defined as the fraction of successful estimation runs within 1000 replicates. In general, the estimation method was considered to be robust if its successful estimation rate was higher than 90%.
Part 2
Systematic assessment of the identifiability of both the operational model and the general operational model
Structural identifiability analysis
The original form of the operational model (Equation (1)) has been extended into the general operational model (Equation (2), the same as Equation 5 in van der Westhuizen et al., 2014) to account for non‐zero basal (Basal), non‐unity slope factor (n) and an estimable maximal system response (Em) (van der Westhuizen et al., 2014).
| (2) |
Here, Em is the system maximal response, Basal is the baseline response in the absence of ligand and n is the slope factor. These three parameters are system parameters. Note, in this expression, it is assumed that the basal activity of the system is constant over both time and applied ligand concentrations. Further generalization is possible but not considered here. Both KA and R are drug‐specific parameters. Conventionally, the parameters KA and R are transformed into logarithms (i.e. ). Note here that this re‐parameterization does not affect the structural identifiability of the model.
The structural identifiability analysis (a formal assessment of the model to determine if the parameters could be uniquely estimated) was performed on both the Black and Leff operational model (Equation (1)) and the general operational model (Equation (2)) in POPT_I. A generic study design with sampling concentrations log(A) from −13 to −4, increment of 1, was assumed for both models. An arbitrary set of parameter values was used (Table 1). [Since this work is dependent on the particular set of parameter values, then the structural identifiability analysis is said to be local – meaning the model is identifiable (or not) based on a specific set of parameter values. This does not affect interpretation of this work.] Structural identifiability was assessed for the Black and Leff operational model based on four scenarios: (i) all the model parameters (R0, KE, KA) were considered to be unknown and estimable; (ii) R0 was assumed to be known and fixed; (iii) KE was assumed to be known and fixed; and (iv) R0 and KE were reduced into one single parameter τ, and both τ and KA were considered to be unknown and estimable. For the general operational model, four scenarios were evaluated for the identifiability analysis: (i) all the model parameters (Em, log(KA), log(R)) were considered to be unknown and estimable; (ii) Em was assumed to be known and fixed; (iii) log(KA) was assumed to be known and fixed; and (iv) log(R) was assumed to be known and fixed.
Table 1.
The parameter values for structural identifiability analysis of the operational model
| Parameters | Operational model | General operational model |
|---|---|---|
| n | – | 1 |
| Em | – | 1 |
| Basal | – | 0.1 |
| R0 | 10 | – |
| KE | 10 | – |
| τ | 1 | |
| log(KA) | −8 | |
| log(R) | 8 | |
| Sampling concentrations: log (A) | From −13 to −4, increased by 1 | |
| Random noise levels: log(σ2) | −7, −6, −5, −4, −3, −2, −1, 0, 1, and 2 | |
Deterministic identifiability analysis
A deterministic identifiability analysis (assessment of SEs of the parameter estimates) was performed on both the operational model and the general operational model. A similar parameter set‐up was used as in the structural identifiability analysis. Details are provided in Table 2. A proportional measurement error with 10% coefficient of variation was assumed for data arising under both models. The deterministic identifiability was assessed for each value of τ. In terms of the general operational model, three arbitrary sets of the parameter values were used and each stood for one of the following circumstances: (i) a pair of highly efficacious ligands; (ii) one highly efficacious ligand and one less efficacious ligand; and (iii) a pair of low‐efficacy ligands (Table 3). Efficacy is defined based on τ values. Under each circumstance, two scenarios were evaluated for the deterministic identifiability: (i) Em was assumed to be known and fixed; and (ii) KA values of both ligands were assumed to be known and fixed.
Table 2.
The parameter values for deterministic identifiability analysis of the operational model
| Design | Value | |
|---|---|---|
| log(A) | From −13 to −4, increased by 1 | |
| Random noise | – | |
| prop. err | 0.1 | |
| Parameters | – | |
| τ | From 0.1 to 100, increased by 0.1 | |
| KA | 1.0E − 8 | |
| R |
|
Table 3.
The parameter values for deterministic identifiability analysis of the general operational model
| Setting | Ligand pair study | ||||||
|---|---|---|---|---|---|---|---|
| High + higha | High + low | Low + low | |||||
| Ligand I | Ligand II | Ligand I | Ligand II | Ligand I | Ligand II | ||
| Individual parameters | τ | 15 | 25 | 15 | 0.8 | 0.8 | 0.4 |
| log(KA) | ‐8 | −7 | −8 | −7 | −7 | −8 | |
| log(R) | 9.18 | 8.40 | 9.18 | 6.90 | 6.90 | 7.60 | |
| Design | log(A) | From −13 to −4, increased by 1 | |||||
| System parameters | Em | 1 | |||||
| Basal | 0.1 | ||||||
| n | 1.0 | ||||||
| prop. err | 0.1 | ||||||
High = high efficiency and low = low efficiency.
Evaluation of the effects of parameter mis‐specification on the quantification of ligand bias
Current estimation methods for the quantification of ligand bias
In current practice, three methods have been adopted for the estimation of the general operational model. In method I, the value of system maximal response (Em) is set to the empirically measured response of a known maximal stimulant (e.g., forskolin for cyclic AMP and phorbol 12‐myristate 13‐acetate for phosphorylated ERK) or the common maximal response among multiple ligands (Kenakin et al., 2012). In method II, the equilibrium dissociation constant (KA) is fixed to a previously estimated value from a separate binding assay (Rajagopal et al., 2011). In method III, a slight modification is made into the operational model framework (van der Westhuizen et al., 2014). In this method, ligands are subjectively classified into two categories: full and partial agonists, based on the value of observed maximal response of each ligand (Emax, i). For partial agonists, the concentration–response curve is directly fitted to the general operational model, whereas for full agonists, one more constraint is applied with KA arbitrarily assigned to 1 mol·L−1 (the identity for most mathematical operations), a value typically 6 to 8 orders of magnitude from expected.
SSE study I: evaluation of the effects of mis‐specified Em
SSE study I was performed to evaluate the effects of mis‐specified Em on the quantification of ligand bias. For the simulation step, a generic study design for the sampling concentrations (Table 4) was assumed for all the SSE units and three arbitrary sets of the parameter values (Table 4) were used with the only difference in slope factor (n=[0.7, 1, 1.5]). Then, in the estimation step, for these three simulated datasets, each was used to estimate the parameters using estimation method I with Em fixed to three different values 0.8, 1(true) or 1.2. Therefore, there were nine SSE units in this SSE study.
Table 4.
The parameter values for the SSE studies
| Design | Impact of Em mis‐specification | Impact of KA mis‐specification | Evaluation of method IV | |||
|---|---|---|---|---|---|---|
| log(A) | From −13 to −4, increased by 1 | From −13 to −4, increased by 0.5 | From −13 to −4, increased by 0.5 | |||
| System parameters | – | – | – | |||
| n | 0.7, 1, 1.5 | Ranging from 0.5 to 2 | Ranging from 0.5 to 2 | |||
| Em | 1 | 500 | 500 | |||
| Basal | 0.1 | 10 | 10 | |||
| prop. err | 0.1 | 0.1 | 0.1 | |||
| Individual parameters | Ligand I | Ligand II | Ligand I | Ligand II | Ligand I | Ligand II |
|---|---|---|---|---|---|---|
| τ | 1.5 | 0.8 | 6 | 2 | 0.6 | 0.2 |
| log(KA) | −8 | −7 | −8 | −7 | −8 | −7 |
| log(R) | 8.176 | 6.903 | 8.778 | 7.301 | 7.778 | 6.301 |
| Δ log (R) | 1.273 | 1.477 | 1.477 | |||
SSE study II: Evaluation of the effects of mis‐specified KA
SSE study II was conducted to evaluate the effects of mis‐specified KA on the quantification of ligand bias. In the simulation step, a generic study design for the sampling concentrations (Table 4) was assumed for all the SSE units and 10 arbitrary sets of the parameter values (Table 4) were used with the only difference in slope factor (n=[0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.25, 1.5, 1.75, 2]). The value of τ for the reference ligand was assigned to a large number (Table 4) to represent full agonist (i.e. highly efficacious ligand). In the following, each simulated data were estimated by two different estimation methods: method II with KA values fixed to true or method III with KA of full agonist arbitrarily assigned to 1 mol·L−1. In the final step, the post‐estimation analysis was applied to get summarized outcomes from these 20 SSE units.
Assessment of the relaxation of the need for a full agonist in quantifying functional selectivity
Method IV for the quantification of ligand bias
The current estimation method for the general operational model requires a full agonist to have been identified within the study. We propose a generalization to this estimation method (termed method IV here) to account for the situation when only low‐efficacy ligands are present. The key steps were listed:
-
1
Fit the classical Emax model (Equation (3)) to the data from every ligand. For each pathway, the value of n and Basal are shared for all the ligands and there is no constraint on the values of Emax and EC50.
| (3) |
Here, Basal and n are system parameters shared among different ligands. Emax and logEC50 are ligand‐specific parameters
-
2
Select the ligand with maximal Emax,i from the current study and set as if it were a full agonist (termed pseudo full agonist). Classify all the remaining ligands as partial agonists.
-
3
For partial agonists, the concentration–response curve is directly fitted with the general operational model, whereas for the pseudo full agonist, the value of KA is set to 1 mol·L−1. For each pathway, the values of n, Basal and Em are shared for all the ligands and there is no constraint on the values of log(R) and log(KA).
An illustrating example with step‐by‐step analysis processes and results is included in the Supporting Information.
SSE study III: Evaluation of the performance of method IV
SSE study III was performed to evaluate the performance of method IV by comparing to methods I and II. The same set‐up was used for the simulation as for SSE study II, except that the values of τ were smaller in SSE study III (Table 4) to represent low‐efficacy ligands. Then, for the parameter estimation, each simulated data were analysed by three different estimation methods: method I with Em set to true; method II with KA values set to true; and method IV. Finally, the results of a total of 30 SSE units were obtained from the post‐estimation analysis.
Results
Systematic assessment of the identifiability of both the operational model and the general operational model
Structural identifiability of the operational model
Given pharmacological response data only, the original form of the operational model (Equation (1)) was confirmed as not structurally identifiable. As conceptually demonstrated in Equation (4) (a re‐expression of Equation (1) by dividing KE), there were infinite possible combinations of R0 and KE that rendered the same result. For example, the two parameter sets, (R0 = 100, KE = 20, KA = 10−8) and (R0 = 10, KE = 2, KA = 10−8), produced exactly identical curves.
| (4) |
Structural identifiability analysis was performed in Equation (1). As shown in Figure S1A, the result indicated that this equation was unidentifiable when all parameters were considered to be estimable. Fixing either R0 or KE rendered the model structurally identifiable. In the absence of measuring (or estimating) R0 or KE from an additional experiment, it is not possible to distinguish their values. In order to solve this problem and as indicated by the work of Black and Leff, R0 and KE are therefore reduced into a single identifiable quantity ( ), defined as the transducer ratio τ. This yielded the reduced form of the operational model, Equation (5), which was structurally identifiable (Figure S1B).
| (5) |
Deterministic identifiability of the operational model
It was seen from the results of a deterministic identifiability analysis (Figure 1) that the operational model (Equation (5)) generally yielded appropriately low RSE% values (<50%) for τ and KA for standard study designs. However, it was also evident that the precision of the estimate of both KA and τ decreased with increasing values of τ, indicating that the operational model would not be deterministically identifiable for the large values of τ, even though this model is structurally identifiable (Figure 1). This is conceptually demonstrated in Equations (6) and (7): when values of τ greatly exceed 10 (i.e. highly efficacious ligand), Equation (5) is well approximated by Equation (6), which is then unidentifiable. Equation (6) is re‐expressed as Equation (7) by dividing KA. We now see that τ and KA only appear as the ratio when τ exceeds 10 and hence there will be infinite possible combinations of τ and KA that provide indistinguishable results (i.e. the model is structurally unidentifiable).
| (6) |
| (7) |
Figure 1.
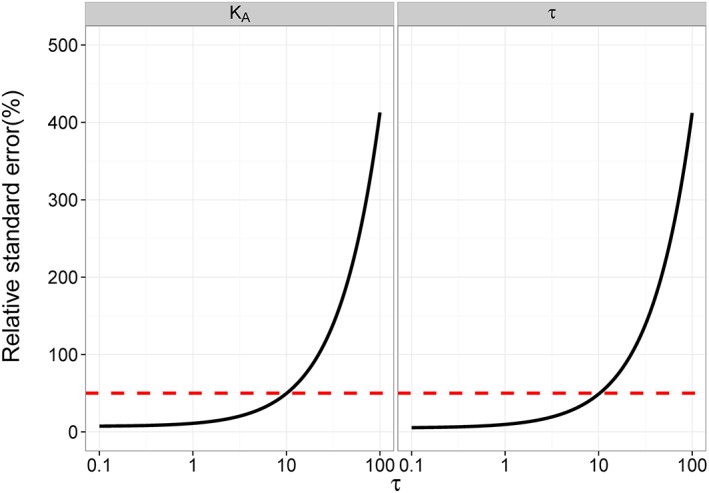
The RSE of estimated parameters versus τ for Equation (5). In this study, a generic study design with sampling concentrations log(A) from −13 to −4, increment of 1, was adopted. A proportional measurement error with 10% coefficient of variation were assumed. KA was set to an arbitrary value, 10−8 mol·L−1. The deterministic identifiability was assessed for each value of τ, ranging from 0.1 to 100. The left panel is for KA and the right panel is for τ. The red dashed line indicates the 50% RSE, considered as the threshold for precise estimation.
In order to circumvent this problem, the transduction coefficient (R) was introduced, defined as the ratio between transducer ratio (τ) and equilibrium dissociation constant (KA). Substituting R into Equation (5) yielding Equation (8):
| (8) |
A deterministic identifiability analysis was also performed on Equation (8). Contrary to the behaviour of KA, the RSE of R is now independent of the value of τ (Figure S2), indicating that the transduction coefficient (R) could be precisely estimated, even for highly efficacious ligands. In this sense, R was not only a combination of efficacy and affinity, as originally described, but also the minimal robust element that could be directly derived from the operational model analysis for quantifying agonism.
Structurally identifiability of the general operational model
Structural identifiability analysis was performed on Equation (2). As shown in Figure S3A, the result indicated that this equation was unidentifiable when all parameters were considered to be estimable. Furthermore, case deletion assessment (Figure S3B–D) identified that the general operational model had one unidentifiable parameter and one of Em, log(KA), or log(R) would be required to be fixed to yield a structurally identifiable model. However, since log(R) is regarded as the target from these analyses, only Em or log(KA) could be considered to be fixed. Note here that neither n nor Basal affects the structural identifiability of the model.
Deterministic identifiability of the general operational model
A deterministic identifiability analysis was performed on Equation (2) for a pair of ligands. As shown in Table 5, in general, with fixed Em or KA, the target parameter R could be precisely estimated with low RSE% values (<50%), when at least one highly efficacious ligand existed. For a pair of low‐efficacy ligands, estimation of R became less precise and fixing Em gave more precise parameter estimation of R than fixing KA. For all highly efficacious ligands, given only pharmacological response data, KA could not be precisely estimated (RSE% values >100%), consistent with previous findings in the operational model.
Table 5.
The results of deterministic identifiability analysis of the general operational model
| Scenario | Fixed parameters | Em RSE(%) | KA RSE(%) | R RSE(%) | |
|---|---|---|---|---|---|
| Ligand pair | High + higha | Em | – | 109.6b, 172.3 | 24.6, 23.7 |
| KA1, KA2 | 5.2 | – | 27.6, 27.5 | ||
| High + low | Em | – | 120.9, 47.3 | 27.9, 44.5 | |
| KA1, KA2 | 6.6 | – | 29.3, 20.3 | ||
| Low + low | Em | – | 75.8, 67.4 | 76.1, 88.4 | |
| KA1, KA2 | 80.9 | – | 159.8, 147.9 | ||
High = high efficacy and low = low efficacy.
If the RSE value is less than 50%, the parameter it describes is interpreted as precisely estimable.
Evaluation of the effects of parameter mis‐specification on the quantification of ligand bias
The source of parameter mis‐specification addressed here was restricted to some unavoidable cases, that is, theoretically inevitable mis‐specification or simply fixing the parameter to an (arbitrary) value for convenience. Note that the effects of mis‐specified KA arising from binding assay experimental error, while potentially important, was not considered on the performance of method II and was beyond the scope of current evaluation.
In method I, Em was prone to mis‐specification. In real cases, the true value of Em is rarely known and often empirically approximated from the maximal observed response among a number of ligands or the response to a known maximal stimulant (e.g. forskolin for cyclic AMP) (Evans et al., 2011; Kenakin et al., 2012). In so doing, Em is set to the lower bound of its true value. On the other hand, KA is simply fixed to an (arbitrary) value for convenience in method III. Instead of plugging in estimated KA values from independent binding assays (method II), the KA values of full agonists were arbitrarily fixed to 1 mol·L−1. This value greatly exceeds the biologically reasonable range of possible values of KA (10−4~10−12 mol·L−1). In the following, we evaluate the effects of parameter mis‐specification on quantification of ligand bias under mis‐specification of Em and KA.
The influence of the mis‐specified Em
In the case where the slope factor (n) is equal to one, an exact numerical evaluation was performed to explore the effects of the mis‐specification of Em (see Appendix A). It is clearly shown that the mis‐specified value of Em leads to an inaccurate estimation of R. Here, we are referring to the mean error in the estimate of R, which we specify as the true value minus the estimated value [we use mean error to avoid the use of bias in two different settings (statistical and pharmacological)]. The mis‐specification of R has a similar effect on different ligands. Therefore, the normalization process would cancel out this estimation mean error, and the estimation of Δ log (R) would remain accurate. In other words, the estimation of Δ log (R) is tolerant to the mis‐specification of Em.
For the case where the slope factor is different from unity, a stochastic simulation‐estimation study was performed to explore the effect of the mis‐specification of Em. In Table 6, it is noted that estimation of log(R) is inaccurate with the mis‐specified Em. For instance, in the case that n is equal to 0.7 and Em is underestimated by 20%, the estimated log(R) values for ligands I and II were 3–5% greater than their true values (i.e. negligibly affected). The estimation mean error of ligand bias caused by the mis‐specification of Em appears therefore to be largely cancelled out via the normalization process.
Table 6.
The results from the evaluation of the effects of the mis‐specified E m on the estimation of log(R) and Δ log (R)
| n | E m assigned value | log(R) | Δ log (R) | Successful estimation rate (%) | |
|---|---|---|---|---|---|
| Ligand I median [95% CI] | Ligand II median [95% CI] | Median [95% CI] | |||
| 0.7 | 0.8 | 8.40 [7.92–8.84] | 7.15 [6.59–7.70] | 1.25 [0.86–1.70] | 98.4 |
| 1(true) | 8.18 [7.52–8.79] | 6.93 [6.24–7.63] | 1.25 [0.86–1.70] | 98.1 | |
| 1.2 | 8.02 [7.22–8.73] | 6.77 [5.95–7.56] | 1.25 [0.85–1.70] | 97.9 | |
| 1 | 0.8 | 8.28 [7.82–8.81] | 7.03 [6.43–7.62] | 1.27 [0.92–1.65] | 98.2 |
| 1(true) | 8.18 [7.55–8.89] | 6.93 [6.17–7.66] | 1.26 [0.91–1.65] | 97.5 | |
| 1.2 | 8.09 [7.34–8.80] | 6.83 [5.98–7.60] | 1.27 [0.91–1.65] | 95.3 | |
| 1.5 | 0.8 | 8.19 [7.73–8.66] | 6.94 [6.34–7.40] | 1.26 [0.94–1.63] | 93.4 |
| 1(true) | 8.20 [7.58–8.72] | 6.94 [6.25–7.45] | 1.27 [0.96–1.62] | 94.0 | |
| 1.2 | 8.17 [7.49–8.71] | 6.91 [6.13–7.45] | 1.27 [0.97–1.62] | 91.2 | |
The influence of mis‐specified KA
As shown for the mis‐specification of Em, we can exactly determine the effect of the mis‐specification of KA on estimation mean error (detailed in Appendix B). Through the derivation, it is evident that the mis‐specification of KA would lead to inaccurate estimation of R. However, again, this affects all ligands in question equally, and hence, estimation of Δ log (R) remains accurate.
When the slope factor was different from unity, we performed a stochastic simulation‐estimation study to explore the influence of the mis‐specification of KA. In Figure 2, it is demonstrated that Δ log (R) calculated from method III (red) is essentially accurate, even when the slope factor n departs from unity. It is also seen that arbitrarily assigning KA to 1 mol·L−1 (method III, red line) is indistinguishable from the result produced from plugging in the true values of KA (method II, blue line), indicating that the influence of this mis‐specification of KA on the quantification of ligand bias is trivial.
Figure 2.
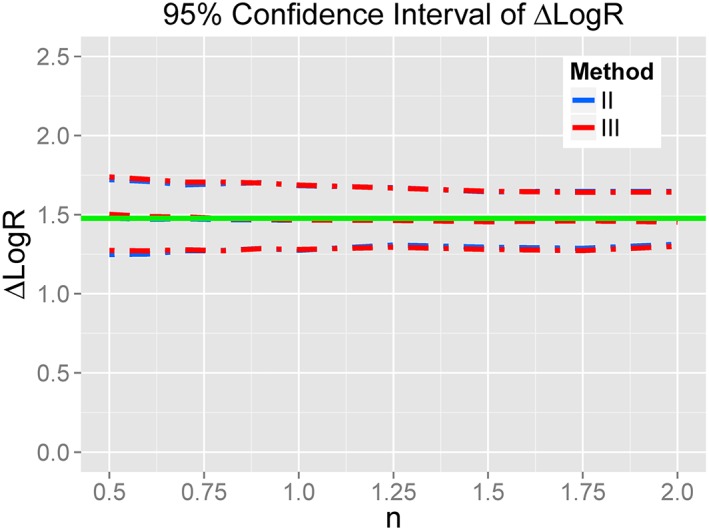
Values of Δ log (R), with its 95% CI, over different values of n. The green line shows the true value. Dashed line indicates the median estimated value and the dash‐dot line the 95% CI of estimated value. Blue indicates the method of assigning KA to measured values from binding assay (method II); red indicates the method of arbitrarily fixing KA of full agonists to 1 (method III). The successful estimation rates of three methods were all higher than 95%.
Assessment of the relaxation of the need for a full agonist in quantifying functional selectivity
It was shown in the deterministic identifiability analysis that estimation of log(R) after fixing Em (method I) or fixing KA (method II) became less precise in the absence of highly efficacious ligands (Table 5). Moreover, the application of method III was restricted, by definition, to cases wherein a full agonist (highly efficacious ligand) was used in the experiment. Method IV was proposed to relax the need for a full agonist in method III. In this case, Em was taken to be the highest efficacy level observed within the range of ligands considered.
A stochastic simulation‐estimation study was performed to compare the performance of method IV with other estimation methods, that is, methods I (Em set to the system maximal response) and II (KA set to the value from a previous binding experiment). Method III was excluded from this comparison because it, by definition, could only be applied to the case that a full agonist was present.
The method IV estimation of log(R) was found to be robust (using GraphPad Prism v7.0), with a successful estimation rate close to 100%. Methods I and II, however, had quite poor rates of successful estimation (less than 60%), especially for large values of n (Figure 3A). This suggests that method IV is more robust than typical analysis methods. Furthermore, in Figure 3B, it was clear that the Δ log (R) calculated using method IV was either accurate or minimally inaccurate within the normal range of n (from 0.5 to 2).
Figure 3.
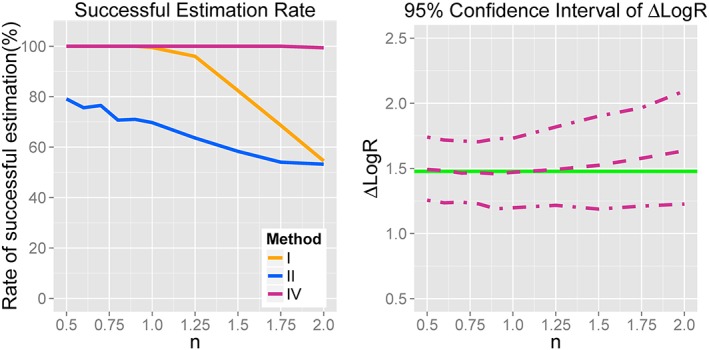
Performance comparison of method IV and other estimation methods. (A) The successful estimation rates for three estimation methods over the range of n. Method I involves assigning Em to known system maximal response; Method II involves assigning KA to measured values from binding assay; Method IV involves arbitrarily fixing KA of pseudo full agonists to 1. (B) Values of Δ log (R), with its 95 % CI, over the normal range of n for Method IV. Green line indicates the true value. Dashed line indicates the median value of estimated value. Dash‐dot line indicates the 95% CI of estimated value.
An exact numerical evaluation (detailed in Appendix C) supports these findings, showing that method IV yields an accurate Δ log (R). As demonstrated before, the influence of mis‐specified KA can be cancelled out through the normalization process. Hence, the estimation of Δ log (R) is accurate using method IV. As demonstrated in Appendix C, fixing KA for a given partial agonist to an arbitrarily large value (1 mol·L−1) forces the apparent value of τ (τ′) to be sufficiently large for estimation of R to be precise, despite its lower efficacy. Furthermore, it is noted in the deterministic identifiability analysis that a large value of τ contributes to the precise estimation of transduction coefficient (R). Hence, R and therefore Δ log (R) can be precisely estimated in method IV.
Discussion and conclusions
Functional selectivity describes the ability of ligands to differentially regulate several different signalling pathways when coupled to a single receptor (Clarke and Berg, 2010). This is a complicated pharmacological process involving multiple biological steps (e.g. receptor binding, cellular and intracellular signalling), and how these multiple signalling pathways interact with the receptor is still unclear (Kenakin and Christopoulos, 2013b). Due to the complexity of functional selectivity, the implementation of a full model that can accommodate multiple receptor states where each state links to a signalling pathway remains impractical (Weiss et al., 1996; Ehlert, 2008; Stein and Ehlert, 2015). Therefore, it has been necessary to use a simplified model. Several simplified models have been proposed, such as the three‐state model (Leff et al., 1997), the operational model (Black and Leff, 1983), the operational model with non‐zero constitutive activity (Slack and Hall, 2012) and the conformation‐based operational model (Roche et al., 2013). Among them, the simplest version is the operational model (Black and Leff, 1983), which has been widely used to quantify functional selectivity (Kenakin et al., 2012).
The purpose of the current study is to gain a more in‐depth understanding of the application of the operational model for quantification of functional selectivity. To do this, we first systematically assessed identifiability of the operational model and the general operational model (where basal and system maximum are also considered as parameters). In so doing, additional rationale has been provided for utilization of current metrics for the quantification of functional selectivity. Second, current estimation methods for the quantification of ligand bias were evaluated via both exact (algebraic) and numerical (stochastic simulation‐estimation) approaches, with the goal of providing a better understanding of the effect of parameter mis‐specification. Finally, based on the insights from these evaluations, the current method was further generalized into a more robust and objective procedure that has the potential to simplify current analyses.
In many cases, metrics arise from a need to solve the mathematical issue of quantification. For instance, the parameter τ was introduced to reduce two entangled parameters, R0 and KE, into one single parameter (Black and Leff, 1983). While this parameter may not have biological meaning, its form is a necessary part of the application of the operational model. Likewise, the transduction coefficient R, the ratio of τ to KA, was initially constructed to simultaneously account for both affinity and efficacy of a ligand (Kenakin and Miller, 2010). However, we see that this was also required mathematically to ensure that the model parameters were able to be estimated with reasonable precision. The issue of parameter estimation is only evident for highly efficacious ligands, where the value of τ is sufficiently large (say, 10) such that the model collapses to the ratio of τ to KA (namely, R). In other words, with only functional response assay data (and no binding data), R is the minimal element that can be directly derived from the operational model.
The normalized transduction coefficient, Δ log (R), was initially designed to cancel out the system bias and observation bias in the in vitro assays (Kenakin et al., 2012). Through our analysis, we have found that this metric could also cancel out the possible estimation mean error introduced by the mis‐specification of fixed parameters. In other words, the value of Δ log (R) would be accurate even when Em and KA were unknown and their values fixed (hence mis‐specified). This makes Δ log (R) an important, robust quantity in current practice. Therefore, there is no need to run a separate assay to determine an accurate estimate of Em or KA, when the aim of study is to quantify ligand bias based on ΔΔ log (R). In so doing, our work helps alleviate the concern that may arise on fixing KA to a non‐physiological value (1 mol·L−1), instead of plugging in realistic value estimated from binding assay (Rajagopal, 2013; Onaran et al., 2014).
In this work, we propose a generalization of the accepted method III, whereby each experiment must include a full agonist which is used as an approximation to the system maximum (Em). Compared to the accepted method, the only modification made in the proposed method (method IV) is to relax the requirement of a full agonist and select the ligand with the highest efficacy level among the tested ligands as if it were a full agonist (termed a ‘pseudo full agonist’). Hence, method IV inherits most of the advantages and limitations of method III; only functional assay data are required, and the estimation of operational model parameters is inaccurate but tolerated due to the subsequent normalization. We also found that method IV provides more precise estimation results even in the absence of highly efficacious ligands. As efficacy profiling of ligands is not required, method IV (using the maximum effect from the entire range of ligands as an approximation to the system Em) therefore has the potential to be applied to large‐scale screening to accelerate the discovery of novel lead compounds with desirable features of functional selectivity.
The choice of the various methods (I–IV) for estimating the parameters from the operational model largely depends on the aim of the work and the available data. If the aim is solely to calculate, Δ log (R) and/or ΔΔ log (R) for the quantification of ligand bias, it is our recommendation that method IV be chosen. However, if an accurate estimate of Em, KA, R and τ is the target, then methods I or II would be more appropriate. In addition, with more information at hand (e.g. binding assay data and separate Em information), it is possible to gain insights into the system via methods I or II, which is not available from methods III or IV where these values are compressed (Buchwald, 2017).
A limitation of the current study is that we did not consider biological constraints associated with different pathways. In this work, we consider a range of values of n to encompass values that are seen in empirical applications of the operational model. We do not attempt to provide a mechanistic interpretation of the value. Method II, in its original form (Rajagopal et al., 2011), fixes the KA from different pathways to the same empirical dissociation constant, determined from a binding assay under conditions that would limit the formation of a receptor ternary complex. However, the feasibility of this biological constraint is still under debate (Rajagopal, 2013; Kenakin and Christopoulos, 2013a). There is emerging evidence that a single value of KA cannot describe data from a ligand that acts as the weak agonists in two pathways with very different EC50 values (Kenakin and Christopoulos, 2013a). Through the theoretical analysis from (cubic) ternary complex model, the binding affinity of agonist can be affected by allosteric modulation of effector (G protein) and different receptor states (Weiss et al., 1996; Ehlert, 2008; Stein and Ehlert, 2015). This may explain the reason why a single binding affinity may be insufficient to describe a biological system. Therefore, in the evaluation of the methods in this work, we allowed the KA values to be different in different pathways. In so doing, the performance of the current method II (without the potentially necessary biological constraint on KA) should always be superior to its original version (which included the biological constraint).
It is noted that in Figure 2 that the 95% CI becomes narrower along the range of evaluated n values (i.e. yields more precise parameter estimation). Yet, in Figure 3A, there is a decrease in the successful estimation fraction with an increase in n, and Figure 3B shows wider 95% CI with the increment of n (i.e. less precise estimation). These directly opposite behaviours may be due to the difference of the ligand efficacy in two scenarios presented in the two figures. Figure 2 is a case of a highly efficacious ligand (large value of τ, τ is greater than 1) whereas Figure 3 considers low efficacious ligands (low value of τ, τ is less than 1). From the equation , when τ is greater than 1, the increment of n would increase the value of (more efficacious), while, when τ is less than 1, the increment of n would decrease the value (less efficacious). Hence, it is speculated that for the same method, more efficacious ligands will have a narrower 95% CIs (i.e. more precise estimation).
Our work provides a formal assessment of the issues pertaining to identifiability and other mathematical observations that have been raised by others (Ehlert, 2005; Kenakin et al., 2012; Rajagopal, 2013; Kenakin and Christopoulos, 2013a; van der Westhuizen et al., 2014). For instance, it was noted that two different parameter sets were able to produce nearly identical curves in the general operational model (Kenakin et al., 2012), which is a function of observability (rather than identifiability, per se). It has also been reported that separate estimation of τ or KA values for full agonists from direct fitting of the operational model to a concentration–response curve was usually not possible (Rajagopal, 2013; van der Westhuizen et al., 2014), which was explored here with deterministic identifiability. To our knowledge, the current study provides the first formal assessment of the identifiability of commonly used models in functional selectivity, illustrating the utility of identifiability analysis tools developed in the field of pharmacometrics (Bazzoli et al., 2010; Shivva et al., 2013). This recent trend in quantitative pharmacology sees the development of more mechanism‐based models, which are inevitably more complicated in their interrelationships but are built from the building blocks provided by standard receptor theory (Wajima et al., 2009; Peterson and Riggs, 2012; Benson et al., 2014). It is therefore likely that the models explored here, based on the operational model, will form the basis of many other models within quantitative systems pharmacology, which require appropriate mathematical underpinning.
In conclusion, we have systematically assessed the identifiability of the operational model and its variants and demonstrated that current methods for quantifying ligand bias is tolerant to mis‐specification of those parameters that are set to fixed constants. Furthermore, an objective method is proposed that relaxes the need for specific choice of ligands in any given experiment and provides accurate estimates of biased ligand profiles.
Author contributions
X.Z. designed and performed experiments, analysed the data and wrote the paper. D.B.F. analysed the data and wrote the paper. M.G. designed experiments, analysed the data and wrote the paper. S.B.D. designed experiments, analysed the data and wrote the paper.
Conflict of interest
The authors declare no conflicts of interest.
Declaration of transparency and scientific rigour
This http://onlinelibrary.wiley.com/doi/10.1111/bph.13405/abstract acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research recommended by funding agencies, publishers and other organisations engaged with supporting research.
Supporting information
Figure S1 log|MF| vs. log residual variance for operational model. A) all parameters estimated from operational model (Eq. 1) with data from functional assay; B) reduced operational model (Eq. 5) with data from functional assay. |MF|: the determinant of the Fisher Information Matrix. The criteria for claiming identifiability of a model: (i) log|MF| should have a continuous linear log–log relationship with the log of the random noise and (ii) |MF| should approach infinity as residual variance approaches zero.
Figure S2 The relative standard error of estimated parameters vs. τ for Eq. 8. In this study, a generic study design with sampling concentrations log (A) from −13 to −4, increment of 1, was adopted. A proportional measurement error with 10% coefficient of variation were assumed. KA was set to an arbitrary value, 10−8 mol L−1. R was defined as the ratio of τ and KA. The deterministic identifiability was assessed for each value of, ranging from 0.1 to 100. The left panel is for KA and the right panel is for R. The red dashed line indicates the 50% relative standard error, considered as the threshold for precise estimation.
Figure S3 log|MF| vs. log residual variance for general operational model (Eq. 2). A) all parameters estimated (E m , Basal, n,log (K A), log (R)); B) E m fixed; C) log (K A) fixed; D) log (R) fixed.
Figure S4 Concentration–response curves for cAMP formation showing pplss‐3HA‐hCB1 HEK signalling, on stimulation with 2.5 μM FSK and a panel of six agonists, following >16 h pretreatment in the presence of PTX. The data is fitted by Method IV.
Table S1 The estimation of transduction coefficient (log (R)) via Method IV.
Acknowledgements
X.Z. was supported by University of Otago Doctoral Scholarship.
Appendix A. Theoretical assessment of the influence of the mis‐specified Em on the quantification of ligand bias
A.1.
From Equation (A1)
| (A1) |
the location and asymptote are defined as follows:
| (A2) |
| (A3) |
| (A4) |
Here, Basal and Em were the true system parameter values shared by all ligands, and τi and KAi were the true parameter values for ith ligand.
Since these constraints (i.e. Equations (A2)–(A4)) need to be met by all the workable parameter sets, the links between true parameter values and mis‐specified parameter values were set‐up as follows:
| (A5) |
| (A6) |
| (A7) |
Here, the prime symbol denotes the corresponding mis‐specified parameter values.
The general form for the mis‐specified value of Em was defined as follows:
| (A8) |
Here, α is a scalar that quantifies the difference between true parameter value (Em) and mis‐specified parameter value ( ). The value of α should be larger than the maximal value of . Doing so ensures that is larger or equal to the maximal observed response among all the ligands.
Substituting Equations (A5) and (A8) into Equations (A6)–(A7) for ligand one yielded the expressions for and :
| (A9) |
| (A10) |
By definition, R (transduction coefficient) is the ratio between τ and KA. So was calculated as follows:
| (A11) |
Similarly, was derived as follows:
| (A12) |
Finally, Δ log (R′) was derived by taking the difference between two ligands:
| (A13) |
Through the derivation above, mis‐specified value of Em would lead to inaccurate estimation of R, while the estimation of Δ log (R) could still be accurate when the slope factor was equal to unity. The estimation mean error caused by the mis‐specification of Em has been fully cancelled out in this situation. In other words, the estimation of Δ log (R) was robust to the mis‐specification of Em.
Appendix B. Theoretical assessment of the influence of the mis‐specified KA on the quantification of ligand bias
B.1.
In a two ligand system, choosing the ligand with higher efficacy as the reference ligand and fixing its equilibrium dissociation constant to an arbitrary large value yielded Equation (A14):
| (A14) |
Here, β was the scaling factor quantifying the difference between true parameter value (KA1) and mis‐specified parameter value ( ). The value of β should be larger than 1.
Substituting Equation (A5) and (A14) into Equations (A6)–(A7) and solving the equation set for ligand one yields the expressions for other parameters:
| (A15) |
| (A16) |
Here, γ was equal to .
By definition, R (transduction coefficient) was the ratio between τ and KA. So was calculated as follows:
| (A17) |
At the same time, Basal′ and were system parameters shared between two ligands. Substituting them into Equations (A6) and (A7) for ligand two yielded the expressions for and :
| (A18) |
| (A19) |
Similarly, was derived:
| (A20) |
Combining Equations (A17) and (A20) yielded the expression for Δ log (R′):
| (A21) |
Through the derivation above, it was clearly shown that a mis‐specified value of KA could lead to inaccurate estimation of R, while the estimation of Δ log (R) was still accurate when the slope factor was equal to unity. The estimation mean error caused by the mis‐specification of KA has been completely cancelled out via normalization process.
Appendix C. Theoretical assessment of the feasibility of method IV
C.1.
Method IV could be considered a natural generalization of method III. The requirement of full agonist was relaxed into the ligand with highest efficacy among all the ligands in the study.
The general operational model has only one unidentifiable parameter, that is, fixing either Em or KA will render the model structurally identifiable. Therefore, with mis‐specified KA, the estimated values of other parameters have to change accordingly in line with the constraints from observed features of the concentration response curve (e.g. Emax and EC50).
The location parameter EC50 of the general operational model was derived as follows:
| (A22) |
Similarly, this constraint should also be applied to the case that KA was fixed to 1 mol·L−1, as shown in Equation (A23).
| (A23) |
Transforming Equation (A23) yielded the expression for the apparent value of τ (denoted here as τ′) when KA was mis‐specified to 1 mol·L−1:
| (A24) |
As the normal value of EC50 was much smaller than 1 mol·L−1 (10−4~10−12 mol·L−1), the apparent value (τ′) appeared to be much larger than 1. In other words, setting KA to 1 ensured the apparently high efficacy of the ligand. In method IV, fixing KA to 1 mol·L−1 was not the result from a full agonist, but rather a ‘pseudo full agonist’ was created by fixing KA to 1 mol·L−1 for the highest efficacy agonist in the set of compared agonists. Furthermore, as noted in the previous deterministic identifiability analysis, the large apparent value of τ (i.e. highly efficacious ligand) could also substantially improve the estimation precision of parameter R.
Method IV could also be considered as the generalization of method I. The asymptote parameter Emax of the general operational model was derived as follows:
| (A25) |
Similarly, this constraint should also be applied to the pseudo full agonist, as shown in Equation (A26).
| (A26) |
Reorganizing Equations (A26) yields (A27):
| (A27) |
As demonstrated before, when KA was assigned to 1 mol·L−1, the apparent value of τ (τ′) was much larger than 1. Therefore, could be reduced to Emax, that is, Em was implicitly fixed to the Emax value of the pseudo full agonist in method IV, rather than the system maximal response.
Zhu, X. , Finlay, D. B. , Glass, M. , and Duffull, S. B. (2018) An evaluation of the operational model when applied to quantify functional selectivity. British Journal of Pharmacology, 175: 1654–1668. doi: 10.1111/bph.14171.
References
- Bazzoli C, Retout S, Mentre F (2010). Design evaluation and optimisation in multiple response nonlinear mixed effect models: PFIM 3.0. Comput Methods Programs Biomed 98: 55–65. [DOI] [PubMed] [Google Scholar]
- Bellman R, Åström KJ (1970). On structural identifiability. Math Biosci 7: 329–339. [Google Scholar]
- Benson N, Metelkin E, Demin O, Li GL, Nichols D, van der Graaf PH (2014). A systems pharmacology perspective on the clinical development of fatty acid amide hydrolase inhibitors for pain. CPT Pharmacometrics Syst Pharmacol 3: e91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black JW, Leff P (1983). Operational models of pharmacological agonism. Proc R Soc Lond B Biol Sci 220: 141–162. [DOI] [PubMed] [Google Scholar]
- Buchwald P (2017). A three‐parameter two‐state model of receptor function that incorporates affinity, efficacy, and signal amplification. Pharmacol Res Perspect 5: e00311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AJ (1926). The antagonism of acetyl choline by atropine. J Physiol 61: 547–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke WP, Berg KA (2010). Use of functional assays to detect and quantify functional selectivity. Drug Discov Today Technol 7: e31‐e36. [DOI] [PubMed] [Google Scholar]
- Clarke WP, Bond RA (1998). The elusive nature of intrinsic efficacy. Trends Pharmacol Sci 19: 270–276. [DOI] [PubMed] [Google Scholar]
- Ehlert FJ (2005). Analysis of allosterism in functional assays. J Pharmacol Exp Ther 315: 740–754. [DOI] [PubMed] [Google Scholar]
- Ehlert FJ (2008). On the analysis of ligand‐directed signaling at G protein‐coupled receptors. Naunyn Schmiedebergs Arch Pharmacol 377: 549–577. [DOI] [PubMed] [Google Scholar]
- Evans BA, Broxton N, Merlin J, Sato M, Hutchinson DS, Christopoulos A et al (2011). Quantification of functional selectivity at the human α1A‐adrenoceptor. Mol Pharmacol 79: 298–307. [DOI] [PubMed] [Google Scholar]
- Guedj J, Thiebaut R, Commenges D (2007). Practical identifiability of HIV dynamics models. Bull Math Biol 69: 2493–2513. [DOI] [PubMed] [Google Scholar]
- Kenakin T (2014). A Pharmacology Primer: Techniques for More Effective and Strategic Drug Discovery. Elsevier, Amsterdam. [Google Scholar]
- Kenakin T, Christopoulos A (2013a). Measurements of ligand bias and functional affinity. Nat Rev Drug Discov 12: 483. [DOI] [PubMed] [Google Scholar]
- Kenakin T, Christopoulos A (2013b). Signalling bias in new drug discovery: detection, quantification and therapeutic impact. Nat Rev Drug Discov 12: 205–216. [DOI] [PubMed] [Google Scholar]
- Kenakin T, Miller LJ (2010). Seven transmembrane receptors as shapeshifting proteins: the impact of allosteric modulation and functional selectivity on new drug discovery. Pharmacol Rev 62: 265–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenakin T, Watson C, Muniz‐Medina V, Christopoulos A, Novick S (2012). A simple method for quantifying functional selectivity and agonist bias. ACS Chem Nerosci 3: 193–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavielle M, Aarons L (2016). What do we mean by identifiability in mixed effects models? J Pharmacokinet Pharmacodyn 43: 111–122. [DOI] [PubMed] [Google Scholar]
- Leff P, Scaramellini C, Law C, McKechnie K (1997). A three‐state receptor model of agonist action. Trends Pharmacol Sci 18: 355–362. [DOI] [PubMed] [Google Scholar]
- Onaran HO, Rajagopal S, Costa T (2014). What is biased efficacy? Defining the relationship between intrinsic efficacy and free energy coupling. Trends Pharmacol Sci 35: 639–647. [DOI] [PubMed] [Google Scholar]
- Peterson M, Riggs M (2012). Predicting nonlinear changes in bone mineral density over time using a multiscale systems pharmacology model. CPT Pharmacometrics Syst Pharmacol 1: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajagopal S (2013). Quantifying biased agonism: understanding the links between affinity and efficacy. Nat Rev Drug Discov 12: 483–483. [DOI] [PubMed] [Google Scholar]
- Rajagopal S, Ahn S, Rominger DH, Gowen‐MacDonald W, Lam CM, DeWire SM et al (2011). Quantifying ligand bias at seven‐transmembrane receptors. Mol Pharmacol 80: 367–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roche D, Gil D, Giraldo J (2013). Multiple active receptor conformation, agonist efficacy and maximum effect of the system: the conformation‐based operational model of agonism. Drug Discov Today 18: 365–371. [DOI] [PubMed] [Google Scholar]
- Shivva V, Korell J, Tucker IG, Duffull SB (2013). An approach for identifiability of population pharmacokinetic‐pharmacodynamic models. CPT Pharmacometrics Syst Pharmacol 2: e49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slack RJ, Hall DA (2012). Development of operational models of receptor activation including constitutive receptor activity and their use to determine the efficacy of the chemokine CCL17 at the CC chemokine receptor CCR4. Br J Pharmacol 166: 1774–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein RS, Ehlert FJ (2015). A kinetic model of GPCRs: analysis of G protein activity, occupancy, coupling and receptor‐state affinity constants. J Recept Signal Transduct 35: 269–283. [DOI] [PubMed] [Google Scholar]
- Urban JD, Clarke WP, von Zastrow M, Nichols DE, Kobilka B, Weinstein H et al (2007). Functional selectivity and classical concepts of quantitative pharmacology. J Pharmacol Exp Ther 320: 1–13. [DOI] [PubMed] [Google Scholar]
- van der Westhuizen ET, Breton B, Christopoulos A, Bouvier M (2014). Quantification of ligand bias for clinically relevant β2‐adrenergic receptor ligands: implications for drug taxonomy. Mol Pharmacol 85: 492–509. [DOI] [PubMed] [Google Scholar]
- Wajima T, Isbister GK, Duffull SB (2009). A comprehensive model for the humoral coagulation network in humans. Clin Pharmacol Ther 86: 290–298. [DOI] [PubMed] [Google Scholar]
- Weiss JM, Morgan PH, Lutz MW, Kenakin TP (1996). The cubic ternary complex receptor–occupancy model I. Model description. J Theor Biol 178: 151–167. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 log|MF| vs. log residual variance for operational model. A) all parameters estimated from operational model (Eq. 1) with data from functional assay; B) reduced operational model (Eq. 5) with data from functional assay. |MF|: the determinant of the Fisher Information Matrix. The criteria for claiming identifiability of a model: (i) log|MF| should have a continuous linear log–log relationship with the log of the random noise and (ii) |MF| should approach infinity as residual variance approaches zero.
Figure S2 The relative standard error of estimated parameters vs. τ for Eq. 8. In this study, a generic study design with sampling concentrations log (A) from −13 to −4, increment of 1, was adopted. A proportional measurement error with 10% coefficient of variation were assumed. KA was set to an arbitrary value, 10−8 mol L−1. R was defined as the ratio of τ and KA. The deterministic identifiability was assessed for each value of, ranging from 0.1 to 100. The left panel is for KA and the right panel is for R. The red dashed line indicates the 50% relative standard error, considered as the threshold for precise estimation.
Figure S3 log|MF| vs. log residual variance for general operational model (Eq. 2). A) all parameters estimated (E m , Basal, n,log (K A), log (R)); B) E m fixed; C) log (K A) fixed; D) log (R) fixed.
Figure S4 Concentration–response curves for cAMP formation showing pplss‐3HA‐hCB1 HEK signalling, on stimulation with 2.5 μM FSK and a panel of six agonists, following >16 h pretreatment in the presence of PTX. The data is fitted by Method IV.
Table S1 The estimation of transduction coefficient (log (R)) via Method IV.


