Population Pharmacokinetics of Finafloxacin in Healthy Volunteers and Patients with Complicated Urinary Tract Infections

ABSTRACT

Finafloxacin is a novel fluoroquinolone with increased antibacterial activity at acidic pH and reduced susceptibility to several resistance mechanisms. A phase II study revealed a good efficacy/safety profile in patients with complicated urinary tract infections (cUTIs), while the pharmacokinetics was characterized by highly variable concentration-versus-time profiles, suggesting the need for an elaborated pharmacokinetic model. Data from three clinical trials were evaluated: 127 healthy volunteers were dosed orally (n = 77) or intravenously (n = 50), and 139 patients with cUTI received finafloxacin intravenously. Plasma (2,824 samples from volunteers and 414 samples from patients) and urine (496 samples from volunteers and 135 samples patients) concentrations were quantified by liquid chromatography-tandem mass spectrometry (LC-MS/MS). NONMEM was used to build a population pharmacokinetic model, and pharmacokinetic/pharmacodynamic relationships were investigated via simulations and logistic regression. A two-compartment model with first-order elimination described the data best (central volume of distribution [V_c] and peripheral volume of distribution [V_p] of 47 liters [20%] and 43 liters [67%], respectively, and elimination clearance and intercompartmental clearance of 21 liters/h [54%] and 2.8 liters/h [57%], respectively [median bootstrap estimates {coefficients of variation}]). V_c increased with body surface area, and clearance was reduced in patients (−29%). Oral absorption was described best by parallel first- and zero-order processes (bioavailability of 75%). No pharmacodynamic surrogate parameter of clinical/microbiological outcome could be identified, which depended exclusively on the MIC of the causative pathogens. Despite the interindividual variability, the present data set does not support covariate-based dose adjustments. Based on the favorable safety and efficacy data, the clinical relevance of the observed variability appears to be limited. (This study has been registered at ClinicalTrials.gov under identifier NCT01928433.)

INTRODUCTION

Finafloxacin is a novel fluoroquinolone that exhibits enhanced antibacterial activity under acidic conditions (1) and in the presence of several fluoroquinolone resistance determinants when present alone or in combination (2). Because of the acidic environment prevailing in many infectious sites, the enhanced activity at lower pH may increase the efficacy of finafloxacin in the treatment of a number of bacterial infections (3). Complicated urinary tract infections are so far frequently being treated with expanded-spectrum fluoroquinolones, but the number of resistant strains is steadily increasing (4), and their activities decrease at an acidic pH (5), which emphasizes the need for novel antibacterial drugs. Two recent studies of finafloxacin, in which healthy volunteers received single and multiple oral (p.o.) (6) or intravenous (i.v.) (7) administrations, indicated a favorable safety profile but also moderate to high pharmacokinetic (PK) variability and rather complex absorption and/or distribution patterns. Specifically, a preliminary evaluation of pharmacokinetic data from studies II and III indicated that more than two compartments would be needed to describe concentration-time curves appropriately (A. Dalhoff, unpublished data). So far, it is not known whether these observations can be directly transferred to patients with, e.g., urinary tract infections and whether they are of any clinical relevance. The goal of this study was to develop a population pharmacokinetic model that appropriately integrates pharmacokinetic data from three clinical trials and thus enables descriptions of interindividual variability (IIV), the pharmacokinetic behavior of finafloxacin, and its relationship to covariates and pharmacodynamic (PD) target parameters.

RESULTS

Data.

A total of 266 subjects, with 77 healthy subjects receiving oral administrations (trial I), 50 healthy subjects receiving intravenous administrations (trial II), and 139 evaluable patients receiving intravenous administrations (trial III), were available for this evaluation. A total of 3,235 plasma samples (1,293 in trial I, 1,531 in trial II, and 414 in trial III) and 633 urine samples (496 from healthy volunteers and 135 from patients) were analyzed. A total of 145 urine samples collected during 5 collection intervals were available from 29 healthy subjects receiving single doses, and 351 urine samples collected during 11 collection intervals (0 to 12 h and 12 to 24 h on days 1 and 7 and 0 to 24 h on days 2 to 6, 8, and 9) were available from 32 healthy subjects receiving multiple doses. For a single subject receiving multiple doses, the last collection interval was missing. Urine samples were available from 52 patients (samples from 0 to 6 h after the third dose were available for all 52 patients, samples from 6 to 12 h were missing for three patients, and samples from 12 to 24 h were missing for 18 patients). Summary statistics and noncompartmental analyses of the data from healthy volunteers were reported previously (6, 7). For summary statistics and frequencies of covariates among patients, see Table 1. Weight, height, and age showed some intercorrelation (Pearson correlation coefficients of 0.38, 0.23, and −0.38 for weight/height, weight/age, and height/age, respectively). Information on microbiological, clinical, and combined outcomes was available for 115, 127, and 111 of 139 patients treated with finafloxacin, respectively. Successful microbiological, clinical, and combined outcomes were observed for 92, 108, and 89 of 139 patients, respectively. MICs were available for most patients (117 patients [84% of all patients treated with finafloxacin]) and ranged from ≤0.03 mg/liter to >32 mg/liter. A total of 48 out of 52 patients with urine measurements received comedications, of which 34 were previously identified to have a potential influence on renal finafloxacin excretion (see Table S1 in the supplemental material) (Dalhoff, unpublished). Finafloxacin concentrations in plasma and urine were quantified by liquid chromatography-tandem mass spectrometry (LC-MS/MS), with lower limits of quantification of 5 ng/ml in plasma and 100 ng/ml in urine; the absolute accuracy and precision for plasma (urine) measurements were <5.86% (6.50%) and 6.73% (5.93%), respectively.

TABLE 1.

Summary statistics of demographic data^a

Trial	No. of patients	Median wt (kg) (range)	Median ht (cm) (range)	Median age (yr) (range)	No. of male patients
I	77	75.3 (61–97.7)	176.7 (161–190)	42.5 (19–55)	71
II	50	76.5 (50.9–112.4)	174.5 (138–200)	41.5 (19–63)	42
III	139	73.5 (64–140)	164 (145–186)	61 (19–90)	21

^aSummary statistics of demographic data from healthy volunteers receiving oral (trial I) or intravenous (trial II) administrations and from patients receiving intravenous administrations (trial III) of finafloxacin. Medians and ranges (minimum to maximum) are presented.

Exploratory analysis.

Two implausible plasma concentrations were excluded from the analysis: one was most likely quantified from a blood sample taken from the same vein in which finafloxacin was administered, and one predose measurement was most likely confused with a postdose measurement, both of which resulted in extremely high concentrations that were not in line with other measurements from the respective patients. Concentrations that were below the quantification limit (BQL) were omitted since only ≤2.5% of all measurements were below the limit of quantification.

Population pharmacokinetic analysis. (i) Basic model.

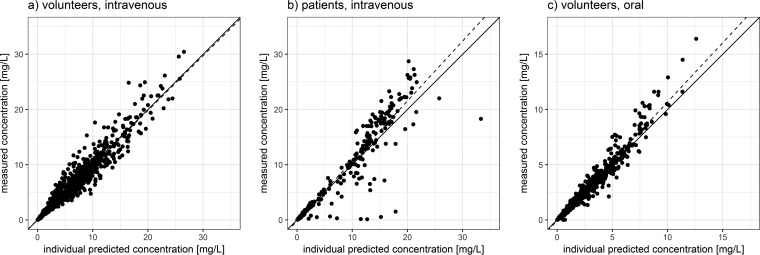
A model consisting of two compartments with linear elimination kinetics appropriately described the plasma concentration data from healthy volunteers receiving intravenous infusions (R² = 0.95) (Fig. 1a), although a slight misspecification with underpredictions of early concentrations was evident. Interindividual variabilities and interoccasional variabilities (IOVs) were highest for clearance, intercompartmental clearance (Q), and the peripheral volume of distribution (V_p) (coefficient of variation [CV] of ≥50%). Further increases in model complexity were not supported by the data since highly instable and implausible estimates were obtained when assuming nonlinear elimination or further compartments. Individual predicted-concentration-versus-measured-concentration plots and visual predictive checks (VPCs) (see Fig. S2 and S3 in the supplemental material) showed that the model provided a good description of the data; therefore, the two-compartment model was accepted for further analysis. Urine data from healthy volunteers receiving intravenous infusions, modeled by an output compartment capturing a fraction of the eliminated drug, could be described well by the model (R² = 0.92). Subsequently, the model was fitted to a joint data set comprising data from healthy subjects receiving intravenous infusions and patients. Obtained estimates for all parameters except for elimination clearance (CL) did not change relevantly (change of <10%) (Table 2). For elimination clearance, a decrease in the respective point estimate (23 liters/h to 19.4 liters/h) and an increase in the coefficient of variation (31% to 47%) were observed. The estimated fraction of finafloxacin excreted renally was distinctly lower and more variable in patients than in healthy volunteers. The resulting fits of patient data were appropriate (R² = 0.87 for patient plasma data) (Fig. 1b), while urine data from patients were not described well by the model (R² = 0.34), and approaches to handle the distinct differences in renal excretion between healthy volunteers and patients were not successful. This included especially the estimation of separate renal excretion parameters in patients and volunteers and the incorporation of information on concomitant medication.

FIG 1.

Plots of individual predicted versus measured plasma concentrations stratified by trial. Plots of individual predicted versus measured plasma concentrations of finafloxacin in healthy volunteers receiving intravenous administrations (a), patients receiving intravenous administrations (b), and healthy volunteers receiving oral administrations (c), as obtained from the final model. Solid line, unity line; dashed line, line of best fit.

TABLE 2.

Point estimates and coefficients of variation of a basic model fitted to intravenous data from healthy volunteers and healthy volunteers/patients^a

Parameter	Point estimate (coefficient of variation [%])
	Volunteers	Volunteers/patients
CL (liters/h)	23 (31)	19.4 (47)
Vc (liters)	52 (23)	49.8 (25)
Q (liters/h)	2.96 (41)	2.97 (42)
Vp (liters)	47.6 (57)	48.7 (58)

^aShown are point estimates (coefficients of variation) of clearance (CL), central volume of distribution (V_c), peripheral volume of distribution (V_p), and intercompartmental clearance (Q) obtained when fitting a two-compartment model solely to data from healthy volunteers receiving intravenous infusions or from healthy volunteers and patients. A distinct change was observed for CL only, with a point estimate reduction and an increase in the coefficient of variation by >10%.

(ii) Dose dependency of pharmacokinetic parameters.

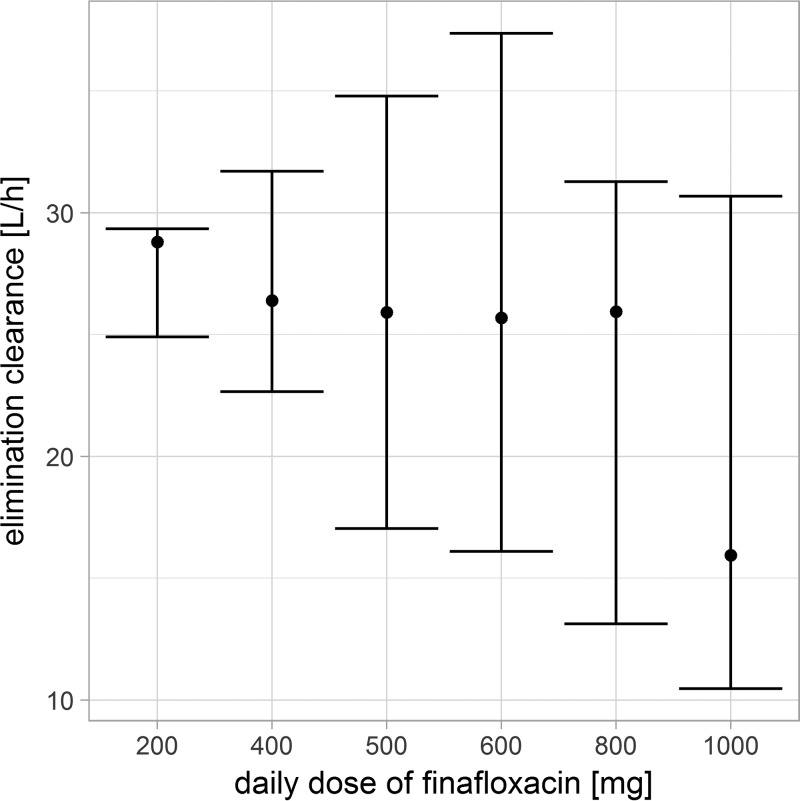
The evaluation of individual elimination clearances (empirical Bayes estimates) of healthy volunteers stratified by dose levels revealed a tendency toward diminished clearances at the highest dose of 1,000 mg (Fig. 2). Therefore, clearances were estimated separately for doses of 200 to 800 mg and a dose of 1,000 mg, which indicated a reduction in clearances from 24 liters/h at doses of 200 to 800 mg to 22 liters/h at a dose of 1,000 mg. Estimating clearances for a dose of 1,000 mg improved the model slightly (change in objective function value [dOFV] of −4.9 points), but further dose-specific clearance estimations as well as a functional relationship between dose and clearance were not supported by the data. To evaluate the hypothesis of saturable renal excretion, which might explain the dose dependency of clearance, models with both a dose-constant first-order elimination and a saturable (i.e., Michaelis-Menten kinetics) elimination route in parallel were tested. However, the possible dose dependency was not explained by such a saturable elimination route.

FIG 2.

Empirical Bayes estimates of elimination clearances stratified by the dose level of finafloxacin. Empirical Bayes estimates of elimination clearances are stratified by the dose (200 to 1,000 mg/day) from healthy volunteers receiving intravenous infusions of finafloxacin. Dots, medians; bars, 90% intervals. A trend toward diminished clearances can be seen at the highest dose of 1,000 mg.

(iii) Covariate model.

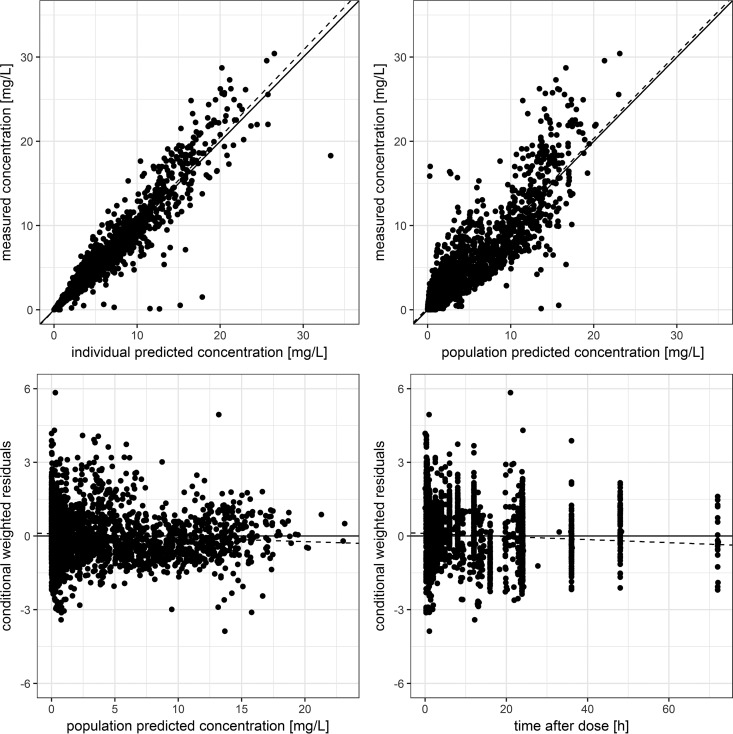
A basic covariate model was identified based on data from volunteers and patients receiving intravenous infusions. The central volume of distribution (V_c), V_p, and Q were found to be related to total body weight (TBW) (each dOFV of less than −6.63). The inclusion of lean body mass (LBM) was not significantly better than the inclusion of TBW, while body surface area (BSA) provided a significant decrease in the OFV when used as a covariate on V_c compared to TBW (dOFV of −15.3 for BSA versus TBW). Therefore, V_c was scaled with BSA, while V_p and Q were scaled with TBW. Subsequently, CL was found to be related to gender (dOFV of −14) and patient status (binary covariate indicating whether a subject was a healthy volunteer or a patient [dOFV of −22]). No significant relationship between CL and TBW, LBM, or BSA was found. Since gender and patient status were related (i.e., most of the patients were female, and patient status was linked to a more distinct decrease in the OFV), patient status was primarily chosen for inclusion. The additional inclusion of gender was then no longer supported. The final forward model comprised the effect of TBW on V_p and Q, BSA on V_c, and patient status on CL. The backward elimination step indicated that TBW covariate relationships could be dropped without increasing the OFV significantly (increase in the OFV of ≤6.64). Therefore, the final covariate model comprised the effect of BSA on V_c and patient status on CL. Although changes in the OFV were significant, BSA and patient status explained only a small amount of variability (absolute reductions in the CV for CL and V_c of 4.7% and 7.4%, respectively). The resulting covariate equation for the central volume of distribution is shown in equation 1. For bootstrap estimates of the resulting final model in healthy volunteers and patients receiving intravenous infusions of finafloxacin, see Table 3. A goodness-of-fit (GOF) plot of the final model including covariate relationships is shown in Fig. 3 and in Fig. S1 in the supplemental material. For VPCs, see Fig. S2 to S5 in the supplemental material.

$$V_{\text{c}}=46.85\times {\left(\frac{\text{BSA}}{1.8251}\right)}^{1.5}$$ (1)

TABLE 3.

Final bootstrap parameter estimates of pharmacokinetic and covariate parameters for plasma and urine data^a

Parameter	Median value	95% CI	IIV (%)	IOV (%)
Intravenous data
CL (liters/h)	20.9	18.5, 23.4	54	8
Vc (liters)	46.9	45.1, 49.0	20	8
Q (liters/h)	2.80	2.47, 3.17	57	18
Vp (liters)	43.1	37.2, 49.8	67	22
BSA on Vc	1.50	0.96, 1.96
Patient status on CL	−0.29	−0.38, −0.18
FER1	0.40	0.38, 0.43	19
FER2	0.21	0.17, 0.26	62
Additive RUV, plasma	0.001	0.001, 0.002
Proportional RUV, plasma	0.24	0.22, 0.26
Additive RUV, urine	0.001	0.001, 0.154
Proportional RUV, urine	0.33	0.29, 0.36
Oral data
F	0.75	0.59, 0.79	33	32
f1st	0.77	0.77, 0.95	39	36
Ka (h−1)	6.61	3.19, 6.61	33	168
LAG1 (h)	0.22	0.14, 0.24	30	28
D0 (h)	7.77	7.39, 12.17	31	31
LAG2 (h)	0.54	0.41, 1.13	33	32
Proportional RUV	0.14	0.13, 0.24
Additive RUV	0.03	0.00, 0.03

^aMedian estimates as well as 95% confidence intervals (CIs) of population pharmacokinetic parameters from bootstrap statistics (n = 1,000) based on intravenous (healthy volunteers and patients) and oral (healthy volunteers) data. Shown are percent coefficients of variation for interindividual variability (IIV) and interoccasion variability (IOV). BSA, body surface area (given parameter estimates are exponents of BSA values normalized to a standard individual with a weight of 70 kg and a height of 172 cm); FER, fraction of finafloxacin excreted unchanged renally in healthy volunteers (FER₁) and patients (FER₂); F, absolute oral bioavailability; f_1st, fraction of drug absorbed by a first-order process; K_a, absorption rate constant for a first-order process; LAG₁, lag time for a first-order process; D₀, duration of a zero-order process; LAG₂, lag time of a zero-order process; RUV, residual unexplained variability given a combined additive- and proportional-error model.

FIG 3.

Goodness-of-fit plots of the final model incorporating the whole data set. Shown are goodness-of-fit plots of the final model incorporating plasma data from healthy volunteers receiving oral or intravenous administrations and from patients receiving intravenous administrations. The top row shows individual and population predicted versus measured plasma concentrations; the bottom row shows population predicted concentrations and the time after dose versus conditional weighted residuals. Solid lines indicate the unity line (top) or the line of zero residuals (bottom); dashed lines indicate lines of best fit.

Since patients received higher doses of finafloxacin (800 mg), a dose-dependent decrease in clearance could have contributed to the possibly reduced clearance in patients. Therefore, the separation of a dose-dependent from a study-dependent change in clearance was evaluated by introducing a separate clearance population estimate for higher doses of at least 800 mg. This was not supported by the data since no model improvements could be observed.

(iv) Oral absorption model.

Upon the inclusion of data from healthy volunteers receiving oral administrations of finafloxacin, parameter estimation became unstable, and basic pharmacokinetic parameters, which do not depend relevantly on the route of administration, changed clearly. This was attributed to the highly variable absorption pattern, which could not be described well by a first-order process in many subjects, and the resulting instability of the model. Therefore, a sequential approach was chosen: median bootstrap estimates of clearances, volumes of distribution, and respective variability estimates, obtained from the previously developed model of intravenous data, were used, and oral absorption parameters were estimated in a subsequent step. A first-order absorption model was not capable of describing the characteristics of the absorption process appropriately, while a mixed-order absorption model with lag times provided reasonable parameter estimates (see Table 3 for bootstrap estimates) and appropriately described the concentration-time profiles following oral administrations (R² = 0.97) (Fig. 1c). A VPC confirmed the aptness of the resulting model (see Fig. S6 and S7 in the supplemental material).

(v) Pharmacokinetic parameters at steady state.

Area under the concentration-time curve (AUC) values from Monte Carlo simulations were 41% higher for patients than for healthy volunteers, which is a consequence of the reduced clearance in patients (Table 4). The observed increase in the plasma half-life (T_1/2) in patients of 30% is also a direct consequence of the reduced elimination clearance. Maximum concentrations (C_max), the times at which C_max was reached (T_max), and terminal elimination half-lives differed only marginally (≤14%).

TABLE 4.

Pharmacokinetic steady-state plasma parameters from simulated intravenous administration of 800 mg finafloxacin per day^a

Parameter	Median value for trial (95% prediction interval)
	II	III
AUC (mg · h/liter)	38 (15–96)	54 (22–134)
AUCW (mg · h/liter)	39 (15–101)	53 (19–143)
Cmax (mg/liter)	14 (9–23)	16 (10–27)
Tmax (h)	1.12 (1.01–1.37)	1.13 (1.01–1.45)
T1/2 (P) (h)	1.66 (0.67–4.0)	2.15 (0.87–5.27)
T1/2 (T) (h)	12.5 (6.21–25.2)	13.3 (6.5–27.1)

^aShown are plasma predictions (medians and 95% prediction intervals) of the AUC normalized to a body weight of 75 kg (AUC^W), the maximum attained concentration (C_max), the time at which the maximum concentration was reached (T_max), as well as plasma (P) and terminal (T) elimination-half-lives (T_1/2) given a simulated intravenous administration of 800 mg finafloxacin per day at steady state. Presented values were calculated via a Monte Carlo simulation using covariate data from all healthy volunteers from trial II and data from all patients from trial III.

Pharmacodynamic analysis.

In the simulated patient population, median AUCs of 31 mg · h/liter (95% interval, 12 to 78 mg · h/liter) for oral administration and 54 mg · h/liter (95% interval, 22 to 133 mg · h/liter) for intravenous administration were attained. Interoccasional variability contributed less variability, with median AUCs of 31 mg · h/liter (95% interval, 23 to 39 mg · h/liter) for oral infusions and 55 mg · h/liter (95% interval, 48 to 63 mg · h/liter) for a typical subject receiving intravenous short-duration infusions. Simulations were not conducted for urine concentrations since no appropriate model for urinary excretion in patients could be identified. Since BSA was a covariate on the volume of distribution only, no relationship between the AUC (median and 95% interval) and BSA was to be expected. This was confirmed by the simulations.

A significant relationship between the time that the concentration exceeded the MIC (T>MIC) and primary clinical (P = 0.02), microbiological (P < 0.01), and combined (P < 0.01) outcomes was identified in the logistic regression analysis (see Table S2 in the supplemental material). For the AUC/MIC ratio, the typical pharmacodynamic surrogate parameter for fluoroquinolones, no relationship could be identified (P ≥ 0.53). Sensitivities and specificities based on areas under the receiver operating characteristic (ROC) curves were low (83 to 85% and 50 to 67%, respectively) (Table S3), and statistical significance between T>MIC and all outcome parameters vanished when subjects with a T>MIC of 0% were omitted from the analysis. This indicated that the model merely classified subjects with less-susceptible pathogens, who are probably prone to therapeutic failure. Logistic regression on data from patients with a T>MIC that was neither 0% nor 100% was not feasible since this group consisted of only 23 patients.

DISCUSSION

A two-compartment model with mixed-order oral absorption and linear elimination appropriately integrated data across three clinical trials, thus being able to describe interindividual variability and the previously reported complex pharmacokinetic behavior of finafloxacin.

The previously reported moderate to high interindividual variability in healthy subjects could be confirmed and was also observed in patients, which might be of clinical significance for treatment with finafloxacin. Several findings may have contributed to the observed distribution pattern, among which were especially the distinct inter- and intraindividual pharmacokinetic variabilities, the tendency toward diminished clearances at a dose of 1,000 mg, and the variable oral absorption pattern. Owing to the reduced elimination clearance, systemic exposure was higher in patients than in healthy volunteers. This might be beneficial for the attainment of sufficient plasma levels for the treatment of bacterial infections but also demands further evaluations with regard to side effects. The latter is attenuated by the favorable safety and tolerability results of trial III (MerLion Pharmaceuticals GmbH).

The observed reduced and variable urinary recovery in urinary tract infection (UTI) patients is in accordance with data from numerous previously reported studies. Reduced urinary recovery rates have been reported, for example, for norfloxacin, ofloxacin, enoxacin, and ciprofloxacin, which were linked to considerably higher serum concentrations in UTI patients than in healthy volunteers (8–12). Reduced urinary recovery in UTI patients may be due to several factors. First, urine measurements are principally error prone and might not have been complete. Although some efforts have been made to increase the validity of urine collections and measurements by introducing, e.g., para-aminobenzoate as a marker for collection completeness (13, 14), it seems noteworthy that related studies showed that up to 50% of urine collections were not complete. Such incomplete collections might have contributed to the impaired estimation of renal excretion in this study. Second, comedications might have affected renal excretion. Comedications of nonsteroidal anti-inflammatory drugs (NSAIDs), statins, and diuretics are known to impair renal tubular secretion mechanisms. Previous finafloxacin PK studies in healthy volunteers revealed that renal clearance exceeded typical glomerular filtration rates, indicating that finafloxacin is also excreted by tubular secretion (7). Therefore, it appears likely that the renal excretion of finafloxacin was reduced by an inhibition of tubular secretion. NSAIDs are additionally known to reduce glomerular filtration, which might have added to the reduced tubular secretion. Especially for paracetamol, acute and chronic renal injuries have been described (15, 16). Likewise, metamizole may cause acute renal injury (17). However, this hypothesis could not be verified in trial III due to the small data set, which demands further investigations. Third, an age-related reduction of renal function might have contributed to reduced urinary recovery, which has been reported for other fluoroquinolones (8–12). All patients in these studies were more than 60 years old. However, it is unlikely that one factor alone caused the reduced urinary recovery of fluoroquinolones in UTI patients.

As indicated by the Monte Carlo simulations, the influence of interindividual variability is far more pronounced than that of interoccasion variability, which is an advantage in terms of stable target attainment over the course of therapy that lasts for several days. Limited variability in target attainment was also observed for oral administrations despite the high interindividual variability in the respective pharmacokinetic parameters. The PK/PD parameter that would predict the efficacy of finafloxacin best is currently not known, and additional in vitro and/or in vivo studies need to be conducted to this end. The typical target parameter for fluoroquinolones is the AUC/MIC ratio (18). Because the AUC/MIC ratio at steady state depends only on dose, bioavailability, clearance, and MIC, bioavailability should be the main parameter related to the absorption model that is of interest, which is in line with the simulation results. The bioavailability of finafloxacin was estimated to be high and with low to moderate variability, which is expected to be beneficial in terms of transitions from i.v. to p.o. administrations, which may be linked to a reduced need for hospitalization and, consequently, reduced costs and resistance development (19–22). It remains to be evaluated whether the simulation results reflect male patients well, since most patients in trial III were female.

It must be emphasized that this assessment might change remarkably if T>MIC or the C_max/MIC ratio would turn out to be the appropriate PK/PD parameter for finafloxacin. Indeed, only T>MIC was linked to clinical and microbiological outcomes in our model. This result is remarkable at first glance, but it is most probably an artifact. According to the ROC analysis, the resulting model had poor predictive abilities, and it was driven exclusively by MIC values of pathogens that were resistant to finafloxacin. For such pathogens, the T>MIC inherently drops to zero, since the respective MICs of ≥32 mg/liter were not exceeded in any patient. Therefore, the T>MIC becomes a marker for resistant pathogens. This reasoning is supported by the reevaluation of the logistic model without subjects who reached a T>MIC of 0%, in which no significant PK/PD parameter was identified. An additional clue might be that mean T>MIC values for subjects with therapeutic failure versus success did not differ significantly after the exclusion of subjects with a T>MIC value of 0%. To appropriately identify PK/PD relationships for finafloxacin in patients with cUTI, a data set with a higher number of subjects and with a larger number of patients with intermediate MICs is probably needed since the present data set was imbalanced: the majority of treatments was successful. It would also have been interesting to investigate relationships between urine concentrations of finafloxacin and therapeutic outcomes since bacterial killing in UTIs might also depend on antibiotic concentrations in urine (23–25). Unfortunately, this was not feasible because the model of renal excretion turned out to be inappropriate to describe urinary excretion in patients. Thus, the main conclusion on PK/PD relationships is that the data set does not support outcome probability modeling.

In summary, pharmacokinetic parameters of finafloxacin have high interindividual variability. However, the present data set does not support covariate-based dose adjustments, and the clinical relevance of the observed variability appears to be limited according to the favorable safety and efficacy data. Further evaluations of PK/PD relationships are needed.

MATERIALS AND METHODS

Study design.

The investigated data originated from two clinical trials of finafloxacin in healthy subjects, which were described previously (trials I and II) (6, 7), and a clinical trial of finafloxacin in hospitalized patients with complicated urinary tract infections or acute complicated or uncomplicated pyelonephritis (trial III). Healthy volunteers received single or multiple ascending doses of finafloxacin either orally (25 to 1,000 mg per day) (trial I) or by intravenous infusions (200 to 1,000 mg per day) (trial II), with plasma as well as urine samples being taken by using a dense sampling scheme. In trial II (trial I), 1,531 plasma (1,293 plasma) and 496 urine samples were taken, and finafloxacin concentrations were quantified. More information on these trials was reported previously (6, 7). In trial III, subjects were assigned at random to treatment with intravenous short-duration infusions (duration of 60 min) of 800 mg finafloxacin for 5 or 10 days or of ciprofloxacin for 10 days. Per protocol, all patients received a once-daily, intravenous, short-duration infusion (duration of 60 min) of finafloxacin or ciprofloxacin for at least 3 days, followed by orally administered finafloxacin or ciprofloxacin for up to 5 or 10 days, respectively. A total of 151 patients received at least one dose of finafloxacin. Of these patients, data for 139 subjects who provided valid pharmacokinetic samples, i.e., who received at least three consecutive infusions of finafloxacin and from whom blood samples were drawn correctly according to the study protocol, were included in the present analysis. After the second infusion, three venous blood samples were drawn from each patient. The first sample was collected right before the administration of the third dose, and the second sample was collected at the end of the third infusion. A third sample was collected within 23 h after the third infusion. From 52 randomly selected subjects receiving finafloxacin, urine was collected in three fractions (0 to 6, 6 to 12, and 12 to 24 h) after the third dose. Body weight, height, sex, age, concomitant medications, and the clinical and microbiological outcomes were recorded for all patients. Outcome data were binary, i.e., indicating success or failure after treatment with finafloxacin or ciprofloxacin. All patients received information on the investigated drug, the conduct of the study, and potential risks and gave written informed consent. The studies were conducted in accordance with guidelines on good clinical practice, the current revision of the Declaration of Helsinki, and International Conference on Harmonization (ICH) guidelines. The investigation was approved by the Ethics Committee of the Justus Liebig University, Giessen, Germany (ClinicalTrials.gov identifier NCT01928433).

Bioanalytics.

LC-MS/MS analyses were carried out by using a Shimadzu chromatographic system coupled to an API 4000 mass spectrometer (Ab Sciex) by electrospray ionization in the positive mode and a reverse-phase column (LichroCart Purospher RP-18, 3 by 125 mm). Solvents used were acetonitrile-water with 0.1% formic acid. Plasma samples were supplemented with methanol and then extracted with acetonitrile–0.1% formic acid, and urine samples were diluted with water–0.1% formic acid before analysis.

Population pharmacokinetic analysis.

Time-concentration profiles of plasma and urine data were inspected visually to identify implausible data prior to the population pharmacokinetic analysis. BQL concentrations were omitted if the number of such measurements was sufficiently low (i.e., <5% of all concentration measurements). Alternatively, standard methods to treat BQL data, such as the M3 method (26), were evaluated. R software (27) was used for data set preparation and visualization. The population pharmacokinetic analysis was carried out by using NONMEM 7.3 nonlinear mixed-effects modeling software (Icon Development Solutions, Ellicott City, MD, USA) in conjunction with Perl-speaks-NONMEM (28). The first-order conditional estimation with interaction (FOCE-I) method was used for parameter estimation. The population pharmacokinetic model was developed empirically, starting with one compartment and linear kinetics. In each modeling step, the likelihood ratio test (LRT), with a drop in the objective function value of at least 3.84 points being considered statistically significant (P = 0.05); standard GOF plots; and VPCs (29) were used to judge changes made to the structural and stochastic model. Final parameters were assessed via bootstrap statistics with 1,000 samples. The modeling process started with data from healthy volunteers receiving intravenous infusions, which constituted a rich data set with dense sampling, followed by modeling the sparse patient data and oral absorption of healthy volunteers. This approach was chosen since patient data were sparse and therefore could not be modeled without the support of rich data from healthy volunteers. For orally administered finafloxacin, a first-order absorption model was considered and extended to more-complex absorption models empirically. Urine data were incorporated into the model by estimating the fraction of the eliminated drug being renally excreted unchanged. Drug amounts in urine were then modeled by estimating the cumulative amount of finafloxacin excreted during the respective collection interval. For covariate modeling, a manual stepwise approach was chosen. Body weight and patient status, i.e., whether a subject was a healthy volunteer or a patient, were defined as the main covariates of interest. The former was selected since pharmacokinetic parameters often scale with body weight (30), and the latter was chosen since differences between patients and volunteers were of special interest. Body surface area (31) and lean body mass (32) were investigated as alternatives to total body weight. In cases where eta shrinkage was not >20% (33), covariates were screened by visual inspection of plots of empirical Bayes estimates of individual pharmacokinetic parameters versus potential covariates. Final covariate inclusion was based on the LRT and decreases in estimated interindividual variability. After the inclusion of all significant covariates, a backward elimination step was used to eliminate covariates that were not significant (P ≤ 0.01, i.e., a change in the objective function of at least 6.64 points) in the final model. For the final covariate model evaluation, 95% confidence intervals from bootstrap statistics were assessed.

The stochastic part of the model consisted of interindividual and interoccasional variability terms for all estimated pharmacokinetic parameters assuming lognormal distributions (see equation 2). The covariance of individual parameter estimates was estimated if computationally feasible. In subjects receiving multiple doses, each administration with at least two related concentration measurements was defined as a new occasion. Pharmacokinetic parameters were therefore defined as follows, with PK_i,j representing individual pharmacokinetic parameter i of subject j, θ_pop being the population estimate, and IIV and IOV being the individual and occasion-specific deviations from the population estimate, respectively:

$${\text{PK}}_{i,j}={\text{θ}}_{pop}\times e^{\text{IIV}\hspace{0.17em}+\hspace{0.17em}\text{IOV}}$$ (2)

A Monte Carlo simulation with 2,000 samples per subject was conducted for subjects receiving short-duration (duration of infusion of 60 min) intravenous infusions of 800 mg finafloxacin per day at steady state. Covariate characteristics from the volunteers and patients from trials II and III were used, and concentration-time profiles were simulated by random sampling from lognormal distributions of pharmacokinetic parameters based on median bootstrap estimates from the population pharmacokinetic model. Distributions were truncated by omitting samples drawn from the upper/lower 1% to avoid unreasonable pharmacokinetic parameters. AUC, C_max, T_max, as well as plasma and terminal T_1/2 values were calculated from this simulation. AUCs were additionally normalized to a standard body weight of 75 kg (AUC^W). Plasma half-lives were defined as the ratios of CLs to central volumes of distribution. Terminal elimination half-lives were equal to plasma half-lives in the case of a one-compartment model and were calculated from microrate constants in the case of a two-compartment model with linear elimination (34).

Pharmacodynamic analysis.

A main target of interest was the AUC since it is a valid predictor of treatment efficacy for most fluoroquinolones (35). Therefore, AUCs from the above-described Monte Carlo simulation were evaluated. To contrast the potential impacts of interindividual versus interoccasional variabilities on target attainment, simulations were additionally conducted by omitting IIV and simulating concentration-time profiles over a time course of 2,000 days with daily random variability. This long time frame was chosen to approximate the distribution of AUCs between occasions, which provides insight into the stability of target attainment over a treatment course of several days. Additionally, a pharmacodynamic model to predict the probability of successful microbiological and/or clinical outcomes was investigated via logistic regression. Available binary outcome data, indicating clinical and/or microbiological success, were visualized with regard to individual AUC/MIC ratios, T>MIC, and C_max/MIC ratios from urine and plasma data estimated for a time window of 24 h after the third administration of finafloxacin using the population pharmacokinetic model. For low (≤0.03 mg/liter) (36 patients) and high (≥32 mg/liter) (11 patients) MIC values, no specific MIC value was available. Either the respective patients were omitted or the MIC values were replaced by a value of 0.03 or 32 mg/liter. Both approaches were conducted in parallel, and results were compared to avoid the introduction of bias due to the censored data. The statistical significance of individual parameter inclusion in a logistic regression model was investigated, and ROC curves were used to assess the predictive capabilities of the resulting model (36). Parameter thresholds for outcome classification were determined by using the Youden index (37).