Ligand Binding Pathways and Conformational Transitions of the HIV Protease

Abstract

It is important to determine the binding pathways and mechanisms of ligand molecules to target proteins to effectively design therapeutic drugs. Molecular dynamics (MD) is a promising computational tool that allows us to simulate protein–drug binding at an atomistic level. However, the gap between the time scales of current simulations and those of many drug binding processes has limited the usage of conventional MD, which has been reflected in studies of the HIV protease. Here, we have applied a robust enhanced simulation method, Gaussian accelerated molecular dynamics (GaMD), to sample binding pathways of the XK263 ligand and associated protein conformational changes in the HIV protease. During two of 10 independent GaMD simulations performed over 500–2500 ns, the ligand was observed to successfully bind to the protein active site. Although GaMD-derived free energy profiles were not fully converged because of insufficient sampling of the complex system, the simulations still allowed us to identify relatively low-energy intermediate conformational states during binding of the ligand to the HIV protease. Relative to the X-ray crystal structure, the XK263 ligand reached a minimum root-mean-square deviation (RMSD) of 2.26 Å during 2.5 μs of GaMD simulation. In comparison, the ligand RMSD reached a minimum of only ~5.73 Å during an earlier 14 μs conventional MD simulation. This work highlights the enhanced sampling power of the GaMD approach and demonstrates its wide applicability to studies of drug–receptor interactions for the HIV protease and by extension many other target proteins.

Graphical abstract

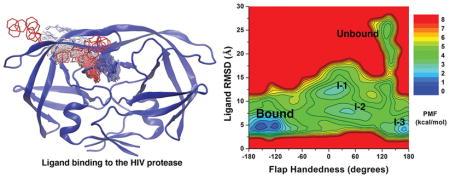
Understanding the binding pathways and mechanisms of small molecule ligands to target proteins is important for the discovery and development of effective drugs.^1–3 The HIV protease is a retroviral aspartyl protease that plays a crucial role in the HIV life cycle.⁴ The protease cleaves synthesized polyproteins, e.g., Gag and Gag-Pol, to create protein subunits of an infectious mature HIV.⁵ Therefore, the HIV protease has served as one of the major drug targets for the treatment of AIDS. Numerous X-ray crystal structures of the HIV protease have been determined over the past 30 years.⁶ More than 100 inhibitors that interfere with the protein functions have been identified.^7,8 Structural dynamics of the protease in the ligand-free (apo) and ligand-bound (holo) forms have also been extensively studied.^9–11 However, the mechanisms of ligand binding and the correlations with protein conformational changes remain poorly understood.

The structure of HIV protease is a homodimer with C₂ symmetry. Two glycine-rich loops, called “flaps”, which are highly dynamic, play an integral role in gating access of the ligands to the active site (Figure 1A).⁶ Three major conformations of the flaps were identified: “open”, “semi-open”, and “closed”. Both experimental and computational studies suggested that the apoprotein predominantly adopts the “semi-open” conformation, while the holoprotein exhibits the “closed” conformation.^12–14 The orientation of the flaps is defined as handedness. There are two handedness states, semi-open and closed, which are correlated with the apo and holo forms of the protein, respectively.^11,15 Because the flap conformation and handedness of the HIV protease are distinct between the apo-and holoprotein forms, large-scale conformational transitions of the protein are expected during ligand binding. In addition, we chose XK263 as a sampling ligand. In particular, the cyclic urea compound XK263 has been identified as a small, fast, and tight binder of the HIV protease with high hydrophobicity.¹⁶ The k_on and K_d of XK263 are ~10⁹ M⁻¹ s⁻¹ and ~10⁻⁹ M (approximately −11 kcal/mol), respectively.¹⁷

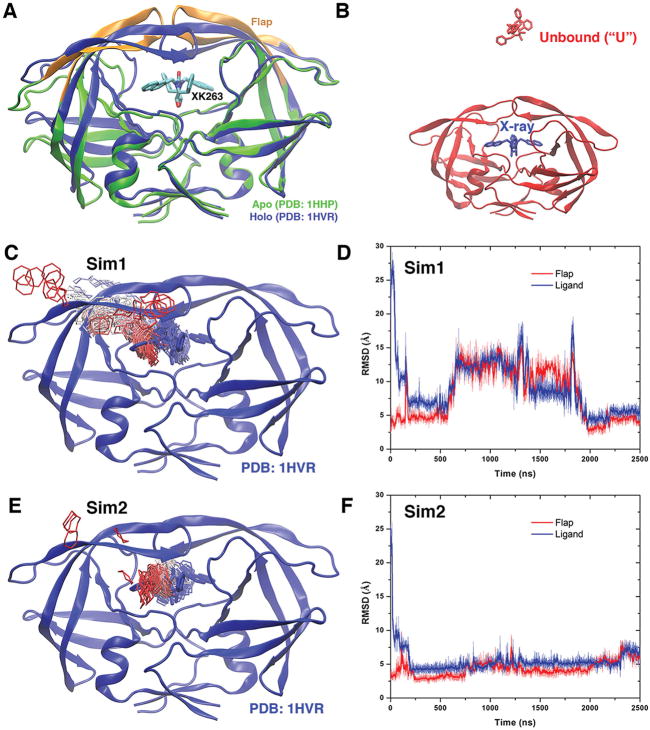
Figure 1.

(A) X-ray crystal structures of the HIV protease in the apo form (Protein Data Bank entry 1HHP, green) and holo form that is bound by the XK263 ligand molecule (Protein Data Bank entry 1HVR, blue). The ligand is shown as sticks and the protein as ribbons. Protein residues Lys43–Tyr59 in the flaps of two protein monomers are colored orange. (B) Simulation starting structure of the HIV protease in which the ligand molecule (red sticks) is placed ~20 Å from the protein surface in the unbound (“U”) state. A virtual ligand molecule of the X-ray conformation is colored blue for reference. (C) During the “Sim1” GaMD trajectory, the XK263 ligand molecule binds to the active site of the HIV protease within 2500 ns, for which the center ring of XK263 is represented by lines and colored by simulation time in a red–white–blue (RWB) color scale. The 1HVR X-ray conformation is colored blue for reference. (D) Root-mean-square deviations (RMSDs) of the ligand molecule and protein flaps relative to the 1HVR X-ray conformation are plotted for “Sim1”. Thick lines depict the running average over 5 ns time windows. (E and F) Ligand binding pathway and ligand and flap RMSDs obtained from the “Sim2” GaMD trajectory, respectively. Ligand pathways and RMSDs of the ligand molecule and protein flaps are presented in Figure S1 for the other eight GaMD simulations, during which the ligand minimum RMSD is >3 Å (Table 1).

Because ligand binding to proteins typically occurs on microsecond to millisecond time scales, Brownian dynamics simulations with coarse-grained models have been widely applied in computational studies.^18,19 However, this model has not been able to capture ligand binding and protein conformational changes at the atomistic level. Recently, remarkable advances in both available computational power and the development of the underlying techniques required to make effective use of new technologies offering this computational power have enabled all-atom molecular dynamics (MD) simulations of protein–ligand association processes.^20–25 MD simulations utilizing these technologies have been able to successfully capture the ligand binding processes that start from initial diffusion in the solvent to entry into the binding pocket and finally binding to the target site of the protein kinases and G-protein-coupled receptors (GPCRs).^20,21,26

Conventional MD (cMD) simulations have also been applied to study association of the ligand to the HIV protease, which have shown that switches of the hydrogen bonds and different chemical properties of the ligands play important roles in the ligand binding process.^16,27 However, even a 14 μs cMD simulation could not reproduce the final bound conformation of XK263.¹⁶ Compared with the X-ray crystal structure, the ligand reached a minimum root-mean-square deviation (RMSD) of 5.73 Å. The deficiency may result from both the lack of effective sampling power and the short time scale, from a biological perspective, of the cMD simulation. Moreover, the insufficient sampling precludes free energy calculations of the ligand binding intermediate states. Therefore, enhanced sampling is needed to obtain a more complete picture of the protein–ligand binding process.

To achieve both unconstrained enhanced sampling and energetic reweighting for free energy calculations of large biomolecules like proteins, Gaussian accelerated MD (GaMD) has been developed by applying a harmonic boost potential to smooth the biomolecular potential energy surface.²⁵ GaMD greatly reduces the energy barriers and accelerates conformational transitions and ligand binding by orders of magnitude.^22,28,29 Moreover, because the boost potential follows a Gaussian distribution, the original free energy profiles of biomolecules can be recovered through a cumulant expansion to the second order.²⁵ GaMD solves the energetic reweighting issue as encountered in the previous accelerated MD (aMD) method.³⁰ It allows us to quantitatively characterize conformational changes in complex biomolecules, including the fast-folding proteins,^25,31 GPCRs,²⁸ and CRISPR-Cas9 (clustered regularly interspaced short palindromic repeats-CRISPR-associated protein 9).²⁹ Compared with other enhanced sampling methods such as metadynamics³² and adaptive biasing force (ABF),³³ GaMD does not require predefined collective variables, which is advantageous for studying, among other things, the complex protein–ligand binding process.²⁵

In this study, GaMD was applied to simulate ligand binding to the HIV protease. Microsecond-time-scale GaMD simulations provided significantly improved sampling compared with that of the cMD simulations. The entire pathways for association of XK263 with the HIV protease were successfully simulated, and several key intermediate states were also identified during ligand binding using GaMD. Correlations between the ligand motions and conformational changes of the HIV protease were further examined. Although GaMD-derived free energy profiles were not fully converged because of insufficient sampling of the complex system, the simulations still allowed us to characterize key ligand binding intermediates and overall protein structural dynamics.

METHODS

Gaussian Accelerated Molecular Dynamics

Gaussian accelerated molecular dynamics (GaMD) enhances the conformational sampling of biomolecules by adding a harmonic boost potential to reduce the system energy barriers. Details of the method have been described in previous studies,^25,31 and a brief summary is provided here. When system potential V(r) is lower than a reference energy E, the modified potential V*(r) of the system is calculated as

$$\begin{gathered} V\ast (\mathbf{r})=V(\mathbf{r})+\mathrm{\Delta }V(\mathbf{r}) \\ \mathrm{\Delta }V(\mathbf{r})=\{\begin{array}{cc}\frac{1}{2}k{[E-V(\mathbf{r})]}^2& V(\mathbf{r})<E\\ 0& V(\mathbf{r})\ge E\end{array} \end{gathered}$$ (1)

where k is the harmonic force constant. The two adjustable parameters E and k can be determined on the basis of three enhanced sampling principles.²⁵ The reference energy needs to be set in the following range:

$$V_{max}\le E\le V_{min}+\frac{1}{k}$$ (2)

where V_min and V_max are the system minimum and maximum potential energies, respectively. To ensure that eq 2 is valid, k has to satisfy the equation k ≤ 1/(V_max − V_min). Let us define k ≡ k₀[1/(V_max − V_min)], then 0 < k₀ ≤ 1. The standard deviation of ΔV needs to be small enough (i.e., narrow distribution) to ensure proper energetic reweighting:³⁴ σ_ΔV = k(E − V_avg)σ_V ≤ σ₀, where V_avg and σ_V are the average and standard deviation of the system potential energies, respectively, and σ_ΔV is the standard deviation of ΔV with σ₀ as a user-specified upper limit (e.g., 10k_BT) for proper reweighting. When E is set to the lower bound E = V_max according to eq 2, k₀ can be calculated as

$$k_0=min(1.0,k_0^{\prime })=min\left(1.0,\frac{{\sigma }_0}{{\sigma }_V}\times \frac{V_{max}-V_{min}}{V_{max}-V_{\text{avg}}}\right)$$ (3)

Alternatively, when the threshold energy E is set to its upper bound E = V_min + 1/k, k₀ is set to

$$k_0=k_0^{″}\equiv \left(1-\frac{{\sigma }_0}{{\sigma }_V}\right)\frac{V_{max}-V_{min}}{V_{\text{avg}}-V_{\text{avg}}}$$ (4)

if $k_0^{″}$ is found to be between 0 and 1. Otherwise, k₀ is calculated using eq 3.

For energetic reweighting of GaMD simulations, the probability distribution along a selected reaction coordinate A(r) is written as p*(A), where r denotes the atomic positions {r₁, …, r_N}. Given the boost potential ΔV(r) of each frame, p*(A) can be reweighted to recover canonical ensemble distribution, p(A), as

$$p(A_j)=p\ast (A_j)\frac{{\langle {\mathrm{e}}^{\beta \mathrm{\Delta }V(\mathbf{r})}\rangle }_j}{{\sum }_{i=1}^M{\langle p\ast (A_i){\mathrm{e}}^{\beta \mathrm{\Delta }V(\mathbf{r})}\rangle }_i},j=1,\dots ,M$$ (5)

where M is the number of bins, β = k_BT, and 〈e^βΔV(r)〈_j is the ensemble-averaged Boltzmann factor of ΔV(r) for simulation frames found in the jth bin. To reduce the energetic noise, the ensemble-averaged reweighting factor can be approximated using cumulant expansion:^35,36

$$\langle {\mathrm{e}}^{\beta \mathrm{\Delta }V}\rangle =exp\left\{\sum _{k=1}^{\infty }\frac{{\beta }^k}{k!}{C}_k\right\}$$ (6)

where the first three cumulants are given by

$$\begin{gathered} C_1=\langle \mathrm{\Delta }V\rangle \\ {C}_2=\langle \mathrm{\Delta }{V}^2\rangle -{\langle \mathrm{\Delta }V\rangle }^2={{\sigma }_{\mathrm{\Delta }V}}^2 \\ {C}_3=\langle \mathrm{\Delta }{V}^3\rangle -3\langle \mathrm{\Delta }{V}^2\rangle \langle \mathrm{\Delta }V\rangle +2{\langle \mathrm{\Delta }V\rangle }^3 \end{gathered}$$ (7)

When the boost potential follows a near-Gaussian distribution, cumulant expansion to the second order (or “Gaussian approximation”) provides an approximation for free energy calculations.³⁴ The reweighted free energy F(A) = −k_BT ln p(A) is calculated as

$$F(A)=F\ast (A)-\frac{1}{\beta }\sum _{k=1}^2\frac{{\beta }^k}{k!}{C}_k+F_{\mathrm{c}}$$ (8)

where F*(A) = −k_BT ln p*(A) is the modified free energy obtained from a GaMD simulation and F_c is a constant.

System Setup

The X-ray crystal structure of the apo HIV protease was taken from Protein Data Bank (PDB) entry 1HHP (2.70 Å resolution).⁶ The XK263 ligand was extracted from the 1HVR X-ray structure of the HIV protease (1.80 Å resolution).⁸ To simulate the ligand binding process, the XK263 ligand was initially placed ~20 Å from the active site of apo HIV protease (see Figure 1B). The Amber FF99SB and general Amber force field (GAFF) were applied to the HIV protease and XK263, respectively.^37,38 Cl⁻ ions were added to neutralize the system using the ion parameters developed by Joung and Cheatham.³⁹ Energy minimization was performed on the hydrogen atoms, protein side chains, and the entire system for 500, 5000, and 5000 steps, respectively. The structure was then solvated in a rectangular box of TIP3P water molecules with ~12 Å between the box edge and the solutes.⁴⁰ Periodic boundary conditions were applied for the simulation system, and long-range electrostatics were accounted for using the particle mesh Ewald summation method.⁴¹

Simulation Protocol

The Amber 14 package with an efficient GPU implementation of GaMD^25,42,43 was applied for simulation of the HIV protease. Bonds containing hydrogen atoms were restrained with the SHAKE algorithm,⁴⁴ and a 2 fs time step was used. The Langevin thermostat with a damping constant of 2 ps⁻¹ was also used to maintain a temperature of 300 K. Electrostatic interactions were calculated using the particle mesh Ewald summation⁴¹ with a direct space cutoff of 12.0 Å. The simulation started with gradual heating of the complex system to 50, 100, 150, 200, 250, and 300 K for 10 ps at each temperature. To ensure that the system reached equilibrium, a 20 ns cMD simulation was further performed at 300 K with the isothermic–isopressure (NPT) ensemble.

The GaMD simulation proceeded with a 10 ns short cMD simulation to collect the potential statistics (e.g., the maximum, minimum, average, and standard deviation values of the system potential) for calculating the GaMD acceleration parameters, a 50 ns equilibration after adding the boost potential, and finally 10 independent GaMD production runs with randomized initial atomic velocities. The GaMD simulation was performed at the “dual-boost” level by setting the reference energy to the lower bound, i.e., E = V_max.²⁵ One boost potential is applied to the dihedral energetic term and another to the total potential energetic term. The average and standard deviation of the system potential energies were calculated every 200000 steps (400 ps). The upper limit of the boost potential standard deviation, σ₀, was set to 6.0 kcal/mol for the dihedral and total potential energetic terms. A list of GaMD production runs with 500–2500 ns durations (total of ~13.8 μs) is provided in Table 1. Simulation frames were saved every 0.1 ps for further analysis.

Table 1.

Summary of 10 GaMD Simulations Performed on Binding of the XK263 Ligand Molecule to the HIV Protease^a

	duration (ns)	ΔV_total (kcal/mol)		ΔV_dih (kcal/mol)		minimum ligand RMSD (Å)
		ΔVavg	σΔV	ΔVavg	σΔV
Sim1	2500	7.41	2.93	6.42	2.45	2.26
Sim2	2500	7.43	2.94	6.59	2.48	2.73
Sim3	1445	7.42	2.93	6.44	2.45	7.69
Sim4	2434	7.46	2.95	6.17	2.38	8.74
Sim5	2436	7.48	2.95	6.62	2.47	5.40
Sim6	500	7.42	2.94	6.61	2.47	6.36
Sim7	500	7.44	2.94	6.57	2.48	17.46
Sim8	500	7.43	2.93	6.3	2.41	19.37
Sim9	500	7.42	2.93	6.29	2.42	21.55
Sim10	500	7.43	2.94	6.09	2.37	20.72

^aΔV_total and ΔV_dih are the boost potential applied to the total potential and dihedral energy terms of the system, respectively.

Simulation Analysis

CPPTRAJ⁴⁵ and VMD⁴⁶ were used to analyze the GaMD simulation trajectories. Because ligand binding triggers major conformational changes mainly in the two flaps of the HIV protease based on the X-ray structures^6,8 and previous studies,^11–16 RMSDs were calculated for the two protein laps (residues Lys43–Tyr59) and the diffusing XK263 ligand relative to the 1HVR PDB structure of the holo HIV protease (Figure 1A). The dihedral angle of the C_α atoms of the Tyr59-Gly51-Gly51′-Tyr59′ motif was also calculated to characterize the protein flap handedness.

The PyReweighting³⁴ toolkit was used to reweight the GaMD simulation to compute the potential of mean force (PMF) profiles. A bin size of 1 Å was used for the RMSDs and 6° for the dihedral angle. The cutoff was set to 500 frames for the PMF calculations. Two-dimensional (2D) PMF profiles were obtained for binding of ligand to the HIV protease regarding the ligand RMSD versus the protein flap RMSD and handedness, and the protein flap handedness versus the flap RMSD (Figures 2–4).

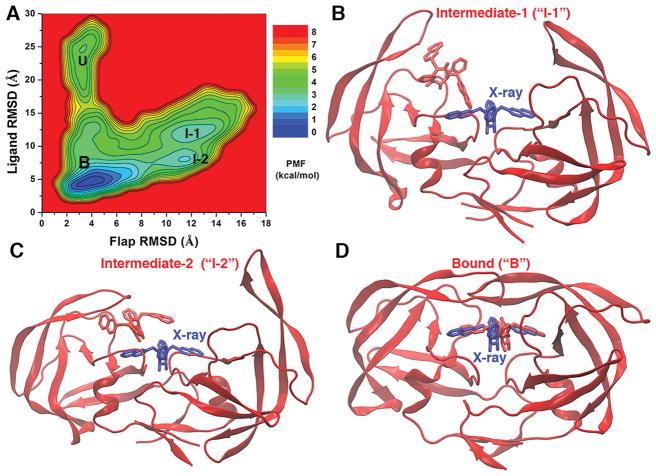
Figure 2.

(A) 2D potential of mean force (PMF) calculated with the protein flaps and ligand molecule RMSDs by combining the “Sim1” and “Sim2” GaMD trajectories, during which the XK263 ligand molecule was observed to bind the protein active site. Four low-energy conformational states are labeled, including the unbound (“U”), intermediate-1 (“I-1”), intermediate-2 (“I-2”), and bound (“B”) forms. (B–D) Structural conformations of the HIV protease in the “I-1”, “I-2”, and “B” states, respectively. The unbound (“U”) conformation is shown in Figure 1B. The evolving protein (ribbons) and ligand molecule (sticks) are colored red, and the X-ray conformation of the bound ligand molecule is colored blue for comparison.

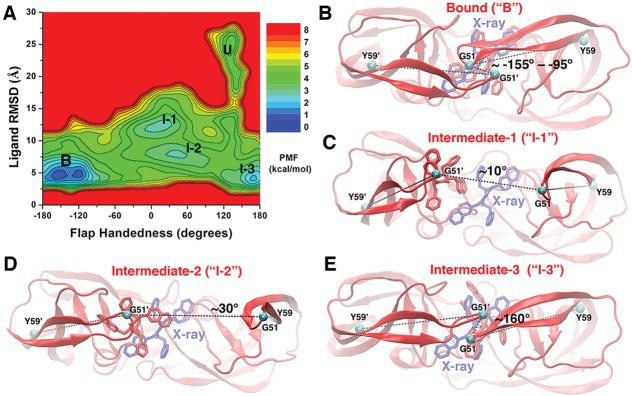
Figure 4.

(A) 2D PMF profile of the flap handedness and ligand molecule RMSD calculated by combining the “Sim1” and “Sim2” GaMD trajectories, during which the XK263 ligand molecule was observed to bind to the protein active site. Five low-energy conformational states are labeled, including the unbound (“U”), intermediate-1 (“I-1”), intermediate-2 (“I-2”), intermediate-3 (“I-3”), and bound (“B”) forms. (B–E) Structural conformations of the HIV protease in the bound (“B”), intermediate-1 (“I-1”), intermediate-2 (“I-2”), and intermediate-3 (“I-3”) states, respectively. The unbound (“U”) conformation is shown in Figure 1B. The evolving protein (ribbons) and ligand molecule (sticks) are colored red, and the X-ray conformation of the bound ligand molecule is colored blue. The dihedral angle of the C_α atoms (cyan spheres) of the Tyr59-Gly51-Gly51′-Tyr59′ motif is shown as in Figure 3.

RESULTS

Binding of the XK263 ligand molecule to the active site of the HIV protease was observed in two 2500 ns GaMD production trajectories (“Sim1” and “Sim2” in Table 1), during which the minimum RMSD of the diffusing ligand relative to the X-ray structure reached <3 Å. Meanwhile, the HIV protease underwent large-scale conformational changes. The protein flaps switched from the semi-open conformation in the apo form to the closed conformation in the holo form and visited distinct intermediate conformational states during ligand binding. In the other eight GaMD production trajectories (“Sim3” to “Sim10” in Table 1), the XK263 ligand bound to other regions of the protein (including the “front”, “left”, and “right”), being consistent with observations obtained from previous Brownian dynamics and MD simulations.^16,27,47 No complete ligand binding to the protein active site was observed in these eight GaMD trajectories, and the minimum ligand RMSDs were >3 Å (see the ligand pathways and RMSD plots in Figure S1). Because we aimed to determine the complete ligand binding pathways, the “Sim1” and “Sim2” GaMD trajectories were used for further analysis.

Ligand Pathways

During the “Sim1” GaMD trajectory, starting from free diffusion in the solvent (unbound state) (Figure 1B), the XK263 ligand molecule first attached to one of the two protein flaps within ~20 ns, entered the protein binding site, and induced the protein flaps to open near ~600 ns. Then, the two protein flaps spent ~1400 ns in rearranging their conformations, with large fluctuations in the RMSDs of both protein flaps and ligand during ~600–2000 ns (Figure 1C). Finally, the two protein flaps changed back to the closed conformation and locked the ligand molecule at the protein active site (Figure 1C and Movie S1). Relative to the 1HVR X-ray structure, the ligand reached a minimum RMSD of 2.26 Å near ~2000 ns (Figure 1D).

A similar pathway of ligand binding to the active site of the HIV protease was observed in the “Sim2” GaMD trajectory (Figure 1E and Movie S2). The RMSD of the ligand relative to the 1HVR X-ray structure approached a minimum of 2.74 Å near ~720 ns in “Sim2” (Figure 1F). However, the two protein flaps opened in “Sim2” for a significantly shorter period of time (~250 ns) before closing back to the ligand-bound conformation than in “Sim1” (~1400 ns). The protein flaps also underwent a smaller conformational change in “Sim2” with an RMSD of ≲8 Å (Figure 1F), compared with an RMSD of ≲15 Å in “Sim1” (Figure 1D).

Protein Conformational Changes

As shown in Figure 2A, a 2D PMF profile was calculated with regard to RMSDs of the two protein flaps and the XK263 ligand relative to the 1HVR X-ray structure by combining the “Sim1” and “Sim2” GaMD trajectories. Four low-energy conformational states, including the unbound (“U”), intermediate-1 (“I-1”), intermediate-2 (“I-2”), and bound (“B”) states, were identified from the PMF profile. Figure S2 shows distribution anharmonicity of ΔV of frames found in each bin of the 2D PMF, along with the reweighted PMF profiles obtained through cumulant expansion to the first, second, and third orders. Overall, the ΔV anharmonicity is close to zero (Figure S2A), justifying the use of Gaussian approximation or cumulant expansion to the second order for energetic reweighting (Figure 2A). In comparison, the PMF profile obtained with cumulant expansion to the third order appeared to be too noisy with free energy values of ≲20 kcal/mol (Figure S2D). Additionally, we calculated 2D PMF profiles for each individual GaMD trajectory (Figure S3), as well as all 10 GaMD trajectories combined (Figure S4). PMF profiles of the individual GaMD trajectories exhibited significant differences, largely because of the different ligand pathways and protein flap dynamics depicted in Figure S1. Nevertheless, the four unbound, intermediate-1, intermediate-2, and bound states identified in Figure 2A remained as low-energy wells in the 2D PMF profile obtained by combining all 10 GaMD trajectories. Therefore, although the presented free energy profiles were still not converged because of insuficient sampling of the complex system, the GaMD simulations allowed us to identify the low-energy states mentioned above. Furthermore, the conformational transition from the unbound to the intermediate states exhibited a free energy barrier higher than the transition between the intermediate and bound states (Figure 2A and Figure S4).

In the unbound state, the HIV protease adopted the “semi-open” conformation, which is the same as in the protein apo form (Figure 1B). Compared to the 1HVR X-ray structure, RMSDs of the two protein flaps and the XK263 ligand were ~2.9 and ~24.3 Å, respectively, in the unbound state (Figure 2A). When the ligand bound to the active site, the flaps changed to the “closed” conformation (Figure 2D). Furthermore, two key intermediate conformations “I-1” and “I-2” of the HIV protease are shown in panels B and C of Figure 2, respectively. In intermediate “I-1”, both protein flaps were widely open with an ~11.1 Å RMSD and the XK263 ligand moved toward one of the two flaps with an ~12.7 Å RMSD (Figure 2A,B). The flank rings of the XK263 ligand formed nonpolar interactions with hydrophobic residues, including Val32′, Ile47′, Ile50′, Pro81′, and Val82′, in the protein flap. In the “I-2” intermediate, a flap tended to close, while the other flap remained fully open as in the “I-1” conformation (Figure 2C). A hydrogen bond was formed between the oxygen atoms of XK263 and residues Asp25′ and Ile50′ to further stabilize the protein–ligand interactions. At this stage, RMSDs of the XK263 ligand and the two protein flaps became ~8.6 and ~13.0 Å, respectively (Figure 2A).

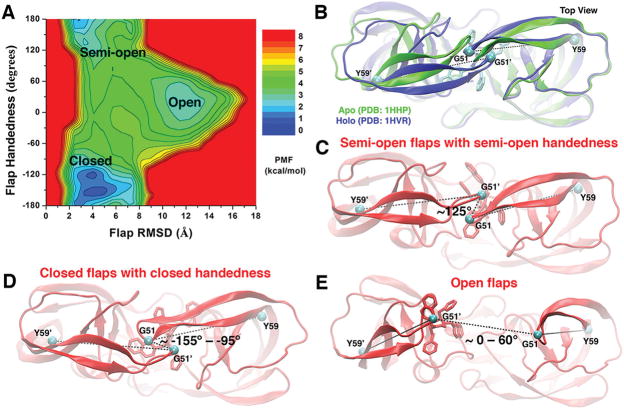
To study the handedness of the two protein flaps in the HIV protease, we define a “handedness dihedral” as the dihedral angle formed by the C_α atoms of the Tyr59-Gly51-Gly51′-Tyr59′ motif. In the X-ray structures, the handedness dihedral of the apo HIV protease is 123.87° and that of the holoprotein −97.09° (Figure 3B). Hence, the positive and negative dihedrals represent conformations of the protein semi-open and closed handedness, respectively. Figure 3A shows a 2D PMF calculated for the protein flap handedness versus the flap RMSD. Three low-energy conformational states of the protein flaps were identified, including the “semi-open flaps with semi-open handedness”, “closed flaps with closed handedness”, and “fully open flaps” states. In the apo form, the protein adopted the semi-open flaps with semi-open handedness state, for which the flap RMSD is ~3 Å and the handedness dihedral is ~125° (Figure 3C). Then, the protein flaps visited the fully open state, for which the flap RMSD increased to ~12 Å and the handedness dihedral is within a range of 0–60° (Figure 3E). This state corresponds to the “I-1” and “I-2” intermediates shown in Figure 2. The fully open protein flaps allowed the ligand to rearrange its conformation in a large space. Finally, the closed flaps with closed handedness were found in the ligand-bound (holo) protein, in which the flap RMSD was found within the range of 2.5–5 Å and the handedness dihedral angle shifted to approximately −155° to −95° (Figure 3D).

Figure 3.

(A) 2D PMF profile of the protein flap RMSD and handedness calculated by combining the “Sim1” and “Sim2” GaMD trajectories, during which the XK263 ligand molecule was observed to bind the protein active site. Three low-energy conformational states of the protein flaps are labeled, including the “open”, “semi-open”, and “closed” states. (B) Top view of the X-ray crystal structures of the HIV protease in the apo (PDB entry 1HHP, green) and XK263-bound holo (PDB entry 1HVR, blue) forms. The ligand is shown as sticks and the protein as ribbons. The dihedral angle of the C_α atoms (cyan spheres) of the Tyr59-Gly51-Gly51′-Tyr59′ motif is used to characterize the flap handedness. (C–E) Conformational states of the HIV protease: “semi-open” flaps with “semi-open” handedness, “closed” flaps with “closed” handedness, and “open” flaps, respectively. The evolving protein is shown as ribbons and the ligand molecule as sticks.

Correlations between Ligand Binding and Protein Conformational Changes

A 2D PMF profile of the ligand RMSD versus protein handedness dihedral was calculated to examine the correlation between ligand binding and handedness changes of the HIV protease. In addition to the unbound, bound, and intermediate “I-1” and “I-2” conformations, the PMF calculation revealed another low-energy intermediate “I-3” state (Figure 4A). In the “I-3” state, the XK263 ligand reached the target site, being quite similar to the final 1HVR X-ray crystal conformation with an RMSD of only ~4.8 Å. However, the handedness dihedral of two protein flaps in intermediate “I-3” was ~160°. The flaps remained in the “semi-open” handedness state as in the ligand-unbound (apo) protein (Figure 4E). In contrast, the flap handedness dihedral was approximately −155° to −95° in the “closed” ligand-bound state (Figure 4B). When the protein flaps are open, the handedness dihedral is ~10° and ~30° in the intermediate “I-1” (Figure 4C) and “I-2” (Figure 4D) states, respectively. Figure S5 also depicts front views of the protein in the intermediate and ligand-bound states. These results suggest correlations between ligand binding and large-scale conformational changes of the HIV protease.

DISCUSSION

In this study, long-time-scale GaMD enhanced simulations were performed for 2500 ns to successfully sample ligand binding pathways and correlated conformational changes of the HIV protease. GaMD provided significantly enhanced sampling compared with that of cMD simulations. Figure S6 plots the RMSDs of the XK263 ligand relative to the 1HVR X-ray crystal conformation obtained from a previous ~14000 ns Anton cMD simulation¹⁶ and two 2500 ns GaMD simulations (“Sim1” and “Sim2” listed in Table 1). Relative to the X-ray crystal structure, the XK263 ligand reached a minimum RMSD of 2.26 Å during 2500 ns GaMD simulations. In comparison, the ligand RMSD reached a minimum RMSD of only 5.73 Å during the Anton simulation. This was already captured during the initial 200 ns GaMD trajectories as shown in the inset of Figure S6.

The 2D PMF plots derived from the GaMD simulations showed that the association of the XK263 ligand with the HIV protease involved several key steps. In the ligand-free state, the protein adopted semi-open flaps with semi-open handedness, as described in the apoprotein crystal structure. Next, the ligand anchored to one of the protein flaps via strong hydrophobic interactions, inducing conformational changes in the protein. The two protein flaps were able to open and close in intermediate conformational states to allow the ligand to move in, accompanying switches of the flap handedness orientations. The magnitude of flap motions could vary as observed in the GaMD simulations presented here. Finally, the XK263 bound to the active site and the HIV protease changed to the closed ligand-bound conformation. The conformational transition between the unbound and intermediate states exhibited the highest free energy barrier (Figure 2A and Figure S4) and thus appeared to be the rate-limiting step during association of the XK263 ligand, although the anisotropic diffusion of the flexible flaps and other factors could affect the ligand binding rate, as well.⁴⁸ The binding mechanism of the XK263 obtained from the GaMD simulations is consistent with those from previous cMD studies;^16,27 i.e., an induced-fit model is more suitable for describing binding of XK263 to the HIV protease than a conformational-selection mechanism is.^16,49

Because of the limited time scale and sampling power, the previous cMD simulations did not capture the final ligand-bound state. The ligand was trapped in the low-energy wells, such as the intermediate “I-3” state in Figure 4. In comparison, the GaMD simulations achieved complete sampling of the XK263 binding process, during which the ligand reached the active site with a <3 Å RMSD compared with the 1HVR X-ray structure of the HIV protease.⁸ Furthermore, the GaMD simulations allowed us to characterize low-energy intermediate conformational states of the HIV protease during binding of the XK263 ligand. However, it is important to note that only two ligand binding events were captured in the HIV protease even with the GaMD enhanced sampling and the simulation-derived free energy profiles were not converged. Refining the free energy profiles and achieving sampling convergence are subject to future developments in the computing power and methodology.

Although the XK263 ligand has been considered as a small and fast binder of the HIV protease, computer simulations of the ligand association paths are still very challenging. Compared to the protein kinases or GPCRs, for which the ligand binding paths may be well-defined,^20,21 the HIV protease binders could approach the protein active site from many different directions. The complete ligand binding to the HIV protease involves not only large conformational changes of the protein flaps between the open and closed states but also motions in the flap handedness orientations. This makes sampling of the entire ligand binding process difficult. Because the XK263 molecule is a hydrophobic ligand, the main driving force for its association is nonpolar interaction. Few formations and breaks of hydrogen bonds among the ligand, protein, and solvent molecules were detected during the simulations. However, the binding mechanism might be different for polar ligands of the HIV protease.¹⁶ Therefore, simulations of different binders and various protein systems will be needed in the future to gain a complete picture of protein–ligand binding mechanisms. GaMD simulations presented here will be useful for guiding future studies of drug–receptor interactions.