A prediction-based alternative to P values in regression models

Graphical Abstract

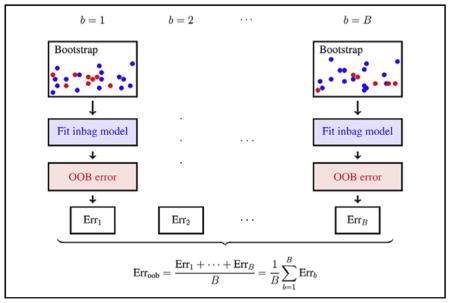
Prediction error calculated using in-sample (blue) and out-of-sample (red) bootstrap data.

Statisticians have discussed for decades the problems associated with P values and have diligently tried to provide researchers with simple guidelines for their correct use. Despite all of this, controversies and frustrations remain. Scientists, who are often forced to use P values, are now openly questioning and debating their validity as scientific tools. “P values, the ‘gold standard’ of statistical validity, are not as reliable as many scientists assume,” is the leading assertion of the Nature article, “Scientific Method: Statistical Errors.”¹ Consider also the recent action of the journal of Basic and Applied Social Psychology, which announced it would no longer publish papers containing P values. In explaining their decision for this policy,² the editors stated that hypothesis significance testing procedures are invalid and that P values have become a crutch for scientists dealing with weak data. Even the American Statistical Association has weighed in on the topic, recently issuing a formal statement on P values,³ the first time in its history it had ever issued a formal statement on matters of statistical practice.

Part of this frustration stems from the need for the P value to be something for which it was never designed. Researchers want to make context-specific assertions about their findings; they especially want a statistic that allows them to make assertions regarding scientific effect. Because the P value cannot do this, and because the terminology is confusing and stifling, this leads to misuse and confusion. Another problem is correctness of the model under which the P value is calculated. If model assumptions do not hold, the P value itself becomes statistically invalid. Researchers rarely test for model correctness, and when they do, they often use goodness of fit. But goodness-of-fit measures are notoriously unreliable for assessing model validity.⁴ All of this implies that a researcher’s findings, which hinge so much on the P value being correct, could be suspect without their even knowing it. This nonrobustness of the P value is further compounded by other conditions typically outside of the control of the researcher, such as the sample size, and collinearity, which have enormous effects on its efficacy.

In this article, we focus on the use of P values in regression models and present a new approach to the problem. As readers are aware, the P value from the coefficient estimate of a variable is typically used to assess its contribution to the regression model. We present a different strategy by using a quantity we call the variable importance (VIMP) index. Unlike the P value, which assesses a variable in terms of statistical significance, and thus gives no insight into how important a variable is to the scientific problem, VIMP measures the importance of a variable in terms of prediction error. The prediction error is a quantity that describes how well a model performs over new data without making any assumptions regarding the truth of the model. VIMP quantifies how much a variable contributes to the prediction performance of a model and provides an interpretable measure of the scientific importance of a variable that is robust to model assumptions. We call this measure the predictive effect size. We also discuss a marginal VIMP index, which measures how much a model would improve when a specific variable is added to it. We call this the discovery effect size.

PREDICTION ERROR

Typically, prediction error is estimated using cross-validation. In cross-validation, the data are split into separate parts, with one part being used to fit the model, and the remaining used to calculate the prediction error. The procedure is repeated over several distinct splits and values averaged. Out-of-bag (OOB) estimation is a variation of cross-validation but possesses certain superior statistical properties due to its connection to leave-one-out cross-validation.^5–7 We use OOB prediction error to calculate VIMP.

Calculating the OOB prediction error begins with bootstrap sampling. A bootstrap sample is a sample of the data obtained by sampling with replacement. On average, because of replicated values, a bootstrap sample contains only 63.2% of the original data, which is referred to as the inbag data. The remaining 37% of the data, which is out-of-sample, is called the OOB data. The OOB error for a model is obtained by drawing a bootstrap sample, fitting the model to the inbag (bootstrapped) data, and then calculating its prediction error on the OOB data. This procedure is repeated many times. The OOB prediction error is the averaged value. More technically, if Err_b is the OOB prediction error using the bth bootstrap sample (from a total of B bootstrap samples) the OOB error is

$${\text{Err}}_{\text{oob}}=\frac{1}{B}\sum _{b=1}^B{\text{Err}}_b.$$

The Central Figure provides an illustration of this concept.

VIMP Index

The VIMP index for a variable β is obtained by a slight modification to the aforementioned procedure (for notational simplicity, we will use β to refer to both the variable and its regression coefficient). After fitting the model to the inbag data, the regression coefficient for β is set to zero. The prediction error using the OOB data is then calculated using the modified regression equation. The VIMP index is the difference between this new modified error and the prediction error from the original (nonmodified) regression model. This value will be positive if β is predictive because the prediction error for the modified equation will increase relative to the original prediction error. Averaging this over the bootstrap samples yields the VIMP index. More formally, let Err_β,_b be the OOB prediction error for β from the modified regression equation and let Err_b be the OOB prediction error for the nonmodified model. The VIMP index for β is

$${\mathit{\Delta }}_{\beta }=\frac{1}{B}\sum _{b=1}^B[{\text{Err}}_{\beta ,b}-{\text{Err}}_b].$$

As just discussed, a positive value indicates a variable β with a predictive effect. A formal description of the VIMP algorithm is provided in the Appendix E1.

RISK FACTORS FOR SYSTOLIC HEART FAILURE

To illustrate VIMP, we consider a survival data set previously analyzed in Hsich and colleagues.⁸ The data involve 2231 patients with systolic heart failure who underwent cardiopulmonary stress testing at the Cleveland Clinic. Of these 2231 patients, during a mean follow-up of 5 years, 742 died. In total, 39 variables were measured for each patient, including baseline characteristics and exercise stress test results. Specific details regarding the data are discussed in the work of Hsich and colleagues.

We used Cox regression, with all-cause mortality used for the survival endpoint (as was done in the original analysis). Prediction error was assessed by 100 times 1 minus C, where C was taken to be Harrell’s concordance index. Recall that C calculates the fraction of times a procedure ranks 2 individuals correctly in terms of their risk over permissible pairs of individuals. Subtracting C from 1 and scaling by 100 conveniently converts the concordance index to a percentage between 0 and 100, with 0%representing a perfect procedure and 50% representing random guessing. This means that a VIMP index of 5% indicates a variable that improves by 5% the ability of the model to rank patients by their risk. We emphasize once again that because calculations are based on OOB data, and hence are cross-validated, this reflects a 5% increase in performance for new patients.

Table 1 presents the results from the Cox regression analysis. Included are VIMP indices and other quantities obtained from B = 1000 bootstrapped Cox regression models. Column β̂ lists the coefficient estimate for each β variable, and β̂_inbag is the averaged coefficient estimate from the 1000 bootstrapped models. These 2 values agree closely, which is to be expected if the number of iterations B is selected suitably large. Table 1 has been sorted in terms of the VIMP index, δ_β. Interestingly, ordering by VIMP does not match ordering by P value. For example, insulin-treated diabetes has a near-significant P value of 6%; however, its VIMP of 0.07% is relatively small compared with other variables. The top variable peak VO₂ has a VIMP of 1.9%, which is more than 27 times larger.

TABLE 1.

Results from analysis of systolic heart failure data

Variable	Cox regression		VIMP			Marginal VIMP
	β̂	P value	β̂inbag	Δβ	Errstep	${\mathit{\Delta }}_{\beta }^{\text{marg}}$
Peak VO2	−0.06	.002	−0.06	1.94	32.40	0.25
BUN	0.02	.000	0.02	1.67	30.81	0.37
Exercise time	0.00	.008	0.00	1.37	30.80	0.08
Male	0.47	.000	0.47	0.52	30.01	0.37
beta-blocker	−0.23	.006	−0.23	0.30	29.34	0.16
Digoxin	0.36	.000	0.36	0.30	29.00	0.22
Serum sodium	−0.02	.071	−0.02	0.20	28.93	0.07
Age	0.01	.022	0.01	0.18	28.99	−0.03
Resting heart rate	0.01	.058	0.01	0.14	28.93	0.04
Angiotensin receptor blocker	0.26	.067	0.27	0.13	28.92	0.02
LVEF	−0.01	.079	−0.01	0.11	28.86	0.03
Aspirin	−0.21	.018	−0.21	0.11	28.83	0.03
Resting systolic blood pressure	0.00	.158	0.00	0.07	28.83	0.00
Diabetes insulin treated	0.26	.057	0.25	0.07	28.87	−0.02
Previous CABG	0.11	.316	0.12	0.07	28.86	−0.02
Coronary artery disease	0.12	.284	0.12	0.06	28.92	−0.04
Body mass index	0.00	.800	0.00	0.00	28.96	−0.05
Potassium-sparing diuretics	−0.14	.134	−0.14	−0.03	28.97	−0.01
Previous MI	0.29	.012	0.30	−0.03	29.02	−0.01
Thiazide diuretics	0.04	.707	0.04	−0.04	29.07	−0.05
Peak respiratory exchange ratio	0.12	.701	0.12	−0.04	29.12	−0.05
Statin	−0.12	.183	−0.13	−0.04	29.19	−0.07
Antiarrhythmic	0.04	.700	0.04	−0.04	29.25	−0.06
Diabetes, noninsulin-treated	0.01	.930	0.00	−0.05	29.30	−0.06
Dihydropyridine	0.03	.851	0.03	−0.05	29.35	−0.05
Serum glucose	0.00	.486	0.00	−0.05	29.42	−0.07
Previous PCI	−0.06	.557	−0.06	−0.05	29.48	−0.05
ICD	0.04	.676	0.03	−0.05	29.55	−0.07
Anticoagulation	−0.01	.933	−0.01	−0.06	29.61	−0.06
Pacemaker	−0.02	.851	−0.01	−0.06	29.67	−0.06
Current smoker	0.03	.807	0.03	−0.06	29.74	−0.06
Nitrates	−0.04	.623	−0.04	−0.06	29.80	−0.06
Serum hemoglobin	0.00	.923	0.01	−0.06	29.87	−0.07
Black	0.07	.589	0.06	−0.07	29.95	−0.08
Nondihydropyridine	−0.30	.510	−0.51	−0.07	30.03	−0.08
Loop diuretics	−0.07	.541	−0.08	−0.07	30.09	−0.06
ACE inhibitor	0.10	.371	0.11	−0.09	30.15	−0.06
Vasodilators	−0.08	.606	−0.07	−0.09	30.25	−0.09
Creatinine clearance	0.00	.624	0.00	−0.11	30.31	−0.06

VIMP, Variable importance; VO₂, oxygen consumption; BUN, blood urea nitrogen; LVEF, left ventricular ejection fraction; CABG, coronary artery bypass grafting; MI, myocardial infarction; PCI, percutaneous coronary intervention; ICD, implantable cardioverter defibrillators; ACE, angiotensin-converting enzyme.

MARGINAL VIMP

Peak oxygen consumption (VO₂), blood urea nitrogen (BUN), and treadmill exercise time are the top 3 variables identified by the VIMP index. Following these are an assortment of variables with moderate VIMP: sex, use of beta-blockers, use of digoxin, serum sodium level, and age of the patient. Then are variables with small but non-zero VIMP, starting with patient resting heart rate and terminating with presence of coronary artery disease. VIMP indices become zero or negative after this. These latter variables, with zero or negative VIMP indices, can be viewed as “noisy” variables that degrade model performance. This can be seen by considering the column labeled as Err_step. This equals the OOB prediction error for models formed using variables ordered by VIMP. For example, the third line, 30.80, is the OOB error for the model using top 3 variables. The fourth line is the OOB error for the top 4 variables, and so forth. Table 1 shows that Err_step decreases for models with positive VIMP, but rises once models begin to include noisy variables with zero or negative VIMP.

The entry Err_step in Table 1 is the motivation for our marginal VIMP index. Relative to its previous entry, Err_step estimates the effect of a variable when added to the current model. For example, the effect of adding exercise time to the model with peak VO₂ and BUN is the difference between the second row (model 2), 30.81, and the third row (model 3), 30.80. The effect of adding exercise time is therefore 0.01 (30.81 minus 30.80). This is much smaller than the VIMP index for exercise time, which equals 1.37. These values differ because the stepwise error rate estimates the effect of adding treadmill exercise time to the model with Peak VO₂ and BUN. We call this the discovery effect size of the variable. Marginal VIMP (see entry ${\mathit{\Delta }}_{\beta }^{\text{marg}}$ in Table 1) is a generalization of this concept. It calculates the discovery effect of a variable by comparing the prediction error of the model with and without the variable added. The Appendix E1 presents a formal description of this algorithm. We summarize the difference between marginal VIMP and the VIMP index as follows:

• VIMP is calculated by setting a variable’s regression coefficient to zero

• Marginal VIMP removes a variable and refits the model with the remaining variables

Table 1 reveals that marginal VIMP is generally much smaller than the VIMP index. This is to be expected because of the large number of variables in the model, because as the number of variables becomes large, it will be difficult for the addition of a single variable to the model to improve prediction performance. However, Table 1 shows there are a small collection of variables whose discovery effect are relatively large compared with their VIMP index. The most interesting is sex (see row entry “Male”), which has the largest discovery effect among all variables (being tied with BUN). The explanation for this is that adding sex to the model supplies new information not contained in other variables. Marginal VIMP is in some sense a statement about correlation. For example, correlation of exercise time with peak VO₂ is 0.87, whereas correlation of BUN with peak VO₂ is −0.40. This allows BUN to have a high discovery effect when peak VO₂ is included in the model, while exercise time cannot.

ROBUSTNESS OF VIMP TO THE SAMPLE SIZE

Here, we demonstrate the robustness of VIMP to sample size changes. We use the systolic heart failure data as before, but this time using only a fraction of the data. We used a random 10%, 25%, 50%, and 75% of the data. This process was repeated 500 times independently. For each data set, we saved the P values and VIMP indices for all variables. Figure E1 displays the logarithm of the P values from the experiment (large negative values correspond to near zero P values). Figure E2 displays the VIMP indices. What is most noticeable is that VIMP indices are informative even in the extremely low sample size setting of 10%. For example, VIMP interquartile values (the lower and upper ends of the boxplot) are above zero for peak VO₂, BUN, and treadmill exercise time, showing that VIMP is able to consistently identify the top 3 variables even with limited data. In contrast, for the low sample setting of 10%, no variable had a median log P value below the threshold of log(0.05), showing that no variable met the 5% level of significance on average. Furthermore, even with 75% of the data, the upper end of the boxplot for exercise time is still above the threshold, showing its significance is questionable.

MISSPECIFIED MODEL

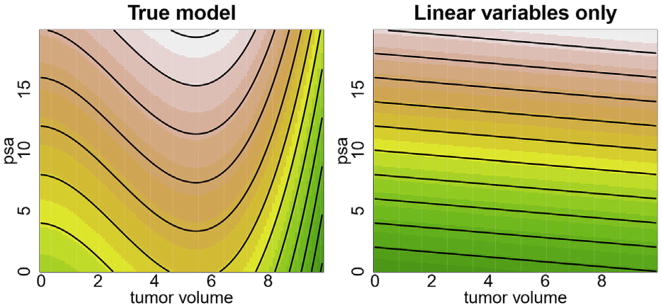
We used the following simulation (n = 1000) from a Cox regression model to demonstrate robustness of VIMP to model misspecification. The first 2 variables are “prostate-specific antigen (psa)” and “tumor volume” and represent variables associated with the survival outcome. The remaining 3 variables are noise variables with no relationship to the outcome. These are called X₁, X₂, X₃. The variable psa has a linear main effect, but tumor volume has both a linear and nonlinear term. The true regression coefficient for psa is 0.05, and the coefficient for the linear term in tumor volume is 0.01. A censoring rate of approximately 70%was used. The log of the hazard function used in our simulation is given in the left panel of Figure 1. Mathematically, our log-hazard function assumes the following function:

$$log(\mathrm{h}(\mathrm{t}))={\alpha }_0+0.05\times \text{psa}+0.01\times \text{tumor}\text{volume}+\psi (\text{tumor}\text{volume}),$$

where ψ(x) = 0.04x² − 0.005x³ is a polynomial function with quadratic and cubic terms. The right panel of Figure 1 displays the log-hazard for the misspecified model that does not include the nonlinear term for tumor volume.

FIGURE 1.

Log-hazard function from Cox simulation example. The left panel displays the true log-hazard function, which includes the nonlinear term for tumor volume. The right panel displays the log-hazard function, assuming linear variables only. psa, Prostate-specific antigen.

We first fit a Cox regression model to the data using only linear variables as one might typically do. This model was bootstrapped B = 1000 values and VIMP and marginal VIMP calculated. This entire procedure of simulating a data set, fitting a Cox model and 1000 bootstrapped Cox models, was repeated M = 1000 times. The results from these 1000 experiments were averaged. These values are summarized in Table 2. The table shows that the P value has no difficulty in identifying the strong effect of psa, which is correctly specified in the model. However, the P value for tumor volume is 0.267, indicating a nonsignificant effect. The P value tests whether this coefficient is zero, assuming the model is true, but the problem is that the fitted model is misspecified. The estimated Cox regression model inflates the coefficient for tumor volume in a negative direction (estimated value of −0.03, but true value is 0.01) in an attempt to compensate for the nonlinear effect that was excluded from the model. This leads to the invalid P value. In contrast, both the VIMP and marginal VIMP values for tumor volume are positive. Although these values are substantially smaller than the values for psa, VIMP is still able to identify a predictive effect size associated with tumor volume. Once again, this is possible because VIMP is based on prediction error, which does not require the underlying model to be correct. Also, notice that all 3 noise variables are correctly identified as uninformative. All have negative VIMP values.

TABLE 2.

Results from analysis of simulated Cox regression data set

	β̂	P value	β̂inbag	δβ	${\mathit{\Delta }}_{\beta }^{\text{marg}}$
psa	0.05	.001	0.05	6.32	6.34
Tumor volume	−0.03	.267	−0.03	0.14	0.15
X1	0.00	.490	0.00	−0.25	−0.25
X2	0.00	.486	0.00	−0.25	−0.25
X3	0.00	.493	0.00	−0.27	−0.27

The model is misspecified by failing to include the nonlinear term for tumor volume. The overall OOB model error is 43%. OOB, Out-of-bag; psa, prostate-specific antigen.

Typically, a standard analysis would end after looking at the P values. However, a researcher with access to the entire Table 2 might be suspicious of the small positive VIMP of tumor volume and its negative coefficient value, which is unexpected from previous experience. This combined with the high OOB model error (equal to 43%) should alert them to consider more sophisticated modeling. This is easily done using standard statistical methods. Here we use B-splines⁹ to add nonlinearity to tumor volume. This expands the design matrix for the Cox regression model to include additional columns for the B-spline expansion of tumor volume.

The results from the B-spline analysis are displayed in Table 3. As before, the entire procedure was repeated M = 1000 times, with values averaged. Notice the large value of VIMP for tumor volume, which shows the effectiveness of the B-splines in identifying the true effect. The same holds true for the P value, which is now very small for tumor volume. However, the P value is very sensitive to the distribution of the data and can easily become unstable. To demonstrate this, we altered the simulation to introduce a positive correlation between psa and tumor volume (correlation of approximately 0.71). This creates collinearity in the variables which heavily affects the P value. The right-hand side of Table 3 with the heading “correlated” displays the results from this analysis. The correlation leads to the very misleading result that although tumor volume is highly significant, psa is not. In contrast, VIMP is able to maintain large positive values for both variables even in the presence of the high collinearity.

TABLE 3.

Results from Cox regression simulation using B-splines to model nonlinearity in tumor volume

	P value	δβ	${\mathit{\Delta }}_{\beta }^{\text{marg}}$	Correlated
				P value	δβ	${\mathit{\Delta }}_{\beta }^{\text{marg}}$
psa	.001	4.20	4.23	.135	2.17	1.09
Tumor volume	.008	2.27	2.31	.006	3.93	4.49
X1	.490	−0.20	−0.20	.484	−0.21	−0.21
X2	.483	−0.20	−0.20	.489	−0.23	−0.23
X3	.490	−0.21	−0.21	.505	−0.25	−0.25

psa, Prostate-specific antigen.

DISCUSSION

In this article, we introduced VIMP as an alternative approach to P values in regression models. Although VIMP has not been used in this context before, variable importance is a fairly old concept used in machine learning. One of its earliest uses was for variable ranking in Classification and Regression Trees (see Chapter 5 of Breiman and colleagues).¹⁰ The idea was later extended to variable selection in random forest regression and classification models.^4,11 See also Ishwaran and colleagues¹² for applications to random survival forest models. What we have done here is to take regression methods with which all the readership will be familiar, borrow from these concepts used in machine learning, which with readers may not be familiar, and apply them in an understandable way to come up with the VIMP index, a new statistic that can supplant P values.

One of the strengths of VIMP is that it provides an interpretable measure of effect size robust to model misspecification. It uses prediction error based on OOB data and replaces statistical significance with predictive importance. The VIMP framework is feasible to all kinds of models including not only parametric models, such as those considered here, but also nonparametric models such as those used in machine learning. This latter point, of using VIMP with machine learning methods, brings up an important issue regarding the distinction between robustness of VIMP and power of the underlying model. VIMP is robust in the sense that because it is based on prediction error, it does not require the model to be true to be valid, but this should not be interpreted to mean VIMP can identify signal in any setting. To be effective in scenarios in which data complexity exists (for example, presence of interactions or nonlinear effects, and general violation of parametric assumptions), the underlying model must have power to discern these effects. In very complex settings, we should turn to machine learning methods over parametric models to improve power. This then allows the VIMP calculated under these more powerful models to be better able to discern signal.

We discussed 2 types of VIMP measures: the VIMP index and the marginal VIMP. The scientific application will dictate which of these is more suitable. VIMP indices are appropriate in settings in which variables for the model are already established and the goal is to identify the predictive effect size. For example, if several genetic markers are already identified as a genetic cause for coronary heart disease risk, VIMP can provide a rank for these and estimate the magnitude each marker plays in the prediction for the outcome. Marginal VIMP is appropriate when the goal is new scientific discovery. For instance, if a researcher is proposing to add a new genetic marker for evaluating coronary heart disease risk, marginal VIMP can yield a discovery effect size for how much the new proposed marker adds to previous risk models.

From a statistical perspective, VIMP indices are an OOB alternative to the regression coefficient P value. An important feature is that degrees of freedom and other messy details required with P values when dealing with complex modeling are never an issue with VIMP. Marginal VIMP is an OOB analog to the likelihood-ratio test. In statistics, likelihood-ratio tests compare the goodness-of-fit of 2 models, one of which (the null model with certain variables removed) is a special case of the other (the alternative model with all variables included). Marginal VIMP compares the prediction precision of these two scenarios.

There are some limitations to VIMP. Researchers will need to be diligent in reporting the measure of prediction performance used in their VIMP analyses. Because VIMP interpretation depends implicitly on the performance measure, these 2 values must go hand in hand. Researchers will also need to familiarize themselves with performance measures that have universal meaning and which are appropriate for VIMP. In survival analysis, the Harrell concordance index is appropriate. For example, a 0.05 VIMP value for 2 different variables from 2 different survival datasets is comparable—both imply a 5% improvement in the ability to rank a patient’s risk. In logistic regression analysis, users can report misclassification error, which lends itself to a VIMP interpretation of improved ability to classify patients. However, mean squared error (MSE), which is a common measure of performance used in linear regression, is not appropriate because of its lack of scale invariance and interpretation. Instead, standardized MSE, defined as the MSE divided by the variance of the outcome, should be used. Standardized MSE can be converted to the percent of variance explained by a model which has an intuitive and universal interpretation. Another limitation of VIMP is that it is more computationally demanding. In place of having to fit one model, the researcher will be required to fit a thousand or more models. This will take more time, but computational solutions such as parallel processing can help tremendously. The Appendix E1 discusses this in greater depth.

One of the tremendous advantages of VIMP is that it removes the arbitrariness of having to select a cutoff value. Regardless of the problem, a VIMP of zero always represents an appropriate cutoff, as it reflects the point at which a variable no longer contributes predictive power to the model. Of course, in practice one may observe VIMP values close to zero, and the meaning of what constitutes being “zero” may be unclear. However, this poses a challenge only in the sense that we must assess whether the variable is truly predictive or not, not whether zero is a reasonable VIMP cutoff value. To answer the question of whether the observed VIMP really differs from zero, we must estimate its standard error. Although not described here, it turns out that fast and efficient subsampling algorithms are available for accurate estimation of VIMP standard error. Thus, if the observed VIMP exceeds the zero cutoff value, up to a tolerance depending on the estimated standard error, we can be confident that the variable is adding predictiveness to the model.

Central Message.

We replace P values with VIMP, which measures predictive and discovery effect sizes for a variable that are valid whether the regression model is correct or not.

APPENDIX E1. CALCULATING THE VIMP INDEX FOR A VARIABLE

The variable importance (VIMP) index for estimating the predictive effect size for a variable is obtained by a slight extension to the out-of-bag (OOB) error rate calculation. For concreteness, call the variable of interest β and let δ_β denote its VIMP index. The VIMP index δ_β is calculated by averaging the VIMP index for β from each bootstrap sample b, which we denote by δ_β,b. This latter value is calculated as follows. For a given bootstrap sample b, take the OOB data for β and “noise it up.” Noising the data is intended to destroy the association between β and the outcome. Use this altered OOB data to calculate the prediction error for the model. Call the noised-up prediction error Err_β,b. The VIMP index for β for the b bootstrap sample is

$${\mathit{\Delta }}_{\beta ,b}={\text{Err}}_{\beta ,b}-{\text{Err}}_{\mathrm{b}}.$$

The prediction error for the noised-up data will increase if β has a real effect in the model. Hence, comparing this prediction error to the original prediction error will yield a positive VIMP index δ_β,b if β is predictive. The VIMP index for β is obtained by averaging these values over the bootstrap realizations:

$${\mathit{\Delta }}_{\beta }=\frac{1}{B}\sum _{b=1}^B{\mathit{\Delta }}_{\beta ,b}=\frac{1}{B}\sum _{b=1}^B[{\text{Err}}_{\beta ,b}-\text{Er}{r}_b].$$

It follows that a large positive value indicates a variable β that has a large test-validated effect size (predictive effect size). Algorithm 1 provides a formal statement of this procedure. We make several remarks regarding the implementation of Algorithm 1.

ALGORITHM 1.

VIMP index for a variable β

1:	for b = 1, …, B do
2:	Draw a bootstrap sample of the data; fit the model to the bootstrap data.
3:	Calculate the prediction error, Errb, using the OOB data.
4:	Noise up the OOB data for β; use this to calculate the OOB error, Errβ;b.
5:	Calculate the bootstrap VIMP index δβ;b = Errβ;b − Errb.
6:	end for
7:	Calculate the VIMP index by averaging: ${\mathit{\Delta }}_{\beta }={\sum }_{b=1}^B{\mathit{\Delta }}_{\beta ,b}/B$.
8:	The OOB error for the model can also be obtained using ${\text{Err}}_{\text{oob}}={\sum }_{b=1}^B{\text{Err}}_b/B$
As stated the algorithm provides a VIMP index for a given variable β but in practice one applies the same procedure for all variables in the model. The same bootstrap samples are to be used when doing so. This is required because it ensures that the VIMP index for each variable is always compared with the same value Errb. Because all calculations are run independently of one another Algorithm 1 can be implemented using parallel processing. This makes the algorithm extremely fast and scalable to big data settings. The most obvious way to parallelize the algorithm is on the bootstrap sample. Thus on a specific computing machine on a cluster a single bootstrap sample is drawn and Errb determined. Steps 4 and 5 are then applied to each variable in the model for the given bootstrap draw. Results from different computing machines on the computing cluster are then averaged as in Steps 7 and 8. Noising up a variable is typically done by permuting its data. This is called permutation noising up and is used for nonparametric regression models. In the case of parametric and semiparametric regression models (such as Cox regression) in place of permutation noising up the regression coefficient estimate for b is set to zero. Setting the coefficient to zero is equivalent to setting the OOB data for β to zero and is a special feature of parametric models that provides a more direct and convenient way to noise up the data. As a side effect the algorithm can also be used to return the OOB error rate for the model Erroob (see Step 8). This can be useful for assessing the effectiveness of the model and identifying poorly constructed models. Algorithm 1 requires being able to calculate prediction error. The type of prediction error used will be context specific. For example in linear regression prediction error can be measured using mean squared error or standardized mean squared error. In classification problems prediction error is typically defined by misclassification. In survival problems a common measure of prediction performance is Harrell’s concordance index. Thus unlike the P value the interpretation of the VIMP index will be context specific.

CALCULATING THE MARGINAL VIMP

The marginal VIMP is calculated by a simple modification to Algorithm 1. In place of noising up a variable β, a second model is fit to the bootstrap data, but with β removed. The OOB error for this model is compared with the OOB error for the full model containing all variables. Averaging these values over the bootstrap realizations yields ${\mathit{\Delta }}_{\beta }^{\text{marg}}$. Algorithm 2 provides a formal description of the procedure.

ALGORITHM 2.

Marginal VIMP index for a variable β

1:	for b = 1, …, B do
2:	Draw a bootstrap sample of the data; calculate the model OOB prediction error, Errb.
3:	Fit a second model, but without β, and calculate its OOB prediction error, ${\text{Err}}_{\beta ,b}^{\text{marg}}$
4:	end for
5:	Calculate the marginal VIMP by averaging: ${\mathit{\Delta }}_{\beta }^{\text{marg}}={\sum }_{b=1}^B[{\text{Err}}_{\beta ,b}^{\text{marg}}-{\text{Err}}_b]/B$