Population Pharmacokinetic/Pharmacodynamic Modeling of Depot Testosterone Cypionate in Healthy Male Subjects

Abstract

A randomized, double‐blind clinical trial was conducted to investigate long‐term abuse effects of testosterone cypionate (TC). Thirty‐one healthy men were randomized into a dose group of 100, 250, or 500 mg/wk and received 14 weekly injections of TC. A pharmacokinetic/pharmacodynamic (PK/PD) model was developed to characterize testosterone concentrations and link exposure to change in luteinizing hormone and spermatogenesis following long‐term TC administration. A linear one‐compartment model best described the concentration‐time profile of total testosterone. The population mean estimates for testosterone were 2.6 kL/day for clearance and 14.4 kL for volume of distribution. Weight, albumin, and their changes from baseline were identified as significant covariates for testosterone. The estimated potency of total testosterone (tT) with respect to suppression of luteinizing hormone (LH) synthesis was 9.33 ng/mL. Simulation based on the indirect response model suggests the suppression of endogenous testosterone secretion, LH synthesis, and spermatogenesis was more severe and of greater duration in the 250 mg and the 500 mg dose groups.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Long‐term excessive dosing of anabolic steroids can lead to serious health risks. One of the most significant physiologic changes induced by the use of testosterone esters is a dose‐dependent impairment of normal testicular androgen secretion and spermatogenesis.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study characterizes and quantifies changes in testosterone and LH concentration, and spermatogenesis following long‐term TC administration.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ The study developed a PK/PD model based on a randomized three‐arm (100 mg, 250 mg, and 500 mg/week) clinical trial, which quantified the relationship between testosterone exposure after exogenous administration and suppression of LH and spermatogenesis. Model results showed that the suppression of endogenous testosterone secretion, LH synthesis, and spermatogenesis was more severe and of greater duration in the 250 mg and the 500 mg dose groups.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS

☑ This PK/PD model provides a framework to quantify and predict the change in LH and spermatogenesis after exogenous testosterone administration. The average concentration of tT in the past 18 weeks was found to have the strongest association with suppression of spermatogenesis.

Endogenous testosterone is responsible for stimulation and development of male sex organs and for maintenance of secondary male characteristics.1 An abnormally low level of testosterone is referred to as hypoandrogenism, in men it may result in decreased sex hormone production and deficiency in gamete production and regulation. Depot‐testosterone (testosterone cypionate (TC)) is an oil‐soluble ester of the hormone testosterone and is indicated for hormone replacement therapy in men who have symptoms of deficiency or absence of endogenous testosterone.2 It can be used to treat both congenital and acquired hypoandrogenism.3

Aside from the therapeutic indications, the illegal use of TC and other anabolic steroids by athletes to gain an unfair advantage in athletic competitions have been reported for over 50 years.4, 5, 6 Numerous studies have shown that long‐term use or excessive dosing of anabolic steroids can lead to serious health risks. One physiologic change is a dose‐dependent impairment of normal testicular androgen secretion and spermatogenesis.7, 8, 9 This effect is believed to result from the suppression of circulating luteinizing hormone (LH) and follicle stimulating hormone through a feedback loop system of the hypothalamic‐pituitary‐gonadal (HPG) axis.9, 10 Most studies evaluating anabolic steroid use are observational and retrospective with studied doses substantially lower than the dose commonly used by illicit steroid users.11, 12, 13, 14

A randomized, double‐blind, placebo‐controlled study was conducted by MacIndoe et al.11 to investigate the effects of weekly TC injections upon the HPG axis. Our main objective of developing a pharmacokinetic/pharmacodynamic (PK/PD) model based on these data is to characterize and quantify the effect of long‐term administration of supratherapeutic doses of TC on suppression of LH synthesis and spermatogenesis. This information may help us better understand the effect of the illegal use of anabolic steroids on the impairment of testicular androgen secretion.

METHODS

Study design

The study design of the trial has been published elsewhere.11 In summary, this is a randomized, double‐blind clinical trial in which 31 healthy male subjects were randomized into the 100 mg/wk (n = 10), 250 mg/wk (n = 10), and 500 mg/wk (n = 11) dose groups. The high dosing regimens of 250 mg/week and 500 mg/week resemble doses illegally used by athletes. The study included two consecutive weekly injections of TC placebo, followed by 14 consecutive weekly TC injections. This dosing regimen was chosen to mimic the common cycling duration observed in the community.6 After the last weekly injection of active agent, the subjects received 12 consecutive weeks of TC placebo injections.

All blood samples were collected between 7 am and 9 am. After the last injection of TC, serum was obtained for total testosterone (tT) and free testosterone (fT) determinations at biweekly intervals of 7 days. The tT and fT values measured in samples drawn immediately postdose, after 8 hours, and then daily for 26 consecutive days after the last active TC injection were used to determine their elimination. Biweekly luteinizing hormone releasing hormone (LHRH) stimulation tests were performed 7 days after the last injection of either placebo or testosterone to assess pituitary gonadotropin secretion. Venous blood samples for LH and follicle stimulating hormone were obtained before and 30, 60, and 120 minutes after the intravenous infusion of 100 mcg LHRH. Semen samples were obtained by masturbation at baseline (week 0), and weeks 2, 16, 21, 28, and, in some subjects, at week 40, and assessed for total and motile sperm concentrations. Subjects were asked to be sexually abstinent for 24 hours before sample collection.

Model building

Nonlinear mixed effects modeling was performed using NONMEM version 7.2. The PK/PD data analysis was performed sequentially. The PK model for tT was first fitted to the data, and the PD model for suppression of LH synthesis, and spermatogenesis was then sequentially fitted conditional on fixed individual PK parameters. Detailed description of model development, model evaluation, and covariate selection can be found in the Supplementary Material. A variety of compartmental models were evaluated with the modeling attempts to fit the interplay between testosterone and LH guided by the known physiology in the HPG axis. Potential covariates (all covariates listed in Table 1) were selected based on the physiological plausibility and prior knowledge from published literature. The potential covariates were tested in a stepwise manner on clearance (CL), volume (V), and absorption rate Ka, as implemented in PsN.15 Effect of covariates was illustrated using simulations that accounted for parameter precision of fixed effects.

Table 1.

Baseline demographic characteristics, protein levels, and laboratory test values of 31 healthy volunteers.

Characteristic	Median (range)
	100 mg (N = 10)	250 mg (N = 10)	500 mg (N = 11)
Baseline tT, ng/mL	6.44 (4.04–9.5)	5.93 (4.2–10.6)	5.78 (2.31–9.48)
Baseline fT, ng/dL	2.41 (1.58–4.17)	2.38 (0.28–3.55)	2.44 (1.08–3.09)
Age, years	26.5 (22–32)	25.5 (22–39)	30 (21–39)
Weight, kg	82.2 (61.7–115)	88.8 (61.7–105)	84.7 (60.7–115)
Blood urea nitrogen, mg/dL	14.5 (10–17)	15 (9–18)	15 (8–19)
Serum creatinine, mg/dL	1.05 (0.8–1.5)	1.1 (1–1.2)	1 (0.9–1.2)
Creatinine clearance, mL/min	124 (89.6–179)	123 (90.4–153)	125 (84.3–166)
Albumin, g/dL	4.55 (4.4–6.9)	4.55 (4.3–5.1)	4.6 (1.6–5)
Globulin, g/dL	2.75 (2–3.1)	2.9 (2.4–3.5)	3 (2.8–3.2)
Thyroxine‐binding globulin, ug/mL	19.5 (10–31)	18.5 (11–26)	21 (14–26)
Sex hormone‐binding globulin, nmol/L	26 (17–46)	24.5 (11–48)	22 (13–47)
Alkaline phosphatase, IU/L	63.5 (52–89)	52 (41–97)	67 (50–98)
Lactate dehydrogenase, IU/L	157 (141–194)	158 (121–196)	143 (111–184)
AST, IU/L	23 (17–32)	20.5 (14–53)	18 (12–34)
ALT, IU/L	22 (16–52)	27.5 (12–47)	19 (10–40)
GGT, IU/L	22 (10–54)	20 (10–54)	18 (10–58)
Total bilirubin, mg/dL	7.25 (6.9–8.1)	7.5 (6.8–8.4)	7.6 (7.1–8)
Direct bilirubin, mg/dL	0.2 (0.2–0.4)	0.25 (0.1–0.4)	0.3 (0.1–0.5)
Triglyceride, mg/dL	110 (40–335)	122 (43–532)	123 (58–538)
Cholesterol, mg/dL	199 (140–238)	184 (139–224)	198 (162–241)
HDL, mg/dL	39 (27–70)	39 (21–54)	33 (22–47)
LDL, mg/dL	125 (65–186)	116 (79–162)	136 (79–181)

ALT, alanine aminotransferase; AST, aspartate aminotransferase; GGT, gamma‐glutamyl transferase; HDL, high‐density lipoprotein; LDL, low‐density lipoprotein; fT, free testosterone; tT, free testosterone.

RESULTS

Population pharmacokinetics of testosterone cypionate

Baseline demographic characteristics and laboratory tests for 31 subjects are summarized in Table 1. Overall, 729 tT and 379 LH serum samples were available. Among these observations, 299 tT samples were obtained within 26 days from the last dose. These samples were used to determine the main PK parameters.

The data were best fit using a one‐compartment model with linear elimination and first‐order absorption. Following the cessation of TC administration, tT concentrations were lower than pretreatment concentrations initially and then slowly returned back to baseline. Initially, the inhibition of endogenous testosterone was modeled with constant reduction of its secretion rate in prespecified intervals from week 4 to week 19 to derive post hoc PK parameters as inputs for PD model development. The model was then updated with an indirect maximum effect (E _max) model to describe the positive regulation of LH on testosterone secretion. The individual post hoc LH prediction from the PD model was used in this indirect model because of different sampling time of testosterone and LH.

The differential equation describing the testosterone PKs is shown below:

$$\frac{d\left(ABS\right)}{d\left(t\right)}=-ka\hspace{0.17em}\ast ABS$$

$$\frac{d\left(Te\right)}{d\left(t\right)}={\beta }_i+ka\ast ABS-\frac{CL}{V}\hspace{0.17em}\ast Te$$

$${\beta }_i={\beta }_{base}+E_{\text{max}}\ast \frac{L{H}^{\lambda }}{L{H}^{\lambda }+L{H_{50}}^{\lambda }}$$

where ka is the first‐order absorption rate, and CL and V are clearance and central volume of distribution. The tT secretion rate ${\beta }_i$ is equal to ${\beta }_{base}$ plus upregulation through LH concentration. The initial condition for Te was estimated as fixed parameter with random effect during model development. The E _max represents the maximum effect of LH on endogenous testosterone secretion, and LH, LH₅₀, and $\lambda$ represent LH concentration, the LH concentration when its upregulation on endogenous testosterone secretion reaches half of the maximum effect, and hill coefficient.

The final PK parameters for total testosterone are shown in Table 2. The CL/F and V/F for tT were estimated to be 2.6 (kL/day) and 14.4 kL in healthy men with median covariate values. The median post hoc half‐life was calculated to be 4.05 days for tT. The E _max and $L{H}_{50}$ describing the positive regulation of LH concentration on the testosterone secretion rate were estimated to be 12.5 mg/day and 12.9 IU/L. The estimates of CL and V were insensitive to the inclusion of LH upregulation on the endogenous secretion rate; the difference in mean post hoc CL and V was found to be within 20% when compared to the model without LH upregulation. A combined additive and proportional model was applied to model the residual error.

Table 2.

Population pharmacokinetic parameter estimates and bootstrap results for total testosterone in 31 healthy volunteers.

Parameter	Final model	Bootstrapa
	Estimate	Median	RSE (%)	95% CI
CL/F, kL/day	2.6	2.6	4.53	(2.42–2.8)
V/F, kL	14.4	14.4	12.1	(11.9–17.6)
Ka, $\mathrm{d}\mathrm{a}{\mathrm{y}}^{-1}$	1.22	1.22	44.9	(0.785–2.67)
${\beta }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$, mg/day	6.24	6.25	23.3	(3.53–8.09)
$Lambda\left(\lambda \right)$	1.18	1.43	55.9	(0.43–2.74)
$E_{\text{max}}$, mg/day	12.5	12.3	25.2	(7.75–18)
$L{H}_{50}$, IU/L	12.9	12.7	63.1	(0.892–23.7)
A_0, TC	6.24	6.21	5.82	(5.63–6.85)
${\theta }_{\mathrm{B}\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{u}\mathrm{m}\mathrm{i}\mathrm{n}-\mathrm{V} }$	−1.55	−1.84	58.7	(−3.56 to −0.842)
${\theta }_{\mathrm{C}\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{u}\mathrm{m}\mathrm{i}\mathrm{n}-\mathrm{V} }$	−0.27	−0.27	25.4	(−0.369 to −0.108)
${\theta }_{\mathrm{B}\mathrm{W}\mathrm{T}-\mathrm{V} }$	1.71	1.77	36.7	(0.776–2.98)
${\theta }_{\mathrm{B}\mathrm{W}\mathrm{T}-\mathrm{C}\mathrm{L} }$	0.785	0.793	17.4	(0.595–1.03)
${\theta }_{\mathrm{C}\mathrm{W}\mathrm{T}-\mathrm{C}\mathrm{L} }$	0.016	0.016	45.2	(0.00382–0.0254)
${\sigma }^2 \mathrm{a}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}$	0.261	0.191	105	(0.00261–0.839)
${\sigma }^2 \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}$	0.057	0.057	18.7	(0.039–0.073)
IIV_CLb	9.66% (25.2)	8.60%	57.3	(2.98%–12.29%)
IIV_V	37% (14.6)	35.9%	52.8	(18.3%–51.7%)
IIV_Ka	53.9% (42.5)	52.4%	89.7	(0.54%–87.5%)
IIV_ $E_{\text{max}}$	45.3% (16.3)	43.1%	71.6	(14.5%–66.3%)
IIV_ $\lambda$	75.9% (25.3)	72.9%	47.4	(40.0%–99.6%)
IIV_A_0, TC	13.6% (49.6)	13.3%	77.1	(0.14%–21.3%)

CI, confidence interval; CL, clearance; E _max, maximum effect; IIV, inter‐individual variability; RSE%, percentage of relative standard error; TC, testosterone cypionate; V, volume.

^aMedian, RSE, and 95% CIs were calculated based on 500 nonparametric bootstrap results.

^bShrinkage of IIV parameters was reported along with parameter estimates.

Significant covariates for tT included baseline weight, baseline albumin, and change in weight and albumin from baseline. Power models for baseline weight and albumin, linear models for change in albumin, and exponential models for change in weight resulted in the lowest objective function values (OFVs). The Forest plot of covariate effects (Figure 1) illustrates that albumin, change in albumin from baseline, and change in weight from baseline are not clinically important for the testosterone PK parameters, as the majority of 95% confidence interval (CI) of these covariate effects fall within the interval of 0.8 to 1.25. On the other hand, a heavier subject (95th percentile, 110 kg) is estimated to have a 1.23 (95% CI = 1.16–1.32) and 1.58 (95% CI = 1.17–2.3) fold higher CL/F and V/F compared to a typical subject (median = 85 kg), respectively, suggesting weight had a modest effect on TC PKs. However, considering the natural variation in testosterone concentrations, weight‐based dosing is not likely to be needed for an i.m. injection of TC. Of 496 observations for covariates weight, albumin, and globulin, missing values were replaced by the previous measurements in 30 (6.05%), 9 (1.81%), and 10 (2.02%) time points, respectively. Basic goodness of fit (GOF) plots for tT are shown in Supplementary Figure S1. Prediction‐corrected visual predictive checks (VPCs) stratified on dose groups are shown separately for intensive and extensive sampling periods in Figure 2 . Overall, the GOF plots and the prediction‐corrected VPCs indicated that the model adequately describes the central tendency and the variability of the PK profile of testosterone.

Figure 1.

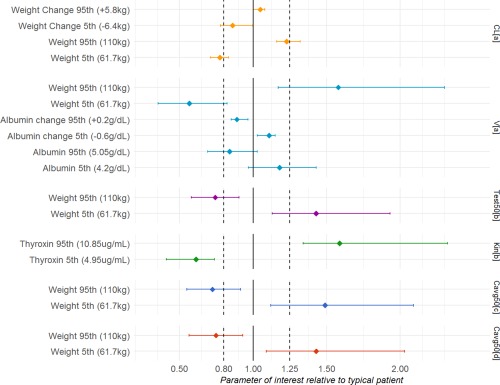
Effect of baseline and time‐varying covariates on pharmacokinetic parameters (clearance (CL) and volume (V)) and pharmacodynamic parameters for suppression of luteinizing hormone (half‐maximal inhibitory concentration (IC₅₀), K_in) and spermatogenesis ( $\mathrm{C}\mathrm{a}\mathrm{v}{\mathrm{g}}_{50}$). Error bars indicate 95% confidence interval based on a nonparametric bootstrap.

Figure 2.

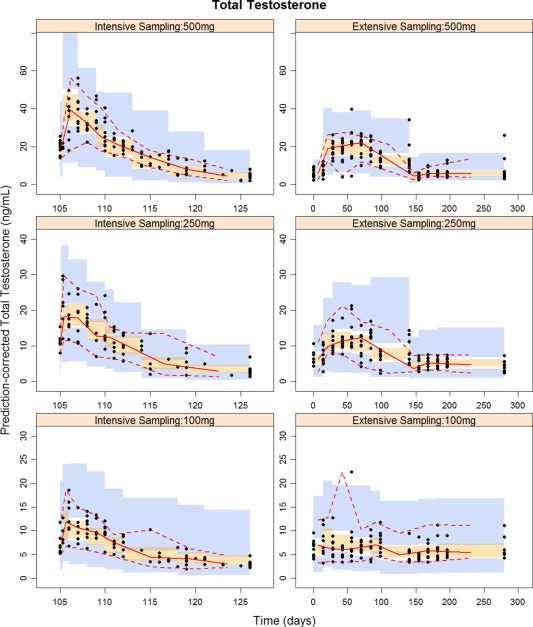
Prediction‐corrected visual predictive check for total testosterone obtained from 1,000 simulations stratified on dose and sampling period. Black solid points are observed concentrations. Red solid and dashed lines represent 2.5th, 50th, and 97.5th percentiles of observed data. The shaded areas indicate simulation‐based 95% confidence intervals around the median (orange) and the 2.5th and 97.5th percentiles (blue) from 1,000 simulations with the final model. Note: All subjects received 14 weekly injections of testosterone cypionate (TC) from week 2 to week 15. Intensive pharmacokinetic sampling was collected immediately postdose, at 8 hours, and then daily for 26 consecutive days after the last active TC injection (week 15).

Suppression of luteinizing hormone and spermatogenesis

The PD end point was chosen to be the LH concentration at 30 minutes after the stimulation test (LH30). An indirect effect model best described the LH30 observations:

$$\frac{\mathrm{d}\left(\mathrm{L}{\mathrm{H}}_{30}\right)}{\mathrm{d}\left(\mathrm{t}\right)}={\mathrm{K}}_{\mathrm{i}\mathrm{n}}\left(1-\mathrm{I}\mathrm{N}\mathrm{H}\right)-{\mathrm{K}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\ast {\mathrm{L}\mathrm{H}}_{30}$$

INH describes the inhibitory effect of testosterone on LH synthesis using sigmoid $E_{\mathrm{m}\mathrm{a}\mathrm{x}}$ model with effect compartment: INH =  ${\mathrm{C}}_{\mathrm{e}}^{\lambda }$/( ${\mathrm{C}}_{\mathrm{e}}^{\lambda }+{\mathrm{T}\mathrm{C}}_{50}^{\lambda }$). $\mathrm{T}\mathrm{h}\mathrm{e} {\mathrm{C}}_{\mathrm{e}}$ is the hypothetical effect compartment concentration accounting for the lag between the increase in testosterone and the loss of LH. $\text{The} \mathrm{T}{\mathrm{C}}_{50}$ is the tT concentration when LH synthesis is inhibited by half. The $E_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is fixed to 1 as LH synthesis is fully inhibited during the study. The initial condition for $\mathrm{L}{\mathrm{H}}_{30}$ is equal to K_in divided by K_out. The final PD model estimates and covariate‐parameter relationships are shown in Table 3. The $\mathrm{T}{\mathrm{C}}_{50}$ and $\lambda$ were estimated to be 9.33 ng/mL and 18.3, respectively. Baseline weight and thyroxin were found to be significant covariates for $\mathrm{I}{\mathrm{C}}_{50}$ and K_in. Based on the Forest plot of covariate effects shown in Figure 1, the 95% CI of effects of weight on $\mathrm{T}{\mathrm{C}}_{50}$ and thyroxin on $K_{in}$ were almost fully outside of the specified interval 0.8 to 1.25, indicating potential clinical significance. The $\mathrm{T}{\mathrm{C}}_{50}$ of a heavier subject (95th percentile, 110 kg) is estimated to be 0.74 (95% CI = 0.58–0.91) fold of that of a typical subject with median weight (85 kg). Simulated LH profiles in subjects with different body weights and thyroxin values are shown in Supplementary Figure S2. Based on simulation, LH suppression in volunteers with larger body weight is estimated to last longer. No difference in simulated LH suppression was identified among volunteers with different thyroxin values. Sensitivity analyses were also conducted to fit the same indirect response model to end points LH60 and LH120. All models had similar parameter estimation and comparable performance.

Table 3.

Population pharmacodynamic estimates and bootstrap results of suppression of LH synthesis and sperm count following long‐term dosing of testosterone cypionate in 31 healthy volunteers.

Parameter	Final model	Bootstrapa
	estimate	Median	RSE (%)	95% CI
LH
Kin, IU/day	1.7	1.7	14.4	(1.36–2.16)
Kout, L/day	0.11	0.11	10.8	(0.093–0.133)
${\mathrm{T}\mathrm{e}\mathrm{s}\mathrm{t}}_{50},$ ng/mL	9.33	9.35	5.62	(8.55–10.1)
$Lambda,\hspace{0.17em}\lambda$	18.3	18.7	21.6	(13.6–27.3)
${\mathrm{k}}_{\mathrm{e}0},$ mL/day	0.0321	0.0318	11.2	(0.0261–0.0377)
${\sigma }^2 \mathrm{a}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}$	0.397	0.395	10.8	(0.331–0.463)
${\theta }_{\mathrm{B}\mathrm{w}\mathrm{t}-\mathrm{I}\mathrm{C}50 }$	−1.14	−1.13	38.9	(−1.88 to −0.494)
${\theta }_{\mathrm{B}\mathrm{t}\mathrm{h}\mathrm{y}\mathrm{r}\mathrm{o}\mathrm{x}\mathrm{i}\mathrm{n}-\mathrm{K}\mathrm{i}\mathrm{n} }$	1.19	1.22	27.1	(0.916–1.96)
IIV_Kinb	39.2% (14)	37.6%	51.4	(21.5%–52.4%)
IIV_ ${\mathrm{I}\mathrm{C}}_{50}$	27.7% (53.5)	27.1%	32.2	(19.0%–33.3%)
IIV_ $\lambda$	42.2% (7.2)	38.0%	103	(0.42%–71.6%)
IIV_ ${\mathrm{k}}_{\mathrm{e}0}$	46.6% (0.5)	45.2%	43.7	(31.1%–64.3%)
Sperm count
Kin,/day	6.17	6.40	58.5	(4.92–9.02)
Kout,/day	0.0696	0.0714	59.3	(0.0616–0.0966)
${\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{g}}_{50},$ ng/mL	8.68	8.74	10.5	(7.3–10.3)
$Lambda,\hspace{0.17em}\lambda$	11.3	11.7	31.5	(6.89–19.7)
$Phi\left(\varphi \right)$	4.65	4.58	19.2	(3.67–6.47)
${\theta }_{\mathrm{B}\mathrm{w}\mathrm{t}-{\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{g}}_{50} }$	−1.27	−1.25	37.5	(−2.06 to −0.536)
${\sigma }^2 \mathrm{a}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}$	0.429	0.421	19	(0.311–0.56)
IIV_Kin b	46.8% (14.2)	45.8%	35.2	(31.6%–59.3%)
IIV_ $Phi\left(\varphi \right)$	234% (35.9)	214%	73.6	(110%–377%)
IIV_ ${\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{g}}_{50}$	23.2% (18.6)	22.4%	57.4	(9.33%–31.53%)
IIV_ $\lambda$	100% (28.9)	98.3%	60.6	(63.8%–159.7%)

CI, confidence interval; LH, luteinizing hormone; RSE%, percentage of relative standard error.

^aMedian, RSE, and 95% CIs were calculated based on 500 nonparametric bootstrap results.

^bShrinkage of IIV parameters was reported along with parameter estimates.

Semenogram data were available in 29 subjects, with two subjects not providing sample due to vasectomies. A total of 159 sperm samples were obtained over the 40 weeks of study. A total of 11 subjects missed 15 of 174 (8.6%) planned visits for collection of sperm samples; 7 subjects (24.1%) missed the sample collection at the end of the study, which might bias the estimate of suppression level of spermatogenesis at that time point. Because there is a very high correlation between sperm count and sperm motility (adjusted R² = 0.87), the sperm count was used as the main PD end point. An indirect effect model best described the sperm counts over time, the differential equation of which is the same as the indirect model used to fit LH suppression. The average tT concentration across different time periods (from Cavg since the beginning to Cavg in the past week) preceding each observation were selected to represent testosterone exposure and its associations with suppression of spermatogenesis. The inhibition of testosterone dosing on spermatogenesis over time was best described by an indirect sigmoid E _max model without effect compartment: $INH=1-E_{\text{max}}\ast Cav{g}^{\lambda }/(Cav{g}^{\lambda }+Cav{g}_{50}^{\lambda })$. Cavg in the past 18 weeks (Cavg_18 weeks) was found to best describe the effect of exogenous testosterone administration on suppression of spermatogenesis (with lowest OFV). The Cavg_18 weeks for semen data measured at a time <18 weeks (baseline and between 2 and 16 weeks) is the average concentration from beginning to the time of measurement. Logistic transformation was applied on $E_{\text{max}}$ in order to constrain its value between 0 and 1: $E_{\text{max}}=\frac{\exp \left(PHI\right)}{1+\exp \left(PHI\right)}.$ An additive error model was applied to PHI, and exponential error models were applied to K_in, $\lambda ,\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d} \mathrm{C}\mathrm{a}\mathrm{v}{\mathrm{g}}_{50}.$ A sensitivity analysis using sperm motility as the PD end point with the same indirect response model was also conducted and had similar parameter estimation and comparable performance. Final PD model estimates for suppression of sperm counts and sperm motility are shown in Table 3 and Supplementary Table S1. ${\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{g}}_{50}$ was estimated to be 8.68 ng/mL. Baseline weight was found to be a significant covariate for $\mathrm{C}\mathrm{a}\mathrm{v}{\mathrm{g}}_{50}$. The ${\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{g}}_{50}$ of a heavier subject (95th percentile, 110 kg) was estimated to be 0.72 (95% CI = 0.55–0.91) fold of that of a typical subject with median weight (85 kg).

Basic GOF plots were plotted against observations of LH and sperm counts and motility in Supplementary Figure S3. The visual predictive checks (VPC) for LH and sperm counts are shown in Figure 3. Overall, diagnostic plots show that indirect response models were able to describe the suppression of LH synthesis and spermatogenesis after long‐term dosing of TC.

Figure 3.

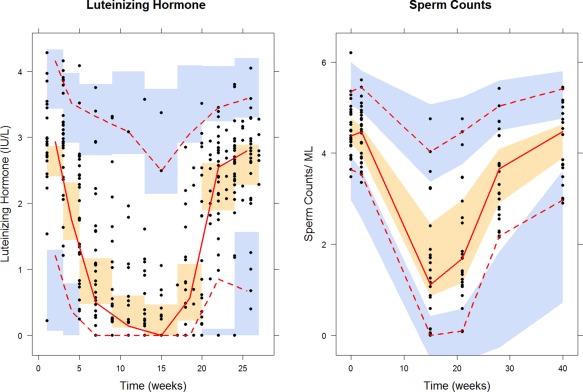
Visual predictive checks for luteinizing hormone (left) and sperm counts (right) obtained from 1,000 simulations. Black solid points are observed concentrations. Red solid and dashed lines represent 2.5th, 50th, and 97.5th percentiles of observed data. The shaded areas indicate simulation‐based 95% confidence intervals around the median (orange) and the 2.5th and 97.5th percentiles (blue) from 1,000 simulations with the final model.

The magnitude and variability of suppression of LH and sperm counts based on post hoc parameters at each dose level were summarized and shown in Figure 4. Both the observed data (black dots) and suppression level generated from post hoc parameters (colored line and areas) suggest the suppression of LH was more severe in the 250 mg and the 500 mg groups, whereas the suppression is variable in the 100 mg group. The median suppression level for the 100 mg group was >90% and has a wide CI during 14 weeks of active TC dosing. On the other hand, the lower bound of 90% CI of suppression level was higher than 98% from week 7 to week 16 in the 250 mg group and from week 12 to week 17 in the 500 mg group. The recovery of suppression of LH synthesis was also found to be slower in the 500 mg group compared to the 250 mg and the 100 mg groups. The median suppression level dropped to below 10% in week 10 after the last testosterone administration in the 500 mg group, compared after week 5 in the 100 mg group and week 6 in the 250 mg group.

Figure 4.

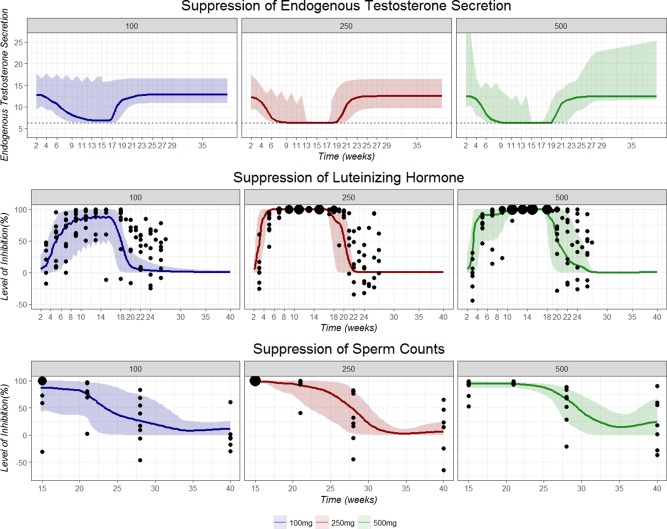
Summary of level of suppression of endogenous testosterone secretion (top), luteinizing hormone synthesis (LH; middle), and sperm counts (bottom) over time during and after testosterone cypionate dosing based on post hoc parameters from 31 subjects. Colored solid lines represent the median suppression level. Horizontal dashed line represents basal endogenous testosterone secretion independent of LH upregulation. Shaded areas indicate 95% confidence interval of the suppression level. Blue: 100 mg, Red: 250 mg, and Green: 500 mg. Black solid points represent the observed percentage change of variable of interest (LH30 or sperm counts) from baseline. The size of black points represents the frequency of observations.

Similarly, the suppression of sperm counts was much more severe in the high dose groups (Figure 4). At the end of 14 weeks of TC dosing, the sperm count was found to be completely suppressed in both the 250 mg and the 500 mg groups. The median suppression level at week 15 in the 250 mg and the 500 mg groups were simulated to be 98.2% and 94.9%, respectively. The recovery of sperm secretion (K_in) also seems to be slower in the higher dose group, with the median suppression level estimated to be 66.9% for 500 mg group, 48.4% for 250 mg group, and 26.6% for the 100 mg group at week 28, respectively. At the end of the study period (week 40) the sperm secretion (K_in) almost returned to normal in the 100 mg and the 250 mg groups, but the sperm counts in some subjects are still lower than baseline values (suppression level = 24.0; 95% CI = 0–67%). As there were 7 subjects (24.1%) who missed the semen collection at the end of the study, a sensitivity analysis including 22 subjects with complete data only was conducted, and parameter estimates were very similar (data not shown).

DISCUSSION

Following the depot administration of TC, the PKs of tT were satisfactorily described by the one‐compartmental model with first‐order absorption. The limited number of samples in the absorption phase (1–2 samples per subject) prevents using a more plausible absorption model for the high lipophilicity of testosterone in an oil base and administered i.m., such as a mixed zero‐order and first‐order model with lag time.16 This could lead to flip‐flop PKs and can cause difficulties in estimation and interpretation of PK parameters.17 The half‐life of testosterone undecanoate (TU) following oral administration is around 150 minutes,18 which is very different from the half‐life estimate of 21–34 days following the i.m. injection of TU reported by Behre et al.19 The large difference in half‐lives of TU between oral and i.m. formulation suggests that flip‐flop PKs are occurring with testosterone esters, which is also reported in the published literature20 and for the i.m. injection of nandrolone.21 The i.m. injection of TC is also likely to have flip‐flop kinetics, in such a scenario, diffusion and release from an oily depot site is the rate‐limiting step to systemic availability.

Endogenous testosterone secretion was described by the combination of basal testosterone secretion and positive regulation by LH. The LH stimulates Leydig cell production of testosterone. The interplay between LH and testosterone after treatment with gonadotropin‐releasing hormone (GnRH) agonists and antagonists has also been described previously.22 The positive regulation of LH was completely suppressed between week 13 and week 17 for the 100 mg group and between week 7 and week 19 for the 250 mg and the 500 mg dose groups, which is consistent with the clinical observation that it took shorter time to observe the loss of basal and LHRH‐stimulated LH in the 250 mg and the 500 mg groups. The mean post hoc endogenous testosterone secretion rate at baseline in PK models for tT models was 12.5 mg/day. It is suggested that men produce between 4 and 11.8 mg of testosterone per day,23 which is slightly lower than our model estimate. However, there is wide variability in normal testosterone concentrations with ranges reported between 300 and 1,000 ng/dl,24 our model estimates of endogenous testosterone secretion rate are consistent with reported values and close to reported physiological values. The endogenous testosterone secretion rate over time is presented in Figure 4. Inhibition of endogenous secretion lasted longer and was more severe in the 250 mg and the 500 mg groups. The upregulation of LH on endogenous testosterone secretion was completely lost during week 9 to week 19 in both the 250 mg and the 500 mg groups. The endogenous testosterone secretion rate returned to baseline at approximately week 23 in all three dose groups. The parameter estimates (LH50 = 12.9 IU/L; E _max = 12.5) of downregulation of endogenous testosterone through inhibition of LH was slightly different from those reported by Tornøe et al.22 (LH50 = 5.18 IU/L; E _max = 77.5), but they are not directly comparable because we use different differential equation to fit the interplay between LH and testosterone secretion.

Inclusion of time‐varying covariates besides resulted in lower interindividual variability on the main PK tT parameters. However, changes in weight and albumin concentrations were likely not clinically significant. Analysis of covariate effects suggests baseline weight is the only potential covariate of clinical importance for the PKs of TC.

It is difficult to calculate the PK parameters of TC using traditional noncompartmental methods, especially when the endogenous testosterone secretion rate is suppressed during the course of TC administration and the testosterone secretion rate is regulated by the LH‐testosterone feedback loop system in HPG axis. Our estimated post hoc median tT half‐life was 4.05 days, which is shorter than the mean reported elimination half‐life of 6.9 days determined using a noncompartmental analysis.11 Such inconsistency is believed to result from failure to consider endogenous testosterone production. When we assume endogenous testosterone secretion is 0 in the PPK analysis, the median estimated half‐life increases to 6.87 days.

There are no population PK data available for the long‐term supratherapeutic administration of testosterone ester. The developed model‐based PPK approach allowed us to estimate endogenous testosterone production rate during and after TC administration.

After characterizing the PKs of long‐term TC dosing in healthy male subjects, the PD model was sequentially developed. An indirect response model was used to describe the change of LH30 during and after TC dosing. The LH concentration after a stimulation test was chosen as the PD marker in part because the response of LH to the stimulation test was different across all three TC dose groups. The lag between loss of basal and stimulated LH levels has been previously observed.25 The ability of exogenous testosterone administration to suppress LH release was incorporated into the PD model. A sigmoid ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ model was applied to link testosterone concentrations with its inhibitory effect on LH synthesis. The addition of an effect compartment accounted for the lag between loss of LH and the increase in testosterone concentration.

We developed a PD model to describe the inhibition of spermatogenesis during TC dosing and the subsequent recovery. The effect of average tT concentration during different dosing intervals preceding each sperm observation was tested on spermatogenesis in the indirect sigmoid E _max model. The average testosterone concentration in the past 18 weeks preceding each observation was found to result in the lowest OFV. The effect of tT Cavg across different time periods on suppression of sperm counts was also tested. Bias in VPC and simulation results was identified using exposure metrics with shorter observation periods than 14 weeks. The requirement of long‐time PK measurement preceding each semen data aligns well with the clinical observation that suppression level of spermatogenesis at 13 weeks after the last active TC administration was still high in both the 250 mg and 500 mg dose groups, although it may limit the practical applicability of the model. To the best of our knowledge, this is the first time the relationship between testosterone exposure after exogenous administration and suppression of spermatogenesis has been quantified. The Cavg of testosterone in the past 18 weeks was found to have the strongest association with suppression of spermatogenesis and also provided information regarding the duration of effect of TC administration on spermatogenesis.

Most studies evaluating abuse effects of androgen steroids are observational studies and study designs are often not randomized, double‐blind, or placebo‐controlled. Subjects are usually exposed to a dose much lower than what is commonly used by illicit steroid users and administered for only a short period. The untoward effects of anabolic steroids on a healthy body, therefore, may be underestimated in the literature. To best of our knowledge, this is the first time a mechanistic population PK/PD model has been developed to quantify the relationship between testosterone exposure after exogenous administration and subsequent suppression of LH and spermatogenesis during and after long‐term supratherapeutic administration of testosterone ester in healthy subjects. Tornøe et al.22 developed a PK/PD model of HPG axis describing the changes in LH and testosterone concentrations after treatment with GnRH agonist triptorelin and GnRH receptor blocker degarelix. Pechstein et al. adequately described the PK/PD relationship between plasma levels of Cetrorelix and testosterone suppression following a single i.v. and s.c. dosing. However, only one single i.v. or s.c. administration was given to healthy subjects in both studies and neither captured the change in spermatogenesis. The proposed PK/PD model in our analysis allows for the quantification and comparison of the suppression of LH synthesis and spermatogenesis at various time points during and after administration of exogenous testosterone esters. We were also able to extrapolate the recovery of LH secretion and spermatogenesis in future time points based on post hoc parameters.

One limitation of the current study is PPK model was developed based on the data from 31 healthy subjects, the precision of estimated covariate effects (Figure 1) was expected to be relatively low due to the small sample size. Re‐estimation of the PK parameters may be necessary if the current PPK model is going to be applied to the patient population. A series of physiological changes in renal function, body composition, or protein concentrations is likely to affect the binding affinity of testosterone as well as the PK profile of exogenous testosterone administration in the elderly patients.26, 27 Certain patient populations may also have lower levels of endogenous testosterone secretion, and altered ${\beta }_{base}$ compared with our model estimates. The small sample size (N = 31) may limit the precise estimation of suppression level of LH and spermatogenesis. The LH suppression for the 250 mg and 500 mg doses during TC administration were consistent and severe, whereas it was variable for the 100 mg dose. The variability of LH recovery after TC administration was large in all three groups. Similarly, for spermatogenesis, suppression at week 15 and week 21 were precisely estimated but recovery was estimated with wide CIs. The study design did not follow subjects long enough to allow observation of complete recovery from inhibition of spermatogenesis, which may have contributed to the high uncertainty in the estimates of K_in and K_out.

In summary, we developed a PK/PD model to characterize the PK profile of tT following long‐term weekly injection of TC, and linked testosterone exposure to the PD effects, including suppression of LH synthesis and spermatogenesis and their recovery during TC dosing in healthy men. Our model supports the finding that the suppression of endogenous testosterone secretion, LH synthesis, and spermatogenesis is more severe and of greater duration in subjects receiving higher TC doses.

Source of Funding

This project was supported by a grant from the National Institute on Drug Abuse at the National Institutes of Health R01DA008347.

Conflict of Interest

The authors declared no conflict of interest.

Author Contributions

Y.B. and D.J.M. wrote the manuscript. P.P. designed the research. P.P. performed the research. Y.B., M.E., and D.J.M. analyzed the data.

Supporting information

Supplementary Text

Supplementary Figure S1 Goodness‐of‐fit plots of total testosterone concentrations. Red solid lines are smoothing lines. Black solid lines are lines of identity. Black dots are observed values. Observed concentrations vs. population predictions (top left). Observed concentrations vs. individual predictions (top right). Ideally, the nonparametric smoother (red line) should fall on the line of unity (black line). Absolute individual weighted residuals (|IWRES|) vs. individual predictions (bottom left). The absolute values of IWRES should be randomly distributed without any apparent shape. CWRES vs time (bottom right). The conditional weighted residuals should not show any trend over time.

Supplementary Figure S2 Simulated LH concentration‐time profile during and after TC administration in healthy volunteers with different body weights and thyroxin values. Colored solid lines represent the median simulated suppression level. Shaded areas indicate 95% confidence interval of the simulated suppression level.

Supplementary Figure S3 Goodness‐of‐fit plots of luteinizing hormone (top left), sperm counts (top right) and sperm motility (bottom left) plotted on a double‐logarithmic scale after testosterone administration. Red solid lines are smoothing lines. Black solid lines are lines of identity. Black dots are observed values. Observed concentrations vs. population predictions (top left). Observed concentrations vs. individual predictions (top right). Absolute individual weighted residuals (|IWRES|) vs. individual predictions (bottom left). CWRES vs time (bottom right).

Supplementary Table S1 Population pharmacodynamic estimates and bootstrap results of suppression of sperm motility following long‐term dosing of testosterone cypionate in 31 healthy volunteers.

• Model Files

• Dataset 1

• Dataset 2

• Dataset 3

• Dataset 4