Temperature-induced arousability during sleep is a missing piece in the puzzle for triggers of sudden infant death syndrome.
Abstract
In addition to regular sleep/wake cycles, humans and animals exhibit brief arousals from sleep. Although much is known about consolidated sleep and wakefulness, the mechanism that triggers arousals remains enigmatic. Here, we argue that arousals are caused by the intrinsic neuronal noise of wake-promoting neurons. We propose a model that simulates the superposition of the noise from a group of neurons, and show that, occasionally, the superposed noise exceeds the excitability threshold and provokes an arousal. Because neuronal noise decreases with increasing temperature, our model predicts arousal frequency to decrease as well. To test this prediction, we perform experiments on the sleep/wake behavior of zebrafish larvae and find that increasing water temperatures lead to fewer and shorter arousals, as predicted by our analytic derivations and model simulations. Our findings indicate a previously unrecognized neurophysiological mechanism that links sleep arousals with temperature regulation, and may explain the origin of the clinically observed higher risk for sudden infant death syndrome with increased ambient temperature.
INTRODUCTION
Brief arousals from sleep that appear random in time and occur frequently throughout the entire sleep period are a riddle wrapped up in an enigma. The dynamical aspects of arousals and their neuronal origin are still not understood, and the debate on their physiological function is controversial. Traditionally, arousals have been predominately associated with disease in general and with sleep disorders in particular (1–3). Too many or too few arousals are indicative of adverse clinical conditions such as sleep apnea (4) or sudden infant death syndrome (SIDS) (5, 6), respectively. More recently, it has been suggested that spontaneous arousals are part of healthy sleep regulation and may play a functional role to ensure the reversibility of sleep—that is, without arousals, sleep would be similar to coma (7). In addition, arousals might serve as a means of remote connection between the sleeper and the environment to maintain some level of alertness to external hazards (7).
Arousals and normal wakefulness require the coordinated activity of several wake-promoting cell groups located in the rostral brainstem and posterior hypothalamus (8). These cell groups form the ascending arousal system, which consists of two major pathways. One pathway includes cholinergic neurons that generate cortical activation via innervation of the thalamus and the basal forebrain. Through the second pathway, monoaminergic neurons activate neuronal populations in the lateral hypothalamic area, the basal forebrain, and the cerebral cortex, bypassing the thalamus (9). However, the mechanisms that activate the wake-promoting neurons (WPN) and trigger spontaneous brief arousals, instead of consolidated wakefulness, remain unknown. Here, we hypothesize that spontaneous arousals are caused by inherent stochastic fluctuations in the neuronal membrane potential. These neuronal fluctuations are an intrinsic phenomenon that is observed in the absence of any external stimulation and is termed subthreshold voltage fluctuations (10). Specifically, we hypothesize that the superposition of uncorrelated neuronal noise currents from a group of neurons (each below the firing threshold) in the brainstem wake-promoting system occasionally exceeds the excitability threshold of cortical neurons, thus provoking brief arousals (Fig. 1).
Fig. 1. Schematic representation of our hypothesis that neuronal noise originating from subthreshold voltage fluctuations in WPN triggers spontaneous arousals during sleep.
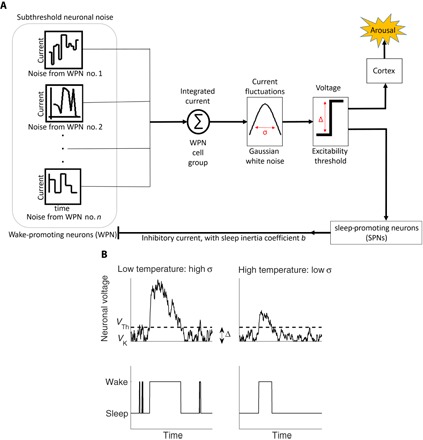
(A) The superposition of the uncorrelated currents from n WPN (connected in parallel) results in a neuronal current that has Gaussian distribution with SD σ (due to central limit theorem; see Materials and Methods). If this superposed neuronal current and its associated voltage exceed an excitability threshold Δ, then it triggers an arousal in the cortex and simultaneously stimulates sleep-promoting neurons (SPNs) in the brainstem. As a consequence, the excited SPNs inhibit the WPN (negative feedback) through an inhibitory current, which ensures sleep inertia and restoring force back to sleep, and thus keeps the arousal brief. (B) Top: Two biased random walk model simulations of the superposed neuronal voltage (that is, the integrated neuronal current) with different values of σ corresponding to low temperature (high σ) and high temperature (low σ). Note that the SD σ is temperature-dependent because high temperatures reduce subthreshold voltage fluctuations leading to lower values of σ, as shown by empirical studies (10, 31). Although the random walk freely moves within the interval [VK,VTh] (corresponding to “sleep state”), there is an inhibitory current once the random walk is above VTh (“wake state”). Bottom: Shown are arousals/wake and sleep bouts corresponding to whether the random walk is above or below the threshold voltage VTh, respectively. Note that at low temperature, wake bouts occur more frequently and have longer durations as compared to high temperature. In our model simulations, the threshold VTh and the potassium Nernst potential VK are approximately constant for different temperatures in agreement with experiments (50); the voltage difference (excitability threshold) is defined as Δ = VTh − VK.
There are two main sources of neuronal subthreshold voltage fluctuations (11): one is due to stochastic openings and closings of voltage-gated membrane channels (mainly potassium channels); the other source is random background synaptic activity. Several studies have demonstrated the neurophysiological significance of subthreshold voltage fluctuations, for example, as a contributor to the stochastic resonance phenomenon that improves the sensory detection of weak signals (12, 13). Other studies relate subthreshold voltage fluctuations in cardiac myocyte ion channels to the intrinsic heart rate fluctuations (14). Here, we show through empirical analyses, analytic derivation, and modeling simulations that neuronal subthreshold voltage fluctuations in WPN are likely the origin of spontaneous brief arousals during sleep.
Subthreshold voltage fluctuations are known to be strongly temperature-dependent and decrease with increasing temperature (10). Therefore, to test our hypothesis that spontaneous arousals originate from subthreshold voltage fluctuations, we investigate sleep under different temperatures. Specifically, we probe whether the arousal frequency and the dynamical characteristics of sleep and wake episodes are correlated with brain temperature. Although our main hypothesis focuses on the origin of spontaneous arousals during sleep in general, the specific temperature effect is expected to be more pronounced in ectothermic organisms that adapt their body temperature to ambient temperatures. Although humans are endotherms with intrinsic temperature regulation, young infants and, in particular, prematurely born babies show ectothermic traits (5, 15): Young infants have still underdeveloped thermal regulation during the first months after birth (5, 16), and premature babies cannot regulate their body temperature at all and therefore need incubator care (15). Moreover, under high room temperature, both young and premature infants show frequent epochs of sleep apnea (5, 17, 18) due to low arousability (5, 18), which may lead to SIDS. However, the mechanism that connects high room temperature with low arousability and the resulting increase in sleep apnea and SIDS events are unknown. Here, we show that neuronal noise due to subthreshold voltage fluctuations is likely to be the missing link between brain/body temperature and arousability from sleep. This study provides a mechanistic picture of the origin of intrinsic arousals during sleep and explains empirically based recommendations that lowering room temperature reduces the risk for SIDS (19) and apnea of prematurity events (17).
During sleep, WPN are inhibited mainly by γ-aminobutyric acid and galanin (8). Nevertheless, WPN maintain a low level of activity because of subthreshold voltage fluctuations, which integrated over many WPN can occasionally exceed the excitability threshold of individual neurons or a group of neurons (Fig. 1A). The resulting arousal is kept brief because of the activity of the still dominant SPNs. The likelihood of crossing the excitability threshold and triggering an arousal is smaller if the SD of the integrated WPN current is smaller—this is the case at higher temperatures where subthreshold voltage fluctuations are reduced. The mechanism we propose is illustrated in Fig. 1B, where two model simulations of a biased random walk (see Materials and Methods) with low and high SD (corresponding to high and low temperature, respectively) yield different lengths and frequencies of arousals, as well as different temporal organization.
RESULTS
Sleep and wake characteristics change under different temperatures
To test our model predictions of the effect of temperature on spontaneous arousals and to support our hypothesis on the role of subthreshold voltage fluctuations in sleep regulation, we perform sleep experiments under different ambient temperatures. For our experiments, we chose zebrafish larvae because zebrafish exhibit similar diurnal sleep/wake (that is, dark/light) cycles as humans (20, 21) and because the zebrafish is an ectothermic animal (22) and, thus, allows testing of the effects of temperature variations on arousal dynamics and sleep/wake characteristics. Because ectotherms cannot regulate their body temperature, the ambient temperature directly translates to body temperature. The optimal water temperature for zebrafish larvae is ~28°C (22, 23). In our experiments, we recorded the sleep/wake behavior of 48 larvae during 48 hours, with two 14-hour light/10-hour dark cycles, at a constant water temperature of 28°C. We also subsequently repeated the measurements at 25°, 31°, and 34°C using a new set of 48 larvae for each temperature recording (in each experiment, the set of larvae is from the same fish line, wild-type AB; see Materials and Methods). Because we are interested in arousals from sleep, we analyzed only the two 10-hour long dark periods (when zebrafish are predominantly sleeping), and we calculated for each temperature the total sleep duration, mean sleep bout duration, number of arousals during sleep, and mean wake bout duration. In accordance with our hypothesis, our analyses show that an increase in temperature decreases the number of arousals as well as the mean arousal/wake bout durations while simultaneously increases total sleep duration and mean sleep bout duration (Fig. 2, A to D; red circles).
Fig. 2. Sleep and wake characteristics of zebrafish larvae (red circles) compared to model simulations (blue squares).
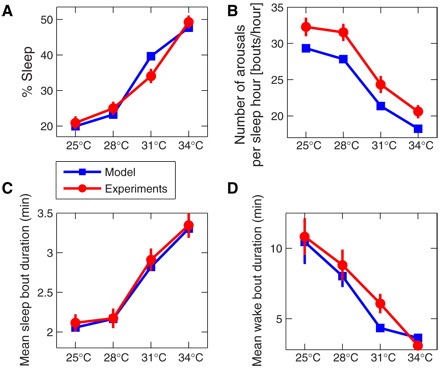
(A) The percent sleep time for zebrafish larvae (blue squares) increases with increasing water temperature—from 20% at 25°C to 50% at 34°C. The same temperature dependence is also obtained for our model simulations, where increasing temperatures are modeled by decreasing neuronal noise levels (as measured by the noise SD σ; for more details, see Materials and Method). (C) The mean sleep bout duration shows similar behavior for increasing temperatures, whereas the number of arousals during sleep [shown in (B)] is decreasing with increasing temperature, with most arousals at low temperatures. Thus, the monotonous increase of total sleep time with increasing temperatures in zebrafish larvae is associated with longer sleep bouts. (D) The mean wake bout duration of zebrafish larvae decreases with increasing temperature, and this trend is also reproduced by our model. The great similarity in (A) to (D) between the experimental measurements obtained for zebrafish larvae under different water temperatures and the model results for different noise levels strongly supports our hypothesis that arousals/brief awakenings from sleep originate from neuronal noise. We examine for each larva the temperature dependence of the sleep/wake parameters in (A) to (D), applying to all 48 larvae in the database a one-way analysis of variance (ANOVA) with repeated measures (comparisons between all temperatures), and we obtain a P < 10−9 (all pairwise multiple comparisons by Tukey’s test yield P < 0.05, except at 25°C versus 28°C for the mean sleep bout duration and at 25°C versus 28°C for number of arousals per sleep hour). In all panels, for each temperature, we present the group average and SE of the 48 larvae during two dark periods (when zebrafish predominantly sleep) with 10-hour duration each, and the model results for each σ are obtained from 48 20-hour independent model simulations matching the duration of the 20-hour dark period. All model parameters are the same for each temperature, only the neuronal noise level σ is changed: For 25°C, we use ; for 28°C, ; for 31°C, ; and for 34°C, , where Δt = 0.08 s is the time resolution of each simulation.
These experimental results are in excellent agreement with the output of our physiologically motivated biased diffusion model that simulates arousals and sleep/wake transitions based on neuronal subthreshold voltage fluctuations (Fig. 1), and where higher temperatures result in lower neuronal noise levels as reflected by lower SD σ. In Fig. 2 (A to D) (blue squares), we show the model simulation data for total sleep duration, mean sleep bout duration, number of arousals, and mean wake bout duration for different values of σ. A monotonous decrease in σ yields the same behavior as the experimental data when temperature monotonically increases, indicating a strong influence of neuronal subthreshold voltage fluctuations on arousability and sleep regulation.
Distributions of sleep and wake bout durations for different temperatures
To obtain a more comprehensive picture of the role of neuronal noise in sleep regulation, we also need information on how different temperatures affect the probability distributions of sleep and arousal durations. As was found earlier for mammals (24), as well as for zebrafish (20), arousal durations exhibit a power-law probability distribution characterized by a scaling exponent α, whereas sleep durations follow an exponential distribution with characteristic time scale τ. In Fig. 3 (A and B), we show the sleep and wake distributions measured for a group of 48 zebrafish larvae at different water temperatures, 25°, 28°, 31°, and 34°C. The scaling exponent α for the wake durations and the exponent τ for the sleep durations consistently increase from low to high water temperatures.
Fig. 3. Cumulative probability distributions of sleep and wake bout durations for zebrafish larvae at different water temperatures compared to model simulations with different neuronal noise levels.
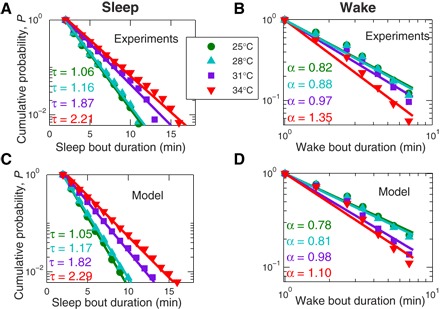
Consistent with previous findings (20, 24), sleep bout durations are exponentially distributed with characteristic time scale τ, whereas wake bout durations show a power-law distribution characterized by the scaling exponent α. However, the characteristics of these distributions, τ and α, change with temperature. (A) The characteristic sleep time monotonically increases from τ = 1.06 min at 25°C to τ = 2.21 min at 34°C. (B) The power-law scaling exponent of the wake distributions increases with increasing temperatures from α = 0.82 at 25°C to α = 1.35 at 34°C. These empirically obtained sleep and wake distributions for zebrafish larvae are well reproduced by our model simulations with different temperatures (that is, different values of the neuronal noise level σ: for 25°C ; for 28°C, ; for 31°C, ; and for 34°C, ) that yield the same type of distributions and temperature dependence as the experimental data. Moreover, we obtain practically matching values for τ and α between zebrafish measurements and the model simulations for each temperature and the corresponding noise level σ, consistent with our conclusions from Fig. 2. For all simulations in (C) and (D), we choose the same parameters for the inhibitory current (sleep inertia) coefficient b = 20 mV2/Δt and the excitability threshold (sleep depth) parameter Δ = 10 mV to best match our empirical observations in (A) and (B). Both α and τ values and their SDs (which are of the order 10−2 or lower) were calculated using the maximum likelihood estimation (MLE) method (see Materials and Methods) (41) on the pooled data of all larvae at a given temperature, and these estimates for α and τ are not affected by particular bin selection for the distribution.
Next, we compare zebrafish sleep/arousal distributions under different water temperatures to predicted values of our model of arousal and sleep regulation under different noise levels. In Fig. 3 (C and D), we show the model results for decreasing neuronal noise levels that simulate the activity of WPN for increasing temperatures. Remarkably, we not only observe the same trend in the probability distributions (increasing exponents α and τ with increasing temperature/noise level) but we also obtain very similar values for the exponents α and τ matching model simulations with the experiments. The fact that the experimental results and the model outputs for sleep/wake characteristics are in good agreement not only in their statistical means (Fig. 2) but also in their respective probability distributions (Fig. 3), strongly supports our hypothesis that arousals are a direct consequence of neuronal noise.
DISCUSSION
Our findings may lead to new insights into the origin and functional role of arousals in general and on the effect of temperature on sleep architecture in particular. We introduce a mechanistic picture on the origin of brief arousals during sleep based on the empirically observed phenomenon of neuronal subthreshold voltage fluctuations. Currently, there is no test to directly and noninvasively measure subthreshold neuronal voltage fluctuations in humans, and our work offers an approach to determine neuronal fluctuations by measuring key parameters that characterize sleep and arousal probability distributions (Fig. 3). This would provide a new diagnostic tool to monitor and better understand neurological diseases related to changes in subthreshold voltage fluctuations.
Specifically, the thermosensitivity of neuronal subthreshold voltage fluctuations explains the lower level of arousability at higher temperatures that for premature babies and young infants may lead to an increased risk of apnea of prematurity and SIDS events (Fig. 4). Reducing the incubator/room temperature increases neuronal noise and therefore increases the frequency and duration of arousals from sleep, thus avoiding potentially fatal epochs of hypoxia in young infants where core body temperature regulation is not fully developed (Fig. 4). In this respect, it is interesting to note that several epidemiological studies have demonstrated a peak occurrence of SIDS during the early morning hours (25–28) and that other investigations, not related to SIDS, found that during sleep, core body temperature in infants significantly increases in the morning hours (29, 30). Furthermore, other epidemiological studies show that the vast majority of SIDS occur during the first 6 months of life, with a peak occurrence at 2 to 3 months of age (19). Intriguingly, this peak in SIDS occurrence coincides with the time period when thermoregulation in infants is not yet fully developed, and therefore, infants are most susceptible to ambient temperatures.
Fig. 4. The possible effect of ambient temperatures on apnea of prematurity and SIDS.
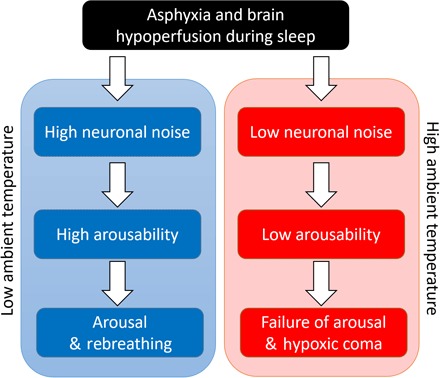
Asphyxia and brain hypoperfusion that can occur in infants during sleep may result in a life-threatening event (5). Depending on the level of arousability, this event may lead to either arousal and rebreathing or to failure of arousal and hypoxic coma. High neuronal noise generated at low ambient temperature yields higher arousability that in turn increases the probability for arousal and rebreathing. In contrast, low neuronal noise at high ambient temperature yields lower probability of arousal and can therefore result in hypoxic coma for the vulnerable infant. Note that very young infants show certain ectothermic traits (similar to fish) because their thermoregulation is not fully developed until the age of 6 months (52), and thus, they are more susceptible to higher ambient temperature and in higher risk for SIDS. Notably, after age of 6 months, the percent of SIDS occurrence drastically decreases (19). The proposed mechanism here indicates that the clinically observed correlation between high ambient temperature and high risk for SIDS is associated with decline in the arousability of sleep-regulatory neuronal circuits that is due to reduction in neuronal noise at high temperature.
Earlier experimental work on neurons demonstrated a clear temperature dependence of neuronal noise—with increasing temperature neuronal noise decrease (10, 31). Although these original experiments were not done in the context of sleep or SIDS, our modeling approach indicates that integrated neuronal noise as a function of temperature plays a key role in the arousability from sleep. Therefore, the temperature dependence of neuronal noise is the likely mechanism that links all empirical findings listed above into a unified picture that explains the occurrence of SIDS at a particular time of the day and for the particular age of the infants. Elevated circadian temperature in the morning hours combined with higher ambient temperature and high susceptibility of infants to ambient temperature can dramatically reduce arousability (Fig. 5 and fig. S3), and thus is the plausible reason for SIDS, as also demonstrated by our model. Our proposed mechanism is further supported by empirical studies showing that infants who later succumbed to SIDS have exhibited less waking (that is, arousability) and more sleep during the early morning hours compared to age-matched control subjects (6, 32).
Fig. 5. Schematic presentation of the physiological importance of the degree of arousability for a group of healthy infants and infants with low neuronal noise levels.
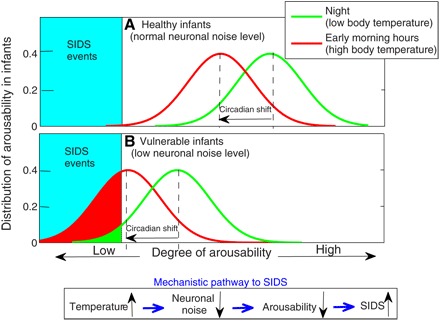
(A and B) Circadian temperature variations play a role for increased risk of SIDS events. Circadian rhythms in infants lead to increasing body temperature in the early morning hours (29, 30). These independent empirical observations combined with the mechanism we propose indicate that the circadian phase associated with the early morning hours is characterized by reduced arousability in infants. For vulnerable infants that are characterized by low level of neuronal noise, identical circadian temperature influences as observed in the healthy infants could further suppress neuronal noise and thus shift the arousability toward a “critical low point,” contributing to increased risk for SIDS events in the morning hours. We note that the superposition of the circadian temperature peak combined with elevated ambient temperature can lead to an even higher risk for SIDS (Fig. 4). Taking into account the intrinsic risk factors for SIDS (5), low levels of neuronal noise in the vulnerable infant [as in (B)] may be due to genetic or developmental factors. Elevated room temperature, extensive crib bedding, bed sharing, infections, and prone sleeping position, all factors that can contribute to higher body temperature (and hence to lower levels of neuronal noise and arousability), are known to be extrinsic risk factors for SIDS (5). Our empirical analyses (fig. S2) show a similar strong dependence of arousability on core body temperature also in adults with higher arousability between 4 a.m. and 6 a.m., when core body temperature reaches a minimum (53, 54).
Although the above-mentioned empirical facts provide indirect evidence of the link between temperature, arousability, and SIDS, our model offers a first unified theoretical framework to link these findings. We start from neuronal considerations (temperature dependence of neuronal noise) and predict system-level empirical observables that match our model predictions with experimental results on the arousability of zebrafish larvae (Fig. 2) and human subjects (fig. S2). The neurophysiological mechanism that allows manipulation of arousability through ambient temperature (as shown in the zebrafish experiment) is likely to be effective in young infants and is currently the only plausible reason for SIDS.
Previous studies show that adult rats and adult humans have more frequent and longer wake epochs at lower ambient temperatures (33, 34). Because adult rats and adult humans are endotherms (and therefore their body temperature is not much affected by reasonable changes in ambient temperatures), the temperature-dependent change in arousability could be attributed to metabolic changes that are responsible for keeping the body temperature constant. To exclude the metabolic influence on arousability, we studied zebrafish larvae (an ectothermic animal), and we propose that our results may also be tested on infant mammals, which have ectothermic traits after birth (15, 35). Moreover, earlier work (36) has shown that during the first few weeks, newborn rats do not exhibit the scale-invariant temporal organization and power-law characteristics in arousal dynamics that we report in our study. Therefore, future work could investigate the temperature dependence of arousability in, for example, newborn rats during the first 2 weeks of life.
In the context of the reported findings here, it is interesting to note that ambient temperature has been related to workplace productivity, performance, ability to concentrate, and the overall well-being (37, 38), with highest productivity at around 22° to 23°C, and that office temperatures below and above this optimal range have a negative effect on concentration. On the basis of the presented data analyses and model simulations here, one could speculate that the negative impact on concentration at lower than optimal temperatures is due to a “hyperactivity” state triggered by higher neuronal noise levels. On the contrary, higher than optimal temperatures might negatively affect concentration because of increased sleepiness.
We anticipate that our findings will initiate further experiments on the correlation between arousals and the level of subthreshold neuronal noise. For example, arousal events could be matched with the activity of WPN in the brain that is measured directly by neuroluminescence in transgenic zebrafish larvae or by membrane potential fluctuations in sleeping mammalian animals. Understanding the role of neuronal noise for the static characteristics and temporal dynamics of arousals can help design a new generation of sleeping aids that directly target the intrinsic neuronal noise to improve sleep quality in adults (that is, by reducing neuronal noise) or to increase arousability in young and premature infants through increased neuronal noise. Such medications might help in particular patients with chronic insomnia who suffer from hyperarousals during nocturnal sleep (2). For young and premature infants prone to SIDS and apnea-of-prematurity events (for example, because of family history of SIDS or because of very low birth weight), new medications that elevate neuronal noise levels should be considered not only to lower the risk of potentially life-threatening events but also to reduce the negative effects of these conditions on the development of infants.
MATERIALS AND METHODS
In this section, we present the setup of our animal experiments as well as the analytic framework and details of our model simulations. Our analytic derivations of the effect of neuronal noise on sleep are based on statistical physics tools. In particular, we used a Fokker-Planck formalism and properties of the Wiener process to calculate the temperature dependence of arousability and the probability distribution of arousals and sleep durations as found in our experiments. For our biased diffusion model, we used the biophysical characteristic that the neuronal current is proportional to the derivative of the neuronal voltage.
Zebrafish experimental protocol
Zebrafish were raised and maintained under 14-hour light (wake) followed by 10-hour dark (sleep) cycles (39). Embryos were generated by natural spawning and raised in egg water (0.2 mg/liter of Instant Ocean, 3 g/liter mM CHNaO3, and 0.15% methylene blue dissolved in reverse osmosis purified water) (39). The fish line included in this study was wild-type AB. Zebrafish larvae were maintained at 28 ± 0. 5°C under a 14-hour/10-hour light/dark regime until 5 days postfertilization (dpf). After 5 dpf, 48 larvae were individually placed into separate wells of a 48-well plate filled with 1 ml of fish water, for acclimation and habituation. Data recording of activity and sleep/wake architecture characterization of zebrafish larvae started at 6 dpf, and larvae were kept on 14-hour light/10-hour dark cycles for a total of 48 hours. Larvae activity was recorded automatically in 1-min time intervals using the DanioVision tracking system (Noldus Information Technology). Water temperature was kept constant throughout the entire 48-hour experiment by using a thermostat and a water circulation pump. The experiment was repeated for different water temperatures using a new set of 48 larvae for each temperature, that is, 25°, 28° (the optimal temperature for zebrafish), 31°, and 34°C. For each 1-min time interval, each larva was assigned either a wake or a sleep state depending on the level of activity (39, 40). An overview of the group average (all 48 larvae) of total sleep duration in 1-hour intervals across 48 hours shows a diurnal rhythm pattern (fig. S1). All animal protocols were reviewed and approved by the Bar-Ilan University Bioethics Committee.
Sleep and wake bout distributions
For each individual larva, mean durations of sleep and wake bouts were calculated. The number of arousals is equal to the number of wake bouts within the two 10-hour dark periods during the 48-hour recording, and the percent sleep time was calculated as the total sum of sleep bout durations divided by 20 hours. Comparison between all temperatures in Fig. 2 was obtained from the P values for multiple comparisons one-way ANOVA. In addition, Tukey’s test was used to compare between the group averages at different temperatures.
Statistical analysis and maximum likelihood estimation
The power-law exponent α of the wake distributions and the characteristic time τ of the exponential sleep distributions were determined by maximum likelihood estimation (MLE) (41, 42) on the pooled data of all zebrafish larvae measured at a given temperature. MLE analysis is unbiased by particular bin selections of the probability distribution.
The exponent τ of the sleep distribution was calculated from the exponential probability , where x is the variable (that is, sleep bout duration) and M is the minimum sleep bout duration to be included in the calculation. The likelihood L of all N variables is given by
and the maximum of L is obtained when d(ln L)/dτ = 0
Therefore, the estimated τ is
| (1) |
as expected for exponential distributions. The error of estimating τ is determined by the Cramér-Rao bound
where Jτ is the Fisher information of τ. Therefore, the lower bound of the SD of τ is
| (2) |
The power-law scaling exponent α was calculated for the probability density function f(x) = (α/M) ⋅ (x/M)− α − 1, where x is the wake bout durations and M is the shortest wake bout duration. As for the exponential (see above), the likelihood L of all N variables is
and the maximum likelihood is obtained by d(ln L)/dα = 0
Thus, the estimated α is
| (3) |
The SE is obtained by the Cramér-Rao bound
Jα is the Fisher information of α, and the (lower bound) SD of α is calculated as
| (4) |
Biased diffusion model to simulate sleep/wake transitions at different temperatures
Here, we introduce a theoretical framework to investigate the effects of different subthreshold neuronal noise levels on sleep and arousal/wake behavior. To this end, we investigated a random walker with different noise levels (SD of the steps) σ. The random walker represents the superposition of the subthreshold neuronal noise from a group of neurons in the wake-promoting system during sleep. Neuronal noise results from random openings and closings of ion channels in the membrane as well as from synaptic noise and leads to fluctuations in the current and voltage of the neurons. Those fluctuations in a single neuron are below the excitability threshold to provoke neuronal firing (hence, they are called subthreshold voltage fluctuations) (10); however, they may facilitate the synchronous activity and bursting of neighboring neurons. Although the current fluctuations of a single neuron Ii cannot be considered Gaussian noise (11), the superposition of the currents from a large enough ensemble of neurons (n > 30), which can be modeled as parallel components (43, 44) with I = ∑iIi, follows a Gaussian distribution, as dictated by the central limit theorem (45). The relationship between the current I and voltage V is given by the Hodgkin-Huxley model, which relates to the axon’s membrane lipid bilayer as a capacitance C and to the ion channels as electrical conductances (resistor-capacitor circuit) (46), and where C ⋅ dV/dt is equal to the current. If the current I is Gaussian white noise, then the voltage V can be described as a Wiener process (Brownian noise). Therefore, during sleep, the resulting voltage of the WPN is given by
| (5) |
where w is a standard Wiener process and σ is the SD of the voltage fluctuations. Note that because subthreshold voltage fluctuations change with temperature (for example, higher temperature decreases neuronal subthreshold voltage fluctuations) (10), different values of the parameter σ reflect different temperatures in our model.
The absolute minimum of V is due to the Nernst potential of potassium ions, and thus, in our simulations, if the Wiener process for the voltage gives a value V that is below −Δ, we set V = −Δ (phenomenologically, Δ is the lower boundary for “sleep depth”)
| (6) |
A value of V < 0 relates to sleep, whereas V ≥ 0 relates to arousal. Note that for simplification, Δ and 0 represent relative values of the Nernst potential of potassium ions and the excitability voltage, respectively. When an arousal occurs, we assume that the sleep-promoting neuronal centers in the brain increase their inhibition of the wake-promoting centers to restore sleep. During arousals, the dynamics of the random walker can be written as
| (7) |
The electrical current I = −b ⋅ C/(V + 1) originates from the SPNs during an arousal to restore sleep by lowering the voltage back to V < 0 (that is, the sleep state). Phenomenologically, this “sleep-restoring” current may lead to the physiological state of sleep inertia that is the tendency to return to sleep. Because I ∝ 1/(V + 1), the sleep-restoring current is negligible in consolidated wakefulness when V ≫ 0. The coefficient of proportionality b ⋅ C is in units of electrical power.
Effect of neuronal noise on the characteristic time of sleep durations
During sleep, −Δ ≤ V ≤ 0, we integrate Eq. 6 and obtain
| (8) |
| (9) |
| (10) |
Averaging yields
| (11) |
| (12) |
| (13) |
In Eq. 8, the maximum voltage during sleep is V = 0, whereas the minimum voltage is −Δ. The variance of the standard Wiener process differential dw is its time interval dt (47), yielding Eq. 12. Finally, because the probability distribution of sleep bout durations decays exponentially with the characteristic time constant τ, we obtain from Eq. 13
| (14) |
Effect of neuronal noise on the power-law exponent of wake durations
As has been shown previously from experimental data (24, 48, 49), wake bout durations follow a power-law distribution with power-law exponent α. Moreover, it has been shown that α ≈ b, where b is the bias of the random walker (24). Here, we determine the relationship between σ (the SD of the subthreshold neuronal noise) and α.
For V > 0, dividing both sides of Eq. 5 by σ yields
After defining a normalized voltage variable s = V/σ, we obtain
| (15) |
Comparing Eqs. 15 and 5 leads to a new rescaled bias coefficient bnew = b/σ2 and to
| (16) |
Note that because of the change in the denominator from V + 1 to s + 1/σ in Eq. 15, the relationship in Eq. 16 is only an approximation.
Probability distribution of the neuronal voltage during wake
We apply the Fokker-Planck formalism on Eq. 7 with a drift term −b/(V + 1) and a diffusion term σ
| (17) |
where P is the voltage probability. Assuming that the probability P does not change in time, we can write dP/dt = 0, and therefore
| (18) |
Using separation of variables yields
| (19) |
where c is an integration constant. Equation 19 shows that the voltage during arousal follows a power-law distribution similar to the arousal durations. Another conclusion from Eq. 19 is that increasing σ2 is equivalent to decreasing b (see also Eq. 16 and Fig. 6, C to F).
Fig. 6. Simulation results for the effect of the excitability threshold Δ (related to sleep depth), b (related to sleep inertia) on the cumulative probability distributions P of sleep and wake bouts, and different neuronal noise levels σ (related to different temperatures).
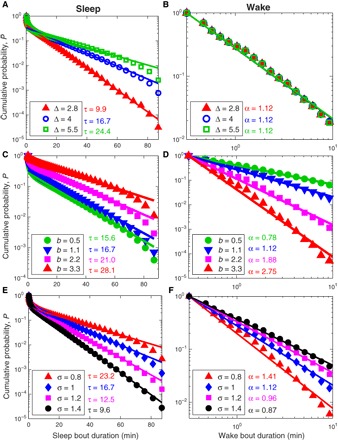
(A) Increasing the excitability threshold Δ leads to longer sleep bouts as reflected by higher values of τ. In contrast, wake bout durations remain unaffected and show similar distributions for different values of Δ as shown in (B). (C) Increasing b leads to longer sleep bouts (that is, larger values of τ) and (D) to larger values of the power-law exponent α for wake bout durations. Changing the noise level σ affects both the sleep bout durations (E) and the wake bout durations (F), however in different ways. Although higher values of σ (for example, due to lower temperatures) decrease the mean sleep bout duration and the exponent τ, wake bout durations increase and α decreases. For all simulations, we use b = 1.1 and Δ = 4.0, and the results are consistent with Eqs. 14 and 16.
Simulations for different model parameters
Our model has three parameters: sleep depth Δ (that is related to the neuronal excitability threshold), the subthreshold neuronal noise level σ, and a parameter b that is related to sleep inertia (and to an inhibitory current originating from clusters of SPNs). In Fig. 6, we show how changing those three parameters affects the probability distributions of sleep and wake bout durations.
Figure 6 (A and B) demonstrates how changing Δ affects sleep and wake probabilities in the model. It shows that as Δ increases, the characteristic time constant of sleep bout durations τ increases as well (Fig. 6A). In contrast, changing Δ does not affect the probability distribution of wake bout durations (Fig. 6B). This is expected from the formulation of the model equations, where Δ is a parameter only for sleep (Eq. 6) and not for wake (Eq. 7).
In Fig. 6 (C and D), we probed the effect of changing the parameter b. Figure 6 (C and D) shows that the characteristic time constant of sleep bout durations τ and the power-law exponent for wake bout durations α both increase when b increases—increasing τ relates to increased sleep bout duration, whereas, in contrast, increasing α leads to decreasing arousal/wake bout durations. Although b directly enters into Eq. 7 and therefore the effect on the wake bout durations is obvious (see also Eq. 16), its effect on sleep is indirect through a weaker versus stronger drive back to sleep, that is, dV < 0 versus dV ≪ 0 that leads to an initial voltage after the transition from wake to sleep of V < 0 versus V ≪ 0, respectively.
Changing the noise level σ, which corresponds to the subthreshold neuronal voltage fluctuations, has major effects on both sleep and wake bout distributions (even for small changes in σ). This is depicted in Fig. 6 (E and F). Increasing σ decreases the time constant τ (shorter sleep bouts) and decreases the exponent α (longer arousals and wake bouts). This can also be seen from Eqs. 14 and 16. Note that determining τ in the model simulations via Eq. 14 is more precise than estimating α, because Eq. 16 is only an approximation. As we discuss in the main text of the paper, the neuronal noise level σ is strongly related to the body temperature, that is, with increasing temperature, arousal/wake frequency and duration decrease as result of decreasing neuronal noise level.
Note that we relate the differences in sleep and wake characteristics at different temperatures (Figs. 2 and 3, main text) to changes in the neuronal noise level σ alone and that we do not consider temperature effects on the excitability threshold (sleep depth) Δ or on the inhibitory current coefficient b (sleep inertia). This is justified because (i) Δ does not change much within a physiologically relevant range of temperatures (50) and changing Δ does not affect arousal characteristics (Fig. 6, A and B), and (ii) the energy efficiency for single action potentials that we can relate to our parameter b only increases significantly for extreme hypothermia (51).
Supplementary Material
Acknowledgments
We thank J. W. Kantelhardt for the discussions and D. Zada for the technical support and assistance in the zebrafish experiment. Funding: This research was supported by a Shulamit Aloni Fellowship of the Ministry of Science, Technology and Space, Israel (grant no. 3-13276 to H.D.), the United States–Israel Binational Science Foundation (grant nos. 2012219 to P.C.I. and S.H., and 2011335 to L.A.), the Israel Science Foundation (grant nos. 690/15 to L.A. and 1657/16 to R.P.B.), the Legacy Heritage Biomedical Program of the Israel Science Foundation (grant no. 992/14 to L.A.), the German Israeli Foundation (grant no. I-1372-303.7/2016 to R.P.B.), NIH (grant no. 1R01-HL098437 to P.C.I.), the W. M. Keck Foundation (grant to P.C.I.), and a Marie Curie Fellowship (grant no. IIF 628159 to R.P.B.). Author contributions: H.D. and R.P.B. conceived the project, designed the simulations, and proposed the experiments. I.E. and L.A. designed and performed the zebrafish experiments and wrote the corresponding text in Materials and Methods. H.D. and R.P.B. designed the neuronal-based sleep model (with input from P.C.I. and S.H.). H.D. and R.P.B. proposed the relevance of this work to SIDS appearance. H.D. proposed the concept of neuronal noise (subthreshold voltage fluctuations) as the source of short sleep arousals, performed the simulations, and developed the analytical framework using Fokker-Planck equations and properties of the Wiener process. H.D., P.C.I., and R.P.B designed the figures and wrote the manuscript with contributions from S.H. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaar6277/DC1
section S1. Sleep behavior of zebrafish larvae
section S2. Sleep behavior of healthy adult humans under different circadian temperatures
section S3. Occurrence of SIDS and heat loss versus infant age
section S4. Model parameters to simulate the sleep/wake statistics of zebrafish larvae
fig. S1. Sleep behavior of zebrafish larvae across 48 hours under 14-hour light/10-hour dark cycles at different temperatures.
fig. S2. Experimentally obtained sleep and wake characteristics for adult subjects as a function of core body temperature during the night (red circles) compared to our model simulations (blue squares).
fig. S3. Occurrence of SIDS and heat loss versus infant age.
REFERENCES AND NOTES
- 1.Broughton R. J., Sleep disorders: Disorders of arousal? Science 159, 1070–1078 (1968). [DOI] [PubMed] [Google Scholar]
- 2.Mahowald M. W., Schenck C. H., Insights from studying human sleep disorders. Nature 437, 1279–1285 (2005). [DOI] [PubMed] [Google Scholar]
- 3.Bonnet M., Carley D., Carskadon M., Easton P., Guilleminault C., Harper R., Hayes B., Hirshkowitz M., Ktonas P., Keenan S., Pressman M., Roehrs T., Smith J., Walsh J., Weber S., Westbrook P., Jordan B. Atlas Task Force , EEG arousals: Scoring rules and examples. A preliminary report from the Sleep Disorders Atlas Task Force of the American Sleep Disorders Association. Sleep 15, 173–184 (1992). [PubMed] [Google Scholar]
- 4.Strollo P. J. Jr, Rogers R. M., Obstructive sleep apnea. N. Engl. J. Med. 334, 99–104 (1996). [DOI] [PubMed] [Google Scholar]
- 5.Kinney H. C., Thach B. T., The sudden infant death syndrome. N. Engl. J. Med. 361, 795–805 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schechtman V. L., Harper R. M., Wilson A. J., Southall D. P., Sleep state organization in normal infants and victims of the sudden infant death syndrome. Pediatrics 89, 865–870 (1992). [PubMed] [Google Scholar]
- 7.P. Halász, R. Bódizs, Dynamic Structure of NREM Sleep (Springer Science & Business Media, 2012). [Google Scholar]
- 8.Saper C. B., Scammell T. E., Lu J., Hypothalamic regulation of sleep and circadian rhythms. Nature 437, 1257–1263 (2005). [DOI] [PubMed] [Google Scholar]
- 9.Brown R. E., Basheer R., McKenna J. T., Strecker R. E., McCarley R. W., Control of sleep and wakefulness. Physiol. Rev. 92, 1087–1187 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Steinmetz P. N., Manwani A., Koch C., London M., Segev I., Subthreshold voltage noise due to channel fluctuations in active neuronal membranes. J. Comput. Neurosci. 9, 133–148 (2000). [DOI] [PubMed] [Google Scholar]
- 11.Manwani A., Koch C., Detecting and estimating signals in noisy cable structures, II: Information theoretical analysis. Neural Comput. 11, 1831–1873 (1999). [DOI] [PubMed] [Google Scholar]
- 12.Jung P., Stochastic resonance and optimal design of threshold detectors. Phys. Lett. A 207, 93–104 (1995). [Google Scholar]
- 13.Gailey P. C., Neiman A., Collins J. J., Moss F., Stochastic resonance in ensembles of nondynamical elements: The role of internal noise. Phys. Rev. Lett. 79, 4701 (1997). [Google Scholar]
- 14.Dvir H., Zlochiver S., Interbeat interval modulation in the sinoatrial node as a result of membrane current stochasticity—A theoretical and numerical study. Biophys. J. 108, 1281–1292 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brück K., Temperature regulation in the newborn infant (part 1 of 3). Neonatology 3, 65–81 (1961). [Google Scholar]
- 16.Fleming P. J., Azaz Y., Wigfield R., Development of thermoregulation in infancy: Possible implications for SIDS. J. Clin. Pathol. 45, 17–19 (1992). [PubMed] [Google Scholar]
- 17.Daily W. J. R., Klaus M., Belton H., Meyer P., Apnea in premature infants: Monitoring, incidence, heart rate changes, and an effect of environmental temperature. Pediatrics 43, 510–518 (1969). [PubMed] [Google Scholar]
- 18.Kahn A., Sawaguchi T., Sawaguchi A., Groswasser J., Franco P., Scaillet S., Kelmanson I., Dan B., Sudden infant deaths: From epidemiology to physiology. Forensic Sci. Int. 130, 8–20 (2002). [DOI] [PubMed] [Google Scholar]
- 19.American Academy of Pediatrics Task Force on Sudden Infant Death Syndrome , The changing concept of sudden infant death syndrome: Diagnostic coding shifts, controversies regarding the sleeping environment, and new variables to consider in reducing risk. Pediatrics 116, 1245–1255 (2005). [DOI] [PubMed] [Google Scholar]
- 20.Sorribes A., Þorsteinsson H., Arnardóttir H., Jóhannesdóttir I. Þ., Sigurgeirsson B., de Polavieja G. G., Karlsson K. Æ., The ontogeny of sleep-wake cycles in zebrafish: A comparison to humans. Front. Neural Circuits 7, 178 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Elbaz I., Foulkes N. S., Gothilf Y., Appelbaum L., Circadian clocks, rhythmic synaptic plasticity and the sleep-wake cycle in zebrafish. Front. Neural Circuits 7, 9 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Scott G. R., Johnston I. A., Temperature during embryonic development has persistent effects on thermal acclimation capacity in zebrafish. Proc. Natl. Acad. Sci. U.S.A. 109, 14247–14252 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kimmel C. B., Ballard W. W., Kimmel S. R., Ullmann B., Schilling T. F., Stages of embryonic development of the zebrafish. Dev. Dyn. 203, 253–310 (1995). [DOI] [PubMed] [Google Scholar]
- 24.Lo C.-C., Amaral L. A. N., Havlin S., Ivanov P. Ch., Penzel T., Peter J.-H., Stanley H. E., Dynamics of sleep-wake transitions during sleep. EPL (Europhys. Lett.) 57, 625 (2002). [Google Scholar]
- 25.A. Bergman, Sudden infant death syndrome in King County, Washington: Epidemiologic aspects, in Sudden Infant Death Syndrome, C. G. Ray, J. B. Beckwith, Eds. (University of Washington Press, 1970), pp. 47–54. [Google Scholar]
- 26.Norvenius S. G., Sudden infant death syndrome in Sweden in 1973–1977 and 1979. Acta Paediatr. 76, 1–138 (1987). [DOI] [PubMed] [Google Scholar]
- 27.Nelson E. A. S., Taylor B. J., Mackay S. C., Child care practices and the sudden infant death syndrome. J. Paediatr. Child Health 25, 202–204 (1989). [DOI] [PubMed] [Google Scholar]
- 28.A.-C. Dämmig, Sudden infant death syndrome. Epidemiologische und ausgewählte histomorphologische Untersuchungen zum Risikoprofil des plötzlichen Säuglingstodes (SIDS) unter besonderer Berücksichtigung des Risikofaktors Hyperthermie/Schwitzen–Eine rechtsmedizinische Studie, thesis, Universität Giessen (2016). [Google Scholar]
- 29.Kleitman N., Titelbaum S., Hoffmann H., The establishment of the diurnal temperature cycle. Am. J. Physiol. 119, 48–54 (1937). [Google Scholar]
- 30.Wailoo M. P., Petersen S. A., Whittaker H., Goodenough P., Sleeping body temperatures in 3–4 month old infants. Arch. Dis. Child. 64, 596–599 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Reig R., Mattia M., Compte A., Belmonte C., Sanchez-Vives M. V., Temperature modulation of slow and fast cortical rhythms. J. Neurophysiol. 103, 1253–1261 (2010). [DOI] [PubMed] [Google Scholar]
- 32.Schechtman V. L., Harper R. K., Harper R. M., Aberrant temporal patterning of slow wave sleep in siblings of SIDS victims. Electroencephalogr. Clin. Neurophysiol. 94, 95–102 (1995). [DOI] [PubMed] [Google Scholar]
- 33.Shapiro C. M., Allan M., Driver H., Mitchell D., Thermal load alters sleep. Biol. Psychiatry 26, 736–740 (1989). [DOI] [PubMed] [Google Scholar]
- 34.Kumar V. M., Body temperature and sleep: Are they controlled by the same mechanism? Sleep Biol. Rhythms 2, 103–124 (2004). [Google Scholar]
- 35.Fowler S. J., Kellogg C., Ontogeny of thermoregulatory mechanisms in the rat. J. Comp. Physiol. Psychol. 89, 738–746 (1975). [DOI] [PubMed] [Google Scholar]
- 36.Blumberg M. S., Seelke A. M. H., Lowen S. B., Karlsson K. Æ., Dynamics of sleep-wake cyclicity in developing rats. Proc. Natl. Acad. Sci. U.S.A. 102, 14860–14864 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.O. Seppänen, W. J. Fisk, Q. H. Lei, Effect of temperature on task performance in office environment, in 5th International Conference on Cold Climate Heating, Ventilation and Air Conditioning, Moscow, Russia, 21 to 24 May 2006. [Google Scholar]
- 38.I. Balazova, G. Clausen, J. H. Rindel, T. Poulsen, D. P. Wyon, Open-plan office environments: A laboratory experiment to examine the effect of office noise on human perception, comfort and office work performance, in Proceedings of the 11th International Conference on Indoor Air Quality and Climate, 17 to 22 August 2008. [Google Scholar]
- 39.Elbaz I., Yelin-Bekerman L., Nicenboim J., Vatine G., Appelbaum L., Genetic ablation of hypocretin neurons alters behavioral state transitions in zebrafish. J. Neurosci. 32, 12961–12972 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Prober D. A., Rihel J., Onah A. A., Sung R.-J., Schier A. F., Hypocretin/orexin overexpression induces an insomnia-like phenotype in zebrafish. J. Neurosci. 26, 13400–13410 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Clauset A., Shalizi C. R., Newman M. E. J., Power-law distributions in empirical data. SIAM Rev. 51, 661–703 (2009). [Google Scholar]
- 42.A. Leon-Garcia, Probability, Statistics, and Random Processes for Electrical Engineering (Pearson Education, 2008). [Google Scholar]
- 43.Eichner H., Klug T., Borst A., Neural simulations on multi-core architectures. Front. Neuroinform. 3, 21 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Prieto A., Prieto B., Ortigosa E. M., Ros E., Pelayo F., Ortega J., Rojas I., Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 214, 242–268 (2016). [Google Scholar]
- 45.A. Papoulis, S. U. Pillai, Probability, Random Variables, and Stochastic Processes (Tata McGraw-Hill Education, 2002). [Google Scholar]
- 46.B. Hille, Ionic Channels of Excitable Membranes (Sinauer Sunderland, 2001), vol. 507. [Google Scholar]
- 47.R. Durrett, Probability: Theory and Examples (Cambridge Univ. Press, 2010). [Google Scholar]
- 48.Lo C.-C., Chou T., Penzel T., Scammell T. E., Strecker R. E., Stanley H. E., Ivanov P. Ch., Common scale-invariant patterns of sleep–wake transitions across mammalian species. Proc. Natl. Acad. Sci. U.S.A. 101, 17545–17548 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lo C.-C., Bartsch R. P., Ivanov P. Ch., Asymmetry and basic pathways in sleep-stage transitions. Europhys. Lett. 102, 10008 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Szabo T. M., Brookings T., Preuss T., Faber D. S., Effects of temperature acclimation on a central neural circuit and its behavioral output. J. Neurophysiol. 100, 2997–3008 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yu Y., Hill A. P., McCormick D. A., Warm body temperature facilitates energy efficient cortical action potentials. PLOS Comput. Biol. 8, e1002456 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bach V., Telliez F., Krim G., Libert J. P., Body temperature regulation in the newborn infant: Interaction with sleep and clinical implications. Clin. Neurophysiol. 26, 379–402 (1996). [DOI] [PubMed] [Google Scholar]
- 53.Duffy J. F., Dijk D.-J., Klerman E. B., Czeisler C. A., Later endogenous circadian temperature nadir relative to an earlier wake time in older people. Am. J. Physiol. 275, R1478–R1487 (1998). [DOI] [PubMed] [Google Scholar]
- 54.Czeisler C. A., Duffy J. F., Shanahan T. L., Brown E. N., Mitchell J. F., Rimmer D. W., Ronda J. M., Silva E. J., Allan J. S., Emens J. S., Dijk D.-J., Kronauer R. E., Stability, precision, and near-24-hour period of the human circadian pacemaker. Science 284, 2177–2181 (1999). [DOI] [PubMed] [Google Scholar]
- 55.Klösch G., Kemp B., Penzel T., Schlögl A., Rappelsberger P., Trenker E., Gruber G., Zeitlhofer J., Saletu B., Herrmann W. M., Himanen S. L., Kunz D., Barbanoj M. J., Röschke J., Värri A., Dorffner G., The SIESTA project polygraphic and clinical database. IEEE Eng. Med. Biol. Mag. 20, 51–57 (2001). [DOI] [PubMed] [Google Scholar]
- 56.C. M. Atkinson, Developmental changes in the human infant: Patterns of endocrine excretion, body temperature and sweating between 1 and 4 months of age, thesis, Department of Pre-Clinical Sciences, University of Leicester (1995). [Google Scholar]
- 57.Rutter N., Hull D., Response of term babies to a warm environment. Arch. Dis. Child. 54, 178–183 (1979). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.T. M. Mauro, Fitzpatrick’s Dermatology in General Medicine (The McGraw-Hill Companies, 2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaar6277/DC1
section S1. Sleep behavior of zebrafish larvae
section S2. Sleep behavior of healthy adult humans under different circadian temperatures
section S3. Occurrence of SIDS and heat loss versus infant age
section S4. Model parameters to simulate the sleep/wake statistics of zebrafish larvae
fig. S1. Sleep behavior of zebrafish larvae across 48 hours under 14-hour light/10-hour dark cycles at different temperatures.
fig. S2. Experimentally obtained sleep and wake characteristics for adult subjects as a function of core body temperature during the night (red circles) compared to our model simulations (blue squares).
fig. S3. Occurrence of SIDS and heat loss versus infant age.


