Crystal structure and equation of state of Fe-Si alloys at super-Earth core conditions

This is the first direct determination of Fe-Si alloy structures at pressures found in the cores of super-Earth planets.

Abstract

The high-pressure behavior of Fe alloys governs the interior structure and dynamics of super-Earths, rocky extrasolar planets that could be as much as 10 times more massive than Earth. In experiments reaching up to 1300 GPa, we combine laser-driven dynamic ramp compression with in situ x-ray diffraction to study the effect of composition on the crystal structure and density of Fe-Si alloys, a potential constituent of super-Earth cores. We find that Fe-Si alloy with 7 weight % (wt %) Si adopts the hexagonal close-packed structure over the measured pressure range, whereas Fe-15wt%Si is observed in a body-centered cubic structure. This study represents the first experimental determination of the density and crystal structure of Fe-Si alloys at pressures corresponding to the center of a ~3–Earth mass terrestrial planet. Our results allow for direct determination of the effects of light elements on core radius, density, and pressures for these planets.

INTRODUCTION

From cosmochemical and geophysical constraints, Earth’s core is composed of iron alloyed with nickel and some amount of lighter elements such as H, C, S, O, and Si. The outer and the inner cores have a density deficit of ~10% and 4 to 5% compared to Fe, respectively. In addition to density, light elements affect the seismic velocity and phase diagram of Fe, both of which can be compared to geophysical observations [see Hirose et al. (1) for a review]. The abundance and identification of the core light elements are crucial for constraining the bulk chemistry of Earth, the process of core formation, and its subsequent thermal and magnetic field evolution (1).

Light elements likely also play an important role in the cores of extrasolar planets (2). The most abundant population of exoplanets detected to date fall within a size range between Earth and Neptune (3). Although a variety of planetary styles are possible in this range, mass-radius observations show that many of these planets have compositions (rock + metal) comparable to the terrestrial planets of our solar system (4). Theoretical and numerical models of the interior structure of these “super-Earth” planets have been constructed to address questions about their bulk chemistry and thermochemical evolution (5–7). Knowledge of the physical properties of a range of geological materials under very high pressure and temperature conditions is needed as input into such models (8); however, these are often highly uncertain because the requisite P-T conditions are far beyond the range of those accessible by standard experimental techniques such as diamond anvil cells (DACs).

A number of lines of evidence make silicon one of the most promising candidates for a major light element of the core. Si is highly abundant cosmochemically, not highly volatile, and forms a continuous solid solution with iron over a wide compositional range. One long-standing geochemical conundrum is that Earth’s mantle has a deficiency in Si relative to the composition of the chondritic meteorites, a geochemical proxy for primitive solar system material from which Earth is believed to have formed (9). Sequestration of 5 to 10% Si in the core can explain this discrepancy, reconciling bulk silicate Earth and chondritic compositions of this major element (9). Recent partitioning experiments conducted under reducing conditions also propose a core composition of 8 to 9 weight % (wt%) Si with 2 to 4 wt% O (10). As a consequence, the phase diagram and equation of state (EOS) of Fe-Si alloys has attracted intense interest in recent years.

A number of static diamond anvil cell experiments have explored the high P-T phase diagram of Fe-Si alloys (11–15). Most of the studies are limited to pressures below 200 GPa and thus not able to directly constrain these properties at the conditions of most of Earth’s core. Shock wave experiments on Fe-Si alloys can provide important information on liquid properties relevant to the outer core (16, 17), but because of the sample heating on compression, these data cannot address the nature of the solid phase of Earth’s inner core. In recent years, ramp dynamic compression techniques have demonstrated experimental access to terapascal pressures within the solid state (18). In ramp compression, dissipative heating is reduced, and the compression path is close to that of an isentrope, and as a result, the solid state is maintained to peak pressure. Combining dynamic compression with nanosecond x-ray diffraction has enabled the structure of materials to be studied under these extreme conditions (18, 19).

We present the first measurements of structure and density (ρ) of Fe-Si alloys up to 1300 GPa, more than three times the central pressure of Earth and close to the conditions expected at the center of a 3–Earth mass terrestrial-type exoplanet (20). We explore the effect of silicon content by studying two compositions: 7 wt% Si (hereafter Fe-7Si), which represents a potential terrestrial composition, and 15 wt% Si (Fe-15Si), a silicon-enriched composition. Our study provides the first direct determination of the lattice structure and equation of state of Fe-Si alloys that can be used to create data-based models of exoplanets and eliminate the need to rely on long extrapolations of low-pressure data.

RESULTS

High-pressure ramp-compression experiments were conducted using the Omega Laser at the Laboratory for Laser Energetics, University of Rochester. Composite laser drives composed of three to seven individual beams were used to ramp compress Fe-7Si and Fe-15Si alloys in target packages affixed to the front of a powder x-ray diffraction with image plates (PXRDIP) diagnostic box (Fig. 1). Laser pulse shaping produces an ablatively driven ramp-compression wave followed by a pressure hold period within the diamond/Fe-Si/window sample (Fig. 1B) (18, 19, 21). Using this approach, Fe-7Si samples were compressed to pressures between 131 and 1314 GPa, and Fe-15Si were compressed to pressures between 105 and 1260 GPa. Laser velocimetry was used to determine each sample’s pressure history (see Materials and Methods) (22).

Fig. 1. Experimental setup for laser ramp-compression experiments.

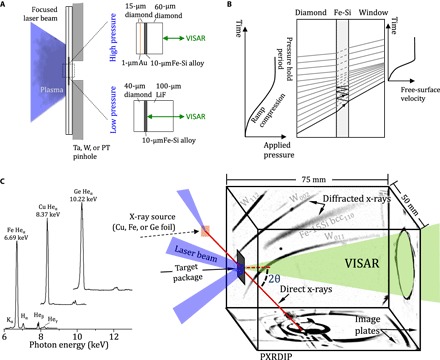
(A) The laser drive is focused to an 800-μm spot on the front diamond surface of C/Au/C/Fe-Si/C or C/Fe-Si/LiF target packages, which are centered over a 300-μm-diameter pinhole. (B) Ablation of the surface of the diamond pusher creates a rapidly expanding plasma that launches a pressure wave through the pusher/sample/window interfaces. For the thin samples used in this experiment, reverberations within the Fe-Si alloy layer due to impedance mismatches across the boundaries rapidly equilibrates the pressure. (C) Schematic of the PXRDIP diagnostic. Quasi-monochromatic x-rays emitted by a laser-generated plasma from a Cu, an Fe, or a Ge foil (left, recorded x-ray emission spectra) diffract from the target package and are recorded by image plates that line the box interior. A rear aperture provides access for velocity interferometry (VISAR).

Quasi-monochromatic x-rays of ~1-ns duration were generated using 16 to 18 Omega laser beams focused onto foils of Fe, Cu, or Ge positioned 24.3 mm from the sample and 45° away from the target normal. Measured spectra of laser-generated plasmas demonstrate emission of predominately helium-α–like x-rays (Fig. 1C), which diffract from the target package and are further filtered before being recorded by image plates (see Materials and Methods) (19). These pulses are timed relative to the drive such that diffraction is recorded at peak sample compression.

Examples of raw and processed image plates are shown in Fig. 2. At low pressure, three diffraction peaks of Fe-7Si were observed, consistent with the characteristic triplet (100, 002, and 101) of the hexagonal close-packed (hcp) structure (Fig. 2, A and C). At higher pressure, only two diffraction peaks were observed, consistent with the two stronger hcp reflections (100 and 101, fig. S4). Measured interatomic spacings (d-spacings) are consistent with DAC measurements of Fe-6.5Si and Fe-8.7Si up to 196 GPa despite minor differences in composition (Fig. 3A) (11, 23).

Fig. 2. X-ray diffraction patterns of Fe-Si samples.

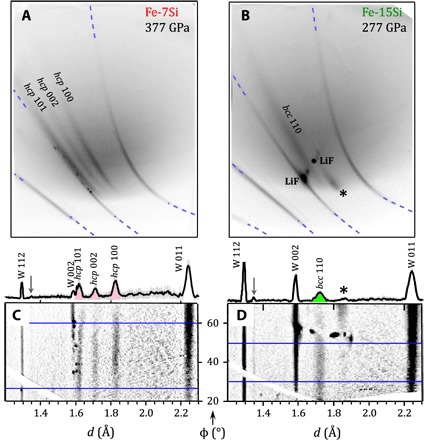
(A and B) Examples of raw (unprocessed) image plate panels. Image plate positions were calibrated using ambient pressure W-pinhole diffraction lines (dashed blue lines). (C and D) Projection of the above image plates into d-spacing − φ coordinates. The one-dimensional (1D) x-ray diffraction patterns at top were integrated over the region between the blue horizontal lines. Diffracted peaks from Fe H_α radiation (6.963 keV) are also observed (gray arrows). Asterisks (*) in (B) and (D) denote an extended feature which has a d-spacing consistent with either hcp (100) or diamond (111), as discussed in the text.

Fig. 3. Measured diffraction peaks and density of Fe-Si alloys as a function of pressure.

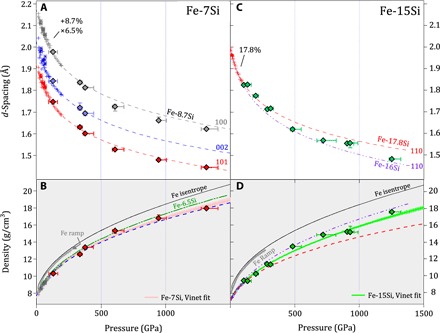
From measured (A) d-spacings of ramp-loaded Fe-7Si, we determine (B) the density of the hcp structure as a function of pressure. A Vinet equation of state fit to the data along the ramp-compression path is compared to measured and extrapolated diamond anvil cell experiments: *, green dash-dotted line = Fe-6.5Si (23); +, blue dashed line = Fe-8.7Si (11). (C) d-spacing and (D) density of ramp-loaded Fe-15Si interpreted as a bcc structure. Measured/extrapolated isotherms: +, red dashed line = Fe-17.8Si (11); purple dash-dotted line = Fe-16Si (14). For comparison, the pressure-density path of ramped Fe to 300 GPa (26) and the Fe-isentrope from Sesame EOS table 2150 (27) are shown.

The calculated ratio of the c and a lattice parameters of hcp-structured Fe-7Si at each pressure is shown in Fig. 4. We find a general increasing trend of c/a with pressure (and concomitant temperature) when using the two stronger x-ray diffraction peaks (100 and 101). Including the 002 reflection, most sensitive to the c axis yet much weaker and therefore more poorly constrained, the c/a falls closer to the trends determined by DAC experiments (23, 24).

Fig. 4. c/a ratio as a function of pressure for Fe-7Si.

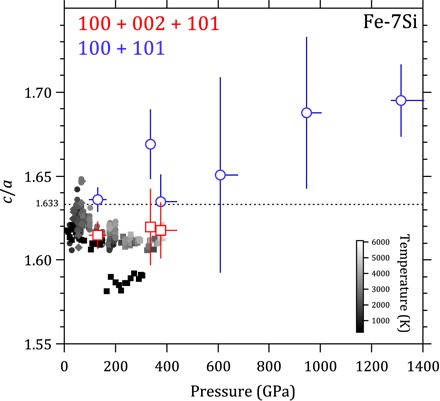
The unit cell ratios of hcp-structured Fe-7Si alloy were calculated from the x-ray diffraction patterns using all three observed hcp reflections (red squares) or only the two stronger reflections (blue circles). Low-pressure DAC data (gray symbols) predict a relatively modest increase in c/a ratio with increasing temperature (15, 23), approaching closer to the ideal hcp ratio of 1.633.

In contrast to Fe-7Si, only a single strong peak was observed from Fe-15Si over the pressure range studied (Fig. 2, B and D). To determine the structure type consistent with this line, we evaluated several candidate structures [hcp, bcc (body-centered cubic), and fcc (face-centered cubic)] and ruled out diffraction line assignments if either the resulting density was unreasonable or the expected diffraction intensity of the peak was unacceptably low given the absence of higher intensity peaks. Of all the structures considered, only the (110) diffraction line of the bcc phase provided a combination of reasonable density and x-ray diffraction intensity (see fig. S1A). A summary of experimentally determined d-spacing, pressure, and density for Fe-7Si and Fe-15Si is shown in table S1.

The calculated densities of Fe-7Si and Fe-15Si are compared to previous work in Fig. 3 (B and D). Our ramp-compressed Fe-7Si data are consistent with extrapolated equations of state measured in DAC studies of Fe-6.5Si and Fe-8.7Si (11, 23). Ramp-compressed Fe-15Si is also roughly consistent with the extrapolated equation of states of Fe-16Si and Fe-17.8Si despite some scatter in the extrapolated curves (11, 14).

DISCUSSION

Our study provides the first direct experimental constraints on phase relations and structures in the Fe-Si system above 400 GPa. We observe hcp- (Fe-7Si) and bcc-phase (Fe-15Si) stability to as high as 1314 GPa with no evidence that any additional phases are stabilized in this system. Current static equation of state determinations for Fe-Si alloys extend to about 400 GPa (15, 23)—our work extends this by over three-fold. The measured density of Fe-Si alloys is in the range of 17 to 18 g/cm³ at the peak pressure, yielding a compression of 2.5 relative to ambient values (Fig. 3).

Fe-Si equation of state to terapascal pressures

The P − ρ compression data were fit to a Vinet equation of state (25) to constrain the bulk modulus, K₀, and its pressure derivative, K₀′. We fix the initial volume, V_0, of Fe-7Si and Fe-15Si to their ambient pressure values: 11.658 Å per atom and 11.266 Å per atom, respectively. Fitting of Fe-7Si gives the values K₀ = 136.2 ± 20 GPa and K₀′ = 5.97 ± 0.47. Comparison to extrapolated static compression studies shows good agreement (Fig. 3B). When K₀′ is fixed to 5 [consistent with the range of reported values (4.7 to 5.5) from static compression studies on compositions containing 6.5 to 9 wt% Si (11, 15, 23)], the resulting K₀ value is 183.4 ± 7.4 GPa.

Fitting of Fe-15Si gives the values K₀ = 227.9 ± 24 GPa, K₀′ = 4.74 ± 0.34, or K₀ = 210.3 ± 4.9 GPa when K₀′ is fixed to 5. Our results are consistent with static compression data in that the addition of silicon increases the bulk modulus of Fe-Si alloys. Beyond this, it is difficult to draw comparisons between ramp-compressed Fe-15Si and static experiments, which exhibit considerable scatter. Contributing to this uncertainty is the limited pressure range of static measurements and the combination of more than one phase into the EOS fits: D03/B2 (11, 13) and hcp/B2 (14).

It is also of interest to compare ramp-compressed Fe-Si alloys to pure iron. Figure 3 (B and D) shows the pressure-density relationship of Fe measured in ramp-compression experiments (26), and calculated from a tabular equation of state along an isentrope (27). For isentropic compression of Fe, the temperature increase is calculated to be 650 K at 1300 GPa, with a density difference from the 300 K isotherm of <−0.5% (27). Ramp compression produces a near isentropic compression path and therefore, comparisons between our measured P − ρ data to static EOS’s are readily made. Deviations from ideal isentropic (reversible) flow occur in materials with strength, where additional sample temperature increases can occur from work heating (28). The strength of Fe-Si alloys at high pressure is not known, and therefore, the deviation from an isentrope is difficult to quantify.

By comparing our data to an isentropic compression curve for pure Fe [Sesame EOS table 2150 (27)], a tabular equation of state consistent with experimental ramp-compression data (26, 29), the density reduction of iron due to Si incorporation can be characterized to ultrahigh pressures for the first time (Fig. 5). At Earth inner core conditions, the density reduction due to Si incorporation is 8.3 ± 0.9% for Fe-7Si and 16 ± 0.7% for Fe-15Si. At 1300 GPa, these values become 8.8% and 13.2%, respectively. The density reduction due to Si incorporation is only weakly sensitive to pressure.

Fig. 5. Density difference between Fe and Fe-Si.

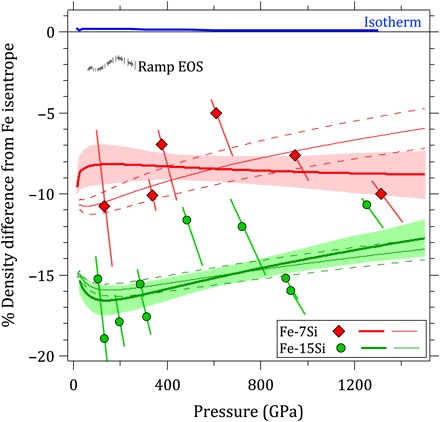
Percent density difference for measured P − ρ of Fe-7Si (diamonds) and Fe-15Si alloys (circles) with respect to the Fe end-member isentrope from Sesame EOS table 2150 (27). Red and green curves represent Vinet EOS fits to our data with V₀ fixed (filled 68% band) and V₀, K′ fixed with K′ = 5 (dashed lines). Also shown are percent density differences with ramp EOS measurements on Fe (dashed gray) (26) and the Sesame EOS table 2150 300-K isotherm (blue trace) (27). We note that the Fe isentrope used here is in agreement with recent experimental results from laser-ramp experiments (29).

Fe-Si phase diagram

Temperature is not directly measured in these ramp-compression experiments, so implications for the high pressure P-T diagram of Fe-Si alloys rely on estimates of achieved temperature. Bounds can be placed from experimental considerations (such as compression path and dissipative mechanism) and comparisons with multi-shock iron experiments (see Materials and Methods and fig. S2 for more discussion).

The phase diagram of the Fe-Si system has been studied at high pressures and temperatures both theoretically and by DAC experiments (12–14, 30–37). The vast majority of diamond anvil experiments are limited to 200 GPa or below, although recent studies have extended to as high as 400 GPa and 6000 K (23). In general, these studies show that the addition of Si to iron stabilizes the cubic B2 structure with respect to both the fcc phase (γ-Fe) at lower pressures and the hcp phase (ε-Fe) at higher pressures (see fig. S2). Theoretical studies have suggested that the presence of Si in the core may lead to stabilization of the fcc (35) or bcc phase at inner core pressures (33).

Our results for Fe-7Si at 131 to 377 GPa are consistent with diamond anvil experiments (13, 23) in that we observe that the sample has transformed from the ambient bcc structure to an hcp phase. DAC studies show that for Fe-9Si, single-phase hcp is stable at lower temperatures, whereas the coexistence of Si-rich B2 and Si-poor hcp phases is observed at higher temperatures up to at least 400 GPa (13, 23). Our observation of only the hcp phase suggests that the pressure-temperature path followed by our ramp-compression experiments lies below the hcp + B2 phase field. The amount of Si required to satisfy the density deficit of the core is estimated to be in the range of 4.5 to 12% for the outer core and 6 to 8% for the inner core (14, 31). Our observation of the hcp phase in Fe-7Si at pressures of the inner core (330 to 360 GPa) supports the stability of the hcp phase for geophysically relevant Si contents, although structure changes at temperatures closer to the core liquidus cannot be ruled out.

Under static compression, further addition of Si expands the stability field of coexisting hcp + B2, where, for Fe-16Si, a mixture of hcp and B2 phases was observed at all temperatures investigated at 140 GPa in DAC experiments (13). For our Fe-15Si composition at 105 to 311 GPa, we observed only one diffraction peak corresponding to bcc, which is consistent with the B2 structure. The B2 phase is an ordered version of the bcc structure, with Fe and Si occupying different sites. On the basis of only one observed diffraction peak, the bcc and B2 structures cannot be distinguished. Our observation of the bcc phase is consistent with static compression studies, which report increased stability of the B2 phase with respect to hcp with increased silicon content (11), and suggests that the high-temperature mixed-phase region of hcp + B2 is limited in extent and that the temperatures in our ramp-compression experiments lie below this boundary.

These results are seemingly in conflict with static compression studies that predict a large stability field of mixed hcp + B2 (13, 24). Considering the extreme pressures (hundreds of gigapascals) and the time scale (nanoseconds) of our experiments, however, it is possible that we may not observe the dissociation into Si-rich B2 and Si-poor hcp phases because requisite diffusion of Fe and Si into distinct phases may not be achievable in time for observation by in situ x-ray diffraction. That is, ordering of Fe and Si may be kinetically inhibited, and therefore, over the time scales of our experiments, Fe-15Si remains in the bcc phase. The other potential interpretation of our results is that Fe-15Si remains in the B2 structure at high pressures, and that the previously reported hcp + B2 mixed-phase region in diamond cell experiments could be due to pressure or temperature gradients rather than a coexistence of phases.

For Fe-15Si, we also observe diffraction features from the single-crystal diamond or LiF. These are often elongated at higher pressure due to deformation and break up of the single crystal under compression (Fig. 2, B and D, and figs. S3 and S4). However, one of these features (as indicated by an asterisk in Fig. 2, B and D, and fig. S3) is ambiguous in that it has a d-spacing that could be assigned to either the (111) peak of diamond or the (100) peak of the hcp structure of Fe-15Si (see also fig. S1A). We assign this peak to diamond (111) due to both the difference in texture and peak intensity considerations: If the observed diffraction peaks corresponded to hcp (100), then we would also expect to see the hcp (101) reflection with comparable intensity, but this is not present in our diffraction patterns. Similar features attributed to diamond based on d-spacing and texture have been been observed in previous ramp-compression studies on other materials (18). However, if the hcp phase is highly textured such that only the hcp (100) reflection is visible, then the coexistence of B2 + hcp would provide an alternative interpretation of the data.

Implications for exoplanet interior modeling

Although interior structure models for exoplanets may be nonunique, they are useful for investigating the plausible range of interior dynamics and evolution in these bodies (6, 7, 38, 39). For large rocky exoplanets (super-Earths), interior models have so far made the simple assumption of a pure iron core (5, 40). However, the incorporation of light elements into the core, as expected geochemically, may affect a number of properties of these bodies including the mass-radius relation, the core size, and the internal pressure and gravity distributions (2). The amount and type of light elements incorporated will depend on the P-T dependence of element partitioning behavior and the details of core formation processes. The effect of pressure on Si solubility in iron is currently uncertain (41).

Kepler-10b is a representative example of a super-Earth exoplanet with a radius of 1.47 (0.03) R_E and a mass of 3.72 (0.42) M_E (42), where R_E and M_E are the radius and mass of Earth, respectively. We have constructed a model of this planet as composed of a silicate mantle and an iron-rich core and used it to illustrate how light element incorporation influences our interpretation of planetary interiors. The mantle is assumed to have a Mg/Fe composition of Mg# = Mg/(Mg + Fe) = 0.9 and is divided into three layers as a result of structural phase transitions. The uppermost mantle consists of 80 volume % olivine and 20% enstatite. The middle layer contains perovskite and ferropericlase, and the lowermost mantle is composed of post-perovskite and ferropericlase. We compare three cases: a pure Fe core, an Fe-7Si core, and an Fe-15Si core. The interior structure is calculated by solving the coupled differential equations for hydrostatic equilibrium, mass within a sphere, and the equation of state of each component with solutions constrained to reproduce the observed mass and radius of the planet (2, 43). Interior models for Fe and Fe-Si cores are shown in Fig. 6. Addition of the light element silicon to the core increases its radius and reduces the planet’s central pressure and density. In the case of Kepler-10b, incorporation of 15 wt% Si increases the core radius by 16% while decreasing the central density and pressure by 20 and 14%, respectively. Thus, the incorporation of light elements into exoplanetary cores may have important effects on the range of possible interior structures.

Fig. 6. Modeled interior profiles of Kepler-10b.

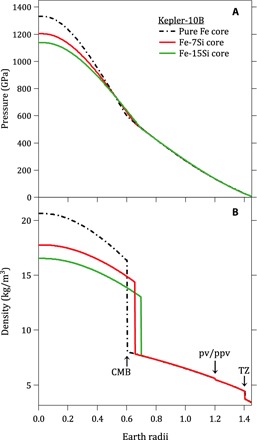
Given the observational constraints on Kepler-10b (3.72 M_E, 1.47 R_E), end-member interior models can be compared to explore the impact of light-element substitution within the core. A simple two-layer planet, core + mantle, with substitution in the core of our measured P − ρ relationship for Fe-15Si (green trace) for that of pure iron (black trace) has a large effect on the modeled pressure and density profiles. CMB, core-mantle boundary; pv/ppv, perovksite-structured bridgmanite→post-perovskite; TZ, transition zone (olivine→bridgmanite + periclase).

CONCLUSIONS

This study provides the first direct determinations of the structure of Fe-Si alloys at pressures spanning the range encountered in Earth and super-Earth planets. Our results indicate that the crystal structure of Fe-Si alloys in planetary cores will depend on the Si content. For modest Si contents up to at least 7 wt %, the crystal structure remains hcp, but the B2 phase becomes stabilized at a Si content of 15 wt %. Further comparison with static compression data will be necessary to better assess the role of kinetic factors in these high–strain rate experiments.

The peak pressure achieved here corresponds to those pressures expected at the center of a ~3–Earth mass terrestrial exoplanet. For such super-Earth planets, it has been shown that the core size is one of the interior features that can be constrained from mass and radius measurements (44). Our study pushes the pressure barriers of x-ray diffraction to unprecedented conditions, a record at 1314 GPa, and provides the first direct experimental data for Fe-Si alloys that can be used to create data-based models of exoplanets and eliminate the need to rely on long extrapolations of low-pressure static data. Future high-pressure studies on Fe-alloying elements, such as oxygen, will further improve super-Earth interior modeling.

MATERIALS AND METHODS

Sample preparation, PXRDIP experiments

The Fe-Si starting materials (99.97% purity) were obtained from ACI Alloys. Fe-7Si (Fe_0.87Si_0.13) crystallizes in the bcc structure [I$\overline{\mathit{m}}$3m, a = 2.8568(1) Å] under ambient conditions, whereas the Fe-15Si (Fe_0.74Si_0.26) composition adopts the Fe3Si–type structure [F$\overline{\mathit{m}}$3m, a = 5.65886(7) Å]. Granules (100 mesh) were ground in an alumina mortar and pestle under ethanol for several hours until grains were ~10 μm. Powdered alloy was compressed into foils using DACs with 500-μm culets to 2 GPa and heated on a hot plate at 125°C for 4 hours. This method produced ~10-μm-thick foils of >400-μm diameter.

Target packages consisted of the ~10-μm-thick sample sandwiched between two single crystals. Experiments aimed at achieving lower pressures (<350 GPa) used a 〈110〉 diamond ablator/pusher and a <100> LiF window, whereas those for higher pressure used diamond for both the pusher and the window (Fig. 1A). High-pressure targets included a thin (<1 μm) vapor-deposited Au layer that acted to shield the sample from preheating by x-rays emitted from the drive plasma (19). Individual material layers were glued together to form the final target assembly with an estimated glue thicknesses of ~1 μm. The equation of state and thickness of each glue layer was explicitly treated in the pressure determination calculations.

Each target package was centered over a Ta, W, or Pt pinhole (100 to 160 μm thick, 300-μm-diameter hole), which collimated the x-rays with an angular resolution of ~0.8° and ensured that only x-rays diffracted from the compressed sample were recorded on the image plate. Diffraction peaks from the edges of the uncompressed pinhole that appear as sharp, extended lines (delineated by dashed blue lines in Fig. 2, A and B) were used to calibrate image plate location relative to the sample position.

Use of 12.5-μm-thick Fe or Cu filters over each image plate suppressed helium-like β and γ x-rays in addition to filtering the Bremsstrahlung continuum x-ray emission from the drive plasma, which is the dominant source of noise recorded by the image plates. All foils were also supplemented with 25-μm-thick kapton filters.

As the laser intensity is increased to achieve higher pressures, the Bremsstrahlung x-ray background increases in intensity and shifts to higher photon energies, which renders spectral decoupling (signal/noise resolution at the He_α energy) progressively more difficult. For experiments up to terapascal pressures, use of higher energy (10.22 keV) He_α radiation from a Ge foil significantly improved the signal-to-noise ratio. In this case, 50- to 150-μm-thick Al filters placed in front of the image plates further reduced the plasma background. To maximize the ionization efficiency of the Ge x-ray source, the surface was primed with an initial low-power laser pulse (red laser profile in Fig. 7A), a technique shown previously to significantly enhance the Ge-He_α emission (45).

Fig. 7. Timing and pressure determination of an Fe-15Si ramp-compression experiment (diamond window).

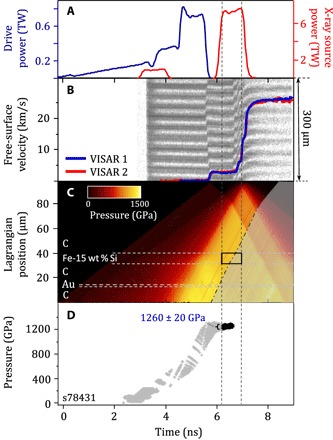
(A) Composite laser drive for shot #78431 (1260 ± 20 GPa) (blue trace). X-rays are generated using a pair of square pulses (red trace). (B) A VISAR interferogram with extracted free-surface velocity history from two VISAR channels. (C) Calculated map of pressure distribution throughout the target package, where the horizontal dashed lines indicate material boundaries in Lagrangian coordinates. Shaded in light gray, predicted pressure release waves (see Materials and Methods). (D) Calculated pressure history of the Fe-Si sample, integrated over the x-ray probe time (vertical dashed lines).

The data from five separate image plates were combined and projected into 2θ − φ coordinates, where 2θ is the diffraction angle and φ is the azimuthal angle about the incident x-ray beam (fig. S3). In these coordinates, diffraction data project as straight lines of constant 2θ. Bragg peaks were fit with Gaussian curves in 2θ and converted to d-spacing, d = λ/(2 sin θ), where λ is the wavelength of the He_α probe. Example x-ray diffraction patterns for all shots are shown in fig. S4. The features observed on the patterns can all be attributed to the sample, pinhole, or single crystal–like reflections from the diamond or LiF windows.

Pressure determination with diamond windows

Sample pressure is determined using VISAR, which for the case of Fig. 7B monitored the free-surface velocity of the diamond window through the 300-μm pinhole. The interferometer recorded the phase change of Doppler-shifted reflected light using two channels with differing velocity sensitivities (22). The measured diamond free-surface velocity, u_fs(t) (Fig. 7B, blue/red trace), served as a boundary condition for a backward characteristics analysis to determine pressure history at the sample position (18, 19, 46). In Fig. 7C, pressure as a function of Lagrangian position and time was calculated using the experimentally measured stress-density-Lagrangian sound-speed relationship for diamond (47).

The characteristics analysis implicitly assumes isentropic compression, in which the experimentally measured compression path for diamond is reversible upon release (47). For experiments at pressures above 800 GPa, where no full-density diamond ramp EOS data exist, an extrapolation of the lower pressure diamond EOS was used (47). An example of calculated P(x, t) is shown in Fig. 7C. The Fe-15Si sample layer pressure versus time, calculated at the intersection of each characteristic, is shown in Fig. 7D. The calculated pressure and distribution within the sample during the x-ray probe period was based on a histogram peak and full-width analysis.

Uncertainty in the strength of diamond on compression and release contributed to the pressure uncertainty. Under laser-driven ramp compression to 800 GPa, diamond was reported to have a yield strength of 69 to 96 GPa, which was maintained to peak pressure (47, 48). In contrast, under shock compression, single-crystal diamond exhibited a complete loss of strength for pressures above the elastic limit (48). Despite its high compressive strength, the diamond is comparatively weak under tension with a spall strength of less than 16 GPa (49).

To determine the uncertainty in sample pressure due to the uncertainty in the strength of diamond, two bounding cases for diamond pressure-density response are considered (see fig. S5A). By applying the characteristics analysis approach to data simulated with a 1D hydrocode (HYADES) (50), in which diamond strength is maintained at all times, we estimate a maximum uncertainty contribution of up to +50 GPa in the sample pressure due to diamond strength uncertainty. We incorporate this value into our pressure estimate as a systematic source of error. The final pressure uncertainties are reported in table S1.

Effect of pressure release

At cessation of laser power, a pressure release fan originating at the drive surface propagates through the target package at the local sound speed. For the shot described in Fig. 7, the laser turned off at 5.75 ns and the initial pressure release wave (dot-dashed curve in Fig. 7C) was estimated to reach the diamond free surface at ~8.5 ns. Although diamond is strong under compression, it has a low tensile strength (49). Interaction of the release wave reflected from the free surface with the oncoming release wave resulted in the production of negative stresses, brittle failure, and the formation of a spall layer that accelerates away from the diamond sample (49, 51). Thus, at late times, and at peak u_fs(t), the VISAR measures the velocity of the spall layer (51). As a result, the VISAR-determined u_fs(t) can no longer be used at these times in the characterisitics analysis. The shaded region in Fig. 7C shows the P (x, t) region affected by pressure release but not explicitly treated by the characteristics analysis.

For some shots, the pressure release wave arrives at the Fe-Si sample during the x-ray probe period. The effect of pressure release on the characteristics-determined Fe-Si pressure was studied in detail with HYADES hydrocode simulations (50), which model pressure conditions within the sample in a forward calculation while explicitly treating pressure release due to the end of a finite laser drive (for example, Fig. 7). Modeling confirms that sample pressure drops precipitously upon arrival of this pressure release wave, which means that released material does not contribute to the measured high-pressure diffraction peaks. Therefore, the pressure-released region of the sample was not considered in our determination of Fe-Si pressure and uncertainty.

Pressure determination with LiF windows

An example of pressure determination for low-pressure experiments is shown in Fig. 8. For diamond/FeSi/LiF targets, the FeSi-LiF particle velocity as a function of time, u(t), was measured. Figure 8B shows recorded u(t) profiles for two independent VISAR channels, corrected for the density dependence of the LiF window refractive index [non–temperature-corrected model in the study of Davis et al. (52)] and averaged over the 300-μm field of view.

Fig. 8. Timing and pressure determination of an Fe-15Si ramp-compression experiment (LiF window).

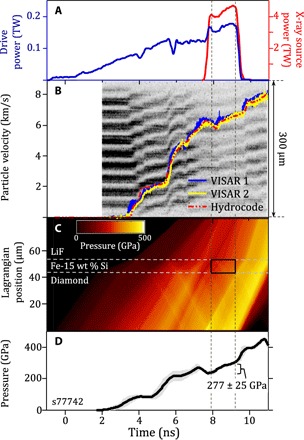
(A) Composite laser drive for shot #77742 (277 ± 25 GPa) (blue trace). X-rays are generated using square pulses (red trace). (B) Raw interferogram from VISAR records sample-LiF particle velocity, which is reproduced by hydrocode simulations (red dashed curve) to determine (C) pressure history in the target package. The black rectangle represents the sample pressure conditions during the x-ray probe period (bounded by vertical dashed lines). (D) Calculated pressure history of the Fe-15Si sample.

To determine the pressure within the sample, we simulated the experiments with HYADES (50). The code calculates the 1D hydrodynamic flow of pressure waves through the target assembly using EOS descriptions of each target material and an initial estimate of an applied pressure drive input, P(t). A scaling law relates diamond ablation pressure to laser intensity, I(t): P(t) [GPa] = 42 [I(t) (TW/cm²)]^0.71 (21).

A series of forward calculations were run with iterative adjustments of P(t) until convergence was reached between the calculated and measured u(t) (red dot-dashed trace in Fig. 8B). The pressure reported here is described by the peak and distribution of a histogram within the sample during the probe period (Fig. 8, C and D). Additional contributions to pressure uncertainty that are small relative to the calculated pressure distribution and thus neglected are uncertainties in laser beam timing (50 ps), VISAR timing (50 ps), sample thicknesses (1 μm), LiF EOS and refractive index uncertainty (see below), and the deviations between the model and the experimental u(t). On the basis of measurements of x-ray emission versus time for select shots, we assumed that He_α x-rays generated by the x-ray source beams were evenly distributed in time over a period bounded by 95% of the peak laser power on the leading and falling edge of the laser pulse profile (red curve in Fig. 8A). A summary of laser power, pressure, and sample velocity as a function of time for all shots is shown in fig. S6.

The Sesame EOS tables (53) used in the hydrocode calculations for LiF (#7271) and diamond (#7830) were in good agreement with pressure-density and sound-speed measurements (48, 52, 54). The EOS of chromium (#3070) (ρ₀ = 7.19 g/cm³) was used to represent that of the Fe-Si sample due to its similar pressure–particle velocity relationship (see fig. S5B) (16, 17, 53). Upon loading, the pressure wave reverberates within the thin Fe-alloy layer due to impedance mismatches, rapidly equilibrating pressure across the diamond/sample/LiF interfaces. Simulations confirm that the pressure in the sample is insensitive to its assumed EOS and starting density after two pressure wave reverberations.

Pressure-temperature path

Ramp compression produces less dissipative heating than shock loading, resulting in P-T states below melt to very high pressures (18). Although temperature was not directly measured in our experiments, bounds can be placed from experimental considerations.

Laser compression of the diamond produced a two-wave structure with an elastic shock of amplitude ~74 to 104 GPa followed by ramp loading to the peak pressure (47). The diamond elastic shock was transmitted into the Fe-Si sample with an amplitude of ~60 to 90 GPa due to the impedance mismatch. A lower bound on the temperature of our samples can thus be obtained from the temperature jump due to this initial shock followed by the additional temperature rise due to isentropic loading up to peak pressure (fig. S2). On the basis of comparison with P-T calculations for Fe-19.8Si (16), we assume that the P-T description of Fe from the study of Kerley (27) is representative of the states generated in our Fe-7Si and Fe-15Si samples (see fig. S2).

Plastic work heating will result in a further temperature increase beyond that of isentropic compression alone (47, 55). The melting curve of the Fe-Si alloys would provide an extreme upper bound to the temperature in these experiments because our diffraction measurements indicate that our samples remain solid up to peak pressure, but the effect of Si on the melting point is not well characterized at these extreme pressures. Figure S2 shows the melting curve of Fe extrapolated to high pressures (56). Static diamond anvil experiments show that the phase diagram of Fe-Si was characterized by a single-phase hcp structure at lower temperatures and a mixture of hcp + B2 phases at higher temperatures, as discussed above. Our observation of the hcp phase only for the Fe-7Si composition indicates that our sample temperatures are below the B2 + hcp→hcp phase boundary.

Constraints on temperatures can also be explored by reference to multishock experiments on iron to 560 GPa (55). This study used extended x-ray absorption fine structure spectroscopy to infer temperatures along off-Hugoniot states (fig. S2). There, it was concluded that a significant component of the temperature increase, above the expected double-shock P-T path, was attributable to work heating due to a significant increase in the strength of iron under high–strain rate compression. Our study was thus consistent with a broad range of possible sub-solidus temperatures in these Fe-Si alloys (fig. S2). Estimated temperatures within the cores of large rocky extra-solar planets of 2.5 to 5 Earth masses in size fall within the bounds of possible temperatures in these experiments (20). Future studies into the strength response of both sample and window materials would improve both the accuracy and the precision of pressure and temperature determination in ramp-compression experiments.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaao5864/DC1

fig. S1. Consideration of alternate structures for Fe-15Si.

fig. S2. Constraints on the P-T phase diagram for Fe-7Si and Fe-15Si.

fig. S3. Example of projected image plates, from shot s77742.

fig. S4. X-ray diffraction patterns as a function of pressure.

fig. S5. Equation of state models used for pressure determination.

fig. S6. Summary of laser power, interface velocity, and sample pressure history for Fe-7Si and Fe-15Si ramp-compression experiments.

table S1. Data summary.

References (57–60)