Abstract
Basal ganglia dysfunction in Parkinson’s disease (PD) is thought to generate deficits in action control, but the characterization of these deficits have been qualitative rather than quantitative. Patients with PD typically show prolonged response times on tasks that instantiate a conflict between goal-directed processing and automatic response tendencies. In the Simon task, for example, the irrelevant location of the stimulus automatically activates a corresponding lateralized response, generating a potential conflict with goal-directed choices. We applied a new computational model of conflict processing to two sets of behavioral data from the Simon task to quantify the effects of PD and dopaminergic (DA) medication on action control mechanisms. Compared to healthy controls (HC) matched in age gender and education, patients with PD showed a deficit in goal-directed processing, and the magnitude of this deficit positively correlated with cognitive symptoms. Analyses of the time-course of the location-based automatic activation yielded mixed findings. In both datasets, we found that the peak amplitude of the automatic activation was similar between PD and HC, demonstrating a similar degree of response capture. However, PD patients showed a prolonged automatic activation in only one dataset. This discrepancy was resolved by theoretical analyses of conflict resolution in the Simon task. The reduction of interference generated by the automatic activation appears to be driven by a mixture of passive decay and top-down inhibitory control, the contribution of each component being modulated by task demands. Our results suggest that PD selectively impairs the inhibitory control component, a deficit likely remediated by DA medication. This work advances our understanding of action control deficits in PD, and illustrates the benefit of using computational models to quantitatively measure cognitive processes in clinical populations.
Keywords: Parkinson’s Disease, Computational Modeling, Action Control, Dopamine, Basal Ganglia
Introduction
Computational models of cognition provide a quantitative account of behavioral data, and decompose performance into psychologically meaningful processes. These models force researchers to be explicit about underlying assumptions, and are increasingly used in clinical research to isolate impaired cognitive processes associated with disorders (Aschenbrenner, Balota, Gordon, Ratcliff, & Morris, 2016; Frank, 2005; Frank, Seeberger, & O’Reilly R, 2004; Ho et al., 2014; Lee, Abramyan, & Shankle, 2015; Ratcliff, Perea, Colangelo, & Buchanan, 2004; Shankle et al., 2013; White, Ratcliff, & Vasey, 2015; White, Ratcliff, Vasey, & McKoon, 2010a, 2010b). A growing body of evidence suggests that basal ganglia dysfunction in Parkinson’s disease (PD) is associated with deficits in action control mechanisms, particularly in times of response conflict (e.g., Chan, Armstrong, Pari, Riopelle, & Munoz, 2005; Praamstra, Plat, Meyer, & Horstink, 1999; Praamstra & Plat, 2001; Praamstra, Stegeman, Cools, & Horstink, 1998; Wylie, Ridderinkhof, Bashore, & van den Wildenberg, 2010; Wylie, Stout, & Bashore, 2005). Interpretation of data has been driven primarily by qualitative theories. The present study uses a new computational model of conflict tasks (Ulrich, Schröter, Leuthold, & Birngruber, 2015) to shed light on the nature of action control deficits in PD.
The effect of PD on action control mechanisms
Learning complex motor skills such as driving a car or playing the violin is a slow and effortful process that engages goal-directed systems. Motor plans become increasingly automatic with extensive training (Logan, 1988; Shiffrin & Schneider, 1977; Servant, Cassey, Woodman, & Logan, 2017). Although automatic response tendencies are an important component of adaptive behavior, they can sometimes conflict with goal-directed actions (Kornblum, Hasbroucq, & Osman, 1990). Theories of conflict processing generally assume that top-down inhibitory mechanisms are engaged to suppress automatic response tendencies and achieve goals (Ridderinkhof, 2002; Van den Wildenberg et al., 2010; but see Hommel, 1993, 1994).
Patients with PD typically show prolonged response times (RT) compared to healthy controls (HC) on tasks that instantiate a conflict between automatic response tendencies and goal-directed actions (e.g., Chan et al., 2005; Praamstra & Plat, 2001; Praamstra et al., 1998; van Wouwe et al., 2016; van Wouwe et al., 2014; Wylie et al., 2012; Wylie et al., 2010; Wylie et al., 2005; Wylie et al., 2009a, 2009b). This finding has been interpreted as reflecting a deficit in inhibitory control, resulting in a greater sensitivity to interference. Recent studies, however, suggest that goal-directed processing is also impaired in PD (de Wit, Barker, Dickinson, & Cools, 2011; Sharp, Foerde, Daw, & Shohamy, 2016).
Both goal-directed and inhibitory processes are mediated by basal ganglia circuits, and by dopaminergic (DA) projections in those circuits (Aron, 2007; Aron & Poldrack, 2006; Balleine & O’Doherty, 2010; Frank, 2006; Jahanshahi, Obeso, Rothwell, & Obeso, 2015; Yin & Knowlton, 2006). PD severely compromises the brain’s DA system, leading to altered processing in the basal ganglia (Bernheimer, Birkmayer, Hornykiewicz, Jellinger, & Seitelberger, 1973; Kordower et al., 2013; Redgrave et al., 2010; Robbins & Cools, 2014). Understanding the nature of these alterations is critical for developing efficient therapeutics. In the present work, we use a computational model of conflict tasks to decompose cognitive processes involved in action control, and quantify the effects of PD and DA medication.
Simon task: measuring response conflict
The Simon task offers one of the most sensitive experimental measures of conflict between goal-directed and automatic actions (Hommel, 2011; Kornblum et al., 1990). Participants are instructed to issue a left or right hand button press response to an attribute (e.g., the color) of a spatially lateralized stimulus. Responses are typically slower and less accurate when the location of the stimulus and the response signaled by the imperative attribute do not correspond (e.g., a left hand response to a stimulus presented to the right visual half-field) than when they do, a phenomenon known as the Simon effect (Simon & Small, 1969). Theories of this effect assume that the irrelevant location of the stimulus automatically primes a corresponding lateralized response (De Jong, Liang, & Lauber, 1994; Hommel, 1993; Kornblum et al., 1990; Ridderinkhof, 2002). Plots of accuracy data as a function of RT quantiles (i.e., conditional accuracy functions, or CAFs) provide support in favor of this hypothesis (Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988; Ridderinkhof, 2002; Servant, Montagnini, & Burle, 2014). For corresponding trials, accuracy is high and relatively constant over the distribution of RTs. By contrast, non-corresponding trials are associated with an early reduction of accuracy (Figure 2A, upper panel), betraying a fast response capture by the location of the stimulus. Electrophysiological recordings have provided converging findings. Early electrical activations of the motor cortex and response agonist muscles associated with the spatially-driven response hand have been observed in non-corresponding trials (Coles, Gratton, Bashore, Eriksen, & Donchin, 1985; C. W. Eriksen, Coles, Morris, & O’Hara, 1985; Leuthold, 2011; Servant, White, Montagnini, & Burle, 2015, 2016).
Figure 2.
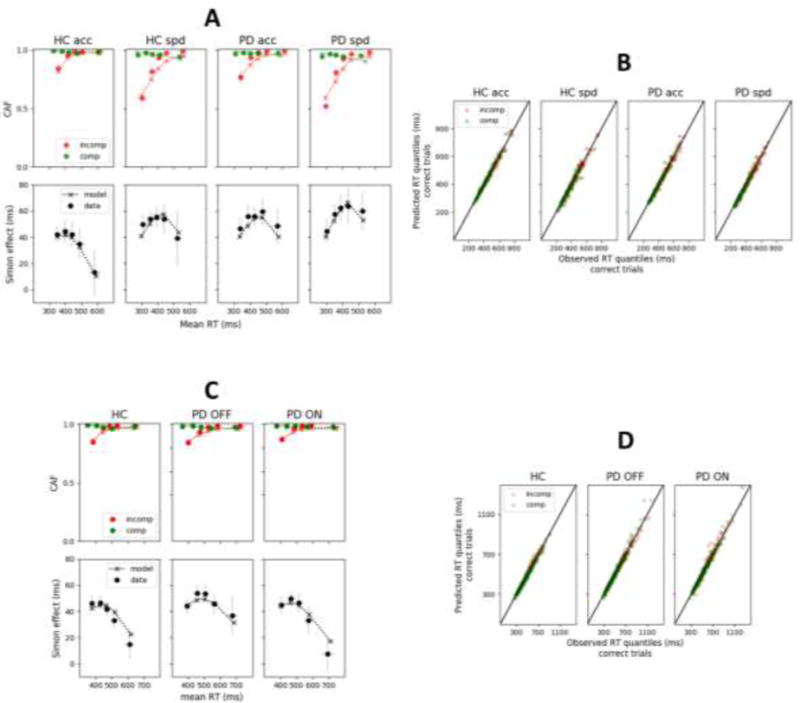
A and C: Observed (datapoints) versus predicted (x’s) conditional accuracy functions (CAFs) and delta plots for each group and condition of Dataset 1 (panel A; van Wouwe et al., 2014) and Dataset 2 (panel B, van Wouwe et al., 2016) averaged across subjects. Each datapoint is accompanied by a 95% confidence interval assuming a student’s t distribution. B and D: Observed (x-axis) versus predicted (y-axis) RT quantiles of correct responses across individual subjects and conditions from Dataset 1 (Panel B) and Dataset 2 (Panel D). comp: compatible stimulus-response; incomp: incompatible stimulus-response.
Theories explaining the Simon effect differ with respect to the evolution of the location-based automatic response priming. Distributional analyses of RT have revealed that the magnitude of the Simon effect decreases as processing time increases. This dynamic is best appreciated with the delta plot technique (De Jong et al., 1994). Delta plots represent the difference (y-axis) against the average (x-axis) of equivalent RT quantiles between non-corresponding and corresponding conditions (Figure 2A, lower panel). Decreasing delta plots have consistently been observed for healthy subjects, showing that the Simon effect is maximal early in the course of processing and decreases for higher RT quantiles (Pratte, Rouder, Morey, & Feng, 2010; Proctor, Miles, & Baroni, 2011; Schwarz & Miller, 2012). Ridderinkhof’s (2002) activation-suppression theory asserts that the location-based automatic response priming is actively suppressed by a top-down inhibitory process that takes time to build (see also Van den Wildenberg et al., 2010). Other theories propose that the automatic response priming passively decays over time (e.g., Hommel, 1993, 1994, 2011). Our model-based analyses offer quantitative estimates of the buildup and reduction of automatic response priming, providing insight into these theoretical alternatives.
Comparisons of CAFs and delta plots from PD patients and HC matched in age, gender and education in the Simon task have revealed consistent patterns. The early dip of accuracy observed on CAFs in the non-corresponding condition does not generally differ between PD and HC, suggesting that the strength of automatic response capture by the location of the stimulus is similar (van Wouwe et al., 2016; van Wouwe et al., 2014; Wylie et al., 2010). Delta plots, however, show an effect of disease, with a less negative-going delta plot slope for PD than HC. This effect has been interpreted in the context of the activation-suppression model (Ridderinkhof, 2002). Specifically, the shallower delta plot observed for PD is thought to reflect a deficit in top-down inhibitory response control (Wylie et al., 2010). Interestingly, delta plots are normalized by DA medication, suggesting that the deficit in inhibitory control is linked to basal ganglia dysfunction induced by DA depletion (van Wouwe et al., 2016).
It should be emphasized that theories of the Simon effect introduced so far are qualitative. In the present work, we sought to provide a quantitative account of behavioral data from PD patients and HC using a computational model of conflict tasks (Ulrich et al., 2015). This model, introduced below, has proven to account for RT distributions and accuracy data observed in the Simon task, and corresponding neurophysiological dynamics (Servant et al., 2016).
The Diffusion Model of conflict tasks (DMC)
The DMC (Ulrich et al., 2015) is an extension of the diffusion model for decision-making (Ratcliff, 1978). The diffusion model has been widely employed in basic and clinical research to decompose behavioral performance from two-choice RT tasks into psychologically interpretable processes (Ratcliff & McKoon, 2008; Ratcliff, Smith, Brown, & McKoon, 2016; White et al., 2010b). The model assumes that task-relevant sensory information is continuously accumulated until it reaches a threshold level, and then the decision terminates in a choice and the response is executed. Noise in physical stimulations and sensory systems makes the process stochastic, potentially leading to an incorrect choice (Brunton, Botvinick, & Brody, 2013; Ratcliff, 1978). The diffusion model has four main parameters (Figure 1, left). The rate of task-relevant sensory information accumulation is called the drift rate (v); it is determined by the quality of the sensory information and the efficiency of attentional processes. Decision thresholds (b: correct choice; -b: incorrect choice) regulate the speed/accuracy strategy. Lower thresholds produce faster but less accurate responding. The starting point (z) of the accumulation process indexes response bias. The process is biased toward the response associated with the nearest threshold. The decision time is the latency between the onset of the accumulation process and the first crossing of a decision threshold. A residual processing latency (Ter), comprising sensory encoding and motor execution components, is added to the decision time to produce a RT. The model predicts the shape of RT distributions for correct and incorrect responses, which can be specified by the probability density function or from computer simulations. These predictions can be fit to data to extract underlying parameters (Ratcliff & Tuerlinckx, 2002).
Figure 1.
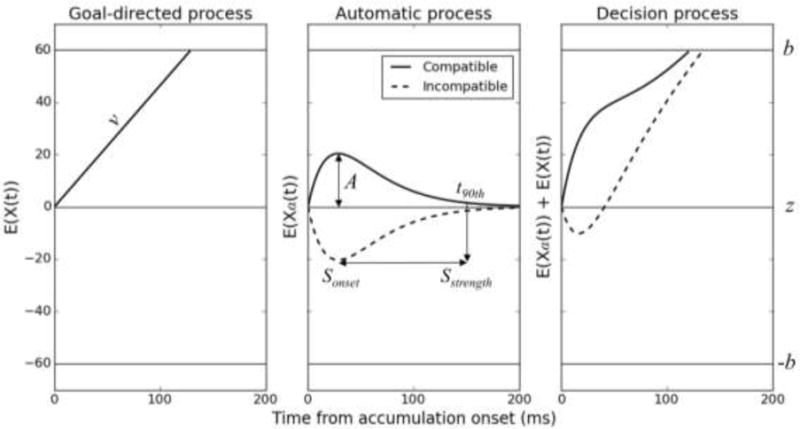
Architecture of the diffusion model of conflict tasks (DMC). The decision process is the sum of automatic and goal-directed decision activations. The goal-directed decision activation X(t) is similar to the standard drift diffusion model. The automatic decision activation Xa(t) has a pulse-like gamma shape. b: correct decision threshold (incorrect threshold is at –b); v: drift rate of the goal-directed process; A: peak amplitude of the gamma function; Sonset: suppression onset, corresponding to the peak latency of the gamma function [Sonset = τ(a − 1)]; t90th: 90th percentile of the gamma percent point function (i.e., the latency at which 90% of the gamma automatic activation has been emitted); Sstrength: suppression strength, defined as t90th - Sonset.
The DMC extends the diffusion model framework by incorporating components of automatic processing. Performance is determined by the sum of automatic and goal-directed decision activations, an architecture reminiscent of a model of automaticity proposed by Logan (Logan, 1980). Contrary to its predecessor, however, the DMC assumes that the contribution of automatic processes is short-lived in conflict tasks such as the Simon task (Ellinghaus, Karlbauer, Bausenhart, & Ulrich, 2017; Lu & Proctor, 1995; Simon, Acosta, Mewaldt, & Spiedel, 1976). The automatic decision activation Xa(t) is modeled as a pulse-like gamma function that favors the correct response in corresponding trials and the incorrect response in non-corresponding trials (Figure 1, middle). Its expected mean as a function of time is described by the following equation:
Where a, τ and A are the shape, characteristic time and peak amplitude of the gamma function respectively. The peak amplitude A quantifies the strength of the automatic activation: the higher the peak amplitude, the stronger the automatic activation. In corresponding trials, automatic and goal-directed processes converge to activation of the correct choice, thereby facilitating RT and accuracy. In non-corresponding trials, the automatic activation favors the incorrect choice, triggering fast errors and slowing down RT (Figure 1, right).
The DMC can be used to distinguish passive decay from activation-suppression theories. Decay theory interprets the gamma function as the growth and decay of automatic activation. Activation-suppression theory interprets the gamma function as the activation and inhibition of automatic activation. Decay should depend primarily on time, not strategy, whereas inhibition should depend on strategy. We address this issue in the discussion section. For now, we assume that the automatic activation is actively suppressed. The onset latency and strength of suppression can be derived from the gamma parameters. The onset of suppression Sonset corresponds to the peak latency of the automatic activation, Sonset = τ(a − 1). Let t90th denote the latency at which 90% of the automatic activation has been emitted. Technically speaking, t90th corresponds to the 90th percentile of the gamma percent point function. Suppression strength Sstrength can be estimated by computing the difference between t90th and Sonset (Figure 1, right). The larger Sstrength, the less efficient the suppression.
The aim of the present work was to provide a model-based analysis of action control mechanisms in PD. We fit the DMC to Simon task behavioral data from PD and HC matched in age, gender and education (van Wouwe et al., 2014; referred to as Dataset 1) to quantify the efficiency of goal-directed (parameter v) and inhibitory (gamma-derived statistics Sonset and Sstrength) processes. We also measured the strength of the location-based automatic activation (parameter A). Dataset 1 was well suited for these purposes because it contained sufficient trials per condition and a speed-accuracy manipulation, which further constrained model fits. Finally, we fit another Simon task dataset from PD ON versus OFF DA medication (van Wouwe et al., 2016; referred to as Dataset 2) to quantify the effect of DA medication on goal-directed and inhibitory processes.
Methods
A brief overview of critical details about participants and experimental procedures for Dataset 1 (van Wouwe et al., 2014) and Dataset 2 (van Wouwe et al., 2016) is recounted below.
Participants
Participants with PD were diagnosed by a neurologist specialized in movement disorders. Ratings on the Hoehn and Yahr scale (Hoehn & Yahr, 1967) and the Unified Parkinson’s Disease Rating Scale (UPDRS) indicated mild to moderate disease severity. All participants met the following exclusion criteria: (i) schizophrenia, bipolar disorder or other psychiatric disease known to affect cognitive functions and (ii) severe mood disorder or medical condition known to interfere with cognition (e.g., diabetes, pulmonary disease).
Dataset 1 featured 21 PD patients and 21 HC matched in age, gender, education, and Mini-Mental Status Exam scores (MMSE; Folstein, Folstein, & McHugh, 1975). MMSE scores ranged 27–30, i.e. well beyond the standard cut-off of 24 indicating cognitive impairment (Tombaugh & McIntyre, 1992). Nineteen of the 21 PD patients were taking DA medication, and were tested during the optimal “ON” phase of their DA medication cycle.
Dataset 2 contained 55 PD patients and 56 HC matched in age, gender, and education. PD patients were tested in their optimal ON phase of their DA medication cycle (condition ON) versus after a 36- to 48 hr withdrawal from their DA medication (condition OFF). The order of visits was counterbalanced across patients. MMSE scores were not available. Instead, PD patients completed the Montreal Cognitive Assessment (MoCA) test (Nasreddine et al., 2005). Ratings indicated very mild to minimal gross cognitive difficulties (all scores ≥ 23).
Procedure
Subjects from Dataset 1 completed 20 blocks of 40 trials from a Simon task featuring a speed-accuracy manipulation. A central fixation cross was presented at the center of the screen during the whole duration of each block of trials. Stimuli (blue and green circles) were presented to the left or right of fixation for 250 ms. A response deadline was set at 1200 ms. The interstimulus interval was 1250 ms. In each group, half of the subjects gave a right hand response to blue stimuli and a left hand response to green stimuli. This mapping was reversed for the other half. Speed and accuracy instructions were alternated between blocks. At the end of each block, subjects were given a feedback on their performance to ensure compliance with instructions.
Subjects from Dataset 2 completed 4 blocks of 60 trials. The task was similar to that used for Dataset 1 except that (i) subjects always had to respond as fast and as accurately as possible (no speed-accuracy manipulation), (ii) the response deadline was fixed at 1500 ms, and (iii) the intertrial interval was 1750–2250 ms (randomly jittered using a rectangular distribution).
DMC fitting procedure
The DMC was fit to behavioral data from each subject individually using a procedure developed by Ratcliff and collaborators (Ratcliff & Smith, 2004; Ratcliff & Tuerlinckx, 2002). The model was simultaneously fit to correct and error RT distributions (.1, .3, .5, .7, .9 quantiles) and to accuracy data. Because the number of errors Ne was generally low, particularly in the corresponding condition, we used an adaptive procedure that only considered the median RT of errors if 0 < Ne ≤ 5, three RT quantiles (.3, .5, .9) if 5 < Ne ≤ 10, and five RT quantiles (.1, .3, .5, .7, .9) if Ne > 10. Because the DMC is mathematically intractable (Ulrich et al., 2015), computer simulations were performed using an integration constant dt = 1 ms to obtain model predictions. The magnitude of within-trial noise, called diffusion coefficient, was fixed at 4 (arbitrary value) to satisfy a mathematical scaling property of the model (Ulrich, Schröter, Leuthold, & Birngruber, 2016). Because left and right responses were equiprobable, we assumed an unbiased starting point (z = 0, halfway between correct and incorrect decision thresholds). Data and model predictions were compared through a chi-square statistic. For a standard Simon task with corresponding and non-corresponding conditions (Dataset 2), the chi-square statistic has the following form:
Where Ni is the number of observations per condition i. pij and πij are, respectively, the observed and predicted proportions of trials in bin j of condition i, which sum to 1 across each pair of correct and error distributions. The variable B represents the number of bins bounded by RT quantiles across each pair of correct and error distributions. Consequently, we have B = 8 if 0 < Ne ≤ 5, B = 10 if 5 < Ne ≤ 10, and B = 12 if Ne > 10. The chi-square statistic was minimized with the Simplex algorithm (Nelder & Mead, 1965) to obtain best-fitting parameters. Because Simplex is sensitive to the initial parameter guess, we used 40 different starting points drawn from uniform distributions bounded by previous fits of the model to data (Servant et al., 2016; Ulrich et al., 2015). Twenty-five thousand trials per condition were simulated for each minimization cycle. Next, we submitted the two best parameter sets (obtained from different starting points) to additional Simplex runs, and simulated 50,000 trials per condition and minimization cycle. The DMC and fitting procedure were programmed in python. Codes were run on Vanderbilt’s advanced computing center for education and research.
Model selection
We tested different DMC variants and compared their goodness-of-fit performance using chi-square tests for nested models (for a similar approach, see Boucher, Palmeri, Logan, & Schall, 2007; Logan, Yamaguchi, Schall, & Palmeri, 2015). The test statistic is the difference χ2Model A - χ2Model B summed over subjects, where Model A is nested in Model B. The number of degrees of freedom for the test is the difference in the number of free parameters multiplied by the number of subjects.
The DMC has 6 main parameters: upper (correct) decision threshold (b; incorrect threshold is at -b), drift rate for the goal-directed process (v), mean non-decision time (Ter), peak amplitude (A; positive in corresponding trials, negative in non-corresponding trials), shape (a), and characteristic time (τ) of the gamma automatic activation. Ulrich et al. (2015) further incorporated intertrial variability in nondecision time and starting point, two assumptions inherited from the standard diffusion model (Ratcliff, 2013; Ratcliff & Rouder, 1998). We thus evaluated the goodness-of-fit of 3 nested DMC variants: a model without intertrial variability, a model with intertrial variability in nondecision time (normally distributed with mean Ter and standard deviation σTer), and a model with intertrial variability in nondecision time and starting point (uniformly distributed with range σz). To account for the speed-accuracy manipulation in Dataset 1, we further compared unconstrained models (all parameters free to vary between speed and accuracy conditions) against models in which one or more parameters were fixed across conditions. Although speed pressure is considered to mainly affect decision thresholds in the diffusion model framework (Bogacz, Wagenmakers, Forstmann, & Nieuwenhuis, 2010; Ratcliff & Smith, 2004), recent modeling and neurophysiological studies suggest that it might also affect other parameters such as drift rate (Cassey, Heathcote, & Brown, 2014; Heitz & Schall, 2012; Rae, Heathcote, Donkin, Averell, & Brown, 2014) and nondecision time (Spieser, Servant, Hasbroucq, & Burle, 2016; White, Ratcliff, & Starns, 2011). Spieser et al. (2016) found an effect of speed pressure on the electromyographic (EMG) activity of response agonist muscles in a flanker task (B. A. Eriksen & Eriksen, 1974). Specifically, the motor time (latency between the onset of EMG activity and the mechanical response) was significantly shorter under speed than accuracy instructions, and accounted for more than 20% of the total effect on global RT. In light of these findings, we let the nondecision time parameter (Ter) of the DMC model free to vary across speed-accuracy instructions.
Parameter recovery
Computational models are only useful as measurement tools if their parameters can be adequately recovered. Stochastic models with a high number of free parameters (such as diffusion models) can be associated with parameter tradeoffs and a sloppy spectrum of parameter sensitivities (e.g., Gutenkunst et al., 2007). White, Servant, and Logan (2017) recently conducted a parameter recovery study on the main parameters of the DMC. The quality of the recovery monotonically increased as the number of trials per condition increased, and was generally better for basic diffusion model parameters (b, v, Ter) than for parameters driving the gamma automatic activation (a, τ, and A). For the range of trials in Datasets 1 and 2 (100–200 trials per condition), the corresponding trial range in the parameter recovery study yielded correlations between simulated and recovered parameters of 0.81-.99 for basic diffusion model parameters and .4-.65 for gamma parameters. Among gamma parameters, the peak amplitude A showed the best recovery results (0.59–0.65). In addition, gamma-derived statistics showed good recovery (suppression onset Sonset: 0.88–91; suppression strength Sstrength: .77-.83), validating their use in the present work1.
Results
Fits to Dataset 1 (van Wouwe et al., 2014)
Figure 2A shows CAFs (upper panel) and delta plots (lower panel) averaged across subjects for each group and condition of Dataset 1. Each datapoint is accompanied by a 95% confidence interval assuming a student’s t distribution. van Wouwe et al. (2014) constructed delta plots from 10 RT quantiles. We instead represented delta plots from the 5 RT quantiles (.1, .3, .5, .7, .9) used to fit the model to data. Delta plots constructed from 5 versus 10 RT quantiles exhibited very similar trends. Their slope was generally more negative-going for HC than PD, and more negative-going for the accuracy than the speed condition. By contrast, CAFs appeared relatively similar between HC and PD groups. CAFs were constructed by sorting the RT data into 5 bins of equal size. Accuracy in each bin (y-axis) was plotted against the corresponding mean RT (x-axis). CAFs showed the typical early dip of accuracy in the non-corresponding condition. This dip was more pronounced under speed pressure, showing that the proportion of fast errors increased.
We fit five nested DMC variants to data to identify the model that provided the best fit. All parameters of Models 1, 2 and 3 were free to vary across speed and accuracy conditions. Model 1 contained the main DMC parameters (b, v, Ter, a, τ, and A). Model 2 incorporated intertrial variability in nondecision time (σTer). Model 3 incorporated intertrial variability in nondecision time and starting point (σz). We found that intertrial variability in nondecision time was critical to capture the shape of RT distributions for both HC (Model 1 - Model 2: χ2(42) = 1775, p < .001) and PD (Model 1 - Model 2: χ2(42) = 2117, p < .001). The goodness-of-fit for Model 3 was significantly better than Model 2 (HC: χ2(42) = 106, p < .001; PD: χ2(42) = 252, p < .001), presumably because σz captured fast guesses in the speed condition. Consistent with this hypothesis, marginal χ2 differences between Model 2 and Model 3 were larger in the speed (HC: χ2 = 81; PD: χ2 = 176) than the accuracy condition (HC: χ2 = 25; PD: χ2 = 76).
We then compared Model 3 against a nested model in which the drift rate for the goal-directed process (v) was constrained to be fixed across speed-accuracy instructions (Model 4). The goodness-of-fit for Model 3 was significantly better than Model 4 (HC: χ2(21) = 1161, p < .001; PD: χ2(21) = 1656, p < .001). Constraining v to be fixed across speed-accuracy instructions prevented the DMC from capturing accuracy data. We finally considered a nested model in which gamma parameters were fixed across speed-accuracy instructions (Model 5). Model 5 failed to capture the shape of RT distributions (HC: χ2(63) = 1162, p < .001; PD: χ2(63) = 1808, p < .001).
CAFs and delta plots predicted by Model 3 averaged across subjects are shown in Figure 2A (dashed lines). The model captures all trends of the data, and the majority of predictions fall into 95% confidence intervals. Observed versus predicted RT quantiles of correct responses across individual subjects are displayed in Figure 2B. Datapoints are gathered around the ideal x = y line for each group and experimental condition, diagnostic of a good fit.
The best-fitting parameters for Model 3 averaged across subjects are shown in Table 1. We conducted mixed-design analyses of variance (ANOVAs) to assess the effects of disease (between-subjects) and speed-accuracy (within-subjects) on model parameters. The strength of the automatic activation, as quantified by the peak amplitude of the gamma (A), did not differ between PD and HC, F(1, 40) = 1.06, p = .31. By contrast, the onset of suppression (Sonset) was significantly delayed for PD than HC, F(1, 40) = 15.11, p < .001. Suppression strength was also less efficient for PD than HC, as revealed by larger values of Sstrength, F(1, 40) = 7.56, p = .009. Although the effect of disease on the drift rate of the goal-directed process (v) failed to reach significance F(1, 40) = 1.76, p = .19, drift rate values were numerically smaller for PD than HC.
Table 1.
Best-fitting DMC parameters to Dataset 1 (van Wouwe et al., 2014) averaged across subjects.
| HC accuracy | HC speed | PD accuracy | PD speed | |
|---|---|---|---|---|
|
|
||||
|
DMC parameters
|
||||
| b | 65.8 | 54.5 | 63.3 | 54.2 |
| v | 0.486 | 0.418 | 0.457 | 0.387 |
| A | 25.1 | 27.2 | 22.5 | 25.9 |
| a | 2.3 | 2.5 | 2.5 | 2.8 |
| τ (ms) | 41.2 | 52.4 | 59.1 | 54.2 |
| Ter (ms) | 324 | 292 | 312 | 283 |
| σTer (ms) | 42.7 | 48.5 | 46 | 47.2 |
| σz | 43.9 | 48.1 | 46.8 | 53 |
|
Gamma-derived statistics
|
||||
| Sonset (ms) | 47.1 | 69.2 | 80.5 | 86.2 |
| Sstrength (ms) | 120 | 158 | 179 | 170 |
Note. The DMC was simulated with an integration constant dt = 1 ms and a diffusion coefficient fixed at 4. b: upper (correct) decision threshold (incorrect threshold is at –b); v: drift rate of the controlled process; Ter: mean nondecision time; σr: intertrial variability in nondecision time; σz: intertrial variability in starting point; A, a, τ: peak amplitude, shape, and characteristic time of the gamma automatic activation; Sonset: suppression onset, corresponding to the peak latency of the gamma automatic activation [Sonset = τ(a−1)]; Sstrength: suppression strength, computed as t90th - Sonset where t90th is the 90th percentile of the gamma percent point function (i.e., the latency at which 90% of the gamma automatic activation has been emitted). Parameters Ter, σr, τ, and gamma-derived statistics Sonset and Sstrength are in milliseconds (ms). Other parameters are in units of diffusion coefficient (arbitrary).
Speed pressure significantly lowered decision thresholds F(1, 40) = 40.55, p < .001, consistent with previous work on the standard diffusion model (e.g., Ratcliff & Smith, 2004). We also found significant effects of speed pressure on the drift rate of the goal-directed process (v; F(1, 40) = 20.9, p < .001) and the peak amplitude of the automatic activation (A; F(1, 40) = 5.06, p = .03), suggesting that speed pressure altered the efficiency of goal-directed processing and increased the sensitivity to irrelevant stimulus information. Non-decision times (Ter) were significantly faster in the speed than the accuracy instructions F(1, 40) = 62.39, p < .001, consistent with EMG results of Spieser et al. (2016). The magnitude of the effect (30 ms) was close to that observed on the EMG motor time (23 ms). No other main effects nor interactions between disease and speed-accuracy instructions reached significance (all ps > .1).
To facilitate comparison between Datasets 1 and 2, we computed an additional mixed-design ANOVA on model parameters, considering only those 19 PD patients that were tested in their optimal ON phase of their DA medication cycle. This analysis revealed similar findings with one exception: the effect of disease on the drift rate of the goal-directed process was marginally significant, F(1, 38) = 3.50, p = .069. Note that empirical delta plot patterns/analyses remained similar when considering PD ON patients only (Appendix A).
To summarize, model fits to Dataset 1 showed that the strength of the automatic response capture by the irrelevant location attribute of the stimulus was similar between PD and HC. However, inhibitory control was delayed and less efficient for PD compared to HC, resulting in a longer-lasting interference. The modeling also suggests a deficit in goal-directed processing in PD, although this effect failed to reach statistical significance.
Fits to Dataset 2 (van Wouwe et al., 2016)
Figure 2C displays CAFs (upper panel) and delta plots (lower panel) averaged across subjects for each group (HC, PD OFF DA medication, PD ON) of Dataset 2. van Wouwe et al. (2016) showed that the delta plot slope was less negative-going for PD OFF than HC, and did not differ between PD ON and HC. The latter appears in sharp contrast with empirical findings from Dataset 1. Remember that 90% of PD patients in Dataset 1 were tested during the optimal ON phase of their DA medication cycle, and their delta plot was significantly less negative-going compared to HC. This discrepancy between studies will be thoroughly discussed in the general discussion.
We fit Model 1 (main DMC parameters), Model 2 (DMC with intertrial variability in nondecision time σTer) and Model 3 (DMC with intertrial variability in nondecision time and starting point σz) to behavioral data from each subject. Consistent with previous fits, we found that intertrial variability in nondecision time was critical to capture the shape of RT distributions for all groups (Model 1 - Model 2; HC: χ2(56) = 1512, p < .001, PD OFF: χ2(55) = 1346, p < .001, PD ON: χ2(55) = 1094, p < .001). The goodness-of-fit of Model 3, however, was not significantly better than Model 2 (HC: χ2(56) = 65, p = .18, PD OFF: χ2(55) = 53, p = .53, PD ON: χ2(55) = 43, p = .89). Thus, intertrial variability in starting point was not necessary for good fits. Predicted CAFs and delta plots averaged across subjects are displayed in Figure 2C (dashed lines). The model captures all trends of the data, and the majority of predictions fall into 95% confidence intervals.
The best-fitting parameters averaged across subjects are shown in Table 2. As a first step, we conducted independent t-tests to assess the effect of disease (comparison PD OFF versus HC) on model parameters2. The strength of the automatic activation (A) did not differ between PD OFF and HC t(109) = 0.12, p = .99, consistent with previous findings. Although suppression onset (Sonset) was delayed and suppression strength (Sstrength) reduced for PD OFF relative to HC, these modulations failed to reach significance (t(109) = −1.12, p = .27 and t(109) = −.92, p = .36 respectively). Disease significantly altered the drift rate of the goal-directed process (v), t(109) = 2.09, p = .039. No other comparison reached significance (all ps > .1).
Table 2.
Best-fitting DMC parameters to Dataset 2 (van Wouwe et al., 2016) averaged across subjects.
| HC | PD OFF | PD ON | ||
|---|---|---|---|---|
|
|
||||
|
DMC parameters
|
||||
| b | 66.3 | 70.2 | 72.1 | |
| v | 0.485 | 0.437 | 0.434 | |
| A | 25.8 | 25.8 | 24.4 | |
| a | 2.3 | 2.5 | 2.4 | |
| τ (ms) | 49 | 52 | 53.5 | |
| Ter (ms) | 350 | 362 | 365 | |
| σTer (ms) | 47.6 | 55 | 53.7 | |
|
Gamma-derived statistics
|
||||
| Sonset (ms) | 62.5 | 76.5 | 65.7 | |
| Sstrength (ms) | 146 | 159 | 158 | |
As a second step, we performed paired t-tests to assess the effect of DA medication on model parameters (comparison PD OFF versus ON). Although suppression onset occurred earlier for PD ON than PD OFF, this effect failed to reach significance, t(54) = .95, p = .35. No other comparison reached significance. For completeness, we computed independent t-tests between HC and PD ON. Consistent with results reported for PD OFF, this analysis revealed a significantly reduced drift rate of the goal-directed process (v) for PD ON compared with HC, t(109) = 2.17, p = .033. No other comparison reached significance.
To summarize, modeling results for Dataset 2 showed that PD impairs goal-directed processing. Contrary to Dataset 1, we found no effect of disease on inhibitory control parameters. In addition, we found no evidence for a modulatory role of DA medication on any of the model parameters.
Discussion
The aim of the present work was to provide a model-based analysis of action control mechanisms in PD and HC matched in age, gender, and education. Previous studies suggest a deficit in the ability to resolve conflict between goal-directed processing and automatic response tendencies in PD, but the nature of this deficit remains unclear. We modeled two Simon task behavioral datasets (van Wouwe et al., 2014, 2016) with the DMC (Ulrich et al., 2015) to decompose cognitive processes involved in action control, and quantify the effects of PD and DA medication. Our results indicate some inconsistencies between the two datasets that we sought to explain and reconcile in the following sections3.
A deficit in inhibitory control in PD?
The modeling of Dataset 1 (van Wouwe et al., 2014; Simon task featuring a speed-accuracy manipulation) and Dataset 2 (van Wouwe et al., 2016; standard Simon task) showed that the strength of the location-based automatic activation, as quantified by the peak amplitude of the gamma function A, was similar for PD ON and HC subjects. This finding suggests that disease doesn’t affect response capture. Although suppression statistics Sonset and Sstrength were significantly larger for PD ON than HC in Dataset 1, these effects were not replicated in Dataset 2. This failure reflects inconsistencies in delta plot patterns between the two studies. Ulrich et al. (2015) demonstrated that the slope of the delta plot predicted by the DMC is largely determined by the onset of suppression (Sonset). Specifically, the slope of the delta plot becomes more positive as Sonset increases. Consistent with our modeling, van Wouwe et al. (2014) found a significantly more positive-going delta plot for PD ON than HC in both accuracy and speed conditions. This modulation, however, was not replicated in their subsequent work (van Wouwe et al., 2016): delta plots were not significantly different between PD ON and HC. As we discuss below, the discrepancy might be caused by a variation in the amount of inhibitory control engaged in the two Simon task variants.
Qualitative theories of the Simon effect diverge as to whether the location-based automatic activation decays passively (Hommel, 1993, 1994, 2011) or is actively suppressed (Ridderinkhof, 2002). As outlined in the Introduction section, passive decay should depend primarily on time, and should be the same regardless of subjects’ speed-accuracy strategy. Consequently, decay theory predicts a similar time-course of the automatic activation across speed and accuracy instructions, consistent with the modeling of Dataset 1. Neither the main effect of speed pressure nor the interaction between disease and speed pressure on suppression statistics (Sonset and Sstrength) reached statistical significance. However, a rapid look at model parameters in Table 1 shows that suppression onset (Sonset) is delayed and suppression strength (Sstrength) is weaker under speed pressure for HC only. Indeed, separate ANOVAs for HC and PD showed a marginally significant effect of speed pressure on Sonset and Sstrength for HC (F(1, 20) = 4.14, p = .055 and F(1, 20) = 3.04, p = .096 respectively), but not for PD (all ps > .1), suggesting that (i) an inhibitory control component also contributes to the reduction of the automatic activation and (ii) this component might be selectively impaired in PD. The contribution of the two components (passive decay and active suppression) to the reduction of the automatic activation might be largely determined by context, which might explain why empirical findings currently favor both accounts (e.g., Hommel, 1993, 1994; Ridderinkhof, 2002). Arguably, demands on inhibitory control processes were generally higher for Dataset 1 than Dataset 2, due to the incorporation of a speed-accuracy manipulation. If PD selectively impairs the inhibitory control component, we would thus expect an effect of disease on suppression parameters in Dataset 1 only. This is exactly what we found. Our modeling results are thus consistent with the view that inhibitory control mechanisms are impaired in PD (e.g., Chan et al., 2005; Praamstra & Plat, 2001; Praamstra et al., 1998; van Wouwe et al., 2016; van Wouwe et al., 2014; Wylie et al., 2012; Wylie et al., 2010). They also suggest that the reduction of interference in the Simon task is driven by a mixture of inhibitory control and passive decay, the contribution of each component being modulated by context. This hypothesis deserves further investigation. Context may refer to the environment or the way the task is performed. A recent study showed a decrease of the Stroop effect when subjects were standing than when they were sitting, suggesting that body posture modulates cognitive control mechanisms (Rosenbaum, Mama, & Algom, 2017). Context also refers to experimental manipulations such as urgency, proportion of non-corresponding trials, or relevance of the location attribute of the stimulus. For example, Ridderinkhof (2002) intermixed regular color-Simon trials with 25% of trials in which subjects had to respond on the basis of the location of the stimulus (context where location was the target aspect of the stimulus, condition ‘CLT’) versus 25% of trials in which subjects had to respond to the shape of the stimulus (context where location could always be ignored, condition ‘CLI’). Demands on inhibitory control processes should be stronger for CLI than CLT. Accordingly, the slope of the delta plot was more positive for CLT than CLI. This path of research should be pursued in order to better understand the relative contributions of decay versus inhibitory control to the reduction of interference in the Simon task.
An alternative, although not necessarily exclusive, explanation of the empirical and modeling inconsistencies between Datasets 1 and 2 concerns variations in DA-related variables between samples of PD patients. DA medication daily dose intensity, as quantified by Levodopa Equivalent Daily Dose (LEDD), was higher on average for PD patients from Dataset 2 (M = 732; SD = 431) than PD patients from Dataset 1 (M = 547; SD = 244). PD might thus impair inhibitory control mechanisms, but this deficit might be improved by DA medication. van Wouwe et al. (2016) reported a significantly more positive delta plot for PD OFF compared with PD ON and HC, although the amplitude of the modulation was small (see Figure 2C, lower panel). Accordingly, our modeling revealed a numerical trend for delayed suppression in PD OFF compared to PD ON and HC (Table 2). This numerical trend, however, was small and non-significant. Noise in model fits4 might have hurt our ability to detect a significant effect of DA medication on suppression parameters, if this effect does exist. To get further insight into the relationship between DA medication and inhibitory control, we computed the Pearson correlation coefficient between LEDD and suppression parameters (Sonset and Sstrength) in each dataset and condition. We found a significant correlation between suppression strength (Sstrength) and LEDD in the speed condition of Dataset 1, r = −.48, p = .039. The higher the LEDD, the stronger the suppression. No other correlation reached statistical significance (all ps > .1). Consequently, DA medication likely improves the PD-related deficit in inhibitory control, but this effect might be hard to detect in Dataset 2 due to (i) the small contribution of inhibitory control to performance and (ii) noise in model fits.
A recent meta-analysis of studies comparing performance from PD patients and HC on tasks that presumably engage inhibitory control suggests that disease duration interacts with DA medication to produce modulations of performance (Manza, Amandola, Tatineni, Li, & Leung, 2017). Specifically, DA medication seems to improve inhibitory control for PD patients with shorter disease duration. However, the average disease duration was close between the two samples of PD ON patients from Dataset 1 (M = 6.4 years) and Dataset 2 (M = 6 years). In addition, we did not find any significant correlation between disease duration and suppression parameters (Sonset and Sstrength) in each Dataset (all ps > .1). Consequently, disease duration is unlikely to have played a modulatory role in the present empirical and modeling findings.
To summarize, our analyses suggest that PD impairs inhibitory control, a deficit likely remediated by DA medication. They also suggest that the reduction of interference in the Simon task is driven by a mixture of inhibition control and passive decay, the contribution of each component being modulated by context.
The effect of PD on goal-directed processing
Beyond parameters related to the location-based automatic activation, our modeling revealed a lower rate of task-relevant sensory evidence accumulation (parameter v) in PD than HC, demonstrating a deficit in goal-directed processing. The rate of task-relevant sensory evidence accumulation in the diffusion model framework is thought to depend on the efficiency of sensory encoding and attentional processes (Ratcliff & Smith, 2004; Smith & Ratcliff, 2009; White et al., 2011). The model, however, does not allow for decomposition of these two processing components.
The effect of disease on goal-directed processing was significant in Dataset 2, but only marginally significant in Dataset 1. The comparison between PD ON and OFF in Dataset 2 suggests that this deficit is not related to DA-related variables: drift rate values were very similar between the two groups of patients (PD ON: v = 0.434; PD OFF: v = 0.437). Beyond differences in DA-related variables, samples of PD patients from Datasets 1 and 2 differ in terms of cognitive symptoms. PD patients from Dataset 1 showed high cognitive functioning, as indicated by scores at ceiling on the MMSE (range 27–30). However, the sample of PD patients from Dataset 2 allowed from mild to minimal gross cognitive difficulties (range 23–30 on the MoCA). Consequently, the deficit in goal-directed processing might be mediated by cognitive symptoms. To test this hypothesis, we computed the Pearson correlation coefficient between the drift rate of the controlled process (parameter v) and MoCA scores for PD patients from Dataset 2. This correlation was high and significant for both groups (PD ON: r = .46, p < .001; PD OFF: r = .35, p < .001, see Figure 3), showing that greater cognitive difficulties are associated with slower goal-directed processing. This finding appears consistent with the lack of effect of DA medication on parameter v, as MoCA is typically used to assess extra-basal ganglia progression of PD to frontal areas (e.g., Nazem et al., 2009; but see discussion below)5.
Figure 3.
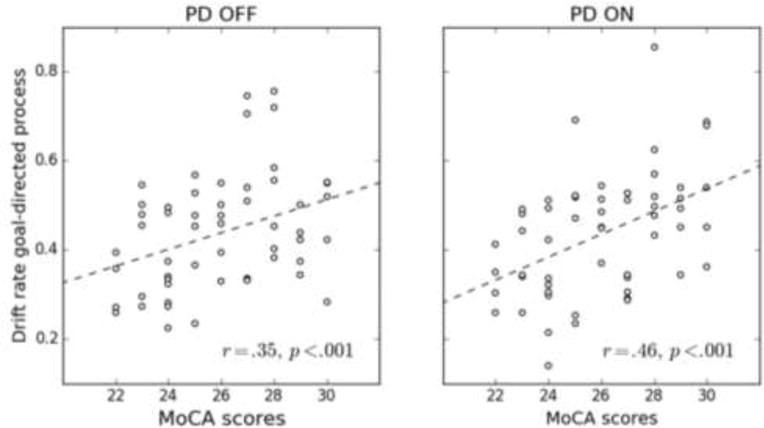
Correlation between the drift rate of the goal-directed process (parameter v) and MoCA scores for PD OFF (left panel) and PD ON (right panel) patients from Dataset 2 (van Wouwe et al., 2016). Also shown are lines of best fit (dashed lines).
Our findings add to the growing body of evidence showing a deficit in goal-directed processing in PD (de Wit et al., 2011; Sharp et al., 2016). In addition, they suggest that cognitive impairment is an important mediator of the goal-directed deficit, which might explain discrepant results in the literature (Redgrave et al., 2010; Robbins & Cools, 2014). However, grey zones remain. De Wit et al. (2011) did not find an effect of DA medication on goal-directed processing, consistent with our findings. By contrast, Sharp et al. (2016) found that the deficit in goal-directed processing in PD was completely restored by DA medication. The reason for this discrepancy is unclear. Neuroimaging studies have shown that the striatal DA deficit in PD is a strong predictor of frontal lobe executive dysfunction (Bruck et al., 2001; Jokinen et al., 2009), consistent with positive results of Sharp and colleagues. However, DA-independent factors such as the deterioration of cholinergic pathways, β-amyloid plaque and Lewy body depositions in PD also contribute to frontal dysfunction (e.g., Bohnen et al., 2012; Jellinger, 2006). In addition, the neurobiological effects of DA medication remain poorly characterized, and variations in DA medication type (e.g., DA agonist monotherapy, levodopa monotherapy) and LEDD between samples might contribute to the discrepant results.
To summarize, our model-based analyses suggest that PD impairs inhibitory control, a deficit likely remediated by DA medication. They also suggest that the reduction of interference in the Simon task is driven by a mixture of inhibition control and passive decay, the contribution of each component being modulated by context. Consequently, observed variations in delta plot patterns should be interpreted with caution. Finally, our modeling highlights a deficit in goal-directed processing in PD, mediated by early cognitive symptoms and extra-basal ganglia progression of PD to frontal areas. This work illustrates the benefit of using computational models to quantitatively measure cognitive processes in clinical populations.
Highlights.
We used a new computational model of action control to characterize and quantify the effects of Parkinson’s disease (PD) and dopaminergic medication (DA).
Relative to healthy controls, PD patients showed a deficit in inhibitory control.
The PD-related deficit in inhibitory control is likely remediated by DA medication.
PD patients also showed a deficit in goal-directed processing, and the magnitude of this deficit correlated with cognitive symptoms.
Acknowledgments
This work was supported by NEI grant R01-EY021833 and the Vanderbilt Vision Research Center P30-EY008126. It was conducted in part using the resources of the Advanced Computing Center for Research and Education (ACCRE) at Vanderbilt University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
To simplify parameter estimation, Ulrich et al. (2015) fixed the shape parameter (a) of the gamma function at 2. With this constraint, the characteristic time parameter τ corresponds to the onset of suppression Sonset = τ(a − 1) = τ. White et al. (2017) conducted an additional parameter recovery study on the DMC and fixed a at 2. The recovery for Sonset (.8-.82) was poorer than for the unconstrained DMC model variant (0.88-.91). Consequently, we treated the shape parameter of the gamma as a free parameter in our modeling.
Because the sampling distribution of model parameters is unknown, we also conducted permutation tests. t-tests and permutation tests yielded virtually similar results. For sake of clarity and brevity, we only report results from t-tests.
To facilitate comparison between the 2 datasets, we only consider modeling results from the 19 PD ON patients from Dataset 1 in the discussion section.
Dataset 2 featured a relatively small number of trials per condition (see Methods), which necessarily alters the validity of parameter estimates (White et al., 2017).
For completeness, we computed the correlation between MoCA scores and suppression parameters (Sonset and Sstrength) for each group of PD patients from Dataset 2. These correlations were not significant (all ps > .1).
References
- Aron AR. The neural basis of inhibition in cognitive control. Neuroscientist. 2007;13(3):214–228. doi: 10.1177/1073858407299288. [DOI] [PubMed] [Google Scholar]
- Aron AR, Poldrack RA. Cortical and subcortical contributions to Stop signal response inhibition: role of the subthalamic nucleus. J Neurosci. 2006;26(9):2424–2433. doi: 10.1523/jneurosci.4682-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aschenbrenner AJ, Balota DA, Gordon BA, Ratcliff R, Morris JC. A diffusion model analysis of episodic recognition in preclinical individuals with a family history for Alzheimer’s disease: The adult children study. Neuropsychology. 2016;30(2):225–238. doi: 10.1037/neu0000222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, O’Doherty JP. Human and rodent homologies in action control: corticostriatal determinants of goal-directed and habitual action. Neuropsychopharmacology. 2010;35(1):48–69. doi: 10.1038/npp.2009.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernheimer H, Birkmayer W, Hornykiewicz O, Jellinger K, Seitelberger F. Brain dopamine and the syndromes of Parkinson and Huntington. Clinical, morphological and neurochemical correlations. J Neurol Sci. 1973;20(4):415–455. doi: 10.1016/0022-510x(73)90175-5. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Wagenmakers EJ, Forstmann BU, Nieuwenhuis S. The neural basis of the speed-accuracy tradeoff. Trends Neurosci. 2010;33(1):10–16. doi: 10.1016/j.tins.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Bohnen NI, Muller ML, Kotagal V, Koeppe RA, Kilbourn MR, Gilman S, Frey KA. Heterogeneity of cholinergic denervation in Parkinson’s disease without dementia. J Cereb Blood Flow Metab. 2012;32(8):1609–1617. doi: 10.1038/jcbfm.2012.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucher L, Palmeri TJ, Logan GD, Schall JD. Inhibitory control in mind and brain: an interactive race model of countermanding saccades. Psychol Rev. 2007;114(2):376–397. doi: 10.1037/0033-295x.114.2.376. [DOI] [PubMed] [Google Scholar]
- Bruck A, Portin R, Lindell A, Laihinen A, Bergman J, Haaparanta M, Rinne JO. Positron emission tomography shows that impaired frontal lobe functioning in Parkinson’s disease is related to dopaminergic hypofunction in the caudate nucleus. Neurosci Lett. 2001;311(2):81–84. doi: 10.1016/s0304-3940(01)02124-3. [DOI] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, Brody CD. Rats and humans can optimally accumulate evidence for decision-making. Science. 2013;340(6128):95–98. doi: 10.1126/science.1233912. [DOI] [PubMed] [Google Scholar]
- Cassey P, Heathcote A, Brown SD. Brain and Behavior in Decision-Making. PLoS Comput Biol. 2014;10 doi: 10.1371/journal.pcbi.1003700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan F, Armstrong IT, Pari G, Riopelle RJ, Munoz DP. Deficits in saccadic eye-movement control in Parkinson’s disease. Neuropsychologia. 2005;43(5):784–796. doi: 10.1016/j.neuropsychologia.2004.06.026. [DOI] [PubMed] [Google Scholar]
- Coles MG, Gratton G, Bashore TR, Eriksen CW, Donchin E. A psychophysiological investigation of the continuous flow model of human information processing. Journal of Experimental Psychology: Human Perception and Performance. 1985;11(5):529–553. doi: 10.1037//0096-1523.11.5.529. [DOI] [PubMed] [Google Scholar]
- De Jong R, Liang CC, Lauber E. Conditional and unconditional automaticity: a dual-process model of effects of spatial stimulus-response correspondence. Journal of Experimental Psychology: Human Perception and Performance. 1994;20(4):731–750. doi: 10.1037//0096-1523.20.4.731. [DOI] [PubMed] [Google Scholar]
- de Wit S, Barker RA, Dickinson AD, Cools R. Habitual versus goal-directed action control in Parkinson disease. J Cogn Neurosci. 2011;23(5):1218–1229. doi: 10.1162/jocn.2010.21514. [DOI] [PubMed] [Google Scholar]
- Ellinghaus R, Karlbauer M, Bausenhart KM, Ulrich R. On the time-course of automatic response activation in the Simon task. Psychol Res. 2017 doi: 10.1007/s00426-017-0860-z. [DOI] [PubMed] [Google Scholar]
- Eriksen BA, Eriksen CW. Effects of noise letters upon the identification of a target letter in a nonsearch task. Perception & Psychophysics. 1974;16:143–149. doi: 10.3758/BF03203267. [DOI] [Google Scholar]
- Eriksen CW, Coles MGH, Morris LR, O’Hara WP. An electromyographic examination of response competition. Bulletin of the Psychonomic Society. 1985;23:165–168. [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12(3):189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Frank MJ. Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J Cogn Neurosci. 2005;17(1):51–72. doi: 10.1162/0898929052880093. [DOI] [PubMed] [Google Scholar]
- Frank MJ. Hold your horses: a dynamic computational role for the subthalamic nucleus in decision making. Neural Netw. 2006;19(8):1120–1136. doi: 10.1016/j.neunet.2006.03.006. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Seeberger LC, O’Reilly R C. By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science. 2004;306(5703):1940–1943. doi: 10.1126/science.1102941. [DOI] [PubMed] [Google Scholar]
- Gratton G, Coles MG, Sirevaag EJ, Eriksen CW, Donchin E. Pre- and poststimulus activation of response channels: a psychophysiological analysis. Journal of Experimental Psychology: Human Perception and Performance. 1988;14(3):331–344. doi: 10.1037//0096-1523.14.3.331. [DOI] [PubMed] [Google Scholar]
- Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput Biol. 2007;3(10):1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasher L, Stoltzfus ER, Zacks RT, Rypma B. Age and inhibition. J Exp Psychol Learn Mem Cogn. 1991;17(1):163–169. doi: 10.1037//0278-7393.17.1.163. [DOI] [PubMed] [Google Scholar]
- Heitz RP, Schall JD. Neural mechanisms of speed-accuracy tradeoff. Neuron. 2012;76(3):616–628. doi: 10.1016/j.neuron.2012.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho TC, Yang G, Wu J, Cassey P, Brown SD, Hoang N, Yang TT. Functional connectivity of negative emotional processing in adolescent depression. J Affect Disord. 2014;155:65–74. doi: 10.1016/j.jad.2013.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehn MM, Yahr MD. Parkinsonism: onset, progression and mortality. Neurology. 1967;17(5):427–442. doi: 10.1212/wnl.17.5.427. [DOI] [PubMed] [Google Scholar]
- Hommel B. The relationship between stimulus processing and response selection in the Simon task: Evidence for a temporal overlap. Psychological Research. 1993;55(4):280–290. doi: 10.1007/BF00419688. [DOI] [Google Scholar]
- Hommel B. Spontaneous decay of response-code activation. Psychological Research. 1994;56(4):261–268. doi: 10.1007/BF00419656. [DOI] [PubMed] [Google Scholar]
- Hommel B. The Simon effect as tool and heuristic. Acta Psychologica. 2011;136(2):189–202. doi: 10.1016/j.actpsy.2010.04.011. [DOI] [PubMed] [Google Scholar]
- Jahanshahi M, Obeso I, Rothwell JC, Obeso JA. A fronto-striato-subthalamic-pallidal network for goal-directed and habitual inhibition. Nat Rev Neurosci. 2015;16(12):719–732. doi: 10.1038/nrn4038. [DOI] [PubMed] [Google Scholar]
- Jellinger KA. The morphological basis of mental dysfunction in Parkinson’s disease. J Neurol Sci. 2006;248(1–2):167–172. doi: 10.1016/j.jns.2006.05.002. [DOI] [PubMed] [Google Scholar]
- Jokinen P, Bruck A, Aalto S, Forsback S, Parkkola R, Rinne JO. Impaired cognitive performance in Parkinson’s disease is related to caudate dopaminergic hypofunction and hippocampal atrophy. Parkinsonism Relat Disord. 2009;15(2):88–93. doi: 10.1016/j.parkreldis.2008.03.005. [DOI] [PubMed] [Google Scholar]
- Kordower JH, Olanow CW, Dodiya HB, Chu Y, Beach TG, Adler CH, Bartus RT. Disease duration and the integrity of the nigrostriatal system in Parkinson’s disease. Brain. 2013;136(Pt 8):2419–2431. doi: 10.1093/brain/awt192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kornblum S, Hasbroucq T, Osman A. Dimensional overlap: cognitive basis for stimulus-response compatibility–a model and taxonomy. Psychological Review. 1990;97(2):253–270. doi: 10.1037/0033-295x.97.2.253. [DOI] [PubMed] [Google Scholar]
- Lee MD, Abramyan M, Shankle WR. New methods, measures, and models for analyzing memory impairment using triadic comparisons. Behav Res Methods. 2015 doi: 10.3758/s13428-015-0662-4. [DOI] [PubMed] [Google Scholar]
- Leuthold H. The Simon effect in cognitive electrophysiology: A short review. Acta Psychol (Amst) 2011;136(2):203–211. doi: 10.1016/j.actpsy.2010.08.001. [DOI] [PubMed] [Google Scholar]
- Logan GD. Attention and automaticity in Stroop and priming tasks: Theory and data ☆. 1980;12(4):523–553. doi: 10.1016/0010-0285(80)90019-5. [DOI] [PubMed] [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Logan GD, Yamaguchi M, Schall JD, Palmeri TJ. Inhibitory control in mind and brain 2.0: blocked-input models of saccadic countermanding. Psychol Rev. 2015;122(2):115–147. doi: 10.1037/a0038893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu CH, Proctor RW. The influence of irrelevant location information on performance: A review of the Simon and spatial Stroop effects. Psychon Bull Rev. 1995;2(2):174–207. doi: 10.3758/bf03210959. [DOI] [PubMed] [Google Scholar]
- Manza P, Amandola M, Tatineni V, Li Cs R, Leung HC. Response inhibition in Parkinson’s disease: a meta-analysis of dopaminergic medication and disease duration effects. NPJ Parkinsons Dis. 2017;3 doi: 10.1038/s41531-017-0024-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasreddine ZS, Phillips NA, Bedirian V, Charbonneau S, Whitehead V, Collin I, Chertkow H. The Montreal Cognitive Assessment, MoCA: a brief screening tool for mild cognitive impairment. J Am Geriatr Soc. 2005;53(4):695–699. doi: 10.1111/j.1532-5415.2005.53221.x. [DOI] [PubMed] [Google Scholar]
- Nazem S, Siderowf AD, Duda JE, Have TT, Colcher A, Horn SS, Weintraub D. Montreal cognitive assessment performance in patients with Parkinson’s disease with “normal” global cognition according to mini-mental state examination score. J Am Geriatr Soc. 2009;57(2):304–308. doi: 10.1111/j.1532-5415.2008.02096.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A Simplex Method for Function Minimization. The Computer Journal. 1965;7:308–313. doi: 10.1093/comjnl/7.4.308. [DOI] [Google Scholar]
- Praamstra P, Plat EM, Meyer AS, Horstink MW. Motor cortex activation in Parkinson’s disease: dissociation of electrocortical and peripheral measures of response generation. Mov Disord. 1999;14(5):790–799. doi: 10.1002/1531-8257(199909)14:5<790::aid-mds1011>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- Praamstra P, Plat FM. Failed suppression of direct visuomotor activation in Parkinson’s disease. J Cogn Neurosci. 2001;13(1):31–43. doi: 10.1162/089892901564153. [DOI] [PubMed] [Google Scholar]
- Praamstra P, Stegeman DF, Cools AR, Horstink MW. Reliance on external cues for movement initiation in Parkinson’s disease. Evidence from movement-related potentials. Brain. 1998;121(Pt 1):167–177. doi: 10.1093/brain/121.1.167. [DOI] [PubMed] [Google Scholar]
- Pratte MS, Rouder JN, Morey RD, Feng C. Exploring the differences in distributional properties between Stroop and Simon effects using delta plots. Atten Percept Psychophys. 2010;72(7):2013–2025. doi: 10.3758/app.72.7.2013. [DOI] [PubMed] [Google Scholar]
- Proctor RW, Miles JD, Baroni G. Reaction time distribution analysis of spatial correspondence effects. Psychon Bull Rev. 2011;18(2):242–266. doi: 10.3758/s13423-011-0053-5. [DOI] [PubMed] [Google Scholar]
- Rae B, Heathcote A, Donkin C, Averell L, Brown S. The hare and the tortoise: emphasizing speed can change the evidence used to make decisions. J Exp Psychol Learn Mem Cogn. 2014;40(5):1226–1243. doi: 10.1037/a0036801. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. Parameter variability and distributional assumptions in the diffusion model. Psychol Rev. 2013;120(1):281–292. doi: 10.1037/a0030775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 2008;20(4):873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Perea M, Colangelo A, Buchanan L. A diffusion model account of normal and impaired readers. Brain Cogn. 2004;55(2):374–382. doi: 10.1016/j.bandc.2004.02.051. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling Response Times for Two-Choice Decisions. Psychological Science. 1998;9:347–356. doi: 10.1111/1467-9280.00067. [DOI] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111(2):333–367. doi: 10.1037/0033-295x.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, Brown SD, McKoon G. Diffusion Decision Model: Current Issues and History. Trends Cogn Sci. 2016;20(4):260–281. doi: 10.1016/j.tics.2016.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin & Review. 2002;9(3):438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redgrave P, Rodriguez M, Smith Y, Rodriguez-Oroz MC, Lehericy S, Bergman H, Obeso JA. Goal-directed and habitual control in the basal ganglia: implications for Parkinson’s disease. Nat Rev Neurosci. 2010;11(11):760–772. doi: 10.1038/nrn2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridderinkhof KR. Activation and suppression in conflict tasks: Empirical clarification through distributional analyses. In: Prinz W, Hommel B, editors. Common mechanisms in perception and action. Attention and Performance, XIX. Oxford: Oxford University Press; 2002. pp. 494–519. [Google Scholar]
- Robbins TW, Cools R. Cognitive deficits in Parkinson’s disease: a cognitive neuroscience perspective. Mov Disord. 2014;29(5):597–607. doi: 10.1002/mds.25853. [DOI] [PubMed] [Google Scholar]
- Rosenbaum D, Mama Y, Algom D. Stand by Your Stroop: Standing Up Enhances Selective Attention and Cognitive Control. Psychol Sci. 2017 doi: 10.1177/0956797617721270. 956797617721270. [DOI] [PubMed] [Google Scholar]
- Schwarz W, Miller J. Response time models of delta plots with negative-going slopes. Psychonomic Bulletin and Review. 2012;19(4):555–574. doi: 10.3758/s13423-012-0254-6. [DOI] [PubMed] [Google Scholar]
- Servant M, Montagnini A, Burle B. Conflict tasks and the diffusion framework: Insight in model constraints based on psychological laws. Cogn Psychol. 2014;72:162–195. doi: 10.1016/j.cogpsych.2014.03.002. [DOI] [PubMed] [Google Scholar]
- Servant M, White C, Montagnini A, Burle B. Using Covert Response Activation to Test Latent Assumptions of Formal Decision-Making Models in Humans. J Neurosci. 2015;35(28):10371–10385. doi: 10.1523/jneurosci.0078-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Servant M, White C, Montagnini A, Burle B. Linking Theoretical Decision-making Mechanisms in the Simon Task with Electrophysiological Data: A Model-based Neuroscience Study in Humans. J Cogn Neurosci. 2016:1–21. doi: 10.1162/jocn_a_00989. [DOI] [PubMed] [Google Scholar]
- Servant M, Cassey P, Woodman GF, Logan GD. Neural Bases of Automaticity. J Exp Psychol Learn Mem Cogn. 2017 doi: 10.1037/xlm0000454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shankle WR, Pooley JP, Steyvers M, Hara J, Mangrola T, Reisberg B, Lee MD. Relating memory to functional performance in normal aging to dementia using hierarchical Bayesian cognitive processing models. Alzheimer Dis Assoc Disord. 2013;27(1):16–22. doi: 10.1097/WAD.0b013e31824d5668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp ME, Foerde K, Daw ND, Shohamy D. Dopamine selectively remediates ‘model-based’ reward learning: a computational approach. Brain. 2016;139(Pt 2):355–364. doi: 10.1093/brain/awv347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiffrin RM, Schneider WE. Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychological Review. 1977;84:127–190. [Google Scholar]
- Simon JR, Acosta E, Mewaldt SP, Spiedel CR. The effect of an irrelevant directional cue on choice reaction time: Duration of the phenomenon and its relation to stages of processing. Perception & Psychophysics. 1976;19(1):16–22. doi: 10.3758/BF03199380. [DOI] [Google Scholar]
- Simon JR, Small AM., Jr Processing auditory information: interference from an irrelevant cue. Journal of Applied Psychology. 1969;53(5):433–435. doi: 10.1037/h0028034. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. An integrated theory of attention and decision making in visual signal detection. Psychol Rev. 2009;116(2):283–317. doi: 10.1037/a0015156. [DOI] [PubMed] [Google Scholar]
- Spieser L, Servant M, Hasbroucq T, Burle B. Beyond decision! Motor contribution to speed-accuracy trade-off in decision-making. Psychon Bull Rev. 2016 doi: 10.3758/s13423-016-1172-9. [DOI] [PubMed] [Google Scholar]
- Tombaugh TN, McIntyre NJ. The mini-mental state examination: a comprehensive review. J Am Geriatr Soc. 1992;40(9):922–935. doi: 10.1111/j.1532-5415.1992.tb01992.x. [DOI] [PubMed] [Google Scholar]
- Ulrich R, Schröter H, Leuthold H, Birngruber T. Automatic and controlled stimulus processing in conflict tasks: Superimposed diffusion processes and delta functions. Cogn Psychol. 2015;78:148–174. doi: 10.1016/j.cogpsych.2015.02.005. [DOI] [PubMed] [Google Scholar]
- Ulrich R, Schröter H, Leuthold H, Birngruber T. Corrigendum to Automatic and controlled stimulus processing in conflict tasks: Superimposed diffusion processes and delta functions [Cogn. Psychol. 78 (2015) 148-174] Cogn Psychol. 2016;91:150. doi: 10.1016/j.cogpsych.2016.11.003. [DOI] [PubMed] [Google Scholar]
- Van den Wildenberg WP, Wylie SA, Forstmann BU, Burle B, Hasbroucq T, Ridderinkhof KR. To head or to heed? Beyond the surface of selective action inhibition: a review. Front Hum Neurosci. 2010;4:222. doi: 10.3389/fnhum.2010.00222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wouwe NC, Kanoff KE, Claassen DO, Spears CA, Neimat J, van den Wildenberg WP, Wylie SA. Dissociable Effects of Dopamine on the Initial Capture and the Reactive Inhibition of Impulsive Actions in Parkinson’s Disease. J Cogn Neurosci. 2016;28(5):710–723. doi: 10.1162/jocn_a_00930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wouwe NC, van den Wildenberg WP, Claassen DO, Kanoff K, Bashore TR, Wylie SA. Speed pressure in conflict situations impedes inhibitory action control in Parkinson’s disease. Biol Psychol. 2014;101:44–60. doi: 10.1016/j.biopsycho.2014.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White CN, Ratcliff R, Vasey MW. Anxiety-related threat bias in recognition memory: the moderating effect of list composition and semantic-similarity effects. Cogn Emot. 2015:1–15. doi: 10.1080/02699931.2015.1070120. [DOI] [PubMed] [Google Scholar]
- White CN, Ratcliff R, Vasey MW, McKoon G. Anxiety enhances threat processing without competition among multiple inputs: a diffusion model analysis. Emotion. 2010a;10(5):662–677. doi: 10.1037/a0019474. [DOI] [PubMed] [Google Scholar]
- White CN, Ratcliff R, Vasey MW, McKoon G. Using diffusion models to understand clinical disorders. J Math Psychol. 2010b;54(1):39–52. doi: 10.1016/j.jmp.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie SA, Claassen DO, Huizenga HM, Schewel KD, Ridderinkhof KR, Bashore TR, van den Wildenberg WP. Dopamine agonists and the suppression of impulsive motor actions in Parkinson disease. Journal of Cognitive Neuroscience. 2012;24(8):1709–1724. doi: 10.1162/jocn_a_00241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie SA, Ridderinkhof KR, Bashore TR, van den Wildenberg WP. The effect of Parkinson’s disease on the dynamics of on-line and proactive cognitive control during action selection. Journal of Cognitive Neuroscience. 2010;22(9):2058–2073. doi: 10.1162/jocn.2009.21326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie SA, Stout JC, Bashore TR. Activation of conflicting responses in Parkinson’s disease: evidence for degrading and facilitating effects on response time. Neuropsychologia. 2005;43(7):1033–1043. doi: 10.1016/j.neuropsychologia.2004.10.008. [DOI] [PubMed] [Google Scholar]
- Wylie SA, van den Wildenberg WP, Ridderinkhof KR, Bashore TR, Powell VD, Manning CA, Wooten GF. The effect of Parkinson’s disease on interference control during action selection. Neuropsychologia. 2009a;47(1):145–157. doi: 10.1016/j.neuropsychologia.2008.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie SA, van den Wildenberg WP, Ridderinkhof KR, Bashore TR, Powell VD, Manning CA, Wooten GF. Neuropsychologia. Vol. 47. England: 2009b. The effect of speed-accuracy strategy on response interference control in Parkinson’s disease; pp. 1844–1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ. The role of the basal ganglia in habit formation. Nat Rev Neurosci. 2006;7(6):464–476. doi: 10.1038/nrn1919. [DOI] [PubMed] [Google Scholar]


