Electrostatic Correlations in Polyelectrolyte Solutions

Abstract

The major attribute of polyelectrolyte solutions is that all chains are strongly correlated both electrostatically and topologically. Even in very dilute solutions such that the chains are not interpenetrating, the chains are still strongly correlated. These correlations are manifest in the measured scattering intensity when such solutions are subjected to light, X-ray, and neutron radiation. The behavior of scattering intensity from polyelectrolyte solutions is qualitatively different from that of solutions of uncharged polymers. Using the technique introduced by Sir Sam Edwards, and extending the earlier work by the author on the thermodynamics of polyelectrolyte solutions, extrapolation formulas are derived for the scattering intensity from polyelectrolyte solutions. The emergence of the polyelectrolyte peak and its concentration dependence are derived. The derived theory shows that there are five regimes. Published experimental data from many laboratories are also collected into a master figure and a comparison between the present theory and experiments is presented.

INTRODUCTION

When similarly charged polymer chains are dispersed in polar solvents such as water, they are strongly correlated in space even under extremely dilute conditions. Every polymer chain is subjected to fields from all other chains even under conditions where the average distance between any two chains is several orders of magnitude larger than their radius of gyration. Such long-ranged correlations present difficulties in interpreting experimental data from light-, X-ray-, and neutron-scattering measurements. The challenge becomes much more complicated when the polymer chains interpenetrate into each other by gaining entropy and mitigating the Coulomb repulsion between them. A theoretical formulation of electrostatic correlations of polyelectrolyte chains, where each chain is itself a topologically correlated object, is a difficult task. The theoretical framework necessary to treat such strongly correlated polymer system was created by Sir Sam Edwards [1, 2].

Sir Sam Edwards opened the gateway to modern polymer physics by mapping the various chain conformations of a flexible polymer chain as a collection of different paths of an electron in a self-generated potential field. He showed that a polymer chain can be equivalently treated as a field theory problem and that the probability distribution of a chain with a certain end-to-end distance is simply a Feynman path integral used in field theory. During the pre-Edwards days, polymer chains were treated as random walks made of contiguous segments, with potential interactions among distant segments treated only perturbatively. When many polymer chains are present in a solution, only theories pertinent to small molecular systems, such as the Bragg-Williams theory and Weiss theory of magnetism, were in practice, without the capacity to treat conformational fluctuations of polymer chains [3].

Edwards’ entrance to the field of polymers changed the scene completely. His theory attracted other great physicists such as de Gennes into the polymer field. Since Edwards’ field theoretic methods enabled calculations of correlations of polymer concentration fluctuations, new efforts were also initiated to measure such correlations using neutron scattering and other techniques. Stoked by such new efforts, the field of polymer science emerged as an extremely active research area with tremendous progress in the fundamental understanding of the collective behavior of polymers.

Sam Edwards contributed to solving many of the most difficult problems in polymer physics: size, shape, and fractal nature of an isolated polymer chain, structural correlations in solutions, knots in polymers, entanglements, polymer dynamics, rubber elasticity, phase transition in liquid-crystalline polymers, and polymer glasses. It all started with the introduction of a Hamiltonian (now known as the Edwards Hamiltonian) in his original field theory formulation [1] of a single chain and the subsequent discovery [2] that the inter-segment excluded volume interactions inside a chain are screened by the collective behavior of other interpenetrating chains, beyond a certain distance, now known as the Edwards length. He also invented the replica trick in the context of the physics of rubber where certain degrees of freedom are quenched while the others are allowed to explore the phase space. Edwards’ scientific interests were not confined only to polymers. Other subjects of his interest include electrons in disordered media, turbulence, spin glasses, and granular media.

Indeed, Sam Edwards was a great scientist. As a person, he was even greater. He was kind and generous in sharing his ideas and wisdom with students. His hospitality to visitors and colleagues was legendary.

Returning to the scientific subject of the paper, extensive experiments were conducted on polyelectrolyte solutions using light, X-ray, and neutron scattering [4–17]. For salt-free polyelectrolyte solutions, the most characteristic feature of the dependence of scattering intensity on the scattering wave vector k is the presence of a scattering peak, known as the polyelectrolyte peak, at k_m. When sufficient amount of small molecular electrolyte is added, this peak disappeared. The peak position for salt-free polyelectrolyte solutions depends on the polyelectrolyte concentration C, and this dependence can be cast empirically as

$$k_m~C^{\mathrm{\delta }}.$$ (1)

The value of δ changes from 1/3 to 1/2, and then to 1/4, as the polyelectrolyte concentration is progressively increased, with crossover behaviors between the various regimes.

It is widely recognized that δ = 1/3 corresponds to infinitely dilute solutions where the average spacing between any two adjacent chains scales (geometrically) as C^−1/3. For semidilute solutions, where C is above the overlap concentration C*, but not very high, the scaling arguments [18] show that the correlation length ξ scales as C^−1/2. Hence it has been argued [4] that a Bragg-like peak is expected at k_m ∼ ξ⁻¹ ∼ C^1/2. The calculations of scattering intensity in the semidilute salt-free polyelectrolyte solutions reported so far in the literature show that k_m ∼ C^1/4 instead. These calculations are based on the random phase approximation (RPA) originally introduced by Edwards for uncharged polymer solutions [2]. When RPA is used, Edwards showed that the contribution to the free energy of the solution from polymer chain conformations (for uncharged polymers) is negative [2, 19],

$$\frac{F_{pf}}{k_{B}T}=-\frac{V}{24\mathrm{\pi }}\frac{1}{{\xi }_E^3},$$ (2)

where k_BT is the Boltzmann constant times the absolute temperature, V is the volume of the solution, and ξ_E is the Edwards length proportional to C^−1/2. Therefore, the fluctuation contributions to the osmotic pressure Π_pf = −∂F_pf/∂V and the osmotic compressibility ∂Π_pf/∂C are negative. This implies that the polymer solutions are thermodynamically unstable unless the mean field terms arising from translational entropy and two-body interactions dominate. On the other hand, experiments and scaling arguments show that the osmotic pressure Π in semidilute solutions of uncharged polymers is dominated by Π_pf and that Π ∼ +C^9/4 [20]. The discrepancy between RPA and experiments in both the sign and the value of the exponent should be noted. Edwards recognized that this misfit lies in keeping only the one-loop calculation in RPA and ignoring higher order correlations as depicted in Fig. 1a. When the higher order correlations are treated, although approximately, it was possible [21] to show that

$$\frac{F_{pf}}{k_{B}T}=+\frac{V}{24\mathrm{\pi }}\frac{1}{{\xi }^3},$$ (3)

with ξ progressively changing from C^−3/4 behavior in the semidilute regime (strong concentration fluctuations) to C^−1/2 behavior in the concentrated regime (weak concentration fluctuations).

Fig. 1.

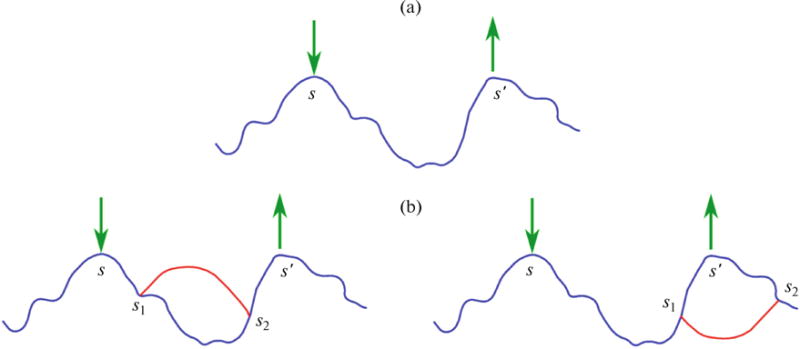
(Color online) Polymer diagrams. (a) One-loop diagram used in RPA. The segments s and s′ interact with each other, mediated by the potential fields (denoted by green arrows) generated by all other chains in the solution. (b) Higher order correlations involve additional segments s1 and s2. The diagram on the left can be effectively accounted for in RPA by appropriate geometrical summation, but the diagram on the right must be accounted for in addition to RPA [21, 27].

The scattering intensity from polyelectrolyte solutions has been calculated by several authors [4, 22–26]. The key result is that k_m ∼ ξ⁻¹ ∼ C^1/4. This result is essentially based on the implementation of RPA and hence it suffers from the same difficulty as in the situation for uncharged polymers (Eq. (2)). Now, not only the osmotic pressure contribution from chain fluctuations is negative, but also the osmotic compressibility is negative and divergent as the polyelectrolyte concentration is reduced (∂Π/∂C ∼ −1/C^1/4). Therefore, it is necessary to go beyond RPA and consider higher order diagrams depicted in Fig. 1b. The present author performed such a higher order calculation and showed that [27]

$$\frac{F_{pf}}{k_{B}T}=\{\frac{\frac{V}{24\sqrt{2\mathrm{\pi }}}\frac{1}{{\xi }_2^3}\text{salt}-\text{free}}{\frac{V}{24\mathrm{\pi }}\frac{1}{{\xi }_1^3}\text{salty}}$$ (4)

where ξ₂ crosses from ξ₂ ~ C^−1/2 in semidilute conditions to ξ₂ ~ C^−1/4 in concentrated conditions for salt-free solutions. In salty solutions, ξ₁ crosses from ξ₁ ∼ C^−3/4 in semidilute conditions to ξ₁ ∼ C^−1/2 in concentrated conditions, as known for solutions of uncharged polymers.

The primary goal of the present paper is to derive full interpolation formulas for the scattering intensity of polyelectrolyte solutions at various concentrations above C* by heavily relying on the author’s earlier work [27] and in the spirit of the Edwards methodology of collective coordinates [2, 19].

In addition, formulas for scattering intensity at concentrations below the overlap concentration are derived by identifying two regimes: ‘gas-like’, when chains are far away from each other such that they are not correlated even electrostatically, and ‘liquid-like’, when chains are electrostatically correlated but not yet overlapping with each other. Finally, a comment is made related to the anomalous enhancement of scattering intensity at very small scattering angles in addition to the occurrence of the polyelectrolyte peak for salt-free polyelectrolyte solutions.

THEORY

Consider a system of n flexible polyelectrolyte chains each containing N segments, n_c counterions, n_γ ions of species γ from dissolved salt, and n_s solvent molecules in volume V. Let α be the fixed degree of ionization per chain so that each of the N α segments of the chain carries a charge of ez_p where e is the electronic charge. The total number of counterions is n_c = αNz_pn/z_c where z_c is the valency of the counterion. Let ez_i be the charge of the i-th charged species. Following Edwards [1], we represent the polymer chain as a continuous curve of length L = Nℓ, where ℓ is the Kuhn step length. The Helmholtz free energy F of the system is given by

$$\begin{gathered} e^{-\frac{F}{k_{B}T}}=\frac{1}{n!n_c!n_s!{\displaystyle \prod { }_{\gamma }{n}_{\gamma }!}}{\displaystyle \int {\displaystyle \prod _{\mathrm{\alpha }=1}^n\mathcal{D}[{\mathbf{R}}_{\mathrm{\alpha }}]}}{\displaystyle \int {\displaystyle \prod _i^{n_c+n_s+{\displaystyle {\sum }_{\gamma }{n}_{\gamma }}}d{\mathbf{r}}_i}} \\ \times \exp {\{-\frac{3}{2{\mathcal{l}}^2}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}\left(\frac{\partial {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})}{\partial s_{\mathrm{\alpha }}}\right)}}}^2 \\ -\frac{1}{2}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \sum _{\mathrm{\beta }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}}{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\beta }}}{U}_{pp}[{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})-{\mathbf{R}}_{\mathrm{\beta }}(s_{\mathrm{\beta }})]}} \\ -{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}}{\displaystyle \sum _{i=1}^{n_s}{U}_{ps}[{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})-{\mathbf{r}}_i]}-\frac{1}{2}}{\displaystyle \sum _{i=1}^{n_s}{\displaystyle \sum _{j=1}^{n_s}{U}_{ss}({\mathbf{r}}_i-{\mathbf{r}}_j)}} \\ -{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}}{\displaystyle \sum _{i=1}^{n_c+{\displaystyle {\sum }_{\gamma }{n}_{\gamma }}}{U}_{pi}[{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})-{\mathbf{r}}_i]}} \\ -\frac{1}{2}{\displaystyle \sum _{i=1}^{n_c+{\displaystyle {\sum }_{\gamma }{n}_{\gamma }}}{\displaystyle \sum _{j=1}^{n_c+{\displaystyle {\sum }_{\gamma }{n}_{\gamma }}}{U}_{ij}[({\mathbf{r}}_i-{\mathbf{r}}_j)]}}\}. \end{gathered}$$ (5)

Here Rα(s_α) is the position vector of the arc length variable s_α(0 ≤ s_α ≤ N) of the α-th chain. U_pp(r) is the interaction energy between two segments of the chain separated by a distance r,

$$U_{pp}(\mathbf{r})=w\mathrm{\delta }(\mathbf{r})+\frac{{\mathrm{\alpha }}^2{z}_p^2{\mathcal{l}}_B}{r},$$ (6)

where w is the Edwards excluded volume pseudopotential, which is related to the Flory-Huggins parameter χ according to $w=\left(\frac{1}{2}-\chi \right){\mathcal{l}}^3$. δ(r) is the Dirac delta function and r = |r|. The second term on the right hand side of Eq. (6) represents the Coulomb interaction energy between the segments, where ℓ_B is the Bjerrum length

$${\mathcal{l}}_B=\frac{e^2}{4\mathrm{\pi }{\epsilon }_0\epsilon k_{B}T},$$ (7)

with ε₀ and ε being the permittivity of vacuum and the uniform dielectric constant of the solution, respectively. In writing this second term, we have assumed that the total charge Nαz_pe of the chain is uniformly distributed along the chain skeleton. The short-ranged interactions between the polymer segments and solvent molecules and between solvent molecules are given by

$$U_{ps}(\mathbf{r})=w_{ps}\mathrm{\delta }(\mathbf{r})\text{and}{U}_{ss}(\mathbf{r})=w_{ss}\mathrm{\delta }(\mathbf{r}),$$ (8)

where w_ps and w_ss are the corresponding pseudopotential excluded volume parameters. The electrostatic interactions between charged segments and various ions are given by

$$U_{pi}(\mathbf{r})=\frac{\mathrm{\alpha }{z}_p{z}_i{\mathcal{l}}_B}{r}\text{and}{U}_{ij}(\mathbf{r})=\frac{z_i{z}_j{\mathcal{l}}_B}{r}.$$ (9)

Integration over the positions of counterions, salt ions, and solvent molecules gives within the Debye-Hückel theory of electrolyte solutions [27]

$$F=F_b+F_p,$$ (10)

where F_p denotes the free energy contribution from all chains and F_b denotes that of the neutralizing background. As derived in [27],

$$\begin{gathered} \frac{F_b}{k_{B}TV}=C_s\ln C_s-C_s+C_c\ln C_c-C_c \\ +{\displaystyle \sum _{\gamma }[C_{\gamma }\ln C_{\gamma }-C_{\gamma }]+\frac{1}{2}{w}_{ss}{C}_s^2+}{w}_{ps}C{C}_s-\frac{{\mathrm{\kappa }}^3}{12\mathrm{\pi }}, \end{gathered}$$ (11)

where C_i is the number concentration of the i-th species, C_i = n_i/V. The inverse Debye length κ is defined by

$${\mathrm{\kappa }}^2=\frac{4\mathrm{\pi }{\mathcal{l}}_B}{V}\left(z_c^2{n}_c+{\displaystyle \sum _{\gamma }{z}_{\gamma }^2{n}_{\gamma }}\right).$$ (12)

It should be noted that the expression for F_b given by Eq. (11) is strictly valid only in the region of validity of the Debye-Hückel theory, namely the local electric potential being less than k_BT. Extensions can be made to go beyond the linearized Poisson-Boltzmann formalism [28, 29].

The polymer contribution to the free energy, F_p, is given by

$$\begin{gathered} e^{\frac{F_p}{k_{B}T}}=\frac{1}{n!}{\displaystyle \int {\displaystyle \prod _{\mathrm{\alpha }=1}^n\mathcal{D}[{\mathbf{R}}_{\mathrm{\alpha }}]}} \\ \times \exp \{-\frac{3}{2{\mathcal{l}}^2}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}\left(\frac{\partial {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})}{\partial s_{\mathrm{\alpha }}}\right)}}^2} \\ -\frac{1}{2}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \sum _{\mathrm{\beta }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}}{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\beta }}v[{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})-{\mathbf{R}}_{\mathrm{\beta }}(s_{\mathrm{\beta }})]}}}\} \end{gathered}$$ (13)

where

$$v(\mathbf{r})=w\mathrm{\delta }(\mathbf{r})+w_c\frac{e^{-\mathrm{\kappa }r}}{4\mathrm{\pi }r},$$ (14)

with w_c defined as

$$w_c\equiv 4\mathrm{\pi }{\mathrm{\alpha }}^2{z}_p^2{\mathcal{l}}_B.$$ (15)

Defining the local monomer concentration c(r) as

$$c(\mathbf{r})={\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}\mathrm{\delta }(\mathbf{r}-{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }}))}}$$ (16)

and its Fourier transform as

$$c_{\mathrm{k}}=\frac{1}{V}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}{e}^{i\mathbf{k}\cdot {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})},}}$$ (17)

Eq. (13) becomes

$$\begin{gathered} e^{-\frac{F_p}{k_{B}T}}=\frac{1}{n!}{\displaystyle \int {\displaystyle \prod _{k>0}\mathrm{\delta }{c}_k}}{\displaystyle \int {\displaystyle \prod _{\mathrm{\alpha }=1}^n\mathcal{D}[{\mathbf{R}}_{\mathrm{\alpha }}]}} \\ \times \exp \{-\frac{3}{2{\mathcal{l}}^2}{{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{n}{\int }}d{s}_{\mathrm{\alpha }}}\left(\frac{\partial {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})}{\partial s_{\mathrm{\alpha }}}\right)}}^2 \\ -\frac{V}{2}{v}_0{C}^2-V{\displaystyle \sum _{k>0}{v}_k{c}_k{c}_{-k}}\} \\ \times {\displaystyle \prod _{k>0}\mathrm{\delta }\left[c_k-\frac{1}{V}{\displaystyle \sum _{\mathrm{\alpha }=1}^n{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}{e}^{i\mathbf{k}\cdot {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})}}}\right]}. \end{gathered}$$ (18)

Here c_k with k > 0 are chosen as independent components as c_k and c_−k are related by $c_{-k}=c_k^{\ast }$. v_k is the Fourier transform of v(r) of Eq. (14),

$$v_k=w+\frac{w_c}{k^2+{\mathrm{\kappa }}^2},$$ (19)

with w_c given by Eq. (15) and the zero-wave vector limit of v_k given by

$$v_0=w+\frac{w_c}{{\mathrm{\kappa }}^2}.$$ (20)

The coupling among all chains can be decoupled into n effective chains by parameterizing the definition of c_k in Eq. (18) in terms of a functional variable ϕ_k with the result [2, 19]

$$e^{-\frac{F_p}{k_{B}T}}=\frac{1}{n!}{\displaystyle \int {\displaystyle \prod _{k>0}\mathrm{\delta }{c}_k{e}^{-\frac{V}{2}{v}_0{C}^2-V{\displaystyle {\sum }_{k>0}{v}_k{c}_k{c}_{-k}}}}}{e}^{-\frac{U_0(\{c_k\})}{k_{B}T}},$$ (21)

where

$$e^{-\frac{U_0(\{c_k\})}{k_{B}T}}={\displaystyle \int {\displaystyle \prod _{k>0}\frac{d{\mathrm{\varphi }}_k}{{\mathrm{\pi }}^2}}}{(G(\mathrm{\varphi }))}^n{e}^{i{\displaystyle {\sum }_{k\ne 0}{c}_k{\mathrm{\varphi }}_{-k}}},$$ (22)

with

$$\begin{array}{r}G(\mathrm{\varphi })\equiv {\displaystyle \int \mathcal{D}[{\mathbf{R}}_{\mathrm{\alpha }}]\exp \{-\frac{3}{2{\mathcal{l}}^2}{\displaystyle \underset{0}{\overset{N}{\int }}d{s}_{\mathrm{\alpha }}}}{\left(\frac{\partial {\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})}{\partial s_{\mathrm{\alpha }}}\right)}^2\\ +{\displaystyle \underset{0}{\overset{N}{\int }}ds\mathrm{\varphi }[{\mathbf{R}}_{\mathrm{\alpha }}(s_{\mathrm{\alpha }})]}\}.\end{array}$$ (23)

The label α for the chain is unnecessary in the above equation as all chains are now decoupled and every effective chain is the same. In the above equation, ϕ(r) is defined as

$$\mathrm{\varphi }(\mathbf{r})\equiv -\frac{i}{V}{\displaystyle \sum _{k\ne 0}{\mathrm{\varphi }}_{-k}{e}^{i\mathbf{k}\cdot \mathbf{r}}}.$$ (24)

Using the identity

$${(G(\mathrm{\varphi }))}^n=n!{\displaystyle \underset{C}{\int }\frac{d\mathrm{\mu }}{2\mathrm{\pi }i}\frac{1}{{\mathrm{\mu }}^{n+1}}{e}^{\mathrm{\mu }G(\mathrm{\varphi })}},$$ (25)

Eq. (22) becomes

$$e^{-\frac{U_0(\{c_k\})}{k_{B}T}}=n!{\displaystyle \underset{C}{\int }\frac{d\mathrm{\mu }}{2\mathrm{\pi }i}\frac{1}{{\mathrm{\mu }}^{n+1}}{\displaystyle \int {\displaystyle \prod _{k>0}\frac{d{\mathrm{\varphi }}_k}{{\mathrm{\pi }}^2}{e}^{\mathrm{\mu }G(\mathrm{\varphi })+i{\displaystyle {\sum }_{k\ne 0}{c}_k{\mathrm{\varphi }}_{-k}}}}}}.$$ (26)

Adding and subtracting $\overline{G}$ in the argument of the exponential in this equation, where $\overline{G}$ is the average of G(ϕ) over the ϕ-field, we get

$$e^{-\frac{U_0(\{c_k\})}{k_{B}T}}={\overline{G}}^n{\displaystyle \int {\displaystyle \prod _{k>0}\frac{d{\mathrm{\varphi }}_k}{{\mathrm{\pi }}^2}{e}^{\mathrm{\mu }G(\mathrm{\varphi })-\mathrm{\mu }\overline{G}+i}}}{\displaystyle {\sum }_{k\ne 0}{c}_k{\mathrm{\varphi }}_{-k}}.$$ (27)

Writing μG(ϕ) as quadratic in ϕ_k,

$$\mathrm{\mu }G(\mathrm{\varphi })=\mathrm{\mu }G(0)-\frac{1}{2V}{\displaystyle \sum _{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}}{\mathrm{\varphi }}_k{\mathrm{\varphi }}_{-k},$$ (28)

we get

$$\mathrm{\mu }\overline{G}=\mathrm{\mu }G(0)-\frac{1}{2}{\displaystyle \sum _{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}}{\mathrm{\Delta }}_k,$$ (29)

where the effective interaction Δ_k is defined by

$${\mathrm{\Delta }}_k=\frac{1}{V}\langle {\mathrm{\varphi }}_k{\mathrm{\varphi }}_{-k}\rangle ,$$ (30)

with the angular brackets denoting the average over the ϕ-field. Therefore, Eqs. (27)–(29) yield

$$\begin{gathered} e^{-\frac{U_0(\{c_k\})}{k_{B}T}}={\overline{G}}^n{e}^{\frac{1}{2}{\displaystyle {\sum }_{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}{\mathrm{\Delta }}_k}} \\ \times {\displaystyle \int {\displaystyle \prod _{k>0}\frac{d{\mathrm{\varphi }}_k}{{\mathrm{\pi }}^2}{e}^{-\frac{1}{2V}{\displaystyle {\sum }_{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}{\mathrm{\varphi }}_k{\mathrm{\varphi }}_{-k}+i}{\displaystyle {\sum }_{k\ne 0}{c}_k{\mathrm{\varphi }}_{-k}}}}}. \end{gathered}$$ (31)

Substituting this result into Eq. (21) gives

$$\begin{gathered} e^{-\frac{F_p}{k_{B}T}}=\frac{{\overline{G}}^n}{n!}{e}^{-\frac{V}{2}{v}_0{C}^2+\frac{1}{2}{\displaystyle {\sum }_{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}{\mathrm{\Delta }}_k}}{\displaystyle \int {\displaystyle \prod _{k>0}\mathrm{\delta }{c}_k}} \\ \times {\displaystyle \int {\displaystyle \prod _{k>0}\frac{d{\mathrm{\varphi }}_k}{{\mathrm{\pi }}^2}{e}^{-V{\displaystyle {\sum }_{k>0}{v}_k{c}_k{c}_{-k}-\frac{1}{2V}}{\displaystyle {\sum }_{k\ne 0}\frac{{\mathcal{E}}_k}{v_k}{\mathrm{\varphi }}_k{\mathrm{\varphi }}_{-k}}+i{\displaystyle {\sum }_{k\ne 0}{c}_k{\mathrm{\varphi }}_{-k}}}}}. \end{gathered}$$ (32)

Performing the δc_k integrals in Eq. (32) gives the effective interaction

$${\mathrm{\Delta }}_k=\frac{1}{V}\langle {\mathrm{\varphi }}_k{\mathrm{\varphi }}_{-k}\rangle =\frac{v_k}{(1+{\mathcal{E}}_k)}.$$ (33)

Therefore, ${\mathcal{E}}_k$ defined through Eq. (28) is related to Δ_k by the above equation. It must be remarked that the inverse Fourier transform of Δk gives the effective pairwise interaction Δ(r) between any two segments of a labeled chain in the solution. The properties of Δ(r) are already discussed in Ref. [27].

Performing the δφ_k integrals in Eq. (32) gives

$$\langle c_k{c}_{-k}\rangle =\frac{1}{V{v}_k}\frac{{\mathcal{E}}_k}{(1+{\mathcal{E}}_k)},$$ (34)

with the angular brackets denoting averaging over concentration fluctuations. The scattering intensity I(k) at the scattering wave vector k is

$$I(k)=V\langle c_k{c}_{-k}\rangle =Cg(k),$$ (35)

where g(k) is the scattering function per segment,

$$g(k)=\frac{1}{C{v}_k}\frac{{\mathcal{E}}_k}{(1+{\mathcal{E}}_k)}.$$ (36)

By redefining ${\mathcal{E}}_k$ as

$${\mathcal{E}}_k\equiv C{v}_k{\zeta }_k,$$ (37)

Eqs. (33) and (36) yield

$${\mathrm{\Delta }}_k=\frac{v_k}{(1+C{v}_k{\zeta }_k)},$$ (38)

and

$$g(k)=\frac{{\zeta }_k}{1+C{v}_k{\zeta }_k}.$$ (39)

ζ_k follows from the calculation of Δ_k as presented in the next section.

The general relation between the scattering function per segment g(k) and the effective interaction Δk follows from Eqs. (38) and (39) as

$${\mathrm{\Delta }}_k=v_k-Cg(k)v_k.$$ (40)

Performing integrations over both δc_k and δϕ_k in Eq.(32) gives the free energy contribution F_p from all polymer fluctuations as

$$\begin{gathered} \frac{F_p}{k_{B}T}=-n\ln \overline{\mathrm{G}}+\ln n!+\frac{V}{2}{v}_0{C}^2 \\ -\frac{V}{2}{\displaystyle \sum _{k\ne 0}\left[\frac{{\mathcal{E}}_k}{v_k}{\mathrm{\Delta }}_k+\ln \left(\frac{{\mathrm{\Delta }}_k}{v_k}\right)\right]}. \end{gathered}$$ (41)

RESULTS

The effective interaction energy between segments is given by Eqs. (33) and (38) as

$${\mathrm{\Delta }}_k=\frac{v_k}{(1+{\mathcal{E}}_k)}=\frac{v_k}{(1+C{v}_k{\zeta }_k)}.$$ (42)

As derived in Ref. [27] by approximately accounting for the higher order terms depicted in Fig. 1b, ζ_k is given by Eq. (3.19) of [27]. In the present paper, the combinatorial numerical factor β in Eq. (3.19) of [27] is taken as unity. The result is

$${\zeta }_k\equiv \frac{1}{k^2{\lambda }^2},$$ (43)

with

$$\frac{1}{{\lambda }^2}=\frac{6}{\mathcal{l}{\mathcal{l}}_1}\frac{1}{\left(1+\frac{9}{\mathrm{\pi }{\mathcal{l}}^2{\mathcal{l}}_1^2}{\mathcal{A}}_{\lambda }\right)},$$ (44)

where ${\mathcal{A}}_{\lambda }$ and ℓ₁ are given by Eqs. (3.30) and (3.40) of Ref. [27], respectively. The limits of ${\mathcal{A}}_{\lambda }$for salt-free (κ → 0) and salty (κ ≫ 0) conditions are

$${\mathcal{A}}_{\lambda }=\{\begin{array}{lll}\frac{w_c}{2}{\left(\frac{C{w}_c}{{\lambda }^2}\right)}^{-3/4}\hfill & \mathrm{\kappa }\to 0,\hfill & w=0\hfill \\ v_0{\left(\frac{C{v}_0}{{\lambda }^2}\right)}^{-1/2}\hfill & \mathrm{\kappa }\gg 0\hfill & \hfill \end{array}$$ (45)

For the salt-free condition, the electrostatic interaction between segments dominate over the short-ranged excluded volume interaction and so w is taken as zero in this limit. Defining correlation lengths ξ₁ and ξ₂ for salty and salt-free conditions according to

$${\xi }_1\equiv {\left(\frac{C{v}_0}{{\lambda }^2}\right)}^{-1/2},\mathrm{\kappa }\gg 0$$ (46)

and

$${\xi }_2\equiv {\left(\frac{C{w}_c}{{\lambda }^2}\right)}^{-1/4},\mathrm{\kappa }\to 0,w=0$$ (47)

we get from Eqs. (44) and (45)

$$\frac{1}{{\xi }_1^2}=\frac{6C{v}_0}{\mathcal{l}{\mathcal{l}}_1}\frac{1}{\left(1+\frac{9v_0}{\mathrm{\pi }{\mathcal{l}}^2{\mathcal{l}}_1^2}{\xi }_1\right)},\mathrm{\kappa }\gg 0$$ (48)

and

$$\frac{1}{{\xi }_2^2}=\frac{6C{w}_c}{\mathcal{l}{\mathcal{l}}_1}\frac{1}{\left(1+\frac{9w}{\sqrt{2}\mathrm{\pi }{\mathcal{l}}^2{\mathcal{l}}_1^2}{\xi }_2^3\right)},\mathrm{\kappa }\to 0,w=0$$ (49)

The effective Kuhn length ℓ₁ representing the renormalization by the effective interaction Δ between the segments is given by ([27])

$${\mathcal{l}}_1^3\left(\frac{1}{\mathcal{l}}-\frac{1}{{\mathcal{l}}_1}\right)=\frac{12}{\mathrm{\pi }{\mathcal{l}}^2}{v}_0{\xi }_1\mathrm{\kappa }\gg 0$$ (50)

and

$${\mathcal{l}}_1^3\left(\frac{1}{\mathcal{l}}-\frac{1}{{\mathcal{l}}_1}\right)=\frac{6\sqrt{2}}{\mathrm{\pi }{\mathcal{l}}^2}{w}_c{\xi }_2^3\mathrm{\kappa }\to 0,w=0$$ (51)

Based on the above equations, the scattering function g(k) and the effective interaction Δ can be calculated for any polyelectrolyte concentration above the overlap concentration. We provide here only the asymptotic limits where analytical results are readily available.

Salty Solutions : (κ ≫ 0)

Combining Eqs. (43) and (46),

$${\zeta }_k=\frac{1}{k^{2}C{v}_0{\xi }_1^2},$$ (52)

so that from Eqs. (38) and (39),

$${\mathrm{\Delta }}_k=v_0\frac{k^2}{(k^2+{\xi }_1^{-2})},$$ (53)

and

$$g(k)=\frac{1}{C{v}_0}\frac{1}{(1+k^2{\xi }_1^2)}.$$ (54)

For semidilute conditions, $v_0{\xi }_1/{\mathcal{l}}^2{\mathcal{l}}_1^2\gg 1$, Eqs. (48) and (50) give

$${\xi }_1=2^{-5/4}{\left(\frac{3}{\mathrm{\pi }}\right)}^{1/2}{v}_0^{-1/4}{C}^{-3/4}{\mathcal{l}}^{-1/2},$$ (55)

$${\mathcal{l}}_1=2^{1/4}{\left(\frac{3}{\mathrm{\pi }}\right)}^{1/2}{v}_0^{1/4}{C}^{-1/4}{\mathcal{l}}^{-1/6}.$$ (56)

For concentrated conditions, $v_0{\xi }_1/{\mathcal{l}}^2{\mathcal{l}}_1^2\ll 1$, ℓ₁ = ℓ, and

$${\xi }_1=\frac{1}{\sqrt{6}}{v}_0^{-1/2}{C}^{-1/2}\mathcal{l}.$$ (57)

For salty conditions, the scattering intensity I(k) = Cg(k) is written as

$$I(k)=\frac{1}{v_0}\frac{1}{(1+k^2{\xi }_1^2)},$$ (58)

where ξ₁ is proportional to $v_0^{-1/4}{C}^{-3/4}$ and $v_0^{-1/2}{C}^{-1/2}$, respectively, in semidilute and concentrated solutions. The free energy is given in [27] with the contribution from polymer fluctuations being positive at all concentrations. The scattering intensity given by the above formula depends on the scattering wave vector k monotonically as shown in Fig. 2a (for v₀ = 1nm³).

Fig. 2.

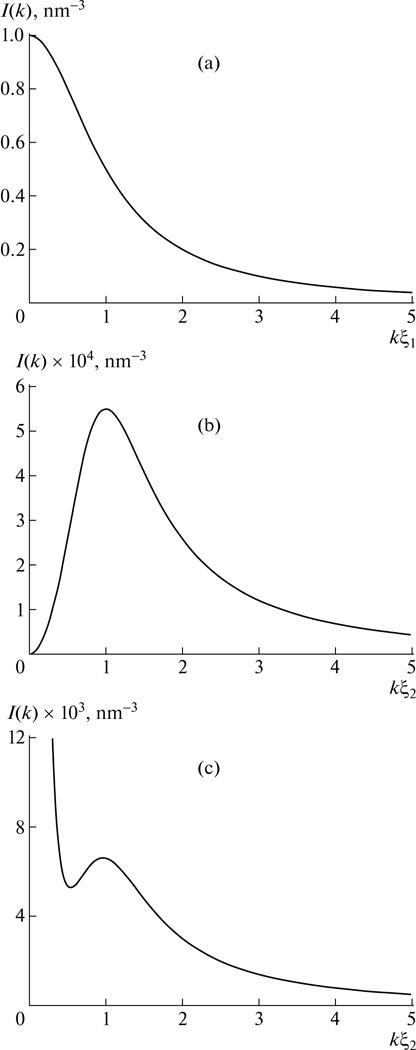
Dependence of scattering intensity I(k) on the angular averaged scattering wave vector k. (a) Salty conditions, using Eq. (58) for v₀ = 1 nm³. (b) Salt-free conditions, using Eq. (62) for w_c = 8.8 nm and ξ₂ = 10 nm. (c) Influence from the presence of aggregates, using Eq. (69) for w_c = 8.8 nm; ξ₂ = 3 nm, and R_g,agg = 300 nm.

Salt-Free Solutions : (κ → 0)

Combining Eqs. (43) and (47),

$${\zeta }_k=\frac{1}{k^{2}C{w}_c{\xi }_2^4},$$ (59)

and from Eqs. (38) and (39),

$${\mathrm{\Delta }}_k=w_c\frac{k^2}{(k^4+{\xi }_2^{-4})},$$ (60)

and

$$g(k)=\frac{1}{C{w}_c}\frac{k^2}{(1+k^4{\xi }_2^4)}.$$ (61)

Therefore, the scattering intensity I(k) = Cg(k) follows as

$$I(k)=\frac{1}{w_c}\frac{k^2}{(1+k^4{\xi }_2^4)}.$$ (62)

For semidilute conditions, $w_c{\xi }_2^3/{\mathcal{l}}^2{\mathcal{l}}_1^2\gg 1$, Eqs. (49) and (51) give

$${\xi }_2={\left(\frac{3}{2\sqrt{2}\mathrm{\pi }}\right)}^{1/2}{\left(\frac{6\sqrt{2}}{\mathrm{\pi }}\right)}^{-1/6}{w}_c^{-1/6}{\mathcal{l}}^{-1/3}{C}^{-1/2},$$ (63)

$${\mathcal{l}}_1={\left(\frac{3}{2\sqrt{2}\mathrm{\pi }}\right)}^{1/2}{\left(\frac{6\sqrt{2}}{\mathrm{\pi }}\right)}^{1/6}{w}_c^{1/6}{\mathcal{l}}^{-2/3}{C}^{-1/2}.$$ (64)

On the other hand, for concentrated solutions, $w_c{\xi }_2^3/{\mathcal{l}}^2{\mathcal{l}}_1^2\ll 1$, ℓ₁ = ℓ, and

$${\xi }_2=6^{-1/4}{w}_c{ }^{-1/4}{\mathcal{l}}^{1/2}{C}^{-1/4}.$$ (65)

The scattering intensity given by Eq. (62) exhibits the polyelectrolyte peak as illustrated in Fig. 2b, by choosing the typical values of w_c and ξ₂ as 8.8 and 10 nm, respectively. In general, the peak position k_m is given by

$$k_m=\frac{1}{{\xi }_2}.$$ (66)

For semidilute solutions, k_m ∼ C^1/2 and only for very high concentrations, k_m ∼ C^1/4,

$$k_m~\{\begin{array}{cc}{C}^{1/2}& C>C^{\ast }\\ C^{1/4}& C\gg C^{\ast }\end{array}$$ (67)

At all concentrations, the contribution from chain fluctuations to the total free energy of the system remains positive ([27]).

For polyelectrolyte concentrations sufficiently larger than the concentration of added salt, dynamic light scattering shows [4] two modes of relaxation, known as the fast and slow modes. Concomitant to the onset of the slow mode, the scattering intensity at very small angles is anomalously high [4]. It has been widely recognized that the slow mode arises from aggregates of many chains which are present in the background of homogeneously distributed polyelectrolyte chains. Although these aggregates constitute only a minor amount in the solution, they can scatter significantly. We approximate their scattering per segment by

$$I_{\mathit{agg}}(k)=\frac{1}{\left(1+\frac{1}{3}{k}^2{R}_{g,\mathit{agg}}^2\right)},$$ (68)

where R_g,_agg is the radius of gyration of the aggregate. Adding this to the scattering intensity for the salt-free solution (Eq. (62)),

$$I(k)=\frac{1}{w_c}\frac{k^2}{(1+k^4{\xi }_2^4)}+\frac{1}{(1+\frac{1}{3}{k}^2{R}_{g,\mathit{agg}}^4)}.$$ (69)

A typical plot of I(k) versus k is given in Fig. 2c for the choice of w_c = 8.8 nm, ξ₂ = 3 nm, and R_g,agh = 300 nm.

DISCUSSION

The dependence of the polyelectrolyte peak position on the concentration and the crossover from k_m ∼ C^1/2 in semidilute solutions to k_m ∼ C^1/4 for very concentrated solutions are derived above for C > C*. When the chains are not interpenetrating (for C < C*), the long-ranged electrostatic correlations are still significant making interpretation of scattering data extremely difficult [30, 31].

For C < C*, the polyelectrolyte solutions can be further classified into electrostatically uncorrelated ‘gas-like’ dilute regime and electrostatically correlated ‘liquid-like’ dilute regime [4, 20].

Electrostatically Uncorrelated Dilute ‘Gas-Like’ Regime

When the polyelectrolyte concentration is extremely low, the average separation distance Λ between any two chains is so large that the strength of the electrostatic interaction between them is vanishingly small. Under these conditions,

$$C=\frac{nN}{V}~\frac{nN}{n{\mathrm{\Lambda }}^3}$$ (70)

so that

$$k_m~\frac{1}{\mathrm{\Lambda }}~C^{1/3}.$$ (71)

Defining the polyelectrolyte concentration C_κ as the concentration at which the average distance between any two chains is the Debye length,

$$C_{\mathrm{\kappa }}~\frac{nN}{n{\mathrm{\kappa }}^{-3}}~N{\mathrm{\kappa }}^3,$$ (72)

the ‘gas-like’ regime corresponds to 0 < C < C_κ.

Electrostatically Correlated Dilute ‘Liquid-Like’ Regime

In this regime, C_κ < C < C*, the average distance Λ between two chains is shorter than the Debye length and yet the chains have not overlapped, such that 2R_g < Λ < κ⁻¹. Under these conditions, the structure factor S(k), which is proportional to the scattering intensity I(k), is approximately the product of the form factor P(k) and the inter-molecular structure factor given by [32]

$$S(k)=P(k)\left[1-\frac{C}{N}Q(k)\right],$$ (73)

where Q(k) depends on the pair-potential U(r) between two chains, with center of mass separation distance r, according to

$$Q(k)={\displaystyle \int d\mathbf{r}}\left[1-e^{\frac{U(\mathbf{r})}{k_{B}T}}\right]e^{i\mathbf{k}\cdot \mathbf{r}}.$$ (74)

For a pair of polyelectrolyte chains in dilute solutions, U(r) has recently been derived [30] as

$$\begin{gathered} \frac{U(r)}{k_{B}T}=\frac{1}{2}\frac{N^2{w}_c}{4\mathrm{\pi }r}{e}^{{\mathrm{\kappa }}^2{R}_g^2/3}[e^{\mathrm{\kappa }r}\text{erfc}\left(\frac{\mathrm{\kappa }{R}_g}{\sqrt{3}}-\frac{\sqrt{3}}{2}\frac{r}{R_g}\right) \\ -e^{\mathrm{\kappa }r}\text{erfc}\left(\frac{\mathrm{\kappa }{R}_g}{\sqrt{3}}+\frac{\sqrt{3}}{2}\frac{r}{R_g}\right)]. \end{gathered}$$ (75)

Here, erfc is the complementary error function [33]. For κR_g < 3r/2R_g, this result reduces to the physically apparent screened Coulomb potential between two chains,

$$\frac{U(r)}{k_{B}T}=N^2{w}_c\frac{e^{-\mathrm{\kappa }r}}{4\mathrm{\pi }r},r>2R_g$$ (76)

Substituting this result in Eq. (74) and performing the high-temperature expansion as usual [32], we get in the limit of 2kR_g ≪ 1,

$$Q(k)=\frac{N^2{w}_c}{k^2}.$$ (77)

The form factor for a polyelectrolyte chain in dilute solutions can be approximated as

$$P(k)=\frac{1}{{\left(1+\frac{2\nu }{3}{k}^2{R}_g^2\right)}^{1/2\nu }}.$$ (78)

where ν is the effective size exponent defined by R_g ∼ N^ν. The value of ν is between the good solution limit of 0.6 and the rod-like limit of 1.0. The above form of P(k) is chosen so that it gives the correct result for extracting R_g from scattering experiments in the limit of kR_g ≪ 1 and the correct fractal dimension for kR_g ≫ 1,

$$P(k)=\{\genfrac{}{}{0ex}{}{1-\frac{1}{3}{k}^2{R}_g^2+\cdots k{R}_g\ll 1}{~\frac{1}{N{k}^{1/\nu }}k{R}_g\gg 1}$$ (79)

Combining Eqs. (73), (77) and (78),

$$S(k)=\frac{1}{{\left(1+\frac{2\nu }{3}{k}^2{R}_g^2\right)}^{1/2\nu }}\left(1-\frac{CN{w}_c}{k^2}\right).$$ (80)

This exhibits a maximum at

$$\begin{array}{c}{k}_m^2=\frac{1}{2}[CN{w}_c(1+2\nu )\\ +\sqrt{C^2{N}^2{w}_c^2{(1+2\nu )}^2+12CN{w}_c/R_g^2]}.\end{array}$$ (81)

For sufficiently large values of CNw_cR_g > 1, this result gives

$$k_m\simeq {\left(\frac{1}{2}+\nu \right)}^{1/2}\sqrt{CN{w}_c},$$ (82)

so that a general result for the polyelectrolyte peak in dilute solutions with electrostatic correlations is

$$k_m~C^{1/2}.$$ (83)

Therefore, the exponent for the concentration dependence of k_m is the same for both the dilute correlated regime and the semidilute regime. However, the numerical prefactor can be slightly different as pointed out by Ref. [4].

Putting all of the above results together, five regimes may be identified for salt-free polyelectrolyte solutions, as sketched in Fig. 3. (i) Infinitely dilute, electrostatically uncorrelated ‘gas-like’ regime, 0 < C < C_κ with k_m ∼ C^1/3; (ii) dilute, electrostatically correlated ‘liquid-like’ regime, C_κ < C < C* with k_m ∼ C^1/2; (iii) semidilute, C* < C < C** with k_m ∼ C^1/2; (iv) concentrated, C** < C < C*** with k_m ∼ C^1/4; and (v) hydrated melt, C*** < C.

Fig. 3.

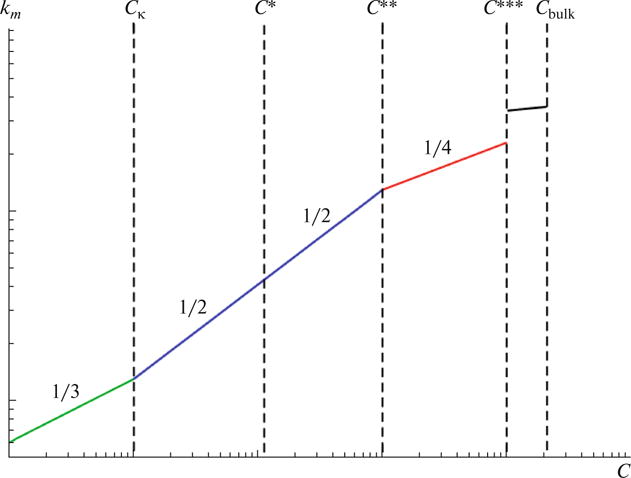
Five regimes for the concentration dependence of the polyelectrolyte peak in salt-free polyelectrolyte solutions: (i) Infinitely dilute, electrostatically uncorrelated ‘gas-like’ regime, 0 < C < Cκ; (ii) dilute, electrostatically correlated ‘liquid-like’ regime, C_κ < C < C*; (iii) semidilute, C* < C < C**; (iv) concentrated, C** < C < C***; and (v) hydrated melt, C*** < C. The values of the exponent δ in k_m ~ Ĉ^δ for the various regimes are shown in the figure. The prefactors in the two regimes of 1/2 slope are different.

The extensive literature on the investigations of the concentration dependence of k_m in salt-free aqueous solutions of sodium poly(styrene sulfonate) of different molecular weights, using light, X-ray, and neutron scattering is summarized in Fig. 4. The presence of different concentration regimes and crossover behaviors between these regimes are evident from Fig. 4. For each molar mass, the overlap concentration is estimated by using the formula

$$C^{\ast }=\frac{M}{\frac{4}{3}\mathrm{\pi }{R}_g^3\mathcal{N}},$$ (84)

where M is the molecular weight and $\mathcal{N}$ is the Avogadro number. For a rigid rod of contour length L, R_g is $L/\sqrt{12}$. Since we know that a flexible polyelectrolyte chain is never fully extended in the experimental situations of interest [34], we may take the span along the most extended direction as L/2, a value typically observed in computer simulations of short polyelectrolyte chains [35]. Therefore,

$$C^{\ast }=\frac{144\sqrt{3}}{\mathrm{\pi }}\frac{M}{\mathcal{N}{L}^3}.$$ (85)

This is the lowest bound for C*, because the radius of gyration is smaller than $L/2\sqrt{12}$ for all molecular weights considered in Fig. 4.

Fig. 4.

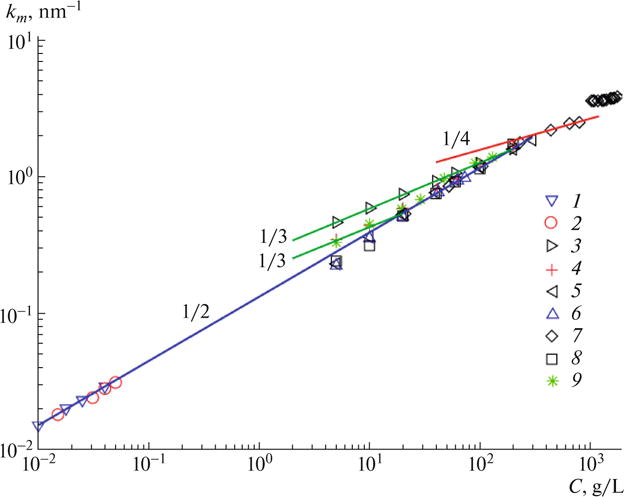
Dependence of k_m on polyelectrolyte concentration C in salt-free aqueous solutions of sodium poly(styrene sulfonate) at various molecular weights and using different radiation. (1) light, M = 780 kDa, Drifford (780k) [7]; (2) light, M = 1132 kDa, Johner (1132k) [11]; (3) X-ray, M = 8 kDa, Kaji (8k) [9]; (4) X-ray, M = 18 kDa, Kaji (18k) [9]; (5) X-ray, M = 100 kDa, Kaji (100k) [9]; (6) X-ray, M = 220 kDa, Kaji (220k) [9]; (7) X-ray, M = 252 kDa, Nishida (252k) [14]; (8) X-ray, M = 1200 kDa, Kaji (1200k) [9]; (9) neutrons, M = 72 kD, Nierlich (72k) [5]. The slopes of 1/3, 1/2, 1/2, and 1/4, expected respectively for infinitely dilute ‘gas-like’, dilute ‘liquid-like’, semidilute, and concentrated, are included as guides.

The overlap concentration C*, estimated by using Eq.(85), for the molar masses of 8, 18, 72, 100, 220, 252, 780, 1132, and 1200 kDa are 1218, 240, 15, 7.8, 1.61, 1.22, 0.13, 0.06, and 0.054 g/L, respectively. The light scattering data of Drifford and Dalbiez [7] on M = 780kDa and Johner et al. [11] on M = 1132 kDa are for C < C*, showing $k_m~\sqrt{C}$. The small angle X-ray (SAXS) data of Kaji et al. [9] on M = 100, 220, and 1200 kDa are for C > C* showing again $k_m~\sqrt{C}$. Similarly, the neutron scattering data of Nierlich et al. [5] exhibit $k_m~\sqrt{C}$ behavior for C > C*. For M = 18 kDa, C* = 240 g/L and the SAXS data [9] for C < C* show both the ‘gas-like’ regime with k_m ∼ C^1/3 (for C ≪ C*) and the ‘liquid-like’ regime with $k_m~\sqrt{C}$. For M = 8 kDa, SAXS data [9] show only the ‘gas-like’ regime as C* is much above the concentrations investigated for this molar mass. The SAXS data of Nishida et al. [14] for M = 252 kDa at concentrations 200–700 g/L (much above C* = 1.22 g/L) show the k_m ~ C^1/4 law, expected for very concentrated solutions. The data [14] for M = 252 kDa at C ~ 1000 g/L represent essentially molten sodium poly(styrene sulfonate). The above described experimental observations are consistent with the theoretical derivations derived in Fig. 3 for the concentration dependence of the polyelectrolyte peak position in salt-free conditions.

As a side remark, it may be mentioned that the above results for the free energy can be used to determine the phase diagram of polyelectrolyte solutions. As has been previously demonstrated by the author and his collaborators, it is critical to use the above expression which goes beyond the one-loop RPA in calculating the phase diagrams for salt-free solutions [36–39]. It is also essential to recognize that the charge of the polyelectrolyte chain is not a fixed number but it self-regulates as the polymer conformation changes due to changes in polymer concentration, salt concentration, dielectric constant, and temperature, etc. [38, 40]. For example, the daughter phases have different charges from the mother phase in a phase-separating polyelectrolyte solution, resulting in a new universality class of phase behavior [38]. The calculations of phase diagrams for salt-free polyelectrolyte solutions, based on one-loop RPA, suffer from the same difficulty mentioned in the introduction that the osmotic compressibility becomes negative. Such an unphysical result from the one-loop RPA has necessitated artificial devices such as arbitrary cutoffs [24, 26, 29, 41]. There are opportunities to implement the theory presented here and go beyond the Debye-Hückel description for the electrostatic interaction among the various ions.

CONCLUSIONS

We have derived expressions for the scattering intensity of radiation from solutions of flexible polyelectrolyte molecules as functions of polymer concentration. Five regimes have been identified, and the concentration dependencies of the polyelectrolyte peak in these regimes are derived. Also, the essential experimental data from the literature on aqueous solutions of sodium poly(styrene sulfonate) using light, X-ray, and neutron scattering, are collected here. The derived theoretical results are consistent with the experimental data obtained in many laboratories worldwide. The theoretical work presented here would not have been possible without the pioneering field theory technique introduced by Sir Sam Edwards.