Ten simple rules for neuroimaging meta-analysis

Abstract

Neuroimaging has evolved into a widely used method to investigate the functional neuroanatomy, brain-behaviour relationships, and pathophysiology of brain disorders, yielding a literature of more than 30,000 papers. With such an explosion of data, it is increasingly difficult to sift through the literature and distinguish spurious from replicable findings. Furthermore, due to the large number of studies, it is challenging to keep track of the wealth of findings. A variety of meta-analytical methods (coordinate-based and image-based) have been developed to help summarise and integrate the vast amount of data arising from neuroimaging studies. However, the field lacks specific guidelines for the conduct of such meta-analyses. Based on our combined experience, we propose best-practice recommendations that researchers from multiple disciplines may find helpful. In addition, we provide specific guidelines and a checklist that will hopefully improve the transparency, traceability, replicability and reporting of meta-analytical results of neuroimaging data.

Introduction

Over the last two decades, neuroimaging has evolved into a widely used method to investigate functional neuroanatomy, brain-behavior relationships, and pathophysiology of brain disorders. However, single imaging studies usually rely on underpowered studies with small sample sizes, which leads to many missed results (Button et al., 2013) and pushes researchers towards analyses and thresholding procedures that increase false positives (Eklund et al., 2016; Wager et al., 2007; Wager et al., 2009; Woo et al., 2014). In addition, results are strongly influenced by experimental and analyses procedures (Carp, 2012) and replication studies are rare. Thus, it is increasingly difficult to sift through the enormous neuroimaging literature and distinguish spurious from replicable findings, and even harder to gauge whether effects in individual studies can be generalized to a task or patient group in a way that is robust to variation in the specific task and details of analysis choices performed. Furthermore, due to the large number of studies, it is challenging to keep track of the wealth of findings (Radua and Mataix-Cols, 2012). Thus, there is a need to quantitatively consolidate effects across individual studies in order to overcome problems associated with individual neuroimaging studies.

One potent approach to synthesizing the multitude of results in an unbiased fashion is to perform a meta-analysis. There are two general approaches to neuroimaging meta-analyses: image-based and coordinate-based meta-analyses. Image-based meta-analyses are based on the full statistical images of the original studies, whereas coordinate-based meta-analyses only use the x,y,z-coordinates (and in some cases their z-statistic) of each peak location reported in the respective publication. Image-based meta-analyses allow for the use of hierarchical mixed effects models that account for intra-study variance and random inter-study variation (Salimi-Khorshidi et al., 2009) as the full information required for this is provided in image form. However, due to the fact that whole-brain statistical images are rarely shared (but see Gorgolewski et al., 2015; http://neurovault.org, for recent approaches of sharing unthresholded statistical images in an online database), most meta-analytic research questions cannot yet be addressed with image-based meta-analysis. In contrast, while coordinate-based meta-analyses use a sparser representation of findings, almost all individual neuroimaging studies provide their results as coordinates in standardized anatomical space (either MNI (Collins et al., 1994) or Talairach (Talairach and Tournoux, 1988) space). Thus, coordinate-based meta-analyses allow us to capitalize on much of the published neuroimaging literature, and provide a quantitative summary of these results to answer a specific research question. There are different approaches to coordinate based meta-analysis, including (multilevel) kernel density analysis (KDA, MKDA; e.g., Wager et al., 2004; Wager et al., 2007; Pauli et al. 2016), gaussian-process regression (GPR; Salimi-Khorshidi et al., 2011), activation likelihood estimation (ALE; Eickhoff et al., 2012; Eickhoff et al., 2009; Turkeltaub et al., 2002; Turkeltaub et al., 2012), parametric voxel-based meta-analysis (PVM; Costafreda et al., 2009), signed differential mapping (SDM; Radua and Mataix-Cols, 2009). A revised version of SDM, termed effect-size SDM (ES-SDM), also allows for the combination of coordinate-based results and statistical images (Radua et al., 2012).

Despite the increasing use of meta-analytic approaches in the last few years, there is a lack of concrete recommendations regarding how to perform neuroimaging-based meta-analyses, report findings, or make results available for the whole neuroimaging community to foster reproducibility of neuroimaging meta-analytic results. For individual MRI experiments, such guidelines have already been developed (COBIDAS; Nichols, 2015). However, best practices for neuroimaging meta-analyses differ from those of individual imaging studies (and also from those of effect-size based meta-analyses of behavioral studies, (e.g., MARS; (American Psychological Association, 2010)). Thus, the aim of this paper is twofold. First, we provide best-practice recommendations that should be considered carefully when performing neuroimaging meta-analyses and help researchers to make informed and traceable decisions. Second, we set standards regarding which information should be reported when publishing meta-analyses to enable other researchers to replicate the study. While these recommendations are primarily relevant to coordinate-based meta-analyses, most of them also hold true for image-based meta-analyses.

1. Be specific about your research question

The critical first step of any meta-analysis is to specify as precisely as possible the research question and the approach towards investigating it. For most functional neuroimaging meta-analyses (this decision is not relevant for structural imaging studies), the researcher must first decide which paradigms to include in the meta-analysis. For example, a researcher interested in cognitive action control may want to know which regions are consistently found activated or deactivated across experiments that required participants to inhibit a prepotent response in favor of a non-routine one. For this example, the question arises if one should include all experiments that test cognitive action control, no matter what paradigm was used (e.g., Stop-signal, Go/No-Go, Stroop, Flanker tasks…), or limit the analysis to a specific paradigm (e.g., Stop-signal task). Considering the consequences for interpretation, the latter case would be specific to the cancelling of an already initiated action, while a meta-analysis across all paradigms would focus on the higher order supervisory control processes necessary in all paradigm types. Importantly, if one decides to include different paradigms, it may be helpful to ensure that the distribution of experiments is relatively balanced across tasks. However, in this context, it should be noted, that if there is enough literature available, there is the possibility to not only calculate one main meta-analysis, but rather also sub-analyses which may focus on more specialized processes (e.g., different paradigm classes) or groups (e.g. different patient samples). For example, one could plan to calculate a general meta-analysis across Stop-signal, Go/No-Go, Stroop and Flanker tasks and then also individual sub-analyses for each paradigm. Convergence across paradigms could be then tested by overlapping the results of the different sub-analyses, or quantitatively using an omnibus test of difference in reported activation pattern (Tench et al., 2014). However, these choices of sub-analyses should have a rationale and be made beforehand and not after inspecting the data (see below). Importantly, brain processes may not always be organized by named task type and minor variations in paradigms can produce large changes in cognitive strategies. As an example, Gilbert et al. (2006) showed that across diverse cognitive domains differences in reaction times between experimental and control conditions are differentially associated with the lateral versus medial rostral prefrontal cortex. That is, when performing a meta-analysis the researcher should carefully select the respective experiments, focusing not only on the paradigm name but also check if the process involved in the respective contrast really reflects the critical cognitive process.

In addition to specifying the paradigms for the analysis, inclusion and exclusion criteria need to be specified. There are general criteria that should be applied. These general criteria refer to only including whole brain experiments (see details below) and only including experiments from which coordinates or statistical images in standard anatomical space can be obtained (see details below). For ES-SDM, another general criteria is to only include experiments that report activations and deactivations (or increases and decreases when comparing groups). Additionally, specific criteria that depend on the particular research question must be specified. Beyond included tasks and paradigms, these specific criteria can relate to analyses and methods. For example, the question might arise if one should only include functional imaging (fMRI) studies (e.g., Kurkela and Dennis, 2016) or studies using either fMRI or positron emission tomography (PET) (e.g., Langner and Eickhoff, 2013; zu Eulenburg et al., 2012).

Examples of other specific inclusion and exclusion criteria relate to aspects of the analysis (e.g. inclusion of only main effects or also of interactions, restricting the meta-analysis to only experiments reporting results on a certain statistical threshold) or to characteristics of the subject group (for example including only healthy subjects or only group comparisons, inclusion of only a specific age range of subjects). Importantly, it should always be kept in mind that the criteria one applies have an impact on how heterogeneous (or homogeneous) the sample of experiments is. Moreover, inclusion and exclusion criteria influence whether or not the sample of experiments is representative for the entire neuroimaging literature available for a specific topic and thus the quality of inclusion. In general, quality of inclusion is given when doing a systematic literature search. However, under certain circumstances it might be limited. For example, when the process investigated and the corresponding inclusion criteria and terminology are defined based on the work of one specific author doing a lot of experiments in this field. This could lead to including only the work of this specific author while concurrently excluding work defining the process a bit different. This emphasizes the need for detailed reporting which experiments are excluded from the meta-analysis and the reasons for doing so.

For research questions regarding group effects there are additional considerations, which have to be taken into account. First of all, there is the question if the focus is on within- (e.g. a specific patient group) or between-group effects (e.g. comparison between patients and controls). When the focus is on between-group effects there are two ways to plan the project: on the one hand, there is the possibility to calculate a meta-analysis across all experiments comparing the groups of interest (e.g. schizophrenia versus controls). On the other hand, two meta-analyses can be calculated, one across experiments in one group (e.g. schizophrenia) and one across experiments of the other group (e.g. controls). In this case, one should make sure that there are no systematic thresholding differences in the original experiments (such as e.g. the results coming from the controls are all corrected, while results from patients are all uncorrected) as this will bias the meta-analytic results. Afterwards a group comparison can be done by doing a contrast analysis between the two meta-analyses (see Spreng et al., 2010). While the former approach is most common, the latter might be an option especially when there are only few experiments reporting between group effects. Importantly, depending on whether the group comparison is done on the experimental or meta-analytic level, interpretation of results changes. That is, while results of meta-analyses across experiments of group comparisons reflect “convergence of differences in brain activation between groups”, a meta-analytic contrast analyses reveals “differences in convergence of brain activation between groups”.

Once a set of papers has been selected, there is also the question of which specific contrasts to include. That is, a paper (which refers to a published item) often reports different analyses or contrasts (which are in the terminology of meta-analyses most frequently called experiments). For example, a paper uses the Go/No-Go (with 75% Go and 25% No-Go trials) task and reports three different contrasts: Go>Rest, No-Go>Rest, No-Go>Go. While the first contrast does not reflect cognitive action control processes necessary to suppress a dominant action plan, the latter two do test for regions involved in these supervisory control processes. Thus, the question arises, if one should include both relevant contrasts or rather only one of the two (see rule 5 for recommendations regarding multiple contrasts per paper).

Additionally, it is also important to decide across which processes and modalities the meta-analysis should be calculated. For example, does it make sense to pool across task fMRI and connectivity experiments? Technically, everything is possible. However, the interpretation of the meta-analytic results crucially depends on the inclusion/exclusion criteria and the experiments on which the analysis is based.

In summary, the first step of a neuroimaging meta-analysis is to specify the research question as precisely as possible, which includes the definition of the process investigated, specification of paradigms and contrasts included as well as the general and specific inclusion and exclusion criteria.

2. Consider the power of the meta-analysis

An important aspect when planning a meta-analysis is the question of how many experiments are necessary in order to be able to perform a robust analysis. Obviously the higher the sample size, the better the power. However, meta-analyses always face a trade-off between number of included experiments (power) and their quality and heterogeneity (Müller et al., 2016). That is, in order to increase the number of experiments an investigator might include experiments that are more heterogeneous in task and design (e.g., include all possible paradigms investigating cognitive action control) or feature lower quality. Thus, when planning a meta-analysis, there is always the challenge to find a balance between homogeneity and power. However, there are conceptual limitations for power, as consolidation of the literature about a specific research field only makes sense if there is enough literature. Thus, when specifying the research question, the literature should always be screened beforehand in order to estimate if there is a reasonable number of experiments to include. This is particularly important for coordinate-based meta-analyses; for image-based analyses, where a random effects approach is generally used, an insufficient number of studies will likewise hamper power due to limited degrees of freedom to estimate between-study variability. For both approaches the generalization of results is questionable when including only a small number of experiments. The key problem with a low number of experiments, at least in ALE based meta-analyses, is that results can be strongly driven by only a few experiments (Eickhoff et al., 2016b). Thus, when pooling across different analytical and experimental approaches (e.g., Go-No-Go and Stop-Signal), this fact can lead to a problem of generalization as only specific types of experiments could drive the results. In general, a meta-analysis aims to pool across different approaches and tasks in order to investigate effects consistent across strategies (Radua and Mataix-Cols, 2012). However, in the event that results can be driven by only a few experiments as is the case for small samples, the generalizability of effects is more questionable.

Based on a recent simulation study (Eickhoff et al., 2016b), a recommendation was made to include at least 17–20 experiments in ALE meta-analyses in order to have sufficient power to detect smaller effects and to also make sure that results are not driven by single experiments. Of course, this can only been seen as rough recommendation as the required number of experiments of a meta-analyses is strongly dependent on the expected effect size. Thus, in cases where a strong effect is expected, smaller sample sizes may be sufficient to perform reliable meta-analyses. However, analyses with expected small and medium effect sizes (which is often the case) that include a lower number of experiments should be treated with caution.

That said, the experiments must fully meet the inclusion criteria. Thus, a sound meta-analysis aims to include many experiments but it may have to discard large numbers of them in order to meet the inclusion criteria.

Thus, a crucial consideration when planning and performing a (coordinate-based) meta-analysis is whether there are enough experiments available that meet all inclusion criteria to ensure that the meta-analysis has adequate sensitivity to detect effects of the expected magnitude, while maximizing ability to generalize to as broad a population of studies of interest as possible.

3. Collect and organize your data

After the research question has been specified, data collection can start. Usually it begins with a thorough literature search, using different search engines. For neuroimaging the most commonly used ones are Pubmed (https://www.ncbi.nlm.nih.gov/pubmed), Web of Science (https://webofknowledge.com), and Google Scholar (https://scholar.google.com/). By using combinations of different keywords restricting the search to specific experiments (e.g. “Go/No-Go”), study types (e.g. “fMRI”) or/and populations (e.g. “human”), potential studies for the meta-analysis can be identified (one can also potentially use less conventional selection strategies; e.g., the Neurosynth or Brainmap database allow researchers to identify papers of, for example, a specific topic). Furthermore, reference tracing in already identified articles as well as in review articles usually helps to complete the literature search. Importantly, everything that is done should be tracked. That is, search engines, keywords and date boundaries should be recorded, along with how many papers were identified by the search, how many of them were excluded, and the reasons for rejection. Any resultant manuscript should provide this information in the methods section. In fact, many journals require “Preferred Reporting Items for Systematic Reviews and Meta-Analyses” (PRISMA) workflow charts for publications of meta-analyses, which graphically illustrate exactly this information. Keeping detailed records during search and selection of experiments eliminates the need to repeat the literature search later.

After identification of all potential papers, the data need to be organized, and all necessary information for the analysis must be extracted. First, the selected experiments should be examined for fulfillment of all inclusion criteria. Thus, each publication must provide a minimum of information required to determine eligibility for inclusion in the meta-analysis. This information refers to coordinates, sample size, and inference/acquisition space. In coordinate-based meta-analyses an experiment can only be included when it reports its results as x/y/z coordinates in standard space (i.e. MNI or TAL), provides the number of included subjects, results are based on whole-brain analysis without small volume corrections, and both increases and decreases are reported (for ES-SDM). Z-statistics (or equivalents such as t-statistics or uncorrected p-values) are needed for GPR and are strongly suggested for ES-SDM. This should always be taken into account when choosing a meta-analytic approach: While GSP and ES-SDM use the z-statistics of the reported results in each experiment; the remaining methods treat all foci equally.

In cases where it is difficult to identify the standard space used or if a whole-brain analysis was conducted, contacting the authors and asking for further information can help to provide this specific information.

It can be very useful to create a table that details all the information that has been extracted from each included experiment. This gives a good overview of the experiments and can help to identify on which criteria to aggregate the experiments (e.g., an overall analysis across all experiments of cognitive action control) and for performing specific sub-analyses (e.g. only No-Go vs. Go experiments, only corrected results, etc.). Furthermore, this table can later be helpful when writing the manuscript as each included experiment should be described and reported in detail.

In summary, for every neuroimaging meta-analysis data collection and organization should be carried out in a precise and conscientious fashion, which includes tracking all steps of the literature search and data selection.

4. Ensure that all included experiments use the same search coverage and identify and adjust differences in reference space

An important aspect for coordinate-based meta-analyses is that convergence across experiments is tested against a null-hypothesis of random spatial associations across the entire brain under the assumption that each voxel has a priori the same chance of being activated (Eickhoff et al., 2012; Radua and Mataix-Cols, 2009; Wager et al., 2007). Therefore, it is a prerequisite that all experiments that are included in a meta-analysis come from the same original search coverage (most commonly the whole brain). Inclusion of heterogeneous region-of-interest (ROI) or small volume corrected (SVC) analyses would violate this assumption and lead to inflated significance for those regions that come from overrepresented ROI/SVC analyses. For example, let’s assume that all of the included experiments of the cognitive control meta-analysis performed a ROI/SVC analysis on the anterior cingulate cortex (ACC) and most of them reported activation in this structure. Significant convergence is almost guaranteed when testing against a null-hypothesis of random spatial convergence across the entire brain. However, this result would only be a confirmation of the bias of investigating activity during cognitive action control solely in the ACC. Thus, in general ROI /SVC analyses should not be included in a meta-analysis.

Importantly, excluding all experiments that used ROI analyses may itself lead to a bias as a critical amount of studies may not be considered in the meta-analysis. To avoid neglecting the importance of e.g. small regions that are commonly used as ROIs the researcher should report how many experiments using ROI analyses were excluded from the meta-analysis and acknowledge those regions that are commonly used as ROIs in their introduction and discussion section.

However, it should be noted that inclusion of ROI analyses may be valid if the whole meta-analysis focuses on just a specific region of interest. Importantly, in this case the null-space has to be adapted to the ROI, i.e. testing against random spatial association across the ROI only. For example, one could ask if and where in the ACC experiments of cognitive action control converge, include also ROI-based experiments and model the null space accordingly with a mask of the ACC. This approach, however, may not be a reasonable solution for small regions as here due to spatial uncertainty of the fMRI signal compared to the size of the region it may not be meaningful to ask where exactly in the ROI the signal converges. Furthermore, in their standard implementation, only few available software tools for neuroimaging meta-analysis offer such ROI meta-analysis (e.g. ES-SDM). Moreover, all included experiments need to fulfill the criteria of having used a mask that includes the same ROI. For some cases this is conceivable; for example, the amygdala where most experiments use standard masks. However, other regions such as the DLPFC are less suitable as they are anatomically less well defined with different authors using different masks.

SVC analyses may be potentially included if peaks in the regions liberally thresholded are discarded unless they meet the statistical threshold used in the rest of the brain. For example, if an experiment applies a threshold of t > 2 in regions with SVC and t > 4 in the rest of the brain, peaks of the SVC could also be included if they reach a t > 4. In other words, one would simulate that the more conservative threshold used in the rest of the brain was also applied to the regions with SVC. If this is done, this should definitely be reported in the publication of the meta-analysis by indicating for each experiment which coordinates exactly have been discarded.

Importantly, potential experiments should not only be checked for classical (explicit) ROI analyses but also for so-called “hidden” ones. That is, sometimes the inference space is also reduced by, for example, partial brain coverage during image acquisition. While exclusion of explicit ROI analyses is most of the time applied in meta-analyses, hidden ROI analyses are often included. However, strictly speaking, those hidden ROI analyses act in the same way as explicit ones. Some papers report partial brain coverage by for example stating that acquisition of slices “started at the temporal pole up to the hand motor area” or make clear that the whole brain was covered. However, in other cases only minimal information on image acquisition is given and it is up to the investigator to decide if the whole brain was covered or not. In general, if a paper does provide in detail the scanner parameters one can easily see if the requirement of whole brain coverage is met or not. What is needed is slice thickness, number of slices, gap as well as the field of view (alternatively to FOV: matrix and voxel size). As an approximation, the average brain has a width of 140 mm (right-left), a length of 167 mm (posterior-anterior) and a height of 93 mm (inferior-superior NOT including the cerebellum) (Carter, 2014). Thus, by using the scanner parameters provided in the method section of the papers it can be estimated if the whole brain was covered during image acquisition or not. For example, ten slices of 4 mm each does not cover the whole brain. In other cases it is trickier and there are also a lot of experiments that scan almost the entire brain (i.e. missing only one or two slices). These experiments might be considered for inclusion, but should be reported as experiments with “almost complete brain coverage”. One potential solution for this problem can also be to use a reduced null space, thus raising the statistical threshold. In the KDA approach such a restrictive null space is implemented by using a gray matter mask with border (e.g. Kober and Wager, 2010).

In contrast to ROI and partial brain coverage, more debatable cases are functional neuroimaging studies that use masking or conjunctions. For example, a comparison of brain activity between a No-Go and Go condition could be masked by the positive main effect of the No-Go condition in order to mask out deactivations. These masking procedures are particularly applied when interactions are investigated (e.g., Remijnse et al., 2009). In general, for individual fMRI studies masking and conjunctions are perfectly reasonable and important. However, in the strict sense, inclusion of these analyses is also questionable as they do reduce the inference space to only regions of the masking contrast. This may be less critical if the original contrast used for masking was whole brain. Depending on the specific research question researchers should carefully consider if experiments using masking contrasts or those scanning almost the entire brain are included, and transparently report which experiments used an inference space that is restricted.

In addition to using the same search coverage all included experiments should also be in the same reference space. As mentioned above, one of the general inclusion criteria is to only include experiments reporting their results in a standard reference space. This is usually the case for all experiments investigating effects in a group of (and not individual) subjects. That is, for every fMRI and PET group-analysis, imaging data is normalized into a standard space in order to be able to investigate effects across subjects. There are two standard spaces used in neuroimaging, the Talairach and Tournoux (TAL; Talairach and Tournoux, 1988) and the Montreal Neurological Institute (MNI; Collins et al., 1994) space. Importantly, coordinates in MNI space differ from those in TAL (Brett et al., 2001), with brains in MNI being larger than those in TAL space (Lancaster et al., 2007). Thus, to perform a meta-analysis across different experiments it is useful and recommended to convert all results into the same space. There are different approaches to transformation--for example, the (older) Brett transformation (Brett et al., 2001; Brett et al., 2002) or the one introduced by Lancaster et al. (2007). However, before adjusting for differences in space, the standard space that was used for normalization has to be determined for each and every included experiment. Usually this information can be found in the method section. However, sometimes it is not explicitly stated, or authors give inconsistent information.

So, how can one determine in which space the coordinates were reported? This information can be derived from i) specifications of the space by the authors (e.g. stating in the method section: “All coordinates are reported in MNI space”) ii) the template (e.g. MNI152 template) and/or iii) the software (i.e. SPM, FSL, AFNI, BrainVoyager, Freesurfer) used for normalization and iv) descriptions of transformations (e.g. for example stating “resulting MNI coordinates were transformed into TAL using the Brett transformation”). For example, an experiment reporting MNI coordinates that used FSL and an MNI template for normalization and not saying anything about transformation into TAL is clearly in MNI space. However, sometimes it is a little bit trickier, when for example the software and/or template used do not fit the author’s statement. A common example would be a paper reporting TAL coordinates in the tables but using SPM with the standard SPM template (which is in MNI space) for normalization without reporting a transformation of coordinates. A rule of thumb is that coordinates of experiments where authors used SPM (version SPM99 and later) or FSL with normalization to the software’s standard template and do not report any transformation should be treated as being in MNI as these software packages use MNI as standard space. When AFNI, Brainvoyager or Freesurfer was used, there is unfortunately no such general rule of thumb and one must rely on the author’s description. This is because these software packages either specifically ask into what space the data should be normalized to or do not document the standard space well. Additionally, in cases of uncertainty, the anatomical space can also be confirmed by contacting the corresponding author.

In summary, classical ROI analyses and small volume corrected results as well as experiments with only partial brain coverage should ideally be excluded from meta-analyses in order to avoid biased results. In addition, inclusion of results using masking or conjunctions is also questionable and should potentially be considered for exclusion from the meta-analysis depending on the specific research question. Moreover, in order to adjust for differences in reference spaces between experiments, for each experiment included in the meta-analysis, the standard space in which the results are reported has to be determined.

5. Adjust for multiple contrasts

When selecting which contrast to include in the meta-analysis, it is important to note that inclusion of multiple experiments (or contrasts) from the same set of subjects (either within or between papers) can create dependence across experiment maps that negatively impacts the validity of meta-analytic results (Turkeltaub et al., 2012). This is problematic, as multiple experiments from one subject group that reflect similar cognitive processes (like in our example cognitive action control delineated by the No-Go>Rest and No-Go>Go experiment) are not independent (Turkeltaub et al., 2012). Thus, when planning a meta-analysis, one needs to clarify how multiple experiments reflecting a similar process from the same sample are dealt with. One approach would be to adjust for within-group effects by, e.g. pooling the coordinates from all relevant contrasts (in this case No-Go>Go and No-Go>Rest) into one experiment (Turkeltaub et al., 2012), averaging the contrast maps of a sample and adjusting the variance (Rubia et al., 2014; Alegria et al., 2016), or combining the contrast maps of a sample using a weighted mean depending on the amount of information of each contrast in each voxel (Alústiza et al., 2016).

If the adjustment for multiple contrasts is not an option, one may prefer to include only one experiment per subject group. This could be to only include the contrast that most strongly reflects the process that the meta-analysis aims to investigate (e.g. Cieslik et al., 2015). For example, this would be including only the No-Go>Go and excluding the No-Go>Rest (as it reflects more than just supervisory control processing) contrast from the meta-analysis. Alternatively, based on the research question one could also decide to include the more lax contrast (e.g. No-Go>Rest). However, in this case the researcher should be aware about the interpretation of the results as such a meta-analysis will not only reveal regions associated with the process of interest (e.g. supervisory control) but also other more general functions (e.g. visual processing).

Thus, when multiple experiments from the same subject group are included in the meta-analysis a crucial consideration is how to adjust for repeated measures.

6. Double check your data and report how you did it

Most authors that plan and perform a meta-analysis do the literature search as well as the extraction of relevant coordinates and meta-data manually and non-automatically. On the one hand, this leads to very detailed and flexible literature search and extraction of relevant information, but on the other hand also makes the process error-prone. For example, mistakes can happen when transferring coordinates and their signs, or a statement about a transformation from MNI to TAL might be missed. Therefore, to avoid errors in the data, any manual data extraction should be double-checked (or duplicated), ideally by a second investigator. Having two investigators ensures that different people agree on which experiments meet the general and specific inclusion and exclusion criteria as well as about the quality of inclusion (i.e. a selection bias is less likely with two investigators). In addition, duplication or double-checking of the recorded data either by the same or different investigators ensures the correctness of the space (MNI or TAL) and the correctness of the coordinates (e.g., in some older publications left and right is switched which can easily be missed). A helpful way for double-checking the coordinates is to either read them backwards or doing the coding horizontally but check them vertically. However, in any case, copy-paste from a PDF into an excel file is prone to errors and should be avoided.

If ES-SDM is done and a map is recreated for each experiment, one can check that the map and their peaks approximate the reports and figures of the paper. In this context, for all neuroimaging meta-analyses it might be helpful to view the included coordinates on the used template space. Importantly, most analyses tools exclude coordinates which are outside the template mask. For analyses across a small amount of experiments this might be undesired and have an effect on the results. In this case, one might decide to adjust the foci so that they still fall into the template space (see Fox et al., 2015 for an example of adjustment). However, all adjustments have to be reported and described in detail as well as the rationale for doing so should be specified. Another option for performing quality control would be to use automated experiment diagnostics. For example, Tench et al. (2013) identified outliers among included experiments by determining the overlap of foci between experiments. However, this automated approach does not fully replace manual quality control as it typically only detects extreme outliers and misses errors like incorrect space specifications or sign mistakes. In contrast to manual extraction of data, there is also the option of collecting data in an automated fashion (e.g., Daniel et al., 2016; Yang et al., 2015; Laird et al., 2015). That is, databases like BrainMap (https://www.brainmap.org/) (Fox and Lancaster, 2002; Laird et al., 2005) or Neurosynth (http://neurosynth.org/) (Yarkoni et al., 2011) that synthesize neuroimaging literature can be used to automatically extract meta-data. This approach comes with the advantage of faster and less error-prone coordinate extraction, but with the downside that experiment selection is less specific and that application of some inclusion/exclusion criteria is not possible. In addition, these databases include only a sample of the available neuroimaging literature. While a fully automated meta-analysis may be viable in situations where there are hundreds or thousands of applicable experiments (and the high error rate in individual experiments may be more than offset by a huge increase in signal), the vast majority of applications require that the data derived from automated data extraction be carefully inspected and corrected.

In summary, in order to avoid errors and to increase the replicability of the meta-analysis, the eligibility of all experiments based on the pre-specified inclusion and exclusion criteria, as well as the correctness of all data used in the final meta-analysis must be double-checked.

7. Plan the analyses beforehand and consider registering your study protocol

As in other neuroimaging studies, a researcher performing a meta-analysis has a lot of “degrees of freedom”. This refers to choices of the statistical tests, number of analyses performed but also to the inclusion and exclusion of experiments (Simmons et al., 2011). Thus, standard concerns about p-hacking also apply to coordinate-based meta-analyses. Therefore, all choices and analyses should be planned beforehand and inclusion and exclusion criteria not be modified based on the observed results (e.g., repeat the analysis after excluding specific paradigms until significant findings are found). Such practices would result in p-values that don’t have their nominal value anymore and that are thus meaningless.

To increase transparency and traceability, we strongly recommend that study aims, hypotheses and all analytic details are registered on a publicly available website or database, such as PROSPERO (https://www.crd.york.ac.uk/PROSPERO/) prior to start of the literature search. Any deviations from the registered protocol, or any non-planned analyses, must be clearly marked as post-hoc or non-prespecified in the resulting manuscript.

8. Find a balance between sensitivity and susceptibility to false positives

As in most neuroimaging studies, multiple statistical tests are performed in a neuroimaging meta-analysis (e.g. for all voxels of the brain), and the researcher performing it must balance between sensitivity and susceptibility to false positives. On the one hand, by not correcting for multiple comparisons, one is certainly more sensitive to discover meaningful (smaller) effects (Lieberman and Cunningham, 2009). Thus, a meta-analysis that aims to maximize sensitivity might show unthresholded whole brain maps if the fact that false positives are not controlled for is clearly indicated and the explorative nature of the results highlighted. However, a lack of control for multiple comparisons also comes with the concurrent downside of a potential contamination of the meta-analytic results (which in turn may strongly influence the future literature) by chance discoveries. Hence, in the majority of cases meta-analytic results should be reported following correction for multiple comparisons. There are different options to account for multiple comparisons in meta-analyses, like controlling for the family-wise error (FWE) or the false discovery rate (FDR), on the voxel- or cluster-level. Voxel-wise FDR correction has become the most widely used correction approach for neuroimaging meta-analysis. However, it has been argued that this correction approach is not adequate for topographic inference on smooth data (Chumbley and Friston, 2009), which also includes neuroimaging meta-analysis data. In addition, for ALE a previous simulation study demonstrated that voxel-wise FDR correction features low sensitivity as well as an increased risk of finding spurious clusters (Eickhoff et al., 2016b). Regarding FWE, its use in current neuroimaging meta-analytic methods is in some way limited by the fact that meta-analytic p-values are not reflecting the probability that a voxel shows an effect by chance. Thus, even if these p-values would be corrected for multiple comparisons, the researcher wouldn’t know if the probability of detecting an effect by chance is small or large. Therefore, the use of FWE in current voxelwise meta-analyses should be considered an informal control of the false positive rate, unless results are exclusively interpreted in terms of spatial convergence in the specific null space (see later).

In general, for ALE meta-analyses (and possibly also other coordinate-based meta-analyses) cluster-level FWE correction seems to be the most reasonable approach, as it entails low susceptibility to false positives in terms of convergence (Eickhoff et al., 2016b). Importantly, on the voxel-level a cluster forming threshold of p<0.001 and a cluster-level threshold of p<0.05 is recommended.

For ES-SDM, a previous simulation showed that an uncorrected threshold of p=0.005 with a cluster extent of 10 voxels and SDM-Z>1 adequately controlled the probability of detecting an effect by chance, and it is thus recommended (Radua et al., 2012). However, this is again an informal control of the false positive rate and could be too conservative or too liberal in other datasets, it must be understood as an approximation to corrected results.

In summary, when doing a meta-analysis a researcher should aim to achieve high sensitivity but additionally also low susceptibility to false positives. To avoid problems such as p-hacking, control of error rates should be specified a priori as part of the design of the study, and could be liberal or conservative to emphasize sensitivity or specificity respectively. A lack of control of the false positive rate might be acceptable providing that a post-hoc estimate of a relevant error rate is given to enable the reader to judge the strength of evidence of a true effect.

9. Show diagnostics

Another important part of meta-analytic studies are diagnostics, i.e. post-hoc analyses providing more detailed information on the revealed clusters of convergence or effect. This can be done by, for example, showing the experiments contributing to a cluster, creating funnel plots or additional heterogeneity analyses using I² and meta-regressions (usually done for ES-SDM). Importantly, these additional diagnostics can reveal valuable information on the clusters found in the meta-analysis.

There are different ways to determine the contribution of experiments. One is to identify and count all experiments that report foci directly lying in a specific cluster or within a specific localization uncertainty range (for example 2 standard deviations; cf. Purcell et al., 2011; Turkeltaub et al., 2011). Alternatively, contributions can also be estimated by determining for each included experiment, how much it contributes to the summarized test-value (e.g. ALE, density) of a specific cluster (this method was for example used in Cieslik et al., 2016 and a similar approach in Etkin and Wager, 2007). This is done by computing the ratio of the summarized test-values of all voxels of a specific cluster with and without the experiment in question, thus estimating how much the summarized test-value of this cluster would decrease when removing the experiment in question. Another alternative for evaluating the contribution would be to test for robustness of results by using jackknife analyses (e.g., Radua and Mataix-Cols, 2009; Radua et al., 2012). This approach tests how stable results are when iteratively repeating the meta-analysis, always leaving one experiment out.

Yet another way is to create a funnel plot, i.e. a scatterplot of the effect sizes and their variances (or the sample size of the studies). With this plot, one can observe how many studies found a relevant effect-size in that voxel, or whether a meta-analytic finding is mostly driven by small studies, which could be an indicator of potential publication bias. To note, interpretation of these plots must be appropriate to the context of CBMA, e.g. many studies may have an effect size of zero if they reported no peaks in the proximity of the voxel.

Examining contributions can also help to identify if results might be driven by experiments featuring specific characteristics, which would allow more specific interpretation of the results. For example, let’s assume that an overall meta-analysis across different tasks of cognitive action control (Go/No-Go, Stop-Signal, Stroop) reveals a widespread fronto-parietal network. When checking the contribution of each cluster of this network the researcher discovers that only experiments that used a Stop-Signal task contributed to the finding in the left anterior insula. This would imply a more specific interpretation for the role of the left anterior insula, by linking it more to the specific process of cancellation of an already initiated action, rather than a general role in supervisory control. Of course, it is important to remember that post-hoc analysis choices made only after inspecting one’s data or results (e.g., analyzing subsets of studies separately, on the basis of apparent heterogeneity) are more likely to be spurious (Gelman & Loken, 2013, Forstmeier et al., 2016). Consequently, such post-hoc conclusions should be explicitly treated as exploratory in one’s manuscript, pending confirmation of the new hypotheses in independent datasets.

In summary, diagnostics provided by contributions, funnel plots and heterogeneity analysis provide important information about the interpretation of results.

10. Be transparent in reporting

As replication of study results becomes more and more important in the field of neuroimaging, and data science in general (Diggle, 2015), it is also crucial for meta-analysts to describe and report their specific research question as well as methods and results with sufficient detail and transparency to allow replication by an independent researcher. Providing such detailed reports is sometimes difficult as many journals have word-limits. However, in these cases all necessary information should be provided in the supplementary material.

Reporting of the research question and the specification of the process investigated should be precise. This also implies a detailed and in depth report of all of the inclusion and exclusion criteria as well as the motivation for selecting these criteria.

Also, all steps of the meta-analytic study should be reported, ideally in a flow-chart, including literature search, selection process, experiment classifications into different subgroups, different meta-analyses conducted and potential further calculations of conjunctions, meta-analytic contrasts or other analyses. In this context, the number of papers and experiments (which are often different) included in total, as well as in each sub-analysis, should be reported.

Importantly, not only the papers that were included in the meta-analysis must be reported but also the specific contrasts (experiments) included. A paper often reports more than one experiment. If only the papers are listed, the list of specific experiments included in the analysis cannot be replicated. For example, let’s again take the example of a paper that reports 4 different experiments; two of a Go/No-Go task (No-Go>Rest and No-Go>Go) and two of a Stop-Signal task (Stop>Rest, Stop>No-Stop). Let’s assume that, based on the specification of the research question, both tasks are included, but only contrasts that test against a control condition. Thus, inclusion of this paper should be reported, as well as the more specific information that the coordinates resulted from the No-Go>Go and Stop>No-Stop contrasts were considered. The best way of reporting this is a table.

In this context the publication of the meta-analysis should also provide details on how multiple contrasts from the same subject group were handled (see rule 5). When again taking the same example, one must report if the two contrasts of the same paper (Go/No-Go and Stop-Signal) were treated as one or as two separate experiments and which adjustment was conducted if treated as one.

In general, in order that every reader can easily retrace fulfillment of the inclusion/exclusion criteria, detailed information of each included experiment should be provided. This can be in the form of a table in the supplement material (cf. Müller et al., 2016). In particular, this table should list the following information (some of them were already mentioned before): number of subjects, specific characteristics of the subjects, task description, stimuli used, coordinate space as well as contrast calculated including source of coordinates (e.g. table number from the original paper).

Furthermore, if any additional information from authors of an included experiment was received, which is not part of the original publication (for example, a paper where only results of ROI analyses are reported and where one received the whole brain results from the author), it is essential to report this information in the method section. In the following there is a summary and checklist with all the information that should be reported:

• Research question

• Detailed inclusion and exclusion criteria and the motivation why they were applied

• All steps of the meta-analytic study ideally in a flow-chart

• Number of experiments included in each analysis

• All experiments (not only the reference of the publications) incorporated

• Handling of multiple experiments from the same subject group

• Detailed information on each included experiment (number of subjects, specific characteristics of the subjects, task description, stimuli used, coordinate space, contrast calculated including source of coordinates)

• Any additional data received from the authors which is not reported in their publication

Besides detailed description in the method section, the reporting of results should also be standardized. Thus, also for meta-analytic approaches test statistics and descriptive statistics should be reported.

Furthermore, it is desirable that results are made available for the neuroscience community. In particular, sharing the meta-analytic results, e.g. on an open source platform such as ANIMA (http://anima.fz-juelich.de/) (Reid et al., 2016) or Neurovault (http://neurovault.org/) (Gorgolewski et al., 2015), allows other authors to compare their own results with meta-analytic clusters. In addition, not only sharing of meta-analytic results but also sharing of all the extracted data is very useful for the neuroimaging community. For example, it is not only possible to extract data from the BrainMap database but also to submit data to it. Thus, data manually gathered for the purpose of a meta-analysis can be contributed to the database. In summary, publication of meta-analysis should be detailed and transparent including all the information necessary to allow replication of the study.

How to discuss the results of coordinate-based meta-analysis in terms of convergence

Finally, we want to raise the issue of how coordinate-based meta-analytic results can be interpreted. In general, neuroimaging meta-analyses consolidate the findings of different experiments that report activation (in task-based fMRI meta-analysis) or gray matter (in VBM meta-analysis) differences between conditions or groups. However, this specific difference information, that is the sign of the effect, of individual neuroimaging experiments is, strictly speaking, lost in a coordinate-based meta-analysis. Importantly, for image-based meta-analyses and ES-SDM, information about activation/deactivation is still preserved. Thus, results of image-based approaches can still be interpreted as strength of decrease/increase of activation or gray matter. In contrast, coordinate-based meta-analytic approaches always test for spatial convergence of neuroimaging findings across experiments in the specific null space. This implies that significant effects can only be interpreted as convergence but not as strength or decrease/increase of activation or gray matter. For example, let’s assume that the meta-analysis across experiments reporting greater activation in a No-Go compared to a Go condition reveals a significant convergence in the right anterior insula. From this result one can conclude that experiments testing for greater activation in a No-Go compared to a Go condition converge in the right anterior insula, or in other words, that greater activation for No-Go compared to Go conditions is more frequently reported in the right anterior insula than in the remaining gray matter +/− white matter and cerebrospinal fluid. Nevertheless, results are often discussed as increased or decreased activations/gray matter, which is conceptually incorrect.

Similarly, when calculating contrasts between coordinate-based meta-analyses, the results can only be interpreted in terms of stronger convergence and not as activation/gray matter differences (again, this does not apply to image-based meta-analyses or ES-SDM). Let’s again take an example where two meta-analyses are performed, one across Go/No-Go experiments and one across Stop-Signal experiments and then a contrast between those two meta-analyses is performed. From this contrast analysis one cannot derive brain regions showing stronger activity in the Go/No-Go compared to the Stop-Signal task, but rather regions where there is significantly stronger convergence of experiments of the one compared to the other task. It is very likely that a meta-analytic contrast very well reflects results of contrasts of individual neuroimaging experiments. However, a coordinate-based meta-analytic contrast-analysis is only testing for differences in convergence and should be interpreted in this way.

Therefore, as many coordinate-based neuroimaging meta-analysis approaches look for convergence of neuroimaging findings across experiments, results should be interpreted in terms of convergence or as regions that are consistently found to be associated to a specific process or group across experiments in the null space. Image-based meta-analyses do not suffer from this limitation, which provides yet another incentive for researchers to adopt such procedures whenever possible.

Open issues

Even though there are general best-practice recommendations we can give for neuroimaging meta-analyses, there are still some aspects that need to be further discussed.

First, there is the problem of publication bias that should be addressed. That is, there is in general in science a bias to publish mainly significant results while experiments failing to reject the null-hypothesis are often not reported (Ioannidis et al., 2014; Rosenthal, 1979). For conventional effect-size meta-analyses this file-drawer problem can be detected and has major implications and should always be considered when interpreting results (Ahmed et al., 2012; Kicinski, 2014). However, coordinate-based neuroimaging meta-analyses are conceptually different, testing for spatial convergence of effects across experiments with the null-hypothesis of random spatial convergence (Rottschy et al., 2012). Thus, a limitation of most coordinate-based algorithms (not for ES-SDM) is that they are insensitive to non-significant results and publication bias may go unnoticed. It is therefore particularly important to be transparent in reporting. Additionally, in neuroimaging meta-analyses the publication bias may derive rather from the pressure that every (expensive) imaging study must always yield “something to publish”. That is, due to the high analytical flexibility in neuroimaging (Carp, 2012), different ways of data-analysis, inference and thresholding might be used until a (desired) significant result is found. This might lead to a publication bias of less relevant and possibly random results, which, unfortunately, also affect the outcome of meta-analyses, leading to more heterogeneity and thus less likelihood to find significant convergence. In this context, the confirmation bias might also play a role. That is, the (unconscious) habit to search, interpret and publish data in a way that it is in line with existing theories and hypotheses (Forstmeier et al., 2016). That is, results may be more likely to be published if they conform with brain regions that are thought to be involved in a specific process. Thus, in neuroimaging meta-analyses, besides the classical publication bias, the confirmation bias as well as analytical flexibility play a crucial role which may lead to publication of more random results.

Another aspect to consider is the handling and inclusion of so-called “grey literature”. When conducting a meta-analysis, especially with research questions where only a few experiments exist, one may consider contacting authors to get additional results and coordinates. On the one hand, there is the possibility to decide to only consolidate results that are published (e.g., Cieslik et al., 2016) and thus to only include experiments that have passed a peer-review process. However, on the other hand, there is also the legitimate decision to include also unpublished data (e.g., Langner and Eickhoff, 2013) in order to increase the number of experiments and to get more appropriate contrasts. There is no general rule or recommendation we can give with regard to this decision. However, no matter the decision, one should always be transparent, i.e. report in the method section of the publication all information that was additionally included but not provided in the original publication.

Summary

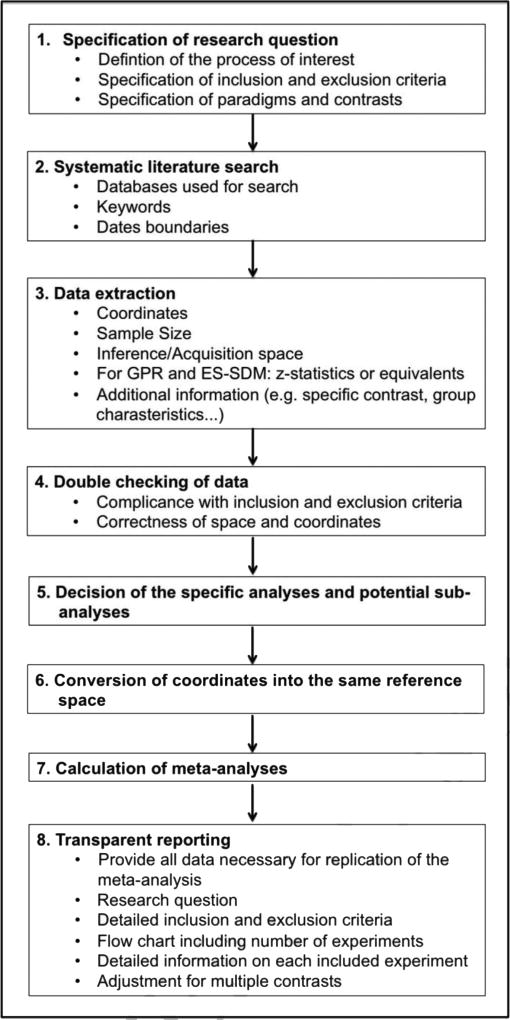
Conducting a meta-analysis at first glance seems straightforward. However, when reviewing the literature and coding the experiments problems may arise which authors may handle different. This can lead to diversity between different meta-analyses investigating the same topic (see also Müller et al., 2016). Thus, meta-analyses require a consistent approach if they are to be interpretable. We here tried to formulate some best practice rules that should be applied when conducting a neuroimaging meta-analysis. However, meta-analyses will always involve to some extent subjective decisions, which may account for the diversity of included experiments and results. It is essential that these subjective decisions and their motivation are transparently reported in the publication of the meta-analysis. Therefore, in order to be able to fully reconstruct a meta-analysis, detailed description of inclusion/exclusion criteria and their motivation as well precise reporting of included papers and contrasts and of analyses conducted are needed. Prior registration of the study protocol in a public database, such as PROSPERO, allows for maximum transparency and traceability. Figure 1 illustrates the important steps when conducting a meta-analysis, while Table 1 provides a formal checklist of all the aspects a researcher performing a meta-analysis should consider. We recommend all authors of neuroimaging meta-analyses to fill out this checklist and provide as supplemental material in their papers.

Figure 1.

Flow-chart illustrating the important steps of a meta-analysis

Table 1.

Checklist for neuroimaging meta-analyses

The research question is specifically defined	YES, and it includes the following contrasts: _____________________ vs ______________________ _____________________ vs ______________________ _____________________ vs ______________________ _____________________ vs ______________________ _____________________ vs ______________________ _____________________ vs ______________________
The literature search was systematic	YES, it included the following keywords in the following databases: ______________________________________
Detailed inclusion and exclusion criteria are included	YES, and reasons of non-standard criterion were: ______________________________________
Sample overlap was taken into account	YES, using the following method: ______________________________________
All experiments use the same search coverage (state how brain coverage is assessed and how small volume corrections and conjunctions are taken into account)	YES, the search coverage is the following: ______________________________________ __________________________________________________________________________________________________________________
Studies are converted to a common reference space	YES, using the following conversion(s): ______________________________________
Data extraction have been conducted by two investigators (ideal case) or double checked by the same investigator (state how double-checking was performed)	YES, the following authors: _______ checked inclusion criteria _______ extracted coordinates _______ extracted other info: _____________ _______ double-ckecked the following data:____
The paper includes a table with at least the references, basic study description (e.g. for fMRI tasks, stimuli), contrasts and basic sample descriptions (e.g. size, mean age and gender distribution, specific characteristics) of the included studies, source of information (e.g. contact with authors), reference space	YES, and also the following data: ______________________________________
The study protocol was previously registered and all analyses planned beforehand, including the methods and parameters used for inference, correction for multiple testing, etc	YES:
	1)The meta-analysis was registered before starting the search at ___________________________ (registration number ______________ ) 2)Any non-planned analyses are clearly stated as post-hoc or non-prespecified in the paper. 3)The meta-analysis used the default methods and parameters of the software, with the following exceptions ______________________
The meta-analysis includes diagnostics	YES, the following: ______________________________________

Highlights.

• Meta-analyses require a consistent approach but specific guidelines are lacking

• Best-practice recommendations for conducting neuroimaging meta-analyses are proposed

• We set standards regarding which information should be reported for meta-analyses

• The guidelines should improve transparency and replicability of meta-analytic results