Abstract
Genetic resources are an important source of genetic variation for plant breeding. Genome-wide association studies (GWAS) and genomic prediction greatly facilitate the analysis and utilization of useful genetic diversity for improving complex phenotypic traits in crop plants. We explored the potential of GWAS and genomic prediction for improving curd-related traits in cauliflower (Brassica oleracea var. botrytis) by combining 174 randomly selected cauliflower gene bank accessions from two different gene banks. The collection was genotyped with genotyping-by-sequencing (GBS) and phenotyped for six curd-related traits at two locations and three growing seasons. A GWAS analysis based on 120,693 single-nucleotide polymorphisms identified a total of 24 significant associations for curd-related traits. The potential for genomic prediction was assessed with a genomic best linear unbiased prediction model and BayesB. Prediction abilities ranged from 0.10 to 0.66 for different traits and did not differ between prediction methods. Imputation of missing genotypes only slightly improved prediction ability. Our results demonstrate that GWAS and genomic prediction in combination with GBS and phenotyping of highly heritable traits can be used to identify useful quantitative trait loci and genotypes among genetically diverse gene bank material for subsequent utilization as genetic resources in cauliflower breeding.
Keywords: cauliflower, gene bank, genome-wide association study, genomic prediction, genotyping-by-sequencing, GenPred, Shared Data Resources, Genomic Selection
Wild ancestors, landraces, old varieties, and breeding stocks of crop plants that are preserved in ex situ gene banks are an important resource of genetic diversity for introducing favorable alleles into modern cultivars. Adaptation to unfavorable environmental conditions, disease resistance, and nutritional value are traits for which new alleles can be found in genetic resources (Hawkes 1991). The improvement of quantitative traits such as yield with genetic resources is more challenging because of deleterious alleles and missing adaptation to modern agricultural practices. However, new improvement strategies may be used for such traits (Longin and Reif 2014). Molecular breeding methods such as association mapping and genomic selection combined with current sequencing technology offer new possibilities for an efficient utilization of genetic resources (Tester and Langridge 2010; Bevan et al. 2017).
Cauliflower (Brassica oleracea var. botrytis, 2n = 2× = 18) is an important vegetable crop, owing to its high nutritional value (Picchi et al. 2012). With an annual production area of ∼1.4 million ha and 24 million tons harvested in 2014 (http://faostat.fao.org/), cauliflower is of great economic importance, particularly in Asia. The most important trait and yield determinant is the cauliflower curd (edible, often white inflorescence meristem; Li et al. 2017), but response to vernalization is also an important agronomic trait, and genotypes with obligate and facultative vernalization requirements have been identified (Matschegewski et al. 2015).
Genome-wide association studies (GWAS) have been carried out in major cereal crops, including maize (Li et al. 2012), rice (Norton et al. 2014), barley (Gawenda et al. 2015), and wheat (Edae et al. 2014). In Brassicaceae, GWAS have mainly been conducted in rapeseed (Brassica napus) to dissect the genetic basis of disease resistance (Jestin et al. 2011), seed oil content and quality (Zou et al. 2010; Rezaeizad et al. 2011), seed weight and quality (Li et al. 2014), seed glucosinolate content (Hasan et al. 2008), and several morphological and phenological traits (Cai et al. 2014). Recently, GWAS was used in cauliflower to identify flowering-related quantitative trait loci (QTL) (Matschegewski et al. 2015), which are useful for breeding varieties adapted to different temperature regimes. For example, expression analysis identified a homolog of the Arabidopsis thaliana CDAG1 (Curd Development Associated Gene 1) gene in cauliflower, whose overexpression increased curd yield (Li et al. 2017).
In addition to genetic mapping, genomic selection (Meuwissen et al. 2001) has become an important method in plant breeding (Schmid and Thorwarth 2014). Genomic selection is based on the prediction of breeding values based on marker information alone. A training population with genotypic and phenotypic information is used to estimate marker effects with a statistical model, which is then applied to calculate the breeding values of the potential selection candidates in the breeding population (Heffner et al. 2009). Cross-validation allows selection of the best model for a certain population, trait, and genetic architecture (Crossa et al. 2010). Genomic selection provides several benefits in both animal and plant breeding (Hayes et al. 2009; Heffner et al. 2009; Jannink et al. 2010), including more rapid breeding cycles and fewer field trials, leading to increased genetic gain per time unit at a lower cost (Schaeffer 2006; König et al. 2009; Heffner et al. 2010). Genomic prediction has been successfully applied in wheat (Poland et al. 2012b), maize (Crossa et al. 2013), and soybean breeding (Jarquín et al. 2014). In Brassicaceae, one study investigated the potential of genomic selection in rapeseed (Würschum et al. 2014) and concluded that it is a promising method for rapeseed breeding.
Advances in sequencing technology allow the detection of single-nucleotide polymorphisms (SNPs) from large and diverse germplasm collections (Crossa et al. 2013). Genotyping-by-sequencing (GBS) generates tens of thousands of molecular markers at low cost (Elshire et al. 2011; Poland et al. 2012b; Sonah et al. 2013) and is an efficient tool for plant genetics and breeding (Poland and Rife 2012; Fu et al. 2014; Tardivel et al. 2014). It has been successfully used for genomic selection in wheat, maize, and soybean (Poland et al. 2012a; Crossa et al. 2013; Jarquín et al. 2014), and in GWAS of morphological traits and flavonoid pigmentation in maize and sorghum, respectively (Romay et al. 2013; Morris et al. 2013). Recently, Zhao et al. (2016) used specific-locus amplified fragment sequencing to create a genetic map of cauliflower. One disadvantage of GBS is a high proportion of missing data, which may be alleviated by genotype imputation (Poland and Rife 2012), although the value of imputation for association mapping and genomic prediction is debated (Marchini and Howie 2010; Rutkoski et al. 2013).
In this study, we combined GBS with a phenotypic analysis of cauliflower genetic resources to investigate the potential of GWAS for the identification and genomic prediction for the selection of useful genetic variation in cauliflower breeding. More specifically, the main objectives of this study were (1) to identify SNP markers that are associated with phenotypic variation in curd-related traits using GWAS, (2) to quantify the predictive ability of genomic prediction models for curd-related traits in diverse cauliflower genotypes obtained from ex situ gene banks, and (3) to evaluate the effect of data imputation on association mapping and genomic prediction. We show that GWAS identifies genomic regions harboring potentially useful variation and that genetic resources are suitable for genomic prediction of phenotypic variation in highly heritable traits.
Materials and Methods
Plant materials and phenotyping
A total of 192 cauliflower accessions representing a wide range of morphological diversity and geographical origins were obtained from the gene banks of the United States Department of Agriculture (USDA) and from the Leibniz-Institut für Pflanzengenetik und Kulturpflanzenforschung (IPK) Gatersleben, Germany. Detailed information about accessions is given in Supplemental Material, Table S1 in File S1. All accessions were phenotyped for curd-related traits in replicated field trials at two locations (experimental stations: Heidfeldhof and Kleinhohenheim in Stuttgart, Germany), for three successive growing seasons (June 2011, April 2012, and August 2012). The field experiment was conducted in randomized complete block design with two replications (Yousef et al. 2015). Five ripened curds were harvested from each plot and used to measure six traits that reflect various aspects of curd development and morphology according to Lan and Paterson (2000).
Curd width (cm): width of the curd.
Cluster width (cm): width of the largest floral cluster.
Number of branches: number of branches within the curd that originated from the main stem.
Apical shoot length (cm): stem length from the apical meristem to where the closest first-rank branch originated from the main stem.
Nearest branch length (cm): length of the branch that is nearest to the apical meristem.
Days to budding: number of days from planting to appearance of the first floral bud.
Genotyping and marker imputation
We genotyped the material with the original GBS protocol using the ApekI restriction enzyme (Elshire et al. 2011). The sequencing and bioinformatic analyses of our material are described in Yousef et al. (2017). Briefly, 192 genotypes were sequenced as two sequencing libraries of 96 individuals on an Illumina HiSeq 1000, using a set of in-house scripts and public sequence analysis tools including bwa (Li and Durbin 2009) and FastQC (http://www.bioinformatics.babraham.ac.uk/projects/fastqc/). Eighteen genotypes with <300,000 reads were excluded from further analyses, which resulted in a total sample of 174 accessions for further analyses. The preprocessed reads were aligned to the genome of B. oleracea sp. capitata (Liu et al. 2014) using bwa. SNP calling was performed with SAMtools (Li and Durbin 2009), bcfutils, vcfutils, and custom Python scripts. The vcf file was parsed to retain only SNP positions with a coverage of ≥30, and ≥10 reads confirming the variant nucleotide. In the end, 120,693 SNPs were detected with 19.02–76.73% of missing values per genotype (File S2).
We imputed missing genotypes with fastPHASE (Scheet and Stephens 2006) and BEAGLE (Browning and Browning 2007); both use a hidden Markov model to cluster haplotypes but they differ in the underlying model. The fastPHASE method uses an expectation–maximization algorithm for parameter estimation and fixes the number of haplotype clusters in the model. By contrast, BEAGLE uses empirical frequencies and allows the cluster number to be changed at each locus for a better fit to the localized linkage disequilibrium (LD) (Pei et al. 2008). We used fastPHASE as the main imputation method because we expected it to perform better than BEAGLE with our data set, which is characterized by a low LD, small sample size, and high marker density. The advantages of imputation methods under different scenarios were described by Browning and Browning (2011). We included BEAGLE for comparison for some analyses, but used only fastPHASE-imputed data for the GWAS to keep the number of analyses manageable. SNP markers with minor allele frequency (MAF) and any missing values were excluded from further analyses, which resulted in a total of 675 markers (unimputed data set). Next, SNP alleles were imputed with fastPHASE (Scheet and Stephens 2006) and markers with a MAF were excluded, which resulted in a total of 64,372 SNPs (imputed data set with fastPHASE). Genomic prediction was conducted with a third data set, in which SNP alleles were imputed with BEAGLE 4 (Browning and Browning 2007) and markers with a MAF were excluded, which resulted in a total of 62,566 SNPs (imputed data set with BEAGLE).
Analysis of phenotypic variation
The effects of the genotype and environment (environment was treated as the combination of location and season) and their interactions with phenotypic variation were evaluated using analysis of variance with the aov function of R (R Core Team 2015). Details of the phenotypic data analysis are described in Yousef et al. (2015). A mixed-effects model was fitted using restricted maximum likelihood (REML) with the lmer function from the R package lme4 (version 1.0-5) (Bates et al. 2014):
| (1) |
where are the adjusted means of the genotype in the environment, m is the overall mean, is the effect of the genotype, is the effect of the environment, and the genotype × environment interaction. All effects were considered as random, except the intercept, which was treated as a fixed effect. Variance components of this model were used to calculate broad sense heritability for each trait according to Nyquist and Baker (1991) as
| (2) |
where is the broad sense heritability, is the genetic variance, is the genotype-by-environment variance, is the error variance, r is the number of replications, and e is the number of environments. Best linear unbiased predictors (BLUPs) for the genotypic effects were extracted from model (1) and used to calculate the genetic correlation () among all traits. The genetic and phenotypic correlation coefficients are based on the Pearson correlation coefficient.
Population structure and LD
We used a discriminant analysis of principle components (DAPC) to infer clusters of genetically related individuals by using a k-means algorithm as implemented by Jombart and Ahmed (2011). LD between adjacent markers was calculated and the LD decay over distance for each chromosome was assessed. To identify differences in LD levels between the complete sample and the clusters identified by k-means, we used PLINK (Purcell et al. 2007) to calculate LD as:
| (3) |
where is the frequency of haplotypes with allele a at one locus and allele b at the other locus (VanLiere and Rosenberg 2008). The extent of background LD was estimated as the correlation of the 95% percentiles of all pairwise markers between chromosomes (Breseghello and Sorrells 2006). Additionally, we analyzed the persistence of linkage phase between DAPC-inferred clusters and the whole sample to validate whether a marker effect estimated in one cluster will contribute to the prediction ability in other clusters. Persistence of linkage phase is calculated as correlation coefficient r by:
| (4) |
where As a measure of LD, r ranges from −1 to 1 (De Roos et al. 2008). Persistence of linkage phase is expressed as correlation of r between the same chromosomes of each cluster. The number of markers differed between clusters; therefore, we averaged the correlation of r values between clusters over groups of 50 markers.
Association mapping
GWAS was performed with the R (R Core Team 2015) implementations of the Efficient Mixed Model Association eXpedited (EMMAX; Kang et al. 2010) and the Multi Locus Mixed Model (MLMM Segura et al. 2012) methods. The MLMM analysis was conducted with R scripts available at https://github.com/Gregor-Mendel-Institute/mlmm. EMMAX is a method that uses a linear model in combination with a marker-derived relationship matrix to correct for population structure. The linear model has the form:
| (5) |
where is the vector of phenotypes; is a matrix containing the markers; is the vector of fixed-effects coefficients; is an incidence matrix; is the random effect, where , with representing the relationship between genotypes inferred from genetic markers; and is the residual effect with . Additive genetic variance () and environmental variance () are derived from the REML estimates. Variance components are only calculated once and are taken as fixed in EMMAX, which speeds up computation (Kang et al. 2010). MLMM uses the same linear model as EMMAX, but additionally includes significant SNPs as covariates in the model by using a forward–backward stepwise algorithm with reestimation of variance parameters ( and ) at each step.
Following Utz et al. (2000), the proportion of phenotypic variance explained by a QTL was calculated as:
| (6) |
where is the coefficient of determination, z is the number of predictors (number of significant SNPs in GWAS), and N is the number of observations. The proportion of genotypic variance explained was calculated as:
| (7) |
where is the heritability of a given trait as defined in equation (2).
Confounding effects due to population structure were evaluated with the inflation factor λ, which is the ratio of the observed median to the expected median of a test statistic distribution (Devlin and Roeder 1999). Values close to 1 indicate no inflation. The significance threshold was set for the unimputed and imputed data for each trait separately using the false discovery rate (FDR; Benjamini and Hochberg 1995), where FDR values are computed from the P-values. The FDR was set to 0.2 for all data sets.
Genomic prediction
We evaluated three different genomic prediction methods, namely genomic BLUP (GBLUP), ridge regression BLUP (RRBLUP), and BayesB. The GBLUP model uses a realized relationship calculated from genetic markers (Habier et al. 2013) and is defined as:
| (8) |
where is an n × 1 vector of random effects and is the design matrix. Genetic values are modeled as random effects with with as the genetic variance and the realized relationship matrix.
An RRBLUP model (Meuwissen et al. 2001) was used to estimate the marker effects and to calculate the prediction ability. The model is of the form:
| (9) |
where is the vector of n phenotypic records, is a vector of fixed effects that represents the overall mean, is an n × 1 vector of random effects, and is the marker matrix. The residuals follow a normal distribution where is the identity matrix. The GBLUP and RRBLUP implementations of the synbreed R package (Wimmer et al. 2012) were used.
Additionally, a BayesB (Meuwissen et al. 2001) model as implemented in the BGLR R package (Pérez and de los Campos 2014) was used to estimate marker effects and to calculate prediction ability. BayesB uses the same linear model as RRBLUP, but a prior for the marker effects is modeled as mixture of a point of mass at zero and a slab that has a scaled-t density. Following Pérez and de los Campos (2014), the notation of the prior distribution is:
| (10) |
where β represents the vector of regression coefficients and is the respective variance. Parameter π is the proportion of nonzero effects and follows a β prior distribution, which implies the possibility of variable selection. , , , and represent the normal, chi-squared, β, and γ density distributions, respectively (Pérez and de los Campos 2014). BayesB was chosen over other Bayesian models such as BayesA and BayesC because it assumes an a priori distribution of marker effects following a mixture distribution with point mass at zero and a scaled-t slab similar to BayesA, and utilizes both shrinkage and variable selection, similar to BayesC (Pérez and de los Campos 2014). The hyper-parameters were chosen according to the default values in BGLR.
Since population structure can inflate prediction ability (Guo et al. 2014), we estimated the effect of population structure on prediction ability by directly correcting the kinship matrix in the GBLUP model for confounding effects of population structure (Thorwarth et al. 2017). The corrected kinship matrix was calculated with PC-Relate (Conomos et al. 2016). Prediction ability was defined as correlation between observed phenotypic and predicted genotypic values [] and was calculated by a five-fold cross-validation with 10 replications for each trait. To test whether genotypic effects in the genomic prediction and GWAS were caused by the same QTL, the position of SNPs with the greatest effects in genomic prediction models were compared with the most significant SNPs in the GWAS.
Data availability
Raw sequence data have been submitted to the Sequence Read Archive under accession number PRJEB8701. SNP calls are available on figshare at https://doi.org/10.6084/m9.figshare.5709784. Best Linear Unbiased Estimators (BLUEs) of phenotypic data are provided as supplementary material (File S2).
Results
Phenotypic analysis of the six yield-related traits
The 174 gene bank accessions were evaluated for six curd-related traits and exhibited a large phenotypic variation in all traits (Yousef et al. 2015). For example, number of days to budding ranged from 45 to 118 d with an average of d, and curd width ranged from 11.11 to 15.29 cm with an average of cm (Table S2 in File S1). Analysis of variance showed that all traits were strongly affected by genotype (G), environment (E) and genotype by environment interaction (G × E; ). Broad-sense heritability () differed strongly between traits. The traits of cluster width and number of days to budding showed moderate (56%) and high (94%) heritabilities, respectively. Furthermore, the traits of curd width and cluster width showed high phenotypic () and genotypic () correlations (Table S3 in File S1), as did apical length and nearest branch length ( and ). Number of days to budding was negatively correlated with number of branches ( and ).
Analyses of population structure and LD decay
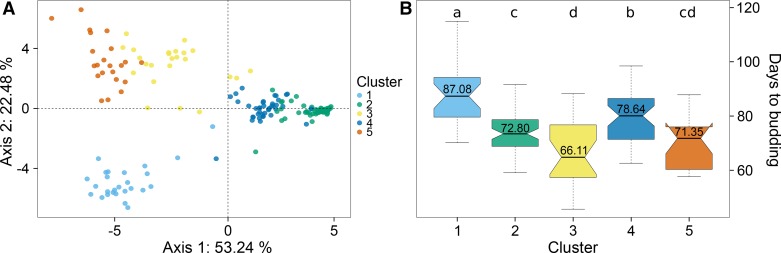
We inferred five genetic clusters (Figure 1A) by k-means clustering (Figure S1 in File S1). The clusters are differentiated by geographic origin and flowering time. Cluster 1 (n = 25) consists of geographically diverse accessions (Table S4 in File S1) without a distinct geographic origin, but differs from the other clusters by its high average time to flowering (Figure 1B). Clusters 2 (n = 56) and 4 (n = 40) consist of predominately European accessions that differ by their mean time to budding. Clusters 3 (n = 24) and 5 (n = 22) consist mainly of Asian accessions that also differ by mean time to budding.
Figure 1.
(A) Discriminant analysis of principal components plot for the five inferred clusters using the k-means algorithm (Jombart and Ahmed 2011). (B) Boxplots for number of days to budding for each DAPC-inferred cluster. Letters above boxplots display Tukey-test results. Clusters with the same letter are not significantly differentiated from each other. Values within boxplots display the mean time to budding for each cluster.
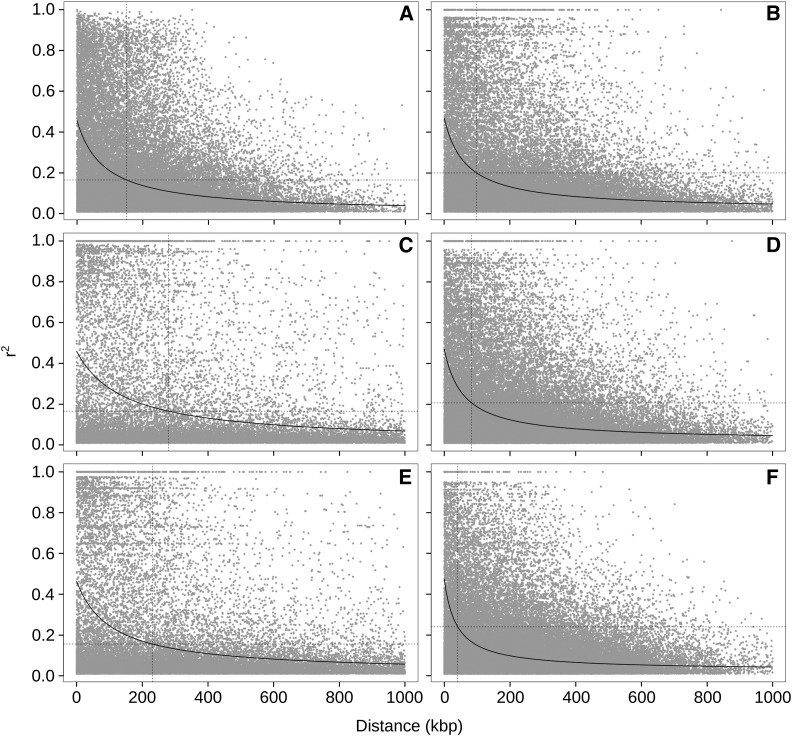
We next tested whether the five clusters also differ by the extent of genome-wide LD, which may reflect differences in the breeding history. Based on the method described by Breseghello and Sorrells (2006), we estimated background LD as intersecting with the nonlinear regression curve at ∼151 kbp (Figure 2). The extent of LD is influenced by population structure and history, and we therefore calculated LD parameters for each cluster. Clusters 1, 3, and 5 show a rapid decay in comparison with the whole population, with an average background LD of , and 0.24, extending to ∼98, ∼83, and ∼41 kbp (Figure 2). Clusters 2 and 4 have lower background LD values of 0.17 and 0.16, but higher long-range LD with averages of ∼280 and ∼231 kbp.
Figure 2.
LD decay in the whole population (A) and clusters 1–5 (B–F). The dashed horizontal line indicates the average background LD of all chromosomes of a respective population. The dashed vertical line indicates the maximum distance between linked markers and is used as reference point for the LD decay.
The average persistence of linkage phase is moderate between all clusters except for cluster 5, which reaches the expectation value of independent segregation (50%) for unlinked markers between clusters already at close distances in comparison with cluster 2 and cluster 4 (Figure S2 in File S1), indicating a stronger differentiation between those clusters.
GWAS of six yield-related traits
Since the accessions show a strong population structure, we conducted a GWAS with models that correct for population structure and used the λ parameter to assess how well a correction was achieved. Overall, both GWAS methods showed λ values close to 1 (reflecting a good correction) for all traits and data (imputed vs. unimputed; Table S5 in File S1), which shows that the two methods account sufficiently well for population structure.
In total, 24 SNPs are associated with at least one of the six curd-related traits (Figure S3 in File S1; FDR). With EMMAX, six of 675 unimputed SNPs were associated with the traits of curd width, cluster width, number of branches, and number of days to budding. Only three SNPs of the imputed data set were associated with number of days to budding using EMMAX. Significant SNPs between the imputed and unimputed data sets differ from each other; using the imputed SNPs we identified an additional putative major QTL on chromosome O6 (Figure S4 in File S1 and Table 1). MLMM identified nine SNPs associated with apical length, number of branches, nearest branch length, or number of days to budding using the unimputed data set, whereas in total six SNPs from the imputed data set were associated with either apical length or number of days to budding (Table 1).
Table 1. Overview of significant associations detected with EMMAX and MLMM.
| Rank | B. oleracea | A. thaliana | Variance explained | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Trait | Chr | Pos | Method | RR | BayesB | Gene ID | Ortholog | Description | Phenotypic | Genetic | MAF |
| Apical Length | 2 | 26,787,029 | MLMMI | 30,559 | 29,378 | Bol035969 | AtSec6 | Cell growth | 4.1 | 37.3 | 0.05 |
| Apical Length | 3 | 20,986,662 | MLMMI | 2397 | 1712 | Bol035507 | AT1G53730 | Protein coding | 11.6 | 105.3 | 0.03 |
| Apical Length | 6 | 4,914,166 | MLMMI | 4902 | 1785 | Bol032997 | — | Protein kinase | 10.6 | 96.0 | 0.08 |
| Apical Length | 6 | 34,494,415 | MLMMU | 2111 | 1194 | Bol040102 | AT1G71780 | Biological processes | 2.2 | 20.3 | 0.13 |
| Cluster Width | 2 | 5,063,181 | EMMAXU | 8 | 4 | Bol007138 | AT1G03220 | Proteolysis | 19.1 | 34.1 | 0.22 |
| Curd Width | 2 | 3,528,844 | EMMAXU | 1 | 1 | Bol021232 | AT5G19110 | Heat stress | 14.4 | 32.6 | 0.44 |
| Curd Width | 2 | 5,063,181 | EMMAXU | 6 | 4 | Bol007138 | AT1G03220 | Proteolysis | 12.1 | 27.4 | 0.22 |
| Length of Nearest Branch | 9 | 25,012,587 | MLMMU | 2 | 2 | Bol012235 | — | unknown | 7.9 | 158.7 | 0.06 |
| Number of Branches | 6 | 2,323,306 | EMMAXU | 2 | 2 | Bol035509 | AT1G75310 | Protein binding | 6.2 | 23.7 | 0.06 |
| Number of Branches | 6 | 2,323,306 | MLMMU | 2 | 2 | Bol035509 | AT1G75310 | Protein binding | 6.2 | 23.7 | 0.06 |
| Number of Branches | 7 | 41.524,584 | EMMAXU | 1 | 1 | Bol024369 | AT2G17050 | NBS gene family | 8.5 | 32.6 | 0.21 |
| Number of Branches | 7 | 41,524,584 | MLMMU | 1 | 1 | Bol024369 | AT2G17050 | NBS gene family | 8.5 | 32.6 | 0.21 |
| Number of Days to Budding | 1 | 37,688,065 | EMMAXU | 1 | 1 | Bol023068 | AT3G09240 | Signaling pathway | 13.5 | 14.4 | 0.2 |
| Number of Days to Budding | 1 | 37,688,065 | MLMMU | 1 | 1 | Bol023068 | AT3G09240 | Signaling pathway | 13.5 | 14.4 | 0.2 |
| Number of Days to Budding | 2 | 2,708,156 | MLMMU | 5 | 6 | Bol024638 | AT5G10090 | Flowering related | 16.4 | 17.4 | 0.57 |
| Number of Days to Budding | 2 | 2,708,163 | MLMMU | 6 | 5 | Bol024638 | AT5G65160 | Flowering related | 16.4 | 17.4 | 0.57 |
| Number of Days to Budding | 2 | 2,708,182 | MLMMU | 7 | 4 | Bol024638 | AT5G65180 | Flowering related | 16.4 | 17.4 | 0.57 |
| Number of Days to Budding | 6 | 2,949,314 | EMMAXI | 1861 | 572 | Bol026132 | AT1G75010 | Flowering | 25.2 | 26.8 | 0.05 |
| Number of Days to Budding | 6 | 2,949,314 | MLMMI | 1861 | 572 | Bol026132 | AT1G75010 | Flowering | 25.2 | 26.8 | 0.05 |
| Number of Days to Budding | 7 | 936,738 | EMMAXI | 2 | 5 | Bol027177 | — | unknown | 4.2 | 4.5 | 0.36 |
| Number of Days to Budding | 7 | 936,738 | MLMMI | 2 | 5 | Bol027177 | — | unknown | 4.2 | 4.5 | 0.36 |
| Number of Days to Budding | 7 | 936,770 | EMMAXI | 1 | 1 | Bol027177 | — | unknown | 6.4 | 6.8 | 0.23 |
| Number of Days to Budding | 7 | 936,770 | MLMMI | 1 | 1 | Bol027177 | — | unknown | 6.4 | 6.8 | 0.23 |
| Number of Days to Budding | 7 | 41,524,584 | MLMMU | 2 | 3 | Bol024369 | AT2G17050 | NBS gene family | 4.1 | 4.4 | 0.21 |
The Rank column indicates which rank the significant association had among marker effects in the genomic prediction with ridge regression (RR) or BayesB methods. The last letter in the Method column indicates in which data set the QTL was discovered (U, unimputed, I, imputed). Phenotypic and genotypic variance indicate the percentage of variance explained by the respective SNP. Chr, chromosome; MAF, minor allele frequency; Pos, position.
Of the 24 SNPs significantly associated with the six traits, six QTL were identified by EMMAX and by MLMM. Moreover, one SNP (C02:5063181) was associated with both curd width and cluster width. Another SNP (C07:41524584) was associated with number of days to budding and number of branches (Table 1). We identified minor-effect QTL related to apical length, number of branches, and nearest branch length. Taken together, the results indicate that the imputation slightly increased the number of significantly associated SNPs.
Further, we tested whether SNPs identified as significantly associated with phenotypic variation also contribute to population structure (expressed as high DAPC loadings using only the imputed data; Figure S5 and S6 in File S1). For the traits of curd width and cluster width, no significant SNP detected by the GWAS was linked to a SNP with a high DAPC loading (Figure S5 in File S1), but for number of days to budding the significant association detected on chromosome O6 is located close to SNPs with high DAPC loadings (Figure S6 in File S1). This suggests that SNPs linked with flowering time variation also contribute to population differentiation.
Genomic prediction with GBLUP and BayesB
Finally, we tested whether genomic prediction of phenotypic traits can be carried out with genetically diverse gene bank accessions to select new genetic resources for breeding purposes. The average prediction ability for each trait was calculated using five cross-validations with 10 replications; it ranged from 0.13 to 0.65 with GBLUP (Table 2) and from 0.09 to 0.66 with BayesB (Table 3) for the different traits and data sets. The prediction ability for RRBLUP was the same as for GBLUP, and we used RRBLUP estimates of marker effects for comparison with GWAS results. For all traits and both methods (GBLUP and BayesB), average prediction abilities were higher with imputed than with unimputed data, but the differences were minor (0.42 vs. 0.39).
Table 2. Prediction ability for six curd-related traits with different data sets using GBLUP.
| Imputed Data | |||||
|---|---|---|---|---|---|
| Trait | Unimputed Data | BEAGLE | fastPHASE | Corrected | Mean |
| Curd Width | 0.38 | 0.45 | 0.45 | 0.45 | 0.43 |
| Cluster Width | 0.62 | 0.65 | 0.65 | 0.59 | 0.63 |
| Number of Branches | 0.34 | 0.38 | 0.38 | 0.31 | 0.35 |
| Apical Length | 0.13 | 0.13 | 0.14 | 0.08 | 0.12 |
| Nearest Branch | 0.22 | 0.27 | 0.28 | 0.21 | 0.25 |
| Number of Days | 0.63 | 0.63 | 0.64 | 0.39 | 0.57 |
| Mean | 0.39 | 0.42 | 0.42 | 0.34 | 0.39 |
Unimputed: prediction ability using 675 SNPs. Imputed: prediction ability using BEAGLE and fastPHASE imputed data. Corrected: prediction ability for the GBLUP model with a realized relationship matrix corrected for population structure.
Table 3. Prediction ability for six curd-related traits with different data sets using BayesB.
| Imputed Data | ||||
|---|---|---|---|---|
| Trait | Unimputed Data | BEAGLE | fastPHASE | Mean |
| Curd Width | 0.35 | 0.40 | 0.44 | 0.40 |
| Cluster Width | 0.60 | 0.64 | 0.66 | 0.64 |
| Number of Branches | 0.38 | 0.35 | 0.41 | 0.38 |
| Apical Length | 0.09 | 0.12 | 0.10 | 0.10 |
| Nearest Branch | 0.23 | 0.28 | 0.29 | 0.26 |
| Number of Days | 0.66 | 0.66 | 0.61 | 0.64 |
| Mean | 0.39 | 0.41 | 0.42 | 0.40 |
Unimputed: prediction ability using 675 SNPs. Imputed: prediction ability using BEAGLE and fastPHASE imputed data.
With BayesB, prediction ability ranged from 0.09 to 0.66 (Table 3). Imputation resulted in slightly higher prediction abilities for all traits, except for number of days to budding. The prediction ability of fastPHASE was slightly higher than with BEAGLE for all traits except number of days to budding and apical length (Table 3). To compare the GWAS with the genomic prediction results, we ranked the marker effects estimated by RRBLUP and BayesB in descending order and compared them with the 24 significant associations detected by EMMAX and MLMM. Of these 24 SNPs, 18 also produced the largest marker effects and were among the top eight SNPs with the highest P-values in the GWAS (Table 1).
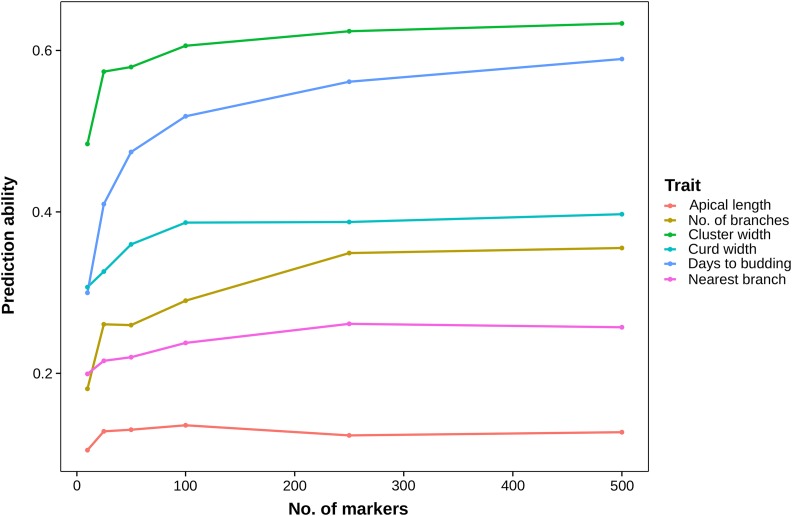
We assessed the influence of population structure on prediction ability using cross-validation. A correction for population structure resulted in a minor decrease in prediction ability for most traits, except curd width. The decrease in prediction ability was substantial for number of days to budding (0.64 to 0.39; Table 2). To test the influence of population structure on prediction ability, we randomly sampled subsets of markers and observed fairly high prediction abilities for small marker numbers (<100; Figure 3). Another approach to characterize the effect of population structure on prediction ability is to estimate the phenotypic variance explained by the first three principal components of a principal component analysis (Table S6 in File S1). According to this analysis, population structure had a strong effect on the genomic prediction ability of cluster width (40.01% variation explained by principal component 1), curd width (16.37% by principal component 1), and number of days to budding (27.66% by principal component 2). The variance explained by principal components was marginal for the other traits.
Figure 3.
Effect of increasing the number of markers, included in a five-fold cross-validation with 10 replications using a standard GBLUP model, on prediction ability. Values represent averages of 100 runs. 10, 25, 50, 100, 250 and 500 markers, respectively, were sampled randomly for each run.
Discussion
Phenotypic variation
Our sample of cauliflower accessions could be grouped into distinct genetic clusters that also differed in phenotypic traits. Heritability estimates of the traits of cluster width, curd width, and number of days to budding were similar to previous studies (Lan and Paterson 2000; Matschegewski et al. 2015) and indicate a sufficient quality of the field trial data for GWAS and genomic prediction. Heritabilities for number of branches, apical length, and nearest branch were very low, which reflects a low data quality or a more complex genetic architecture.
Strong population structure and differences in LD decay
A comparison of the population structure inferred by genetic markers and the passport data indicates limitations of available passport data. Among the 93 USDA accessions in the sample, 49 have a European origin according to their passport data. Of these, 24 (49%) cluster with the European accessions from IPK and the remaining 25 (51%) are distributed between cluster 1 (late flowering, geographically diverse accessions) and cluster 5 (predominately Asian accessions). This is unexpected under the assumption of a strong correlation between geographic origin and genetic relationship, but may be explained by incomplete passport data. Data about the seed donor but not the collection site were available for 79 of 93 USDA accessions (85%), and in these cases the true geographic origin could not be verified. For this reason, the analysis of genetic relationship allows a putative geographic origin of accessions to be assigned and can be used to complement missing passport data.
Genome-wide LD levels in the complete sample, which we measured as LD decay, were fairly high for an outcrossing species. The maximum physical distance for genetic linkage is reached at 151 kbp using the whole population. This value is comparable with that of self-fertilizing species, but lower than a previous estimate for cauliflower of up to 400 kbp (Matschegewski et al. 2015). A comparison of LD decay and background LD for the complete sample and each inferred cluster revealed differences between these groups. For example, the high LD in clusters 2 and 4 that consist mainly of European cultivars suggests that breeding and small population size likely contributed to the observed differences.
The highest level of long-range LD is located on chromosome O4 in accessions of clusters 2 and 4 (data not shown). This chromosome harbors multiple paralogs of the BolbZIP gene family, which is involved into cold stress tolerance (Hwang et al. 2016). Although this trait was not evaluated in our field trials, we hypothesize that selection for cold tolerance in European varieties may explain the higher level of LD.
Finally, we compared the persistence of linkage phase between clusters (Figure S2 in File S1). The proportion of markers in the same linkage phase was moderate between most clusters, but slightly lower between clusters 2 and 5 and clusters 4 and 5, which indicates that genomic prediction ability is mainly influenced by the genetic relationship of individuals and not by a persistent linkage of marker alleles with causal QTL in different clusters.
Significant marker–trait associations in a GWAS of traits with a high heritability
The phenotypic differences in flowering time and curd width between genetic clusters suggest a genetic basis for these differences. We used two GWAS methods for the imputed and unimputed SNP data to map QTL controlling these traits and identified 24 SNPs that were associated with at least one of the six phenotypic traits. The genomic locations of SNPs associated with flowering time (e.g., time to budding) coincide well with QTL regions identified in previous studies. For example, a SNP on chromosome O6 explained 26.8% of variation and was close to a QTL detected by Hasan et al. (2016). Another SNP found on chromosome O2 explains 16.4% of the phenotypic variation for the same trait and maps to a known QTL (Okazaki et al. 2007; Uptmoor et al. 2008; Matschegewski et al. 2015). The last of these studies also demonstrated the influence of QTL on chromosome O2 on time to flowering. The QTL region harbors a homolog of the A. thaliana Flowering Locus C (FLC) gene, which controls vernalization and has a major influence on flowering time.
A third SNP on chromosome O1 explained 13.5% of genetic variation. It is located in a genomic region that harbors an ortholog to the A. thaliana the flowering time gene VRN1 (Matschegewski et al. 2015). Additional SNPs that explain a minor proportion of the genetic variation for flowering time are located on chromosome O7 but have not been described in literature.
The GWAS also identified three polymorphisms on chromosome O2 that are associated with curd width and cluster width. Strongly associated polymorphisms overlapped for these traits, which can be explained by the fact that the two traits are highly correlated with each other (Table S3 in File S1). The SNPs explain between 27.4 and 34.1% of the genetic variation and therefore seem to be linked to a major QTL. These SNPs are located in genes whose A. thaliana orthologs regulate response to heat stress, which is consistent with the observation that temperature has a strong effect on cauliflower curd development (Matschegewski et al. 2015). Hasan et al. (2016) identified a QTL on the same chromosome (O2), which was only expressed under high-temperature conditions (27°).
The differences between the two GWAS methods (EMMAX and MLMM) may result from the small sample size. Sample size has a great influence on detection power for complex traits in GWAS (Korte and Farlow 2013). However, small samples are sufficient to detect major QTL, because simulations show that QTL explaining 10% of genetic variance can be identified in a sample of 100 genotypes (Gawenda et al. 2015). As an example, a flowering time QTL caused by variation in the vernalization response gene FRIGIDA was found in a sample of only 107 natural accessions of A. thaliana (Atwell et al. 2010). We therefore consider our sample of 174 individuals sufficiently large to reliably detect major QTL for highly heritable traits such as flowering time regulation, curd width, and cluster width.
Evaluation of genomic prediction in cauliflower genetic resources
Genomic prediction is a useful method for characterizing gene bank accessions, because it may allow phenotyping to be restricted to a subset of accessions in order to predict trait values for the complete collection. We used GBLUP and BayesB for prediction, because these models have a good performance, stable prediction ability, and are suited for different genetic architectures (Meuwissen et al. 2001; Heslot et al. 2012). Genomic prediction worked best for traits with a high heritability such as number of days to budding and cluster width, and less well for the traits of apical length and length of nearest branch (Table 2 and Table 3). In addition to a low heritability, the precise phenotyping of the latter two traits is challenging, and measurement errors result in biased estimates of variance components and adjusted means that affect prediction ability.
Since this is the first study that uses genomic prediction in cauliflower, we can only compare our results with those for other Brassica species. Prediction abilities for number of days to budding and curd width are similar to those for flowering time (0.70) and grain yield (0.50) in rapeseed (B. napus) (Würschum et al. 2014), a close relative of B. oleracea, which suggests that genomic selection is a robust and promising breeding method for Brassica species. Prediction ability is influenced by the presence of population structure (Thorwarth et al. 2017). If both training and validation sets for genomic selection show a population structure, a correction for structure reduces prediction ability (Guo et al. 2014). The effect of population structure on prediction ability depends on the trait. For the trait days to budding, prediction ability decreased from 0.64 to 0.39 after correction, whereas a correction had no effect on prediction ability of the other five traits.
The strong effect of structure correction on prediction ability for flowering is consistent with our observation that this trait differs significantly between genetic clusters. Mainly loci close to the putative QTL on chromosome O6 seem to contribute to population differentiation (measured as high loading values in the DAPC analysis) and are close to SNPs linked to flowering time QTL in the GWAS. This indicates that selection for different flowering time or adaption to different areas contributed to the genetic population structure (Matschegewski et al. 2015). For the other traits such as curd with or cluster width there is no such overlap, which may be explained by a more complex genetic architecture of these traits.
Genomic prediction models simultaneously utilize all SNPs for calculating the breeding value. RRBLUB and BayesB estimate marker effects, which can be used for comparison with GWAS models that consider each SNP separately. We found strong overlaps of significant SNPs in the GWAS, with the highest marker effects obtained from the genomic prediction models (Table 1). This overlap reflects the similarity of the statistical models used for GWAS and genomic prediction, and suggests that these SNPs are linked to robust QTL. In summary, a comparison of putative causal SNPs identified by GWAS, the estimation of marker effects in genomic prediction, and the analysis of allele contribution to population structure (DAPC loading) may be considered as validation of significant marker–trait associations and provides useful information to improve genetic analysis (Spindel et al. 2016; Bian and Holland 2017).
The success of genomic prediction depends on the method used and the size of the training set. We observed only minor differences between GBLUP and BayesB regarding their mean prediction ability over all traits and data sets (Table 2 and Table 3). This observation confirms earlier work that Bayesian models do not outperform GBLUP (Bao et al. 2014). Since GBLUP is computationally less expensive and much simpler to implement than BayesB, our results suggest that GBLUP can be recommended for genomic selection in cauliflower breeding. The size of the training set is another point to consider, because larger training sets improve prediction ability and allow a robust estimation of marker effects (Windhausen et al. 2012). We provide a first assessment of genomic prediction in a small sample of genetically diverse cauliflower gene bank material, but larger training sets are required, especially for traits with a complex genetic architecture (>1000; Thorwarth et al. 2017).
Imputation effect on GWAS and genomic prediction results
Although GBS is an efficient method for obtaining large numbers of polymorphisms, the resulting data have a high proportion of missing values. Imputation of missing data may be used to overcome this limitation. In our GWAS analysis, we obtained fewer significant associations (10) with the imputed data than with unimputed data (14; Figure S3 in File S1). However, imputation may improve the power of GWAS because in the imputed data only we identified one additional QTL for flowering time on chromosome O6, which was also found by Hasan et al. (2016). However, several QTL observed in the unimputed data were not identified in the imputed data. One explanation for this discrepancy is significance levels that are based on marker number. For quantitative traits that are influenced by QTL with small effects, a Bonferroni correction of P-values in GWAS may be too conservative and result in a high proportion of false negatives (Perneger 1998). Therefore, we used the FDR, which is the expected proportion of significant associations that are false positives. It is defined as , where i is the rank of the ascending P-values, n is the number of markers (tests), and Q is the FDR (Benjamini and Hochberg 1995). We used a FDR of 0.05, which implies that 20% of the observed significant associations are false positives. A smaller or higher Q value will lead to a more stringent or a more relaxed threshold, respectively. For example, with an FDR value 5% we observed 10 and with an FDR of 30% we obtained a total of 35 significant associations with EMMAX and MLMM. It should be noted that FDR thresholds are specific for each combination of traits and data sets, and for this reason the identification and implementation of optimal significance thresholds is still debated (Sham and Purcell 2014). Thus, a careful assessment of different thresholds together with the ranking of marker effects and a comparison of the DAPC loadings can help to improve the conclusions drawn from GWAS studies and validate the robustness of putative QTL.
The difference in the number of significant associations between the unimputed and imputed data sets is also influenced by the imputation method. The fastPHASE method is not well suited for GBS data, because a parameter vector of allele frequencies has to be estimated for each SNP. As fastPHASE performs best with SNPs genotyped in many individuals (Scheet and Stephens 2006), the high proportion of missing data reduces the average number of individuals available per SNP. As the second imputation method, we used BEAGLE, which performs well with medium to large sample sizes (>1000 individuals), but not as well as fastPHASE when compared for small samples of 100 individuals, as demonstrated by Browning and Browning (2011). The clustering approach of BEAGLE flexibly changes cluster numbers to better accommodate local LD patterns, but in general neither method can cope very well with a large amount of missing data as observed in this study (Yang et al. 2014; Xavier et al. 2016).
The imputation of missing markers slightly improved prediction ability for most traits, consistent with previous studies that revealed only minor advantages of imputation, particularly in self-fertilizing crops with a slow LD decay (Rutkoski et al. 2013; Poland et al. 2012a; Jarquín et al. 2014). Prediction ability is mainly determined by relatedness and less by linkage between marker and QTL, as indicated by the linkage phase analysis. For this reason, imputation has little influence on prediction ability, because small numbers of high-quality SNPs are sufficient to capture the relationship structure among individuals.
In summary, there was only a minor advantage of imputation for GWAS and genomic prediction with our sample. However, the rapid development of genome sequencing technologies and rapidly decreasing costs will alleviate the problem of missing data for genomic prediction, as genome resequencing will uncover most genetic variation, in particular for crops with small genome sizes such as B. oleracea (Golicz et al. 2016).
Implications for the utilization of genomic resources
Breeding populations of cauliflower are characterized by a low genetic diversity (Golicz et al. 2016), which limits the potential for improving varieties that meet the expectations of growers and consumers. We showed that both GWAS and genomic prediction contribute to the genetic analysis of complex traits and to the identification of novel and potentially useful genetic variation in gene bank material (Yu et al. 2016). Our study also provides a perspective with respect to the utilization of ex situ conserved gene bank accessions. Our sample was randomly selected and represents a broad genetic and geographic diversity. We achieved reasonable genomic prediction abilities, although genetic clustering inflates prediction ability if the cluster structure is correlated with trait distribution. For this reason, genotyping whole collections of gene bank accessions and the phenotyping of a sufficiently large subset allows the prediction of relevant phenotypic traits in the whole collection and the subsequent selection of accessions for further use as genetic resources. This will contribute to an efficient description and utilization of ex situ conserved germplasm resources.
Supplementary Material
Supplemental material is available online at www.g3journal.org/lookup/suppl/doi:10.1534/g3.117.300199/-/DC1.
Acknowledgments
We thank Thomas Müller for his support in genotypic data analysis. We are grateful to the USDA and IPK gene banks for sending us the seeds. This work was funded by a DAAD GERLS Fellowship to E.A.A.Y. and an endowment of the Stifterverband der Deutschen Wissenschaft to K.J.S. The authors declare that they have no conflict of interest.
Author contributions: P.T., E.A.A.Y., and K.J.S. designed the study. E.A.A.Y. analyzed the phenotypic data. P.T. performed the remaining analyses (population structure, LD, GWAS, genomic selection, and imputation). P.T. and E.A.A.Y. wrote the first version of the manuscript. P.T. and K.J.S. wrote the final version of the manuscript.
Footnotes
Communicating editor: J.-L. Jannink
Literature Cited
- Atwell S., Huang Y. S., Vilhjálmsson B. J., Willems G., Horton M., et al. , 2010. Genome-wide association study of 107 phenotypes in a common set of Arabidopsis thaliana inbred lines. Nature 465: 627–631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao Y., Vuong T., Meinhardt C., Tiffin P., Denny R., et al. , 2014. Potential of association mapping and genomic selection to explore PI 88788 derived soybean cyst nematode resistance. Plant Genome 7 DOI:10.3835/plantgenome2013.11.0039 [Google Scholar]
- Bates D., Maechler M., Bolker B., Walker S., 2014. lme4: linear mixed-effects models using Eigen and S4. R package version 1: 1–23. [Google Scholar]
- Benjamini Y., Hochberg Y., 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57: 289–300. [Google Scholar]
- Bevan M. W., Uauy C., Wulff B. B., Zhou J., Krasileva K., et al. , 2017. Genomic innovation for crop improvement. Nature 543: 346–354. [DOI] [PubMed] [Google Scholar]
- Bian Y., Holland J., 2017. Enhancing genomic prediction with genome-wide association studies in multiparental maize populations. Heredity 118: 585–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breseghello F., Sorrells M. E., 2006. Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics 172: 1165–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning S. R., Browning B. L., 2007. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am. J. Hum. Genet. 81: 1084–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning S. R., Browning B. L., 2011. Haplotype phasing: existing methods and new developments. Nat. Rev. Genet. 12: 703–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai D., Xiao Y., Yang W., Ye W., Wang B., et al. , 2014. Association mapping of six yield-related traits in rapeseed (Brassica napus L.). Theor. Appl. Genet. 127: 85–96. [DOI] [PubMed] [Google Scholar]
- Conomos M. P., Reiner A. P., Weir B. S., Thornton T. A., 2016. Model-free estimation of recent genetic relatedness. Am. J. Hum. Genet. 98: 127–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., Campos G. l., Perez P., Gianola D., Burgueno J., et al. , 2010. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 186: 713–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., Beyene Y., Kassa S., Perez P., Hickey J. M., et al. , 2013. Genomic prediction in maize breeding populations with genotyping-by-sequencing. G3(Bethesda) 3: 1903–1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Roos A. P. W., Hayes B. J., Spelman R. J., Goddard M. E., 2008. Linkage disequilibrium and persistence of phase in Holstein-Friesian, Jersey and Angus cattle. Genetics 179: 1503–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin B., Roeder K., 1999. Genomic control for association studies. Biometrics 55: 997–1004. [DOI] [PubMed] [Google Scholar]
- Edae E. A., Byrne P. F., Haley S. D., Lopes M. S., Reynolds M. P., 2014. Genome-wide association mapping of yield and yield components of spring wheat under contrasting moisture regimes. Theor. Appl. Genet. 127: 791–807. [DOI] [PubMed] [Google Scholar]
- Elshire R. J., Glaubitz J. C., Sun Q., Poland J. A., Kawamoto K., et al. , 2011. A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS One 6: e19379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y.-B., Cheng B., Peterson G. W., 2014. Genetic diversity analysis of yellow mustard (Sinapis alba L.) germplasm based on genotyping by sequencing. Genet. Resour. Crop Evol. 61: 579–594. [Google Scholar]
- Gawenda I., Thorwarth P., Günther T., Ordon F., Schmid K. J., 2015. Genome-wide association studies in elite varieties of German winter barley using single-marker and haplotype-based methods. Plant Breed. 134: 28–39. [Google Scholar]
- Golicz A. A., Bayer P. E., Barker G. C., Edger P. P., Kim H., et al. , 2016. The pangenome of an agronomically important crop plant Brassica oleracea. Nat. Commun. 7: 13390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Z., Tucker D. M., Basten C. J., Gandhi H., Ersoz E., et al. , 2014. The impact of population structure on genomic prediction in stratified populations. Theor. Appl. Genet. 127: 749–762. [DOI] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Garrick D. J., 2013. Genomic BLUP decoded: a look into the black box of genomic prediction. Genetics 194: 597–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan M., Friedt W., Pons-Kühnemann J., Freitag N. M., Link K., et al. , 2008. Association of gene-linked SSR markers to seed glucosinolate content in oilseed rape (Brassica napus ssp. napus). Theor. Appl. Genet. 116: 1035–1049. [DOI] [PubMed] [Google Scholar]
- Hasan Y., Briggs W., Matschegewski C., Ordon F., Stützel H., et al. , 2016. Quantitative trait loci controlling leaf appearance and curd initiation of cauliflower in relation to temperature. Theor. Appl. Genet. 129: 1273–1288. [DOI] [PubMed] [Google Scholar]
- Hawkes J., 1991. The importance of genetic resources in plant breeding. Biological Journal of the Linncan Society 43: 3–10. [Google Scholar]
- Hayes B., Bowman P., Chamberlain A., Goddard M., 2009. Invited review: genomic selection in dairy cattle: progress and challenges. J. Dairy Sci. 92: 433–443. [DOI] [PubMed] [Google Scholar]
- Heffner E. L., Sorrells M. E., Jannink J.-L., 2009. Genomic selection for crop improvement. Crop Sci. 49: 1. [Google Scholar]
- Heffner E. L., Lorenz A. J., Jannink J.-L., Sorrells M. E., 2010. Plant breeding with genomic selection: gain per unit time and cost. Crop Sci. 50: 1681. [Google Scholar]
- Heslot N., Yang H.-P., Sorrells M. E., Jannink J.-L., 2012. Genomic selection in plant breeding: a comparison of models. Crop Sci. 52: 146. [Google Scholar]
- Hwang I., Manoharan R. K., Kang J.-G., Chung M.-Y., Kim Y.-W., et al. , 2016. Genome-wide identification and characterization of bzip transcription factors in Brassica oleracea under cold stress. BioMed Res. Int. 2016: 4376598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jannink J.-L., Lorenz A. J., Iwata H., 2010. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9: 166–177. [DOI] [PubMed] [Google Scholar]
- Jarquín D., Kocak K., Posadas L., Hyma K., Jedlicka J., et al. , 2014. Genotyping by sequencing for genomic prediction in a soybean breeding population. BMC Genomics 15: 740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jestin C., Lodé M., Vallée P., Domin C., Falentin C., et al. , 2011. Association mapping of quantitative resistance for Leptosphaeria maculans in oilseed rape (Brassica napus L.). Mol. Breed. 27: 271–287. [Google Scholar]
- Jombart T., Ahmed I., 2011. Adegenet 1.3–1: new tools for the analysis of genome-wide SNP data. Bioinformatics 27: 3070–3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H. M., Sul J. H., Service S. K., Zaitlen N. A., Kong S.-y., et al. , 2010. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 42: 348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korte A., Farlow A., 2013. The advantages and limitations of trait analysis with gwas: a review. Plant Methods 9: 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- König S., Simianer H., Willam A., 2009. Economic evaluation of genomic breeding programs. J. Dairy Sci. 92: 382–391. [DOI] [PubMed] [Google Scholar]
- Lan T.-H., Paterson A. H., 2000. Comparative mapping of quantitative trait loci sculpting the curd of Brassica oleracea. Genetics 155: 1927–1954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F., Chen B., Xu K., Wu J., Song W., et al. , 2014. Genome-wide association study dissects the genetic architecture of seed weight and seed quality in rapeseed (Brassica napus L.). DNA Res. 21: 355–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Peng Z., Yang X., Wang W., Fu J., et al. , 2012. Genome-wide association study dissects the genetic architecture of oil biosynthesis in maize kernels. Nat. Genet. 45: 43–50. [DOI] [PubMed] [Google Scholar]
- Li H., Liu Q., Zhang Q., Qin E., Jin C., et al. , 2017. Curd development associated gene (cdag1) in cauliflower (Brassica oleracea l. var. botrytis) could result in enlarged organ size and increased biomass. Plant Sci. 254: 82–94. [DOI] [PubMed] [Google Scholar]
- Liu S., Liu Y., Yang X., Tong C., Edwards D., et al. , 2014. The Brassica oleracea genome reveals the asymmetrical evolution of polyploid genomes. Nat. Commun. 5: 3930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longin C. F. H., Reif J. C., 2014. Redesigning the exploitation of wheat genetic resources. Trends Plant Sci. 19: 631–636. [DOI] [PubMed] [Google Scholar]
- Marchini J., Howie B., 2010. Genotype imputation for genome-wide association studies. Nat. Rev. Genet. 11: 499–511. [DOI] [PubMed] [Google Scholar]
- Matschegewski C., Zetzsche H., Hasan Y., Leibeguth L., Briggs W., et al. , 2015. Genetic variation of temperature-regulated curd induction in cauliflower: elucidation of floral transition by genome-wide association mapping and gene expression analysis. Front. Plant Sci. 6: 720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H., Hayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris G. P., Rhodes D. H., Brenton Z., Ramu P., Thayil V. M., et al. , 2013. Dissecting genome-wide association signals for loss-of-function phenotypes in sorghum flavonoid pigmentation traits. G3(Bethesda) 3: 2085–2094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton G. J., Douglas A., Lahner B., Yakubova E., Guerinot M. L., et al. , 2014. Genome wide association mapping of grain arsenic, copper, molybdenum and zinc in rice (Oryza sativa L.) grown at four international field sites. PLoS One 9: e89685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyquist W. E., Baker R., 1991. Estimation of heritability and prediction of selection response in plant populations. Crit. Rev. Plant Sci. 10: 235–322. [Google Scholar]
- Okazaki K., Sakamoto K., Kikuchi R., Saito A., Togashi E., et al. , 2007. Mapping and characterization of FLC homologs and QTL analysis of flowering time in Brassica oleracea. Theor. Appl. Genet. 114: 595–608. [DOI] [PubMed] [Google Scholar]
- Pei Y.-F., Li J., Zhang L., Papasian C. J., Deng H.-W., 2008. Analyses and comparison of accuracy of different genotype imputation methods. PLoS One 3: e3551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez P., de los Campos G., 2014. Genome-wide regression and prediction with the BGLR statistical package. Genetics 198: 483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perneger T. V., 1998. What’s wrong with Bonferroni adjustments. BMJ 316: 1236–1238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picchi V., Migliori C., Scalzo R. L., Campanelli G., Ferrari V., et al. , 2012. Phytochemical content in organic and conventionally grown Italian cauliflower. Food Chem. 130: 501–509. [DOI] [PubMed] [Google Scholar]
- Poland J., Endelman J., Dawson J., Rutkoski J., Wu S., et al. , 2012a Genomic selection in wheat breeding using genotyping-by-sequencing. The Plant Genome Journal 5: 103. [Google Scholar]
- Poland J. A., Rife T. W., 2012. Genotyping-by-sequencing for plant breeding and genetics. The Plant Genome Journal 5: 92. [Google Scholar]
- Poland J. A., Brown P. J., Sorrells M. E., Jannink J.-L., 2012b Development of high-density genetic maps for barley and wheat using a novel two-enzyme genotyping-by-sequencing approach. PLoS One 7: e32253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M. A. R., et al. , 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81: 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team , 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. [Google Scholar]
- Rezaeizad A., Wittkop B., Snowdon R., Hasan M., Mohammadi V., et al. , 2011. Identification of QTLs for phenolic compounds in oilseed rape (Brassica napus L.) by association mapping using SSR markers. Euphytica 177: 335–342. [Google Scholar]
- Romay M. C., Millard M. J., Glaubitz J. C., Peiffer J. A., Swarts K. L., et al. , 2013. Comprehensive genotyping of the USA national maize inbred seed bank. Genome Biol. 14: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutkoski J. E., Poland J., Jannink J.-L., Sorrells M. E., 2013. Imputation of unordered markers and the impact on genomic selection accuracy. G3(Bethesda) 3: 427–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer L. R., 2006. Strategy for applying genome-wide selection in dairy cattle. J. Anim. Breed. Genet. 123: 218–223. [DOI] [PubMed] [Google Scholar]
- Scheet P., Stephens M., 2006. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am. J. Hum. Genet. 78: 629–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid K., Thorwarth P., 2014. Genomic selection in barley breeding. Springer Berlin Heidelberg 69: 367–378. [Google Scholar]
- Segura V., Vilhjálmsson B. J., Platt A., Korte A., Seren U., et al. , 2012. An efficient multi-locus mixed-model approach for genome-wide association studies in structured populations. Nat. Genet. 44: 825–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham P. C., Purcell S. M., 2014. Statistical power and significance testing in large-scale genetic studies. Nat. Rev. Genet. 15: 335–346. [DOI] [PubMed] [Google Scholar]
- Sonah H., Bastien M., Iquira E., Tardivel A., Légaré G., et al. , 2013. An improved genotyping by sequencing (GBS) approach offering increased versatility and efficiency of SNP discovery and genotyping. PLoS One 8: e54603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spindel J., Begum H., Akdemir D., Collard B., Redona E., et al. , 2016. Genome-wide prediction models that incorporate de novo gwas are a powerful new tool for tropical rice improvement. Heredity 116: 395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tardivel A., Sonah H., Belzile F., O’Donoughue L. S., 2014. Rapid identification of alleles at the soybean maturity gene E3 using genotyping by sequencing and a haplotype-based approach. Plant Genome 7 DOI:10.3835/plantgenome2013.10.0034 [Google Scholar]
- Tester M., Langridge P., 2010. Breeding technologies to increase crop production in a changing world. Science 327: 818–822. [DOI] [PubMed] [Google Scholar]
- Thorwarth P., Ahlemeyer J., Bochard A.-M., Krumnacker K., Blümel H., et al. , 2017. Genomic prediction ability for yield-related traits in German winter barley elite material. Theor. Appl. Genet. 130: 1669–1683. [DOI] [PubMed] [Google Scholar]
- Uptmoor R., Schrag T., Stützel H., Esch E., 2008. Crop model based QTL analysis across environments and QTL based estimation of time to floral induction and flowering in Brassica oleracea. Mol. Breed. 21: 205–216. [Google Scholar]
- Utz H. F., Melchinger A. E., Schön C. C., 2000. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics 154: 1839–1849. [PMC free article] [PubMed] [Google Scholar]
- VanLiere J., Rosenberg N., 2008. Mathematical properties of the r2 measure of linkage disequilibrium. Theor. Popul. Biol. 74: 130–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wimmer V., Albrecht T., Auinger H.-J., Schon C.-C., 2012. Synbreed: a framework for the analysis of genomic prediction data using R. Bioinformatics 28: 2086–2087. [DOI] [PubMed] [Google Scholar]
- Windhausen V. S., Atlin G. N., Hickey J. M., Crossa J., Jannink J.-L., et al. , 2012. Effectiveness of genomic prediction of maize hybrid performance in different breeding populations and environments. Genetics 2: 1427–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Würschum T., Abel S., Zhao Y., 2014. Potential of genomic selection in rapeseed (Brassica napus L.) breeding. Plant Breed. 133: 45–51. [Google Scholar]
- Xavier A., Muir W. M., Rainey K. M., 2016. Impact of imputation methods on the amount of genetic variation captured by a single-nucleotide polymorphism panel in soybeans. BMC Bioinformatics 17: 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y., Wang Q., Chen Q., Liao R., Zhang X., et al. , 2014. A new genotype imputation method with tolerance to high missing rate and rare variants. PLoS One 9: e101025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousef E. A. A., Lampei C., Schmid K. J., 2015. Evaluation of cauliflower genebank accessions under organic and conventional cultivation in Southern Germany. Euphytica 201: 389–400. [Google Scholar]
- Yousef T., Müller T., Schmid K. J., 2017. Comparative analysis of genetic diversity and differentiation of cauliflower (Brassica oleracea var. botrytis) accessions from two ex situ genebanks. bioRxiv. https//.org/10.1101/238840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X., Li X., Guo T., Zhu C., Wu Y., et al. , 2016. Genomic prediction contributing to a promising global strategy to turbocharge gene banks. Nat. Plants 2: 16150. [DOI] [PubMed] [Google Scholar]
- Zhao Z., Gu H., Sheng X., Yu H., Wang J., et al. , 2016. Genome-wide single-nucleotide polymorphisms discovery and high-density genetic map construction in cauliflower using specific-locus amplified fragment sequencing. Front. Plant Sci. 7: 334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou J., Jiang C., Cao Z., Li R., Long Y., et al. , 2010. Association mapping of seed oil content in Brassica napus and comparison with quantitative trait loci identified from linkage mapping. Genome 53: 908–916. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Raw sequence data have been submitted to the Sequence Read Archive under accession number PRJEB8701. SNP calls are available on figshare at https://doi.org/10.6084/m9.figshare.5709784. Best Linear Unbiased Estimators (BLUEs) of phenotypic data are provided as supplementary material (File S2).