Abstract
Salmonid rickettsial syndrome (SRS), caused by the intracellular bacterium Piscirickettsia salmonis, is one of the main diseases affecting rainbow trout (Oncorhynchus mykiss) farming. To accelerate genetic progress, genomic selection methods can be used as an effective approach to control the disease. The aims of this study were: (i) to compare the accuracy of estimated breeding values using pedigree-based best linear unbiased prediction (PBLUP) with genomic BLUP (GBLUP), single-step GBLUP (ssGBLUP), Bayes C, and Bayesian Lasso (LASSO); and (ii) to test the accuracy of genomic prediction and PBLUP using different marker densities (0.5, 3, 10, 20, and 27 K) for resistance against P. salmonis in rainbow trout. Phenotypes were recorded as number of days to death (DD) and binary survival (BS) from 2416 fish challenged with P. salmonis. A total of 1934 fish were genotyped using a 57 K single-nucleotide polymorphism (SNP) array. All genomic prediction methods achieved higher accuracies than PBLUP. The relative increase in accuracy for different genomic models ranged from 28 to 41% for both DD and BS at 27 K SNP. Between different genomic models, the highest relative increase in accuracy was obtained with Bayes C (∼40%), where 3 K SNP was enough to achieve a similar accuracy to that of the 27 K SNP for both traits. For resistance against P. salmonis in rainbow trout, we showed that genomic predictions using GBLUP, ssGBLUP, Bayes C, and LASSO can increase accuracy compared with PBLUP. Moreover, it is possible to use relatively low-density SNP panels for genomic prediction without compromising accuracy predictions for resistance against P. salmonis in rainbow trout.
Keywords: disease resistance, genomic selection, Oncorhynchus mykiss, reliability, GenPred, Shared Data Resources
In 1989, Piscirickettsia salmonis was identified as a pathogenic bacterium causing salmonid rickettsial syndrome (SRS) in farmed coho salmon (Oncorhynchus kisutch) in Chile (Branson and Diaz-Munoz 1991; Cvitanich et al. 1991). Since then, P. salmonis has been confirmed as the causative agent for SRS in coho salmon, Atlantic salmon (Salmo salar), and rainbow trout (Oncorhynchus mykiss) in several countries, including Norway, Canada, Scotland, Ireland, and Chile (Fryer and Hedrick 2003; Rozas and Enríquez 2014). The economic losses related to SRS in Chile in the year 2012 were US$450 million, owing to mortality, antibiotic treatment, and vaccinations (Camussetti et al. 2015)
Currently, treatment for bacterial diseases in the aquaculture industry is predominantly based on antibiotics (Peña et al. 2016). Although several vaccines are available for prevention of SRS, none of them provide complete protection against P. salmonis in field conditions (Kuzyk et al. 2001; Tobar et al. 2011). In addition, selective breeding can be used to alleviate disease problems. The levels of genetic variation for resistance to P. salmonis, with heritability values ranging from 0.11 to 0.41, have demonstrated the feasibility to improve the trait by means of artificial selection in salmon breeding populations (Yáñez et al. 2013, 2014, 2016a; Lhorente et al. 2014).
With the recent advances in genotyping methods and the development of single-nucleotide polymorphism (SNP) panels for salmonids (Houston et al. 2014; Palti et al. 2015; Yáñez et al. 2016b; Macqueen et al. 2017), genetic markers linked with quantitative trait loci (QTL) can be identified and implemented in breeding programs through marker-assisted selection (MAS) (Yáñez et al. 2014). For example, in Atlantic salmon, one major QTL for infectious pancreatic necrosis virus resistance was detected, explaining 29 and 83% of the phenotypic and genetic variances, respectively (Gheyas et al. 2010; Houston et al. 2010, 2008a,b). This QTL has been successfully used in MAS programs in this species (Moen et al. 2015). However, genome-wide association studies (GWAS) in Atlantic salmon suggested that resistance against P. salmonis is a trait with moderate polygenic control, with many markers explaining a small proportion of the genetic variance (Correa et al. 2015). The complexity of this trait and the absence of QTL with major effects suggest that the implementation of MAS could be not successful in this particular case. By contrast, genomic selection (GS) will be the most appropriate way to incorporate the genomic information and accelerate the genetic progress for traits where the markers have small effects.
Genomic evaluations using dense SNP markers have been shown to increase accuracy of estimated breeding values (EBV) compared with pedigree-based methods for different economically important traits in Atlantic salmon (Ødegård et al. 2014; Tsai et al. 2015, 2016; Bangera et al. 2017; Correa et al. 2017; Sae-Lim et al. 2017) and rainbow trout (Vallejo et al. 2016, 2017). Different GS methods have been tested and prediction accuracy varies depending on the method used, which mainly differ with respect to the assumption about marker effects and the genetic relationship matrix calculation. The genomic best linear unbiased predictor (GBLUP) assumes that all marker effects come from a normal distribution (Meuwissen et al. 2001; VanRaden 2008), and the relationship matrix is calculated using genomic information only. The single-step GBLUP (ssGBLUP) assumes the same normal distribution for marker effects; however, it uses a combination of pedigree and genomic information to determine the additive genetic relationship matrix (Aguilar et al. 2010). In general, Bayesian methods assume more flexible and nonnormal distributed marker effects. For instance, the Bayes C method assumes that SNP effects have independent and identical mixture distributions (Habier et al. 2011), whereas the Bayesian Lasso (LASSO) assumes a double exponential prior distribution for variances of SNP marker effects (Aguilar et al. 2010).
The performances of the different GS methods have been tested for different livestock species and traits (Hayes et al. 2010; Colombani et al. 2013; Chen et al. 2014; Neves et al. 2014). The best method in terms of accuracy will depend on some factors, such as the number of phenotyped animals, heritability, effective population size, size of the genome, marker density, and genetic architecture of the trait (Daetwyler et al. 2008; Goddard 2009; Meuwissen 2009). In general, Bayesian methods outperform the GBLUP method for traits that are affected by a few large QTL, whereas for traits that are affected by many QTL with small effects, GBLUP would likely perform better than or similar to the Bayesian methods (Chen et al. 2014). Furthermore, Hayes et al. (2010) suggested that results obtained from cattle may not be relevant for other species, owing to the larger linkage disequilibrium (LD) blocks in bovine than other species.
Therefore, it is valuable to compare the accuracies of different GS methodologies to identify the method that will result in the highest accuracy for the genetic evaluation of resistance to one of the most important bacterial diseases affecting sea rearing of rainbow trout, which in turn is one of the most widely distributed aquaculture species in the world. In addition, GS can be implemented using a cost-effective individual genotyping strategy using low-density panels without much loss of information (Cleveland and Hickey 2013). Recent empirical studies have demonstrated that low-density panels are sufficient to get higher accuracy using genomic EBV (GEBV) than EBV obtained from pedigree-based BLUP (PBLUP) for resistance against P. salmonis (Bangera et al. 2017) and sea lice (Tsai et al. 2016; Correa et al. 2017) in Atlantic salmon.
The objectives of this study were: (i) to compare the accuracy of EBV using PBLUP with that using GBLUP, ssGBLUP, Bayes C, and LASSO; and (ii) to test the accuracy of genomic prediction and PBLUP using different marker densities (0.5, 3, 10, 20, and 27 K) for resistance against P. salmonis in rainbow trout.
Materials and Methods
Challenge test and phenotypes
The rainbow trout (O. mykiss) used in this study were obtained from the breeding nucleus of Aguas Claras S.A. (Puerto Montt, Chile) and were challenge-tested for resistance against P. salmonis at Aquainnovo’s Aquaculture Technology Center Patagonia, Puerto Montt, Chile (Flores-Mara et al. 2017). The fish used in this study were from the year-class 2011, which has undergone three generations of selection for growth, carcass quality, and appearance traits. Juveniles from 105 families (representing progeny from 105 dams and 48 sires) were reared in separate tanks until being individually tagged using a passive integrated transponder tag at an average weight of 7 g. After tagging, the animals were communally reared in a single tank for ∼7 months before being transferred to Aquainnovo’s research station (Lenca River, Xth Region, Chile). The fish were subjected to acclimation period during 20 d at the research station. After this period, a total of 2416 juveniles (with an average of 23 fish per family and ranging from 15 to 30 individuals) were experimentally challenged with P. salmonis. Before the challenge test, all fish were proven to be negative to the presence of infectious salmon anemia virus, infectious pancreatic necrosis virus, and Renibacterium salmoninarum by real-time PCR, and Flavobacterium spp. by culture. Fish were infected by injecting 0.2 ml of an LD50 (median lethal dose) inoculum of P. salmonis through intraperitoneal (IP) injection. Post IP injection, infected fish were equally distributed by family into three different tank replicates (used as fixed effect for PBLUP and genomics models). The challenge test continued for 32 d, and mortality and weight at the end of the experiment were recorded in all fish. All surviving fish at day 32 were anesthetized and killed. Tissue samples (fin clips) for genomic DNA isolation were taken from all dead and surviving fish and preserved in 95% ethanol at −80°.
Resistance to SRS was defined as the number of days to death (DD), with values ranging from 5 to 32; and binary survival (BS), scored as 1 if the fish died during the challenge test and 0 if the fish survived until the end of the challenge test.
Genotypes
The genotyped individuals were selected to obtain a balanced number of animals per family (mean = 19, range from 12 to 26) and maintain the phenotypic variance. Genomic DNA was extracted from fin clip samples from 2130 fish (average of 19 fish per family, range from 12 to 26 fish) using a commercial DNeasy Blood & Tissue Kit, Qiagen, following the manufacturer’s instructions. The fish were genotyped using a commercially available 57 K Affymetrix Axiom SNP array, designed by the National Center for Cool and Cold Water Aquaculture at the United States Department of Agriculture (Palti et al. 2015).
The genotypes were subjected to quality control (QC) using Affymetrix’s Axiom Analysis Suite software, using the default settings (dish QC ≥ 0.82 and genotype call rate ≥ 97% for each sample). Additional QC steps were conducted by filtering out SNPs and samples with a Hardy–Weinberg equilibrium test p-value < 0.00001, SNP call rate lower than 0.90, and minor allele frequency lower than 0.01.
Statistical models
Pedigree-based BLUP:
The pedigree-based variance components and EBV were estimated using BLUP and were compared with genomic evaluations. The model used was as follows:
where is a vector of phenotypes (DD or BS), is a vector of fixed effects (tank and body weight), is a vector of random additive polygenic genetic effects that follows a normal distribution ∼N(0, A), and are incidence matrices, is the additive relationship matrix, is the random residual error with a distribution , and is the identity matrix (Lynch and Walsh 1998). Body weight was included as a covariate in the analysis given that it significantly (p < 0.05) affected both traits. This was most likely because inoculum was IP-injected in the same dose for all fish, disregarding their initial size.
Genomic BLUP:
The SNP-based variance components and GEBV were estimated using GBLUP, in a similar way to the PBLUP model (M1), as implemented in the BLUPF90 software package (Misztal et al. 2016). The GBLUP model is a modification of the PBLUP method, where g is a vector of random additive genetic polygenic effects with a distribution ∼Nand is the genomic relationship matrix as described by VanRaden (2008). The G matrix is constructed based on all markers, and it can differ from the pedigree-based numerator relationship matrix (A), in that it can potentially have some negative off-diagonal values when individuals are molecularly less related than average pairs of animals in the sense of identity by state if the population were in Hardy–Weinberg equilibrium (Toro et al. 2002). The variance components, PBLUP, and GBLUP solutions for the breeding values were obtained using a restricted maximum likelihood method implemented in AIREMLF90, from the BLUPF90 family of programs (Misztal et al. 2016).
Single-step GBLUP:
The ssGBLUP model is similar to the PBLUP model (M1) except for the use of a combined genomic and pedigree relationship. The kinship matrix used was H (Aguilar et al. 2010), in which genotype and pedigree data are combined. The inverse of the matrix H is:
| (1) |
where is the inverse numerator relationship matrix for all animals, is the inverse of a pedigree-based relationship matrix for genotyped animals only, and is the inverse genomic relationship matrix.
The EBV and the GEBV for DD were analyzed as linear traits using AIREMLF90 and BLUPF90. BS was analyzed using a threshold model (including a probit link function to transform event incidence to liability) by means of a Bayesian approach implemented in the THRGIBBS1F90 module from the BLUPF90 family of programs (Misztal et al. 2016). For Bayesian analysis (THRGIBBS1F90) 200,000 iterations were used in the Gibbs sampling, with a burn-in period of 20,000 iterations, and samples were saved every 50 cycles. Visual inspection of trace plots of the posterior variance components generated by POSTGIBBSF90 were used for QC purposes regarding convergence.
Bayes C:
Bayes C fits a mixture model that assumes some known fraction of markers have zero effects, and it has been shown that Bayes C is less sensitive to prior assumptions than, e.g., Bayes B (Habier et al. 2011). All model parameters for Bayes C are defined as in M1, except the elements of vector which was calculated for each fish as:
where is the vector of the genotypes for the ith SNP for each animal; is the random allele substitution effect of the ith SNP; and δi is an indicator variable (0,1) sampled from a binomial distribution with parameters determined such that 1% of the markers were included in the model. The prior assumption is that SNP effects have independent and identical mixture distributions, where each marker has a point mass at zero with probability π and a univariate normal distribution with probability 1 − π having a null mean and variance , which in turn has a scaled inverse chi-squared prior, with and degrees of freedom (d.f.) and scale parameter (or ) (Fernando and Garrick 2013). For the additive variance, d.f. = 4 was used so the data would not overwhelm the prior if many loci were fitted, considering that, for Bayes C, a common locus variance is assumed and estimated by combining information from the prior and the data, and each fitted locus contributes to estimation of the common locus variance from the data (Fernando and Garrick 2013). The residual variance d.f. values were chosen based on those used in previous studies (Peters et al. 2012; Santana et al. 2016; Wolc et al. 2016; Yoshida et al. 2017).
Bayesian Lasso:
LASSO (Legarra et al. 2012) appears to be an interesting alternative method for performing regression on markers, suggesting that a double exponential prior may be a better choice than the Bayes A method, when most markers do not have an effect. The parameters for the LASSO method are defined as above in M1, except for an a priori distribution of individual SNP effects (ai) which was calculated as:
where is the individual variance for each SNP, estimated conditionally on a regularization parameter λ (initial value was which was estimated using an a priori gamma distribution bounded between 0 and 107.
The Bayes C and LASSO analyses were performed using GS3 software (Legarra et al. 2012). A total of 200,000 iterations were used in the Gibbs sampling, with a burn-in period of 20,000 cycles where results were saved every 50 cycles. Convergence and autocorrelation were assessed by visual inspection of trace plots of the posterior variance components.
Genetic parameters and heritability:
The total additive genetic variance () was estimated using relationship matrices A, G, and H for PBLUP, GBLUP, and ssGBLUP, respectively. For both DD and BS, the heritabilities were computed using the following equation:
| (2) |
For Bayesian models, the total additive genetic variance was estimated as the sum of the additive marker and the polygenic pedigree ()-based additive genetic variance , and the heritability was computed as:
| (3) |
Prediction accuracy:
The predictive abilities of different models were assessed using a fivefold cross-validation scheme. Briefly, all phenotyped and genotyped animals were randomly separated into five validation sets. The genomic predictions of the validation data sets were determined one at a time, where the phenotypic records of the validation fish (20% of the population) were set to missing and all remaining individuals with phenotypes and genotypes (80% of the population) were used as the training data set. For ssGBLUP, training and validation data sets were separated as described above, with the addition of 100% of the animals with only phenotypes (n = 482) into the training set.
Accuracy was used to assess the performance of each model for the validation set, and was estimated as:
| (4) |
where is the correlation between the EBV or GEBV of a given model (predicted for the validation set using information from the training set) and the record phenotype, and is the square root of the pedigree-based estimate of heritability (Legarra et al. 2008; Ødegård et al. 2014).
In addition, the prediction accuracies obtained using different SNP densities were tested for all the methods. The 0.5 K, 3 K, 10 K, and 20 K SNP densities were randomly selected five times for each test method from the ∼27 K SNP that passed QC.
The bias of EBV prediction was obtained as the regression coefficient of phenotyped animals and EBV or GEBV, for PBLUP and genomics methods (GBLUP, ssGBLUP, Bayes C, and LASSO) in the validation data.
Data availability
All phenotypic and genotypic data used in the current study can be found at the Figshare public repository (https://figshare.com/s/5219597a19f23873fda3).
Results
Descriptive statistics and genetic parameters
Summary statistics for both traits and covariates (body weight at the end of the challenge test) are presented in Table 1. The average DD ranged from 22 to 24 d and from 23 to 25 d between tanks for phenotyped (n = 2320) and genotyped (n = 1844) animals, respectively. The proportion of cumulative mortality ranged from 0.59 to 0.65 d and from 0.52 to 0.60 d between tanks for phenotyped and genotyped animals, respectively. The average body weights at the end of the challenge test were 165.3 g (SD = 40.44 g) and 168.8 g (SD = 41.37 g) for phenotyped and genotyped fish, respectively. A total of 1934 animals and 27,490 SNP (27 K) passed QC.
Table 1. Summary statistics for resistance against Piscirickettsia salmonis for phenotyped and genotyped rainbow trout.
| Traits | Tank | Na | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|---|
| Phenotyped fish | ||||||
| Days to death (d) | 1 | 819 | 23.59 | 8.07 | 5 | 32 |
| 2 | 805 | 22.82 | 8.03 | 6 | 32 | |
| 3 | 792 | 22.13 | 8.27 | 7 | 32 | |
| Binary survival (1 or 0) | 1 | 819 | 0.59 | 0.49 | 0 | 1 |
| 2 | 805 | 0.65 | 0.48 | 0 | 1 | |
| 3 | 792 | 0.65 | 0.48 | 0 | 1 | |
| Final challenge weight (g)b | — | 2320 | 165.30 | 40.44 | 46 | 295 |
| Genotyped fish | ||||||
| Days to death (d) | 1 | 669 | 24.92 | 7.64 | 10 | 32 |
| 2 | 641 | 24.01 | 7.78 | 11 | 32 | |
| 3 | 624 | 23.25 | 8.07 | 11 | 32 | |
| Binary survival (1 or 0) | 1 | 669 | 0.52 | 0.50 | 0 | 1 |
| 2 | 641 | 0.59 | 0.49 | 0 | 1 | |
| 3 | 624 | 0.60 | 0.49 | 0 | 1 | |
| Final challenge weight (g)b | — | 1844 | 168.80 | 41.37 | 66 | 295 |
Number of fish.
Used as covariable.
Variance components estimates for all the models are presented in Table 2. For both DD and BS, the additive genetic variance and heritability were higher for genomic methods compared with PBLUP. For PBLUP the heritabilities were 0.38 and 0.54 for DD and BS, respectively. For genomic prediction methods the heritability values ranged from 0.45 to 0.57 and from 0.54 to 0.62 for DD and BS, respectively. For both traits, the lowest and the highest heritability estimates when using genomic prediction methods were obtained from the GBLUP and Bayes C methods, respectively.
Table 2. Estimates of residual variance (), total additive genetic variance (), and heritability (h2) for resistance against Piscirickettsia salmonis in rainbow trout.
| Methods | Traits | |||||||
|---|---|---|---|---|---|---|---|---|
| Days to death | Binary survival | |||||||
| a | h2 | SEb | a | h2 | SEb | |||
| PBLUP | 23.017 | 37.375 | 0.381 | 0.059 | 1.177 | 1.005 | 0.539 | 0.053 |
| LASSO | 29.031 | 32.840 | 0.468 | 0.037 | 1.342 | 1.000 | 0.569 | 0.042 |
| GBLUP | 27.313 | 33.813 | 0.447 | 0.037 | 1.249 | 1.005 | 0.554 | 0.036 |
| ssGBLUP | 34.585 | 34.376 | 0.502 | 0.037 | 1.355 | 1.004 | 0.574 | 0.035 |
| BAYES C | 41.580 | 31.030 | 0.566 | 0.041 | 1.782 | 1.000 | 0.624 | 0.055 |
Total additive genetic variance for PBLUP, ssGBLUP, and GBLUP was for LASSO and BAYES C it was + (polygenic effect).
SE or SD for Bayesian methods.
Accuracy of different methods and marker densities
Based on the fivefold cross-validation, the prediction accuracy of GEBV from genomic methods outperformed that of the EBV from PBLUP (Table 3). Within all genomic methods, the accuracies predicted for DD were higher than those for BS, with a low SE of the estimate (Table 3).
Table 3. Mean accuracy, bias, and SE of EBV and GEBV for resistance against Piscirickettsia salmonis using a 27 K SNP panel.
| Methods | Traits | |||||||
|---|---|---|---|---|---|---|---|---|
| Days to death | Binary survival | |||||||
| Accuracy | SE | Biasa | SE | Accuracy | SE | Biasa | SE | |
| PBLUP | 0.613 | 0.097 | 1.053 | 0.113 | 0.470 | 0.105 | 0.269 | 0.109 |
| LASSO | 0.784 | 0.069 | 0.968 | 0.069 | 0.591 | 0.090 | 0.253 | 0.041 |
| GBLUP | 0.785 | 0.064 | 1.026 | 0.092 | 0.598 | 0.082 | 0.240 | 0.049 |
| ssGBLUP | 0.798 | 0.061 | 1.035 | 0.091 | 0.608 | 0.082 | 0.267 | 0.048 |
| BAYES C | 0.859 | 0.061 | 1.063 | 0.102 | 0.614 | 0.086 | 0.240 | 0.045 |
Regression for the EBV obtained by PBLUP and GEBV predicted with the different genomic methods.
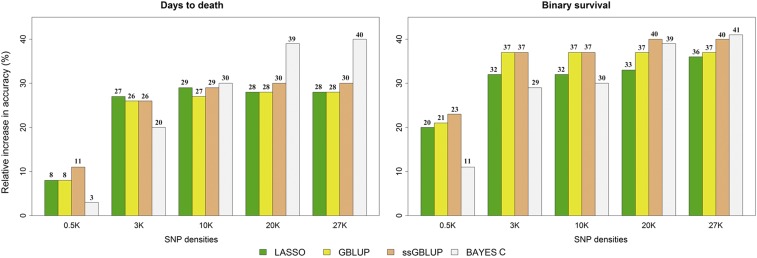
The relative increase in accuracy of predicted GEBV compared with EBV from PBLUP varied moderately between models and traits at 27 K marker density (Figure 1). For both traits, the Bayes C method resulted in higher relative improvement in accuracy (>40%). On the other hand, LASSO and GBLUP resulted in the lowest relative increases in accuracy, and were the same (28%) for DD and similar for BS (LASSO = 36% and GBLUP = 37%) (Figure 1).
Figure 1.
Relative increase in accuracy of different genomic selection methods for traits days to death and binary survival compared with PBLUP in rainbow trout using different SNP chip densities (0.5, 3, 10, 20, and 27 K).
For marker density equal to 20 K, the Bayes C and ssGBLUP methods were most favorable in terms of relative increase in accuracy for DD and BS, respectively (Figure 1). At marker densities of 3 K and 10 K, ssGBLUP and GBLUP resulted in the same relative increase in accuracy for BS (Figure 1). By contrast, for DD the Bayesian methods had better performance. The ssGBLUP method performed slightly better than the other genomics methods at the lowest marker density (0.5 K), especially compared with Bayes C, which showed the lowest increase in accuracy for both traits (<11%). Nevertheless, the relative increases in accuracy of predicted GEBV from all genomic models were superior to those of EBV from PBLUP, even at the lowest marker density of 0.5 K for both traits. In general, the relative increase in accuracy was considerably more evident for BS than DD.
The GEBV estimated using GBLUP had the smallest departure from unity for DD. By contrast, the Bayes C method resulted in the most biased estimate (1.035). The bias values for EBV and GEBV for BS were considerably lower than 1.0 for all methods and ranged from 0.24 to 0.27, which indicates that all results for BS were upward biased (Table 3).
Discussion
Heritability for pedigree-based and genomic models
Low to moderate heritability estimates (from 0.16 to 0.24) have been reported for SRS resistance in Atlantic salmon (Yáñez et al. 2013, 2014) and coho salmon (Yáñez et al. 2016a) using a pedigree-based method to analyze a trait defined similarly to DD and BS. The comparatively higher estimates of heritability reported using genomic information compared with PBLUP in our study are in accordance with what has been reported in other fish species (Tsai et al. 2016; Bangera et al. 2017; Correa et al. 2017; Vallejo et al. 2017). Vallejo et al. (2016, 2017) also estimated a similar range of heritability using genomic models (0.26–0.54) and PBLUP (0.31–0.48) for bacterial cold water disease resistance in rainbow trout.
Prediction accuracy
The relatively high accuracy achieved in the present study for genomic methods suggested that the strong relationship between the animals in the training and validation data sets, and the small effective population size of this breeding population, could contribute to the accuracy values. This in turn could result in extensive LD and a smaller number of effective chromosome segments to be estimated. The GEBV prediction accuracy for resistance against cold water disease in rainbow trout was estimated using different methods by Vallejo et al. (2017), and the accuracies reported were similar of magnitude for survival days (0.63–0.71) and survival status (0.66–0.71).
In Atlantic salmon, Bangera et al. (2017) and Correa et al. (2017) showed that the relative increase in GEBV prediction accuracies from different models compared with PBLUP was up to 30 and 22% higher for resistance against SRS and Caligus rogercresseyi, respectively. However, improvement in accuracy values in the current study varied from 28 to 41%; this was still lower than the values reported by Vallejo et al. (2017), which ranged from 83 to 109% for bacterial cold water disease resistance in rainbow trout. We speculate that in the study of Vallejo et al. (2017), the use of a larger number of animals with phenotype in the training data set (7893 vs. 2417) resulted in a higher relative increase in accuracy. Furthermore, Piyasatian et al. (2007) suggested that high heritability of a trait (>0.45 in the present study) reduced the benefit of GS over PBLUP.
Effect of marker density on accuracy
Genotyping of large numbers of selection candidates with high-density panels may not be cost-effective if the economic benefit per animal is low compared with the cost of genotyping (Habier et al. 2009), as in aquaculture species. The use of low-density panels, with considerable reduction in cost of genotyping, is a potential cost-effective approach to implement GS. Previous studies in Atlantic salmon reported that low-density panels between 5 and 10 K were sufficient to obtain reliable increases in accuracy (even close to the maximal accuracy of high-density panels) compared with PBLUP (Tsai et al. 2015, 2016; Correa et al. 2017). The lowest-density SNP panel (0.5 K) used in our study resulted in the lowest accuracies, mainly for DD, as a result of insufficient LD between the markers owing to the large distance between the randomly selected low-density markers (Bangera et al. 2017).
We suggest that the considerable gain in GEBV accuracy obtained in different genomic prediction methods using markers above 10 K was because of the high LD between the randomly selected markers. All low-density panels showed improved GEBV accuracy over PBLUP (Figure 1); higher accuracy of genomic prediction can be obtained by using high-density panels, as also shown by Ødegård et al. (2014) and Bangera et al. (2017). Therefore, to implement cost-effective GS, a strategy of genotyping of the selection candidates with a low-density panel (e.g., 500 SNPs) followed by imputation to a high-density panel (e.g., 50 K) could be used (Tsai et al. 2017). Imputing from 0.25 to 0.5 K to a high-density panel and using the imputed genotypes for genomic prediction was shown to achieve a similar level of accuracy compared with using true genotypes in Atlantic salmon (Tsai et al. 2017).
Comparison of models at different marker densities
The GBLUP approach assumes polygenic control of the trait and makes use of all genotyped SNPs for calculating the genomic relationship matrix. By contrast, Bayesian models assume that a few markers explain the genetic variance of a trait (Habier et al. 2007; Hayes et al. 2009; de los Campos et al. 2013). Thus, Bayesian methods are expected to perform better than GBLUP when several moderate- to large-effect QTL are controlling the trait. In this study, two GBLUP and two Bayesian methods were tested to compare the accuracy of genomic predictions from different GS models with those obtained by ordinary PBLUP.
All genomic prediction methods outperformed PBLUP at different SNP densities (Figure 1). For both traits, the Bayes C method had the highest accuracy (>40% relative increase over PBLUP) at the highest SNP density (27 K). The GBLUP and ssGBLUP methods showed a constant relative increase in accuracy from 3 K to 27 K SNP panels, mainly for BS. Interestingly, for the 0.5 K SNP panel, ssGBLUP resulted in the highest accuracies for both traits, suggesting that for very low-density panels, the use of additional animals with only phenotypes in the training set can improve the accuracy of predictions. Furthermore, ssGBLUP could be used as a strategy to reduce the genotyping costs and still achieve higher GEBV accuracies compared with PBLUP. As has been reported previously, the use of information from genotyped and nongenotyped individuals (Lourenco et al. 2014) and the increase in accuracy when compared with PBLUP (Chen et al. 2011; Christensen et al. 2012) are among the advantages of using ssGBLUP.
The use of progressively more markers in the GBLUP method might have resulted in better capturing of genetic relationships, whereas Bayes C was more effective in capturing LD between markers and QTL when more markers were used (Bermingham et al. 2015). Furthermore, fitting 1% of the SNPs with larger effect in the Bayes C method resulted in the highest relative increase in accuracy. This is most likely owing to the genetic architecture of P. salmonis resistance in rainbow trout. In a previous GWAS in the same population, P. salmonis resistance was suggested to be under oligogenic control (data not published), with a few SNPs showing moderate to large effects (the top 10 SNPs explained >50% of the genetic variance; results not shown).
Bayes C outperformed ssGBLUP at 20 and 27 K SNP densities for DD, and had slightly lower performance for BS. However, for lower SNP densities, the Bayes C method had lower accuracy (Figure 1 and Table 3). The large distance between the low-density SNPs results in lower LD between the markers and QTL. The possibility of exclusion of the SNPs with moderate to high effects during the process of random selection might have resulted in lower relative accuracies in Bayes C.
Several other studies also reported that GEBV estimated by Bayesian methods outperformed EBV estimated using pedigree-based methods, and even other genomic methods (i.e. GBLUP and ssGBLUP) (Neves et al. 2014; Vallejo et al. 2016, 2017; Bangera et al. 2017; Correa et al. 2017). A disadvantage in using Bayesian methodologies (e.g., Bayes C) is the considerably higher computational time, which could increase linearly depending on the number of markers fitted in the model (Bermingham et al. 2015). Considering the similarity in accuracies between Bayes C and ssGBLUP, and the highest accuracies for the low-density panels (Figure 1 and Table 3), the ssGBLUP method may be a more flexible and computationally efficient alternative.
Bias
GEBV bias was calculated as the regression of EBV on GEBV. A regression coefficient equal to one is indicative of predictions that are on a scale similar to that of the GEBV, whereas a regression <1 or >1 indicates that GEBV is overestimated or underestimated, respectively. Here, we found bias values somewhat below unity for BS, indicating that GEBV was underregressed compared with EBV, and suggesting that the genetic trends could be underestimated and have negative impact in selection schemes. Other studies reported bias values <1 for BS, and similar bias values to those of the present work for DD (Vallejo et al. 2016, 2017; Bangera et al. 2017).
Implications
Our results showed that using genomic information for estimating breeding values achieved higher accuracies compared with using only pedigree information for both DD and BS. Using 20 K and 3 K SNP panels for DD and BS, respectively, was enough to improve accuracy to similar values to those obtained for 27 K SNP chip density. Given the economic importance of resistance against P. salmonis in rainbow trout, and the efficacy of genomic prediction over pedigree-based methods, we suggest that selective breeding using genomic information will be an important component to control SRS and reduce losses in aquaculture systems.
Acknowledgments
Aguas Claras S.A. provided funding for the experimental challenge test and fish used in this study. This work was partially funded by grants from Corporación de Fomento de la Producción (11IEI-12843), Fondo Nacional de Desarrollo Científico y Tecnológico Regular (no. 1171720), and Núcleo Milenio de Salmónidos Invasores. G.M.Y. acknowledges support from a Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP process numbers 2014/20626-4 and 2015/25232-7) doctoral fellowship. R.C. acknowledges support from a National Council for Scientific and Technological Development fellowship (process number 308636/2014-7). The authors declare that they have no conflicts of interest.
Footnotes
Communicating editor: D. J. de Koning
Literature Cited
- Aguilar I., Misztal I., Johnson D. L., Legarra A., Tsuruta S., et al. , 2010. Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 93: 743–752. [DOI] [PubMed] [Google Scholar]
- Bangera R., Correa K., Lhorente J. P., Figueroa R., Yáñez J. M., 2017. Genomic predictions can accelerate selection for resistance against Piscirickettsia salmonis in Atlantic salmon (Salmo salar). BMC Genomics 18: 121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bermingham M. L., Pong-Wong R., Spiliopoulou A., Hayward C., Rudan I., et al. , 2015. Application of high-dimensional feature selection: evaluation for genomic prediction in man. Sci. Rep. 5: 10312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branson E. J., Diaz-Munoz D. N., 1991. Description of a new disease condition occurring in farmed coho salmon, Oncorhynchus kisutch (Walbaum), in South America. J. Fish Dis. 14: 147–156. [Google Scholar]
- Camussetti M. A., Gallardo A., Aguilar D., Larenas J., 2015. Análisis de los Costos por la Utilización de Quimioterápicos y Vacunas en la Salmonicultura. Salmonexpert, Puerto Montt, Chile. [Google Scholar]
- Chen C. Y., Misztal I., Aguilar I., Tsuruta S., Meuwissen T. H. E., et al. , 2011. Genome-wide marker-assisted selection combining all pedigree phenotypic information with genotypic data in one step: an example using broiler chickens. J. Anim. Sci. 89: 23–28. [DOI] [PubMed] [Google Scholar]
- Chen L., Li C., Sargolzaei M., Schenkel F., 2014. Impact of genotype imputation on the performance of GBLUP and Bayesian methods for genomic prediction. PLoS One 9: e101544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen O. F., Madsen P., Nielsen B., Ostersen T., Su G., 2012. Single-step methods for genomic evaluation in pigs. Animal 6: 1565–1571. [DOI] [PubMed] [Google Scholar]
- Cleveland M. A., Hickey J. M., 2013. Practical implementation of cost-effective genomic selection in commercial pig breeding using imputation. J. Anim. Sci. 91: 3583–3592. [DOI] [PubMed] [Google Scholar]
- Colombani C., Legarra A., Fritz S., Guillaume F., Croiseau P., et al. , 2013. Application of Bayesian least absolute shrinkage and selection operator (LASSO) and BayesCπ methods for genomic selection in French Holstein and Montbéliarde breeds. J. Dairy Sci. 96: 575–591. [DOI] [PubMed] [Google Scholar]
- Correa K., Lhorente J. P., López M. E., Bassini L., Naswa S., et al. , 2015. Genome-wide association analysis reveals loci associated with resistance against Piscirickettsia salmonis in two Atlantic salmon (Salmo salar L.) chromosomes. BMC Genomics 16: 854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correa K., Bangera R., Figueroa R., Lhorente J. P., Yáñez J. M., 2017. The use of genomic information increases the accuracy of breeding value predictions for sea louse (Caligus rogercresseyi) resistance in Atlantic salmon (Salmo salar). Genet. Sel. Evol. 49: 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cvitanich J., Garate O., Smith C. E., 1991. The isolation of a rickettsia‐like organism causing disease and mortality in Chilean salmonids and its confirmation by Koch’s postulate. J. Fish Dis. 14: 121–146. [Google Scholar]
- Daetwyler H. D., Villanueva B., Woolliams J. A., Schaeffer L., Crawford A., 2008. Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS One 3: e3395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G., Vazquez A. I., Fernando R., Klimentidis Y. C., Sorensen D., 2013. Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet. 9: e1003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernando R. L., Garrick D., 2013. Bayesian methods applied to GWAS. Methods Mol. Biol. 1019: 237–274. [DOI] [PubMed] [Google Scholar]
- Flores-Mara R., Rodríguez F. H., Bangera R., Lhorente J. P., Neira R., et al. , 2017. Resistance against infectious pancreatic necrosis exhibits significant genetic variation and is not genetically correlated with harvest weight in rainbow trout (Oncorhynchus mykiss). Aquaculture 479: 155–160. [Google Scholar]
- Fryer J. L., Hedrick R. P., 2003. Piscirickettsia salmonis: a Gram-negative intracellular bacterial pathogen of fish. J. Fish Dis. 26: 251–262. [DOI] [PubMed] [Google Scholar]
- Gheyas A. A., Houston R. D., Mota-Velasco J. C., Guy D. R., Tinch A. E., et al. , 2010. Segregation of infectious pancreatic necrosis resistance QTL in the early life cycle of Atlantic Salmon (Salmo salar). Anim. Genet. 41: 531–536. [DOI] [PubMed] [Google Scholar]
- Goddard M., 2009. Genomic selection: prediction of accuracy and maximisation of long term response. Genetica 136: 245–257. [DOI] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Dekkers J. C. M., 2007. The impact of genetic relationship information on genome-assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Dekkers J. C. M., 2009. Genomic selection using low-density marker panels. Genetics 182: 343–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Kizilkaya K., Garrick D. J., Meuwissen T., et al. , 2011. Extension of the Bayesian alphabet for genomic selection. BMC Bioinformatics 12: 186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B. J., Visscher P. M., Goddard M. E., Heinkel J., Wimmers K., et al. , 2009. Increased accuracy of artificial selection by using the realized relationship matrix. Genet. Res. 91: 47. [DOI] [PubMed] [Google Scholar]
- Hayes B. J., Pryce J., Chamberlain A. J., Bowman P. J., Goddard M. E., 2010. Genetic architecture of complex traits and accuracy of genomic prediction: coat colour, milk-fat percentage, and type in Holstein cattle as contrasting model traits. PLoS Genet. 6: e1001139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houston R. D., Gheyas A., Hamilton A., Guy D. R., Tinch A. E., et al. , 2008a Detection and confirmation of a major QTL affecting resistance to infectious pancreatic necrosis (IPN) in Atlantic salmon (Salmo salar). Dev. Biol. (Basel) 132: 199–204. [DOI] [PubMed] [Google Scholar]
- Houston R. D., Haley C. S., Hamilton A., Guy D. R., Tinch A. E., et al. , 2008b Major quantitative trait loci affect resistance to infectious pancreatic necrosis in Atlantic salmon (Salmo salar). Genetics 178: 1109–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houston R. D., Haley C. S., Hamilton A., Guy D. R., Mota-Velasco J. C., et al. , 2010. The susceptibility of Atlantic salmon fry to freshwater infectious pancreatic necrosis is largely explained by a major QTL. Heredity (Edinb) 105: 318–327. [DOI] [PubMed] [Google Scholar]
- Houston R. D., Taggart J. B., Cézard T., Bekaert M., Lowe N. R., et al. , 2014. Development and validation of a high density SNP genotyping array for Atlantic salmon (Salmo salar). BMC Genomics 15: 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzyk M. A., Burian J., Machander D., Dolhaine D., Cameron S., et al. , 2001. An efficacious recombinant subunit vaccine against the salmonid rickettsial pathogen Piscirickettsia salmonis. Vaccine 19: 2337–2344. [DOI] [PubMed] [Google Scholar]
- Legarra A., Robert-Granié C., Manfredi E., Elsen J.-M., 2008. Performance of genomic selection in mice. Genetics 180: 611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legarra A., Ricard A., Filangi O., 2012. GS3: Genomic Selection, Gibbs Sampling, Gauss Seidel.
- Lhorente J. P., Gallardo J. A., Villanueva B., Carabaño M. J., Neira R., et al. , 2014. Disease resistance in Atlantic salmon (Salmo salar): coinfection of the intracellular bacterial pathogen Piscirickettsia salmonis and the sea louse Caligus rogercresseyi. PLoS One 9: e95397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenco D. A. L., Misztal I., Tsuruta S., Aguilar I., Ezra E., et al. , 2014. Methods for genomic evaluation of a relatively small genotyped dairy population and effect of genotyped cow information in multiparity analyses. J. Dairy Sci. 97: 1742–1752. [DOI] [PubMed] [Google Scholar]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantiative Traits. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Macqueen D. J., Primmer C. R., Houston R. D., Nowak B. F., Bernatchez L., et al. , 2017. Functional annotation of all salmonid genomes (FAASG): an international initiative supporting future salmonid research, conservation and aquaculture. BMC Genomics 18: 484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H., 2009. Accuracy of breeding values of “unrelated” individuals predicted by dense SNP genotyping. Genet. Sel. Evol. 41: 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misztal I., Tsuruta S., Lourenco D., Masuda Y., Aguilar I., et al. , 2016. Manual for BLUPF90 Family of Programs. University of Georgia, Athens, GA. [Google Scholar]
- Moen T., Torgersen J., Santi N., Davidson W. S., Baranski M., et al. , 2015. Epithelial cadherin determines resistance to infectious pancreatic necrosis virus in Atlantic salmon. Genetics 200: 1313–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neves H. H., Carvalheiro R., Brien A. M. O., Utsunomiya Y. T., do Carmo A. S., et al. , 2014. Accuracy of genomic predictions in Bos indicus (Nellore) cattle. Genet. Sel. Evol. 46: 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ødegård J., Moen T., Santi N., Korsvoll S. A., Kjøglum S., et al. , 2014. Genomic prediction in an admixed population of Atlantic salmon (Salmo salar). Front. Genet. 5: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palti Y., Gao G., Liu S., Kent M. P., Lien S., et al. , 2015. The development and characterization of a 57K single nucleotide polymorphism array for rainbow trout. Mol. Ecol. Resour. 15: 662–672. [DOI] [PubMed] [Google Scholar]
- Peña B., Isla A., Haussmann D., Figueroa J., 2016. Immunostimulatory effect of salmon prolactin on expression of Toll-like receptors in Oncorhynchus mykiss infected with Piscirickettsia salmonis. Fish Physiol. Biochem. 42: 509–516. [DOI] [PubMed] [Google Scholar]
- Peters S. O., Kizilkaya K., Garrick D. J., Fernando R. L., Reecy J. M., et al. , 2012. Bayesian genome-wide association analysis of growth and yearling ultrasound measures of carcass traits in Brangus heifers. J. Anim. Sci. 90: 3398–3409. [DOI] [PubMed] [Google Scholar]
- Piyasatian N., Fernando R., Dekkers J., 2007. Genomic selection for marker-assisted improvement in line crosses. Theor. Appl. Genet. 115: 665–674. [DOI] [PubMed] [Google Scholar]
- Rozas M., Enríquez R., 2014. Piscirickettsiosis and Piscirickettsia salmonis in fish: a review. J. Fish Dis. 37: 163–188. [DOI] [PubMed] [Google Scholar]
- Sae-Lim P., Kause A., Lillehammer M., Mulder H. A., 2017. Estimation of breeding values for uniformity of growth in Atlantic salmon (Salmo salar) using pedigree relationships or single-step genomic evaluation. Genet. Sel. Evol. 49: 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santana M. H. A., Junior G. A. O., Cesar A. S. M., Freua M. C., Gomes R. C., et al. , 2016. Copy number variations and genome-wide associations reveal putative genes and metabolic pathways involved with the feed conversion ratio in beef cattle. J. Appl. Genet. 57: 495–504. [DOI] [PubMed] [Google Scholar]
- Tobar J. A., Jerez S., Caruffo M., Bravo C., Contreras F., et al. , 2011. Oral vaccination of Atlantic salmon (Salmo salar) against salmonid rickettsial septicaemia. Vaccine 29: 2336–2340. [DOI] [PubMed] [Google Scholar]
- Toro M., Barragán C., Óvilo C., Rodrigañez J., Rodriguez C., et al. , 2002. Estimation of coancestry in Iberian pigs using molecular markers. Conserv. Genet. 3: 309–320. [Google Scholar]
- Tsai H.-Y., Hamilton A., Tinch A. E., Guy D. R., Gharbi K., et al. , 2015. Genome wide association and genomic prediction for growth traits in juvenile farmed Atlantic salmon using a high density SNP array. BMC Genomics 16: 969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai H.-Y., Hamilton A., Tinch A. E., Guy D. R., Bron J. E., et al. , 2016. Genomic prediction of host resistance to sea lice in farmed Atlantic salmon populations. Genet. Sel. Evol. 48: 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai H.-Y., Matika O., Edwards S. M., Antolín–Sánchez R., Hamilton A., et al. , 2017. Genotype imputation to improve the cost-efficiency of genomic selection in farmed Atlantic salmon. G3 7: 1377–1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejo R. L., Leeds T. D., Fragomeni B. O., Gao G., Hernandez A. G., et al. , 2016. Evaluation of genome-enabled selection for bacterial cold water disease resistance using progeny performance data in rainbow trout: insights on genotyping methods and genomic prediction models. Front. Genet. 7: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejo R. L., Leeds T. D., Gao G., Parsons J. E., Martin K. E., et al. , 2017. Genomic selection models double the accuracy of predicted breeding values for bacterial cold water disease resistance compared to a traditional pedigree-based model in rainbow trout aquaculture. Genet. Sel. Evol. 49: 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRaden P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91: 4414–4423. [DOI] [PubMed] [Google Scholar]
- Wolc A., Arango J., Settar P., Fulton J. E., O’Sullivan N. P., et al. , 2016. Mixture models detect large effect QTL better than GBLUP and result in more accurate and persistent predictions. J. Anim. Sci. Biotechnol. 7: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yáñez J. M., Bangera R., Lhorente J. P., Oyarzún M., Neira R., 2013. Quantitative genetic variation of resistance against Piscirickettsia salmonis in Atlantic salmon (Salmo salar). Aquaculture 414–415: 155–159. [Google Scholar]
- Yáñez J. M., Houston R. D., Newman S., 2014. Genetics and genomics of disease resistance in salmonid species. Front. Genet. 5: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yáñez J. M., Bangera R., Lhorente J. P., Barria A., Oyarzun M., et al. , 2016a Negative genetic correlation between resistance against Piscirickettsia salmonis and harvest weight in coho salmon (Oncorhynchus kisutch). Aquaculture 459: 8–13. [Google Scholar]
- Yáñez J. M., Naswa S., López M. E., Bassini L., Correa K., et al. , 2016b Genome-wide single nucleotide polymorphism (SNP) discovery in Atlantic salmon (Salmo salar): validation in wild and farmed American and European populations. Mol. Ecol. Resour. 16: 1002–1011. [DOI] [PubMed] [Google Scholar]
- Yoshida G. M., Lhorente J. P., Carvalheiro R., Yáñez J. M., 2017. Bayesian genome-wide association analysis for body weight in farmed Atlantic salmon (Salmo salar L.). Anim. Genet. 48: 698–703. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All phenotypic and genotypic data used in the current study can be found at the Figshare public repository (https://figshare.com/s/5219597a19f23873fda3).