Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2018 Mar 15;4(4):477–483. doi: 10.1021/acscentsci.7b00625

Increasing Elasticity through Changes in the Secondary Structure of Gelatin by Gelation in a Microsized Lipid Space

Atsushi Sakai †, Yoshihiro Murayama †, Kei Fujiwara ‡, Takahiro Fujisawa §, Saori Sasaki §, Satoru Kidoaki §, Miho Yanagisawa †,*
PMCID: PMC5920605  PMID: 29721530

Abstract

graphic file with name oc-2017-00625j_0007.jpg

Even though microgels are used in a wide variety of applications, determining their mechanical properties has been elusive because of the difficulties in analysis. In this study, we investigated the surface elasticity of a spherical microgel of gelatin prepared inside a lipid droplet by using micropipet aspiration. We found that gelation inside a microdroplet covered with lipid membranes increased Young’s modulus E toward a plateau value E* along with a decrease in gel size. In the case of 5.0 wt % gelatin gelled inside a microsized lipid space, the E* for small microgels with R ≤ 50 μm was 10-fold higher (35–39 kPa) than that for the bulk gel (∼3 kPa). Structural analysis using circular dichroism spectroscopy and a fluorescence indicator for ordered beta sheets demonstrated that the smaller microgels contained more beta sheets in the structure than the bulk gel. Our finding indicates that the confinement size of gelling polymers becomes a factor in the variation of elasticity of protein-based microgels via secondary structure changes.

Short abstract

We found that the elasticity of gelatin microgel greatly varies by gelation in a microsized lipid space via secondary structure transition of gelatin in nanoscale.

Introduction

Polymer microgels in the size range 1–1000 μm are indispensable for biomedical, cosmetic, and food materials.1,2 A hallmark feature of microgels is their high surface-to-volume ratio, which allows an instantaneous response to environmental changes.3,4 Due to this property, microgels have become a featured material for application in drug delivery systems5 and stem cell culturing.6,7 Furthermore, recent studies have used microgels as a model cytoskeleton to elucidate the physicochemical and mechanical properties of cells.8,9

The size, shape, and mechanical properties of microgels are important factors for optimized applications. Recent progress in emulsion polymerization and droplet-based microfluidics has enabled the synthesis of monodisperse spherical and capsule-shaped microgels of the desired sizes.10−12 Furthermore, the selective polymerization of droplets in an aqueous two-phase system (ATPS) enables the functionalization of microgels into complex shapes.13−16 However, the mechanical properties of microgels have been poorly documented due to the difficulty in characterizing the floating spherical microgel in solution using conventional methods such as atomic force microscopy (AFM).

The mechanical properties of microgels have not been as commonly reported as those of large bulk gels. For example, Weitz et al. have reported methods to measure the elasticity of single microgels by an image analysis of the deformed microgels in ATPS droplets and micropipets17,18 that indicated that microgels of polyacrylamide show higher elasticity than its bulk gels.17 Furthermore, physicochemical analyses have shown that microsized space and boundary conditions arising due to surrounding surfactants like lipids result in various unexpected properties of the components inside the confined space.15,19,20 Thus, it is plausible that the preparation process determines the mechanical properties of microgels.

Herein we have investigated the elasticity of microgels prepared inside lipid droplets by using micropipet aspiration, and compared it with that of bulk gels. We found that the gelation of gelatin in a microsized lipid space remarkably increases its elasticity with a varying secondary structure of gelatin. Our results provide important information that confinement effects are critical to determining the mechanical properties of microsized hydrogels of biopolymers and biomimetic polymers prepared via emulsion polymerization.

Results and Discussion

Microgel Preparation and Elastic Measurements

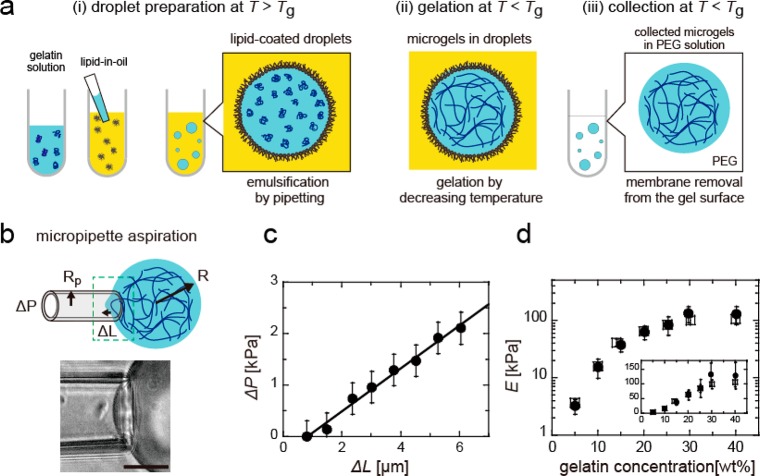
We prepared gelatin microgels inside droplets coated with a lipid layer (Figure 1a). The gelatin solution was confined inside the droplet (before gelation) at a temperature above the gelation temperature Tg, and then gelled over 24–26 h at temperatures below Tg. The microgel size was constant before and after gelation (Figure S1). For elasticity measurement, the microgel was collected from the droplet and added to the 3.0 wt % PEG 20k solution, and the lipid membrane covering the microgel surface was removed. To confirm the removal of lipid membranes, we visualized the membrane and gelatin gel using two different dyes (Figure S2). By comparing the fluorescence images of the microgels before and after the addition of PEG, we confirmed that this process removed the lipid membrane from the microgel surface.

Figure 1.

Figure 1

Open in a new tab

(a) Preparation of gelatin microgels: (i) Above the gelation temperature Tg, the gelatin solution was entrapped in lipid-coated droplets via pipetting. (ii, iii) After gelation at T < Tg, the microgels were collected from the lipid droplets by adding a PEG solution. (b) Measurement of Young’s modulus of the collected microgels via micropipet aspiration. ΔP is the aspirate pressure, ΔL the protrusion length of microgel into the micropipet, and Rp the inner radius of the micropipet. The scale bar represents 20 μm length. (c) Linear relationship between the applied pressure ΔP and aspiration length ΔL inside the micropipet. (d) Young’s modulus E of bulk gels with ∼1.5 mm thickness at various gelatin concentrations, obtained using micropipet aspiration (closed circles) and AFM (squares). The inset represents the plot for a linear scaling of E (on the y-axis).

Micropipet aspiration was used to measure Young’s modulus of the microgels (Figure 1b). In the measurement of the elasticity of the nonflat microgels floating in a solution, the micropipet aspiration method has an advantage over AFM measurements via microindentation because the micropipet can trap the microgel and directly deform it by aspiration. The micropipet aspiration technique has been used for the mechanical characterization of cells21,22 and liposomes23 but not polymer gels. Therefore, we first examined the reliability of this method by comparing the obtained E for flat bulk gels with those obtained via conventional AFM measurements. The bulk gels were cut into small pieces (larger than 1.0 mm) and suspended in the 3.0 wt % PEG 20k solution prior to micropipet aspiration to ensure that the conditions are similar to those used for the microgels. For AFM measurements too, the bulk gels were covered with the 3.0 wt % PEG 20k solution.

The gels were gradually aspirated into the micropipet by increasing the aspiration pressure ΔP. The protrusion length ΔL increased linearly with ΔP, as plotted in Figure 1c. According to eq 1, we derived E from the slope for bulk gels for different gelatin concentrations ranging from 5.0 to 40 wt %. Figure 1d shows the E values obtained by micropipet aspiration and AFM measurements. The E values obtained by both the methods are almost equal, and the gelatin concentration dependence of E qualitatively agrees with previous reports.24 Therefore, we conclude that the micropipet aspiration technique is suitable for measuring the elasticity of gels. Moreover, the E values are constant and independent of micropipet size Rp and bulk gel size R under the condition that the ratio is smaller than a critical value, i.e., Rp/R < 0.4 (Figures S3, S4). Therefore, we performed the following experiments under the condition of Rp/R < 0.4.

Effect of Lipid Membrane on the Elasticity of Bulk Gels

As a first step to reveal the mechanical properties of microgels, we investigated the effect of a lipid membrane on the elasticity of the gelatin gel. We measured Young’s modulus of a flat bulk gel containing 5.0 wt % gelatin that was partially covered with a PC membrane before gelation (Figure 2a (i, ii)). After removing the membrane, we measured the local elasticity using AFM (Figure 2b (i, ii)). The thickness of the bulk gels was approximately 1.5 mm.

Figure 2.

Figure 2

Open in a new tab

(a) Schematic of flat bulk gels partially covered with a PC membrane prior to (upper) or after gelation (lower). (b) Local Young’s modulus E of 5.0 wt % gelatin bulk gels (i, iii) with and (ii, iv) without the membrane, as obtained using AFM.

The value of E for the bulk gel previously in contact with the lipid membrane was 7.6 ± 2 kPa (Ebulkm; average (av) ± standard error (SE), number of measurements N = 8). This is about twice as large as that for the bulk gel without contact with the lipid membrane: Ebulk0 = 2.6 ± 0.3 kPa (N = 7). We confirmed the relationship Ebulkm > Ebulk0 by measuring the elasticity of cut pieces of the bulk gels in the PEG solution using micropipet aspiration.

The value of E for the bulk gel covered with a lipid membrane after gelation was 1.9 ± 0.5 kPa (N = 5; Figures 2a and 2b (iii)), which is similar to that for the bulk gel without the membrane: 2.6 ± 0.5 kPa (N = 6; Figures 2a and 2b (iv)). These results indicate that coverage with a lipid membrane prior to gelation increased the elasticity of a gelatin gel, and suggest that the gelation process determines mechanical properties even in the case of bulk gels.

Elasticity of Differently Sized Microgels

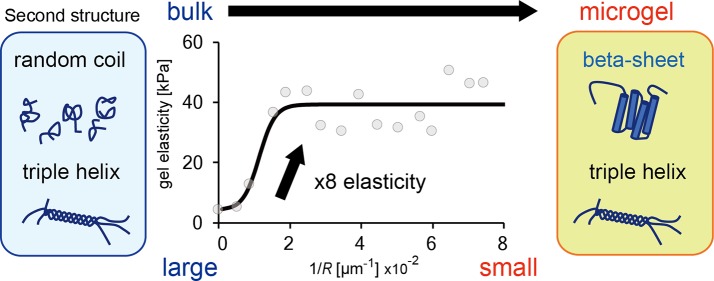
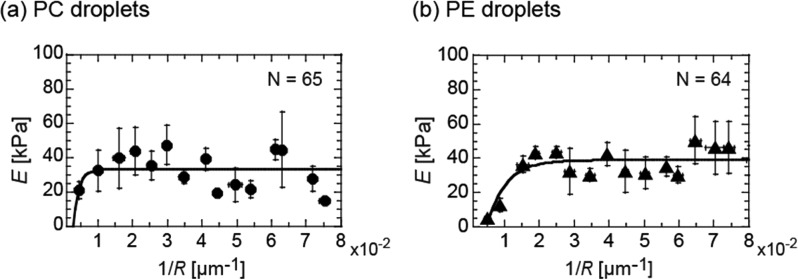
Because reducing the gel size increases the surface area to volume ratio, the effect of a lipid membrane on gel elasticity is expected to be enhanced when the gel size decreases. To investigate the microgel size effect, we measured E of spherical microgels and plotted them as a function of the radius R (ranging from 12 to 300 μm), as shown in Figure 3a. The radius R refers to the size of collected microgels after membrane removal. In the case of smaller microgels with 1/R ≥ 1 × 10–2 [μm–1] (i.e., R ≤ 100 μm), the E values are independent of the microgel size R. The average value is 35.3 ± 3 kPa (N = 55), corresponding to the saturation point E* obtained by fitting the data with a simple exponential saturation curve (solid line, Figure 3a).

Figure 3.

Figure 3

Open in a new tab

Size dependence of Young’s modulus E of microgels of gelatin 5.0 wt % prepared inside (a) PC and (b) PE droplets. The solid lines are fits to the data with a simple exponential saturation curve.

In these experiments, we used a PC membrane to cover the gelatin surface. To investigate whether the E* value depends on the lipid affinity of gelatin, we used another species of lipids, PE, having a far higher affinity to gelatin than PC.15Figure 3b shows the E value of microgels as a function of R for PE. The E values increase toward a plateau value E* ∼ 39 kPa along with a decrease in microgel size. This E* value corresponds to the average value for smaller microgels with 1/R ≥ 2 × 10–2 [μm–1] (i.e., R ≤ 50 μm); 38.7 ± 3 kPa (N = 43). Since the E* values of PC and PE are similar, this is mainly determined by the size of confinement in the lipid droplet and not the affinity of the lipid for gelatin. In addition, the E* value of 35–39 kPa for 5.0 wt % gelatin microgels is significantly larger than that of the bulk gel of gelatin 5.0 wt % with membrane Ebulkm = 7.6 kPa (Figure 2b (i)), and similar to that of the bulk gel of ∼15 wt % gelatin without the membrane (Figure 1d).

The increase in E of microgels was not due to condensation by PEG, since all the microgels never shrank but rather swelled upon collection in a 3.0 wt % PEG solution. We compared the radius of collected microgels R with the initial droplet size before their collection in the PEG solution (R0). The swelling ratio R/R0 is plotted against 1/R for three different temperatures (Figure 4). The value of R/R0 increases with an increase in 1/R from 1 and approaches 1.9 for smaller microgels with 1/R ≥ 3 × 10–2 [μm–1] (R ≤ 33 μm) for all temperature conditions. Since this R dependence of the swelling ratio is similar to that of E (Figure 3) and swelling behavior is determined by the nanostructure of the gels, it is expected that the increase in E of a small microgel was a result of a change in gel structure of the gelatin molecules.

Figure 4.

Figure 4

Open in a new tab

Swelling ratios of 5.0 wt % gelatin microgels through collection in a 3.0 wt % PEG 20k solution at 30 °C (red), 27 °C (black), and 21 °C (blue), respectively. R and R0 are the radii of the collected microgels and initial lipid droplets in oil, respectively. The solid line represents a saturation curve obtained from a simple exponential fit to the measured data.

Circular Dichroism (CD) Spectroscopy

To reveal the nanostructure of the microgels, we analyzed the secondary structure of gelatin in microgels and bulk gels using circular dichroism (CD) spectroscopy (Figure 5). The CD spectra of the bulk gels show two prominent peaks: a positive peak centered around 220 nm, corresponding to the collagen triple helices, and a negative peak centered around 200 nm, corresponding to random coils (Figure 5a, black), as has been reported previously.25,26 Compared with the bulk gels, the microgels maintained the positive peak at 220 nm and showed a drastic decrease in the negative peak at 200 nm (Figure 5a, blue). In the case of the liquid phase, the CD spectra of both the bulk solution and microdroplets show negative peaks at 200 nm corresponding to random coils (Figure 5b). The difference in the peak height might reflect an increase of random coil. These results demonstrate that the small microgels prepared inside lipid droplets contain similar quantities of triple helices but a different secondary structure that causes the decrease in the negative peak observed at around 200 nm.

Figure 5.

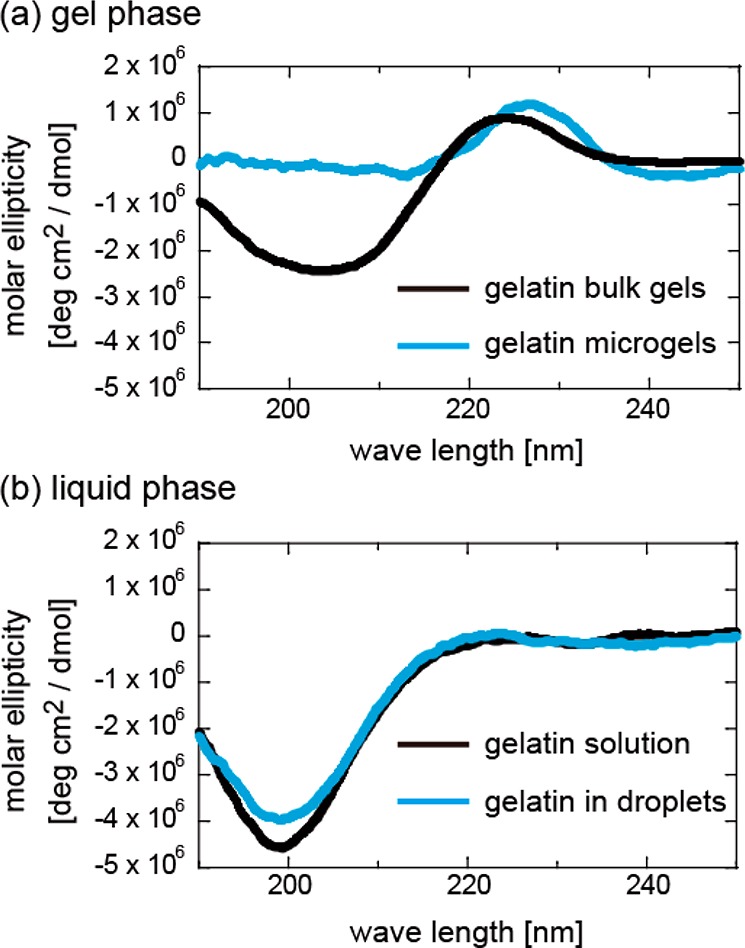
Figure 5

Open in a new tab

(a) CD spectra of a cut piece of bulk gels (black) and collected microgels (blue) of gelatin 5.0 wt %. Both the samples were immersed in a 3.0 wt % PEG solution. (b) The CD spectra of the gelatin solution in bulk (black) and lipid droplets (blue).

Amyloid Structures in Gelatin Microgels

Two mechanisms can be used to explain the diminishment of the 200 nm peak: (i) the fraction of random coil becoming high enough to cancel the peak and (ii) the diminishment of random coil through conversion to an ordered structure. Since the increase of random coils does not seem to explain the high elasticity of microgels, we assumed that the random coils converted to assembled β sheet rich structures, since the positive peak at 197 nm (for the β sheet)27 can cancel the negative peak at 200 nm. In addition, the slight peak shift to the higher wavelength side (Figure 5a) supports the β sheet formation, because the negative peak of β sheet centered at 218 nm can partially cancel the positive peak centered at 222 nm of collagen triple helices to shift the apparent peak to longer wavelength.

To verify this assumption, we tried to visualize the existence of a β sheet rich structure (like the amyloid structure) using Thioflavin T (ThT) in the following experiment. We added ThT to the gelatin microgels before gelation and analyzed the intensity IThT after 18 h of incubation. Figure 6a shows an example of the fluorescence image of droplets with different radii R0 and their intensity curves along the cross-sectional line. The values of IThT are homogeneous in a microgel, and their magnitude is larger for smaller microgels, which indicates that the smaller microgels contained more assembled β sheet rich structures. Such higher values of IThT for microgels (compared to the bulk gels) were also observed upon ThT addition in the collected microgels (Figure S5). We plot the R0 dependence of IThT normalized by that of the bulk gel (Ibulk) in Figure 6b. The magnitude of IThT/Ibulk increases with a decrease in R0 and reaches a saturation value at around 1/R0 = 14 × 10–2 [μm–1] (i.e., R0 ∼ 7 μm). The tendency of the ThT fluorescence intensity of small microgels to be higher than that of the bulk gels is in common with that for gel elasticity (Figure 3) and swelling ratio (Figure 4).

Figure 6.

Figure 6

Open in a new tab

(a) Confocal image of 5.0 wt % gelatin microgels in lipid droplets containing Thioflavin T (ThT) of different radii R0: (i) 22 μm, (ii) 6 μm, and (iii) 9 μm. The corresponding intensity profiles along the cross-sectional line are shown. (b) Average intensity inside the droplets normalized by that of the bulk gel IThT/Ibulk plotted against 1/R0.

The IThT increased as soon as the temperature dropped below the gelation point and saturated within 1 h. In considering whether this rapid increase of IThT is related to the higher E of the microgels, the microgel elasticity at 1 h after temperature reduction was measured. The microgels incubated for 1 h at 27 °C had an elasticity E = 27.1 ± 2.3 kPa (N = 10; 15 μm < R < 25 μm), which was similar to that of the microgels incubated for 24 h at 27 °C, E* ∼ 35 kPa (Figure 3a).

Furthermore, smaller microgels with R < 20 [μm] showed a slightly higher melting temperature than the gelatin bulk gel at ∼30 °C depending on the triple helix structure (Figure S6), resembling the gels formed by assembled β sheet rich structures that exhibited high melting temperatures.28,29

To further confirm the secondary structure change, we also analyzed the microgel structure by using Fourier transform infrared spectrometry (FT-IR). Absorbance difference between microgels and bulk gels of 5.0 wt % gelatin in PEG solution shows increase of peaks at 1620–1640 cm–1 (amide I band assigned to β sheet) and decrease of peaks at 1640–1660 cm–1 (amide I band assigned to α helix and random coil) (Figure S7). These results also support the enrichment of β sheet structure in gelatin microgels.

The high elasticity exhibited by the β sheet structure matches a previous study that revealed that the elasticity of various peptide-based gels with β sheet structures reaches tens of kPa.30 In addition, the conversion and assembly of a β sheet rich structure is known to be induced by lipids.31 These results strongly support that the high E of the microgel is due to the conversion of random coils into an assembled β sheet structure by the gelation present inside the microsized lipid space. Increase of the surface elasticity of the bulk gel covered with lipid membranes prior to gelation (Figure 2) indicates that lipid membrane promotes the secondary structure change of gelatin. We confirmed that the addition of 10–20 mM liposomes with a radius <500 nm to the bulk gels before gelation did not vary the elasticity, 3.1 ± 0.3 kPa (N = 4). Thus, the ratio of surface area of the lipid membrane to entrapped volume of the gelatin gel is the important parameter for increasing the gel elasticity.

Although the magnitude of E* = 35–39 kPa for the small microgel can be obtained by increasing the gelatin concentration (Figure 1d), it is not possible to change the gelation rate and melting temperature of the gelatin gel derived from a triple helix. We found that microgels form self-assembled β sheet structures through their microsized confinements in the lipid droplets. This structural change increased not only gel elasticity but also gelation rate and melting point. These are great advantages for the further application of gelatin-based microgels and represent important knowledge of the physicochemical properties of the biopolymer microgels obtained by gelation inside microsized space and the cytoskeleton gels in artificial and live cells.

Conclusion

We investigated Young’s modulus of a gelatin microgel by establishing a micropipet aspiration method and found that the gelation prepared inside a microsized lipid space increased the elasticity of the resultant gelatin gels. The magnitude of E increased with a decrease in the microgel radius R and approached E* (= 35–39 kPa) in the case of small microgels with R ≤ 50 μm; this value is significantly larger than that of the bulk gel (by ∼3 kPa). Analyzing the secondary structures of gelatin in microgels indicated that the increase in E can be attributed to the conversion of the secondary structure in the gel to assembled β sheet structure. Our findings demonstrate that the confinement size of a gelling polymer can be varied to control the mechanical properties of biopolymer gels.

Materials and Methods

Materials

1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine (PC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (PE), and polyethylene glycol (molecular weight 20,000; PEG 20k) were purchased from Wako Pure Chemical Industries (Osaka, Japan). Mineral oil was purchased from Nacalai Tesque (Kyoto, Japan), while alkali-treated gelatin was supplied by Nitta Gelatin Co. (Osaka, Japan). The average molecular weight of the gelatin as determined by gel-permeation chromatography was 190 kDa. Fluorescein isothiocyanate isomer I (FITC; Sigma-Aldrich Japan, Tokyo, Japan) and Rhodamine B labeled 1,2-dihexadecanoyl-sn-glycero-3-phosphatidylethanolamine (Rho-PE) (Invitrogen; Carlsbad, CA, USA) were used as fluorescent dyes for the gelatin and lipid, respectively. Thioflavin T (ThT; Wako Pure Chemical Industries) was used to detect β sheet rich structures like the amyloid structures. All the materials were used without further purification.

Preparation of Microgels inside Lipid Droplets and Their Collection

The spherical microgels were prepared using gelatin droplets coated with a lipid layer in an oil phase (Figure 1a). First, dry films of the lipids were formed at the bottom of a glass tube. The mineral oil was added to the lipid films followed by 90 min of sonication. The final concentration of the lipid/oil solution was approximately 1 mM. The gelatin was dissolved in water at 65 °C (above the gelation temperature Tg) for 1 h. To prepare the droplets, 10 vol % of the gelatin polymer solution was added to the lipid/oil solution at 65 °C. After emulsification via pipetting, we placed an aliquot containing the gelatin droplets on a silicone-coated cover glass to prevent the droplets from sticking to the glass plate. The samples were gradually cooled to 27 °C (<Tg) at a rate of approximately 0.2 °C/min and gelated by allowing them to stand for 24–26 h. Young’s modulus of the microgels was measured after collection by adding a 3.0 wt % PEG 20k solution to the microgel droplets in oil, as has been previously reported.15 This procedure disrupted the lipid membrane and exposed the microgel in the PEG aqueous phase.

Preparation of Bulk Gels

As a control sample, we prepared a bulk gel by sandwiching the gelatin solution between two glass slides. The volume was greater than 200 μL and thickness approximately 2 mm, which was large enough for the gel to not be affected by the bottom glass slide, as has been previously reported.32 In addition, we cut an approximately 0.5 mm thick portion of the gel surface to eliminate the influence of the glass slide on gel elasticity. During the analysis of the effect of membrane on bulk gel elasticity, we deposited the lipid-in-oil on the gelatin substrate, where the lipids spontaneously formed a membrane on the surface. We removed the lipid membrane by adding PEG prior to elasticity measurement, as was the case with the microgels.

Measurement of the Elasticity of Microgels Using Micropipet Aspiration

To measure Young’s modulus E of the microgels, we used micropipet aspiration (Figure 1b). Unlike a previous study in which the elasticity of a microgel was determined by aspirating it into a tapered micropipet, this method allowed us to measure the local elasticity of a microgel surface.17 We derived E from the following expression for a homogeneous half-space model.21,22

graphic file with name oc-2017-00625j_m001.jpg 1

Here, ΔP is the aspirate pressure, ΔL the protrusion length of microgel into the micropipet, and Rp the inner radius of the mouth of the micropipet. Φ is a constant determined by the geometry of the micropipet, and was fixed as 2.0, which is similar to the values observed in previous reports.21,22 We aspirated the gel by using a micropipet manipulator system (MMO-202ND and MN-4; Narishige, Tokyo, Japan) and microinjector (IM-11-2; Narishige) with a differential pressure transducer (DP15; Validyne, Northridge, CA) equipped with a microscope (Axiovert 40CFL; Carl Zeiss, Göttingen, Germany). We prepared a glass micropipet having a tip inner diameter of approximately 5 to 40 μm by pulling glass capillaries (GC-1; inner diameter 0.5 mm, Narishige) using a puller (PC-10; Narishige), microforge (MF-900; Narishige), and polishing machine (EG-401; Narishige).

Measurement of the Elasticity of Bulk Gels Using AFM

To determine the value of E of bulk gels, we also used an atomic force microscope (MFP-3D; Asylum Research) equipped with a tetrahedral cantilever (OMCL-AC240TS-C3; Olympus, Japan). The E value of the gels was determined by deforming the surface and fitting the force–indentation curve to the Hertz (Sneddon’s variation) model:33

graphic file with name oc-2017-00625j_m002.jpg 2

Here, F is the applied force calculated using κ, and δ the indentation length according to the difference between the piezo height and cantilever deflection. The elastic modulus (E) and Poisson’s ratio (ν) together define the material properties. Poisson’s ratio ν was assumed to be 0.5 because the gelatin gel was considered incompressible, as has been previously reported.34 The cantilever properties were defined by the opening angle α (=34°) and cantilever spring constant κ. A thermal vibration based program installed in the AFM instrument was used to calculate κ. The cantilever was calibrated before each experiment, and the average κ for the experiments was 2 N/m. By analyzing the approach curve, we obtained E.

Circular Dichroism Spectroscopy

The circular dichroism (CD) spectra of gelatin samples were detected in the far-UV region (190 to 300 nm) using a CD spectropolarimeter (J-720W, JASCO, Tokyo, Japan). Approximately 20 μL of the samples in the gel (at 27 °C) and sol (liquid) (at 65 °C) phases were scanned at 0.2 nm intervals and an optical path of 40 and 10 μm for the gel and sol phases, respectively. The data obtained in millidegrees with ten computer-averaged scans for each sample were further converted to molar ellipticity (deg cm2 dmol–1) using a mean residue weight of 100. As mentioned in Preparation of Microgels inside Lipid Droplets and Their Collection, the collected microgels were immersed in a 3.0 wt % PEG 20k solution. The concentration of the gelatin microgels used for CD analysis was 0.2 ± 0.1 wt % (14 ± 7 μM). To approximate the situation of mobile microgels in PEG, we cut bulk gels into approximately 0.5 mm parts and immersed them in a PEG solution with gelatin concentration 6.6 μM. As a sol sample, we prepared a 0.5 wt % gelatin solution (34 μM) and 0.2 ± 0.1 wt % gelatin droplets in an oil phase (14 ± 7 μM). The PEG and oil are invisible in the far-UV CD spectra.

Thioflavin T Fluorescence Assay

To estimate the amount of self-assembled β sheet structures in gelatin gels, we added a fluorescent dye detecting β sheet rich amyloid 5 μM Thioflavin T (ThT) to the gelatin solution before gelation and collected microgels in the 3.0 wt % PEG solution (refer to Preparation of Microgels inside Lipid Droplets and Their Collection). The incubation time at 27 °C was 18 h. The ThT intensity per unit volume IThT was obtained from the center of the cross-sectional image showing gelatin droplets of radius R > 5 μm by using a confocal laser scanning fluorescence microscope (CLSM; Olympus IX83 with FV1200). Thioflavin T excited by a 473 nm laser was collected with a band-pass filter (in the wavelength range 490–590 nm). The intensity IThT was analyzed by using the ImageJ software (National Institutes of Health) and normalized to the average intensity of the corresponding bulk gel, Ibulk.

Fourier Transform Infrared Spectrometry

To obtain Fourier transform infrared spectrometry (FT-IR) spectra, gelatin samples were prepared similarly to the method for CD spectroscopy. To avoid 1640 cm–1 absorbance of H2O, PEG solution and gelatin were prepared using D2O. The infrared spectrum of gels was measured by using a CaF2 transmission cell in an ALPHA FT-IR Spectrometer (Bruker, Billerica, MA, USA).

Acknowledgments

This work was supported by JSPS KAKENHI (M.Y.: No. 15H05463, No. 15KT0081, No. 16H00796, and No. 16H01443) and cooperative research program of “Network Joint Research Center for Materials and Devices” (20161280). We thank Ms. Michiko Maeda (Keio University) for her technical assistance in FT-IR measurements.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00625.

  • Microscopic image of microgels inside droplets (S1), fluorescence image of microgels before and after the collection in PEG solution (S2), pipet size dependence of derived microgel elasticity (S3), elasticity of a cut bulk gel piece (S4), fluorescence image of collected microgels after the addition of Thioflavin T (S5), size distribution of collected microgels below and above sol–gel transition temperature of gelatin (S6), and FT-IR spectra of microgels (S7) (PDF)

Author Contributions

Y.M. and K.F. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

oc7b00625_si_001.pdf (474.2KB, pdf)

References

  1. Saunders B. R.; Vincent B. Microgel particles as model colloids: theory, properties and applications. Adv. Colloid Interface Sci. 1999, 80 (1), 1–25. 10.1016/S0001-8686(98)00071-2. [DOI] [Google Scholar]
  2. Fernandez-Nieves A.; Wyss H.; Mattsson J.; Weitz D. A.. Microgel suspensions: fundamentals and applications; John Wiley & Sons: Weinheim, 2011. [Google Scholar]
  3. Cai W. S.; Gupta R. B. Fast-responding bulk hydrogels with microstructure. J. Appl. Polym. Sci. 2002, 83 (1), 169–178. 10.1002/app.10034. [DOI] [Google Scholar]
  4. Shimanovich U.; Efimov I.; Mason T. O.; Flagmeier P.; Buell A. K.; Gedanken A.; Linse S.; Akerfeldt K. S.; Dobson C. M.; Weitz D. A.; Knowles T. P. Protein microgels from amyloid fibril networks. ACS Nano 2015, 9 (1), 43–51. 10.1021/nn504869d. [DOI] [PubMed] [Google Scholar]
  5. Li Y.; Meng H.; Liu Y.; Narkar A.; Lee B. P. Gelatin Microgel Incorporated Poly(ethylene glycol)-Based Bioadhesive with Enhanced Adhesive Property and Bioactivity. ACS Appl. Mater. Interfaces 2016, 8 (19), 11980–11989. 10.1021/acsami.6b01364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Velasco D.; Tumarkin E.; Kumacheva E. Microfluidic encapsulation of cells in polymer microgels. Small 2012, 8 (11), 1633–1642. 10.1002/smll.201102464. [DOI] [PubMed] [Google Scholar]
  7. Morimoto Y.; Takeuchi S. Three-dimensional cell culture based on microfluidic techniques to mimic living tissues. Biomater. Sci. 2013, 1 (3), 257–264. 10.1039/C2BM00117A. [DOI] [PubMed] [Google Scholar]
  8. Kurokawa C.; Fujiwara K.; Morita M.; Kawamata I.; Kawagishi Y.; Sakai A.; Murayama Y.; Nomura S. M.; Murata S.; Takinoue M.; Yanagisawa M. DNA cytoskeleton for stabilizing artificial cells. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (28), 7228–7233. 10.1073/pnas.1702208114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kumar R. K.; Yu X.; Patil A. J.; Li M.; Mann S. Cytoskeletal-like supramolecular assembly and nanoparticle-based motors in a model protocell. Angew. Chem., Int. Ed. 2011, 50 (40), 9343–9347. 10.1002/anie.201102628. [DOI] [PubMed] [Google Scholar]
  10. Shum H. C.; Abate A. R.; Lee D.; Studart A. R.; Wang B.; Chen C. H.; Thiele J.; Shah R. K.; Krummel A.; Weitz D. A. Droplet microfluidics for fabrication of non-spherical particles. Macromol. Rapid Commun. 2010, 31 (2), 108–118. 10.1002/marc.200900590. [DOI] [PubMed] [Google Scholar]
  11. Theberge A. B.; Courtois F.; Schaerli Y.; Fischlechner M.; Abell C.; Hollfelder F.; Huck W. T. Microdroplets in microfluidics: an evolving platform for discoveries in chemistry and biology. Angew. Chem., Int. Ed. 2010, 49 (34), 5846–5868. 10.1002/anie.200906653. [DOI] [PubMed] [Google Scholar]
  12. Wang J. T.; Wang J.; Han J. J. Fabrication of advanced particles and particle-based materials assisted by droplet-based microfluidics. Small 2011, 7 (13), 1728–1754. 10.1002/smll.201001913. [DOI] [PubMed] [Google Scholar]
  13. Ma S.; Thiele J.; Liu X.; Bai Y.; Abell C.; Huck W. T. Fabrication of microgel particles with complex shape via selective polymerization of aqueous two-phase systems. Small 2012, 8 (15), 2356–2360. 10.1002/smll.201102715. [DOI] [PubMed] [Google Scholar]
  14. Choi C. H.; Weitz D. A.; Lee C. S. One step formation of controllable complex emulsions: from functional particles to simultaneous encapsulation of hydrophilic and hydrophobic agents into desired position. Adv. Mater. 2013, 25 (18), 2536–2541. 10.1002/adma.201204657. [DOI] [PubMed] [Google Scholar]
  15. Yanagisawa M.; Nigorikawa S.; Sakaue T.; Fujiwara K.; Tokita M. Multiple patterns of polymer gels in microspheres due to the interplay among phase separation, wetting, and gelation. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (45), 15894–15899. 10.1073/pnas.1416592111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hu Y.; Wang S.; Abbaspourrad A.; Ardekani A. M. Fabrication of shape controllable Janus alginate/pNIPAAm microgels via microfluidics technique and off-chip ionic cross-linking. Langmuir 2015, 31 (6), 1885–91. 10.1021/la504422j. [DOI] [PubMed] [Google Scholar]
  17. Wyss H. M.; Franke T.; Mele E.; Weitz D. A. Capillary micromechanics: Measuring the elasticity of microscopic soft objects. Soft Matter 2010, 6 (18), 4550–4555. 10.1039/c003344h. [DOI] [Google Scholar]
  18. Abate A. R.; Han L.; Jin L.; Suo Z.; Weitz D. A. Measuring the elastic modulus of microgels using microdrops. Soft Matter 2012, 8 (39), 10032–10035. 10.1039/c2sm26108a. [DOI] [Google Scholar]
  19. Kato A.; Yanagisawa M.; Sato Y. T.; Fujiwara K.; Yoshikawa K. Cell-Sized confinement in microspheres accelerates the reaction of gene expression. Sci. Rep. 2012, 2, 283. 10.1038/srep00283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ao M.; Xu G.; Kang W.; Meng L.; Gong H.; Zhou T. Surface rheological behavior of gelatin/ionic liquid-type imidazolium gemini surfactant mixed systems. Soft Matter 2011, 7 (3), 1199–1206. 10.1039/C0SM00556H. [DOI] [Google Scholar]
  21. Theret D. P.; Levesque M.; Sato M.; Nerem R.; Wheeler L. The application of a homogeneous half-space model in the analysis of endothelial cell micropipette measurements. J. Biomech. Eng. 1988, 110 (3), 190–199. 10.1115/1.3108430. [DOI] [PubMed] [Google Scholar]
  22. Hochmuth R. M. Micropipette aspiration of living cells. J. Biomech. 2000, 33 (1), 15–22. 10.1016/S0021-9290(99)00175-X. [DOI] [PubMed] [Google Scholar]
  23. Kwok R.; Evans E. Thermoelasticity of large lecithin bilayer vesicles. Biophys. J. 1981, 35 (3), 637–652. 10.1016/S0006-3495(81)84817-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Uricanu V.; Duits M. H.; Nelissen R.; Bennink M. L.; Mellema J. Local structure and elasticity of soft gelatin gels studied with atomic force microscopy. Langmuir 2003, 19 (20), 8182–8194. 10.1021/la0347004. [DOI] [Google Scholar]
  25. Usha R.; Ramasami T. Stability of collagen with polyols against guanidine denaturation. Colloids Surf., B 2008, 61 (1), 39–42. 10.1016/j.colsurfb.2007.07.005. [DOI] [PubMed] [Google Scholar]
  26. Pelc D.; Marion S.; Pozek M.; Basletic M. Role of microscopic phase separation in gelation of aqueous gelatin solutions. Soft Matter 2014, 10 (2), 348–356. 10.1039/C3SM52542B. [DOI] [PubMed] [Google Scholar]
  27. Wei Y.; Thyparambil A. A.; Latour R. A. Protein helical structure determination using CD spectroscopy for solutions with strong background absorbance from 190 to 230nm. Biochim. Biophys. Acta, Proteins Proteomics 2014, 1844 (12), 2331–2337. 10.1016/j.bbapap.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Marchesan S.; Styan K.; Easton C.; Waddington L.; Vargiu A. Higher and lower supramolecular orders for the design of self-assembled heterochiral tripeptide hydrogel biomaterials. J. Mater. Chem. B 2015, 3 (41), 8123–8132. 10.1039/C5TB00858A. [DOI] [PubMed] [Google Scholar]
  29. Kopeček J.; Yang J. Peptide-directed self-assembly of hydrogels. Acta Biomater. 2009, 5 (3), 805–816. 10.1016/j.actbio.2008.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. De Leon Rodriguez L. M.; Hemar Y.; Cornish J.; Brimble M. A. Structure-mechanical property correlations of hydrogel forming beta-sheet peptides. Chem. Soc. Rev. 2016, 45 (17), 4797–824. 10.1039/C5CS00941C. [DOI] [PubMed] [Google Scholar]
  31. Terakawa M. S.; Yagi H.; Adachi M.; Lee Y. H.; Goto Y. Small liposomes accelerate the fibrillation of amyloid beta (1–40). J. Biol. Chem. 2015, 290 (2), 815–826. 10.1074/jbc.M114.592527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Domke J.; Radmacher M. Measuring the elastic properties of thin polymer films with the atomic force microscope. Langmuir 1998, 14 (12), 3320–3325. 10.1021/la9713006. [DOI] [Google Scholar]
  33. Radmacher M.; Fritz M.; Hansma P. K. Imaging soft samples with the atomic force microscope: gelatin in water and propanol. Biophys. J. 1995, 69 (1), 264–270. 10.1016/S0006-3495(95)79897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sheppard S.; Sweet S.; Benedict A. J. Elasticity of purified gelatin jellies as a function of hydrogen-ion concentration. J. Am. Chem. Soc. 1922, 44 (9), 1857–1866. 10.1021/ja01430a003. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc7b00625_si_001.pdf (474.2KB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES