Signal intensity analysis and optimization for in vivo imaging of Cherenkov and excited luminescence

Abstract

During external beam radiotherapy (EBRT), in vivo Cherenkov optical emissions can be used as a dosimetry tool or to excite luminescence, termed Cerenkov-excited luminescence (CEL) with microsecond-level time-gated cameras. The goal of this work was to develop a complete theoretical foundation for the detectable signal strength, in order to provide guidance on optimization of the limits of detection and how to optimize imaging, near real time frame rates. The key parameters affecting photon production, propagation and detection were considered and experimental validation with both tissue phantoms and a murine model are shown. Both the theoretical analysis and experimental data indicate that the detection level is near a single photon-per-pixel for the detection geometry and frame rates commonly used, with the strongest factor being the signal decrease with the square of distance from tissue to camera. Experimental data demonstrates how the SNR improves with increasing integration time, but only up to the point where the dominance of camera read noise is overcome by stray photon noise that cannot be suppressed. In a fixed geometry and camera, the signal to background ratio limits the detection of light signals, and the observed in vivo Cherenkov emission is on the order of 100× stronger than CEL signals. As a result, imaging signals from depths < 15mm is reasonable for Cherenkov light, and depths < 3mm is reasonable for CEL imaging. The current investigation modeled Cherenkov and CEL imaging of two oxygen sensing phosphorescent compounds, but the modularity of the code allows for easy comparison of different agents or alternative cameras, geometries or tissues.

Introduction

Cherenkov based dosimetry or luminescence imaging have recently been developed for sensing within a range of applications including radiation therapy dosimetry.^1–6 This light intensity is an example of a signal that is linearly related to the applied radiation to the tissue.^2,7 In general, the light signals available to be detected are quite low, being near the single photon per pixel level for most detection systems. The detection approaches to dealing with these signals are advanced, but the choice of ideal detection device strongly depends upon knowledge of the signal intensity, especially at this range where it could be below or above the single photon per pixel level.⁸ In this study, a rigorous theoretical analysis of the signal level available was completed and validated through both ex vivo and in vivo experiments, in order to assess where optimizations might best be made.

There are a number of single photon detection strategies using specialized signal processing to ensure that the signal read out from the camera is real, and not attributed to noise. One of the dominant factors in deciding the detection scheme is the speed of readout desired, because the number of photons per pixel per unit time will affect the acceptable noise and readout noise. Long integration times of seconds to minutes can be achieved with low noise cameras such as a cooled CCD. However, when the readout time is the range of milliseconds, then the ideal choice might be a cooled sCMOS sensor. Yet again when the timing of acquisition needs to be in the microsecond range, then few options exist for this fast gating, other than a time-gated image intensifier. In the application of Cherenkov mediated imaging from a linear accelerator, this latter approach is required, with fast temporal gating, with on and off times in the nanosecond range. As result, much of this study focuses on an image intensified camera, where the initial detection event occurs at the entry photocathode, and after amplification, follows through to a phosphor plate.

The photon budget considers several parameters, including: the number of Cherenkov source photons, attenuation due to tissue optical properties, lens type and placement, photocathode quantum efficiency, micro-channel plate gain, phosphor plate quantum efficiency, and CCD efficiency. Noise introduced by the photocathode, CCD, and analog-to-digital converter (ADC) are also considered. Where possible, the budget tracks photon wavelength within the range of 350–900nm with 10nm resolution. A series of Python scripts were developed to track the photon counts at each stage, from Cherenkov emission through digitization at the ADC.

The scheme of how to maximize the signal to noise in these cameras depends upon a better understanding of the signal and noise levels. This current investigation provides the basis for a photon budget for both Cherenkov emission imaging, as well as Cherenkov excited luminescence (CEL) imaging from two phosphorescent compounds used experimentally. The work begins with an in depth theoretical treatment of all aspects of the imaging situation which affect the signal strength, and then progresses to experimental studies that are used to validate the predictions. Ultimately the results of this study can then guide optimization with this type of camera, or alternatively other detection systems which are optimized for single photon imaging.

Theory

Signal Source

Cherenkov photons are generated over a wide spectral range, but within the UV/optical/NIR range the distribution is proportional to 1/λ², as described by the Frank-Tamm formula, which can be used to calculate the number of emitted Cherenkov photons for a given input phase velocity (β) and target refractive index (n).^9,10 Extensive Monte Carlo simulations have been performed previously to relate the Cherenkov photon fluence to EBRT dose rates (Gy/sec).⁷ These spectrally-resolved photon fluence values can then be used to estimate the number of Cherenkov photons produced during CEL imaging.

CEL imaging relies upon the emission of Cherenkov photons to excite a localized phosphorescent compound within the medium. Unlike fluorescence imaging, which generally use an external light source for excitation, CEL is accomplished through the local production of photons within a target, such as tissue. Localized Cherenkov photons are produced when high-energy charged particles, such as electrons, move through a dielectric medium at a speed faster than the phase velocity of light for the given target.⁹ For medical-imaging applications the high-energy electron source is generally caused by either a radioisotope implanted in the target tissue,^11–13 or from an external beam radiotherapy (EBRT).^1,2,14 This paper will focus on the latter, although Monte Carlo simulations have been used to relate the photons generated by the two sources.^7,15,16

Tissue Optical Properties

While the Cherenkov emission spectrum is heavily UV/blue-weighted, with in vivo imaging, much of this spectrum is attenuated due to tissue optical properties. Tissue is composed of several smaller structures, each with unique absorption and scattering properties. The bulk summation of these optical properties can be assessed based on estimates of the proportions of contributing factors such as hemoglobin, water, and lipids. These estimates can then be applied to Monte Carlo simulations for boundary interactions, or applied to diffusion theory estimates of light propagation deeper in tissue.

When Cherenkov photons are emitted deep within tissue, surface detection will be red-shifted due to the light attenuation introduced by tissue.² Additionally, the light scattering in tissue further increases pathlength of travel, compounding the absorption due to blood, and as a result the dominant light signal available is within the 650–950nm range. Since there are reduced numbers of Cherenkov photons in this part of the spectrum, the overall signal is reduced and the detection is more difficult. It has been a bit unclear if the optimal excitation of a CEL should be in the blue or red wavelengths, but recent data suggests that red excitation is superior to blue for maximal CEL signal.¹⁷ The red Cherenkov photons produced within tissue can be absorbed and re-emit photons at a longer NIR wavelength, which travel further in tissue. Several factors come into play when selecting an appropriate compound. As with fluorescence imaging, the quantum yield (Φ) of the compound is one important factor which dictates the efficiency of the compound. In CEL imaging time gating is used to separate Cherenkov emissions from luminescence, so phosphorescence lifetime (τ) is also an important factor. Medical Linear accelerators have a 3–4 microsecond radiation pulse, and so this moderate pulse time limits most time gating to the microsecond regime. The luminescent agents which are available with microsecond lifetimes are phosphorescent. It has not been feasible to detect fluorescent agents which by definition have nanosecond lifetimes, other than through wavelength filtering and continuous wave detection.¹⁷ In medical applications biocompatibility and the ability to target areas of interest are also important factors, however these are outside the scope of the current investigation.

Detection Hardware

In EBRT, a linear accelerator delivers 3–4 microsecond bursts of radiation at a specific duty cycle, often in the range of 100–400 Hz, which can be synchronized to the gating of the shutter of a sensitive camera. The speed of this gating is not conducive to mechanical shuttering, requiring the use of electronic gating approaches such as an image intensifier can. In previous work, an ICCD was chosen as the optimal camera for both sensitivity and time-gating reasons.⁸ This current investigation focuses on time-gated discrimination of Cherenkov emission and luminescence, and what level of signal is available within this constraint, however the estimation of photon levels can also be applied to assess the applicability of other camera systems.

Camera position and lens selection are two factors that influence resolution, field of view, and photon sensitivity. Several other inherent camera properties can also influence detection. In an ICCD, the intensifier has three components: the photocathode, microchannel plate (MCP), and phosphor screen, which each play a role in the sensitivity. The photocathode converts photons to electrons by the photoelectric effect. Then a high voltage applied across the MCP attracts the electrons to the nearest channel, where they are multiplied through multiple wall collisions, often to 10,000× more than the entering electron numbers. This amplified electron flow then exits the MCP onto a phosphor screen, which converts these fast electrons into photons. The phosphor screens have a certain quantum efficiency (QE) for producing light from these electrons, and then this optical signal must be imaged by a camera, like a CCD or CMOS sensor, for pixelated electronic imaging. In the case studied here, the CCD converts these photons back to an electric charge, based on the QE of the sensor. Other CCD properties like dark current and full well capacity will also influence detection. The analog to digital converter (ADC) will also introduce a certain amount of uncertainty when quantizing the analog signal into bins with 16-bit resolution. The readout noise is also usually a dominant factor in what is detectable with a sensor, and so determining how fast to read the signal or how long to integrate for is often determined by the intensity of the signals on the chip.

Environmental conditions may also impact the ability to discriminate signal from background. While time-gating reduces the impact of ambient lighting during Cherenkov detection, ambient light is unnecessary background and often needs to be minimized. Within the ICCD a certain level of effective background illumination (EBI) will be introduced by the intensifier. Additionally, thermal dark noise (σ_D) and shot noise (σ_S) will be introduced by the CCD. For detection, usually the target signal must be greater the sum of the noise components, or else more elaborate methods for signal averaging or signal processing must be employed.

Methods

A photon budget for EBRT CEL imaging was developed based on previously reported camera configurations and imaging geometries. Estimates of photon counts were made between 350nm and 900nm with a 10nm resolution for each step in the Cherenkov and CEL imaging process. The estimates in the following section are for quanta (photons or electrons) as they travel from their source through the final step of being detected and digitized at a single (2×2-binned) pixel with the resolution of 315μm (0.1mm²).

The input parameters for each component in the imaging system are provided in the supplementary material (S1). Python code was developed to read this input file and determine the quanta at each stage based on the input radiation dose and total exposure time. The quanta for wavelengths of interest are recorded in an output file which is organized by tissue depth of the source photons. Output files were created for Cherenkov detection (S2), and phosphorescence detection (S3).

Cherenkov

Previous Monte Carlo simulations documented by Glaser et al. ⁷ provide the fluence rate over a wide spectral range for Cherenkov photons produced in tissue as the result of an external 6MV X-ray photon beam. This average fluence rate (nW/cm²) is provided as a function of radiation dose rate (Gy/sec) and can be converted to photon flux (photons/cm²) by accounting for the energy at each wavelength. The photon flux is then dependent on the radiation dose rate, which can be simplified to be assumed at a standard 0.1Gy/sec (600MU/min, the standard Monitor Unit rate of the Varian Clinac2100CD at 6MV). The Varian higher energy clinical linear accelerator (Clinac 2100C) referenced in previous CEL publications provides a 3–4μs radiation pulse at a variable repetition rate of 60Hz–360Hz, but commonly at 360 Hz for the higher MU/min.^6,8,18

The number of Cherenkov photons can then be estimated for the area detected by a single pixel (0.1mm²) based on the total dose delivered. For simplicity, this is calculated for the following: a single pulse (0.028 cGy), 30 pulses (0.83 cGy), 60 pulses (1.67 cGy), and 7200 pulses (2 Gy), where 2Gy is a typical daily dose given during fractionated radiotherapy.

Luminescence

The number of photons absorbed by a phosphorescent compound is governed by the molar extinction coefficient and concentration of the compound. The quantum yield provides a metric of how efficiently the compound emits photons when one is absorbed. Two phosphorescent compounds are considered in this photon budget: PtG4 (λ_Ex: 435nm, 623nm, λ_Em: 772nm)¹⁹ and Ir(btp)₂(acac) (λ_Ex: 337nm, 480nm, λ_Em: 620nm)²⁰. It is assumed 50μL of a 50μM solution is injected into a tumor with a total volume of 250mm³. So, assuming the compound is distributed homogenously throughout the tumor and does not leak, the final concentration in the tumor would be 10uM or a total number of 0.25 nanomols. Since both compounds have primary excitation peaks below 500nm, it can be assumed the Cherenkov-excitation must originate within 1mm (defined as d₀ in Table 1) due to the attenuation of shorter wavelengths in tissue.

Table 1.

Parameters considered in photon budget and typical range of quanta available at each stage.

Component	Parameters		Parameter range		Quanta range (N/mm2)
Radiation	γ− (MV) or e− (MeV), Dose (Gy), Rate (Gy/s)		6–18(MV), 6–18(MeV), 0–2(Gy), 0.017 – 0.1 (Gy/s)
Cherenkov	β, n		0.81–0.98, 1.3–1.5		1.0E+07–2.0E+11
Tissue μ-environment	$ex{p}^{-d_0{\mu }_a}({\text{mm}}^{-1})$		d0: <1mm μa: 0.02–20.0 (mm−1)		8.0E+06–2.0E+11
Luminescence	Φ (%), τ (μs)		0.01–0.3, 1–300 (μs)		8.0E+04–6.0E+10
Tissue diffusion	$ex{p}^{-d_1{\mu }_{\mathit{eff}}}({\text{mm}}^{-1})$		d1: 1–20 (mm) μeff: 0.1–10.0 (mm−1)		5.0E+02–5.0E+07
Camera placement	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${d_2}^2$}\right.$		d2: 300–2000 (mm)		1.0E−04–6.0E+02
Lens	$\frac{2si{n}^{-1}(NA)}{\pi }$		NA: 0.09–0.42		7.0E−06–2.0E+02
	Signal	Background	Signal	Background	Signal	Background
Photocathode	QE(λ) (%)	EBI (ph/pix/s)	0.01–0.35	0.002–0.02	7.0E−08–6.0E+01	8.0E−08–1.0E−04
MCP	Gain		104–107		7.0E−04–6.0E+08	8.0E−04–1.0E+03
Phosphor plate	η (ph/e)	τ (ms)	95–200	0.2μs–3ms	7.0E−02–1.0E+11
Coupling	50%		30–80 %		3.0E−02–6.0E+10
CCD	QE(λ) (%)	σS, σD	0.3–0.5	$\sqrt{N}$, <2	1.0E−02–2.0E+10
ADC	Rate (MHz)	Read noise (e−)	2–32	10–70 (e−)

Tissue Optics

Tissue optical properties from previously published Monte Carlo simulations of photon interactions with a multi-layer skin model were adapted for the present investigation.² The spectral distribution of the absorption coefficient (μ_a) and the reduced scattering coefficient (μ_s’) were used to calculate the effective attenuation coefficient (μ_eff) using (1):

$${\mu }_{\mathit{eff}}(m{m}^{-1})=\sqrt{3{\mu }_a({\mu }_a+{\mu }_s^{\text{'}})}$$ (1)

For a diffuse approximation of the number of photons present at a given distance the Beer-Lambert Law can be applied with the effective attenuation coefficient as shown in (2):

$$I_{d_1}=I_{0}ex{p}^{-d_1{\mu }_{\mathit{eff}}}$$ (2)

Where d₁ is the distance (mm) from the photon source to tissue surface and I₀ is the number of photons at the source. This approximation can be applied to estimate either the number of Cherenkov photons, or the number of Cherenkov-excited luminescent photons which reach the surface.

System Configuration

Two specific combinations of camera position and lens specification were considered as a way to demonstrate practical set ups. First, a 135mm f/1.8 lens positioned 1.3m from the target, and secondly a 50mm f/1.2 lens positioned 0.63m from the target. The numerical aperture can be approximated from the f-number using (3) and (4) to determine the acceptance angle:

$$NA~\frac{1}{2\ast f\_\mathit{number}}$$ (3)

$$\theta =si{n}^{-1}(NA)$$ (4)

Since it was assumed that the light at the surface of the target tissue would emit light isotopically, only half the emitted light would leave the tissue and the total light captured by the lens (N_lens) must be adjusted using (5):

$$N_{\mathit{lens}}=\frac{2\theta }{\pi }$$ (5)

The photons would then diffuse from the source proportional to 1/d₂², where d₂ is the distance from the target to the lens, assuming each point on the tissue acts like an isotropic emitter. Since the 50mm f/1.2 lens positioned 0.63m collects more photons, only values using this lens configuration are reported in the simulation output files (S2–S3). Additionally, experimental validation reported in subsequent sections uses a 50mm f/1.2 at this approximate distance.

Image Intensifier

The photocathode QE is applied to the number of photons collected by the lens to determine the number of electrons entering the next stage of the intensifier. The current photon budget assumed that the photocathode is a filmless Gen III device with high red quantum efficiency²¹, so that the photocathode introduces noise in the form of EBI, which is near 0.02 photoelectrons/pixel/second at room temperature and an order of magnitude lower with active cooling.²¹ So, the total input EBI (N_EBI) is calculated using (6):

$$N_{\mathit{EBI}}=\mathit{EBI}(e/p/s)\ast N_{\mathit{pixels}}\ast t(\mathit{sec})$$ (6)

Where N_pixels is 4 because of the 2×2 pixel binning, and t is the total exposure time while the intensifier is on, which is the product of the gate width and number of accumulations on chip (AOC).

Multiple stages of MCPs can be chained together where typical amplification values are approximately 10⁴ (single stage), 10⁶ (double stage), 10⁷ (triple stage). These amplification values are used to determine the number of detected electrons which interact with the phosphor screen. The amplification is also applied to N_EBI to determine the background noise levels.

Two phosphor screens were considered: P43 and P46. P43 has a higher quantum efficiency (200 photons/electron) but a longer decay time (1.5–3.2 ms), whereas P43 has a lower quantum efficiency (95 photons/electron), but quicker decay time (0.2–20 us).²² The P43 and P46 phosphor screens emit photons at different wavelengths, which must be considered when factoring the CCD detection QE.

CCD Sensor

The CCD can be coupled to the intensifier by fibers, or with an air gap. The former is slightly more efficient, but with added cost, whereas the latter is more economical, but less efficient. A coupling efficiency of 50% is used in this budget. The noise characteristics of the CCD must also be combined with the EBI noise introduced at the photocathode. The CCD noise is characterized as shot noise (σ_S), which is defined by the square root of the number of incident photons, and dark current noise (σ_D) which is provided as a device specification.²¹ The total CCD noise is given by (7):

$$\mathit{Nois}{e}_{\mathit{CCD}}=\sqrt{{{\sigma }_S}^2+{{\sigma }_D}^2}$$ (7)

While the CCD noise, combined with the EBI provides a lower limit of detection, the full-well capacity of the CCD pixel provides and upper limit, and the current budget assumes a full well capacity of 130 ke⁻ per pixel.²¹ Since 2×2 pixel binning is assumed, this value is quadrupled. After the CCD converts the photons to electrons, the analog-to-digital converter (ADC) will introduce a certain amount of uncertainty, between 10 e⁻ and 70 e⁻, based on the rate of conversion, between 2 MHz and 32 MHz, respectively.²¹

Phantom Imaging

A mouse phantom (XFM-2X Fluorescence Phantom, PerkinElmer) with μ_eff ∈ [0.1, 3] mm⁻¹, and spectral response similar to tissue, was used for experimental validation of the Cherenkov photon sensitivity. As shown in Figure 1, a linear accelerator (Varian, Clinac 2100C, California, USA) produced a 6MV X-ray photon beam which was shaped by the multi-leaf-collimator (MLC) into a 5mm thick sheet across the midline of the phantom. A PiMAX4 ICCD (Princeton Instruments, New Jersey, USA) was triggered by the LINAC to acquire images 0.03μs after the beginning of the radiation pulse and for a gate width of 3.25μs, which is within the duration of each radiation pulse. The number of AOC was varied, while keeping the total dose fixed at 100MU (1Gy). The photocathode was not actively cooled during imaging, but the CCD was kept at −20°C.

Figure 1.

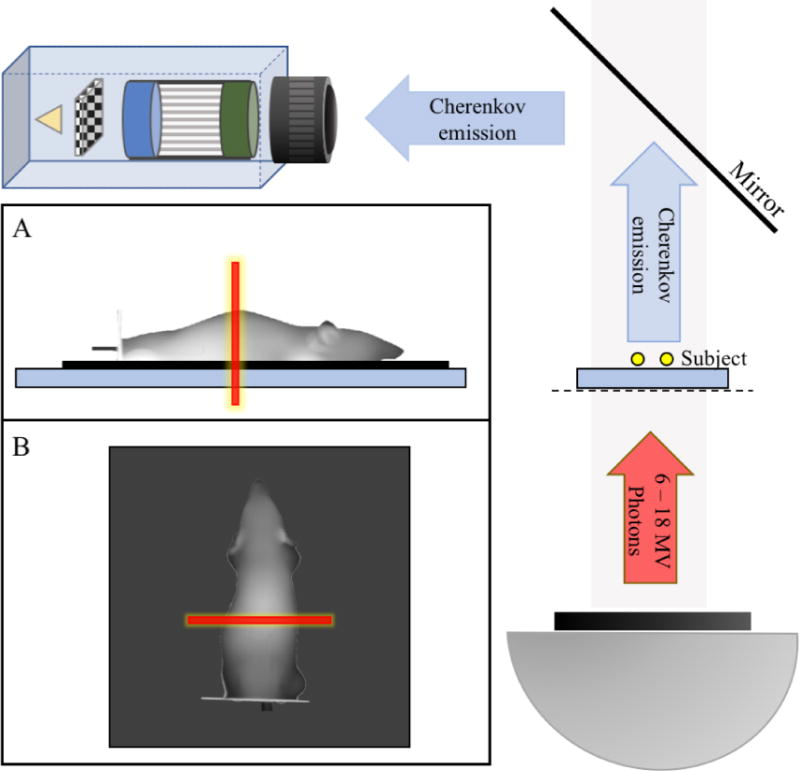
Geometry of the imaging system used for experimental validation. The LINAC gantry head is placed below the subject, providing a source of high energy photons. The subject is placed on the treatment couch with a mirror above to redirect photons towards the camera. (A) Side-view representation of the mouse phantom showing the radiation sheet in red. The mouse is placed on a 0.5–1.0cm thick water phantom to account for the buildup region of the radiation dose. (B) Top-view or camera-view representation of the mouse as seen by the ICCD with the radiation sheet superimposed.

In vivo Imaging

Human breast adenocarcinoma (MDA-MB-231) cells were implanted subcutaneously in two locations on the left and right lower flank of two nude mice. The tumors were allowed to grow until they were visible, but not ulcerated, approximately 100–250 mm³. Each mouse was anesthetized using isoflurane during imaging and placed prone on a black surface. Each tumor was injected with 50μL of a 50μM solution of each phosphorescent compound (0.25 nmol). Imaging was performed during anesthesia and 30 minutes after sacrifice, and a warming pad was used to regulate the mouse temperature for the duration of imaging.

Similar to the ex vivo phantom imaging, a linear accelerator produced a 6MV X-ray photon beam which was shaped by the multi-leaf-collimator (MLC) into a 5mm thick sheet. However, in this experiment the radiation sheet traveled orthogonally from the ventral to dorsal region of the mouse, scanning from a position cranial to the tumor and moving in the caudal direction. A PiMAX4 ICCD was triggered by the LINAC to acquire images 4.26μs after the beginning of the pulse, so each frame is collected after the radiation pulse. Data from approximately 65 pulses were accumulated on chip before being read off the CCD. The gate width was between 5 and 10 times the deoxygenated effective lifetime of the given phosphorescent compound. The photocathode was not actively cooled during imaging, but the CCD was kept at −20°C.

Results and Discussion

The parameters considered for each component of the imaging system are presented in Table 1, with corresponding typical ranges expected in EBRT. The associated quanta estimates using these ranges are also provided to demonstrate the magnitude of changes between elements. A more detailed breakdown of these interactions using a specific set of input parameters are provided in the following sections and the supplementary material.

Cherenkov Emission

The Cherenkov photon density in tissue due to a 6MV photon beam is given in Figure 2A for doses ranging from 0.03cGy to 2Gy. Tissue acts as a long pass filter as can be seen in Figure 2B and 2D. Shorter wavelength light is attenuated, so even though more Cherenkov photons are generated at shorter wavelengths, much of the detected signal originating from depths greater than 1mm in the tissue will be due to longer wavelengths. Figure 2D shows the Cherenkov photon budget for a source 3mm deep in tissue, where wavelengths shorter than 600nm are just above the noise floor, whereas wavelengths longer than 600nm are about two orders of magnitude above the noise floor. If we assume 30 pulses, corresponding to a dose of 0.83cGy, are accumulated on chip, then there are enough Cherenkov photons to be distinguished from the background, as shown in Figure 2D where all the lines are above the silver shaded region at the CCD.

Figure 2.

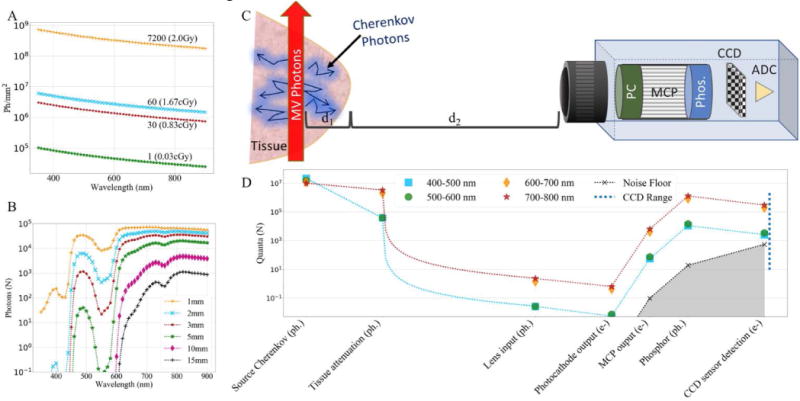
(A) Cherenkov photons produced in 1 mm² as the result of: a single radiation pulse (0.03cGy), 30 pulses (0.83cGy), 60 pulses (1.67cGy), and 7200 pulses (2Gy). (B) Cherenkov photon attenuation of 30 pulses (0.83cGy) observed at the tissue surface for photons emitted at various depths (d₁). (C) Schematic depicting imaging system and components of interest. (D) Photon budget for a Cherenkov source at 3mm below the tissue surface (d1) generated by a 0.83cGy dose, as detected by a 2×2 binned-pixel. The blue dotted line at right represents the usable dynamic range of the sensor.

Camera properties, such as lens placement also have a large impact on the detectable signal. Without accounting for distance, the f/1.2 lens can capture a maximum of 27.4% of the emitted light, while the f/1.8 captures up to 17.9%, however, when distance to the object is considered, the intensity obeys an inverse square relation, dramatically reducing the detected signal. The photon budget indicates the lens may only receive approximately a single photon for each binned-pixel. While this value is small, the intensifier can amplify the signal sufficiently for detection by the CCD.

The first stage of the intensifier, the photocathode, introduces a small amount of background intensity. The EBI is also amplified through the next two stages of the intensifier, depicted by the silver shaded region in Figures 2D and 3D. Cooling can help reduce the EBI by reducing the background by 10–20×, however this has little impact on the detectable Cherenkov signal as shown in Figure 4 where the ratio remains the same after cooling.

Figure 3.

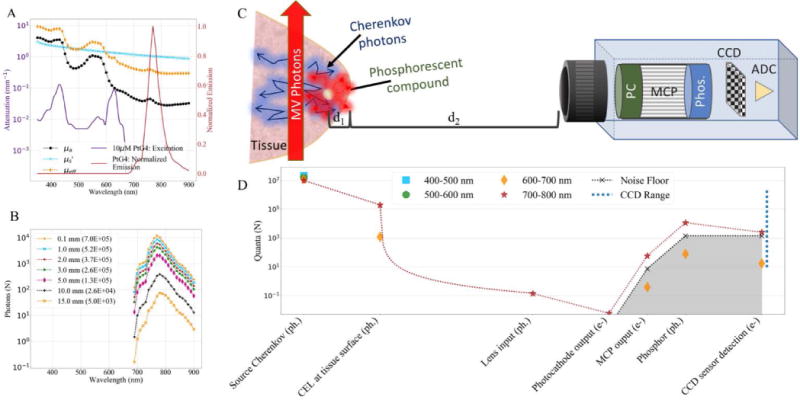
(A) Approximate tissue attenuation coefficients overlaid with extinction coefficient for 10μM PtG4 (left y-axis), and corresponding normalized emission spectrum (right y-axis). (B) Simulated photon count of CEL caused by 0.83cGy dose for a PtG4 source at various depths (d₁) within tissue. (C) Schematic depicting imaging system and components of interest. (D) Photon budget for PtG4 CEL source at 3mm below the tissue surface (d₁) generated by a 0.83cGy dose, as detected by a 2×2 binned-pixel. The blue dotted line at right represents the usable dynamic range of the sensor.

Figure 4.

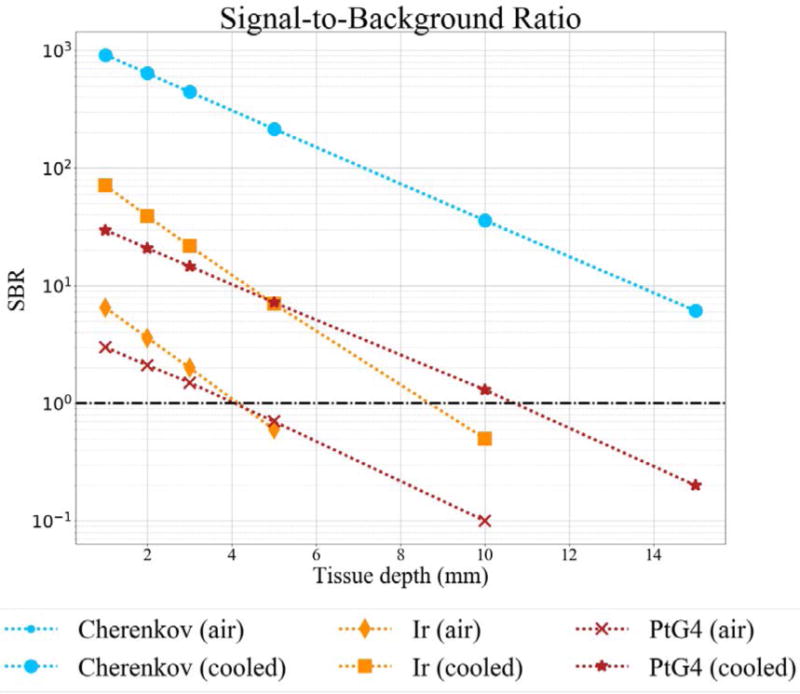
Theoretical Signal-to-Background ratio for Cherenkov and CEL detection with a photocathode room temperature, and cooled with dry nitrogen. Cherenkov values are the same.

Cherenkov-excited Luminescence

While it is possible to detect Cherenkov-photons with sufficient signal at depths of centimeters, it is not an ideal modality for targeted imaging often used to determine properties of subcutaneous lesions. Phosphorescent compounds can be used to absorb Cherenkov photons in tissue at depths of greater than a centimeter. The two compounds investigated in this study, PtG4 and Ir(btp)₂(acac) absorb photons at shorter wavelengths and emit longer wavelengths after the 4μs radiation pulse has stopped. Figure 3A shows the excitation and emission spectrum of PtG4, where the excitation overlaps with much of the Cherenkov emission. Even though both these compounds have quantum yields much lower than 1, the longer wavelengths are less affected by tissue attenuation and there is still sufficient signal for detection. The number of phosphorescence photons originating from a 10uM PtG4 inclusion at various tissue depths (d₁) is shown in Figure 3B. Since the phosphorescence shifts the output to a longer wavelength, there are no photons within the 400–500 or 500–600nm range shown beyond the Cherenkov source for the photon budget depicted in Figure 3D. Additionally, for this compound the photons between 600–700nm are not detectable without further processing because they are below the noise floor, shown as the silver shaded region.

As with the Cherenkov detection, the distance from the camera to the object of interest (d₂) has a very strong influence on the final signal due to the 1/d₂² relation. Since phosphorescence imaging has a lower overall signal than Cherenkov imaging, camera placement is one method that could greatly improve system sensitivity.

Since phosphorescence images are acquired after the 4μs radiation pulse and generally have a longer gate width (55μs–300μs), the EBI will have a larger influence because this background signal is directly related to the gate width and the number of accumulations on chip. The estimated signal and background intensities based on the simulated photon budget are summarized in Table 2 and used to calculate the signal-to-background ratios in Figure 4. Since EBI impacts phosphorescence detection more so than Cherenkov detection, background reduction through photocathode cooling will more positively influence CEL imaging, as can be seen in Figure 4. Without cooling, the photon budget indicates Ir(btp)₂(acac) is detectable at depths of approximately 3.5mm in tissue, and PtG4 is detectable at depths of approximately 3mm, however, with cooling these values increase to 8mm and 10mm, respectively. The difference in slope is due to the comparison of different wavelength ranges, where both Cherenkov and PtG4 have their highest SBR in the 700–800nm range, whereas Ir(btp)₂(acac) has a peak emission at 620nm, so the 500–600nm range was used to compute SBR for this compound.

Table 2.

Summary of photon budget parameters for different source depths in tissue, using optimal wavelength range.

Imaging Type	Cherenkov						CEL: PtG4						CEL: Ir
Pulses	30
Dose (cGy)	0.83
Gate Width (us)	4						300						55
Wavelength (nm)	700–800						700–800						600–700
Depth	1	2	3	5	10	15	1	2	3	5	10	15	1	2	3	5	10	15
Source	9.76E+06						9.76E+06						1.21E+07
Tissue output	6.78E+06	4.71E+06	3.28E+06	1.59E+06	2.67E+05	4.58E+04	3.98E+05	2.80E+05	1.97E+05	9.75E+04	1.71E+04	3.07E+03	1.40E+05	7.68E+04	4.28E+04	1.39E+04	9.89E+02	8.25E+01
Lens output (f/1.2 0.63m)	4.67E+00	3.25E+00	2.26E+00	1.10E+00	1.84E−01	3.16E−02	2.74E−01	1.93E−01	1.36E−01	6.72E−02	1.18E−02	2.12E−03	9.68E−02	5.29E−02	2.95E−02	9.57E−03	6.82E−04	5.69E−05
Photocathode output	1.31E+00	9.07E−01	6.31E−01	3.06E−01	5.09E−02	8.69E−03	1.15E−02	8.09E−03	5.69E−03	2.82E−03	4.93E−04	8.82E−05	4.54E−03	2.48E−03	1.38E−03	4.48E−04	3.19E−05	2.66E−06
MCP output (Single stage)	1.31E+04	9.07E+03	6.31E+03	3.06E+03	5.09E+02	8.69E+01	1.15E+02	8.09E+01	5.69E+01	2.82E+01	4.93E+00	8.82E−01	4.54E+01	2.48E+01	1.38E+01	4.48E+00	3.19E−01	2.66E−02
Phosphor screen output (P43)	2.61E+06	1.81E+06	1.26E+06	6.12E+05	1.02E+05	1.74E+04	2.30E+04	1.62E+04	1.14E+04	5.63E+03	9.86E+02	I.76E+02	9.08E+03	4.96E+03	2.77E+03	8.97E+02	6.38E+01	5.32E+00
CCD detection	4.96E+05	3.45E+05	2.40E+05	1.16E+05	1.93E+04	3.30E+03	4.38E+03	3.07E+03	2.16E−03	1.07E+03	1.87E+02	3.35E+01	1.72E+03	9.43E+02	5.25E+02	1.70E+02	1.21E+01	1.01E+00
Photocathode EBI	9.60E−06						7.20E−04						1.32E−04
MCP EBI	9.60E−02						7.20E+00						1.32E+00
Phosphor screen EBI	1.92E+01						1.44E+03						2.64E+02
CCD noise	5.41E+02						3.49E+01						2.05E+01
Total noise	5.41E+02						1.44E+03						2.65E+02
Approximate Pixel Intensity	62518	43438	30207	14648	2439	416	552	387	272	135	24	4	217	119	66	21	2	0
Approximate Noise Intensity	68						182						33
Signal to Background Ratio	917.1	637.2	443.1	214.9	35.8	6.1	3.0	2.1	1.5	0.7	0.1	0.0	6.5	3.6	2.0	0.6	0.0	0.0

Experimental validation

Phantom Imaging

Images of the mouse phantom acquired during the radiation pulse show detectable Cherenkov signal. As the number of AOC are increased, the image signal increases as seen in Figures 5. Higher AOC increase the signal intensity, but also increase radiation dose and background intensity levels.

Figure 5.

Cherenkov image frames of a mouse phantom captured with varying numbers of accumulations on chip (AOC).

To further quantify the relation of the signal and background, two regions of interest were defined for each image stack. The Cherenkov signal is defined as the region within the white boundary in Figure 6A, which is where the radiation beam is delivered to the mouse phantom. The background is defined as the region outside of the green boundary around the mouse phantom. The normalized distribution of pixel intensities for each region are shown for a Cherenkov image collected using 2 AOC as shown in Figure 6A–C. The distribution of the background appears Gaussian and pixel intensity is centered at 600 counts, which is the offset used by the PiMAX, whereas the distribution of the detected Cherenkov photons centered at 705 and follows a Poison distribution. As the number of accumulations increases, the variability of the pixel intensities for both regions grow, however it increases more rapidly for the background region. The ratios of the median pixel intensity for each region provides the signal-to-background ratio, as shown in Figure 6E for a single frame. Since there is an offset used in the camera, the signal-to-noise ratio is calculated as:

$$\mathit{SNR}=\frac{\mathit{Med}(\mathit{Beam})-600}{{\sigma }_{Bg}}$$ (8)

where σ_Bg is the standard deviation of pixel intensities in the background region. While both SBR and SNR increase with the number of AOC, the radiation dose required to capture each image also increases as shown in the upper x-axis of Figures 6D and 6E. The SNR was also determined for a fixed radiation dose of just under 7cGy by taking the temporal median of the acquired image frames, where 2 frames were used from the set of images acquired with 128 AOC, and 128 frames were used from the set acquired with 2 AOC. These parameters more closely match previously reported acquisition settings where temporal median filtering is often used to reduce noise from high-energy particles.^8,14,17 In this setting it can be seen in Figure 5E that the SNR plateaus between 64 and 128 AOC.

Figure 6.

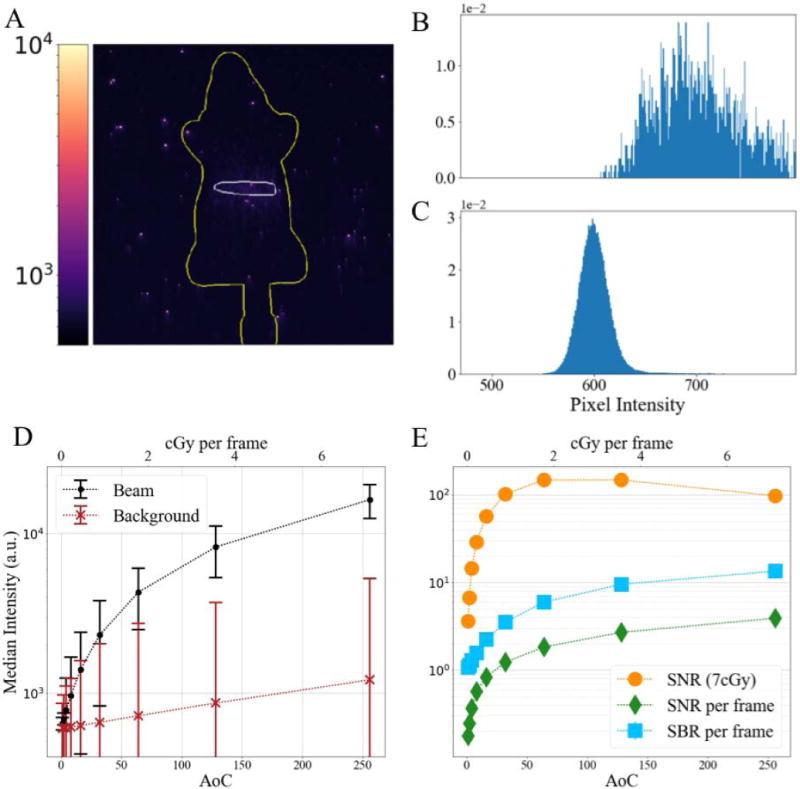
(A) Cherenkov image frame of a mouse phantom captured using 2 accumulations on chip; (B) Normalized histogram of intensity count for region of image receiving radiation dose (inside white area in (A)); (C) Normalized histogram of intensity count for background area around mouse phantom (outside green area in (A)); (D) Median pixel intensity of previously defined regions for different AOCs, where error bars show standard deviation of pixel intensities in region; (E) Signal-to-background ratio and signal to noise ratio for varying AOCs

In this phantom study, the image stacks captured with lower AOC values have lower photon flux due to the shorter CCD exposure times. In this region (<64 AOC) the primary factors contributing to noise are dark current and read noise from the ADC. In the read-noise-limited detection the signal is expected to increase linearly with the number of exposures, while the noise remains relatively constant. So, in this region, combining multiple exposures will increase the SNR by the square root of the number of exposures. However, as the photon flux increases with longer CCD exposure times (>64AOC), the primary factors contributing to noise are EBI from the photocathode and shot-noise in the CCD. In this photon-limited-noise region combining additional frames does not improve the overall SNR, as seen in Figure 6E. While the SNR should remain relatively unchanged, a single frame may still contain artifacts from high-energy particles, so in practice multiple frames are still acquired using a temporal median filter to reduce their influence on the final image.

In vivo imaging

Data collected from in vivo imaging of mice with subcutaneous tumors injected with PtG4 and Ir(btp)₂(acac) produce a detectable signal in a single frame. Tumors were estimated to be between 100 and 250 mm³ which corresponds to an approximate average dimension between 4.6 and 6.3 mm.

Approximating the thickness of mouse skin to be between 0.5 and 1.5 mm, and assuming there is additional tissue between the surface and tumor, we can estimate the phosphorescent signal will diffuse between 1 and 4mm in tissue before reaching the surface. From Figure 4 we see the estimated signal-to-background ratio in this range is estimated to be between 3.0 – 1.1 and 6.5 – 1.3 for PtG4 and Ir(btp)₂(acac), respectively.

A single frame for both Cherenkov and PtG4 phosphorescence detection are shown in Figure 7B and C, respectively. The Cherenkov image was collected using 32 accumulations on chip with a gate width of 3.5us, for a total dose of 0.89cGy. The phosphorescence frame was collected with 64 accumulations on chip and a gate width of 300us, for a total dose of 1.78cGy. From these images, we observe the Cherenkov pixel intensity values are on the order of 10⁴ counts, whereas the phosphorescence is an order of magnitude weaker, even though the Cherenkov image received half the dose. While the photon budget indicates the Cherenkov pixel intensity should be approximately 100× higher than the PtG4 intensity for equal radiation dose, as shown in Table 2, or 50× for half the dose, the in vivo PtG4 is localized below the skin whereas the Cherenkov originates at multiple locations within the mouse, which can account for the slight discrepancy.

Figure 7.

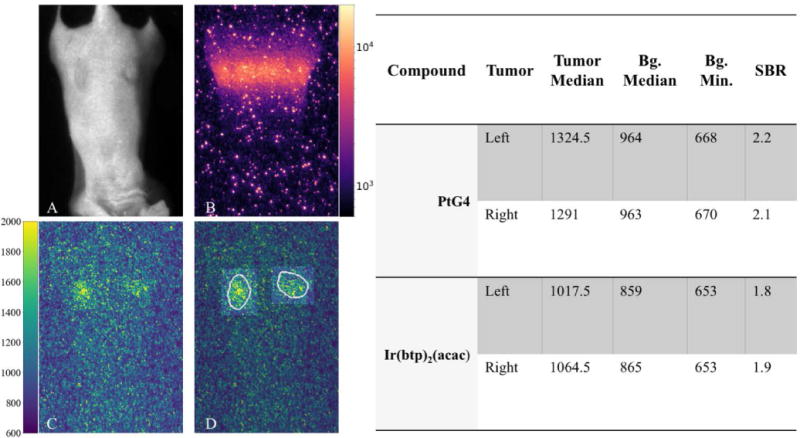
(A) Room-light image of mouse with two flank tumors injected with PtG4. (B) Single Cherenkov frame of interest during scanned imaging. (C) Single phosphorescence frame. (D) Regions of interests identified on phosphorescence frame, which were used to generate values shown in table.

While the photon budget indicates Cherenkov imaging exhibits a relatively strong signal with low background, the impact of high-energy particles observed as high-intensity speckle (Figure 7B) cannot be fully ignored, however, it can be overcome with temporal-median filtering. The short gate width and low number of accumulations needed to acquire an adequate Cherenkov frame help keep the background levels low, although higher photon counts will increase the CCD shot noise which can explain why in Table 2 Ir(btp)₂(acac) has lower noise than the Cherenkov image, even though the CEL image uses a longer gate width.

Regions of interest for each tumor were created from a processed image set. Briefly, a processed image set is created by temporally and spatially median filtering multiple frames. Temporal median filtering can be achieved because the MLC scans the radiation beam across the midline of the mouse and multiple frames are acquired at each MLC position, which provides the opportunity to take the median of sequential frames. A maximum intensity projection is performed on the resulting image stack, and a threshold is used to identify the area of maximum phosphorescence (white boundary in Figure 7D). The background is defined as the area outside of the tumor regions and is also overlaid as the darker area around the tumors in the phosphorescence frame shown in Figure 7D. There is a small amount of padding between the tumor and background regions to avoid diffusion of the phosphorescent signal and to account for a certain amount of uncertainty in tumor and injection locations. The median value of each region is determined for each frame and these values were used to calculate the SBR. The PiMAX4 adds an arbitrary offset to the pixel values of approximately 600 counts, so this is accounted for in this experiment by subtracting the background minimum from both regions in the same frame as shown in (9).

$$\mathit{SBR}=\frac{\mathit{Med}(\mathit{Tumor})-\mathit{Min}(Bg.)}{\mathit{Med}(Bg.)-\mathit{Min}(Bg.)}$$ (9)

The maximum experimentally determined SBR for PtG4 was found to be between 2.1 and 2.2, and between 1.8 and 1.9 for Ir(btp)₂(acac), which are both within the estimated ranges of the photon budget. Additionally, if we subtract the arbitrary offset, the median pixel values for the tumors are similar to those estimated by the photon budget, with the photon budget only slightly underestimating the actual values.

While phosphorescence lifetime is not directly considered in the photon budget, experimentally the gate width is generally set between 5–10 times the deoxygenated lifetime (τ₀). By accounting for gate width in the photon budget, we are indirectly compensating for the needed shift in detection time. While this works to reduce the noise floor, as can be observed when comparing the estimated noise intensity of PtG4 and Ir(btp)2(acac) (Table 2), there are practical limitations in applicable lifetimes.

The time between radiation pulses is one factor that will limit the maximum lifetime when choosing a phosphorescent compound. The LINAC generates radiation pulses at a repetition rate between 2.7 and 17ms (600MU/min–100MU/min), where the slower rates require longer treatment times, which can be impractical for in vivo imaging applications. Additionally, the phosphor plate in the image intensifier also has a decay which is generally provided in technical specifications. For example, P43 the decay to 10% or 1% the original signal is 1.5 and 3.2 ms, respectively, whereas P46 is ranges from 0.2 and 20 μs at the sacrifice of quantum efficiency and spatial resolution.²² In the current experiments a dose rate of 500MU/min, corresponding to a repetition rate of 3.3ms, was used to reduce the impact of ghosting between frames, which could be introduced at higher dose rates due to the limitations of the P43 decay time.

Shorter lifetimes can be difficult to discriminate from the radiation-induced Cherenkov light. The LINAC radiation pulse does not immediately turn off, and both stray charge and Cherenkov emissions may be detected during the transition phase. Phosphorescent compounds with lifetimes in this range (<4.5us) will be difficult to detect. While Ir(btp)₂(acac) has a deoxygenated effective lifetime beyond this range, when it is in a well-oxygenated environment it may be more difficult to detect, whereas PtG4 can be detected both in the presence and absence of oxygen.

Conclusions

Imaging system

There are many factors that influence the detection of Cherenkov emission and Cherenkov-excited luminescence in vivo. While there are detectable signals in both imaging modalities, photon flux during imaging can be very close to the noise floor, but discriminating the signal from the noise can be improved by optimizing several camera parameters. Phantom experiments demonstrated how SNR saturates when increasing the camera AOC value. This is thought to be the transition between the read-noise-limited and photon-noise-limited regimes. This transition point is where the SNR can be maximized without unnecessary increases to radiation dose. However, the transition point will change based on camera parameters such as positon, ADC rate, and cooling temperature, as well as the inherent photon flux of the system being imaged.

As can be observed in Table 1, and Figures 2C and 3C, detection signal is most sensitive to camera-to-target distance. The inverse square relation of distance from the source can be accommodated by designing the optical path such that the camera is placed proximal to the target, without placing the camera hardware in the path of the radiation beam.

While the intensifier can overcome the low photon count, the CEL signals are still very low and the system is noise-limited. While additional MCP stages could theoretically help improve the overall signal, this comes at great cost. Additionally, if the EBI is greater than the photon count at the photocathode, additional MCP stages will not improve the problem. Maintaining low noise levels is particularly important with CEL imaging, where photocathode cooling may produce an up to 3× increase in depth sensitivity.

In vivo properties

While we have observed in vivo Cherenkov emission to be on the order of 100× stronger than Cherenkov-excited phosphorescence for the compounds discussed in this investigation, much of Cherenkov light is being absorbed by nearby tissue, and thus never reaches the surface for detection. This absorption-dominated process can still be leveraged by localizing compounds which shift this energy to longer wavelengths which are impacted less by absorption. At these longer wavelengths, light attenuation in tissue is dominated by scatter and can travel further distances.

Tissue optical properties have a large impact on the overall signal, which is observed at greater depths. This is less of a concern for the implementation of Cherenkov for surface dosimetry. However, using CEL the detection of signals at depths is generally very important. One method to reduce the impact of this issue is to identify a phosphorescent compound with an emission less influenced by absorption. As can be seen in Figure 4 Ir(btp)₂(acac) has a more negative slope than PtG4, so while Ir(btp)₂(acac) has a slightly higher SBR at shallow depths, PtG4 is more robust at depth due to its emission peak at 772 nm, as opposed to the Ir(btp)₂(acac) emission peak at 620nm.

To optimize CEL, compounds which are excited by wavelengths shorter than approximately 500nm should be located as close to the targeted tissue as possible to maximize the energy transfer. The multiple dendritic chains of PtG4 allow it to circulate in blood with little degradation, whereas Ir(btp)₂(acac) can be endocytosed by cells.^20,23 While both methods can deliver the compound to the tumor microenvironment, they are not molecularly targeted, which could further enhance the in vivo applications of CEL imaging.

Model

The current investigation was limited to Cherenkov detection, and detection of CEL for two specific phosphorescent compounds. The input parameters for this model are organized in a single spreadsheet (S1), which allows for easily incorporating changes to the imaging environment. Additionally, simulating other compounds with known extinction coefficient, quantum yield, and lifetime would be trivial, as no code would need to be modified. While more detailed Monte Carlo simulations could be developed, the current model provides an estimate of which compounds warrant further investigation.

Supplementary Material

Data set S1

S1: Photon budget input parameters (S1_Photon_Budget_inputs.xlsx)

Data set S2

S2: Cherenkov photon budget output for select parameters organized by Cherenkov source depth in tissue (S2_Photon_Budget_outputs_30pulses_Cherenkov.xlsx)

Data set S3

S3: CEL photon budget for PtG4 and Ir(btp)₂(acac) for select parameters organized by depth of the phosphorescent compound in tissue (S3_Photon_Budget_outputs_30pulses_Phosphorescence.xlsx)