Abstract
Objectives
The long term goal of this research is to determine if the middle ear muscle reflex can be used to predict the number of healthy auditory nerve fibers in hearing impaired ears. In this study we develop a high-impedance source and an animal model of the middle ear muscle reflex and explore the influence of signal frequency and level on parameters of the reflex to determine an optimal signal to examine auditory nerve fiber survival.
Design
A high-impedance source was developed using a hearing aid receiver attached to a 0.06 diameter 10.5cm length tube. The impedance probe consisted of a microphone probe placed near the tip of a tube coupled to a sound source. The probe was calibrated by inserting it into a syringe of known volumes and impedances. The reflex in the anesthetized rat was measured with elicitor stimuli ranging from 3 kHz to 16 kHz presented at levels ranging from 35 to 100 dBSPL to one ear while the reflex was measured in the opposite ear containing the probe and probe stimulus.
Results
The amplitude of the reflex increased with elicitor level and was largest at 3 kHz. The lowest threshold was ~54 dBSPL for the 3 kHz stimulus. The rate of decay of the reflex was greatest at 16 kHz followed by 10 kHz and 3 kHz. The rate of decay did not change significantly with elicitor signal level for 3 and 16 kHz, but decreased as the level of the 10 kHz elicitor increased. A negative feedback model accounts for the reflex decay by having the strength of feedback dependent on auditory nerve input. The rise time of the reflex varied with frequency and changed with level for the 10 and 16 kHz signals but not significantly for the 3 kHz signal. The latency of the reflex increased with a decrease in elicitor level, and the change in latency with level was largest for the 10 kHz stimulus.
Conclusion
Because the amplitude of the reflex in rat was largest with an elicitor signal at 3 kHz, had the lowest threshold, and yielded the least amount of decay, this may be the ideal frequency to estimate auditory nerve survival in hearing impaired ears.
I. Introduction
Damage to cochlear structures, such as inner hair cells, leads to degeneration of auditory nerve fibers (Suzuka and Schuknecht, 1988; Nadol, 2001; Sugawara et al., 2004), and consequently alterations in central auditory physiology (Salvi et al., 2000). This occurs on a time scale of hours to years, and leaves the spiral ganglion cells with a short peripheral process. The connections from the spiral ganglion cells to the cochlear nucleus are generally maintained although the morphology of the connections is altered (Ryugo et al., 1998). Eventually, spiral ganglion cell bodies and their central processes degenerate. The time scale, however, depends on species, ranging from months in rodents to years in humans. Although this classic description of auditory nerve degeneration as a secondary effect of loss of inner hair cells is still true, recent evidence indicates that even temporary damage to the cochlea without loss of hair cells can cause auditory nerve degeneration (Kujawa and Liberman, 2009; Fernandez et al., 2015; Kujawa and Liberman, 2015). Moreover, both animal and human studies show that this degeneration progresses with aging (Sergeyenko et al. 2013; Makary et al, 2011).
Importantly, the loss of auditory nerve fibers alone does not influence hearing threshold. As early as the 1950’s Schucknect and Woellner (1955) showed that eliminating 50% of the auditory nerve had no effect on behavioral auditory thresholds (i.e. audiogram) in cat. The presence of normal hearing thresholds with nerve damage is termed “Hidden Hearing Loss”, and recent evidence indicates that this may be due to loss of low spontaneous rate fibers (Lin et al., 2011). Low spontaneous rate fibers code for high signal levels and are believed to be used for listening in a background of noise (Liberman et al., 2016). High spontaneous rate fibers code for low-level sounds. Unfortunately, damage due to noise exposure and aging causes degeneration of the low spontaneous rate fibers. Thus hearing threshold is not altered, but hearing with noise in the background is reduced; one of the most common complaints of patients with hearing loss.
A problem with current clinical diagnostic tests is that they do not identify the underlying anatomic damage that creates hearing loss. Hearing tests provide only a rough estimate of the underlying pathology (Otte et al., 1978; Salvi et al., 1983; Humes et al., 1984). With promising developments in gene therapy and stem cell transplantation for hair cell and neural recovery, it is important to develop new diagnostic procedures that define the locus of insult for targeting therapeutic agents as well as monitoring recovery after therapeutic intervention. In this study we begin to develop a biomarker of auditory nerve survival. This could be important for patients with hearing loss for many reasons: 1) identifying the targets for genetic and stem cell treatment to cure hearing loss, 2) predicting which patients will be good hearing aid users, 3) predicting candidacy for a cochlear implant (which requires auditory nerve survival), and 4) diagnosing the patient with “Hidden Hearing Loss” so that counseling regarding noise hazards and other aural rehabilitation procedures can be implemented.
Presently, hearing tests are not sensitive to auditory nerve degeneration. However, in an animal model it has been shown that the amplitude of wave 1 of the auditory brainstem response, which is generated by auditory nerve fibers, is reduced in animals with neural degeneration (Lin et al., 2011). Wave 1 of the auditory brainstem response can be recorded in humans and, with more research developing procedures to reduce between-patient variability, it may be a biomarker of auditory nerve degeneration (Stamper and Johnson, 2015). Another approach for developing a test of auditory nerve degeneration is to use the middle ear muscle (MEM) reflex. Importantly, the MEM reflex is sensitive to alterations of the auditory nerve. Stretching the auditory nerve experimentally (Borg, 1977) or space-occupying tumors in the cerebellar pontine angle, causes the amplitude of the reflex to decay during continuous stimulation (Mangham, Lindeman, and Dawson, 1980). Recently, Valero and colleagues, 2016 showed that the MEM reflex was altered in mice with “normal hearing” but with reduced synaptic ribbons. Presently the MEM reflex is routinely used in the audiology clinic making translation from animal to human studies possible. Decay in the amplitude of the reflex during acoustic stimulation is one of the parameters that the audiologist uses to diagnose vestibular schwannomas, and interestingly may be a unique signature to pathology of the auditory nerve. Lesions in the brainstem can eliminate the contralateral reflex, and thus reflex decay does not occur (Borg, 1977). In the present study we report on normative values of the MEM reflex in rat with the long term goal of using this model to determine the ability of the MEM reflex to estimate auditory nerve survival.
II. Theory
Sound pressure is related to impedance by,
| (1) |
where P is sound pressure in Pascals, U is volume velocity in m3/sec, and Z is acoustic impedance in Ohms. Contraction of the MEM reflex will change Z thereby changing P if U remains constant. The ideal situation is to have a speaker deliver a probe signal to the ear at a constant volume velocity independent of the load impedance coupled to the source, in our case the impedance at the entrance of the rat ear canal Zec. In such a system changes in Zec produce proportional changes in P. With real sound sources, the change in sound pressure produced by a change in Zec depends on the construction of the source and the ratio of the magnitudes of Zec and the impedance associated with the sound source. Thus, changes in Z are reflected in changes in the sound pressure of the probe signal. However, the ability to measure a change in sound pressure depends on the acoustics in the experiment. In figure 1 the corresponding Norton circuit of a speaker attached to a tube delivering Us (source volume velocity) is illustrated. Together they are considered the source, for which the impedance is designated as Zs (source impedance). Once inserted into the ear canal, the volume of air in the canal, middle ear and structures, and inner ear together constitute the load impedance Zec (ear canal impedance) and are in a parallel combination to the source. To record the MEM reflex a microphone is placed along with the tube into the ear canal. The sound pressure in the canal is
Figure 1.
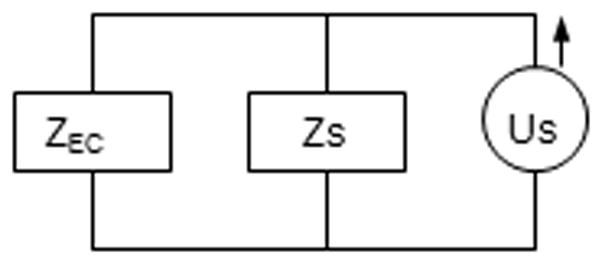
Circuit model of the acoustic environment to measure the MEM reflex. Us represents the acoustic volume velocity, Zs the impedance of the source and, Zec the input impedance looking into the ear canal.
| (2) |
which shows that the sound pressure in the canal is influenced by the impedance of the speaker/tube combination and microphone (Zs). Equation 2 is a specific case of equation 1 and by allowing Zs ≫> Zec, changes in Zec produce proportional changes in the Z of the parallel combination and proportional changes in Pec such that Pec ~ UsZec. Moreover, small values of Zs create a measured sound pressure that will estimate only a fraction of the actual impedance, and because of the sensitivity and noise floor of the microphone, will limit the ability to quantify a change in sound pressure. Thus, the idea is to create a probe with infinite impedance (Zs much greater than Zec).
We created a high Zs by attaching a small diameter tube to a hearing aid speaker. Data from Ravicz et al. (1992) indicated that /Zec/, where / / indicates magnitude, for gerbil and other rodents with the bulla open was approximately 1,000 CGS Ohms at 800 Hz. Lower frequencies were considered but /Zec/ was much larger at lower frequencies making it difficult to construct a probe with an impedance higher than /Zec/. Using a mathematical model of a cylinder including viscothermal properties (Matlab code provided by Doug Keefe Boys Town, Personal Communication, code based on Benade, 1968), we determined that a tube length of 10.5 cm and an inner diameter of 0.06 cm would provide a high impedance (36,192 cgs Ohm). Moreover, when placed into the first-author’s ear, the signal was still audible. Although the tube had a high impedance, this did not guarantee that /Zs/ was larger than /Zec/, because /Zs/ is a combination of the tube impedance, as well as the speaker and probe-microphone impedance. Thus, after attaching the tube to the hearing aid speaker, we determined if this source acted as a constant volume velocity high /Zs/ source over the range of /Z/ that was likely to occur in the animal’s ear.
The probe was sealed with clay into a 1.0. cm3 syringe (figure 2, top panel). The sound pressure at 800 Hz was measured with a microphone (Etymotic ER7C) as a function of distance between the probe and plunger of the syringe. Sound pressures were measured at 11 different volumes (from 0.3 cc to 0.15 cc) and converted to a DC signal using a rectifier circuit, amplified, and monitored on an oscilloscope. The /Z/ of the syringe was estimated from a mathematical model of a cylinder (Benade, 1968). Figure 2 shows proportionality of the measured sound pressure and the test impedance for three different input signal levels and three repeated measures. Linear regression showed a significant linear relation between sound pressure (microphone voltage) and /Z/. This indicates that over the expected ranges of /Z/ that should occur in the animal’s ear, sound pressure is proportional to /Z/, i.e. equation 2 with Zs ≫> Zec and Pec ~ UsZec, and the probe acts as constant velocity high impedance source. Moreover, with larger input levels the slope increases, indicating that the probe provides a larger output volume velocity at higher input levels, with slopes of 2.5, 5.7, and 13.4 mV/Ohm, respectively, for the same change in impedance. In this study we chose to use the highest signal level so that the microphone signal could more easily be recorded above the noise floor. Reliability between the three different trials for each probe signal level was high (r > 0.98) indicating that the probe provides repeatable data.
Figure 2.
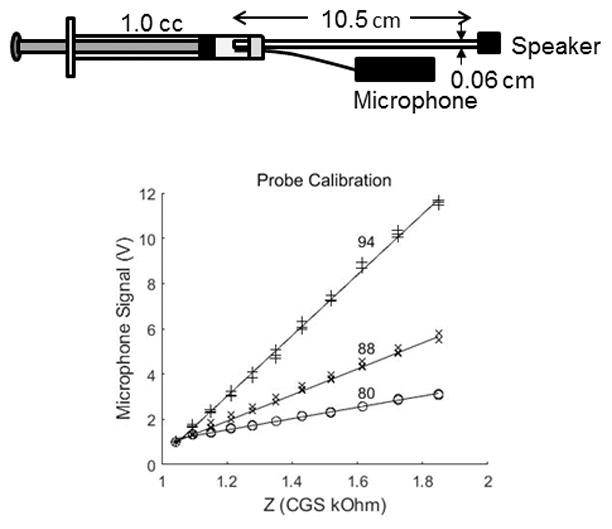
Dimensions of the probe and its insertion into the 0.3 cm3 syringe cavity used for calibration (top panel). Calibration of the probe at three different signal levels (80, 88, and 94 dBSPL) developed to record the impedance (Zec) at 800 Hz in the reflex recording ear (bottom panel). The probe was sealed into the cavity and the sound pressure was recorded, converted to a DC signal, and amplified. The volume of the syringe was changed and the voltage from the microphone recorded. Estimates of the impedance of the syringe were obtained from a mathematical model of a closed cylinder with viscothermal losses.
III. Methods
A. Subjects
Nineteen Long Evans rats weighing between 50–250 grams with normal hearing (estimated by a positive startle reflex) were used as subjects. This animal model was chosen because Murata et al. (1986) has shown through electromyographic and cochlear microphonic recordings in the chloralose-anesthetized rat has a measurable MEM reflex. Moreover, Relkin et al. (2005) demonstrated in ketamine-anesthetized rat, that middle-ear muscles altered distortion product otoacoustic emissions.
B. Equipment
In the ear with the elicitor stimulus (ear used to evoke the reflex), sound was delivered via an ER-2 headphone attached to a speculum that was sealed into the ear canal. Sound pressure was monitored with a microphone (Etymotic ER7C) to determine elicitor signal levels. In the opposite ear, an 800 Hz probe stimulus was delivered at 94 dBSPL and monitored with the assembly described in the theory section above. The probe signal recorded by the microphone was low-pass filtered at 1500 Hz (Krohn-Hite model 3700) rectified and amplified by a homemade circuit with a time constant of < 1 msec and amplification factor of 200. A screw pot on the circuit was used to adjust the baseline DC sound pressure level to 1 volt before the reflex was initiated and the differential changes in sound pressure were recorded. The output of the circuit was digitized at 50 kHz for 10 seconds by a Link Instruments DS0–8500 storage oscilloscope and stored on a personal computer. The contralateral reflex was chosen over the ipsilateral reflex simply for technical reasons. At this stage of instrumentation development, it was easier to separate the elicitor signal and probe signal physically in different ears rather than via filtering and other signal processing methods.
C. Procedures
Animals were initially sedated with KAX (ketamine, 180 mg/ml; atropine, 0.54 mg/ml; xylazine 24 mg/ml) at a dose of 0.1–0.2 mL/100 gram animal and 1/3 dose given every 30 minutes to maintain anesthesia. Body temperature was maintained at 37 degrees Celsius with a heating blanket (Harvard Homeothermic). The pinna and muscle surrounding the bulla of the probe-stimulus ear was removed and a small (~ 1mm) hole was made in the bulla. The hole was important for equalizing middle ear sound pressure. This became apparent in our pilot experiments as the MEM reflex disappeared after 10–20 minutes of a successful recording, but could be restored after opening the bulla to equalize middle ear sound pressure. The probe assembly was mounted on a micromanipulator and then positioned into the ear canal. The 800 Hz probe signal was delivered and monitored on an oscilloscope while the ear canal was sealed with Otoferm (Dreve). A sealed canal was crucial for obtaining the desired signal level and measuring the MEM reflex.
The probe stimulus was recorded for two seconds, followed by a simultaneous presentation of the probe and elicitor tone for six seconds. This was followed by a subsequent recording of the probe signal alone for two seconds. This constituted one trial. No signal averaging was done, and the time between single-trial runs was controlled manually and thus the time varied between animals. The reflex elicitor signals were 3, 10, and 16 kHz with elicitor levels ranging from 100 to 35 dBSPL in 5 dB increments.
D. Data Analysis
D.1 Dependent Variables
Figure 3 illustrates a schematic of the onset and decay of the reflex induced change in impedance where q is the baseline impedance measured by the probe. Latency is defined as the time between the onset of the elicitor and the onset of the reflex, and reflex amplitude is height a. The decay time and rise time of the reflex are defined as 1/b and 1/c in the equation under the solid line in the figure (or equation 4 below). Reflex threshold is the signal level just above which no response was obtained.
Figure 3.
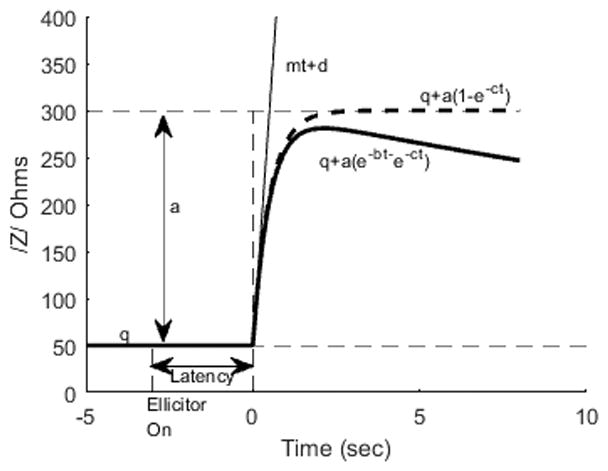
A schematic of the time course of the impedance magnitude change in response to the elicitor tone in the contralateral ear. The baseline impedance value measured with the probe tone without the elicitor is q. The impedance is increased by the elicitor with an initial slope and intercept of mt+d (Eqn 3, thin solid line). The latency between elicitor onset and the impedance change is calculated as the difference in time between the elicitor onset and the time point where mt+d=q. The time course of the evoked impedance change is approximated by a response of amplitude a and the time course defined by the solid line Z=q+a(e−bt−e−ct). Notably, as the size of b goes to zero, the curves becomes the growing saturating exponential curve, q+a(1−e−ct).
Latency was obtained by fitting the following piecewise function
| (3) |
to the impedance versus time curve using least squares regression in matlab. Here q is a constant until the amplitude of /Z/ continuosly increases, then, from this location, a linear equation with slope m and intercept d was fit to 80% of the peak amplitude of the /Z/. Latency was obtained by solving equation 3 for t when q = mt + d. Reflex threshold was obtained via observation by two investigators monitoring the reflex on the computer and was defined as the signal level where the response differed from the noise floor. The other variables, amplitude (a), decay time (1/b), and rise time (1/c) were obtained by fitting the nonlinear function
| (4) |
to the impedance time waveform (see statistics below).
D.2 Statistics
The influence of frequency on threshold was determined by pair-wise T-tests. For the other dependent variables the influence of frequency and signal level on the reflex were obtained using linear and nonlinear regression. The influence of level and elicitor frequency on latency was obtained using a random intercept linear model fitted with Stata (StataCorp LP, College Station, TX). A random intercept linear model is the usual linear regression model with the additional assumption that each animal has its own intercept. That is, the intercept is treated as a number that changes from animal to animal. This approach incorporates in the statistical analysis the fact that each animal is unique, allows separating the within-animal variability from the between-animal variability, and results in a better fit of the regression equation to the data (Hedeker and Gibbons, 2006). The influence of signal level and frequency on the parameters of equation 4 were determined by treating them as functions of signal level such that
| (5) |
| (6) |
| (7) |
where level is in dBSPL. The parameters with subscripts zero and one indicate the intercept and slope respectively and quantify the effect of signal level on the MEM reflex for a particular frequency. Equations 4–7 were estimated by fitting a nonlinear regression model of /Z/ simultaneously to all animals, all levels (above threshold) and all frequencies taken together. Since there may be animal heterogeneity, correlations across time points within an animal may occur. Thus, robust standard errors that account for this correlation were used. Briefly speaking, standard errors measure the reliability of the parameter estimates used to build the confidence intervals. Robust standard errors are usually recommended for longitudinal data such as those analyzed in this paper (Davidian and Giltinan, 1995). This technique is preferable over fitting each animal and then averaging the parameters because it reduces the standard errors and therefore improves the reliability of parameter estimates. The influence of signal level on the parameter a was considered significant if the p value of a Wald test for a1 (equation 5) was ≤ 0.05. This test compared the maximum likelihood estimator of a1 with its standard error (Hedeker and Gibbons, 2006). Joint Wald tests comparing simultaneously several intercepts and/or slopes in equations 5–7 between frequencies were also conducted (Davidian and Giltinan, 1995; StataCorp. 2013). The influences of signal level and frequency on the parameters b and c were examined analogously.
Within-animal reliability of the reflex was determined by intraclass correlations computed in five animals between the first and second time-domain recordings. The intraclass correlation was computed for each animal separately and for each elicitor level and frequency. The intraclass correlations were averaged across animals. Intraclass correlation was used instead of correlation to account for possible magnitude differences as well as the shape of the reflex function.
IV Results
A. Artifact
Figure 4 shows the MEM reflex in an animal before and after sacrifice. The reflex elicitor signal was 3 kHz and presented at 120 dBSPL. When the animal is alive, Z changes by approximately 350 Ohms. After sacrifice the response was absent indicating that the measured response was not due to electrical artifact or the signal crossing from the elicitor ear to the probe ear.
Figure 4.
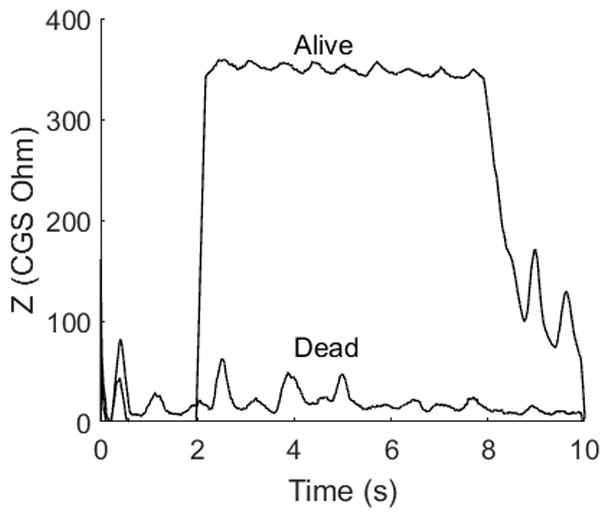
Checking for instrumentation and biologic artifact. The MEM reflex was recorded in one animal at 120 dBSPL at 3 kHz before and after sacrifice. No reflex was recorded after sacrifice indicating that the response was not due to acoustic crossover or other instrumentation issues.
B. Group Data
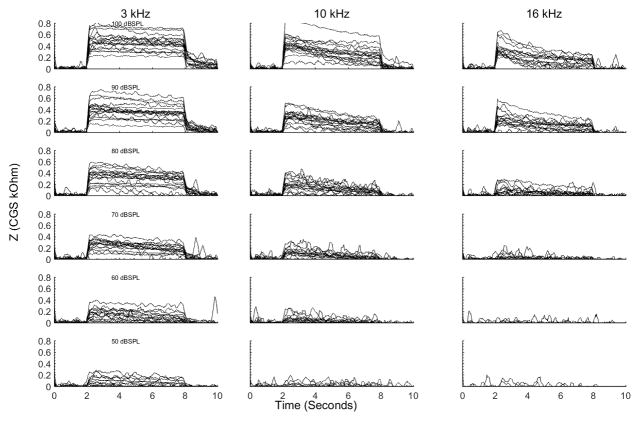
The MEM reflex from all animals at 3, 10, and 16 kHz and from elicitor levels ranging from 100 to 50 dBSPL in 10 dB increments is illustrated in figure 5. The amplitude and decay of the reflex varied across animals, frequency, and level. The amplitude of the reflex was largest at 3 kHz followed by 10 and 16 kHz. At all three frequencies the amplitude decreased as elicitor level decreased, reaching threshold that varied with signal frequency. Threshold (Table 1) was significantly lower (as indicated by a t-test) at 3 kHz than 10 kHz (t18 = −5.52, p < 0.001) and 16 kHz (t18 = −10.98, p < 0.001). Threshold at 10 kHz was lower than 16 kHz (t16 = −8.27, p < 0.001, 16 kHz MEM reflexes were not attempted on 2 of the 19 animals). The rate of reflex decay was largest at 10 kHz at lower stimulus levels and 16 kHz at the highest stimulus levels.
Figure 5.
MEM reflex from all of the animals used in this study. The magnitude of the reflex was largest at 3 kHz, followed by 10 kHz, and 16 kHz. The decay of the reflex increased as signal level decreased, with higher decay rates at 10 and 16 kHz than at 3 kHz.
Table 1.
MEM Reflex Threshold
| Frequency | 3,000 Hz | 10,000 Hz | 16,000 Hz |
|---|---|---|---|
| Mean (dBSPL) | 53.68 | 64.21 | 76.18 |
| St. Dev. | 14.89 | 14.84 | 10.39 |
The within-animal reliability was obtained in five animals in which the MEM reflex was recorded twice, once with a descending elicitor signal level and a second time with an ascending elicitor signal level. Reliability was quantified by computing the intraclass correlation (ICC) between the two waveforms for each animal and then averaged across animals. The ICCs from mid to high signal levels were 0.67–0.92 for 3 kHz; 0.65–0.95 for 10 kHz; and 0.44–0.97 for16 kHz, indicating good to excellent reliability (Cicchetti, 1994) within an animal in a single recording session.
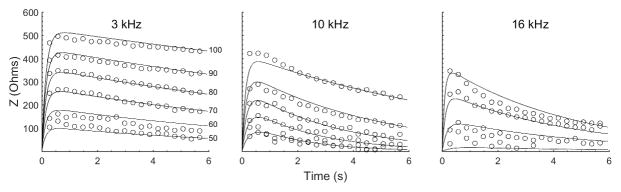
The trends in the group data were quantified using equation 4 and the nonlinear regression model. This allowed us to determine the influence of both elicitor signal level and frequency on the parameters of equation 4, hence on the MEM reflex. The two-time constant model (equation 4) fit quite well to the data from all animals as illustrated in figure 6 with an overall r2 = 0.88. The level dependence of the model parameters slope and intercept were fit to straight lines and the 95% confidence intervals relating the effect of signal level on the MEM reflex (i.e. equations 5–7) for each frequency are provided in table 2.
Figure 6.
Mean MEM reflex (circles) for the three frequencies at select levels, and the fit (lines) of the statistical model given by equation 4. The lines were obtained from the parameters of a nonlinear model that combined the data from all animals. The model fit well with r2 = 0.88. Time zero is when the reflex activating signal was initiated and lasted for 6 seconds.
Table 2.
Level Effect on Amplitude, Decay Time and Rise Time of Reflex Response.
| Parameters | 3 kHz | 95% CI | 10 kHz | 95% CI | 16 kHz | 95% CI |
|---|---|---|---|---|---|---|
| a0 Intercept | −314.89 | (−501.22, −128.57) | −301.83 | (−530.23, −73.44) | −800.95 | (−940.16, −661.73) |
| a1 Slope | 8.42 | (5.73, 11.12) | 7.19 | (4.29, 10.08) | 11.74 | (9.62, 13.85) |
| b0 Intercept | 0.18 | (0.084, 0.28) | 1.06 | (0.79, 1.33) | 0.13 | (−0.21, 0.47) |
| b1 Slope | −0.0015 | (−0.0025, −0.00047) | −0.0096 | (−0.012, −0.0070) | 0.00085 | (−0.0029, 0.0046) |
| c0 Intercept | 7.23 | (0.17, 14.29) | −1.85 | (−4.54, 0.84) | −15.27 | (−18.12, −12.41) |
| c1 Slope | −0.0077 | (−0.088, 0.073) | 0.0913 | (0.061, 0.12) | 0.26 | (0.21, 0.31) |
CI: Confidence interval.
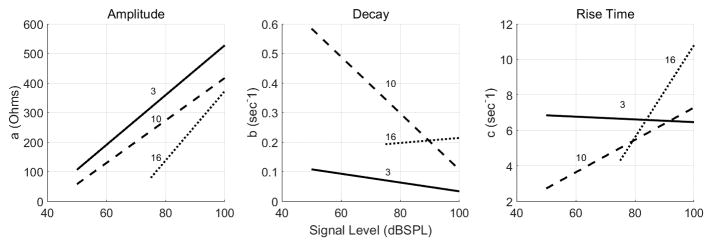
The amplitude of the reflex, a, significantly increased with signal level (left panel of Figure 7). This is also indicated by the 95% confidence intervals for the slopes (a1), which do not contain zero at each of the frequencies (second row of table 2). A Wald test of the joint null hypothesis that all slopes and intercepts for a in figure 7 are zero, which addressed the question “do the three lines differ?” indicated significant differences across lines (F4,17 = 9.61 p<0.001). This suggested that the amplitude of the reflex differed across frequencies. However, additional joint tests suggested that the intercepts of the linear growths differed significantly across frequencies (F2,17 = 9.61, p = 0.0016 ) but the difference between slopes was borderline significant (F2,17 = 3.3, p = 0.069).
Figure 7.
The influence of signal level and frequency on the parameters obtained from equation 4 and quantified by equations 5–7. Parameter a reflects the amplitude of the reflex and grows similarly for the three frequencies. Parameter b represents the decay. There were significant differences between the three frequencies. Although 3 and 16 kHz differed from each other, they did not change significantly with signal level. Decay at 10 kHz, however, was influenced by signal level. The parameter c, estimates the rise time of the MEM reflex. The rise time at 3 kHz was not effected by signal level whereas at 10 and 16 kHz, the rise time was greatly influenced by signal level.
The rate of decay of the reflex, b, also changed with elicitor level and, moreover, was frequency dependent (middle panel of figure 7). From table 2 (4th row), the confidence interval for b1 did not contain zero for 3 and 10 kHz, indicating that b changed significantly with signal level. As level increased, b decreased (decay time constant = 1/b), indicating that it took longer for the MEM reflex to decay at higher signal levels than at low signal levels (figure 7). The lines relating signal level with b differed significantly across frequencies (Wald test of the joint null hypothesis that all slopes and intercepts were zero: F4,17 = 23.86, p < 0.001). Additional tests indicated that both the intercepts (F2,17 = 28.19, p < 0.001) and slopes (F2,17 = 23.18, p < 0.001), contributed to the significant differences between lines. However, no significant effect of level on b occurred for the 16 kHz elicitor [slope=0.00085, 95% CI (−0.0029, 0.0046); table 2]. The steepest reduction in decay rate for higher signal levels occurred at 10 kHz, ranging from approximately 1.7 seconds (1/b=1/0.6) at 50 dBSPL to 10 seconds (1/b=1/0.1) at 100 dBSPL (figure 7).
Similarly c, the rate of reflex growth (rise time constant = 1/c), changed with level and frequency (right panel of figure 7). The lines relating signal level with c differed significantly across frequencies (joint Wald test: F4,17 = 17.36, p < 0.001). The 95% confidence interval for c1 did not contain zero for 10 kHz and 16 kHz but did for 3 kHz (6th row of table 2). This indicates that the rise time of the reflex (1/c) decreased with increase in signal level for 10 and 16 kHz, although this did not occur at 3 kHz.
The latency of the reflex varied with elicitor level (Figure 8, table 3). The slopes for the three frequencies were negative and significantly different from zero (table 3). The slopes were significantly different across frequencies (Wald X2=8.18, df=2 p=0.017), the steeper slope occurring at 10 kHz (table 3). The initial latencies (i.e. 50 dBSPL) were also significantly different across frequencies (Wald X2 =7.89, df=2, p=0.0193), the higher initial latency occurring at 10 kHz.
Figure 8.
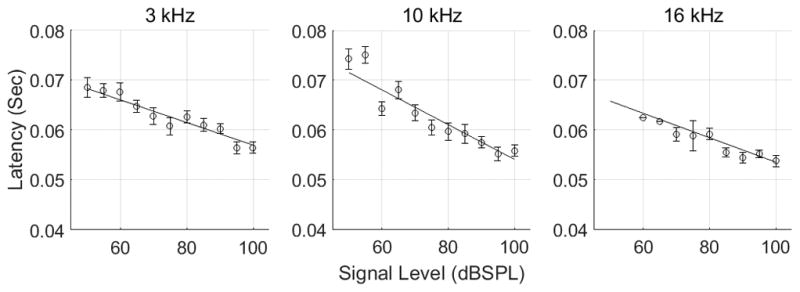
The latency of the reflex varied with signal level. The circles represent the mean (+/− 1 SEM) latency of the reflex obtained by fitting equation 3 to the MEM reflex wave form. The lines are the solution of the linear mixed model. As signal level increased, the latency of the MEM reflex decreased, more so at 10 kHz than at 3 and 16 kHz.
Table 3.
Effect of Level on Latency of Reflex Response
| 3,000 Hz (95% CI) | 10,000 Hz (95% CI) | 16,000 Hz (95% CI) | |
| Intercept (msec) | 79.61 (75.60, 83.62) | 88.96 (83.13, 94.79) | 78.03 (66.29, 89.76) |
| Slope (msec/dBSPL) | −0.227 (−0.277, −0.177) | −0.349 (−0.419, −0.280) | −0.245 (−0.377, −0.113) |
CI: Confidence interval.
C. Model
Similar to Longtin and Derome, (1986), a phenomenological model incorporating a simple negative feedback system can account for many of the features of the effect of elicitor level and frequency on the parameters describing the MEM reflex (Figure 9, top and bottom panels). The input to the brainstem was considered the total output of the auditory nerve (box labeled input), represented by either a few auditory fibers at a high discharge rate or a population of auditory nerve fibers firing at a low discharge rate. We assumed that the total output from the nerve was constant throughout the stimulus. Although this is not necessarily true, given that single auditory nerve fibers show an increased discharge rate at the onset of the stimulus and then a decay to steady state, the time constant of the decay of auditory nerve fibers is on the order of milliseconds whereas the decay of the reflex is on the order of seconds. The output of the auditory nerve is fed into the brainstem which contains an integrator (box labeled with 1/s) followed by a gain (triangle symbol) by which the output of the auditory nerve to the muscle is controlled. The muscle (either stapedius or tensor tympani, box labeled output) is modeled as a first order differential equation or transfer function. Other investigators (Christakos, 1982; Longtin and Derome, 1986) have used second-order models to represent the muscle but these investigators are often modeling the muscle twitch response to a single pulse input. Here we model the muscle during tetanus. We assume that the decay of the MEM reflex is not due to fatigue of the muscle which is supported by Van Den Berge and Wirtz (1989a, 1989b) who showed that both the stapedius and tensor tympani muscles mostly consist of fast oxidative glycolytic fibers which are fast-acting and generally resistant to fatigue. The model contains only two parameters that can be modified to replicate the MEM reflex, the gain (K) and the time required from stimulus to muscle contraction (here indicated as 1/7.23 seconds, but could be modified to account for 10 and 16 kHz stimuli). The bottom panel illustrates the influence of the gain on the simulated MEM reflex. As K is increased, the output of the auditory nerve to the brainstem is less and causes the MEM reflex to decay. K could be modified to account for changes in MEM reflex decay with signal level or frequency. Thus, this model indicates that by simply varying the total output of the auditory nerve, various reflex characteristics can be replicated. This suggests that at high signal levels where outer hair cell motility is saturated, the loss of inner hair cells or auditory nerve fibers should be reflected in the MEM reflex. This is consistent with a result already shown by Valero et al, 2016. Whether threshold, latency, decay time, rise time, or amplitude or a multivariate approach is the important parameter to estimate inner hair cell or neural survival, however, remains to be determined.
Figure 9.
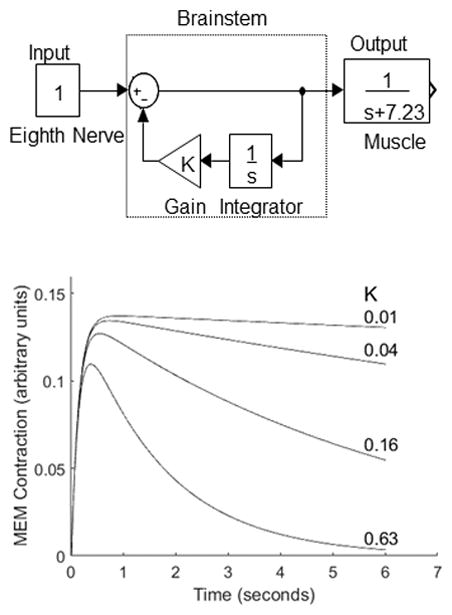
Phenomenological model (top panel) of reflex decay where the input to the middle ear muscle is controlled by an integrator (1/s), where s indicates the Laplace domain, and whose amount of decay can be controlled by a gain K. The muscle is represented by a first order transfer function. The output of the model (bottom panel) illustrates that as the gain (K) increases, there is less input to the muscle and therefore more decay.
V. Discussion
A. Reflex Parameters
The MEM reflex consists of two striated muscles, the stapedius and tensor tympani, located in the middle ear cavity. In response to a loud sound to one ear, these muscles in rodents contract bilaterally and decrease low-frequency sounds entering the cochlea (Van den Berge & Wirtz, 1989). In this study we showed that the MEM reflex could be measured in the rat using a high-impedance probe as a source. The MEM reflex amplitude increased with elicitor signal level but the rate of growth did not differ significantly across frequencies. The increase in the magnitude of the impedance indicates a larger contraction of either the stapedius or tensor tympani muscle, or perhaps both, as elicitor level increased. This reflects a recruitment of neural activity along the MEM reflex neural pathway. For example, in the cochlea, an increase in signal level will displace a large region along the cochlear partition and recruit a broad range of nerve fiber populations. Subsequently at the level of motor neurons, many neurons will be stimulated because motor units respond to a wide range of frequencies (Kobler et al., 1992). In conjunction with an increase in the number of motor units, the discharge rate will also increase with elicitor level (Vacher et al., 1989). Both the increase in the number of motor units and their discharge rate will cause a greater muscle contraction at high elicitor levels than at low levels.
The lowest threshold of the MEM reflex was approximately 50 dBSPL at 3 kHz. This threshold in rats is consistent with Murata et al. (1986) who used the CM to measure contralateral threshold. Curiously the lowest MEM reflex threshold was not at 10 kHz which would be consistent with the audiogram of rat. As suggested by Pilz et al., (1997), opening the bulla would change the middle ear frequency response and could have influenced ours and Murata’s data. It is interesting to note that this threshold is much lower than the MEM reflex in humans which is approximately 70 – 100 dB SPL at low frequencies when measured as a change in sound pressure level in the ear canal, as was done in this study. It is possible that the purpose of the reflex differs between humans and rodents. In humans, because of the high thresholds of the MEM reflex, it may be used for protection from loud sounds. However, given that Feeney et al., (2003) found MEM reflex thresholds near 60 dBSPL in humans, the role of the MEM reflex in human hearing may serve other purposes than protection. In rat, however because of the low threshold, the reflex may be frequently active and perhaps, like bats, used during vocalization to prevent low-frequency upward spread of masking (Suga and Jen, 1975).
The decay of the reflex varied with elicitor signal frequency and level. At 3 kHz the decay was less than at 10 and 16 kHz showing higher decay rates with higher frequencies. Moreover, similar to 16 kHz, the decay at 3 kHz did not change with signal level. By contrast, the decay at 10 kHz was elicitor level dependent, showing higher decay rates with lower elicitor levels. The anatomical location of the MEM reflex decay and why the MEM reflex decays, more at high frequencies than low frequencies is still not clearly understood. We were, however, able to model the decay as an integrator with a gain that is driven by the number of auditory nerve fibers (or total discharge rate of fibers). Thus the auditory nerve plays a role in the reflex decay. Further support comes from the fact that the MEM reflex decay occurs when the auditory nerve is stretched or disrupted by a tumor (Borg, 1977), while this does not seem to happen for brainstem lesions (Borg, 1977). In fact, reflex decay is used in audiology clinics as a marker for a tumor affecting the auditory nerve (Mangham, Lindeman, and Dawson, 1980). Future studies will be required to determine the source and role of the auditory nerve in MEM reflex decay.
The shortest rise time ( ) for the MEM reflex was approximately 90 msec for the 16 kHz signal presented at 100 dBSPL. The rise time increased, or rate of rise decreased, as elicitor level decreased for the 10 and 16 kHz signals with no significant effect of level for the 3 kHz activator. Our results differ from those reported by van den Berge and colleagues (1990), who showed rise time to vary between 7 and 12 msec and decreased with elicitor level. As indicated below, perhaps the difference in anesthesia regimen between their study and ours caused the discrepancy. However, it is worth noting that the short rise times reported by van den Berge are quicker than the twitch response of a single muscle fiber. Teig (1972) reported that, at least in cat, fast twitch muscle fibers had contraction times between 23 and 40 msec, and slow twitch fibers between 58 and 92 msec. These values are much longer than those reported by van den Berg using the change in the CM as a measure of the reflex.
As elicitor level decreased the latency of the reflex increased. Shifts in latency with signal level are common in other auditory physiology measures such as the auditory brainstem response and the compound action potential, and are often interpreted as a shift along the cochlear partition to a region of maximum vibration. In this study the shortest reflex latency was 54 msec at 16 kHz in response to the 100 dBSPL stimulus. This latency is similar to contralateral reflexes in cat at approximately 100 dBSPL at 2 kHz (mean ranging from 48.9 – 53.9 msec after Xylazine or Ketamine; Sims and Horohov, 1986), and 90 dBHL in dog (73.17 +/− 18.02 msec; Sims, Weigel, and Moore, 1986).
Our latency of the MEM reflex is in contrast with other investigators who measured the latency of the MEM reflex in rat. Van den Berg et al. (1990) used cochlear microphonic signals and reported MEM reflex latency to be 12 msec. An electromyographic recording of the tensor tympani muscle by these investigators yielded a latency of 7 msec. Pilz et al. (1997) reported the decrease in the CM after a latency of 10–20 msec for stimuli ranging from 80 to 100 dBSPL. The difference between our results and these investigators is difficult to reconcile. Even extrapolating our results to a higher elicitor level, e.g. 120 dBSPL using the regression equation for 10 kHz, only decreases the latency to 47 msec.
Anesthesia has been shown to influence the MEM reflex and could play a role in the discrepancy of our results and those of previous investigators using rats. Van den Berge used only Ketamine to sedate the animals and Pilz et al. reported that rats were only lightly anesthetized with Ketamine (100 mg/kg) and still showed a blink reflex during recordings. Perhaps that addition of Xylazine in our anesthesia sedation protocol influenced the neural conduction time to elicit the reflex. Oh et al. (2010) reported a slowing of neural conduction time in the sural sensory nerve in mice treated with Xylazine. However, we are not aware of the effects of Xylazine on rat.
Interestingly, the effects of Ketamine and Xylazine on the MEM reflex may be species dependent. Guinan and McCue (1987) showed that MEM reflexes in cat were maintained when anesthetized with Ketamine during the duration of the experiment. Moreover Sims and Horohov reported no influence of Xylazine or Ketamine on the contralateral reflex in cat. In contrast, Thompson and colleagues (1984) indicated that the amplitude of the contralateral reflex was greatly reduced in squirrel monkey even at low doses (i.e 5 mg/kg) of Ketamine. Interestingly, our initial animal species chosen for developing and animal model of the MEM reflex was gerbil. However, we were not successful in measuring the MEM reflex using acoustic means. Even after success with rat, subsequent attempts with gerbil were still not successful. Perhaps, our lack of MEM reflex in the gerbil may be due to a differential effect of Ketamine on the two species.
B. Clinical Relevance
In contrast to rabbits in which both muscles are involved in the reflex to loud sounds (Borg, 1973), the dominant muscle involved in the human acoustic reflex is the stapedius muscle. Thus, one could argue that a rabbit or rodent model is not appropriate for studying the human reflex. This however, depends on the clinical use of the reflex. We believe that although the stapedius and tensor tympani muscles receive input from different nuclei (facial motor nuclei and trigeminal motor nuclei, respectively) both muscle reflexes depend on auditory nerve activity. Thus changes in auditory nerve activity should be reflected in the activity of either or both of the muscle reflexes as measured by changes in impedance.
The MEM reflex, particularly the decay of the reflex, is presently used in the audiology clinic to determine if a patient has a tumor or mass impinging on the auditory nerve (Mangham, Lindeman, and Dawson, 1980). The amplitude of the reflex decays more quickly in these patients than in normal hearing or hearing impaired individuals without a tumor. Because of the sensitivity of the MEM reflex to auditory nerve alterations, we hypothesize that the MEM reflex decay or other parameters may be sensitive to, perhaps, other subtle changes in auditory nerve fibers. For example, degeneration of auditory nerve fibers would result in fewer fibers and decrease the input to the brainstem mechanisms and MEM reflex. This could result in a loss of the amplitude of the reflex, elevated thresholds, or modification of other parameters. If so, a univariate or multivariate approach with a set of MEM reflex parameters may be useful to predict the number of healthy auditory nerve fibers.
Presently, there is some evidence that the MEM reflex may be useful in diagnosing changes in a certain population of auditory nerve fibers. The auditory nerve is made up of nerve fibers that are distinguished by their spontaneous discharge rate. High spontaneous rate fibers discharge at high rates at rest, have low thresholds, and saturate at moderate sound pressure levels. Low spontaneous rate fibers discharge at low rates at rest, have higher thresholds and limited saturation. Previously, as suggested by Kobler and colleagues (1992), the high threshold of the MEM reflex may indicated that the low spontaneous rate fibers were the fibers that contributed to the reflex. This is supported by more recent studies (Valero et al., 2016) who showed a reduced MEM reflex in mice with reduced low spontaneous rate fibers even in mice with normal auditory thresholds. Thus the MEM reflex may be sensitive to changes in the auditory nerve. If this could be verified in humans, the MEM reflex may be a method to identify individuals with reduced low spontaneous rate auditory nerve fibers. Or perhaps, more generally, a parameter of the MEM reflex could be used as a biomarker for auditory nerve degeneration in individuals with sensorineural hearing loss.
Acknowledgments
This research was funded by the National Institutes of Health Division of Communicative Disorders.
The authors wish to acknowledge the reviewers for their comments to improve the manuscript. In addition, the authors thank John Rosowski for serving as a sounding board to clarify our knowledge, and Doug Keefe for help with the tube model.
Bibliography
- Benade AH. On the propagation of sound waves in a cylindrical conduit. The Journal of the Acoustical Society of America. 1968;44(2):616–623. [Google Scholar]
- Borg E. On the neuronal organization of the acoustic middle ear reflex. A physiological and anatomical study. Brain Research. 1973;49(1):101–123. doi: 10.1016/0006-8993(73)90404-6. [DOI] [PubMed] [Google Scholar]
- Borg E. The intra-aural muscle reflex in retrocochlear pathology: a model study in the rabbit. International Journal of Audiology. 1977;16(4):316–330. doi: 10.3109/00206097709071843. [DOI] [PubMed] [Google Scholar]
- Christakos CN. A study of the muscle force waveform using a population stochastic model of skeletal muscle. Biological Cybernetics. 1982;44(2):91–106. doi: 10.1007/BF00317969. [DOI] [PubMed] [Google Scholar]
- Davidian M, Giltinan DM. Nonlinear Models for Repeated Measurement Data. 1. New York: Chapman & Hall/CRC; 1995. [Google Scholar]
- Feeney MP, Keefe DH, Marryott LP. Contralateral acoustic reflex thresholds for tonal activators using wideband energy reflectance and admittance. J Speech Lang Hear Res. 2003;46:128–136. doi: 10.1044/1092-4388(2003/010). [DOI] [PubMed] [Google Scholar]
- Fernandez KA, Jeffers PW, Lall K, et al. Aging after noise exposure: acceleration of cochlear synaptopathy in “recovered” ears. Journal of Neuroscience. 2015;35(19):7509–7520. doi: 10.1523/JNEUROSCI.5138-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guinan JJ, Jr, McCue MP. Assymetries in the acoustic reflexes of the cat stapedius muscle. Hearing Research. 1987;26:1–10. doi: 10.1016/0378-5955(87)90031-1. [DOI] [PubMed] [Google Scholar]
- Hedeker D, Gibbons RD. Longitudinal data analysis. Hoboken: John Wiley & Sons, Inc; 2006. [Google Scholar]
- Humes LE. Noise-induced hearing loss as influenced by other agents and by some physical characteristics of the individual. The Journal of the Acoustical Society of America. 1984;76(5):1318–1329. doi: 10.1121/1.391447. [DOI] [PubMed] [Google Scholar]
- Kobler JB, Guinan JJ, Jr, Vacher SR, et al. Acoustic reflex frequency selectivity in single stapedius motoneurons of the cat. Journal of Neurophysiology. 1992;68(3):807–817. doi: 10.1152/jn.1992.68.3.807. [DOI] [PubMed] [Google Scholar]
- Kujawa SG, Liberman MC. Adding insult to injury: cochlear nerve degeneration after “temporary” noise-induced hearing loss. Journal of Neuroscience. 2009;29(45):14077–14085. doi: 10.1523/JNEUROSCI.2845-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kujawa SG, Liberman MC. Synaptopathy in the noise-exposed and aging cochlea: primary neural degeneration in acquired sensorineural hearing loss. Hearing Research. 2015;330:191–199. doi: 10.1016/j.heares.2015.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberman MC, Epstein MJ, Cleveland SS, Wang H, Maison S. Toward a differential diagnosis of hidden hearing loss in humans. PLOS ONE. 2016 Sep;:1–15. doi: 10.1371/journal.pone.0162726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin HW, Furman AC, Kujawa SG, et al. Primary neural degeneration in the guinea pig cochlea after reversible noise-induced threshold shift. Journal of the Association for Research in Otolaryngology. 2011;12(5):605–616. doi: 10.1007/s10162-011-0277-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longtin A, Derome J. A new model of the acoustic reflex. Biological Cybernetics. 1986;53(5):323–342. doi: 10.1007/BF00336564. [DOI] [PubMed] [Google Scholar]
- Makary CA, Shin J, Kujawa SG, et al. Age-related primary cochlear neuronal degeneration in human temporal bones. Journal of the Association for Research in Otolaryngology. 2011;12(6):711–717. doi: 10.1007/s10162-011-0283-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangham CA, Lindeman RC, Dawson WR. Stapedius reflex quantification in acoustic tumor patients. The Laryngoscope. 1980;90(2):242–250. doi: 10.1288/00005537-198002000-00008. [DOI] [PubMed] [Google Scholar]
- Murata K, Ito S, Horikawa J, et al. The acoustic middle ear muscle reflex in albino rats. Hearing Research. 1986;23(2):169–183. doi: 10.1016/0378-5955(86)90014-6. [DOI] [PubMed] [Google Scholar]
- Nadol JB., Jr . Auditory Neuropathy. San Diego, CA: Singular; 2001. Primary cochlear neuronal degeneration; pp. 99–104. [Google Scholar]
- Oh SS, Hayes JM, Sims-Robinson C, et al. The effects of anesthesia on measures of nerve conduction velocity in male C57Bl6/J mice. Neuroscience Letters. 2010;483(2):127–131. doi: 10.1016/j.neulet.2010.07.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otte J, Schuknecht HF, Kerr AG. Ganglion cell populations in normal and pathological human cochleae. Implications for cochlear implantation. The Laryngoscope. 1978;88(8):1231–1236. doi: 10.1288/00005537-197808000-00004. [DOI] [PubMed] [Google Scholar]
- Pilz P, Ostwald J, Kreiter A, et al. Effect of the middle ear reflex on sound transmission to the inner ear of rat. Hearing Research. 1997;105(1–2):171–182. doi: 10.1016/s0378-5955(96)00206-7. [DOI] [PubMed] [Google Scholar]
- Ravicz ME, Rosowski JJ, Voigt HF. Sound-power collection by the auditory periphery of the mongolian gerbil Meriones unguiculatus. I. Middle-ear input impedance. The Journal of the Acoustical Society of America. 1992;92:157–177. doi: 10.1121/1.404280. [DOI] [PubMed] [Google Scholar]
- Relkin EM, Sterns A, Azeredo W, Prieve BA, Woods CI. Physiological mechanisms of onset adaptation and contralateral suppression of DPOAEs in the rat. J Assoc Res Otolaryngol. 2005;6:119–135. doi: 10.1007/s10162-004-5047-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryugo D, Rosenbaum B, Kim, et al. Single unit recordings in the auditory nerve of congenitally deaf white cats: Morphological correlates in the cochlea and cochlear nucleus. The Journal of Comparative Neurology. 1998;397(4):532–548. doi: 10.1002/(sici)1096-9861(19980810)397:4<532::aid-cne6>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Salvi RJ, Ahroon WA. Tinnitus and Neural Activity. Journal of Speech Language and Hearing Research. 1983;26(4):629–632. doi: 10.1044/jshr.2604.629. [DOI] [PubMed] [Google Scholar]
- Salvi RJ, Wang J, Ding D. Auditory plasticity and hyperactivity following cochlear damage. Hearing Research. 2000;147:261–274. doi: 10.1016/s0378-5955(00)00136-2. [DOI] [PubMed] [Google Scholar]
- Schuknecht HF, Woellner RC. An experimental and clinical study of deafness from lesions of the cochlear nerve. The Journal of Laryngology & Otology. 1955;69(02):75–97. doi: 10.1017/s0022215100050465. [DOI] [PubMed] [Google Scholar]
- Sergeyenko Y, Lall K, Liberman MC, et al. Age-Related Cochlear Synaptopathy: An Early-Onset Contributor to Auditory Functional Decline. Journal of Neuroscience. 2013;33(34):13686–13694. doi: 10.1523/JNEUROSCI.1783-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sim MH, Horohov JE. Effects of xylazine and ketamine on the acoustic reflex and brainstem auditory-evoked response in cat. American journal of veterinary research. 1986;1:102–109. [PubMed] [Google Scholar]
- Sims MH, Weigel JP, Moore RE. Effects of tenotomy of the tensor tympani muscle on the acoustic reflex in dogs. American journal of veterinary research. 1986;5:1022–1031. [PubMed] [Google Scholar]
- Stamper GC, Johnson TA. Auditory function in normal-hearing, noise-exposed human ears. Ear and Hearing. 2015;36(2):172–184. doi: 10.1097/AUD.0000000000000107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- StataCorp. Statistical Software. College Station, TX: StataCorp LP; 2013. Stata: Release 13. [Google Scholar]
- Suga N, Jen PHS. Peripheral control of acoustic signals in the auditory system of echolocating bats. J exp Biol. 1975;62:277–311. doi: 10.1242/jeb.62.2.277. [DOI] [PubMed] [Google Scholar]
- Sugawara M, Corfas G, Liberman MC. Influence of supporting cells on neuronal degeneration after hair cell loss. Journal of the Association for Research in Otolaryngology. 2005;6(2):136–147. doi: 10.1007/s10162-004-5050-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuka Y, Schuknecht HF. Retrograde cochlear neuronal degeneration in human subjects. Acta Oto-Laryngologica. 1988;105(Sup450):1–20. doi: 10.3109/00016488809098973. [DOI] [PubMed] [Google Scholar]
- Teig E. Tension and contraction time of motor units of the middle ear muscles in the cat. Acta Physiologica Scandinavica. 1972;84(1):11–21. doi: 10.1111/j.1748-1716.1972.tb05150.x. [DOI] [PubMed] [Google Scholar]
- Thompson GC, Stach BA, Jerger JF. Effect of Ketamine on the stapedius reflex in squirrel monkey. Achr Otolaryngol, Vol. 1984;110:22–24. doi: 10.1001/archotol.1984.00800270026007. [DOI] [PubMed] [Google Scholar]
- Vacher SR, Guinan JJ, Kobler JB. Intracellularly labeled stapedius-motoneuron cell bodies in the cat are spatially organized according to their physiologic responses. The Journal of Comparative Neurology. 1989;289(3):401–415. doi: 10.1002/cne.902890306. [DOI] [PubMed] [Google Scholar]
- Valero ME, Hancock KE, Liberman CM. The middle ear muscle reflex in the diagnosis of cochlear neuropathy. Hearing Research. 2016;332:29–38. doi: 10.1016/j.heares.2015.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Berge H, Wirtz P. Detailed morphology of the tensor tympani muscle of the rat. an integrated light microscopical, morphometrical, histochemical, immunohistochemical and electron microscopical study in relation to function. Journal of Anatomy. 1989;164:215–228. [PMC free article] [PubMed] [Google Scholar]
- Van den Berge H, Wirtz P. Detailed morphology of the stapedius muscle of the rat. an integrated light microscopical, morphometrical, histochemical, immunohistochemical and electron microscopical study in relation to function. J Anat. 1989;166:157–169. [PMC free article] [PubMed] [Google Scholar]
- Van den Berge HV, Kingma H, Kluge C, Marres E. Electrophysiological aspects of the middle ear muscle reflex in the rat: latency, rise time and effect on sound transmission. Hearing Research. 1990;48(3):209–219. doi: 10.1016/0378-5955(90)90061-s. [DOI] [PubMed] [Google Scholar]