Binding Thermodynamics and Kinetics Calculations Using Chemical Host and Guest: A Comprehensive Picture of Molecular Recognition

Abstract

Understanding the fine balance between changes of entropy and enthalpy and the competition between a guest and water molecules in molecular binding is crucial in fundamental studies and practical applications. Experiments provide measurements. However, illustrating the binding/unbinding processes gives a complete picture of molecular recognition not directly available from experiments, and computational methods bridge the gaps. Here, we investigated guest association/dissociation with β-cyclodextrin (β-CD) by using microsecond-time-scale molecular dynamics (MD) simulations, postanalysis and numerical calculations. We computed association and dissociation rate constants, enthalpy, and solvent and solute entropy of binding. All the computed values of k_on, k_off, ΔH, ΔS, and ΔG using GAFF-CD and q4MD-CD force fields for β-CD could be compared with experimental data directly and agreed reasonably with experiment findings. In addition, our study further interprets experiments. Both force fields resulted in similar computed ΔG from independently computed kinetics rates, ΔG = −RT ln(k_on·C⁰/k_off), and thermodynamics properties, ΔG = ΔH − TΔS. The water entropy calculations show that the entropy gain of desolvating water molecules are a major driving force, and both force fields have the same strength of nonpolar attractions between solutes and β-CD as well. Water molecules play a crucial role in guest binding to β-CD. However, collective water/β-CD motions could contribute to different computed k_on and ΔH values by different force fields, mainly because the parameters of β-CD provide different motions of β-CD, hydrogen-bond networks of water molecules in the cavity of free β-CD, and strength of desolvation penalty. As a result, q4MD-CD suggests that guest binding is mostly driven by enthalpy, while GAFF-CD shows that gaining entropy is the major driving force of binding. The study deepens our understanding of ligand–receptor recognition and suggests strategies for force field parametrization for accurately modeling molecular systems.

Graphical Abstract

1. INTRODUCTION

Molecular recognition determines the binding of two molecules—a common phenomenon in chemical and biological processes. Thus, understanding molecular recognition is of interest in both fundamental studies and has practical applications in chemical industries and drug discovery. Molecular binding can be characterized by thermodynamic and kinetic properties, which are governed by factors such as polar and nonpolar interactions between solutes, solvent effects, molecular diffusion, and conformational fluctuations. Molecular binding affinity is a straightforward characterizer of recognition and can be obtained experimentally by enthalpimetry such as calorimetry.^1,2 However, it is difficult to measure the binding entropy directly from experiments, and it is impossible to measure separate entropy contributions from the solvent and solute. Recent studies have revealed the importance of kinetic properties^3–5 and showed that drug efficacy is sometimes correlated with the kinetic properties better than binding affinity.^6,7 Investigating residence time^8–10 was proposed in the past decade and has become a useful criterion in predicting drug efficacy. Efforts have been devoted to studies of kinetic–structure relations.^11–14 Computational methods, which have the advantage of an atomistic resolution, are useful tools to investigate the fundamentals of thermodynamics and kinetics. With the recent breakthrough in computational powers, molecular dynamics (MD) is able to simulate up to microsecond or millisecond time scale molecular motions.^15,16 Therefore, computational methods can be used to sample a larger time scale of dynamics of host–guest systems and take advantage of numerical methods to directly extract the enthalpic and entropic profiles of both the solvent and the solute as well as the kinetics from unbiased long-time-scale MD. New findings observed from chemical host–guest systems with theoretically sound computational methods have advanced our knowledge of molecular recognition and brought new insights into ligand–protein systems.

Cyclodextrins (CDs) are a class of cyclic oligosaccharide compounds that can be obtained by degradation of starch by α-1,4-glucan-glycosyltransferases. Depending on the number of glucopyranose units (D-glucose), these compounds can be classified into 6 units (α-CD), 7 units (β-CD), 8 units (γ-CD), and CDs of more glucopyranose units. In β-CD (Figure 1), the 7 glucopyranose units (D-glucose) enclose a cavity with a diameter of about 6.5 Å. The glucopyranose units bring the center of the cavity a hydrophobic surface of the carbon chains in the glucopyranose, whereas the rims of β-CD consist of hydrophilic hydroxyl groups. Notably, the wide and narrow rims of β-CD are asymmetrical. Because of the structure and size of the cavity, β-CD can host a wide variety of guest molecules via nonpolar or polar attractions. With these properties, β-CD and its derivatives have many applications in many fields, such as the cosmetics industry, pharmaceuticals, catalysis, and food and agricultural industries.^17–23 Thus, the experimental thermodynamics and kinetics data are available for a variety of β-CD complexes.^24–30

Figure 1.

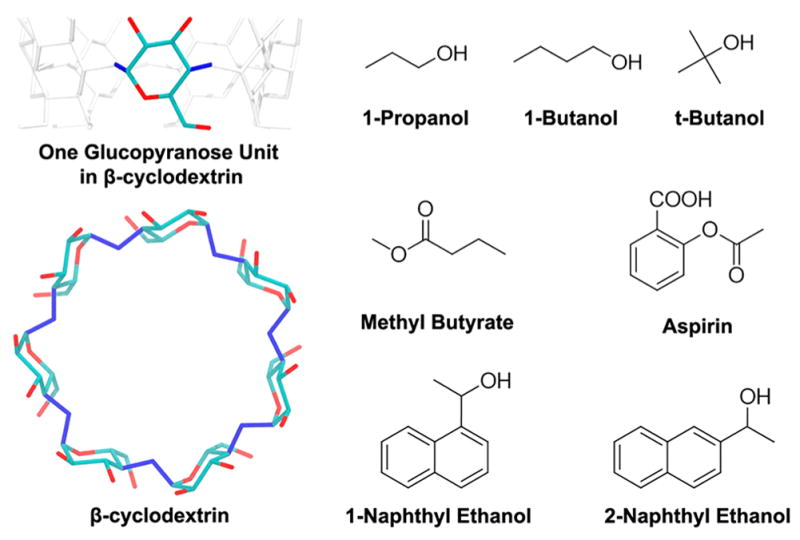
Structure of β-cyclodextrin (β-CD) and the 7 guest molecules. In the structure of β-CD, hydrogen atoms are not shown. For the β-CD internal (vibrational/conformational) entropy calculation, the 14 dihedral angles used to define the conformations of β-CD are in blue.

β-CD consists of 147 atoms, so we can directly investigate the fundamentals of binding thermodynamics and kinetics by MD simulations. Short MD simulations have been used to study ligand binding affinity, dynamics, H bonds, and hydration properties of β-CD complexes.^31–38 Replica exchange molecular dynamics (REMD) and the Mining Minima 2 method were used to thoroughly sample the bound states of various β-CD complexes and accurately evaluate their binding affinities by using an implicit solvent model.^39,40 QM/MM methods were also used to investigate the binding pose, binding enthalpy, and properties of the β-CD cavity.^41–44 In most of these studies, the conformations of β-CD resemble the crystal structures via shorter than 20 ns MD simulations and no further dynamic information from experiments or long-time-scale MD of β-CD complexes. In addition, although the binding affinity decomposition into enthalpy and entropy has been achieved for some ligands, the use of an implicit solvent model and previous computation techniques cannot obtain both solvent and solute entropy contributions that allow direct comparison with experimentally measured ΔH and ΔS. It is still difficult to sample multiple association/dissociation events for kinetic rate calculations. ⁴⁵

The present study applied microsecond-time-scale MD simulations with GPU acceleration to compute binding kinetics and thermodynamics of 7 guests with β-CD to reveal the binding mechanisms. Using two force fields for β-CD, GAFF-CD, and q4MD-CD, we performed simulations that sampled multiple association/dissociation events of the complexes to compute k_on and k_off together with MD of free β-CD and guests and a water box to compute entropy and enthalpy from both contributions of solvent and solutes. The nonpolar interactions between solutes and the water entropy gains on binding were the major driving forces of association, regardless of the use of force fields. However, GAFF-CD provided slightly more flexible β-CD, which produced more complicated H-bond networks between the free β-CD and water molecules in the first hydration shell, thereby resulting in slower k_on and larger desolvation penalty. The study also gives details regarding multiple guest association and dissociation pathways and explains how each decomposed energetic and entropic term contributes to binding kinetics/thermodynamics and binding mechanisms.

2. METHOD

Molecular Systems and Force Fields

We selected 4 weak binders (1-butanol, tert-butanol, 1-propanol, methyl butyrate) and 3 relatively stronger binders (aspirin, 1-naphthyl ethanol, 2-naphthyl ethanol) as the guest molecules (ligands) for the β-CD host–guest complexes. Note that the 3 relatively stronger binders still bind weakly with β-CD (mM binders). The set of data has similar experimental binding affinities (ΔG) by both kinetics and thermodynamic measurements, and the available rate constants are accessible by MD for sampling multiple association and dissociation events. Structures of guests were manually created using Vega ZZ,⁴⁶ and the structure of β-CD was obtained from the Cambridge Crystal Data Center (PDB ID: WEWTOJ) (Figure 1). We used two different force fields for β-CD: Amber general force field (GAFF),⁴⁷ termed GAFF-CD, and q4MD-CD force field.⁴⁸ For simulations with GAFF-CD, we took the partial charge of β-CD from a previous work.⁴⁰ For simulations using q4MD-CD, the partial charge of β-CD was provided in the force field. The guests were modeled by only GAFF, and the partial charges were computed using optimization and then ChelpG atomic charge calculation with the Gaussian package⁴⁹ at the 6-31+g(d,p)/B3LYP level. Initial conformations of the complexes were obtained by manually locating the ligand in the center of the cavity of β-CD. All MD simulations and calculations were repeated in the same setting for the free and bound β-CD with GAFF-CD and q4MD-CD.

Molecular Dynamics Simulations

We performed microsecond- time-scale MD runs for a total of 1–11 μs simulations (Table SI 1) for each β-CD-ligand system, that is, on the complex, the free β-CD, the free ligand, and an empty water box.⁵⁰ For each run, the system was first solvated with exactly 1737 TIP3P water molecules (about 12 Å away from the solute) and then optimized to eliminate possible clashes. The water molecules were then equilibrated at 298 K for 1 ns, followed by an equilibration of the entire system from 200 to 298 K for 150 ps. By using Amber 14 with GPU acceleration, ^47,51 long production runs were performed at 298 K maintained by a Langevin thermostat^52,53 in an NPT (isothermal–isobaric) ensemble. A frame was saved every 1 ps for each run. For postanalysis and numerical calculations we resaved a frame every 10 ps, and the trajectories were visualized by VMD.⁵⁴ Table SI 1 summarizes the total lengths of all MD simulations and numbers of frames used in thermodynamics calculations. We also performed 50 ns MD runs for free β-CD in a vacuum by using GAFF-CD and q4MD-CD to examine the force field parameters, as detailed in SI section 2.

Binding Enthalpy Calculation

The binding enthalpy (ΔH) was calculated by ΔH = 〈E〉_Complex + 〈E〉_Water − 〈E〉_Host − 〈E〉_Guest ⁵⁰ with the periodicity of the water box, where 〈E〉_Complex, 〈E〉_Water, 〈E〉_Host, and 〈E〉_Guest are the averaged potential energies of all molecules from the trajectories of the complex, water, host, and guest, respectively. Note that only the bound state conformations from the trajectories of the complexes were used to compute 〈E〉_Complex. The kinetic energy will be canceled, so it is not evaluated here. The pressure–volume term is negligible in a solvated system. The computed decomposed enthalpy terms are reported in SI section 3. We also computed the surface area, number of H bonds, and number of solvation water (detailed in SI section 4) to explain our decomposed enthalpy terms.

Solute Entropy Calculation

Solute entropy change (ΔS_Solute) and water entropy change (ΔS_Water) are computed separately for binding entropy, ΔS = ΔS_Solute + ΔS_Water, where ΔS_Solute was decomposed into host internal (conformational/vibrational) entropy change (ΔS_Host), guest internal entropy change (ΔS_{Guest Int}), and guest external (translational/rotational) entropy change (ΔS_{Guest Ext}), illustrated as ΔS_Solute = ΔS_Host + ΔS_{Guest Int} + ΔS_{Guest Ext}.

Notably, the host retains its external degrees of freedom, so there is no change of external entropy for the host. The internal entropy changes of the host (ΔS_Host = S_{Host Complex} − S_{Host Free}) and guest (ΔS_{Guest Int} = S_{Guest Int Complex} − S_{Guest Int Free}) were calculated by taking the difference in internal entropies of their free state and bound state by using the Gibbs entropy formula (eq 1)^55,56

$$S_{\text{Int}}=-R\int P({\mathrm{\Omega }}_{\text{Solute}})\text{ln}(P({\mathrm{\Omega }}_{\text{Solute}}))\mathrm{d}{\mathrm{\Omega }}_{\text{Solute}}$$ (1)

where R is the gas constant and P(Ω_Solute) is the probability distribution of conformations (Ω_Solute) defined by key dihedrals in the species, as detailed in SI section 5.

In the free states, both β-CD and ligands can diffuse freely in solution, but ligand diffusion may be restricted after binding into the cavity of β-CD. The external entropy loss of the ligand was calculated as ΔS_{Guest Ext} = S_{Guest Ext Complex} − S_{Guest Ext Free}, where S_{Guest Ext Free} = R ln(8π²/C⁰) is approximately 6.98 kcal/mol at 298 K.^57,58 R is the gas constant, and C⁰ is the standard concentration (1 M). S_{Guest Ext Complex} is the external entropy of the ligands evaluated by numerical integration after aligning the MD trajectories of the complexes to the crystal structure of β-CD

$$S_{\text{GuestExtComplex}}=Rln\left(\int sin(\theta )\mathrm{d}x\mathrm{d}y\mathrm{d}z\mathrm{d}\varphi \mathrm{d}\phi \mathrm{d}\theta \right)$$ (2)

where x, y, and z are the Cartesian coordinates of the ligand translation and ϕ, φ, and θ are the Euler angles of the ligand rotation. The bin size of x, y, and z was 2 Å, and the bin size of ϕ, φ, and θ was 30°. The ϕ and φ were integrated from −π to π, and θ was integrated from −π/2 to π/2.

Water Entropy Calculation

We evaluated the water entropy change on ligand binding (ΔS_Water) from the solvation entropy (ΔS_Solv·) of the free β-CD (ΔS_Solv·Host), free guests (ΔS_Solv·Guest), and the complexes (ΔS_{Solv·Complex}) by ΔS_Solv· = ΔS_Solv·Trans + ΔS_Solv·Rot + ΔS_Solv·Conf. ΔS_Solv· was calculated by the grid cell method.^59–61 In the grid cell method, the water molecules in the water box are treated as if they are vibrating in a local cell and confined by the forces from surrounding water molecules and solutes. In the cell method, ΔS_Solv· decomposes into vibrational (ΔS_{Solv· Vib}) and conformational (ΔS_Solv·Conf) entropies and ΔS_Solv·Vib further decomposes into translational (ΔS_Solv·Trans) and rotational (ΔS_Solv·Rot) entropies. The entropy terms were calculated by using eqs 6.8–6.11 in the SI, and an in-house script was developed to perform the calculations. The changes in water entropy on ligand binding were evaluated by ΔS_Water = ΔS_{Solv·Complex} − ΔS_Solv·Host − ΔS_Solv·Guest. The translational (ΔS_{Water Trans}), rotational (ΔS_{Water Rot}), and conformational (ΔS_{Water Conf}) terms of changes of water entropy on ligand binding were evaluated by the same equation. The setting of solvation water entropy calculation is provided in SI section 6. We counted the number of solvation water molecules in the free guest, free host, and complexes to explain the water entropy calculations, as detailed in SI section 7.

Calculations of the Association and Dissociation Rate Constants

As mentioned previously, our MD simulations can sample multiple association and dissociation events in one long run for each system. We define the bound state for a complex when the center of mass of the ligand is within 7.5 Å from the center of mass of β-CD. Any bound/unbound period that lasted longer than 1.0 ns was counted as one bound/unbound event. Because molecules fluctuate during ligand binding, if a ligand stayed or left β-CD for less than 1.0 ns, we did not consider the motion as a bound/unbound event. The average bound/unbound period lengths were calculated and plugged into eqs 3 and 4 to compute k_on and k_off, where [solute] is the concentration of solute estimated by the averaged size of the water box, as detailed in SI section 8. After obtaining k_on and k_off, we calculated the equilibrium constant K_eq = k_on/k_off. We also estimated the diffusion-controlled association rate constants by using diffusion coefficients and radii of host and guest molecules for comparison, as detailed in SI section 9.

$$k_{\text{on}}=\frac{1}{\text{average}\text{unbound}\text{time}\times [\text{solute}]}$$ (3)

$$k_{\text{off}}=\frac{1}{\text{average}\text{bound}\text{time}}$$ (4)

Binding Free Energy Calculation

The binding free energies can be computed by using the classical thermodynamics and statistical mechanics equations. We evaluated binding free energies (ΔG_Comp1) from the computed binding enthalpy and binding entropy as in eq 5. We also evaluated binding free energies (ΔG_Comp2) from the computed association and dissociation rate constants (k_on and k_off) as in eq 6

$$\mathrm{\Delta }{G}_{\text{Comp}1}=\mathrm{\Delta }H-T\mathrm{\Delta }S$$ (5)

$$\mathrm{\Delta }{G}_{\text{Comp}2}=-\mathit{RT}ln(k_{\text{on}}·C^0/k_{\text{off}})$$ (6)

Uncertainty Evaluation of Computed Properties

We evaluated the uncertainties of the binding enthalpy (ΔH), the entropy change of water (ΔS_Water), the internal entropy change of β-cyclodextrin (ΔS_Host), the internal (ΔS_{Guest Int}) and external (ΔS_{Guest Ext}) entropy change of guests, the total binding entropy (ΔS), the binding free energy from eq 5 (ΔG_Comp1), the association (k_on) and dissociation (k_off) rate constants, and the equilibrium constant (K_eq). The details are provided in SI section 10.

3. RESULTS

We used microsecond-time-scale MD simulations with an explicit solvent model to compute the binding enthalpies, entropies, and association/dissociation rate constants for β-CD with 7 guest molecules (Figure 1). Binding free energy ΔG was computed by using eq 5 (ΔG_Comp1), from the thermodynamic properties, and eq 6 (ΔG_Comp2), from the kinetics binding rate constants. All computed results yielded reasonable agreement with experimental data (Tables 1 and 2 and Figure 2). Two force fields, GAFF-CD and q4MD-CD, were used to assign parameters for β-CD, and all ligands used the GAFF force field. In general, ΔG computed with GAFF-CD is slightly more positive than the experimental data, and binding is driven by entropy. In contrast, q4MD-CD yields slightly more negative computed ΔG than experimental data, and binding is driven by enthalpy. Here we were able to separate enthalpy and entropy calculations, and we therefore use directly computed ΔH and −TΔS to investigate their contributions of a guest and β-CD binding.

Table 1.

Binding Free Energies (ΔG), Enthalpies (ΔH), and Entropies (−TΔS) of β-Cyclodextrin (β-CD) with 7 Guests from Experiments and Calculations by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	ΔGComp1	ΔH	−TΔS
1-propanol	−1.54 ± 0.93	0.54 ± 0.74	−2.08 ± 0.19
1-butanol	1.01 ± 0.59	2.99 ± 0.52	−1.98 ± 0.06
methyl butyrate	−2.40 ± 0.52	1.88 ± 0.47	−4.29 ± 0.05
tert-butanol	0.38 ± 0.46	2.86 ± 0.40	−2.48 ± 0.06
1-naphthyl ethanol	−3.01 ± 0.31	−1.41 ± 0.28	−1.60 ± 0.03
aspirin	−3.84 ± 0.35	−0.01 ± 0.31	−3.83 ± 0.04
2-naphthyl ethanol	−2.93 ± 0.30	−0.88 ± 0.27	−2.05 ± 0.03
calculated (q4MD-CD)
guest	ΔGComp1	ΔH	−TΔS
1-propanol	−2.21 ± 0.47	−0.66 ± 0.41	−1.55 ± 0.06
1-butanol	−1.33 ± 0.34	−0.85 ± 0.30	−0.48 ± 0.04
methyl butyrate	−4.17 ± 0.38	−2.00 ± 0.33	−2.17 ± 0.05
tert-butanol	−2.50 ± 0.38	−2.87 ± 0.33	0.37 ± 0.05
1-naphthyl ethanol	−5.53 ± 0.32	−5.44 ± 0.29	−0.09 ± 0.04
aspirin	−6.33 ± 0.37	−4.30 ± 0.33	−2.03 ± 0.05
2-naphthyl ethanol	−4.32 ± 0.31	−4.03 ± 0.28	−0.29 ± 0.03
experimental
guest	ΔG	ΔH	−TΔS
1-propanol24	−0.88 ± 0.09	1.43 ± 0.48	−2.34 ± 0.57
1-butanol24	−1.67 ± 0.19	0.69	−2.34
methyl butyrate63	−1.99 ± 0.02	/	/
tert-butanol93	−2.22 ± 0.01	/	/
1-naphthyl ethanol29	−4.08 ± 0.01	/	/
aspirin28	−3.74 ± 0.00	/	/
2-naphthyl ethanol29	−3.97 ± 0.07	/	/

^aUnavailable experimental values are marked by /. All values are in kcal/mol.

Table 2.

Association and Dissociation Rate Constants of the 7 β-CD Complexes from Experiments and Calculations by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	kon (1/s·M)	koff (1/s)	Keq (1/M)	ΔGComp2 (kcal/mol)
1-propanol	2.0 ± 0.1 × 108	3.9 ± 0.3 × 108	0.5 ± 0.06	0.40 ± 0.08
1-butanol	2.2 ± 0.1 × 108	1.1 ± 0.2 × 108	2.0 ± 0.3	−0.41 ± 0.10
methyl butyrate	3.9 ± 0.1 × 108	8.0 ± 0.6 × 107	4.9 ± 0.4	−0.94 ± 0.05
tert-butanol	2.3 ± 0.1 × 108	8.5 ± 1.2 × 107	3.2 ± 0.4	−0.69 ± 0.08
1-naphthyl ethanol	8.6 ± 1.1 × 108	1.5 ± 1.9 × 106	558.9 ± 100	−3.75 ± 0.12
aspirin	1.1 ± 0.01 × 109	2.4 ± 0.3 ×107	46 ± 4.3	−2.27 ± 0.06
2-naphthyl ethanol	9.5 ± 0.4 × 108	5.2 ± 0.9 × 106	182 ± 23	−3.08 ± 0.08
calculated (q4MD-CD)
guest	kon (1/s·M)	koff (1/s)	Keq (1/M)	ΔGComp2 (kcal/mol)
1-propanol	1.2 ± 0.02 × 109	1.2 ± 0.02 × 108	10.1 ± 0.2	−1.37 ± 0.01
1-butanol	1.5 ± 0.03 × 109	3.3 ± 0.07 ×107	45.9 ± 1.2	−2.27 ± 0.02
methyl butyrate	1.6 ± 0.1 × 109	1.1 ± 0.1 ×107	146.8 ± 15	−2.95 ± 0.06
tert-butanol	1.1 ± 0.07 × 109	7.2 ± 1.0 × 106	157.5 ± 18	−3.00 ± 0.07
1-naphthyl ethanol	1.2 ± 0.5 × 109	1.4 ± 0.5 × 106	876.0 ± 42	−4.01 ± 0.03
aspirin	3.2 ± 0.3 × 109	3.1 ± 0.9 × 106	1035.3 ± 83	−4.11 ± 0.05
2-naphthyl ethanol	3.91 × 109	5.0 × 105	7788.3	−5.31
experimental
guest	kon (1/s·M)	koff (1/s)	Keq (1/M)	ΔG (kcal/mol)
1-propanol93	5.1 ± 0.7 × 108	1.2 ± 0.07 × 108	4.2 ± 0.6	−0.88 ± 0.09
1-butanol93	2.8 ± 0.8 × 108	3.8 ± 0.6 ×107	7.2 ± 2.0	−1.67 ± 0.19
methyl butyrate63	3.7 ± 0.3 × 108	1.28 ± 0.03 ×107	29 ± 1	−1.99 ± 0.02
tert-butanol93	3.6 ± 0.1 × 108	0.85 ± 0.01 ×107	42.6 ± 1.0	−2.22 ± 0.01
1-naphthyl ethanol29	4.7 ± 1.9 × 108	4.8 ± 1.8 × 105	979 ± 10	−4.08 ± 0.01
aspirin28	7.2 ± 0.04 × 108	1.3 ± 0.03 × 106	549 ± 2	−3.74 ± 0.00
2-naphthyl ethanol29	2.9 ± 1.6 × 108	1.8 ± 0.7 × 105	820 ± 90	−3.97 ± 0.07

^aThe standard deviations of rate constants of β-CD-2-naphthyl ethanol with q4MD-CD are not available because of lack of adequate binding events.

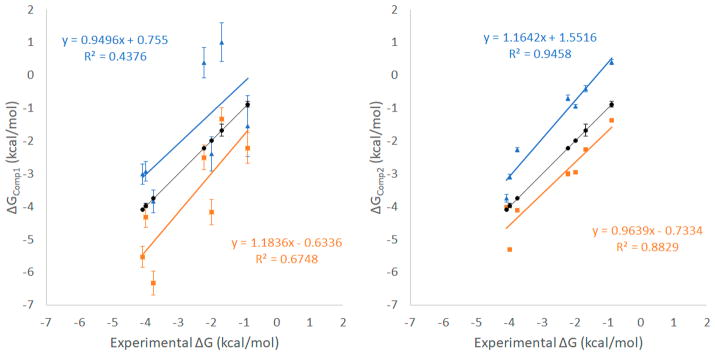
Figure 2.

Correlations between ΔG_Comp1, ΔG_Comp2, and experimental values. Results from GAFF-CD are shown in blue triangles, and results from q4MD-CD are shown in orange rectangles. Experimental values are shown in black circles. Correlations are labeled correspondingly.

Binding Enthalpy and Entropy Calculations

The calculated ΔH, −TΔS, and ΔG_Comp1 by using eq 5 with the GAFF-CD and q4MD-CD force fields are compared with the experimental data in Table 1. The computed ΔG is mostly within 2 kcal/mol of experiments, and they provide a correct trend. Although results from the two force fields reasonably agree with experimental results, GAFF-CD generally underestimated and q4MD-CD overestimated the binding free energy. The intermolecular van der Waals (vdW) attraction between β-CD and a guest is one major driving force for complex formation (Tables 3 and 4) as well as the water entropy gain on binding (Table 5). Interestingly, compared to q4MD-CD, the less negative binding affinities using GAFF-CD are primarily from the larger desolvation penalty, resulting in the less negative binding enthalpy. The host became more flexible and gained configuration entropy on binding, which is another favorable factor in guest binding (Table 5). In contrast, as compared with GAFF-CD, q4MD-CD modeled a significantly smaller desolvation penalty and more negative ΔH, which become the main driving force for binding. However, the systems need to pay a higher cost in entropy (−TΔS) because the host became more rigid in the bound state.

Table 3.

Binding Enthalpy Decompositions of β-CD Complexes by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	ΔH	ΔHHost–Guest	ΔHHost Conf	ΔHGuest Conf	ΔHSolute Inter	ΔHDesolvation	ΔHHost–Water	ΔHGuest–Water	ΔHWater–Water
1-propanol	0.54	−10.64	−0.87	−0.01	−9.76	11.18	12.20	6.92	−7.93
1-butanol	2.99	−15.28	−2.25	0.00	−13.03	18.27	20.55	8.34	−10.62
methyl butyrate	1.88	−19.31	−2.85	0.02	−16.48	21.19	25.58	10.28	−14.67
tert-butanol	2.86	−15.71	−2.55	−0.04	−13.13	18.57	20.71	8.39	−10.53
1-naphthyl ethanol	−1.41	−30.60	−4.45	0.03	−26.18	29.19	35.45	14.93	−21.19
aspirin	−0.01	−31.53	−3.77	0.23	−27.99	31.52	34.60	19.15	−22.22
2-naphthyl ethanol	−0.88	−28.45	−3.97	0.13	−24.61	27.57	33.21	13.76	−19.40
calculated (q4MD-CD)
guest	ΔH	ΔHHost–Guest	ΔHHost Conf	ΔHGuest Conf	ΔHSolute Inter	ΔHDesolvation	ΔHHost–Water	ΔHGuest–Water	ΔHWater–Water
1-propanol	−0.66	−13.61	−2.05	0.04	−11.60	12.95	13.72	7.74	−8.50
1-butanol	−0.85	−16.66	−2.66	0.09	−14.10	15.82	17.72	9.21	−11.10
methyl butyrate	−2.00	−20.61	−3.53	0.18	−17.26	18.61	22.05	11.10	−14.55
tert-butanol	−2.87	−17.38	−3.50	−0.06	−13.82	14.51	16.31	7.87	−9.67
1-naphthyl ethanol	−5.44	−28.56	−3.42	0.20	−25.34	23.12	29.65	14.51	−21.04
aspirin	−4.30	−29.85	−3.39	0.57	−27.03	25.55	28.91	18.17	−21.53
2-naphthyl ethanol	−4.03	−27.41	−3.38	0.16	−24.20	23.38	28.82	13.95	−19.39

^aThe total binding enthalpy (ΔH) is decomposed into solute–solute interaction change (ΔH_Host–Guest) and desolvation energy (ΔH_Desolvation). ΔH_Host–Guest includes conformational enthalpy changes of host (ΔH_{Host Conf}) and guest (ΔH_{Guest Conf}) and host–guest interaction change (ΔH_{Solute Inter}). ΔH_Desolvation decomposes into host–water (ΔH_Host–Water), guest–water (ΔH_{Guest–Water}), and water–water (ΔH_{Water–Water}) interaction changes. All values are in kcal/mol.

Table 4.

Decompositions of Host–Guest Interaction Change (ΔH_{Solute Inter}) into van der Waals and Coulombic Energies by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	ΔHSolute Inter	ΔHSolute Inter (vdW)	ΔHSolute Inter (Coul)
1-propanol	−9.76	−6.08	−3.68
1-butanol	−13.03	−10.33	−2.7
methyl butyrate	−16.48	−14.33	−2.16
tert-butanol	−13.13	−10.8	−2.32
1-naphthyl ethanol	−26.18	−23.57	−2.61
aspirin	−27.99	−22.76	−5.22
2-naphthyl ethanol	−24.61	−21.72	−2.89
calculated (q4MD-CD)
guest	ΔHSolute Inter	ΔHSolute Inter (vdW)	ΔHSolute Inter (Coul)
1-propanol	−11.6	−9.67	−1.93
1-butanol	−14.1	−12.09	−2.01
methyl butyrate	−17.26	−15.12	−2.14
tert-butanol	−13.82	−12.39	−1.43
1-naphthyl ethanol	−25.34	−22.76	−2.57
aspirin	−27.03	−22.15	−4.88
2-naphthyl ethanol	−24.2	−21.45	−2.75
Units: kcal/mol

^aΔH_{Solute Inter} is decomposed into van der Waals energy (ΔH_{Solute Inter (vdW)}) and Coulombic energy (ΔH_{Solute Inter (Coul)}). All values are in kcal/mol.

Table 5.

Binding Entropy Decomposition of β-CD Complexes by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	−TΔSWater	−TΔSHost	−TΔSGuest Int	−TΔSGuest Ext	−TΔS
1-propanol	−3.32 ± 0.18	−0.52 ± 0.01	0.00 ± 0.00	1.75 ± 0.00	−2.08 ± 0.19
1-butanol	−2.37 ± 0.06	−1.20 ± 0.00	−0.05 ± 0.00	1.64 ± 0.00	−1.98 ± 0.06
methyl butyrate	−4.00 ± 0.04	−1.58 ± 0.00	−0.10 ± 0.00	1.39 ± 0.00	−4.29 ± 0.05
tert-butanol	−2.22 ± 0.05	−1.84 ± 0.00	0.00 ± 0.00	1.57 ± 0.00	−2.48 ± 0.06
1-naphthyl ethanol	−2.28 ± 0.02	−1.24 ± 0.00	0.00 ± 0.00	1.92 ± 0.00	−1.60 ± 0.03
aspirin	−4.08 ± 0.03	−1.53 ± 0.00	0.12 ± 0.00	1.67 ± 0.00	−3.83 ± 0.04
2-naphthyl ethanol	−2.33 ± 0.02	−1.33 ± 0.00	0.00 ± 0.00	1.61 ± 0.01	−2.05 ± 0.03
calculated (q4MD-CD)
guest	−TΔSWater	−TΔSHost	−TΔSGuest Int	−TΔSGuest Ext	−TΔS
1-propanol	−3.36 ± 0.05	0.21 ± 0.00	0.02 ± 0.00	1.57 ± 0.00	−1.55 ± 0.06
1-butanol	−2.31 ± 0.03	0.25 ± 0.00	−0.17 ± 0.00	1.74 ± 0.00	−0.48 ± 0.04
methyl butyrate	−4.12 ± 0.04	0.22 ± 0.00	−0.11 ± 0.00	1.84 ± 0.00	−2.17 ± 0.05
tert-butanol	−1.84 ± 0.05	0.45 ± 0.00	0.00 ± 0.00	1.76 ± 0.00	0.37 ± 0.05
1-naphthyl ethanol	−2.17 ± 0.03	0.12 ± 0.00	0.00 ± 0.00	1.95 ± 0.01	−0.09 ± 0.04
aspirin	−3.81 ± 0.04	0.11 ± 0.00	−0.16 ± 0.00	1.82 ± 0.00	−2.03 ± 0.05
2-naphthyl ethanol	−2.31 ± 0.03	0.03 ± 0.00	0.00 ± 0.00	1.99 ± 0.01	−0.29 ± 0.03

^a−TΔS_Water, −TΔS_Host, −TΔS_{Guest Int}, −TΔS_{Guest Ext}, and −TΔS are the entropy change of water, internal entropy change of β-cyclodextrin, internal and external entropy change of guests, and the total binding entropy at 298 K. All values are in kcal/mol.

Unlike for experiments and most calculations that measured ΔG and ΔH, we independently computed ΔH and −TΔS. Nevertheless, we still observed entropy–enthalpy compensation in our systems with different force fields, so the compensation in these systems indeed has a physical implication and is not an artifact from the mathematics of eq 5. We compared the calculated ΔH and −TΔS for 1-propanol and 1-butanol for which experimental data are available. Both experiments and calculations with GAFF-CD showed a small positive ΔH, which slightly opposed binding, but the systems gained more entropy to compensate for losing enthalpy on binding. Although only 2 guests studied here have experimental ΔH and −TΔS, the binding data for other alcohols of β-CD with calorimetry (ITC) and UV experiments commonly show gaining entropy, and enthalpy was not the predominant determinant for binding in all cases (Figure SI 7). The following subsections present results of the binding enthalpy of solute–solute and solute–solvent and the binding entropy of solutes and solvent.

Changes of Enthalpy from Different Components

We evaluated the absolute values of binding enthalpy by using potential energies 〈E〉 from microsecond-time-scale MD trajectories of the four species, and the convergences of the enthalpy calculations were first examined (Figures SI 8–10). For all simulations, the potential energy reaches a stable value within a fluctuation of 0.4 kcal/mol, which is also within reported experimental uncertainty.^{24,28,29,62,63} The fluctuations of potential energies of β-CD-1-propanol, β-CD-1-butanol, and β-CD-tert-butanol complexes are larger with GAFF-CD than the other systems. The fractions of the bound states of these systems are lower than with the other systems; thus, the smaller numbers of sampling result in larger fluctuations.

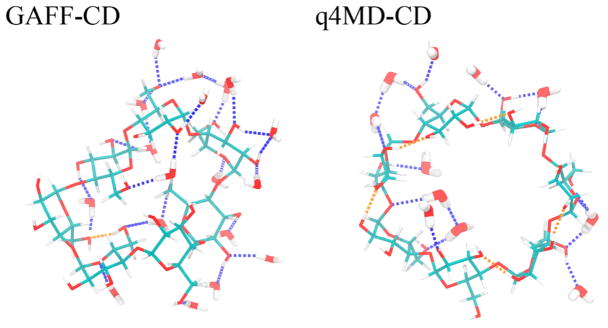
To understand binding enthalpies, we decomposed the calculated values into various contributions (Table 3). We also provide the decompositions into vdW and Coulombic interactions for ΔH_{Solute Inter}, ΔH_{Host Conf}, ΔH_Host–Water, and ΔH_{Guest–Water} (Tables 4, 6, and 7). Regardless of the type of force field used, we immediately noticed that ΔH_Host–Guest data are all favorable (negative), and stronger binders such as naphthyl ethanol and aspirin have large negative ΔH_Host–Guest value,~–30 kcal/mol (Table 3). However, ΔH_Desolvation largely compensates for the solute–solute attraction, for significantly smaller ΔH, ranging from 3.0 to −1.4 kcal/mol with GAFF-CD and from −0.9 to −5.7 kcal/mol with q4MD-CD. The computed ΔH with GAFF-CD yielded positive values for weak binders (ΔG > −2.0 kcal/mol), which has been seen in experiments (see Figure SI 7). In contrast, ΔH values are all negative with q4MD-CD. On binding, both β-CD and the guest desolvate water molecules and lose interactions with water molecules; thus, ΔH_Host–Water and ΔH_{Guest–Water} values are all positive. The values are larger for stronger binders; presumably, guests such as naphthyl ethanols have larger sizes as compared with weaker/small binders such as propanol. The water molecules released after binding regain interactions with other water molecules, thereby resulting in all negative ΔH_{Water–Water} values. However, this term is not negative enough to counterbalance the loss from water–solute interactions. As a result, desolvation enthalpy is inevitably all positive and becomes the major force that opposes binding. Of note, the desolvation penalty from the polar contribution is the major force that opposes binding with GAFF-CD, which results from losing more intermolecular H bonds between water molecules and β-CD (Table 7). The partial charges and the nonpolar attractions between guests and β-CD modeled with both force fields are highly similar. However, different parameters for the bonded terms result in different modeled β-CD conformations, which significantly changes the H-bond networks between water molecules and β-CD. As illustrated in Figure 3 and Table SI 2, the conformation results in breaking more intermolecular H bonding and larger desolvation penalty in GAFF-CD on guest binding.

Table 6.

Decompositions of β-CD Conformational Enthalpy Change (ΔH_{Host Conf}) into Bonded, van der Waals, and Coulombic Energies by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	ΔHHost Conf	ΔHHost Conf (Bonded)	ΔHHost Conf (vdW)	ΔHHost Conf (Coul)
1-propanol	−0.87	1.37	1.76	−4.00
1-butanol	−2.25	3.97	5.22	−11.44
methyl butyrate	−2.85	4.65	6.01	−13.51
tert-butanol	−2.55	5.05	6.07	−13.67
1-naphthyl ethanol	−4.45	6.23	8.71	−19.39
aspirin	−3.77	5.89	7.95	−17.62
2-naphthyl ethanol	−3.97	5.54	8.15	−17.66
calculated (q4MD-CD)
guest	ΔHHost Conf	ΔHHost Conf (Bonded)	ΔHHost Conf (vdW)	ΔHHost Conf (Coul)
1-propanol	−2.05	−0.38	1.79	−3.46
1-butanol	−2.66	−0.38	1.95	−4.23
methyl butyrate	−3.53	−0.47	2.29	−5.34
tert-butanol	−3.50	−0.83	2.18	−4.86
1-naphthyl ethanol	−3.42	0.62	2.57	−6.62
aspirin	−3.39	0.34	2.44	−6.16
2-naphthyl ethanol	−3.38	0.21	2.57	−6.16

^aΔH_{Host Conf} is decomposed into bonded energy (ΔH_{Host Conf (Bonded)}), van der Waals energy (ΔH_{Host Conf (vdW)}), and Coulombic energy (ΔH_{Host Conf (Coul)}). All values are in kcal/mol.

Table 7.

Decompositions of Host–Water (ΔH_Host–Water) and Guest–Water (ΔH_{Guest–Water}) Interaction Enthalpy Changes into van der Waals and Coulombic Energies by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	ΔHHost–Water	ΔHHost–Water (vdW)	ΔHHost–Water (Coul)	ΔHGuest–Water	ΔHGuest–Water (vdW)	ΔHGuest–Water (Coul)
1-propanol	12.20	1.34	10.85	6.92	2.12	4.80
1-butanol	20.55	0.12	20.44	8.34	4.15	4.19
methyl butyrate	25.58	0.64	24.94	10.28	5.79	4.49
tert-butanol	20.71	−1.38	22.09	8.39	4.16	4.23
1-naphthyl ethanol	35.45	0.91	34.54	14.93	9.62	5.32
aspirin	34.60	0.40	34.20	19.15	9.13	10.02
2-naphthyl ethanol	33.21	1.54	31.66	13.76	9.29	4.47
calculated (q4MD-CD)
guest	ΔHHost–Water	ΔHHost–Water (vdW)	ΔHHost–Water (Coul)	ΔHGuest–Water	ΔHGuest–Water (vdW)	ΔHGuest–Water (Coul)
1-propanol	13.72	4.08	9.63	7.74	3.85	3.89
1-butanol	17.72	5.45	12.27	9.21	4.99	4.22
methyl butyrate	22.05	6.51	15.54	11.10	6.34	4.77
tert-butanol	16.31	4.75	11.56	7.87	5.12	2.75
1-naphthyl ethanol	29.65	8.63	21.02	14.51	9.60	4.91
aspirin	28.91	7.75	21.16	18.17	9.35	8.82
2-naphthyl ethanol	28.82	8.95	19.87	13.95	9.37	4.59

^aΔH_Host–Water and ΔH_{Guest–Water} decompose into van der Waals energy (ΔH_{Host–Water (vdW)} and ΔH_{Guest–Water (vdW)}) and Coulombic energy (ΔH_{Host–Water (Coul)} and ΔH_{Guest–Water (Coul)}) terms. All values are in kcal/mol.

Figure 3.

Hydrogen-bond (H-bond) patterns of representative free β-CD conformations with GAFF-CD and q4MD-CD. With GAFF-CD, there are 18 water molecules forming H bonds with β-CD, 24 H bonds with water (blue dotted lines), and 1 intramolecular H bond (orange dotted lines). With q4MD-CD, there are 11 water molecules forming H bonds with β-CD, 16 H bonds with water, and 5 intramolecular H bonds.

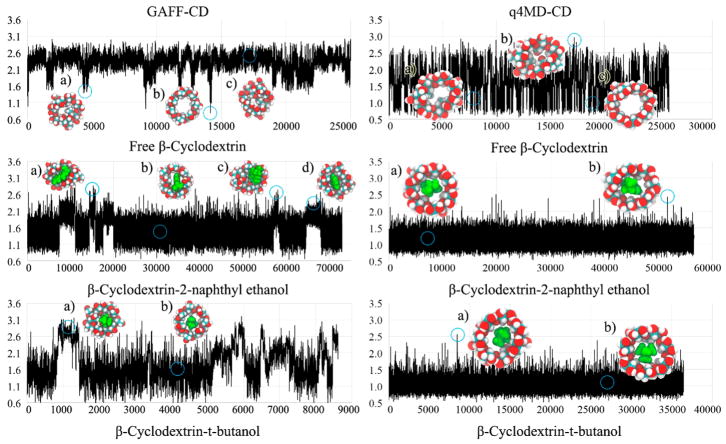
Strong enough intermolecular attraction ΔH_{Solute Inter} is always required for molecular recognition, and vdW attraction was the major driving force for all guests (Table 4). The loss of intramolecular H bonds of β-CD on guest binding is compensated by the intermolecular Columbic attraction in the bound state (ΔH_{Host Conf (Coul)} in Table 6). Although the values of ΔH_Host–Guest with both force fields are similar, the decomposition shows significantly larger numbers of each contribution to ΔH_{Host Conf}, such as ΔH_{Host Conf (vdW)} and ΔH_{Host Conf (Coul)} of β-CD, with GAFF-CD (Table 6) because of larger conformational changes after ligand binding. The free β-CD prefers flipping 2 glucopyranose units instead of holding an open cavity, as shown in the crystal structure (Figure 4, GAFF-CD free β-CD a and c compared to low population of b). The glucose rings flipped outward during ligand binding, which lost more water molecules to allow the binding site of β-CD to be accessible for guests to bind. In contrast, q4MD-CD appeared to have crystal-like host structures in both the free and the bound states. Note that in vacuum, both GAFF-CD and q4MD-CD sampled predominantly crystal-like host structures (Figure SI 1), which indicates that the glucose ring flipping is largely induced by the hydration shell. GAFF-CD not only changed host conformations upon ligand binding but also makes the host more flexible.

Figure 4.

RMSD plots and representative conformations of β-CD for free β-CD, β-CD-2-naphthyl ethanol complex, and β-CD-tert-butanol complex with GAFF-CD and q4MD-CD. RMSD (Å) are computed against the crystal structure by using conformations chosen every 100 ps from all conformations of free β-CD and bound-state conformations of complexes. Representative conformations are shown near the labels (a–d) and circles on the plots. In the representative conformations, ligands are in green.

Changes of Solute Entropy on Ligand Binding

Solute entropy, also termed configuration entropy, reflects the flexibility of a molecular system. Here we used numerical integration to compute each entropy term by eq 1 for internal (conformational/vibrational) and eq 2 for external (translational/rotational) solute entropy. We used the well-defined dihedral distribution analyzed from our MD trajectories to compute internal solute entropy, as detailed in SI section 5. For the small and weak binding guests studied here, the internal solute entropy of a guest is nearly identical when the guest is in the free solution or bound to β-CD, suggesting a weak correlation between internal degrees of freedom and external translational and rotational degrees of freedom (Table 5 and SI Movie). The external and internal entropy terms therefore can be computed separately in our systems. The calculated entropy values are shown in Table 5. A system is well known to lose configuration entropy because the intermolecular attractions inevitably rigidify the 2 molecules on binding.^39,40,64,65 For example, a drug binding to HIV protease can result in >10 kcal/mol entropic penalty from rigidifying conformational and vibrational degrees of freedom.⁶⁶ Additional loss of the configuration entropy also comes from translational and rotational entropy of a ligand, >7 kcal/mol, by confining itself in a snug binding site.^57,58 Postanalyzing our MD trajectories showed that all guests and β-CD were not markedly rigidified in the bound state. The guests lost ~1.5–2 kcal/mol external entropy, and β-CD was slightly more flexible, gaining 0.5–1.8 kcal/mol internal entropy with GAFF-CD or being unchanged with q4MD-CD on guest binding (Table 5). Even though different force fields for the host yield considerable differences in β-CD fluctuations, the variation in internal entropy of guests (−TΔS_{Guest Int}) is negligible. Also, the interactions between β-CD and guests are not large enough to strongly confine a guest to a handful of well-defined bound guest conformations, thereby allowing a guest to freely tumble and diffuse in the cavity of β-CD. Figure SI 11 illustrates that ligands can pose a wide collection of locations and orientations covering the center and top regions of the binding site, thereby resulting in a small reduction of −TΔS_{Guest Ext}.

Changes of Water Entropy on Ligand Binding

Water entropy is one major driving force in ligand binding in these systems, contributing from −2 to −4 kcal/mol to the free energy of binding (Tables 1 and 5). Gaining water entropy dominates in the binding of all guests to β-CD with GAFF-CD and the first 3 weaker binders to β-CD with q4MD-CD. The change in water entropy (−TΔS_water) is a combined effect from rearranging water molecules, which affects their vibrational and conformational entropy, and from releasing the water molecules residing in the cavity of β-CD or interacting with the guest after the complex is formed (Tables 8 and SI 3–6). We used a grid cell theory approach to calculate the water entropy over the space near the solute, as compared with the entropy estimated for the bulk solvent. We also used an alternative method that computes the molar entropy of water when different solutes are present to approximate −TΔS_water (detailed in SI section 6). Both methods agree with each other. The theory and implementation were first validated by comparing our computed molar entropy of bulk water at 298 K, 5.26 kcal/mol (Tables SI 3–5), with the standard molar entropy of water at 298 K, 4.98 kcal/mol. The rigid water TIP3P model performed very well in reproducing standard molar entropy, as reported here and previously, with a two-phase thermodynamic method.^67,68

Table 8.

Decompositions of Water Entropy Change by Using GAFF-CD and q4MD-CD Force Fields^a

calculated (GAFF-CD)
guest	−TΔSWater Trans	−TΔSWater Rot	−TΔSWater Vib	−TΔSWater Conf	−TΔSWater
1-propanol	−2.02	−0.91	−2.92	−0.39	−3.32
1-butanol	−1.18	−0.73	−1.90	−0.47	−2.37
methyl butyrate	−1.92	−1.36	−3.28	−0.72	−4.00
tert-butanol	−1.16	−0.46	−1.63	−0.59	−2.22
1-naphthyl ethanol	−1.12	−0.18	−1.30	−0.98	−2.28
aspirin	−2.36	−0.91	−3.26	−0.82	−4.08
2-naphthyl ethanol	−1.15	−0.24	−1.38	−0.95	−2.33
calculated (q4MD-CD)
guest	−TΔSWater Trans	−TΔSWater Rot	−TΔSWater Vib	−TΔSWater Conf	−TΔSWater
1-propanol	−1.93	−0.90	−2.83	−0.53	−3.36
1-butanol	−1.13	−0.47	−1.60	−0.71	−2.31
methyl butyrate	−1.80	−1.46	−3.26	−0.86	−4.12
tert-butanol	−0.77	−0.33	−1.10	−0.74	−1.84
1-naphthyl ethanol	−0.70	−0.37	−1.07	−1.10	−2.17
aspirin	−1.99	−0.86	−2.85	−0.96	−3.81
2-naphthyl ethanol	−0.80	−0.47	−1.26	−1.04	−2.31

^aThe binding water entropy (−TΔS_Water) decomposes into translational (−TΔS_{Water Trans}), rotational (−TΔS_{Water Rot}), vibrational (−TΔS_{Water Vib} = −TΔS_{Water Trans} + −TΔS_{Water Rot}), and conformational (−TΔS_{Water Conf}) terms. All values are in kcal/mol.

Table 5 lists the changes in water entropy on each guest binding to β-CD, and the contribution from each decomposed entropy term is in Tables SI 3–5. Using different force fields to model β-CD did not change the computed −TΔS_Water, so solute flexibility does not play an important role in water entropy calculations. Aspirin and methyl butyrate have more water entropy gains on binding than do other guests. The 2 guests have more polar functional groups to capture nearby water molecules in their free state, and after forming the complex with β-CD, these water molecules are released, which results in gaining more entropy on binding.

Figure 5 reveals the fluctuation of water molecules presented in the grid space in a pure water box and when β-CD, 2-naphthyl ethanol, or the complex is present using GAFF-CD. The behavior of water molar entropy in q4MD-CD is similar to GAFF-CD, so only one force field is presented in this figure. The averaged jiggling of water molecules is quantified by computed translational, rotational, and conformational entropy, as shown in columns 2–4 of Figure 5, and the darker grid indicates that water molecules in this cell are less mobile. We used an in-house multilayer visualization program to display the decomposed entropy terms for each grid, and the layer through the center of the solute was selected in the figure. In general, the translational entropy decreases at the surface of the solute because the existence of the solute hinders free diffusion of water molecules. In free β-CD and 2-naphthyl ethanol, the translational entropy of water decreases ~0.2–0.4 kcal/mol around the solutes, as shown by darker cells in the vicinity of each solute in Figures 5B–D.

Figure 5.

Water entropy decompositions of pure water and in the vicinities of free β-CD, free 2-naphthyl ethanol, and β-CD-2-naphthyl ethanol complex in GAFF-CD. From top to bottom are pure water (A), free β-CD (B), free 2-naphthyl ethanol (C), and β-CD-2-naphthyl ethanol complex (D). Plane of the spatial grid in the figures is shown in green in the first column. From left to right are total entropy (1, S_Water), translational entropy (2, S_{Water Trans}), rotational entropy (3, S_{Water Rot}), and conformational entropy (4, S_{Water Conf}). Each column has a separate color bar (values in kcal/mol). Red areas are regions occupied by the solute molecules, and water entropy cannot be calculated.

The rotational entropy increases on the hydrophobic surface and decreases near hydrophilic regions. For example, with free 2-naphthyl ethanol, the rotational entropy increases ~0.2–0.3 kcal/mol near the carbon chains or benzene ring and in the hydrophobic cavity of free and bound β-CD (see lighter cells in Figure 5B and 5C). The nonpolar surface may promote water tumbling, but forming H bonds with a polar group decreases rotational entropy by ~0.2–0.5 kcal/mol near the hydroxyl group of 2-naphthyl ethanol. The conformational entropy is correlated with the density of water molecules (eq 6.6 in SI). The cavity of β-CD is large enough to hold ~5–6 water molecules, on average, and the waters slightly decrease their conformational entropy by 0.2–0.3 kcal/mol because the cavity restrains the rearrangement of water molecules. However, the water is not frozen in the cavity and keeps the fluid-like property, for no significant decrease in translational water entropy. Because the density of water fluctuates during the MD simulations, except for water molecules in the vicinity of solutes, conformational entropy of waters in the bulk solvent or surrounding a solute does not noticeably differ.

Binding Kinetics

Calculations of Association and Dissociation Rate Constants

The fast kinetics of guest binding to β-CD allowed for directly assessing the association (k_on) and dissociation (k_off) rate constants from the bound and unbound lengths during microsecond-long unguided MD simulations. Table 2 summarizes the calculated k_on and k_off for systems modeled by GAFF-CD and q4MD-CD. The diffusion-controlled limit for the molecular systems is approximated by k_{on_diffuse} = 4πDR, where D is the diffusion coefficient obtained by our MD simulations (4 × 10⁻⁹ m²/s for a guest such as aspirin and 7 × 10⁻¹⁰ m²/s for β-CD, regardless of force field used) and R is the sum of the radius of β-CD and a guest (~10 Å). The estimated diffusion-controlled association rate constants for all systems are k_{on_diffuse} ≈ 3–4 × 10¹⁰ 1/Ms by using the approximated size of each molecule and the diffusion coefficient obtained by MD (Table SI 8). The modeled k_on by using GAFF-CD agrees very well with the experimental data, and all guests showed 2 orders of magnitude slower k_on than k_{on_diffuse}. Using q4MD-CD slightly overestimated k_on for all guest binding, and the value is 1 order of magnitude slower than k_{on_diffuse} because of the spatial factor. Because β-CD does not require considerable conformational changes or slow transition to acquire all guests, experiments revealed no differences in k_on for different guests. However, k_on modeled with GAFF-CD shows that larger guests such as aspirin and naphthyl ethanols associate marginally faster to β-CD, with k_on values close to 10⁹ 1/Ms, as compared with smaller guests such as butanols, with k_on ≈ 2–3 × 10⁸ 1/Ms. The faster association from modeling may result from stronger intermolecular attraction that can more easily retain the guest once 2 molecules collide. In contrast, because k_on modeled with q4MD-CD is already fast and close to k_{on_diffuse}, a small difference is observed, with k_on ≈ 1–4 × 10⁹ 1/Ms.

The difference in computed k_on with the two force fields and from experimental k_on result from the intermolecular attractions and the desolvation process. Guest diffusing on the cyclodextrin surface is unlikely due to weak intermolecular interactions, and the β-CD surface features a restricted target area (window areas). Assuming no intermolecular attraction, successful binding occurs only with the first collision occurring in the window areas of the cavity (~2.5% of the entire surface), which are the areas covering the top and bottom entrance of the cavity. With q4MD-CD, modeled k_on is 20 times slower than k_{on_diffuse}, and ~5% of molecular encounters result in successful binding. Therefore, the restricted target area is the main contribution to a slower k_on. Using the same concept, less than 1% of the initial association results in a stable complex modeled with GAFF-CD, except for aspirin and 2-naphthyl ethanol. The chief reason that causes further slowdown in k_on with GAFF-CD is the desolvation process during association. Although the tilt glucose rings in the free β-CD may partly occlude the cavity, rotating the 2 dihedrals in C–O–C for different glucose ring tilting is nearly barrierless. Replacing water molecules that formed the H-bond network with the free β-CD creates an energy barrier and results in unsuccessful binding, even for a guest already diffused to the cavity. Note, successful binding was considered only when a complex was formed for longer than 1 ns in MD simulations.

In contrast to k_on, k_off modeled by q4MD-CD agrees very well with experiments; however, with GAFF-CD, all guests left β-CD approximately one order faster than the measured k_off values. Because of the faster k_off, the equilibrium constants (K_eq) are systematically smaller than the experimental values, except for 1-naphthyl ethanol. The dissociation rate constants are directly proportional to how long a guest can stay in the pocket of β-CD, also termed residence time in the drug discovery community. Different force field parameters can largely affect k_off. The longer average bound time indicates more negative ΔH (Table 3), in which ΔH computed with q4MD-CD is stronger than that with GAFF-CD. However, longer bound time does not always require stronger intermolecular attractions, and Table 3 shows that the water effects can be the major differentiating factors. Of note, we sampled hundreds of bound/free states during long simulations (Tables SI 10 and 11), but these are still less than the real experiments.

For the weak binders, we observed one direct association/dissociation pathway in which a guest diffused into the window of the cavity and then stayed with β-CD. The association perturbed the conformations of β-CD to get rid of hydrated waters and flip glucopyranose. We term this pathway the direct binding pathway (SI Movies 1, 2, 7, and 8). For the relatively strong binders such as aspirin, for which k_on is 3- to 10-fold faster than weak binders modeled by both force fields, we observed one more association/dissociation pathway, termed the sticky binding pathway (SI Movies 3–6 and 9–12). The stronger intermolecular attractions allow the guest to stay on the surface of β-CD for surface diffusion to reach the cavity. This situation largely increases the possibility of binding events because the guests can overcome the limitation of a restricted target area of the surface. Note that unlike some ligand–protein binding in which the large biomolecular system needs longer than a microsecond time scale for both molecules to arrange to form a complex, binding processes of guest–β-CD are very fast, in the subnanosecond range, without large binding energy barriers. Nevertheless, the intermolecular attractions, possible surface diffusion and desolvation process still play a key role in controlling binding kinetics.

4. DISCUSSION

This study demonstrates that unbiased MD simulations can be used to computeCD–guest binding kinetics and thermodynamics. The kinetic properties and binding enthalpies can be extracted directly from the simulations, but postprocessing of the MD trajectories by using numerical integration and the grid cell method is needed to compute solute and solvent entropy of binding. Computed values with both force fields, GAFF-CD and q4MD-CD, agree well with experimental measures; however, values strikingly differ depending on whether the binding is driven by enthalpy or entropy.

The binding free energy computed from the kinetic data (ΔG_Comp2) correlate better with experiments (Figure 2) compared with ΔG_Comp1 computed from ΔH – TΔS. The calculation only needs one long MD run that includes both solutes in one water box. Equation 6 may be rewritten as $\mathrm{\Delta }{G}_{\text{Comp}2}=-\mathit{RT}ln(\frac{1}{\text{average}\text{unbound}\text{time}\times [\text{solute}]}·C^0/\frac{1}{\text{average}\text{bound}\text{time}})$. The numbers of bound and unbound events for computing the average time are nearly identical from the same one MD run; thus, another equation to describe binding free energy may be $\mathrm{\Delta }{G}_{\text{Comp}3}=-\mathit{RT}ln(\frac{\text{total}\text{bound}\text{time}}{\text{total}\text{unbound}\text{time}\times [\text{solute}]}·C^0)$. From classical statistical mechanics, the probability of observing a bound complex during this long MD run is $P_{\text{bound}}=\frac{{\int }_{\text{bound}}{\mathrm{e}}^{-E_{\text{bound}}(r)/RT}\mathrm{d}r}{{\int }_{\text{all}}{\mathrm{e}}^{-E(r)/RT}\mathrm{d}r}$. As a result, ΔG = G_bound − G_unbound = −RT ln(P_bound/P_unbound), which is the same as equation ΔG_Comp3. The enthalpy change is also available from the average energy of the bound and unbound states in the trajectories of the complexes, ΔH_{Bound–unbound} = 〈H_bound〉 − 〈H_unbound〉. The computed enthalpy changes are highly similar to the values computed using four separated MD runs (Figure SI 12 and Table 1). This study aims to investigate the kinetic properties in addition to binding affinities; thus, ΔG_Comp3 was not used to obtain the results. However, for other weak binding systems that k_on and k_off measurements are not available and for the research that focuses on binding free energies, we suggest that one can run a long MD simulation to obtain ΔG and ΔH. It is worth mentioning that although directly computing entropy changes is not needed if ΔG and ΔH are available, the calculation allows researchers to investigate the water effects in a great detail. The calculations also bring further insights into contributions regarding water entropy and solute configuration entropy to binding. However, because configuration entropy calculations inevitably need multidimension integral, a larger error than ΔG computed from k_on and k_off is anticipated.

Intuitively, a more negative binding enthalpy ΔH modeled by q4MD-CD is likely a result of the Lennard–Jones parameters, which could result in more optimized ΔH_Host–Guest.⁶⁹ Nevertheless, in the decomposed term ΔH_{Solute Inter} of ΔH_Host–Guest, the computed ΔH_{Solute Inter (vdW)} and ΔH_{Solute Inter (Coul)} show that both force fields model highly similar intersolute attractions, and the main determinant is from water. Both force field parameters allow the sugar ring to flip in the free states, and β-CD can easily adjust to an open cavity conformation when forming a complex with a guest. Therefore, unlike existing study showing that substituents attached to decorated β-CDs block a guest from binding,⁷⁰ the ring flipping itself in our study did not hinder guest binding. However, more flipped sugar rings modeled by GAFF-CD allow the formation of more H bonds between waters and β-CD and a more structured H-bond network as compared with conformations modeled by q4MD-CD. Therefore, the cavity more energetically accommodates stable water molecules, which results in large enthalpy penalty on desolvating those water molecules. The Coulombic term ΔH_{Host–Water (Coul)} becomes the essential energy term that opposes binding due to breakage of β-CD–water H bonds, and the value is significantly larger with GAFF-CD. We suspected that the bonded parameters with GAFF-CD may highly prefer sugar ring flipping in the free states. However, the MD simulations in vacuum showed that both GAFF-CD and q4MD-CD highly prefer wide-open, crystal structure-like conformations in the free states (Figure SI 1). Because β-CD is reasonably flexible, in particular, with GAFF-CD modeling, adding explicit water molecules easily induces the conformation changes. A “slaving” model in which water drives protein fluctuations was proposed.⁷¹ Recently, a direct measurement of hydration water dynamics in protein systems illustrated that the surface hydration-shell fluctuation drives protein side-chain motions.⁷² Here we showed that the water molecules are highly responsible for molecular recognition in both thermodynamics and kinetics.

Without considering other factors, the theoretical k_on may be estimated by multiplying the restricted target area by the diffusion-controlled limit k_{on_diffuse},⁷³ 2.5% × 4 × 10¹⁰ 1/Ms = 10⁹ 1/Ms, which is close to the modeled k_on of most guests binding with q4MD-CD. To increase an association rate faster than the theoretical value 10⁹ 1/Ms, when the initially collision did not bring a guest to the restricted target area, intermolecular attractions kept the guest in close proximity to β-CD until the guest reached the cavity. This situation can be observed during MD simulations, as illustrated in the sticky binding pathways with the relatively tighter binder aspirin. Note no long-range electrostatic attractions for rate enhancement because of the neutral molecules. A guest always needs to compete with water molecules during binding. Therefore, k_on can be slower than the theoretical value 10⁹ 1/Ms if there exist barriers from removing stable water molecules in the hydration shell. The desolvation barrier increases when the free β-CD forms a larger number of H bonds between water molecules modeled by GAFF-CD, which results in more unsuccessful guest binding and slower k_on. As a result, although a less wide-open cavity conformation in free β-CD may seem to directly lead to a slower k_on in GAFF-CD, the direct cause is from paying a higher cost to disturb its solvation shell. After forming a complex with a guest, β-CD gained a few kcal/mol, showing a more negative ΔH_{Host Conf} on binding. A similar finding from investigating binding free energy barriers for a drug binding a protein showed that desolvation of the binding pocket contributes the most to the free energy cost, as opposed to reorganizing the protein binding pocket.⁷⁴ However, for molecular systems that encounter large-scale conformational changes and/or induce fit during ligand binding, rearranging conformations may still significantly affect the association rate constants,⁷⁵ and the kinetic property can be highly system dependent. With q4MD-CD, because water molecules form a less stable H-bond network, the role of desolvation in binding kinetics is not as important as with GAFF-CD.

Unlike desolvation effects, which are quite different from the 2 force fields, another dominant but similar driving force for binding from both force fields is the attractive component of the vdW energy, ranging from −6 to −23 kcal/mol. This driving force may be expected because of the nonpolar property of the β-CD cavity and the neutral guests. This term mainly accounts for dispersion forces between β-CD and guests in the force field parameters and is similar for both force fields, with a trend that larger guests have more negative ΔH_{Solute Inter (vdW)}. In experiments, measuring the separate contributions for binding from dispersive interactions and classical hydrophobic effects in aqueous environment is challenging, and the absolute values from the dispersive interactions are not available experimentally.^76,77 As compared with the vdW attraction, the Coulombic attraction between β-CD and guests is significantly weaker because the guests are not highly charged molecules and few intermolecular H bonds are formed in the complex. The intermolecular attractions are balanced by the enthalpy penalty from disrupting attractions between waters and solutes and gaining water–water enthalpy for those water molecules replaced by a guest, which results in merely a few kcal/mol net enthalpy changes on binding. One may consider hydrophobic effects as the major contributions to β-CD and guest recognition.⁷⁸ Of note, although the pocket of β-CD is nonpolar, it is a very tiny cavity and the rims of β-CD consist of several hydroxyl groups. On binding, ~20–25 water molecules were replaced by a larger guest, which agrees with experimental measurement⁷⁹ (Table SI 6). However, not all replaced water molecules are “unhappy”. Therefore, although the replaced water molecules also regain water–water attractions in the bulk solvent, the costs to replace the stable water molecules result in the large desolvation penalty. This differs from the binding in a completely hydrophobic cavity, where the enthalpic gain from water–water attraction dominates in the binding process.⁸⁰

The systems did not encounter large solute entropy loss, which contrasts with several existing publications that suggested loss of configuration entropy when a drug binds its target protein.^{65,66,81–83} Unlike most drug-like compounds, which fit tightly to their target protein pocket, our guests only loosely fit in the cavity of β-CD. Therefore, the mobility of β-CD is not reduced considerably by a guest. With GAFF-CD, the hydrated water molecules in the cavity of free β-CD showed an ordered H-bond network and slaved the conformational motions of β-CD. On ligand binding, a bound guest did not form a stable H-bond network with β-CD; thus, β-CD showed a slightly increased flexibility. The guests were also able to form various contacts with β-CD. Similar to alternative contacts provided by the hydrophobic binding pocket of protein systems,⁸⁴ we did not observe rigidity of β-CD with GAFF-CD.

The enthalpy and entropy balance may follow immediately from eq 5, ΔG_comp1 = ΔH − TΔS.^64,85,86 Therefore, it has been suggested that the entropy–enthalpy compensation is from a much smaller range of experimentally measured ΔG for a series of ligands than the range of ΔH. Different from most experimental techniques, we computed the entropy and enthalpy terms separately and still observed the entropy–enthalpy compensation. Our guests were all weak binders and did not have a wide spectrum of ΔG. The computed range of ΔH is in a similar ballpark as ΔG, and the range of −TΔS is relatively smaller than ΔG and ΔH. As a result, the enthalpy change mostly governs if a guest is a stronger or weaker binder. Our calculations reveal the physical basis of larger range of ΔH and more similar −TΔS. The enthalpy calculations are based on energy functions in the force fields, but the Gibb’s entropy formula is based on the distribution of the microstates (eq 1). Unlike protein systems with numerous rotatable bonds and a larger binding site to mostly enclose a ligand, a guest is not completely confined within the cavity of β-CD and the host remains highly flexible. Interestingly, −TΔS_water is similar in both force fields, and −TΔS_water is not simply proportional to the size of a guest. Instead, −TΔS_water relates more to the hydrophilicity of a guest such as 1-propanol, methyl butyrate, and aspirin when forming a complex with β-CD. The free guests reduce more entropy of water in their solvation shell, and these solvation waters gain more entropy on guest binding. For q4MD-CD, because the free β-CD generally has a more open cavity, more waters were released on binding (Table SI 6). However, the ring flipping conformation modeled by GAFF-CD produces a more structured H-bond network for the first hydration shell. As a result, although fewer water molecules were released on binding, those waters gained more entropy than those of β-CD with q4MD-CD, which resulted in a similar computed −TΔS_water from both force fields. The results suggest that as in enthalpy, entropy calculations feature a fine balance.

Force field parameters are critical for accurate modeling and successful prediction.^87–90 In this study, we used GAFF for β-CD (GAFF-CD) and for all guests and q4md-CD a specialized force field for CDs that combines Amber99SB and GLYCAM04 to match experimental geometries from crystal structures and NMR.⁴⁸ It is common practice to seek agreement between the calculated and the experimental binding affinities/binding free energies for validating and improving the parameters of force fields or solvent models. Using computed thermodynamics and kinetics (eqs 5 and 6), both force fields for β-CD showed reasonable agreement with experimental binding affinities, which validated the parameters used. Interestingly, different force fields concluded different driving forces, with GAFF-CD and q4MD-CD showing an entropy- and enthalpy-driven binding, respectively. In addition, GAFF-CD yielded better agreement between computed and experimental association rate constants. Using only binding free energy in the training set for parametrization was suggested to risk an incorrect entropy–enthalpy balance; therefore, binding enthalpy needs to be considered for optimizing parameters.⁶⁹ With continuing growth in computer power, for molecular systems with fast association/dissociation rate constants, we suggest considering computed binding kinetics for validating and optimizing force field parameters as well. Our studies also showed the importance of and challenge in correctly modeling multiple conformations in which solvent effects may be remarkable and experimental structures are not available. Although our preliminary studies indicated that using TIP3P and TIP4P water models did not yield different sampled conformations during MD simulations, other molecular systems may be more sensitive to the solvent effects with different water models. In the future, we envision a more careful force field optimization that considers binding free energy, enthalpy–entropy balance, and kinetic properties. We also anticipate further investigation into the role of water in the binding kinetics of various guests to a pocket with different polar and/or nonpolar properties.^91,92

5. CONCLUSION

In this work, we performed microsecond-time-scale MD simulations with GPU acceleration for 7 chosen β-CD complexes. The computed thermodynamic and kinetic properties agree with experimental values reasonably well. The binding of β-CD complexes is mainly driven by the nonpolar attraction between β-CD and the guest and the entropy gain of desolvated water molecules, regardless of the force field used. With both force fields, the ligands have only a small entropy penalty, and the entropy term also contributes to the binding process. GAFF-CD reproduced more favorable binding entropy and less favorable binding enthalpy due to stronger desolvation penalty than did q4MD-CD. As compared with GAFF-CD, q4MD-CD produced more rigid dynamics of free β-CD. However, the conformational rearrangement did not contribute to the differences in thermodynamics and kinetics modeled by the 2 force fields, and the real determinant was the different H-bond networks between the solvation water molecules and free β-CD. With GAFF-CD, β-CD forms more H bonds with solvation waters in a more distorted conformation; on ligand binding, the ligand needs to pay more enthalpic penalties to remove these stable H-bonded waters, which results in the stronger desolvation enthalpy. In the bound state, free β-CD forms fewer H bonds with its environment and thus becomes more flexible and gains configuration entropy. Although we computed ΔH and −TΔS separately, the compensation is observed. In general, hydrogen bonding between water molecules and the solute can significantly influence solute conformations and fluctuations, contribute to desolvation penalty, and slow down the association processes. The water entropy change, which is a fine balance between numbers of released waters and stable waters in the cavity of a receptor, may play an important role in governing ligand–receptor binding. Our study also showed that different force field parameters can yield the same computed ΔG but different entropy and entropy balance.