Abstract
Cartilage is composed of cells and an extracellular matrix, the latter being a composite of a collagen mesh interpenetrated by proteoglycans responsible for tissue osmotic swelling. The matrix composition and structure vary through the tissue depth. Mapping such variability requires tissue sectioning to gain access. The resulting surface roughness, and concomitant proteoglycan loss contribute to large uncertainties in elastic modulus estimates. To extract elasticity values for the bulk matrix which are not obfuscated by the indeterminate surface layer, we developed a novel experimental and data analysis methodology. We analyzed the surface roughness to optimize the probe size, and performed high-resolution (1 µm) elasticity mapping on thin (~12 µm), epiphyseal newborn mouse cartilage sections cut parallel to the bone longitudinal axis or normal to the articular surface. Mild fixation prevented the major proteoglycan loss observed in unfixed specimens but not the stress release that resulted in thickness changes in the sectioned matrix. Our novel data analysis method introduces a virtual contact point as a fitting parameter for the Hertz indentation model that minimizes the effects of surface roughness and corrects for the finite section thickness. Our estimates of cartilage elasticity converge with increasing indentation depth and, unlike previous data interpretations, are consistent with linearly elastic material. A high cell density that leaves narrow matrix septa between cells may cause the underestimation of elastic moduli, whereas fixation probably causes an overestimation. The proposed methodology has broader relevance to nano- and micro-indentation of soft materials with multiple length scales of organization and whenever surface effects (including roughness, electrostatics, van der Waals forces, etc.) become significant.
Graphical abstract

INTRODUCTION
The key functions of cartilage tissues in vertebrates are the growth of bones during skeleton development, and the cushioning and lubrication of bones in articular joints. These functions require cartilage to withstand repetitive and prolonged mechanical loads. Cartilage consists of cells, chondrocytes and an extracellular matrix. The cells make and maintain their matrix, while the matrix determines the load-bearing capacity. The matrix consists of negatively charged aggrecan bottlebrushes, assembled on hyaluronic acid chains, to form a supramolecular assembly that interpenetrates a collagen network1, 2. The charge-repulsion and counter-ion influx induced by the entanglement of negatively-charged molecules within the collagen network produce a high swelling pressure equilibrated by the collagen network that is under tension3, 4. This balance between the swelling pressure and matrix tension enables cartilage tissue to bear compressive loads.
The quantitative relationships between composition, structure and mechanics are not well understood. The concentrations and arrangement of matrix components varies across the cartilage tissue5, 6, and with growth, age, and disease7–9. Understanding how these local variations contribute to cartilage function (i.e., load-bearing) is a problem which requires the characterization of local and bulk matrix mechanical properties of a soft, rich composite structure with several scales of organization10, 11.
Estimates of cartilage elasticity depend strongly on the length scale of the measurement, even qualitatively12. Unconfined compression studies for millimeter-sized matrix regions show the matrix stiffness decreasing from resting to the proliferative/hypertrophic zone of the porcine cartilage growth plate11. However, atomic force microscopy (AFM) indentation with nanometer-sized probes in a rabbit growth plate shows the stiffness increasing across the same region, and possibly reflecting the calcium deposition pattern within the growth plate13. Macroscale indentation experiments report elasticity to be of the order of MPa14, 15, whereas nanoscale indentations report it to be of the order of tens of kPa16. Indentations with nanoscale (sharp) probes appear to be picking up the mechanics of individual macromolecules and produce a bimodal distribution of elasticity, as collagen or the much softer aggrecan molecule is indented16–18. On the other hand, macroscale mechanics as measured by indentation seem to describe the composite elasticity of the stiffer matrix and the relatively compliant cells14, 19.
As the complications associated with the measurement of elasticity for tissues with hierarchical, multi-scale organization such as cartilage became clearer, researchers have arrived at more consistent measures showing cartilage extracellular matrix elastic moduli to be in the range of a few MPa, across species, although outstanding questions remain. This has resulted in a better understanding of measurements at the macro-, micro- and nanoscale. For example, Cao et al. measured the elastic modulus of murine knee tibial plateau to be ~2 MPa using macroscale (~110 µm probe) indentations20 and obtained somewhat lower values for human and for rat. Stolz et al. measured 1.3 MPa, for murine femur cartilage, using micro-indentation and obtained similar values for human femoral joint cartilage21. Nia et al. also measured mouse femur matrix elasticity to be ~2 MPa and showed that aggrecan depletion leads to a significant decrease in the elastic modulus (~0.4 MPa)22. Interestingly, for human tissue, they did not detect overall changes as osteoarthritis progressed21. Studies of several osteoarthritis animal model systems have shown significant changes in elasticity, both increases23 and decreases21, 24.
Apart from measuring physically different characteristics, the nanoscale measurements are affected by surface roughness. The surface roughness is introduced when the cartilage tissue is cut to expose regions across the tissue depth where its composition and structure vary. It has been reported that the elasticity modulus in the different zones of the growth plate cartilage increases with indentation depth12. Darling et al.25 reported a three-fold increase in elasticity when indentation forces were increased from 5 to 50 nN. While the depth-dependent changes might describe a cartilage matrix that is stiffening in a nonlinear way, the initial low values of elasticity could also be attributed to the presence of a rough layer atop the tissue section25. These defects either represent intrinsic roughness from exposed macromolecules and their assemblies, or are introduced when the cartilage tissue is cut to expose deeper regions. This roughness cannot be described in detail or modeled and, therefore, to extract bulk matrix properties, indentation measurements need to account for the effect of this surface roughness.
In this work, methodology was developed for obtaining bulk matrix elasticity profiles across the tissue thickness with micrometer resolution from sections of cartilage. The goal was to extract bulk matrix properties that characterize the underlying surface defects and roughness of the cartilage matrix.
Mouse cartilage was used to develop our approach for extracting bulk matrix elasticity for two reasons. Firstly, the study of mouse cartilage will be useful since mouse is a widely-used animal model of human disorders. Secondly, such an approach will provide access to a wide variation of cartilage compositions and structures which occur in model mice subject to various treatments and genetic modifications. We used newborn epiphyseal cartilage because it consists of continuously connected and yet functionally and structurally different cartilage zones. A complexity with mouse cartilage is that, unlike the cartilage of large animals, it is densely populated with chondrocytes, leaving relatively thin matrix septa between cells, and imposing geometric constraints on the force curve measurements and data interpretation.
All these complexities necessitated the development of a novel approach to the force curve analysis based on (i) the exploration of surface topography, to ensure that applied indentions were deep enough so as to probe the bulk matrix; (ii) the exploration of the loss of macromolecules from cartilage sections, to ensure that the measurements were performed on tissue that was as close as possible to the native state; (iii) the choice of the optimal indenter size that could probe areas large enough to even out surface roughness but small enough to separate matrix and cell regions; (iv) the development of a novel force curve fitting approach that introduced an effective or virtual contact point between the indenter and the matrix underlying the rough surface layer, and minimized the contribution of this layer; and (v) corrections for the effect of the rigid substrate on the apparent elasticity at large indentations and an evaluation of matrix thickness changes across the sample by measuring section thickness at every probed location. It was shown that this approach not only corrects for the force contribution from the superficial layer, but also produces matrix contact points and elasticity that are nearly independent of the indentation depth. Using this methodology, the elastic modulus of the matrix was evaluated, and its variability across different tissue zones and uncertainties was estimated. Finally, future directions for reducing these uncertainties are proposed.
METHODS
Sample preparation
Cartilage samples were prepared as detailed in our previous study26. Briefly, proximal halves of femurs were dissected from a 0.5-day old wild type mouse and fixed in 1% paraformaldehyde solution (from a freshly open ampule, methanol-free, ThermoFisher Scientific, MA) in PBS buffer for 6 hours at room temperature. Each specimen was embedded into an aqueous solution of 20% 10 kDa polyvinylpyrrolidone and 20% 360 kDa polyvinylpyrrolidone, and cryo-sectioned with a D-profile tungsten carbide knife at −25°C, near the mid-coronal plane of the femur, according to the protocol optimized for hard tissues27. Sections were completely demineralized in 0.25 M EDTA for 5 min to improve attachment to the glass slide, trimmed with a blade where the mineralized growth plate cartilage converts into bone, and washed with PBS containing 0.5 mM CaCl2 (to replenish strongly bound Ca++ ions to proteins). Sections were adhered to a positively charged slide (Superfrost Plus, Daigger Scientific, IL) in a PBS droplet, air-dried after aspiration of the droplet, washed with purified water and hydrated in PBS.
AFM imaging of section topography
AFM imaging was performed on the hydrated sections using a fluid cell of an AFM instrument (Bioscope Catalyst, Bruker) that sits atop an inverted optical microscope with 10×/0.3NA and 50 ×/0.5NA objectives and off-axis, top-down illumination. Selected sample areas ~10×10 µm2 were imaged using the Peak-Force tapping (PFT/QNM, Bruker) imaging modality with sharp tips (7 nm nominal radius of curvature) of etched silicon probes (FESP, Bruker) having a nominal stiffness of 2.8 N/m with ~30 nm/pixel lateral resolution.
AFM force spectroscopy
AFM force spectroscopy was performed on hydrated sections. Indentation was performed using 5 µm diameter silica microspheres (Polysciences, Inc., Warrington, PA) attached to cantilevers of stiffness in the range of 3 to 5N/m (NanoandMore, Watsonville, CA) using UV-curable epoxy. The stiffness of each cantilever was estimated using the thermal calibration method. The exact microsphere diameter was measured by comparing against a control length under a microscope. The ramp rate for indentations was typically 15–20 µm/sec. Deflection sensitivities were measured at the beginning and end of each experiment by indenting the glass surface.
Force-indentation curves were acquired on the cartilage sections along the indentation pathway shown in Fig. 1A. This pathway started near the articular surface facing the joint cavity and ended at the region in which mineralized growth plate cartilage converts to bone. To indent along the pathway, the glass slide bearing the section was cut and oriented so that the lines composing the pathway fell along either the x- or y-axis of the AFM stage scanner.
Fig. 1.
(A) Optical transmission image of a demineralized 12 µm section from the epiphyseal proximal femur cartilage of a 0.5-day old mouse. Red dashed lines mark the pathway along which the force-indentation curves were acquired. The boxes mark the regions magnified in panels B,C and D. (B,C) Higher magnification images of the section at the articular (B) and growth plate (C) regions acquired before demineralization. The double arrow marks the zone of hypertrophic chondrocytes. (D) Detailed image showing indentation lines along which the indentation was performed. Also shown is the 100 µm offset between the centers of successive indentation lines, resulting in 20 µm overlaps between them.
The “autoramp” feature of the instrument software (Nanoscope v.8.15) was used to indent points along a straight line of certain length, which we call the indentation line, Fig. 1A,D. Each indentation line was 120 µm long with indentation points spaced 1 µm apart. To span the mm distance from the glass slide into the tissue along the pathway, Fig. 1A, the centers of successive indentation lines were offset by 100 µm, Fig. 1D. This introduced an overlap of 20 µm on either side of the indentation lines, which was used for correcting errors in x- y- and z-displacements between consecutive lines (see below). The 1 µm resolution for the indentation points was necessary to obtain smooth profiles of tissue thickness and elasticity along the indentation lines, so that cell and matrix regions could be easily identified.
Three elastic models for force curve analyses
The resulting force curves were analyzed using three contact mechanics models for a spherical probe. The first model is the classical, half-space model derived by Hertz which assumes that the indentation, δ, is much smaller than the probe radius,
| (1) |
where E is the elastic modulus, R is the probe radius and ν is the Poisson’s ratio, assumed to be equal to 0.5 for an incompressible material.
The second model is the correction of the Hertz approximation for a finite thickness sample bonded to a rigid substrate19,
| (2a) |
where χ is determined by the ratio of the contact circle radius a (where ), and the sample thickness h,
| (2b) |
The third model is the exact model of spherical indentation of a half-space. It is computed implicitly via a system of two equations derived by Sneddon20,
| (3a) |
As this implicit function is cumbersome for implementing in numerical fitting, we expanded the ratio F/δ3/2 in power series of δ and obtained an approximate expression in explicit form,
| (3b) |
This equation is accurate to within 0.01% at indentations δ ≤ R (Fig. 2), and was used for the analyses instead of Eq. 3a. This third model was used to check whether the Hertz approximations are in significant error for the higher indentations used here.
Fig. 2.
Relative error in the approximate expression given in Eq. 3b (FS) for the exact half-space elastic model in Eq. 3a (F), as a function of indentation δ relative to the probe radius.
Force curve fitting
Typical indentation raw data are acquired in the form d =d(z), where d is the AFM cantilever deflection and z is the vertical position of the probe. Hence, if the physical contact occurs at point (z0, d0), the indentation at a point (z,d) along the curve will be δ = (z−z0)−(d−d0). Prior to fitting, raw data curves, d = d(z), were converted into force, F, versus separation, w,
| (4) |
where k is the spring constant of the cantilever. In these coordinates, the contact point is defined as w0 (z0 − d0), the indentation as δ =w−w0 and the force relevant to the mechanics’ models as Fdata =k(d−d0).
However, the physical contact point is not rigorously defined at the molecular scale because molecular interactions extend over a range of distances. Typically, the contact point (CP) is estimated from the force curve as the point at which non-zero force appears, or at which the slope of the curve starts to increase nonlinearly. In our case, the probe is indenting a matrix whose surface is intrinsically rough due to the finite size of the matrix macromolecules and the potential damage from tissue sectioning. In such a case, the cantilever force at the shallow indentations may be due to incomplete contact and the corresponding initial strain does not homogeneously transmit to the bulk matrix underneath. Therefore, the point at which force is detected does not represent contact with the bulk material.
A way to account for this indeterminate layer at the surface, is to indent deeper than the surface layer and to introduce an “effective” Hertz contact point, (zH, dH), (abbreviated as HCP) with an offset zero force, k (d-dH), that gives the best fit for the bulk matrix at indentations deeper than the surface layer. Hence, we replace the physical CP coordinates with these new, effective HCP coordinates. We use the latter along with the elastic modulus, E as fitting parameters. The algorithm allows for this effective HCP to float off the actual data set where, conventionally, the physical CP lies.
We estimate the vector p of the three fitting parameters, (E, zH, dH), via least square minimization using the standard Newton-Raphson procedure. We minimize the sum S of residuals Ri squared,
| (5a) |
| (5b) |
where Fdata is the experimentally measured force at different z values, i0 and N are respectively the first and the last data points (points with the lowest and highest z-values) selected for fitting, and Ffit is the appropriate fitting model. Starting from initial guess values (or previous values) of the parameters pk, we obtain an improved estimation, pk+1 → pk + Δp, where
| (6) |
and
is the Jacobian of the residual function.
An important difference between our implementation and the conventional fitting procedures is that because of the square root term in Eqs. 1, 2 and 3b, the leading term FH(δ), of the force functions for δ<δH has only imaginary terms. The imaginary terms at these indentations are mathematical artifacts with no physical meaning (for the Hertz model, the force is zero at negative indentations). The same holds true for the first derivatives of the force functions needed to compute the Jacobian. These terms are eliminated in the calculation of the fitted force vector by requiring the algorithm to proceed only with the physically-meaningful real values of the first order terms in all three models. To clarify, to compute Δp (Eq. 6), the residuals of Eq. 5b were computed as
| (7) |
where FH is the standard Hertz term (Eq. 1), CX stands for the correction terms to the Hertz model in Eqs. 2 and 3b, respectively (CX =1 for the standard Hertz model) and wH is the indentation at the HCP, wH = zH−dH. Notice that when computing the Jacobian, the real parts of FH (wi − wH) and its first derivatives with respect to the three parameters were used.
The above procedure is mathematically equivalent to using a continuous, piecewise function Ffit(w) which combines one of the elastic models FX(w) (Eqs. 1,2, or 3b) at indentations deeper than wH with a horizontal line at shallower indentations,
| (8) |
where
For fitting we selected ranges of data starting at short distances before the physical or slope contact point (SCP) and up to the maximum force. That reduced the effect of the non-contact region on the algorithm performance which remained robust and insensitive to the chosen distance from the SCP. As a convergence criterion, we used norm (root mean squared sum of residuals) < 1E-06 nN.
The convergence of the Newton-Raphson procedure depends on the goodness of the initial guess for p. We used as initial guesses, z0 (for the parameter zH) and E in p from the slope and intercept of a straight-line fit to the Hertz equation (Eq. 1) rearranged as
| (9) |
after the data were shifted to zero deflection (or force) at the SCP. For the initial guess of dH, we used the value of d at the initial guess of zH.
Section thickness measurement and correction
We estimated local section thickness as the difference between the SCP on the glass slide adjacent to the tissue section and the SCP at each indentation point on the tissue section. This was possible with our specific AFM instrument whose piezo-drive has a z-range of about 25 µm, which is significantly higher than the section thickness. Since the x,y-range of the instrument is limited to ~150 µm, we needed to use the motorized stage to map the whole section and we used the SCPs along overlapping indentation lines (Fig. 3B) to correct for the poor control of the motor displacements.
Fig. 3.
Loss of glycosaminoglycans (GAGs) and non-collageneous core proteins (NCPs) from a hydrated 12 µm section of unfixed cartilage from a 0.5-day old mouse, measured by high-definition infrared hyperspectral imaging. The curves were derived from the data, their fitting models, and the averaged fitting parameters given in Supplementary Fig. S1F.
Each force curve was analyzed twice. In the first round of analysis, SCPs and, subsequently HCPs were determined using the half-space model (Eq. 1). The HCPs were used to obtain the section thickness at each indentation point. The thickness was then used as an input constant in the second round of analysis (Eq. 2) in which the elastic modulus, corrected for the finite section thickness, was determined.
All analysis procedures, including the file handling, model fitting, and matrix selection, were automated in Matlab. Finally, profiles of height and elasticity at each indentation line were aligned against the corresponding optical image to pick out matrix regions that were not interrupted by other features (cells, lacuna, pericellular matrix, etc.). These were used to construct an elasticity profile plot showing how the matrix elasticity varied along the probed line.
RESULTS
To evaluate the mechanical properties of different anatomical regions of hydrated cartilage, we prepared a section of a femur head cartilage from a 0.5-day old mouse. The section was demineralized with a chelating agent (EDTA) after cutting, so that minerals present in vivo near the mineralizing end, Fig. 1, did not affect the section attachment to the substrate. The use of EDTA is not expected to alter the structure of the crosslinked tissue or matrix mechanics as we replenished strongly bound calcium after EDTA treatment. We performed indentations in physiological solution without calcium because the absence of weakly bound calcium should have a small effect on matrix osmotic swelling and mechanics.
A low magnification image of the section adhered to a glass slide is shown Fig. 1. The sectioned region spans from the articular surface which faced the joint space in vivo to the mineralizing zone which faced the femur midshaft and at which the conversion of cartilage to bone was occurring. Prior to the analysis of the elastic properties of the extracellular matrix, we explored sample preparation, topography of the section surface, probe size and the effects of indentation depth, and we developed a novel force-displacement curve analysis to address some of the complexities presented by the nature of the sample, as detailed below.
Prevention of loss of macromolecules from hydrated cartilage sections
Sectioning the cartilage to allow for probing the zonal variation of mechanical properties exposes the section surfaces to hydrating solution. It has been reported that proteoglycans diffuse away from a hydrated cartilage specimen if they are not fixed. To evaluate whether or not such a loss is significant on the timescale of the AFM experiments (8–10 hours), we measured the loss of glycosaminoglycans (GAGs) and non-collagenous core proteins (NCPs) from the extracellular matrix of a hydrated 12 µm section of unfixed cartilage.
We used high-definition infrared (HDIR) transmission hyperspectral imaging of hydrated 12 µm sections with 6 µm spatial resolution as detailed in the Supplementary Material. Briefly, we observed a reduction of infrared absorbance by the sections at multiple infrared frequencies. This reduction and the spectroscopic fingerprints of major matrix components suggested that GAG chains and NCPs diffused from the matrix. Figure 3 summarizes the results showing that 23% and 39% of GAGs were lost from the matrix after 0.5 and 23 hours, respectively, after hydration. This loss was concomitant with the loss of 19% and 29% of NCPs after 3 and 22 hours. There could also be a slight loss of collagen (~5% in 23 hours), which was close to the detection limit of our experiment, and, therefore, needs further confirmation. The experiment tracked the loss of matrix components through the full thickness of the sections, while the first 1–2 µm from the surface were indented in our AFM experiments. The loss of these matrix components from this 1–2 µm surface layer of the section may be faster than the observed loss from the full section depth due to slower diffusion of the macromolecular components through the matrix depth.
As the losses were significant on the time scale of our AFM experiment, we fixed whole excised femur specimens mildly with formaldehyde (see Methods). After such fixation, cartilage sections, which were hydrated at 20°C for days, exhibited no losses (data not shown) to within the detection limit of the HDIR experiment (~ 1–2% of GAGs and NCPs and ~4% of collagen). It remains unclear whether the proteoglycan loss was due to physical dissociation of the macromolecules from the collagen matrix and their diffusion out into the PBS bath, or due to protein cleavage by proteases; it is also not known whether protease inhibitors would attenuate this loss.
Matrix roughness and choice of AFM probe, indentation depth and sample thickness
For the AFM probe, we chose a sphere as opposed to a sharp probe. At shallow indentations, a sharp probe would primarily interact with one or a few individual matrix components (collagen fibers, aggrecan molecules, etc.), rather than with the bulk matrix. At larger indentations it would cause large and highly inhomogeneous local strains and possibly damage, resulting in inelastic responses and complicating the interpretation of indentation data.
Our spherical probe would interact with the surface of the sectioned cartilage matrix that is intrinsically rough due to the finite size of the macromolecules and cutting defects. To choose the optimal diameter for our spherical AFM probe we first explored the roughness of the surface of the fixed specimen with a sharp AFM tip. A representative image of the surface height is shown in Fig. 4A. We quantified the roughness within circular regions (the shape of the contact region of a sphere with a flat sample). The resulting peak-to-valley roughness (roughness depth) of circular matrix regions selected away from cell lacunas (dark and bright round regions in Fig. 4A) is shown in Fig. 4B.
Fig. 4.
(A) Height distribution of a region from the cartilage section shown in Fig. 1 measured with a sharp tip. (B) Peak-to-valley roughness curves (solid lines) measured within a circle on the cartilage matrix surface versus the circle diameter. The roughness function is defined as the difference between the 99th and 1st percentiles of physical contact point depths measured by a sharp AFM tip within concentric circles of diameter D. The three representative roughness curves were measured for three anatomically different regions. Each curve is an average of 6–11 curves at 6–11 centers of non-overlapping circles. The bands show the corresponding 68% confidence (one standard deviation) bands of the roughness curves. The superimposed green dashed curves show indentation depth versus contact diameter of spherical probes of various diameters predicted by the exact half-space elastic model (Eq. 3a). (C) Height profiles (blue and red curves) measured along the blue and red lines, respectively, shown in (A). Superimposed are cross-section outlines (green lines) of 5 and 20 µm diameter spheres. (D) Magnified region of the height profiles in (C). Superimposed are cross-section outlines (green lines) of a 5 µm diameter spherical probe indented by 0, 0.5 and 1.5 µm.
The roughness increases with the diameter of the circle, exhibits a crossover at ~0.6 µm diameter, tends to level off at ~1.5 µm diameter and then slowly increases further. The latter increase at larger diameters indicates larger scale roughness, which may be due to cutting defects or the non-uniform expansion or contraction of different regions. Roughness at smaller diameters is likely due to the finite size of matrix macromolecules; it levels off at a depth of ~0.2 µm. This depth is comparable to half the typical sizes of two major macromolecules. These are the 0.3–0.4 µm length of aggrecan (the dominant matrix proteoglycan)28 and the collagen interfibrillar distance of 0.1–0.3 µm29, 30. Note that these components may be cut, and their sizes could be smaller at the surface. The other key sizes of the dominant structural units of healthy cartilage, such as the ~0.04 µm aggrecan diameter28 and the 0.02–0.08 µm collagen fiber diameter30, were not spatially resolved by our measurements. The 0.6 µm crossover is much larger than the characteristic structural length scales of normal hyaline cartilage, and appears to reflect a transition to macroscopic scale of the surface. Note that for some pathological cases21, 31, 32, the collagen fiber thickness can be 0.5–1 µm, an order of magnitude thicker than wildtype, and this may change the section surface roughness and require special consideration of probe geometry, indentation depth and data analysis.
The macromolecules and their assemblies near the section surfaces are removed from their native interacting partners, and distorted or cut, so that their mechanical properties can be different from their properties within the matrix bulk. Therefore, an AFM tip probing the bulk properties should indent substantially deeper than the characteristic size of the 0.2 µm roughness depth. In the meantime, the lateral size of the contact area of the AFM tip with the matrix should be substantially larger than the crossover diameter, that is, larger than 1.5 µm.
These conditions imply that the size of the probe should be sufficiently large. To optimize the probe size, we superimposed the roughness curves with the curves of indentation versus contact diameter for a half-space elastic material in Fig. 4B. This superimposition suggests that the 5 µm sphere that we chose as a probe is large enough to have a contact diameter of 2 µm at 0.4 µm indentation and to flatten out the “macromolecular” roughness, Fig. 4B,C,D. A 2 µm sphere is too small; it would reach the required contact diameter at indentations exceeding the sphere radius, making the interpretation of force-indentation curves less reliable. On the other hand, a 20 µm sphere is too big to indent 0.4 µm without bumping onto adjacent cell structures. Depending on the surface roughness (Fig. 4B), larger spherical probes may be suitable for human and larger animal cartilage with lower cell density and much wider matrix septa.
We chose the 12 µm sample section thickness to avoid cells under the matrix surface on the one hand and, on the other hand, to make the matrix much thicker than the maximal indentation depths of up to 2 µm used in our experiments.
Force curve analysis
Using a 5 µm glass sphere as the AFM probe, we acquired force-indentation curves at multiple regions of the cartilage section and selected curves at the extracellular matrix as described later. The curves exhibited different shapes, most of which could not be fitted well to the elastic models (Eqs. 1–3) using standard methods. The curves appeared to exhibit two distinct regions, a softer, lower indentation (toe region) and a higher indentation that was stiffer. We verified that the curve shapes were not due to local detachment of the section from the slide: we monitored a microscopic video image of the section during indentation and observed no vertical displacement of any section region.
To demonstrate our approach to the fitting of such data, we use one of the curves acquired at the matrix, Fig. 5A. We chose a curve whose lower, softer region was not pronounced. As the tip approached the sample, the curve showed a change in slope exceeding its noise threshold. This marks the physical CP of the probe with the sample, which we abbreviated to SCP. After this point, the curve exhibited a steeper rise. Conventional approaches use SCP as the contact point and fit the rising force with elastic models and a single parameter, the elastic modulus. Clearly, such a fit, shown in Fig. 5A, does not capture the experimental force curve well, giving the impression that the matrix has nonlinear, depth-dependent properties.
Fig. 5.
Fitting a force curve at the matrix using the 1- and 3-parameter methods. (A) The force curve and the fitted curves obtained using the Hertz model with a finite thickness correction, Eq. 2. Shown are the 1-parameter and 3-parameter fits. The top panel shows fitting residuals. The dots mark the positions of the slope and Hertz contact points (SCPs and HCPs). The inset shows details of the fits near the contact points. (B) Elastic modulus (black) and HCP (gray) from fitting the truncated force curve as a function of the maximal truncated indentation using the 3-parameter approach. The black solid and dash-dot and solid curves are the elastic modulus for the same maximal indentations with (Eq. 2) and without (Eq. 1) the thickness correction of the Hertz model, respectively. The dash-dot curve shows the corresponding elastic modulus using the 1-parameter fit. All the parameters converge to specific values as the indentations exceed ~0.6 µm only when the 3-parameter method is used. All forces and indentations are offset by the same values so that the SCP of the force data curve is at zero force and zero indentation.
On the contrary, our novel three-parameter fitting approach resulted in a nearly perfect fit, Fig. 5A, except at the lower part of the curve. This is because we used three adjustable parameters: the elastic modulus, and the two coordinates of the HCP, as independent parameters. For this curve, this approach resulted in an effective HCP that is offset from the SCP by about ~0.1 µm, which is commensurate with the vertical size of the surface roughness, Fig. 4.
Such HCP adjustment reduces the effect of weak forces exerted by the rough layer, so that the matrix appears rather linear with no depth-dependent variation of the elastic modulus. This is indicated by the best-fit HCP and elasticity determined by analyzing the force curves up to different maximal indentations, Fig. 5B. As the maximal indentation increases, the values of both the HCP and elasticity stabilize, indicating that at depths beyond the top layer, the matrix is not strain-stiffening.
Analysis of typical cartilage matrix force curves
Most of the force curves measured at the matrix appeared more complex than the curve in Fig. 5A. We explored the structure of such curves in more detail using the novel fitting approach. We selected a representative curve, Fig. 6A,B, that (i) was measured at the middle point of a relatively wide matrix septum, (ii) had an effective elastic modulus that was middle of the range for such locations and (iii) had a fit quality (root-mean-square of residuals) that was close to the fit quality median of all matrix curves measured. We tested all three fitting models, Eqs. 1, 2a and 3b, and found that they produced comparable results, as shown in Fig. 7, and the same conclusions. Therefore, we used the simplest, half-space Hertz model (Eq. 1) to analyze the selected curve.
Fig. 6.
Fitting analysis of a typical force-indentation curve at the matrix. (A,B) The force curve (grey lines) and its fits with the half-space Hertz model (Eq. 1). Fits with 1-, 2- (A) and 3-parameter (A,B) approaches are shown. The dots mark the slope and Hertz contact points (SCPs and HCPs). The top panels show fitting residuals and mark the ranges of indentations used for fitting. The resulting elastic moduli in MPa are shown next to the corresponding curves (B). The solid fitted line indicates the data range selected and analyzed by our default curve fitting algorithm. The bottom panels in (B) magnify the lower and upper regions of the middle panel (B). Segments of the dashed and dotted fitted curves on the left side of the Hertz contact are omitted for clarity in (B). (C, D) Elastic modulus and HCP resulting from fitting the truncated force curve as a function of truncation position using the novel approach. In (C), the force curve is truncated at deeper (maximal) indentations. In (D), force curve data points between the SCP and given minimal indentation are excluded from the fit. All forces and indentations are offset by the same values so that the SCP of the force data curve is at zero force and zero indentation. The 2-parameter fit was done using NanoScope Analysis v. 1.9 software (Bruker).
Fig. 7.
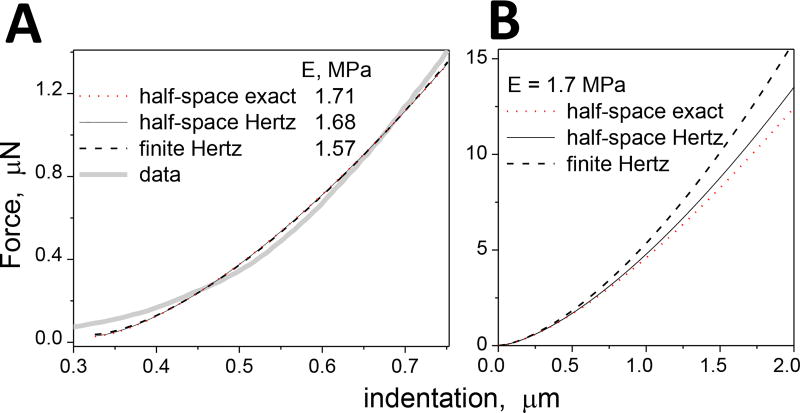
(A) Force-indentation curve at the matrix fitted with the three elastic models. The resulting elastic moduli are shown. (B) Force curves simulated with the three elastic models and an elastic modulus of 1.7 MPa. The measured thickness of 16.7 µm of the matrix in (A) was used for the fitting and simulation with the finite Hertz model.
Typical matrix curves exhibited a crossover point at ~0.5 µm indentation, evident in the force curve shown in Fig. 6B,C,D. This crossover divided the “toe” region at moderate indentations and the steep region at deeper indentations. Fitting of the toe and the steep data ranges using our algorithm suggested that the toe region was softer (~4 times lower effective elastic modulus) than the deep region, Fig. 6B. The effective HCP for the whole curve was offset from the SCP by about ~0.35 µm. We attribute these offset and crossover points to the rough layer at the section surface and the bulk-like layer underneath. The rough layer is expected to be softer than the bulk matrix because it has less material and consists of potentially more loose material; its influence on the force curve should extend to indentations deeper than the 0.2 µm roughness depth, as is the case. Our attribution of the toe region is consistent with curves like the one shown in Fig. 5 which exhibit a less pronounced toe region.
Despite such variability of the rough layer, the matrix layer underneath exhibited similar behavior. We observed this similarity when we reduced the contribution of the toe to the fitted curves. Namely, we successively discarded sets of points from the deepest indentation down to a given maximal indentation (Figs. 5B,6C) or from the SPC up to a given minimal indentation (Fig. 6D). These plots showed that in addition to the several-fold variation of the effective elastic modulus, the effective HCP point shifted by up to 0.3 µm upon fitting progressively deeper indentation ranges. However, the effective elasticity and HCP (nearly) converged to constant values. This convergence suggests that the bulk-like matrix layer does not have appreciable non-linear or depth-dependent elastic properties.
This contrasts with the observation of Park et al.12 who used the conventional one-parameter fit with the Hertz model and reported that the elasticity does not converge as the indentation increases, except at small indentations. We believe that this is a result of the one-parameter fitting rather than a cartilage matrix property. Indeed, when we used the conventional approach to compute effective elasticity as a function of maximal indentation starting from the SPC, the apparent elasticity showed similar behavior (dotted line in Fig. 5B): the elasticity stayed nearly constant at small maximal indentations, but increased monotonically beyond.
This analysis also indicated that indentations of at least 0.6 µm are required to get consistent values of matrix elasticity (Figs. 5B, 6C, D). The higher indentations are necessary so that most force sampling comes from the “intact” bulk region rather than from the rough superficial layer. Therefore, we used an automated, thickness-corrected, three-parameter fitting strategy to fit the data from the SPC up to 0.7–1.8 µm maximal indentations. This reduced the effect of the toe region on the fitted elastic modulus (cf. the solid black curve in Fig. 6B) even when the toe region was relatively pronounced. Although the resulting elastic moduli were in general lower (by ~30%, Fig. 6B,C,D) than the converged values (cf. dashed curve in Fig. 6B) such an underestimation was satisfactory for the goals of this work because it was smaller than the other uncertainties in our measurements (see below).
Effect of finite sample thickness
To select the best elastic model for our analyses, we compared three models. The half-space Hertz model assumes that indentation is much smaller than the contact radius, which is not the case at the deeper indentations of our force curves. However, the resulting error was small, ~2%, and the fitted Hertz and exact curves were barely distinguishable, Fig. 7. The fitted curve of the finite thickness Hertz model was also barely distinguishable from the others, Fig. 7A. However, elastic moduli resulting from the finite thickness model were 10–30% smaller than those of the half-space models, Fig. 7A, because a finite thickness results in steeper force curves for the same elastic modulus, Fig. 7B. To avoid this uncertainty due to potential thickness variability across the sample, we used the finite Hertz model for subsequent analysis.
Sampling mouse cartilage tissue
We applied the above fitting approach to force curves measured across the mouse cartilage section shown in Fig. 1A. We acquired force curves along straight 120 µm segments with 1 µm intervals. The first segment started at the glass slide near the sample. Each next segment overlapped by 10 µm with the previous segment, Fig. 1D. This allowed us to measure sample thickness which we defined as the distance from the glass substrate surface to the top surface of the section determined by the HPC on the force curves. By measuring SCPs around the section, we verified that the tilt of the slide surface across the section was small and had a negligible effect on the measured thickness.
The resulting measurement points passed through the extracellular matrix, cells and empty cell lacunas whose cells fell off during sample preparation, Fig. 8A. We distinguished the matrix curves using optical transmission microscopic images of the measured regions correlated with section thickness profiles, Fig. 8A, and the shapes of the force curves, Fig. 8B. An alternative optical image-guided approach based on immuno-fluorescence labeling of the pericellular matrix has been used previously33 to examine the porcine articular matrix. Force curves at cells appeared less steep than at the matrix, consistent with the cells being much softer than the matrix. Such curves often had abnormal shapes with nearly flat regions, inflection points or maxima (cell 1 in Fig. 8B) and gave poor fits apparently due to complex local topography and structure. Occasionally, force curves at the matrix also had abnormal shapes apparently due to debris. All such curves were discarded.
Fig. 8.
(A) The elastic modulus (Middle) and slope and Hertz contact points (Bottom) extracted from force curves recorded in a cartilage region versus the distance along the dashed stripe shown in the visible microscopic image of the region (Top). The width of the stripe indicates the approximate contact region of the spherical probe indented at maximal indentation. Cells appear as irregular round blobs, and empty cell lacunas as smooth round impressions. Letters C, L and M mark cells, lacunas and matrix, respectively, along the dashed stripe. (B) Representative force-indentation curves at the matrix and cells.
Elastic modulus and thickness profiles
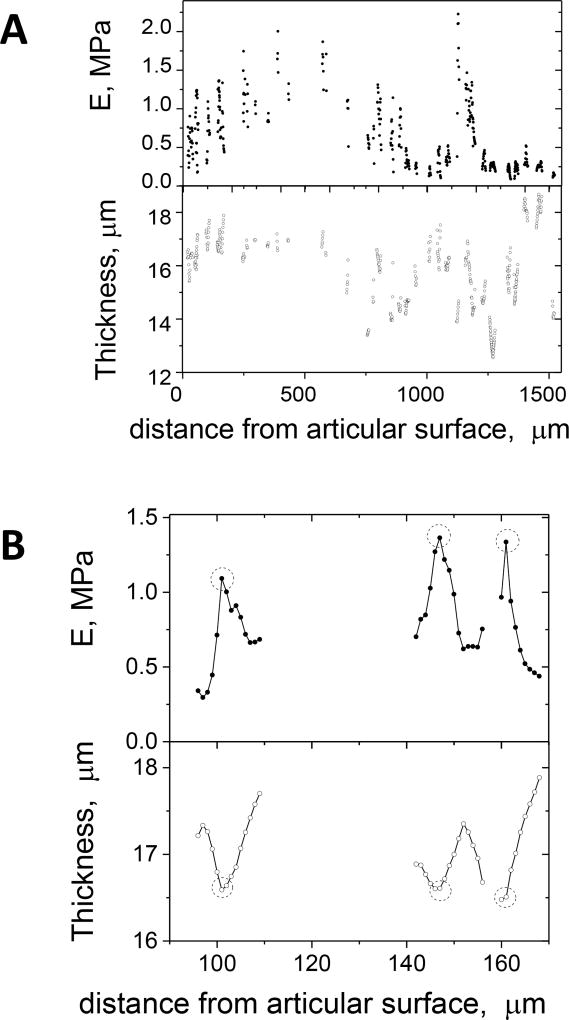
The elastic moduli and corresponding local tissue thickness at selected points (as described above) are shown in Fig. 9A. Notice the apparent global trends and the local scatter of the elastic moduli. A closer look at elasticity profiles showed that much of the local scatter in Fig. 9A came from points probed across matrix septa between cells.
Fig. 9.
Apparent elastic modulus and thickness of the cartilage extracellular matrix plotted versus the anatomical distance from the articular surface along the indentation pathway in Fig. 1A. (A) The full range of selected matrix data points. (B) A selected range of data points (from panel A) passing across three matrix septa. The circles mark points near the middles of the matrix septa.
Representative matrix profiles of effective elastic modulus and sample thickness across three matrix septa are shown in Fig. 9B. The elastic modulus profiles have bell shapes with maxima in the middle of the septa. The elastic modulus dropped about three-fold towards the cells. This could simply be the result of geometry, namely indenting close to a much softer cell or an empty lacuna, or it could be that the pericellular matrix is considerably softer than the matrix farther from the cell33 or a combination of the two. One could argue that, since the peaks of the bell-shaped elasticity profiles are the closest we can get to the true extracellular matrix elasticity, the upper envelope of the scatter seen in the plot of Fig. 9A may be the best representation of extracellular matrix elasticity. This, however, may not be the case because local composition variability, the systematic changes of septa widths along the indentation pathway and the possibility of a softer pericellular matrix introduce large uncertainties to the interpretation of each bell shaped modulus profile and because we sampled a small number of septa.
To examine the global trends of matrix elasticity across different anatomical regions more carefully, we applied a more stringent rule in choosing matrix point data. In Fig. 10, we replotted the elasticity and thickness data points corresponding to the elastic modulus maxima near the middle of matrix septa. This plot shows that the matrix thickness varied between 13 and 17 µm with most of the points being close to 16 µm, Fig. 10. This was significantly thicker than the nominal 12 µm thickness of the section, indicating expansion of the matrix after sectioning.
Fig. 10.
Apparent elastic modulus and thickness of extracellular cartilage matrix as a function of anatomical distance from the articular surface along the indentation pathway in Fig. 1A. Only points measured near the middle of matrix septa (cf. points encircled in Fig. 9B) were selected for this plot. The dashed line indicates the 12 µm nominal thickness of the cartilage section.
The resulting elastic modulus varied within a factor of two within most regions. This local variability may reflect local variability in the structure and composition which can vary by 10–20% within the same region26. In the growth plate region, at 900–1500 µm, the elastic modulus was about four times lower than in the other regions. As the growth plate region (and especially the zone of hypertrophic chondrocytes, Fig. 1C) had substantially thinner matrix septa, the lower effective elastic modulus in this region could be, at least partially, due to this factor, so that the apparent difference between this and the other regions is difficult to interpret. The observed variability of the effective elastic modulus, Fig. 10, was inferred from deep regions of the force-indentation curves because the maximal indentations into the matrix were 0.7–1.8 µm, which was substantially deeper than the ~0.2 µm thick rough superficial layer, Fig. 4.
DISCUSSION
The present cartilage micro-indentation work is a case-study in the typical problems encountered when attempting to obtain meaningful elastic properties from thin or thick samples. Often, such samples not only have multiple length-scales of organization but also have surface properties (roughness, elasticity, charges, etc.) that differ from the bulk material and cannot be simply characterized. The responses of such features to indentation forces are not part of the standard indentation models used to analyze related experimental data.
Cartilage matrix has a soft layer at the cartilage section surface
To be able to evaluate the elasticity of matrix bulk, we explored surface topography of a cartilage section and optimized the probe size and indentation depth for our force curve measurements. We found that sectioning of the cartilage matrix results in a surface layer that is rough (Fig. 4), is softer than the underlying matrix bulk (Fig. 5 and 6B), and has a significant effect on the force curve shape up to indentations of at least 0.5 µm (Figs. 5 and 6).
A soft layer at the section surface of unfixed cartilage has been observed previously and has been ascribed to damage at the cut surface25. Apart from mechanical damage by the cutting knife, the layer could result from dislocation and loss of macromolecules which occur in unfixed cartilage, Fig. 3. We believe the latter to be mostly an intrinsic feature of exposing the cartilage structure rather than a result of major damage by uneven and rough cutting. This is supported by our measurements of the surface roughness scales which are commensurate with the characteristic sizes of matrix macromolecules and their assemblies and distances between them. Matrix macromolecules and their assemblies at the cut surface lose their interaction partners and that allows them to expand into the free space, contributing to the softness of the surface layer. Thus, the tissue sections could be viewed as a two-layer structure. However, the surface layer cannot be simply characterized and modeled for our indentation experiments, so novel force curve fitting methods and experimental protocols had to be devised.
Mild fixation prevents major diffusional loss of proteoglycans
We observed a major loss of GAGs and NCPs in unfixed cartilage matrix, Fig. 3. The lost components were dominated by aggrecan, the major proteoglycan of cartilage matrix, and by NCPs, as indicated by our spectroscopic data (Supplementary Figs. S1C,F). As aggrecan is a key determinant of cartilage mechanical properties, its partial loss could have a major effect on force measurements. We found that mild fixation prevented that loss and so we mildly fixed the tissue before cutting the sections.
Deep indentations and the introduction of a virtual contact point reduce the surface layer effect
As the soft surface layer contributes to the force curve, we had to account for this layer in order to measure the bulk matrix underneath. We greatly reduced its effect by using deep indentations (0.7–1.8 µm), Fig. 6B,C,D, and by developing a novel fitting approach. This approach reduces the contribution of the soft layer by offsetting the effective CP towards indentations deeper than the physical contact point (SCP) of the AFM probe with this surface layer.
The effective elastic modulus may be underestimated
The measured effective elastic modulus may be underestimated compared with that in the matrix in intact tissue for three reasons. Firstly, in our analysis, the soft surface layer has a residual effect on the effective modulus which can result in the underestimation of the bulk modulus by up to 30%, Fig. 6B. Secondly, we observed that the elasticity measurements across septa have a characteristic bell shape with moduli varying by a factor of two to three, Fig. 9. This could be the result of a different composition and structure and, hence, a different elasticity of the pericellular matrix. This would be consistent with previous reports that the pericellular matrix of porcine cartilage is three-to-four times softer that the extracellular matrix33. Another explanation could be that due to the narrowness of the septa, we are indenting near much softer objects like a cell or an empty lacuna. This effect should be more pronounced with deeper indentations which were used in this work. The latter explanation is also consistent with the elastic modulus in the growth plate region, where septa are particularly narrow, being around four times lower than in other regions where septa widths are much wider, Fig. 10. This issue could be resolved by finite-element analysis of the cell/lacunae effect on the force curve, which was beyond the scope of this paper.
The third possible reason for the elastic modulus underestimation may be the measured 20–40% matrix expansion in thickness, compared to the nominal value for the section shown in Figs. 9, 10. The thickness changes have three implications for our data analysis and interpretations. First, the matrix thickness had to be measured and corrected for at every point probed, to estimate the local elastic modulus. Second, the thickness changes indicate that sectioning released stresses present in intact matrix in the tissue. The non-uniform expansion points to the tissue anisotropies and related pre-stress distributions within the intact tissue. Third, the matrix thickness changes can result in elasticity values different from those of the intact matrix in the tissue. If the sectioned matrix expands in all dimensions, the measured values would underestimate the intact values. If the sectioned matrix shrinks in the section plane, the measured values could be under- or overestimated depending on the shrinkage/expansion ratio. The magnitude of such effects is difficult to quantify because the relationships between matrix composition and elasticity are poorly understood and the anisotropy of the expansion is unknown.
A final factor is the specimen fixation necessitated by the observed major loss of GAGs and NCPs in unfixed cartilage matrix, Fig. 3. Fixation has two opposite effects on our effective elastic modulus estimates. Firstly, it introduces additional crosslinks into the matrix, which should increase the elastic modulus and increase the difference between the fixed matrix and intact matrix in native cartilage. On the other hand, such crosslinks prevent the loss of macromolecules from the section and should also reduce the matrix expansion, reducing the difference between the sectioned and native tissue. The combined effect of the fixation is difficult to evaluate and needs to be studied further, which was beyond the scope of this paper. Taking the fixation effect and the possible sources of underestimation, our estimates of matrix elasticity in newborn mouse cartilage are consistent with the elasticity of a few MPa measured with macroscopic probes of native mouse cartilage20. Nonetheless, we expect the fixation to have a similar effect in different specimens (e.g., normal vs pathological) and at different tissue depths of the same specimen, and to have a small effect on the corresponding elasticity differences, provided that the fixation activities and times are similar.
The elastic modulus varies across the mouse cartilage section
Having obtained measurements from all regions of the section along the indentation line, Fig. 1A, we observed an apparent global dependence of the elastic modulus on the anatomical region across the cartilage section, and a local variability of the modulus within each region. It is unclear whether this dependence and local variability result from the moderate dependence and local variability in matrix cartilage composition observed previously across an adjacent section from the same specimen26. The global variability of composition occurs primarily within ~250 µm distance from the articular surface where the collagen concentration in the matrix decreases and the GAG concentration increases. We observe that the effective elastic modulus increases in the same direction. However, this increase is also consistent with the variability of matrix septa width and the possible dependence of the effective elastic modulus on that width: the septa became narrower towards the articular surface and mineralizing zone of the growth plate region; the spike near the distance of 1200 µm in Fig. 9 correlates with septa widths which happened to be much wider than at nearby locations where the indentation lines happened to pass through very narrow septa dividing stacked cells within cell columns, as seen from visible images of the section. As the matrix composition also varies within each region26 and so do the septa widths, we cannot presently discriminate between the contributions of these variabilities to the local variability of matrix elasticity. Altogether, our results indicate that the dependence of matrix elasticity on the anatomical region does not exceed a factor of three.
Our approach improves length-scale invariance of the elastic modulus
An ongoing inconsistency in the cartilage mechanics field is that the elasticity predicted by nanoindentation is orders of magnitude smaller than the elasticity predicted by macroscale indentation (tens of kPa12 vs. MPa20). Our observed convergence of the elasticity with indentation depth suggests that if the rough, surface layer is discounted, the cartilage indeed appears linearly elastic. Moreover, at 0.8 – 1.5 MPa, our estimates of the elastic modulus are closer to those from macroscale measurements20. Our values also agree with other microscale measurements of cartilage matrix in adult mice and other animals21, 22, 24. It is unclear if this agreement is due to similar values of the actual elastic moduli or due to compensating factors. These factors could include the contributions of cells to the macroscale elasticity, the differences in experimental methodologies used, the newborn age of our mouse and the use of a single animal in this methodological work.
The novel force curve fitting approach has broad relevance for soft matter nanoindentation studies
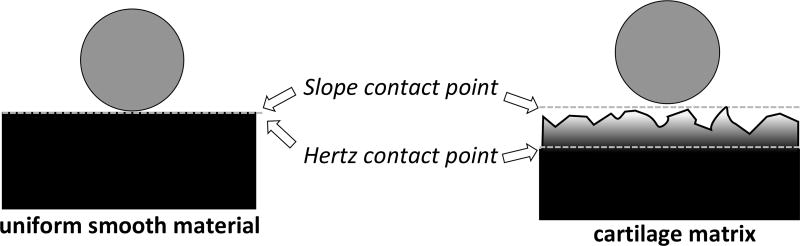
Initial efforts to analyze the acquired indentation data clearly indicated the existence of a surface layer that had very different properties from the bulk matrix underneath. This was obvious from the poor fits obtained by using any of the established fitting strategies, Figs. 5A and 6B. Our approach offers a key distinguishing strategy from other fitting methods of Hertzian mechanics in the literature. Our fitting strategy of using both CP coordinates (zH, dH) as independent fitting parameters allows for the CP to float off the force curve. This addresses the issue of the rough surface layer, because of which the SCP cannot be equated to the idealized HCP for the bulk material under the rough surface. Our method estimates an effective CP for the material underlying the surface layer that cannot be simply characterized, and there is no physical reason requiring this CP to lie on the data curve, Fig. 11.
Fig. 11.
Illustration of Hertz mechanics describing the indentation of a spherical probe into a homogenous layer with a smooth surface (left). In our experiments, however, the surface of the sectioned matrix is rough and softer than the underlying matrix bulk (right). As a result, the effective or Hertz contact point (HCP) predicted by our fitting analysis lies deeper than the physical or slope contact point (SCP) at which the probe starts interacting with the matrix.
Our analysis with this fitting approach suggested that at deeper indentations the contribution of the soft layer was substantially reduced and that there was no appreciable inelastic stiffening, Figs. 5B and 6C,D. Therefore, the resulting effective elastic modulus represents the properties of deeper regions of the matrix in the section. This strategy proved superior to any one-parameter (E) fitting approach, Fig. 6A. It was also superior to two-parameter fitting methods (including our previous method34 and its constrained three-parameter version34, 35) that estimate, in addition to E, one coordinate of the CP and require the CP to lie on the acquired data curve, Fig. 6A. These approaches are appropriate when seeking a CP on a homogeneous sample, but this is not the case here.
Our approach has wider relevance given that, irrespective of the indented object, the region of the shallowest indentation near the CP is often plagued by noise and is affected by other types of interactions (electrostatics, van der Waals, etc.) that are not part of any fitting model. In addition, it has been repeatedly pointed out in the literature that the values of the estimated fitting parameters strongly depend on the choice of contact point12, 25, 36. Our approach is optimized to address this issue too by allowing the effective CP to lie off the force dataset. For these reasons, it may be appropriate to always try and reduce the effect of that shallow indentation region; that is what our approach offers.
CONCLUSIONS
In our effort to map the elastic properties of the extracellular matrix through the thickness of newborn mouse cartilage we encountered several challenges. We overcame some of them by a detailed study of the surface properties of cartilage sections and by optimizing measurement and analysis methods. In particular, we developed a fitting algorithm that substantially reduces the effect of the soft, rough layer present at the cartilage section surface due to intrinsic cartilage matrix structures and possible sectioning damage. Our data analysis suggests that the matrix behaves as a linear elastic material even at relatively high strains. We showed that unfixed cartilage sections lose macromolecules that regulate matrix elasticity and that mild fixation of the specimen prevents that loss. We found that the variation of elastic modulus does not exceed a factor of two to three across anatomically and functionally different zones of newborn mouse cartilage. We observed changes of section thickness relative to nominal thickness which can alter the matrix elastic modulus. The narrow width of matrix septa in mouse cartilage may also result in the underestimation of the modulus. Further studies of the septum width effect, of elasticity differences between the pericellular and extracellular matrix in mice, and of the effect of fixation will allow for more accurate measurement and interpretation of matrix elasticity. This, in turn, will allow for the quantification of the effect of thickness expansion, and a better understanding of the structure-function relationships in cartilage.
Supplementary Material
Acknowledgments
We thank A. Forlino, S. Leikin and A. Pilgrim-Roberts for providing and genotyping mouse samples. We also thank Mr. N. English for assistance with optical image processing. This work was funded by the Intramural Research Programs of the National Institute of Child Health and Human Development (NICHD) and the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health, and a NICHD Director’s Award.
References
- 1.Iozzo R, editor. Proteoglycans: Structure, Biology, and Molecular Interactions. Marcel Dekker Inc; New York: 2000. [Google Scholar]
- 2.Kiani C, Chen L, Wu YJ, Yee AJ, Yang BB. Cell Res. 2002;12:19–32. doi: 10.1038/sj.cr.7290106. [DOI] [PubMed] [Google Scholar]
- 3.Nap RJ, Szleifer I. Biophysical Journal. 2008;95:4570–4583. doi: 10.1529/biophysj.108.133801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chandran P, Horkay F. Acta Biomaterialia. 2012;8:3–12. doi: 10.1016/j.actbio.2011.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Watanabe H, Yamada Y, Kimata K. J Biochem. 1998;124:687–693. doi: 10.1093/oxfordjournals.jbchem.a022166. [DOI] [PubMed] [Google Scholar]
- 6.Poole AR, Matsui Y, Hinek A, Lee ER. Anat Rec. 1989;224:167–179. doi: 10.1002/ar.1092240207. [DOI] [PubMed] [Google Scholar]
- 7.Dudhia J. Cellular and Molecular Life Sciences. 2005;62:2241–2256. doi: 10.1007/s00018-005-5217-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Plaas AHK, Wong-Palms S, Roughley PJ, Midura RJ, Hascall VC. Journal of Biological Chemistry. 1997;272:20603–20610. doi: 10.1074/jbc.272.33.20603. [DOI] [PubMed] [Google Scholar]
- 9.Meder R, De Visser SK, Bowden JC, Bostrom T, Pope JM. Osteoarthritis and Cartilage. 2006;14:875–881. doi: 10.1016/j.joca.2006.03.002. [DOI] [PubMed] [Google Scholar]
- 10.Williams JL, Do PD, Eick JD, Schmidt TL. Journal of Orthopaedic Research. 2001;19:1043–1048. doi: 10.1016/S0736-0266(01)00040-7. [DOI] [PubMed] [Google Scholar]
- 11.Sergerie K, Lacoursière M-O, Lévesque M, Villemure I. Journal of Biomechanics. 2009;42:510–516. doi: 10.1016/j.jbiomech.2008.11.026. [DOI] [PubMed] [Google Scholar]
- 12.Park S, Hung CT, Ateshian GA. Osteoarthritis and Cartilage. 2004;12:65–73. doi: 10.1016/j.joca.2003.08.005. [DOI] [PubMed] [Google Scholar]
- 13.Radhakrishnan P, Lewis N, Mao J. Annals of Biomedical Engineering. 2004;32:284–291. doi: 10.1023/b:abme.0000012748.41851.b4. [DOI] [PubMed] [Google Scholar]
- 14.Simha NK, Jin H, Hall ML, Chiravarambath S, Lewis JL. Journal of Biomechanical Engineering. 2007;129:767–775. doi: 10.1115/1.2768110. [DOI] [PubMed] [Google Scholar]
- 15.Hori RY, Mockros LF. Journal of Biomechanics. 1976;9:259–268. doi: 10.1016/0021-9290(76)90012-9. [DOI] [PubMed] [Google Scholar]
- 16.Loparic M, Wirz D, Daniels AU, Raiteri R, VanLandingham MR, Guex G, Martin I, Aebi U, Stolz M. Biophysical Journal. 2010;98:2731–2740. doi: 10.1016/j.bpj.2010.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prein C, Warmbold N, Farkas Z, Schieker M, Aszodi A, Clausen-Schaumann H. Matrix Biology. 2016;50:1–15. doi: 10.1016/j.matbio.2015.10.001. [DOI] [PubMed] [Google Scholar]
- 18.Stolz M, Raiteri R, Daniels AU, VanLandingham MR, Baschong W, Aebi U. Biophysical Journal. 2004;86:3269–3283. doi: 10.1016/S0006-3495(04)74375-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nguyen BV, Wang QG, Kuiper NJ, El Haj AJ, Thomas CR, Zhang Z. Journal of the Royal Society Interface. 2010;7:1723–1733. doi: 10.1098/rsif.2010.0207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cao L, Youn I, Guilak F, Setton LA. Journal of Biomechanical Engineering. 2006;128:766–771. doi: 10.1115/1.2246237. [DOI] [PubMed] [Google Scholar]
- 21.Stolz M, Gottardi R, Raiteri R, Miot S, Martin I, Imer R, Staufer U, Raducanu A, Duggelin M, Baschong W, Daniels AU, Friederich NF, Aszodi A, Aebi U. Nature nanotechnology. 2009;4:186–192. doi: 10.1038/nnano.2008.410. [DOI] [PubMed] [Google Scholar]
- 22.Nia HT, Gauci SJ, Azadi M, Hung HH, Frank E, Fosang AJ, Ortiz C, Grodzinsky AJ. Journal of Biomechanics. 2015;48:162–165. doi: 10.1016/j.jbiomech.2014.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Candela ME, Wang C, Gunawardena AT, Zhang KR, Cantley L, Yasuhara R, Usami Y, Francois N, Iwamoto M, van der Flier A, Zhang YJ, Qin L, Han L, Enomoto-Iwamoto M. Plos One. 2016;11 doi: 10.1371/journal.pone.0156783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Coles JM, Zhang L, Blum JJ, Warman ML, Jay GD, Guilak F, Zauscher S. Arthritis and Rheumatism. 2010;62:1666–1674. doi: 10.1002/art.27436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Darling EM, Wilusz RE, Bolognesi MP, Zauscher S, Guilak F. Biophysical Journal. 2010;98:2848–2856. doi: 10.1016/j.bpj.2010.03.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mertz EL, Facchini M, Pham AT, Gualeni B, De Leonardis F, Rossi A, Forlino A. The Journal of Biological Chemistry. 2012;287:22030–22042. doi: 10.1074/jbc.M110.116467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aaron JE, Carter DH. The journal of histochemistry and cytochemistry : official journal of the Histochemistry Society. 1987;35:361–369. doi: 10.1177/35.3.2434557. [DOI] [PubMed] [Google Scholar]
- 28.Ng L, Grodzinsky AJ, Patwari P, Sandy J, Plaas A, Ortiz C. Journal of structural biology. 2003;143:242–257. doi: 10.1016/j.jsb.2003.08.006. [DOI] [PubMed] [Google Scholar]
- 29.Aszodi A, Chan D, Hunziker E, Bateman JF, Fassler R. Journal of Cell Biology. 1998;143:1399–1412. doi: 10.1083/jcb.143.5.1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Maroudas A. In: Adult articular cartilage. 2. MAR F, editor. ch. 4. Pitman Medical Publishing Co; London: 1979. pp. 215–290. [Google Scholar]
- 31.Diab M, Wu JJ, Shapiro F, Eyre D. American Journal of Medical Genetics. 1994;49:402–409. doi: 10.1002/ajmg.1320490411. [DOI] [PubMed] [Google Scholar]
- 32.Shapiro F. Calcified Tissue International. 1992;51:324–331. doi: 10.1007/BF00334495. [DOI] [PubMed] [Google Scholar]
- 33.Wilusz RE, DeFrate LE, Guilak F. Journal of the Royal Society Interface. 2012;9:2997–3007. doi: 10.1098/rsif.2012.0314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lin DC, Dimitriadis EK, Horkay F. Journal of biomechanical engineering. 2007;129:904–912. doi: 10.1115/1.2800826. [DOI] [PubMed] [Google Scholar]
- 35.Our previous constrained method searches for the two coordinates of the contact point. Importantly, it excludes all data points for indentations shallower than the current contact point at each iteration step. (Effectively, the theta function in Eq.8 is replaced by a constant equal to 1.) Such exclusion drives the final CP closer to the data curve, so that for force curves with pronounced toe region the result is similar to that of 2-parameter approaches, cf. Fig. 6A.
- 36.Dimitriadis EK, Horkay F, Maresca J, Kachar B, Chadwick RS. Biophysical Journal. 2002;82:2798–2810. doi: 10.1016/S0006-3495(02)75620-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.