PROBABILITY DISTRIBUTION OF DOSE AND DOSE-RATE EFFECTIVENESS FACTOR FOR USE IN ESTIMATING RISKS OF SOLID CANCERS FROM EXPOSURE TO LOW-LET RADIATION

Abstract

This paper presents an analysis to develop a subjective state-of-knowledge probability distribution of a dose and dose-rate effectiveness factor (DDREF) for use in estimating risks of solid cancers from exposure to low-LET radiation (photons or electrons) whenever linear dose-responses from acute and chronic exposure are assumed. A DDREF represents an assumption that the risk of a solid cancer per Gy at low acute doses or low dose rates of low-LET radiation, R_L, differs from the risk per Gy at higher acute doses, R_H; R_L is estimated as R_H/DDREF, where R_H is estimated from analyses of dose-responses in Japanese atomic-bomb survivors. A probability distribution to represent uncertainty in a DDREF for solid cancers was developed from analyses of epidemiologic data on risks of incidence or mortality from all solid cancers as a group or all cancers excluding leukemias, including (1) analyses of possible nonlinearities in dose-responses in atomic-bomb survivors, which give estimates of a low-dose effectiveness factor (LDEF), and (2) comparisons of risks in radiation workers or members of the public from chronic exposure to low-LET radiation at low dose rates with risks in atomic-bomb survivors, which give estimates of a dose-rate effectiveness factor (DREF). Probability distributions of LDEFs and DREFs for solid cancer incidence and mortality were combined using assumptions about the relative weight that should be assigned to each estimate to represent its relevance to estimation of a DDREF. The probability distribution of DDREF for solid cancers developed in this study has a median (50^th percentile) and 90% subjective confidence interval (CI) of 1.3 (0.47, 3.6). The harmonic mean is 1.1, which implies that the arithmetic mean of an uncertain estimate of the risk of a solid cancer per Gy at low acute doses or low dose rates of low-LET radiation is only about 10% less than the mean risk per Gy at higher acute doses. We also evaluated data to define a low acute dose or low dose rate of low-LET radiation, i.e., a dose or dose rate below which a DDREF should be applied in estimating risks of solid cancers.

INTRODUCTION

Risks of cancer in humans from exposure to low-LET radiation (photons or electrons) are estimated primarily on the basis of estimated risks in Japanese atomic-bomb survivors [the Life Span Study (LSS) cohort] who received an acute exposure mainly to high-energy photons, with a smaller contribution from neutrons, at neutron-weighted organ doses up to several Gy (e.g., Preston et al. 2007; Richardson et al. 2009; Ozasa et al. 2012; Hsu et al. 2013). Risks of most solid cancers in the LSS cohort are well described by linear dose-response relationships—i.e., an excess risk of solid cancer incidence or mortality, ℜ, is modeled as ℜ = αD, where D is the dose (Gy) and α (Gy⁻¹) is the model coefficient (e.g., NRC 2006; Preston et al. 2007; Ozasa et al. 2012). However, when estimated risks of solid cancers in the LSS cohort are used to estimate risks in other cases of acute or chronic exposure to low-LET radiation, it is often assumed that the risk per Gy at low acute doses or low dose rates, R_L, differs from the risk per Gy at higher acute doses in the LSS cohort, R_H, by a modifying factor referred to as a dose and dose-rate effectiveness factor (DDREF). In such cases, R_L is estimated as R_H/DDREF.

This paper presents an analysis to develop a subjective state-of-knowledge probability distribution to represent uncertainty in a DDREF for solid cancers induced by low-LET radiation. This distribution is intended for use in estimating risks of solid cancers and their uncertainty whenever linear dose-responses from acute and chronic exposure to low-LET radiation are assumed. The probability distribution of DDREF developed in this study was based on analyses of dose-responses for all solid cancers as a group or all cancers excluding leukemias from acute exposure in the LSS cohort and dose-responses for those cancer groups in radiation workers or members of the public from chronic exposure to low-LET radiation at low dose rates.

As part of this analysis, we also evaluated data to define an acute dose or dose rate of low-LET radiation below which a DDREF should be applied in estimating risks of solid cancers. This evaluation is summarized in an appendix.

Use of a DDREF in estimating risks of solid cancers at low acute doses or low dose rates of low-LET radiation was based originally on two assumptions: (1) the dose-response from acute exposure to low-LET radiation is inherently linear-quadratic—i.e., ℜ = αD + βD²,^‡ where the coefficient β (Gy⁻²) is >0—and (2) the response from chronic exposure to low-LET radiation at low dose rates is determined by the linear term in a linear-quadratic dose-response from acute exposure (ICRP 1977; NCRP 1980). These assumptions were based on (1) observed effects of dose and dose rate on various responses in cells, plants, and laboratory animals, (2) an observed increase in the risk of mortality from all leukemias per Gy with increasing dose in early studies of the LSS cohort, and (3) microdosimetric arguments that responses per Gy at low acute doses (βD² << αD) or low dose rates should be the same (NCRP 1980).

The assumption of a linear-quadratic dose-response from acute exposure to low-LET radiation incorporates a dose-dependent DDREF implicitly; i.e., DDREF = R_H/R_L = [1 + (β/α)D], where β/α (Gy⁻¹), referred to as the curvature parameter, describes the degree of nonlinearity in a dose-response. When β is >0, the response per Gy at low doses is less than at higher doses (DDREF >1). However, an assumption of a linear-quadratic dose-response from acute exposure to low-LET radiation does not have a firm theoretical or experimental basis (e.g., NCRP 2012), and other relationships, such as a supralinear dose-response (DDREF <1), are not excluded.

A probability distribution of DDREF that could be used in estimating risks of leukemias at low acute doses or low dose rates of low-LET radiation was not developed in this study, mainly because, in contrast to dose-responses for most solid cancers, dose-responses for all leukemias as a group in the LSS cohort are well described by linear-quadratic models that incorporate a dose-dependent DDREF (NRC 2006; Richardson et al. 2009; Hsu et al. 2013).^§

A DDREF represents two distinct concepts, which we refer to as a low-dose effectiveness factor (LDEF) and a dose-rate effectiveness factor (DREF). An LDEF is estimated by analyzing possible nonlinearities in dose-responses from acute exposure; i.e., an LDEF is the ratio of a risk per Gy at a high acute dose to a risk per Gy at a low acute dose. For example, analyses of the curvature in dose-responses in the LSS cohort assuming linear-quadratic models give estimates of LDEF. A DREF is estimated by comparing cancer risks in populations that received chronic exposures to low-LET radiation at low dose rates with risks in the LSS cohort assuming linear dose-responses in both populations; i.e., a DREF is the ratio of a risk per Gy in the LSS cohort to a risk per Gy from chronic exposure. Although the concepts of an LDEF and a DREF usually are combined into a DDREF, as we have done in our analysis, we maintained this distinction in evaluating data from specific epidemiologic studies.

This study was carried out to provide input to a future revision of cancer risk models in the Interactive RadioEpidemiological Program (IREP) (Land et al. 2003; Kocher et al. 2008), which is used in adjudicating claims for compensation for cancer under the Energy Employees Occupational Illness Compensation Program Act (EEOICPA). Part B of EEOICPA (U.S. Congress 2000) and its implementing regulations (U.S. DHHS 2002) mandate that cancer risk models in IREP account for uncertainty, and experience with using IREP (Kocher et al. 2008) and other analyses of uncertainties in cancer risk models (NCRP 1997; NRC 2006; U.S. EPA 2011) showed that an uncertainty in DDREF is often an important contributor to an uncertainty in estimated risks of solid cancers from exposure to low-LET radiation.

More generally, the intent of this study was to develop a probability distribution of a DDREF for solid cancers induced by low-LET radiation that is an unbiased representation of the state of knowledge.

DDREFS DEVELOPED IN PRIOR STUDIES

Prior to this study, probability distributions to represent uncertainty in a DDREF for solid cancers induced by low-LET radiation were developed in several other studies. Table 1 presents 90% subjective confidence intervals (CIs) and medians and arithmetic means of those distributions. The bases for those DDREFs are summarized below and described in more detail elsewhere (NCRP 2012; Trabalka et al. 2017). A more recent analysis to estimate DREFs and their uncertainties (Shore et al. 2017) is discussed in a later section.

Table 1.

Probability distributions developed in previous studies to represent uncertainty in DDREF for solid cancers induced by low-LET radiation.

Reference	Cancer outcomes	DDREF
		90% CI	Median	Mean
NCRP (1997)	Solid cancer mortality	(1.25, 4.1)a	2.3	2.5
U.S. EPA (1999)	Solid cancer mortality or incidence	(1.1, 4.3)b	2.0	2.25
Grogan et al. (2000)	Solid cancer mortality excluding lung	(1.0, 4.1)c	2.3	2.4
	Lung cancer mortality	(1.5, 8.3)d	4.5	4.7
Land et al. (2003)	Solid cancer incidence excluding breast and thyroid	(1.0, 3.0)e	1.5	1.8
	Breast and thyroid cancer incidence	(1.0, 3.0)f	1.5	1.6
BEIR VII report (NRC 2006)	Solid cancer incidenceg	(0.9, 2.5)h	1.5	1.6
Jacob et al. (2009)	Solid cancer mortality or incidence	(0.53, 1.96)i	0.83j	NAk
		(0.33, 0.86)	0.48
		(0.65, 2.43)	1.02
U.S. EPA (2011)		Distribution from BEIR VII report

^aPiecewise-linear distribution with most probable value at 2 and lower and upper bounds of (1, 5) based on assessment of curvature in dose-responses for solid cancer mortality or incidence in LSS cohort assuming linear-quadratic models, comparison of risks of lung cancer mortality in medical patients exposed to x rays with risks in LSS cohort, and data on cancer induction in laboratory animals.

^bUniform distribution at values of 1–2 and exponential distribution at values >2 based on distribution recommended by NCRP (1997) and other data in LSS cohort, medical patients exposed to x rays, and laboratory animals.

^cPiecewise-linear distribution with most probable value at 2 and lower and upper bounds of (0.2, 5) based on modification of distribution recommended by NCRP (1997) to include possibility of supralinear response at low acute doses (DDREF <1), as suggested by dose-response for cancer mortality in LSS cohort.

^dPiecewise-linear distribution with most probable value at 4 and lower and upper bounds of (0.2, 10) based on distribution for solid cancer mortality excluding lung and comparison of risks of lung cancer mortality in medical patients exposed to x rays with risks in LSS cohort.

^eDiscrete distribution with most probable values at 1.5 and 2 and lower and upper bounds of (0.5, 5) based mainly on assessment of nonlinearity in dose-response for solid cancer mortality in LSS cohort.

^fDiscrete distribution with most probable value at 1.0 and lower and upper bounds of (0.5, 4) based on distribution for solid cancer mortality excluding breast and thyroid and conclusion that dose-responses for breast and thyroid cancer in LSS cohort showed greater tendency toward linearity.

^gExcluding thyroid and nonmelanoma skin cancers but including lymphomas and multiple myeloma.

^hLognormal distribution with 95% CI of (0.83, 2.7) was based on analysis of curvature in dose-response for solid cancer incidence in LSS cohort assuming linear-quadratic model modified to take into account dose-responses for cancer induction in laboratory animals. Distribution essentially represents an LDEF.

ⁱEntries are reciprocals of upper and lower bounds of 90% CIs of combined ratios of estimated risks in workers or members of the public from chronic exposure to low-LET radiation at low dose rates to estimated risks from acute exposure in LSS cohort, referred to as “risk ratios.” First entry represents main result based on estimated risks from seven studies of cancer mortality in workers or members of the public; second and third entries were based on estimated risks from four studies of cancer mortality and three studies of cancer incidence, respectively. Distributions represent DREFs.

^jEntries are reciprocals of central estimates of combined risk ratios.

^kMeans of probability distributions of combined risk ratios were not reported, and means of corresponding DDREFs are not estimated.

All probability distributions in Table 1 were based mainly or entirely on epidemiologic data; NCRP (1997), U.S. EPA (1999), Grogan et al. (2000), and the BEIR VII committee (NRC 2006) also used data on cancer induction or life shortening due mainly to fatal cancers in laboratory animals. All probability distributions except those from Jacob et al. (2009) were based at least in part on analyses of the curvature in dose-responses for incidence or mortality from all solid cancers in the LSS cohort assuming linear-quadratic models; NCRP (1997), U.S. EPA (1999), and Grogan et al. (2000) also used comparisons of risks of lung cancer in the LSS cohort and in medical patients that received fractionated exposures to x rays. The probability distribution developed by the BEIR VII committee (NRC 2006) essentially represents an LDEF, whereas distributions based on analyses by Jacob et al. (2009) represent DREFs.

In analyses by Jacob et al. (2009), estimated risks of cancer mortality or incidence in several cohorts of radiation workers or members of the public that received chronic exposures to low-LET radiation at low dose rates were compared with age- and sex-matched estimates of risks in the LSS cohort assuming linear dose-responses in all cohorts.^** In each comparison, a probability distribution of the ratio of a risk from chronic exposure to the corresponding risk in the LSS cohort, referred to as a “risk ratio,” was obtained; each risk ratio is the reciprocal of a DREF. Jacob et al. (2009) then derived probability distributions of three overall risk ratios by calculating weighted averages of risk ratios based on estimated risks in selected cohorts of workers or members of the public, with each risk ratio weighted by the reciprocal of its variance. The main result obtained by Jacob et al. (2009) was a weighted average of risk ratios based on results from seven studies of cancer mortality. Two additional overall risk ratios were weighted averages of risk ratios based on results from four studies of cancer mortality or three studies of cancer incidence. Medians and 90% CIs of the three DDREFs in Table 1 are reciprocals of the central estimates and 90% CIs of the overall risk ratios derived by Jacob et al. (2009).

In analyses by the BEIR VII committee (NRC 2006) and Jacob et al. (2009), risks in the LSS cohort were estimated using Dosimetry System 2002 (DS02) (RERF 2005), whereas risks in the LSS cohort used in earlier studies summarized in Table 1 were estimated using DS86 dosimetry (RERF 1987, 1988) and shorter periods of follow-up of the cohort. In addition, the epidemiologic and animal data and subjective judgments that provided the bases for the probability distributions of DDREF developed by NCRP (1997), U.S. EPA (1999), Grogan et al. (2000), and Land et al. (2003) are not as well documented as the more formal quantitative analyses of relevant data by the BEIR VII committee (NRC 2006) and Jacob et al. (2009). For these reasons, we consider that probability distributions based on analyses by the BEIR VII committee (NRC 2006) and Jacob et al. (2009) should be better representations of an uncertain DDREF for solid cancers. In a later section, we compare those distributions with the probability distribution of DDREF for solid cancers developed in this study.

OVERVIEW OF PRESENT STUDY

The probability distribution of DDREF for solid cancers developed in this study was based on a comprehensive evaluation of radiobiologic and epidemiologic data on the effects of dose and dose rate on dose-responses from exposure to low-LET radiation (Trabalka et al. 2017). Radiobiologic data we evaluated included estimates of DDREF from studies of mutagenesis, cell transformation, or chromosome aberrations in cells and studies of induction of cancers or life shortening due mainly to fatal cancers in laboratory animals. However, data from radiobiologic studies were not used in our analysis to estimate a DDREF for solid cancers. Dose-responses from some studies in cells are complex and difficult to interpret, and it is questionable whether data on responses in cells are relevant to cancer induction in humans. Although data on induction of cancers or life shortening due mainly to fatal cancers in laboratory animals should be more relevant to cancer induction in humans, dose-responses from some studies also are complex and difficult to interpret. There also are concerns about extrapolating data in laboratory animals to humans due, for example, to the genetic uniqueness of highly inbred animal strains and differences in the relative frequencies of specific cancer types induced by low-LET radiation in animals compared with humans. From our review, we judged that epidemiologic data were sufficiently abundant and varied that a credible probability distribution of DDREF for solid cancers could be developed without using data in animals.

We developed a subjective state-of-knowledge probability distribution of DDREF for solid cancers from estimates of LDEF based on analyses of the curvature in dose-responses for incidence or mortality from all solid cancers in the LSS cohort assuming linear-quadratic models and estimates of DREF based on comparisons of risks of incidence or mortality from all solid cancers or all cancers excluding leukemias in radiation workers or members of the public from chronic exposure to low-LET radiation at low dose rates with risks of those cancers from acute exposure in the LSS cohort.^††

ESTIMATES OF LDEF AND DREF FOR ALL SOLID CANCERS

Estimates of LDEF

Estimates of LDEF we included in our analysis to estimate a DDREF for solid cancers are summarized in Tables 2 and 3. These LDEFs were derived from analyses of possible nonlinearities in dose-responses for solid cancer incidence or mortality in the LSS cohort assuming linear-quadratic models; in all analyses, doses in the LSS cohort were estimated using DS02 dosimetry. Modeled responses were excess relative risks (ERRs) or excess absolute rates (EARs). Each LDEF is the ratio of an estimated risk per Gy at a high acute dose to an estimated risk per Gy at a dose sufficiently low that the modeled dose-response in the LSS cohort is essentially linear. LDEFs from an analysis of solid cancer mortality using DS02 dosimetry by Preston et al. (2004) were not included in our analysis based on a judgment that those LDEFs were superseded by estimates from a more recent analysis by Ozasa et al. (2012). LDEFs based on the most recent analyses of solid cancer incidence and mortality in the LSS cohort (Grant et al. 2017; Cullings et al. 2017) are discussed in a later section.

Table 2.

Estimates of 50^th percentiles and 90% CIs of LDEF based on analyses of curvature in dose-responses (ERRs) for incidence of all solid cancers in LSS cohort assuming linear-quadratic models^a

Reference	Dose range (Gy)b	Follow-up period	Method of calculation	LDEFc
BEIR VII report (NRC 2006)d	0–1.5	1958–1998	αL/αLQe	1.5 (0.9, 2.4)f
			[1 + (β/α)]g	1.5 (1.0, 2.3)h
Preston et al. (2007)	0–2	1958–1998	[1 + (β/α)]g	1.4 (1.0, 1.9)]i

^aERRs estimated using DS02 dosimetry were sex-averaged and modified by age at exposure and attained age. LDEFs were included in our analysis to estimate DDREF for solid cancers induced by low-LET radiation.

^bRange of neutron-weighted doses to colon, calculated assuming biological effectiveness of neutrons at Hiroshima and Nagasaki relative to high-energy photons of 10, over which ERRs were modeled to estimate LDEF.

^cEstimates are based on assumption that reported MLEs and CIs of ratios of risk coefficients can be represented by Weibull distributions with modes at MLEs.

^dAll solid cancers excluded thyroid and nonmelanoma skin cancers but included lymphomas and multiple myeloma.

^eα_L is ERR per Gy obtained from linear fit to dose-response, and α_LQ (Gy⁻¹) is coefficient of linear term in linear-quadratic fit.

^fEstimate based on reported MLE and 95% CI of α_L/α_LQ [1.3 (0.8, 2.6)]. Reported α_L/α_LQ is estimate of LDEF based only on data in LSS cohort preferred by BEIR VII committee. LDEF recommended by BEIR VII committee based on data in LSS cohort and laboratory animals given in Table 1 differs slightly.

^gα (Gy⁻¹) and β (Gy⁻²) are coefficients of linear and quadratic terms, respectively, in linear-quadratic fit to dose-response, and β/α (Gy⁻¹) is curvature parameter. LDEF is estimate at dose of 1 Gy.

^hEstimate based on reported MLE and 95% CI of β/α [0.3 (−0.1, 1.5) Gy⁻¹].

ⁱEstimate based on reported MLE and 90% CI of β/α [0.3 (0.01, 0.90) Gy⁻¹].

Table 3.

Estimates of 50^th percentiles and 90% CIs of LDEF based on analyses of curvature in dose-responses (ERRs or EARs) for mortality from all solid cancers in LSS cohort assuming linear-quadratic models^a

Reference	Dose range (Gy)	Follow-up period	Method of calculation	LDEFb
Little et al. (2008)	0–4c	1950–2000	[1 + (β/α)]d (ERR model)e	1.34 (1.01, 2.53)f
			[1 + (β/α)]d (EAR model)e	1.51 (1.07, 3.26)g
Ozasa et al. (2012)	0–2h	1950–2003	[1 + (β/α)]d (ERR model)i	3.2 (1.2, 8.3)j
			αL/αLQk (ERR model)i	2.0 (1.0, 6.8)m
	0–4n		[1 + (β/α)]d (ERR model)i	1.11 (0.94, 1.48)o
			αL/αLQk (ERR model)i	1.16 (0.77, 1.90)p

^aERRs and EARs estimated using DS02 dosimetry were sex-averaged. LDEFs were included in our analysis to estimate DDREF for solid cancers induced by low-LET radiation.

^bEstimates are based on assumption that reported MLEs and CIs of risk coefficients or ratios of risk coefficients can be represented by Weibull distributions with modes at MLEs.

^cRange of shielded kerma free-in-air from photons and neutrons. Members of LSS cohort with shielded kerma >4 Gy were omitted. Range of neutron-weighted doses to colon, calculated assuming biological effectiveness of neutrons at Hiroshima and Nagasaki relative to high-energy photons of 10, over which ERRs or EARs were modeled to estimate LDEF was slightly less than range of shielded kerma (Egbert 2005; RERF 2007).

^dα (Gy⁻¹) and β (Gy⁻²) are coefficients of linear and quadratic terms, respectively, in linear-quadratic fit to dose-response, and β/α (Gy⁻¹) is curvature parameter. LDEF is estimate at dose of 1 Gy.

^eERRs and EARs were modified by time since exposure and attained age.

^fEstimate based on reported MLEs and 90% CIs of α [0.347 (0.161, 0.566) Gy⁻¹] and β [0.121 (0.004, 0.246) Gy⁻²] and assumption that α and β are negatively correlated (correlation coefficient of −1). Assumed parameter correlation should result in slight overestimate of uncertainty in LDEF.

^gEstimate based on reported MLEs and 90% CIs of α [5.58 (2.31, 9.40) Gy⁻¹] and β [2.86 (0.66, 5.22) Gy⁻²] and assumption that α and β are negatively correlated (correlation coefficient of −1). Assumed parameter correlation should result in slight overestimate of uncertainty in LDEF.

^hRange of neutron-weighted doses to colon, calculated assuming biological effectiveness of neutrons at Hiroshima and Nagasaki relative to high-energy photons of 10, over which ERRs were modeled to estimate LDEF.

ⁱERRs were modified by age at exposure and attained age.

^jEstimate based on reported MLE and 95% CI of β/α [0.81 (0.08, 8.6) Gy⁻¹]. Reported β/α is estimate of curvature in dose-response preferred by Ozasa et al. (2012).

^kα_L is ERR per Gy obtained from linear fit to dose-response, and α_LQ (Gy⁻¹) is coefficient of linear term in linear-quadratic fit.

^mEstimate based on reported MLEs of α_L (0.44 Gy⁻¹) and α_LQ (0.22 Gy⁻¹), estimated 95% CIs of α_L [(0.33, 0.56) Gy⁻¹] and α_LQ [(0.036, 0.43) Gy⁻¹] (D. Preston, personal communication, November 6, 2016), and assumption that α_L and α_LQ are uncorrelated.

ⁿRange of shielded kerma free-in-air from photons and neutrons, with estimates of shielded kerma >4 Gy truncated to 4 Gy. Range of neutron-weighted dose to colon, calculated assuming biological effectiveness of neutrons at Hiroshima and Nagasaki relative to high-energy photons of 10, over which ERRs were modeled to estimate LDEF was slightly less than range of shielded kerma (Egbert 2005; RERF 2007).

^oEstimate based on reported MLEs of α (0.36 Gy⁻¹) and β (0.038 Gy⁻²), estimated 95% CIs of α [(0.21, 0.53) Gy⁻¹] and β [(−0.043, 0.123) Gy⁻²] (D. Preston, personal communication, November 6, 2016), and assumption that α and β are negatively correlated (correlation coefficient of −1). Assumed parameter correlation should result in slight overestimate of uncertainty in LDEF.

^pEstimate based on reported MLE and 95% CI of α_L [0.42 (0.32, 0.53) Gy⁻¹)], reported MLE of α_LQ (0.36 Gy⁻¹), estimated 95% CI of α_LQ [(0.21, 0.53) Gy⁻¹] (D. Preston, personal communication, November 6, 2016), and assumption that α_L and α_LQ are uncorrelated.

Two different methods were used to estimate LDEFs in Tables 2 and 3. As described in the Introduction, an LDEF was estimated in most cases as [1 + (β/α)D], where α (Gy⁻¹) and β (Gy⁻²) are coefficients of the linear and quadratic terms, respectively, in a fit to a dose-response over a defined dose range assuming a linear-quadratic model and β/α (Gy⁻¹) is the curvature parameter. In all such cases, LDEFs are estimates at a dose (D) of 1 Gy; i.e., LDEF = 1 + (β/α).^‡‡

In the second method, which was preferred by the BEIR VII committee (NRC 2006) and was also used to derive two LDEFs from an analysis of dose-responses for solid cancer mortality in the LSS cohort by Ozasa et al. (2012), an LDEF was estimated as α_L/α_LQ, where α_L is the risk per Gy obtained from a fit to a dose-response over a defined dose range assuming a linear model and α_LQ (Gy⁻¹) is the coefficient of the linear term in a fit over the same dose range assuming a linear-quadratic model. The ratio α_L/α_LQ also is a measure of the curvature in a dose-response. As indicated by results based on analyses by the BEIR VII committee (NRC 2006) in Table 2 and Ozasa et al. (2012) in Table 3, the two methods give roughly equivalent estimates of LDEF.

The LDEF from Preston et al. (2007) in Table 2 and all LDEFs in Table 3 were based on analyses of dose-responses for all solid cancers, whereas LDEFs from the BEIR VII report (NRC 2006) in Table 2 were based on an analysis of a dose-response for all solid cancers excluding thyroid and nonmelanoma skin cancers but including lymphomas and multiple myeloma. LDEFs from the BEIR VII report in Table 2 are not the same as the recommended LDEF from that report in Table 1, which also took into account dose-responses for cancer induction or life shortening due mainly to fatal cancers in laboratory animals.

In estimating LDEFs and their uncertainties in Tables 2 and 3, we assumed that reported central values of LDEFs, risk coefficients, or ratios of risk coefficients we used to derive an LDEF are maximum likelihood estimates (MLEs). We then estimated 50^th percentiles and 90% CIs of LDEFs by assuming that reported LDEFs, risk coefficients, or ratios of risk coefficients and their CIs can be represented by Weibull distributions with modes at the reported central values.^§§ Weibull distributions were chosen for their flexibility in allowing values <0 and in representing highly skewed distributions. When LDEFs were based on reported MLEs and CIs of β and α or α_L and α_LQ separately, we estimated 50^th percentiles and 90% CIs of LDEFs using Monte Carlo uncertainty propagation techniques with 10,000 iterations of stratified (Latin hypercube) random sampling from the assumed Weibull distributions of each coefficient.

Although all LDEFs in Tables 2 and 3 were based on much the same data in the LSS cohort, there are several potentially important differences, including differences in (1) the composition of the LSS cohort, (2) the response under study (solid cancer incidence or mortality), (3) the period of follow-up of the cohort, (4) the cancer types included in “all solid cancers,” (5) the measure of risk analyzed (ERR or EAR), (6) whether members of the LSS cohort with an estimated shielded kerma from photons and neutrons >4 Gy were included in a dose-response analysis, (7) assumed uncertainties in estimated doses and how they were taken into account, (8) the range of doses over which dose-responses were modeled to estimate an LDEF, (9) assumptions about the dependence of risks on age at exposure, attained age, or time since exposure, and (10) the method used to estimate an LDEF [(1 + β/α) at 1 Gy or α_L/α_LQ].

Estimates of LDEF from an analysis of solid cancer mortality in the LSS cohort by Ozasa et al. (2012) in Table 3 show a pronounced effect of the dose range over which the dose-response was modeled. The curvature in the modeled dose-response was substantially greater at colon doses of 0–2 Gy than at doses up to about 4 Gy, where a linear-quadratic fit was nearly indistinguishable from a linear fit, and uncertainties in estimated LDEFs over the lower dose range were much greater. The reported distribution of β/α at doses of 0–2 Gy also is highly skewed, so that the 50^th percentile of LDEF of 3.2 we estimated by assuming a Weibull distribution is substantially greater than the MLE of 1.8. The possibility of a high LDEF from the analysis of solid cancer mortality at colon doses of 0–2 Gy is not apparent in LDEFs for solid cancer incidence at colon doses of 0–1.5 or 0–2 Gy in Table 2.

The pronounced effect of the dose range over which a dose-response for solid cancer mortality in the LSS cohort was modeled on an estimated LDEF and its uncertainty calls into question whether an LDEF based on a linear-quadratic fit to a dose-response over a restricted dose range should be used to modify an estimated risk per Gy based on a linear fit to the same dose-response over a wider dose range. In analyses by the BEIR VII committee (NRC 2006), Preston et al. (2007), and Ozasa et al. (2012), risks per Gy were estimated from linear fits to dose-responses for all solid cancers at colon doses up to nearly 4 Gy, whereas the curvature in those dose-responses was estimated from linear-quadratic fits over a more restricted dose range (0–1.5 or 0–2 Gy). If LDEFs based on analyses over different dose ranges differ significantly, it is not clear which LDEF should be used to modify a dose-response based on an analysis over the full dose range, especially when linear fits over both dose ranges are nearly the same.

Estimates of DREF

Estimates of DREF we included in our analysis to estimate a DDREF for solid cancers are summarized in Table 4. Each DREF is the ratio of an estimated ERR per Gy in the LSS cohort, assuming a linear dose-response, to an estimated ERR per Gy in workers or members of the public from chronic exposure to low-LET radiation at low dose rates, with the risk in the LSS cohort matched by age and sex. We obtained probability distributions of those ratios using Monte Carlo uncertainty propagation techniques with 10,000 iterations of stratified (Latin hypercube) random sampling and an assumption that each ERR per Gy can be represented by a Weibull distribution with mode at the reported MLE or by a normal distribution. A normal distribution was assumed only when we used an ERR per Gy in the LSS cohort of that form reported by Jacob et al. (2009).

Table 4.

Estimates of 50^th percentiles and 90% CIs of DREF obtained by comparing risks (ERRs) of solid cancers in radiation workers or members of the public from chronic exposure to low-LET radiation at low dose rates with age- and sex-matched risks from acute exposure in LSS cohort.^a

Study cohort (reference)	Cancer outcomes	ERR per Gyb		DREF
		Study cohort	LSS cohort
U.K. workers (Muirhead et al. 2009)	Cancer incidence excluding leukemiasc	0.27 (0.04, 0.51)	0.37 (0.29, 0.46)d	1.4 (0.64, 5.9)
Techa River (Russia) (Davis et al. 2015)	Solid cancer incidence	0.77 (0.13, 1.5)e	0.49 (0.39, 0.60)f	0.63 (0.33, 2.2)
U.K. workers (Muirhead et al. 2009)	Cancer mortality excluding leukemiasc	0.28 (0.02, 0.56)	0.30 (0.21, 0.39)d	1.0 (0.39, 5.0)
French, U.K., and U.S. workers (Richardson et al. 2015)	Solid cancer mortality	0.47 (0.18, 0.79)	0.26 (0.19, 0.35)g	0.55 (0.30, 1.5)
Techa River (Russia) (Schonfeld et al. 2013)	Solid cancer mortality	0.61 (0.04, 1.27)e	0.41 (0.30, 0.53)h	0.64 (0.31, 2.7)

^aDREF is ratio of ERR per Gy in LSS cohort assuming linear dose-response to ERR per Gy in workers or members of the public. ERRs in LSS cohort were estimated using DS02 dosimetry. DREFs were included in our analysis to estimate DDREF for solid cancers induced by low-LET radiation.

^bExcept as noted, estimates are MLEs and 90% CIs and were represented by Weibull distributions with modes at MLEs.

^cLymphomas and multiple myeloma were included.

^dEstimate by Jacob et al. (2009) assuming age at exposure 29, attained age 52, and male fraction 0.9 was represented by normal distribution.

^eUncertainty is 95% CI.

^f50^th percentile and 95% CI we estimated using dose-response model for solid cancer incidence developed by BEIR VII committee (NRC 2006) assuming age at exposure 27, attained age 63, and male fraction 0.43 (Krestinina et al. 2007; Davis et al. 2015).

^g50^th percentile and 90% CI we estimated using dose-response model for solid cancer mortality developed by BEIR VII committee (NRC 2006) assuming age at exposure ≥31, attained age 58, and male fraction 0.9 (Richardson et al. 2015). Richardson et al. (2015) compared ERR per Gy in study cohort with ERR per Gy in males in LSS cohort with MLE and 90% CI of 0.32 (0.07, 0.47) assuming age at exposure 35, as estimated by Cardis et al. (2007) using DS86 dosimetry.

^h50^th percentile and 95% CI we estimated using dose-response model for solid cancer mortality developed by BEIR VII committee (NRC 2006) assuming age at exposure 28, attained age 64, and male fraction 0.42 (Eidemüller et al. 2008; Schonfeld et al. 2013).

From our review of published epidemiologic studies (Trabalka et al. 2017), we judged that five studies of risks of solid cancers from chronic exposure to low-LET radiation at low dose rates were suitable for use in estimating a DREF: studies of solid cancer incidence and mortality in U.K. workers by Muirhead et al. (2009), which were included in analyses by Jacob et al. (2009) summarized in Table 1; the International Nuclear Workers Study (INWORKS) of solid cancer mortality in workers in France, the U.K., and the U.S. by Richardson et al. (2015); and studies of solid cancer mortality and incidence in the Techa River cohort in Russia by Schonfeld et al. (2013) and Davis et al. (2015), respectively. The two studies of cancer mortality in workers are not completely independent when Richardson et al. (2015) included risks in U.K. workers from Muirhead et al. (2009) in the INWORKS analysis. Studies of cancer mortality in workers in France (Metz-Flamant et al. 2013) and the U.S. (Schubauer-Berigan et al. 2015) used by Richardson et al. (2015) are more recent than studies of workers in those countries included in analyses by Jacob et al. (2009). DREFs based on recent studies of solid cancer incidence and mortality in Chernobyl emergency workers (Kashscheev et al. 2015) and Mayak workers (Hunter et al. 2013; Sokolnikov et al. 2015; 2017) are discussed in a later section.

DREFs we derived using recent estimates of risks of solid cancer mortality and incidence in the Techa River cohort (Schonfeld et al. 2013; Davis et al. 2015) were included in our analysis despite concerns about the accuracy of estimated doses, which were based on modeling, and other issues, such as uncertainties in disease ascertainment (Kossenko 2010). Our decision to include those studies was based mainly on the consideration that the Techa River cohort is the only population consisting of members of the public of all ages in which estimated risks of all solid cancers have been reported. Earlier estimates of risks of solid cancer mortality and incidence (Krestinina et al. 2005, 2007) were included in analyses by Jacob et al. (2009).

Except for the risks of solid cancer mortality and incidence in U.K. workers from Muirhead et al. (2009), we did not use estimated risks in workers or members of the public included in analyses by Jacob et al. (2009). Estimated risks in workers in 14 countries [risks from a 15-country study with the entire Canadian cohort excluded (Cardis et al. 2007)] and workers in the U.S. (Boice et al. 2006; Wing and Richardson 2005) and France (Telle-Lamberton et al. 2007) were not statistically significant. An estimated risk in another cohort of workers in the U.S. (Stayner et al. 2007), although marginally significant, had a much greater uncertainty and substantially greater MLE than estimated risks in all other worker cohorts. Estimated risks of solid cancer mortality and incidence in Chernobyl emergency workers (Ivanov et al. 2001, 2004, 2006) were judged to be unreliable by the BEIR VII committee (NRC 2006), due to difficulties with follow-up of disease outcomes and a lack of validation of estimated doses. As noted above, more recent estimates of risks of solid cancer mortality and incidence in the Techa River cohort were used in our analysis.

Exclusion from our analysis of all results from the 15-country study of radiation workers by Cardis et al. (2007) was based mainly on two considerations. First, we judged that the entire Canadian cohort should be excluded from the 15-country study because of concerns about the reliability of estimated doses to Atomic Energy of Canada Limited workers who were first monitored during the period 1956–1964 (Zablotska et al. 2014) and the significant impact of the unusually high risk to those workers on results from the 15-country study (Cardis et al. 2007). Then, we excluded results from a 14-country study from our analysis because the estimated risk was not statistically significant, as noted above, and in none of the 14 countries was the estimated risk to workers statistically significant (Cardis et al. 2007).

There are several potentially important complications in estimating a DREF by comparing risks in populations that received chronic exposures at low dose rates with risks from acute exposure in the LSS cohort. Since risks of solid cancers generally depend on age at exposure and attained age, such comparisons require assumptions about an age at exposure and attained age in the LSS cohort that are equivalent to the frequency distributions of ages at exposure and attained ages in the other populations. Such comparisons also assume implicitly that: (1) differences in the relative frequencies of specific solid cancers in the LSS cohort and other populations do not have a significant effect on comparisons of risks of all solid cancers combined; (2) external exposures to neutrons, nonuniform exposures of the whole body from intakes of radionuclides, and nonuniform exposures from uses of external radiation or internally deposited radioactive materials in medicine in other populations are either unimportant or properly accounted for in a dose-response analysis; and (3) uncertainties in transferring estimated risks of all solid cancers in the LSS cohort to other populations, which arise from differences in baseline rates of those cancers in populations of different nationalities (Land et al. 2003; NRC 2006; NCRP 2012; UNSCEAR 2014), are unimportant. DREFs in Table 4 do not account for possible biases and uncertainties in those assumptions. Several differences in various analyses of data in the LSS cohort discussed in the previous section that can lead to differences in estimates of LDEF also can affect estimates of DREF.

DEVELOPMENT OF PROBABILITY DISTRIBUTION OF DDREF

Procedures and assumptions

We developed a probability distribution of DDREF for solid cancers induced by low-LET radiation by combining probability distributions of LDEFs and DREFs in Tables 2–4 using assumptions about the relative weight that should be assigned to each estimate to represent its relevance to estimation of a DDREF. Our judgments about relevance were based on evaluations of the overall quality of the underlying studies, rather than an accounting of reported statistical uncertainties in estimated LDEFs and DREFs only.

Our procedure for combining probability distributions of LDEFs and DREFs for solid cancer incidence and mortality and assumptions about relative weights we assigned to those distributions are described as follows.

Step 1 of Procedure:

• LDEFs for solid cancer incidence in Table 2 were combined by assigning 25% weight to each of the two distributions from the BEIR VII report (NRC 2006) and 50% weight to the distribution from Preston et al. (2007). These assumptions give equal weight to LDEFs from the BEIR VII report (NRC 2006) and Preston et al. (2007).

The weights assigned to the three estimates of LDEF for solid cancer incidence were based on judgments that (1) the two estimates from the BEIR VII report (NRC 2006) are equally relevant to estimation of an LDEF and (2) estimates of LDEF based on analyses by the two expert groups [BEIR VII committee and Radiation Effects Research Foundation (RERF)] are equally relevant to estimation of a DDREF.

• LDEFs for solid cancer mortality in Table 3 were combined by assigning 25% weight to each of the two distributions from Little et al. (2008), 15% weight to each of the two distributions from Ozasa et al. (2012) at colon doses of 0–2 Gy, and 10% weight to each of the two distributions from Ozasa et al. (2012) at a shielded kerma of 0–4 Gy. These assumptions give equal weight to LDEFs from Little et al. (2008) and Ozasa et al. (2012).

The weights assigned to the six estimates of LDEF for solid cancer mortality were based on the following judgments: (1) the two estimates from Little et al. (2008), which were obtained from a study for UNSCEAR, are equally relevant to estimation of an LDEF; (2) the two estimates from Ozasa et al. (2012) based on an analysis at colon doses of 0–2 Gy are equally relevant, as are the two estimates from that study based on an analysis over the full dose range corresponding to a shielded kerma of 0–4 Gy; (3) estimates from Ozasa et al. (2012) based on an analysis at colon doses of 0–2 Gy should be assigned substantially greater weight than estimates from that study based on an analysis over the full dose range; and (4) estimates of LDEF based on analyses by the two expert groups (UNSCEAR and RERF) are equally relevant to estimation of a DDREF. A judgment that estimates of LDEF from Ozasa et al. (2012) based on an analysis at colon doses of 0–2 Gy should be assigned twice the weight as estimates based on an analysis over the full dose range was based on two considerations: (1) Ozasa et al. (2012) preferred an estimate over a limited dose range, as did the BEIR VII committee (NRC 2006) and Preston et al. (2007), and (2) an estimate over the full dose range should still be taken into account to obtain a probability distribution of DDREF that represents the state of knowledge. The issue of selecting an appropriate dose range for estimation of an LDEF is discussed previously.

• DREFs for solid cancer incidence in Table 4 were combined by assigning 80% weight to the distribution based on an estimated risk to U.K. radiation workers from Muirhead et al. (2009) and 20% weight to the distribution based on an estimated risk in the Techa River cohort from Davis et al. (2015).

The low weight assigned to the DREF based on an estimated risk in the Techa River cohort reflects our concerns noted previously about uncertainties in estimated doses and other issues with estimated risks in that cohort.

• DREFs for solid cancer mortality in Table 4 were combined by assigning 40% weight to the distribution based on an estimated risk to U.K. radiation workers from Muirhead et al. (2009), 40% weight to the distribution based on an estimated risk to radiation workers in France, the U.K., and the U.S. (INWORKS) from Richardson et al. (2015), and 20% weight to the distribution based on an estimated risk in the Techa River cohort from Schonfeld et al. (2013).

The rationale for the low weight assigned to the DREF based on an estimated risk in the Techa River cohort is described above. We then judged that estimates of DREF based on analyses by Muirhead et al. (2009) and Richardson et al. (2015) are equally relevant to estimation of a DDREF. As acknowledged previously, those two analyses are not completely independent when risks in U.K. workers were included in the INWORKS analysis. However, we judged that a DREF based on the estimated risk to U.K. workers could be included in our analysis when risks to workers in France and the U.S. that were included in the INWORKS analysis (Metz-Flamant et al. 2013; Schubauer-Berigan et al. 2015) were not statistically significant, nor was the risk from the INWORKS analysis statistically significant when U.K. workers were excluded (Richardson et al. 2015). If the study of U.K. workers were assigned zero weight and the DREF based on the INWORKS analysis were assigned a weight of 80%, DREFs in Table 4 indicate that the result would be a decrease in the median DREF for solid cancer mortality and a narrowing of the 90% CI, especially at the upper bound.

The result of the procedures in Step 1 is two probability distributions of LDEF, one for solid cancer incidence and the other for solid cancer mortality, and two such distributions of DREF. The four probability distributions are summarized in Table 5.

Table 5.

Summary of probability distributions of LDEF, DREF, and DDREF for all solid cancers calculated using stepwise procedures for combining probability distributions of LDEF and DREF from epidemiological studies to obtain preferred DDREF distribution^a

Step in procedure	Type of combined estimate	Percentile of probability distribution
		2.5th	5th	50th	95th	97.5th
Step 1	LDEF for cancer incidence (n = 3)b	0.89	0.96	1.4	2.2	2.4
	LDEF for cancer mortality (n = 6)	0.92	0.97	1.5	5.2	7.0
	DREF for cancer incidence (n = 2)	0.31	0.41	1.2	5.2	8.8
	DREF for cancer mortality (n = 3)	0.26	0.31	0.72	3.1	5.4
Step 2	LDEF for cancer incidence and mortality combined, with relative weights of 2:1 assigned to incidence- and mortality-based distributions	0.90	0.96	1.4	3.0	4.5
	DREF for cancer incidence and mortality combined, with relative weights of 2:1 assigned to incidence- and mortality-based distributions	0.28	0.36	1.0	4.7	7.7
Step 3	DDREF obtained by combining LDEF and DREF distributions from Step 2, with equal weight assigned to each distribution	0.36	0.44	1.3	3.8	6.1
Step 4	Preferred DDREF distribution obtained by truncating distribution from Step 3 by removing values <0.2 and >20	0.39	0.47	1.3	3.6	5.6

^aProbability distributions of LDEF and DREF from epidemiologic studies are summarized in Tables 2–4.

^bEntries in parentheses in Step 1 are number of distributions of LDEF or DREF combined in each calculation.

Our approach to combining probability distributions of LDEF or DREF in Tables 2–4 based on their assigned weights represents an application of multi-model inference (model averaging) described by UNSCEAR (2014).^*** To illustrate the approach to model averaging, the six distributions of LDEF for solid cancer mortality in Table 3 were combined in the following way using Monte Carlo uncertainty propagation techniques with 10,000 iterations of stratified (Latin hypercube) random sampling. Of the 10,000 random samples, 2,500 were obtained from the first distribution and 2,500 from the second distribution based on an analysis by Little et al. (2008), 1,500 were obtained from the first distribution and 1,500 from the second distribution based on an analysis by Ozasa et al. (2012) at colon doses of 0–2 Gy, and 1,000 were obtained from the first distribution and 1,000 from the second distribution based on an analysis by Ozasa et al. (2012) at a shielded kerma of 0–4 Gy. In model averaging, only one probability distribution of an LDEF was sampled at random in each iteration. This approach to sampling was used in all steps in our procedure that involved combining multiple probability distributions.

We did not combine probability distributions of LDEF or DREF by weighting each estimate by the reciprocal of its variance, as in analyses by Jacob et al. (2009) summarized in Table 1. Weighting each estimate by the reciprocal of its variance is most appropriate when all LDEFs or DREFs are statistically independent estimates of the same quantity and are free from bias (systematic error). However, the condition of statistical independence is not met when all LDEFs and DREFs included in our analysis were estimated using much the same data in the LSS cohort. Furthermore, the various estimates of risks in workers or members of the public we used to estimate DREFs do not represent repeated measurements of the same quantity, even when the health effect of concern (e.g., solid cancer incidence) is the same, because characteristics of the study populations can differ in potentially important ways including, for example, their ethnicity, age distributions, time course of exposures, general health status, smoking habits, and baseline rates of specific cancers. Such differences can introduce biases in analyses of dose-responses that are not taken into account when estimated DREFs from different studies are combined by assuming that their uncertainties are due only to reported statistical (random) errors in fits to data on dose-responses using assumed models. Combining estimates of LDEF based only on reported random errors in fits to dose-responses in the LSS cohort also assumes that those LDEFs are repeated measurements of the same quantity and are free from bias. However, these conditions are unlikely to be met when different analysts use different formulations of dose-response models and LDEFs for solid cancer incidence and mortality are not estimates of the same quantity. Our approach to weighting takes these additional concerns into account.

Step 2 of Procedure:

• The two LDEFs obtained in Step 1 were combined by assigning relative weights of 2:1 to the incidence- and mortality-based estimates. The same relative weights were assigned in combining the two DREFs obtained in Step 1.

Our judgment that substantially greater weight should be assigned to LDEFs and DREFs for solid cancer incidence was based on several considerations: (1) accuracy of disease ascertainment is a greater concern in estimating risks of cancer mortality; (2) cancer mortality, but not incidence, can depend on the level and intensity of medical care; (3) estimated risks of mortality are less reliable for cancers that usually are not fatal (e.g., thyroid cancer); (4) risks of cancer incidence, but not mortality, are used in the compensation program for U.S. nuclear energy workers (U.S. DHHS 2002); and (5) use of LDEFs and DREFs for cancer incidence is compatible with risk modeling in IREP (Land et al. 2003; Kocher et al. 2008).

The result of the procedures in Step 2 is a single distribution of LDEF and a single distribution of DREF, with each distribution representing data for solid cancer incidence and mortality combined (see Table 5).

Step 3 of Procedure:

• A probability distribution of DDREF for solid cancers was obtained by assigning equal weight to the probability distributions of LDEF and DREF obtained in Step 2.

As noted previously, there are complications in estimating a DREF that do not affect estimates of LDEF. On this basis alone, LDEFs might be assigned greater weight than DREFs in estimating a DDREF. However, there also are concerns that use of linear-quadratic models to extrapolate observed risks at higher acute doses in the LSS cohort to lower doses where risks are not observable may not be reliable (Trabalka and Kocher 2007; Leenhouts and Chadwick 2011; NCRP 2012). For example, dose-responses for solid cancer mortality based on DS02 dosimetry (Preston et al. 2004; Ozasa et al. 2012) suggest an increase in the risk per Gy at doses <0.3 Gy (LDEF <1) that is not apparent in dose-responses for solid cancer incidence (NRC 2006; Preston et al. 2007), although an increase in the risk per Gy for solid cancer mortality at low doses is not statistically significant. In addition, our intent was to develop a probability distribution of DDREF that would apply to any risk assessment scenario. Based on such considerations, we concluded that there is little justification for assigning greater weight to LDEFs or DREFs in developing a probability distribution of DDREF for solid cancers. The probability distribution of DDREF obtained in Step 3 is summarized in Table 5.

Step 4 of Procedure:

• Our subjective state-of-knowledge probability distribution of DDREF for solid cancers was obtained by truncating the probability distribution of DDREF obtained in Step 3 by removing all values <0.2 or >20.

Truncation of the probability distribution obtained in Step 3 was based mainly on a judgment that the weight of evidence from the distributions of LDEFs and DREFs in Tables 2–4 is that a DDREF for all solid cancers outside the range of 0.2–20 is not credible. This judgment was supported by uncertainties in LDEFs and DREFs for specific solid cancers in humans and data in animals (Trabalka et al. 2017). Truncation removed about 1.3% of the values in the tails of the probability distribution obtained in Step 3. Most of the values removed were <0.2, including values <0 that resulted from negative values in the lower tails of assumed Weibull distributions of uncertain risk coefficients or ratios of risk coefficients we used as inputs to our procedures.

Summary of probability distribution of DDREF for solid cancers

The probability distribution of DDREF for solid cancers we developed using the procedures and assumptions described above is summarized in Tables 5 and 6. A lognormal distribution that approximates our distribution also is summarized in Table 6. That distribution should be convenient for use in most cancer risk assessments that account for uncertainty.

Table 6.

Summary of subjective state-of-knowledge probability distribution of DDREF for solid cancers induced by low-LET radiation developed in this study and approximate lognormal probability distribution.

Distribution	Percentiles					Harmonic meana
	2.5th	5th	50th	95th	97.5th
This study	0.39	0.47	1.3	3.6	5.6	1.1
Approximate lognormal distribution (GM = 1.31, GSD = 1.80)b	0.41	0.50	1.3	3.4	4.2	1.1

^aHarmonic mean is important measure of central tendency when arithmetic mean of uncertain estimate of risk of solid cancers at low acute doses or low dose rates of low-LET radiation is proportional to reciprocal of harmonic mean of uncertain DDREF.

^bGM = geometric mean; GSD = geometric standard deviation.

In addition to selected percentiles, Table 6 gives the harmonic means of the two probability distributions of DDREF.^††† The importance of the harmonic mean as a measure of central tendency is a consequence of DDREF appearing as a divisor in an equation to estimate cancer risks per Gy at low acute doses or low dose rates, R_L, on the basis of estimated risks per Gy at higher acute doses, R_H; i.e., R_L = R_H/DDREF. The arithmetic mean (average) of an uncertain R_L, which is an important and commonly used measure of central tendency, is proportional to the reciprocal of the harmonic mean of an uncertain DDREF, not the reciprocal of its arithmetic mean. Inappropriate use of the arithmetic mean of DDREF would result in an underestimate of the arithmetic mean of R_L.

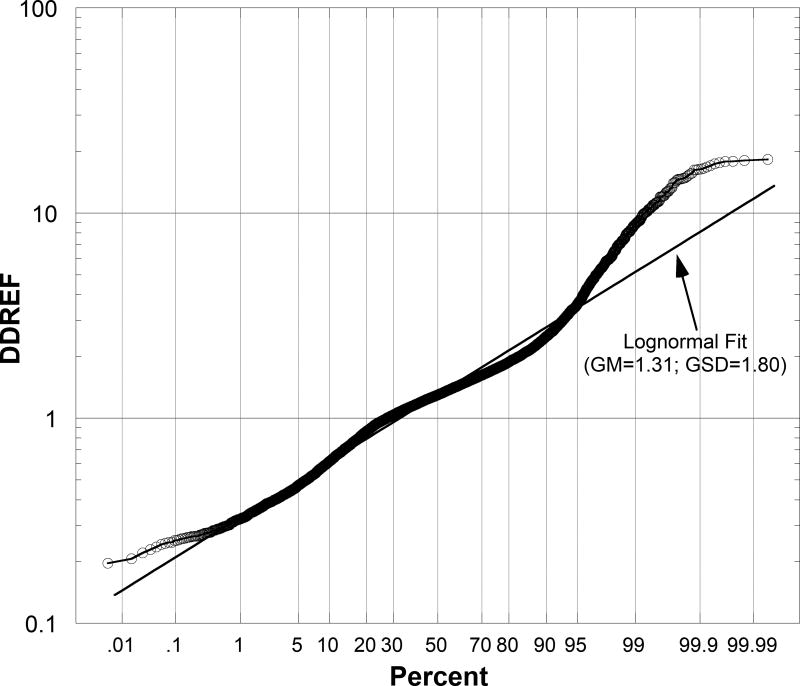
The probability distribution of DDREF we developed and the approximate lognormal distribution are shown in Figure 1 as log-probability plots, in which lognormal distributions lie on a straight line (Chambers et al. 1983). Each circle is a DDREF that resulted from a single iteration of random sampling using the procedures and assumptions described previously. The approximate lognormal distribution gives a good fit to our distribution between the 0.2^nd and 95^th percentiles. Outside that range, the lognormal distribution underestimates DDREFs in our distribution by about 10% or more. An underestimation of DDREF results in an overestimation of cancer risks at low acute doses or low dose rates of low-LET radiation. However, this could be a concern only at the lowest values in probability distributions of estimated risks, which are of lesser importance in most applications of results of cancer risk assessments.

Fig. 1.

Log-probability plots of probability distribution of DDREF for solid cancers induced by low-LET radiation developed in this study (circles) and approximate lognormal distribution with indicated geometric mean (GM) and geometric standard deviation (GSD).

Our probability distribution of DDREF has two important implications for cancer risk assessments. First, as indicated in Figure 1, our distribution gives a substantial weight of about 27% to values <1, i.e., an assumption that the risk of solid cancers per Gy at low acute doses or low dose rates of low-LET radiation is greater than the risk per Gy at higher acute doses in the LSS cohort. This result is a consequence of including DREFs in Table 4 in our analysis, since most values in the distributions of LDEFs in Tables 2 and 3 are >1. Second, the harmonic mean of our distribution in Table 6 implies that the mean (average) of an uncertain estimate of the risk of a solid cancer per Gy at low acute doses or low dose rates of low-LET radiation is only about 10% less than the mean risk per Gy at higher acute doses in the LSS cohort.

The probability distribution of DDREF for solid cancers developed in this study should be suitable for use in estimating risks of specific solid cancers from exposure to low-LET radiation whenever linear dose-responses from acute and chronic exposure are assumed. Our DDREF should not be used to estimate risks of specific solid cancers if nonlinear dose-responses from acute exposure in the LSS cohort are assumed.^‡‡‡

COMPARISONS WITH PRIOR ESTIMATES OF DDREF

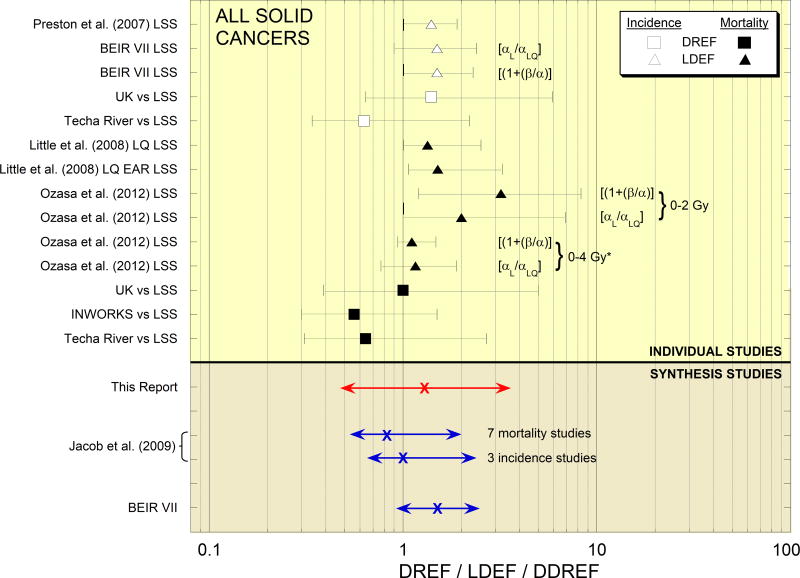
Probability distributions of LDEFs and DREFs included in our analysis, as given in Tables 2–4, are shown in the top portion of Figure 2. The bottom portion compares our probability distribution of DDREF for solid cancers with two distributions of DDREF based on analyses by Jacob et al. (2009) and the distribution of DDREF for solid cancer incidence developed by the BEIR VII committee (NRC 2006), as summarized in Table 1.

Fig. 2.

Estimates of 50^th percentiles and 90% CIs of DREFs or LDEFs for solid cancer incidence or mortality used in this study to develop probability distribution of DDREF for solid cancers induced by low-LET radiation (top) and comparison of our distribution with two distributions of DDREF based on analyses by Jacob et al. (2009) and distribution of DDREF developed by BEIR VII committee (NRC 2006). Distributions from Jacob et al. (2009) are DREFs, and distribution from BEIR VII report (NRC 2006) essentially is an LDEF ^* Range of shielded kerma free-in-air from photons and neutrons (neutron-weighted doses to colon otherwise).

Compared with the probability distribution based on an analysis of seven studies of cancer mortality by Jacob et al. (2009), which has a 50^th percentile and 90% CI of 0.83 (0.53, 1.96) and represents the main result from that study, the lower bound of the 90% CI of our distribution is nearly the same, but our distribution is broader and gives substantially greater weight to values >1. The main reason for these differences is that the analysis by Jacob et al. (2009) considered estimates of DREF only; LDEFs, which tend to be greater than DREFs and give little weight to values <1, were not considered. The DDREF based on three studies of cancer incidence by Jacob et al. (2009), which is similar to the main result from that study, also gives substantially less weight to values >1 than our distribution.

Compared with the probability distribution developed by the BEIR VII committee (NRC 2006), which has a 50^th percentile and 90% CI of 1.5 (0.9, 2.5) and essentially represents an LDEF, our distribution is broader and gives greater weight to values <1. There are two main reasons for these differences: (1) our distribution also takes into account probability distributions of LDEF for solid cancer mortality, some of which give substantial weight to values >3 that are not evident in LDEFs for solid cancer incidence (NRC 2006; Preston et al. 2007); and (2) the BEIR VII committee did not consider DREFs, which tend to be lower than LDEFs and give substantially greater weight to values <1.^§§§

The probability distribution of DDREF developed in this study is unique in that it was based on estimates of LDEF and DREF for solid cancer incidence and mortality. All other analyses to estimate a DDREF prior to this study were based mainly or exclusively on estimates of LDEF or DREF only and, except for analyses by Jacob et al. (2009), data for solid cancer incidence or mortality only. We think that estimates of LDEF and DREF for both endpoints must be taken into account if a probability distribution of DDREF for solid cancers that represents the state of knowledge is to be obtained.

CONSIDERATION OF OTHER RECENT STUDIES

Studies of risks to workers

Recent studies of solid cancer incidence and mortality in Chernobyl emergency workers (Kashcheev et al. 2015) and Mayak workers (Hunter et al. 2013; Sokolnikov et al. 2015; 2017) were not included in our analysis to estimate DREFs. Those studies are discussed below.

Chernobyl emergency workers

Kashcheev et al. (2015) estimated ERRs per Gy in Chernobyl emergency workers of 0.47 [95% CI: (0.03, 0.96)] for solid cancer incidence and 0.58 [95% CI: (0.002, 1.25)] for solid cancer mortality. Kashcheev et al. (2015) estimated comparable ERRs per Gy in the LSS cohort of 0.47 for solid cancer incidence (Preston et al. 2007) and 0.33 for solid cancer mortality (Ozasa et al. 2012). These estimates suggest DREFs of about 1.0 for solid cancer incidence and 0.5–0.6 for solid cancer mortality, both of which are lower than the corresponding 50^th percentiles we obtained in Step 1 of our procedure (see Table 5).

We have two main concerns about the analysis of risks in Chernobyl emergency workers by Kashcheev et al. (2015): (1) the period of follow-up of this cohort was short and most members were still alive; and (2) analyses of dose-responses did not take into account other known risk factors, such as smoking, alcohol consumption, and occupational status.

Mayak workers

Recent analyses of risks of solid cancers in Mayak workers excluded cancers of the lung, liver, and bone, which are important sites of deposition of inhaled plutonium in exposures of many workers. An analysis of the risk of solid cancer incidence by Hunter et al. (2013) found no significant association with external photon exposure when the estimated risk was adjusted for plutonium exposure. We consider that this analysis is inconclusive, given the uncertainty in accounting for exposures to plutonium.

Sokolnikov et al. (2015; 2017) estimate two ERRs per Gy for solid cancer mortality (excluding lung, liver, and bone) associated with external photon exposure in Mayak workers: 0.12 [95% CI: (0.03, 0.21)] in the entire cohort when risks were adjusted for plutonium exposure and monitoring status, and 0.20 [95% CI: (−0.0002, 0.46)] when workers at plutonium and radiochemical plants were excluded. Sokolnikov et al. (2015) estimated a comparable ERR per Gy in the LSS cohort of 0.35 [90% CI (0.19, 0.55)] (Preston et al. 2003). These estimates give DREFs of 3.0 [90% CI: (1.3, 8.7)] based on data in the entire cohort and 1.6 [90% CI: (0.56, 8.1)] when plutonium and radiochemical plant workers were excluded. If we assume that the latter estimate is more reliable when exposures to plutonium presumably were unimportant, that DREF tends to be higher and more uncertain than the DREF for solid cancer mortality we obtained in Step 1 of our procedure (see Table 5).

Before including an estimated risk of solid cancer mortality in Mayak workers in an analysis to estimate DREFs, we believe it would be prudent to await results of a revised cancer risk assessment based on the recently updated dosimetry system (MWDS-2013). The new dosimetry system takes into account shared and unshared uncertainties in model parameters (Birchall et al. 2017), in addition to revised estimates of dose.

Studies of risks in LSS cohort

After completion of our analysis, new analyses of risks of solid cancer incidence and mortality in the LSS cohort were published (Grant et al. 2017; Cullings et al. 2017). Both analyses were based on a revised dosimetry system (DS02R1), and the analysis of cancer incidence also included a longer period of follow-up of the cohort.

Estimate of LDEF for solid cancer incidence

Grant et al. (2017) estimated a common curvature (β/α) in the dose-response for solid cancer incidence in males and females over the full dose range corresponding to a shielded kerma of 0–4 Gy that gives an LDEF at 1 Gy of 1.22 [95% CI: (1.01, 1.60)]. Compared with the estimate from RERF by Preston et al. (2007) based on DS02 dosimetry at colon doses of 0–2 Gy in Table 2, the main effect of the new analysis is a slight reduction in the upper bound of a CI. However, the two estimates are not directly comparable since they were not based on analyses of dose-responses over the same dose range.

Estimates of LDEF for solid cancer mortality

The analysis of solid cancer mortality in the LSS cohort by Cullings et al. (2017) updated the analysis by Ozasa et al. (2012) based on a revision of the dosimetry system only. The following sex-averaged estimates of 50^th percentiles and 90% CIs of LDEFs at 1 Gy for solid cancer mortality from the analysis by Cullings et al. (2017) based on DS02R1 dosimetry can be compared with the corresponding estimates from the analysis by Ozasa et al. (2012) based on DS02 dosimetry in Table 3:

$$\begin{gathered} \text{Colon doses of }0–2\text{ Gy}- \\ [1+(\mathrm{\beta }/\mathrm{\alpha })]5.1(1.4,16) \\ {\mathrm{\alpha }}_{\mathrm{L}}/{\mathrm{\alpha }}_{\text{LQ}}2.2(1.1,8.4) \end{gathered}$$

$$\begin{gathered} \text{Full dose range }(\text{shielded kerma of }0-4\text{ Gy})- \\ [1+(\mathrm{\beta }/\mathrm{\alpha })]1.19(0.95,1.54) \\ {\mathrm{\alpha }}_{\mathrm{L}}/{\mathrm{\alpha }}_{\text{LQ}}1.21(0.79,1.99) \end{gathered}$$

The two LDEFs over the full dose range are nearly the same as the estimates from Ozasa et al. (2012). At colon doses of 0–2 Gy, the main change in LDEF calculated as α_L/α_LQ is an increase in the upper bound of the CI. However, when LDEF is calculated as [1 + (β/α)], which gave the LDEF preferred by Ozasa et al. (2012), the 50% percentile and upper bound of the CI both increase substantially. The analysis based on DS02R1 dosimetry again shows a pronounced effect of the dose range over which the dose-response is modeled on an estimated LDEF.

Dependence of LDEFs on sex

Grant et al. (2017) and Cullings et al. (2017) also analyzed the dependence of dose-responses for solid cancer on sex. For solid cancer incidence, Grant et al. (2017) reported a significant difference in the shapes of the dose-responses in males and females over the full dose range based on DS02R1 dosimetry: a curvature of 1.3 per Gy (LDEF at 1 Gy of 2.3), indicative of a significant nonlinearity, in males compared with 0.084 per Gy (LDEF at 1 Gy of 1.08), consistent with linearity, in females.

For solid cancer mortality, Cullings et al. (2017) reported estimates of the curvature in dose-responses over the full dose range based on DS02R1 dosimetry of 0.12 (LDEF at 1 Gy of 1.12) in males and 0.13 (LDEF at 1 Gy of 1.13). In contrast to the finding by Grant et al. (2017) for solid cancer incidence, no dependence on sex was found in the dose-responses for solid cancer mortality, and both dose-responses are consistent with linearity.

Cullings et al (2017) also analyzed the sex-dependence of dose-responses for solid cancer mortality at colon doses of 0–2 Gy based on DS02R1 dosimetry. In males, the estimated curvature in the dose-response of 1.14 per Gy (LDEF at 1 Gy of 2.1) was not statistically significant, but the estimated curvature of 1.01 per Gy (LDEF at 1 Gy of 2.0) in females was statistically significant, i.e., indicative of nonlinearity. When compared with estimates over the full dose range given above, the LDEFs in males and females at colon doses of 0–2 Gy tend to be higher, as in the analyses of sex-averaged LDEFs for solid cancer mortality.

Given the inconsistencies in estimates of LDEF described above, we believe it is premature to attempt to account for possible sex-dependencies of LDEFs for solid cancer incidence or mortality in estimating a DDREF. The statistically significant sex-dependence in dose-responses for solid cancer incidence reported by Grant et al. (2017) calls for further investigation. Analyses of possible differences in dose-responses for specific solid cancers in males and females in the LSS cohort are potentially important in resolving this matter.

Recent analysis to estimate DREFs

In a recent analysis, Shore et al. (2017) used the same approach as in an analysis by Jacob et al. (2009) described previously to estimate ratios of risks from chronic exposure of workers or members of the public at low doses to age- and sex-matched risks from acute exposure in the LSS cohort, referred to as risk ratios. Reciprocals of these risk ratios are DREFs. Estimated risk ratios from studies of different cohorts of workers or members of the public were combined by weighting each estimate by the reciprocal of its variance. Shore et al. (2017) included 19 studies of solid cancer mortality and three studies of solid cancer incidence in their analysis; estimated risks in the LSS cohort were obtained from Ozasa et al. (2012) and Preston et al. (2007).

Analyses by Shore et al. (2017) give the following six estimates of DREFs and their 95% CIs depending on the studies of chronic exposures that were taken into account:

• [1]2.8 (1.8, 7.1), all mortality studies;
• [2]3.0 (1.9, 7.7), all mortality and incidence studies;
• [3]0.89 (0.54, 2.5), all mortality studies except Mayak workers;
• [4]1.9 (1.0, 11), all mortality and incidence studies except mortality in Mayak workers;
• [5]0.94 (0.55, 3.3), 16 mortality studies with mean dose <100 mGy;
• [6]1.7 (0.94, 10), 16 mortality and two incidence studies with mean dose <100 mGy.

Exclusion of the study of mortality in Mayak workers in two cases was based on the finding that the first two estimates of DREF given above were determined mainly by the DREF based on that study. For example, the DREF from the study of Mayak workers contributed 91% of the total weight to the estimate based on all mortality studies, due to its much lower uncertainty (variance) compared with the variances of all other DREFs. The study of Mayak workers was excluded from the last two estimates, since the mean dose was >100 mGy.

If the study of Mayak workers is included, the two estimates of DREF by Shore et al. (2017) clearly tend to be substantially greater than one. This result differs from the previous estimate based on seven mortality studies by Jacob et al. (2009) in Table 1 and our estimates of DREF for solid cancer mortality obtained in Step 1 of our procedure and solid cancer mortality and incidence obtained in Step 2 (see Table 5). If the study of Mayak workers is excluded, as in our analysis, the four remaining estimates of DREF by Shore et al. (2017) still tend to be greater than the corresponding estimates in Table 5, but the differences are smaller. The third and fourth estimates by Shore et al. (2017) are the most comparable to our estimates in Table 5.

SUMMARY AND CONCLUSIONS

From an evaluation of estimated risks of incidence or mortality from all solid cancers or all cancers excluding leukemias from acute exposure in the LSS cohort and risks of those cancers in radiation workers or members of the public from chronic exposure to low-LET radiation at low dose rates, we developed a subjective probability distribution that is intended to represent the state of knowledge of a DDREF for solid cancers induced by low-LET radiation. This DDREF distribution can be used in estimating risks of solid cancers at low acute doses or low dose rates of low-LET radiation and their uncertainty whenever linear dose-responses from acute and chronic exposure are assumed.

A DDREF represents two distinct concepts, referred to as a low-dose effectiveness factor (LDEF) and a dose-rate effectiveness factor (DREF). LDEFs were estimated from analyses of the curvature in dose-responses for solid cancer incidence or mortality in the LSS cohort, and DREFs were estimated by comparing risks of solid cancer incidence or mortality in workers or members of the public at low dose rates with risks in the LSS cohort. Probability distributions of uncertain LDEFs or DREFs for solid cancer incidence or mortality were combined using judgments about the relative weight that should be assigned to each estimate to represent its relevance to estimation of a DDREF. Estimates of LDEF or DREF for solid cancer incidence were assigned twice the weight as estimates for solid cancer mortality, and combined estimates of LDEF and DREF for either outcome were weighted equally.

The probability distribution of DDREF for solid cancers developed in this study has a 50^th percentile and 90% subjective CI of 1.3 (0.47, 3.6). This distribution gives a weight of about 27% to an assumption that the risk of a solid cancer per Gy at low acute doses or low dose rates of low-LET radiation is greater than the risk per Gy at higher acute doses in the LSS cohort (DDREF <1). Since probability distributions of LDEF generally give little weight to values <1, the substantial weight given to DDREFs <1 in our distribution is a consequence of including estimates of DREF. Our probability distribution of DDREF also gives a weight of about 17% to values >2. The harmonic mean of our distribution is 1.1, which implies that the mean risk per Gy at low acute doses or low dose rates of low-LET radiation is only about 10% less than the mean risk per Gy at higher acute doses.

Our analysis is unique in two respects. First, a probability distribution to represent uncertainty in a DDREF for solid cancers induced by low-LET radiation was developed from estimates of LDEF and DREF for solid cancer incidence and mortality and their uncertainties: four data sets in all.

Second, we assigned subjective weights to estimates of LDEF or DREF to be combined based on judgments about their relevance to estimation of a DDREF, rather than a reliance on their reported statistical uncertainties only. Our judgments about relevance were based on evaluations of the overall quality of the underlying studies. If we had weighted each estimate by the reciprocal of it variance, as in analyses by Jacob et al. (2009) and Shore et al. (2017), the uncertainty in an estimated DDREF would have been determined mainly by estimates of LDEF and DREF with the smallest reported uncertainties, and the uncertainty in DDREF would have been substantially smaller than the uncertainty we estimated. Our concern about the approach to weighting used by Jacob et al. (2009) and Shore et al. (2017) is the underlying assumption that each estimate of LDEF and DREF to be combined represents a direct measurement of the same quantity and is free from systematic errors (i.e., each estimate is directly relevant, without bias), conditions which generally are not met.

By including estimates of LDEF and DREF for solid cancer incidence and mortality and by combining those estimates based on judgments about their relevance to estimation of a DDREF, our intent was to develop a probability distribution of DDREF that is an unbiased representation of the state of knowledge and is suitable for use in assessments of risks of solid cancers from exposure to low-LET radiation that account for uncertainty. Our approach to meeting this intent was based on the beliefs that (1) LDEFs and DREFs for solid cancer incidence and mortality must be taken into account and (2) combining different estimates based only on their statistical uncertainties from fits to dose-responses using assumed models leads to probability distributions of DDREF that are overly confident representations of the present state of knowledge.

We also discussed DREFs based on estimates of risks in workers that were not taken into account in our analysis, estimates of LDEFs based on the most recent analyses of dose-responses for solid cancer incidence and mortality in the LSS cohort, and a recent analysis to estimate DREFs. Those studies along with ours illustrate that all analyses to estimate a DDREF are representations of data available at a particular time and are subject to change as new data are developed. All analyses, including evaluations of uncertainty, also are based to some extent on the use of judgment. Additional studies of risks to workers and a possible sex-dependence of LDEFs should be especially important in revising estimates of a DDREF.

APPENDIX

DEFINING A LOW ACUTE DOSE AND LOW DOSE RATE

In using a DDREF to estimate risks of solid cancers from exposure to low-LET radiation, it is necessary to define a low acute dose and a low dose rate, i.e., an acute dose or a dose rate from chronic exposure below which a DDREF should be applied. As part of this study, we evaluated data to define upper bounds of a low acute dose and a low dose rate.

Definition of low acute dose

An upper bound of a low acute dose of low-LET radiation can be defined as the lowest dose at which significant deviations from linearity in a modeled dose-response are observed (NCRP 1980). For example, UNSCEAR (1993) defined an upper bound of a low acute dose as the dose at which the quadratic term in a modeled linear-quadratic dose-response for mortality from all cancers excluding leukemias in the LSS cohort contributed about 20% of the estimated risk, i.e., a dose of about 0.2(β/α)⁻¹ Gy, where β/α (Gy⁻¹) is the curvature parameter. Using this definition, UNSCEAR (1993) estimated an upper bound of a low acute dose of 200 mGy. More recent recommendations by expert groups include 10 mGy (NCRP 2001), 100–200 mGy (ICRP 2005), and 100 mGy (NRC 2006; ICRP 2007; UNSCEAR 2008).

In IREP, an upper bound of a low acute dose is considered to be uncertain and is represented by a loguniform probability distribution over the range of 30–200 mGy (Land et al. 2003; Kocher et al. 2008). The approach in IREP also is unique in assuming that a DDREF is phased in gradually as an acute dose decreases below an uncertain value in that range (Land et al. 2003; Kocher et al. 2008).

We estimated an upper bound of a low acute dose of low-LET radiation from an evaluation of dose-responses for solid cancer incidence and mortality in the LSS cohort, results from other epidemiologic studies, a variety of radiobiologic data in cells and laboratory animals, and microdosimetric considerations (Trabalka et al. 2017).

In evaluating data in the LSS cohort, we assumed that an upper bound of a low acute dose can be defined as the dose at which the quadratic term in a modeled dose-response for all solid cancers contributes about 5% of the estimated risk. With this assumption, dose-responses for solid cancer mortality (Preston et al. 2004; Pierce et al. 2008; Little et al. 2008) and incidence (NRC 2006; Preston et al. 2007) based on DS02 dosimetry indicated an upper bound of a low acute dose in the range of about 10–200 mGy. This range was based on fits to dose-responses assuming linear-quadratic models, except an upper bound at the low end of this range was based on a fit assuming a linear-quadratic-exponential model (Little et al. 2008).

Other epidemiologic studies that support an assumption of an upper bound of a low acute dose as low as 10 mGy include studies of childhood cancer following in utero exposure (Doll and Wakeford 1997; UNSCEAR 2000; Ron 2003) and breast cancer incidence in medical patients who received x-ray fluoroscopy treatments (Preston et al. 2002). Support for a low acute dose as low as 10 mGy also is provided by data on tumor induction in laboratory animals (Ullrich et al. 1987; Bartstra et al. 2000), data on oncogenic cell transformation (NCRP 2001), and microdosimetric considerations (Trabalka et al. 2017). Studies of thyroid cancer incidence in children from external radiation (Ron et al. 1995) and brain cancer incidence from computed tomography (CT) scans in children and adolescents (Pearce et al. 2012) suggest that an upper bound of a low acute dose is less than 100 mGy. There are no epidemiologic or radiobiologic data to suggest that an upper bound of a low acute dose is substantially greater than 200 mGy.

On the basis of these considerations, we concluded that a low acute dose of low-LET radiation can be defined as a dose less than an uncertain value in the range of 10–200 mGy. As in IREP (Land et al. 2003; Kocher et al. 2008), an uncertain upper bound of a low acute dose can be represented by a loguniform probability distribution that would be phased in gradually as an acute dose decreases below an uncertain value in that range. This approach to representing the uncertainty in defining a low acute dose of low-LET radiation is intended for use in cancer risk assessments that fully account for uncertainty.

Definition of low dose rate

An upper bound of a low dose rate from chronic exposure to low-LET radiation can be defined as the highest dose rate at which the dose-response is linear, whatever the total dose. Recommendations by expert groups include a dose rate averaged over a period of about one hour of 0.1 mGy min⁻¹ (UNSCEAR 1993), 2 mGy min⁻¹ (ICRP 1991), and 0.01 mGy min⁻¹ (NRC 2006). The recommendation by ICRP (1991) was not retained in a later report (ICRP 2007), and the basis for the recommendation by the BEIR VII committee (NRC 2006) was not documented.

The upper bound of 0.1 mGy min⁻¹ recommended by UNSCEAR (1993) was based on studies of cancer induction in laboratory animals from chronic exposure to ¹³⁷Cs gamma rays at varying dose rates (e.g., Ullrich and Storer 1978, 1979a, 1979b). At the lowest dose rates of about 0.06–0.07 mGy min⁻¹, dose-responses appeared to be linear and the response per Gy was substantially lower than at higher dose rates. The lowest dose rates in the animal studies were rounded up to give an estimated upper bound of 0.1 mGy min⁻¹ (UNSCEAR 1993). However, there is considerable uncertainty in this estimate. Since only a limited number of widely separated dose rates were used in studies of cancer induction in animals evaluated by UNSCEAR (1993), the yield of tumors per Gy could have been about the same at dose rates several times higher. The yield per Gy also could have been substantially less at lower dose rates that could not be investigated in the animal studies.

UNSCEAR (1993) also estimated an upper bound of a low dose rate on the basis of microdosimetric considerations. By assuming that an upper bound could be defined as the dose rate below which only a single track of low-LET radiation would traverse a cell nucleus during a period characteristic of the time required for repair of damage to DNA (a period of perhaps a few hours), an estimate of 10⁻³ mGy min⁻¹ was obtained (UNSCEAR 1993). This dose rate is two orders of magnitude lower than the estimate based on studies of cancer induction in animals.

The upper bound of 0.1 mGy min⁻¹ recommended by UNSCEAR (1993) was adopted by Land et al. (2003) and expressed as a dose rate of 6 mGy h⁻¹ averaged over a period of a few hours, whatever the total dose. From an evaluation of epidemiologic and radiobiologic data and microdosimetric considerations (Trabalka et al. 2017), we judged that there was little justification for revising this assumption. However, the uncertainty in the assumed upper bound probably is at least several-fold. Land et al. (2003) also recommended that users of IREP apply a full DDREF at any dose rate from low-LET radiation below the assumed upper bound.

Distinction between acute and chronic exposure

In many situations, exposure to low-LET radiation is easily characterized as acute or chronic and, therefore, the applicability of a possible DDREF in assessing risks of solid cancers is easily determined from an estimated acute dose or dose rate from chronic exposure. For example, exposures of the public to radionuclides routinely released to the environment from nuclear facilities and exposures of workers who spend substantial portions of their working days in designated radiation zones clearly are chronic, whereas infrequent exposures to medical×rays from routine dental examinations or from CT scans to monitor the outcome of prior treatments for cancer clearly are acute.

When exposures are highly fractionated (i.e., there are multiple exposures at small fractions of the total dose from all exposures), as occur in some medical treatments with external radiation, it may not be straightforward to determine whether exposures should be considered chronic, in which case a DDREF should be applied, or not, depending on the average dose rate over the entire period of exposure whatever the total dose, or acute, in which case a DDREF should be applied to each exposure separately, or not, depending on the dose from each exposure. Land et al. (2003) considered that fractionated exposures should be treated as separate acute exposures if they are separated by five hours or more but should be treated as a single chronic exposure otherwise.^**** For example, on the basis of this criterion, each exposure in a series of daily radiotherapy treatments using external radiation would be considered an acute exposure. However, expert groups have not developed recommendations on conditions under which fractionated exposures should be treated as a single chronic exposure or a sequence of separate acute exposures. When in doubt, we believe that an appropriate way to account for uncertainty is to estimate risks from highly fractionated exposures based on either assumption and average the two estimates by assigning them equal weight.