Identification of curcumin derivatives as human LMTK3 inhibitors for breast cancer: a docking, dynamics, and MM/PBSA approach

Abstract

Human lemur tyrosine kinase-3 (LMTK3) is primarily involved in regulation of estrogen receptor–α (ERα) by phosphorylation activity. LMTK3 acts as key biomarker for ERα positive breast cancer and identified as novel drug target for breast cancer. Due to the absence of experimental reports, the computational approach has been followed to screen LMTK3 inhibitors from natural product curcumin derivatives based on rational inhibitor design. The initial virtual screening and re-docking resulted in identification of top three leads with favorable binding energy and strong interactions in critical residues of ATP-binding cavity. ADME prediction confirmed the pharmacological activity of the leads with various properties. The stability and binding affinity of leads were well refined in dynamic system from 25 ns MD simulations. The behavior of protein motion towards closure of ATP-binding cavity was evaluated based on eigenvectors by PCA. In addition, MM/PBSA calculations also confirmed the relative binding free energy of LMTK3–lead complexes in favor of the effective binding. From our study, novel LMTK3 inhibitors tetrahydrocurcumin, curcumin 4,4′-diacetate, and demethoxycurcumin have been proposed with inhibition mechanism. Further experimental evaluation on reported lead candidates might prove its role in breast cancer therapeutics.

Electronic supplementary material

The online version of this article (10.1007/s13205-018-1239-6) contains supplementary material, which is available to authorized users.

Introduction

The human hormone estrogen plays a vital role in breast cancer growth and cell development (Labrie et al. 1999). Estrogen receptors (ERs) are the specific hormone receptor of estrogen found to be express more in two-thirds of tumor cells compared to normal breast cells (Robinson et al. 2000). Among types of breast cancer, the estrogen receptor-α (ERα) positive breast cancers are very common in metastatic stage of breast cancer (Stebbing et al. 2011). The development of endocrine resistance in human is the major bottleneck for the treatment of ERα positive breast cancer. In case of ERα positive breast cancer, the protein kinase enzymes are found to be novel drug target to overcome the endocrine resistance. Moreover, the kinase inhibitors that target protein kinase enzymes are considered as effective therapeutic agents for breast cancer (Giamas et al. 2007).

Human lemur tyrosine kinase-3 (LMTK3) is identified as novel drug target for breast cancer with extensive screening of human genes involved in ERα positive breast cancer. LMTK3 belongs to protein group of serine/threonine/tyrosine kinases family (Robinson et al. 2000). The primary function of LMTK3 is the regulation of human ERα by phosphorylation activity in breast cancer. The key process of LMTK3 exon sequence change between human and chimpanzees confirmed the major reason for susceptibility of humans to ERα positive breast cancer (Stebbing et al. 2012). In addition, LMTK3 also identified as new potential biomarker for ERα positive breast cancer with positive selection compared with chimpanzee ortholog (Giamas et al. 2011). Due to the critical role of LMTK3 in breast cancer, the design of potential inhibitors against LMTK3 can downregulate mRNA expression of ERα and can be successful in breast cancer treatment in modern era (Johnson and O’Malley, 2011).

Curcumin, a potential anti-cancer agent, found to be more effective in prevention and treatment of various cancers. Basically, curcumin belongs to class of polyphenol compounds derived from the South Asian herb turmeric belongs to Curcuma longa (Creighton et al. 2003). The herb C. longa contains curcuminoids that comprised of curcumin, demethoxycurcumin, and bisdemethoxycurcumin (Jurenka 2009). In Ayurvedic medicine, curcumin is widely used for various treatment aspects due to the therapeutic properties like anti-oxidant, anti-septic, analgesic, anti-malarial, and anti-inflammatory (Aggarwal et al. 2007). The human carcinomas like melanoma, head and neck, breast, colon, pancreatic, prostate, and ovarian cancers are effectively inhibited by curcumin (Wilkenet al. 2011). The key mechanism of inhibitory effects of curcumin compounds against human cancers is by the regulation of biochemical cascades, various transcription factors, growth factors, inflammatory cytokines, protein kinases, and other enzymes (Lin 2007).

Materials and methods

Data set

The three-dimensional structural model of LMTK3 kinase domain (PMDB identifier: PM0078692) reported in our previous study (Anbarasu and Jayanthi 2014) was used as protein target for the inhibitor design. The critical binding of ATP and active residues involved in the binding cavity with LMTK3 was used as target region. Based on rational design, 50 curcumin derivatives were selected as ligand data set and structures retrieved from PubChem database in SDF format. The format conversion of ligands from SDF to PDB format was performed using E-BABEL tool in VCCLAB server (Tetko et al. 2005).

Virtual screening

The initial virtual screening (VS) on the data set was manually done by Lipinski’s Rule of Five filter (Lipinski et al. 1997). Lipinski’s Rule of Five was mainly evaluated the pharmacological properties of the ligands that ensure the oral active drugs. The properties include Molecular weight (mw) less than 500 daltons, logP (octanol–water partition coefficient) less than 5, hydrogen bond acceptors less than 10, and hydrogen bond donors less than 5. After filtering, further virtual screening using molecular docking procedures was carried out for the screened curcumin derivatives. The software AutoDock Vina (Trott and Olson 2010) in PyMOL plugin (Seeliger and de Groot 2010) was used for the identification of hits from the given ligand data set. The input of both protein and ligands was saved in PDB format and used for the docking procedures. To have large search space for the docking, the volume of the grid box was fixed to 27,000 Å. The docking grid box was constructed with center x = 0.04, y = 2.45, z = 1.26, size 60 × 60 × 60 Å, and spacing 0.375 Å that target the ATP-binding cavity of LMTK3. The molecular docking run was set to 100 for effective screening and more specificity. The scoring function of AutoDock Vina was categorized by binding affinity expressed in kcal/mol and ligands with least binding affinity were identified as top hit compounds.

Molecular docking

The re-docking on hits was performed in software AutoDock 4.2 (Morris et al. 1998) in PyMOL plugin for the identification of lead candidates. All the non-polar hydrogens were merged and water molecules were removed. For the molecular docking, the same grid parameters were used as in Vina. Using the genetic algorithm, 100 possible binding conformations were generated in AutoDock. A default protocol was applied in genetic algorithm, with population size of 150 randomly placed individuals; maximum number of 2.5 × 10⁵ energy evaluations, maximum number of 2.7 × 10⁴ generations, gene mutation rate of 0.02, and crossover rate of 0.8 were used. The visualization of molecular docking results was done by LigPlot⁺ for both hydrophobic interactions and hydrogen bond interactions (Laskowski and Swindells 2011).

ADME prediction

To check the pharmacological activity, ADME predictions were carried out for the ligands using QikProp 4.5 module (Schrödinger 2015-3). The pharmacological parameters like Human Oral Absorption, QPPMDCK, QPPCaco, QPlogHER, and QPlogBB were predicted for the analysis. Human oral absorption descriptor predicted the qualitative of oral absorption. QPPMDCK descriptor predicted the apparent MDCK cell permeability in nm/s. MDCK cells are considered to be a good mimic for the blood brain barrier. QPPCaco descriptor predicted apparent Caco-2 cell permeability in nm/s. Caco-2 cells predicted a model for the gut-blood barrier. QPlogHER descriptor predicted IC50 value for blockage of HERG K+ channels. QPlogBB descriptor predicted the brain/blood partition coefficient.

Molecular dynamics (MD) simulations

MD simulations were performed in GROMACS 4.5 (Berendsen et al. 1995) for refinement of binding affinity, analysis the stability of the complex, and evaluate the conformational changes in LMTK3 after ligand binding. The best binding conformation of all three lead complexes from the AutoDock results was used as input for the MD simulations. The force field GROMOS96 43a1 (Lindahl et al. 2001) was used for all simulations and the energy minimization of LMTK3 complex was performed with steepest algorithm. Initially, the topology of ligands from the docked complex was generated using PRODRG server (Schüttelkopf and van Aalten 2004) and partial charges were added for the ligand preparation. After topology generation, the solvation of complex was performed in a dynamic system with cubic box size 1.0 nm and distance between periodic images with minimum of 2.0 nm. The specific water model spc216 was used for the aqueous environment in the dynamic system. The system was energy minimized by steepest descent minimization with emstep of 0.01, emtol of 1000, and steps 100 ps. The Verlet–leap-frog algorithm was used in numerical integration with a 1.0 fs time step length for minimization and 2.0 fs for dynamics. The neutralization of the system was done by adding six chlorine ions and periodic boundary conditions were applied in all directions. LMTK3–ligand complex was well equilibrated by initial simulations in two phases, namely, NVT and NPT. In case of NVT, the complex was simulated at 300 K and with a coupling constant of 0.1 ps for duration 100 ps using leap-frog integrator. The cut-off range for short electrostatic and van der waals interactions was set to 14 Å for both. All bond lengths and hydrogen bonds of the protein were constrained by LINCS algorithm (Hess et al. 1996) and geometry of water molecules was constrained by SETTLE algorithm (Miyamoto and Kollman 1992). After NVT, the complex equilibrated with constant pressure of 1 bar was employed with a coupling constant of 5 ps with steps 100 ps using leap-frog integrator. Particle Mesh Ewald (PME) for long-range electrostatics interactions was set with order 4 and 0.16 fourier spacing. The temperature was set by V-rescale, a modified Berendsen thermostat with reference temperature of 300 K in time constant and Parrinello-Rahman barostat with 1 bar pressure for equilibration ensembles. Finally, the production MD run was performed for duration 25 ns and all MD trajectories were analyzed.

Principal component analysis (PCA)

Principal component analysis (PCA) or essential dynamics was one of the advance methods in MD simulations. PCA was more specific in elucidate the functional relevant motions of protein by the combination of local fluctuations and collective motions. The protocol (Amadei et al. 1993) was used for construction of PCA with the extraction of concerted motion from all trajectories using Cα atoms. The PCA method was based on the construction of covariance matrix with elements C_ij for coordinates i and j:

$${\mathit{C}}_{\mathit{ij}}=⟨\left({\mathit{x}}_{\mathit{i}}-⟨{\mathit{x}}_{\mathit{i}}⟩\right)\left({\mathit{x}}_{\mathit{j}}-⟨{\mathit{x}}_{\mathit{j}}⟩\right)⟩,$$

where x₁,…, x₃N—mass-weighted Cartesian coordinates of an N-particle system and <>—average over all instantaneous structures sampled during the simulations. The symmetric 3 × 3 N matrix C was then process with diagonalization of an orthonormal transformation matrix R:

$$R^T\mathit{CR}=\mathit{diag}\left(k_{2,}.........k_{3N}\right),$$

where k₁ ≥ k₂ ≥ ≥k₃N—eigenvalues and R^T—transpose of R. The eigenvalue was the key property of covariance matrix and consists of energetic contribution of all motion. Eigenvectors were used in evaluation of direction of atomic motion in conformational phase. The eigenvector that contains largest eigenvalue was called as “principal component”. The PCA plot constructed by plotting eigenvectors (eigenvectors 1 and 2 or PCA1 vs PCA2) showed the maximum motion of protein.

The trajectories of LMTK3 complexes were retrieved and analyzed using Gromacs utilities: g_energy to evaluate the various energy contributions in dynamic system, g_rms to analyze the structural deviation through RMSD plot, g_hbond to evaluate inter-hydrogen bond interactions between two groups by NH plot, g_gyrate to identify the compactness of protein during folding–unfolding states through Rg plot, g_sas to evaluate the surface area of the protein accessible to solvent by SASA plot, and, finally, PCA plot to find overall motion of protein by g_covar and g_anaeig utilities. All plots from MD trajectories were plotted using Xmgrace tool (Turner 2005).

Binding free energy calculation: MM/PBSA

The relative binding free energy protein–ligand complex was calculated by g_mmpbsa gromacs utility (Kumari et al. 2014). Molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) calculations from the Gromacs and APBS packages (Baker et al. 2001) were adopted. The binding energy consists of three energetic terms potential energy in vacuum, polar solvation energy, and non-polar solvation energy. Full description of the MM/PBSA protocol was followed from the web page (http://rashmikumari.github.io/g_mmpbsa/). From 25 ns simulations, each trajectory saved at 2 ps frame subjected for the binding free energies that have been calculated from electrostatic, polar salvation, and SASA energies. The default parameters were used in all instances.

Results and discussion

Currently, many protein kinases act as potential drug targets for breast cancer and most of the successful drugs were belongs to kinase inhibition. Especially, ATP-binding cavity was the common target site for the various classes of kinase inhibitors. In this present study, we focused on identification of potent LMTK3 inhibitors (lead candidates) using curcumin derivatives based on rational inhibitor design. The feasible binding mechanism of curcumin derivatives with LMTK3 was evaluated by structure-based virtual screening. We used three-dimensional structural model of human LMTK3 domain characterized with functional kinase domains contains ATP-binding cavity (Supp Fig. 1). In case of LMTK3 kinase activity, ATP-binding cavity in a specific cavity between the hinge of ‘N’ terminal domain and ‘C’ terminal domain was critical for the region of ERα phosphorylation. In deep structural level, our previous study reported the ATP-binding cavity and key residues Tyr185 and Asp284 involved in binding were target region for inhibitor design.

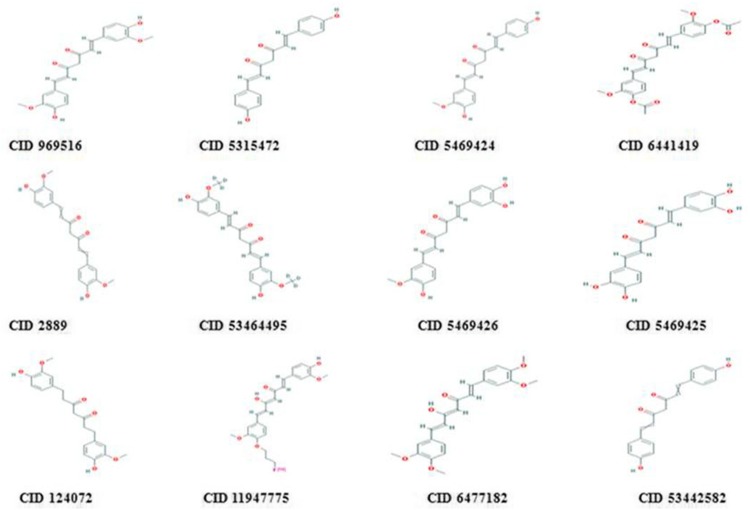
The currently available 50 curcumin derivatives were retrieved from PubChem database and filtered using Lipinski’s Rule of Five. Based on the properties of drug likeness, 12 curcumin derivatives were filtered out from 50 derivatives for virtual screening (Table 1) and 2D chemical structures were shown (Fig. 1). The molecular weight of the screened derivatives in range of 300–400 g/mol and log P in range of 3–4 confirmed the favorable oral activity. The H-bond donor in the range of 1–4 and H-bond acceptor in range of 4–8 confirmed the binding affinity of ligands. Mainly, the basic skeleton of curcumin derivatives contains phenol aromatic rings connected by unsaturated carbonyl groups that characterized the ligand function for potential binding. Thus, the active functional groups in curcumin were more critical in case of virtual screening and molecular docking against ATP-binding cavity of LMTK3.

Table 1.

Lipinski’s Rule of Five of screened curcumin derivatives

Compound ID	CID 969516	CID 5315472	CID 5469424	CID 6441419	CID 2889	CID 53464495	CID 5469426	CID 5469425	CID 124072	CID 11947775	CID 6477182	CID 53442582
Molecular weight (g/mol)	368.37	308.32	338.35	452.45	368.38	374.41	354.35	340.32	372.41	427.45	396.43	428.43
XLogP3-AA	3.2	3.3	3.3	3.4	3.2	3.2	2.9	2.5	2.8	5	4.6	3.2
H-bond donor	2	2	2	0	2	2	3	4	2	2	1	2
H-bond acceptor	6	4	5	8	6	6	6	6	6	7	6	8

Molecular weight < 500, XLogP < 5, H-bond Donor < 5 and H-bond Acceptor < 10

Fig. 1.

2D Chemical structure of screened curcumin derivatives obtained from PubChem database

Virtual screening

From virtual screening, the results showed that curcumin derivatives docked well with LMTK3. The best binding affinity was observed in hit CID 124072 of − 7.8 kcal/mol and lower binding affinity in CID 11947775 of − 4.6 kcal/mol confirmed the changes in binding due to ligand atom interactions with LMTK3. The top four ligands CID 124072, CID 6441419, CID 2889, and CID 5469424 were chosen as hits with binding affinity more than − 7 kcal/mol confirmed the potential binding (Table 2). Hence, the virtual screening method was more useful in identifying the top hits from the curcumin ligand data set.

Table 2.

Virtual screening results of curcumin derivatives against ATP-binding cavity of human LMTK3 from AutoDock Vina

Compound	Binding affinity (kcal/mol)	Conformation
CID 969516	− 6.4	34
CID 5315472	− 6.4	41
CID 5469424	− 7.2	55
CID 6441419	− 7.6	41
CID 2889	− 7.3	72
CID 53464495	− 6.3	25
CID 5469426	− 6.7	63
CID 5469425	− 6.9	18
CID 124072	− 7.8	51
CID 11947775	− 4.6	78
CID 6477182	− 6.6	22
CID 53442582	− 6.4	42

The top hits were highlighted in bold

Molecular docking

After hit identification, re-docking on the same was performed for identification of potential lead candidates with binding pose in AutoDock. With the result of docking run, 100 conformations for each hits were generated and binding mode with least binding energy was selected as best conformation. The post-docking analysis was evaluated by parameters like favorable energy, low inhibition constant, and weak interactions involved between protein/ligand complexes. The energy terms including binding energy, final intermolecular energy, electrostatic energy, and van der Waals energy showed the energy contribution for the favorable docked complex. In LMTK3–ligand complex, weak interactions such as hydrogen bond interactions and hydrophobic interactions play a critical role in ligand recognition and protein stability after ligand binding.

From post-docking analysis (Table 3), three hits CID 124072, CID 6441419, and CID 5469424 showed the favorable binding energy with range − 6 to − 7 kcal/mol that showed the effective docked complex. The binding energy was more reasonable for the changes induced and subsequent rearrangements in protein after ligand binding. Moreover, the effective interaction was further supported by energies like final intermolecular energy, electrostatic energy, and van der Waals energy. From the energy analysis, the LMTK3 inhibition by curcumin hits was mostly by non-polar forces contribution. Besides energy terms, inhibition constant of three hits showed less than 8 µM, supported the docking results, and confirmed the significance of inhibition.

Table 3.

Molecular docking results of top curcumin hits from AutoDock and analyzed in LigPlot⁺

Compound	Binding energy (kcal/mol)	Inhibition constant (µM)	Final intermolecular energy (kcal/mol)	Electrostatic energy (kcal/mol)	vdW + Hbond + desolv energy (kcal/mol)	Hydrogen bonds	Residues involved
CID 124072	− 7.41	3.72	− 9.66	− 0.28	− 9.38	3	Asn261, Lys137, Ser265
CID 6441419	− 7.19	5.40	− 9.72	− 0.19	− 9.53	3	Arg270, Tyr185(2)
CID 5469424	− 6.93	7.39	− 9.71	− 0.27	− 9.44	1	Arg270

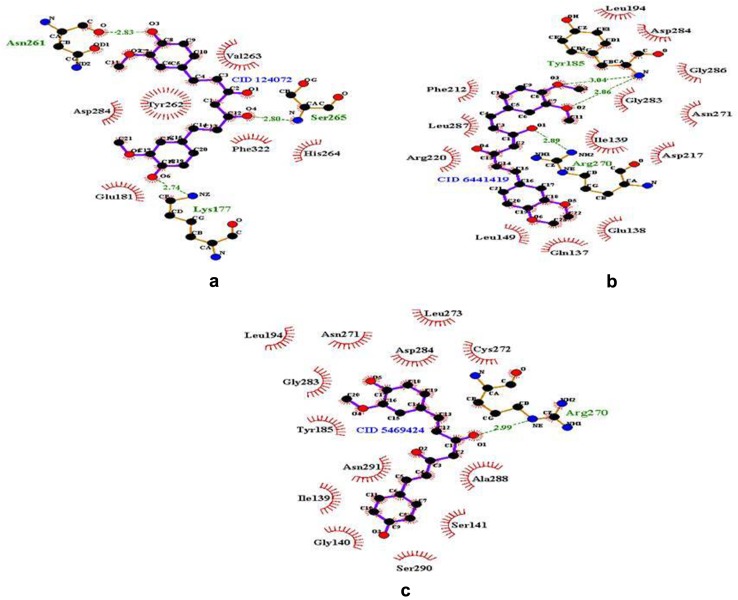
The hydrogen bond and hydrophobic interactions of LMTK3–CID 124072 complex were evaluated using LigPlot⁺. The results showed three hydrogen bonds between the protein and ligand atoms. The interaction residues including Asn261, Lys137, and Ser265 involved in active LMTK3 inhibition. The binding pose of hit CID 124072 clearly suggested the effective inhibition compete with ATP molecule. The hydrogen bond interaction pattern evaluated by atom ‘O’ of Asn261 interact with atom ‘O3’ of ligand, atom ‘N’ of Ser265 interact with atom ‘O4’ of ligand, and atom ‘NE’ of Lys137 interact with atom ‘O6’ of ligand. The hydrophobic interactions were analyzed for LMTK3–CID 124072 complex, six hydrophobic interactions were observed, and residues Glu181, Tyr262, Val263, His264, Asp284, and Phe322 involved in interaction. Especially, key residue Asp284 involved in both hydrogen bond and hydrophobic interactions in CID 124072 which clearly showed its role in stability of the complex (Fig. 2a).

Fig. 2.

Hydrogen bond interactions and hydrophobic interactions of top three lead complexes were visualized in LigPlot⁺. a CID 124072 complex, b CID 6441419 complex, c CID 5469424 complex. Color representation: hydrophobic interactions in red color arc and hydrogen bonds showed in green color dots

In case of LMTK3–CID 6441419 complex, the results showed three hydrogen bonds between the protein and ligand atoms. The interaction residues include Arg270 and Tyr185. The hydrogen bond interaction pattern was evaluated by atom ‘N’ of Tyr185 interact with atom ‘O3’ of ligand, atom ‘N’ of Tyr185 interact with atom ‘O2’ of ligand, and atom ‘NE’ of Arg270 interact with atom ‘O1’ of ligand. In addition, the complex was observed with 13 hydrophobic interactions and residues Gln137, Glu138, Ile139, Leu149, Leu194, Phe212, Asp217, Arg220, Asn271, Gly283, Asp284, Gly286, and Leu287 involved in interaction (Fig. 2b).

In case of LMTK3–CID 5469424 complex, the results showed that one hydrogen bond interaction includes Arg270. The hydrogen bond interaction pattern was evaluated by atom ‘NE’ of Arg270 interact with atom ‘O1’ of ligand. In addition, the complex was observed with 13 hydrophobic interactions were observed and residues Ile139, Gly140, Ser141, Tyr185, Leu194, Asn271, Cys272, Leu273, Glu283, Asp284, Ala288, Ser290, and Asn291 involved in the interaction (Fig. 2c). Thus, hit compounds CID 124072, CID 6441419, and CID 5469424 were identified as novel lead candidates (lead1, lead2, and lead3, respectively) with potent LMTK3 inhibition. The impact of weak interactions in the strong inhibition mechanism was well defined between LMTK3 and lead candidates.

ADME prediction

ADME properties inspected using QIKPROP 4.5 were analyzed and listed (Table 4). Human oral absorption was high with value 3. QPPMDCK was great with more than 500 with permeability to MDCK cells. QPPCaco was great with 500 with permeability to Caco cells. QPlogHER was less than − 5 with permeability to HER. QPlogBB was with range of in range of − 3.0 to 1.2 that cross blood brain barrier. Thus, docking and ADME predictions confirmed the three lead molecules as good inhibitors for LMTK3.

Table 4.

ADME predictions of curcumin leads in QikProp (Schrodinger)

Properties	CID 124072	CID 6441419	CID 5469424
Human oral absorption	3	3	3
QPPMDCK	546.903	711.846	684.179
QPPCaco	525.729	1400.266	794.27
QPlogHER	− 8.975	− 9.412	− 6.385
QPlogBB	− 1.004	− 0.47	− 2.008

Human oral absorption: 1-low, 2-medium and 3 for high; QPPMDCK: < 25 poor, > 500 great; QPPCaco: < 25 poor, > 500 great; QPlogHER: concern below − 5; QPlogBB: − 3.0 to 1.2

Molecular dynamics simulations

After virtual screening and docking analysis, the binding affinity and stability of the lead candidates were further investigated using molecular dynamics simulations with respect to nanosecond scales. MD simulation method mainly considers the receptor flexibility which not involved in molecular docking module. In addition, MD simulation was more powerful technique near to experimental studies for the investigation of protein–ligand complex. From 25 ns production MD run, the analysis was evaluated by group properties like total energy, RMSD, Rg, SASA, inter-hydrogen bond interactions, and advance properties like PCA and MM/PBSA free energy calculations using trajectory files.

The total energy was calculated for the three lead complexes that evaluated the protein stability after lead binding. The total energy of complexes was − 489578, − 489617, and − 467522 kJ/mol, respectively, which showed the stable conformation with LMTK3. The comparison of total energy reported that both complexes possessed the favorable energy during the complex formation in the dynamic system. In addition, other energies like potential energy, kinetic energy, average Coul-SR, and average LJ-SR energies were evaluated and supported the stable energy contributions in LMTK3 (Supp Table 1).

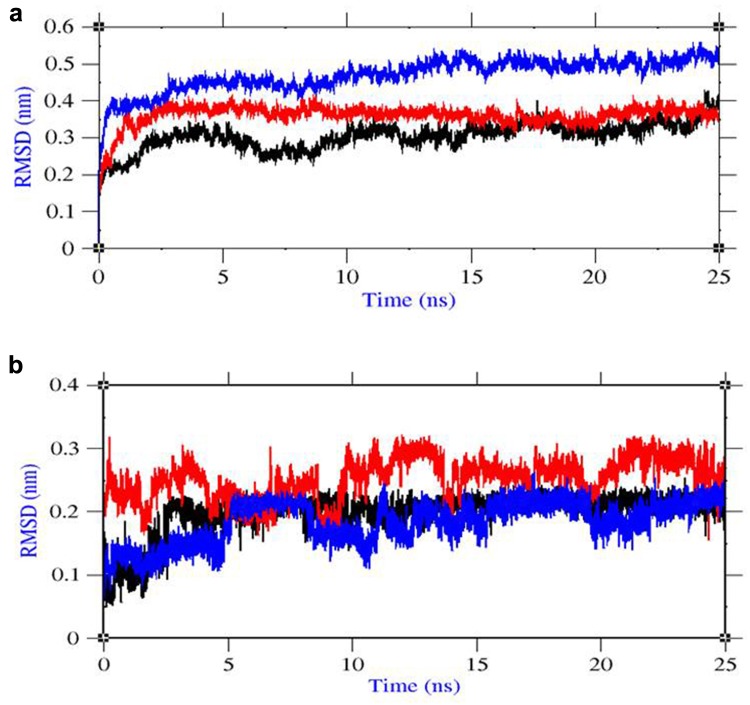
Root mean square deviation (RMSD) was evaluated for the convergence of the protein structure towards an equilibrium state after lead binding. From protein RMSD plot based on backbone atoms, lead1 complex showed until 5 ns that the structure was equilibrated well and started to converge with RMSD range near to 0.3 nm. The RMSD value of lead1 complex was less and clearly explained the less structural deviation after ligand binding. From the RMSD plot of lead2 complex, the structure was equilibrated until 6 ns and then started to converge near to 0.4 nm. From the RMSD plot of lead3 complex, the structure was equilibrated until 5 ns and then started to converge near to 0.5 nm. In comparison with protein RMSD from our previous study, the results showed the high structural deviation until 12 ns due to conformational change after ligand binding and after that the structure started to obtain the stability with less structural deviation at end of 25 ns simulation. After ligand binding, the structural deviation of lead2 and lead3 complex was little higher when compared to lead1 complex (Fig. 3a).

Fig. 3.

Group properties of LMTK3–lead complexes from MD trajectories a RMSD of protein backbone atoms, b RMSD of ligand atoms. Color representation: LMTK3–CID 124072 complex in black, LMTK3–CID 6441419 complex in red, and LMTK3–CID 5469424 complex in blue

From ligand RMSD plot, lead1 complex showed less structural change in ligand structure with RMSD 0.2 nm throughout the simulations which supported the binding affinity. In lead2 complex, the ligand structure showed some change in deviation until 10 ns 0.2–0.3 nm explained the small change in conformation of complex. In lead3 complex, the ligand structure showed some change in deviation until 10 ns 0.1–0.2 nm explained the small change in conformation of complex (Fig. 3b). Thus, the favorable energy and proper convergence of LMTK3 structure after ligand binding explained the stable complex formation.

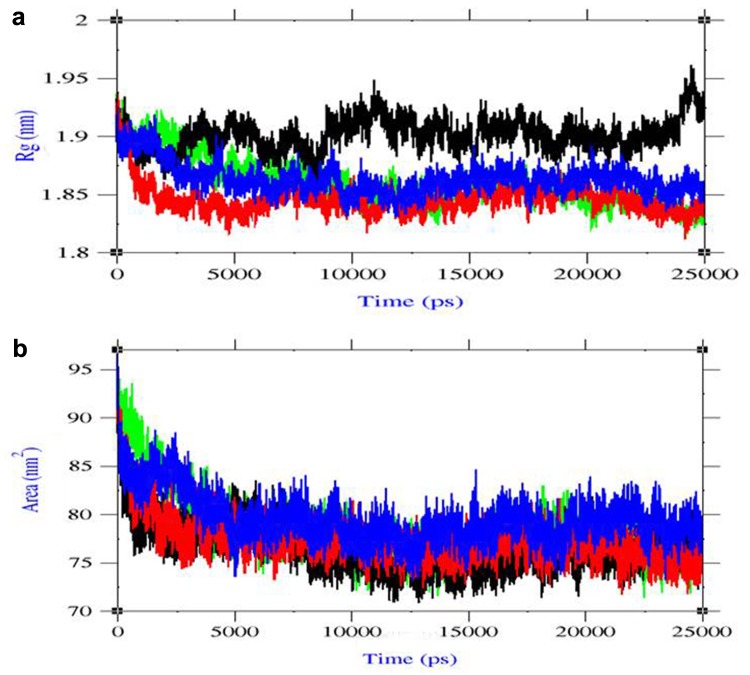
Radius of gyration (Rg) was evaluated the changes in complex compactness which measures the mass of atoms relative to the center of mass of the complex. From our previous study, Rg plot of the LMTK3 apo state was retrieved and Rg was near to 1.9 nm showed the native structure with defined compactness. In case of lead1 complex, the results showed Rg value near to 1.85 nm showed the slight decrease in compactness of the structure compared to LMTK3 in apo state. In case of lead2 complex, the results showed Rg value near to 1.9 nm showed the compactness was near to native LMTK3. In case of lead3 complex, the results showed Rg value near to 1.88 nm showed that the compactness was near to native LMTK3 (Fig. 4a). In comparison with Rg plots, very less change in compactness of protein observed during the complex formation. Solvent accessible surface area (SASA) was the property of protein, where the region is accessible to solvent. From SASA plot, lead1 complex showed value of 70–80 nm², lead2 complex showed 75–80 nm², and lead3 complex showed that 78–85 nm² confirmed the appropriate change in SASA due to ligand binding (Fig. 4b). In comparison with LMTK3 in apo state SASA plot from our previous study, the solvent accessibility in the protein was decreased due to ligand binding and thus favored hydrophobicity related to close of binding cavity.

Fig. 4.

a Radius of gyration (Rg) plot, b Solvent accessible surface area (SASA) plot. Color representation LMTK3 in black, LMTK3–CID 124072 complex in red, LMTK3–CID 6441419 complex in green, and LMTK3–CID 5469424 complex in blue

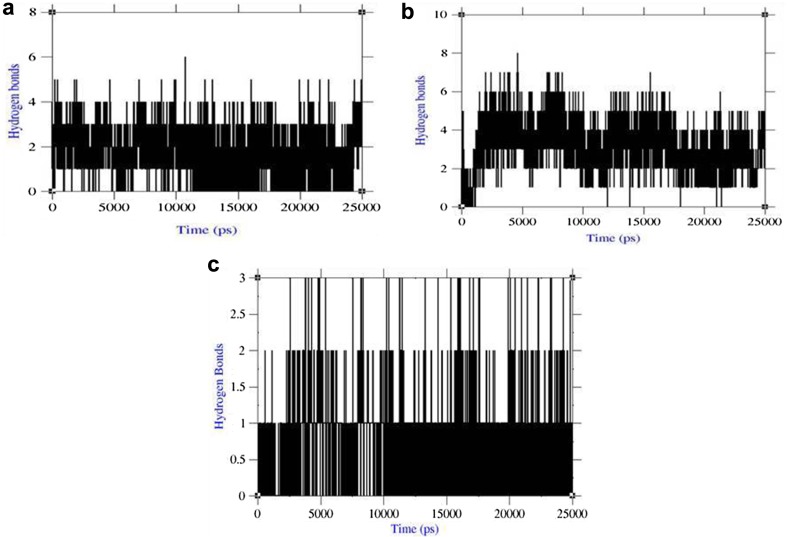
Inter-hydrogen bond interactions between protein and ligands were evaluated for the LMTK3–lead complexes. In case of lead1 complex, NH plot results showed that range of four-to-six hydrogen bond interactions was observed throughout 25 ns simulation and maximum of eight hydrogen bonds (Fig. 5a). NH analysis confirmed strong inhibition of LMTK3 by lead1 in dynamic system as same as docking results inferred with six hydrogen bonds. In case of lead2 complex, the results showed with range three-to-four hydrogen bond interactions were found throughout 25 ns simulation and maximum of six hydrogen bonds as same as docking results (Fig. 5b). In case of lead3 complex, the results showed with range one-to-three hydrogen bond interactions were found throughout 25 ns simulation and maximum of three hydrogen bonds (Fig. 5c). The inter-hydrogen bond interaction pattern suggested the plausible mode of strong binding of lead candidates with LMTK3 favored the inhibition mechanism. Thus, the group properties like total energy, RMSD, Rg, SASA, and inter-hydrogen bonds of lead complexes suggested the refined potent binding with LMTK3. Overall, the property analysis showed that lead1 complex showed better refined binding than other two complexes in the dynamic system.

Fig. 5.

Inter-hydrogen bond interactions. a LMTK3–CID 124072 complex, b LMTK3–CID 6441419 complex, and c LMTK3–CID 5469424 complex

Principal component analysis

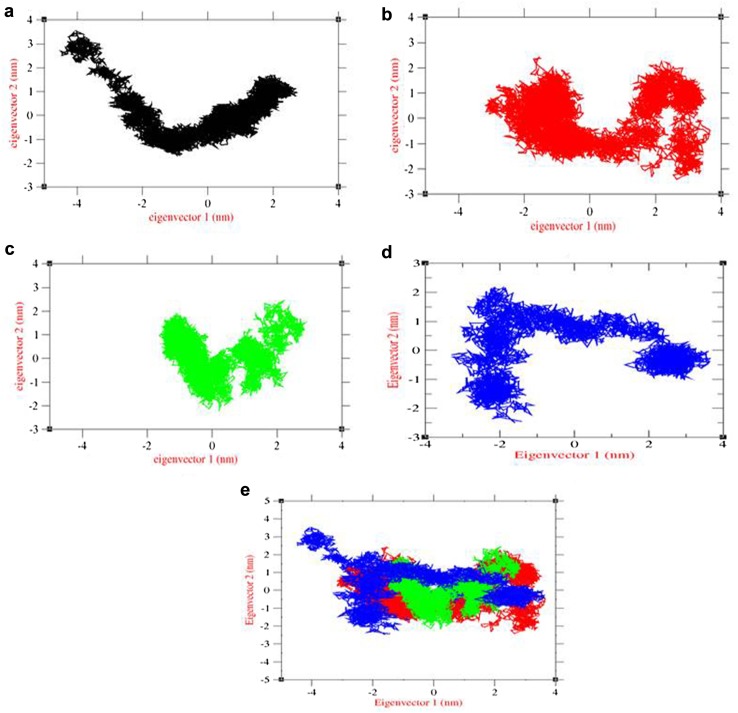
The impact of overall motion of protein due to lead binding was analyzed by principal component analysis (PCA) using construction of eigenvectors. From our previous study, PCA of LMTK3 in apo state was used for the comparison of overall motion in conformational space (Fig. 6a). The corresponding covariance trace value of LMTK3 in apo state was 8.32235 nm². In case of complexes, the covariance trace values of lead1, lead2, and lead3 complexes were 7.61036 nm², 4.62685 nm^2, and 9.2788 nm², respectively. The effect of lead1 binding results in slight change in overall motion of LMTK3 with clusters extended in conformational space when compared to PCA plot of LMTK3 in apo state (Fig. 6b). The effect of lead2 binding results in significant change in overall motion of LMTK3 with clusters compressed in conformational space (Fig. 6c). The effect of lead3 binding results in significant change in overall motion of LMTK3 with clusters extended in conformational space (Fig. 6d). To get the better view of protein motion, combined PCA was plotted and results showed the change in LMTK3 motion due to ligand binding (Fig. 6e). Overall, the PCA plot confirmed the change in protein motion due to lead binding and towards closed conformation of the LMTK3.

Fig. 6.

PCA plot constructed by eigenvector 1 vs eigenvector 2. a LMTK3, b LMTK3–CID 124072 complex, c LMTK3–CID 6441419 complex, d LMTK3–CID 5469424 complex, and e combination of LMTK3 and its lead complexes. Color representation LMTK3 in black, LMTK3–CID 124072 complex in red, LMTK3–CID 6441419 complex in green, and LMTK3–CID 5469424 complex in blue

Binding free energy calculation: MM/PBSA

To evaluate the binding free energy of LMTK3–lead complexes using MM/PBSA method, trajectories from molecular dynamic simulations were retrieved (Guan et al. 2016). The snapshots were extracted at every 10 ps of stable intervals from 25 ns MD trajectory and served as input for the calculation. The binding free energy and its corresponding components obtained from the MM/PBSA calculation of the LMTK3–lead complexes were listed (Table 5). The results indicated that three leads compounds possessed a negative binding free energy with − 141.727, − 151.455, and − 132.758 kJ/mol, respectively. Moreover, van der Waals, electrostatic interactions, and non-polar solvation energy negatively contribute to the total interaction energy, while only polar solvation energy positively contributes to total free binding energy. The relative binding free energies of three LMTK3–lead complexes supported the strong binding in the dynamic system.

Table 5.

Binding free energy results from MM/PBSA calculations. All energies represented in kJ/mol

	Energies	CID 124072	CID 6441419	CID 5469424
Polar energies	Electrostatic	− 98.352	− 84.778	− 96.331
	Polar solvation	220.185	206.011	218.366
Non-polar energies	van der Waal	− 244.230	− 251.165	− 240.121
	SASA	− 19.329	− 21.523	− 14.672
	Binding energy	− 141.727	− 151.455	− 132.758

Conclusion

In the present study on human LMTK3, we attempted to design the potential inhibitors using computational approaches. ATP-binding cavity of LMTK3 was the current target region for screening based on competitive inhibitors. From the virtual screening results, the least binding affinity of curcumin derivatives characterized the strong binding with LMTK3. The screened hits were under further investigation using re-docking and three lead candidates were identified based on binding energy. The effective inhibition mechanism of lead candidates was evaluated by binding mode with least binding energy, low inhibition constant, more number of hydrogen bond interactions, and hydrophobic interactions in ATP-binding cavity involving critical residues. MD simulations on LMTK3/lead complexes confirmed the proper refinement of leads in the dynamic system. The trajectory analyses like total energy, RMSD, Rg, and NH bond analysis characterized by the potential binding of leads favor the effective inhibition. The inter-hydrogen bond interaction pattern confirmed that the high affinity of lead candidates in dynamic system correlated well with molecular docking results. The principal component analysis (PCA) results confirmed the stability of the LMTK3/lead complex with less change in overall motion of protein after ligand binding. In a nutshell, the screened lead candidates tetrahydrocurcumin, curcumin 4, 4′-diacetate, and demethoxycurcumin can act as competitive human LMTK3 inhibitors. Hence, the reported curcumin leads may act as future anti-breast cancer agents that can be confirmed by further experimental methods using in vitro and in vivo studies.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Compliance with ethical standards

Conflict of interest

The authors declare no conflict of interest.