Abstract
Key points
Distinct spiking patterns may arise from qualitative differences in ion channel expression (i.e. when different neurons express distinct ion channels) and/or when quantitative differences in expression levels qualitatively alter the spike generation process.
We hypothesized that spiking patterns in neurons of the superficial dorsal horn (SDH) of spinal cord reflect both mechanisms.
We reproduced SDH neuron spiking patterns by varying densities of KV1‐ and A‐type potassium conductances. Plotting the spiking patterns that emerge from different density combinations revealed spiking‐pattern regions separated by boundaries (bifurcations).
This map suggests that certain spiking pattern combinations occur when the distribution of potassium channel densities straddle boundaries, whereas other spiking patterns reflect distinct patterns of ion channel expression. The former mechanism may explain why certain spiking patterns co‐occur in genetically identified neuron types.
We also present algorithms to predict spiking pattern proportions from ion channel density distributions, and vice versa.
Abstract
Neurons are often classified by spiking pattern. Yet, some neurons exhibit distinct patterns under subtly different test conditions, which suggests that they operate near an abrupt transition, or bifurcation. A set of such neurons may exhibit heterogeneous spiking patterns not because of qualitative differences in which ion channels they express, but rather because quantitative differences in expression levels cause neurons to operate on opposite sides of a bifurcation. Neurons in the spinal dorsal horn, for example, respond to somatic current injection with patterns that include tonic, single, gap, delayed and reluctant spiking. It is unclear whether these patterns reflect five cell populations (defined by distinct ion channel expression patterns), heterogeneity within a single population, or some combination thereof. We reproduced all five spiking patterns in a computational model by varying the densities of a low‐threshold (KV1‐type) potassium conductance and an inactivating (A‐type) potassium conductance and found that single, gap, delayed and reluctant spiking arise when the joint probability distribution of those channel densities spans two intersecting bifurcations that divide the parameter space into quadrants, each associated with a different spiking pattern. Tonic spiking likely arises from a separate distribution of potassium channel densities. These results argue in favour of two cell populations, one characterized by tonic spiking and the other by heterogeneous spiking patterns. We present algorithms to predict spiking pattern proportions based on ion channel density distributions and, conversely, to estimate ion channel density distributions based on spiking pattern proportions. The implications for classifying cells based on spiking pattern are discussed.
Keywords: spiking pattern, Spinal cord, dorsal horn, Neuronal excitability, classification, computational modeling
Key points
Distinct spiking patterns may arise from qualitative differences in ion channel expression (i.e. when different neurons express distinct ion channels) and/or when quantitative differences in expression levels qualitatively alter the spike generation process.
We hypothesized that spiking patterns in neurons of the superficial dorsal horn (SDH) of spinal cord reflect both mechanisms.
We reproduced SDH neuron spiking patterns by varying densities of KV1‐ and A‐type potassium conductances. Plotting the spiking patterns that emerge from different density combinations revealed spiking‐pattern regions separated by boundaries (bifurcations).
This map suggests that certain spiking pattern combinations occur when the distribution of potassium channel densities straddle boundaries, whereas other spiking patterns reflect distinct patterns of ion channel expression. The former mechanism may explain why certain spiking patterns co‐occur in genetically identified neuron types.
We also present algorithms to predict spiking pattern proportions from ion channel density distributions, and vice versa.
Introduction
Neurons can be classified using various criteria such as their electrophysiological properties (including spiking pattern), morphology and expression of neurochemical and genetic markers. Classification schemes ideally consider combinations of factors (e.g. Cauli et al. 2000; Nelson et al. 2006; Ascoli et al. 2008; Hamilton et al. 2012; Zeng & Sanes, 2017) to identify robust clusters representing bona fide neuron ‘types’. Accurately identifying neuron types is critical for studying how developmental programmes lead to neuronal diversity and how that diversity is utilized to form complicated neural circuits. Yet certain populations of neurons seem to defy classification. A good example is neurons in the superficial dorsal horn (SDH) of the spinal cord (Graham et al. 2007a; Todd, 2017).
The SDH – defined as lamina I and II of spinal cord – plays an important role in the early processing of somatosensory information, especially thermal and nociceptive input (for reviews, see Ribeiro‐da‐Silva & De Koninck, 2008; Todd, 2010; Prescott & Ratté, 2012; Cordero‐Erausquin et al. 2016; Peirs & Seal, 2016). Only a minority (∼5%) of neurons in lamina I project to supraspinal targets (Spike et al. 2003). The remaining neurons, including all of those in lamina II, are local interneurons of which roughly one‐third are inhibitory and two‐thirds are excitatory (Polgar et al. 2003). SDH neurons exhibit diverse spiking patterns (Fig. 1 A). Paired recordings (Lu & Perl, 2005) and correlation with immunocytochemical markers (Yasaka et al. 2010) have revealed differences in the spiking patterns of excitatory and inhibitory neurons. Molecular genetic tools have dramatically accelerated this characterization (Duan et al. 2014; Kardon et al. 2014; Peirs et al. 2015; Petitjean et al. 2015; Abraira et al. 2016; Cheng et al. 2017). But genetically identified cell types can be surprisingly heterogeneous when it comes to spiking pattern (Heinke et al. 2004; Punnakkal et al. 2014; Smith et al. 2015). Linking gene expression patterns with electrophysiological phenotype on a cell‐by‐cell basis is now conceivable with the advent of single‐cell RNAseq (Cadwell et al. 2016; Fuzik et al. 2016; Poulin et al. 2016; Johnson & Walsh, 2017), but this will require more detailed understanding of electrophysiological heterogeneity.
Figure 1. Heterogeneous spiking patterns in SDH neurons.
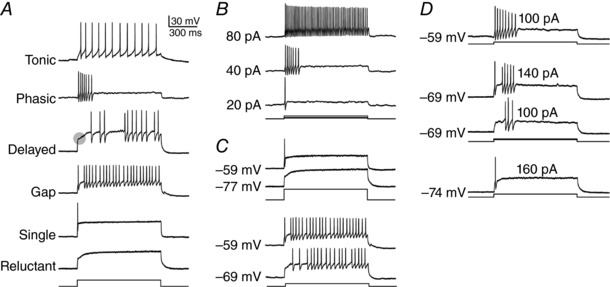
A, sample recordings from five SDH neurons showing the range of spiking patterns evoked by sustained somatic current injection. Note that delayed spiking is preceded by a sharp inflection (shaded circle) indicative of an A‐type potassium current; the inflection is replaced by an initial spike in gap spiking. However, spiking pattern is not a truly innate property of the neuron since it can vary with stimulus intensity (B) or pre‐stimulus membrane potential (C). D, example of a neuron in which different combinations of stimulus intensity and membrane potential yielded four different spiking patterns. Modified from Prescott and De Koninck (2002).
Qualitative differences in spiking pattern are often assumed to arise from qualitative differences in ion channel expression (i.e. expression of different ion channels). But quantitative differences in ion channel expression (i.e. expression of the same ion channels but at different levels, or densities) can also yield distinct spiking patterns if they qualitatively alter spike generation dynamics, which reflect the non‐linear interaction between ion channels (Izhikevich, 2007; Prescott et al. 2008). A qualitative (discontinuous) change in output caused by continuous variation of a parameter is referred to as a bifurcation. Slight variations in ion channel density may cause a neuron to exhibit very different spiking patterns if that variation shifts the neuron across a bifurcation. Variations in stimulus intensity or pre‐stimulus membrane potential can similarly affect the spiking pattern if a bifurcation is crossed. It is, therefore, notable that spiking patterns in some SDH neurons are sensitive to stimulus intensity and/or pre‐stimulus membrane potential (Fig. 1 B–D), as this suggests that some SDH neurons do indeed operate near a bifurcation. A direct corollary of this is that a population of neurons may exhibit different spiking patterns because variation in ion channel expression across the population causes subsets of neurons to operate on opposite sides of a bifurcation. Thus, a population of neurons may exhibit heterogeneous spiking patterns because of qualitative differences in ion channel expression or because an ion channel density distribution straddles a bifurcation (where distribution refers to the variance in ion channel density across neurons). We hypothesized that the latter contributes to explaining the heterogeneous spiking patterns observed in SDH neurons.
To test our hypothesis, we reproduced tonic, single, gap, delayed and reluctant spiking in a simple conductance‐based computer model. Then, following the approach used by Le Franc and Le Masson (2010) to study spiking patterns in deep dorsal horn neurons, we systematically co‐varied the densities of potassium channels responsible for SDH neuron spiking patterns in order to map out parameter combinations where the model switched patterns (i.e. bifurcated). The resulting map reveals which spiking pattern combinations are likely to arise from a single distribution of ion channel densities straddling a bifurcation and which arise from separate ion channel distributions. The implications for SDH neuron classification are discussed.
Methods
Modified Morris–Lecar model
Simulations were conducted using a modified version of the Morris–Lecar model (Rinzel & Ermentrout, 1989; Prescott et al. 2008). The starting model contained only a leak conductance g leak, an instantaneously activating sodium conductance g Na and a delayed rectifier potassium conductance g K,dr. To this model we added a low‐threshold non‐inactivating (Kv1‐type) potassium conductance g K,lt and an inactivating (A‐type) potassium conductance g K,A. Activation of the latter was modelled after Connor and Stevens (1971). The system is described by:
| (1) |
| (2) |
where x corresponds to the gating variables, w, z, a or b. Because m is assumed to activate instantaneously with changes in V, it is always at steady state. Steady‐state activation curves and voltage‐dependent time constants are modelled according to:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
C = 2 μF cm−2, E Na = 50 mV, E K = –100 mV, E leak = –70 mV, = 20 mS cm−2, = 20 mS cm−2, = 2 mS cm−2, ϕw = 0.15, ϕz = 0.15, ϕa = 1.0, ϕb = 1.0, βm = −1.2 mV, βw = −10 mV, βz = −21 mV, γm = 18 mV, γw = 10 mV, γz = 15 mV, and and were set to values identified in the Results, or were systematically varied in 0.1 mS cm−2 increments to map the parameter space giving rise to different spiking patterns. This procedure was repeated across multiple stimulus intensities (from 30 to 110 μA cm−2, at 5 μA cm−2 intervals) and different pre‐stimulus membrane potentials (see Results). Equations were numerically integrated in MATLAB (The MathWorks Inc., Natick, MA, USA) using the Euler method and a 0.1 ms time step. Each simulation was run for 250 ms to reach steady‐state before the application of a stimulating current (I stim) for 400 ms. No dendritic or axonal compartments were included in our model because, although spiking pattern and dendritic morphology are somewhat correlated, there is no evidence of a causal relationship and, furthermore, spiking pattern is defined by the response to somatic current injection (as opposed to dendritic stimulation) and those spikes originate in or near the soma.
After each simulation, neurons were classified as tonic, single, delayed, gap, or reluctant spiking based on the following criteria. Firstly, all neurons that did not spike during stimulation were labelled reluctant spiking. Neurons that produced only one spike, but did not satisfy the criteria for delayed spiking (see below) were labelled as single spiking. The remaining multi‐spike neurons were categorized based on the inter‐spike intervals (ISI) of their initial spikes. Neurons that exhibited an initial spike, but had a delay before the second spike (i.e. a ‘gap’) of greater than 1.5 times the ISI between the second and third spikes were labelled gap spiking. Those that had a delay before firing their first spike of more than 1.5 times the ISI between the first two spikes were labelled delayed spiking. Neurons that fired only one spike with a delay >100 ms were also considered delayed spiking. Neurons firing multiple spikes with neither a gap nor a delay (as defined above) were labelled tonic spiking.
Predicting single neuron conductance densities from spiking pattern sequences
Running the model with specified values of and gives a spiking pattern that depends on I stim. Re‐testing different I stim gives a sequence of spiking patterns. Working in the opposite direction, if one knows the spiking pattern evoked by a certain value of I stim, estimates of and are only weakly constrained (i.e. there are many different potassium channel densities that could yield a given pattern). But if one knows the sequence of spiking patterns evoked by a sequence of I stim, the estimation of and becomes more tightly constrained. To estimate those densities, all points (,) that yield the observed spiking pattern for a given value of I stim were identified, and this was repeated for I stim from 50 to 80 μA cm−2 tested at 5 μA cm−2 intervals. The intersection of those points across planes was then identified, thus revealing values of and that give the correct spiking patterns for all Is tim.
Calculating spiking pattern proportions from the joint distribution of ion channel densities
For a population of neurons, and were assumed to have Gaussian distributions with mean values μK,lt and μK,A, and standard deviations σK,lt and σK,A, respectively. A correlation coefficient ρ (ranging from −1 to 1) must be included to account for any correlation between and . Combining these two univariate normal distributions, and any correlation between them, gives a bivariate normal distribution (BND). The probability density function of the BND is given by:
| (11) |
| (12) |
where x and y represent g K,lt and g K,A, respectively. Equation (12) describes an elliptic paraboloid surface, where cross‐sections parallel to the xy‐plane are ellipses with centre at (μx, μy) = (μK,lt, μK,A) and rotation determined by the correlation coefficient ρ. Integrating the distribution over the region in the parameter space corresponding to a certain spiking pattern yields the volume within that region. Since the total volume under a BND is, by definition, 1, the volume over each spiking pattern region Ri represents the proportion of neurons with spiking pattern i, where i = 1–5 and corresponds to reluctant, single, delayed, gap and tonic spiking, respectively. Hence, the proportion Vi of each firing‐pattern i within a given model neuron population is given by:
| (13) |
The definite double integral in eqn (13) was computed numerically using two‐dimensional trapezoidal integration.
Estimating the joint distribution of ion channel densities from spiking pattern proportions
Working in the opposite direction from the calculations described above, we developed an algorithm to estimate the underlying ion channel distributions that best account for the proportions of different spiking patterns observed within a sample of neurons. Specifically, a geometric‐based optimization algorithm was created to find a BND describing K,lt and K,A such that the BND volume within each spiking pattern region reproduces an observed set of spiking pattern proportions. The algorithm was implemented as follows (where μx , k and μy , k represent the estimation in the k‐th iteration of μK,lt and μK,A, respectively). We started with an arbitrarily chosen BND at the centre of the parameter space (i.e. for a 20 mS cm−2 × 20 mS cm−2 plot, μx ,0 = 10 mS cm−2; μy ,0 = 10 mS cm−2), with no correlation (ρ = 0) and pre‐set σx = σK,lt = 1 mS cm−2 and σy = σK,A = 1 mS cm−2. Volumes under the distribution (V calc) were computed using eqn (13). The calculated proportions V calc,i and the target proportions V target,i were then compared for each firing‐pattern i, yielding a set of error terms E i where:
| (14) |
| (15) |
In words, MaxError is the highest absolute‐value difference between the calculated and target volumes for any spiking pattern. In additional tests, a finite number of samples (n) was randomly drawn from the BND and the target spiking pattern proportion was calculated from the number of samples falling within each spiking pattern region. This models the experimental scenario in which V target, i are estimated from a limited sampling of neurons rather than being strictly known.
Step 1 – modifying ρ. The correlation coefficient ρ was varied systematically from −0.9 to +0.9 by increments of 0.1, thus producing a set of rotated BNDs. MaxError was calculated for each BND and was compared to arbitrarily chosen error thresholds δ = 0.001 and ε = 0.003, which correspond to 0.1% and 0.3% errors, respectively. If MaxError fell below ε, the algorithm proceeded to vary ρ in increments of 0.01 from −0.99 to +0.99. If instead MaxError was less than δ, the algorithm ended (see below). If MaxError remained above δ, the value of ρ yielding the smallest error (ρoptimized) was carried forward to step 2.
- Step 2 – optimizing μ. The next step was to move the centre of the BND from M 0 = (μx ,0, μy ,0) to a new locus M 1 = (μx ,1, μy ,1). To efficiently reduce the error between calculated and target volumes, the centre of the distribution was moved towards regions where V target, i > V calc, i and away from those where V target, i < V calc, i. To determine the direction to move M, the centroid of each region was computed using a weighted average of all points in the region, given by:
where ni is the number of points in Ri, j is any integer ranging from 1 to ni, and pj = (pj , x, pj , y) is the corresponding j‐th point in Ri. Next, the direction from M to each point Ri was determined by drawing a vector from M to each corresponding centroid Ci given by:(16)
To calculate the effect of each region on the centre of the distribution (scaled by the amount of error), each vector was divided by its magnitude to give a unit vector in the direction of each centroid, and was then multiplied by the respective error‐term E i to give a scaled vector where:(17)
Once each error‐scaled vector was determined, M = M0 was moved to a new point M = M 1 by taking the net sum of all vectors and adding the resulting vector to M 0, yielding(18) (19)
where eqn (20) describes the new centre of the BND.(20)
Step 1 was then repeated using the new BND, and MaxError was calculated again for each value of ρ. If MaxError was still >δ for all BNDs centred at M 1, the algorithm repeated Step 2. This sequence was repeated k‐iterations until MaxError fell below δ = 0.001 or the algorithm converged on a point Mk +1. The algorithm returned estimates for the following parameters: μK,lt = μx , k +1, μK,A = μy , k +1, and ρ = ρ optimized. Adding a step to fit σ caused the algorithm to run very slowly; instead, the two‐step algorithm was re‐run with σK,lt and σK,A set, at 0.05 mS cm−2 intervals, to values between 0.4 and 1.6 mS cm−2. Values of σK,lt and σK,A yielding the lowest MaxError were considered the best estimates. This process thus estimated the full set of distribution parameters: μK,lt, μK,A, ρoptimized, σK,lt and σK,A.
All MATLAB code is available at http://prescottlab.ca.
Results
Qualitative reproduction of different spiking patterns in a computational model
Our first step was to reproduce the spiking patterns observed experimentally in SDH neurons during sustained somatic current injection. Sample responses in Fig. 1 A each come from a different neuron, thus highlighting the diversity of spiking pattern across neurons. On the other hand, sample responses in Fig. 1 B–D highlight the sensitivity of spiking pattern within a given neuron to test conditions such as stimulus intensity and/or pre‐stimulus membrane potential. The sensitivity of spiking pattern to test conditions tends to complicate classification, but can be harnessed to strengthen classification and glean addition information if properly addressed (see below and Discussion). All sample responses to somatic current injection in Fig. 1 come from previously published recordings from rat lamina I neurons (Prescott & De Koninck, 2002).
Using a simple conductance‐based model, we sought to identify the minimal changes in ion channel expression required to convert the model between spiking patterns. The starting model – which contains only fast‐activating sodium conductance, delayed rectifier potassium conductance, and a leak conductance – spikes tonically (Fig. 2 A). The ion channels we added to this model were chosen based on past work by us (Prescott et al. 2008; Ratté et al. 2015) and others (Grudt & Perl, 2002; Ruscheweyh & Sandkuhler, 2002; Graham et al. 2007b, 2008; Smith et al. 2015). Adding low‐threshold non‐inactivating (Kv1‐type) potassium conductance g K,lt converted the model to single spiking (Fig. 2 B) whereas adding an inactivating (A‐type) potassium conductance g K,A converted it to delayed spiking (Fig. 2 C). The activation profiles show how each potassium current shapes the spiking pattern. A single spike can occur before g K,lt activates, but all subsequent spikes are prevented because g K,lt does not inactivate. In contrast, g K,A activates quickly enough to prevent spiking at the onset of stimulation, but late spikes occur once g K,A inactivates. Gap spiking (Fig. 2 D), which resembles a mixture of single and delayed spiking, occurs when is low enough that a single spike can occur despite rapid activation of g K,A, but other spikes are delayed until g K,A inactivates. Including high enough densities of g K,A and g K,lt disallowed single and delayed spiking, thus yielding reluctant spiking (Fig. 2 E).
Figure 2. Reproduction of SDH neuron spiking patterns in a computational model.
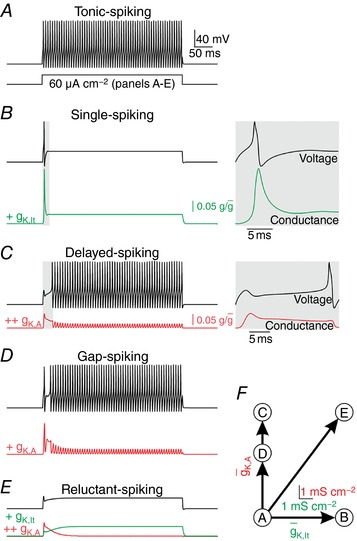
Equivalent stimulation (I stim = 60 μA cm−2) was applied in all panels. Coloured traces show the relative activation (i.e. ) of the added conductance. A, the starting model (with leak conductance, fast‐activating sodium conductance and delayed rectifier potassium conductance) exhibited tonic spiking. B, adding a low‐threshold, non‐inactivating (Kv1‐type) potassium conductance ( = 6 mS cm−2) yielded single spiking. Inset shows horizontally enlarged view of the shaded region on the main trace to highlight that the initial spike occurs before g K,lt activates, and that all subsequent spikes are prohibited since g K,lt does not inactivate. C, adding an inactivating (A‐type) potassium conductance ( = 8 mS cm−2) to the starting model yielded delayed spiking. In this case, spiking occurs only after g K,A inactivates, as highlighted in the inset, which again shows a horizontally enlarged view of the shaded region on the main trace. D, decreasing (to 5 mS cm−2) yielded gap spiking by allowing an initial spike to occur before activation of g K,A but subsequent spikes are delayed until g K,A inactivates. E, adding g K,lt (= 6 mS cm−2) and g K,A (= 8 mS cm−2) to the starting model yielded reluctant spiking because fast activation of g K,A prevents the initial spike while sustained activation of g k,lt prevents late spikes even once g K,A inactivates. F, summary of conductance changes in A–E.
Other ion channels contribute to shaping SDH neuron response properties, such as subthreshold sodium and calcium conductances that encourage temporal summation in tonic‐spiking neurons (Prescott & De Koninck, 2005; Ratté et al. 2015) and adaptation conductances that encourage phasic spiking (Prescott & Sejnowski, 2008). But together, g K,lt and g K,A are sufficient to explain qualitative differences in the pattern of initial spiking, which is the primary basis for electrophysiological classification of SDH neurons. Fig. 2 F shows these spiking patterns relative to the 2‐D space defined by the densities of g K,lt and g K,A.
Quantitative mapping of conductance density to spiking pattern
Next, we systematically co‐varied and to quantify the impact on spiking. The resulting plot (Fig. 3 A) shows five regions, each associated with a different spiking pattern. Whereas broadly separated conductance densities within a region yield the same spiking pattern (notwithstanding quantitative differences), narrowly separated conductance densities straddling a boundary yield distinct patterns (compare traces a–d). However, those boundaries can shift depending on stimulus intensity (Fig. 3 B) or pre‐stimulus membrane potential (Fig. 3 C), meaning the same neuron may exhibit different spiking patterns under different test conditions. For Fig. 3 B and C, each arrow represents a neuron whose spiking pattern (for each test condition) is predicted by the region pierced by that arrow. The sample traces verify these predictions. Traces in the right panel of Fig. 3 C show relative activation of g K,A; less of this conductance is available for activation at the onset of I stim when pre‐stimulus membrane potential is depolarized by a pre‐pulse I pre. These results are consistent with experimental observations illustrated in Fig. 1 B–D.
Figure 3. Relationship between ion channel densities and spiking pattern.
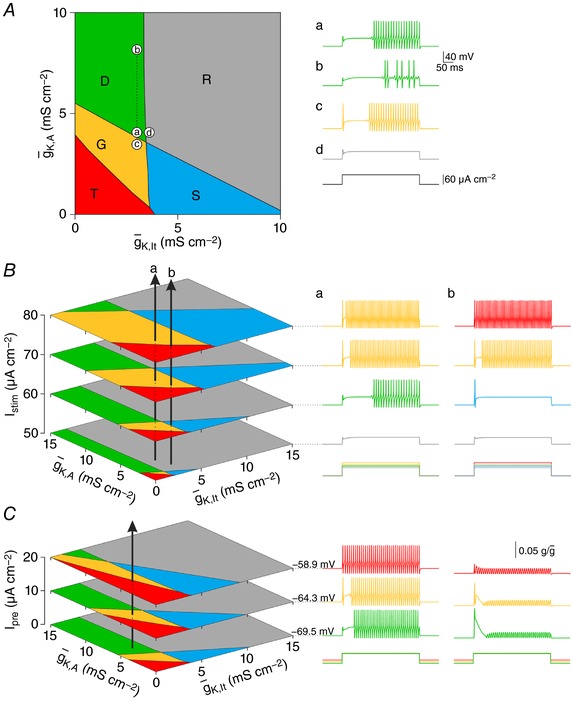
A, systematically co‐varying and revealed that distinct regions in this 2‐D parameter space yield different spiking patterns. Boundaries shown here are based on testing with I stim = 60 μA cm−2. Traces in a–d show sample responses for parameter values labelled on the main plot. Large parameter variations that remain within a region yield the same spiking pattern; compare condition a ( = 3 mS cm−2, = 4 mS cm−2) with condition b ( increased by 4 mS cm−2). In contrast, small parameter variations that cross a boundary yield different spiking patterns; compare condition a with condition c ( reduced by 0.5 mS cm−2) or condition d ( increased by 0.5 mS cm−2). B, boundaries can shift because of stimulus intensity (I stim), meaning a neuron with fixed values of and K,A can exhibit different spiking patterns at different I stim. To illustrate, each vertical arrow on the left panel represents a neuron: for neuron a, = 3 mS cm−2 and = 4 mS cm−2; for neuron b, = 3.5 mS cm−2 and = 2.5 mS cm−2. The spiking pattern at each I stim (illustrated on the right) depends on which region the arrow passes through. C, boundaries can also shift because of pre‐stimulus membrane potential. For these simulations, a subthreshold ‘pre‐pulse’ (I pre) was used to vary the membrane potential before the onset of suprathreshold stimulation. Each plane represents the response to I stim = 60 μA cm−2 after a different pre‐pulse (pre‐stimulus membrane potential is indicated beside each voltage trace). The vertical arrow represents a neuron with = 2 mS cm−2 and = 6 mS cm−2. Traces on the right show the reduced availability of g K,A depending on I pre. By partially inactivating g K,A, subthreshold depolarization reduces the availability of those channels for activation during suprathreshold stimulation, effectively re‐scaling the y‐axis.
On the surface, classification is compromised by the sensitivity of spiking patterns to test conditions. Indeed, if a neuron's spiking pattern is classified using only one or two stimulus intensities and without any regard for membrane potential, the classification has little value. On the other hand, if those sensitivities are thoroughly documented, that information can be used to help infer the ion channel densities in that neuron. To illustrate, Fig. 4 shows sample responses from two model neurons, but now, rather than predicting the spiking patterns at each stimulus intensity based on where the arrows intersect each plane (as in Fig. 3), we invert the problem to ask in what volume each arrow must pass to account for the specific sequence of spiking patterns. A simple algorithm (see Methods) was developed to determine all combinations of K,lt and K,A (shown as light grey regions) that account for the spiking pattern sequences. These areas are smaller than the spiking pattern regions because a sequence of spiking patterns across different stimulus intensities is rarer than the spiking pattern at any one intensity. Likewise, certain spiking pattern sequences are rarer than others: a rare sequence (as for neuron a) will give a more tightly constrained prediction of the underlying ion channel densities than a more common sequence (as for neuron b). For the same reason, testing more stimulus intensities and/or membrane potentials will help refine the prediction. Inferring ion channel densities in this way works best for neurons that operate near a bifurcation (i.e. whose spiking patterns are sensitive to test conditions).
Figure 4. Estimating ion channel densities from spiking pattern sequences.
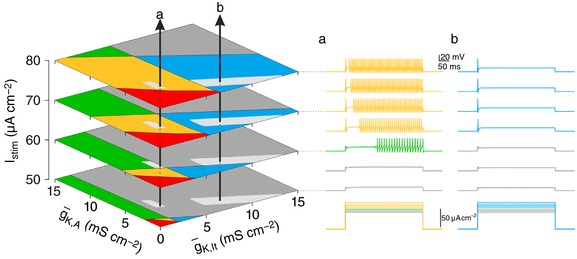
Spiking patterns were determined for I stim between 50 and 80 μA cm−2, at 5 μA cm−2 increments for two neurons labelled a and b on left. Planes are shown for only a subset of I stim. To estimate the channel densities in neurons a and b, we determined all combinations of K,A and K,lt that could produce that sequence. The grey patches shown on each plane together demarcate the volume in which each arrow must exist. The spiking pattern sequence for neuron a leads to a more tightly constrained estimate of ion channel densities than does the sequence for neuron b.
Estimating spiking pattern proportions from ion channel density distributions
Whereas each neuron is represented by a single point on the x–y plane based on its particular expression of g K,lt and g K,A, a set of neurons of the same type will be represented by a cloud of points. The distribution of those points was assumed to be Gaussian based on random variation in and . The univariate distributions describing and are represented by bell‐shaped curves shown respectively on the x‐ and y‐axes of plots in Fig. 5. These univariate distributions combine to form a joint (or bivariate) distribution represented by colour on each plot. If and are uncorrelated (i.e. expression of one channel is independent of the other channel), the joint distribution will be circular when the standard deviations of the two univariate distributions are equal (Fig. 5 A) or elliptical when the standard deviations are unequal (Fig. 5 B). If and are positively or negatively correlated (quantified as the correlation coefficient ρ), the joint distribution will take a slanted elliptical shape but, notably, this is not reflected in the univariate distributions (Fig. 5 C and D).
Figure 5. Estimating spiking pattern proportions from ion channel density distributions.
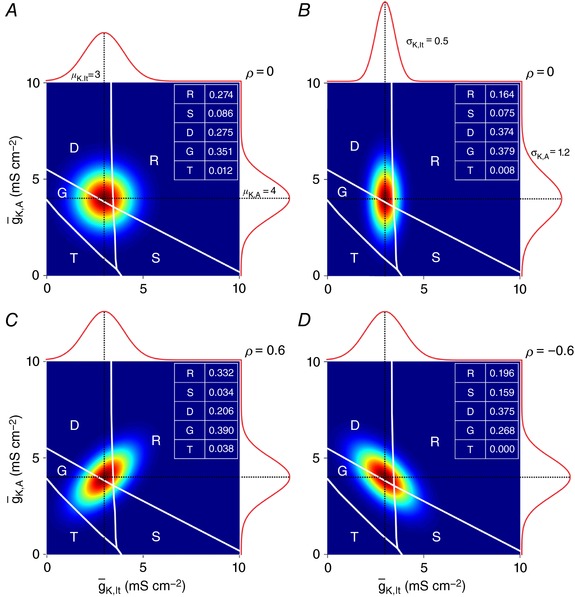
Within a set of neurons, K,lt and K,A are likely to exhibit variability consistent with a Gaussian distribution. Univariate distributions describing K,lt and K,A, which are represented by curves on the edges of each graph, combine to give a joint distribution represented by colour (where dark red indicates the highest probability). In all panels, μK,lt = 3 mS cm−2 and μ,A = 4 mS cm−2. A, if the widths of the two univariate distributions are equal (σK,lt = σK,A = 1 mS cm−2), the joint probability distribution is circular. B, if the widths are unequal (σK,lt decreased to 0.5 mS cm−2 and σK,A increased to 1.2 mS cm−2), the joint probability distribution becomes elliptical. Correlations between and and , although not reflected in the univariate distributions, are important for describing the joint distribution, with a positive correlation (ρ > 0) yielding a slanted ellipse whose long axis has a positive slope (C), whereas a negative correlation (ρ < 0) yields slanting in the other direction (D). Since the total volume under these joint probability distributions equals 1, the volume sitting over each spiking pattern region represents the proportion of neurons exhibiting that pattern. Spiking pattern proportions are shown in the table on each plot.
Within a set of neurons, different neurons may exhibit distinct spiking patterns if the joint distribution of ion channel densities straddles one or more spiking pattern boundaries. Thus, to describe spiking within a set of neurons, one must determine the proportion of different spiking patterns (see insets on Fig. 5). We can estimate those proportions by projecting the joint distribution of ion channel densities onto the spiking pattern regions and calculating the portion of that distribution that sits over each region (see Methods). To do this, one must know the mean (μ) and standard deviation (σ) of the univariate distributions describing and , plus the correlation coefficient (ρ). Each univariate distribution can be characterized with experiments conducted in separate sets of neurons, but determining ρ requires measurements of and in the same neuron, which can be prohibitively difficult (e.g. drugs used to isolate one current for voltage clamp measurements may preclude measurement of the other current). Consequently, correlations are often neglected despite theoretical work showing that they are important (Marder & Taylor, 2011). As shown in Fig. 5, differences in correlation can yield very different spiking pattern proportions.
Estimating ion channel density distributions from spiking pattern proportions
Given the difficulty of measuring correlations in ion channel expression, we sought to invert the approach used in Fig. 5 (i.e. predicting spiking pattern proportions from the joint distribution of ion channel densities) to instead predict ion channel density distributions, most notably ρ, from spiking pattern proportions. To solve this optimization problem, we developed an algorithm that finds the joint distribution of ion channel densities best able to account for a given proportion of spiking patterns. Estimated values of parameters μK,lt, μK,A, and ρ are optimized through a two‐step process that is repeated iteratively to minimize the error between target and predicted spiking pattern proportions, as summarized in Fig. 6 A (see Methods for details). Using an arbitrary distribution, a target spiking pattern proportion was calculated as in Fig. 5 or a number of samples (n sample) were drawn randomly from that distribution and the target proportion was calculated from the fraction of samples falling within each spiking pattern region. The latter approach was used to test the effects of finite sampling. Results of fitting are reported for target proportion determined through the former method unless otherwise indicated.
Figure 6. Estimating ion channel density distributions from spiking pattern proportions.
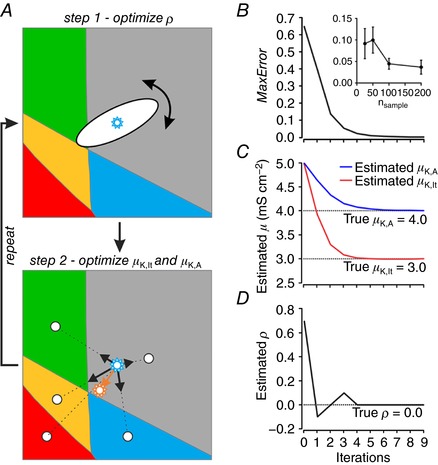
A, schematic representation of the iterative, two‐step process used to estimate the joint distribution of ion channel densities (μK,lt, μ,K,A and ρ) from an observed (target) set of spiking pattern proportions. Starting with arbitrarily chosen parameter values for μ, in step 1, ρ is systematically varied in 0.1 increments to find the value yielding the best match between estimated and target spiking pattern proportions. That value is carried forward to step 2, in which estimates of μK,lt and μ,K,A are updated by drawing vectors from the centre of the joint distribution to the centroid of each spiking pattern region. The length of each vector was adjusted based on the error (see Methods) and the distribution is shifted to the position given by the net vector. Step 1 was then repeated with the updated values of μK,lt and μ,K,A, and so on, until the error decreased below a threshold, after which point ρ was systematically varied in 0.01 increments for greater accuracy. The algorithm continued until the MaxError reached a minimum (B) and estimates of μ (C) and ρ (D) stabilized, which occurred within a few iterations. Data in B–D show results of fitting the spiking pattern proportions from a target distribution with μK,lt = 3 mS cm−2, μ,K,A = 4 mS cm−2, ρ = 0 and σK,lt = σK,A = 1 mS cm−2. In additional tests, n samples were drawn randomly from the target distribution and spiking pattern proportions were determined from the fraction of samples falling within each spiking pattern region. Regardless of how target spiking pattern proportions were generated, the estimation process was the same. Inset in panel B shows MaxError at steady‐state (mean ± standard deviation) as a function of n sample, where each data point is based on five tests.
To start the fitting process, an initial distribution with σK,lt = σK,A = 1 mS cm−2 was created at the centre of the plot (μK,lt = μK,A = 10 mS cm−2 for a 20 × 20 mS cm−2 plane). Neither the starting values of μ nor the dimensions of the plot impact the final outcome (data not shown). The fitting process was repeated for different values of σ (see below). The spiking pattern proportions yielded by this distribution (i.e. the estimated proportions) were calculated as in Fig. 5. In step 1, the value of ρ was systematically varied and predicted proportions were re‐calculated; the value of ρ yielding the smallest error was carried forward to the next step. In step 2, values of μK,lt and μK,A were updated by using the error to scale vectors pointing from the centre of the joint distribution to the centroid of each spiking pattern region, the rationale being to pull the distribution towards regions whose spiking pattern was underestimated and push it away from regions whose spiking pattern was overestimated. The updated values of μK,lt and μK,A were carried forward to a second iteration of step 1, during which ρ was re‐optimized using updated values of μ. These two fitting steps were repeated until the MaxError was minimized (Fig. 6 B) and estimates of μ (Fig. 6 C) and ρ (Fig. 6 D) stabilized, which typically occurred within a few iterations. The inset in Fig. 6 B shows MaxError at steady‐state plotted as a function of the number of neurons used to estimate the target spiking pattern proportion (see above). That relationship argues that reasonably large data sets (∼100 neurons or more) are needed to reliably estimate the target spiking pattern proportion.
To test our method, we fitted sets of spiking pattern proportions generated using arbitrarily chosen ion channel density distributions. As summarized in Table 1 for the estimation of sample distributions shown in Fig. 5 A, C and D, our algorithm was very successful in estimating the ion channel density distribution based on spiking pattern proportions. However, for those examples, estimated values of σ (denoted σestimate) were set to the true values of σ (denoted σtrue) rather than being fitted. To explore the effects of misestimating σ, and thus establish if σ must also be fitted, we fixed σestimate at 1 mS cm−2 and generated joint distributions with σK,lt = σK,A = [0.5, 0.8, 1.0, 1.2, 1.5] mS cm−2. Although all errors were < 5%, they were significantly lower when σestimate = σtrue compared with when σestimate ≠ σtrue (P < 0.001, Kruskal–Wallis test; P < 0.05 for each pairwise comparison to σtrue/σestimate = 1, Tukey tests). Comparing estimated values of μ and ρ against their true values (Fig. 7 B–D) similarly revealed that those estimates were degraded when σestimate ≠ σtrue.
Table 1.
Testing the algorithm with different target neuron population distributions
| Population A | Population C | Population D | ||||
|---|---|---|---|---|---|---|
| Target | Estimated | Target | Estimated | Target | Estimated | |
| Parameter | ||||||
| μK,lt (mS cm−2) | 3 | 2.998 | 3 | 2.999 | 3 | 2.997 |
| μ,K,A (mS cm−2) | 4 | 4.002 | 4 | 4.003 | 4 | 4.003 |
| ρ | 0.00 | 0.00 | 0.60 | 0.61 | −0.60 | −0.60 |
| Proportions | ||||||
| Tonic (T) | 0.274 | 0.273 | 0.332 | 0.333 | 0.196 | 0.195 |
| Single (S) | 0.086 | 0.086 | 0.034 | 0.033 | 0.159 | 0.158 |
| Delayed (D) | 0.275 | 0.276 | 0.206 | 0.206 | 0.375 | 0.376 |
| Gap (G) | 0.351 | 0.351 | 0.390 | 0.390 | 0.268 | 0.268 |
| Reluctant (R) | 0.012 | 0.012 | 0.038 | 0.038 | 0.000 | 0.000 |
| MaxError | ||||||
| From volume | 0.001 | 0.001 | 0.001 | |||
| n sample = 200 | 0.0368 ± 0.0162 | 0.0261 ± 0.0142 | 0.0334 ± 0.0189 | |||
| n sample = 100 | 0.0445 ± 0.0126 | 0.0461 ± 0.0187 | 0.0330 ± 0.0133 | |||
| n sample = 50 | 0.0997 ± 0.0303 | 0.0692 ± 0.0237 | 0.0911 ± 0.0374 | |||
| n sample = 25 | 0.0915 ± 0.0349 | 0.1263 ± 0.0765 | 0.1112 ± 0.0931 | |||
Population A, C, and D refer to conditions shown in the corresponding panels of Fig. 5. MaxError values for target proportions based on random sampling are mean ± standard deviation based on five tests for each condition.
Figure 7. Sensitivity of ion channel density estimation to assumed value of σ.
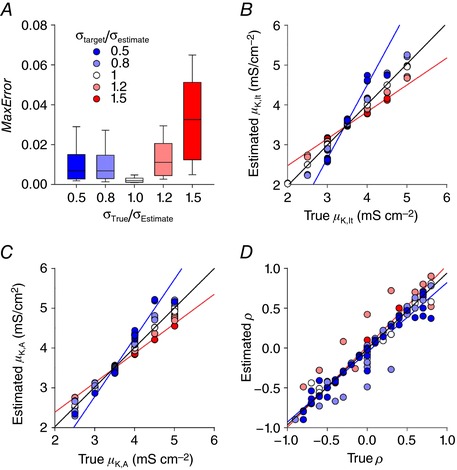
Sets of spiking pattern proportions were calculated for joint distributions with arbitrarily chosen parameter values. σestimate was fixed at 1 mS cm−2 but, unlike previously fitted distributions, σtarget ( = σK,lt and σK,A) took a range of values. Specifically, the algorithm was applied to target distributions where σestimate correctly estimated σtarget = 1.0 mS cm−2 (σtarget/σestimate = 1.0), σtarget was 20% greater or less than estimated (σtarget/σestimate = 1.2 or 0.8, respectively), or σtarget was 50% greater or less than assumed (σtarget/σestimate = 1.5 or 0.5, respectively). N = 40 target distributions belonging to each group were used for testing, each with arbitrarily chosen values of μK,lt, μ,K,A and ρ. A, box‐plot shows the MaxError in the estimated spiking pattern proportions, with box ends and whisker ends representing the 1st/3rd quartiles and 5th/95th percentile, respectively. The median error value of 0.002 when σ was correctly estimated (σtarget/σestimate = 1.0) was significantly less than when σ was misestimated (P < 0.05, Tukey tests). Estimations of μK,lt (B), μ,K,A (C) and ρ (D) are shown relative to their true values. Black lines show the regression using all points; their slopes were all within 5% of the expected value of 1. However, when the regression was calculated using points from σtarget/σestimate = 0.5 (blue) or 1.5 (red), 5 of the 6 values deviated significantly from the expected value of 1 (P > 0.05, one sample t tests with Bonferroni correction).
Having established the need to fit σ, we tried adding a σ‐fitting step into our algorithm. However, this caused the algorithm to run very slowly. We found that it was more efficient to simply re‐run the algorithm with different σestimate values and identify a posteriori which gave the best fit of the spiking pattern proportions. When this was done, error values fell (compare Fig. 8 A to Fig. 7 A) and did not systematically differ with σ (P > 0.05, one sample t test). Moreover, all five parameters were accurately estimated over a range of values (Fig. 8 B–F); specifically, the slope of all regression lines fell within 7% of (and none differed significantly from) the expected value of 1 (P > 0.05, one sample t tests with Bonferroni correction). These results demonstrate that values of all μ and σ could be estimated to within approximately ±0.2 mS cm−2 and ρ could be estimated within ±0.2 based on the conditions tested. Sources of neuronal heterogeneity not accounted for in our neuron model and any inaccuracies in the initial measurement of spiking pattern proportions will tend to reduce performance below these benchmarks (see Discussion).
Figure 8. Estimating ion channel distributions, including σ, from spiking pattern proportions.
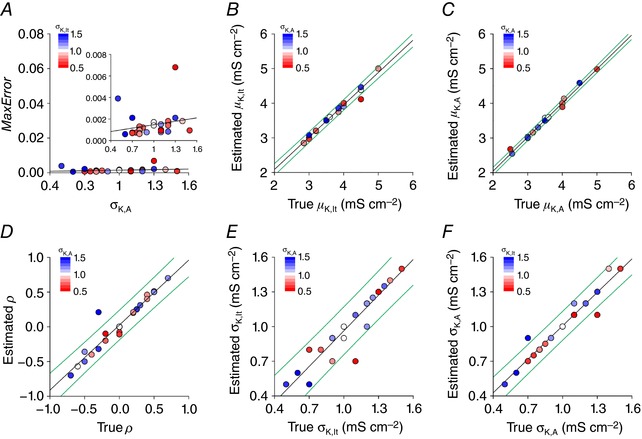
Values of σestimate for σK,lt and σK,A were independently varied between 0.4 and 1.7 mS cm−2 by increments of 0.1 mS cm−2. The two‐step algorithm explained in Fig. 6 was re‐run for all combinations of σestimate values. Values of σK,lt and σK,A yielding the least error after fitting the remaining parameters (μK,lt, μ,K,A, ρ) were considered the best estimates. This approach was tested on N = 29 target distributions. A, MaxError plotted against true σK,A on the x‐axis and σK,lt represented in colour. Scaling of the y‐axis on the main graph is the same as for Fig. 7 A for comparison; inset shows enlarged view. Slope of the regression line did not deviate significantly from 0 (P > 0.05, one‐sample t test). Plotting estimated vs. true values of μK,lt (B), μ,K,A (C), ρ (D), σK,lt (E) and σK,A (F) revealed the accuracy with which each parameter was estimated. Regression lines are shown in black, with the 95% prediction intervals shown in green. No regression line slopes deviated significantly from the expected value of 1 (P < 0.05, one sample t tests with Bonferroni correction).
Discussion
In this study, we reproduced five of the spiking patterns observed in SDH neurons by varying the densities of just two ion channels, namely, a low‐threshold non‐inactivating potassium conductance g K,lt and an inactivating (A‐type) potassium conductance g K,A. Systematically co‐varying those two conductances revealed boundaries that represent the transition between spiking patterns. Le Franc and Le Masson (2010) used a similar approach to study spiking patterns in deep dorsal horn neurons, but we are not aware of previous studies like this in the superficial dorsal horn. The boundaries we found imply that subtle changes in or can cause a neuron to switch spiking patterns. Yet the regions in parameter space associated with each spiking pattern are themselves quite large, implying that the same spiking pattern (notwithstanding quantitative differences) can arise from a broad range of and , so long as a boundary is not crossed. This combination of observations has important implications for (i) classifying neurons based on spiking pattern and (ii) ascribing different spiking patterns to unique ion channel expression patterns. We will discuss each point and will summarize the tools we have developed to address these issues.
Anyone with first‐hand experience recording from SDH neurons will appreciate that classifying those neurons by spiking pattern is more of an art than a science. The same is true to varying degrees for other neuron populations, but this is not the sort of information that is well documented in publications. That said, some SDH cell types are more distinguishable than others. For example, tonic‐spiking neurons tend to spike repetitively over a broad range of stimulus intensities, irrespective of pre‐stimulus membrane potential, and they also exhibit features such as rebound spiking and a biphasic afterhyperpolarization that distinguishes them from other cell types (Prescott & De Koninck, 2002). Punnakkal et al. (2014) found that nearly all genetically defined GABAergic and glycinergic neurons in the SDH were tonic spiking, which contrasts with the heterogeneity they observed for glutamatergic neurons (see below). Although other cell types can spike repetitively, especially in response to strong stimulation, they tend to exhibit single or delayed spiking for stimulus intensities near rheobase. And unlike the voltage‐insensitivity of tonic spiking, single‐spiking neurons can switch to reluctant spiking and delayed‐spiking neurons can switch to gap spiking depending on membrane potential (Fig. 1 C). Such observations cast doubt on whether distinctions between single and reluctant spiking or between delayed and gap spiking are legitimate. But more importantly, those observations reveal that some neurons operate near spiking pattern boundaries (or bifurcations). We have shown here that boundaries shift with changes in stimulus intensity or pre‐stimulus membrane potential (Fig. 3), thus allowing a given neuron to exhibit more than one spiking pattern. Indeed, our simulations specifically predict voltage‐dependent switching between single and reluctant spiking, and between delayed and gap spiking. The observation of temperature‐dependent switching between delayed and reluctant spiking (Graham et al. 2008) is also consistent with our simulations insofar as those two spiking patterns also share a boundary. Specifically, temperature will quantitatively alter ion channel gating, but would not be expected to qualitatively alter the spiking pattern unless a bifurcation occurred.
An association between single and delayed spiking may seem unlikely given how distinct those patterns are, yet our simulations indicate that these two patterns can arise from similar ion channel densities. Gap spiking helps reveal the ‘missing link’ between them. Notably, single and delayed spiking can occasionally be observed in the same neuron (Fig. 1 D) and are disproportionately found in neurons with multipolar (or radial/vertical) morphology (Prescott & De Koninck, 2002) and in neurons defined by expression of calretinin (Smith et al. 2015) or vesicular glutamate transporter type 2 (Punnakkal et al. 2014). Conversely, neither single nor delayed spiking is commonly observed in inhibitory neurons defined by expression of parvalbumin (Hughes et al. 2012) or prion protein (Ganley et al. 2015). Of all the spiking patterns, phasic spiking tends to be the most promiscuous. Together, these observations suggest that tonic spiking occurs almost exclusively amongst inhibitory neurons whereas delayed, gap, single and reluctant spiking are associated with excitatory neurons. That said, the four different spiking patterns do not imply that there are four different excitatory cell types (each defined by expression of a distinct set of ion channels); instead, those four spiking patterns likely represent a single cell population in which variations in and straddle the intersection of two spiking pattern boundaries.
The above conclusion is seemingly inconsistent with Abraira et al. (2016) who reported delayed spiking in certain sets of inhibitory neurons and tonic spiking in certain sets of excitatory neurons. But the samples of delayed spiking they showed for inhibitory neurons lack the inflection association with an A‐type potassium current (see Fig. 1 A) and the sample of tonic spiking they showed for a parvalbumin‐expressing excitatory neuron could be considered phasic spiking (see Fig. 1 B). Their ‘regular spiking’ cells align better with our definition of tonic spiking. In other words, the inconsistencies are arguably superficial, based on nuanced criteria that form the basis for this sort of phenomenological classification. The potential for confusion speaks to the need for mechanism‐based classification schemes. In other words, functional classification should become more of a science and less of an art. Cluster analysis based on quantifiable metrics is a must, but the choice of metrics should be guided by putative ionic mechanisms (e.g. measuring the delay to spiking for test stimuli applied at different membrane potentials to rule in/out the contribution of an A current). The modelling and quantitative analysis presented in this study aim to help shift the field in that direction.
Though spiking pattern‐based classification is compromised by the sensitivity of spiking patterns to test conditions, carefully documenting that sensitivity can help constrain estimates of the underlying ion channel densities (Fig. 4). Moving from the characterization of single neurons to the characterization of neuronal populations, spiking pattern heterogeneity can help inform our understanding of the underlying distributions of ion channel density. As demonstrated in Figs 6, 7, 8, the proportion of different spiking patterns observed within a population can be used to estimate ion channel density distributions, including any correlations in the expression of different ion channels. We are not aware of any past studies that have used this approach and, in that respect, the success of our algorithm represents proof‐of‐principle demonstration that this approach can work. But notably, such an approach requires that data are collected in a standardized way, and from many neurons (to ensure that the population is appropriately sampled). Even then, our modelling has neglected sources of neuronal heterogeneity that may compromise the ability to estimate ion channel distributions. First, even if our model included all the ion channels expressed in real neurons, the densities of channels that we did not systematically vary (i.e. leak conductance, fast sodium conductance, and delayed rectifier potassium conductance) would also vary between neurons, and this additional heterogeneity would blur the spiking pattern boundaries plotted on planes defined by and . That said, >2 ion channel densities could be co‐varied during initial mapping, in which case boundaries currently depicted as lines on a plane would become manifolds within a higher dimensional space; this is harder to visualize but is still computationally feasible. Second, real neurons express other ion channels that were not included in our model, and even if those channels are not necessary to explain each spiking pattern, heterogeneity in their expression may also contribute to blurring the spiking pattern boundaries. Addressing these and other sources of heterogeneity (e.g. expression of ion channels in the dendrites and variations in dendritic morphology) is computationally feasible but requires larger data sets than can be acquired by painstakingly patching one neuron at a time. As higher throughput recording methods are developed, and larger data sets are collected, analysis of those data using these computational tools will become practicable. The collation of data across labs into databases like NeuroElectro (Tripathy et al. 2014) will also facilitate such efforts. But even if the data are available, one must develop a valid computational model of the cells of interest in order to fit its parameters to the data.
Our results also highlight how correlations in ion channel expression may influence spiking pattern proportions. Specifically, in Fig. 5 we show that the same univariate distributions of and can yield different spiking pattern proportions depending on if and how the densities of those channels are correlated. Such correlations are often overlooked, but can reveal themselves during computational modelling, when the average neuron (in functional terms) is not recapitulated by endowing the model with the average densities of conductances known to be expressed in that cell type (Golowasch et al. 2002). Correlations in ion channel expression levels have been documented experimentally (MacLean et al. 2003; Bergquist et al. 2010; Cao & Oertel, 2011), as have correlations in the voltage dependencies of co‐expressed channels (Amendola et al. 2012). Such correlations emerge via co‐regulation of ion channels by homeostatic (O'Leary et al. 2013) or neuromodulatory (Khorkova & Golowasch, 2007) processes, and are important for enabling robust regulation of cellular function (Zhao & Golowasch, 2012; Golowasch, 2014). But whereas most past work has focused on maintaining cellular function on the basis of different ion channel combinations, where compensation for one channel by another channel naturally leads to correlations (Hudson & Prinz, 2010), our results suggest that functional heterogeneity may also depend on correlations. The algorithm we have developed provides a novel tool to predict correlations on the basis of that heterogeneity.
To conclude, we have used computational modelling to reproduce five of the spiking patterns by which SDH neurons are often classified. Our results demonstrate that different combinations of two potassium channels can account for that heterogeneity. By mapping the relationship between channel densities and spiking pattern, our results reveal the relationship between different spiking patterns (i.e. which patterns share a boundary), which in turn predicts the switching between certain spiking patterns based on factors like stimulus intensity or membrane potential. Together with past observations, our data suggest that certain spiking patterns do not reflect cell types with distinct ion channel expression patterns, but, rather, suggest that certain spiking patterns result from continuous variations in ion channel densities that manifest distinct spiking patterns because of the inherent non‐linearity of the spike generation process. These are important issues to consider for making neuron classification schemes more robust and for ensuring efficient identification of the molecular basis of important functional differences.
Additional information
Competing interests
The authors have declared that no competing interests exist
Author contributions
Simulations were performed in the laboratory of SAP. AB and SAP conceived the design of the study. AB conducted all simulations. AB and SAP analysed and interpreted the data. AB and SAP wrote the manuscript. SAP supervised the project. Both authors have read and approved the final version of the manuscript, and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all persons qualified for authorship are listed as authors.
Funding
This work was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada and by an Ontario Early Researcher Award to SAP.
Acknowledgements
We wish to thank Graham Pitcher, Frances Skinner and Stéphanie Ratté for helpful feedback on the manuscript.
Biography
Arjun Balachandar is a medical student at the University of Toronto with a strong interest in basic neuroscience, neurology and neurosurgery. He completed his undergraduate studies in Honours Neuroscience at McGill University, after which he began research under the guidance of Steven Prescott at SickKids Hospital. He is particularly interested in applying computational modelling to understand the biophysical basis for neural information processing at the cellular and network levels, especially pain‐related sensory information and how chronic pain arises from aberrations in that processing. He hopes to pursue a career as a clinician–scientist, translating basic science research to clinical applications.

Linked articles This article is highlighted by a Perspective by Tadros et al. To read this Perspective, visit https://doi.org/10.1113/JP275870.
Edited by: Ian Forsythe & Jesper Sjöström
References
- Abraira VE, Kuehn ED, Chirila AM1, Springel MW, Toliver AA, Zimmerman AL, Orefice LL, Boyle KA, Bai L, Song BJ, Bashista KA, O'Neill TG, Zhuo J, Tsan C, Hoynoski J, Rutlin M, Kus L, Niederkofler V, Watanabe M, Dymecki SM, Nelson SB, Heintz N, Hughes DI & Ginty DD (2016). The cellular and synaptic architecture of the mechanosensory dorsal horn. Cell 168, 295–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amendola J, Woodhouse A, Martin‐Eauclaire MF & Goaillard JM (2012). Ca2+/cAMP‐sensitive covariation of IA and IH voltage dependences tunes rebound firing in dopaminergic neurons. J Neurosci 32, 2166–2181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ascoli GA, Alonso‐Nanclares L, Anderson SA, Barrionuevo G, Benavides‐Piccione R, Burkhalter A, Buzsáki G, Cauli B, Defelipe J, Fairén A, Feldmeyer D, Fishell G, Fregnac Y, Freund TF, Gardner D, Gardner EP, Goldberg JH, Helmstaedter M, Hestrin S, Karube F, Kisvárday ZF, Lambolez B, Lewis DA, Marin O, Markram H, Muñoz A, Packer A, Petersen CC, Rockland KS, Rossier J, Rudy B, Somogyi P, Staiger JF, Tamas G, Thomson AM, Toledo‐Rodriguez M, Wang Y, West DC & Yuste R (2008). Petilla terminology: nomenclature of features of GABAergic interneurons of the cerebral cortex. Nat Rev Neurosci 9, 557–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergquist S, Dickman DK & Davis GW (2010). A hierarchy of cell intrinsic and target‐derived homeostatic signaling. Neuron 66, 220–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cadwell CR, Palasantza A, Jiang X, Berens P, Deng Q, Yilmaz M, Reimer J, Shen S, Bethge M, Tolias KF, Sandberg R & Tolias AS (2016). Electrophysiological, transcriptomic and morphologic profiling of single neurons using Patch‐seq. Nat Biotechnol 34, 199–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao XJ & Oertel D (2011). The magnitudes of hyperpolarization‐activated and low‐voltage‐activated potassium currents co‐vary in neurons of the ventral cochlear nucleus. J Neurophysiol 106, 630–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauli B, Porter JT, Tsuzuki K, Lambolez B, Rossier J, Quenet B & Audinat E (2000). Classification of fusiform neocortical interneurons based on unsupervised clustering. Proc Natl Acad Sci USA 97, 6144–6149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng L, Duan B, Huang T, Zhang Y, Chen Y, Britz O, Garcia‐Campmany L, Ren X, Vong L, Lowell BB, Goulding M, Wang Y & Ma Q (2017). Identification of spinal circuits involved in touch‐evoked dynamic mechanical pain. Nat Neurosci 20, 804–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor JA & Stevens CF (1971). Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. J Physiol 213, 31–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero‐Erausquin M, Inquimbert P, Schlichter R & Hugel S (2016). Neuronal networks and nociceptive processing in the dorsal horn of the spinal cord. Neuroscience 338, 230–247. [DOI] [PubMed] [Google Scholar]
- Duan B, Cheng L, Bourane S, Britz O, Padilla C, Garcia‐Campmany L, Krashes M, Knowlton W, Velasquez T, Ren X, Ross SE, Lowell BB, Wang Y, Goulding M & Ma Q (2014). Identification of spinal circuits transmitting and gating mechanical pain. Cell 159, 1417–1432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuzik J, Zeisel A, Mate Z, Calvigioni D, Yanagawa Y, Szabo G, Linnarsson S & Harkany T (2016). Integration of electrophysiological recordings with single‐cell RNA‐seq data identifies neuronal subtypes. Nature Biotech 34, 175–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganley RP, Iwagaki N, del Rio P, Baseer N, Dickie AC, Boyle KA, Polgar E, Watanabe M, Abraira VE, Zimmerman A, Riddell JS & Todd AJ (2015). Inhibitory interneurons that express GFP in the PrP‐GFP mouse spinal cord are morphologically heterogeneous, innervated by several classes of primary afferent and include lamina I projection neurons among their postsynaptic targets. J Neurosci 35, 7626–7642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J (2014). Ionic current variability and functional stability in the nervous system. Bioscience 64, 570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Goldman MS, Abbott LF & Marder E (2002). Failure of averaging in the construction of a conductance‐based neuron model. J Neurophysiol 87, 1129–1131. [DOI] [PubMed] [Google Scholar]
- Graham BA, Brichta AM & Callister RJ (2007a). Moving from an averaged to specific view of spinal cord pain processing circuits. J Neurophysiol 98, 1057–1063. [DOI] [PubMed] [Google Scholar]
- Graham BA, Brichta AM & Callister RJ (2008). Recording temperature affects the excitability of mouse superficial dorsal horn neurons, in vitro. J Neurophysiol 99, 2048–2059. [DOI] [PubMed] [Google Scholar]
- Graham BA, Brichta AM, Schofield PR & Callister RJ (2007b). Altered potassium channel function in the superficial dorsal horn of the spastic mouse. J Physiol 584, 121–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grudt TJ & Perl ER (2002). Correlations between neuronal morphology and electrophysiological features in the rodent superficial dorsal horn. J Physiol 540, 189–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton DJ, Shepherd GM, Martone ME & Ascoli GA (2012). An ontological approach to describing neurons and their relationships. Front Neuroinform 6, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinke B, Ruscheweyh R, Forsthuber L, Wunderbaldinger G & Sandkuhler J (2004). Physiological, neurochemical and morphological properties of a subgroup of GABAergic spinal lamina II neurones identified by expression of green fluorescent protein in mice. J Physiol 560, 249–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson AE & Prinz AA (2010). Conductance ratios and cellular identity. PLoS Comput Biol 6, e1000838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes DI, Sikander S, Kinnon CM, Boyle KA, Watanabe M, Callister RJ & Graham BA (2012). Morphological, neurochemical and electrophysiological features of parvalbumin‐expressing cells: a likely source of axo‐axonic inputs in the mouse spinal dorsal horn. J Physiol 590, 3927–3951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM (2007). Dynamical Systems in Neuroscience. MIT Press, Cambridge, MA, USA. [Google Scholar]
- Johnson MB & Walsh CA (2017). Cerebral cortical neuron diversity and development at single‐cell resolution. Curr Opin Neurobiol 42, 9–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kardon AP, Polgar E, Hachisuka J, Snyder LM, Cameron D, Savage S, Cai X, Karnup S, Fan CR, Hemenway GM, Bernard CS, Schwartz ES, Nagase H, Schwarzer C, Watanabe M, Furuta T, Kaneko T, Koerber HR, Todd AJ & Ross SE (2014). Dynorphin acts as a neuromodulator to inhibit itch in the dorsal horn of the spinal cord. Neuron 82, 573–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khorkova O & Golowasch J (2007). Neuromodulators, not activity, control coordinated expression of ionic currents. J Neurosci 27, 8709–8718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Franc Y & Le Masson G (2010). Multiple firing patterns in deep dorsal horn neurons of the spinal cord: computational analysis of mechanisms and functional implications. J Neurophysiol 104, 1978–1996. [DOI] [PubMed] [Google Scholar]
- Lu Y & Perl ER (2005). Modular organization of excitatory circuits between neurons of the spinal superficial dorsal horn (laminae I and II). J Neurosci 25, 3900–3907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLean JN, Zhang Y, Johnson BR & Harris‐Warrick RM (2003). Activity‐independent homeostasis in rhythmically active neurons. Neuron 37, 109–120. [DOI] [PubMed] [Google Scholar]
- Marder E & Taylor AL (2011). Multiple models to capture the variability in biological neurons and networks. Nat Neurosci 14, 133–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson SB, Sugino K & Hempel CM (2006). The problem of neuronal cell types: a physiological genomics approach. Trends Neurosci 29, 339–345. [DOI] [PubMed] [Google Scholar]
- O'Leary T, Williams AH, Caplan JS & Marder E (2013). Correlations in ion channel expression emerge from homeostatic tuning rules. Proc Natl Acad Sci USA 110, E2645–E2654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirs C & Seal RP (2016). Neural circuits for pain: recent advances and current views. Science 354, 578–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirs C, Williams SP, Zhao X, Walsh CE, Gedeon JY, Cagle NE, Goldring AC, Hioki H, Liu Z, Marell PS & Seal RP (2015). Dorsal horn circuits for persistent mechanical pain. Neuron 87, 797–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petitjean H, Pawlowski SA, Fraine SL, Sharif B, Hamad D, Fatima T, Berg J, Brown CM, Jan LY, Ribeiro‐da‐Silva A, Braz JM, Basbaum AI & Sharif‐Naeini R (2015). Dorsal horn parvalbumin neurons are gate‐keepers of touch‐evoked pain after nerve injury. Cell Rep 13, 1246–1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polgar E, Hughes DI, Riddell JS, Maxwell DJ, Puskar Z & Todd AJ (2003). Selective loss of spinal GABAergic or glycinergic neurons is not necessary for development of thermal hyperalgesia in the chronic constriction injury model of neuropathic pain. Pain 104, 229–239. [DOI] [PubMed] [Google Scholar]
- Poulin JF, Tasic B, Hjerling‐Leffler J, Trimarchi JM & Awatramani R (2016). Disentangling neural cell diversity using single‐cell transcriptomics. Nat Neurosci 19, 1131–1141. [DOI] [PubMed] [Google Scholar]
- Prescott SA & De Koninck Y (2002). Four cell types with distinctive membrane properties and morphologies in lamina I of the spinal dorsal horn of the adult rat. J Physiol 539, 817–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA & De Koninck Y (2005). Integration time in a subset of spinal lamina I neurons is lengthened by sodium and calcium currents acting synergistically to prolong subthreshold depolarization. J Neurosci 25, 4743–4754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y & Sejnowski TJ (2008). Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS Comput Biol 4, e1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA & Ratté S (2012). Pain processing by spinal microcircuits: afferent combinatorics. Curr Opin Neurobiol 22, 631–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA & Sejnowski TJ (2008). Spike‐rate coding and spike‐time coding are affected oppositely by different adaptation mechanisms. J Neurosci 28, 13649–13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Punnakkal P, von Schoultz C, Haenraets K, Wildner H & Zeilhofer HU (2014). Morphological, biophysical and synaptic properties of glutamatergic neurons of the mouse spinal dorsal horn. J Physiol 592, 759–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratté S, Lankarany M, Rho YA, Patterson A & Prescott SA (2015). Subthreshold membrane currents confer distinct tuning properties that enable neurons to encode the integral or derivative of their input. Front Cell Neurosci 8, 452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribeiro‐da‐Silva A & De Koninck Y (2008). Morphological and neurochemical organization of the spinal dorsal horn In Science of Pain, ed. Basbaum AI. & Bushnell MC, pp. 279–310. Academic Press, New York. [Google Scholar]
- Rinzel J & Ermentrout B (1989). Analysis of neural excitability and oscillations In Methods in Neuronal Modeling, eds Koch C. & Segev I. MIT Press, Cambridge. [Google Scholar]
- Ruscheweyh R & Sandkuhler J (2002). Lamina‐specific membrane and discharge properties of rat spinal dorsal horn neurones in vitro. J Physiol 541, 231–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith KM, Boyle KA, Madden JF, Dickinson SA, Jobling P, Callister RJ, Hughes DI & Graham BA (2015). Functional heterogeneity of calretinin‐expressing neurons in the mouse superficial dorsal horn: implications for spinal pain processing. J Physiol 593, 4319–4339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spike RC, Puskar Z, Andrew D & Todd AJ (2003). A quantitative and morphological study of projection neurons in lamina I of the rat lumbar spinal cord. Eur J Neurosci 18, 2433–2448. [DOI] [PubMed] [Google Scholar]
- Todd AJ (2010). Neuronal circuitry for pain processing in the dorsal horn. Nat Rev Neurosci 11, 823–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd AJ (2017). Identifying functional populations among the interneurons in laminae I‐III of the spinal dorsal horn. Mol Pain 13, 1744806917693003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tripathy SJ, Savitskaya J, Burton SD, Urban NN & Gerkin RC (2014). NeuroElectro: a window to the world's neuron electrophysiology data. Front Neuroinform 8, 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yasaka T, Tiong SY, Hughes DI, Riddell JS & Todd AJ (2010). Populations of inhibitory and excitatory interneurons in lamina II of the adult rat spinal dorsal horn revealed by a combined electrophysiological and anatomical approach. Pain 151, 475–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng H & Sanes JR (2017). Neuronal cell‐type classification: challenges, opportunities and the path forward. Nat Rev Neurosci 18, 530–546. [DOI] [PubMed] [Google Scholar]
- Zhao S & Golowasch J (2012). Ionic current correlations underlie the global tuning of large numbers of neuronal activity attributes. J Neurosci 32, 13380–13388. [DOI] [PMC free article] [PubMed] [Google Scholar]


